Dominant Gating Governing Transient GABA_A Receptor Activity: A First Latency and P_o/oAnalysis

Abstract

Steady-state, single-channel gating of GABA_Areceptors (GABARs ) is complex. Simpler gating may dominate when triggered by rapid GABA transients present during fast inhibitory synaptic transmission and is critical to understanding the time course of fast IPSCs. We studied the single-channel activity of expressed α1β1γ2 GABARs in outside-out patches from human embryonic kidney 293 cells triggered by rapidly applied GABA (10–2000 μm) pulses (2–300 msec). Activation was analyzed with the time to first channel opening after GABA presentation, or first latency (FL). FL distributions are monoexponential at low GABA concentrations and biexponential above 30 μm GABA. The fast rate increases supralinearly to a plateau of ∼1100 sec⁻¹, the apparent activation rate. The slow rate and amplitude are insensitive to GABA concentration. The results argue that doubly liganded receptors can rapidly desensitize before opening. Gating after the first opening was quantified with analysis of open probability conditioned on the first opening (P_o/o).P_o/o functions are biexponential, dominated by a fast component, and insensitive to GABA concentration. This suggests that open channels convert primarily to fast but also to slow desensitized states. Furthermore, dual modes of fast desensitization may influence IPSC amplitude and thereby synaptic efficacy. The findings provided for the construction of a mathematical gating model that accounts for FL and P_o/o functions. In addition, the model predicts the time course of macroscopic current responses thought to mimic IPSCs. The results provide new insights into dominant gating that is likely operational during fast GABAergic synaptic transmission.

GABA is the primary inhibitory neurotransmitter in the mammalian CNS. After release from a presynaptic terminal, GABA binds to postsynaptic GABA_Areceptors (GABARs) and induces conformational changes culminating with the opening of an integral, anion-selective pore. Extensive studies on single GABARs under equilibrium conditions have advanced our understanding of microscopic channel properties and revealed that channel gating is complex, with multiple open and closed states (Hamill et al., 1983; Bormann and Kettenmann, 1988; Macdonald et al., 1989; Twyman et al., 1990). During fast inhibitory synaptic transmission, however, a rapid, high GABA concentration transient in the cleft likely triggers IPSCs (Maconochie et al., 1994). Thus, during synaptic transmission, only a subpopulation of states may be visited primarily. Investigations of macroscopic current responses from rapidly perfused membrane patches have provided a fundamental understanding of the underlying IPSC time course (Maconochie et al., 1994; Jones and Westbrook, 1995; McClellan and Twyman, 1999). However, macroscopic currents report average GABAR activity, which may obscure important gating that can be observed at the level of single channels.

In this study, we identify dominant states governing transient GABAR activity through the analysis of single-channel behavior. Single-channel analysis using first latency (FL) (Aldrich et al., 1983) and conditional open probability (P_o/o) (Sigworth, 1981; Yue et al., 1990) have been used to probe the function of voltage-gated ion channels. This approach coupled with recent advances in the technology of rapid solution application provides a unique platform for studying the function of GABARs under transient agonist conditions. First latency is the time from GABA presentation to the first single-channel opening and reflects events underlying activation.P_o/o reports activity after the first opening. The combination of these two functions completely describes channel gating (Colquhoun and Hawkes, 1995). We believe this is the first use of this powerful combination of experimental and analytical techniques to probe the behavior of a ligand-gated ion channel.

Here, outside-out membrane patches containing expressed α1β1γ2 GABARs were rapidly perfused with GABA pulses (10–2000 μm; 2–300 msec). First latency andP_o/o analyses were performed on idealized single-channel traces. Salient features of the computed functions identified the underlying dominant states and connectivity. First latency analysis indicates that two pathways diverge from a doubly liganded closed state, one leading to a fast desensitized state and the other to a single open state.P_o/o analysis suggests that an open channel undergoes, at the least, conformational changes primarily to a second distinct fast desensitized state but also a slow desensitized state likely lying within and beyond the activation cascade. Furthermore, dual modes of fast desensitization heavily influence channel peak open probability, which points to a new role of desensitization in determining synaptic efficacy by modulating the amplitude of IPSCs. A parsimonious mathematical model derived from these gating subschemes quantitatively accounts for FL andP_o/o functions and predicts the time course of macroscopic currents that replicate IPSCs. Overall, the findings provide novel insight into dominant GABAR gating likely involved in fast inhibitory synaptic transmission.

MATERIALS AND METHODS

Cell culture and transient transfection. Transformed HEK-293 cells, purchased from American Type Culture Collection (Bethesda, MD), were plated on 18 × 18 mm glass coverslips in 60 × 15 mm Falcon dishes (Becton Dickinson, Lincoln Park, NJ) and cultured in minimum essential medium (MEM) supplemented with 10% fetal bovine serum (FBS) and 1% each of penicillin, streptomycin, and glutamine (all from Life Technologies, Grand Island, NY). After incubation in 37°C, 5% CO₂ for 48 hr, cells were transiently transfected using a lipofection technique described previously (Gingrich et al., 1995) with cDNAs encoding mouse brain α1, β1, and γ2 subunits (kindly provided by Dr. David Burt, University of Maryland) inserted individually into the plasmid pCI-neo (Promega, Madison, WI). Briefly, aliquots of lipofection reagent (Lipofectamine, Life Technologies) and appropriate plasmids (1:1:1 by weight, α1/β1/γ2) were mixed in a modified, serum-free medium (Optimem, Life Technologies), and incubated at room temperature for 10 min. Cells were washed with PBS (Life Technologies), and supplemented MEM was replaced with Optimem, followed by addition of liposome-plasmid-containing solution. After a 6–8 hr incubation period (37°C, 5% CO₂), cells were washed with PBS and returned to supplemented MEM for further incubation. Cells were ready for electrophysiological recording 48 hr after transfection.

Electrophysiological recordings. Coverslips with transfected cells were transferred to the lid of a culture dish mounted on the stage of an Olympus IMT-2 (Olympus, Lake Success, NY) inverted microscope with Hoffman modulated optics. The cells were immersed in a modified Tyrode's solution containing (mm) 132 NaCl, 4.8 KCl, 1.2 MgCl₂, 1 CaCl₂, 10 HEPES, 5 dextrose, pH 7.3. Glass pipettes were prepared from borosilicate glass (Corning Pyrex, Corning, NY) with a multistage puller (Flaming Brown model P-97, Sutter Instrument Company, Novato, CA), fire polished (MF-9 Microforge, Narishige, Greenvale, NY), and coated with Sylgard (Dow Corning Company, Midland, MI). Recording pipettes were filled with (in mm): 140 CsCl, 1 MgCl₂, 5 MgATP, 10 HEPES, and 10 EGTA. Open tip resistances were typically 5–10 MΩ under these ionic conditions. Currents were recorded with the outside-out configuration of the patch-clamp technique (Hamill et al., 1981) using an Axopatch 200A amplifier (Axon Instruments, Foster City, CA). Macropatch currents were those recorded from outside-out membrane patches with sufficient channel number such that measured currents reflected macroscopic gating. These currents were filtered at 1–2 kHz (−3 dB, four-pole Bessel) and sampled at 12.5 kHz. Single-channel currents were filtered at 2 kHz (−3 dB, four-pole Bessel) and sampled at 25 kHz. Digitized data were collected and stored on an IBM-compatible (Gateway 2000 4DX-2–66) computer running the Axobasic environment (Axon Instruments) using software of our own design. Data were collected at room temperature (20–23°C). The chloride potential is 0 mV under these ionic conditions, resulting in inward currents (outward Cl⁻ movement) at a holding potential of −70 mV throughout our experiments.

Rapid solution changes. GABA (Sigma, St. Louis, MO), stored in aliquots of 10 mm and diluted to the desired concentrations, both in Tyrode's solution, was transiently applied to patches via an electromechanical solution changer. Control and test solutions were gravity-fed separately into the lumens of dual-barreled pipettes constructed from pulled borosilicate theta tubing (Sutter Instrument Company). Test solutions containing GABA were applied by delivering a filtered (model LPF-100B, four-pole Bessel, 200 Hz; Warner Instrument Corporation, Hamden, CT) voltage pulse to a high-voltage amplifier (model P-275.10, Physik Instruments, Waldbronn, Germany) that drove the macro-block translator such that a dual-barreled pipette tip moved a short distance. In this way, control and test streams bathing the membrane patch could be interchanged rapidly. GABA pulses were applied every 15 sec (GABA in micromolar, duration in milliseconds): 10, 300; 30, 200; 100–2000, 100. Macropatch current responses to brief (2 msec), high-concentration GABA (2000 μm) pulses replicated IPSCs (Jones and Westbrook, 1995). At the end of the experiment, the membrane patch was ruptured, and open-tip junction potential current responses were obtained using half-diluted Tyrode's solution. This response was taken to represent the GABA time course during the experiment. Experiments were included only if the time course approximated a pulse with 10–90% rise time < 300 μsec. In preliminary experiments, the variability of the wash-in latency was <120 μsec (SEM). This was reported by the time to reach the half-amplitude point of the junction potential response during repetitive pulsing when the wash-in criterion was satisfied.

Data analysis. Single-channel events were detected by half-height criterion (Sachs et al., 1982) and idealized with custom software running in the Axobasic environment (Axon Instruments). The primary conductance opening was 29 pS. Subconductance openings (22 pS) were infrequent (<5%) and excluded during idealization when these openings reached a clear plateau (see Fig. 3A, ○). The number of active channels in a patch (n) was determined by the stacking of unitary events, which is a good estimator, especially for n < 4 (Horn, 1991), over the course of 100–200 sweeps of channel activity. A typical patch contained two to three active channels. Patches were included only if channel activity was stationary, which was confirmed by a quasi-linear dependence of the integral of sweep open probability (P_o) over sweep number. Sweep open probability was computed by integrating idealized records over the sweep period. Dwell time histograms were binned logarithmically (Sigworth and Sine, 1987) and fitted by a maximum likelihood method. Transformed, multi-exponential, probability density functions were fit to dwell time histograms only considering durations more than three times the system dead time (t_d ∼0.1 msec). The number of fitted exponential components was increased until additional functions failed to improve the fit. Idealized records were used to construct ensemble currents, first latency distributions,P_o/o functions, and dwell time histograms.

Fig. 3.

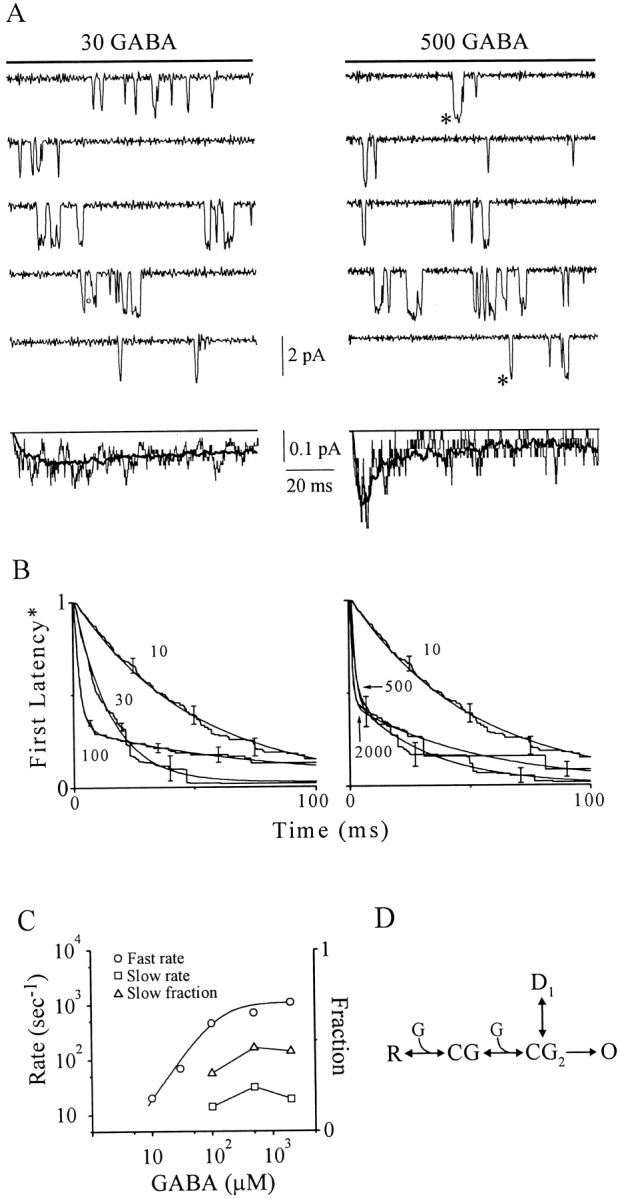
First latency analysis of activation.A, Representative, nonconsecutive single-channel traces evoked by GABA pulses (solid lines) at indicated concentrations (in micromolar) from individual single-channel patches. Downward current deflections denote channel opening. Ensemble average currents (below, irregular lines) are similar to the time course of representative macropatch currents at these concentrations (heavy lines). Open circlemarks a subconductance opening excluded from single-channel analysis. At the higher concentration (500 μm), delayed first openings, occurring after the ensemble current peak, are indicated (asterisks). B, Single-channelFirst Latency* functions (corrected for a slow desensitized state; see Materials and Methods) at indicated GABA concentrations, in micromolar (means ± SEM; n= 3–5). Superimposed relationships (smooth lines) are delayed monoexponential (10 and 30 μm) and biexponential (100–2000 μm) function fits to the data (see Materials and Methods). The fit to the 100 μm response is difficult to visualize because it nearly overlies the empirical response at all time points. C, Concentration–response relationships for rates (fast and slow) and slow fraction derived from parameters from multiexponential function fits in B. The fast rate (open circles) is well fit (smooth line) by a logistical function [Rate = Rate_max × (1 + (EC₅₀/[GABA])^slope)⁻¹, where Rate_max is maximum rate (1100 sec⁻¹), EC₅₀ is concentration of half-maximal rate (125 μm), and slope is related to the Hill coefficient (1.47)]. D, An activation gating scheme that reconciles the empirical findings from first latency* functions (see Results).

First latency distributions were created using standard histogram techniques (Aldrich et al., 1983). Plateau values were corrected for the probability of a channel residing in a long-lived desensitized state. Complemented distribution functions were then constructed, andnth rooted to compensate for n-channel patches (Aldrich et al., 1983). This function is denoted first latency* (FL*) to indicate correction for null sweeps arising from a long-lived desensitized state.

Precise determination of n from multichannel patches is necessary to construct single-channel first latency functions. We therefore investigated the accuracy of the channel estimator using single-channel simulations of the model that accounts for many features of GABAR gating (see Fig. 6A). A single-channel simulator (implemented in Matlab v5.1; Mathworks, Natick, MA) was used to determine the probability of n and n −1 overlapped openings in response to 100 msec GABA (100 μm) pulses (delivered every 15 sec; 150 applications; five separate trials) for n-channel patches (n = 2–5). The probability of observing noverlapped openings is appreciable for n = 2 or 3 (0.45 and 0.15, respectively), the typical numbers of detected channels in an experimental patch. When n was increased to 4 or 5, the probability of n overlapped openings was markedly reduced (<0.02), whereas the probability of observing n −1 overlapped openings was high (0.3 and 0.1, respectively). This suggests that n − 1 channels will likely be detected when n > 3. Consequently, the calculated single-channel first latencies may be shifted erroneously, to a small degree (∼30%), to briefer times resulting from (n − 1)th rooting of complemented distribution functions.

Fig. 6.

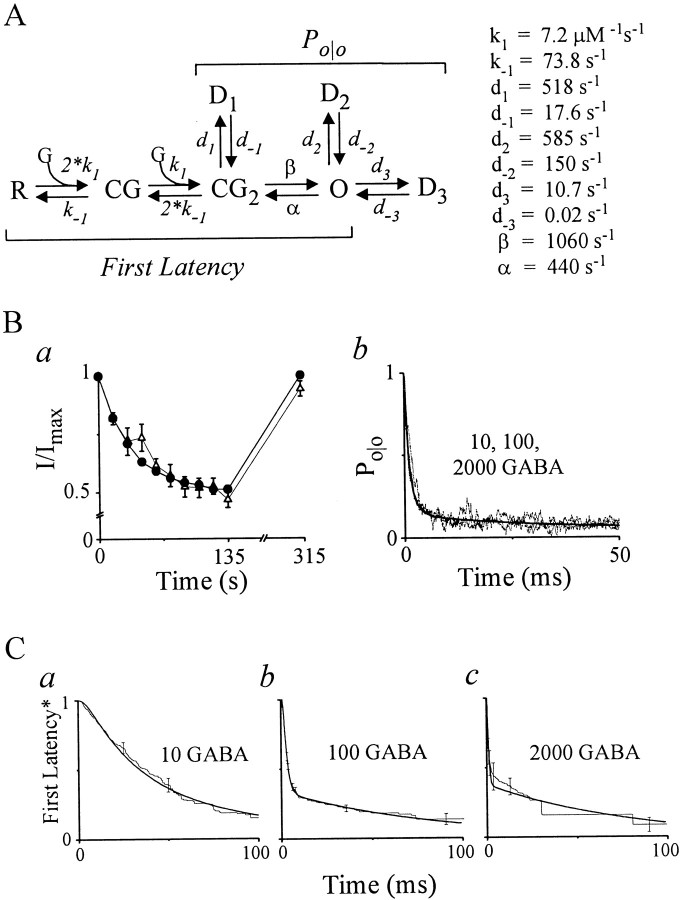
Mathematical model of dominant GABAR gating during transient GABA. A, Left, Gating model formed by combining subschemes separately proposed for first latency and P_o/o functions. Bracketsencompass states and gating that primarily contribute to each function. A resting channel (R) sequentially binds two molecules of GABA (G) to either open (O) (fast component in FL* functions) or rapidly desensitize (D₁). Channel emerges from D₁, to subsequently open, giving rise to the slow component in the FL*. Open channels rapidly desensitize to D₂ or convert transiently to CG₂ before finally desensitizing to D₁. D₃ likely accounts for apparent null sweep grouping and macropatch amplitude decrement.Right, Parameter values of model (see Results).B, C, Model reproduces empirical responses used in its construction. Response of peak amplitudes of macropatch currents during pulse trains (Ba),P_o/o (Bb), and FL* (Ca–c) for the indicated conditions (GABA in micromolar). Model simulations are superimposed (connected filled circles in Ba;smooth solid lines in Bb,Ca–c). Experimental results replotted from Figures 2B, 3B, and4B.

P_o/o functions were constructed as described by Yue et al. (1990) and give the probability of a channel being open at time t given that it was first open at timet_j(P_o/o(t,t_j)). For single-channel patches, idealized traces with openings occurring during a conditioning window centered at t_j were aligned at the first open point to t_j. These traces were then averaged and normalized by the unitary current to yieldP_o/o. For multichannel patches, the algorithm calculates the conditional expectation value (E_o/o) (Imredy and Yue, 1994) for the number of channels open at time t, given that the first opening occurred at time t_j.P_o/o was then evaluated according to the relation:

$$P_{\text{o}\Vert \text{o}}(t,t_{\text{j}})=E_{\text{o}\Vert \text{o}}(t,t_{\text{j}})-(n-1)·P_{\text{o}}(t+t_{\text{j}}),$$ Equation 1

where P_o(t +t_j) is the unconditional probability that a channel is open at time (t +t_j). The convolution (Eq. 2) of the first latency probability density function [f(t)] andP_o/o(t) specifies the time-dependent channel open probability [P(t)], which is a scaled version of the macroscopic current [I(t); n = channel number; γ = unitary conductance; ΔV = electrochemical driving force]) (Eq. 3):

$$P(t)=\underset{0}{\overset{\text{t}}{\int }}f(\tau )·P_{\text{o}\Vert \text{o}}(t-\tau )d\tau ,$$ Equation 2

$$I(t)=n·\gamma ·\mathrm{\Delta }V·P(t).$$ Equation 3

Up to a two-exponential function [A₁exp(−(t −t_D)/τ₁) + A₂exp(−(t −t_D) /τ₂) + B:A_n is the nth component amplitude;B is a constant or plateau; t is time (milliseconds); t_D is a time (milliseconds) delay; τ_n is thenth component time constant (milliseconds)] was fit to the time courses of experimental peak amplitude current decrement, FL* functions, P_o/o functions, and the decay of ensemble currents. Fitting used Origin v3.0 (MicroCal, Northampton, MA), in which the final “goodness of fit” was judged by eye. Fits to macroscopic peak amplitude decrement used a zero time delay (t_D = 0) and a non-zero constant (B > 0). Fits to FL* values used a time delay (t_D > 0) to account for an initial sigmoidal period and a constant of zero (B = 0). Fits to P_o/o values included a constant of zero (B = 0) and a zero time delay (t_D = 0). Fits to the decay phase of ensemble currents used a time delay (t_D > 0) equal to the time of peak current and a constant of zero (B = 0).

Model simulation and parameter estimation. The seven-state dominant gating model was implemented in Matlab v5.1 (Mathworks, Natick, MA) by solving the matrix equation:

$$X(t)={\text{e}}^{Q(\text{t})}·X(0)$$

where X(t) is a 7 × 1 state variable vector indicating the occupation of the states (i.e., R, CG, CG₂, D₁, O, D₂, D₃) at timet, X(0) = [1 0 0 0 0 0 0]^T initial state vector at time 0 assuming all channels in the resting R state, andQ(t) = the 7 × 7 state transition matrix of rate constants governing the transition rates between all connected states. The single open state is O, the singly and doubly liganded receptors are CG and CG₂, respectively, and the three desensitized states are D₁, D₂, and D₃ (see Fig.6A). The simulation period was divided into GABA wash-in and wash-out, and changes in concentrations were assumed to be instantaneous. Parameter optimization used a least squares technique that simultaneously used mean empirical FL* andP_o/o values at 10, 100, and 2000 μm GABA as performance targets.

RESULTS

GABA induces single-channel activity in rapidly perfused, outside-out membrane patches from cells expressing α1β1γ2 GABARs

We focused initially on dominant features of GABAR activation by exploring first latencies. Figure1A shows consecutive single-channel traces evoked by rapidly applied, periodic GABA pulses delivered to an outside-out membrane patch that contained a single, active α1β1γ2 GABAR. Single-channel openings are marked by downward current deflections manifesting a primary conductance state of 29 pS. Patches from untransfected cells showed no activity. First latencies range from milliseconds to tens of milliseconds. Individual traces show openings that occur singly and in bursts. Long closed periods are interposed between openings, consistent with channel entry into desensitized states. The junction potential current response recorded at the end of the experiment reports the test solution time course at the tip of the recording pipette and presumably GABA time course at the extracellular membrane surface during experimentation. The ensemble average current overlies a representative macropatch current recorded under the same conditions, which argues that channel density fails to influence channel gating. This is essential to extending single-channel findings to macroscopic responses.

Fig. 1.

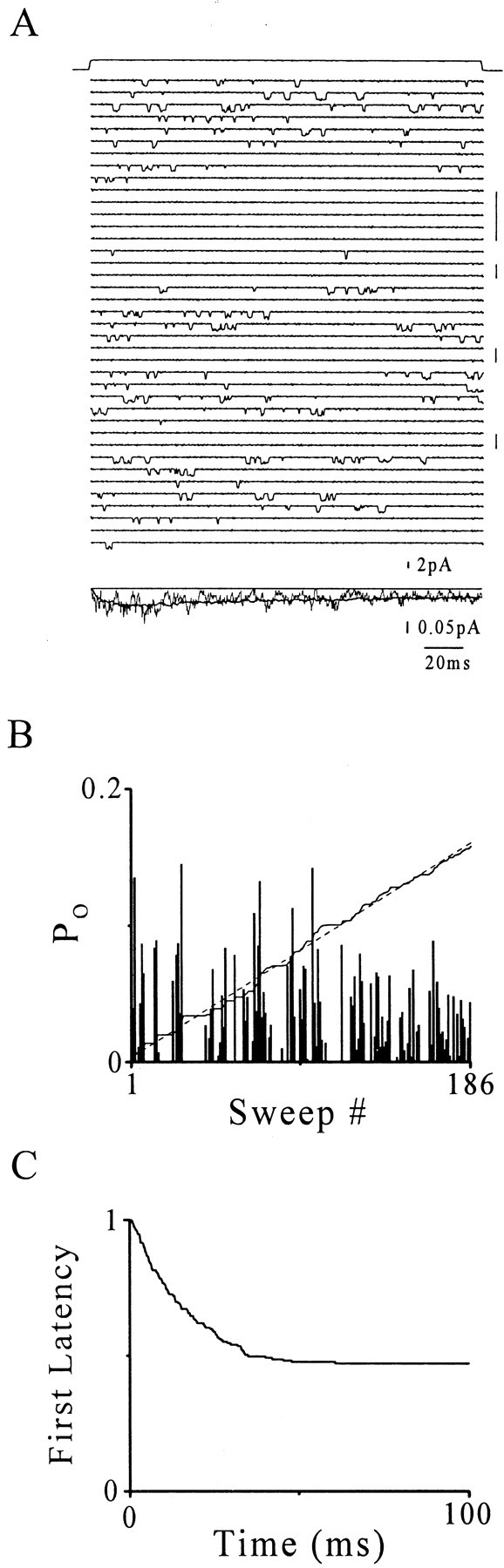
Single-channel activity from a rapidly perfused, outside-out membrane patch from a cell expressing α1β1γ2 GABARs.A, Top, Liquid junction potential response (see Materials and Methods) representing the time course of the GABA pulse (upward deflection, 30 μm; 200 msec) that was delivered every 15 sec. Middle, Consecutive sweep voltage-clamp current records show single-channel activity triggered by GABA pulses. Downward current deflections mark openings of a single α1β1γ2 GABAR with a primary conductance state of 29 pS (holding potential = −70 mV). Vertical bars mark periods of apparent null clustering. Bottom, Ensemble current average (irregular line) and superimposed representative normalized macropatch current collected under the same conditions (heavy line). The vertical scale bars reflect single-channel amplitudes. B, Sweep open probability (P_o) plotted versus sweep number (see Materials and Methods). Integral of P_o(irregular line, arbitrarily scaled) over sweep number is shown. An appropriately scaled linear function (dashed line) overlies the integral of P_odemonstrating quasi-linearity, which indicates that channel activity is stationary over the data collection period (see Results).C, First latencies given as a complement of the distribution.

Markov models have been used widely to describe ion channel gating where the random nature of transitions between conformational states can be described by a Poisson process. A key feature of such a process is the stationary increment assumption (Ross, 1997) and is fundamental to single-channel analysis. We were concerned about whether channel activity was stationary during these experiments because data collection periods lasted up to 50 min, which arose from infrequent collection (every 15 sec) of sweep records to maximize recovery from slow desensitized states (Haas and Macdonald, 1999). We investigated this issue by first plotting sweep open probability (P_o) versus sweep number (Fig.1B). P_o was then integrated over sweep number and plotted on the same axes with arbitrary scaling. A quasi-linear dependence on sweep number, and therefore time, indicates stationary function. Only patches meeting this criterion were included in the data set.

Figure 1C shows the corresponding FL function in a complement of the distribution form, which conveys the probability that the first opening will occur at a time after that specified on the abscissa. This function concisely conveys FL information for all 186 sweeps from this patch and shows that most first openings occurred within 40 msec. The plateau (∼0.5) reports the probability that a channel will fail to open during a given GABA application. Indeed, inspection of individual sweep records reveals sweeps without activity (nulls). These can be explained by either a resting, closed channel converting to a desensitized state during the present GABA pulse before opening or a long-lived, desensitized state persisting from the previous pulse. Null sweeps appeared to cluster, thus arguing for the latter possibility. Single-channel analysis assumes that the receptor is in the same resting conformation before each GABA application. Therefore, to further investigate for a persistent, slow desensitized state, single-channel protocols were applied in macropatch current experiments.

GABARs enter a long-lived, desensitized state

Figure 2A shows macropatch current responses to GABA pulses (100 msec, 2000 μm) delivered every 15 sec. Current time course initially shows a rapid downward increase representing channel activation that is followed by decay reflecting fast desensitization. The peak amplitude of subsequent responses progressively declines until an apparent plateau is reached around the eighth pulse. Preparation stability was ensured by the return to control amplitude of a response evoked 180 sec after the pulse train. The results support GABA-induced entry into a desensitized state sufficiently long-lived to accumulate from pulse to pulse. For accumulation to occur, the recovery time constant must be on the order of the interstimulus interval (15 sec). This finding was confirmed in grouped data (Fig. 2B) in which peak amplitudes declined in a monoexponential manner to a plateau of ∼0.5. A plateau is consistent with a pseudo-equilibrium condition established between pulse-induced entry into and interstimulus recovery from a long-lived, desensitized state. According to this reasoning, approximately half the channels are unavailable for activation at the end of the pulse train. Once the mean probability of this state is determined for a given experimental protocol, null sweeps and FL values can be corrected. Therefore, macropatch current experiments were performed for all protocols, mean responses were calculated, and monoexponential fitting were performed. Derived plateau values were plotted for each protocol and designated by GABA concentration (Fig. 2C). This slow desensitized state accords with reports from heterologous expression systems (Haas and Macdonald, 1999) and neuronal cells (Bai et al., 1999).

Fig. 2.

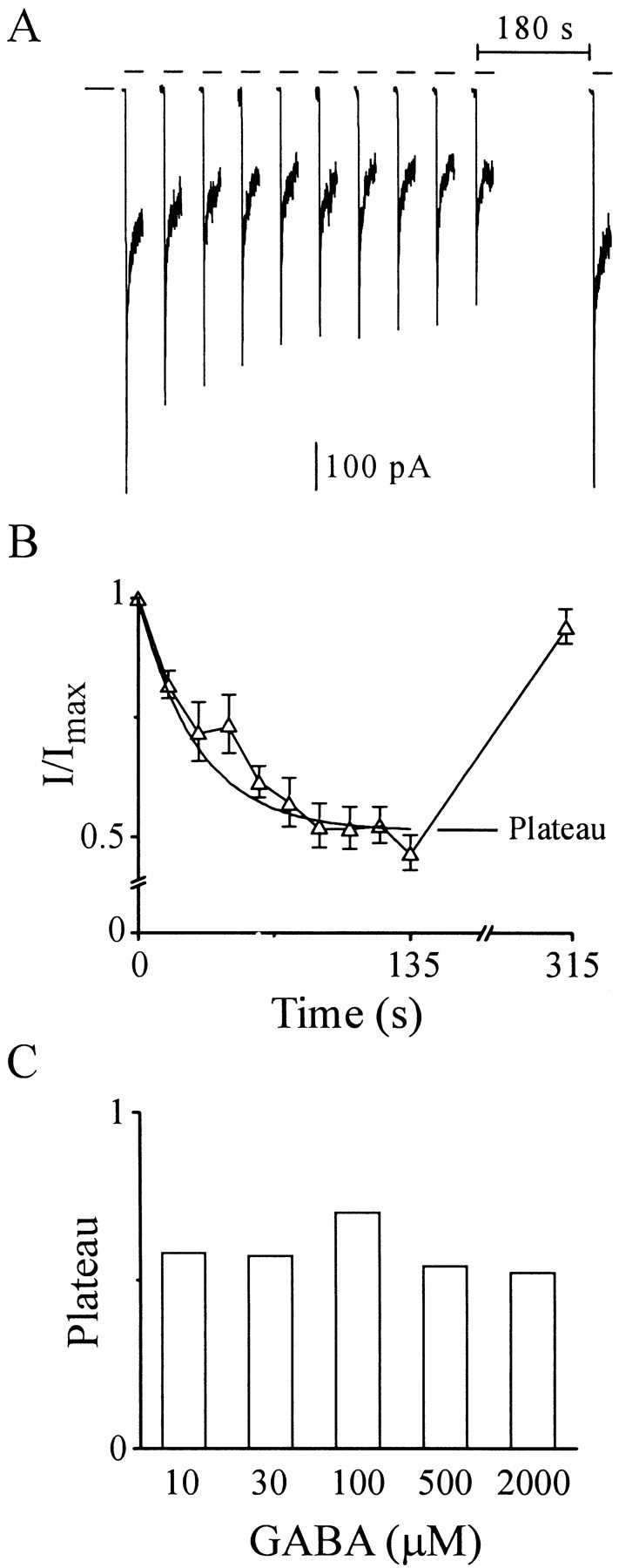
Peak amplitude of macropatch currents decreases during trains of GABA pulses. A, Macropatch currents triggered by GABA (2000 μm) pulses (100 msec) every 15 sec (series of short horizontal bars). Single long bar on left marks baseline. Deactivation time course has been truncated for clarity. B, Peak current amplitudes (I) fromA normalized to the amplitude of the first pulse (I_max) and plotted versus time of pulse (means ± SEM; n = 3). A monoexponential function fit is shown (smooth solid line) with a plateau of 0.52 (see Materials and Methods). C, Bar graph of plateau values derived from monoexponential fitting to macroscopic peak amplitude decrement for single-channel GABA pulse protocols (10 μm, 300 msec; 30 μm, 200 msec; and 100–2000 μm, 100 msec) with a period of 15 sec.

Increasing GABA concentration shortens first latencies and reveals a slow component of activation

Figure 3B shows first latency functions corrected for nulls (FL*) associated with a slow desensitized state. The function at 10 μm GABA exhibits a brief delay followed by a slow decline, which is well fit by a delayed monoexponential function without a constant (see Materials and Methods). The FL* at 30 μm GABA is also monoexponential but is accelerated relative to 10 μm GABA, consistent with enhancement of forward rate constant(s). Increasing GABA concentration to 100 μm continues to accelerate the fast component and introduces a second slow monoexponential component. Higher GABA concentrations (>100 μm) caused little additional acceleration of the fast component without changing the slow.

We explored gating reflected in FL* values by examining the dependence of exponential parameters on GABA concentration (Fig.3C). The fast rate increases supralinearly (slope factor related to the Hill coefficient of 1.47) from 20 sec⁻¹ to a plateau of 1100 sec⁻¹, suggesting that at least two GABA molecules must bind to trigger channel opening. The plateau value represents the apparent forward activation rate constant. The slow fraction and rate appear insensitive to GABA concentration, suggesting the involvement of slowly activating, maximally liganded receptors. Figure 3D shows a simple gating scheme that reconciles these findings. A resting channel (R) binds a single GABA molecule (G) to achieve the singly liganded closed state (CG). GABA binding to a second identical site leads to a doubly liganded closed state (CG₂). CG₂ may activate directly by converting to an open state (O), thereby giving rise to the fast component in FL* values. Alternatively, CG₂ may convert initially to a fast desensitized state (D₁), where it dwells until returning to CG₂, whereupon it activates to O to be reported by the slow component.

Open probability conditioned on the first opening (P_o/o) is biphasic and GABA insensitive

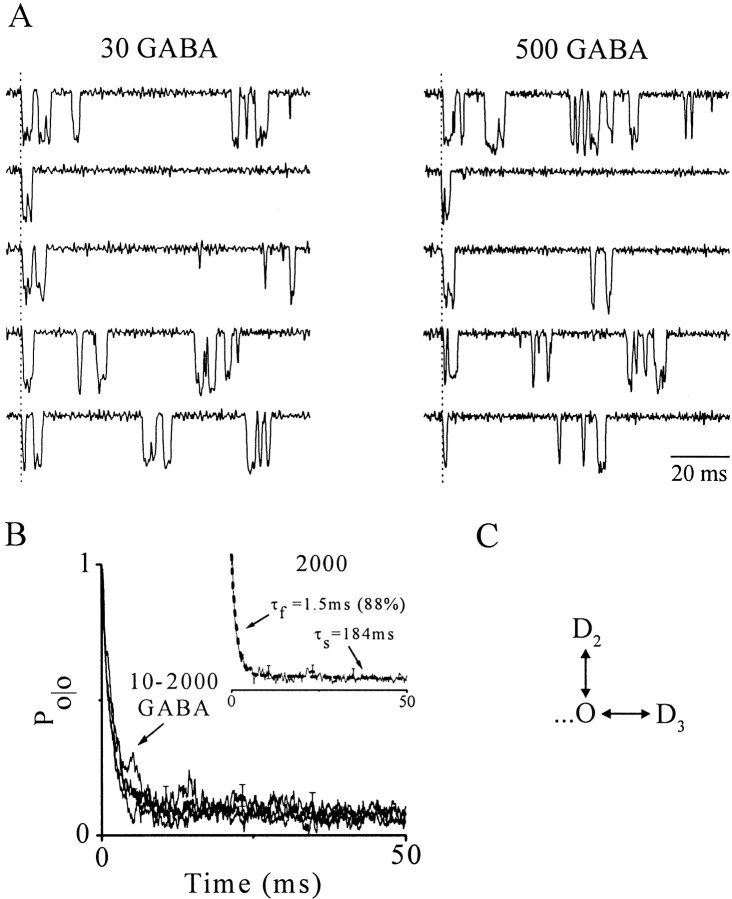
We next considered channel gating subsequent to the first opening. Figure 4A shows representative single-channel traces aligned at the first opening by eye for comparison. Gating after the first opening is qualitatively similar at both concentrations and is characterized by openings that occur singly and in bursts separated by long closed intervals. We quantitatively analyzed this gating using conditional open probability analysis (Sigworth, 1981; Yue et al., 1990) (see Materials and Methods). Specifically, we constructedP_o/o functions that report open probability conditioned on the first opening, which likely emphasizes transitions to deeper states at high GABA concentrations (>100 μm). Figure 4B shows meanP_o/o values over a range of GABA concentrations. These functions nearly superimpose, indicating that gating subsequent to the first open event is insensitive to GABA concentration and therefore implicates states that are maximally liganded. The function time courses are biphasic, dominated by a fast component, and fit well with a biexponential function. The results are reconciled by a simple gating scheme in which the open state converts to adjacent fast (D₂) and slow (D₃) desensitized states (Fig. 4C); however, maximally liganded closed states preceding the open state may also be involved.

Fig. 4.

Open probability conditioned on the first opening (P_o/o). A, Nonconsecutive, single-channel records evoked by 30 and 500 μm GABA from patches in Figure 3A, with first openings aligned at the dotted vertical lines by eye for comparison. Sweeps with similar gating across concentrations were paired for comparison. B, MeanP_o/o functions for indicated GABA concentrations (micromolar) that nearly superimpose. For clarity, error bars are shown only for the 2000 μm decay (means ± SEM; n = 3–5). Inset, Biexponential fit (dashed line) to the 2000 μm response with indicated parameters. C, A simple gating scheme consistent with P_o/o findings in which open channels (O) convert to adjacent fast and slow desensitized states (D₂ and D₃, respectively). Dotted line represents states that may contribute toP_o/o but are not shown (see Results and Discussion).

Convolution of FL probability density andP_o/o reproduces the macroscopic current time course

Single-channel open probability [P(t)] is a scaled version of the macroscopic current time course and can be calculated by convolving (see Materials and Methods) the first latency probability density function (f) with theP_o/o function (Fig.5, A and B, respectively). If our analytical techniques are correct, then the computed P(t) will duplicate gating manifest in ensemble current averages derived from the same single-channel data. Figure 5C shows that computed P(t) accurately reproduces the time course of the mean ensemble current average, thereby confirming the validity of our approach.

Fig. 5.

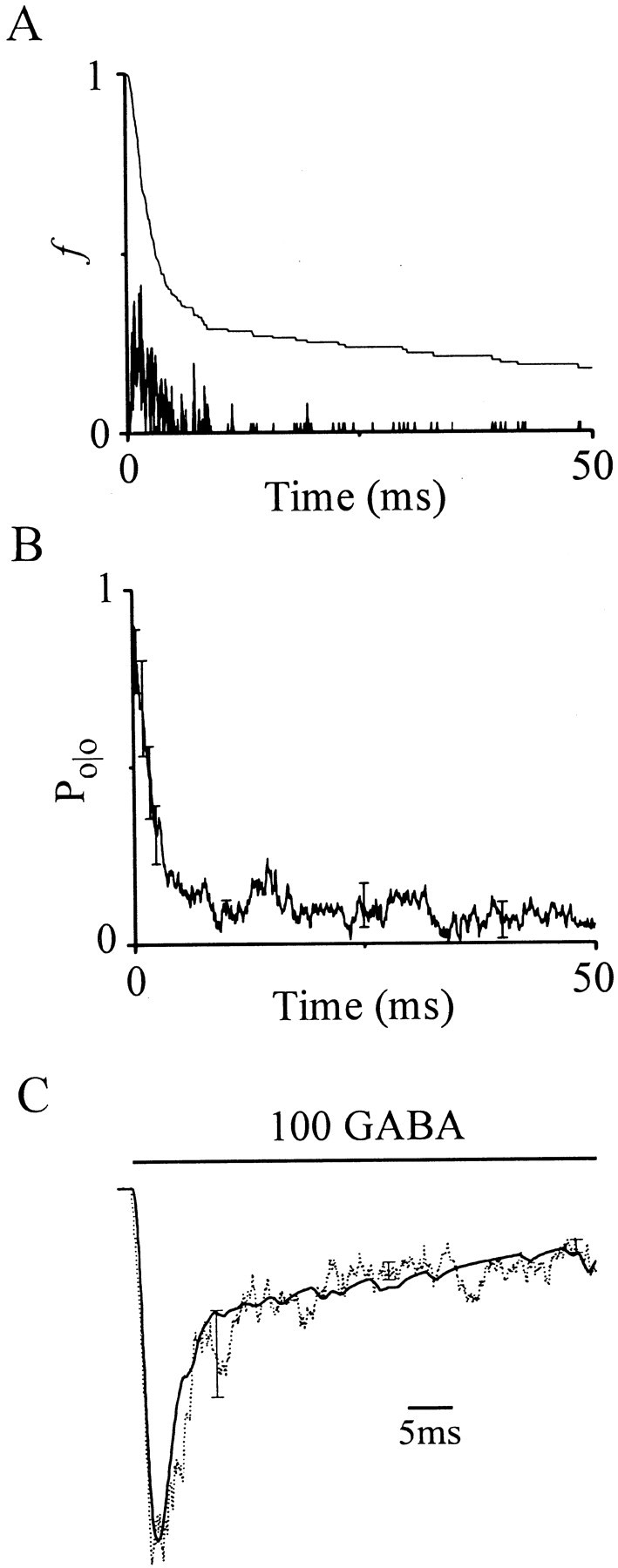
Single-channel open probability derived from convolution of first latency and P_o/oreproduces the time course of macroscopic current. Calculation of single-channel open probability [P(t)] induced by a long 100 μm GABA pulse. A, First latency probability density function (f, vertical lines) composed of first latencies collected from all patches at this concentration (n = 3). Mean complement of the distribution (smooth line) replotted from Figure3B for reference. B, MeanP_o/o function replotted from Figure4B (±SEM). C, Plot of single-channel open probability [P(t), solid line)] constructed by convolving f withP_o/o (see Materials and Methods) and ensemble average current (dotted line; mean ± SEM;n = 3). Horizontal bar marks GABA pulse. Responses were normalized and peaks aligned in time to facilitate comparison of time courses.

A parsimonious gating model accounts for FL* andP_o/o values and predicts the properties of microscopic and macroscopic gating

As a first attempt to construct a parsimonious model of dominant GABAR gating, we simply combined the gating subschemes separately proposed for FL* and P_o/ofindings at the single open state (Fig.6A). We then estimated model parameters using empirical FL* andP_o/o values as performance targets (see Materials and Methods) to determine all final values except those (d₃,d₋₃) related to the slow desensitized state (D₃). These were manually adjusted to account for the amplitude decrement of macropatch currents (Fig. 2B). From this point forward, all parameter values were held constant (Fig. 6A,right), which defined the final model. The final model precisely accounts for empirical FL* values (Fig.6Ca–c), P_o/ovalues (Fig. 6Bb), and the amplitude decrement of macropatch currents (Fig. 6Ba), all of which were used in its construction. The ability of a fully defined model to account for data used in its construction is a minimum criterion. However, model prediction of empirical data not considered during its construction is remarkable and represents predictive value. This feature enhances the credibility of the model structure. A credible model may then provide new insight into processes underlying predicted empirical responses as well as point to new lines of experimentation. We therefore tested for this quality.

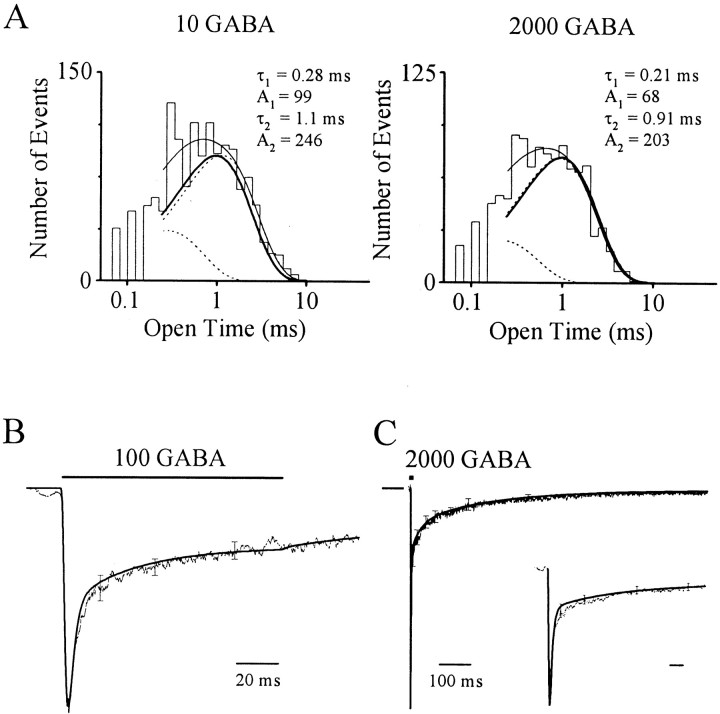
Previous studies have identified up to three distinct open states for GABARs (Twyman et al., 1990; Haas and Macdonald, 1999) in contrast to the single open state in this model. To investigate this divergence we first characterized open states manifest in our single-channel data. Open time histograms (OTHs) (see Materials and Methods) at low GABA concentration (10 μm) exhibited two kinetically distinct open states (Fig. 7A,left). We considered the primary feature of the OTH as the single longer open state, because it carries >90% of the charge as a result of its mean lifetime (τ ∼ 1 msec) and higher relative frequency. A 200-fold concentration increase induces little change in the OTH (Fig. 7A, right). Comparable findings were made in at least two other patches at each concentration. The findings suggest a single dominant open state that is maximally liganded. The findings from empirical OTHs are predicted by the model because it has a single maximally liganded open state with a dwell time of ∼1 msec. This conclusion is demonstrated by model OTHs that closely approximate empirical OTHs at both concentrations (Fig.7A).

Fig. 7.

Model predicts mean open time and macroscopic GABAR gating. A, Log-binned open time histograms at 10 and 2000 μm GABA. Maximum likelihood fits of transformed biexponential functions (thin line) and individual components (dashed lines). Thick linesrepresent model open time histograms. B, Macropatch current (irregular line; mean ± SEM;n = 3) evoked by the indicated GABA pulse (bar). The model response [simulatedP(t), smooth line] normalized for peak amplitude accurately predicts the empirical time course. C, Macropatch current response (irregular line; mean ± SEM; n = 4) to a brief (2 msec) high concentration GABA (2000 μm) pulse marked by filled square, which replicates an IPSC. Long horizontal bar at left indicates baseline. Normalized model response (smooth line) reproduces the empirical time course. Inset, The same responses on an expanded timescale. Calibration: 10 msec.

The main focus of this study is to understand the dominant gating underlying the time course of IPSCs. If the model predicted the time course of IPSCs then it could provide new insight into the underlying gating. Therefore, we first considered whether the model predicts the time course of empirical macroscopic currents triggered by long GABA pulses. Figure 7B shows that the model predicts the mean macropatch current response triggered by a 100 μm GABA pulse lasting 100 msec. We next considered IPSCs. The IPSC time course in cultured neurons is mimicked by macropatch current responses induced by brief (<5 msec) pulses of saturating GABA concentrations (>1 mm) (Maconochie et al., 1994; Jones and Westbrook, 1995). We therefore tested the ability of the model to predict the time course of such replicated IPSCs in our experimental preparation. Figure 7Cshows a mean macropatch current response trigged by a brief (2 msec), high concentration GABA (2000 μm) pulse. The time course is complex, manifesting rapid activation, followed by rapid decay over milliseconds and a slow decay phase lasting for hundreds of milliseconds. Remarkably, the normalized model response to the same stimulus precisely predicts the empirical response such that the two are nearly indistinguishable, even when focusing on the first 100 msec of the response (Fig. 7C, inset). The results demonstrate that the model reproduces the gating underlying replicated IPSCs. If these findings generalize to native synaptic receptorsin vivo, then they point to dominant gating operational during fast GABAergic synaptic transmission.

Model parameter sensitivity analysis and dual modes of fast desensitization influence model peak open probability and synaptic efficacy

The role of model states and gating transitions in performance is investigated by examining model sensitivity to changes in associated parameters (parameter sensitivity analysis). Charge transfer mediated by receptor activity is a primary determinant of synaptic efficacy. We used the integral of model open probability [P(t)] induced by brief, high concentration GABA pulses as an index (ΣP) of charge transfer because they are proportional. We examined changes in ΣP to fivefold increases in parameter values (Fig.8A).k₁ caused no change in ΣPbecause forward rates are already sufficiently high to reduce the probability of R and CG₁ states to near zero during the pulse. k₋₁ induced a small change (<20%), which was less than expected. Changes ink₋₁ would likely affect the slow decay occurring over hundreds of milliseconds, but ΣP was computed for only the first 50 msec of the response. However, marked changes (>50%) in ΣP occur with rate constants governing conformational changes involved in channel opening (β and α), an intuitive result. ΣP is also strikingly sensitive to entry rate constants for desensitization (d₁ and d₂), suggesting that the associated states (D₁ and D₂) play an important role in shaping IPSC morphology, consistent with a previous report (Jones and Westbrook, 1995). To gain deeper insight into the influence of both fast desensitized states, we investigated the effects ofd₁ and d₂ onP(t), FL*, andP_o/o.

Fig. 8.

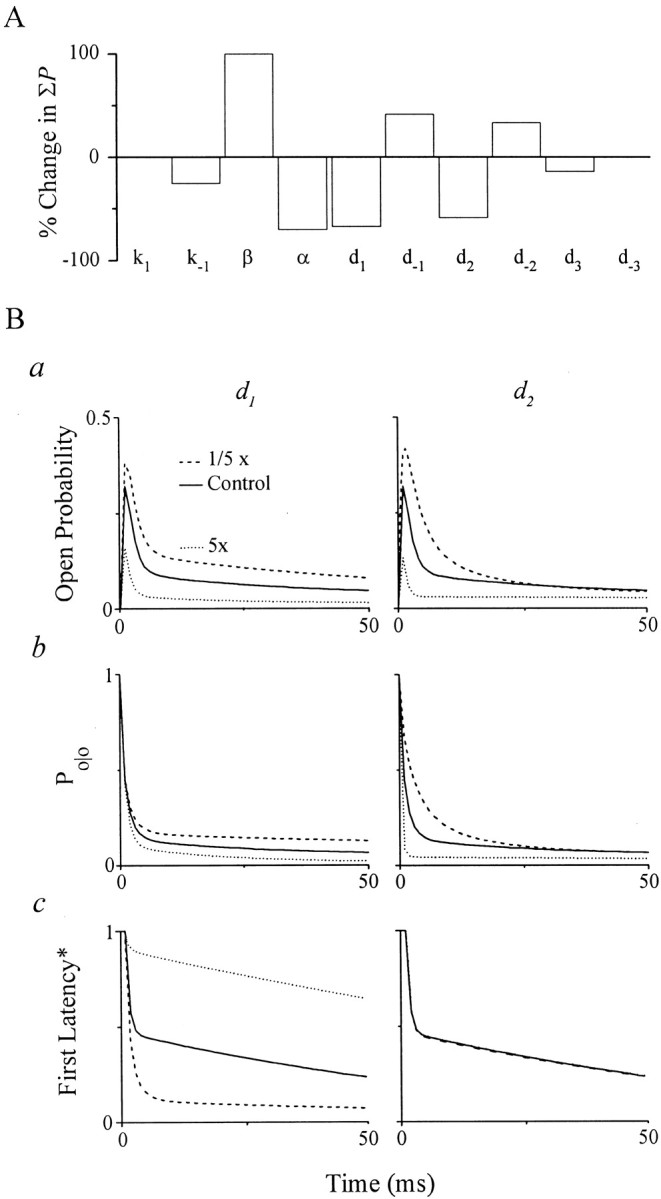
Model parameter sensitivity analysis.A, Percentage change in simulated integral of single-channel open probability (ΣP) during the first 50 msec of a replicated IPSC induced by a brief, high concentration GABA pulse (2000 μm, 2 msec) for a fivefold increase in the indicated model parameters. ΣP is proportional to the total charge transfer. B, Control responses (solid lines) and those with a fivefold increase (dotted lines) or a fivefold decrease (dashed lines) in d₁ ord₂ (as indicated). Model open probability (a), P_o/o(b), and FL* (c) functions at the same GABA concentration (2000 μm).P_o/o and FL* functions are model responses to 100 msec GABA pulses (see Results).

Increasing d₁ depressed peak open probability (P_max) by more than twofold and enhanced the amplitude of the fast component of decay (Fig.8Ba, left).d₁ promotes entry into D₁ and thereby reduces the fast component of the FL* (Fig. 8Bc, left). The slow activation component is markedly enhanced, which primarily affectsP(t) after the peak, thereby underscoring the utility of first latency analysis. This change enhanced the amplitude of the fast component, accelerated the slow component, and depressed the apparent plateau of the P_o/o (Fig.8Bb, left). This indicates that D₁, in addition to D₂, contributes importantly to gating after the first opening and thusP_o/o. Examination of related rate constants (Fig. 6A) support this conclusion. Overall, the simple subscheme proposed earlier (Fig. 4C) must be extended to include these states, which is reflected in the identification of subgroups of states and transitions underlyingP_o/o (Fig. 6A). Decreasing d₁ had the expected converse effects on P(t), FL*, andP_o/o.

Increasing d₂ suppressedP_max, accelerated the fast component, and decelerated the rate and increased the amplitude of the slow component. d₂ promotes entry into D₂ and thereby markedly acceleratesP_o/o decay and depresses the apparent plateau (Fig. 8Bb, right), whereas it has no effect on FL* (Fig. 8Bc, right). The marked depression of P_max arises from increased transitions from O to D₂, which blunts the probability of O. Decreasing d₂ caused converse effects on P(t), FL*, andP_o/o. The results identify key model states and support the involvement of fast desensitization in shaping the IPSC time course (Jones and Westbrook, 1995). Notably, they point to a second important role of fast desensitized states in synaptic efficacy by influencing peak open probability and IPSC amplitude.

Dominant gating underlying replicated IPSCs

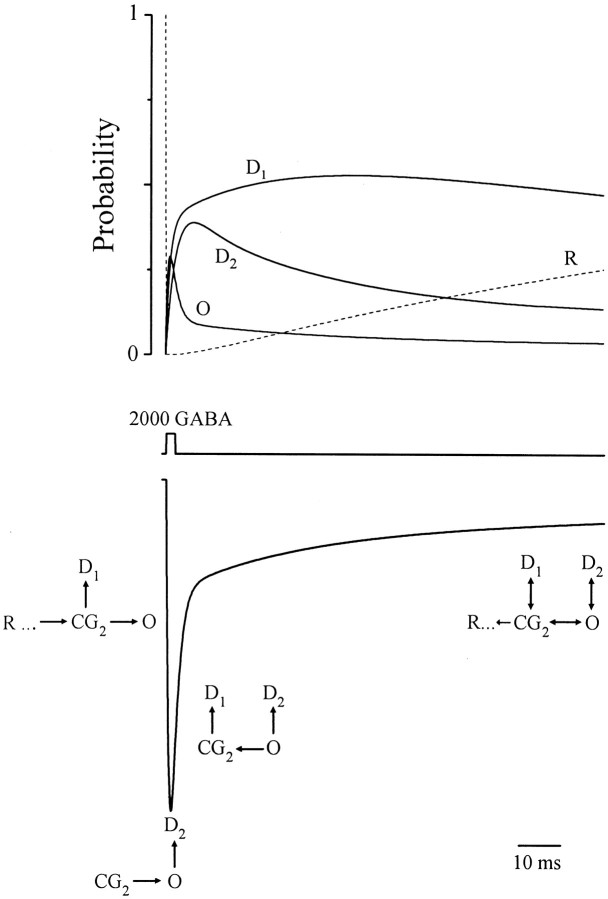
The central goal of this study was to identify the dominant gating underlying the time course of IPSCs. The GABAR response to brief, high concentration GABA pulses “mimics” or replicates IPSCs (Jones and Westbrook, 1995). The time course of replicated IPSCs in our preparation is predicted by the model (Fig. 7C). Therefore, we examined model function to gain new insight into the gating underlying IPSCs. Figure 9(top) shows the probability time course of states that play key roles in model IPSCs. Open probability rises to a peak within 1 msec and is followed initially by a fast and then a slow phase of decay. During early activation, before the peak, open probability is reduced by rapid entry into D₁, which is reported by the early rapid rise of D₁. A channel in CG₂ has nearly a 30% chance of converting directly to D₁. Given the long lifetime of D₁ (∼50 msec), it will not contribute to the peak, and therefore P_max will be depressed proportionately. Late in activation,P_max is further blunted by >20% as O converts to D₂, which is reflected by the early rapid rise of D₂. Therefore, both fast desensitized states influence P_max and consequently synaptic efficacy. The fast decay of open probability results from continued conversion of O into D₂and eventually D₁ as indicated by increasing probability of these states. A slow phase of decay, which begins around 10 msec, is governed overall by GABA unbinding that is reported by increasing probability of R. During this phase, there is a quasi-equilibrium established among O, CG₂, D₁, and D₂ except that D₁ does not join until after 50 msec. Channel bursting arises from interconversions among O, CG₂, and D₂, and long closed intervals result from sojourns to D₁ in a manner proposed by Jones and Westbrook (1995). Figure 9(bottom) summarizes these findings for a model IPSC.

Fig. 9.

Model gating underlying primary phases of replicated IPSCs. Top, Probability of resting (R) (dashed line), open (O), and desensitized states (D₁ andD₂) (solid lines) during replicated IPSC (bottom) triggered by a brief (2 msec) high concentration (2000 μm) GABA pulse (middle trace). See Results. Bottom, Replicated model IPSC to the same GABA pulse is coarsely divided into four phases: early activation, activation to peak current, fast decay, and slow decay. Early activation, rapid downward current deflection, results from fast transition from R to CG₂. This reduces the R probability to zero during the pulse. The number of channels directly converting to O is reduced by those entering D₁. Peak amplitude is determined in part by early activation, but also by rapid conversion of O to D₂ that depresses the peak. Fast decay phase is the rapid current decay after the peak, which is attributable to continued transitions to D₁ and D₂. Finally, slow decay is primarily governed by slow ligand unbinding that is impeded by a relatively fast pseudo-equilibrium among CG₂, O, D₁, and D₂.

DISCUSSION

We investigated dominant gating governing GABAR activity triggered by transient GABA application with a unique combination of experimental and analytical techniques. The findings provide new insight into the dominant states and connectivity operative during transient GABAR activity. The primary results are as follows: doubly liganded closed channels can visit an adjacent fast desensitized state before opening; open channels rapidly convert to a second distinct fast desensitized state; a doubly liganded state(s) undergoes a conformational change to a slow desensitized state; and dual fast desensitized states may affect synaptic efficacy by influencing IPSC amplitude. Finally, a mathematical gating model predicts the time course of replicated IPSCs and thus provides new insight into the underlying GABAR gating.

Comparison of the dominant-gating model with previous models

Work by Weiss and Magleby (1989), Macdonald et al. (1989), andTwyman et al. (1990) investigating steady-state, single-channel activity of native GABARs provided a foundation for microscopic gating. In these studies, many conformational states were observed and represented in subsequent models. Furthermore, these studies have direct physiological relevance to extrasynaptic receptor function triggered by low GABA concentration under ambient conditions (Isaacson, 2000). Our focus here was dominant gating triggered by transient GABA application and specifically inhibitory synaptic transmission, which are conditions in which some channel states may be visited with low probability.

Maconochie et al. (1994) studied gating manifest in macropatch current time course induced by rapidly applied GABA pulses to outside-out, membrane patches from cerebellar neurons. This work was the first to investigate gating during GABAR activation. Current activation was monoexponential, wherein the derived rate manifests low and high concentration asymptotes. The findings supported a simple gating model with an “inactive pool” and an “active pool.” The inactive pool contains resting states that undergo rapidly equilibrating binding reactions when GABA is presented. Activation is a transition to the active pool governed by effective forward (β*) and reverse (α*) rate constants. First latency analysis allows detection of slower components of activation likely obscured in macroscopic current desensitization. In this way, we identified sojourns to a fast desensitized state (D₁) before opening, which underlies a second major component of GABAR activation.

A limitation of our study, as well as that of Maconochie et al. (1994), is that rate constants may be effective because transitions that equilibrate more rapidly than activation cannot be excluded. If such gating is present, then subsequent models are incomplete. The associated states can be identified by detailed single-channel analysis (Macdonald et al., 1989; Twyman et al., 1990) that could be applied to our transient single-channel data to refine our current model, if necessary. Another limitation of our study is the restricted range of GABA concentrations. At lower concentrations, different gating may dominate, but our focus was on gating underlying the IPSC time course.Maconochie et al. (1994) studied responses triggered by nanomolar GABA levels to define a low concentration activation rate asymptote of ∼10 sec^−-1, which likely represents the unbinding rate constant and is on the same order of magnitude that we report.

The critical role of desensitized states in IPSC relaxation was proposed by Jones and Westbrook (1995). This work complemented that ofMaconochie et al. (1994) by identifying gating that dominates GABAR deactivation. The authors suggested that brief, high-concentration GABA transients are sufficient to drive channels into a doubly liganded, fast desensitized state (D_fast). D_fast is similar to D₁ of our model, and we extend its role to modulation of channel activation. In addition, our results point to a second distinct, fast desensitized state (D₂), suggested by the simultaneous consideration of FL* and P_o/ovalues. FL selectively considers states leading to the first opening. These findings led us to propose a simple gating subscheme (Fig. 3D) in which the associated rate constants (Fig.6A) are constrained by FL* empirical data. Consideration of prospective gating that may underlie theP_o/o time course indicated that, whereas CG₂ and D₁contribute to this time course, the model accounted for both FL* andP_o/o values by adding D₂ in the manner shown (Figs. 4C,6A). Our work provides new insight into connectivity and points to an important role for a second fast desensitized state (D₂). D₂ appears similar to a closed state (2AC₂) that accounts for intraburst closures in a model of GABARs from spinal cord neurons (Twyman et al., 1990). 2AC₂ is analogous to D₂ because it also causes closures from the most probable open state (O₂) and has coarsely similar entry and exit rates. These observations support the notion that dominant states identified in this study are a subset of those described by Twyman et al. (1990).

Slow GABAR desensitization has been reported previously (Celentano and Wong, 1994; Jones and Westbrook, 1995; Haas and Macdonald, 1999). The associated long-lived desensitized state may play a tonic inhibitory role at GABAergic synapses (Brickley et al., 1996; Overstreet et al., 2000) and is a potential drug target (Bai et al., 1999). Our model lacks a monoliganded slow desensitized state (D_slow) in contrast to Jones and Westbrook (1995), which would manifest in FL* values as an additional GABA-sensitive component and produce increasing null sweeps at lower agonist concentrations. Neither is apparent in our FL* data, but a minor contribution by such a mechanism cannot be excluded. D_slow appears similar to D₃, which accounts for null sweep grouping and amplitude decrement of macroscopic currents during pulse trains. Model simulations show that a brief high concentration GABA pulse causes 20% of resting channels to enter D₃, although it is distal to O. Our FL* results suggest that D₃ is doubly liganded, on the basis of the above arguments. However, D₃ adjacency to O is arbitrary because similar model behavior can be achieved when D₃ adjoins D₂ and other rates are adjusted slightly. Other connectivity is possible as long as D₃ is doubly liganded. D₃ is consistent with previous reports of slow GABAR desensitization (Celentano and Wong, 1994; Bai et al., 1999; Haas and Macdonald, 1999).

Haas and Macdonald (1999) proposed gating models to account for subunit-dependent, divergent GABAR activity. The authors adapted a previous model (Twyman et al., 1990) to address desensitization. For α1β3δ GABARs, two open states connected to two nonconducting states and a separate slow desensitized state were required. For α1β3γ2L GABARs, the model needed three open states, each connected to three nonconducting states, and three desensitized states. Clearly, quantitative models differ for receptors with different subunits. However, studies of GABARs with closely related subunit compositions [α1β1γ2 and α2β1γ2 (Lavoie et al., 1997) or α1β2γ2 and α3β2γ2 (Gingrich et al., 1995)] suggest that a difference in the binding affinity for GABA could account for quantitative differences between these receptors.

Dual fast desensitized states

Our modeling efforts indicated an important role of dual fast desensitized states in determining peak open probability and consequently synaptic efficacy (Fig. 8). However, our simulatedP_max of ∼0.3 is less than previous reports for GABARs, with values of ∼0.6 (Newland et al., 1991; Jones and Westbrook, 1995). The low P_maxobserved here is explained by channels delayed in D₁ during activation and rapid desensitization of open channels to D₂. We were concerned that the rapid desensitization observed in our preparation may be anomalous. We quantified the time course of fast desensitization by fitting a multiexponential function to mean ensemble current averages (0.5 mm GABA: τ_fast = 4.1 msec, 0.77 relative amplitude; data not shown), because fast desensitized states are reflected in rapid macroscopic desensitization. These findings are similar to those from recombinant rat α1β3γ2 receptors (1 mm GABA: τ_fast = ∼8 msec, ∼0.5 relative amplitude) (Haas and Macdonald, 1999) and human α1β1γ2 receptors (1 mm GABA: τ_fast = 12.4 msec, 0.5 relative amplitude) (McClellan and Twyman, 1999), which point to similar underlying microscopic gating. Jones and Westbrook (1995)reported slower rapid desensitization (10 mmGABA: τ_fast = 81 msec, 0.26 relative amplitude), which accords with the divergence inP_max arising from differences in fast desensitization. This may arise from variations in subunit composition or factors that are unique to either recombinant receptors or ex vivo receptors from native cells in culture.

Jones and Westbrook (1995) suggested an important role of desensitized states in shaping IPSC relaxation. Desensitized states affected synaptic efficacy by prolonging the charge transferred during an IPSC. Our results point to a second important mechanism by which desensitization influences synaptic efficacy: dual modes of fast desensitization modulate peak open probability and therefore the peak of IPSCs.

This work demonstrates the powerful utility of first latency and conditional open probability analysis in identifying dominant states and connectivity that underlie the kinetics of GABAR opening and closing. We add this approach to those already applied to probe GABAR gating (Weiss and Magleby, 1989; Twyman et al., 1990; Maconochie et al., 1994; Jones and Westbrook, 1995). In combination with site-directed mutagenesis, these analyses could yield the structural basis for transition rate constants and provide insight into the mechanism of clinically relevant drugs. Finally, these results provide new information regarding dominant GABAR gating induced by transient GABA and extend earlier findings regarding gating underlying the time course of IPSCs.