Long-Range Synchrony in the γ Band: Role in Music Perception

Abstract

Synchronization seems to be a central mechanism for neuronal information processing within and between multiple brain areas. Furthermore, synchronization in the γ band has been shown to play an important role in higher cognitive functions, especially by binding the necessary spatial and temporal information in different cortical areas to build a coherent perception. Specific task-induced (evoked) γ oscillations have often been taken as an indication of synchrony, but the presence of long-range synchrony cannot be inferred from spectral power in the γ range. We studied the usefulness of a relatively new measure, called similarity index to detect asymmetric interdependency between two brain regions. Spontaneous EEG from two groups—musicians and non-musicians—were recorded during several states: listening to music, listening to text, and at rest (eyes closed and eyes open). While listening to music, degrees of the γ band synchrony over distributed cortical areas were found to be significantly higher in musicians than non-musicians. Yet no differences between these two groups were found at resting conditions and while listening to a neutral text. In contrast to the degree of long-range synchrony, spectral power in the γ band was higher in non-musicians. The degree of spatial synchrony, a measure of signal complexity based on eigen-decomposition method, was also significantly increased in musicians while listening to music. As compared with non-musicians, the finding of increased long-range synchrony in musicians independent of spectral power is interpreted as a manifestation of a more advanced musical memory of musicians in binding together several features of the intrinsic complexity of music in a dynamical way.

Widespread oscillatory activity, particularly in the γ range (>30 Hz) has attracted the attention of researchers studying different cognitive phenomena in human and mammalian species (for review, see Basar-Eroglu et al., 1996;Tallon-Baudry and Bertrand, 1999). Synchronous 40 Hz oscillations, found in the olfactory system of the rabbit (Freeman, 1978), were supposed to play a key role in the detection of different odors (Freeman and Skarda, 1985). Furthermore, spatially distributed cells in the visual cortex of both the anesthetized (Gray et al., 1989) and the alert cat (Gray and DiPrisco, 1997) produced oscillations in the γ band in response to visual stimuli. Evidence of precise phase locking across different cortical areas with zero phase lag in this frequency range was also reported in alert cats during visual discrimination task (Roelfsema et al., 1997). In humans, transient phase locking at ∼40 Hz generated in the contralateral and parietal cortical areas was found during selective attention (Desmedt and Tomberg, 1994). It has been postulated (Bressler et al., 1993; Tallon-Baudry et al., 1998) that the γ band serves as a mechanism for the visual representation of objects and as a means of “binding” various intricate aspects of object perception into a unitary whole. These interpretations are supported by observations that have shown enhanced 40 Hz activities during the perception of multistable figures (Keil et al., 1999) and animated unstable human postures (Solbounov et al., 2000). Recently, it has been demonstrated that binding-related γ oscillations are also produced in the brain of 8-month-old infants during the perception of illusory figures (Csibra et al., 2000).

So far, most of the researches investigating the role of the γ band were concentrated on visual tasks, whereby only few attempts were made with other cognitive tasks (Jokeit and Makeig, 1994; Joliot et al., 1994). Furthermore, more attention was paid to the detection of the γ oscillations, whereby the functional relationships between distant multiple cortical areas were not considered. It has been demonstrated that during a face recognition task neuronal assemblies not only synchronize locally in the γ range but are also locked in phase across distances without any time lag (Rodriguez et al., 1999). Coherence in the γ range was also enhanced between two regions of the brain receiving two classes of stimuli involved in an associative-learning procedure in humans (Miltner et al., 1999). Recently, Haig et al. (2000) reported the occurrence of a significant late poststimulus γ-synchrony response for task-relevant stimuli, whereas for task-irrelevant stimuli no such response was found. All these results indicate that synchrony in the γ band provides important insight into the understanding of the cognitive functioning of our brain.

The main goal of this paper was to examine, under the presumption of a binding function of the γ band, (1) whether differences in the γ-band synchrony with respect to the EEG at rest may also be found in listening tasks (listening to text or to music) in groups of musicians and non-musicians, and (2) whether differences can be found in the degree of the γ-band synchrony between these two groups. Our hypothesis was that if the γ band serves as a binder also in the auditory category, the degree of long-range synchrony should be significantly higher in musicians than non-musicians while listening to music, whereas no large differences should exist between these two groups for other conditions such as listening to text or at rest.

MATERIALS AND METHODS

Experimental methods. Twenty male subjects belonging to two broad groups: musicians (10 subjects with mean age of 25.7 years and at least 5 years of musical education on any instrument) and non-musicians (10 subjects with mean age of 25.4 years without any musical education) were chosen for this study. All subjects were right-handed and gave consent before the recording. The subjects were instructed to listen for 5 min attentively to a piece of music composed by J. S. Bach (French Suite No. 5 for Harpsichord, Gigue: the piece was not familiar to the subjects), and to a text of neutral content (a short story, “Versuendigung gegen die Nachwelt” by H. Weigel, read by C. Hoerbiger, 2 min). Periods of EEG at rest with eyes closed and with eyes open were recorded before, between, and after each task. Eyes were closed during both listening tasks.

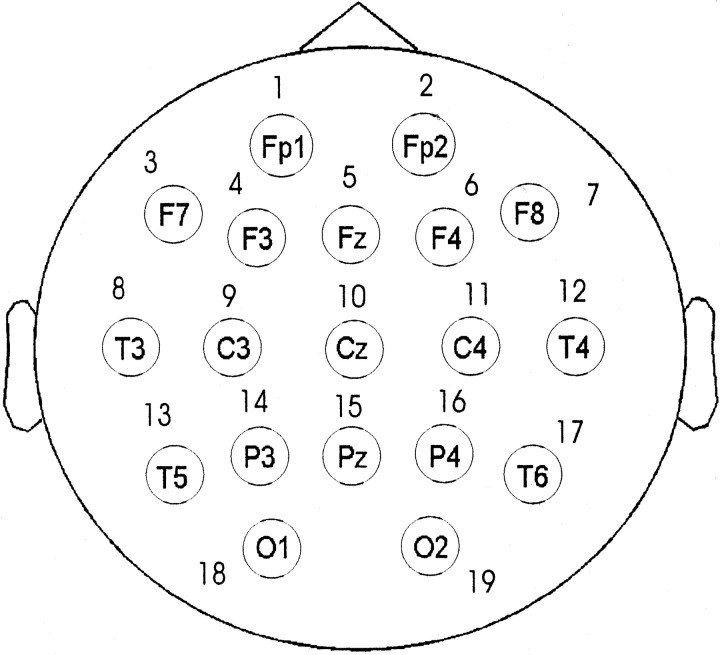
Nineteen gold-cup electrodes (Fp1, Fp2, F7, F3, Fz, F4, F8, T3, C3, Cz, C4, T4, T5, P3, Pz, P4, T6, O1, and O2 numbered as 1, … , 19), equally distributed over the skull according to the so-called 10–20 system (Jasper, 1958), were placed (Fig.1). EEG signals were recorded with respect to the averaged signals from both earlobes. Sampling frequency was 128 Hz, and analog-to-digital precision was 12 bit. For each task as well as for resting conditions, 90 sec of EEG data, visually free from eye-movement artifacts, were considered. Every signal originating from an electrode was first normalized to zero mean, and a second order polynomial was fitted and subtracted from the original signal to remove any baseline drift. Because we were interested in the γ band, the mean and polynomial subtracted signal was bandpass filtered using a sixth-order Butterworth filter with cutoff frequencies of 30 and 50 Hz. Here, the γ band is regarded as the signal lying strictly between 30 and 50 Hz (Galambos, 1992). In this notion, the oscillations in the γ band represent a brain state, which can be operationally distinct and separable, although the brain might be simultaneously active in other modes.

Fig. 1.

Spatial positions of the 19 electrodes and their designations according to the International 10–20 electrode placement system (Jasper, 1958).

Classical analysis of synchrony. Traditionally, correlation and magnitude squared coherence are the two most commonly used measures to detect synchrony in neurophysiological signal analysis. Let {x(k)} and {y(k)} be two EEG signals from two electrodes. The cross-correlation or covariance between these two signals is:

$$c_{x,y}=\frac{1}{N} \sum _{k=1}^N(x(k)-x_m)(y(k)-y_m)$$ Equation 1

where N is the length of each signal, andx_m andy_m are the mean values of {x(k)} and {y(k)}, respectively. A non-vanishing value of c indicates a linear dependency between two signals, but the opposite conclusion is not always true. The counterpart of covariance in frequency domain is coherence, which measures the linear association in specific frequency range. To obtain the coherence λ_x,y, one has to estimate the following:

$${\lambda }_{x,y}^2(f)=\frac{\Vert P_{\text{xy}}(f){\Vert }^2}{\langle P_{\text{xx}}(f)\rangle \langle P_{\text{yy}}(f)\rangle }$$ Equation 2

whereP_xx(f) andP_yy(f) are the power spectra of the two signals, andP_xy(f) is the cross-spectrum between two signals. To increase the confidence level of coherence estimation, several epoch lengths must be averaged. Generally speaking, coherence measures the phase consistency of the two signals as a function of frequency: at frequency f,λ_x,y = 1 indicates that the two signals maintain the same phase difference in every epoch, whereas λ_x,y = 0 indicates that the phase difference varies from epoch to epoch. However, it has been shown that coherence is not a reliable indicator of phase coupling, and the value of coherence can be low even when the phases of two systems are synchronized (Lachaux et al., 1999; Rosenblum et al., 2000). Furthermore, both of these measures (covariance and coherence) are symmetric and can detect only linear dependencies. To determine the asymmetric nature of interaction between different cortical areas, a relatively new measure, called similarity index (SI), based on dynamical system theory (the foundation of nonlinear time series analysis) has been used (Arnhold et al., 1999). The method is briefly sketched later. For comparison, the results based on coherence have also been included in this study.

SI. The construction of state space trajectory is an important step in nonlinear time series analysis (Takens, 1981). Because one has only indirect access to the original dynamical system itself (i.e., the brain) through the time series (i.e., EEG), one has to reconstruct a suitable state space for the original system from the time series to characterize the underlying dynamics. By using the method of delays based on the embedding theorem (Takens, 1981; Sauer et al., 1991), it is possible to obtain a set of reconstructed state space vectors x(k) = [x(k),x(k − τ), … , x(k − (m − 1)τ)], where m and τ are embedding dimension and time delay, respectively. For a smooth one-to-one mapping between the reconstructed and the original state space, the embedding theorem requires m ≥ (2d_f + 1), where d_f is the box counting or fractal dimension of the original state space. The values ofm and τ can be estimated from the time series by different methods (Kantz and Schreiber, 1997). Once the state space vectors are constructed for the two signals {x(k)} and {y(k)}, for each state space vector pairx(k) and y(k), theirR nearest neighbors are chosen from their individual state spaces. Nearest or true neighbors means that the Euclidean distances between x(k) and these vectors are smaller than the distance between x(k) and any other state space vector. Let the time indices of such nearest neighbors in two state spaces be denoted asr_k(i) ands_k(i), i = 1,… , R, respectively. The squared mean distance from these neighbors is given by:

$$D_k^R(x)=\frac{1}{R} \sum _{i=1}^R\parallel x(k)-x(r_k(i)){\parallel }^2$$ Equation 3

Accordingly, the set of mutual neighbors ofx(k) are those vectorsx(s_k(i)) that bear the time indices of the R nearest neighbors ofy(k). The conditional distance can be defined as:

$$D_k^R(x\Vert y)=\frac{1}{R} \sum _{i=1}^R\parallel x(k)-x(s_k(i)){\parallel }^2$$ Equation 4

Should the two signals be identical, both sets (true and mutual) of neighbors are equal; increasing differences between the two sets of neighbors imply weaker relationship between the two signals. For independent systems,D ${}_{\text{k}}^R$(x y) >>D ${}_{\text{k}}^R$ (x), whereas for strongly dependent systemsD ${}_{\text{k}}^R$(x y) ≈D ${}_{\text{k}}^R$ (x). Therefore, the assessment of the interdependence consists in quantifying the difference between both sets of neighbors. This is usually performed by means of an index that measures the similarity or dissimilarity between all vectors and their corresponding true and mutual neighbors. The similarity between the local geometry of the state spaces can be computed as:

$$S^R(x\Vert y)=\frac{1}{N} \sum _{k=1}^N \frac{D_k^R(x)}{D_k^R(x\Vert y)}$$ Equation 5

We call this measure SI. In an analogous way,S^R (y‖x) is also computed. The higher the values of S^R(x‖y) and S^R(y‖x), the stronger is the degree of synchrony or interdependency, i.e., the connectivity between the two systems is strongly bidirectional. If S^R(x‖y) < S^R(y‖x), the system associated with signal {x(k)} has more influence on the system associated with signal {y(k)} than vice versa. By this way, the nature of asymmetric coupling can be represented. If one system is found to exert more influence on the other, the former possesses higher complexity or higher degrees of freedom. It is to be noted that the similarity index is sensitive only to those degrees of freedom, which operate in the amplitudes of the order of mean distances (Eqs. 3, 4) in the state spaces. This index has been found to be useful for simulated models (Schmitz, 2000) and also for real life signals (Pereda et al., 2001).

For each task as well as for resting conditions, the record of 90 sec EEG was divided into 15 nonoverlapping windows; for each window,S (Eq. 5) was computed for all possible combinations of electrodes; their values were stored in a 19 × 19 matrix, which may be asymmetric. These 15 matrices were further compared statistically as described later. In this study, we have chosen the following embedding parameters: embedding dimension (m) = 10 (time samples), time delay (τ) = 2 (time samples), and the number of true (and mutual) neighbors (R) = 10.

The method of obtaining similarity index is graphically represented in Figure 2. For the sake of clarity, only one reference vector (x(k) or y(k)) is chosen from two individual state spaces. It is clear that the true neighbors always resemble the reference vector in terms of similarity in pattern, whereas the patterns of mutual neighbors may or may not be similar depending on the degree of interdependency.

Fig. 2.

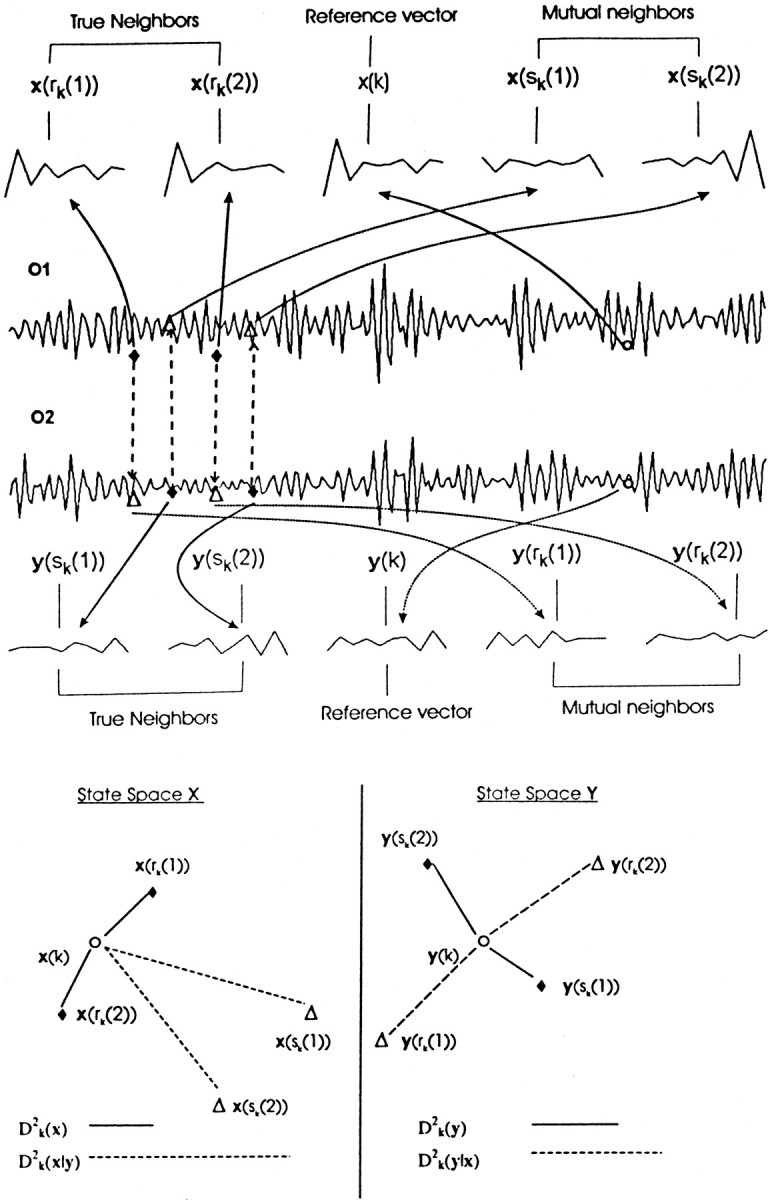
Top, Pictorial descriptions of true and mutual neighbors. Two simultaneous EEG epochs filtered in the γ band (1.8 sec each) of two channels (O1 and O2 represented by system x and y, respectively) for a musician while listening to music. For a reference vector (o), the nearest or true neighbors (filled diamonds) and mutual neighbors (open triangles) are shown. For the sake of clarity only two vectors (r = 2 in Eq. 3and 4) are used. For the reference vector x(k), its nearest neighbors are x(r_k(1)) and x(r_k(2)), whereas for the simultaneous reference vector y(k), its two true neighbors (filled diamonds) are y(s_k(1)) and y(s_k(2)). The mutual neighbors of x(k) are those vectors x(s_k(1)) and x(s_k(2)) (open triangles) simultaneous to the nearest neighbors of y(k), which consequently bear the same time indices. In an analogous way, the mutual neighbors of y(k) are y(r_k(1)) and y(r_k(2)). All these vectors are shown with the reconstruction parameters m = 10 andτ = 2. Bottom, The reconstructed state spaces of X and Y, in which both the actual (solid lines) and conditional (dashed lines) distances are displayed for comparison. Similarity index S (Eq. 5) for x(k) is simply the ratio between both distances. In the top half, note that the pattern for x(k) is similar to that of its nearest neighbors but does not match that of its mutual neighbors; this fact is more prominent in distance measures. For this chosen example,D²_k(x‖y) >D²_k(y‖x) which leads toS(Y‖X) > S(X‖Y), i.e., X has more influence on Y than vice versa. We would like to emphasize that this index has to be calculated for all possible reference vectors and finally averaged to get the final value of similarity index.

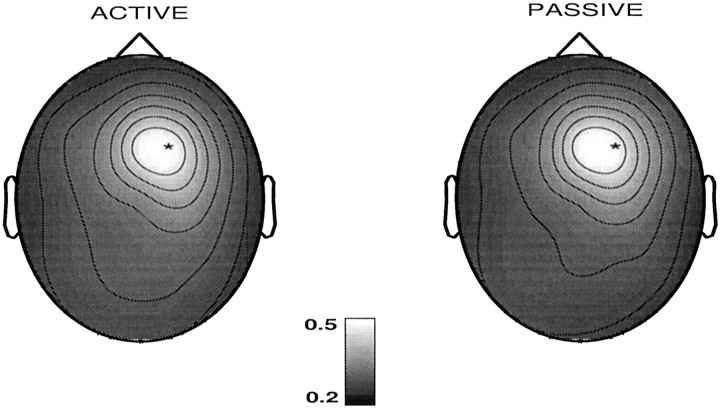
Figure 3 describes the scalp maps for the SI of electrode F4 in a musician (Vp. 632) while listening to music. For this subject, the influences between this electrode region and the other electrode regions are mainly symmetric, the active and passive regions being quite similar. The strong interdependencies between F4, C4, and Fz are also evident.

Fig. 3.

Scalp maps of the similarity indices for one electrode F4 (marked by the asterisks) for a subject (musician) while listening to music. Left, The electrode region was considered as active or influencing other electrode regions (S(j‖F4), j = 1, … , 19). Right, The electrode region was considered as passive or being influenced by the other electrode regions (S(j‖F4)).S(F4‖F4) is set to the mean of the maximum and minimum of S values in each plot for better visual clarity.

Spatial synchrony. To measure the global spatial synchronization, a linear complexity measure was used (Wackermann, 1999). Nineteen EEG channels ({x₁(k)}, {x₂(k)}, … . , {x₁₉(k)}), filtered in the γ band, are stacked column-wise to form a multichannel EEG matrix of size N × 19, where N is the number of time samples. Each row (u_k) of this matrix corresponds to the vector representing the spatial distribution of the γ-band signal over the entire scalp at the kth instant of time. The covariant matrix (of size 19 × 19) of the multichannel EEG matrix is formed as:

$$C=\frac{1}{N} \sum _{k=1}^N u_k^T{u}_k$$ Equation 6

The eigenvalues {ε₁, ε₂, … , ε₁₉} (Golub and Van Loan, 1996) of the symmetric positive semidefinite matrix C are computed and subsequently normalized as:

$${\xi }_i={\epsilon }_i/\sum _i{\epsilon }_i(i=1,\dots ,19)$$

The complexity measure Ω is defined as follows:

$$log\mathrm{\Omega }=\sum _{i=1}^{19} {\xi }_{i}log{\xi }_i$$ Equation 7

Ω approximately quantifies the amount of spatial synchronization over the entire scalp and is closely related to the intrinsic dimensionality (Fukunaga, 1990). Ω varies from 0 for a one-dimensional distribution (all channels are completely correlated yielding perfect synchrony) to 19 for identically distributed white noise (no correlation between channels corresponding to the absence of synchrony). Thus, the degree of spatial synchronization decreases monotonically with increase of Ω. Here, Ω was computed for data window of 6 sec with overlapping segment of 3 sec.

Statistical analyses. To compare the values of similarity indices between the two groups, we have performed a normalization procedure, where the indices for non-musicians are considered as reference. For example, {S_nm(j‖i)} is the set of values of SI between electrode pairs i and jconsidering the influence of the ith electrode on thejth electrode for the group of non-musicians (in this study, each set associated with every electrode pair contains 150 values (10 subjects × 15 windows)); let μ_nm(j‖i) and u_nm(j‖i) be the mean and variance of the set {S_nm(j‖i)}. Say, the SI for an identical electrode pair for a musician isS_m(j‖i); the relative synchrony of interdependency value is computed as:ς(j‖i) = (S_m(j‖i) − μ_nm(j‖i))/√u_nm(j‖i). If ς(j‖i) > 2.33, it can be inferred that the degree of interdependency between electrode pairi and j, assuming the ith electrode influencing the jth electrode, is higher in musicians than non-musicians with >99% statistical significance (Theiler et al., 1992); for ς(j‖i) < −2.33, the interdependency is significantly higher in non-musicians. In a similar way, ς(i‖j) can also be obtained considering the influence of the jth electrode on theith electrode. If any electrode is found to exert influence on many other electrodes, that electrode is considered to be acting as a diverging (differentiating) node, whereas if it is influenced by many other electrodes, it is considered as a converging (integrating) node. In this way, a comprehensive insight into the underlying differentiation and integration properties of cortical areas associated with each electrode location can be obtained.

EEG at rest with eyes closed (no-task or baseline condition) was also considered in this study. To find the change in interdependency pattern while listening to music or text as compared with rest, paired Wilcoxon test is applied to find statistical differences between the values of SI of task conditions (listening to music or listening to text) from no-task condition. The level of significance is set to 99% (p < 0.01). Thus, by measuring the degree of differences between groups and/or tasks and not highlighting the absolute values of S, interdependency between near and distant electrode regions can be treated in an equivalent way.

RESULTS

Power analysis

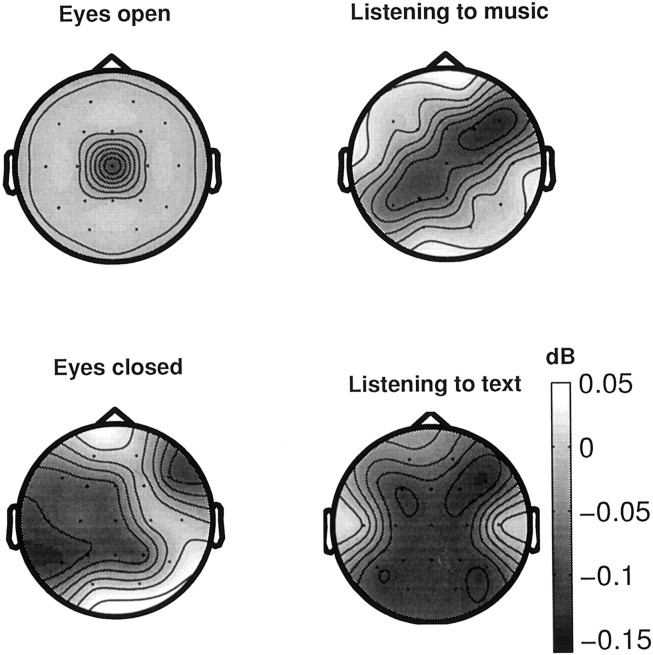
Power in the γ band is obtained by estimating power-spectral density of each signal by using a fast Fourier transform algorithm (Matlab; MathWorks Inc., Natick, MA) and averaging over overlapping windows of 3 sec with overlapping segment of 1 sec. When spectral power is compared (paired Wilcoxon test, significance level; p < 0.05) between task and baseline (eyes closed) conditions within each group, posterior electrodes are mainly found to be significant for both tasks in both groups. Figure4 shows the difference (musicians vs non-musicians) in scalp maps of power spectra in the γ band between the two groups in different states. An overall tendency toward higher spectral power for non-musicians as compared with musicians has been found. C4 showed higher power in non-musicians while resting with eyes open, whereas several cortical regions, mostly in the left hemisphere (F7, F3, T3, C3, T5, P3), showed significantly higher γ-band power at rest with eyes closed. While listening to music, enhancement of power in non-musicians was obtained for electrodes F4, F8, Cz, P3, and T3. The most significant increases of power in non-musicians as compared with musicians occurred while listening to text: except temporal electrodes (T3 and T4), all other electrodes showed large and significant increase of power in the γ band in non-musicians.

Fig. 4.

Scalp topographies of the γ band spectral power differences (expressed in decibels) between musicians and non-musicians during no-task (eyes open and eyes closed), and task (listening to music and to text) conditions. Results were averaged over overlapping windows and subjects within each group. Nonsignificant differences (set to zero) appeared in light gray. At rest with eyes open, spectral power was higher in non-musicians only in central electrode; when eyes were closed at resting conditions, γ band power was higher for multiple electrode regions (except frontal and occipital electrodes) in non-musicians. For task conditions, spectral power was higher (more black) for various electrode locations in non-musicians as compared with musicians; this effect was even more pronounced while listening to text.

Differences in interdependencies between the two groups

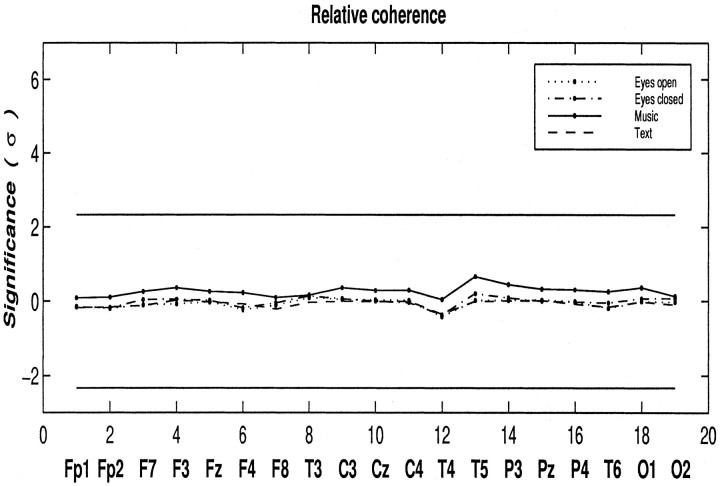
Coherence values (Eq. 2) in the γ band are computed between all possible combinations of electrodes. The segmentation scheme is the same as for power analysis. Because no consistent peaks of coherence are observed, the mean coherence for the entire γ band is used for statistical analysis. Figure 5 shows the relative γ band coherence expressed in ς for musicians as compared with non-musicians. Although the musicians show weak tendencies to higher coherence than non-musicians only while listening to music, no significant differences are found between the two groups in the degree of coherence values in any state (task or no-task).

Fig. 5.

Degree of the relative γ band coherence, expressed in ς for musicians relative to non-musicians at different states: eyes open (dotted line), eyes closed (dash–dot line), listening to music (solid line), and listening to text (dashed line), respectively. The two horizontal lines denote the level of significance (p < 0.01). No significant differences are evident between the two groups. Coherence is slightly but not significantly increased in musicians while listening to music.

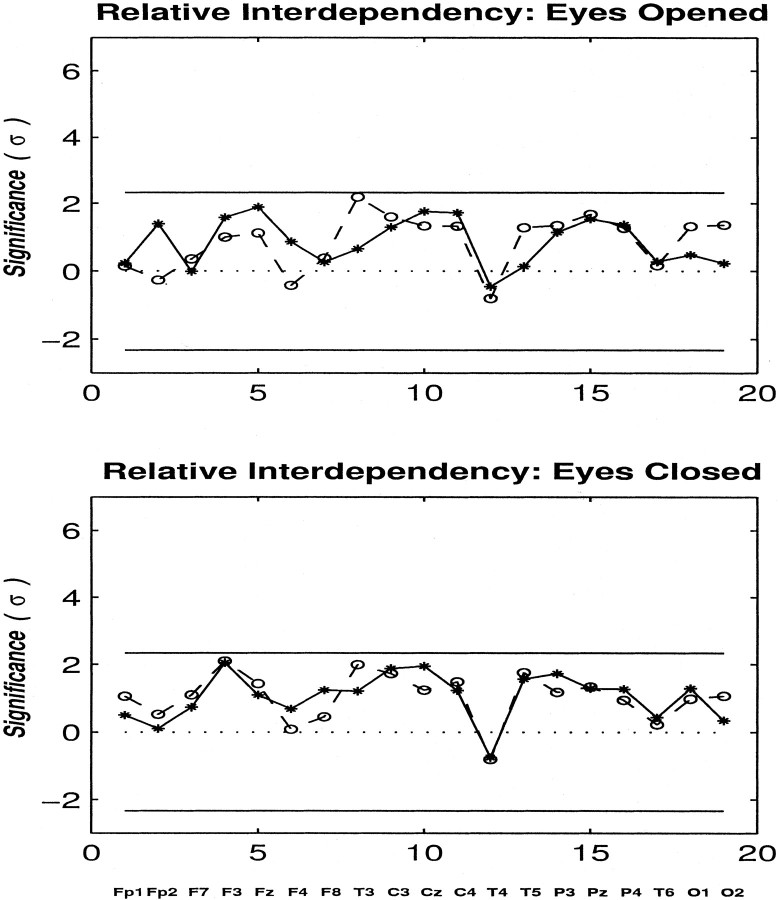
Figure 6 shows the relative interdependencies (measured by SI) in units of ς for musicians as compared with non-musicians in both resting conditions, eyes closed and eyes open, respectively. As described in the previous section,S (Eq. 5) is asymmetric, thus, each electrode has two characteristics: the ability of influencing others and the ability of being influenced by others. The two profiles depicted in each figure show the averages of these two features for each electrode region. Degrees of asymmetry (although not significant) are higher during opened than closed eyes. Thus, no significant differences in the values of S are found between the two groups. This fact may be expected because musical training, by common sense, should not produce higher (or lower) degrees of interdependency in the brain when no task was apparently involved.

Fig. 6.

Profiles showing the degrees of relative interdependencies (in units of ς) in the γ band for musicians relative to non-musicians at resting conditions: with eyes open (top) and eyes closed (bottom). Results were averaged over windows, subjects within each group, and for all possible electrode combinations for each electrode. For profile connected by an asterisk, significance level was computed while assessing the degree of influence of each electrode region on other electrode regions (“diverging node”). The other profile connected by an open circle exhibits the average property of each electrode considering it being influenced by others (“converging node”). The two horizontal lines (ς = ±2.33) represent the line of significance (p < 0.01) i.e., any entry above the higher line indicates that the degree of interdependency in musicians is significantly higher than non-musicians and any entry below the lower line indicates higher interdependency in non-musicians. No significant differences were found between the two groups at resting conditions.

Analogous profiles are shown in Figure7 while both groups were listening to music and to text. Interestingly, several cortical regions associated with multiple electrode locations (F3, Fz, F4, C3, Cz, C4, T5, P3, Pz, T6) are found to be highly significant for musicians while listening to music. In particular, right midfrontal (F4) and frontobasal cortical regions (F8) exhibit more influences on other cortical regions in musicians (“diverging nodes”). Midline posterior parietal regions (Pz) act more as passive zones (“converging nodes”), which are likely to be influenced by various cortical regions. On the other hand, the values of ς are found to be nearly zero for all electrodes while listening to text. Thus, no significant differences in the degree of interaction in the γ band between musicians and non-musicians are found during listening to text.

Fig. 7.

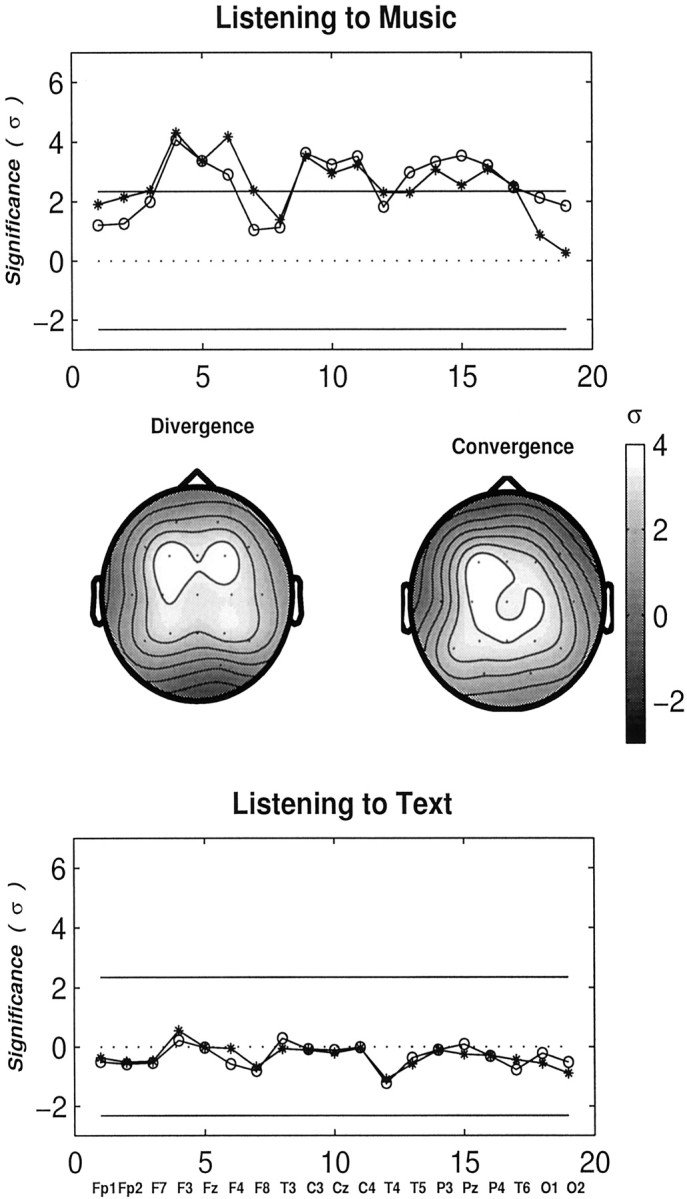
Profiles showing the degrees of relative interdependencies (in units of ς) in the γ band for musicians relative to non-musicians at task conditions columns: listening to music (top), and to a text of neutral content (bottom). Symbols are the same as in Figure 6. Large and significant increases in long-range synchrony in the γ band over multiple electrode regions are found in musicians while listening to music, particularly in and near midline regions. These profiles are also presented as scalp maps exhibiting the two different attributes (convergence and divergence) of individual electrode regions. ς is coded from black to white as the value increases. Text processing does not produce any difference between the two groups.

Differences in interdependencies between task and no-task conditions

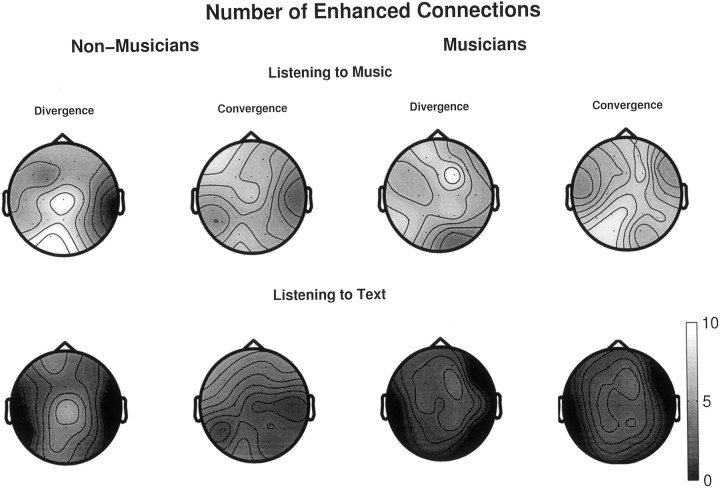
Earlier figures have clearly shown the enhanced degrees of interdependencies between various cortical regions in musicians while listening to music. As compared with resting conditions, attentively listening to music (or to a text) is a higher cognitive task that calls for enhanced coordination between several brain regions even for a naive listener. To obtain more insight into the possible transfer of information between brain regions, the values of S (Eq. 5) are statistically compared between task and resting condition, and the total number of electrode pairs with significantly higher S, which are involved at task condition, are plotted in Figure8 as scalp maps. These maps or topographies show the average activity of each electrode region where averaging is done over all possible combinations of pairs of electrodes and over subjects within each group (here, the statistical comparison between task and no-task condition was initially performed for each subject and finally averaged). In spite of these grand-averaging, several noteworthy features are found: (1) for both groups, listening to music produced higher degrees of interdependency reflected in a larger number of enhanced electrode pairs than listening to text, (2) the degree of asymmetry of the profiles is higher in non-musicians than in musicians: in non-musicians, frontal regions are found to be more passive, whereas posterior regions are found to be more active for both tasks. The fact that both groups have comparable numbers of enhanced connections for listening tasks might seem contradictory at first sight because the degree of S has earlier been shown to be significantly higher for musicians. But in comparing the connectivity pattern of task condition with respect to resting condition, various levels of significance (i.e., p < 0.01 orp < 00.001) were treated in a similar fashion. Thus, both cognitive tasks have produced significant effects in the cooperation among cortical areas in both groups, yet the level of significance is much higher for musicians while listening to music but not while listening to text.

Fig. 8.

Scalp maps for both groups showing the numbers of connections (electrode pairs) associated with each electrode with significantly higher values of S while listening to music and to text as compared with the values of S at rest with eyes closed. Here also, the scalp maps of the two different attributes (divergence and convergence) of individual electrode regions are shown. For both groups, listening to music produced higher synchronization than listening to text. However, the degree of asymmetries of several cortical regions, especially in frontal and occipital regions while listening to music, is higher for non-musicians than musicians.

Spatial synchrony

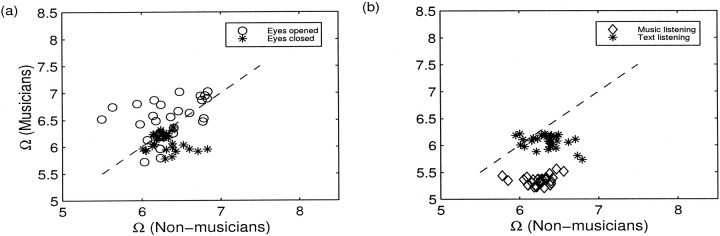
The degree of spatial synchrony (Ω as described by Eq. 7) or the overall linear independency is plotted in Figure9 for both groups for all time windows. While listening to music, a clear separation is evident between the two groups, where the degrees of spatial synchrony, reflected by the low values of Ω, are much higher in musicians. Also, the resting state with eyes open is associated with higher Ω than with eyes closed. Interestingly, musicians show an overall tendency toward higher spatial synchronization (lower values of Ω) except during eyes open condition.

Fig. 9.

Scatter plots of the measure of spatial synchrony Ω for two groups for resting conditions with eyes closed (asterisks) and eyes open (open circles) (a), and task conditions while listening to music (open diamonds) and to text (asterisks) (b). Ω was computed with overlapping window length of 6 sec, which overlaps over 3 sec; the abscissa and ordinate of each entry represent the value of Ω of each time window for non-musicians and musicians, respectively. Thediagonal indicates the line of equality between two groups. Note the clear separation in the degree of spatial synchronization between the two groups while listening to music: musicians have significantly lower Ω, implying higher spatial synchrony.

DISCUSSION

In this study, the degree of interdependency between distributed cortical regions has been assessed primarily by a measure (SI) based on nonlinear dynamical system theory. This measure has the inherent capability of detecting asymmetric coupling, whereas the commonly used measures to detect hidden synchrony are usually symmetric. The degree of the γ band long-range synchrony has been measured in subjects while listening to music, to text, as well as at rest with no-task involved.

Power analysis

Apart from questions of mutual dependencies, the power spectrum of musicians versus non-musicians was examined as an indicator of the degree of the local involvement of brain regions. The major finding in this respect was the higher γ power in non-musicians as compared with musicians over several electrode regions. Generally, an increase in spectral power at an electrode location can be attributable to an enhancement of local increased in-phase activity of neuronal assemblies or to the recruitment of additional synchronous neuronal populations (Srinivasan et al., 1999). Across local synchronization, interdependency measures such as SI can detect long-range synchronization between distant brain regions. In non-musicians, local increase in spectral power was accompanied by a decrease in interdependency; thus, neuronal assemblies were involved more locally, whereas, at the same time, they were functionally less connected with distant brain regions. Therefore, the spectral power is not an appropriate indicator of the degree of long-range synchronization, which seems to be an essential requirement for the performance of various cognitive tasks (Bressler et al., 1993; Miltner et al., 1999).

Interdependency analysis and the role of the γ band synchrony

In interdependency analysis, the following main observations were made: (1) the degrees of interdependencies were increased under task with respect to no-task condition; (2) the degrees of interdependencies or the strength of coupling between distributed cortical areas were significantly higher in musicians while listening to music. These increases were found over multiple cortical areas; and (3) no differences in the degree of interdependency were found between the two groups while listening to text or at resting conditions.

A growing body of literature (Singer and Gray, 1995; Tallon-Baudry and Bertrand, 1999 and references therein) suggests that fast (>30 Hz) oscillatory synchronization of brain areas may serve to establish dynamic relations between neuronal assemblies; therefore, this mechanism might pave a way to the solution of the binding problem inherent to cognitive functions such as scene segmentation and object representation. In a similar way, because visual objects have many different attributes (i.e., shape, size, depth, color, etc.), that have to be integrated for realizing objects as such, any complex music has various acoustic attributes (i.e., pitch, timbre, rhythm, harmony, melody, contour, etc.). For the realization of music as a specific entity, all these acoustic attributes have to be bound in a dynamical way; every attentive listener even including a naive one performs this binding task, but subjects with professional musical training do the same in a more efficient way because of their higher ability to discriminate between different musical attributes and to mentally follow and reconstruct acoustic architectonic structures. One possible reason why the long-range γ-band synchrony was found to be higher in musicians may be attributable to their higher ability of binding musical attributes because of their professional training. Moreover, attentively listening to music is associated with anticipation: we anticipate what we already know; thus, anticipation is based on past musical memories. Therefore, a trained musician as compared with a non-musician implicitly retrieves a larger repertoire of musical patterns from his memory while listening to music, although a given piece of music is unknown to him. Listening to text, on the other hand, obviously involves similar memory contents in both groups. This view is supported by the lack of differences in the γ-band synchrony between the two groups while listening to text and under resting conditions.

Spatial synchrony

Using a linear measure of signal complexity (Ω) to characterize the spatial synchrony taking 19 channels together, it was found that musicians showed significantly higher spatial (or global) synchronization than non-musicians while listening to music. The degree of interdependency (measured by SI) was already shown to be higher in musicians for distributed cortical areas, or in another words, the cortical areas acted more independently in non-musicians. Thus, in non-musicians, brain regions were functionally more localized while listening to music i.e., they were more isolated from other brain regions; this fact was reflected in the high values of Ω revealing spatial desynchronization.

Remarks

Several critical points have to be discussed. It is well known that the γ band has much smaller amplitudes than signals in α or θ band, and there is interference with muscle activities. For the following reasons it seems unlikely that our results are caused by muscles: (1) most emphasis is put on synchrony measure rather than the raw amplitude of the signal, (2) temporal electrodes T3 and T4 are usually the most contaminated by muscles, yet the values of ς for these two electrodes are insignificant (Fig. 7), whereas significant differences were found over distributed cortical areas; thus, the enhanced γ band synchrony for musicians is even present when temporal electrodes are excluded from the study. Second, one might ask whether similar enhancement of the γ band synchrony could be found for other pieces of music. In the same group of subjects, we found that musicians have significantly higher phase synchronization than non-musicians while listening to different pieces of music, including a non-rhythmic synthesized computer music (Bhattacharya and Petsche, 2001b). So, attentively listening to any kind of music most likely results in higher interdependency in musicians than non-musicians. The correlation between selective attention and the synchronization in the γ band, mostly measured by spectral power, is well known (Sheer, 1989; Desmedt and Tomberg, 1994; Fries et al., 2001). However, it has to be noted that both groups were paying attention to both listening tasks, although differences were found only while listening to music. Third, the EEG recorded at any region of the scalp approximately quantifies the summed electrical potentials generated by postsynaptic dendritic currents from pyramidal neurons in a certain volume of tissue under the electrode. Thus, EEG does not measure dynamic processes but represents the summation of dynamical processes; on the other hand, the similarity index, theoretically, has been proposed to find the coupling between two distinct dynamical processes. Generally speaking, the possible substrates of synchrony between neuronal assemblies are the existence of groups of neurons interconnected by mutual excitatory and inhibitory synaptic connections and/or the presence of in-phase neuronal firing in different assemblies. Thus, if S between two signals from two electrodes is high, the functional integration manifested by synaptic connections or the enhanced in-phase firing between neuronal assemblies in the associated cortical regions underlying the two electrodes will also be high. In the present paper, this working scheme of interpretation has been adopted, although we think that it will be important to apply this measure on the data from unit recording to get clearer insight. Finally, the cutoff of ς was based on the assumption of a Gaussian distribution, which might not be fulfilled always, and, further, the results (Figs. 6-8) provide an average representation across electrodes. After applying a nonparametric statistical test (paired Wilcoxon) between the two groups while listening to music, 309 electrode pairs of a possible 342 electrode pairs showed significantly higher interdependency in musicians, and only nine electrode pairs showed higher interdependency in non-musicians. In this paper, the significance level was computed for all possible electrode pairs separately, and finally the results were averaged for the compaction of information; after grand-averaging, any value of ς associated with any electrode region above the significance cutoff should necessarily imply that this electrode region was strongly connected with many other electrode regions, albeit distant. Because near and distant electrode pairs were treated in an identical way, the synchronization reported here is indeed of long range. Thus, the adopted scheme of quantifying the statistical difference between the two groups is found to be reasonable, and it is most likely that the reported enhanced interdependency in musicians while listening to music is associated with functional cooperation among multiple cortical areas.

Possibilities of other significant frequency bands

Another pertinent question is whether similar results can be obtained for other frequency bands. In a parallel study, we have found that musicians showed significantly higher phase synchronization only in the γ band while listening to music (Bhattacharya and Petsche, 2001a). According to an earlier report, binding of the visual features of a complex object can be accomplished within ∼100 msec (König et al., 1995). Oscillations in the α or lower frequency ranges would be too slow to establish synchrony within the required time. On the other hand, binding cannot either be accomplished by very high frequency oscillations for the following reason: simulation studies have indicated that reciprocally coupled oscillators can be entrained when the conduction delays in the network are less than one-third of the average period time (König and Schillen, 1994), otherwise synchrony without phase lag would not be possible. Interestingly, long-range synchrony in the cortex occurs consistently with almost zero (<3 msec) phase lag (Engel et al., 1991;Roelfsema et al., 1997), whereas much greater phase lag would be expected from the slow speed of axonal conduction across the corpus callosum (Innocenti, 1980). Considering all these constraints and the coupling delays, it has been postulated that if oscillation indeed is an essential requirement for the establishment of long-range synchrony, the γ band would be the most suitable candidate for integration (König et al., 1995).

It should be noted that the mere occurrence of oscillations in the γ band, as commonly believed, should not be taken as the hallmark of underlying synchrony, rather the synchrony measures directly reflect the underlying binding process (Rodriguez et al., 1999). The mechanisms by which such coherent high-frequency oscillations are generated and subsequently synchronized are not clearly known, and no claim in this regard can be made by the data obtained by macroscopic EEG electrodes. Furthermore, the role of other frequencies in establishing this enhanced synchrony in the γ band cannot be ruled out either. Recently, in animal studies, strong phase coupling was found between the γ band and α, θ bands, which supports the hypothesis that γ band represents bottom-up processing, and lower frequencies represent top-down processing (von Stein et al., 2000). This is an objective for future researches to investigate whether similar coupling between different frequencies can also be found for music perception, which inherently calls for the integration between bottom-up and top-down processing.

Conclusion

By using a recent index to detect functional coupling, this study demonstrates that musicians' brains show significantly higher interdependency in the γ band between distributed cortical areas as compared with non-musicians while listening to music. No significant differences were found between the two groups for other conditions. The similarity index was found to be more useful in the detection of hidden functional interdependencies than classical indices like coherence. It has also been shown that long-range synchrony in the γ band contains more information than the γ band spectral power in understanding higher cognitive functioning, and furthermore, that this long-range synchrony in the γ band is not an exclusive property of visual-feature binding, as commonly believed. Instead, this synchrony could provide a platform for large-scale general cognitive integration. Finally, if our hypothesis about the potential role of long-range synchrony in high-frequency band stands correct, the enhancement in the cooperation between multiple cortical areas should be present during the performance of any higher cognitive task in which several complex attributes must be bound together to complete the task; furthermore, the degree of this enhancement should be correlated with training in similar tasks.