The Design Principles of Biochemical Timers: Circuits That Discriminate Between Transient and Sustained Stimulation

SUMMARY

Many cellular responses for which timing is critical display temporal filtering – the ability to suppress response until stimulated for longer than a given minimal time. To identify biochemical circuits capable of kinetic filtering, we comprehensively searched the space of three-node enzymatic networks. We define a metric of “temporal ultrasensitivity”, the steepness of activation as a function of stimulus duration. We identified five classes of core network motifs capable of temporal filtering, each with distinct functional properties such as rejecting high frequency noise, committing to response (bistability), and distinguishing between long stimuli. Combinations of the two most robust motifs, double inhibition (DI) and positive feedback with AND logic (PF_AND), underlie several natural timer circuits involved in processes such as cell cycle transitions, T cell activation, and departure from the pluripotent state. The biochemical network motifs described in this study form a basis for understanding common ways cells make dynamic decisions.

Graphical Abstract

eTOC BLURB

Timing is critical in biological regulation. In many cellular processes, biochemical networks can measure the duration of signaling inputs to coordinate the relative timing of cellular responses. To define biochemical circuits capable of this temporal filtering, we comprehensively searched the space of three-node biochemical networks. We identified five classes of core network motifs capable of temporal filtering with distinct functional properties and mechanisms. These core network motifs provide insight into how cells can interpret dynamic information and temporally coordinate events.

INTRODUCTION

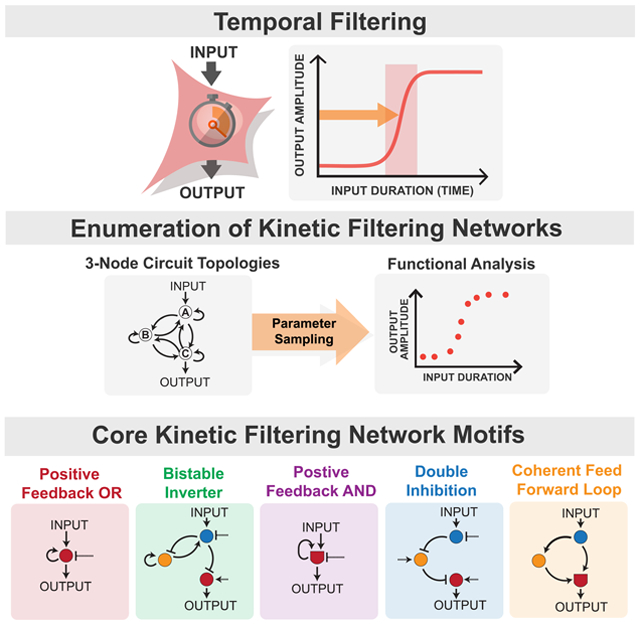
Timing is critical in biological regulation. How do cells tell time and measure the duration of events? In many processes, cells display temporal filtering or temporal thresholding -- the ability to measure the duration of time that they experience a given input, and to only respond after a given threshold duration of stimulation (Fig 1A). Closely related behavior has also been referred to as kinetic proofreading (Hopfield, 1974) or persistence detection (Mangan and Alon, 2003). Temporal filtering is important for several types of physiological behaviors. Signaling networks downstream of receptors must filter noisy, transient environmental fluctuations to distinguish them from real, more sustained signals (Hopfield, 1974). Kinetic filters can absorb and dissipate these transient inputs. Measuring stimulation time also allows cells to trigger a response to an initial cue only after a specific delay, which can be critical for coordinating the relative timing of events, especially in complex, sequential processes such as the cell cycle or development. Finally, there is increasing appreciation that biological information can be encoded dynamically, e.g. in features such as input duration or frequency (Batchelor et al., 2011; Locke et al., 2011; Purvis and Lahav, 2013; Suel et al., 2007), and cellular circuits that can measure duration of stimulation undoubtedly play a key role in interpreting and decoding this kind of more complex temporal information.

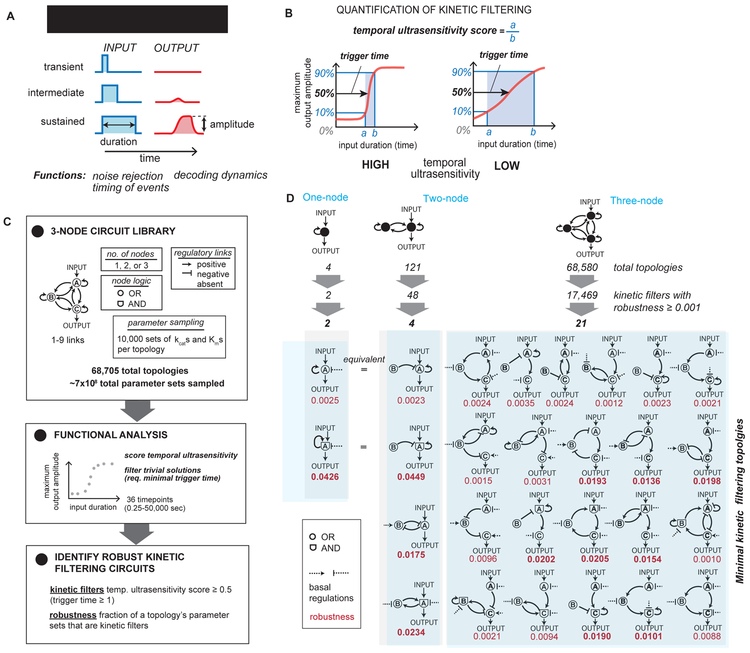
Figure 1. Enumeration of 1-, 2-, and 3-node networks finds 25 minimal kinetic filtering circuits that distinguish between transient and sustained inputs.

(A) Kinetic filtering circuits respond to sustained but not transient stimuli, allowing cells to perform time-sensitive functions. (B) Temporal ultrasensitivity score quantifies kinetic filtering by measuring steepness of activation over stimulus time, defined by taking the ratio of input duration required for 10% activation to input duration required for 90% activation. Trigger time, the duration of input yielding 50% activation, measures the duration of stimulus necessary to trigger response. (C) To identify kinetic filtering architectures, temporal ultrasensitivity score and trigger time were measured over an enumerated space of 68,705 circuit topologies and 10,000 sampled parameter sets per topology testing with 36 specific input pulse durations between 0.25 and 50,000 seconds. Parameter sets were considered to show kinetic filtering if temporal ultrasensitivity score ≥ 0.5 and trigger time ≥ 1s. A topology’s robustness is defined as the fraction of its sampled parameter sets that show kinetic filtering. See Figure S1 for details on simulating enzymatic circuits with OR and AND nodes. (D) Number of topologies, kinetic filters with robustness ≥ 0.001, and minimal kinetic filters in 1-, 2-, and 3-node networks. Minimal kinetic filtering topologies are topologies with robustness ≥ 0.001 where removal of any link decreases robustness below 0.001 (Figure S2D). Two 2-node minimal kinetic filters are topologically identical to 1-node minimal kinetic filters with regulatory node B taking the place of the basal regulator. Circuits with robustness ≥ 0.01 are indicated in bold.

How can biochemical circuits function as kinetic filters? There have been few studies that systematically explore and compare which signaling circuit architectures can kinetically filter stimuli and measure time. Although some circuits that can serve as kinetic filters have been analyzed, for many biological examples, the precise molecular circuitry or mechanism responsible for the measurement of stimulus time is not known. Some specific classes of circuits have been noted to be able to serve as kinetic filters. These include extended multistep cascades (Hopfield, 1974; Samoilov et al., 2002), as well as coherent feed forward loops that have both long (multi-step) and short branches of transmission that are simultaneously required for output (Mangan and Alon, 2003; Murphy et al., 2002). In transcriptional networks, positive feedback has also been proposed to play a role in noise suppression (Hornung and Barkai, 2008). But are these the only solutions for effective kinetic filtering? If there are more families of solutions, how do they compare with one another in terms of efficiency and various functional tradeoffs? As we begin to explore how the cell coordinates and interprets complex dynamic information, it will be important to have a road map to help identify and classify the general types of molecular circuits that will emerge.

Coarse-grained network enumeration offers a computational approach to identify classes of biochemical network architectures that can achieve a given target function (Chau et al., 2012; Lim et al., 2013; Ma et al., 2006; 2009; Adler et al., 2017; Schaerli, et al., 2014). Comprehensive, unbiased enumeration of a space of simple circuits allows identification of core solutions and evolutionary starting points for more complex networks. A set of core solutions forms the basis for understanding and cataloging natural timing circuits as well as providing blueprints for designer synthetic circuits that can measure time.

Here we apply this approach to search the full space of all possible 1-, 2-, and 3-node enzymatic networks and identify the classes of network architectures that can robustly achieve kinetic filtering. To identify kinetic filters, we defined a new metric – temporal ultrasensitivity – to measure the steepness with which activation of a system occurs as a function of increasing stimulus duration. As the name implies, temporal ultrasensitivity is an analog of concentration ultrasensitivity – the measure of the steepness of a system’s dose-response (Goldbeter and Koshland, 1981; Altszyler et al., 2016). In natural cellular processes, such as in cell cycle transitions or differentiation, the features of temporal ultrasensitivity and delayed trigger time contribute to the robustness of signaling responses (Yang and Ferrell, 2013; Trunnell et al., 2011; Wang et al., 2009). Here we find five classes of simple network motifs that can achieve kinetic filtering, including the previously characterized coherent feed forward loop (Mangan and Alon, 2003; Mangan et al., 2003). Two of these motifs can be optimized to yield kinetic filters with both sharp temporal ultrasensitivity and long trigger time (duration of input required for half-maximal response). In contrast, the other motifs identified can robustly achieve high temporal ultrasensitivity only at a lower range of trigger times. We identify key mechanistic properties that allow for longer trigger times while retaining sharp activation dynamics.

These findings and the tradeoffs associated with each class of motif suggest particular functional roles of each subtype. Convergent motifs among natural kinetic filters responsible for cell cycle transition circuits and T cell activation among other functions is a combination of the two most robust classes uncovered in our search, which are predicted to combine both long, tunable trigger times with committed, temporally ultrasensitive switching. We also predict other types of combined circuit motifs that would have particular kinetic filtering properties.

Our understanding of how cells respond to the complex dynamic information they receive, and how they control their own responses over time, is currently relatively primitive. The design principles of kinetic filtering circuits explored in this study may provide a road map for uncovering such temporal regulatory mechanisms.

RESULTS

Defining kinetic filtering: temporal ultrasensitivity and trigger time

We use two parameters to quantitatively define a kinetic filter (Fig 1B). First, trigger time is the input duration required to achieve half-maximal response; second, temporal ultrasensitivity is the steepness of the response vs input duration curve. Analogous to concentration-based ultrasensitivity (Goldbeter and Koshland, 1981), temporal ultrasensitivity quantifies the sharpness of a signaling network’s kinetic filtering thresholding behavior, implying a steep temporal dose response curve where input stimulation with durations shorter than the trigger time result in minimal or no activation of the network, and inputs longer than the trigger time result in maximal activation. Networks that perform as kinetic filters can thus be defined as those that show temporal ultrasensitivity or trigger times above a minimum cutoff value. Because temporal ultrasensitivity is sensitive to left-right translations, we consider all circuits with temporal ultrasensitivity exceeding the cutoff value to be equally temporally ultrasensitive.

Circuit enumeration and analysis of robust kinetic filtering

To identify the simplest kinetic filtering circuits, we enumerated the space of 1-, 2-, and 3-node enzymatic circuits, as described previously (Ma et al., 2009), and measured each topology’s temporal ultrasensitivity and trigger time under multiple parameter sets (Fig 1C). Here we focused on enzymatic nodes, where each node is modeled with standard Michaelis-Menten parameters. Each node is at a fixed total concentration partitioned into active and inactive states. A regulatory link between nodes indicates that the active state of the upstream node catalyzes the conversion of the downstream node between its active and inactive state (Fig S1).

In this model, nodes that integrate two regulatory inputs exhibit “AND” or “OR” logic. Here we do not define these as absolute Boolean operators, but rather use this nomenclature to describe whether the effects of two different upstream regulatory links are either multiplicative (“AND”) or additive (“OR”) (Fig S1). In an enzymatic framework, AND logic can be implemented as, for example, activation of a kinase requiring phosphorylation by two other kinases. Both logics are sampled in this enumeration because prior work has shown that some key kinetic filters require specific integrating node logic (Mangan and Alon, 2003). These classes of nodes only describe two extreme models of two-input integration where both inputs are absolutely needed or both equally activating, but many intermediate behaviors are also possible, such as integrating nodes in which the weights of activation by each link are different (one input link is weak activator; other is strong). Individual nodes may also have basal activation or inactivation, independent of regulatory links between nodes.

Altogether, we search a space of 68,705 possible network architectures and quantify temporal ultrasensitivity and trigger time for each architecture. We measure these behaviors by tracking maximal output at any time during the simulation, since we also wanted to be able to capture networks that may require a substantial delay after the stimulus pulse to develop its full output. For all simulated networks, we assume that concentrations of individual enzymatic nodes operate in regimes where stochastic effects are minimal.

To capture only the kinetic filters with very strong all-or-none response to input duration, we applied a high stringency cutoff for temporal ultrasensitivity satisfied by <1% of simulated circuits (Fig S2A). Relaxing the cutoff for temporal ultrasensitivity from 0.5 to 0.4 yielded similar results for the types of motifs observed. Additionally, we required the circuits display a minimum trigger time of 1s (compared to tested input durations of up to 50,000s) to exclude circuits with trivially short trigger times (Fig S2B), as a single-node circuit without feedback can exhibit sufficiently steep temporal dose response when the requirement on trigger time is relaxed as long as the kinetics of input activation are sufficiently slow. These cutoffs yield circuits with steep dynamic activation thresholds, but with a range of trigger times. We then quantified the robustness of each topology’s kinetic filtering by measuring the fraction of a topology’s tested parameter sets that satisfy the performance cutoffs (Dassow et al., 2000; Hornung and Barkai, 2008; Ma et al., 2009). A higher robustness implies that the topology’s performance is more robust to changes in parameter values. High robustness circuits are thought to represent the most likely solutions to emerge from a random evolutionary process (Lim et al., 2013).

We explored network space using a two-phase search strategy. First, we searched the network space with a low-stringency robustness cutoff, where only very low-robustness networks were eliminated, in order to cast a wide net to find all minimal network motifs than can perform kinetic filtering. We can search this set of architectures for clusters of core kinetic filtering network motifs. In the second phase, we searched for optimal kinetic filters, which are likely to be more complex networks, by applying a much higher robustness cutoff. We could then identify whether particular kinetic filtering motifs identified in the first search were enriched within this more selective set of network architectures.

Over 25% of all the enumerated topologies satisfied the low stringency robustness cutoff, but only 83 topologies met the high robustness cutoff (Fig S2C). We first describe phenotypic clustering of the large set of topologies and define the main classes of minimal kinetic filtering motifs, then explore motif enrichment in the smaller, higher-performing set of topologies.

Low-stringency search and phenotypic clustering identifies five classes of kinetic filtering networks

Of the 17,469 topologies that passed the low-stringency robustness cutoff, many are likely to be redundant – closely related networks that contain the same core motif that executes kinetic filtering. To reduce this large set of topologies to a minimal core set of non-redundant architectures, we systematically tested the effect of link pruning on robustness (Chau et al., 2012) (Fig S2D). We considered a minimal kinetic filtering architecture to be one in which removal of any single link in the network resulted in a drop in robustness below the 0.001 cutoff.

After this pruning procedure, 25 topologies were classified as minimal kinetic filtering architectures (Fig 1D). Each of the 17,469 kinetic filters in the low-stringency robustness set contains at least one of these 25 minimal kinetic filters as a core substructure, and the most robust kinetic filters often contain multiple minimal architectures. The minimal architectures thus form a basis set for analysis and classification of kinetic filters.

In the enumerative network search, we focus on the temporal ultrasensitivity score to define minimal motifs that function as kinetic filters. To investigate whether the minimal topologies could be clustered by more specific functional behaviors, we evaluate six additional metrics (Fig 2A). We consider two metrics that are independent of the kinetic properties of the circuit: 1) trigger time, the input pulse duration required to achieve 50% maximal activation in the temporal dose response, as described in Figure 1B and 2) whether the network exhibited long-term memory, defined as final output concentration divided by maximum output concentration, for a fixed input pulse duration. We also consider four metrics dependent on circuit kinetics, which describe the dynamics of the circuit on and off transition for a given input pulse duration. These dynamic metrics include 3) time for turning the circuit on (the time required for output to reach 50% maximum amplitude after application of input), 4) steepness of the circuit turning on (time required for output to reach 10% maximum amplitude divided by time required to reach 90% amplitude), 5) time to turn the circuit off (time required for output to decrease to 50% maximum amplitude after the input was turned off), and 6) steepness of the circuit turning off (time required for output to decrease to 10% maximum amplitude after the input was turned off divided by time required to reach 90% of maximum amplitude after the input was turned off). We measured these “phenotypic” metrics for each parameter set of all the minimal topologies that were above our kinetic filtering metric cutoffs, a total of 2896 topology/parameter combinations. Metrics 2-6 were measured for a single input pulse of duration 50,000 seconds.

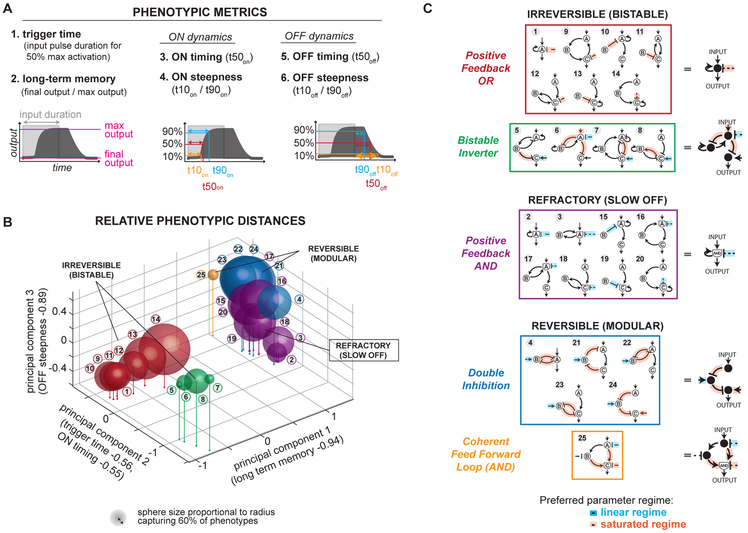
Figure 2. Minimal kinetic filters of 1, 2, and 3 nodes phenotypically cluster into five groups.

(A) Metrics used to cluster minimal kinetic filters by phenotypic features. For metrics 2-5, a single input pulse of duration 50,000s was applied. Measurements of ON dynamics are relative to input ON time, and measurements of OFF dynamics are relative to input OFF time. OFF dynamics were not measured for circuits where max output = final output. Phenotypic metrics were measured for all parameter sets of minimal kinetic filters with temporal ultrasensitivity ≥ 0.5 and trigger time ≥ 1s (total of 2,896 parameter sets distributed across 25 topologies in Figure 1D). (B) Location of minimal kinetic filters in 3D space of first 3 principal components of 6 phenotypic metrics. See Figure S3 for singular values and composition of each principal component. Each sphere is centered at the mean principal component value observed over all kinetic filtering parameter sets of each minimal kinetic filtering architecture. Sphere size is proportional to radius capturing 60% of observed phenotypes. (C) Minimal kinetic filters cluster into 5 phenotypic groups that each share structural features. Archetypal topologies (right column) are the simplest topology in each phenotypic group. Circuit links where kinetic filtering requires Michaelis-Menten kinetics to be in the linear or saturated regime are indicated in blue and orange respectively.

Principal component analysis was performed on these phenotypic metrics for the set of minimal kinetic filtering topologies (Fig S3). Figure 2B presents each minimal topology as a sphere in principal component space with center at the mean principal component value across the topology’s kinetic filtering parameter sets and radius reflecting the amount of phenotypic variation within that topology.

The minimal kinetic filters fall into five functional clusters (Fig 2C). Principal component 1, consisting mainly of the long-term memory metric, divides the minimal kinetic filters into two groups, one with long-term memory and one without. The circuits with long-term memory are irreversible and bistable and are further divided by principal component 2 into two subtypes: positive feedback circuits with OR logic (PFB_OR) and a class that we refer to as bistable inverters (BI).

Among the circuits without long-term memory, principal component 3 distinguishes between a class of kinetic filters that turn off slowly and gradually, requiring a long refractory period -- positive feedback circuits with AND logic (PFB_AND) -- from kinetic filters that turn off quickly and steeply and are thus considered the most reversible. Principal component 2 further divides the reversible circuits into two subtypes, double inhibition (DI) circuits and coherent feed forward loops with AND logic (CFFL).

Mechanisms of the five core kinetic filtering motifs

How does each of these five classes of core motifs achieve kinetic filtering behavior? Here we describe in detail the activation trajectories for each of these core classes, using ideal parameter sets that display kinetic filtering, and summarize their basic mechanisms. Parameter constraints observed for the four most robust classes are summarized in Fig S4.

Coherent feed forward loops (CFFL) have been previously identified as being capable of kinetic filtering (Mangan and Alon, 2003). These topologies use a fast arm/slow arm mechanism for kinetic filtering, where the output node shows AND logic and is only activated if it receives simultaneous signals from both the fast arm (a measure for whether the input is still present) and the slow arm (a measure of whether input was also on some time ago). A representative coherent feed forward loop timecourse (Fig 3A) shows that output node C is only activated when both active A and active B are above a threshold concentration; thus, trigger time is largely determined by the time required to transmit signal through the slower arm of the network, or the difference between the slow and fast arms. Short inputs are filtered because they do not last long enough to allow both the long and short arm of the network to be simultaneously activating the terminal AND node (node C). CFFL circuits are reversible after removal of input and turn off sharply. They can, however, display a moderate lag in initiating shutoff, which is dependent on how long the pool of active node A remains after removal of input.

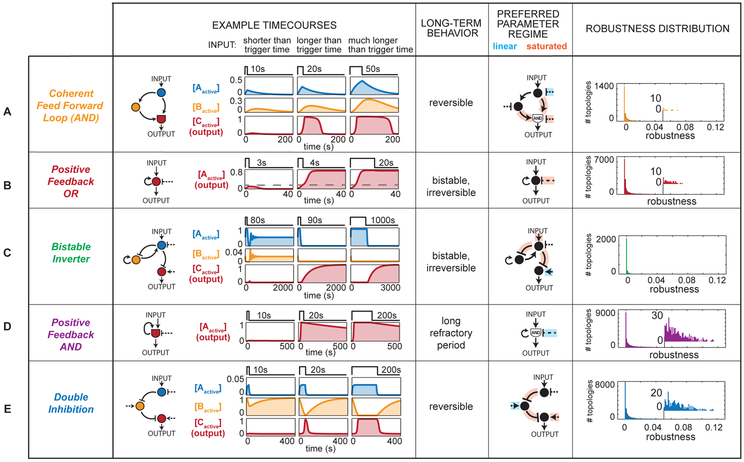
Figure 3. Representative timecourses, preferred parameter regimes, and robustness of five classes of kinetic filters.

Each circuit is shown responding to input shorter than trigger time, just longer than trigger time, and far longer than trigger time. Distributions of parameter values used to identify preferred regimes are shown in Figure S4. The dashed line in row B indicates the output concentration separating the attractor OFF and ON states. See Table S1 for parameter values used in example timecourses. Robustness score distributions across all topologies for each minimal kinetic filtering motif are shown. A topology was considered to contain a double inhibition motif if it contained at least one double inhibition minimal kinetic filter, and analogously for each of the other kinetic filtering classes. All topologies that do not contain motifs in any of the 5 classes have robustness < 0.001.

Bistable memory circuits, such as the positive feedback OR circuit (PFB_OR), can also achieve kinetic filtering. These circuits simply require a given time of input stimulation to pass the tipping point or separatrix, resulting in switching from the OFF state to the ON state (Fig 3B). The PFB_OR motif requires only a single node to achieve a bistable circuit. Here activation of the OR node (node A) by input results in positive feedback stimulation to the node, which, once at sufficiently high levels to counter the basal inactivating activity, can self-sustain activation of the OR node even in the absence of input. Short inputs are filtered because they leave the level of activated node A below the threshold required for locking ON.

Another kinetic filtering motif that results in long-term memory is the bistable inverter (BI) class (Fig 3C). This highly unusual class of circuits exhibits behavior where the output only switches ON after input has been halted. To serve as a kinetic filter, the A and B nodes begin in activated states. The output node (node C) is thus initially off, because node A represses C. Upon input stimulation, the negative feedback relationship between B and A nodes initiates oscillations in the activity of both A and B, but if stimulation is long enough, then B becomes completely deactivated. In the absence of active B, when input is halted, the activity of node A falls to zero. Because node A was the only deactivator of the output node C, output will now turn on. In short, this type of kinetic filter requires a minimal input stimulation duration to “prime” the system and eliminate active B (Fig S6). This priming time defines the minimal trigger time of the kinetic filter. The priming period can be followed by a holding time of variable length as long as input is sustained, but immediately after the input is switched off, the output will turn ON irreversibly. This highly unusual motif has not been, to our knowledge, characterized in known examples of kinetic filters, but it is possible that this sort of two-phase switch may be useful for particular biological behaviors.

Positive feedback loop AND (PFB_AND) circuits are another simple class of motifs capable of kinetic filtering (Fig 3D). In this case the integrating node (node A) must be simultaneously stimulated by input and positive feedback in order for the system to strongly activate output. Initial input can lead to low levels of activation of A, if the basal deactivators of A are weak (here an “AND” gate is not an absolute Boolean gate, but one in which the integration of two activating stimuli is multiplicative rather than additive). Nonetheless this buildup of initial amounts of activating A can be very slow and tuned by the strength of the basal opposing activity. If the input is on long enough to build up enough active A to trigger positive feedback, then A will turn on synergistically because of dual AND activation. In this case, the system does not formally display memory after input is removed, since it does turn off eventually. However, most parameters that lead to kinetic filtering also lead to an extremely slow inactivation of the system. Here the biggest difference between the PFB_AND and PFB_OR circuits is that the AND motif has a much stronger dependence on positive feedback in order to increase the level of active A. It is important to remember that our coarse grained search considered only two types of integrating node behaviors, and it is certainly possible that there could exist related positive feedback circuits in which the key integrating node has intermediate behaviors such as an OR gate where the weights of activation are much stronger for the positive feedback stimulation compared to the direct input stimulation. In this case, one would expect to obtain a kinetic filter that was like the PFB_AND motif in that it would require a long period of direct input stimulation to initiate build up of active A, but also like PFB_OR in that it could eventually lock on in a fully bistable manner.

The final major class of minimal kinetic filters is the double inhibition (DI) motif (Fig 3E). Networks in this class share a cascade with two successive inhibitory regulatory relationships. The central node (here B) starts with high activity and acts as an inhibitor of system output (node C). Input stimulation inhibits the inhibitor to switch on the system. DI motifs can act as kinetic filters when the central inhibitor node (here node B), acts as a buffer to absorb system input. Although input might immediately decrease node B activity, this does not register as a change in C node activity until after a longer duration of stimulation (trigger time) when the level of B has dropped very low. Trigger time is determined by the overall rate of decrease in B node activity, which is dependent not only on input, but is also opposed by the basal activation of B; higher basal activation can yield longer trigger times. DI motifs are reversible: after removal of input, the system rapidly returns to its initial steady state. The DI motif can be arranged as a sequential element between input and output nodes as described above, but can also be found in a double inhibition feedback loops as long as a terminal element of the DI motif has a positive regulatory relationship with the output node.

The most robust kinetic filtering networks are enriched for DI and PFB_AND motifs

To identify which of the five core motifs can give rise to the most robust kinetic filtering networks, we imposed a high-stringency robustness cutoff of 0.08 on the ~70,000 sampled topologies (Fig S5A). All 83 circuits in the high-robustness set contained DI and/or PFB_AND motifs but none of the other three core architectures (Fig S5B), although minimal versions of DI and/or PFB_AND motifs are not robust enough to meet this cutoff. Of the 83 highly robust kinetic filters, 25 have only PFB_AND motifs, 9 have only DI motifs, and 49 have both PFB_AND and DI motifs: combining DI and PFB_AND in the same circuit increases robustness. The distributions of robustness of architectures containing each of the five core motifs (Fig 3) show that circuits containing DI and PFB_AND motifs achieve much higher degrees of robust kinetic filtering than circuits containing CFFL and PFB_OR motifs, and circuits containing BI motifs are the least robust. The strong enrichment for both DI and PFB_AND motifs in the most robust kinetic filtering architectures prompted us to explore why these motifs may act as better kinetic filters than other related motifs.

Why double inhibition cascades are better kinetic filters than double activation cascades

The more robust DI motif and the less robust CFFL motif are structurally analogous – the slow arm of the CFFL motif, which plays a major role in trigger time, is a double activation cascade, in contrast to the double inhibition motif. We examined the trigger time distributions of all DI parameter sets above our functional cutoffs, and found that they display trigger times ranging from 1s to >10,000s. Under the same range of sampled parameters, CFFL circuits are limited to trigger times under 100s (Fig 4A). When we examine the trigger times and temporal ultrasensitivity found with 10,000 random parameter sets imposed on archetypical DI or CFFL architectures, we find that DI circuits can occupy the quadrant with both high trigger time and high temporal ultrasensitivity (Fig 4B). In contrast, the CFFL circuits appear to have constraints that lead to a tradeoff between temporal ultrasensitivity and trigger time in the parameter sets that lead to kinetic filtering (Fig S7).

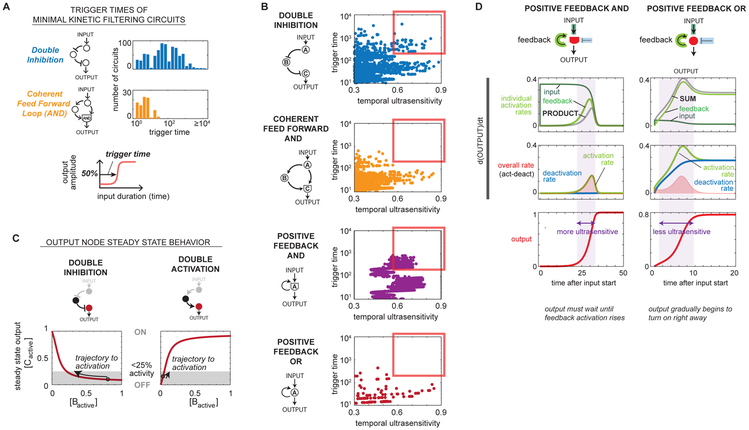
Figure 4. Turning off a deactivator more effectively buffers against partial activation by subthreshold length inputs.

(A) Histogram of observed trigger times minimal kinetic filtering circuits. Parameter sets of minimal double inhibition topologies (#4, #21-24 in Figure 2C, total 798 parameter sets) and the coherent feed forward loop topology (#25 in Figure 2C, total 88 parameter sets) satisfying temporal ultrasensitivity score ≥ 0.5 and trigger time ≥ 1s were measured for trigger time. (B) An archetypal architecture for each kinetic filtering motif was sampled for 50,000 parameter sets over the same range as the sampling used in the enumerative search (k_cat 0.1 to 10, K_m 0.001 to 100, evenly in log space by Latin hypercube). Shown in each plot are the temporal ultrasensitivity score and trigger time for each parameter set of the archetypal topology that resulted in temporal ultrasensitivity score ≥ 0.3 and trigger time ≥ 10s (DI: 1328 parameter sets; CFFL: 1078 parameter sets; PFB_AND: 2135 parameter sets; PFB_OR: 115 parameter sets). (C) Steady state output changes at a more gradual pace with changing regulator concentration in double inhibition circuits compared to double activation circuits. In both circuits, we solved for steady state output node concentration as a function of [B] with K_mBC = 0.5, k_catBC = 1, K_m basal activator/deactivator = 0.5, k_cat basal activator/deactivator = 1, concentration of basal act./deact. = 0.1. (D) Positive feedback AND circuits are better kinetic filters than positive feedback OR circuits because they require output to remain low until feedback activation rises. Activation rate consists of activation due to input and activation due to feedback, which are multiplied in AND circuits and summed in OR circuits. Shaded region delineates the zone between 5% and 95% output activation.

These differences between the behavior of DI and CFFL kinetic filters likely result from intrinsic differences between turning on an output by activating an activator versus inhibiting an inhibitor. To illustrate this point, we directly contrast a double inhibition circuit with a double activation circuit modeled with identical parameters — a double activation circuit is simply a coherent feed forward loop with the short arm removed. In Fig 4C we solve for the steady state concentration of active output node (node C) as a function of the fraction of active regulator node (node B). In both cases, output is initially low prior to input and increases the longer input is applied. For double inhibition circuits, the shape of the steady state output curve dictates that output remains low for a wide range of node B concentration; only after the amount of active B has been driven below a threshold does the fraction of active output (node C) begin to rapidly increase. Thus for double inhibition circuits, trigger time can be tuned to be very long, with minimal activation before reaching the trigger time. In contrast, for double activation circuits, output increases substantially with even a small initial increase in node B. Trigger time is thus limited by the shape of the output activation curve being steepest at low concentrations of node B, the early phase of the stimulation trajectory. However, activation cascades that are highly cooperative may also be able to maintain minimal changes in output for small increases in input.

This simple observation that double inhibition cascades will have intrinsically distinct temporal activation properties from double activation cascades is related to earlier work from Savageau on the noise resistance of different regulatory schemes (Savageau, 1977). Systems that switch on by double inhibition cascade are more noise-resistant than systems that switch on by activation cascade because of the intrinsic difference in which regimes of the dose-response curve are steep or shallow.

Why Positive Feedback AND motifs are better kinetic filters than Positive Feedback OR motifs

We then compared why the PFB_AND motif is a more robust kinetic filter than the closely related PFB_OR motif. Taking the archetypical kinetic filter of each architecture and carefully dissecting the trajectory of output activation, we observe that for the PFB_AND motif, minimal output activation occurs until the feedback activation loop has been triggered, as would be expected for the AND integration of the central node (Fig 4D). Feedback activation can trigger only very late in the trajectory because activation requires accumulation of the activated node, which can only occur through leaky activation induced by direct input activation.

In contrast, the PFB_OR circuit is able to immediately show gradual activation of the central node, because the OR integration allows activation by the direct input even in the absence of positive feedback. Thus, the PFB_OR circuit activation trajectory is inherently less steep than the equivalent PFB_AND circuit.

DISCUSSION

General classes of signaling networks capable of kinetic filtering and their potential functional roles

Here we have used coarse-grained network enumeration to identify classes of biochemical enzymatic networks that can achieve kinetic filtering – the ability of a system to respond only after input stimulation has sustained for a given threshold duration. Networks that execute kinetic filtering can play a central role in filtering transient noise, interpreting complex dynamic inputs, and controlling the timing of a sequence of events. Given the growing appreciation of the importance of dynamics in cellular information processing, it will be critical to understand the mechanisms that can be used for kinetic filtering and recognize and classify the networks that are found in cells (Purvis and Lahav, 2013). The design principles of such kinetic filters may also allow us to design cellular circuits with precision temporal control (Lim et al., 2013).

Kinetic filters must be able to absorb and dissipate input pulses that are shorter than a threshold triggering time, thus suppressing the resulting output. Here we focus on two behavioral parameters of the network: the trigger time -- the threshold stimulus duration time required to achieve half-maximal output, and temporal ultrasensitivity – the steepness of system activation as a function of input duration. Ideal kinetic filters can be considered to have both high temporal ultrasensitivity and high trigger times.

Our metric of temporal ultrasensitivity is analogous to the cooperativity index used to describe concentration-based ultrasensitivity. While well-established, this metric is sensitive to right translations: a temporal dose response of identical steepness will have a poorer score if trigger time is higher. Our analysis has focused on general properties of broad classes of circuits, but future work on kinetic filters may benefit from exploring other metrics capable of distinguishing subtle behaviors such as thresholding and switching (Gunawardena, 2005). Such alternative metrics might include direct fitting of a Hill function to the transition region to disentangle the steepness of the response from the trigger time in the temporal ultrasensitivity score. In addition, characterization of these motifs assuming dynamic noise and perturbations such as cell division will further inform our understanding of the robustness of these networks.

When we perform an exhaustive search for enzymatic networks capable of kinetic filtering, we identify five classes of architectures. Some classes (PFB_OR, CFFL) require tradeoffs between high temporal ultrasensitivity and long trigger time, while others (PFB_AND, DI) allow simultaneous optimization of trigger time and temporal ultrasensitivity. These findings suggest different potential functional roles for these different classes of circuits (Fig 5A). The CFFL can effectively filter against activation by relatively transient noise, since this would only require optimization of a high temporal ultrasensitivity without a long trigger time. DI and PFB_AND circuits may be better as kinetic filters that also incorporate a longer timer or delay function, since they can exhibit long trigger time without sacrificing temporal ultrasensitivity. Finally, PFB_AND circuits could also be used in cases where memory or a long turn-off lag is needed, while CFFL and DI would be more suited to cases where rapid shut-off is optimal.

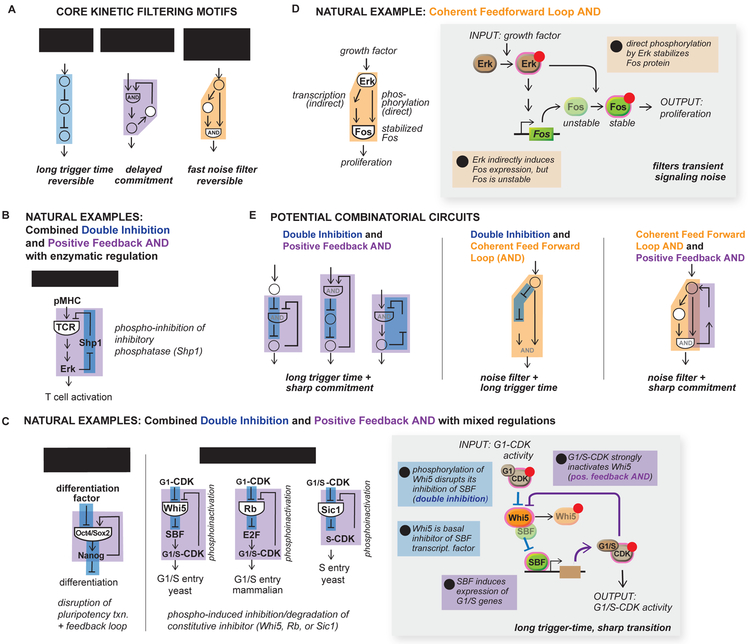
Figure 5. Natural examples of kinetic filters feature both core and combinatorial kinetic filtering motifs.

(A) Double inhibition, positive feedback AND and coherent feed forward loop AND form the core set of kinetic filtering motifs. (B) T cell activation is regulated by enzymatic networks that contain combined double inhibition and positive feedback AND motifs. (C) Pluripotent state exit in embryonic stem cells and cell cycle transitions in both mammalian and yeast cells are controlled by double inhibition and positive feedback AND architectures with mixed enzymatic and transcriptional regulation. (D) Erk activation of cFos is mediated by networks containing a coherent feedforward loop AND motif (E) Core kinetic filtering motifs can be combined to yield hybrid phenotypes.

Combined DI and PFB_AND network in T cell activation

This analysis predicts that one should be able to find these circuit types in natural kinetic filtering systems, although some might be preferred for a given functional context. There are several signaling systems that are known to display kinetic filtering. Here we examine these natural evolved systems and compare them with the motifs identified in this theoretical study.

Several natural kinetic filters seem to have converged upon a similar combination of both the DI and PFB_AND motifs, the two most robust kinetic filtering architectures identified in this work. Committed activation of T cells upon antigenic peptide-MHC engagement is thought to involve kinetic filtering (Davis et al., 1998). Activation is only observed with peptide-MHC complexes with sufficiently long engagement times. One of the key proteins thought to play a role in this kinetic filtering is the negatively regulatory phosphatase Shp1 (Altan-Bonnet and Germain, 2005; Feinerman et al., 2008). Examination of the Shp1 network reveals a combined DI and PFB_AND circuit (Fig 5B). Shp1 acts as an inhibitor that removes activating phosphorylation on the T cell receptor (TCR) and some of its downstream effectors. Activation of the TCR leads to its own phosphorylation, and in subsequent steps, activation of the downstream MAPK Erk. Active Erk can in turn phosphorylate Shp1 in a manner that is thought to lead to its dissociation from the TCR complex.

Although all parameters of the circuit have not been experimentally determined, measurements of native TCR signaling (Altan-Bonnet and Germain, 2005) indicate that known parameters for individual nodes and the trigger time of the circuit operate in regimes expected by the model. The estimated k_cat of ERK activation (2.6 s⁻¹) and SHP-1 phosphatase activity (5.4 s⁻¹) exhibit fast kinetics as predicted by the model. In addition, the measured trigger times of the circuit (30 – 90s) are within model expectations.

Convergence on combined DI and PFB_AND motifs in stem cell exit from pluripotency and cell cycle transition control networks

Many if not most signal-processing networks in cells employ mixed rather than solely enzymatic regulation. We expect that similar circuit behaviors of buffering input and slow accumulation of output can result when DI and PFB_AND motifs respectively appear in non-enzymatic networks, and the resulting circuits can exhibit kinetic filtering behavior through similar mechanisms as we observed in enzymatic circuits.

Pluripotent embryonic stem cells differentiate only in response to sustained but not transient differentiation signals (Sokolik et al., 2015). The circuit that induces differentiation (or exit from the pluripotent state) has a combined DI and PFB_AND motif. The Oct4-Sox2-Nanog maintains the pluripotent state through an autoregulatory positive feedback loop, thus acting as a repressor of differentiation. Differentiation factors induce the switch by disrupting the Oct4-Sox2-Nanog complex through competitive binding, leading to Nanog degradation and thereby relief of the repression of differentiation (double inhibition) (Fig 5C).

Recent studies have observed that several phase transitions in the cell cycle utilize convergent regulatory networks (Fig 5C) (Bertoli et al., 2013; Skotheim et al., 2008; Yang et al., 2013). In each of these cases, the networks contain integrated DI and PFB_AND motifs. In key cell cycle transitions, the cell starts with high activity of the cyclin dependent kinase (CDK) in complex with an initial phase. The cell must then sharply transition to the next phase, associated with a sharp increase in the next phase cyclin-CDK complex. These combination DI and PFB_AND networks appear to be optimal to drive this transition in a temporally sharp and decisive manner.

All of these circuits, even though they operate at different stages of the cell cycle, or in different organisms, have a central inhibitor that initially prevents output, i.e. next phase cyclin-CDK activity. For yeast entry into START (the G1/S transition), the inhibitor is the protein Whi5, which binds to and inhibits the transcription factor SBF. The transition initiates with a double inhibition cascade: when Whi5 is phosphorylated by the initial phase G1/Cdk enzyme, it initiates release from SBF, which in turn allows SBF to initiate expression of G1/S phase genes, including the G1/S cyclins. This results in increase in G1/S Cdk enzyme, the next phase cyclin/CDK complex, which then acts in a strong positive feedback manner to even more strongly phosphorylate and inactivate Whi5. Here, because Whi5 requires priming phosphorylation by the G1-CDK complex, but is more efficiently phosphorylated by the G1/S Cdk enzyme, it approximates an AND gate. Overall, this system shows a very sharp temporal transition after a long delay, followed by a strong commitment to the next phase, a combination of behaviors that the DI/PFB_AND hybrid network should be ideal for. Here the central inhibitory node (Whi5 = node B) is not an enzyme, as in the case of the network models used in our coarse-grained search, but is instead a stoichiometric inhibitor. This particular molecular manifestation of the network is expected to show temporal ultrasensitivity as long as the binding of Whi5 to SBF is sufficiently tight (Fig S8).

The identical hybrid network is observed in other cell cycle transitions. In mammalian G1/S entry, the protein Rb serves as the central inhibitory node analogous to Whi5, even though it is evolutionarily unrelated (Bertoli et al., 2013). Rb is an inhibitor of a transcription complex, and Rb’s function is in turn initially inhibited by G1-CDK mediated phosphorylation. Rb’s inhibition leads to expression of the G1/S cyclins, leading to positive feedback when the G1/S CDK enzyme strongly phosphorylates Rb.

In the case of the yeast S phase entry, the protein Sic1 serves as a central inhibitory node. Sic1 is a direct inhibitor of the S-Cdk complex, but is initially phosphorylated by the earlier stage G1/S-CDK enzyme. In a DI motif, phosphorylation of Sic1 leads to its degradation, initiating activation of the next phase G1-CDK enzyme. This leads to positive feedback, since the G1-CDK enzyme more strongly phosphorylates Sic1, leading to its even more rapid degradation.

CFFL motifs in natural kinetic filtering circuits: Erk activation of cFos

One classical example of kinetic filtering is the activation of the cFos protein only in response to sustained activation of the mitogen activated protein kinase (MAPK) Erk (Fig 5D). In this case, activation of cFos occurs through a CFFL network (Murphy et al., 2002). Erk activation of transcription factors leads to increased transcription of the cFos gene. The cFos protein is, however, rapidly degraded, so it does not accumulate. Erk also directly phosphorylates the cFos protein, resulting in cFos stabilization. Here Erk-mediated transcription of cFos serves as the slow branch of the CFFL network, while direct Erk phosphorylation of cFos serves as the fast branch. cFos accumulation acts as an AND gate, since both cFos transcription and phosphorylation are required.

It is hard to know exactly why the somewhat less robust CFFL architecture is used in this case. One possibility is that in some cases (e.g. EGF stimulation), Erk activation occurs in pulses, where the frequency of pulses can convey information (Albeck et al., 2013). For a downstream output to effectively integrate multiple Erk pulses only when they are relatively close together would require a system that neither shuts off immediately nor has an extremely long lag time. The CFFL may be ideal for this kind of frequency-encoded information, since the DI networks shut off extremely fast, and the PFB_AND networks show very long turn-off lag.

Other potential combinatorial kinetic filtering networks

Some of the best-characterized cellular systems that display kinetic filtering contain combinations of the ideal core motifs identified in our analysis. We predict several other possible combinatorial motif circuits to have useful combinations of behaviors. Three-node hybrid DI and PFB_OR circuits exhibit both delayed appearance of output, a DI feature, and bistability, a PFB_OR feature (Fig S9). A DI and CFFL combination circuit (Fig 5E) is expected to yield both a long trigger time and intermediate off-kinetics. Such a circuit could be used to integrate multiple wide pulses of input. Combining CFFL and PFB_AND could lead to efficient transient noise filtration combined with a committed transition. These networks built of multiple combinations of the core kinetic filtering motifs require more than three nodes, and thus would not have been identified from our enumeration of 3-node networks.

It is likely that the core motifs identified here could be combined together, both sequentially or in an interlinked manner to build even more effective kinetic filters with longer trigger times, or in a way that can overcome particular functional tradeoffs of the individual simpler motifs. We have previously found that a similar combinatorial use of minimal motifs leads to more robust cell polarization circuits (Chau et al., 2012). Multiple kinetic filters could be linked together in higher order sequences of events that control processes like the cell cycle or trafficking that require distinct steps to occur in a defined order. It is also possible that these minimal motifs could be combined with oscillatory networks to yield timer systems that combine pulsatile clock-like mechanisms with kinetic filtering (Suel et al., 2007).

While our analysis has focused on enzymatic networks to limit the scope of enumeration, many physiological circuits combine multiple types of regulation. Future work should explore circuits with transcriptional and mixed regulation, as natural circuits may take advantage of different inherent timescales of each regulation type to produce kinetic filtering architectures that are not possible with purely enzymatic circuits.

Evolutionary choice of signaling enzyme regulatory mechanisms may be linked to dynamic response behaviors

The diverse dynamic behaviors examined here may also explain why particular molecular mechanisms of regulation are chosen for different signaling enzymes. One of the most prevalent molecular mechanisms to gate signaling enzyme activity is regulation via an inhibitory domain that can act in trans or in cis (autoinhibition). Activation can thus occur via double inhibition or relief of autoinhibition. Although these mechanisms of enzyme regulation are very similar at a molecular level, this study suggests that when incorporated into circuits, the two molecular switches will have very different dynamical properties. At a network level, circuits with core nodes that rely on regulation by relief of autoinhibition will behave like conventional activation cascades, which can switch on faster but are less likely to have sharp temporal ultrasensitivity. In contrast, systems with an unlinked inhibitor could achieve much sharper temporal ultrasensitivity. It will be interesting to explore whether known signaling systems that use trans inhibition (e.g. protein kinase A, which is regulated by an inhibitory subunit that dissociates upon cAMP binding) are associated with robust time delays, while those that use cis -inhibition (e.g. Src kinases, which are regulated by intramolecular autoinhibitory domain interactions) are associated with faster, more immediate processes.

Conclusions

The motifs and understanding that emerge from this enumerative circuit analysis provide a useful roadmap for more deeply and predictively understanding how cells interpret dynamic information. These mechanisms can help understand why particular network perturbations that might disrupt timing control could contribute to diseases such as cancer. The motifs that emerge also provide a catalog by which to define key dynamical control elements within complex cellular networks mapped by proteomic and genomic methods. Further computational and experimental exploration of natural biological circuits will uncover the prevalence and functions of these minimal motifs and combinations thereof for cellular signaling.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Wendell Lim (wendell.lim@ucsf.edu).

METHOD DETAILS

Simulation of biochemical circuits

Reactions were modeled with total quasi-steady-state Michaelis-Menten kinetics (Ciliberto et al., 2007; Gomez-Uribe et al., 2007; Tzafriri, 2003). Nodes were converted between active and inactive states according to network linkages, where positive regulations catalyzed activations and negative regulations catalyzed deactivations (Fig S1). The total concentration of each node was held constant at 1. For nodes operating under OR logic, Michaelis-Menten expressions for incoming links were added. For nodes operating under AND logic, Michaelis-Menten expressions for incoming links of the same sign were multiplied, and expressions for incoming links of opposite signs were added. Each circuit was numerically integrated with a fifth-order embedded Runge-Kutta formula (Press et al., 2002). Active concentrations of each node were initialized to 0.1 and allowed to come to steady state before the application of input.

To enumerate circuit topologies, we allowed each link to be positive, negative, or absent. We discarded topologies where the input signal did not reach the output node. Circuits with regulations on a non-input, non-output node that did not in turn regulate another node were also discarded. For AND logic topologies, we discarded all circuits where the node with AND logic did not have two regulatory links of the same sign, counting input as a positive regulation.

In addition to the regulations between nodes A, B, and C, a circuit had additional constitutive activators and deactivators as needed such that no node had only activators or only deactivators (Fig S1). Constitutive activators and deactivators had constant concentration of 0.1. Up to 26 parameters were sampled for each circuit: k_cat and K_m for each of the nine possible circuit links, three possible constitutive activators and deactivators, and the input link. Node concentration was held constant at 1.0 and not sampled. Only the active fraction of a specific node can catalyze other reactions at a given time. All parameter samplings used the Latin hypercube method (Iman et al., 1980) with range 0.1 to 10 for k_cat and 0.001 to 100 for K_m; this range is roughly physiological with units of seconds and μM. 10,000 parameter sets were sampled for the enumerative search and 100,000 for determining parameter regime restrictions.

Quantification of circuit performance

Input pulses of duration 0.25, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 800, 1000, 2000, 3000, 5000, 6000, 8000, 10000, 20000, and 50000 seconds were applied separately to each parameter set of each topology. Input amplitude was set to 0.1 for all simulations to allow for comparison between circuits. Maximum output amplitude was measured over the period covering both the duration of the input pulse as well as a post-pulse recovery period lasting until the system came to steady state. Circuits that failed to reach steady state within 86,400 simulation seconds were removed from consideration. Inverting circuits whose output decreased with application of input were also discarded.

Temporal ultrasensitivity was quantified by plotting the circuit’s maximum output amplitude for each duration of input and measuring the temporal ultrasensitivity score (TU score) of the resulting curve (Fig 1B). TU score was defined as the ratio of input duration yielding 10% of maximum response to input duration yielding 90% of maximum response, analogous to cooperativity score in classical dose response curves (Goldbeter and Koshland, 1981). The 10% and 90% input durations were determined by interpolating a linear fit between the simulated input durations bracketing the 10% and 90% response amplitudes respectively. The response threshold T was determined by linear fit to identify input duration at 50% maximum output amplitude.

Maximal response (Rmax) and difference between maximal and minimal response (ΔR) were also measured for each circuit. Circuits with Rmax < 0.001 or ΔR/Rmax < 0.5 were considered to have insufficient response amplitude and were not considered to be kinetic filters.

QUANTIFICATION AND STATISTICAL ANALYSIS

Simulation of enzymatic circuits and calculations of dose response features were performed in C++. Python 2.7 was used for simulation management and data analysis. Hierarchical clustering was performed using Cluster (Cluster 3.0 for Max OS X within the C Clustering Library v1.36) with Euclidean distances and centroid linkage and visualized with Java TreeView. Principal components were calculated using the SciPy v0.11.0 linalg.svd singular value decomposition package.

DATA AND SOFTWARE AVAILABILITY

Circuit simulation, dose response measurement, topology generation, and parameter sampling software are available in the Github repository https://github.com/jgerardin/persistence-detection

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Circuit simulator and dose response feature calculator	This study	https://github.com/jgerardin/persistence-detection
Topology generation and parameter sampling scripts	This study	https://github.com/jgerardin/persistence-detection
Cluster for phenotypic clustering	de Hoon 2004	https://www.encodeproject.org/software/cluster/
SciPy linalg.svd for principal component analysis	SciPy	https://www.scipy.org
Java TreeView	Saldanha 2004	http://jtreeview.sourceforge.net/

HIGHLIGHTS.

• Many biochemical networks exhibit temporal filtering to coordinate timing of events

• Enumeration of three-node networks reveals five motifs capable of kinetic filtering

• Each core network motif exhibits distinct mechanisms and functional properties

• Several natural timer circuits contain combinations of the two most robust motifs