Can one concurrently record electrical spikes from every neuron in a mammalian brain?

Abstract

The classic approach to measure the spiking response of neurons involves the use of metal electrodes to record extracellular potentials. Starting over 60 years ago with a single recording site, this technology now extends to ever larger numbers and densities of sites. We argue, based on the mechanical and electrical properties of existing materials, estimates of signal-to-noise ratios, assumptions regarding extracellular space in the brain, and estimates of heat generation by the electronic interface, that it should be possible to fabricate rigid electrodes to concurrently record from essentially every neuron in the cortical mantle. This will involve fabrication with existing yet nontraditional materials and procedures. We further emphasize the need to advance materials for improved flexible electrodes as an essential advance to record from neurons in brainstem and spinal cord in moving animals.

eTOC blurb

Understanding cognition can, in principle, require simultaneous records of spikes from every neuron in cortex. Can this be achieved? The results from back-of-the-envelope calculations show that such measurements may be obtained using electrodes fabricated with existing yet nontraditional materials and procedures.

Electrical recordings are the sine qua non for the measurement of computations in the nervous system. It is thus of fundamental interest to ask if, as a matter of principle, one can record spikes from all neurons in a mammalian brain. And, if not, from what fraction of the brain can one record? In this regard, the discussions that led to the United States BRAIN Initiative were convened with a working title of ÒThe Brain Activity MapÓ (Alivisatos et al., 2012). The prospects for such a dynamic map (Buzsáki et al, 2015), with a corresponding connectome (Denk and Horstmann, 2004) to map all chemical and resistive connections among neurons, forms the basis for modeling and ultimately understanding brain function (Kleinfeld et al., 2011; Plaza et al., 2014; Rubinov et al., 2015). Here we discuss the physical limits to obtain the brain-wide activity map in a mammal. The corresponding connectivity map could be obtained via transmission electron microscopy (Kasthuri et al., 2015) or focused ion beam milling combined with scanning electron microscopy (Knott et al., 2008; Hayworth et al., 2019). As demonstrated for nonmammalian species (Kornfeld and Denk, 2018), there are no fundamental barriers beyond the constraints of experimental time and the current need for substantial human curating.

Both optical and electrical approaches have been taken to measure neuronal activity across many sites, albeit the most pervasive is optical imaging using a fluorescent indicator of intracellular Ca ²⁺ concentration (Grienberger and Konnerth, 2012). While no doubt useful, [Ca ²⁺] transients are only an approximate reflection of spiking (Theis et al., 2016). The advent of genetically expressible voltage sensors may obviate this problem (Platisa and Pieribone, 2018). Yet currently available sensors, while impressive for recording local network activity in vivo (Adam et al., 2019), appear insufficiently sensitive for brain-wide imaging and require sparsely labeled brain regions to prevent cross-talk from obfuscating the desired signals. Lastly, the photon budget to simultaneously image large numbers of neurons, and the technology to image at all depths throughout cortex without deleterious aberrations (Ji, 2017; Liu et al., 2019), remains an elusive goal. Our focus here is on a classical approach, that of measuring extracellular electrical potentials (Lemon, 1984). These signals depend on current flow through the extracellular space during the propagation of an action potential. While the signal-to-noise ratio can be quite high, it is important to recall that isopotential neurons, e.g., electrically compact cells, will not generate an extracellular signal (Jack et al., 1974). This contingency, however, seems unlikely to apply to neurons that are present in neocortex.

A corollary of our query is that of sufficiency. That is, from what fraction of all cells does one need to record to determine how few neurons are needed to quantize the neuronal basis of perception or behavior? This question is bound up in the issue of the dimensionality of neuronal computations (Ganguli and Sompolinsky, 2012; Gao et al., 2017; Stringer et al., 2019), i.e., how fine a sensory field is perceived, or how finely controlled is motion within a motor act? Further, the question of sufficiency is likely to be widely variable for different parts of the brain (Lehky et al., 2014; Schoelvinck et al., 2015). Thus we focus on the reductionist issue of fundamental physical limits, practical limits, and numbers.

Theory, together with transport and mechanical parameters for known materials, places physical limits on the dimensions of wires. For example, how stiff does a sensor carrier need to be before it buckles in the insertion process? What force is required to insert a probe of a given cross-section? How thick a wire does one require to propagate a signal without appreciable attenuation at action potential frequencies? For concreteness, we discuss a cylindrical probe of diameter d_shaft with recording sites distributed along the length of the shank. We consider the case of neocortex with dimensions appropriate for mouse through marmoset. We ask if, in principal, enough multi-electrode shanks could be inserted into the cortex to reliably record spikes from all neurons. Conversely, if we set an upper limit for displaced brain tissue, this same calculation can be used to estimate the fraction of neurons whose spiking could be detected with available probes.

We first establish the essential parameters for the electrical measurement process. We then consider physical arguments for the size and density of electrode carriers and electrodes that will enable electrical recordings with high signal-to-noise ratios. Lastly, we discuss potential physiological constraints, including the thermal load from the associated electronics.

1. Neuroelectric Scales

The electrical capture length for extracellular recording from a neuron, denoted D, is key. The average density of neurons in murine cortex is ρ = 1×10 ⁵ /mm ³ (Petersen, 2007; Tsai et al., 2009), which roughly translates to a cube that is ${\rho }^{1/3}\approx 20\mu \text{m}$ on edge per neuron. The range of extracellular spike detection is an issue of signal amplitude relative to that of background spiking activity. While detection of spikes more than 100 µm from the originating soma has been demonstrated for the largest cortical pyramidal neurons (Buzsáki, 2004), the detection length is less well defined for smaller neurons. A conservative estimate of the range of detection is the electronic length for a propagating action potential. This length is set by the ratio of current flow through the membrane, which is dominated by sodium conductance during an action potential, to current flow that is along the axis of the axon (Jack et al., 1974). Typically, ${\lambda }_{AP}\approx \text{Å}20\hspace{0.17em}\mu \text{m}$, which matches the neuronal spacing ${\rho }^{1/3}\approx 20\mu \text{m}$. Thus we take D = 20 µm as the maximum length between a neuron and an electrode for reliable recording. Clearly, there are significant variations in neuronal size and D will depend on cell geometry and levels of channel expression.

The second scale is the bandwidth of neuronal signaling, which we denote as f_AP. The spectral density of the action potential extends to 10 kHz (Fee et al., 1996), so that we assign f_AP = 10 kHz. We note in passing that the collective activation of sodium channels in the axon hillock has a frequency components up 40 kHz (Naundorf et al., 2006), yet these are not essential to the detection of a spike.

2. Metrology

What is the minimum distance between electrode shanks? We put the issue of displacement of brain tissue by the electrodes aside for the moment. Ideally, the shanks should be spaced at nominally 2D ≈ 40 µm, so that each neuron is, on average, within one electronic length of a shank. The shanks are chosen to be arranged in a triangular array with a spacing of 2D = 40 µm (Figure 1a).

Figure 1. Schematic of the proposed stiff electrode.

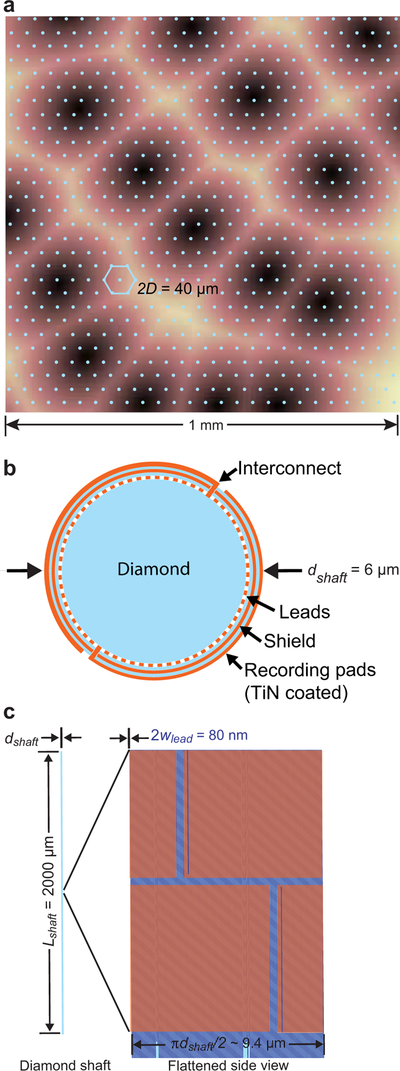
(a) The proposed triangular grid of electrodes spaced on top of primary vibrissa sensory cortex. Image from Knutsen et al. (2016). (b) The electrode is constructed of a diamond shaft that is covered with five layers. First is the leads and the mineral insulation between leads, second is mineral insulation, third is a conduction shield, fourth is a second is mineral insulation, and fifth is the electrode pads. Each pad is connected to one lead via a thru-hole interconnects that pierce the shield. Illustration is not to scale. (c) The multi-electrode shaft with an expanded view of the face to show the arrangement of pads.

With the above parameters for detection range and bandwidth, we can estimate limits to the diameter of the electrode. This shank should have the smallest feasible tissue displacement, contain recording sites of sufficient density to resolve the signals from the full density of neurons, and have a mechanical strength sufficient to insert into cortex.

3. Design Considerations for Rigid Probes

With the knowledge of the necessary insertion force, we can now estimate the diameter of our canonical shank. With additional information, we can further estimate the number and size of the electrode pads and leads.

A critical limit for the fabrication of the thinnest usable rigid probe is the buckling force at the time of insertion of the electrode into cortex. This constrains the dimensions of the shank. The ideal material for a rigid shank, i.e., the stiffest and thus most resistant to buckling, is diamond, with Young’s modulus E = 1.2 N/µm ². By comparison, E = 0.2 N/µm ² for silicon. We choose a recording depth of L_shaft = 2000 µm, which is appropriate for mouse through marmoset cortex. Recent measurements of the force required to insert cylindrical electrodes into mouse cortex, ex vivo, with diameters ranging from 7.5 to 100 µm, yield a penetration force of F_i = F₀ (1 + d / d₀), with F₀ = 8×10 ⁻⁶ N and d₀ = 1 µm (Obaid et al., 2018). Note that the penetration force reported for a 100 µm diameter probe is about 6-times less than that was reported for inserting electrodes in monkey cortex (Reitboech, 1983). Lastly, the sustaining force to insert the electrode did not exceed the penetrating force down to at least 1500 µm of insertion depth (Obaid et al., 2018).

Our dimensional estimates (Box 1) for diamond shanks supports the use of cylindrical electrodes that are at least 4 µm in diameter. We choose the larger value of d_shaft = 6 µm, based on electrical considerations (Box 2), for which the volume fraction of the brain occupied by the electrodes, denoted Θ, is Θ ≈ 0.02. This value for the volume fraction is ten-fold less than the mean extracellular volume fraction (Tonnesen et al., 2018).

Box 1. Dimensional estimates for a rigid electrode array.

• What is the shank diameter required for insertion? Standard formula for the threshold force, F, at the onset of buckling of a solid cylindrical beam (Timoshenko and Young, 1945) give

  $$F={\left(\frac{\pi }{4}\right)}^{3}E{\left(\frac{d_{\text{shaft}}^2}{L_{\text{shaft}}}\right)}^2,$$

  with the beam taken to be rigidly supported on one end. We equate F with F_i, approximated as F_i ≈ ( F₀ / d₀) d_shaft, take E as the Young’s modulus for diamond, and estimate a minimum diameter of d_shaft = 4 µm to insert a diamond shaft into cortex without the electrode buckling. A larger value may be required to penetrate the dura, recalling that $F\propto d_{\text{shaft}}^4$, and/or to accommodate sufficient numbers of electrode pads.
• What is the volume fraction of the brain occupied by the electrodes? Geometry sets this fraction at

  $$\mathrm{\Theta }=\frac{\pi }{8\sqrt{3}}{\left(\frac{d_{\text{shaft}}}{D}\right)}^2.$$

  This fraction is Θ = 0.009 for d_shaft = 4 µm and Θ ≈ 0.02 for d_shaft = 6 µm. The fraction must be small compared to the volume fraction of extracellular space, denoted α. Super-resolution imaging data from hippocampal slice shows that the fractional volume varies across anatomical locations (Tonnesen et al., 2018); it is α = 0.05 in stratum pyramidalis, the cell layer, up in α = 0.36 in fibrous regions, and has a mean value of $\overline{\alpha }=0.19$. These values can change by 1.5-fold with neuromodulator concentration (Ding et al., 2016). Data from in vivo reports give similar values for $\overline{\alpha }$ (Sykov‡ and Nicholson, 2008).
• How many recording pads are required to cover the shank? The number of cells probed by one shank is

  $$N=2\sqrt{3}\hspace{0.17em}\rho \hspace{0.17em}{D}^2{L}_{\text{shaft}},$$

  which yields N = 280. We set the number of recording pads equal to the target number of neurons to minimize, but not obviate, complications from spike sorting (Hill et al., 2011; Barnett et al., 2017). The surface of the shank is covered with one layer of lead wires, to bring signals to the surface of the brain. The overlaying layer is a mineral insulator, followed by a ground plane to shield the leads from the electrodes and a second mineral insulator layer. The final, or fifth layer, contains the recording pads. Thru-holes connect each pad to the underlying wire (Figure 1b,c).
• What is the size of the leads and pads? We choose to wrap the leads for the N electrodes along the entire circumference of the first layer. We assume an equal lead width and separation distance of w_lead. This gives

  $$\begin{gathered} w_{\text{lead}}=\frac{\pi d_{\text{shaft}}}{2N} \\ =\frac{\pi }{4\sqrt{3}}\frac{1}{\rho D^2}\frac{d_{\text{shaft}}}{L_{\text{shaft}}}, \end{gathered}$$

  which yields w_lead = 35 nm. Each electrode pad occupies an area with dimensions $\pi d_{\text{shaft}}/2=9\mu \text{m}$ wide by 2 L_shaft/N = 14 µm high, in which space remains for the inclusion of insulating gaps between pads. This corresponds to an area of A_pad = 126 µm².

Box 2. Electrical noise and shunting for a rigid electrode array.

• How much thermal noise is generated by the recording pads? There are two types of electrode interfaces, Faradaic and non-Faradaic, that transform electrical signals between the ionic conduction in solution and the electronic conduction in gold or other metals (Bard and Faulkner 2000). Non-Faradaic electrodes, also known as ideal polarizable electrodes, refer to interfaces for which no electrochemical, i.e., reduction-oxidation, reactions take place. Faradaic electrodes make use of reduction-oxidation processes at the extracellular solution to metal interface. Faradaic electrodes are characterized by a shot noise component that is associated with the electrochemical processes.

  For electrophysiology, non-Faradaic electrodes are preferred. In this case, the electrical noise from the electrodes is solely thermal in origin and is associated primarily with resistances of the double-layer at the extracellular solution to metal interface, as well as any access resistances to the bulk electrolyte and tissue. Under the assumption that the resistance of the double-layer dominates the losses, the root-mean-square (RMS) thermal noise is

  $$\delta V_{\text{pad}}=\sqrt{\frac{k_{B}T}{C_{\text{pad}}}},$$

  which is derived by equating the noise energy $1/2\hspace{0.17em}{C}_{\text{pad}}\hspace{0.17em}\delta V_{\text{pad}}^2$ with the equipartition energy 1 / 2 k_BT, where k_B is the Boltzman constant and T is the temperature. A large electrode capacitance is clearly preferred based on noise considerations. The capacitance given by

  $$C_{\text{pad}}={ϵ}_o{ϵ}_{\text{double}}\frac{A_{\text{pad}}}{t_{\text{double}}}.$$

  The double layer is characterized by a thickness t_double = 0.3 nm and relative dielectric constant ϵ_double = 2, for which C_pad = 7 pF. The addition of a coating of titanium nitride (TiN) to the face of the electrode will dramatically increase the value of the surface area of the pad. The increase in area exceeds one hundred-fold at the onset on testing (Jun et al., 2017) and diminishes to a worst case of twenty-fold under chronic, in vivo recording conditions (TDH, unpublished observations). Thus C_pad is conservatively replaced by C_{pad, TiN} = 150 pF and the estimated RMS noise is $\delta V_{\text{pad}}=5.2\hspace{0.17em}\mu \text{V}$ over the bandwidth associated with the double layer.

  The noise will be reduced if the spectral bandwidth of the neuronal activity, f_AP, is less than the bandwidth, denoted f_pad, associated with the electrode and double layer. This bandwidth is found from input resistance between the neuron and the electrode times the capacitance, where the input resistance is estimated as the spreading resistance over a separation distance D, i.e.,

  $$R_{\text{input}}=\frac{{\rho }_{brain}}{4\pi \overline{\alpha }D},$$

  where we have corrected for the volume fraction, $\overline{\alpha }$ (Weissberg, 1963). The resistivity of cerebral spinal fluid in neocortex, denoted ${\rho }_{brain}$, is estimated to be in the range 2–4 Ω m (Logothetis et al., 2007). Thus R_input ≈ 60 kΩ so that f_pad = 1/2 πR_input C_{pad, TiN} = 18 kHz, or 4-times f_AP. Thus the filtered noise level will be $\delta V_{\text{pad}}=5.2/\sqrt{18/10}\hspace{0.17em}\hspace{0.17em}\mu \text{V}=4\mu \text{V}$.
• How much thermal noise is generated by the leads to the recording pads? The resistance of a gold, 35 nm thick by 35 nm wide wire is R_lead = 30 kΩ. The corresponding RMS thermal noise, also referred to as Johnson noise, is

  $$\delta V_{\text{lead}}=\sqrt{4k_{B}T{R}_{\text{lead}}{f}_{\text{AP}}}.$$

  We estimate $\delta V_{\text{lead}}=4\mu \text{V}$. The noise from the leads and electrode pads are, for our design, nominally equal.
• What is the expected noise from passive tissue? The electrode thermal noise must be compared with the variability in the extracellular signal that arises from background neuronal activity in cortex. The spreading resistance between a signal and a reference electrode spaced a distance Δd apart is $R_{\text{spreading}}={\rho }_{brain}/4\pi \overline{\alpha }\Delta d$. The corresponding thermal noise is

  $$\begin{gathered} \delta V_{\text{spreading}}=\sqrt{4k_{B}T{R}_{\text{spreading}}{f}_{\text{AP}}} \\ =\sqrt{k_{B}T\frac{{\rho }_{brain}}{\pi \overline{\alpha }\Delta d}{f}_{\text{AP}}}. \end{gathered}$$

  For a reference spaced Δd =10 mm from the main electrodes,$\delta V_{\text{spreading}}=130\hspace{0.17em}\text{nV}$. This is negligible compared to the noise of the electrodes.
• Is the capacitive coupling between electrodes leads deleterious? The coupling between neighboring leads and leads and electrode pads can both attenuate and corrupt the measured signal. For our geometry (Figure 1b) and interposed short and long leads,

  $$\begin{gathered} C_{\text{lead}}={ϵ}_o{ϵ}_{\text{dielectric}}\frac{L_{\text{shaft}}}{2}{w}_{\text{lead}}\sum _{n=1}^N\frac{1}{\frac{d_{\text{shaft}}}{2}\text{cord}\left(2\pi \frac{n}{N}\right)-w_{\text{lead}}} \\ ={ϵ}_o{ϵ}_{\text{dielectric}}{L}_{\text{shaft}}\sum _{n=1}^{N/2}\frac{1}{\frac{2N}{\pi }\text{sin}\left(\pi \frac{n}{N}\right)-1}, \end{gathered}$$

  where the sum accounts for coupling to all leads. The coupling between the leads and the pads is prevented by the incorporation of a ground plane with via holes between the layer of pads and that of leads (Figure 1b).
  We use ϵ_dielectric = 5 for diamond and estimate C_lead = 0.1 pF. This value is negligible compared to both the capacitance of the pad and the capacitance of the gate of a field effect transistor (FET) at the input of an ultra-low noise amplifier (Wattanapanitch et al., 2007). The roll-off frequency for attenuation of high frequency components of the signal is $f_{3\text{dB}}=1/(2\pi R_{\text{lead}}{C}_{\text{lead}})=5\hspace{0.17em}\text{MHz}$ for a lumped parameter model, or over two orders-of-magnitude larger than f_AP. Lastly, as a design rule, the expression for C takes on a simple scaling in the limit of large N, i.e.,

  $$\underset{N\to \infty }{\text{lim}}{C}_{\text{lead}}\to \frac{{ϵ}_o{ϵ}_{\text{dielectric}}{L}_{\text{shaft}}}{2}{\text{log}}_{\text{e}}\left(\frac{4}{\pi }N\right),$$

  where 436.00 in Dwight (1961) was used.
• What is the expected signal strength? The signal strength from the electrode can be attenuated by the capacitance divider formed between the electrode capacitance and the input capacitance of the first-stage amplifier. Thus

  $$\frac{\Delta V_{\text{meas}}}{\Delta V_{\text{cell}}}\approx \frac{C_{\text{pad, TiN}}}{C_{\text{pad, TiN}}+C_{\text{input}}}.$$

  The input capacitance of an an ultra-low noise amplifier is less than 1 pF (Wattanapanitch et al., 2007). Thus ΔV_meas/ΔV_cell ≈ 1. The maximum voltage for extracellular signals ranges from ΔV_cell = 300 µV (Hill et al., 2011) to ΔV_cell = 1 mV (Lemon, 1984), so a conservative upper bound is ΔV_meas < 300 µV. High values of C_{pad, TiN} values are clearly preferred to maximize the input signal as well as reduce thermal noise from the electrode.

The mechanical and electrical properties of currently available materials allow, in principle, for spikes to be recorded from all neurons in a slab equivalent to that of the cortical mantle of mouse or marmoset (Boxes 1 and 2). The proposed design, constrained by neuronal density and the extracellular volume, consists of electrode shafts arranged on a triangular lattice, spaced 2D = 40 µm. Each multi-site electrode shaft has 280 pads, 9 µm in width with a 14 µm pitch, on a shaft that is 6 µm in diameter and 2000 µm in length. The pads are joined to insulated leads by thru-hole interconnects. We next ask if the geometry and size of the electrodes are consistent with signal-to-noise and bandwidth constraints for the detection of neuronal spikes.

The estimated RMS noise, which is dominated by the thermal noise of the electrode pad, is $\sqrt{\delta V_{\text{pad}}^2+\delta V_{\text{lead}}^2+\delta V_{\text{tissue}}^2}\approx 6\mu \text{V}$. Thus the estimated peak signal-to-RMS-noise ratio of the probe should exceed 50:1 for an action potential amplitude of ΔV_meas = 300 µV. Note that the measured fluctuations in vivo will further contain nonstationary contributions from active sources, including spiking by distant neurons and other fast ionic processes. A RMS value of $\delta V_{\text{RMS}}=25\mu \text{V}$ was reported for regularly spiking neurons in primary vibrissa cortex (Fee et al., 1996). Including these physiological sources, the estimated signal-to-RMS-noise ratio of the probe drops to 12:1.

Our estimates are conservative. The minimum diameter of the electrode required to forestall buckling may be reduced by sharpening the electrode tip (Obaid et al., 2018). Further, a guide tube may be used to reduce the unsupported length of the electrode. Past work also suggests the utility of dissolvable supports (Weltman et al., 2016) and microfluidic injection systems (Vitale et al., 2018). Lastly, the noise of the implanted electrode pads will decrease with improvements in the stability of coatings. In addition to TiN, poly(3,4-ethylenedioxythiophene (PEDOT) (Charkhkar et al., 2016; Ludwig et al., 2011; Rivnay et al., 2015), sputtered Pt (Whalen III et al., 2006), and IrOx (Negi et al., 2010) are other materials to consider.

3.1. Comparison with the state-of-the-art rigid probes

The status of current high-density density probes was reviewed by Steinmetz, Koch, Harris and Caradini (2018). Prominent among recent probes is the Neuropixels probe (Jun et al., 2017) (Figure 2), with a cross-section of 20 µm by 70 µm, about 50-times larger than that in our theoretical example (Figure 1a), and with electrodes on only one face. If we maintain the same filling-factor of Θ = 0.02, this suggests that Neuropixels probes can be placed as close as 2D = 165 µm and, for a λ_AP approximately 20 µm capture distance, record spikes from 0.01 to 0.02 of all neurons. The initial use of Neuropixels probes in mouse cortex yielded 0.6 to 1.0 neurons per site across 100 sites (Steinmetz et al., 2018), which is consistent with recording the majority of neurons within the capture distance of a single probe.

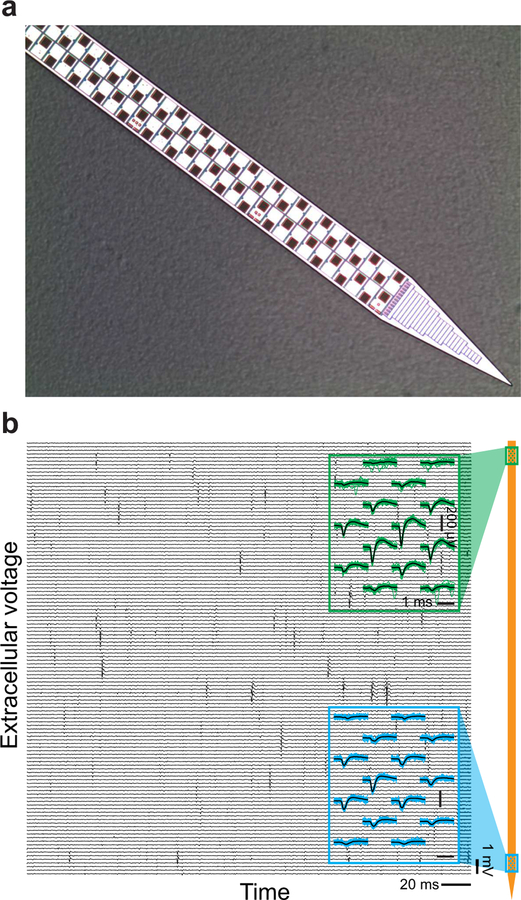
Figure 2. A state-of-the-art rigid probe.

(a) Photograph of the distal 68 sites of the 960 sites on a shank of a Neuropixels probe. The shank is 10 mm long, 70 µm wide, and 24 µm thick, with 12 µm by 12 µm TiN recording sites pitched at 2 per 20 µm of shank length. (b) Two example recordings from Neuropixels probe pads. The probe was chronically implanted in rat prefrontal cortex one day prior to data acquisition. Blue traces and green traces are 30 raw traces in the vicinity of a spike near the top (green) and bottom (blue) of the probe; black lines are average of those traces. Adapted from Jun et al. (2017).

4. Considerations for Flexible Shanks

We shift our attention to electrodes with flexible shafts or, simply, soft wires. Though less mature than rigid electrodes, flexible electrodes have, in the ideal case, the advantage of bending with changes in local brain shape and size over the course of the day. This is essential for recording in flexible structures, like the hindbrain. Further, increasing evidence suggests that more flexible electrodes promote more stable neural interfaces (Xie et al., 2014; Fu et al., 2016; Luan et al., 2017; Yang et al 2019). Flexible electrodes can be driven into the brain with retractable support rods and thus provide a strategy to record in hindbrain, spinal cord, and even cortex where a rigid connection between the brain and the world is deleterious. As a matter of principle, the wires can be sufficiently fine to occupy a negligible volume fraction (Box 2).

We estimate that the same 280 electrode pads per shank target may be accommodated by a flexible rectangular shank with a 10 µm width and 1.5 µm thickness. Most estimates of the rigid probe (Box 1) apply to flexible shanks except for several points (Box 3).

Box 3. Estimates for a flexible electrode array.

• What is the minimal thickness of a flexible probe? While mineral-based materials work as insulators for rigid shanks, they can easily crack on a flexible shank. Polymers are typically used as insulators for flexible probes and a thickness of approximately 500 nm is typically required. Taking d_lead = 40 nm, 300 leads can readily fit in two 10-µm-wide lead layers and three insulator layers, yielding an overall thickness of 1.5 µm and cross-sectional area of 15 µm ² (Figure 3a).

• What is the shuttle diameter required for insertion? The shuttle should have a cross section similar to that of the rigid probe (Felix et al., 2013; Zhao et al., 2019) (Box 1), i.e., 6 µm diameter for diamond.

• How should the array be transiently attached the shuttle for insertion? Temporarily attaching the flexible probe to the shuttle can be achieved with geometrical anchors (Luan et al., 2017), or water soluble adhesives (Felix et al., 2013; Zhao et al., 2019).

• What is the tissue displacement? The total displacement for the flexible probe is half of that for the rigid probe, or Θ = 0.01. The shuttle will transiently triple the volume occupied by the flexible electrode alone. Yet this increase in negligible if the shanks are inserted sequentially. On the other hand, there is potential for tissue damage during the process of insertion per se (Na et al., 2019; Zhao et al., 2019; Ferro et al. 2018; Joo et al 2019).

4.1. Comparison with the state-of-the-art flexible probes

The thinnest multi-channel flexible probes are currently fabricated with thicknesses of approximately 1 µm. To achieve the highest contact density, e-beam lithography is most promising for its approximately 10-nm spatial resolution (Luan et al., 2017; Wei et al., 2018; Yang et al., 2019) (Figure 3). This and related approaches (Chung et al., 2019) provide proof of the viability of flexible electrodes, although the demonstrated channel count per shank is about 20-times less than proposed array. In principle, the resolution of electron beam lithography should permit the fabrication process at a much higher electrode count but is limited by currently available back-end electronics.

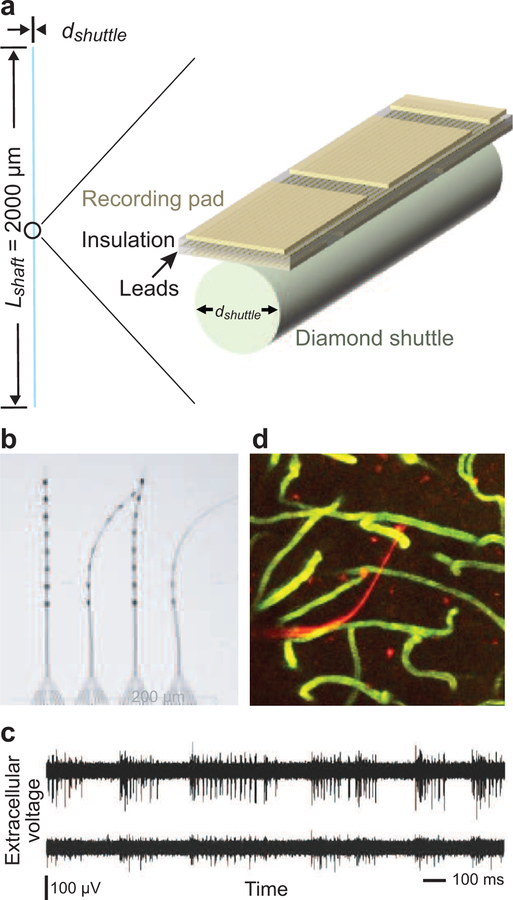
Figure 3. A state-of-the-art flexible probe.

(a) The electrode is constructed of gold pads and epoxy insulators. A diamond shank provides temporary rigidity for insertion. (b) A flexible multi-channel neural probe fabricated by electron beam lithography, with a shank width of 8 µm, thickness of 0.8 µm, and electrode pad size of 5 µm by 15 µm. (c) Representative electrical traces from the probe in panel b. (d) Three dimensional reconstruction of vasculature by in vivo two-photon microscopy (Kleinfeld et al., 1998) around a probe (red). Data obtained two months after implantation and shown as a maximum projection 100Ð320µm below the pia. Adapted from Wei et al. (2018).

It is also important to note that even brittle materials can be rendered flexible if they are sufficiently thin. Bending stiffness scales roughly with the cube of the film thickness. For the example of silicon, this allows a reduction in bending stiffness from roughly 2 Nm for a standard 500 µm thick silicon to only 5 µNm for silicon thinned to a thickness of 12 µm. The resulting nearly six-order-of-magnitude increase in mechanical compliance allows many of the properties of more flexible materials to be achieved. For the particular case of silicon, this permits the design of flexible probes that incorporate electronics to be produced in state-of-the-art fabrication lines.

5. Interface Electronics and Power Limits

The signal from each electrode needs to be electronically buffered, i.e., transformed from a high impedance source to a low-impedance driver, amplified, and digitized. This task is performed by a FET placed at the top of the electrode. This transistor and the associated downstream amplification and digitization electronics will generate heat that must be dissipated in the air above the animal. The channel densities that we propose are high, i.e., $N/\sqrt{3}{D}^2=2.6{\text{x10}}^5\hspace{0.17em}\hspace{0.17em}{\text{channels/mm}}^2$ or twenty million channels across the readily accessible 8 mm by 10 mm cortical mantle in mice.

How much power can be safely dissipated? Recent studies on the suppression of neuronal activity by heating through the absorption of light (Owen et al., 2019) suggest that the threshold thermal load is roughly 0.06 W/mm²; similar conclusions are found for light-induced vasodilation (Rungta et al 2017). This is likely to be an underestimate as heating was local in these studies, yet it provides a guide and suggests the need for an electronic interface that dissipates less than 0.2 µW per channel. Recalling that thermal conduction by diamond is 30,000 × that of air, essentially all of the heat will flow into the brain unless steps are taken block this flow. For example, a gap between the electrode and the electronics that is comprised of epoxy-silica should reduce the conduction of heat into the brain by a factor of 0.4.

5.1. Feasibility of ultra-low power amplification

Amplifiers for neuronal recording whose power dissipation is close to the fundamental physical limits set by input-referred thermal noise in transistors have already been built (Wattanapanitch et al., 2007; Sarpeshkar 2010; Wattanapanitch et al., 2011). Such amplifiers have a power dissipation that is inversely proportional to the square of the input-referred noise as well as linear in the required bandwidth; 22.8 in Sarpeshkar (2010). A relevant design was configured for an input-referred noise of 3.1 µV RMS and a 5.3 kHz bandwidth and realized with a gain of nearly 100, an input capacitance significantly less than 1 pF, and a ”1/f” noise that is negligible for spike recording. The concomitant measured dissipation was 7.6 µW per channel. This implies a dissipation of $7.6\mu \text{W}\times {(3.1\mu \text{V/6}\mu \text{V})}^2\hspace{0.17em}\times (10\hspace{0.17em}\text{kHz}/5.3\hspace{0.17em}\text{kHz})=3.8\hspace{0.17em}\mu \text{W}$ per channel, or 1.5 W/mm ², using the 6 µV RMS noise floor of our electrodes. This value, however, exceeds the target value for power dissipation.

A novel technique known as adaptive power biasing permits the power dissipation of a large, multi-channel electrode to be reduced by over an order of magnitude (Sarpeshkar 2010; Wattanapanitch et al., 2011). The statistics of multi-channel arrays are such that their input-referred noise varies over a probability distribution. Thus one low-noise amplifier can measure, calibrate, digitally store, and bias all other amplifiers in a multi-channel system such that each channel only dissipates power that is appropriate to the noise floor of the associated electrode pad. The method is effective precisely because the mean power dissipation of an amplifier in a multi-channel array, which is inversely proportional to the square of the input-referred noise, is significantly lower than that of an array of amplifiers designed for a fixed input noise; e.g., our estimated mean RMS noise floor of 6 µV. Thus, for our electrode array, we estimate that we could dissipate less than 0.15 W/mm², on average. This value is less than the target value for power dissipation, and thus supports the feasibility our approach.

Additional decrements on power dissipation can occur by increasing the acceptable noise floor toward the value with background activity, i.e., $\delta V=25\mu \text{V}$, mindful of the quadratic decrement in power dissipation with increasing amplifier noise. Further improvements may also be achieved with lower supply voltages and, as in the case of Neuropixels probes (Jun et al., 2017), by disabling unused channels.

5.2. Digitization

What of the power costs of digitization? Electronics with adaptive or programmable gain and analog-to-digital converters (ADCs) can provide a large dynamic range of operation, i.e., peak signal-relative to noise, and good bit precision while maintaining low power dissipation. As an example (Wattanapanitch et al., 2011), capacitively coupled ADCs with programmable gain can readily digitize amplified action potentials that range in amplitude from 10 µV, i.e., at the noise-floor and thus amplified with the highest gain, to 3 mV, i.e., amplified with the lowest gain, with 8-bit precision over a 12-bit dynamic range. Well known techniques for ultra low power subthreshold digital design can ensure that switching power dissipation is minimized, so that the lionÕs share of power dissipation originates from the neural amplifiers and not the ADCs (Sarpeshkar 2010).

A final point is data transmission. The bit rate per square millimeter for 8-bits of digitization depth and $f_{\text{AP}}=10\hspace{0.17em}\text{kHz}$ is $2f_{\text{AP}}N/(\sqrt{3}{D}^2)\times 8=65\hspace{0.17em}\text{GHz}$. From all of cortex, the rate is about 5 THz. This is well within the capacity of a single fiber optic transmission line (Stark et al., 2001). Nonetheless, one may wish to transmit only segments of the data with potential spikes. Each action potential will contribute to multiple electrode pads, so that the detection of action potentials is a source localization problem. The fraction of active electrodes at a given time can be estimated for the case of asynchronous activity and action potentials that contribute to a subset, denoted n, of the electrodes on a shank, where each spike occurs at an average rate of r and lasts for Δt. The fraction of time that an electrode is active is then $p=1-{(1-r\Delta t)}^n$; we assume a spread of ± 100 µm (Figure 2), implying n = 14 for a 14 µm pitch (Figure 1c), and take Δt = 2 ms and r = 10/s. We find p = 0.25, implying that the bit rate per square millimeter can drop to 16 GHz and the bit rate for the cortical mantle drops to nearly 1 THz. The data rate can be reduced further with optimized compression schemes.

6. Biomechanics of Probe Insertion

Compression of the brain during the insertion of either rigid or flexible shanks could pose complications. First, it is simply unknown if neocortex can be compressed to 0.98 of its original volume. This presumably can occur given the ability of the brain to accommodate tumors of roughly 0.1-times the cortical volume before there are clinical indicators (Jalali et al., 2010). It is entirely possible that the compression would lead solely to changes in the volume of ventricles. Second, even if the brain can perform normally in a reduced volume, the act of inserting electrodes can lead to dysfunction from the compression of the pia and upper layers of cortex during insertion. Established procedures may obviate this issue, such as the use of a weak vacuum to stabilize the surface of the brain onto a mesh of guide tubes (Ventakachalam et al., 1999) and vibro-cutting of the dura and pia (Gilleland et al., 2015). Other factors should be considered as well, particularly the insertion speed (Rousche and Normann, 1992; Maynard et al., 1997; Nicolelis et al., 2003; Rennaker et al., 2005; Felix et al. 2013) and possible enzymatic treatment of the pia (Paralikar and Clement 2008).

The vasculature could pose challenges in gaining access to all locations, as the pial surface of cortex is covered with venules and arterioles. These two classes of vessels overlap with each other but not within a class. Together, they roughly cover 0.1 of the surface of mouse cortex. It may be possible to penetrate through vessels with a sharp tip at the end of the shank and have the vessel seal; such tests remain unreported. While sparse blockage to surface arterioles is tolerated, blockage of a penetrating vessel will lead to an approximately 500 µm diameter infarct (Shih et al., 2013). A second issue is the potential lesions of microvessels, which in mice occupy close to 0.01 of the cortical volume, have mean diameter of 2.5 µm, and have no directional bias (Blinder et al., 2013). We reanalyzed published data (Blinder et al., 2013) and estimate that the probability of encountering a microvessel varies as $1-e^{-z/z_o}$ with insertion depth, z, and z_o = 300 µm. Nonetheless, it is likely, based on experience with silicon shaft electrodes, that microvessels splay and are spared from damage with a slowly inserted shaft. Further, sparse blockage of microvessels is tolerated (Shih et al., 2013).

7. Discussion

The essence of our analysis is that basic physical estimates suggest the utility of moving toward a program of all-cortex, if not all brain, spike-based electrical imaging through the adoption of non-traditional materials and the extension of current fabrication processes. Practical limits exist in terms of fabrication processes. For example, one can only pull a wire to be so thin, or reliably deposit a layer of insulation above a minimum thickness. Economics will limit the choice of materials. Electronic heating and power considerations, while likely to be challenging, do not appear to be insurmountable with respect to fundamental limits. All told, our analysis points to the adoption of an engineering-based feasibility study for rigid electrodes.

Soft electrodes represent an emerging technology (Xie et al., 2014; Luan et al., 2017; Zhao et al., 2017; Chung et al., 2019). Beyond issues of scientific investigation, particularly in subcortical regions, they may have extensive utility in brain-machine interfaces that involve the brainstem and spinal cord. Our analysis points to the adoption of a discovery-based program to explore soft materials for flexible electrodes.

7.1. Epilog

The practical problems that must be overcome for electrode technology to reach its full potential appear daunting but can be addressed and likely surmounted. The insertion of a dense array of shanks, one shank every 40 µm, will pose significant challenges, as the pitch is one tenth that of the ”Utah” array (Maynard et al., 1997) (Blackrock Microsystems). Signal processing at the head of the shank will definitely be required. Automation for craniotomies (Jeong et al., 2012) and automated shank insertion will likely be required. The vasculature will likely occupy some of the space assumed for this array of shanks. Lastly, while spikes appear to be the major currency of neuronal computation, the brain-wide measurement and understanding of subcellular electrodynamics, certainly down to the level of fine dendrites (HŠusser et al., 2000; Moore et al., 2017; Ranganathan et al., 2018), represents an important albeit futuristic goal.

Highlights.

• Physical limits do not preclude simultaneous recordings of all spikes in neocortex.

• Future electrodes need nontraditional materials and fabrication procedures.

• Challenges for dense recording include heat dissipation from interface electronics.