PAMAM: Power Analysis in Multi-ancestry Admixture Mapping

Abstract

Admixed populations arise when two or more previously isolated populations interbreed. Admixture mapping (AM) methods are used for tracing the ancestral origin of disease susceptibility genetic loci in the admixed population such as African American and Latinos. AM is different from genome-wide association studies (GWAS) in that ancestry rather than genotypes are tracked in the association process. The power and sample size of AM primarily depends on proportion of admixture and differences in the risk allele frequencies among the ancestral populations. Ensuring sufficient power to detect the effect of ancestry on disease-susceptibility is critical for interpretability and reliability of studies using AM approach. However, there is no power and sample size analysis tool exist for admixture mapping studies in admixed population. In this study, we developed PAMAM to estimate power and sample size for two-way and three-way population admixture. PAMAM is the first web-based bioinformatics tool developed to calculate power and sample size in admixed population under a variety of genetic and disease phenotype models. It is a valuable resource for investigators to design a cost-efficient study and develop grant application to pursue AM studies. PAMAM is built on JavaScript back-end with HTML front-end. It is accessible through any modern web-browser such as Firefox, Internet Explorer, and Google Chrome regardless of operating system. It is a user-friendly tool containing links for support information including user manual and examples, and freely available at https://research.cchmc.org/mershalab/PAMAM/login.html.

Introduction

A major gene flow episode in the form of population admixture began in the last 400 years in the Americans that primarily involved the interbreeding of three geographically separated ancestral populations (Smith et al., 2004). The first ancestral population is the Native American population, the second is the migrating population from Europe, and the third is the transatlantic slave trade movement of West Africans to the North and South Americas. In the Americas, interbreeding brought together ancestral genomes from these continental populations (Figure 1). African Americans, a two-way admixed population primarily admixture between European and African ancestries (Bryc, Auton, et al., 2010), and Latinos, a three-way admixed population consisting of primarily genomic admixture from European, African, and Native American ancestries (Bryc, Velez, et al., 2010), are the most widely studied in disease genetics, population genetics, anthropology and forensics and genetic testing (Brown et al., 2017; Cheng et al., 2009; Sofer et al., 2017). Additionally, multi- ancestry admixed populations such as those in Brazil and South Africa are under intensive admixture mapping (AM) studies (Kehdy et al., 2015; Petersen et al., 2013; Turner & Houle, 2018). An admixed samples from recently admixed individuals have genomes that are a mosaic of segments each originating from different ancestral populations. The goal of AM study is to identify the risk-associated allele (for a given disease) based on the likelihood of observing an association between a given ancestral allele(s) with disease risk (Mersha, 2015). The general hypothesis of AM is that among the affected samples of admixed individuals, the disease-causing genetic variants are transmitted in higher proportion from the ancestral population(s) with the higher frequency of risk allele than non-affected sample’s variants (McKeigue, 2005; Montana & Pritchard, 2004; Zhu, Cooper, & Elston, 2004).

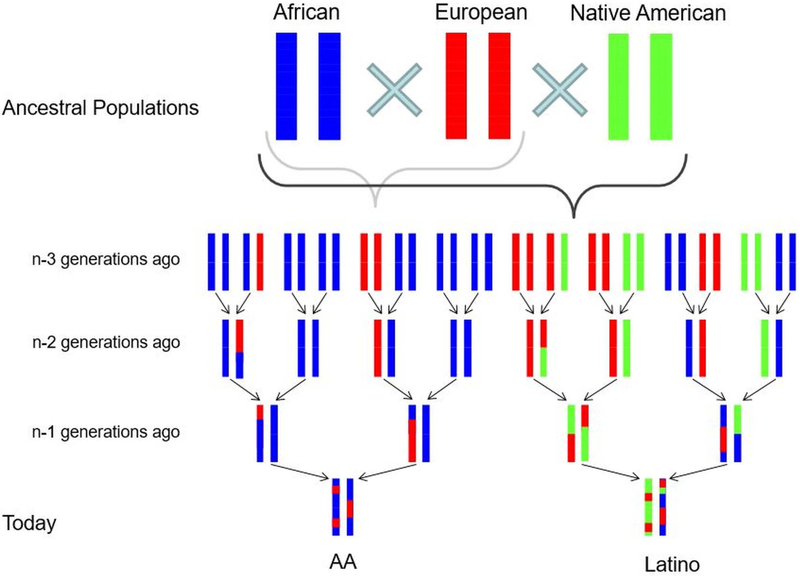
Figure 1: Schematic view of population admixture in America.

Figure shows an overview of admixture process of three ancestral populations, African, European, and Native American in the American continent. African Americans (AA) are two-way admixture of African and European; Latinos are three-way admixture of African, European, and Native American.

Because of genetic heterogeneity within an individual due to genetic admixture, power and sample size calculation methods developed for GWAS of European descent that assume genetic homogeneity (e.g., Genetic Power Calculator (Purcell, Cherny, & Sham, 2003), CaTS (Skol, Scott, Abecasis, & Boehnke, 2006), and GAS Power Calculator (Johnson & Abecasis, 2017)), are not applicable for mixed ancestry samples including African Americans and Latinos. While admixed populations can be challenging for GWAS due to population stratification which can lead to spurious associations (Baye, 2011; Freedman et al., 2004; He et al., 2011; Marchini, Cardon, Phillips, & Donnelly, 2004; Price et al., 2006). AM has many advantages over GWAS because admixture tests: 1) are not affected by population structure since the excess of ancestry is being tested at each marker position (Montana & Pritchard, 2004) and, 2) allow for the efficient detection of genomic regions with an exponentially smaller sample size and increased power in detecting disease signals because of reduced number of independent tests in comparison to GWAS (Shriner, Adeyemo, & Rotimi, 2011).

With the advances in high-throughput technologies and access to low-cost sequencing and genotyping data from diverse populations, the relevance of AM is ever increasing and so is the necessity of easily accessible analytical tools for power and sample size. The underlying power to detect the true effect on the disease under investigation determine the interpretability and replicability of a given study. Theoretically, a larger sample size may provide power to detect smaller effect, but in reality, clinical samples are often limited and/or the cost of sampling is high. On the other hand, larger sample results in wastage of resources and the researchers’ time. Studies with low power have poor translation and would likely results in failure of the research projects and loss of resources. Such situations can be avoided by “a priori” power and sample size study design (Turner & Houle, 2018). Granting agencies often require the power analysis to demonstrate the interpretability, viability, and success of the proposed research projects (Purcell et al., 2003). Thus, striking a balance between sample size and statistical power is an essential part of a study design.

Multiple online tools exists to calculate power and sample size for homogeneous populations (Johnson & Abecasis, 2017; Purcell et al., 2003). These methods are not applicable for mixed ancestry samples such as African Americans or Latinos. The objective of this study was to develop a freely available online tool called Power Analysis for Multi-ancestry Admixture Mapping (PAMAM) for power and sample size calculation for two-and three-way ancestry admixed populations. For admixture analysis, PAMAM performs the power and/or sample size calculation based on flexible user specified parameters for dichotomous as well as quantitative traits. For dichotomous trait, PAMAM performs power and sample size analysis under both case-only and case-control study designs. Case-only study design reduces the need for a large control sample size, which can be particularly difficult to ascertain in admixed populations. Even though the approach is currently implemented for two- and three-way admixture events, the analytical framework can be generalize and extended to more than three-way admixture analysis. To our knowledge, PAMAM is the first online tool developed to determine power and sample size calculation for admixed populations and freely available for the research community including investigators planning a priori and post-hoc power calculations to report expected and observed power, respectively.

Implementation

Architecture overview

PAMAM is a web accessible, graphical user interface application tool that can run on any modern browsers in any operating system. The web interface is built using HTML in the front-end while the back-end analytical and graphical algorithms are implemented in JavaScript. The web interface allows user to either display the information on the browser or to download to the client-side local hard drive.

PAMAM work flow

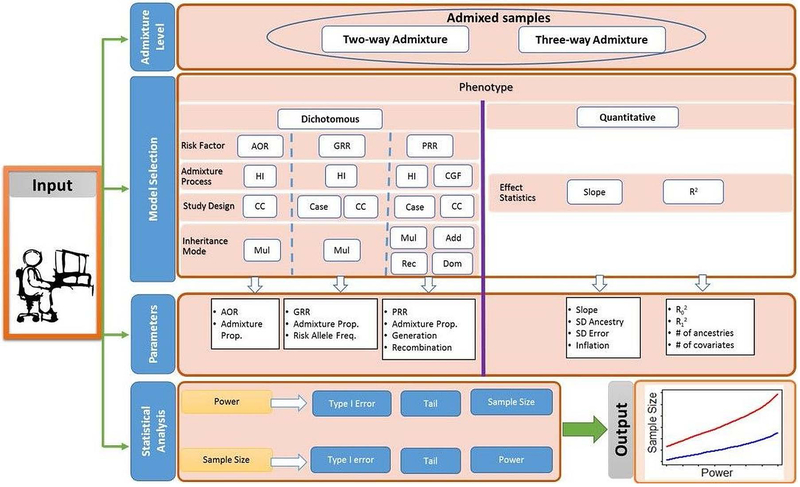
Figure 2 describes the work flow of PAMAM implementation. The entire process is divided into input and output sections. The input section constitutes four different stages: admixture level, model building, parameter specifications, and statistical analysis as described below.

Figure 2: Workflow of PAMAM Summarizing the Study Design and Approach.

AOR = Ancestry Odds Ratio, GRR = Genotype Risk Ratio, PRR = Parental (ancestral) risk ratio; HI = Hybrid Isolation, CGF = Continuous Gene Flow; CC = Case-Control; Mul = Multiplicative, Add = Additive, Rec = Recessive, Dom = Dominant, R² = (multiple) squared correlation.

Admixture level:

The power analysis using PAMAM starts with selection of admixture level of the samples where users will select one of the two options: ‘two-way admixture’ or ‘three-way admixture’ event. Two-way admixture option is applicable if the data constitutes the admixture samples with two ancestral population, such as African Americans. If the data represent samples from the admixture of three ancestral populations, such as Latinos, then the power analysis can be performed with ‘three-way admixture’ option.

Model building:

The ‘model building’ step is the second step of the PAMAM implementation where users will select the phenotype category as ‘Dichotomous’ or ‘Continuous’ to initiate the analysis. Following the selection, the system will prompt to provide required input information for model building. For two-way admixture under the dichotomous phenotype, users will select one of the risk factors – ancestral odds ratio (AOR), genotype risk ratio (GRR), or the parental risk ratio (PRR) followed by the admixture process. Hybrid-isolation (HI) is the default choice for AOR and GRR while for PRR, it could be selected between the HI or CGF. Next, a case-only or a case-control study design will be selected. For AOR risk factor, only case-control design is applicable. The last input for ‘Model Building’ is the selection of mode of disease inheritance. Again, the default is multiplicative mode for all the risk factors. Additionally, four different modes: multiplicative, additive, recessive, and dominant are available under PRR. However, for the three-way admixture, only the GRR based model is implemented in PAMAM and accordingly, only the GRR-based input options available for the analysis. Under the continuous phenotype, users will select model based on one of the two effect statistics: ‘Slope’ or ‘R²’. In PAMAM, slope-based model is only applicable for two-way admixture whereas the R² based model is available for both two-way and three-way admixture analyses. The slope-based method is appropriate for post-hoc analysis when the estimates of the required parameters are available from the sample.

Parameter specification:

Under the discrete phenotype, the set of parameters depends on the risk factors. The required set of input parameters under each risk factors are listed in the Figure 1. Under the continuous phenotype and ‘Slope’ statistics, the required inputs include slope, the standard deviation of the ancestry proportion (SD Ancestry), the standard deviation of the error (SD Error), and inflation factor (the multiple R² between the ancestry variables and other covariates). For the R² statistics, the multiple R² under the null and alternate model, # of ancestries for the admixed samples, and # of covariates are required.

Statistical analysis:

In this step, users select desired power or sample size. Type I error rate is required for all type of analysis. Type I error is the probability of a false positive result, that is, the probability of rejecting a null hypothesis that is true, usually set at 0.05. For the power analysis, sample size is required while for the sample size calculation, power is required. By default, all the analyses will be carried out as one-sided test, but it can be changed to two-sided by choosing the option available under the tab ‘Side’. In accordance with the study hypothesis, one can employ directional or non-directional tests of statistical significance as one-sided or two-sided, respectively. The selection of side will only affects the results for two-way admixture because the power analyses for two-way admixture is approximated using the standard normal distribution (see the Analytical Approach section for detail).

The output section constitutes the numerical and graphical display and results. Once the input information from all the four input stages are submitted, the tool will perform the appropriate analysis and generate output tables and graphs. One of the output tables provides the summary information from user’s input. Other tables correspond to the output graph of the power vs sample size. For a case-control study, two power graphs will be generated - one for power vs cases with fixed control and other for power vs control with fixed cases. Data tables can be further exported as a comma separated text file or as an excel file.

PAMAM application

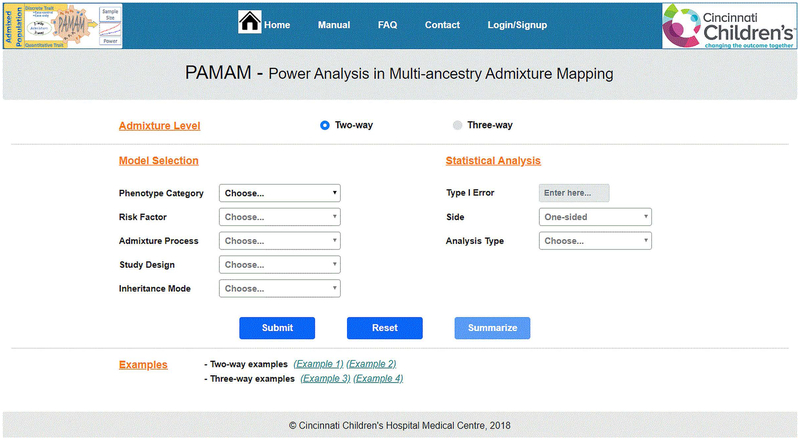
PAMAM begins with the web interface that constitutes the input section of webpage (Figure 3). As detailed above, users will select admixture level of the sample data or target population, build the admixture analysis model suitable for the available information, and provide the model-specific set of parameters and select the statistical analysis. Data will be inputted into the system in real-time and calculation is carried out on-the-fly. Data are entered by simple clicking on the tab, selecting the options from drop-down menu, or keyboarding the numerical values such as type I error, sample size or power. Optionally, the sample size and the power can be inputted through the associated sliding ruler. Once all the input information are provided, a single click of the ‘Submit’ button will generate the results on the output section. The ‘Summarize’ button will then be activated and can be used to generate the summary table of input information. The ‘Reset’ button will nullify all input information and return users to the homepage. The computation time depends on whether we are conducting a 2-way or 3-way admixture analysis. Though the power analysis can be computed within 1-2 seconds, the sample size analysis for three-way quantitative trait may take longer time than other analyses. For example, .the sample size calculation for two-way admixture takes about 0.1 seconds, while similar analysis for three-way admixture takes about 6-10 seconds, which is based on the computer with following configuration - processor: inter(R) Core (TM) i5-7300U CPU @ 2.60 GHz; RAM = 8.00 GB; Operating system: 64-bit Windows 10 Enterprise.

Figure 3: PAMAM web interface.

It is designed as an architecture consisting of four layers where a user selects admixture level, build the model, specific the parameter and conduct the statistical analysis in a single click. The web interface allows user to either display the information on the browser or to download to a local hard drive.

Examples for power and sample size analyses

a). Two-way admixed populations: Dichotomous trait

Suppose a study is planned for admixture mapping for discrete phenotype on samples from two-way admixed populations X and Y, with X being the high risk population. Previous studies on the similar target population have found the 80% of the genomes in the admixed population is contributed from X. The investigators want to collect enough samples to detect the ancestral risk variants with genotype risk ratio = 2.5 and 80% power under the significance level of α = 2.5 × 10⁻⁵ (type I error rate). This level of significance is equivalent to 5 false positive discovery among the 2000 independent test (0.05/2000). Note that, for admixture mapping, the genome wide significance level is much larger than that for the association mapping (Shriner et al., 2011). As an example, let us say from prior reference data on an admixed population between X and Y, an investigator found that the risk allele frequencies were 0.4 and 0.1, respectively, and a 70% genomic contribution from the population X. Let us assume the risk ratio of interest is genotype risk ration (GRR). The investigator start building the admixture mapping model by selecting the discrete phenotype then GRR risk factor, the default HI process followed by case-only study design with multiplicative mode (default). Once this stage is complete, investigator will input the parameters – GRR = 2.5, Admixture proportion = 0.70, Risk Allele Freq = (0.4, 0.1) (comma separated). On the ‘Statistical Analysis’ stage, investigator selects ‘Sample size’ and enter type I error = 0.000025, Side = ‘One-sided’, and power = 0.80. On the output window, the case-only sample size is shown as n = 590. The accompanying graph shows the sample size required for different powers for the model with the inputted information (Figure 4A). This allows users to recognize the sample size needed to achieve specified power. By switching to the case-control design, the investigator find the required total sample as n = 2392 with assumption of equal cases and controls (so 1196 cases and 1196 controls).

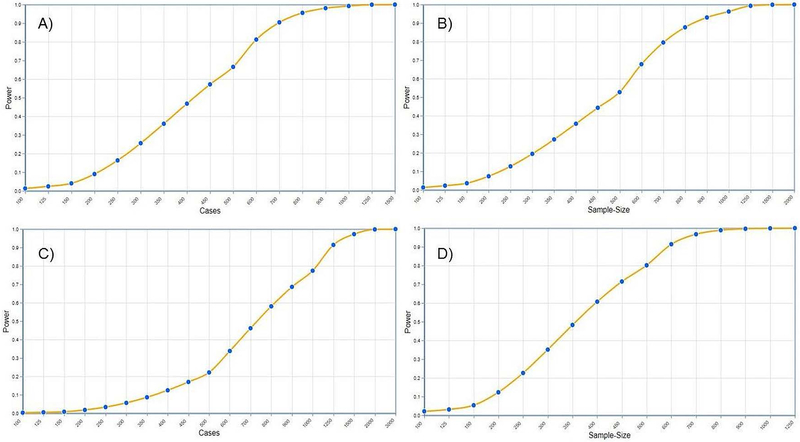
Figure 4: Power vs sample size plots.

Figure shows the power vs sample size plots of different admixture mapping models. A) Two-way admixture mapping for discrete trait with following inputs - admixture process = hybrid-isolation, study design = case-only, inheritance mode = multiplicative, grr = 2.5, admixture proportion = 0.8, allele frequencies = (0.4, 0.1), type I error rate = 0.000025, side = one; B) Two-way admixture mapping for quantitative trait with inputs - effect statistics = slope, slope = 0.35, SD error = 0.72, SD ancestry = 0.4, type I error rate = 0.000025, side = one; C) Three-way admixture mapping for discrete trait with inputs - admixture process = hybrid-isolation, study design = case-only, inheritance mode = multiplicative, grr = 2.5, admixture proportion = (0.67, 02, 0.13), allele frequencies = (0.4, 0.2, 0.1), type I error rate = 0.000025; D) Three-way admixture mapping for quantitative trait with inputs - multiple R² = (0.1,0.15), type I error rate = 0.000025.

b). Two-way admixed populations: Quantitative trait

Suppose an admixture mapping analysis is carried out for a quantitative trait using 750 samples from a two-way admixed population X and Y with admixture proportion from population for X is 0.80. Using this information, the investigators may want to perform the post hoc power analysis at type I error rate 0.000025 (adjusted for multiple testing). From the analysis, following information are derived: Slope (α₁) = 0.30, Standard error (σ) = 0.72, SD of ancestry (σ_u) = 0.40, Sample size = 750. Assume an inflation ($r_u^2$ ) of 0.1 due to single covariate ‘age’ in the model is expected.

Using PAMAM, the investigator can obtained an estimate of power. For example, under the ‘Model Selection’ section of ‘Quantitative’ trait would be selected for the ‘Phenotype Category’ and ‘Slope’ as the effect statistics. Then, the following parameters can be entered: Slope = 0.35, SD Ancestry = 0.40, SD Error = 0.72, Inflation = 0.1. In the ‘Statistical Analysis’ section, “Type I Error” = 0.000025; Side = ‘One-sided’; ‘Analysis Type’ = ‘Power’, and ‘Sample Size’ = 750 can be entered. After submitting these information, the investigator will find that the power of the study is 0.84. Further comparison of power for different sample sizes can be performed from the accompanying graph (Figure 4B).

c). Three-way admixed populations: Dichotomous trait

For an AM study with three ancestries, say X₁, X₂, X₃, an investigator first want to determine sample size. Suppose that the estimated admixture proportions of X₁, X₂, X₃, ancestries of the target admixed population can be well approximated with 0.67, 0.20, and 0.13, respectively. In addition, risk allele frequencies for X₁, X₂, X₃ were 0.4, 0.2, and 0.1, respectively. The investigators want to collect enough samples to detect the ancestral risk variants with genotype risk ratio = 2.5 and 80% power under the significance level of α = 2.5 × 10⁻⁵ (type I error rate). On the PAMAM window, the investigator could select “Three-way admixture” option and proceed to the model building stage with following inputs: GRR = 2.5, Admixture Proportion = (0.67, 0.20, 0.13), Risk Allele Freq = (0.4, 0.2, 0.1). On the ‘Statistical Analysis’ stage, investigator selects ‘Sample size’ and enter type I error = 0.000025, tail = 1, and power = 0.80. For the case-only study, the sample size required for this study is 1035 cases. Figure 4C shows the accompanying power graph for various sample size for case-only study. Under the case-control study design, the investigator will find the sample sizes needed for this study would be 1950 cases and 1950 controls.

d). Three-way admixed populations: Quantitative trait

Suppose we plan a three-way admixture mapping study of a quantitative trait. The environmental and demographic covariates explained 10% of the phenotype variation. We would like to have enough samples in the study to detect loci whose ancestry could explain additional 5% (or more) of the phenotype variation beyond that of the covariates with at least 80% power at type I error rate (α) = 0.000025 (after adjusting for multiple testing). We can use the PAMAM tool to estimate the sample size needed to achieve the desired power of the study. The required input information are multiple R² under null and alternate hypotheses, which are equal to 0.1 and 0.15 respectively, type I error rate (α) = 0.000025, and power = 0.80. The total sample size needed for this study with 80% power is N = 500. Figure 4D shows the output power graph for varying sample sizes.

Power comparison between theoretical and simulation studies

To estimate sample size and statistical power for admixture mapping theoretically, we assume that the true ancestry at each marker is known and all individuals have the average ancestry equal to the global admixture proportion. In practice, the ancestry information need to be estimated and the above theoretical assumptions do not meet. The power calculated from the PAMAM is expected to be in the upper bond compared with power achieved from real datasets (Montana & Pritchard, 2004). To illustrate the actual power vs estimated/theoretical power scenarios, we performed an admixture mapping analysis on simulated case-control data for a two-way admixed population with ancestral populations X and Y. The simulation approaches is described as follow-

Step 1: Set the disease prevalence for X and Y as k₁ = 0.2 and k₂ = 0.1, respectively. Population X is the high risk population.

Step 2: Estimate the population specific risk allele frequencies p₁ and p₂. Assuming a multiplicative mode of inheritance with genotype risk ratio (λ) = 2.5, and the penetrance (f₀) = 0.05, the risk allele frequencies can be estimated solving the following equation for p_j, j = 1, 2.

$$f_0(1-p_j{)}^2+2\lambda f_0{p}_j(1-p_j)+f_0{\lambda }^2{p}_j^2=k_j.$$

Step 3: Assuming Hardy-Weinberg Equilibrium (HWE), generate M individuals from each population X and Y. We set M = 10,000.

Step 4: Generate the first generation of admixed population. We generated a set of 5,000 individuals, 60% of the samples carrying the genotype from population X and 40% carrying admixed genotype with 1 allele from each population at random. This ensured the total contribution of alleles from population X among the set of individuals was 80% (global admixture proportion).

Step 5: Simulate n^th generation of admixed population. Following the hybrid-isolation model, we allowed random mating within the individuals generated from Step 4 with no additional genomic contribution from either ancestral population until 8^th generation. We allowed population growth per generation (approximate 1.5 times) and simulated the genotype for 100,000 admixed individuals.

Step 6: Assign the case-control status for the admixed individuals. The case-control status for the admixed samples were assigned based on the penetrance function (f₀) = 0.05 and the genotype risk ratio (λ) = 2.5.

Step 7: Assign the global ancestry for each individual. The global ancestry of each individual was sampled from the beta distribution, Beta(α = 12, β = 3) with mean ancestry = 0.8.

Step 8: Compute the ancestral odds ratio. The estimated ancestral odds ratio was 1.636.

Step 9: Estimate actual and theoretical power of admixture mapping for different sample size. We randomly sampled n (= 300, 400,…,1000) cases and equal controls and perform the case-control admixture mapping test at type I error rate = 0.000025. We performed 10,000 resampling for each n, and computed the power as the proportion test with significance p-value ≤ 0.000025. Similarly, theoretical power was computed for each n, using the PAMAM tool with estimated ancestral adds ratio = 1.636, admixture proportion = 0.8, type1.error = 0.000025 and side = 1 (one-sided test).

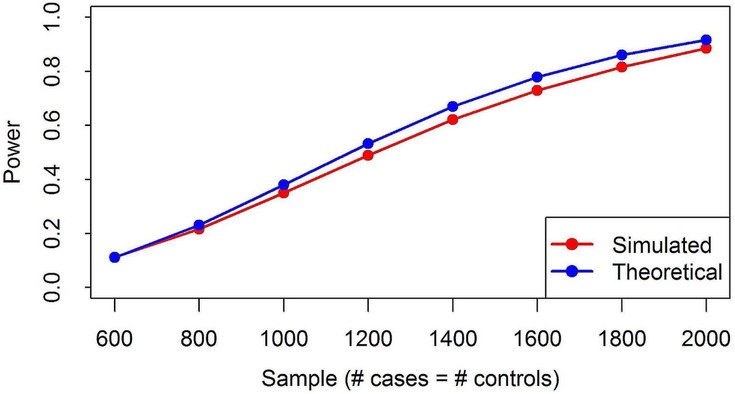
Based on our simulation, power in simulated data is slightly lower but highly comparable with the theoretical results (Figure 5), indicating that the underlying theoretical assumptions has only small effect on the actual power of the admixture mapping.

Figure 5. Power comparison between theoretical and simulation studies.

Figure shows the comparison of theoretical power computed based on PAMAM and the power from simulation. X-axis shows the total sample size with equal cases and controls. Power is computed for the ancestral odds ratio = 1.636, admixture proportion = 0.8, type1.error = 0.000025 and side = 1.

Conclusion

Multi-parental admixed populations, such as the African American or Latino populations, are increasingly being used for genetic studies via admixture mapping. However, there were no specialized analytic software to determine power and sample size in admixed population limited, which limits the utility of mixed ancestry population in genetics/genomics studies. To overcome analytic limitations, we have developed a web-based tool, PAMAM, for power and sample analysis in admixed populations. PAMAM is built on JavaScript, run on most of the modern browsers independent of operating system and no installation is needed. To our knowledge, PAMAM is the first online tool to implement power and sample size analysis for admixed populations with two and three ancestral populations. There is widespread applicability and importance of admixture mapping in studies with samples from admixed populations. We hope the tool serve as convenient platform for such analysis which will benefit the scientific communities and clinicians working on admixed samples. We welcome user’s feedbacks to improve the PAMAM features.

In summary, we developed PAMAM, which is powered by the back-end computational pipeline for various power and sample size calculation algorithms. The front-end user interfaces provide a wealth of user-specified settings including model selection for study design, genetic inheritance, and visualization and downloading results. In this study, we achieved the following three goals: (1) Develop power and sample size calculator for mapping risk loci in two-way and three-way admixed populations in discrete traits; (2) Develop power and sample size calculator for mapping risk loci in two-way and three-way admixed populations in quantitative traits; and (3) Develop an online tool for power and sample size calculation tool and make freely available at https://research.cchmc.org/mershalab/PAMAM/login.html.

Analytical Approach

PAMAM is developed for power analysis of two-way and three-way admixture mapping studies for both dichotomous and quantitative trait outcomes. Analytical approaches are presented below:

Two-way admixture:

For dichotomous traits, both case-only and cases-control study designs were analyzed under the framework of one-sample and two-sample binomial test of proportion and for quantitative traits, linear regression models with and without covariates were implemented. In case-only study design, the average ancestry proportion at a marker, say Π₁, will be compared with global ancestry proportion Π₀ for the significant differences. The power (1 – β) and sample size (n₁) were computed as:

$$1-\beta =P\left(Z>\frac{\sqrt{V_0}{Z}_{\alpha }-\mid {\Pi }_1-{\Pi }_0\mid }{\sqrt{V_0}{V}_1}\right),n_1=\frac{1}{2}{\left(\frac{z_{\beta }\sqrt{{\Pi }_1(1-{\Pi }_1)}+z_{\alpha }\sqrt{{\Pi }_o(1-{\Pi }_0)}}{{\Pi }_1-{\Pi }_0}\right)}^2,$$ (1)

Where β is the type II error rate, α is the type I error rate (potentially adjusted for the multiple testing if required), $V_0=\frac{{\Pi }_o(1-{\Pi }_0)}{2n_1}$, and $V_1=\frac{1}{V_0}\left(\frac{{\Pi }_1(1-{\Pi }_1)}{2n_1}\right)=\frac{{\Pi }_1(1-{\Pi }_1)}{{\Pi }_0(1-{\Pi }_0)}$ are variance under the null and alternate model. In the case-control study design, the average ancestry proportion at a marker among cases, say Π₁, will be compared with average ancestry proportion at the same marker among controls, say Π₀, for the significant differences. Then, the power (1 – β) and sample size (n) for the case-only design were computed as:

$$1-\beta =P\left(Z>\frac{\sqrt{V_0}{Z}_{\alpha }-\mid {\Pi }_1-{\Pi }_0\mid }{\sqrt{V_0{V}_1}}\right),n=\frac{1}{2}{\left[\frac{z_{\beta }\sqrt{{\Pi }_1(1-{\Pi }_1)+{\Pi }_0(1-{\Pi }_0)}+z_{\alpha }\sqrt{2{\Pi }_0(1-{\Pi }_0)}}{{\Pi }_1-{\Pi }_0}\right]}^2,$$ (2)

where β is the type II error rate, α is the type I error rate (potentially adjusted for the multiple testing if required), $V_0=\frac{{\Pi }_0(1-{\Pi }_0)}{2n_1}+\frac{{\Pi }_0(1-{\Pi }_0)}{2n_2}$, $V_1=\frac{1}{V_0}\left[\frac{{\Pi }_1(1-{\Pi }_1)}{2n_1}=\frac{{\Pi }_0(1-{\Pi }_0)}{2n_2}\right]$ are the variance under null and alternate model. The sample size in equation (2) is computed by assuming equal sample size for both case and control i.e. n = n₁ = n₂.

Additionally, the power analysis of quantitative traits is based on the linear regression model

$$v={\beta }_0+{\beta }_{1}u+\zeta W+ϵ,$$

where v be the (normalized) phenotype measurement, u be the excess ancestry proportion, W is a vector of the covariates, β₀is the intercept, β₁is the coefficient of ancestry effect, ζ is a vector of covariates effect, and ϵ~N(0, σ²) is the residual. For type I error rate α (adjusted for the multiple testing) and the type II error rate β, the power and sample size of the test are estimated using normal approximation which are derived to be as

$$1-\beta =P\left(Z>z_{\alpha }-\frac{{\widehat{\beta }}_1}{SE({\widehat{\beta }}_1)}\right),n=\frac{{\sigma }^2(z_{\alpha }+z_{\beta }{)}^2}{{\alpha }_1^2{\sigma }_u^2(1-r_u^2)}.$$ (3)

Here, ${\widehat{\beta }}_1$ is the estimate of β₁ and $SE({\widehat{\beta }}_1)=\frac{\sigma }{{\sigma }_u\sqrt{n(1-r_u^2)}}$ is the standard error of ${\widehat{\beta }}_1$ with σ = standard error of the model, σ_u= standard deviation of the variable u, and $r_u^2$ = multiple R² from the linear model regressing u against the rest of the covariates in the model. When there is no covariates on the model, then $r_u^2=0$ can be used in equation (3).

In general, the power and sample size analysis given by (1) and (2) depend on the approximation of admixture proportion Π₁. We have implemented the genotype risk ratio based approach (Montana & Pritchard, 2004), parental risk ratio based approach (Zhu et al., 2004), and ancestral odds-ratio based approaches under different disease inheritance mode as detailed in Gautam et al. (Gautam, Altaye, Xie, & Mersha, 2017). For details of the analytical approaches for admixture mapping under various disease outcomes and models please refer Gautam et al (Gautam et al., 2017).

Three-way admixture:

Similar to two-way admixture, the analyses for dichotomous trait can be performed in the framework of case-only and case-control study design. For the case-only study, the analysis will be performed under a Chi-square goodness of fit test, comparing the expected population distribution of multinomial admixture proportion with an expected distribution under a disease model. For the case-control studies, the association between the trait and ancestry is modeled under a Chi-square test of independence. For quantitative trait, a linear multinomial regression model will be used to access the association between the phenotype and ancestries and the power and sample size analyses will be performed for a desired level of association as measured by the multiple correlation (R²). Suppose we have a recently admixed population resulting from an admixture of three ancestral populations X₁, X₂, and X₃ with admixture proportions θ₁, θ₂, and θ₃, respectively, the proportion of alleles from the population X_i at given marker locus is θ_i.

Dichotomous Trait

In dichotomous traits, an admixture mapping analysis would measure a significance deviation in the admixture proportion in the study samples from the expected population proportions of X₁, X₂, and X₃, which can be achieved by either case-only or case-control study design.

Case-only admixture mapping:

Suppose M cases were selected from an admixed population. We further assume that at disease-susceptibility marker L with risk allele 0, the risk allele frequencies were f₁, f₂, and f₃ in the populations X₁, X₂, and X₃, respectively. We assume that the ancestry at marker L is known without error, and the number of ancestral alleles from X₁, X₂, and X₃ are given by (n_1, n₂, n₃) with n₁+ n₂ + n₃ = N (= 2M). The estimated ancestry proportion at L are ${\widehat{\theta }}_1=\frac{n_1}{N}$, ${\widehat{\theta }}_2=\frac{n_2}{N}$, ${\widehat{\theta }}_3=\frac{n_3}{N}$, respectively. We can use a Chi-square goodness of fit test to compare the expected distribution (θ₁, θ₂, θ₃) and observed distribution (${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$, ${\widehat{\theta }}_3$) under a large sample assumption. The null and alternate hypotheses for the goodness of fit test –as follows:

$$\begin{gathered} \text{H0}:({\theta }_1,{\theta }_2,{\theta }_3)=({\widehat{\theta }}_1,{\widehat{\theta }}_2,{\widehat{\theta }}_3) \\ \text{H1}:({\theta }_1,{\theta }_2,{\theta }_3)\ne ({\widehat{\theta }}_1,{\widehat{\theta }}_2,{\widehat{\theta }}_3),\text{i.e. at least one of the}{\theta }_j\ne {\widehat{\theta }}_j. \end{gathered}$$

The test statistics under the null hypothesis is computed as:

$$T=N{\sum }_j({\widehat{\theta }}_j-{\theta }_j{)}^2∕{\theta }_j.$$

Under the H0, $T\sim {\chi }_2^2$ distribution with 2 degree of freedom. Under some local alternate hypothesis (p₁, p₂, p₃), $T\sim {\chi }_2^2(\delta )$, a non-central chi-square distribution with non-central parameter δ with 2 degree of freedom where $\delta ={\text{lim}}_{\mathrm{N}\to \infty }N{\sum }_j\frac{(p_j-{\theta }_j{)}^2}{{\theta }_j}$ exists and finite (Chow, Shao, & Wang, 2008; Drost, Kallenberg, Moore, & Oosterhoff, 1989).

Let α be the type I error rate after multiple testing correction and β be the type II error rate. Let $C=P({\chi }_2^2(0)>1-\alpha )$ be the critical value under the null. When the sample size N is large, $N{\sum }_j\frac{(p_j-{\theta }_j{)}^2}{{\theta }_j}$ is a reasonable approximation of the δ (Drost et al., 1989). Using $\delta =N{\sum }_j\frac{(p_j-{\theta }_j{)}^2}{{\theta }_j}$, the power of the Chi-square goodness of fit test can be computed as:

$$1-\beta =P({\chi }_2^2(\delta )>C).$$ (4)

The sample size to achieve power = (1- β) will be estimated using

$$N=\delta ∕w^2$$ (5)

where $\mathrm{w}=\sqrt{{\sum }_j\frac{(p_j-{\theta }_j{)}^2}{{\theta }_j}}$ is the effect size, and δ is the non-central parameter estimated by solving the equation $P[{\mathrm{X}}_2^2(\delta )\le C]=\beta$ (Chow et al., 2008). Finally, the sample size to achieve the power is given by M = N/2.

Case-control admixture mapping:

In the case-control admixture mapping, the access ancestry in the cases and the access ancestry in the control are compared. We assume that the control is the ideal sample representing the population, so the test becomes equivalent to comparison of ancestry proportions in cases and controls. We use a chi square test of independence between the disease status (case, control) and ancestry (X₁, X₂, X₃) to estimate the power or sample size of the case-control mapping.

If M₁ and M₂ be the number the sample sizes for cases and controls, then the number of alleles in cases and controls are N₁ = 2M₁ and N₂ = 2M₂. The observed count of ancestry alleles at a locus in cases and controls can be summarized in 2×3 table as follows:

	X1	X2	X3	Total
Case	n11	n12	n13	N1
Control	n21	n22	n23	N2
	N.1	N.2	N.3	N

The chi-square test statistics for independence is $T={\sum }_{i=1}^2{\sum }_{j=1}^3\frac{(n_{ij}-N_{.j^{\ast }}{N}_i{)}^2}{N_{.j^{\ast }}{N}_i}$. Under the null hypothesis of no association between disease and ancestry, $T\sim {\chi }_2^2$, a chi square distribution with degree of freedom 2. Under some alternative hypothesis, $T\sim {\chi }_2^2(\delta )$, a non-central chi-square distribution with non-central parameter δ with 2 degree of freedom where $\delta ={\text{lim}}_{\mathrm{N}\to \infty }N{\sum }_{i=1}^2{\sum }_{j=1}^3\frac{(p_{ij}-p_{.j^{\ast }}{p}_{i.}{)}^2}{p_{.j^{\ast }}{p}_{i.}}$, where p_ij, p_.j, and p_i. cell and marginal probabilities respectively, provided the limit exists (Chow et al., 2008).

Let α be the type I error rate after multiple testing correction and β be the type II error rate. Let $C=P({\chi }_2^2(0)>1-\alpha )$ be the critical value under the null. Then, the power of the Chi-square test of independence is computed as:

$$1-\beta =P({\chi }_2^2(\delta )>C)$$ (6)

The non-centrality parameter δ in (6) will be estimated using the following equation:

$$\delta =N{\sum }_{i=1}^2{\sum }_{j=1}^3\frac{(p_{ij}-p_{.j^{\ast }}{p}_i{)}^2}{p_{.j^{\ast }}{p}_i},\text{under some alternate hypothesis.}$$

For sample size estimation to achieve power = (1- β), the non-centrality parameter δ will be estimated by solving the $P[{\mathrm{X}}_2^2(\delta )\le C]=\beta$ for δ. The total sample size N will be estimated as follow:

$$N=\frac{\delta }{{\sum }_{i=1}^2{\sum }_{j=1}^3\frac{{\left(p_{ij}-p_{.j^{\ast }}{p}_i\right)}^2}{p_{.j^{\ast }}{p}_i}}$$ (7)

We assume equal cases and controls to compute the sample size for cases and controls.

Next, we describe the approach of estimating the admixture proportion under the alternate hypothesis for a diseased-susceptibility marker with a given genotype risk ratio and under the multiplicative mode of inheritance. Similar approach was used for two-way admixture in Montana and Pritchard (Montana & Pritchard, 2004).

Estimating the ancestry proportion under alternate hypothesis:

The power and sample size computations using equations (4) - (7) required the admixture proportion/joint distribution under some alternate hypothesis. An appropriate alternate hypothesis can be constructed from the population specific parameters such as disease risk, allele frequencies, population admixture proportions, and disease inheritance.

Let f₁, f₂, and f₃ risk allele frequencies at disease-susceptibility marker L in the three ancestral populations X₁, X₂, X₃ respectively. Let (θ₁, θ₂, θ₃) be the admixture proportion at the marker under null model. Let γ be the genotype relative risk, assumed to be constant across all three populations. Under multiplicative mode of inheritance, the ancestry proportion under the disease model, (p₁, p₂, p₃), can be computed as:

$$p_i={\theta }_i\frac{1+f_i(\gamma -1)}{1+\stackrel{‒}{f}(\gamma -1)},$$

where $\stackrel{‒}{f}=p_1{f}_1+p_2{f}_2+p_3{f}_3$ is the allele frequency in the admixed population.

For the case-only study, (p₁, p₂, p₃) will be used as the alternate hypothesis for power and sample size estimation. However, for the case-control study, we further need to construct the alternate hypothesis, which is the joint distribution of disease status and ancestry, using the ancestry estimates (p₁, p₂, p₃) for cases and (θ₁, θ₂, θ₃) for controls. If M₁ and M₂ are the number of cases and number of controls and N₁ = 2M₁ and N₂ = 2M₂ be the respective allele counts, then the joint distribution can be tabulated as follow:

	X1	X2	X3	Total
Case	N1p1	N1p2	N1p3	N1
Control	N2θ1	N2p2	N2p3	N2
	N.1	N.2	N.3	N

For the power analysis using equation (3), the non-central parameter δ can be estimated using equation (4) with cell probabilities from the table above. For sample size estimation, we assume equal cases and control (i.e. N₁ = N₂ ➔ M₁ = M₂) and cell probabilities can be recalculated and the sample size can be estimated using equation (5). Note that N is the total alleles count from cases and controls, so we will have M₁ = M₂ = 0.25N.

Quantitative Trait

The association between the quantitative trait and the multiple ancestry can be studied in the framework of the linear multiple regression analysis. Let y_i be the phenotype measurement and θ_i = (θ_1i, θ_2i, θ_3i) be the admixture proportion of i-th individual at a disease susceptibility marker locus. Since θ_1i + θ_2i + θ_3i = 1, without loss of generality, we use θ_1i and θ_2i be the independent component on the model. If W_i be the vector of covariates, then a multiple regression model between the phenotype and the ancestry can be expressed as

$$y_i=a+b_1{\theta }_{1i}+b_2{\theta }_{2i}+\zeta W_i+{ϵ}_i,$$ (8)

where a is the intercept, b₁ and b₂ are the slope parameters, ζ be the vector of the covariates effect, and ${ϵ}_i\sim N(0,{\sigma }_{ϵ}^2)$ is the residual. Covariates may include age, gender, age of disease onset, medication status, individual’s average ancestry, and other clinical genotypes and environmental exposure factors. A significant nonzero b₁ or b₂ or both indicate a possible association between the phenotype and the ancestries. The null and alternate hypotheses of the test can be expressed as -

$${\mathrm{H}}_0:{\mathrm{b}}_1={\mathrm{b}}_2=0{\text{vs. H}}_1:\text{at least one of the}{\mathrm{b}}_1\text{or}{\mathrm{b}}_2\text{is non-zero.}$$

During the planning stage of analysis, the sample information, and hence b₁ and b₂, are unknown. So, it is practical to perform the power analysis unconditional to data by setting some desired level of relationship such as the multiple R² between phenotype and independent variables (Gatsonis & Sampson, 1989). Cohen proposed an approximation for power and sample size analysis using multiple R² from linear multiple regression based on the approximate non-central F-distribution (Cohen, 1988). Gatson and Sampson further suggested that the approximation of Cohen is highly accurate for power and sample size approximation for linear multinomial regression (Gatsonis & Sampson, 1989). In this article, we performed the power and sample size analysis of (8) using the multiple R² as proposed by Cohen (Cohen, 1988).

Let $R_1^2$ and $R_0^2$ be the multiple correlation of (8) with and without the ancestry information, then the null and alternate hypotheses can be equivalently expressed as-

$${\mathrm{H}}_0:{\mathrm{R}}^2=R_0^2{\text{vs. H}}_1:{\mathrm{R}}^2>R_0^2(=R_1^2).$$ (9)

The model (9) provides a test for non-zero gain in proportion of explained variation of Y (phenotype) by using the ancestries in the model. The Cohen’s measure of effect size (f²) based on the model (9) is given by $f^2=\frac{R_1^2-R_0^2}{1-R_1^2}$. Under the null hypothesis f²~F_u,v, a central F-distribution with numerator degree of freedom (u) and the denominator degree of freedom (v). If k = # of ancestries and w = # of covariates in the model (8), we will have the numerator degree of freedom (u) = k −1 (= 2 for three-way admixture), the denominator degree of freedom (v) = N - u - w - 1. Under the alternate hypothesis, f² is approximated as non-central F-distribution with the con-centrality parameter (δ) = f²(u + v + 1). If α be the level of significance, C = P(F_u,v ≥ α) is the critical value, and β be type II error rate, then the power of the test (9), 1 – β, can be estimated as

$$1-\beta =P(F_{u,v}(\delta )\ge C).$$ (10)

On the other hand, if β be the type II error rate, for the sample size estimation, we first estimate the non-centrality parameter δ by solving the equation P(F_u,v(δ) < C) – β = 0 for δ. Note that both δ and C in the equation are functions of v. So, the equation (10) will be, in turn, solve for the denominator degree of freedom $(v)=\frac{\delta }{f^2}-u-1$, and the approximated sample size is

$$N=u+v+w+1.$$ (11)

The post-hoc power analysis of the test (10) depends on the f², the number of the variables under the null and alternate models, the sample size, and the type I error rate. Alternately, for the sample size analysis, one can provide f², the number of the variables under the null and alternate models, the type I error rate, and the power or the type II error rate (β).

When there is no covariates in the model, we can set $R_0^2=0$, and w =0 in the above computation. Accordingly, the effect size becomes $f^2=\frac{R_1^2}{1-R_1^2}$. The power and sample size are again computed as before using (10) and (11).

In PAMAM, the power and sample size approximations are performed using equations (10) and (11) when covariates are present, and using (11) when no covariate presents.

Generalize model for multi-ancestry power and sample size analysis

The power and sample size estimations described for the three-way admixture mapping in equations (4) - (7) can be generalized for multi-ancestry admixture populations with more than three ancestries. For a case-only admixture mapping on admixed population consisting of k ancestries (k ≥ 3), the computation of $\delta =N{\sum }_j\frac{(p_j-{\theta }_j{)}^2}{{\theta }_j}$ in (4) and $w=\sqrt{{\sum }_j\frac{(p_j-{\theta }_j{)}^2}{{\theta }_j}}$ in (5) hold with summation over j = 1 to k. Similar generalization of the equations (6) and (7) can be applied for case-control admixture mapping. In either scenario, the underlying chi-square distribution has degree of freedom k −1. Additionally, the power and sample size analysis of quantitative traits using (10) and (11) can be generalized for multi-way admixture analysis with more than three-way admixture by simply adjusting the numerator degree of freedom (u). Note that if k = # of ancestries, then u = k-1.

Tool and Code Availability

We have implemented the proposed PAMAM method in JavaScript. PAMAM tool is freely available from https://research.cchmc.org/mershalab/PAMAM/login.html. A user manual is available to download from the website. We have further developed R codes implementing the PAMAM algorithm for two-way and three-way power and sample size analyses. The R codes are freely available under the GNU General Public License on the Mersha Lab GitHub page: https://github.com/MershaLab/PAMAM

List of abbreviations

PAMAM

Power analysis of multi-ancestry admixture mapping

AM

Admixture mapping

GWAS

Genome wide association study

AOR

Ancestry adds ratio

GRR

Genotype risk ratio

PRR

Parental risk ratio

HI

Hybrid-isolation

CGF

Continuous gene flow