Precise Burst Synchrony in the Superior Colliculus of the Awake Cat during Moving Stimulus Presentation

Abstract

This study aimed to characterize the synchrony that occurs between cell discharges in the superior colliculus of the awake cat. We trained cats to perform a visual fixation in the presence of a visual moving stimulus and then recorded 686 pairs of neighboring cells in the superior colliculus during task performance. A new method to assess the significance of precise discharge synchronization is described, which permits analysis of nonstationary data. Of 181 pairs with sufficient data for quantitative analysis, 125 showed a cross-correlation histogram (CCH) with features assessed as significant using this approach. CCHs frequently showed an isolated central peak (41 of 125) or a peak flanked by one or two troughs (68 of 125), and in a few cases an oscillatory pattern of ∼65 Hz (16 of 125). This is in contrast to the oscillation frequency reported for the visual cortex and shows that oscillations in the superior colliculus probably arise from a cortex-independent mechanism.

Our method also permits direct quantification of the correlation shift predictors, assessing precise time locking of spikes to the stimulus. Only 1 of 125 cross-correlation shift predictors had a significant central peak, meaning that most of the CCH features were not related to cell discharges time-locked to the stimulus presentation.

Further investigation using a burst-jittering method showed that synchrony in the superior colliculus is attributable to precise synchronization of short bursts of spikes. Such synchrony could be related to the network dynamics and the common inhibitory feedback from local interneurons, which would act as temporal selectors of the cells with greatest or fastest response.

Synchronous neuronal activity at the millisecond time scale has been described in the mammalian visual cortex (Griffith and Horn, 1963) and in many other regions of the brain (Singer and Gray, 1995). Although this phenomenon has aroused interest for some time, its functional significance remains uncertain and has become an object of speculation and controversy (Usrey and Reid, 1999). Synchrony could be related to information transfer by synfire chains (Abeles, 1991), information storage in potentiated synapses (Singer, 1995; Whittington et al., 1997), a time advance coding scheme (Hopfield 1995, 1996), tag transmission in binding theory (Roelfsema and Singer, 1998), or to timed neuronal selection for temporal pattern recognition (Laurent, 1996; Parodi et al.,1996). Similarly, coincident bursts have also been suggested to play a role in synaptic plasticity and information processing (Lisman, 1997).

Determining the time during an experiment when synchrony occurs could shed light on its possible function (Vaadia et al., 1995; Riehle et al., 1997). However, this is a difficult statistical problem, because it requires a method capable of quantifying the excess of synchronous spikes, termed coincident events (CEs), even when the neural firing rates covary with the animal's performance, behavior, or attention (Pauluis and Baker, 2000). Without such precise quantification, it is not possible to show that the information provided by the CEs differs from that contained by the firing rate variation.

The superior colliculus (SC) has long been known as a sensorimotor interface that controls rapid orientation movements (Sparks, 1986;Grantyn, 1988). The ventral part of the superficial laminae of the SC receives direct afferent input from the retina and visual cortex layers V and VI pyramidal cells (magnocellular pathway). Cortical projections maintain topographic alignment with the retinal input, so that the central 10° of the visual field are represented proximally by >30% of the SC. Cells in the superficial and intermediate layers are visually responsive, exhibit a phasic response to the onset and offset of a stationary spot of light, and respond vigorously to stimuli moving at 0.5–30°/sec (sometimes up to 800°/sec). Conversely, the response of cells in deep layers exhibits dramatic adaptation to repetitive stimulation (Sparks, 1986; Grantyn, 1988).

The visual processing of moving visual stimuli performed in the SC suggests that, as in the visual cortex, the SC may be a structure in which synchrony is important for information processing. However, collicular and corticotectal multiunit cross-correlations observed in the anesthetized cat exhibit much broader peaks than in the cortex (average width at half height, 51 msec; Brecht et al.,1998). Such broad temporal dispersion is thought to be related to a simultaneous activation of both cells or to the presence of large bursts in their discharges, but not especially to a temporally precise coding (Nelson et al., 1992; Nowak et al.,1995).

Given the major role of the SC in gaze and attention orientation (Goldberg and Wurtz, 1972; Wurtz et al., 1982; Robinson and Kertzman, 1995), we studied spike train correlations in the SC of awake cats. The animals performed a fixation task to a central target while a light spot moved in the visual field. We used new quantification methods that relied on instantaneous discharge probability estimates to calculate the expected correlation on a single-trial basis (Pauluis and Baker, 2000).

A preliminary account of this work has been presented previously in abstract form (Pauluis et al., 1999).

MATERIALS AND METHODS

Experiments were performed on two adult cats selected after a few weeks of training on gaze orientation tasks. The care and use of animals was in accordance with the guidelines of the Society for Neuroscience and the American Physiological Society.

General

Two cats were prepared for chronic gaze recording by undergoing a first surgery. Anesthesia was induced with xylazine (2 mg/kg, i.m.) and, after 20 min, with ketamine hydrochloride (10 mg/kg, i.m.). Deep anesthesia was maintained throughout with additional injections of both drugs. A scleral search coil (three turns of 20-mm-diameter Teflon-insulated stainless steel wire; Cooner Wire Company, Chatsworth, CA) was implanted under the conjunctiva. The animal was placed in a Horsley–Clarke apparatus, and a head implant was constructed from dental cement and anchored to the skull with stainless steel screws. A fixation device was embedded in dental cement to fix the head during experiments.

After recovery from the surgery, cats underwent a second stereotaxic procedure under deep anesthesia. A craniotomy was performed to allow access of microelectrodes into both SCs, and a stainless steel recording chamber was added to the head implant on the midline at stereotaxic coordinate anterior, +2.

Behavioral paradigms

Cats were trained to perform fixation and saccade tasks for food reward. The target spots were projected on a tangential screen by oscilloscopes controlled with an 80486 personal computer (digital-to-analog converter frequency; 100 Hz).

Moving stimulus paradigm. All trials started with an auditory click followed after 300 msec by the appearance of a small fixation point (FP) of 0.5° and a larger stimulus point (SP) (disk ∼3.0°) both at the center of the visual field (Fig.1A). The cat had 1200 msec to begin fixating and was required to maintain fixation for 500–1200 msec (Fig. 1C). Then, the SP moved slowly toward the periphery with fixed velocity (5–70°/sec), amplitude (5–35°), and direction, which could be chosen either specifically or randomly (Fig. 1B). The SP was the stimulus for the recorded cells. At the end of the ramp, the SP was switched off for 300 msec. A new SP appeared then at the center and started to move after 60 msec. This was repeated up to four times. During the whole paradigm the cat was not allowed to follow the stimulus and had to maintain fixation within 3° of the FP to receive a food reward.

Fig. 1.

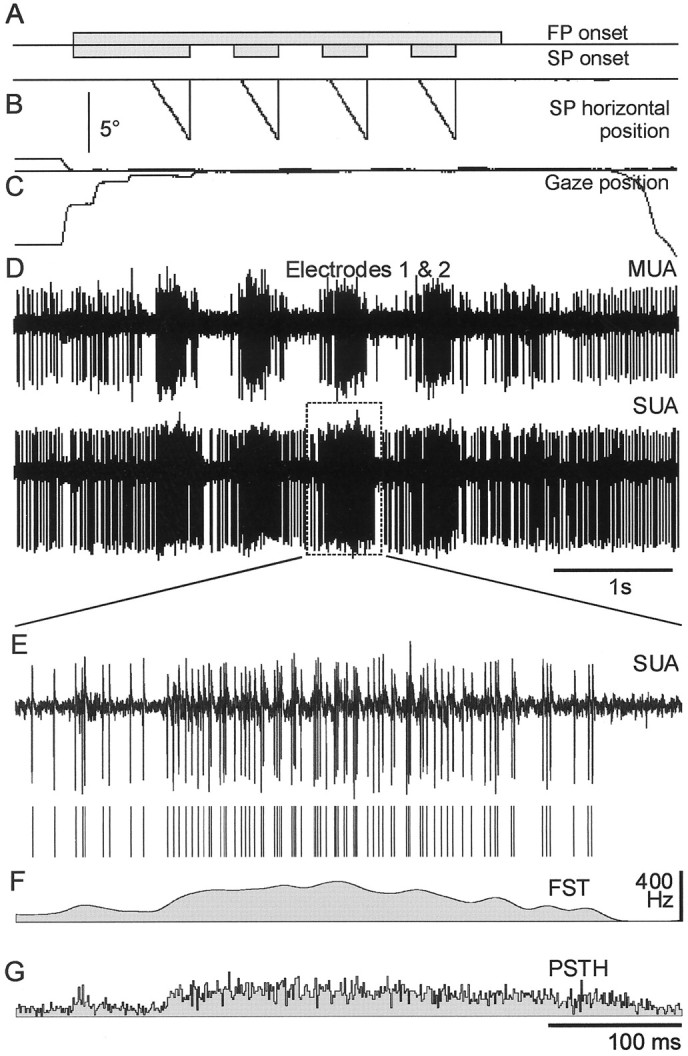
Set up and instantaneous discharge probability estimates. A light spot was presented in the center of the screen and was moved at a uniform velocity (15°/sec) toward the periphery while the cat was continuously fixating another central point. The onsets of the fixation point (FP) and stimulus point (SP) are shown in A. During the fixation task, the SP was moved toward the periphery, as illustrated inB. The FP and eye positions are presented inC. Cellular activities were recorded from two independent electrodes (D). Result of spike discrimination (E) is shown for a single stimulus presentation. After window discrimination, this train was classified as a single-unit activity, and the other was classified as a multiunit activity. In this study, the estimate of the instantaneous discharge probability (F) is the spike train (E), filtered with a 10 msec Gaussian kernel (filtered spike train). This measure is contrasted with the commonly used PSTH (G) calculated from 80 trials which, in this case, underestimates the discharge probability because the data were not stationary during the 80 trials, as in many experiments on awake animals.

Cats were typically capable of 2 hr of sustained task performance, performing a total of 300–800 trials in blocks of 20–80.

Recording and data collection

Neuronal discharge was recorded extracellularly with two commercially available tungsten microelectrodes (impedance, 0.15–0.6 MΩ at 1 kHz; FHC, Bowdoinham, ME). The two electrodes were mounted on a double hydraulic microdrive (model MO-95B; Narishige, Tokyo, Japan) fitting a single recording chamber and were driven independently. Electrode penetrations were made vertically through a single guide tube (21 gauge; horizontal distance between electrode tips, >300 μm). The guide tube was inserted afresh each session through the dura to a depth of 5 mm above the SC. Neural activity was conventionally amplified (gain, 5000 or 10,000; Neurolog NL-100 and NL-104; Digitimer), filtered (300 Hz to 6 kHz; Neurolog NL-125; Digitimer), and displayed. System noise level was 30 μV because of the magnetic search coil fields. Cross-talk between the two channels was never observed.

Eye position was measured with the magnetic search coil technique (magnetic field frequencies, 50 and 75 kHz). The target and stimulus positions were generated by an 80486 personal computer and data acquisition card (model AT-MIO-16E; National Instrument) that also drove the food reward pump and controlled a constant current stimulus isolator (WPI) for electrical stimulation.

The two independent electrodes were positioned in the SC just below the first layer of spontaneously active cells in dim light. As the track was continued deeper, cell discharges showed more and more adaptation to the visual stimulation, preventing reliable recording for more than a few trials. For this reason, most of the cells were recorded in the superficial and intermediate layers (a depth of 0.5–2 mm below the SC surface).

After a recording session, if the track location was new or if the electrode location was uncertain, we used a stimulation paradigm. After initial fixation of a single FP in the center, the FP was turned off and, after an interval of 50 msec, a stimulation train was delivered (500 μsec pulse width; 200 Hz; 200 msec duration; 20 μA). At the end of the stimulation train, a new target appeared randomly 10° to the right or to the left of the FP, and the cat had to fixate this new target for food reward. The direction and amplitude of evoked short-latency saccadic eye movements permitted precise assessment of the electrode position (Roucoux and Crommelinck, 1976).

All of the data related to the gaze and stimulus positions, to the stimulation, and to the reward were digitized at 2 kHz, whereas the extracellular activities were sampled at 20 kHz (Pentium-Pro 200 MHz; model AT-MIO-64-E3; National Instruments). Some data files were transferred immediately after the set of trials onto another computer (Pentium-Pro 200 MHz) to assess the fine temporal relationship between the spike trains. If the cell discharges were not correlated, they were discarded after a few sets. At the end of the recordings for each day, raw data were stored on digital compact disks for further off-line analysis.

In the final recording session, electrolytic lesions were made with stainless steel electrodes to mark the SC (20 sec, 20 μA anodal pulse). The animal was then anesthetized with xylazine (2 mg/kg, i.m.) followed by pentobarbital sodium (40 mg/kg, i.p.). After transcardial injection of heparin, the animal was perfused with 0.9% saline and then with potassium ferrocyanate diluted in neutral formalin, to color iron deposits. The brain was removed and placed into a solution of formalin with 15 and then 30% sucrose until it sank. The SC was blocked, frozen, and cut into 30 μm transversal sections. One section of three was mounted onto chrome–alum-coated slides.Postmortem histological processing confirmed that the marker lesion sites were located in the anterior two-thirds of the SC at the expected depth.

Data analysis

To remove movement artifacts and to sort two or more spike waveforms, we used a program based on multiple level discriminators set sequentially on a plot of superposed spike waveforms (Matlab 5.0). We compared this simple method to a more time-consuming principal component analysis (Eggermont, 1990), and they appeared equally efficient. To ensure that a single cell was recorded, an autocorrelation histogram (ACH) was constructed (0.1 msec bin width). The waveform was attributed to a single cell only if the measured absolute refractory period was at least 0.75 msec [minimum interval observed by DeBusk et al. (1997) in the cat striate cortex was 0.73 msec]. From this processing, it was usually possible to isolate one or more waveforms from a single channel and to classify them as originating from a single or multiple units. No attempt was made to separate overlapping spikes. All the waveforms from a given electrode that did not satisfy the absolute refractory period criterion were pooled together into one channel of multiunit activity.

Before considering the temporal relationship between two different cell discharges, we checked whether the same cells could have been recorded on both electrodes simultaneously. This was achieved by a high-precision cross-correlation histogram (CCH) (0.1 msec bin width; lags, 2 msec). If the same cell was recorded on both electrodes, it is expected that the CCH peak would be very narrow and very high. There could be a short time lag because the spike waveforms could be slightly different. Nine recordings were excluded from the analysis because the CCHs exhibited a very narrow central peak (0.1–0.2 msec width).

We also characterized the interspike interval (ISI) distribution by the proportion of ISIs shorter than 3 msec. This proportion was used by Gray and McCormick (1996) to characterize the chattering cells that had 27.5 ± 10.8% of their ISIs shorter than 3 msec (n = 11). Although this proportion has been previously applied to single-unit recordings, we extended its use to the multiunit activities for descriptive purpose only, because only a small number of different cells were present in a single channel of multiple unit activity thanks to the spike wave discrimination. The term “bursting train” is used here to describe the recordings in which ≥25% of the ISIs were shorter than 3 msec.

Other analysis always took place during a period that started 80 msec after the movement beginning, that is after the strongest effect in the cell discharge caused by movement onset, and ended at the movement offset, that is before the offset response.

Instantaneous discharge probability. To determine the significance of cross-correlation peaks, one approach is to assume that the time-dependent discharge probability of each cell is equal to its peristimulus time histogram (PSTH). This would correspond to the joint peristimulus time histogram (JPSTH) method (Palm et al., 1988; Aertsen et al., 1989). However, this method encounters problems if the discharge is variable from one trial to the next. Because the cat's attention was changing considerably throughout the recording session, there was some trial-to-trial covariation in the neuron firing rate. We therefore chose to use instead the second alternative i.e., to estimate the instantaneous discharge probability directly from the spike train (Abeles, 1982; Palm et al., 1988). These instantaneous discharge probability estimates were used to calculate the expected correlation on a single-trial basis. Single-trial expectations were then summed to obtain the expected correlation caused by firing rate covariation. The assumptions made to estimate the instantaneous firing rate are then critical for the interpretation of results. Because we analyzed the spike train correlation during a period without any sudden change in the stimulus presentation, we expect the instantaneous firing rate to vary smoothly during this time. Therefore, we used a simple Gaussian kernel estimator to assess the instantaneous discharge probability. The spike train was simply filtered by convolution with a Gaussian function (SD, 10 msec; Fig. 1F; Silverman, 1986). This means that only synchrony that is more precise than the 10 msec SD of the Gaussian kernel used to estimate the instantaneous discharge probability will test as significant using our analysis.

CCH. Synchronization was quantified by means of the CCH (Fig. 2A). The CCH counts, when divided by the number of trigger spikes, represent the conditional probability of the occurrence of a response spike if a trigger spike occurred. When two spike trains are independent, the CCH is flat, i.e., the conditional probability remains constant whatever the time interval. If the CCH is not flat, there is some functional correlation between the cells (Perkel et al., 1967; Moore et al., 1970).

Fig. 2.

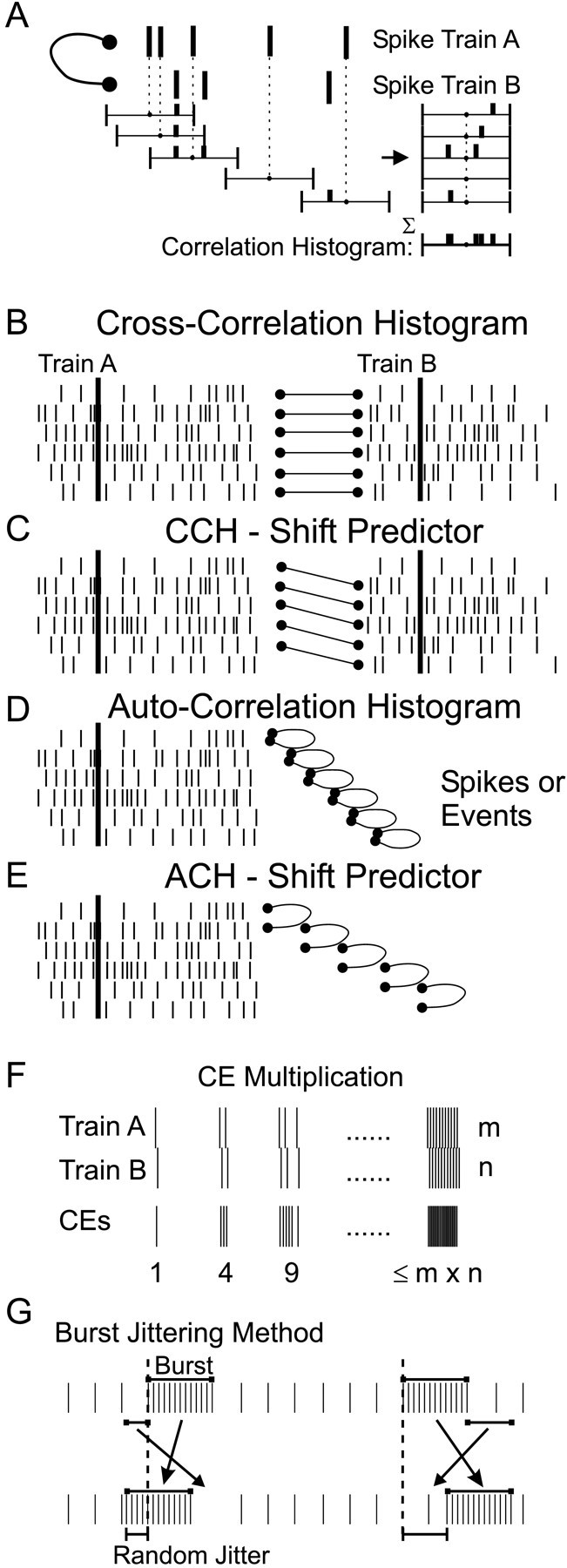
The counting process involved in the CCH and related measures. A, For each spike of the train A, spikes of train B occurring within a fixed window relative to the spike of A cause the corresponding bins of the CCH to be incremented. The sum of all these windows gives the CCH. B, Correlation is calculated from two spikes train of the same trial. C,Conversely, the CCH shift predictor is calculated between thenth trial of A and the (n + 1)th trial of B.D, To calculate an ACH, the same train is used twice.E, Again, the ACH shift predictor involves thenth trial and the (n + 1)th trial, both related to the same cell. F, When two spikes occur within a time delay corresponding to the CCH central peak, they are termed a CE. This definition also assumes that the maximum number of CEs within this time window is the product of the number of spikes. G, During burst jittering, the whole burst is shifted with a random delay, and the spikes that are at the target location are swapped with the original burst.

All analysis was performed on the CCH smoothed by means of a 5 msec window average, advanced in 1 msec time steps. Significance was assessed assuming that the spike distribution in each window followed a Poisson distribution, using a threshold of p < 0.001. The probability that the number of coincidences c will be at least as many as the number observed, C, given thatE are expected, was calculated as Equation 1:

$$P(c\ge C)=1-\sum _{i=0}^{i=C-1} \frac{e^{-E}{E}^{\text{i}}}{\text{i}!}$$ Equation 1

This method for significance quantification is independent of the bin width, but still requires that the event probability is very small and independent from the occurrence of the other events (Poisson process).

To measure stimulus-locked changes in excess synchronization, we calculated the time-resolved CCH. An example is displayed in Figure5C. The abscissa X corresponds to time relative to the stimulus movement onset, whereas the ordinate Y is the lag time relative to each spike of cell 1. It is exactly as if the CCH was plotted in a gray scale as a function of peristimulus time, like in a raw JPSTH (Palm et al., 1988; Aertsen et al., 1989). For each trial, we calculated the time-resolved cross-correlation and its expectation function, using the instantaneous frequency estimate of the two cells. The time-resolved cross-correlation and its expected value were then summed across trials and compared (1 msec bins). The CCH could be extracted from the time-resolved CCH by summing along the stimulus-related time axisX (see Fig. 5G).

Fig. 5.

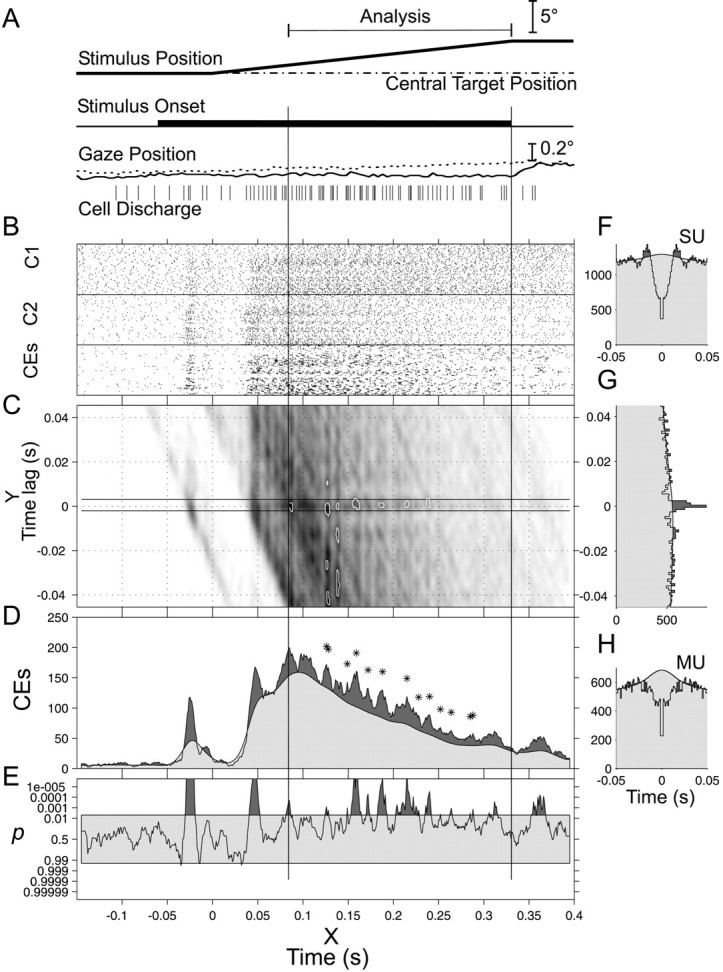
Time-resolved cross-correlation.A, Schematic representation of stimulus time course, along with the gaze position and spike train of the single trial shown in Figure 1E. B, After off-line discrimination, action potentials were plotted in the two top rasters. Their cross-correlation is shown in G, and the delay defining a CE was determined from the significant bins of the central peak (−1.5 to +2.5 msec). The CEs were displayed in the third raster of B. The texture is more contrasted in the CE raster than in the spike rasters because CE calculation enhances burst coincidences. C, The smoothed time-resolved cross-correlation is shown on a gray scale. The CEs are shown inside the two horizontal lines. The expected value of the time-resolved cross-correlation was calculated from the instantaneous discharge probabilities for each trial and then summed. The first percentile of most significant p after filtering is highlighted by the white curves. The CCH (G) was calculated as the bin sum along the abscissa between 80 and 333 msec (vertical lines). The time-resolved cross-correlation can also be summed along the y-axis between −1.5 and +2.5 msec to give the CE count shown inD (dark gray). The expected CE count is calculated similarly and shown in light gray. The significant peaks are marked by a star(p < 0.005 in a 9 msec window). The ACHs for each spike train are shown in F andH. The central bin is set to the value of the adjacent ones. In E, the significance test of the CE count is plotted as a surprise test: log_{10((1 − P)/P)}. Each time the p values pass below 0.005, the curve is shaded in dark gray, and the corresponding point in D is marked by astar. Same experiment as in Figure 1.can also be summed along the y-axis between −1.5 and +2.5 msec to give the CE count shown in D (dark gray). The expected CE count is calculated similarly and shown in light gray. The significant peaks are marked by astar (p < 0.005 in a 9 msec window). The ACHs for each spike train are shown in Fand H. The central bin is set to the value of the adjacent ones. In E, the significance test of the CE count is plotted as a surprise test: log_{10((1 − P)/P)}. Each time the p values pass below 0.005, the curve is shaded in dark gray, and the corresponding point in D is marked by astar. Same experiment as in Figure 1.

The peak width was determined from the CCH by the intersections of the observed and expected count curves. The high level of confidence used (p < 0.001) ensured that the detected peaks were visible to the naked eye and obviated the need for an additional criterion on the peak amplitude. The peak with the highest amplitude was called the “central peak” and was characterized by the relative modulation amplitude (RMA), calculated as the ratio of the peak amplitude to the expected value: (max − expect)/expect (Engel et al., 1990, 1991a,b,c; Brecht et al., 1999) and by the peak width at half-height. The RMA is related to the factork, which is the ratio of maximum peak count to the expected count: max/expect (Sears and Stagg, 1976; Kirkwood and Sears, 1982). Hence, RMA = (max − expect)/expect = k− 1, which has also been described as the relative peak height (Cope et al., 1987).

If there was more than one central peak within ±70 msec, the other significant peaks were called “satellite peaks” and were taken as evidence for an oscillatory correlation.

CCH shift predictors. When spikes are produced in response to a stimulus, the stimulus could synchronize the recorded cells. This stimulus-related synchronization was quantified by the shift predictor (Perkel et al., 1967; Palm et al., 1988). These predictors are computed similarly as for the CCH (Fig.2B), except that the spike trains correlated are related to two successive trials (Fig. 2C). If the stimulus direction was varied (30 recordings), the shift predictor was computed with the next trial in the same direction. The expectation of the shift predictor was also calculated using the instantaneous discharge probability estimates, as explained for the time-resolved cross-correlation. Significant peaks in the shift predictor then indicated precise time locking of spikes to the stimulus presentation.

ACH. Autocorrelation histograms were also computed for each spike train (Fig. 2D), and the presence of satellite peaks was used to quantify whether the discharge was oscillatory (see Fig. 5F,H). Statistical requirements for significance were similar to the CCH.

An ACH shift predictor (Fig. 2E) was computed between the nth and (n + 1)th trials. The expectation was calculated on a single-trial basis, using the instantaneous discharge probability, as explained for the time-resolved cross-correlation. Significant peaks in the ACH shift predictor indicated that spikes were time-locked to the stimulus.

CEs. If a central peak was observed in the CCH, we used the number of significant bins of the smoothed histogram to define the time delay during which a spike occurring in both cells was called a CE. In the example of Figure 5, four windows centered at −1, 0, 1, and 2 msec were significant, so that each time a spike of the second cell occurred between 1.5 msec before and 2.5 msec after a spike of cell one, it was considered as a CE. The CE definition was thus directly related to the CCH peak, in contrast to previous definitions that have used an arbitrary allowed interval (Grün, 1996; Riehle et al.,1997). The moment of each CE was determined as the mean time between the two spikes: (t₁ −t₂)/2 (Pauluis and Baker, 2000). This definition allowed two CEs to occur by chance exactly at the same moment. If the two cells fired together in a short burst, the number of CEs would be the product of the number of spikes in each burst (Fig.2F). This multiplicative property mirrors the way in which bursts of spikes contribute to the CCH.

Once the CEs had been defined, it was possible to calculate their ACH and ACH shift predictor, which we will denote CE–ACH and CE–ACH shift predictor. This allowed the characterization of oscillations and stimulus time locking in the CEs.

Burst perturbation analyses. Many cells recorded in this study showed burst discharges. Spike bursts invalidated the Poisson assumption we made for statistical testing (Eq. 1). To asses the influence of this firing pattern on our results, we designed a control analysis. The bursts in spike trains, defined as a succession of ISIs <3 msec, were located. This arbitrary value is convenient and comes from the definition of the chattering cells in the visual cortex (Gray and McCormick, 1996). The spikes of each burst were deleted and then added back to the spike train after a random shift (uniform distribution), which was the same for the spikes belonging to the same burst (Fig. 2G). Any spikes that originally fell within the new location of the burst were moved to the part of the spike train from which the burst had been removed. This technique ensured that the number of short ISIs was constant or even increased, whereas the precise timing of the spike bursts was destroyed. All measures were then recalculated to assess the impact of burst precision on our statistical procedures.

The same jittering method was applied to CE trains to test whether the time precision of CE bursts was relevant to our findings.

RESULTS

Correlation histograms

Of 686 pairs of spike trains tested for cross-correlation, 181 were selected as having a reasonable amount of data (>500 spikes in each train and mean cross-correlation count per bin >15). A significant central peak in the CCH was found in 125 recordings (Table1). Fourteen of one hundred twenty-five (14 of 125) CCHs involved the activity of two single units, and the others were from multiunit activities (39 of 125 involved a single and a multiunit activity, and 72 of 125 involved two multiunit activities). Only three CCHs were obtained from cells recorded with the same electrode. In the selected set of recordings with sufficient data (n = 362 = 2 × 181 trains), the proportion of recordings that had >25% of their ISIs shorter than 3 msec was 32.6% (“bursting trains”). This proportion was not significantly different in units that were part of a pair showing a CCH peak (34.0%; n = 250; binomial test). In these data, we conclude that bursts do not predispose to significant CCH central peaks.

Table 1.

Quantitative results

	Number of recordings
# Pairs	686
# CCH with >500 spikes & offset >15	181
# Pairs with CCH peak	125
# CCH with significant satellite peak (s)	16
# CCH with significant trough(s)	68
# Trains with >500 spikes	435
# ACH peaks ≤ 8 msec	17
# ACH peaks > 8 msec	40
# CCH-SP offset >15:	123
# Significant CCH-SP	1
# Significant ACH-SP	8
# CE-ACH-SP offset >15:	63
# CE-ACH-SP with central peak	47
# ACH-CE with satellite peaks	42

The main results for pooled recordings are detailed in this table. The number of pairs considered was 686. Only 181 recordings were obtained from trains of >500 spikes each and exhibiting mean CCH level larger than 15 spikes per window. The number of pairs with significant CCH peak is then given, with the number of pairs having significant satellite peaks and troughs. There were 435 trains that exhibited >500 spikes. The number of satellite peaks in ACH are presented separately with the assumption that a peak at ≤8 msec means that the cells could be bursting and that a longer delay means an oscillatory discharge (Fig. 3D). As shown in the second part, only eight trains showed a discharge that was time-locked to the stimulus presentation. In only one CCH, the central peak could be related to this time locking. In contrast, the CEs seemed strongly time-locked to the stimulus presentation, and they exhibited satellite peaks very often.

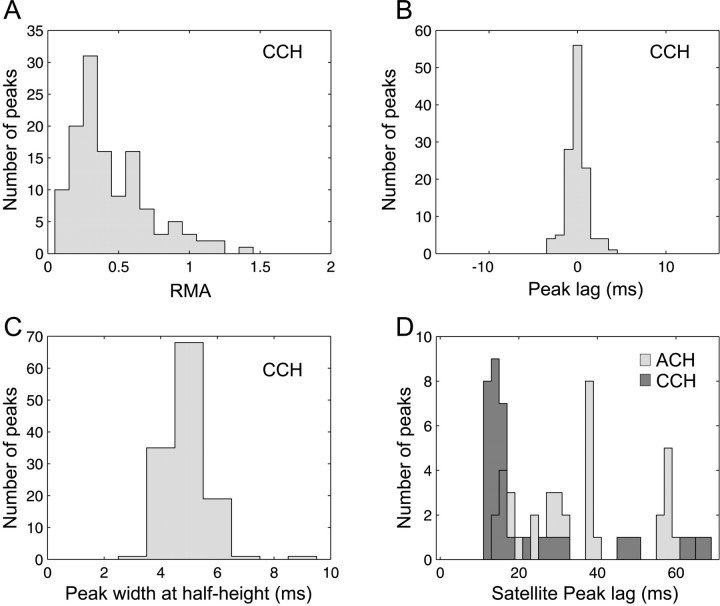
The properties of the significant CCH central peaks are described in Figure 3. The RMA is plotted in Figure3A. Except in few cases, the RMA was >0.1, which has been used previously as a significance threshold (Engel et al.,1990).

Fig. 3.

CCH. After filtering, the central peaks in CCHs were quantified by their RMA: (max − expect.)/expect. The RMA distribution is shown inA. B, The peak lag distribution is precisely centered on 0 msec (mean, 0.02 ± 1.19 msec SD;n = 125), and the peak width at half height is shown in C to be centered on 5 msec. D,Satellite peaks were identified in ACHs, and their delay distribution is shown in light gray. Some satellite peaks were also found in the CCHs and are displayed in dark gray. Most such peaks were found between 12 and 18 msec (55–85 Hz), but they represented <15% of the recordings (Table 1).

The distribution of the central peak time lag is shown in Figure3B and is well centered on 0 msec. Figure3C displays the distribution of the width at half height for the central peak. Peaks were narrow, corresponding to the “Tower” type of Nelson et al., (1992): as noted in Materials and Methods, our analysis technique was specifically designed to detect such narrow peaks. Only 16 recordings showed significant satellite peaks at nonzero lag (Fig. 3D, dark gray).

Shift predictors were constructed by cross-correlating one spike train recorded during a given trial with the other spike train recorded during the next trial (Perkel et al., 1967). The use of an instantaneous discharge probability estimate allowed direct significance quantification for the shift predictors. Only one of the CCH shift predictors showed significant features, in contrast to the preponderance of central peaks in the CCHs. This indicates that only one of the CCH central peaks could be attributable to spike time locking to the stimulus presentation.

Examples of ACHs are shown in Figure 5, F and H. Among trains with >500 spikes (n = 435), a significant peak within 8 msec of zero lag in the ACH was found in 17 recordings (Table 1); we interpreted these peaks as indicating a stereotyped burst discharge.

Satellite peaks in ACHs at >8 msec lag were found in 40 of 435 trains (see Fig. 5F). Figure 3D shows the distribution of their time lags in light gray; this has a first mode centered on 16 msec (63 Hz), and some others at 30 and 40 msec. A similar distribution was found for the CCH satellite peaks (dark gray, 16 recordings). Only eight spike trains exhibited a significant peak in the ACH shift predictor (Table 1), illustrating that these cells had a discharge that could be time-locked to the stimulus presentation.

Although oscillatory synchronization as assessed from the presence of satellite peaks was rare, >50% (68 of 125) of the CCH central peaks were flanked by one or two significant troughs. In these 68 recordings, it is possible that correlated spike trains with a narrow central peak would have produced a smoothed central can also be summed along the y-axis between −1.5 and +2.5 msec to give the CE count shown in D (dark gray). The expected CE count is calculated similarly and shown in light gray. The significant peaks are marked by a star(p < 0.005 in a 9 msec window). The ACHs for each spike train are shown in F andH. The central bin is set to the value of the adjacent ones. In E, the significance test of the CE count is plotted as a surprise test: log_{10((1 − P)/P)}. Each time the p values pass below 0.005, the curve is shaded in dark gray, and the corresponding point in D is marked by astar. Same experiment as in Figure 1.peak in the expected CCH calculated from the instantaneous firing rates, leading to the erroneous detection of troughs in the difference. However, if we modified the instantaneous discharge estimate by extending the Gaussian kernel from 10 to 150 msec SD, we still obtained 64 recordings with significant troughs, making it unlikely that the troughs were artifactually generated in this way.

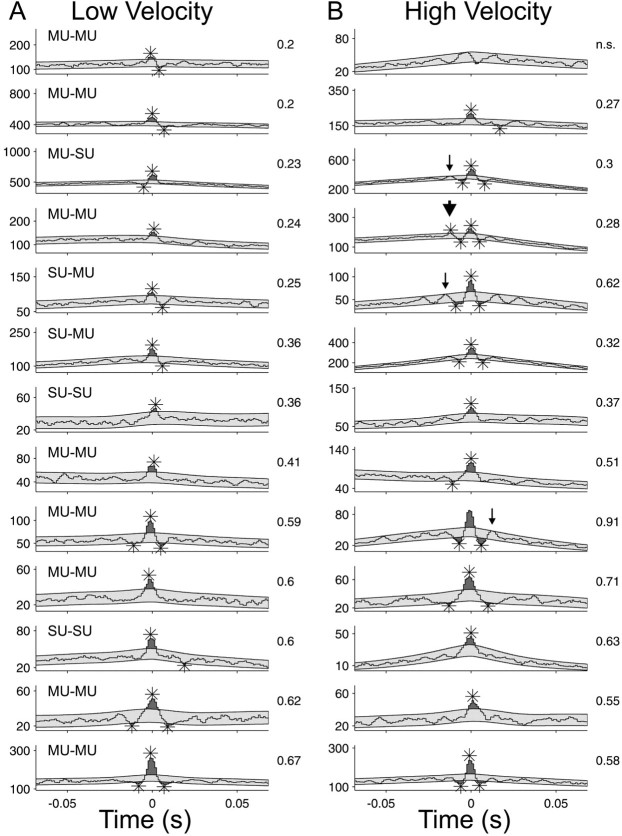
We could not detect any effect of the stimulus velocity on cellular synchronization; Figure 4 provides a summary for the 13 pairs on which this was tested. With increasing velocity, the maximum firing rate increased slightly, but this did not reach significance (mean difference, 18.4 spikes/sec ± 13.1 SE;p = 0.08; paired t test). Raw CCHs computed for lower velocities (5–35°/sec) are displayed in the left column, and those for higher velocities are displayed in the right (15–70°/sec). Visual inspection reveals that the peak shapes were remarkably constant irrespective of the stimulation velocity. There was no consistent trend in synchrony strength with stimulus velocity, as measured by the RMA (displayed on the right side of each CCH). There was a slight tendency for an increase in synchronous oscillations at the high velocity: a significant (p < 0.001) satellite peak appeared in one data set (large arrowhead), and also in three others if the significance level was relaxed to p< 0.0025 (small arrows).

Fig. 4.

Stimulus velocity testing. Thirteen pairs were tested for low (A, 5–35°/sec) and high (B, 15–70°/sec) stimulus velocities, and the resulting CCHs were compared. Smoothed CCHs are shown for every set of data, and the expected CCH ± 3 SD has been shaded in light gray (p < 0.001;√count). Stars denote significant peaks and troughs. The RMA is indicated in the top right corner of each CCH. Nine of 13 peaks increased their RMA when the stimulus velocity increased. The CCH shift predictors were flat in all cases.

Coincident event analyses

Coincident event distribution

The following analyses were performed to assess the distribution of CEs in the poststimulus time average to shed light on their origin (Fig. 5D,E). Figure5B shows the response of two cells during the presentation of a moving stimulus (Fig. 5G). The corresponding ACHs are shown in Figure 5, F and H.

The time-resolved cross-correlation histogram is displayed in Figure5C. After testing for significance and filtering (two-dimensional Gaussian convolution 2 msec SD), significant regions (p < 0.01) were highlighted by a white line. From ∼130–250 msec, the dark spots on the zero-lag axis are surrounded by two brighter traces, resembling eraser marks, which denote troughs either side of the central peak in the CCH. The raw CCH is plotted in Figure 5G and corresponds to the sum of the time-resolved cross-correlation along the stimulus time axis, between 80 and 333 msec. The CCH expectation (calculated from the instantaneous firing rates) is superimposed in light gray. The number of adjacent significant windows in the CCH is shown by the two horizontal lines on both sides of 0 msec lag in the time-resolved cross-correlation histogram (bins, −1 to +2 msec; Fig. 5C). All the points between these two lines were called CEs. Such events were summed and plotted in Figure 5B as rasters (CEs) and in Figure5D as a PSTH (dark gray curve), on which is superposed the corresponding expectation (light gray). The coincidence count (Fig.5D) was then tested to quantify CE excess significance, assuming that the CEs follow a nonstationary Poisson distribution with rate equal to the sum of the single-trial CE expectations (compare Eq.1). Significant excess in a particular time window during the period of 80–333 msec is indicated on Figure 5D by a star. Significance is plotted as a surprise measure (cf. Aertsen et al., 1989) in Figure 5E.

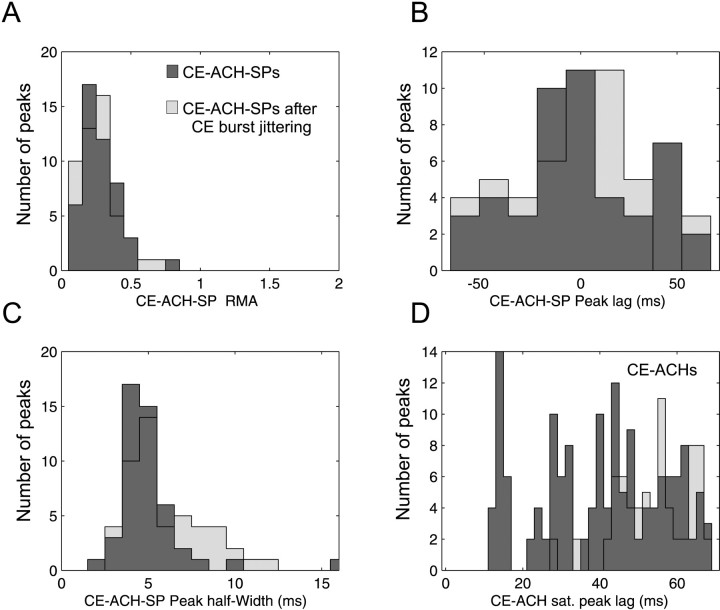
Such an analysis shows when CEs were present in excess during the poststimulus time. To address the issue of the distribution of CEs across time and to show how the CE density could vary from trial to trial, we computed the CE–ACH shift predictor for the complete set of trials in each of the 125 experiments with a significant CCH peak. Peaks in the CE–ACH shift predictor indicate that the CEs tended to occur at similar times after the stimulus from one trial to the next. Forty-seven recordings exhibited peaks in both the CCH and the CE–ACH shift predictor, suggesting that CEs could be stimulus locked in this way. This is in contrast to the fact that only one CCH shift predictor and only eight ACH shift predictors were peaked (Table 1).

Figure 6 shows the results of correlation analysis performed on CEs. The distribution of the RMA of the significant central peak of the CE–ACH shift predictor is shown in Figure 6A. The peak lag distribution is shown in Figure 6B. The peak lag of the CE–ACH shift predictor was broadly centered on 0 msec. The width of CE–ACH shift predictor peaks had a similar distribution to the width of peaks in the CCH (Figs. 3C, 6C). Finally, we performed autocorrelation analysis on CEs, and satellite peaks were found at ∼15 and 30 (Fig. 6D), as for spike train autocorrelation (Fig. 3D; 42 CE–ACHs vs 55 cells).

Fig. 6.

CE–ACH shift predictor and CE–ACH. CEs were found to be time-locked to the stimulus presentation in 47 recordings (dark gray). The background light grayhistograms refer to the results obtained after CE burst jittering (see Results). A, Peaks did not have a large amplitude. B, Peak lag distribution was broadly centered on 0 msec (−0.9 msec ± 32.3 SD; n = 47).C, The peak width at half height was similar to that for CCH peaks. D, Autocorrelation performed on CEs revealed more satellite peaks than any other correlation measure, with a mode of ∼15, and then possibly at 30 and 45 msec.

Effect of burst discharge on statistical measures

Fifty percent of the recordings with a significant peak in the CE–ACH shift predictor were from bursting trains (>25% ISIs shorter than 3 msec; n = 94), and 32.6% of pairs with peaked CCH came from bursting trains; these proportions were significantly different (p < 0.001, binomial test). The statistical tests used to detect peaks assumed that spike trains could be approximated by Poisson processes, an assumption clearly violated when bursts are present. We therefore tested whether the results obtained above could have been influenced by the presence of bursts in the spike trains. Rather than attempt to generate a more appropriate theoretical statistical model for the spike trains, we used the empirical burst-jittering analysis described in Materials and Methods (Fig. 2G), in which whole bursts were randomly swapped with other nearby segments of the original spike train. This was designed to destroy precise burst synchronization between the two simultaneously recorded neurons, while maintaining the bursting nature of the individual spike trains.

When jittering was applied to bursts in the original spike trains, of 125 CCHs with significant peaks, only 62 remained significant after the application of a random jitter with maximum size ±10 msec. This number remained fairly constant for larger jitters up to ±50 msec. We can therefore be confident that at least half of the CCH central peaks were caused by burst synchronization and were not an artifact of cell bursting.

A contrasting result was obtained when burst jittering was applied to the CE trains. Of 63 recordings suitable for CE analysis, between 46 and 51 showed significant CE—ACH shift predictors for jitters from ±1 to ±50 msec; this compared with 47 significantly peaked CE–ACH shift predictors in the original data. The number of significant peaks was thus essentially unaffected by the burst jittering. Measurements made from these peaks, for the largest jitter tested (±50 msec), are shown in light gray in Figure 6. Surprisingly, the distribution of most of the measures was also qualitatively unaffected, even by this considerable jittering of the bursts. Peaks were no larger (Fig.6A), similarly timed (Fig. 6B), and of comparable width (Fig. 6C). The only difference was that the jittered CE trains did not show an oscillatory peak in the ACH (Fig. 6D; no isolated peak at 16 msec lag).

We conclude that the presence of peaks in many of the CCHs results from genuine short-term synchronization of bursting spike trains and is not solely a statistical artifact caused by the presence of bursts. However, the apparent precise time locking of CEs to the stimulus, as indicated by the presence of features in the CE–ACH shift predictors, is by contrast likely to result from an artifactual influence of CE bursts on the statistical calculations.

Single-trial analysis

An important advantage of our method based on the instantaneous discharge rate is that it allows inspection and significance assessment of single trials, provided that enough spikes were collected. This is accordingly examined below.

Figure 7 illustrates how the CE count varied with trial repetition in a single recording session. This experiment was the first one of the day, so attention was probably sustained for an especially long time at the beginning of the session. There were 80 trials, each 333-msec-long; these are plotted sequentially along the abscissa in Figure 7A. The observed number of CEs is described by the dark gray histogram and the expected CE count by the overlying light gray area. Cells discharged at much higher rates during the first trials, which produced the higher expected CE count at that time. However, a clear CE excess persisted throughout.

Fig. 7.

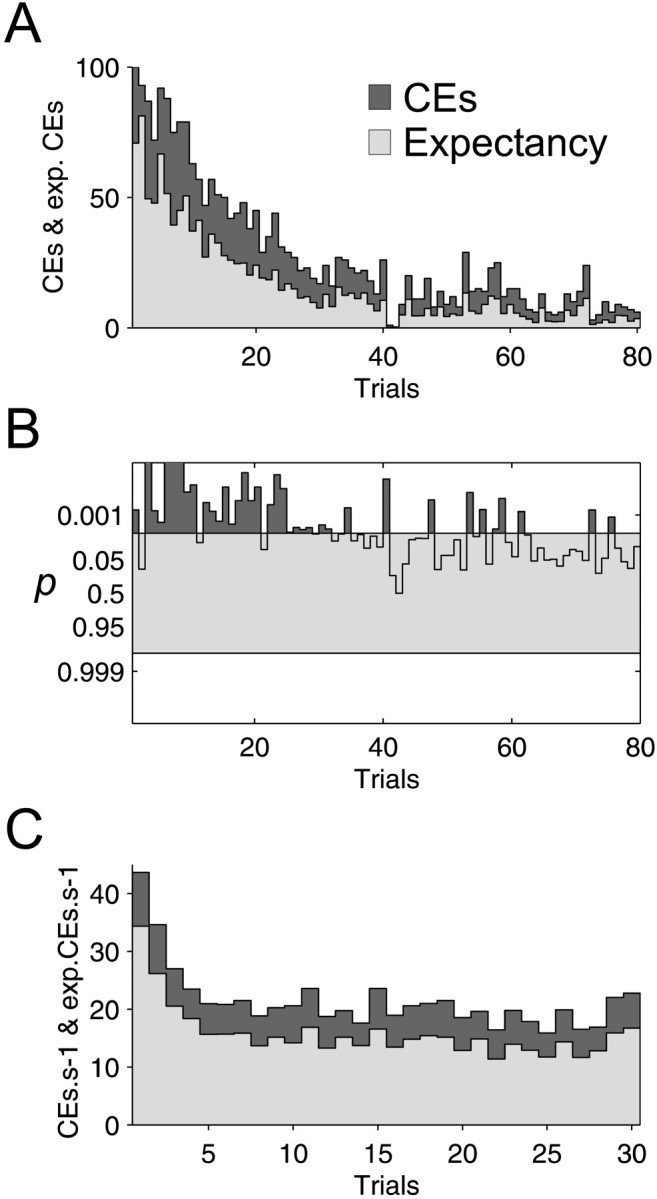
Trial repetition. Instantaneous discharge probability estimates allow quantification of the CE excess on a single-trial basis. A, CE (dark gray) and expected CE count (light gray) are shown for all trials.B, The surprise test on each trial was positive more often during the first part of the experiment than during the second one. C, CE count and expectation were averaged for all 81 data sets, presenting at least one CCH peak and composed of 31–40 trials. On average, the decrease in CE expectation occurred within the first five trials. This contrasts with A, but this experiment in A was the first of the day, and attention could have been longer sustained.

The surprise test for each trial is presented in Figure 7B. CE excess failed consistently to test as significant for the later trials, because of the low number of counts expected reducing the power of the statistical tests.

CE rates from recordings with a significant cross-correlation peak were averaged for each trial. Figure 7C shows this average for 81 experiments composed of 30–40 trials and that were recorded at different moments of different days (average trial duration, 1 sec). This confirms the results of the single cell pair shown in Figure 7,A and B. Cells are usually more responsive during the first five trials; however, the CE excess remained significant (p < 10⁻⁹) and fairly constant during the whole recording session.

DISCUSSION

Methodological considerations

The method developed in the present study offers many advantages over the usual JPSTH method (Aertsen et al., 1989). First, it is able to cope with highly nonstationary data because the CE estimate is adjusted for each trial separately and, in each trial, for every moment with the requested precision (here 10 msec SD). Nearly every trial can be included securely in the rasters, even if cell firing rates are much lower or much higher than in the other trials. Such trials with covariant and unexplained discharge variations are pernicious when included in JPSTH because they are not described adequately by the PSTH and consequently bias the CE expectation. This leads to the assessment of large cross-correlation peaks caused by patterns of covariant activities (Brody, 1999a,b; Pauluis and Baker, 2000). A way to control for this problem is to show that the expected CCH offset fits well the observed CCH offset for the each period of the experiment. This simple check is not performed in some CE analysis (Riehle et al.,1997). The method used here is based on the calculation of the CE expectation for each single trial and compensates very simply for this kind of problem. Second, it offers a quantitative approach to test significance of any correlation measure, including the shift predictors. Their significance was quantified previously by recursion or by comparison with the shuffled predictor. Third, when this method is coupled to traditional perturbation methods like burst jittering, it enables direct quantification of the spike or burst precision. Fourth, it allows trial by trial CE significance calculation, an ability that permitted the quantification of the effect of trial repetition and of which more sophisticated experimental paradigms could make use.

Precise burst synchrony in the superior colliculus

One of the main results of the present study is the direct evidence for precise burst synchrony in the visual response of collicular cells of the awake cat. Lisman (1997) suggested that in some regions, single spikes are just noise. It has been shown recently byLivingstone et al. (1996) that in the primary visual cortex of alert monkeys only bursts provided a clear indicator of the presence of a visual stimulus. Burst discharges in the SC have been reported previously by Mandl (1993) in the pretrigeminal cat during moving visual stimulus presentation, and 25% of the responding cells exhibited a 60–80 Hz burst frequency. We were able to show that such cells synchronize their short spike bursts with a precision of few milliseconds.

In contrast, Brecht et al. (1996, 1998, 1999) reported previously that synchrony takes place in the SC of the anesthetized cat with a wide time course: the mean width at half height was 51 msec for corticotectal interactions, and similar values were found for intracollicular interactions (>20 msec). However, Brecht et al. (1999) assessed CCH peaks by fitting a generalized Gabor function to the CCHs (König, 1994). Broad peaks could possibly be better identified than thin ones because curve fitting favors identification of large trends over narrow peak characterization, whereas our method assumes that wide peaks are caused by firing rate covariation.

In awake cats, the CCH peak width at half height was on average 5 msec (Fig. 3C). In awake animals in comparison to the anesthetized state, the temporal relationship changes from a coactivation pattern to precise synchrony, which is very interesting because the SC can be regarded as an attentive filter (Goldberg and Wurtz, 1972; Robinson and Kertzman, 1995; Kustov and Robinson, 1996) and because attentive tasks enhance synchrony in other brain areas (Murthy and Fetz, 1992, 1996a,b; Roelfsema et al.,1997).

Spike time locking has been described previously in response to a sudden change in the stimulus presentation (Mainen and Sejnowski, 1995). It has also been reported that most cells in the cat LGN and visual cortex could synchronize strongly on a 60 Hz monitor refresh rate (Wollman and Palmer, 1995). Such evident causes of fast stimulus locking are unlikely during our stimulus presentation because we used an oscilloscope with a position increment rate of 100 Hz, and SC oscillations we found had a frequency of 65 Hz. We also took care to start analysis after the fast transient because of the onset of the stimulus displacement and excluded the stimulus offset because such events would have locked the cell discharge. Although the synchrony between spikes is precise, they are not precisely time locked to the stimulus presentation.

It was shown recently that fixational eye movements can cause large response modification in the firing rate of visual cells in the primary cortex and lateral geniculate nucleus (Gur et al., 1997). Although the SC cells we recorded responded strongly to the visual stimulus, we cannot exclude that small eye movements were responsible for part of the synchronization.

Oscillations in the superior colliculus

We found some evidence of oscillation in the SC at 65 Hz. According to previous simulation work (Traub et al., 1996;Pauluis et al., 1999), the oscillation frequency would depend on the physiology of local inhibitory interneurons. Lopez-Barneo and Llinas (1988) estimated the membrane time constant of neurons located in the stratum griseum intermediale of the SC in guinea pig to be 4.13 ± 1.3 (SE) msec (n = 27), a value two times smaller than the shortest cortical membrane time constant (Koch et al., 1996). This could explain the fast oscillations in the SC. The involvement of inhibitory interneurons in network oscillations is also supported by the recent evidence showing inhibitory bursting cells in the intermediate and deep layers of the rabbit superior colliculus, which may form mutual inhibitory connections (Zhu and Lo, 2000).

There were 40 oscillatory ACHs, but many of the CCHs exhibited no satellite peaks (109 of 125). This would be interpreted, if the recordings had been made in the visual cortex, as a lock-in state (Eckhorn, 1994) that probably corresponds to suboptimal stimuli. Because of constraints on the duration of recordings in awake animals, and especially in cats, our stimulus parameters had to be rapidly adjusted to be close to, but probably did not reach, the optimal. Moreover, attention and motivation decreased during the experiment leading to a decrease in the response to the stimulus. Whereas attention modulates the visual response in the SC (Goldberg and Wurtz, 1972), it has been shown that stimulation of the mesencephalic reticular formation increases visually evoked oscillations in anesthetized and awake cat (Metherate et al., 1992; Munk et al., 1996; Steriade et al., 1996).

Another explanation for our failure to detect oscillations could be that although some occurred, their frequency was too irregular to be significant in the CCH. This is supported by the fact that the SC receives both visual afferents from the retina, which have been shown to oscillate at 61–114 Hz in response to visual targets (Neuenswander and Singer, 1996; Castelo-Branco et al., 1998), and from the visual cortex in which moving stimuli induce typically 30–60 Hz oscillations (Gray et al., 1989; Singer and Gray, 1995;Castelo-Branco et al., 1998). Castelo-Branco et al. (1998) suggested that in response to moving stimuli, subcortical (LGN) and cortical oscillations dissociated, but if cortical mechanisms dominated, LGN responses could become phase locked to the cortical oscillations. Some SC cells could receive predominately retinal input, showing 65 Hz oscillations, whereas some others might receive both kinds equally. However, only a few satellite peaks were found to be compatible with the known cortical oscillation frequency, suggesting that in the main SC oscillations arise from a cortex-independent mechanism (Fig. 3D). Our results are in marked contrast to the low-frequency oscillations previously reported in the anesthetized cat (5–20 Hz; Brecht et al., 1999; Chabli et al., 2000).

Trough-peak-trough pattern

In our data, symmetrical troughs flanked many of the CCH peaks. Our previous modeling work has shown the conditions needed to reproduce this pattern (Pauluis, 2000). On the basis of this, we suggest that there are three different states of network dynamics that produce qualitatively different cross-correlation features. First, an isolated central peak is evidence for a common input, which may be either excitatory or inhibitory, and arise from either local or extrinsic circuits (Perkel et al., 1967). Where the central peak is flanked by troughs, this may reflect a common inhibitory feedback acting with delay on the recorded cells, possibly from the local interneurons (Pauluis, 2000). This is however one step short of full oscillatory network activity. Finally, there may be genuine oscillations, leading to satellite peaks in the cross-correlation. Modeling work has shown the importance of mutual inhibition between interneurons to produce oscillatory activity (Wilson and Cowan, 1972; van Vreeswijk et al., 1994; Whittington et al., 1995; Traub et al., 1996; Wang and Buzsáki, 1996; White et al., 1998; Pauluis et al., 1999). The network state leading to a central peak flanked by troughs could therefore be an intermediate stage on the way to sustained oscillations. Our results should encourage experimenters to test the significance of satellite troughs to differentiate this pattern from an isolated central peak or a genuine oscillatory CCH.