Synaptic Depression Mediates Bistability in Neuronal Networks with Recurrent Inhibitory Connectivity

Abstract

When depressing synapses are embedded in a circuit composed of a pacemaker neuron and a neuron with no autorhythmic properties, the network can show two modes of oscillation. In one mode the synapses are mostly depressed, and the oscillations are dominated by the properties of the oscillating neuron. In the other mode, the synapses recover from depression, and the oscillations are primarily controlled by the synapses. We demonstrate the two modes of oscillation in a hybrid circuit consisting of a biological pacemaker and a model neuron, reciprocally coupled via model depressing synapses. We show that across a wide range of parameter values this network shows robust bistability of the oscillation mode and that it is possible to switch the network from one mode to the other by injection of a brief current pulse in either neuron. The underlying mechanism for bistability may be present in many types of circuits with reciprocal connections and synaptic depression.

Rhythmic movements are often produced by neuronal networks known as central pattern generators (CPGs). Many CPGs consist of neurons connected with reciprocal inhibitory connections (Peterson, 1983; Satterlie, 1985; Marder and Calabrese, 1996). Although many neurons in a CPG may show intrinsic oscillatory properties, synaptic connections play a substantial role in shaping the network output (Miller and Selverston, 1982; Marder and Calabrese, 1996).

Short-term synaptic depression is a common feature of CPG synapses (Manor et al., 1997; Parker and Grillner, 1999; Sanchez and Kirk, 2000). In cortical circuits, recent research has identified several functional roles of synaptic depression, including automatic gain control (Abbott et al., 1997), network stabilization (Varela et al., 1999), and synchronization (Tsodyks et al., 2000). Surprisingly, almost nothing is known about the functional roles of synaptic depression in CPGs (Nadim and Manor, 2000).

In oscillatory networks, network characteristics such as cycle period and neuronal voltage ranges often depend on synaptic strength. When the synapse is depressing, synaptic strength depends on the level of recovery that, in turn, depends on these network characteristics. This circular interaction can produce bistability in network operation. In one state, cycle period is long, and the extent of hyperpolarization in the presynaptic cells is large. The inactive state of each presynaptic neuron allows the synapse to recover from depression and strengthen, which in turn hyperpolarizes the postsynaptic neuron and lengthens cycle period. In the other mode, the synapses are depressed and have a small effect on the postsynaptic potential and thus contribute little or nothing to the cycle period. In this mode, the intrinsic properties of the neurons that are involved primarily determine the cycle period. We refer to these two oscillation modes as synapse-controlled (SC) and cell-dominated (CD).

In previous modeling work we showed that bistability could arise in an inhibitory network consisting of a pacemaker neuron receiving feedback from a follower neuron (Nadim et al., 1999). Bistability in this model was based on post-inhibitory rebound in the pacemaker and depression in the synapse from the follower to the pacemaker. However, the synapse from the pacemaker to the follower did not need to be depressing. In this work, we show that bistability can be obtained if both synapses are depressing, even when post-inhibitory rebound properties are weak or absent.

We study this mechanism in the pyloric network of the crab Cancer borealis. The pyloric rhythm is driven by a pacemaker group of three electrically coupled anterior burster (AB) and two pyloric dilator (PD) neurons. A fourth lateral pyloric (LP) neuron inhibits the PD neurons (see Fig. 1A). Our study focuses on this reciprocally inhibitory sub-network (see Fig. 1B). We functionally removed the LP neuron from the network and coupled the PD neurons to a computational LP model neuron with model synapses implemented using the dynamic-clamp technique (Sharp et al., 1993;Manor et al., 1998). We show that when the synapses are depressing, this hybrid biological-model network exhibits two stable modes of oscillation, and transient stimuli can switch the network between modes. This bistability is robust, and random transitions between states do not occur.

Fig. 1.

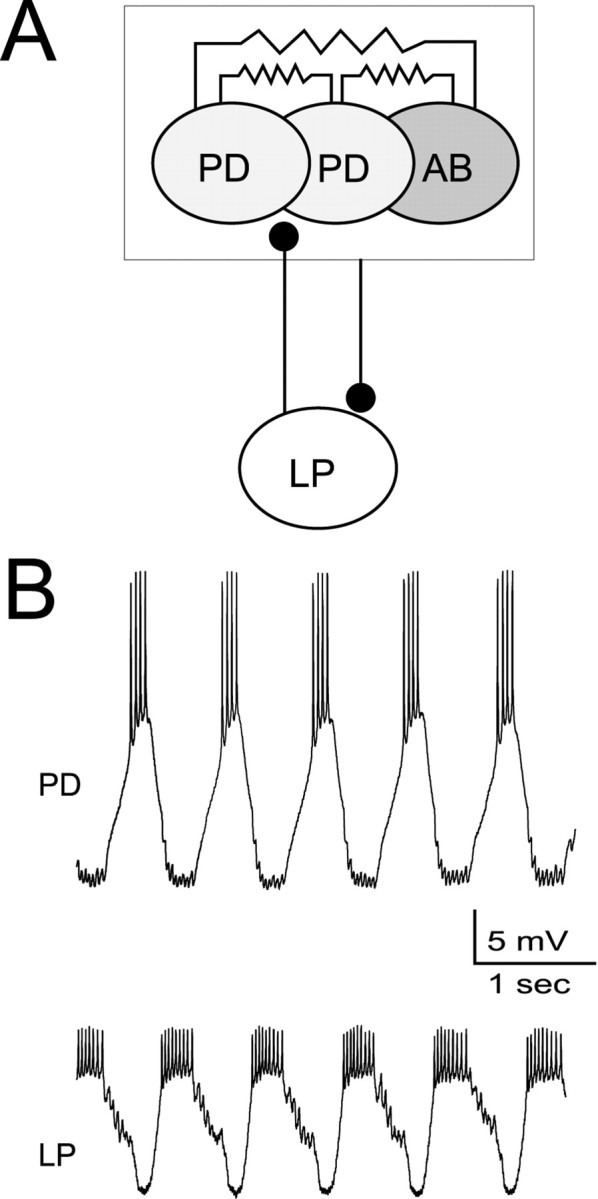
The LP neuron provides inhibitory feedback to the pyloric pacemaker. A, Schematic drawingshows the pyloric pacemaker group consisting of the electrically coupled PD neurons and the AB neuron. The LP neuron is inhibited by the pyloric pacemakers and inhibits the PD neurons. B, Intracellular recordings of the PD and LP neurons show that these two neurons burst rhythmically in alternation.

MATERIALS AND METHODS

Electrophysiology. Crabs (C. borealis) were purchased from local markets in Newark, NJ. The stomatogastric nervous system was dissected from the stomach, pinned in a Petri dish lined with Sylgard 182 (Dow Corning, Corning, NY) and superfused with cold (10–12°C) saline. The saline composition was (in mm): 440 NaCl, 11 KCl, 26 MgCl₂, 13 CaCl₂, 11.2 Trizma base, and 5.1 maleic acid, pH 7.4–7.5. The stomatogastric ganglion was desheathed, and the neurons were identified. The LP and the two PD neurons were impaled with sharp microelectrodes filled with 4 m KAc + 20 mm KCl (15–25 MΩ). One of the two PD neurons was always recorded in two-microelectrode current-clamp mode. The membrane potential of this PD neuron was monitored and used for calculating the artificial PD to LP synaptic current (see below). This current was injected in both PD neurons. Voltage recordings and current injections were done with Axoclamp B1 amplifiers (Axon Instruments, Foster City, CA) in bridge mode. Signals were digitized using a PCI-MIO-16E-1 board (National Instruments, Houston, TX) at a sampling rate of 2.5 kHz.

Coupling model and biological neurons in real time. Although the PD neurons are only a subset of the pacemaker group, all neurons in the pyloric pacemaker group are strongly electrically coupled and coactive (Harris-Warrick et al., 1992b). Hence, for the purpose of this paper, the PD neurons were considered an oscillator (Fig.1).

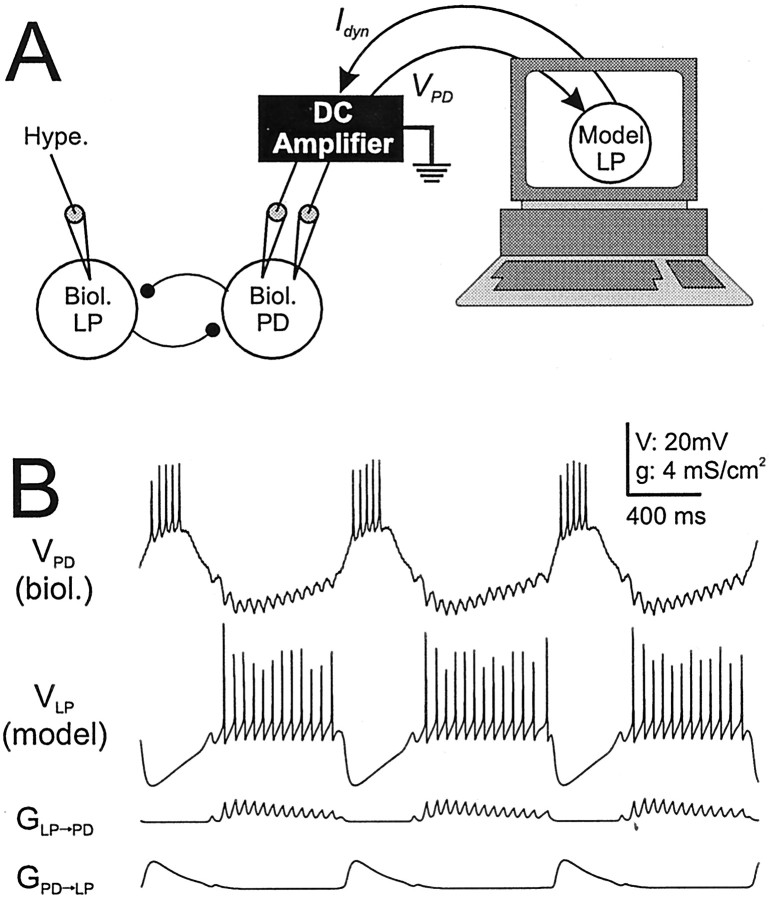
After functional elimination of the biological LP to PD synapse (usually with injection of a 5–10 nA negative DC current into the biological LP neuron), we reciprocally coupled the biological PD neuron and the LP model neuron with model synapses in real time. For this purpose, we wrote a dedicated real-time software in the LabWindows/CVI environment (National Instruments). The software numerically integrated a set of coupled ordinary differential equations describing the voltage and ionic conductances of the LP model neuron and the conductances of the model synapses. The numerical integration of these differential equations was dependent on the continuous acquisition of the PD neuron membrane potential (see below). The synaptic current from the LP model neuron to the PD neuron was calculated by multiplying the LP to PD synaptic conductance by the driving force of the synapse (see the synaptic models below) and was injected into the PD neuron on-line to mimic the biological LP to PD synapse. A schematic of the experimental setup is illustrated in Figure2A. Figure2B is an example that shows the voltages of the biological PD neuron and the LP model neuron and the conductances of both artificial synapses. The different shapes in synaptic conductances are the result of different parameters of these synapses. The IPSPs in the biological PD neuron were fast and corresponded to the individual LP action potentials. In contrast, the inhibition of the LP model neuron was slow and smooth. These distinct synaptic responses are characteristic of the biological synapses (Weimann, 1992).

Fig. 2.

Substitution of the biological LP neuron with an LP model neuron and model synapses. A, The experimental paradigm involves hyperpolarizing the biological LP neuron by injecting a large (5–10 nA) negative DC current to functionally remove the LP neuron from the network. A computer model of the LP neuron is then coupled, in real time, to the biological PD neuron using the dynamic-clamp technique. B, Example of an experiment using the paradigm described in A. The top two traces are the time courses of membrane potentials in the biological PD and LP model neuron. As a result of undersampling, the spikes in the LP model appear to have different heights. Thebottom two traces show the actual conductances of the model synapses.

The LP model neuron. The LP neuron was modeled as a tonic neuron, firing at 15 Hz in agreement with the firing rate of the biological LP neuron in isolation (data not shown). The model included a leak conductance, a fast transient sodium conductance (g_Na), a fast persistent potassium conductance (g_K), a slow hyperpolarization-activated inward conductance (g_h), and a synaptic conductance representing the PD to LP synapse. The dynamics of the LP model neuron voltage is described by the following differential equation: C dV_LP/dt =I_ext − G_leak(V − E_leak) −G_Nam³h(V − E_Na) −G_Kn⁴(V − E_K) −G_hp(V −E_h) −I_PD→LP, where C is the specific membrane capacitance (1 μF/cm²),G_i values are maximal conductances (in mS/cm²: leak 2, Na 10, K 1, h 1), andE_i values are reversal potentials (in mV: leak −40, Na 50, K −80, h 10, PD→LP −80). The last term in the equation is the synaptic current from the PD to LP synapse. Its calculation is described below.

The next family of equations is a set of differential equations governing the behavior of a state variable (activation or inactivation) for an ionic conductance: dx/dt = (x_∞(V_LP) −x)/τ_x(V_LP)x = m, h, n,p, where x_∞(V_LP) are steady-state curves of the form 1/(1 + e^(V−Vx)/k) (V_x in mV: m −28, h −30, n −30, p −64;k in mV: m −10, h 1, n −1, p 3) and τ_x(V) values are associated time constants of the form τ_l + (τ_h − τ_l)/(1 +e^(V−Vm)/k) (V_m in mV: m −28, h −30, n −30, p −64;k in mV: m −10, h 1, n −1, p 3; τ_lin msec: m 0, h 204, n 204, p 500; τ_h in msec: m 0, h 4, n 4, p 500). τ_x = 0 means the variable x is instantaneous.

The model synapses. The synaptic models were developed from experimental measurements of synaptic dynamics, with methods similar toManor et al. (1997). These synaptic models were used to build a reciprocally inhibitory circuit between the PD neuron and the LP model neuron using our software with the dynamic-clamp technique (Sharp et al., 1993; Manor et al., 1998). We define synaptic currents with the following equation: I_pre→post =G_pre→posta d(V_post −E_syn, where G is the maximal conductance of the synapse and E_syn is the reversal potential. d and a describe the depression and activation processes, and their dynamics are governed bydy/dt =y_∞(V_pre −y)/τ_y(V_prey = a, d. The steady state curvesy_∞ have the form 1/(1 +e^(V−Vx)/k). The time constants τ_y have the form τ_l + (τ_h − τ_l)/(1 +e^(V−Vx)/k). In contrast to the parameters for LP model neurons, which are pretuned, the synaptic parameters are tuned for each experiment because they depend on the specific voltage range and response of the PD neuron, which can change from preparation to preparation. We use the notationg_pre→post =G_pre→posta d to denote the actual conductance of the synapse.

Tuning the model parameters. The first step was to construct a depressing synapse from the PD neuron to the LP model neuron so that the LP model neuron was entrained to the PD neuron oscillations without being strongly inhibited. This step was performed out by the following procedure.

(1) The midpoint of the function a_∞for the PD→LP synapse was set at a value approximately in the middle range of the slow-wave oscillations of the PD neuron. The slope of this function was set at a value where the synapse was maximally active at the peak of the slow-wave oscillations and almost completely deactivated at the trough of these oscillations.

(2) τ_a for the PD→LP synapse was independent of voltage and between 25 and 50 msec.

(3) The midpoint of the function d_∞for the PD→LP synapse was set at ∼1–2 mV below the trough of the slow-wave oscillations of the PD neuron. The function was chosen to be steep, so that it went from inactive to maximally active in a 3–4 mV window.

(4) The function τ_d was defined with the same midpoint and slope as d_∞ and was of the same order of magnitude as the oscillation period. Typically, we allowed the value of τ_d to be twice as large during the trough of the PD neuron oscillations (500 msec in the example shown in Fig. 3) compared with the burst phase. This time constant was chosen so that the synapse remained partially depressed (d < 0.1) but had the potential to recover from depression if the PD neuron interburst duration became longer.

Fig. 3.

The two modes of oscillation. Network activity was examined at different values ofG_PD→LP.G_LP→PD was kept fixed at a value of 1.5 nS. Shown are the time courses of the membrane potential of the biological PD neuron, the synaptic current from the LP model to the PD neuron, the membrane potential of the LP model neuron, and the synaptic current from the PD neuron to the LP model neuron withG_PD→LP = 0 (A),G_PD→LP = 2 nS (B),G_PD→LP = 4 nS (C). In A and B, the rhythm is determined by the dynamics of the PD neuron (CD mode). InC, the rhythm is controlled by the dynamics of the synapses (SC mode). The horizontal dotted linessuperimposed on the PD neuron and the LP model neuron voltage traces represent the midpoint of the steady-state depression/recovery curves of the PD to LP synapse and the LP to PD synapse, respectively.D, Steady-state activation and depression/recovery curves for the PD to LP synapse (top panel) and the LP to PD synapse (bottom panel). The voltage range (ordinate) is identical to the voltage range of the traces in A–C. The dotted drop lines represent the midpoint of the depression/recovery curves.

(5) TheG_PD→LPsynapse was set at a value large enough so that the LP model neuron was entrained to the rhythm but not very strongly inhibited.

Because the biological LP→PD synapse produces large action potential-mediated IPSPs in the PD neuron, this synapse was modeled with a high activation threshold so that it was activated by the LP model neuron action potentials (Manor et al., 1997). The LP→PD synapse was modeled as follows.

(1) The midpoint of the sigmoid a_∞ for the LP→PD synapse was set at a value approximately in the middle range of the LP model neuron action potentials. This function is steep, so that it went from 0 to 1 in a 3–4 mV window.

(2) τ_a for the LP→PD synapse was independent of voltage and fast (5–10 msec).

(3) The midpoint of the sigmoid d_∞for the LP→PD synapse was set at ∼1–2 mV below the trough of the slow-wave oscillations of the LP model neuron.

(4) The function τ_d was defined with the same midpoint and slope as d_∞ and was comparable to the d_∞ of the PD→LP synapse.

In some cases we eliminated the capability of a synapse to depress. In the model synapse this was done by setting the state variabled to 1, independent of presynaptic voltage or time. We refer to this type of synapse as “static.”

The symmetric model parameters. In this section we describe the model described in the last section of the results (see Fig. 9). Unlike the LP model, the symmetric model was not used in a coupling with the biological network but was used as a pure computational construct. This model consists of two identical neurons reciprocally coupled with identical depressing synapses. The equations of the model neurons are given by C dV/dt = −G_leak(V − E_leak) −G_inwardm_∞(V) h(V − E_inward)dh/dt = (h_∞(V) −h)/τ_h, where C = 1 μF/cm²,G_leak = 0.4 mS/cm²,G_inward = 0.6 mS/cm²,E_leak = −65 mV,E_inward = 40 mV,m_∞(V) = 1/(1 + exp(−(V + 50)/4),h_∞(V) = 1/(1 + exp((V + 55)/8), and τ_h = 150 msec. The synaptic currents are given byI_syn = G_syna d (V_post −E_syn), whereG_syn is the maximal conductance of the synapse and E_syn is the reversal potential. d and a describe the depression and activation processes, respectively, and their dynamics are governed bydy/dt − (y_∞(V_pre) − y)/τ_y(V_pre)y = a, d.

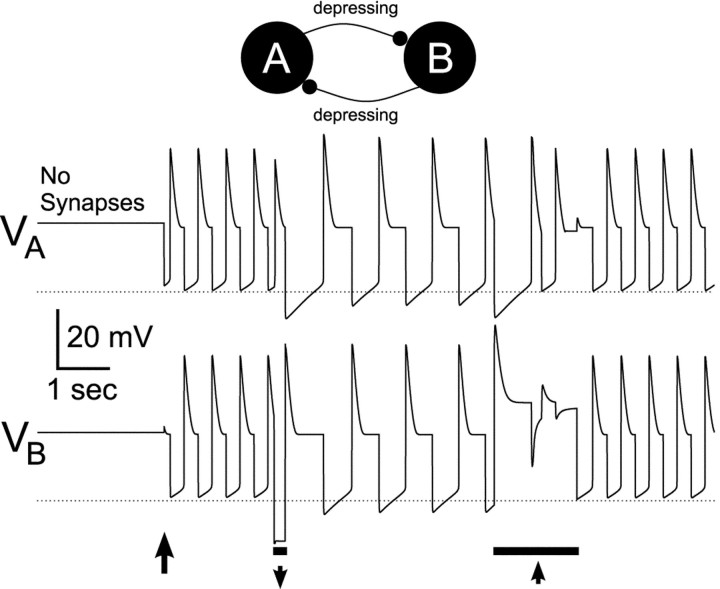
Fig. 9.

Depressing synapses mediate bistability in a symmetric model. A computational model consisting of two identical neurons reciprocally connected via two depressing synapses was constructed. Both model neurons lacked autorhythmic properties but expressed post-inhibitory rebound. Shown are voltage traces of the two neurons. Horizontal dotted lines indicate the midpoint of the depression/recovery curve at −67 mV. With no synaptic connections, the two neurons were quiescent with a membrane potential of −44 mV. When the maximal conductances of both synapses were set to 1 mS/cm² (first arrow), after a small perturbation in neuron B, the two neurons produced alternating rhythmic activity (CD mode). At the time indicated by the left bar, a 200 msec current pulse of −10 μA/cm² was injected into neuron B. This caused the rhythm to switch from CD mode to SC mode. At the time indicated by the right bar, a 1500 msec current pulse of +10 μA/cm² was injected into neuronB. This caused the rhythm to switch back to the CD mode.

The steady-state curves y_∞have the form 1/(1 + exp((V −V_y)/k_y)), where V_a = −52 mV,k_a = −1 mV,V_d = −67 mV, andk_d = 0.5 mV. Time constants are given by τ_a(V) = 5 msec and τ_d(V) = 200–100d_∞(V) msec.

RESULTS

In all experiments we removed the synaptic influence of the LP neuron by injecting a large hyperpolarizing DC current (5–10 nA) into the LP neuron soma. We coupled both biological PD neurons reciprocally to an LP model neuron with artificial synapses (see Materials and Methods). There was no difference in the connections from or to each of the two PD neurons. The artificial synapses were modeled to mimic the time courses and depression properties measured in the biological system (Manor et al., 1997). We systematically examined the effects of varying synaptic strength on the oscillations of the PD neurons.

The effect of maximal conductance of a depressing synapse on the rhythmic activity of a reciprocally inhibitory network

As a first step, we examined the behavior of the network at different values of G_PD→LP, the maximal conductance of the PD to LP synapse (Fig.3). G_LP→PD was kept fixed at a value of 1.5 nS. G_PD→LP was changed from 0 (Fig. 3A) to 2 nS (Fig. 3B) and then to 4 nS (Fig. 3C). After each manipulation, we waited until the rhythmic activity stabilized. We then recorded the membrane potentials of the PD neuron and the LP model neuron. To evaluate the tendency of a synapse to depress and recover from depression when presynaptic voltage changes, we also show the steady-state activation/decay (a_∞) and the depression/recovery (d_∞) curve for the corresponding voltage trace (Fig. 3D). The depression/recovery curve spans the range from 0 (representing a totally depressed state at high voltages) to 1 (representing a totally recovered state at low voltages). The midpoint of the steady-state depression/recovery curve is also represented by the dotted lines in A–C. Also shown are the synaptic currents, I_PD→LP andI_LP→PD. The kinetics of these two synapses are tuned to mimic the kinetics observed in the corresponding biological synapses (Fig. 1B).

When G_PD→LP = 0, the PD neuron produced bursting oscillations at a cycling period of 0.927 ± 0.015 sec, with a duty cycle of 0.41 (Fig. 3A). Within the burst, the PD neuron fired five spikes at a frequency of 16.9 ± 3.0 Hz. The LP model neuron produced a tonic activity at a spike frequency of 14.3 ± 0.04 Hz. Because G_PD→LP = 0, the PD to LP synaptic current I_PD→LP was also zero. However, although G_LP→PD was not zero,I_LP→PD was very small. This occurred because the membrane potential of the LP model neuron was in a voltage range in which the LP to PD synapse never recovered from depression (compare the voltage range of the LP model neuron with the dotted line).

When G_PD→LP was set to 2 nS, there was very little effect on the electrical activity of the PD neuron (Fig. 3, compare A, B). The LP model neuron, on the other hand, became rhythmically active in alternation with the bursting activity in the PD neuron. Within each burst, the LP model neuron produced seven to nine spikes at a frequency of 12.1 ± 0.08 Hz. The voltage range of the LP model neuron remained in the range for which the LP to PD synapse was mostly depressed (compare the voltage range of the LP model neuron with the dotted line). Therefore, the actual conductance of the LP to PD synapse (and thusI_LP→PD) remained very small because the synapse did not recover from depression. In this case, the PD to LP synapse is partially depressed, but the LP to PD synapse is almost completely depressed. As a result, the two cells are in effect coupled in a unidirectional way, and the network operates in a CD mode.

When G_PD→LP was increased to 4 nS (Fig.3C), there was a 38% increase in the cycle period, from 0.927 ± 0.015 sec to 1.275 ± 0.038 sec. In addition, there was a significant effect on the electrical activity of both the PD neuron and the LP model neuron. The burst duration of the PD neuron did not change, but its duty cycle decreased from 0.41 to 0.35. The slope of the PD neuron membrane potential depolarizing phase almost tripled its size (from 0.045 to 0.13 V/sec at −40 mV), suggesting that some intrinsic conductance was activated in the PD neuron. In each burst, the PD neuron produced six spikes at a frequency of 22.7 ± 3.0 Hz. During the PD neuron interburst intervals, the PD neuron membrane potential dropped to voltages where the synapse recovered from depression. Hence, during the PD neuron burst the synaptic current from PD to LP first increased and then decreased as the synapse started to depress. Note that the decaying phase of this current was not monotonic but interrupted by a small increase at the beginning of the LP burst. This occurred because the synapse from PD to LP was large enough to truncate the first spike of the LP burst. As a result, LP inhibition of PD is partially removed during this time, and a small depolarization occurs in the PD neuron. This small depolarization brings the PD neuron back to voltages where transmitter can be released. The LP model neuron produced bursts of action potentials in alternation with the bursts of the PD neuron. Within each burst, the LP model neuron produced 10–11 spikes at a frequency of 14.0 ± 1.0 Hz. During the LP model neuron interburst intervals, the LP model neuron membrane potential also dropped to voltages where the LP to PD synapse recovered from depression. As a consequence of the recovery of both synapses, the coupling between the LP and PD neurons became bidirectional, and the network operated in the SC mode.

In summary, when the strength of the PD to LP synapse was increased beyond a certain level, the network switched from one operational mode (the CD mode) to a completely different operational mode (the SC mode). In the CD mode, the LP to PD synapse had no significant effect on the electrical activity of PD, because it was mostly depressed. In the SC mode, the LP model neuron membrane potential was sufficiently hyperpolarized to allow the LP to PD synapse to recover from depression and affect the network cycle period.

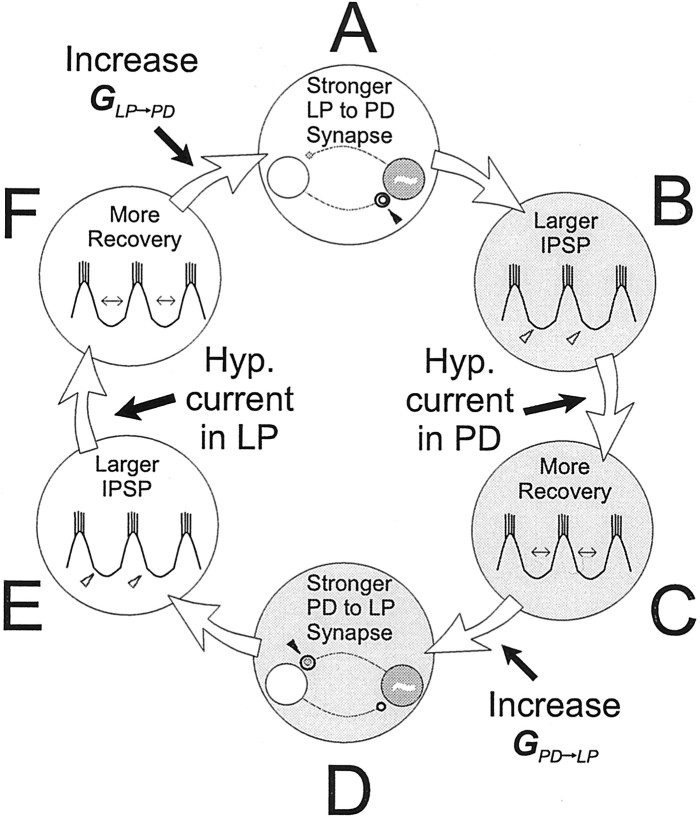
Figure 4 shows a schematic drawing that explains how the network can switch from the CD mode to the SC mode. Originally, the two synapses are weak and depressed, and the oscillation period is determined by the dynamics of the pacemaker PD neuron. An increase in maximal conductance of the LP to PD synapse (Fig. 4A, arrow) increases the actual conductance of this synapse. This causes the PD neuron interburst interval to be longer and the PD neuron membrane potential during this interval to be more hyperpolarized (Fig. 4B). As a result, the PD to LP synapse may recover more from depression (Fig.4C), and the actual conductance of the PD to LP synapse may increase (Fig. 4D). This would increase the duration of the LP neuron interburst interval and the hyperpolarization of the LP neuron during the interval (Fig. 4E). As a result, the LP to PD synapse may recover more from depression (Fig.4F), and thus the actual conductance of the LP to PD synapse may increase (Fig. 4A, new iteration). If the actual conductance of the LP to PD synapse is larger at this point than at the beginning of the previous iteration, a positive feedback loop is engaged. This feedback loop will continue for several cycles, during which the actual conductances of both synapses increase greatly.

Fig. 4.

A regenerative loop can be engaged in the PD–LP neuron circuit when both synapses are depressing. An increase in the strength of the LP to PD synapse (A) generates a larger IPSP in the PD neuron (B). If this IPSP is sufficiently large, the PD to LP synapse recovers from depression (C) and increases in strength (D). This increase, in turn, generates a larger IPSP in the LP neuron (E). If this IPSP is sufficiently large, the LP to PD synapse recovers from depression (F) and increases in strength (back toA), and the process repeats. A transient hyperpolarization of either neuron, or an increase in the maximal conductance of either synapse beyond an associated threshold (indicated by the black arrows), triggers this positive feedback mechanism. This regenerative loop greatly increases the strength of both synapses and yields a longer oscillation period.

A similar feedback loop could be triggered if the maximal conductance of the PD to LP synapse is increased instead. This regenerative process could also be triggered by a transient hyperpolarizing stimulus in one of the two neurons, given during its interburst (for example, a negative current into the PD neuron in Fig. 4C), because this external stimulus would transiently increase the duration of the interburst interval and thus initiate a similar chain of events as described above. The positive feedback loop stops because of several factors, the most important of which is that when the interburst interval is of the same order as the time constant of recovery, the recovery process saturates. In this mode (SC), the interburst interval, and hence cycle period, is controlled by the time constants of depression in the two synapses.

Post-inhibitory cellular mechanisms would augment this regenerative process (Nadim et al., 1999). For example, an increased PD neuron interburst interval (Fig. 4C) could activate (or deinactivate) an inward current, in which case the subsequent PD neuron burst would be stronger in terms of amplitude, slope, number of spikes, or spike frequency. Together with increased synaptic recovery, this effect would contribute to increase the strength of the PD to LP synapse.

Depressing synapses in a reciprocally inhibitory network give rise to hysteresis in the network activity

In the previous section we established the existence of two oscillation modes in our experimental paradigm. In this section, we systematically examine the steady-state effect of synaptic strengths (maximal synaptic conductances) on oscillation period. We fixedG_PD→LP at a value that supported SC oscillations when G_LP→PD was large. Starting with a G_LP→PD value of 0 (where the network operated in the CD mode), we increased G_LP→PDand held it until the cycle period reached a steady-state value. We repeated this step, each time incrementingG_LP→PD by a fixed amount. At small values ofG_LP→PD, we observed no change in the oscillation period. We continued the incremental steps until we observed a clear effect on the oscillation period. This indicated that the network had switched to the SC mode. We then decreasedG_LP→PD in fixed steps back to 0.

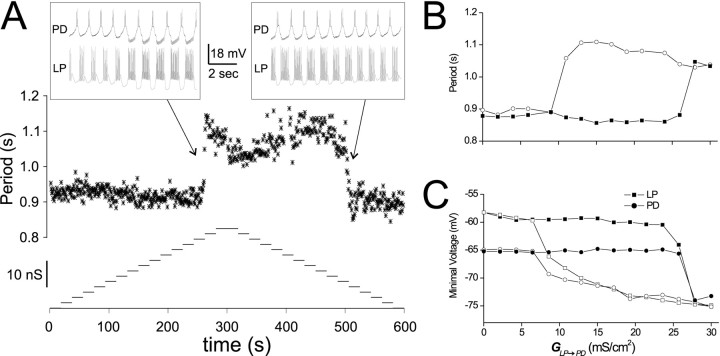
An example of this protocol is shown in Figure5. In this experiment,G_LP→PD was increased every 20 sec in steps of 2 mS/cm². At aG_LP→PD value of ∼26 mS/cm², the oscillation period jumped from 0.9 sec to ∼1.1 sec and stayed at that period asG_LP→PD was increased further (Fig.5A). As we decreased G_LP→PD, the period initially remained at ∼1.1 sec. WhenG_LP→PD decreased below 10 mS/cm², the period returned to 0.9 sec. The slow- and fast-period oscillations corresponded to the CD and SC regimens, respectively. Figure 5B plots the last (steady-state) cycle period within each 20 sec stretch, as a function of the corresponding G_LP→PD value. Figure5C plots the trough voltage values of PD and LP for the same cycles shown in Figure 5B. TheG_LP→PD value at which the network switched from CD to SC mode (the upswing) was larger than the switch value from SC to CD mode (the downswing).

Fig. 5.

Oscillation mode can be switched by changing the maximal synaptic conductance. G_PD→LP was held at a value of 1 mS/cm². Every 20 sec,G_LP→PD was incremented in steps of 2 mS/cm² from 0 to 30 mS/cm² and then stepped back to 0. A, Cycle periods (stars, top trace) are plotted as function of time. Bottom trace showsG_LP→PD values as a function of time.Insets show the voltage traces of the biological PD neuron and LP model neuron at the transitions between the two modes.B, The cycle period at the end of each 20 sec stretch is plotted as a function of the correspondingG_LP→PD. The filled squarescorrespond to the up steps, and the open circlescorrespond to the down steps. C, Trough voltage values of the PD neuron (circles) and the LP model neuron (squares) for the same cycles shown in B.Filled and open symbols represent the up and down steps, respectively.

In addition to varying G_LP→PD in a stepwise manner, we also ramped G_LP→PD up and down (with a slope similar to the step-wise variation) and obtained essentially the same results. In both the step and ramp protocols, similar results were obtained by fixing G_LP→PDand varying G_PD→LP (data not shown).

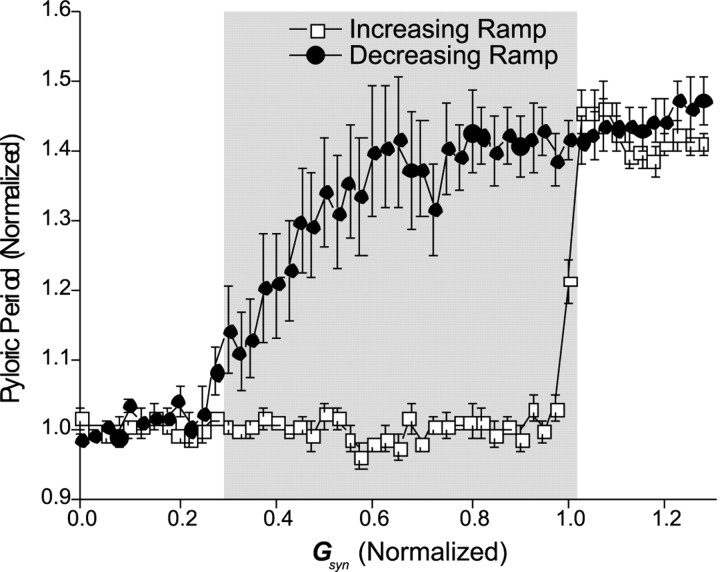
Figure 6 presents averaged data from nine experiments of the protocol in which G_LP→PDwas ramped up and down. In all experiments we began in CD mode. The pyloric period was ∼42% greater (n = 9;p < 0.001, Student's t test) in the SC mode (1501 ± 115 msec, mean ± SEM) than in CD mode (1056 ± 71 msec, mean ± SEM). In different experiments, the oscillation period P_pyl, and the value of G_LP→PD at which the network switched from CD to SC mode (and back) varied. We therefore normalized the data to compare the range of bistability across experiments. We plot the averageP_pyl/P_cell, where P_cell is the mean period in the CD mode, as a function ofG_LP→PD/G_up, where G_up is theG_LP→PDvalue at which the switch from CD to SC mode occurred (Fig. 6). The bistable range (gray rectangle) was defined as those points whereP_pyl/P_celldiffered in the increasing and decreasing arms of the plot (one-way ANOVA on the period differences; Tukey's test; p < 0.05). Note that network bistability occurs over a large range ofG_LP→PD/G_up.

Fig. 6.

Oscillation period shows hysteresis as a function of G_LP→PD. Hysteresis effect of the pyloric period when G_LP→PD was ramped up from 0 (>200–300 sec) until the network switched from CD to SC mode (■) and then ramped back down to 0 (●). For each experiment, pyloric period (P_pyl; mean ± SEM; n = 9) is normalized by the mean periodP_cell in the CD mode.G_LP→PD is normalized byG_up, the value ofG_LP→PD at which the switch from CD to SC mode occurred. Gray rectangle shows the region of bistability (one-way ANOVA on the difference between the periods on the up and down ramps; Tukey's test; p < 0.05).

Network bistability critically depends on both synapses being depressing

We examined whether bistability could occur when only one of the two synapses was depressing or whether it required depression in both synapses. We tested different combinations of depressing and nondepressing (static) synapses. As before, we varied the maximal conductance of one synapse while keeping the other at a fixed value.

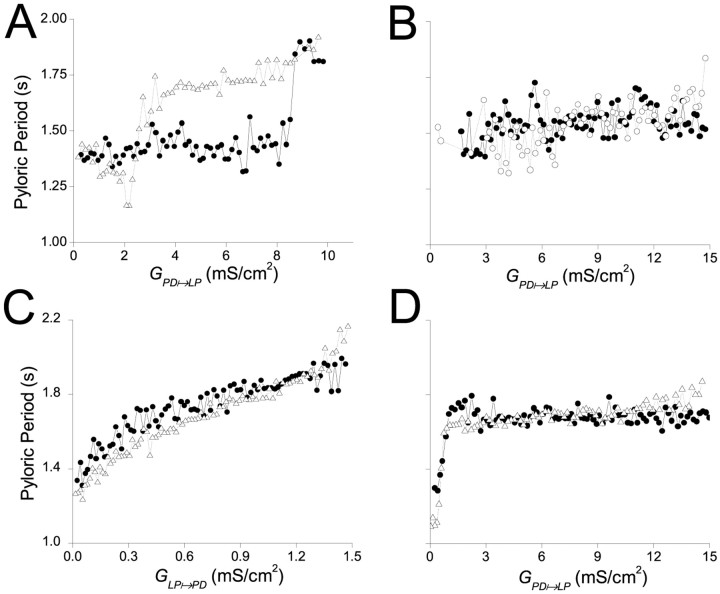
In Figure 7A, both synapses were depressing andG_PD→LPwas varied gradually.G_LP→PDwas held at a fixed value of 0.8 mS/cm², andG_PD→LPwas ramped up (filled circles) from 0 to 10 mS/cm² and then ramped down (open triangles) from 10 mS/cm² to 0 in a total time of 300 sec. At the beginning of the session, the oscillation was in the CD mode. On the ramp up, the oscillation switched from CD mode to SC mode atG_PD→LP= 8.5 mS/cm². On the ramp down, the oscillation switched back to CD mode atG_PD→LP= 2.7 mS/cm². Hence the rhythm showed reversible bistability in the two modes of oscillation. The reversible bistability is manifested as a hysteresis phenomenon. Qualitatively similar results were obtained whenG_LP→PDwas gradually ramped up and down andG_PD→LPwas held at a fixed value (Fig. 6).

Fig. 7.

Two oscillation modes exist only when both synapses are depressing. The maximal synaptic conductance of one synapse was varied by ramping it up (●) and then down (▵) over a total period of 300 sec. A, Both synapses are depressing. G_LP→PD was fixed at 0.8 mS/cm², and G_PD→LP was varied between 0 and 10 mS/cm². B, The PD to LP synapse was depressing, and the LP to PD synapse was static. G_LP→PD was fixed at 0.8 mS/cm², and G_PD→LP was varied between 0 and 15 mS/cm². C, The LP to PD synapse was depressing, and the PD to LP synapse was static. G_PD→LP was fixed at 10 mS/cm², and G_LP→PD was varied between 0 and 1.5 mS/cm². D, Synapses are as in C, butG_LP→PD was fixed at 0.8 mS/cm², and G_PD→LP was varied between 0 and 15 mS/cm².

In Figure 7B, the LP to PD synapse was static, and the PD to LP synapse was depressing.G_LP→PDwas held at a value of 0.8 mS/cm². At the beginning of the sessionG_PD→LPwas 0, and the network was in the CD mode. WhenG_PD→LPwas ramped up and down, the pyloric period remained fixed at ∼1.5 sec. During the ramping ofG_PD→LP, the LP model neuron waveform changed as expected (data not shown). However, because the LP to PD synapse was static, the modified LP model neuron waveform did not produce any change in the actual conductance of the LP to PD synapse, and hence the oscillation remained in the CD mode.

In Figure 7C the LP to PD synapse was depressing, and the PD to LP synapse was static.G_PD→LPwas held at a value of 10 mS/cm². At this value,G_PD→LPwas sufficiently large to allow the LP to PD synapse to recover from depression on a cycle-by-cycle basis. Note that the recovery of the synapse is dependent on the synaptic dynamics (depression and recovery time constants) and not on its maximal conductance. Hence, even whenG_LP→PDwas 0, the synapse was already recovered from depression, although it was not affecting the rhythm. Therefore, asG_LP→PDwas increased from 0, it started to slow down the PD period immediately. The system was in SC mode (i.e., the synapse was not depressed) for all values ofG_LP→PD>0.

As a final test, we studied the behavior of the network when the LP to PD synapse was depressing and the PD to LP synapse was static. This time, however, we ramped the static synapse and heldG_LP→PDfixed at 0.8 mS/cm². In this case, whenG_PD→LPwas 0, the system operated in the CD mode. AsG_PD→LPwas increased, the system immediately switched to SC mode and stayed in this mode for all higher values ofG_PD→LP(Fig. 7D). Therefore, we conclude that hysteresis and bistability occurred in no other case than when both synapses were depressing.

The bistable network can be switched between oscillation modes by injection of a transient current pulse

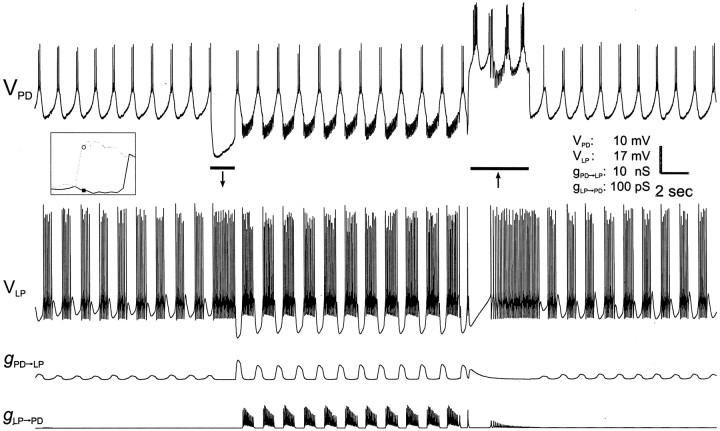
When the network operates in a bistable regime, transient inputs to either neuron can switch the network between oscillatory modes. Figure 8 shows voltage traces of the PD neuron and LP model neuron and conductance traces of the two synapses. The synaptic parameters were adjusted to values within the bistable regime indicated on the inset. The activity of the two neurons started in the CD regimen. The PD to LP synapse was relatively weak and the LP to PD synapse was almost null. As a result, the oscillation was relatively fast. At the time indicated by theleft bar, the PD neuron was injected with a −2 nA, 2 sec current pulse. As a result, the PD neuron hyperpolarized and the LP model neuron fired tonically. As a consequence of the PD neuron hyperpolarization, the PD to LP synapse could recover from depression. At the end of this pulse, the PD neuron rebounded from hyperpolarization to produce a burst. Because the PD to LP synapse had recovered from depression, the LP model neuron was strongly inhibited. This inhibition, in turn, allowed the LP to PD synapse to recover from depression, and after rebound the LP model neuron strongly inhibited the PD neuron. This process triggered the regenerative loop described in Figure 4, and the network switched to the SC mode. At the time indicated by the right bar, the PD neuron was depolarized with a +2 nA, 5 sec pulse. At the beginning of this pulse, the PD neuron depolarization caused a large inhibition in the LP model neuron. However, as a result of depression, the PD to LP synapse weakened, and the LP model neuron started to fire tonically. Tonic activity of the LP model neuron caused the LP to PD synapse to also depress. After termination of the pulse, both synapses were depressed, and the network returned to the CD mode. Note that if the depolarizing pulse had been terminated too early, i.e., before the LP model neuron started to fire tonically, the LP to PD synapse would not have depressed, and the network would have remained in the SC mode.

Fig. 8.

Current–pulse injection switches the network between oscillation modes. The network is the same as in Figure 5.G_PD→LP andG_LP→PD were set at 1 and 10 mS/cm², respectively. With these values, the network operated in its bistability regimen (as indicated by thepoints on the inset). The top two traces are the membrane potentials of the biological PD neuron and the LP model neuron. The bottom two traces are the actual conductances of the PD to LP and LP to PD synapses. The network started in CD mode. At the time indicated by the left bar, a −2 nA, 1.7 sec current pulse was injected into the PD neuron, and the network switched to SC mode. At the time indicated by the right bar, a +2 nA, 4 sec current pulse into the PD neuron switched the network back to the CD mode.

Depressing synapses mediate bistability in other types of reciprocally inhibitory loops

The mechanism described above applies not only when a pacemaker generates the rhythmic activity, but also when rhythmicity emerges from network interactions. To demonstrate this, we constructed a simplified computer model consisting of two identical neurons in which each neuron lacked independent rhythmic capabilities but did exhibit post-inhibitory rebound. We then coupled the neurons using identical depressing synapses. Figure 9 shows the voltage traces of the two neurons. When no synapses were present, the model neurons did not produce oscillations but had a relatively depolarized resting potential (the dotted lines indicate the midpoint of the depression/recovery curve at −67 mV). When the model neurons were connected (indicated by the first arrow), a small perturbation in neuron B triggered an antiphase oscillation between the model neurons, a behavior commonly seen in reciprocally inhibitory pairs of symmetric neurons. In this case, the synapses were relatively (but not completely) depressed, and the oscillation period was insensitive to changes in the maximal conductance of either one of the synapses (data not shown), and the network thus oscillated in a mode equivalent to CD. At the time indicated by the left bar, a brief hyperpolarizing current pulse was injected into neuron B, allowing its synapse to neuron A to recover from depression. This, in turn, allowed the A to B synapse to recover from depression, and the oscillation switched to a distinct mode that had a longer (almost double) period. In this mode, the oscillation period was determined primarily by the maximal synaptic conductances (data not shown), and the network thus oscillated in an SC mode. At the time indicated by the right bar, a 1500 msec current pulse of +10 μA/cm² was injected into neuronB. The long depolarization allowed the B toA synapse to completely depress and caused the rhythm to switch back to the CD mode.

These data show that in a reciprocally inhibitory circuit where both synapses are depressing, bistability can arise when the two neurons are quiescent neurons with high resting membrane potentials. Similar results were obtained when the two neurons were quiescent neurons with low resting membrane potentials, or when the two neurons were endogenous oscillators.

DISCUSSION

Synaptic depression is among the most common forms of short-term plasticity observed in central synapses (Stevens and Wang, 1995). Many rhythmic networks consist of neurons that are reciprocally connected via inhibitory synapses with short-term synaptic depression. In this study we systematically examined the effect of synaptic depression in a small circuit comprising a biological oscillator and a model neuron, coupled with artificial synapses implemented in the dynamic-clamp technique.

Synaptic depression mediates bistability in half-center oscillators

When the synapses between the biological oscillator and the model neuron were both depressing, the network displayed two operational modes. In the CD mode, the synapses were depressed, and the oscillation was determined by the intrinsic dynamics of the pacemaker. If the synapses were allowed to recover from depression, the oscillation period became slower, which further expedited the synapse recovery. This regenerative process switched the oscillation to the SC mode, in which the rhythm was mostly determined by synaptic dynamics. Variation in the maximal conductance of either synapse similarly switch the network between modes. As such, the mode of network oscillation depended only on initial conditions, and transient perturbations could persistently switch the network from one mode to the other.

In this work we distinguished the two modes of oscillation mainly by comparing cycle periods. It should be noted, however, that these two modes also differ in the voltage ranges of the neurons involved, in particular in the level of hyperpolarization during the interburst intervals. In general, it is possible that the two modes of oscillation differ in only one of these two network characteristics and not the other.

Significance of bistability for neuromodulation

In view of the importance of neuromodulation in initiating, modifying, or terminating the activity of neuronal networks, it is interesting to ask what would be the consequences of bistability in neuronal networks, such as the stomatogastric nervous system (Harris-Warrick et al., 1992), that are subject to complex neuromodulation. Modulatory agents modify not only intrinsic properties but also synaptic strength and dynamics (Marder, 1998), and we have shown that these factors are crucial in promoting bistability in reciprocally inhibitory circuits. We therefore discuss several possible implications of bistability for neuromodulation.

First, it has been suggested that bistable dynamic activity of a single neuron permits the effects of a neuromodulator to persist long after the neuromodulator is withdrawn (Canavier et al., 1994). This idea similarly applies to the bistability mechanism described in this paper. A neuromodulator that slows down the rhythm would allow the synapses to recover from depression and switch the network from CD mode to SC mode. Once the network is in the SC mode, the synaptic activity would support a slow rhythm, and the neuromodulator could be removed without affecting network cycle period. A neuromodulator that speeds up the rhythm could be transiently used to switch the network from the SC to the CD mode. Neuromodulators that alter pyloric network period have been described extensively (Hooper and Marder, 1987; Marder and Weimann, 1992; Skiebe and Schneider, 1994; Tierney et al., 1997). It would be interesting to see whether in our experimental framework such modulators could switch the oscillation mode.

Second, the effect of neuromodulation can vary according to the state of the network. For example, in the stomatogastric nervous system, the effects of many peptides vary as a function of network cycle period (Nusbaum and Marder, 1988, 1989; Wood et al., 2000). Hence, it is not only the effect of neuromodulation on cycle period that must be considered, but also the effect of cycle period on neuromodulation. Transient synaptic inputs that rapidly switch the network from one state to another could rapidly alter the effect of a neuromodulator on its targets.

Another implication of bistability is the possibility of “silent neuromodulation.” Neuromodulator effect can be altered by previous exposure to a conditioning neuromodulator, even when the conditioning modulator is applied at subthreshold concentrations (Dickinson et al., 1997). It has been suggested that the conditioning neuromodulator triggers a second-messenger pathway or activates a dormant receptor that can then interact with a different neuromodulator at a later time (Prier et al., 1994). The present study provides an alternative mechanism. If modification of synaptic properties (for example, time constants of depression and recovery) occurs while the network operates in the CD mode, it would be undetected because in this mode cellular properties determine network activity. However, when the network switches into the SC mode, network activity strongly depends on dynamics of the synapses, which would reveal the effects of the previous modification of synaptic properties.

Is the pyloric network bistable?

Under control conditions, the biological pyloric network does not switch from one oscillation mode to another with transient current injection in the LP or PD neuron (data not shown). However, this observation does not imply that the pyloric network cannot operate in a bistable domain. The large parameter range under which network bistability was found implies that the mechanism described here is robust. Moreover, all the properties necessary for the emergence of bistability are present in this network. One possibility is that, under control conditions, the intact pyloric network does not operate within the bistability parameter range. Another possibility is that the network is in the bistability regime, but some secondary mechanism [such as the inhibition of the LP neuron by pyloric neurons other than the pacemakers (Graubard et al., 1983)] forces the network to operate only in one mode. Either of these mechanisms would ensure that the network does not inappropriately switch modes. However, neuromodulatory inputs may bring the system into the bistability regime or remove the restriction on bistability. We are currently examining these possibilities in the pyloric network in the presence of neuromodulators.

The mechanism of bistability: a comparison with other neuronal systems

We have described here a novel type of bistability mediated by short-term synaptic depression in reciprocally inhibitory networks. The core of this mechanism is a cyclic interaction between cycle period and the depression state of synapses. Although this mechanism depends on network connectivity and synaptic dynamics alone, cellular mechanisms such as post-inhibitory rebound properties may also play a role (Nadim et al., 1999).

Among other known mechanisms for bistability, the simplest form is found in neurons that display plateau potentials (Jahnsen and Llinas, 1984; Bal et al., 1988; Hounsgaard et al., 1988; Lechner et al., 1996;Booth et al., 1997; Kiehn and Eken, 1998; Lee and Heckman, 1999;O'Donnell et al., 1999). A plateau neuron makes sharp transitions between a low-voltage equilibrium and a more depolarized potential. In most reported cases of neurons showing plateau potentials, a brief perturbation (such as a short-lasting synaptic input) can trigger transitions between the different states (Marder, 1991). However, this type of bistability is not completely stable, because plateau neurons may switch spontaneously from one state to the other because the intrinsic conductance that supported the plateau potential has slowly inactivated.

Another type of bistability is found in neurons with NMDA-sensitive glutamatergic synapses. In such neurons, NMDA receptors are activated when a transient presynaptic activity coincides with depolarization of the neuron. The activation of these NMDA channels enhances or suppresses a different type of glutamate receptor. This modification can outlast the triggering input for hours or days and is the basis for the induction phase of long-term potentiation and depression (Malenka and Nicoll, 1999).

Bistability may also result from the organization of synaptic connectivity. In models of networks with recurrent excitatory connections, with no external input, neurons of the network spike spontaneously and sporadically. When the external input is increased, recurrent excitation begins and persists after the stimulus is withdrawn (Brunel, 2000; Durstewitz et al., 2000; Tabak et al., 2000). A possible drawback of this type of bistable network is sensitivity to random fluctuations (external noise), which can induce spontaneous transitions between states (Brunel, 2000).

Synaptic depression as an internal mechanism for network reconfiguration

In small neuronal networks, such as the pyloric circuit, network reconfiguration is often used to increase the repertoire of neuronal activities (Marder and Weimann, 1992). External inputs such as command or neuromodulatory neurons have been suggested to play a direct role in the reconfiguration of neuronal networks by changing the network components. We propose that synaptic depression can be used as an internal mechanism that allows the rhythmic network to reconfigure itself as an external signal arrives. Indeed, depressing synapses can be turned on or off by allowing or disallowing them to recover from depression. As a result of the change in synaptic strengths, the network is reconfigured to produce a new output. The change in network output stabilizes the synaptic strengths, which in turn act to stabilize the new pattern of activity. By exploiting these built-in network flexibilities, external neuromodulatory inputs can cause a major reorganization of the network without altering channel voltage dependence or expression, the dependence of transmitter release on calcium concentration, or similar fundamental physical characteristics of membrane and synaptic proteins. The mechanisms described here thus add a new level of complexity in the control of network output.