Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Sep 3;52(18):6889–6897. doi: 10.1021/acs.macromol.9b00753

A Multiscale Model for Solute Diffusion in Hydrogels

Eneko Axpe †,‡, Doreen Chan †, Giovanni S Offeddu §, Yin Chang ∥, David Merida ⊥, Hector Lopez Hernandez †, Eric A Appel †,*
PMCID: PMC6764024  PMID: 31579160

Abstract

graphic file with name ma9b00753_0007.jpg

The number of biomedical applications of hydrogels is increasing rapidly on account of their unique physical, structural, and mechanical properties. The utility of hydrogels as drug delivery systems or tissue engineering scaffolds critically depends on the control of diffusion of solutes through the hydrogel matrix. Predicting or even modeling this diffusion is challenging due to the complex structure of hydrogels. Currently, the diffusivity of solutes in hydrogels is typically modeled by one of three main theories proceeding from distinct diffusion mechanisms: (i) hydrodynamic, (ii) free volume, and (iii) obstruction theory. Yet, a comprehensive predictive model is lacking. Thus, time and capital-intensive trial-and-error procedures are used to test the viability of hydrogel applications. In this work, we have developed a model for the diffusivity of solutes in hydrogels combining the three main theoretical frameworks, which we call the multiscale diffusion model (MSDM). We verified the MSDM by analyzing the diffusivity of dextran of different sizes in a series of poly(ethylene glycol) (PEG) hydrogels with distinct mesh sizes. We measured the subnanoscopic free volume by positron annihilation lifetime spectroscopy (PALS) to characterize the physical hierarchy of these materials. In addition, we performed a meta-analysis of literature data from previous studies on the diffusion of solutes in hydrogels. The model presented outperforms traditional models in predicting solute diffusivity in hydrogels and provides a practical approach to predicting the transport properties of solutes such as drugs through hydrogels used in many biomedical applications.

Introduction

Hydrogels are three-dimensional cross-linked polymer networks mainly composed of water (typically 70%–99%).1 The polymeric network within the liquid provides hydrogels unique properties that make them particularly attractive for biomedical engineering applications.2−5 Clinical use of hydrogels in regenerative medicine and drug delivery critically relies on the diffusion of solutes across the hydrogel matrix, where entrapped cells in 3D tissue engineering scaffolds must be supplied with oxygen and nutrients,6,7 and drug delivery requires controlled release mechanisms.1,8,9 While the translation of these three-dimensional networks to biological systems depends on the diffusion of solutes, quantitatively understanding this dynamic movement of these solutes within a hydrogel network has been challenging.10,11,20−24,12−19

The diffusion of solutes in hydrogels is commonly modeled by one of the following three theoretical frameworks: (i) hydrodynamic theory,25 which considers friction between the solute and the surrounding hydrogel matrix; (ii) free volume theory,26 which assumes that the solute is transported via dynamic empty spaces between molecules; and (iii) obstruction theory,27 which models the polymer net as a barrier for the diffusion of the solute with the liquid. While each of these models is successful at capturing features of experimental diffusion data under some circumstances, they are often not predictive because they are applied outside of experimental regimes for which they are applicable and/or contain unspecified empirical parameters.28,29 Despite the substantial progress made during the past 40 years, a standard model that accurately predicts mass transport in hydrogels is still lacking. As a consequence, time and capital-intensive trial-and-error procedures are often employed to assess the viability tests of specific hydrogel applications. In this paper, a comprehensive model combining three primary theories for the diffusion of solutes in hydrogels at multiple length scales is presented. We call this framework the multiscale diffusion model (MSDM). To test this framework experimentally, we employed a series of hydrogels made of poly(ethylene glycol) (PEG) as a model system on account of their broad use in both tissue engineering30 and drug delivery applications.31,32 To validate our model, we needed to quantify the size of the (sub)nanoscopic free volume holes present within these hydrogels. For that purpose, we used positron annihilation lifetime spectroscopy (PALS), a unique technique capable of measuring these molecular pores in biomaterials under wet conditions. To further test our model, which describes the solute as a hard sphere similar to most traditional models, we perform a meta-analysis of 66 distinct solute/hydrogel combinations reported previously by us and other research groups (Table S1). The model proposed here suggests that diffusion occurs through several complementary mechanisms, described independently in traditional models, and that all mechanisms must be considered together for accurate prediction of solute diffusion.

Results

Model Formulation

The diffusivity (D0) of a solute with hydrodynamic radius (rs) in a pure liquid is given by the hydrodynamic theory, as defined by the Stokes–Einstein equation:33

graphic file with name ma9b00753_m001.jpg 1

where kb is the Boltzmann constant, T is the absolute temperature, and η is the dynamic viscosity of the liquid.

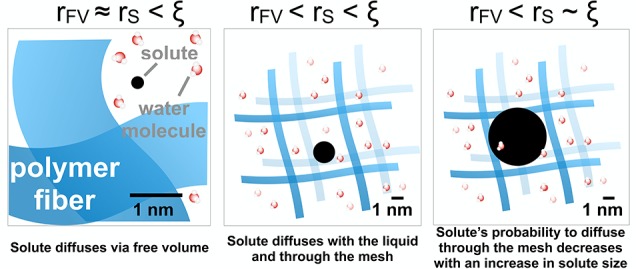
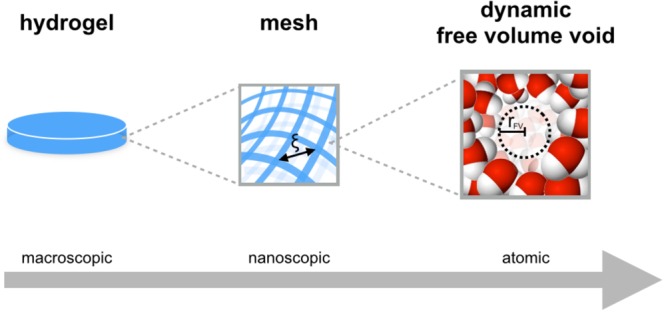
In a hydrogel, solute diffusivity is altered by the presence of the polymer chains, which form a network with open spaces between the chains. The size of these spaces, typically termed the characteristic “mesh size” of the network, can be nano- or microscopic, and the space between polymer chains is filled by aqueous solution. Here, ξ is defined as the correlation length, also known as the average mesh size of the network,34 which can be experimentally measured (e.g., neutron scattering). Another property of relevance is the free volume, formed by dynamic empty voids between all molecules forming the hydrogel structure (e.g., between the water molecules, between the polymer molecules, and at the water/polymer interface). The average size of these pockets is quantified by the free volume void radius (rFV), is atomic in scale, and hence is typically several orders of magnitude smaller than the mesh size (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Scale effects in solute diffusion in hydrogels. The diffusion of a solute within a hydrogel occurs via aqueous solution and through liquid-filled, nano- to microscopic open spaces between the polymer fibers or free volume (dynamic, subnanoscopic, empty voids between the molecules). Which of these mechanisms dominates diffusion depends on the ratio between the hydrodynamic radius of the solute and the radius of the free volume voids in the hydrogel.

In this paper, it is postulated that the solute diffusivity normalized by the diffusivity in pure solvent, D/D0, will be dictated by the probability of diffusing (i) via free volume (FV) voids and/or (ii) alongside aqueous solution through a mesh of size ξ. These events are essentially mutually exclusive as they occur at distinct length scales and thus the probability that a solute will diffuse by both mechanisms simultaneously is essentially zero. Thus

graphic file with name ma9b00753_m002.jpg 2

Based on free volume theory, solute diffusivity in a hydrogel with a given polymer volume fraction, φp, normalized by the solute diffusivity in liquid, was developed by Lustig and Peppas35 as follows:

graphic file with name ma9b00753_m003.jpg 3

Here C is a sieving factor, and Y is the ratio between the critical volume required for the solute diffusion (approximated as the volume of the solute, VS) and the available free volume per molecule in the aqueous solution inside the hydrogel (approximated as the average volume of the free volume voids in the water, VFVW).

Based on obstruction theory, which is derived from Fick’s law, the probability of finding an open space of size ξ between polymer chains of radius (rf) forming the hydrogel network was described by Amsden et al.36 as follows:

graphic file with name ma9b00753_m004.jpg 4

where the polymer mesh within the hydrogel is modeled as a motionless physical obstacle for diffusion of the solute.

Bringing these probabilities together, the following equation is obtained:

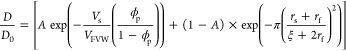graphic file with name ma9b00753_m005.jpg 5

In this equation, a weighting factor A is used to combine solute diffusivities via free volume holes and/or through the mesh such that the total probability for the normalized diffusion to occur by any mechanism is quantified as a number between 0 and 1. Here, the prefactors account for the assumption that the diffusion via free volume dominates when the average radius of the free volume voids is comparable to the hydrodynamic radius of the solute (rFV ∼ rs), whereas the mesh size becomes the limiting factor when the size of the solute is much larger than the free volume voids (rFV ≪ rs). In addition, intermolecular forces are considered negligible in these systems, which is a reasonable assumption based on previous treatments of numerous hydrogel systems and distinct solutes.35,36

In this work we made use of the Gaussian error function, which is classically encountered in many problems in diffusion, as the prefactor. It is well-known that the radius of the free volume holes in many hydrogels and diverse biological tissues follow a Gaussian distribution with an average rFV and a distribution breadth denoted by σVF.37−41 For a particle with radius rs and free volume holes of rFV that are normally distributed, the corresponding error function is 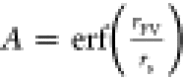Inline graphic. This function describes the probability that a diffusing particle of rs will find a single intermolecular space of rFV, which falls in the range of 0–1 since 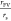Inline graphic is always a positive value. Consequently, the probability of the particle diffusing through other mechanisms (i.e., not via free volume holes) is captured by the complementary error function 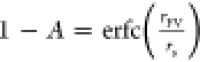Inline graphic. The weighting factor we made use of here is therefore not based on empirical observations and is instead based on a physical theory, encountered in integrating the normal distribution of the radii of the free volume voids normalized by the solute radius. With the inclusion of these functions, the previous equation can be rewritten as follows:

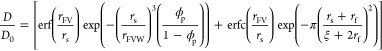graphic file with name ma9b00753_m009.jpg 6

In this equation, the solute is modeled as a hard sphere and the free volume voids in the hydrogel as empty spheres with radius rFV (rFVW in the case of water). While many techniques have been developed to characterize the mesh size and radius of the solute, allowing these parameters to be easily obtained, the free volume of a system is more difficult to characterize and therefore frequently overlooked. In a previous study, the mesh size in our hydrogels was estimated by spherical indentation.42 Though, to validate our MSDM model, shown in eq 6, it was necessary to measure rFV within the PEG hydrogels. For this end, we used positron annihilation lifetime spectroscopy.

Positron Annihilation Lifetime Spectroscopy (PALS)

PALS is a nondestructive technique capable of probing atomic-sized open spaces. The lifetime of positrons implanted in materials is measured, which yields information about the electron density. Particularly, orthopositronium (o-Ps) is a system with a radius of 1.59 Å, consisting of an implanted positron and an electron from the material with parallel spins, formed in the free volume voids (Figure 2A). The o-Ps lifetime is correlated to the size of the free volume voids inside a material, including hydrogels. This difference in size is reflected in the positron lifetime spectra obtained (see representative spectra for PEG5 and PEG25 in Figure 2B). By deconvoluting these raw spectra, we obtain the characteristic average o-Ps lifetime and distribution (Figure 2C). Finally, the o-Ps lifetime is correlated to the average free volume radius (rFV) and distribution (σVF) by a well-established model (Table 1).40,43,44

Figure 2.

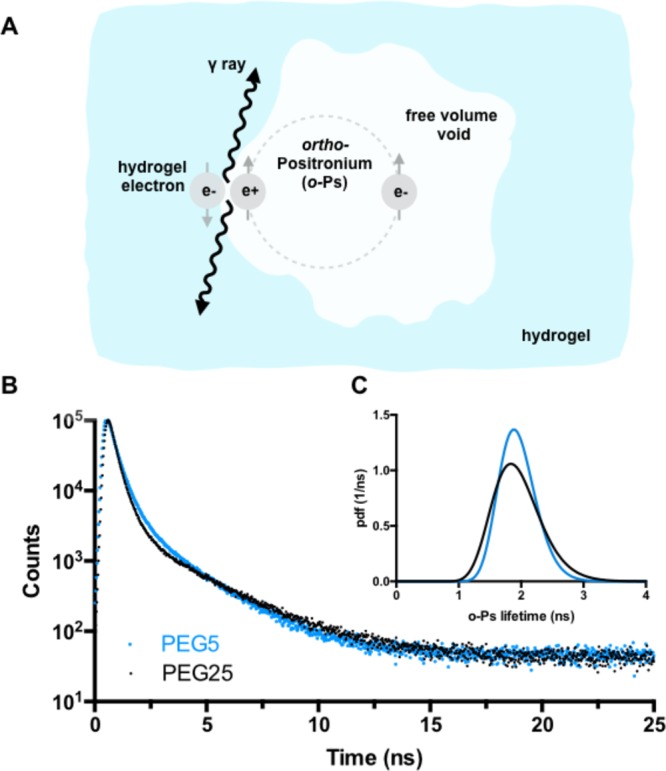
Figure 2

Open in a new tab

(A) In positron annihilation lifetime spectroscopy (PALS) experiments, positrons are implanted in the material. In the free volume voids, orthopositroniums (o-Ps) are formed. In larger free volume voids, the o-Ps will live for longer before annihilating with an electron from the void wall and decaying into two γ-rays. (B) Raw positron lifetime spectra obtained in two different samples, PEG5 and PEG25. (C) Probability density functions of the o-Ps in two different samples, PEG5 and PEG25, extracted by deconvoluting the positronium lifetime spectra.

Table 1. Positron Annihilation Lifetime Spectroscopy (PALS) Data for the PEG Hydrogelsa.

sample χ2 (a.u.) Io-Ps (%) Io-Ps (ns) σo-Ps (ns) rFV (Å) VF (Å3) σVF (Å3)
PEG5 1.08 20 ± 1 1.95 ± 0.06 0.3 ± 0.1 2.80 ± 0.09 92 ± 6 30 ± 10
PEG7 1.02 20 ± 1 1.97 ± 0.08 0.3 ± 0.1 2.82 ± 0.08 94 ± 7 30 ± 10
PEG10 1.05 20.0 ± 0.3 1.97 ± 0.02 0.4 ± 0.3 2.82 ± 0.03 94 ± 2 40 ± 30
PEG25 1.06 17.0 ± 0.5 2.46 ± 0.06 0.5 ± 0.1 3.24 ± 0.08 142 ± 6 80 ± 10
Open in a new tab
a

Values of the intensity of the orthopositronium signal (Io-Ps), orthopositronium Lifetime (τo-Ps) and distribution (σo-Ps), average radius of the free volume voids (rFV), average volume of the free volume voids (VF) and distribution (σVF), and for the different PEG hydrogels tested. χ2 are the χ2 test values.

The average radius of the free volume voids, rFV, was similar for the three most dilute PEG hydrogels tested and was found to be very similar to the free volume in water rFVW (2.69 Å).42,45 In contrast, the rFV determined for the hydrogel system with the highest polymer volume fraction, PEG25, differed by more than 20% from the average radius of the free volume in water. Presumably, the higher polymer content in the latter system introduces significantly more free volume as it contains a greater amount of surface area both between two polymer chains and between water and the polymer chains.

Validation of the Model

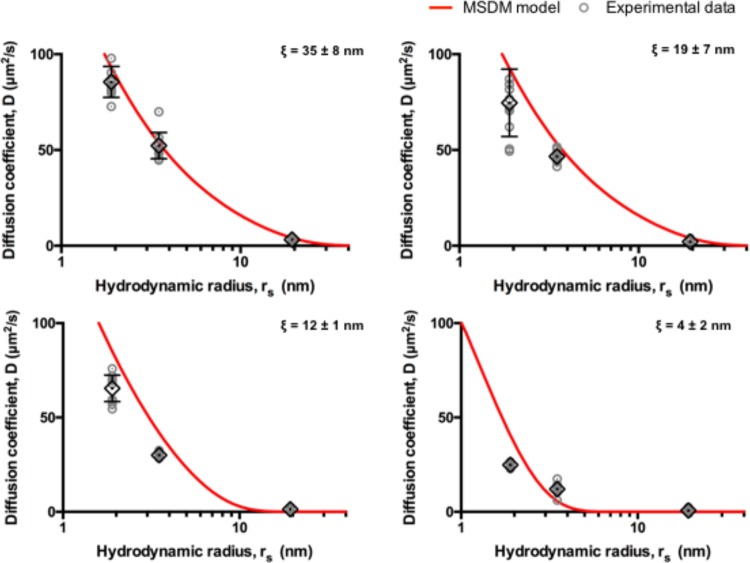
To validate our approach, we used the MSDM model to predict the diffusivity (D) of solutes of various sizes in the series of PEG-based hydrogels with distinct mesh sizes described in the Materials Section (Figure 3). The values for the cross-sectional radius of the hydrated PEG fiber (rf) and the average free volume void size in water (rFVW) were taken from the literature as 5.1 and 2.69 Å, respectively.45,46 It is clear that the predicted diffusivity values decrease monotonically with increasing solute radius (Figure 3), in accordance with physical expectations. We compared these predictions to experimental diffusivity values previously obtained42 by fluorescence recovery after photobleaching (FRAP) for dextran solutes of different sizes (rs = 1.9, 3.5, and 19.4 nm, corresponding to molecular weights of 4, 20, and 2000 kDa, respectively) in these hydrogels (Figure 3).

Figure 3.

Figure 3

Open in a new tab

Diffusivities predicted by the MSDM model compared against experimentally obtained diffusivities. Experimental diffusivities (gray circles; error bars denote mean ± s.d.; n = 10) and predicted diffusivities (solid red lines) are plotted against solute hydrodynamic radius (rs) for PEG hydrogels with different mesh sizes (ξ).

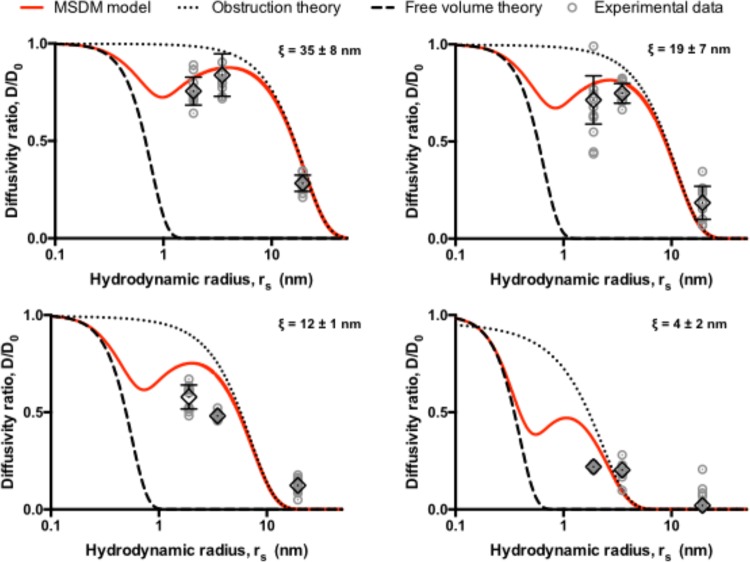
Additionally, we compared the MSDM model to (i) free volume theory as defined by Lustig and Peppas35 (eq 3) with 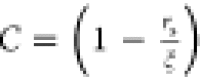Inline graphic and (ii) obstruction theory as developed by Amsden et al. (eq 4).36Figure 4 shows the predictions of the three different models compared to experimental data discussed previously, normalized by their diffusivity in pure liquid (D/D0).47 Again, the values for the cross-sectional radius of the hydrated PEG fiber (rf) and the average free volume void size in water (rFVW) were taken from the literature as 5.1 and 2.69 Å, respectively.45,46 The free volume theory (black dashed line) tends to systematically underestimate the solute diffusivity, while obstruction theory (black dotted line) tends to systematically overestimate the diffusivity values for all but the largest solute (rs = 19.4 nm). Interestingly, experimental data could potentially suggest the presence of a local maximum in the diffusivity ratio for solutes of intermediate size (rs ∼ 1–10 nm) in hydrogels with larger mesh sizes (34.83 and 19.30 nm). Even if more experiments will be needed to confirm this presence of a local maximum, this trend is uniquely captured by the MSDM model, which predicts a local minimum and local maximum in the diffusivity ratio arising at distinct size regimes for the solutes.

Figure 4.

Figure 4

Open in a new tab

Normalized diffusivities predicted by the MSDM model compared against experimentally obtained values. Experimental data (gray circles; error bars denote mean ± s.d.; n = 10) and theoretical predictions (lines) for the normalized diffusivity, D/D0, versus solute hydrodynamic radius (rs) for PEG hydrogels with different mesh sizes (ξ; mean ± s.d.; n = 4). The MSDM model (red solid line) predicts the existence and location of a local minimum and maximum in D/D0, whereas free volume theory (black dashed line) and obstruction theory (black dotted line) do not. These local minima/maxima in D/D0 are reflected in the experimental data.

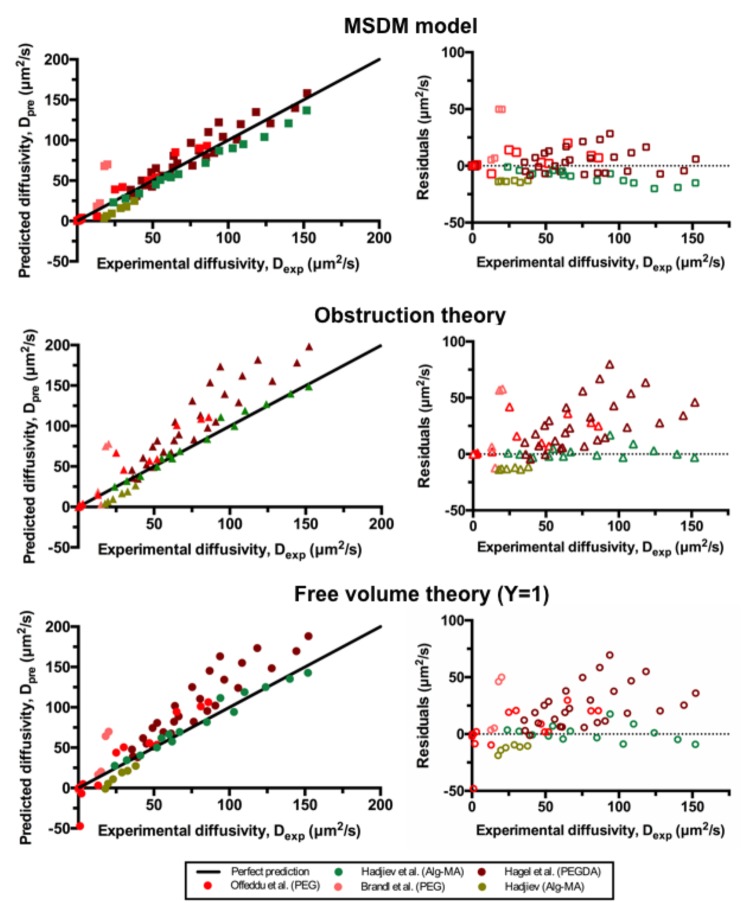
To further validate the MSDM model and quantify the differences in the accuracy between models, we performed an analysis of data obtained by other research groups in previous studies.36,46,48,49 In total, 66 distinct solute/hydrogel combinations using two different hydrogel systems (PEG and alginate) were analyzed (Table S1). Figure 5 shows experimentally obtained solute diffusion coefficients in the hydrogels, plotted versus the prediction from eqs 3, 4, and 6. For this analysis, as free volume hole size data was not available for many of the data sets, two approximations were made: (i) Y = 1 for the free volume theory predictions as previously suggested by the Lustig and Peppas35 and (ii) rFV ≈ rFVW for the MSDM model. When access to PALS equipment is not available, the approximation that rFV ≈ rFVW is appropriate because the free volume holes in hydrogels deviate from those in water only at high polymer concentrations (Table 1). With this, the MSDM model takes into account four independent parameters, while obstruction theory has three and free volume theory has two independent parameters. The MSDM model (R2 = 0.885, calculated with respect to the perfect prediction line) outperforms obstruction theory (R2 = 0.743) and free volume theory (R2 = 0.787) in predicting the experimentally obtained diffusivity more accurately. Moreover, a study of the residuals (Figure 3B) shows that the MSDM mean square error value (MSE) is ∼4 times smaller (185.7) than that for the obstruction theory (710.0) and 3 times smaller than that for free volume theory (564.8).

Figure 5.

Figure 5

Open in a new tab

Parity plot of predicted versus experimental diffusivity. The perfect prediction is illustrated as the 1–1 line plotted in black. The MSDM model (squares) by eq 6 predicts the experimental diffusivity of dextran solutes in both poly(ethylene glycol) hydrogels (PEG)42,46,48 and alginate-based hydrogels36,49 more accurately than eqs 3 and 4—free volume theory (triangles) and obstruction theory (circles). Each color of data points represents a different study of the meta-analysis. In the residuals versus experimental diffusivity plot, the perfect prediction is shown as a black dotted line.

Typical drugs range in diameter from 1 nm (small molecules) to 5 nm (antibodies). For potential drug delivery applications of our model, we analyzed the residuals for the predicted diffusivity values with different models versus solutes with radii within this typical range (rs from 0.5 to 5 nm; Figure S1A). The outcome of this analysis highlights the accuracy of the MSDM model for solutes with sizes that lie within the typical range of size range for drug molecules: 1–5 nm.

Discussion

Here, a predictive model for the diffusion of solutes in hydrogels was formulated combining three traditional theoretical frameworks: hydrodynamic theory, free volume theory, and obstruction theory. It was demonstrated that the MSDM model successfully predicts the diffusion of dextran solutes of multiple sizes in chemically cross-linked PEG and physically cross-linked alginate hydrogels with multiple mesh sizes (66 distinct combinations in total), with an increased qualitative and quantitative accuracy compared to traditional models.

Previous studies1,50 have employed hydrodynamic theory in the form of the Stokes–Einstein equation to predict the diffusivity in hydrogels with a mesh size larger than the solute size. However, this approach appears to be inaccurate, as it overpredicts the experimental diffusivity in hydrogels even if the mesh size exceeds the solute radius by a factor of 18 (in Figure 4, this case would be represented by a horizontal line of D/D0 = 1). On the other hand, free volume theory tends to underestimate the diffusion coefficient unless the solute size is large. Moreover, when using the approximation Y = 1 proposed by Lustig and Peppas,35 the model predicts negative (and, as a consequence, unphysical) values for the diffusion coefficient of solutes with radius 19.4 nm (Table S2). In addition, the MSDM model is notably more accurate (R2 = 0.885, calculated with respect to the perfect prediction line) than the equation developed by Amsden et al.36 based on the obstruction theory (R2 = 0.743).

Most drug molecules have a hydrodynamic radius that falls between 0.5 and 5 nm. In this solute size regime of paramount importance for drug delivery applications, the diffusion behavior is fundamentally not captured by traditional models (Figure S1). By combining these traditional models to create a comprehensive description of solute diffusion, the MSDM model is remarkably more accurate than the any of these models individually. The mean square error is 3–4-fold smaller than traditional theories.

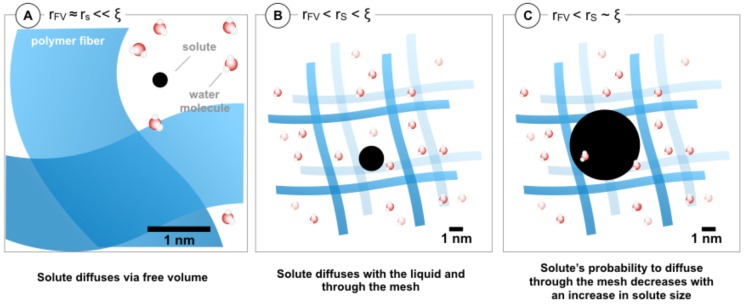
As in traditional frameworks, the diffusivity (D) predicted in the MSDM model decreases monotonically with increasing solute radius (Figure 3). The MSDM theory does not contain any term nor fitting parameter that is empirical. Our approach is entirely probabilistic in nature and begins from the conservation of probability (eq 2), which captures two independent modes of diffusion: (i) via free volume voids and/or (ii) alongside water through the polymer mesh. Both of these diffusion modes contribute to the total probability. The model presented here describes the competition between different mechanisms of diffusion, and three regimes emerge. First, when rs ≈ rFV (and therefore rs ≪ ξ), the MSDM model reduces to the free volume theory:

graphic file with name ma9b00753_m011.jpg 7

In this regime, the solute diffuses via dynamic free volume voids formed in the hydrogel. Here, the probability of finding a free volume void decreases with an increase in the solute size. Second, for larger solutes, the diffusion via this mechanism becomes increasingly unlikely, and a local minimum in the D/D0 prediction is reached (rs ∼ 1 nm for the hydrogels tested; see Figure 4). In this intermediate zone, the probability of the solute to diffuse within the hydrogels via the liquid (instead by free volume voids) starts to gain importance. As the mesh size is still much larger than the solute, it allows its passage. As the solute size increases, both the values for D and D0 decrease, but the D/D0 ratio increases, as there exists a superposition of two diffusion mechanisms in this regime. Finally, a local maximum is reached when the solute size starts to be comparable to the mesh size (rs ≈ ξ and therefore rs ≫ rFV), and the equation presented in this study reduces to the obstruction theory:

graphic file with name ma9b00753_m012.jpg 8

Here, the probability of finding an aperture in the mesh decreases with a further increase in solute size. In other words, this local minimum and maximum indicate a transition in the hinder mechanism of the diffusing particle. Importantly, this local minimum and maximum has been previously shown to be a physical phenomenon, as observed by Hoh and Zia.51,52 Thus, depending on the size scale of solute, the MSDM accounts for different mechanisms of diffusion, as summarized in Figure 6.

Figure 6.

Figure 6

Open in a new tab

MSDM model accounts for different diffusion mechanisms depending on the scale of the solute. (A) When the solute size is comparable to the free volume pockets, the solute will diffuse though free volume. (B) When the solute is substantially larger than the free volume, it will diffuse with the liquid within the hydrogel and cross the mesh. (C) When the solute is larger than the mesh size, the diffusion will be hindered by the polymer fibers of the mesh.

Overall, the MSDM model describes different dominant types of molecular transport depending on the solute size. This model provides valuable information not only for a theoretical understanding of the diffusion in hydrogels but also for practical applications in tissue engineering or drug delivery applications, by potentially predicting more accurately the diffusion of solutes such as growth factors, nanoparticles, or drugs in hydrogels. It is also important to note that solute–gel interactions, including hydrophobic effects, H-bonding, electrostatic, and van der Waals interactions, are present and of considerable importance in several systems. While few studies have explored drug–hydrogel interactions, this could include up to a 25% decrease in diffusivity.53 However, inclusion of such interactions would be incredibly specific to each material, which is not the intention of our model that we hope can be broadly applicable to many systems.46,54 We also want to highlight that for drug delivery systems the process of drug release is dominated by diffusion when the mesh is larger than the drug due to domination of steric interactions; in these cases, drug–gel interactions are not even necessary. Thus, many principles introduced here could be applied to drug delivery.1 In addition, the MSDM model could be used in future studies as a baseline to quantify gel–solute interactions.

The favorable experimental validation of the model presented here is limited to dextran solutes–PEG hydrogels (considered as inert). To fully understand the strengths and weaknesses of the MSDM model, future work across a wide range of hydrogels and solutes is necessary. To apply this model when PALS data are not available, it could be assumed that the available free volume voids in the aqueous solution are much more numerous than those surrounding the polymer network in hydrogels. In other words, the average free volume void size in the hydrogels could be approximated as the one in water. The MSDM model was tested including this approximation (see Figure S2) and obtained good results (R2 = 0.93, calculated with respect to the perfect prediction line for the 12 experimental points, whereas without the approximation the obtained value was R2 = 0.94). The main limitations of the MSDM model, similar to each of the traditional models described above, are that the solute is described as a hard sphere (thus precluding possible shape effects) and that it does not consider possible intermolecular forces between the solute and the polymer. Future studies will investigate the utility of the MSDM model in more complex aqueous systems such as living cells as well as in organogels.

Conclusion

The MSDM model presented here is capable of integrating three different mechanisms for the solute diffusion in hydrogels occurring on various size scales. Compared to previous frameworks, this combined model leads to more accurate predictions of the experimentally measured diffusivity, determined by dextran solutes of different sizes in PEG hydrogels and alginate-based hydrogels with different mesh sizes and free volume properties. Development of tunable and well-defined materials in clinical use, regenerative medicine, and drug delivery relies critically on the ability of solutes (e.g., nutrients or drugs) to move through the material scaffold. The model presented could offer a way to design hydrogels for tissue engineering or drug delivery applications with tailored solute transport properties. The dramatic reduction in costs of fabrication and testing may pave the way to a larger use of hydrogels in biomedical commercial applications. This study can also be a fundamental advance in understanding the physics behind diffusion of solutes in hydrogels.

Methods

Hydrogel Preparation

Poly(ethylene glycol) dimethacrylate (PEGDMA) monomers with a molecular mass of Mn = 1000 g mol–1 as specified by the manufacturer (Polysciences, Inc., USA), were used to fabricate PEG hydrogels with various mesh and free volume void sizes. PEGDMA was dissolved in phosphate-buffered saline (PBS) in weight concentrations of 5, 7, 10, and 25 wt % called PEG5, PEG7, PEG10, and PEG25, respectively. Ammonium persulfate (APS) was used as a free-radical initiator, and N,N,N′,N′-tetramethylethylenediamine (TEMED) was used as an accelerator. APS volumes of 150 μL (10 wt % in H2O) and 75 μL of TEMED were added simultaneously to 10 mL of the precursor solution, vortexed for 10 s to ensure thorough mixing, poured into cylindrical molds 35 mm in diameter, and left overnight to cross-link. Prior to testing, the gels were placed in PBS for 24 h at room temperature to reach swelling equilibrium and to allow the removal of nonreacted monomers.

Positron Annihilation Lifetime Spectroscopy

Two samples from each hydrogel sandwiched the 22NaCl positron source of about 15 μCi from PerkinElmer (USA), protected by two 7.5 μm Kapton foils and sealed by a CAPLINQ (Canada) double-sided sticky Kapton tape. The PAL spectrometer is composed by two H1949-50 Hamamatsu (Japan) photomultipliers added to two BC-422 plastic scintillators from Saint Gobain (USA) performed vertically inside a Radiber S.A. (Spain) FFD-1402 refrigerator. All the electronic modules were purchased from ORTEC (USA). The temperature of the samples was kept constant at 25 °C by a SALICRU (Spain) variable power supply, a 3508 temperature controller from Eurotherm (United Kingdom), a Watlow Europe (Germany) 100 W FIREROD cartridge heater, and a TC S.A. (Spain) PT-100 CS5 (1|5) temperature sensor introduced in an aluminum sample holder. The resolution function was 258 ps, and the detection rate was ∼70 counts s–1. Each positron lifetime spectrum was obtained by ∼3 million counts and analyzed with the LT_polymers software. The Kapton contribution was extracted (19.8%, 0.382 ns) prior to the decomposition of each spectrum into three components. The longest-lived component distribution corresponded to the orthopositronium (o-Ps) lifetime distribution. The Tao–Eldrup equation55,56—based on positronium trapping in spherical voids in polymers—was used to calculate the radius size of the voids:

graphic file with name ma9b00753_m013.jpg 9

where r0 = rVF + ΔrVF and ΔrVF is an empirical parameter fitted as 1.66 Å.57

Acknowledgments

This work was supported by the Center for Human Systems Immunology with Bill & Melinda Gates Foundation (OPP1113682) and a Stanford Bio-X Interdisciplinary Initiatives Program Seed Grant. Dr. Eneko Axpe is thankful for funding support from a postdoctoral fellowship of the Basque Government and for a Marie Skłodowska-Curie Individual Fellowship (INMARE Project No. 796557). Yin Chang acknowledges the Taiwanese Cambridge Trust for her PhD fellowship. Doreen Chan is grateful for an award by the Department of Defense, Air Force Office of Scientific Research, National Defense Science and Engineering Graduate (ND-SEG) Fellowship, 32 CFR 168a, with government support under FA9550-11-C-0028. Authors are very grateful to Prof. Rosanne Zia, Prof. Andrew Spakowitz, and Dr. David Labonte for critical discussions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.macromol.9b00753.

  • Figures S1–S4 as well as Tables S1 and S2 (PDF)

Author Contributions

E.A. conceived the study. E.A. and E.A.A. coordinated the study. E.A., Y.C., D.C., and G.S.O. developed the mathematical model. G.S.O. and Y.C. fabricated the hydrogels. D.M. and E.A. performed the PALS studies. E.A., D.C., H.L.H., and E.A.A. performed the analysis. H.L.H. performed the statistical analysis. E.A., Y.C., D.C., and E.A.A. analyzed the data. All authors participated in the writing of the article.

The authors declare no competing financial interest.

Supplementary Material

ma9b00753_si_001.pdf (702.4KB, pdf)

References

  1. Li J.; Mooney D. J.; Buffle J.; DeRouchey J. E.; Langer R. Designing Hydrogels for Controlled Drug Delivery. Nat. Rev. Mater. 2016, 1 (12), 16071. 10.1038/natrevmats.2016.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Slaughter B. V.; Khurshid S. S.; Fisher O. Z.; Khademhosseini A.; Peppas N. A. Hydrogels in Regenerative Medicine. Adv. Mater. 2009, 21 (32–33), 3307–3329. 10.1002/adma.200802106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hayashi K.; Okamoto F.; Hoshi S.; Katashima T.; Zujur D. C.; Li X.; Shibayama M.; Gilbert E. P.; Chung U.-i.; Ohba S.; Oshika T.; Sakai T.; et al. Fast-Forming Hydrogel with Ultralow Polymeric Content as an Artificial Vitreous Body. Nat. Biomed. Eng. 2017, 1 (3), 0044. 10.1038/s41551-017-0044. [DOI] [Google Scholar]
  4. Peppas N. A.; Hilt J. Z.; Khademhosseini A.; Langer R. Hydrogels in Biology and Medicine: From Molecular Principles to Bionanotechnology. Adv. Mater. 2006, 18 (11), 1345–1360. 10.1002/adma.200501612. [DOI] [Google Scholar]
  5. Chin S. Y.; Poh Y. C.; Kohler A.-C.; Compton J. T.; Hsu L. L.; Lau K. M.; Kim S.; Lee B. W.; Lee F. Y.; Sia S. K. Additive Manufacturing of Hydrogel-Based Materials for next-Generation Implantable Medical Devices. Sci. Robot. 2017, 2 (2), eaah6451 10.1126/scirobotics.aah6451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Lee K. Y.; Mooney D. J. Hydrogels for Tissue Engineering. Chem. Rev. 2001, 101 (7), 1869–1879. 10.1021/cr000108x. [DOI] [PubMed] [Google Scholar]
  7. Novosel E. C.; Kleinhans C.; Kluger P. J. Vascularization Is the Key Challenge in Tissue Engineering. Adv. Drug Delivery Rev. 2011, 63 (4), 300–311. 10.1016/j.addr.2011.03.004. [DOI] [PubMed] [Google Scholar]
  8. Lin C.-C.; Metters A. T. Hydrogels in Controlled Release Formulations: Network Design and Mathematical Modeling. Adv. Drug Delivery Rev. 2006, 58 (12), 1379–1408. 10.1016/j.addr.2006.09.004. [DOI] [PubMed] [Google Scholar]
  9. Zhang S.; Ermann J.; Succi M. D.; Zhou A.; Hamilton M. J.; Cao B.; Korzenik J. R.; Glickman J. N.; Vemula P. K.; Glimcher L. H.; et al. An Inflammation-Targeting Hydrogel for Local Drug Delivery in Inflammatory Bowel Disease. Sci. Transl. Med. 2015, 7 (300), 300ra128 10.1126/scitranslmed.aaa5657. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kosto K. B.; Deen W. M. Diffusivities of Macromolecules in Composite Hydrogels. AIChE J. 2004, 50 (11), 2648–2658. 10.1002/aic.10216. [DOI] [Google Scholar]
  11. Ogston A. G. The Spaces in a Uniform Random Suspension of Fibres. Trans. Faraday Soc. 1958, 54 (0), 1754. 10.1039/tf9585401754. [DOI] [Google Scholar]
  12. Ogston A. G.; Preston B. N.; Wells J. D. On the Transport of Compact Particles Through Solutions of Chain-Polymers. Proc. R. Soc. London, Ser. A 1973, 333 (1594), 297–316. 10.1098/rspa.1973.0064. [DOI] [Google Scholar]
  13. Kosar T. F.; Phillips R. J. Measurement of Protein Diffusion in Dextran Solutions by Holographic Interferometry. AIChE J. 1995, 41 (3), 701–711. 10.1002/aic.690410327. [DOI] [Google Scholar]
  14. Phillips R. J.; Deen W. M.; Brady J. F. Hindered Transport of Spherical Macromolecules in Fibrous Membranes and Gels. AIChE J. 1989, 35 (11), 1761–1769. 10.1002/aic.690351102. [DOI] [Google Scholar]
  15. Johnson E. M.; Berk D. A.; Jain R. K.; Deen W. M. Hindered Diffusion in Agarose Gels: Test of Effective Medium Model. Biophys. J. 1996, 70 (2), 1017–1023. 10.1016/S0006-3495(96)79645-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Johansson L.; Löfroth J. Diffusion and Interaction in Gels and Solutions. 4. Hard Sphere Brownian Dynamics Simulations. J. Chem. Phys. 1993, 98 (9), 7471–7479. 10.1063/1.464686. [DOI] [Google Scholar]
  17. Anderson J. L.; Quinn J. A. Restricted Transport in Small Pores. A Model for Steric Exclusion and Hindered Particle Motion. Biophys. J. 1974, 14 (2), 130–150. 10.1016/S0006-3495(74)70005-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fornasiero F.; Krull F.; Prausnitz J. M.; Radke C. J. Steady-State Diffusion of Water through Soft-Contact-Lens Materials. Biomaterials 2005, 26 (28), 5704–5716. 10.1016/j.biomaterials.2005.02.028. [DOI] [PubMed] [Google Scholar]
  19. Liu D. E.; Kotsmar C.; Nguyen F.; Sells T.; Taylor N. O.; Prausnitz J. M.; Radke C. J. Macromolecule Sorption and Diffusion in HEMA/MAA Hydrogels. Ind. Eng. Chem. Res. 2013, 52 (50), 18109–18120. 10.1021/ie402148u. [DOI] [Google Scholar]
  20. Hoch G.; Chauhan A.; Radke C. J. Permeability and Diffusivity for Water Transport through Hydrogel Membranes. J. Membr. Sci. 2003, 214 (2), 199–209. 10.1016/S0376-7388(02)00546-X. [DOI] [Google Scholar]
  21. Kotsmar C.; Sells T.; Taylor N.; Liu D. E.; Prausnitz J. M.; Radke C. J. Aqueous Solute Partitioning and Mesh Size in HEMA/MAA Hydrogels. Macromolecules 2012, 45 (22), 9177–9187. 10.1021/ma3018487. [DOI] [Google Scholar]
  22. Tegrotenhuis W. E.; Radke C. J.; Denn M. M. Self-Diffusion in Electrostatically Stabilized Colloidal Suspensions Using Brownian Dynamics. Mol. Simul. 1989, 2 (1–2), 3–14. 10.1080/08927028908032780. [DOI] [Google Scholar]
  23. Pimenta A. F. R.; Ascenso J.; Fernandes J. C. S.; Colaço R.; Serro A. P.; Saramago B. Controlled Drug Release from Hydrogels for Contact Lenses: Drug Partitioning and Diffusion. Int. J. Pharm. 2016, 515 (1–2), 467–475. 10.1016/j.ijpharm.2016.10.047. [DOI] [PubMed] [Google Scholar]
  24. Liu D. E.; Dursch T. J.; Taylor N. O.; Chan S. Y.; Bregante D. T.; Radke C. J. Diffusion of Water-Soluble Sorptive Drugs in HEMA/MAA Hydrogels. J. Controlled Release 2016, 239, 242–248. 10.1016/j.jconrel.2016.08.025. [DOI] [PubMed] [Google Scholar]
  25. Cukier R. I. Diffusion of Brownian Spheres in Semidilute Polymer Solutions. Macromolecules 1984, 17 (2), 252–255. 10.1021/ma00132a023. [DOI] [Google Scholar]
  26. Turnbull M. H. C.; Cohen M. H.; Turnbull D. Molecular Transport in Liquids and Glasses. J. Chem. Phys. 1959, 31 (5), 1164–1169. 10.1063/1.1730566. [DOI] [Google Scholar]
  27. Mackie J. S.; Meares P. The Diffusion of Electrolytes in a Cation-Exchange Resin Membrane. I. Theoretical. Proc. R. Soc. London A: Math. Phys. Eng. Sci. 1955, 232 (1191), 498–509. 10.1098/rspa.1955.0234. [DOI] [Google Scholar]
  28. Amsden B. Solute Diffusion within Hydrogels. Mechanisms and Models. Macromolecules 1998, 31 (23), 8382–8395. 10.1021/ma980765f. [DOI] [Google Scholar]
  29. Masaro L.; Zhu X. Physical Models of Diffusion for Polymer Solutions, Gels and Solids. Prog. Polym. Sci. 1999, 24 (5), 731–775. 10.1016/S0079-6700(99)00016-7. [DOI] [Google Scholar]
  30. Zhu J. Bioactive Modification of Poly(Ethylene Glycol) Hydrogels for Tissue Engineering. Biomaterials 2010, 31 (17), 4639–4656. 10.1016/j.biomaterials.2010.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Bunker A. Poly(Ethylene Glycol) in Drug Delivery, Why Does It Work, and Can We Do Better? All Atom Molecular Dynamics Simulation Provides Some Answers. Phys. Procedia 2012, 34, 24–33. 10.1016/j.phpro.2012.05.004. [DOI] [Google Scholar]
  32. Knop K.; Hoogenboom R.; Fischer D.; Schubert U. S. Poly(Ethylene Glycol) in Drug Delivery: Pros and Cons as Well as Potential Alternatives. Angew. Chem., Int. Ed. 2010, 49 (36), 6288–6308. 10.1002/anie.200902672. [DOI] [PubMed] [Google Scholar]
  33. Miller C. C. The Stokes-Einstein Law for Diffusion in Solution. Proc. R. Soc. London, Ser. A 1924, 106 (740), 724–749. 10.1098/rspa.1924.0100. [DOI] [Google Scholar]
  34. de Gennes P.-G.Scaling Concepts in Polymer Physics; Cornell University Press: 1979. [Google Scholar]
  35. Lustig S. R.; Peppas N. A. Solute Diffusion in Swollen Membranes. IX. Scaling Laws for Solute Diffusion in Gels. J. Appl. Polym. Sci. 1988, 36 (4), 735–747. 10.1002/app.1988.070360401. [DOI] [Google Scholar]
  36. Hadjiev N. A.; Amsden B. G. An Assessment of the Ability of the Obstruction-Scaling Model to Estimate Solute Diffusion Coefficients in Hydrogels. J. Controlled Release 2015, 199, 10–16. 10.1016/j.jconrel.2014.12.010. [DOI] [PubMed] [Google Scholar]
  37. Axpe E.; Bugnicourt L.; Merida D.; Goiriena-Goikoetxea M.; Unzueta I.; Sanchez-Eugenia R.; Garcia J. A.; Plazaola F.; Contera S. Sub-Nanoscale Free Volume and Local Elastic Modulus of Chitosan-Carbon Nanotube Biomimetic Nanocomposite Scaffold-Materials. J. Mater. Chem. B 2015, 3 (16), 3169–3176. 10.1039/C5TB00154D. [DOI] [PubMed] [Google Scholar]
  38. Axpe E.; Lopez-Euba T.; Castellanos-Rubio A.; Merida D.; Garcia J. A.; Plaza-Izurieta L.; Fernandez-Jimenez N.; Plazaola F.; Bilbao J. R. Detection of Atomic Scale Changes in the Free Volume Void Size of Three-Dimensional Colorectal Cancer Cell Culture Using Positron Annihilation Lifetime Spectroscopy. PLoS One 2014, 9 (1), e83838 10.1371/journal.pone.0083838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Axpe E.; Garcia-Arribas A. B.; Mujika J. I.; Merida D.; Alonso A.; Lopez X.; Garcia J. A.; Ugalde J. M.; Goni F. M.; Plazaola F. Ceramide Increases Free Volume Voids in DPPC Membranes. RSC Adv. 2015, 5 (55), 44282–44290. 10.1039/C5RA05142H. [DOI] [Google Scholar]
  40. García-Arribas A. B.; Axpe E.; Mujika J. I.; Mérida D.; Busto J. V.; Sot J.; Alonso A.; Lopez X.; García J. A.; Ugalde J. M.; et al. Cholesterol-Ceramide Interactions in Phospholipid and Sphingolipid Bilayers As Observed by Positron Annihilation Lifetime Spectroscopy and Molecular Dynamics Simulations. Langmuir 2016, 32 (21), 5434–5444. 10.1021/acs.langmuir.6b00927. [DOI] [PubMed] [Google Scholar]
  41. Jean Y. C.; Mallon P. E.; Schrader D. M.. Principles and Applications of Positron and Positronium Chemistry; World Scientific: 2003. [Google Scholar]
  42. Offeddu G. S.; Axpe E.; Harley B. A. C.; Oyen M. L. Relationship between Permeability and Diffusivity in Polyethylene Glycol Hydrogels. AIP Adv. 2018, 8 (10), 105006. 10.1063/1.5036999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Giri N.; Del Pópolo M. G.; Melaugh G.; Greenaway R. L.; Rätzke K.; Koschine T.; Pison L.; Gomes M. F. C.; Cooper A. I.; James S. L. Liquids with Permanent Porosity. Nature 2015, 527 (7577), 216–220. 10.1038/nature16072. [DOI] [PubMed] [Google Scholar]
  44. Axpe E.; Lopez-Euba T.; Castellanos-Rubio A.; Merida D.; Garcia J. A.; Plaza-Izurieta L.; Fernandez-Jimenez N.; Plazaola F.; Bilbao J. R. Detection of Atomic Scale Changes in the Free Volume Void Size of Three-Dimensional Colorectal Cancer Cell Culture Using Positron Annihilation Lifetime Spectroscopy. PLoS One 2014, 9 (1), e83838 10.1371/journal.pone.0083838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Kotera K.; Saito T.; Yamanaka T. Measurement of Positron Lifetime to Probe the Mixed Molecular States of Liquid Water. Phys. Lett. A 2005, 345 (1–3), 184–190. 10.1016/j.physleta.2005.07.018. [DOI] [Google Scholar]
  46. Hagel V.; Haraszti T.; Boehm H. Diffusion and Interaction in PEG-DA Hydrogels. Biointerphases 2013, 8 (1), 36. 10.1186/1559-4106-8-36. [DOI] [PubMed] [Google Scholar]
  47. Gribbon P.; Hardingham T. E. Macromolecular Diffusion of Biological Polymers Measured by Confocal Fluorescence Recovery after Photobleaching. Biophys. J. 1998, 75 (2), 1032–1039. 10.1016/S0006-3495(98)77592-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Brandl F.; Kastner F.; Gschwind R. M.; Blunk T.; Teßmar J.; Göpferich A. Hydrogel-Based Drug Delivery Systems: Comparison of Drug Diffusivity and Release Kinetics. J. Controlled Release 2010, 142 (2), 221–228. 10.1016/j.jconrel.2009.10.030. [DOI] [PubMed] [Google Scholar]
  49. Hadjiev N.FRAP Measurements of Solute Diffusion Through Hydrogels. MS diss., Queen’s University, Kingston, Ontario, Canada, 2014. [Google Scholar]
  50. Weber L. M.; Lopez C. G.; Anseth K. S. Effects of PEG Hydrogel Crosslinking Density on Protein Diffusion and Encapsulated Islet Survival and Function. J. Biomed. Mater. Res., Part A 2009, 90 (3), 720–729. 10.1002/jbm.a.32134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Hoh N. J.; Zia R. N. Force-Induced Diffusion in Suspensions of Hydrodynamically Interacting Colloids. J. Fluid Mech. 2016, 795, 739–783. 10.1017/jfm.2016.209. [DOI] [Google Scholar]
  52. Hoh N. J.; Zia R. N. The Impact of Probe Size on Measurements of Diffusion in Active Microrheology. Lab Chip 2016, 16 (16), 3114–3129. 10.1039/C6LC00476H. [DOI] [PubMed] [Google Scholar]
  53. Zustiak S. P.; Boukari H.; Leach J. B. Solute Diffusion and Interactions in Cross-Linked Poly(Ethylene Glycol) Hydrogels Studied by Fluorescence Correlation Spectroscopy. Soft Matter 2010, 6 (15), 3609. 10.1039/c0sm00111b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Rossi F.; Castiglione F.; Ferro M.; Marchini P.; Mauri E.; Moioli M.; Mele A.; Masi M. Drug-Polymer Interactions in Hydrogel-Based Drug-Delivery Systems: An Experimental and Theoretical Study. ChemPhysChem 2015, 16 (13), 2818–2825. 10.1002/cphc.201500526. [DOI] [PubMed] [Google Scholar]
  55. Tao S. J. Positronium Annihilation in Molecular Substances. J. Chem. Phys. 1972, 56 (11), 5499–5510. 10.1063/1.1677067. [DOI] [Google Scholar]
  56. Eldrup M.; Lightbody D.; Sherwood J. N. The Temperature Dependence of Positron Lifetimes in Solid Pivalic Acid. Chem. Phys. 1981, 63 (1–2), 51–58. 10.1016/0301-0104(81)80307-2. [DOI] [Google Scholar]
  57. Nakanishi H. Microscopic Surface Tension Studied by Positron Annihilation. Int. Symp. Positron Annihil. Stud. Fluids 1988, 292–298. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma9b00753_si_001.pdf (702.4KB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES