Counterion-Dependent Mechanisms of DNA Origami Nanostructure Stabilization Revealed by Atomistic Molecular Simulation

Abstract

The DNA origami technique has proven to have tremendous potential for therapeutic and diagnostic applications like drug delivery, but the relatively low concentrations of cations in physiological fluids cause destabilization and degradation of DNA origami constructs preventing in vivo applications. To reveal the mechanisms behind DNA origami stabilization by cations, we performed atomistic molecular dynamics simulations of a DNA origami rectangle in aqueous solvent with varying concentrations of magnesium and sodium as well as polyamines like oligolysine and spermine. We explored the binding of these ions to DNA origami in detail and found that the mechanism of stabilization differs between ion types considerably. While sodium binds weakly and quickly exchanges with the solvent, magnesium and spermine bind close to the origami with spermine also located in between helices, stabilizing the crossovers characteristic for DNA origami and reducing repulsion of parallel helices. In contrast, oligolysine of length ten prevents helix repulsion by binding to adjacent helices with its flexible side chains, spanning the gap between the helices. Shorter oligolysine molecules with four subunits are weak stabilizers as they lack both the ability to connect helices and to prevent helix repulsion. This work thus shows how the binding modes of ions influence the stabilization of DNA origami nanostructures on a molecular level.

DNA origami is a robust and reliable method for designing and constructing uniquely addressable DNA-based nanostructures. By exploiting the programmability of Watson–Crick base pairing, circular single-stranded scaffold strands are folded into preprogrammed 2D or 3D nanostructures using shorter complementary staple strands.¹⁻⁴ Controlled folding is obtained as each staple strand binds to multiple regions of the scaffold strand, forming antiparallel double-stranded DNA (dsDNA) helices interconnected via Holliday junctions or crossovers. Because of their biocompatibility, nontoxicity,⁵⁻⁸ and unique addressability, DNA origami structures have been used as drug delivery vehicles,^7,9,10 artificial lipid membrane channels,^11,12 and as a molecular breadboard for enzymatic and chemical reactions.^13,14 A recent demonstration of the possibilities of DNA origami is the “inside-out virus”, a hollow DNA assembly containing proteins that are released upon transfection into HeLa cells.¹⁵

Although the above examples show the potential of DNA origami in nanomedicine and synthetic biology, applicability is impaired by the lack of structural integrity of DNA origami nanostructures in biologically relevant environments. There are two main reasons for this instability that hinder application of DNA origami nanostructures for biomedical objectives. First, nucleases present in biological environments degrade DNA nanostructures with, depending on the exact design, half-lives in the order of hours to days.¹⁶⁻¹⁸ Second, DNA origami comprises a high density of negatively charged phosphates on the DNA backbone. Though the stability of DNA origami has been shown to be strongly dependent on the exact design of the origami as well as on the identity of the buffer,¹⁹ high concentrations of multivalent cations are therefore required to overcome repulsive forces. In in vitro experiments typically 5–20 mM Mg²⁺ is used, which is an order of magnitude higher than typical in vivo environments.^2,20

Several solutions to these problems have been proposed including encapsulation of the nanostructure in a lipid bilayer membrane,²¹ design of polyhedral nanostructures that remain stable at lower cation concentrations,^22,23 and coating DNA-based nanostructures with cationic polyamines like poly(2-dimethylaminoethyl methacrylate) (PDMAEMA).²⁴ Recently, Ponnuswamy et al. identified poly(l-lysine) (K_n) with n at least 10 as a particularly stabilizing polyamine for DNA origami in low Mg²⁺ environments that also provides protection against nucleases when conjugated to polyethylene glycol (PEG). The authors also identified spermine (Spm⁴⁺) and spermidine as stabilizing polyamines, although these seem to dissociate from the DNA origami over time.²⁵ Oligolysine (Figure S1a) has been studied in relation to DNA vectors as it has been proposed as a transfection agent in gene therapy,^26,27 while Spm⁴⁺ (Figure S1b) and spermidine are naturally occurring molecules involved in DNA condensation and cell longevity.^28,29 Such polyamines and other multivalent cations have been shown to condense double-stranded DNA at certain concentration ranges.³⁰⁻³⁶ Although many studies have been performed on the interaction of DNA with polyamines and Mg²⁺ and Na⁺,³⁷⁻⁴⁶ mechanistic insights into the stabilization of DNA origami and its characteristic crossovers by these cations on a molecular level are still lacking.

Here we present atomistic molecular dynamics (MD) simulations of a 512 base pair DNA origami rectangle with varying concentrations of Mg²⁺ and Na⁺, K₁₀, and Spm⁴⁺ and analyze the stability of the DNA nanostructure in these different environments at time scales up to 100 ns. First, we investigate global structural fluctuations of the origami, after which we focus on local fluctuations and base pair integrity. Finally, we zoom in to analyze the binding of individual ions to the DNA origami at atomistic detail, with a special focus on the crossover-junctions that are characteristic for DNA origami. The root-mean-square deviation and aspect ratio of the origami rectangle reveal a large deviation from the initial structure in environments with only Na⁺. In contrast, structural integrity of the origami is observed in environments with Mg²⁺, Spm⁴⁺, or K₁₀. Analyses of the hydrogen bonding and internal angles reveal that crossovers and nicks are the main hotspots where disruptions of the origami structure occur. We show that Mg²⁺ resides near the DNA origami for extended periods of time compared to Na⁺. By aligning a crossover over multiple timesteps, we demonstrate that Mg²⁺ ions occupy particular locations near the DNA, while Na⁺ ions are more delocalized and at larger distance from the DNA. Although both K₁₀ and Spm⁴⁺ effectively stabilize the DNA origami, the underlying mechanisms for these two polyamines differ significantly. While K₁₀ mainly overcomes repulsion between DNA helices by spanning from one helix to another, Spm⁴⁺ efficiently screens the charges on the DNA backbone by binding in the grooves of the helices along the phosphate groups as well as in between helices. Compared to K₁₀, Spm⁴⁺ also results in higher amine concentrations near the crossovers, preserving the “H”-conformation of crossovers and planarity of the origami. To test whether the observed mechanistic differences between Spm⁴⁺ and K₁₀ depend on their difference in polyvalency, we finally set up one additional simulation containing K₄ as counterions. This work thus reveals the differences in the binding modes of these ions to DNA origami and offers insight into DNA origami stabilization on a molecular level: an important prerequisite for biomedical applicability of these versatile nanostructures.

Results and Discussion

Simulations

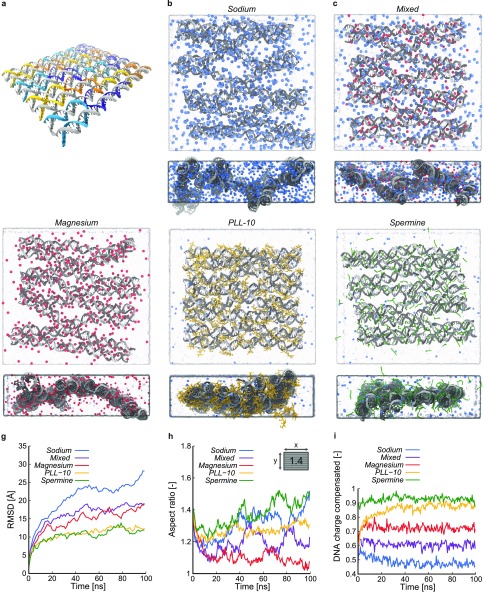
The DNA origami design in our simulations is based on the original 8192 base pair Rothemund rectangle¹ but comprises a reduced number of 512 base pairs to maintain computational feasibility in the atomistic MD simulations (Figure 1a). A schematic representation of our model compared to the original Rothemund rectangle, as well as the full DNA sequence, is shown in Figure S2. An atomistic model of the DNA origami was generated and simulated in five aqueous solutions with distinct ionic content, 10 mM Mg²⁺, which is a typical concentration for in vitro experiments, a mix of 5 mM Mg²⁺ and 10 mM Na⁺, 20 mM Na⁺, K₁₀, and Spm⁴⁺. These are denoted as Magnesium, Mixed, Sodium, PLL-10, and Spermine simulation, respectively. The exact content of each simulation is shown in Table S1. We first performed an equilibration protocol in which the positions of DNA origami backbone atoms are held fixed and ions diffuse toward the DNA origami. After the number of ions near the origami stabilized, all constraints were released and 100 ns MD production runs were initiated. Simulation details, as well as the methods used for solvation and ionization, are described in the Methods Section. Snapshots of the final configurations of the five systems are shown in Figure 1b–f, respectively.

Figure 1.

Overview of the DNA origami rectangle and atomistic MD simulations with various counterions. (a) DNA origami design considered in the MD simulations, with the scaffold strand shown in gray and the staple strands in color. (b–f) Snapshots of the final configurations of the Sodium, Mixed, Magnesium, PLL-10, and Spermine simulation, respectively, with the DNA origami shown in gray, water in light blue, and Na⁺, Mg²⁺, K₁₀, and Spm⁴⁺ in blue, red, yellow, and green, respectively. For each structure, both a top and side view are shown. (g) Root-mean-square deviation (RMSD) of the DNA backbone atoms from their initial positions as a function of time for the five simulations. (h) Aspect ratio of the DNA origami rectangle as a function of time for the five simulations. The inset shows the initial aspect ratio. (i) Fraction of DNA charge compensated by ions within 5 Å of DNA atoms for the Sodium, Mixed, Magnesium, PLL-10, and Spermine simulations as a function of time.

Global Conformational Changes

We first assessed how the different ionic environments affect global deformations of the origami construct. A conventional measure of the global deformations of a structure is the root-mean-square deviation (RMSD). Figure 1g shows the RMSD of the DNA origami backbone atoms from their initial positions as a function of time. For all simulations, the RMSD increases during roughly the first half of the trajectory before reaching a plateau. In the Magnesium, Sodium, and Mixed simulations, a trend of decreasing RMSD values with increasing Mg²⁺ concentration is observed. The Spermine and PLL-10 simulations show similar RMSD values that lie significantly lower than those in the simulations containing Na⁺ and Mg²⁺. These reduced global fluctuations are consistent with the experimental observation that these multivalent ions are able to stabilize DNA origami structures.²⁵ To verify if the simulations reach steady state, we also calculated the RMSD of the backbone atoms from their positions halfway through the simulation (Figure S3), which indicated that after 50 ns, the global conformations of the structures remain largely the same, which made us confident that the time scale of our simulations is sufficiently long.

Since RMSD only shows the average magnitude of deviations from a reference structure, we subsequently explored measures that describe the shape of the origami. As the origami construct is rectangular, an evident measure of the global structure is the aspect ratio, defined as the ratio between the sizes of the origami in the direction of the DNA double helices and in the direction in the origami plane perpendicular to the double helices. In Figure 1h, the aspect ratios of the DNA origami constructs in the five simulations are shown as a function of time. All initial structures, with aspect ratio 1.4, are elongated in the direction along the helices, and all simulations initially show a decreasing aspect ratio in time. While the aspect ratio in the Magnesium simulation stabilizes at a value approaching that of a square origami, the aspect ratio in the Sodium and Spermine simulations rises again after 25 ns. Visual inspection reveals an expansion of the DNA helices perpendicular to the helices in the Sodium simulation as well as a global twist in the structure of the origami. This causes the origami to deviate from an approximately flat rectangle and to extend over the entire simulation box at the end of the simulation, which renders the description of the structure by the aspect ratio of a 2D rectangle rather invalid. In contrast, the origami structure in the Spermine simulation becomes more oblong over time. This increase in aspect ratio originates from a closer packing of the helices, which can be attributed to ability of Spm⁴⁺ to effectively screen the negative charges on the backbone phosphates causing an attractive force between helices. Attraction of parallel DNA helices has been observed in earlier experiments,³¹⁻³⁴ and the mechanism has been debated for many years,⁴⁷ with attempts to describe this effect using counterion correlation theories like the Wigner crystal model,⁴⁸⁻⁵⁰ bridging model,^51,52 or more recently, an overlapping shell model.^53,54 It has been established that polyelectrolytes with a charge of at least three are required to observe this behavior.^32,55 However, whereas these theories are aimed at parallel DNA helices, an essential feature of DNA origami is the connection of helices through Holliday junction-like crossovers, which we will analyze in detail further. The opposite behavior, that is, the observed expansion of the origami perpendicular to the helical axes in the Magnesium, Mixed, Sodium, and to a smaller extent the PLL-10 simulations can analogously be rationalized by a lower efficiency of the ions in these simulations to screen the electrostatic interactions on the DNA backbone compared to Spm⁴⁺, leading to repulsion of neighboring helices and an aspect ratio closer to 1. This is corroborated by a previous work, where a linear relationship between Mg²⁺ concentration and DNA origami area was established.⁵⁶ Also, similar conclusions have been drawn from small-angle X-ray scattering experiments by Qiu et al.^32,57,58

To quantify the screening of the negative charges on the DNA backbone phosphates, we subsequently counted the number of ions condensing on the origami. In Figure 1i, the fraction of DNA charge compensated by ions within 5 Å (the characteristic distance to find bound ions in, see Figure S4, and of the order of the Debye length in physiological solution⁴⁷) of DNA atoms in the Sodium, Mixed, and Magnesium simulations is shown as a function of time. In all cases, this fraction remains constant over time, with higher values in systems containing more Mg²⁺. As the positive charges of K₁₀ and Spm⁴⁺ are centered on their nitrogen atoms, the fraction of DNA charge compensated by these nitrogens within 5 Å of DNA atoms for the PLL-10 and Spermine simulations is plotted in Figure 1i as well. Spm⁴⁺ and K₁₀ both show fractions higher than in the other simulations, which can be attributed to the polyvalency effects of these charged molecules. Bloomfield²⁸ has shown that condensation of DNA occurs when more than 90% of its charge is neutralized. The observed increase in aspect ratio in the Spermine simulation is therefore explained by the high number of Spm⁴⁺ ions, approximately 90%, localized near the origami. The fraction of K₁₀ nitrogens near the origami rises slowly compared to the other ions but steadily reaches a level close to the fraction of Spm⁴⁺ ions. Together, the RMSD, aspect ratio, and ion condensation analyses show that Na⁺ and Mg²⁺ cause larger global conformational changes than do Spm⁴⁺ and K₁₀ and that the change of shape of the origami itself is significantly different in the Spermine simulation. Na⁺ has a lower affinity for the DNA origami than Mg²⁺, followed by K₁₀ and Spm⁴⁺, which cause gradually less repulsion between parallel DNA helices.

Structure and Stability

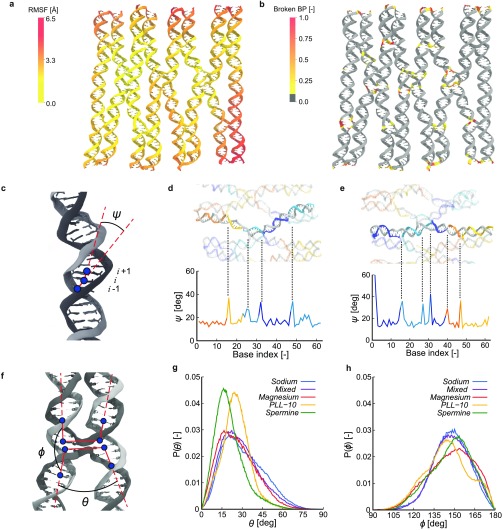
Having established the effect of the different ions on global conformational changes, we next examined the fluctuations of the structures in more detail to obtain insight in local deformations and DNA origami stability. To that end, we calculated the root-mean-square fluctuation (RMSF) for the center of mass for each nucleotide. Figure 2a shows a representation of these RMSF values for the Magnesium simulation, containing the typical ionic environment in in vitro experiments, mapped onto the time-averaged structure. The largest fluctuations in space occur at the edges of the origami, while the center remains rather rigid. The increased fluctuations at the edges of the DNA origami are caused by the lack of crossovers in the edge regions, which comprise a relatively large part of the origami design used in our simulations. The full-size origami typically employed experimentally would have a relatively much larger interconnected part constrained by crossovers. The fluctuations at the edges are also difficult to compare with experiments, as typical DNA origami experiments exclude the edge staples. This is because the ends of the origami helices, where one strand terminates and its complementary forms a U-turn, effectively form blunt ends, causing aggregation between separate origamis.¹ These effects could be diminished by constructing an infinite DNA origami system that binds to itself over the periodic boundaries,⁵⁶ though imposing such strict constraints upon the origami could introduce artifacts in its own. A qualitatively similar picture as observed for Mg²⁺ is displayed for the other ion types (see Figure S5). However, the magnitude of fluctuations clearly differs between simulations and shows a trend comparable to the final RMSD values where the fluctuations in the Sodium simulation are highest and that in the PLL-10 simulation lowest.

Figure 2.

Structural analysis of the DNA origami rectangle. (a) Root-mean-square fluctuations (RMSF) per nucleotide center of mass mapped onto the DNA’s time averaged structure for the Magnesium simulation. (b) Fraction of time the base pairs are broken for the Magnesium simulation mapped onto the DNA’s time averaged structure. (c) Schematic for the definition of helix angles ψ_i for base index i. (d, e) Helix angles ψ_i in the Sodium simulation for helices 4 and 5, respectively. (f) Schematic for the definition of crossover angles θ and ϕ. (g) Probability distributions of the angle θ for all five simulations. (h) Probability distributions of the angle ϕ for all five simulations.

As destabilization of DNA is typically associated with dehybridization of base pairs, we also analyzed whether the base pairs in the initial structure remain intact during the simulations. To this end, we quantified the fractions of time base pairs are broken. A base pair is defined to be intact, that is, not broken, if it has formed two or three hydrogen bonds for A-T and G-C pairs, respectively, where we count a hydrogen bond if the hydrogen-acceptor distance is within 2.9 Å and the donor-hydrogen-acceptor angle is at least 120°. Analysis of the Magnesium simulation (Figure 2b) shows that primarily base pairs near crossover regions and at the edges of the origami are broken. Base pairs in blunt ends at the edges are susceptible to fraying, while bases near crossovers in the center of the origami experience a larger stress from the structure that forces it in a certain conformation, which is not optimal for the formation of DNA base pairs. No clear difference between different ion concentrations or ion types is observed (see Figure S6), which indicates that breaking of base pairs near crossovers is not related to ion types but inherent to the DNA origami. Further research with other DNA origami designs could explain whether this is a design-specific effect or if this is inherent to all DNA origami constructs.

While the RMSF and base pair analyses reveal that the extent of internal instabilities in the origami structures is similar across simulations, small local deformations could still drive structural deformations at the global level. To quantify these local deformations, we studied bending of DNA helices, as well as the angles between two helices in crossover regions for different ion types. First, the angle between the two vectors connecting the centers of mass of three subsequent base pairs is assessed (Figure 2c). In Figure 2d and e, this angle ψ averaged over time is shown as a function of the base index (i) within the two middle helices of the DNA origami for the Sodium simulation as well as a snapshot of the corresponding helices. The angles at crossover locations are clearly larger than those in regions without crossovers, which corroborate recent coarse grained-simulations of a larger DNA origami.⁵⁹ Interestingly, in helix 5 (Figure 2e), an additional peak is observed at base index 38, that is, eight bases away from the nearest crossover. Inspection of the DNA sequence shows that at this position one staple strand ends and another one starts, effectively introducing a nick in the helix. That in helix 4 no clear kink is observed at a similar nick present at base index 22, may be attributed to the presence of a crossover only three bases away. These ψ-profiles repeat across the DNA origami (see Figure S7), matching the inherent periodicity of the design. Since crossover regions are the main difference between DNA origami nanostructures and previous work on the condensation of parallel DNA bundles, we aimed to characterize these regions in more detail. To this end, we defined two more angles, θ and ϕ, described by the four vectors between the centers of mass of base pairs adjacent to the crossovers and those three base pairs away (Figure 2f). Here, θ is defined as the angle between parallel vectors across helices, while ϕ is defined as the angle between antiparallel vectors within a helix. Probability density functions of the angles for all five simulations, averaged over time and all crossovers, are shown in Figure 2g and h. For θ, a trend can be observed in the Sodium, Mixed, and Magnesium simulations where a decreasing amount of Mg²⁺ results in wider angles. This is in line with the difference in aspect ratios in Figure 1h, where we observe that lower Mg²⁺ concentrations lead to stronger repulsion between DNA helices, forcing crossovers in an “X”-conformation. The PLL-10 and, even more strongly, the Spermine simulations display the smallest θ angles, showing that the crossovers retain an “H”-conformation. In contrast, no similar clear trend with Mg²⁺ concentration can be distinguished in the probability distributions of ϕ. Visual inspection reveals that the lack of correlation between θ and ϕ stems from the crossovers moving out of plane, especially in the Sodium and Mixed simulations. However, in the case of the Magnesium simulation, more ϕ angles close to 180° can be observed than in the other simulations, showing that Mg²⁺ ions allow the DNA helices to run relatively straight and that they are less influenced by the presence of crossover junctions. Collectively, these results show that different ions do not affect the structural integrity of the double helices at the time scale of our simulations but influence the global origami structure via the conformations of crossovers and repulsion of parallel helices.

Binding of Ions

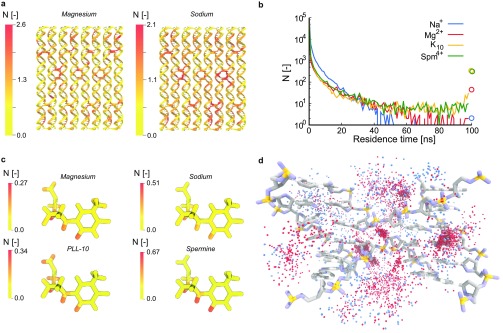
The above results revealed the effect of the distinct ions on conformational changes in the DNA origami structure. To explain the observed structural differences, we subsequently studied the preferential binding mechanisms of the distinct ions by zooming in onto the interactions of the ions with individual nucleotides and atoms in the DNA origami. First, we quantified preferential binding positions on the DNA origami rectangle by time-averaging the number of ions within 5 Å of every nucleotide. The results for the Magnesium and the Sodium simulations are shown in Figure 3a and those of the other simulations in Figures S8 and S9. In all cases, nucleotides at the edge of the origami are observed to bind fewer ions compared to nucleotides in the center of the rectangle, which can be explained by the lower density of negatively charged phosphates at the edges compared to the center, especially at crossover regions. Comparison of the Magnesium and Sodium simulations reveals a more homogeneous distribution of ions over the origami in the latter. This indicates that Na⁺ either has a lower preference for particular locations in the origami, or that Na⁺ ions regularly unbind and bind at other positions, or even diffuse over the surface without forming specific interactions. Spm⁴⁺ and Mg²⁺ show the highest number of charges near crossovers compared to the other ion types. The PLL-10 and Spermine simulations show a slight increase of ions near crossovers, but overall the ions are more randomly distributed over the structure compared to the Magnesium simulation.

Figure 3.

Analysis of binding of ions to the DNA origami. (a) Number of ions within 5 Å of each nucleotide averaged over time in the Magnesium and the Sodium simulation, respectively, mapped onto the initial origami structure. (b) Residence times of ions within 12 Å of the DNA origami. Circles at 100 ns indicate ions that are near the DNA during the full simulation time. (c) Number of ions within 5 Å of each atom in thymine, averaged over time and all thymine nucleotides. (d) Superposition of 100 frames of a crossover region in the Mixed simulation showing Mg²⁺ (red) binding at more defined regions and Na⁺ (blue) binding further away at less defined positions.

Apart from differences in distribution of ions across the DNA origami nanostructure, we also observed differences in the lengths of the time intervals for which ions reside within 12 Å of the origami. These residence times (Figure 3b) are observed to be much shorter for Na⁺ compared to other ions. Only two Na⁺ ions remain within 12 Å of the DNA backbone over a time interval of 60 ns and longer. In contrast, 43 Mg²⁺ ions show residence times of at least the duration of the entire simulation. For K₁₀ and Spm⁴⁺, the majority of charge centers remain near the DNA for the duration of the simulation, consistent with the earlier global ion analysis, which showed that almost all ions are localized near the origami at any given moment in the simulation.

Na⁺ and Mg²⁺ are known to bind sequence-dependently to the major and minor groove with a preference of Mg²⁺ for guanine and adenine in both major and minor grooves.⁶⁰ Na⁺ has also been shown to bind preferentially to thymine in the minor groove but to guanine and adenine in the major groove.⁶¹ Though the origami structure in our simulations differs significantly from the dodecamers used in these studies and does not contain long AT or CG domains, we next averaged the amount of ions within 5 Å of a nucleotide over all nucleotides of the same type to analyze if base type dependent binding of ions plays an important role in this DNA origami. For each nucleotide type, we determined the average amount of ions or nitrogens near a nucleotide (Table S2). These data reveal that in all simulations, adenine and guanine are more subject to ion binding, which can be explained by the higher number of atoms in these bases. However, no further significant preferences for specific nucleotide types were observed.

To investigate possible base type dependent binding of the distinct ions in more detail, we also quantified the average amount of ions near each nucleotide type at the atomistic level. The results for thymine bases in Figure 3c show that Mg²⁺ is often localized near the carbonyl oxygen in the minor groove-side of the nucleotide and near backbone atoms, while it is found very infrequently near other atoms in the thymine base ring. Also for other nucleotides (see Figure S10), Mg²⁺ often appears to bind near minor-groove atoms, mainly in adenine and guanine, and near backbone phosphates. Na⁺ is also found frequently near minor-groove atoms, while little binding is observed near the backbone or the major groove for all nucleotides. For K₁₀, penetration of amines into the grooves of the DNA is relatively uncommon and while some minor groove binding is observed, K₁₀ mainly binds to the DNA backbone. This is in agreement with a recent study that showed that K₆ does not bind strongly to the major and minor groove, especially in AT-rich regions.⁶² In the Spermine simulation, Spm⁴⁺ shows only little binding to phosphate groups in the DNA backbone, and mainly binds to major groove atoms in guanine. This sequence-dependency of Spm⁴⁺ binding has also been observed by Yoo et al., who showed that the methyl group in thymine prevents Spm⁴⁺ binding to the major groove in AT-rich regions, while it does bind in the major groove of GC-rich regions.³⁶ For thymine and adenine, we observe that Spm⁴⁺ binds in the minor groove instead and through visual inspection we observe them in the regions in between helices as well. This has previously been shown to cause a stronger attraction between helices and has been referred to as the “bridging” of Spm⁴⁺ molecules between DNA duplexes.^36,53,63

To visualize the difference between Mg²⁺ and Na⁺ binding, we aligned one crossover junction over 100 frames in the Mixed simulation. In Figure 3d, the crossover and the surrounding ions over all 100 frames are shown. We observe clusters of Mg²⁺ at specific locations near the crossover in line with our previous analysis. These are mainly Mg²⁺-ions with long residence times, while Na⁺-ions are primarily scattered at larger distances from the origami.

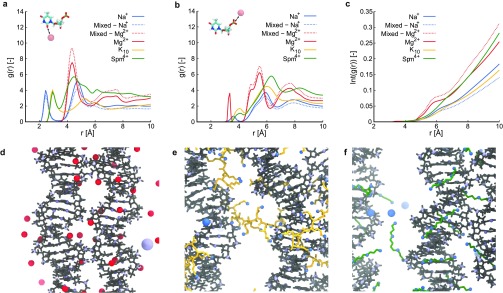
We further quantified the preferential binding positions of ions by determining the radial distribution functions (rdf) between ions and DNA atoms in the minor groove, and between ions and phosphorus atoms in the DNA backbone. For the minor groove-ion-rdf we considered the carboxyl oxygen on thymine and cytosine bases and the hydrogen of the secondary amine in guanine and adenine bases (Figure 4a). The highest peak of Mg²⁺ is located at the same distance as the highest Spm⁴⁺ peak at 4 Å, while the peak of Na⁺ is at a larger distance of 5 Å. In contrast, the rdf for K₁₀ fluctuates around a value of 2 with less defined peaks, indicating that K₁₀ does not bind close to minor groove atoms, corroborating the results in Figures 3c and S10. In the phosphorus-ion-rdf (Figure 4b), the main peak for Spm⁴⁺ at 6.5 Å indicates binding to the grooves, with a smaller one at 4 Å indicating limited direct binding to phosphates. Na⁺ and K₁₀ display a peak at a similar distance of 6 Å, while Mg²⁺ is typically closer to phosphorus at 5.5 Å, which can be an effect of both a higher charge and a smaller ionic radius.

Figure 4.

Illustration of typical binding of ions to DNA origami. (a) Radial distribution function between ions and atoms located in the minor groove of the DNA origami helix. (b) Radial distribution function between ions and phospohorus atoms in the DNA backbone. (c) Integral of the radial distribution function between ions and all phosphorus atoms in the nucleotides forming crossover junctions. (d–f) Zoomed in simulation snapshots illustrating typical binding of Mg²⁺, K₁₀, and Spm⁴⁺, respectively, with DNA origami shown in gray, Mg²⁺ in red, K₁₀ in yellow, Spm⁴⁺ in green, and nitrogen in blue.

As analysis of preferential binding regions on the origami suggested that some ions bind close to crossover regions more frequently than others, we also determined the rdfs between ions and phosphorus atoms of the four nucleotides forming the crossovers. The integrals of these rdfs (Figure 4c) clearly show that mainly Mg²⁺ binds close to crossover phosphates. Also, for Spm⁴⁺ approximately 50% more charge is located within 10 Å of the crossover phosphates compared to K₁₀ and Na⁺. K₁₀ and Na⁺ bind at similar distances further away from the crossover phosphates. This enhanced charge compensation of crossover phosphates compared to other ions explains for the improved ability of Mg²⁺ and Spm⁴⁺ to stabilize crossovers and retain the parallel conformation of adjacent helices.

Together, these results reveal that Mg²⁺ binds closely to the DNA origami and is more likely to bind specific locations near crossovers, which has been shown to rigidify crossovers,^64,65 whereas Na⁺ binds at a larger distance from the origami and rapidly exchanges with the bulk solvent. Spm⁴⁺ binds closely to the DNA origami grooves, aligning with the backbone phosphates and shows, together with Mg²⁺ ions, the highest charge compensation near crossovers, while K₁₀ is able to stabilize DNA origami without binding deeply in the grooves. Snapshots illustrating typical binding of Mg²⁺, K₁₀, and Spm⁴⁺ are shown in Figures 4d, e, and f, respectively. In these snapshots, Mg²⁺ is seen bound in the DNA minor groove, as well as directly near phosphate groups around a crossover, and Spm⁴⁺ bound in, and aligned with, the minor groove. Spm⁴⁺, as mentioned before, is also seen in between neighboring DNA helices, suggesting a mechanism similar to the “bridging” model of DNA helix attraction.^36,53,54,63 K₁₀ reveals a mechanism where part of the peptide binds to one helix and another part to a neighboring helix, effectively spanning over DNA origami helices. Not only does this mechanism explain for the high capability of K₁₀ to stabilize DNA origami but also for the experimentally observed aggregation of DNA origamis in the presence of polylysines with more than 10 units,²⁵ namely by simultaneously binding to helices in different origamis.

DNA Origami Stabilization by K₄

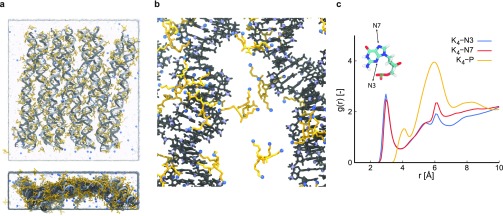
The observation that K₁₀ stabilizes DNA origami by simultaneously binding adjacent DNA helices, while tetravalent Spm⁴⁺ does so by binding closely in the DNA grooves and in between helices, reducing strain on crossovers, triggered us to perform an additional simulation with shorter oligolysines as counterions. For this simulation, denoted as the PLL-4 simulation, we chose K_n molecules with n = 4 to maintain the same charge per molecule as Spm⁴⁺ while retaining the molecular structure of oligolysine. Visual inspection of the final configuration (Figure 5a) shows a larger deviation from the initial structure compared to both the PLL-10 and Spermine simulations. The edges of the origami move outward, indicating that K₄ is less able to reduce the repulsive forces between backbone phosphates. This is confirmed by the RMSD values for the DNA backbone (Figure S11), which are higher than those for the PLL-10 and Spermine simulations. Observing the crossover angles θ and ϕ, we find that both have an increased probability toward angles of 90 deg compared to the Spermine and PLL-10 simulations (Figure S12), indicating that K₄ does not stabilize crossovers efficiently. Radial distribution functions reveal that K₄ side chains bind closely to both the N3 and N7 nitrogens in the minor and major grooves, respectively (Figure 5c). On the level of individual atoms (as in Figure 3c), we observe similar preferential binding as for K₁₀, but with an enhanced preference for the major groove of guanine (see Figure S10). This is explained by the presence of a carbonyl group at the major groove side of guanine, which attracts K₄ side chains more strongly to the major groove compared to adenine. The larger size of K₁₀ as opposed to K₄ causes side chains to be more constrained, reducing their ability to reach into the guanine major groove to form more favorable interactions. Typical binding of K₄ to DNA origami is shown in Figure 5b and shows that the methyl group in the major groove side of thymine prevents binding to AT-rich regions.³⁶ Also, K₄ amine side chains reach toward the major groove side of guanine.

Figure 5.

PLL-4 simulation. (a) Snapshot of the final configuration in two orientations, with the DNA origami shown in gray, water in light blue and Na⁺ and K₄ in blue and yellow, respectively. (b) Zoomed in simulation snapshot illustrating typical binding of K₄, with DNA origami shown in gray, K₄ in yellow, and nitrogen in blue. (c) Radial distribution function between nitrogens in K₄ and minor groove atoms, major groove atoms, and phosphorus atoms in the DNA backbone, respectively. The inset indicates the minor (N3) and major (N7) groove atoms used in the case of guanine.

To confirm if the typical bridging behavior observed for K₁₀ occurs to a lesser degree for K₄, we finally quantified the fractions of molecules that bind to more than one helix at the same time, where binding is again defined as one of the N atoms in the counterion being within 5 Å of any DNA atom in that helix. Averaged over time, 62% of the K₁₀ molecules bind to two helices. In contrast, only 24% of the K₄ molecules bind to more than one helix at the time, while for Spm⁴⁺ this percentage is 23%. Despite its identical structure to K₁₀ and its equal valency to Spm⁴⁺, K₄ can thus neither stabilize the DNA origami by aligning in the DNA grooves like Spm⁴⁺ nor by spanning over helices like K₁₀.

Conclusions

We have used atomistic MD simulations to analyze the effect of various ion types on a 512 bp DNA origami rectangle and the structure of its crossovers. The high spatial-temporal resolution of these simulations provides a molecular picture of DNA origami stabilization that cannot be directly observed experimentally. Na⁺ has been shown to bind only weakly to the DNA origami and to rapidly exchange with the solvent, resulting in a too weak screening of the negative charges on the DNA backbone to prevent repulsion of parallel helices and destabilization of crossovers. In contrast, Mg²⁺ does not only bind to the DNA origami to a higher extent, it also binds more closely and resides at specific locations for extended periods of time, also at crossovers. As a result, it stabilizes the origami by screening the negative charges on the backbone more efficiently and maintaining crossovers in an “H” conformation. Spm⁴⁺ molecules condense even stronger on the DNA and bind especially closely in the minor groove near thymine and adenine, and in the major groove near guanine with long residence times as well as in between helices. Being able to retain the parallel orientation of DNA helices more than the other counterions, Spm⁴⁺ has an increased capability to stabilize crossovers in “H” conformation. This correlates with the prevention of repulsion between DNA helices, resulting in condensation of helices and therefore a higher aspect ratio of the origami compared to the other simulations. K₁₀ molecules show the longest residence times near the origami and bind directly to the backbone rather than penetrating the DNA grooves and keep helices together by simultaneous binding of adjacent helices with its flexible side chains, in this way spanning parallel helices. We thus reveal two main mechanisms of DNA origami stabilization: (i) binding of high charge density ions like Mg²⁺ and Spm⁴⁺ stabilizes crossovers and reduces repulsion of parallel helices and (ii) binding of long flexible ions like K₁₀ that interconnect adjacent helices by simultaneous binding of different parts of the ion. A simulation with K₄, that is, a counterion with the same valency as Spm⁴⁺ and the same molecular structure as K₁₀ but that is too short to span multiple DNA helices and does not have the high charge density of Spm⁴⁺, showed that K₄ is indeed a weaker stabilizer than both K₁₀ and Spm⁴⁺, though still stronger than Na⁺. Altogether, this shows that ions can stabilize DNA origami via distinct mechanisms and that for stabilization either a higher number of weakly binding amines like in K₁₀ or a smaller but stronger binding molecule like Spm⁴⁺ or Mg²⁺ is required.

Combining both strategies, that is, preventing helix repulsion and simultaneously binding adjacent helices, by using mixtures of ion types could lead to enhanced stabilization of DNA nanostructures. For instance, while K₁₀, Spm⁴⁺, and Mg²⁺ have been shown to be efficient stabilizers for the DNA origami nanostructure used in our simulations, K₁₀ may not be able to stabilize larger three-dimensional designs as it is too large to penetrate the structure and neutralize the inner regions of the nanostructure. In this case, optimal stabilization might be obtained by a combination of smaller ions, for example, Mg²⁺ or spermine with a K₁₀ coating on the outside of the DNA nanostructure. Another interesting avenue would be to consider another ion type that integrates both stabilization mechanisms. A promising example in this respect may be a second-generation polypropyleneimine dendrimer, a molecule with structural similarity to Spm⁴⁺ that approaches the length of K₁₀ in its fully extended conformation. In addition, given the apparent importance of high charge density of ions to stabilize crossovers, a third interesting avenue would be the investigation of other compact multivalent ions that have been studied in the context of DNA, for example, cobalt hexammine.^31,53 Though further computational and experimental work is required to determine if such mixtures of ions, dendrimers or other high charge density cations are indeed able to more efficiently stabilize DNA origami, the simulations presented here already shed light on the binding mechanisms of Mg²⁺, Na⁺, K₁₀, Spm⁴⁺, and K₄ to DNA origami at an atomistic level and showed their modes of stabilization. Understanding of these mechanisms of stabilization is an important prerequisite to open up the biomedical applicability of these versatile nanostructures.

Methods

Simulation Setup

The origami rectangle was designed using caDNAno⁶⁶ and subsequently converted into an atomistic representation using a tool developed by Aksimentiev et al.^38,67 This atomistic representation of the DNA origami rectangle was dissolved in aqueous solutions containing different ions: Na⁺, a mix of Na⁺ and Mg²⁺, Mg²⁺, K₁₀, Spm⁴⁺, and K₄, termed the Sodium, Mixed, Magnesium, PLL-10, Spermine, and PLL-4 simulation, respectively. For the Magnesium, Mixed, and Sodium simulations, the DNA origami structure was first solvated in TIP3P water⁶⁸ using VMD’s⁶⁹ solvate tool in a simulation box with dimensions 250 × 70 × 270 ų. Subsequently, using the ionize tool in VMD,⁶⁹ random water molecules were replaced with Mg²⁺ or Na⁺ to neutralize the system and with additional ions to reach excess ion concentrations of 10 mM MgCl₂, 5 mM MgCl₂, and 10 mM NaCl or 20 mM NaCl in the Magnesium, Mixed, or Sodium simulation, respectively. For the PLL-10, Spermine, and PLL-4 simulations, first 100 K₁₀, 250 Spm⁴⁺, and 250 K₄ molecules, respectively, were added to the system using a custom Python script to reach a nitrogen:phosphorus (N:P)-ratio of approximately 1:1. After solvation with TIP3P water in a simulation box with dimensions 250 × 70 × 270 ų, random water molecules were replaced with Na⁺ and Cl^– to reach the same amount of added positive and negative charges in the system as in the other simulations (see Table S1 for details).

Simulation Protocol

The simulation protocol is largely based on the protocol used by Yoo and Aksimentiev.³⁸ All simulations were performed using NAMD⁷⁰ with periodic boundary conditions, the CHARMM36 force field optimized for DNA⁷¹ with improved parameters for ions⁷² and polyamines,⁷³ 1–4 nonbonded exclusions, a 10–12 Å switching scheme for nonbonded interactions, and electrostatic interactions treated using a particle-mesh Ewald scheme with a grid spacing of 1 Å. In the molecular dynamics simulations, temperature was controlled using a Langevin thermostat,⁷⁰ and pressure was controlled at one bar using a Nosé–Hoover barostat.⁷⁴

First, we perform an equilibration protocol. The first step of this protocol comprised 10⁴ steps of energy minimization while keeping the positions of all DNA origami backbone atoms fixed. To ascertain that in the simulations containing Mg²⁺, magnesium hexahydrates were formed, we restrained the six water oxygen atoms closest to each Mg²⁺ ion using harmonic restraints with an equilibrium distance of 1.94 Å and a force constant of 1 kcal/mol/Ų, and performed an additional short minimization to let the system adjust to these restraints. The second step of the equilibration protocol comprised a short NVT molecular dynamics run in which the temperature is increased in a stepwise fashion from 0 to 295 K. To give the ions a more random orientation with respect to the starting structure in the PLL-10, Spermine, and PLL-4 simulations, an NPT run of 0.5–1.5 ns was performed where for each polyamine one atom at its center was kept fixed. The next step of the equilibration protocol comprised an NPT run of 3–4 ns where all ions could freely diffuse toward the origami of which the backbone was still restrained. In these runs a high piston period of 1000 fs was used to prevent the simulation from crashing. Then, for all simulations we released the DNA origami and the hexahydrate restraints and performed another short minimization and NVT run. Finally, we started the 100 ns production run in an NPT ensemble at a temperature of 298 K and a pressure of one bar with a piston period of 200 fs. Simulations were performed partly on our local computing cluster, but mainly on Cartesius, the Dutch national supercomputer.

Analysis

All analyses were performed using in-house developed Python scripts, which made use of the MDAnalysis module to read in trajectory files and perform atom selections.⁷⁵ Radial distribution functions were computed using VMD’s built-in analysis tool.⁷⁶

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.9b05650.

• Figures of molecular structures of K_n and Spm⁴⁺, representation of DNA origami considered, additional data on RMSD, RMSF, broken base pairs, internal angles, and number of ions near origami, tables containing number of ions near distinct nucleotide types and number of molecules (PDF)

The authors declare no competing financial interest.