Engineering and Modeling the Electrophoretic Trapping of a Single Protein Inside a Nanopore

Abstract

The ability to confine and to study single molecules has enabled important advances in natural and applied sciences. Recently, we have shown that unlabeled proteins can be confined inside the biological nanopore Cytolysin A (ClyA) and conformational changes monitored by ionic current recordings. However, trapping small proteins remains a challenge. Here, we describe a system where steric, electrostatic, electrophoretic, and electro-osmotic forces are exploited to immobilize a small protein, dihydrofolate reductase (DHFR), inside ClyA. Assisted by electrostatic simulations, we show that the dwell time of DHFR inside ClyA can be increased by orders of magnitude (from milliseconds to seconds) by manipulation of the DHFR charge distribution. Further, we describe a physical model that includes a double energy barrier and the main electrophoretic components for trapping DHFR inside the nanopore. Simultaneous fits to the voltage dependence of the dwell times allowed direct estimates of the cis and trans translocation probabilities, the mean dwell time, and the force exerted by the electro-osmotic flow on the protein (≅9 pN at −50 mV) to be retrieved. The observed binding of NADPH to the trapped DHFR molecules suggested that the engineered proteins remained folded and functional inside ClyA. Contact-free confinement of single proteins inside nanopores can be employed for the manipulation and localized delivery of individual proteins and will have further applications in single-molecule analyte sensing and enzymology studies.

Sensors capable of the label-free interrogation of proteins at the single-molecule level have applications in biosensing, biophysics, and enzymology.¹⁻³ In particular, the ability to observe the behavior of individual proteins allows one to directly retrieve the rates of kinetic processes and provides a wealth of mechanistic, energetic, and structural information, which are not readily obtained from statistically averaged ensemble (bulk) measurements.¹ To achieve single-molecular sensitivity at high signal-to-noise ratios, the observational volume of the sensor should be similar in size to the object of interest (i.e., zeptoliter range for a protein with a radius of 2.5 nm). Moreover, many kinetic processes have relatively long time scales (e.g., 10^–3 to 1 s) which, in turn, necessitate long observational times to obtain a statistically relevant number of events. Hence, the protein must also remain inside the observational volume for seconds or minutes, a feat that is only possible if the protein is either physically immobilized or trapped in a local energetic minimum that is significantly deeper than the thermal energy.^4,5

To counteract the random thermal motion of nanoscale objects in solution, several optical, microfluidic, and nanofluidic methodologies have been developed over the years. The optical trapping of nanoscale objects (<50 nm radius) requires the sub-diffraction-limited confinement of light,⁶⁻⁸ which can be achieved with photonic^9,10 or plasmonic¹¹⁻¹⁸ nanostructures. Although optical techniques have been shown to be capable of trapping proteins with a radius of ≈2.3 nm,¹⁵ the high optical intensities required and the solid-state nature of the devices tend to not only trap the proteins but also unfold them, limiting the scope of their applicability.^13,18

Microfluidic techniques might offer softer alternatives for the immobilization of single molecules. The anti-Brownian electrokinetic (ABEL) trap makes use of optical tracking to electrophoretically counteract the Brownian motion of individual dielectric particles,¹⁹⁻²² enabling the trapping of proteins down to ≈2.9 nm radius²² and even single fluorophores.²³ Because this technique uses fluorescence microscopy to track the movement of their targets, the observational time window is ultimately limited by the photobleaching of the dye.^19,21

Nanopores, which are nanometer-sized apertures in a membrane separating two electrolyte reservoirs, have been used extensively to study single molecules.^3,24−26 In nanopore analyses, an electric field is applied across the membrane and information about a molecule passing through the pore is collected by monitoring the modulations of the ionic charge current. As proteins typically transit the pore at high velocities (≈10^–3 to 10^–2 m·s^–1),²⁷⁻³⁰ the dwell time (i.e., the duration a molecule of interest spends inside the observable volume) is on the order of 10^–6 to 10^–3 s. These time scales have proven sufficient for obtaining structural information such as protein size, shape, charge, dipole moment, and rigidity,^27,30−33 but they are too brief to efficiently study the enzymatic cycle of the majority of human enzymes (turnover numbers between 10^–3 and 10³ s^–1).

To increase the observation window of proteins by nanopores, researchers have made extensive use of noncovalent interactions. By coating solid-state nanopores with nitrilotriacetic acid (NTA) receptors, the dwell time of His-tagged proteins could be prolonged up to 6 orders of magnitude.³⁴ In another account, the diffusion coefficient of several proteins was reduced 10-fold via tethering to a lipid-bilayer-coated nanopore.^35,36 The decoration of biological nanopores with thrombin-specific aptamers enabled the investigation of the binding kinetics of thrombin to its aptamer³⁷ and the selective detection in the presence of a 100-fold excess of noncognate proteins.³⁸ Electrophoretic translocation of protein–DNA complexes through small nanopores (<3 nm diameter) typically results in the temporary trapping of the entire complex, which has allowed for the study of polymerase enzymes^39,40 and DNA-binding proteins.^41,42 Although promising, none of these approaches could efficiently control the trapping of the protein inside the nanopore or allow observation of enzyme kinetics or ligand-induced conformational changes.

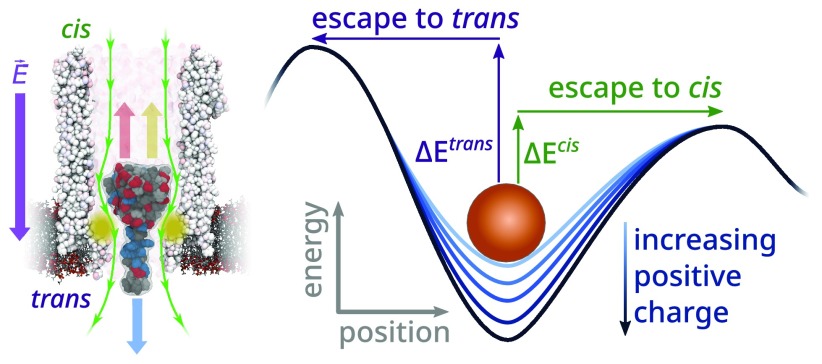
The energetic landscape of a protein translocating through a nanopore stems directly from the electrostatic, electrophoretic, electro-osmotic, and steric forces exerted on it.⁴³ Given the relatively high motility of proteins, the creation of a long lasting (10–100 s), contact-free trap within a spatial region of a few nanometers mandates the presence of a deep potential energy well within the nanopore.⁴⁴ Such a potential profile was achieved by Luchian and co-workers, who showed that the dwell time of a polypeptide inside the α-hemolysin pore could be significantly increased by manipulating the strength of the electro-osmotic flow^45,46 or by placement of oppositely charged amino acids at the polypeptide’s termini.⁴⁷ In a similar approach, a single barnase enzyme was trapped inside α-hemolysin via the addition of a positively charged N-terminal tag.⁴⁸

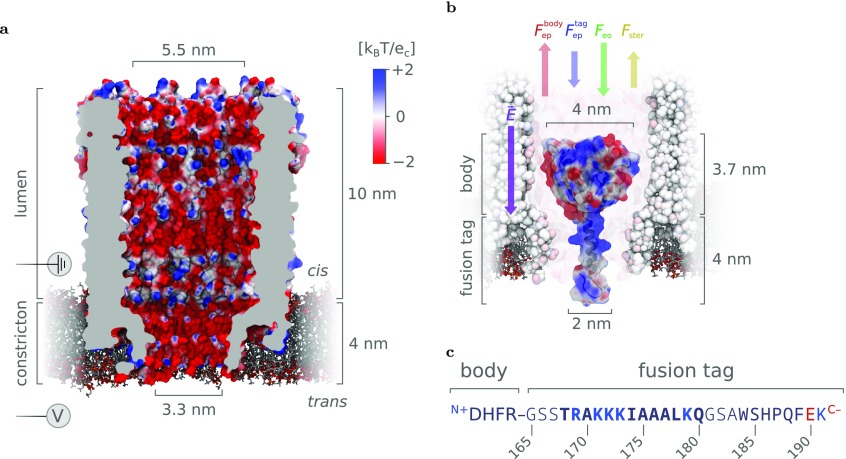
Previous work in the Maglia group on protein analysis with nanopores was centered around the biological nanopore Cytolysin A (ClyA)—a protein with a highly negatively charged interior whose shape can best be described by a large (≈5.5 nm diameter, ≈10 nm height, cis lumen) and a small (≈3.3 nm diameter, ≈4 nm height, trans constriction) cylinder stacked on top of each other (Figure 1a).^38,49 Upon capture from the cis side of the pore, certain proteins exhibited exceptionally long dwell times inside ClyA from seconds up to tens of minutes,^38,49−53 enabling the monitoring of conformational changes⁵³⁻⁵⁵ and even of the orientation⁵⁴ of the proteins inside the nanopore. A subset of the investigated proteins, such as lysozyme, Dendra2_M159A, and dihydrofolate reductase (DHFR), resided inside the nanopore lumen only for hundreds of microseconds and hence could not be studied.^38,50 It was observed that the size of the nanopore plays a crucial role in the effectiveness of protein trapping, as a mere <10% increase of ClyA’s diameter (i.e., by using ClyA nanopores with a higher oligomeric state) is enough to reduce the dwell time of proteins by almost 3 orders of magnitude.⁴⁹ Next to pore size, the charge distribution of proteins can significantly affect their dwell time inside a nanopore. For example, the binding of the negatively charged (−2 e) inhibitor methotrexate (MTX) to a modified DHFR molecule with a positively charged fusion tag at the C-terminus (DHFR_tag) increased the dwell time of the protein inside the ClyA nanopore from ≈3 ms to ≈3 s at −90 mV.⁵⁰

Figure 1.

Trapping of proteins inside the ClyA-AS nanopore. (a) Surface representation of a type I ClyA-AS nanopore—a dodecameric version of the Cytolysin A pore containing eight mutations (C87A, L99Q, E103G, F166Y, I203V, C285S, K294R, H307Y) compared to the wild-type variant from Salmonella typhimurium— embedded in a planar lipid bilayer. The structure was derived through homology modeling from the wild-type crystal structure (PDB ID: 2WCD(56)) using the MODELLER,⁵⁷ VMD,⁵⁸ and NAMD⁵⁹ software packages.⁶⁰ The surface of the pore is colored according to its electrostatic potential in 150 mM NaCl, as calculated by APBS.⁶¹⁻⁶³ (b) Depiction of a single dihydrofolate reductase (DHFR) molecule extended with a positively charged C-terminal polypeptide tag (DHFR₄S) inside a ClyA-AS nanopore. The secondary structure of the tag (primarily α-helical) was predicted by the PEP-FOLD server.^64,65 At negative applied bias voltages relative to trans, the electric field (E⃗) is expected to pull the negatively charged body of DHFR upward (F_ep^body) and the positively charged fusion tag downward (F_ep), while the electro-osmotic flow pushes the entire protein downward (F_eo). Lastly, as the body of DHFR is larger than the diameter of the trans constriction, the force required to overcome the steric hindrance (F_ster) during full cis-to-trans translocation is expected to be significant. (c) Sequence of DHFR₄S fusion tag with its positive and negative residues colored blue and red, respectively. The sequence of the Strep-tag starts at residue 183, and the GSS and GSA linkers are shown in light font. Note that, at pH 7.5, the C- and N-termini contribute one negative charge to the body and one positive charge to the tag, respectively. Images were rendered using VMD.^58,66

In this work, the immobilization of individual Escherichia coli DHFR molecules (Figure 1b) inside the ClyA biological nanopore (specifically type I ClyA-AS,⁴⁹Figure 1a) is investigated in detail. Using nanoscale protein electrostatic simulations as a guideline, our results show that the dwell time of DHFR₄S—a molecule identical to the above-mentioned DHFR_tag aside from the insertion of a single alanine residue at its fusion tag (A174_A175insA, Figure 1c)—inside ClyA can be increased several orders of magnitude by manipulating the distribution of positive and negative charges on its surface. To elucidate the physical origin of the trapping mechanism, a double energy barrier model was developed which—by fitting the voltage dependency of the dwell times for various DHFR mutants—yields direct estimates of the cis and trans translocation rates and the magnitude of force exerted by the electro-osmotic flow on DHFR. Our method provides an efficient means to increase the dwell time of the DHFR protein inside the ClyA nanopore and suggests a general mechanism to tune the dwell time of other proteins, which we believe has significant value for single-molecule sensing and analysis applications.

Results and Discussion

Phenomenology of DHFR Trapped Inside ClyA

To effectively study the enzymes at the single-molecular level, one must be able to collect a statistically significant number (i.e., typically hundreds) of catalytic cycles from the same enzyme. In the case of the E. coli DHFR, which has a turnover number of ≈0.08 s,⁶⁷ this means that the protein must remain trapped inside the pore for tens of seconds. However, as detailed above, such long dwell times were only achieved for DHFR by adding a positively charged polypeptide tag to the C-terminus of DHFR, together with the binding of the negatively charged inhibitor methotrexate (MTX).⁵⁰ Although these long dwell times are encouraging, the requirement for MTX excludes the study of the full enzymatic cycle. Hence, using these previous findings as a starting point, we aim to find out how to prolong the dwell time of a tagged DHFR molecule inside the ClyA-AS nanopore without the use of MTX and to understand the fundamental physical mechanisms that determine the escape of DHFR from the pore.

The structure of DHFR₄S, the tagged DHFR molecule used as a starting point in this work, can be roughly divided into a “body”, which encompasses the enzyme itself and has a net negative charge, N_body = −10 e, and a “tag”, which comprises the C-terminal polypeptide extension and bears a net positive charge, N_tag = +4 e (Figure 1b,c). To capture a tagged DHFR molecule, an electric field oriented from cis to trans (i.e., negative bias voltage) must be applied across the nanopore, which gives rise to an electro-osmotic flow pushing the protein into the pore (F_eo). The electrophoretic force on the body (F_ep^body) strongly opposes this electro-osmotic force but is significantly weakened by the electrophoretic force on the tag (F_ep), allowing the protein to be captured.^38,50,55 As the body and tag of the DHFR molecules bear a significant amount of opposing charges, it is likely that the molecule will align itself with the electric field, where the tag is oriented toward the trans side. In this configuration, the body sits in the ClyA lumen and the tag is located in or near the narrow constriction. Because the body (≈4 nm) is larger than the diameter of the constriction (3.3 nm), the steric hindrance between the body and the pore is expected to strongly disfavor full translocation to the trans reservoir, giving rise to an apparent “steric hindrance” force (F_ster). Finally, Poisson−Boltzman electrostatic calculations calculations showed that the negatively charged interior of ClyA-AS creates a negative electrostatic potential within both the lumen (≈−0.3 k_BT/e) and the constriction (≈−1 k_BT/e) of the pore,⁶⁰ which will result in disfavorable and favorable interactions with the body and the tag, respectively.

Energy Landscape of DHFR in ClyA

To increase the dwell time of DHFR—and to generalize our findings for other proteins—it is necessary to understand how the forces exerted on DHFR inside the pore behave as a function of the experimental conditions (e.g., charge distribution and applied bias). In the absence of specific high affinity interactions, DHFR’s trapping behavior should be chiefly determined by its electrostatic interactions with the pore, whereas the external electrophoretic and electro-osmotic forces can be viewed as modifications thereof. Hence, we will start by investigating the molecule’s electrostatic energy landscape within ClyA in equilibrium where the externally applied electric field vanishes.

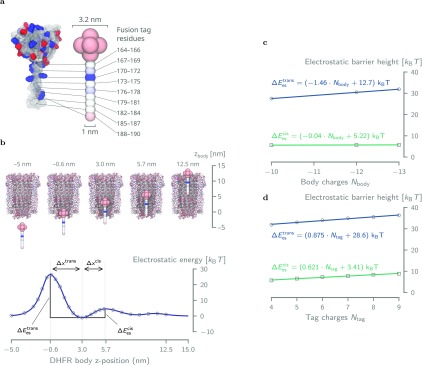
To this end, we used the adaptive Poisson–Boltzmann solver (APBS) to compute the electrostatic energy of a simplified bead-like-tagged DHFR molecule model as it moves through the pore (Figure 2a,b; see Supporting Information section 2 for details).^61−63,68 The bead-like model was chosen such that its body’s size is small enough to pass the constriction without necessitating conformational changes as these cannot be modeled using APBS. Hence, this also means that the magnitude of maxima of the electrostatic energy landscape, which occur when the bead model’s charges come close to the pore’s charges, should be viewed as indicative and not absolute.

Figure 2.

Energy landscape of DHFR₄S inside ClyA. (a) Coarse-grained model of DHFR₄S used in the electrostatic energy calculations in APBS. The body of DHFR consists of seven negatively charged (−1.43 e) beads (1.6 nm diameter) in a spherical configuration (0.8 nm spacing), whereas the tail is represented by a linear string of beads (1 nm diameter, 0.6 nm spacing), each holding the net charge of three amino acids. (b) Electrostatic energy (ΔE_es) resulting from a series of APBS energy calculations where the coarse-grained DHFR₄S bead model is moved along the central axis of the pore. The distances Δx^cis and Δx^trans refer to the distances between the energy minimum near the bottom of the lumen (z = 3 nm) and the maximum at, respectively, cis (z = 5.7 nm) and trans (z = 0.6 nm). (c) Although every additional negative charge to the body of DHFR increases the trans electrostatic barrier by 1.46 k_BT, it has virtually no effect on the cis barrier, which increases only by 0.04 k_BT per charge. (d) Addition of a single positive charge to DHFR’s tag affects the height of the trans and cis much more similarly, with increases of 0.875 k_BT and 0.621 k_BT per charge, respectively.

Nevertheless, the energy profile of the DHFR_tag clearly shows that there is a significant electrostatic barrier, ΔE_es^trans, to overcome when the body of the DHFR moves through the constriction of the pore (Figure 2b). Moreover, we observed a second smaller electrostatic barrier, ΔE_es, toward the cis side so that an energetic minimum exists inside ClyA in which the molecule can reside. The size difference between these two barriers clearly suggests that in the absence of an external force (i.e., at 0 mV bias) the molecule will exit toward cis with overwhelming probability.

To estimate how the charges on DHFR impact its dwell time, we modified the number of charges in the body from −10 to −13 e and recomputed the energy landscape using APBS (Figure 2c). We found that the electrostatic energy barrier toward cis was largely unaffected (0.04 k_BT increase per negative charge), whereas the barrier for trans exit increased significantly (1.46 k_BT increase per negative charge). The latter is a reflection of the highly negatively charged and narrow trans constriction of ClyA.

Contrary to the body of DHFR, the modification of the charge in the tag from +4 to +9 e influenced the heights of both the cis and the trans barrier similarly, with increases of 0.621 k_BT and 0.875 k_BT per positive elementary charge, respectively (Figure 2d). This behavior can be explained by the fact that, at DHFR’s equilibrium position within the pore, the positively charged tag resides in the highly negatively electrostatic well present in the trans constriction of the nanopore (Figure 2b). Moving the molecule from this position into either direction requires this Coulombic attraction to be overcome, which is directly proportional to the number of charges on the tag, irrespective of whether the molecule moves toward cis or toward trans.

Note that when an external electric field is applied, the electrophoretic and electro-osmotic forces must be taken into account. If their net balance is positive (i.e., a net force toward cis) or negative (i.e., a net force toward trans), the electrostatic landscape will be tilted upward and downward, respectively (see Figure S3c). The capture of highly negative charged (−11 e) wild-type DHFR molecules against the electric field⁵⁰ strongly indicates that the electro-osmosis outweighs electrophoresis, and the energy landscape will be shifted downward at trans, resulting in higher and lower barrier heights at cis and trans, respectively. This effectively deepens the energy minimum, which should manifest as an increase of DHFR’s dwell time.

Dwell Time Measurements

The entry of a single protein into ClyA results in a temporary reduction of the ionic current from the “open pore” (I₀) to a characteristic “blocked pore” (I_b) level. Previously, we revealed that the DHFR protein shows a main current blockade with I_res% = I_b/I₀ ≈ 70% (see Figure S4). However, occasionally deeper blocks are observed, which most likely represent the transient visit of DHFR to multiple locations inside the nanopore. Here, we assume that the dwell time (t_d) is simply given by the time from the initial capture to the final release where the current level returns to the open-pore current.

After gathering sufficient statistics for the dwell time events, we computed the expectation value of t_d by taking the arithmetic mean of all dwell time events. This is because the chance for an escape can be modeled as the probability of overcoming a potential barrier whose distribution function is exponential (see Supporting Information section 1). Note that even if the molecule transitions through multiple meta-states with individual rates connecting each of them before it exits, the expectation value is still given by the arithmetic mean (see Supporting Information eq S12).

We observed before that the dwell time of tagged DHFR molecules depends strongly on the applied bias,⁵⁵ that is, exponentially rising with voltage until a certain bias—which we will refer to as the threshold voltage—followed by an exponential fall. This behavior has also been observed for charged peptides in α-hemolysin⁴⁴ and is typical for a decay of a bound state into multiple final states, such as an escape to either cis or trans (see Supporting Information section 1). Therefore, the dwell time of the molecule, as a function of bias voltage, V^bias, can be expressed as the inverse of the sum of two escape rates:⁴⁴

1

where k^cis/trans are the molecule’s escape rates toward cis and trans, respectively. These can be further decomposed into attempted frequencies k₀^cis/trans and bias-dependent barriers in the exponentials. Although this equation can help to qualitatively describe the experimental data, the reduction of the entire protein–nanopore system to four parameters does not allow for their physical interpretation.

Engineering DHFR’s Dwell Time by Manipulation of Its Charge

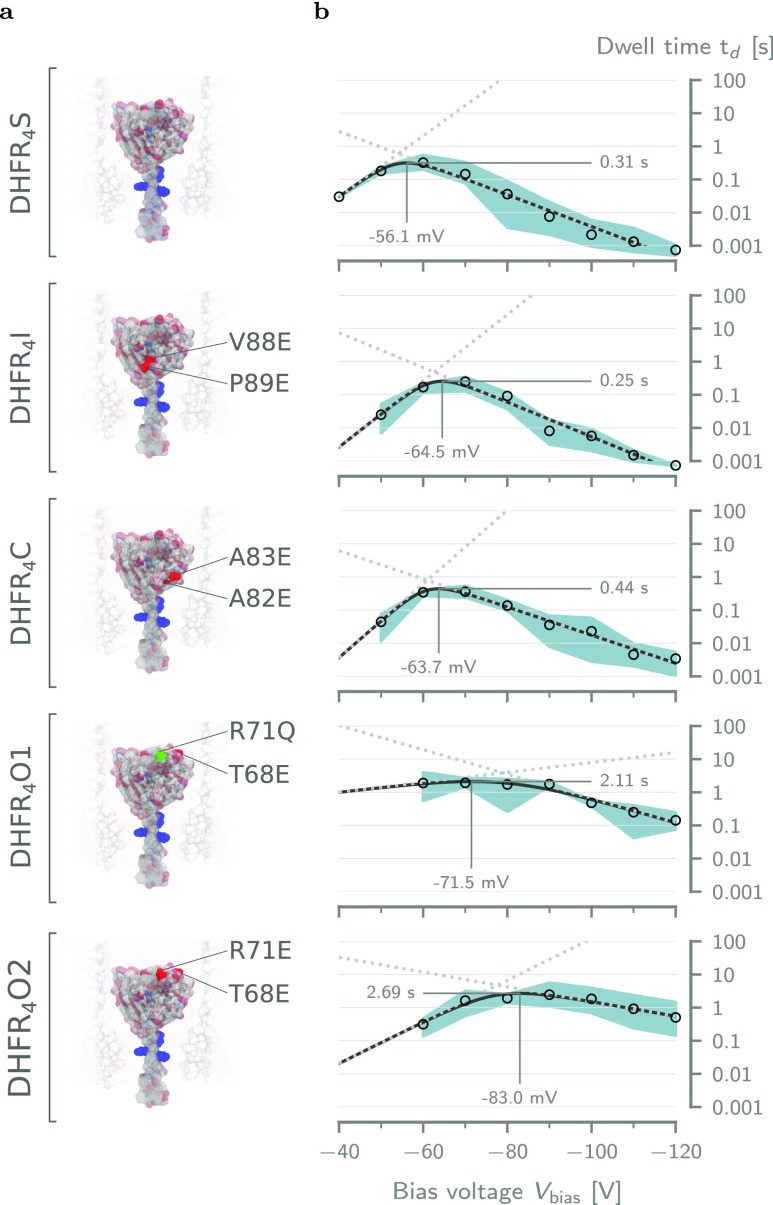
The results from the APBS simulations, together with the previous work with DHFR_tag and MTX,⁵⁰ suggest that the dwell time of DHFR in ClyA can be increased by the manipulation of its charge distribution. To achieve the increase in dwell time without the need for MTX, several nonconserved amino acids on the surface of DHFR₄S were identified and mutated to negatively charged glutamate residues, resulting in the molecules DHFR₄I, DHFR₄C, DHFR₄O1, and DHFR₄O2 (Table 1 and Figure 3a). These mutations modify the number of charges in the body compared to DHFR₄S, and their charges are also in different locations. For convenience, this series of mutations will be referred to as the body charge variations from here on out.

Table 1. Mutations and Charges of All DHFR Variants.

	mutationsa		protein charge at pH 7.5 [e]
name	body (res. 1–163)	tag (res. 164–190)	body	tag	total
DHFR4S			–10	+4	–6
DHFR4I	V88E P89E		–12	+4	–8
DHFR4C	A82E A83E		–12	+4	–8
DHFR4O1	E71Q		–12	+4	–8
DHFR4O2	T68E R71E		–13	+4	–9
DHFR5O1	E71Q	A175K	–12	+5	–7
DHFR7O1	E71Q	A175K A174K A176K	–12	+7	–5
DHFR5O2	T68E R71E	A175K	–13	+5	–8
DHFR6O2	T68E R71E	A175K A174K	–13	+6	–7
DHFR7O2	T68E R71E	A175K A174K A176K	–13	+7	–6
DHFR8O2	T68E R71E	A175K A174K A176K A169K	–13	+8	–5
DHFR9O2	T68E R71E	A175K A174K A176K A169K L177K	–13	+9	–4

^aWith respect to DHFR₄S.

Figure 3.

Effect of the body charge on the dwell time of tagged DHFR. (a) Surface representation of the five tested DHFR₄X body charge mutants. The mutated residues are indicated for each variant. The positive charges in the fusion tag are colored blue. From top to bottom: DHFR₄S, DHFR₄I, DHFR₄C, DHFR₄O1, and DHFR₄O2. (b) Voltage dependence of the average dwell time (t_d) inside ClyA-AS for DHFR mutants in (a). The solid lines represent the voltage dependency predicted by fitting the double barrier model given by eq 1 to the data (see Table S4). The dotted lines represent the dwell times due the cis (low to high) and trans (high to low) barriers. The threshold voltages at the maximum dwell time were estimated by inserting the fitting parameters into eq S25. The error envelope represents the minimum and maximum values obtained from repeats at the same condition. All measurements were performed at ≈28 °C in aqueous buffer at pH 7.5 containing 150 mM NaCl and 15 mM Tris-HCl. Current traces were sampled at 10 kHz and filtered using a low-pass Bessel filter with a 2 kHz cutoff.

We performed ionic current measurements for all body charge variations for a wide range of bias voltages (−40 to −120 mV; see Figures S4 and S5) and extracted the dwell times as shown in Figure 3b. All body charge variations showed the same increase of the dwell time at low electric fields and decreased at high fields. However, we observed differences in the threshold voltage and the magnitude of the maximum dwell time. These differences cannot simply be explained by the total number of charges as DHFR₄I and DHFR₄C have the same charge as DHFR₄O1, but their dwell times are 10-fold lower (Figure 3b). This result implies that the location of the body charge on DHFR plays an important role.

Additional body mutations could potentially compromise the catalytic cycle of DHFR. Hence, we proceeded by systematically increasing the number of positive charges to the fusion tag (N_tag) of DHFR₄O2, the variant that exhibited the longest dwell time, via lysine substitution from 4 e to 9 e (Table 1 and Figure 4). The resulting DHFR_NtagO2 mutants will be referred to as the tag charge variations.

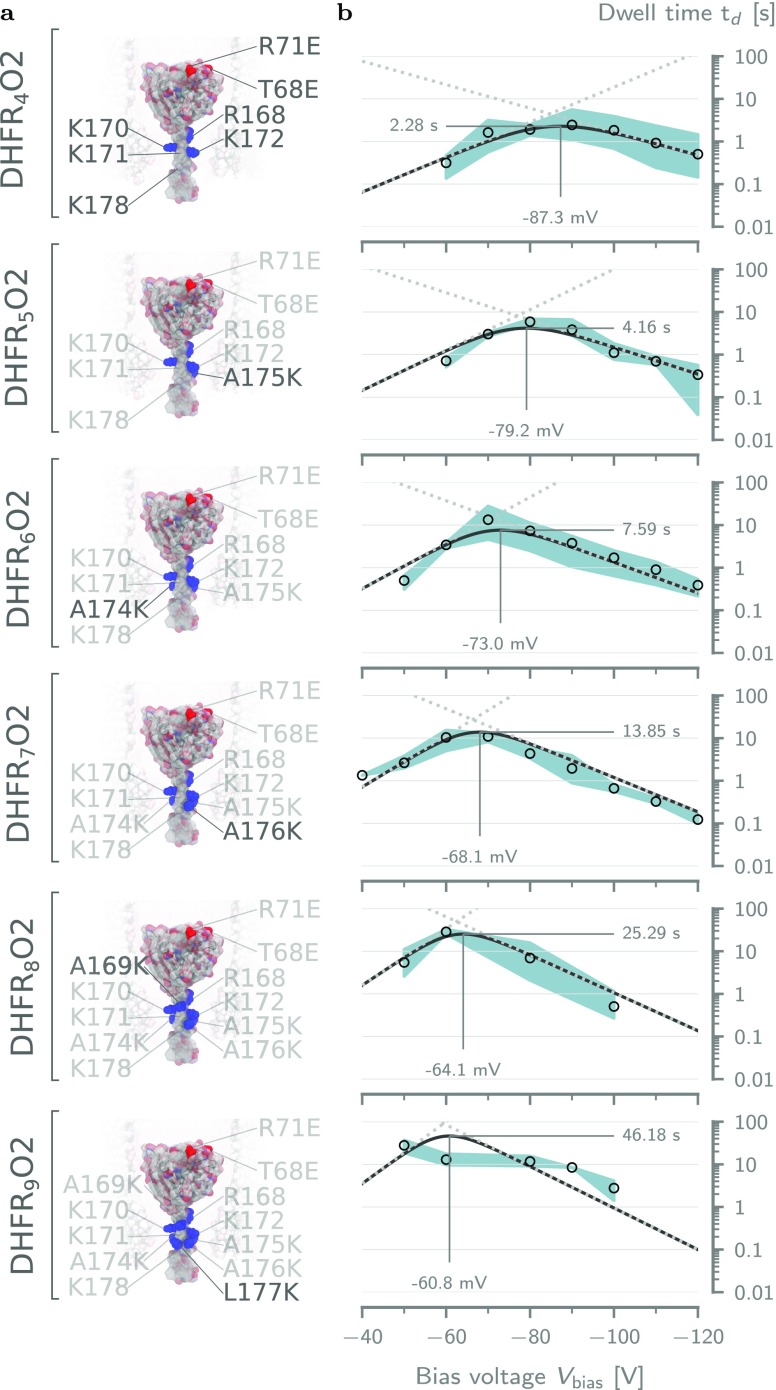
Figure 4.

Effect of the tag charge on the dwell time of DHFR_NtagO2. (a) Surface representations of all DHFR_NtagO2 mutants going from N_tag = 4 (top) to N_tag = 9 (bottom). The positively charged residues in the tag have been annotated and highlighted in blue. (b) Voltage dependencies of the mean dwell time (t_d) for the mutant on the left-hand side, fitted with the double barrier model of eq 6. The annotated threshold voltages were computed by Supporting Information eq S26. Solid lines represent the double barrier dwell time, and the dotted lines show the dwell times due the cis (low to high) and trans (high to low) barriers. Fitting parameters can be found in Table 2. The error envelope represents the minimum and maximum values obtained from repeats at the same condition. Experimental conditions are the same as those in Figure 3.

Subsequent characterization of their the dwell times revealed that the addition of positive charges to the tag significantly increased DHFR’s dwell time (Figure 4b). We observed a similar increase for DHFR₄O1 variants with +5 and +7 tag charge numbers (see Figure S7). This behavior is consistent with the tag being trapped electrostatically inside the negatively charged trans constriction,^44,46,47,60 and it suggests that the tag plays a crucial role in the trapping of DHFR, which was already observed in previous work.⁵⁰

Binding of NADPH Reveals That DHFR Remains Folded Inside the Pore

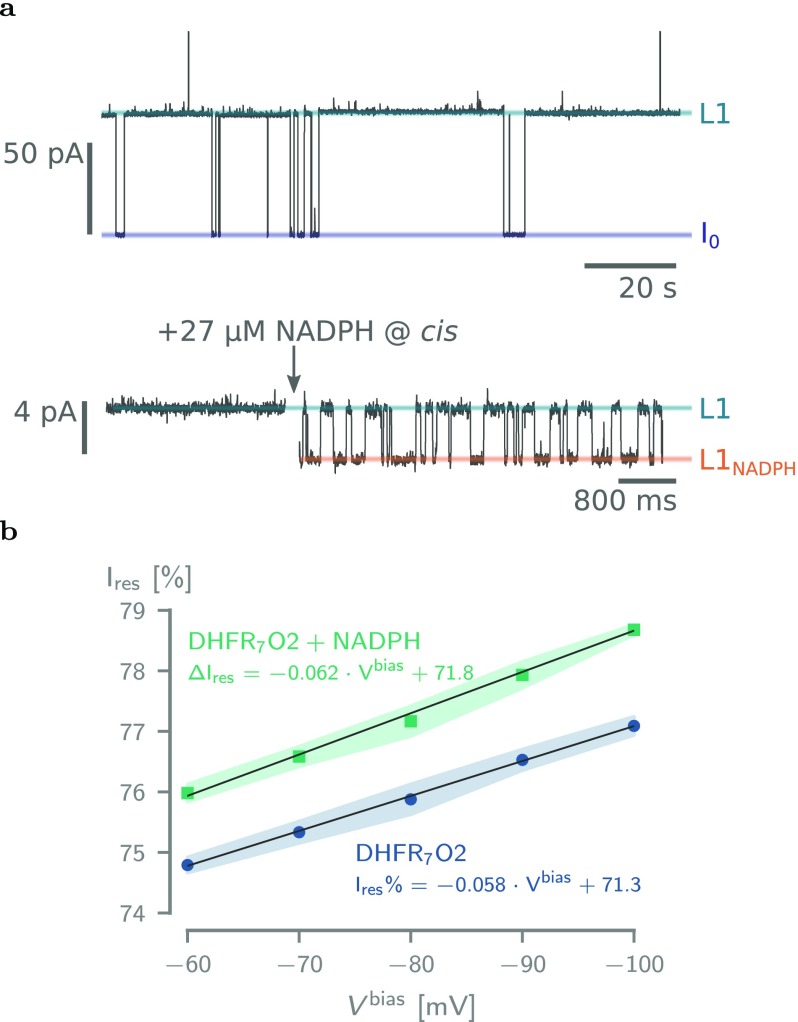
To verify that our DHFR variants remained folded inside the nanopore, we measured and analyzed the binding of NADPH to the enzyme. The addition of the NADPH cofactor to the trans solution of nanopore-entrapped DHFR molecules induced reversible ionic current enhancements that reflect the binding and unbinding of the cofactor to the protein (Figure 5a and Supporting Information Figure S6 and Table S3).

Figure 5.

Binding of NADPH to DHFR₇O2. (a) Top: Typical current trace after the addition of 50 nM DHFR₇O2 to a single ClyA-AS nanopore added to the cis reservoir at −60 mV applied potential. The open-pore current (I₀) and the blocked pore levels (L1) are highlighted. Bottom: Current trace showing the blocked pore current of a single DHFR₇O2 molecule (50 nM, cis) at −60 mV applied potential before (left) and after (right) the addition of 27 μM NADPH to the trans compartment. NADPH binding to confined DHFR molecule is reflected by current enhancements from the unbound L1 to the NADPH-bound L1_NADPH current levels and showed association (k_on) and dissociation (k_off) rate constants of 2.03 ± 0.58 × 10⁶ M^–1·s^–1 and 71.2 ± 20.4 s^–1, respectively (see Table S3). (b) Dependence of the I_res% on the applied potential for DHFR₇O2 and DHFR₇O2 bound to NADPH. All current traces were collected in 250 mM NaCl and 15 mM Tris-HCl, pH 7.5, at 23 °C, by applying a Bessel low-pass filter with a 2 kHz cutoff and sampled at 10 kHz.

Not all DHFR variants were found to be suitable for NADPH-binding analysis: DHFR₅O2 did not dwell long enough inside ClyA-AS at −60 mV (t_d = 0.32 ± 0.17 s) to allow a detailed characterization of NADPH binding, whereas NADPH-binding events to DHFR₈O2 were too noisy for a proper determination of k_on and k_off. No NADPH-binding events to DHFR₉O2 could be observed. NADPH-binding events to the other DHFR variants (DHFR₅O2, DHFR₆O2, and DHFR₇O2) showed similar values for k_on, k_off, and event amplitude (Table S3), suggesting that the binding of NADPH to DHFR inside the ClyA-AS nanopore is not affected by the number of positive charges in the C-terminal fusion tag. Possibly, the inability of DHFR₈O2 and DHFR₉O2 to bind the substrate is due the lodging of DHFR closer to the trans constriction.

Work with solid-state nanopores also previously reported that electric fields inside a nanopore may unfold proteins during translocation,⁶⁹ suggesting that the high degree of charge separation between the body and tag of DHFR might destabilize its structure. To further investigate the effect of the applied potential on the protein structure, we analyzed the dependency of the residual current on the applied potential (Figure 5). We found that the residual current of both the apo-DHFR and the ligand-bound enzyme increased by ≈2.5% from −60 to −100 mV. A voltage-dependent change in residual current is compatible with a force-induced stretching of the enzyme. However, single-molecule force spectroscopy experiments showed that NADPH binding increases the force required to unfold the protein by more than 3-fold from 27 to 98 pN.⁷⁰ As the change of residual current over the potential was identical for both apo- and ligand-bound DHFR (Figure 5), a likely explanation is that, rather than stretching DHFR, the applied bias changes the position of DHFR within the nanopore. Hence, our data suggest that, as previously reported for several other proteins,^52,53 the protein remains folded at different applied bias.

Double Barrier Model for the Trapping of DHFR

Inspired by the strong dependence of the dwell time on the tag charge, we set out to understand the underlying trapping mechanism by building a quantitative model. To this end, we will focus on the data set of the dwell time of DHFR_NtagO2 shown in Figure 4b.

We propose a double barrier model that describes the trapping of the molecule as a combination of escape rates toward cis and toward trans (see Supporting Information section 1.3). Similar to eq 1, the dwell time is defined in terms of the rate k, which in turn is given by the sum of the rate for cis exit and the rate for trans exit. However, now we define the rates in terms of energy barriers:

2

where k₀ is the attempt rate and ΔE^cis/trans are the energy barriers the molecule has to overcome in order to escape toward cis and trans, respectively. These can be readily decomposed into steric, electrostatic, and external contributions:

3a

3b

The steric components ΔE_st,0^cis/trans are defined as those interactions of the molecule with the nanopore that are not electrostatic in nature, such as size- or conformation-related effects as DHFR translocates through the narrow constriction toward trans.

Supported by the APBS simulations (Figure 2b) and the corresponding barrier height to tag charge dependency analyses (Figure 2d), we infer that the electrostatic components ΔE_es^cis/trans can be further decomposed as

4a

4b

where ΔV_tag^cis/trans are the electrostatic potentials associated with the tag charge N_tag for the cis and trans barriers (i.e., the change in barrier height per additional charge in N_tag) and ΔE_es,0 are two constant terms that combine all electrostatic interactions between the protein and the pore that do not depend on N_tag (e.g., body-charge-related interactions with the electric fields in the nanopore).

The external forces acting on a protein trapped inside ClyA under applied bias voltages manifest in the barrier contribution ΔE_ex^cis/trans. They comprise an electrophoretic component ΔE_ep and an electro-osmotic component ΔE_eo^cis/trans. The former results from the strong electric field (≈3.5 × 10⁶ V·m^–1 at −50 mV) and the nonzero net charge on the molecule, whereas the latter springs from the force exerted by ClyA’s electro-osmotic flow, which is strong enough to allow the capture of negatively charged proteins even in opposition to the electrophoretic force.^38,49,50,55 If it is assumed that the bias potential changes linearly over the length of the pore, the external energy barriers are given by (see Supporting Information section 1)

5a

5b

where N_net = N_body + N_tag is the total number of charges on DHFR, L is the length of the nanopore (14 nm), and V^bias is the negative applied bias. The strength of the electro-osmotic force is defined by the equivalent osmotic charge number N_eo—the number of charges that must be added to DHFR to create an equal electrophoretic force on the molecule. Defining the electro-osmotic force in terms of an equivalent osmotic charge number reveals its complete analogy to an electrophoretic force, which has the benefit that the magnitudes of both forces can be readily compared. Moreover, the equivalent osmotic charge number is an invariant related solely to the size and shape of the molecule.

The quantities Δx^cis/trans are defined as the distances from the electrostatic energy minimum to the cis and trans barriers, which depend on the energetic landscape of ClyA and on the precise location of residence of DHFR within the pore. To estimate these values, we can use the APBS simulations (Figure 2b) from which we can read that Δx^trans ≈ 3.5 nm. The cis distance is more difficult to define as the cis electrostatic barrier is much shallower. Without external fields, it has a distance of about ≈2.7 nm, but as we can see in Figure S3c, when the energy landscape is tilted by an external force, the barrier that needs to be overcome is actually located at the cis entrance of the pore. In practice, Δx^cis will need to be adjusted to a value between these two possibilities to give an adequate estimate and hence will be left as a fitting parameter.

Inserting eqs 3–5 into eq 2 yields the final dwell time model:

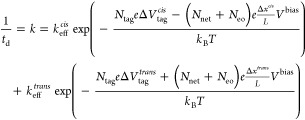6

where the static terms are absorbed into the prefactor to form the effective cis and trans barrier attempt rates k_eff^cis/trans. The formulation of eq 6 offers a compact description of the most salient features of the molecule–nanopore system, and it enables us to describe the dwell time of DHFR inside ClyA quantitatively as a function of the physical properties of the system. Fitting this model to all DHFR_NtagO2 data simultaneously—with both V^bias and N_tag as independent variables—leads to the fitting values in Table 2 and the plots in Figure 4b, which show excellent accuracy considering the simplicity of our model. This is a strong indication that we captured the essence of the trapping mechanism within our model.

Table 2. Fitting Parameters for DHFR_NtagO2.

parameter	description	type	valuea
Vbias	applied bias voltage	independent	40 to 120 mV
Ntag	tag charge number	independent	4 to 9
Nbody	body charge number	fixed	–13
Neo	equivalent osmotic charge number	dependent	15.5 ± 0.9
L	nanopore length	fixed	14 nm
Δxtrans	distance to trans barrierb	fixed	3.5 nm
Δxcis	distance to cis barrierb	dependent	5.21 ± 1.32 nm
ΔVtagtrans	change of ΔEestrans with tag charge	dependent	0.860 ± 0.078 kBT/e
ΔVtagcis	change of ΔEescis with tag charge	dependent	0.218 ± 0.167 kBT/e
ln(kefftrans/Hz)	effective attempt rate for the trans barrier	dependent	–3.44 ± 1.24 (3.21 × 10–2 Hz)
ln(keffcis/Hz)	effective attempt rate for the cis barrier	dependent	7.39 ± 1.02 (1.62 × 103 Hz)

^aErrors are confidence intervals for one standard deviation.

^bRelative to the energetic minimum inside the pore.

Characteristics of the Trapping

As the double barrier model of eq 6 is derived from the underlying physical interactions of the molecule with the nanopore and with the externally applied field, the fitted parameters of Table 2 are physically relevant quantities that describe the characteristics of the system.

The sizes of the electrostatic barriers ΔV_tag^cis/trans that the tag charges experience are in direct relation to the gradients of the barrier sizes computed using the APBS model (Figure 2d). We find that the change of the trans barrier with respect to tag charge, ΔV_tag = 0.860 k_BT, is in excellent agreement with the simulated gradient of 0.875 k_BT/e. The change observed for the cis barrier, ΔV_tag^cis = 0.218 k_BT/e, is approximately 3-fold smaller compared to its APBS value of 0.621 k_BT/e. This deviation likely results from the shallowness of the cis barrier, causing it to disappear when the energy landscape is tilted under an applied bias voltage (see Figure S3b). This gives rise to a cis barrier that lies at a location further away from the electrostatic minimum located inside the trans constriction, effectively limiting the influence of the tag charge number on the barrier height. This claim is further corroborated by the finding that the fitted value of Δx^cis ≈ 5.2 nm, which is almost twice the distance predicted by the APBS simulations and moves that cis barrier much closer to the cis entry.

One of the key insights we obtain from our model is the ability to directly extract information on the strength of the osmotic flow. However, let us first observe that the equivalent electro-osmotic charge number N_eo ≈ 15.5 is much bigger than the net charge of all tag charge variations, N_tag + N_body = −9, ..., −4, and also has the opposite sign. This is in agreement with the earlier assumption that the electro-osmotic force is strong enough to overcome the opposing electrophoretic force and is hence responsible for the capture of the molecule.^38,50 At a bias of V^bias = −50 mV, the electro-osmotic force exerted onto the DHFR molecule, as computed by eq S21, is

7

The magnitude of this force is in line with those found experimentally for DNA⁷¹⁻⁷³ and proteins⁷⁴ in solid-state nanopores.

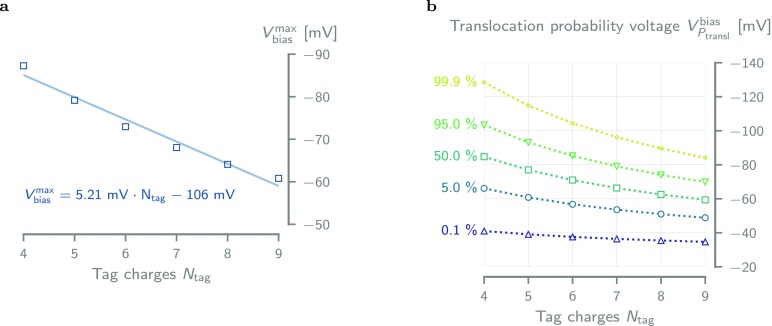
We found the threshold voltages—obtained from the fitted model—to be roughly linearly dependent on the number of tag charges, with a decrease of ≈5 mV per additional positive charge (Figure 6a). This effect is caused by the increase of the net external force on the molecule with increasing tag charge, resulting in a simultaneous lowering of the trans barrier and raising the cis barrier.

Figure 6.

Tag charge dependence of the threshold voltage and translocation probability. (a) Every additional positive charge in the fusion tag of the DHFR_NtagO2 variants increases the threshold voltage (see Supporting Information S26) by ≈5.21 mV. The solid line is a linear fit to the data. (b) Translocation probability voltage V_Ptransl^bias plotted against tag charge for P_transl = 0.1, 5, 50, 95 and 99.9% shows that variants with high tag charge require less bias voltage to fully translocate the pore. Values were obtained through interpolation from eq 8, using the parameters in Table 2.

Another important finding of our model is that the DHFR variations are essentially trapped by the electrostatic forces of the pore on the tag. This can be seen from the direct exponential dependence of the electrostatics on the tag charge as shown in eq 4. If the molecule was trapped as a whole between two barriers, we would rather see a dependence on the net charge on the molecule. Indeed, we verified that such a net charge dependence cannot be fitted to the data. This suggests that the tag acts as an anchor which is located in the electrostatic minimum created by the trans constriction (Figure 2a).

We can also determine the probability of a full translocation of DHFR using

8

where k^cis and k^trans can be computed using the individual components given by eq 6 and the parameters in Table 2. At zero bias and zero tag charge, we find that only 0.002% of DHFR molecules would exit to the trans side, indicating that in the absence of an electrophoretic driving force a cis exit is much more likely than a trans exit. This is in agreement with our expectations because DHFR’s size leads to a significant steric hindrance when it tries to translocate through the nanopore constriction.

Finally, from eq 8, we can compute the voltage V_Ptransl^bias required to obtain a given translocation probability (Figure 6). The number of tag charges significantly lowers the voltage required to achieve full translocation, for example, V_Ptransl for P_transl = 99.9 decreases from −130 mV to −85 mV going from N_tag = +4 to +9. This effect is mainly due to the lowering of the trans barrier height, as the cis escape probability voltage (0.01% line in Figure 6) only changes from −40 mV to −35 mV going from +4 to +9 tag charges. Hence, the higher the tag charge number, the stronger the net external force which pushes the molecule through the trans constriction of the pore.

Conclusions

We showed previously that neutral or weakly charged proteins larger than the trans constriction (>3.3 nm) of ClyA can be trapped inside the nanopore for a relatively long duration (seconds to minutes) and that their behavior can be sampled by ionic current recordings.^{38,49,50,54,55} In contrast, small proteins rapidly translocate through the nanopore due to the strong electro-osmotic flow, and highly negatively charged proteins remain inside ClyA only briefly or they do not enter at all.³⁸

In this work, we use DHFR as a model molecule to enhance and investigate the trapping of small and negatively charged proteins inside the ClyA nanopore.⁵⁵ DHFR (3.5–4 nm) is slightly too large to pass through the trans constriction, and its negatively charged body (N_body = −13 e) only allowed trapping the protein inside the nanopore for a few milliseconds. The introduction of a positively charged C-terminal fusion tag partially counterbalanced the electrophoretic force and introduced an electrostatic trap in the trans constriction of ClyA that increased the DHFR dwell time up to minutes.

The DHFR mutants showed a biphasic voltage dependency which was explained by using a physical model containing a double energy barrier to account for the exit on either side of the nanopore. The model contained steric, electrostatic, electrophoretic, and electro-osmotic components, and it allowed us to describe the complex voltage-dependent data for the different DHFR constructs. Furthermore, fitting to experimental data of a series of DHFR_NtagO2 constructs, in which the positive charge of the tag was systematically increased, enabled us to deduce meaningful values for DHFR’s intrinsic cis and trans translocation probabilities as well as an estimate of the force exerted by the electro-osmotic flow on the protein of 0.178 pN·mV^–1 (e.g., 9 pN at −50 mV, Table 2). We also showed that the APBS simulation results of a simple bead model for the molecule are directly related to the independently fitted parameters of the double barrier model. In conclusion, this means that it should be possible to predict the dwell times of similar experiments by obtaining parameters directly from these types of APBS simulations.

The double barrier model of eq 6 in its current form does not adequately describe the mutations that modify the body charge distribution of DHFR. This is most likely because body charge variations close to the electrostatically trapped tag will impact the height of the barriers more strongly than modifications on the far end of the tag. Although a model accounting for this effect could be made, it would also make the double barrier model significantly more complex without providing any significant advantages over a more comprehensive atomistic simulation. A more detailed discussion can be found in the Supporting Information section 4.

Inside the lumen of ClyA, proteins are able to bind to their specific substrates at all applied potentials tested (up to −100 mV), indicating that the electrostatic potential inside the nanopore and the electrostatic potential originating from the inner surface of the nanopore did not unfold the protein. Therefore, our results indicate that ClyA nanopores can be used as nanoscale test tubes to investigate enzyme function at the single-molecule level. Compared to the wide variety of single-molecule techniques based on fluorescence, nanopore recordings are label-free, which have the advantage of allowing long observation times.

The electrophoretic trapping of proteins inside nanopores is likely to have practical applications. For example, arrays of biological or solid-state nanopores will allow the precise alignment of proteins on a surface. In addition, proteins immobilized inside glass nanopipettes atop a scanning ion conductance microscope^75,76 can be manipulated with nanometer-scale precision, which might be used, for instance, for the localized delivery of proteins. Furthermore, ionic current measurements through the nanopore can be used for the detection of analyte binding to an immobilized protein, which has applications in single-molecule protein studies and small analyte sensing.

Materials and Methods

Electrostatic Energy Landscape Computation

The electrostatic energy landscape of a coarse-grained DHFR molecule translocating through a full-atom ClyA model was computed using the adaptive Poisson–Boltzmann solver (APBS).⁶¹ The full procedure is described in the Supporting Information section 2. In summary, a full atom model of ClyA-AS⁶⁰ was prepared via homology modeling with the MODELLER software package⁵⁷ from the wild-type ClyA crystal structure (PDB ID: 2WCD(56)), and its energy was further minimized using the VMD⁵⁸ and NAMD programs.⁵⁹ A coarse-grained bead model of DHFR—consisting of a “body” of seven negatively charged beads in a spherical configuration and a “tail” of nine smaller beads in a linear configuration with varying charge—was placed a various locations along the central axis of the pore using custom Python code and the Biopython package.⁷⁷ Each atom in the resulting ClyA–DHFR complexes was subsequently assigned a radius and partial charge (according to the CHARMM36 force-field⁷⁸) with the PDB2PQR program,^62,63 and the electrostatic energy was computed with APBS. The net electrostatic energy cost or gain of placing a DHFR molecule at a given location inside ClyA (ΔG^pore+part) is then given by

9

with G^pore+part, G^pore, and G^part being the total electrostatic energies of the ClyA–DHFR complex, the empty ClyA pore, and only the DHFR molecule, respectively.

Protein Mutagenesis, Overexpression, and Purification

All DHFR variants were constructed, overexpressed, and purified using standard molecular biology techniques,^50,55 as described in full detail in the Supporting Information section 5.2. Briefly, the DHFR₄S DNA construct was built from the pT7-SC1 plasmid containing the DHFR-tag construct⁵⁰ by inserting an additional alanine residue at position 175 (located in the fusion tag) with site-directed mutagenesis. All other variants were derived—again using site-directed mutagenesis—either directly from DHFR₄S or from a variant thereof. The plasmids of each DHFR variant were used to transform E. cloni EXPRESS BL21(DE3) cells (Lucigen, Middleton, USA), and the DHFR proteins they encode were overexpressed overnight at 25 °C in a liquid culture. After the bacterial cells were harvested by centrifugation, the overexpressed proteins were released into solution through lysis—using a combination of at least a single freeze–thaw cycle, incubation with lysozyme, and probe–tip sonification. Finally, the DHFR proteins were purified from the lysate with affinity chromotography with Strep-Tactin Sepharose (IBA Lifesciences, Goettingen, Germany), aliquoted, and stored at −20 °C until further use.

ClyA-AS Overexpression, Purification, and Oligomerization

ClyA-AS oligomers were prepared as described previously,⁴⁹ and full details can be found in the Supporting Information section 5.2. Briefly, the ClyA-AS monomers were overexpressed and purified in a manner similar to that for DHFR, with the largest difference being the use of Ni-NTA-based affinity chromotography. After purification, ClyA-AS monomers were oligomerized in 0.5% β-dodecylmaltoside (GLYCON Biochemicals GmbH, Luckenwalde, Germany) at 37 °C for 30 min. The type I oligomer (12-mer) was isolated by gel extraction from a blue native PAGE.

Electrical Recordings in Planar Lipid Bilayers

Electrical recordings of individual ClyA-AS nanopores were carried out using a typical planar lipid bilayer setup with an AxoPatch 200B (Axon Instruments, San Jose, USA) patch-clamp amplifier.^38,79 Briefly, a black lipid membrane consisting of 1,2-diphytanoyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids, Alabaster, USA) was formed inside a ≈100 μm diameter aperture in a thin polytetrafluoroethylene film (Goodfellow Cambridge Limited, Huntingdon, England), separating two electrolyte compartments. Single nanopores were then made to insert into the cis side chamber (grounded) by addition of 0.01–0.1 ng of preoligomerized ClyA-AS to the buffered electrolyte (150 mM NaCl, 15 mM Tris-HCl, pH 7.5). All ionic currents were sampled at 10 kHz and filtered with a 2 kHz low-pass Bessel filter. A more detailed description can be found in the Supporting Information section 5.4.

Dwell Time Analysis and Model Fitting

The dwell times of the DHFR protein blocks were extracted from single-nanopore channel recordings using the “single-channel search” algorithm of the pCLAMP 10.5 (Molecular Devices, San Jose, USA) software suite. The process was monitored manually, and any events shorter than 1 ms were discarded. We processed the dwell time data and fitted the double barrier model to it, using a custom Python code employing the NumPy,⁸⁰ pandas,⁸¹ and lmfit⁸² packages. More details can be found in the Supporting Information sections 5.4 and 5.5.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.8b09137.

• Supplementary text and figures for the full derivation of the double barrier model, details of the APBS simulations, examples of raw current traces of all variants, the on- and off-rates of NADPH binding to DHFR, and all materials and methods (PDF)

Author Contributions

^⊥ K.W., D.R., and A.B. contributed equally to this work.

The authors declare no competing financial interest.