Dynamic Gain Analysis Reveals Encoding Deficiencies in Cortical Neurons That Recover from Hypoxia-Induced Spreading Depolarizations

Abstract

Cortical regions that are damaged by insults, such as ischemia, hypoxia, and trauma, frequently generate spreading depolarization (SD). At the neuronal level, SDs entail complete breakdown of ionic gradients, persisting for seconds to minutes. It is unclear whether these transient events have a more lasting influence on neuronal function. Here, we describe electrophysiological changes in cortical neurons after recovery from hypoxia-induced SD. When examined with standard measures of neuronal excitability several hours after recovery from SD, layer 5 pyramidal neurons in brain slices from mice of either sex appear surprisingly normal. However, we here introduce an additional parameter, dynamic gain, which characterizes the bandwidth of action potential encoding by a neuron, and thereby reflects its potential efficiency in a multineuronal circuit. We find that the ability of neurons that recover from SD to track high-frequency inputs is markedly curtailed; exposure to hypoxia did not have this effect when SD was prevented pharmacologically. Staining for Ankyrin G revealed at least a fourfold decrease in the number of intact axon initial segments in post-SD slices. Since this effect, along with the effect on encoding, was blocked by an inhibitor of the Ca²⁺-dependent enzyme, calpain, we conclude that both effects were mediated by the SD-induced rise in intracellular Ca²⁺. Although effects of calpain activation were detected in the axon initial segment, changes in soma-dendritic compartments may also be involved. Whatever the precise molecular mechanism, our findings indicate that in the context of cortical circuit function, effectiveness of neurons that survive SD may be limited.

SIGNIFICANCE STATEMENT Spreading depolarization, which commonly accompanies cortical injury, entails transient massive breakdown of neuronal ionic gradients. The function of cortical neurons that recover from hypoxia-induced spreading depolarization is not obviously abnormal when tested for usual measures of neuronal excitability. However, we now demonstrate that they have a reduced bandwidth, reflecting a significant impairment of their ability to precisely encode high-frequency components of their synaptic input in output spike trains. Thus, neurons that recover from spreading depolarizations are less able to function normally as elements in the multineuronal cortical circuitry. These changes are correlated with activation of the calcium-dependent enzyme, calpain.

Introduction

Clinically, spreading depolarization (SD) is a major hallmark of focal cortical injury, such as ischemic stroke, mechanical injury, and subarachnoid hemorrhage (Somjen, 2001; Dreier, 2011; Lauritzen et al., 2011; Ayata and Lauritzen, 2015). SDs are transient waves of massive neuronal and glial depolarization that arise spontaneously and progress slowly from the injured tissue into surrounding, ostensibly normal cortex (von Bornstädt et al., 2015). Each SD reflects a complete breakdown in neuronal and glial ionic gradients. Although the functional consequences of cortical SD are not clear, in view of the magnitude of the underlying cellular disturbance, one would expect them to be devastating.

We previously used an in vitro preparation to study the electrophysiological cellular phenomena which accompany exposure of cortical circuitry to hypoxic events, each of which resulted in a brief episode of SD (Revah et al., 2016). At the neuronal level, SD entails a complete, glutamate-dependent breakdown of ionic gradients persisting for seconds to minutes (Rossi et al., 2000; Thompson et al., 2008; Weilinger et al., 2012; Revah et al., 2016). We found that, even though each SD entails a massive increase in intracellular Ca²⁺, neurons recover over the course of a few minutes and can sustain several SDs without obvious electrophysiological consequences (Revah et al., 2016). However, standard biophysical measures provide only partial insight as to the ability of a neuron to function effectively within the context of a neuronal circuit.

In cortical circuits, information is represented by the distributed activity patterns of large populations of nerve cells. Although each cortical neuron receives fluctuating synaptic input from a large number of sources, it generates action potentials (APs) at a relatively low firing rate (usually <5 Hz). At any point in time, individual APs are precisely timed relative to the outputs of other neurons that are part of the same cortical circuit. Thus, at the single-cell level, circuit function depends on the ability of the individual neuron to detect subtle, correlated high-frequency input activity that is hidden in intense, asynchronous background noise, and to encode it in the timing of the output spikes (London et al., 2010). It was recently discovered that cortical neurons exhibit an ultrafast response, as manifested by a high bandwidth dynamic gain, such that the firing across the population can follow rapidly changing, time-dependent inputs with millisecond precision and even lock to fast rhythms in the frequency range of sharp wave ripples (hundreds of Hertz) as precisely as to low-frequency oscillations (Silberberg et al., 2004; Köndgen et al., 2008; Boucsein et al., 2009; Higgs and Spain, 2009, 2011; Tchumatchenko et al., 2011; Broicher et al., 2012; Ilin et al., 2013; Testa-Silva et al., 2014; Doose et al., 2016; Nikitin et al., 2017; Lazarov et al., 2018; Linaro et al., 2018). We now report that the dynamic gain of cortical neurons that recover from SD is significantly narrowed.

Theoretical studies have identified the onset rapidness of the AP at its point of origin as an important parameter that determines the neuron's ability to track high frequencies (Fourcaud-Trocmé et al., 2003; Naundorf et al., 2005; Wei and Wolf, 2011; Eyal et al., 2014). Recently, this was also demonstrated experimentally (Ilin et al., 2013; Lazarov et al., 2018). APs originate in the axon initial segment (AIS), a highly specialized cytoskeletal structure organized around Ankyrin G (AnkG), which is the main scaffold protein responsible for anchoring the ion channels involved in AP initiation (Grubb and Burrone, 2010; Rasband, 2010; Stoler and Fleidervish, 2016). It was shown that, in a mouse model of stroke, arterial occlusion leads to a major disruption of AIS scaffold proteins, due to activation of the Ca²⁺-dependent protease, calpain (Schafer et al., 2009). Here, we report that the narrowed dynamic gain that follows episodes of SD is, indeed, also associated with activation of calpain and structural disruption of the AIS. However, because high-speed fluorescence imaging revealed that the decreased AnkG staining was not associated with changes in distribution of Nav channels along the proximal axon, it is possible that Ca²⁺-dependent AIS changes are not solely responsible for the difference in encoding. Whatever the precise mechanisms, we propose that the circuit function of populations of cortical neurons that have recovered from hypoxic episodes will be severely compromised because they can no longer encode high-frequency input.

Materials and Methods

Animal procedures.

All experiments were approved by the Animal Care and Use Committee of the Hebrew University of Jerusalem, or Ben Gurion University of the Negev. Recordings were made in 300- to 400-μm-thick coronal slices of somatosensory cortex of CD-1 mice of either sex that were 17–24 postnatal days of age. Procedures for preparation and maintenance of slices were similar to those described previously (Fleidervish et al., 2010). Animals of either sex were deeply anesthetized with Nembutal (60 mg/kg) or isoflurane and killed by decapitation; their brains were rapidly removed and placed in cold (4°C), oxygenated (95% O₂/5% CO₂) aCSF. Coronal slices from a region corresponding to the primary somatosensory cortex were cut on a vibratome (Series 1000; Pelco International), or with a VT1200 vibrating blade microtome (Leica Microsystems), and placed in a holding chamber containing aCSF at room temperature for >30 min of recovery. The slices were then transferred to an interface-type chamber for induction of hypoxia and extracellular recordings.

Induction of hypoxia.

Hypoxic episodes were produced by changing the gas flow over the slice from 95% O₂/5% CO₂ to 95% N₂/5% CO₂, as first described by Leblond and Krnjevic (1989). Because this was performed in an interface-type chamber, in which only a thin film of fluid separated slices from the aerating gas, the partial pressure of O₂ drops abruptly throughout the slice after the onset of a hypoxic episode, and an effective equilibrium between the atmosphere and the slice tissue is achieved within seconds. We produced two, 7-min-long hypoxic episodes in the same slice, with a recovery interval between them of 7 min. Since the latency to SD was ∼3 min, the effective time in SD mode was usually 2–3 min.

Electrophysiology.

Whole-cell patch-clamp recordings were made from layer 5 neurons under infrared differential interference contrast microscopic control. Slices were held submerged in a chamber on a fixed stage of an Axioskop FS microscope (Carl Zeiss). Voltage was recorded in whole-cell configuration using an Axoclamp 2B (Molecular Devices) connected to an MU-type headstage (Molecular Devices). Patch pipettes were manufactured from thick-walled borosilicate glass capillaries (outer diameter, 1.5 mm; Hilgenberg) and had resistances of 5–7 mΩ for somatic and extracellular recordings. All recordings were made at 30 ± 2°C. Command voltage protocols were generated, and whole-cell data were acquired online with a Digidata 1320A analog-to-digital interface. Data were low-pass filtered (−3 dB, one-pole Butterworth filter) and digitized at 20–250 kHz. For each neuron, bridge correction and capacitance compensation were performed manually online. Extra care was taken to choose healthy-appearing, neurons with similar somatic morphologies.

Assessing passive and active membrane properties.

The subthreshold membrane properties and the characteristics of the AP were obtained by injecting a series of increasing 500 ms current steps, separated by 2–5 s intervals during which the cell was held at either resting or at −77 mV.

Assessing the frequency response function of layer 5 neurons.

To assess the frequency response of neuronal populations, we somatically injected currents that were composed of a sinusoid signal of frequency f immersed in different realizations of an Ornstein-Uhlenbeck process-based noise with a correlation time of 5 ms. A constant, direct current (DC) was added manually to maintain a target firing rate of ∼5 Hz. Currents were injected in 46 s episodes, with ∼30 s intervals between the injections.

Vector strength.

The vector strength (r) characterizes phase locking of firing of the neurons to the periodic stimulus. For spike times t_j measured in the presence of a sinusoidal stimulus with frequency f, the vector strength is calculated as follows:

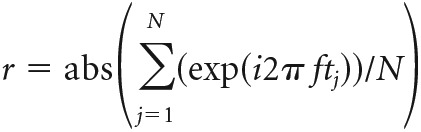To determine the statistical significance of phase locking of recorded spikes to periodic input current stimulation, we used a randomization test, based on Tchumatchenko et al. (2011). This test was performed for spikes recorded for each input frequency f and each cell separately. The value of the experimentally obtained vector strength r was compared with values obtained for datasets of the same size but randomized phase. A total of 10,000 independent realizations of random sets {x′_j}, where each x′_j ε N(0,1), j = 1 … N (number of spikes recorded in a cell in response to the input frequency f), were used to generate 10,000 realizations of phase randomized sets of spike times t′_j = (mod(t_j * f,1) + x′_j)/f. This procedure keeps the number of spikes equal to that obtained experimentally but eliminates any original phase preference. For each of the randomized sets of spike times, the corresponding vector strength r′ was calculated as above with t′_j replacing t_j.

For the r′ distribution, we calculated the 95th percentile, which is the value below which 95% of the randomly drawn r′ can be found. The probability to obtain by chance a value above the 95th percentile is 5%. The 95th percentile of the r′ distribution was taken as the single-cell significance level of vector strength r for the modulation frequency f. The maximal 95th percentile value obtained among cells recorded with the same modulation paradigm is shown in the respective figure as significance levels. Typically, in each cell, responses to all 5 frequencies (f = 50, 100, 200, 500, and 750 Hz) were recorded. Parameters of injected currents were adjusted to obtain similar amplitudes of membrane potential fluctuation and similar firing rates (v = 5 Hz) in all experiments (range: −85 to −45 mV). To obtain these voltage fluctuations, the standard deviation (σ) of the noise was adjusted according to each neuron's intrinsic membrane properties (range 75–150 pA) and the signal-to-noise ratio was constant at 0.37 (SNR = σ/σ + noise).

Dynamic gain calculation.

The frequency transfer function was calculated from responses to injected fluctuating current synthesized as an Ornstein-Uhlenbeck process, using a method based on Higgs and Spain (2009), with standard deviation σ and correlation time τ_corr. APs were detected as crossings of zero voltage, and the spike triggered average (STA) current was calculated for each cell from ∼2500 spikes by averaging stimulus waveform in a temporal window of 1 s centered on the AP time. If the train of APs is idealized as a discrete sequence of numbers with zero for empty samples and 1/dt for samples carrying an AP, then the product of the STA current and the firing rate ν equals the cross-correlation between input current and AP output. The frequency response function (or the dynamic gain), G(f), was then calculated as the ratio between the Fourier transform of this cross-correlation $C\widetilde{C_{I\leftrightarrow AP}}$ and the Fourier transform of the auto-correlation of the input current $\widetilde{A{C}_I}$. The latter is equal to the power spectral density of the input current. We note that, since $C\widetilde{C_{I\leftrightarrow AP}}$ and $\widetilde{A{C}_I}$ are equally affected by the added sinewaves, the frequency response function (i.e., their division) is not biased by them, as follows:

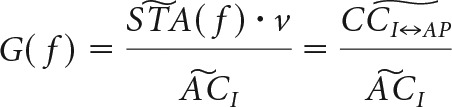To improve signal-to-noise ratio, the complex function G(f) was filtered using a Gaussian window w(f′), centered at frequency f′ = f, with a width of f/2π as follows:

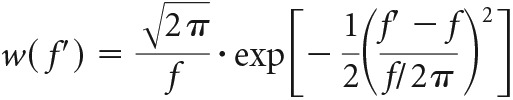This averages out neighboring frequency components of similar amplitude but random phase (i.e., noise). Deterministic frequency components with a phase that changes only mildly within the Gaussian window are not affected by this filtering. Thus:

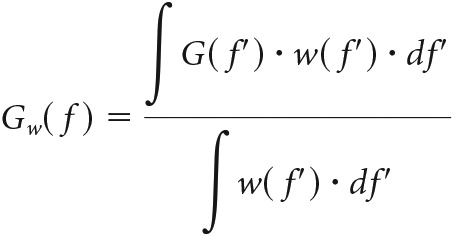To average the gain curves from N cells, we averaged the STA currents. To avoid overrepresentation of cells with a smaller input resistance (i.e., cells that require a larger amplitude of current fluctuations), we weighted the STA curves: $\overline{STA}=\frac{1}{N}·{\displaystyle {\sum }_{i=1}^{N}ST{A}_i·\frac{\overline{\sigma }}{{\sigma }_i}}$ with the average input variance $\overline{\sigma }=\frac{1}{N}·{\displaystyle {\sum }_{i=1}^N{\sigma }_i}$. The average cross-correlation was obtained by multiplication with the average firing rate as follows:

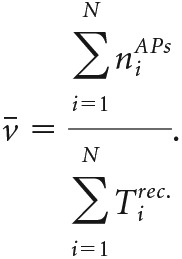Similarly, we averaged the autocorrelations of all stimuli, but using the variance as the normalization, not the standard deviation. The average gain is thus as follows:

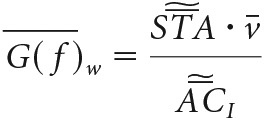For each neuron and for the population average, we calculated the CIs of the gain curve as well as the noise floor by balanced bootstrap. The CI at a given frequency f′ was defined by the 2.5th and the 97.5th percentile of G_BST(f′) for 1000 bootstrap gain curves calculated from 1000 random samples of actual AP times. The noise floor at a certain frequency is understood as 95th percentile of G_BST^rnd(f′) calculated not from measured but from random AP times. To obtain random AP times without changing the statistics of the AP time series, we applied a cyclic shift of the injected current by a random value >5 correlation times. This results in a random triggered average of the input, which replaces the STA current in the calculations for G_BST^rnd.

Analysis of onset rapidness of APs generated during noise injection.

APs were detected when membrane potential crossed 0 mV. The onset rapidness was obtained from the upsampled version of the voltage waveform V(t) and its derivative dV/dt. The resample function in Igor Pro (Wavemetrics) was used to obtain 100 kHz interpolation from the 20 kHz sampled raw data. This resample function obtains intermediate points by applying the sample theorem (i.e., by a convolution with a x/sin(x) kernel). Onset rapidness was calculated as the slope of the phase plot (d/dV (dV/dt)) at 20 V/s. These measures were determined for every spike of every cell fired during the ongoing noise injection. For each cell, we determined a single rapidness value by taking the median of all rapidness values of all APs in a given trial (i.e., a 45-s-long noise file) and then averaging these values across all trials. We tested the reliability of this approach by constructing average AP waveforms for each trial, aligning the first derivatives of individual APs at 20 V/s. Onset rapidness was then determined for the AP waveform obtained by averaging the AP waveforms across trials. The two different ways of obtaining a single value for each cell yielded results that were identical.

Fluorescent imaging of sodium flux during single APs.

Sodium imaging experiments were performed as previously described (Fleidervish et al., 2010; Baranauskas et al., 2013). The pipette solution was supplemented with Na⁺ sensitive dye, SBFI (Invitrogen, 2 mm). SBFI fluorescence was excited by using a high-intensity LED device (385 ± 4 nm, Prizmatix), and the emission was collected by using a modified Olympus U-MNU2 filter set (DC = 400 nm; EM = 420 nm). Changes in fluorescence were acquired using a back-illuminated 80 × 80 pixel cooled camera (NeuroCCD-SMQ; RedShirt Imaging) controlled by Neuroplex software. Images were acquired at 500 frames per second. Indicator bleaching was corrected by subtracting an equivalent trace without electrical stimulation. To improve the signal to noise ratio,15–30 trials were typically averaged.

Solutions.

The aCSF contained the following (in mm): 124 NaCl, 3 KCl, 2 CaCl₂, 2 MgSO₄, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 glucose, pH 7.3, at 37°C when bubbled with a 95% O₂/5% CO₂ mixture. In a voltage-clamp recording, TTX (0.5–1 μm) and Cd²⁺ (200 μm) were added to the aCSF to block currents mediated by voltage-gated Na⁺ and Ca²⁺ channels. The pipette solution for current-clamp experiments contained the following (in mm): 130 K-gluconate, 6 KCl, 4 NaCl, 2 MgCl₂, and 10 HEPES (potassium salt), pH 7.3. For voltage-clamp recordings with Cs⁺, the solutions contained the following (in mm): 135 CsCl, 2 MgCl₂, and 10 HEPES (potassium salt), pH 7.3.

Staining and immunohistochemistry.

The same slices that were used for patch-clamp recording were incubated in the following: (1) 4% PFA and 5% sucrose for 1 h; (2) 5% goat serum 0.1% BSA blocking solution for 1 h; (3) overnight primary antibodies in blocking solution (1:200 AnkG; Neuromab, 1:500 NeuN; Invitrogen); (4) 3 h secondary antibodies (1:500 Alexa-488 Anti-gout; Invitrogen, 1:1000 Alexa-633 anti guinea pig; Invitrogen); and (5) DAPI (Sigma-Aldrich) for 5 min. Images were acquired on a Nikon C2 Plus laser unit docked to a Nikon Ti eclipse unit of a confocal microscope using 20× and 60× (oil-immersion) and processed with ImageJ (National Institutes of Health).

Experimental design and statistical analysis.

Electrophysiological and imaging data analyses were accomplished using Origin 2016 (OriginLab) and Igor Pro 8 (Wavemetrics). If not otherwise noted, values are given as mean ± SE, and Student's t test was used for statistical analysis.

Results

Brief hypoxic episodes have a minimal effect on the excitability of layer 5 neurons

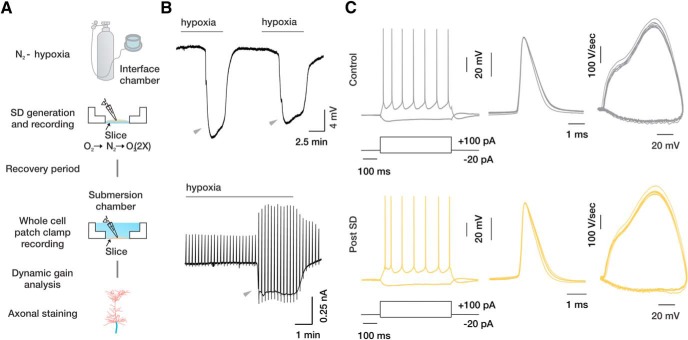
Coronal brain slices were maintained in an interface-type recording chamber (Haas et al., 1979) and subjected to two consecutive, 7 min hypoxic episodes produced by switching the gas flow over the slice from 95% O₂/5% CO₂ to 95% N₂/5% CO₂ (Leblond and Krnjevic, 1989), with 7 min reoxygenation periods between the episodes (Fig. 1A). In all slices, extracellular recording within the cortical gray matter revealed DC shift potentials that typically began 3–5 min after the onset of hypoxia and always lasted until the beginning of reoxygenation (Fig. 1B, top). The DC shift potentials, hallmarks of cortical SD (Dreier, 2011), coincided with rapid, significant increases in holding current and leak conductance, as was evident in whole-cell voltage-clamp recordings from Cs⁺-dialyzed layer 5 cortical neurons in the presence of TTX (1 μm) and Cd²⁺ (200 μm) (Fig. 1B, bottom). Following reoxygenation, whole-cell conductance quickly recovered to prehypoxic values, with a time course that paralleled recovery from the extracellular DC shift (Fig. 1B). After two such hypoxic episodes, slices were held under normoxic conditions for 3–6 h at room temperature. They were then transferred to the submerged slice chamber for whole-cell current-clamp recordings from visually identified layer 5 pyramidal cells at 30°C. Parallel control slices from the same animals were subjected to the same conditions but were not exposed to hypoxia. When depolarized with prolonged, suprathreshold current pulses, both control and recovered neurons responded with trains of repetitive APs (Fig. 1C, left), which showed similar frequency–current relationship. Individual spike properties, including spike amplitude, threshold, and half-width, were also similar (Table 1). Phase plot analysis of the first derivative of the somatic voltage versus the voltage itself shows similar curves for control and posthypoxic neurons (Fig. 1C, middle, right). Both exhibited a typical biphasic pattern. In these plots, the early phase reflects lateral current originating in the axon, and the later phase reflects activation of the somatic Na⁺ channels (Bender and Trussell, 2012). We conclude that, in neurons exposed to hypoxia, as in controls, APs evoked by somatic current injection originate in the AIS. As summarized in Table 1, the statistically significant differences between the recovered neurons and controls were as follows: (1) a higher apparent input resistance (201 ± 22 mΩ, n = 14 vs 129 ± 19 mΩ, n = 11, p < 0.019) and (2) a longer membrane time constant (32 ± 3 ms, n = 14 vs 21 ± 2 ms, n = 11, p < 0.006).

Figure 1.

Effects of brief hypoxic episodes on the electrical properties of layer 5 cortical neurons. A, Experimental design. Slices held in an interface chamber were subjected to two, 7 min hypoxic episodes by switching the gas flow over the slice from 95% O₂ to 95% N₂ (5% CO₂), with an intervening 7 min reoxygenation period. The slices were then allowed to recover <95% O₂. Three to six hours following recovery, they were transferred to a submersion chamber for whole-cell recordings and then fixed and stained for further analysis. B, Representative extracellular field potential recording showing hypoxia-induced SDs (arrowheads) in a cortical slice, seen as DC shifts (top). DC shifts appeared 3–5 min from hypoxia onset and were quickly reversed upon reoxygenation. Bottom, SD recorded in whole-cell voltage-clamp configuration. Several minutes of hypoxia caused a sudden increase in neuronal conductance, evident as a significant increase in holding current (V_hold = −70 mV). The upward deflections in the current signal are the result of slow voltage ramps applied every 11 s (range: −70 to 70 mV). C, Left, Responses of control and recovered neurons (Post SD) to 500 ms hyperpolarizing and depolarizing current steps. Middle, Repetitive APs elicited by depolarizing current steps aligned at voltage of dV/dt_max. Right, APs depicted as phase plots (dV/dt vs voltage) in control and recovered neurons. The biphasic pattern of somatic AP upstroke is preserved in neurons that have recovered from SD.

Table 1.

Intrinsic membrane properties of recovered neurons

	Control (n = 11)		Post SD (n = 14)		p
	Mean	SE	Mean	SE
Apparent input resistance (mΩ)	128.5	18.8	201.2	21.7	0.019*
Membrane time constant (ms)	20.8	2.2	31.6	3	0.006**
Spike amplitude (mV)	92.1	2.1	93.3	2.2	0.72
Spike threshold (mV)	−40.6	1.4	−42.6	1.2	0.31
Spike half-width (ms)	0.9	0.07	1.26	0.1	0.077
Maximum dV/dT (V/s)	458.1	36.6	384.4	28.6	0.12

*P < 0.05;

**P < 0.01.

Neurons that recover from brief hypoxic episodes have a decreased capacity to encode high frequencies

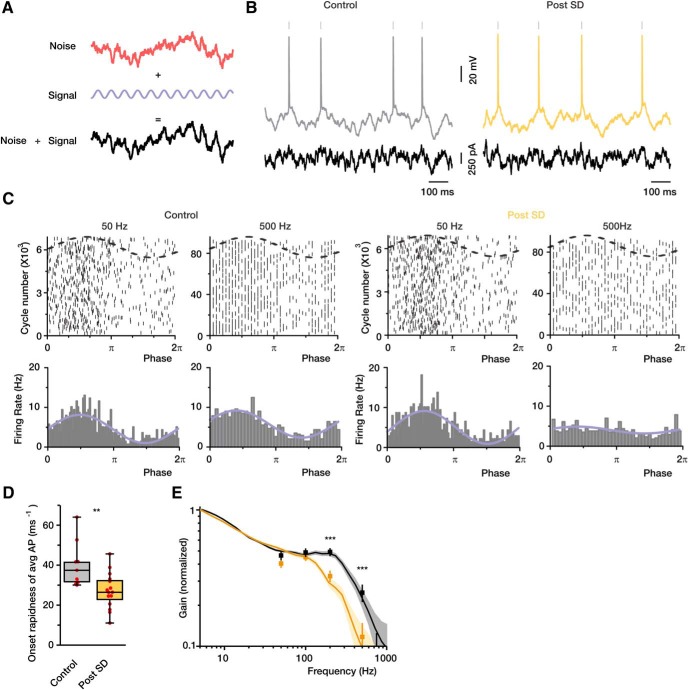
Even though standard single neuron parameters were only minimally altered by exposure to hypoxia, clinical consequences of cortical hypoxia (Dreier, 2011; Lauritzen et al., 2011; von Bornstädt et al., 2015) led us to suspect that the ability of these neurons to function optimally in cortical networks might be compromised. We therefore examined the dynamic gain of neurons, which reflects their ability to encode varying subthreshold inputs. We injected layer 5 neurons with sinewave “signals” at different frequencies buried in background “synaptic noise” (correlation time = 5 ms) (Fig. 2A) and assessed their ability to entrain AP firing at ∼5 Hz. The response to somatic current injection is illustrated in Figure 2B. Figure 2C shows the tracking capability of control versus recovered cells (data were pooled from 3 representative neurons for each group) at two input signal frequencies: 50 and 500 Hz. Raster plots and peristimulus time histograms show the relationship between spike times and the phase of the sinewave. At 50 Hz, spikes in both control and recovery groups clearly clustered at the depolarizing phase of the sinusoid. However, at the higher frequency, the phase-locking capabilities of the neurons that had been exposed to hypoxia were dramatically decreased compared with control neurons. A decreased ability to encode high frequencies has been associated with reduction of the onset rapidness of the spike (Ilin et al., 2013). Indeed, when we analyzed the thousands of spikes that were generated during the noise injection episodes, we found that spikes of recovered neurons had significantly slower onset rapidness (27 ± 9 12 ms⁻¹, n = 15 neurons) compared with controls (40.3 ± 12 ms⁻¹, n = 9 neurons, p < 0.01). To quantify the phase-locking capabilities of the neurons, we used vector strength analysis (see Materials and Methods). At 50 and 100 Hz, there was no significant difference in vector strength between control and recovered neurons; whereas at 200 and 500 Hz, the vector strength was very much higher in controls compared with recovered neurons (Fig. 2E). Dynamic gain analysis, which allowed us to compare the neurons tracking capabilities across a wide range of frequencies, revealed a prominent leftward shift in the gain of neurons that recovered from hypoxia-induced SD (Fig. 2E).

Figure 2.

The encoding capabilities of cortical neurons are reduced following SD. A, Experimental paradigm for testing the encoding capabilities of cortical neurons. For every neuron, a current command containing signal (sinewave) and variable fluctuating background (noise) was synthetized and delivered via the somatic whole-cell pipette. B, Noisy voltage fluctuations and APs elicited by somatic current injection of the noise plus signal function. C, Raster plots of AP times (top) and firing rates (bottom) as a function of the phase of the sinewave. Control and recovered neurons were injected with synthetic currents containing either 50 or 500 Hz sinewave component. The firing rate of the recovered neurons is not affected by the 500 Hz sinewave. D, AP onset rapidness of control (gray) and recovered (yellow) neurons (n = 9 and n = 15, respectively). E, Vector strength and dynamic gain of neuronal responses as a function of input frequency. Pooled data from control and recovered neurons are shown (n = 9 and n = 13 neurons, respectively). Box charts represent median (horizontal line), 25th–75th percentile (box), and extremes. Faded error bars indicate 5%–95% CIs of bootstrapped data (1000 repetitions). **p < 0.01, ***p < 0.001.

Previous studies showed that SD generation can be entirely prevented by exposure to blockers of all ionotropic glutamate and GABA receptors (Rossi et al., 2000; Madry et al., 2010; Revah et al., 2016). We therefore used a mixture containing DNQX (50–100 μm) to block AMPA/kainate receptors, MK-801 (50–100 μm) and APV (50–100 μm) to block NMDA receptors, and BMI (25–50 μm) to block GABA_A receptors to avert hypoxia-triggered SD development. Slices were incubated with the antagonists for at least 30 min before hypoxia onset. This consistently prevented development of DC shift potentials in extracellular recordings and increases in holding current in whole-cell recordings (Fig. 3A,B). Under these conditions, in which neurons were exposed to hypoxia in the absence of SDs, the dynamic gain curve and the cutoff frequency of the recovered cells were not different from that in the control condition (Fig. 3C).

Figure 3.

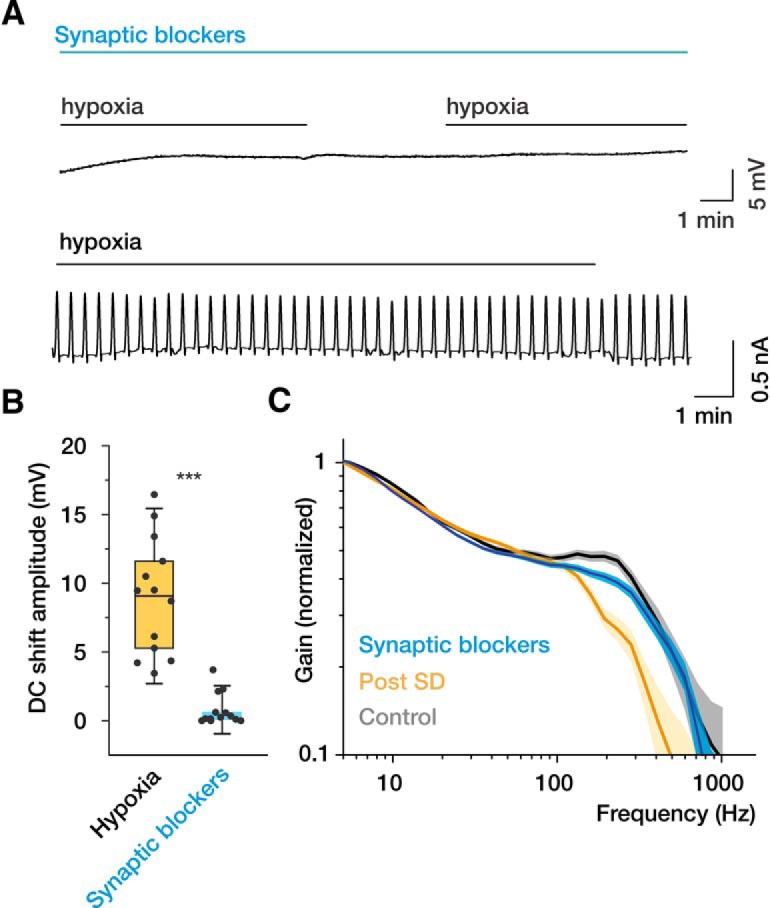
Ionotropic glutamate receptor blockers prevent SD and preserve the high-frequency encoding of the neurons following hypoxia. A, In the presence of the glutamate receptor blockers APV (50 μm), MK-801 (50 μm), DNQX (50 μm), and the GABA_A receptor blocker BMI (25 μm), hypoxia fails to generate SDs (extracellular recording, top) and SD current (whole-cell voltage-clamp recording, bottom). B, Quantification of hypoxia-induced DC shift amplitudes in aCSF and in the presence of ionotropic glutamate receptor blockers. C, In the presence of synaptic blockers, hypoxia has little effect on the dynamic gain of recovered neurons (blue curve, data pooled from 14 neurons). Faded error bars indicate 5%–95% CIs of bootstrapped data (200 repetitions). The dynamic gain curves of control (gray) and recovered (yellow) neurons (Fig. 2) are shown for comparison. Box charts represent median (horizontal line), 25th-75th percentile (box), and standard deviation (bars). n = 13 slices with and n = 13 slices without synaptic blockers. ***p < 0.001.

Hypoxia-induced SD damages the cytoskeleton of the AIS

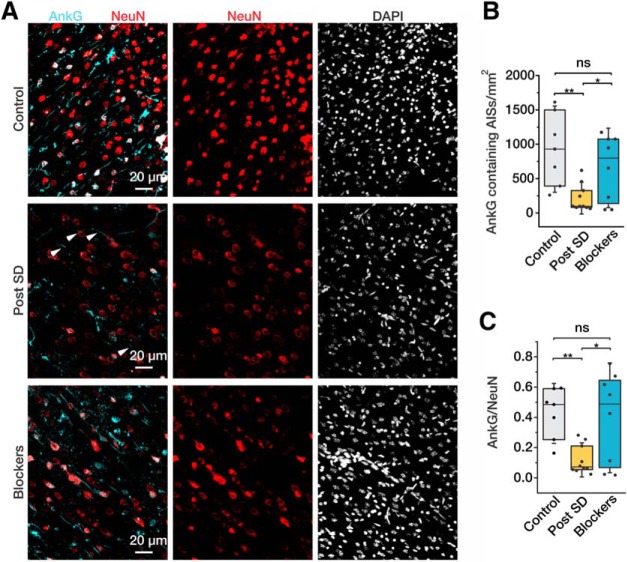
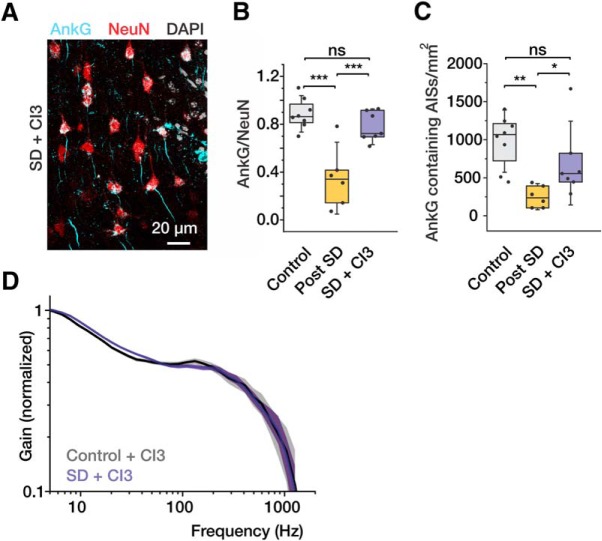
The ability of cortical neurons to encode information depends critically on the integrity of the AP generation mechanism (Naundorf et al., 2005, 2006; Ilin et al., 2013; Eyal et al., 2014), which is located in the distal AIS (Baranauskas et al., 2013). A recent study revealed that the AIS is structurally disrupted in cortical neurons following middle cerebral artery occlusion in vivo or oxygen and glucose deprivation of cultured neurons in vitro (Schafer et al., 2009). To determine whether brief hypoxic episodes have a similar effect in our experiments, in 25 slices electrical recordings were followed by fixation and immunohistochemical staining for the specific cytoskeletal protein, AnkG. In Figure 4A, neuronal cell bodies were stained with NeuN (red) and the AIS was stained for AnkG (cyan). In control slices, most NeuN-stained somata were associated with single AnkG-positive processes (Fig. 4A, left column). In slices maintained under normoxic conditions, 929 ± 198 AnkG-positive AISs were found in a single, 1 mm² confocal optical section (n = 8; Fig. 4B). In slices that were exposed to hypoxia (Fig. 4A, middle column), by contrast, there was a marked loss of AnkG immunostaining with only 216 ± 61 positive AISs detected (n = 10, p < 0.01; Fig. 4B). In slices that had been exposed to hypoxia and SDs, the density of the NeuN-stained cell bodies was reduced, presumably due to neuronal death. We therefore calculated the ratio of AnkG-positive AISs to NeuN-stained cell bodies in each optical field. This ratio was significantly lower in slices that had been exposed to hypoxia and SDs compared with controls (0.11 ± 0.03 vs 0.42 ± 0.06, p < 0.01). The presence of SDs was critical for this decrease in AnkG staining, since, in slices that were exposed to hypoxia in the presence of synaptic blockers, the density of AnkG-positive AISs (656 ± 170) and the AnkG-positive AIS/soma density ratio (0.39 ± 0.1) were similar to those in control (p = 0.31 and p = 0.82, respectively).

Figure 4.

SD leads to decreased AnkG staining. A, Confocal images obtained from coronal cortical slices maintained under control conditions (top) or subjected to two consecutive hypoxic episodes without (middle) or with (bottom) synaptic blockers in the bath. The sections were stained for the AIS cytoskeletal protein, AnkG (cyan), the neuronal marker, NeuN (red), and DAPI (white). The almost complete absence of AIS AnkG immunoreactivity in neurons that have recovered from SDs (Post SD). By contrast, AnkG immunosignal is largely preserved in slices that were treated with synaptic blockers to prevent SD. B, Number of AnkG-positive AISs counted in 1 mm² section in control (gray) and posthypoxia (yellow) slices without and with (blue) synaptic blockers. C, Ratio of the number of AnkG-stained AISs to the number of NeuN-stained neuronal somata in control slices, recovered slices, and slices exposed to synaptic blockers. Box charts represent median (horizontal line), 25th-75th percentile (box), and standard deviation (bars). n = 7, n = 10, and n = 8 slices, respectively. *p < 0.05, **p < 0.01. ns indicates p > 0.05.

AP-associated AIS Na⁺ Influx is not significantly altered in neurons that have recovered from SD

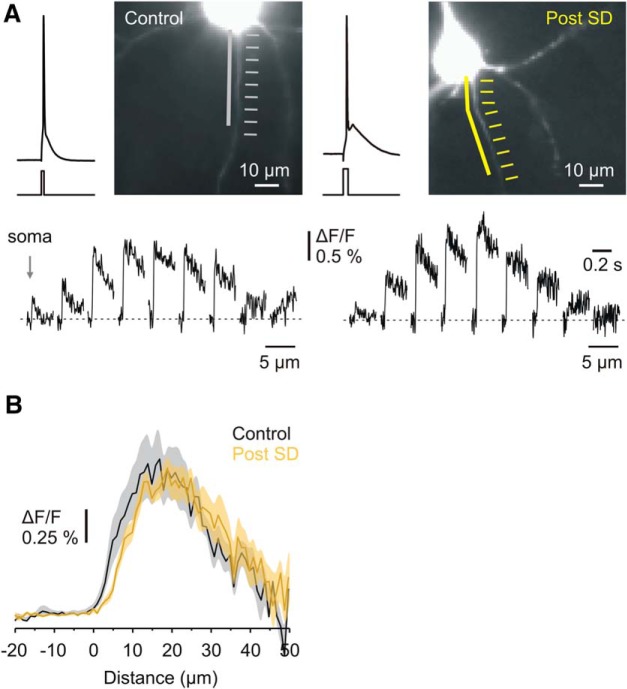
From the above experiment, we conclude that brief transient hypoxic episodes elicit disruption of the AIS scaffold proteins in most of the surviving neurons. This structural damage might be expected to elicit detachment of the Na⁺ channels from the cytoskeleton, which would allow them to diffuse laterally in the neuronal membrane. To find out whether SD indeed induces this effect, we measured AP-elicited Na⁺ transients in the soma and in the first 50 μm of the axons of 11 control and 16 recovered layer 5 pyramidal cells (Fig. 5). We only used single APs to generate [Na⁺]_i increases to minimize diffusion-associated distortion of the [Na⁺]_i–AIS length relationship (Baranauskas et al., 2013). Spatially, peak amplitude of the averaged ΔF/F transients in both control and post-SD neurons grew over the first ∼15 μm of axonal length, reaching a maximal value in a ∼15-μm-long central segment of the AIS, and then declining gradually to nearly zero in the more distal, presumably myelinated region. The mean peak ΔF/F amplitude over the 10-μm-long central AIS of recovered neurons 1.20 ± 0.03% (n = 16; Fig. 5B, black-yellow trace) was not significantly different from that in control neurons (1.29 ± 0.07%, n = 11, p = 0.24, white-gray trace). Thus, despite the morphological damage indicated by decreased antibody staining, the pattern of Na⁺ channel distribution in neurons that have recovered from SD is largely preserved.

Figure 5.

Recovery from SD is not accompanied by an altered distribution of AP-evoked Na⁺ flux along the proximal axon. A, Representative images obtained during Na⁺ imaging experiments from control neurons (left) and neurons that have recovered from SD (right). The white (control) and yellow (recovered) arrows indicate the regions from where fluorescence measurements were obtained. Lines indicate the axonal regions where fast-rising fluorescent signals were detected. Bottom, Averaged ΔF/F transients (n = 30 sweeps) elicited by a single AP in the 5-μm-long axonal segments. B, Mean AP evoked Na⁺ elevations in the soma and axon of control (gray, n = 11) and recovered (yellow, n = 16) neurons. Plotted are mean peak ΔF/F ± SEM values obtained from 1-μm-long segments in the soma and along the axon.

Blockade of calpain activation prevents the decrease in AnkG staining and preserves high-frequency encoding

We previously showed that hypoxia-induced SDs are associated with a very significant increase in intracellular Ca²⁺ (Revah et al., 2016). Several recent studies (Schafer et al., 2009; Hinman (2014); Del Puerto et al., 2015; Hinman et al., 2013; Brocard et al., 2016) showed that oxygen deprivation causes the structural AIS damage through activation of the Ca²⁺-dependent protease, calpain. We therefore tested whether inhibition of calpain can prevent the SD-dependent AIS damage and reduction in encoding capabilities. In neurons from slices that were bathed in calpain inhibitor 3 (CI3) (40 μm) but not exposed to hypoxia, AnkG immunoreactivity, the properties of individual APs, and repetitive firing characteristics were not different than control. In slices that were subjected to hypoxic episodes in the presence of CI3, most NeuN-stained neuronal somata were associated with an AnkG-immunoreactive AISs (Fig. 6A,B). Density of AnkG-positive AISs in recovered slices bathed with CI3 was 692 ± 173 (n = 7 slices) per 1 mm², which was similar to the value in control slices (981 ± 120 per 1 mm²; n = 8, p = 0.18) and significantly higher than in recovered slices that had not been bathed in the calpain inhibitor (259 ± 58 per 1 mm²; n = 6, p < 0.05). In Figure 6C, the ratio of AnkG-positive AIS/soma densities was 0.77 ± 0.04 (n = 7) in CI3-treated slices that had undergone SD. This is slightly, but not significantly, lower than in control slices (0.88 ± 0.04; n = 8, p = 0.12), but significantly higher than in recovered slices bathed in control aCSF (0.35 ± 0.1; n = 6, p < 0.001). Figure 6D shows that the high-frequency tracking ability of neurons in slices that had been challenged with two episodes of hypoxia-induced SD in the presence of CI3 and that of control neurons were not different. We conclude that hypoxia-induced SDs led to a rise in intracellular Ca²⁺ concentration that was sufficient to activate calpain, which, in turn, damaged the cytoskeleton of the AIS (and probably elsewhere in the cell), thereby causing a marked reduction in the neuron's encoding capabilities.

Figure 6.

The calpain blocker, CI3, prevents the effect of SD on AnkG staining and dynamic gain. A, Confocal images obtained from coronal cortical slices subjected to brief hypoxic episodes in the presence of CI3 (40 μm). B, Number of AnkG-positive AISs counted in 1 mm² section in control, recovered, and SD + CI3 slices in n = 8, n = 6, and n = 7 slices, respectively. C, Ratio of the number of AnkG-stained AISs to the number of NeuN-stained neuronal somata in control, recovered, and SD + CI3 slices. D, In the presence of CI3, SD has little effect on dynamic gain (CI3, purple, n = 12 neurons; control, black, n = 6 neurons). Faded error bars indicate 5%–95% CIs of bootstrapped data (1000 repetitions). Box charts represent median (horizontal line), 25th-75th percentile (box), and standard deviation (bars). *p < 0.05, **p < 0.01, ***p < 0.001. ns indicates p > 0.05.

Discussion

Our findings demonstrate that cortical neurons that have recovered from hypoxia-induced SDs and appear normal according to standard electrophysiological excitability measures are, indeed, impaired, in that they lose the ability to code high-frequency inputs. This consequence, which suggests a compromised capacity to function within a circuit, results not from oxygen deprivation itself, but rather from the SDs it generates. Thus, when SD generation was blocked, high-frequency tracking was preserved. Finally, we have shown that the damaged coding capacity is associated with activation of a Ca²⁺-dependent protease, calpain.

SD has no known normal physiological function but is always associated with various neuropathological states usually involving some degree of hypoxia (Takano et al., 2007). Numerous studies have shown that, during the SD itself, each neuron undergoes dramatic ionic and metabolic changes and that, if the SD persists, these inevitably lead to cell death (Kaminogo et al., 1998). Therefore, it was surprising to find that cortical neurons that had ostensibly recovered from brief, hypoxia-induced SDs generated normal-appearing APs and that conventional measures of the health of individual neurons displayed minimal abnormalities. In this study, we have introduced an additional measure of a single neuron's function, developed in theoretical neuroscience studies, that reflects more directly its effectiveness in the context of a functioning neuronal circuit.

In vivo studies in awake, behaving mice reveal that single layer 5 neurons initiate APs at relatively low firing rates (1–20 Hz) (Chorev et al., 2009). This limits the ability of a single neuron's spike train to accurately reflect rapid changes in synaptic input. Thus, coding must occur at the population level (London et al., 2010; Tchumatchenko and Wolf, 2011; Tchumatchenko et al., 2011), as small subsets of neurons respond precisely to correlated input buried in a background of asynchronous synaptic noise (Brunel et al., 2001; Destexhe et al., 2001; Boucsein et al., 2009; Poulet et al., 2012). The dynamic gain of the individual neuron defines the frequencies of background changes to which the circuitry can respond appropriately (Knight, 1972; Higgs and Spain, 2009; Wolf et al., 2014). Theoretical and experimental studies indicate that several cellular mechanisms, including the structure of the background synaptic noise (Brunel et al., 2001) and the onset rapidness of the AP at its site of initiation (Naundorf et al., 2006; Wei and Wolf, 2011; Eyal et al., 2014; Lazarov et al., 2018), critically impact the dynamic gain of cells. We found that, in neurons that had recovered from hypoxia-induced SDs, the dynamic gain decreases rapidly at frequencies >100 Hz, whereas normal layer 5 cortical neurons can track much faster inputs. Since APs in pyramidal neurons originate from the proximal axon, it is reasonable to seek the mechanism underlying the narrowing of the dynamic gain in the unique cytoskeletal organization of the AIS.

The AIS has been shown to be disrupted in the periphery of ischemic stroke following middle cerebral artery occlusion in rats (Schafer et al., 2009; Del Puerto et al., 2015), in areas adjacent to cortical microinfarct in humans (Coban et al., 2017) and in cultured hippocampal neurons following oxygen-glucose deprivation (Schafer et al., 2009). Similarly, we found that, in neurons that recovered from SD, the AISs were almost never stained by AnkG, indicating that they had been damaged. Although functional consequences of this structural damage have not been explored directly, they are generally presumed to be devastating because of the importance of the AIS for synaptic integration and AP generation. Indeed, a structurally intact AIS, with its specialized assembly of voltage-gated channels, cytoskeletal and associated proteins (Rasband, 2010) seems to be prerequisite to its normal function, as even relatively small plastic changes within the AIS (Grubb and Burrone, 2010; Kuba et al., 2010, 2015; Lezmy et al., 2017) elicit significant changes in neuronal excitability. Virtually all these proteins, including α- and β-spectrins, ankyrins, Nav1.2, Nav1.6, and Kv7 channels, are either calpain substrates or subject to calpain-mediated endocytosis (Benned-Jensen et al., 2016). In the AIS, partial proteolysis and loss of anchoring of Na⁺ and K⁺ channels could render these channels nonfunctional and alter their distribution and biophysical properties (Iwata et al., 2004; von Reyn et al., 2012; Brocard et al., 2016). Our physiological recordings indicate that the damage to the AIS was apparently not so severe as to impede its capacity to serve as the neuron's primary site of spike generation. Thus, the neurons still generated apparently normal APs when recorded from the soma. Moreover, imaging revealed that the Nav channels remained anchored to the AIS region. This is similar to a recent report by Brocard et al. (2016) that, following spinal cord injury, calpain is activated in motor neurons, yet Nav channel density in the axon does not decrease. Although we did not directly measure the spike rise time at the initiation site, we did find a decreased onset rapidness of APs as recorded in the soma; we expect that this would be even more pronounced at the axonal site of initiation. Theoretical studies have related ability to track high frequencies with onset rapidness at the site of AP origin (Fourcaud-Trocmé et al., 2003; Wei and Wolf, 2011; Ilin et al., 2013; Eyal et al., 2014). However, in light of our finding that the spatial distribution of Nav channels is not changed, it seems that the precise mechanism by which the AnkG damage affects AP generation has yet to be determined. For example, our imaging data would not reveal possible changes in the kinetics of the Na channels, or of other AIS factors that might contribute to onset rapidness.

Both the absence of AnkG staining and the narrowing of the dynamic gain were prevented by calpain inhibitors. Calpains are activated by high, micromolar-range levels of Ca²⁺ (Goll et al., 2003). Such high concentrations do not normally occur in neurons, and are typically associated with cell death and apoptosis (Orrenius et al., 2003). An exception to this is the SD, during which a complete breakdown of ionic gradients leads to a Ca²⁺ overload that reaches concentrations in the micromolar range (Gniel and Martin, 2010). In a recent study (Revah et al., 2016), we measured Ca²⁺ directly under the somatic membrane and reported that, upon the onset of SD, it can rise to at least 65 μm, a concentration at which calpain is sure to be activated. It is widely believed that the severity of the damage that is caused by an SD is related to the metabolic state of the tissue in which it is triggered (Dreier and Reiffurth, 2015). In our preparation, where the SD was induced by hypoxia, Ca²⁺ begins to rise within seconds of the removal of oxygen, and ∼2 min before the onset of SD (Revah et al., 2016). While this initial rise in Ca²⁺ might not be enough to activate calpain, it could affect multiple cell processes such that the subsequent massive Ca²⁺ rise associated with the SD becomes more damaging. Precisely how this SD-mediated rise produces the change in dynamic gain remains to be elucidated. Because the Ca²⁺ rise occurs throughout the neuron, and calpain is present throughout the neuron, it is possible that molecular changes in other compartments contribute to the effect on neurons that recover from SD. For example, we observed a consistent increase in input resistance and membrane time constant, which could indicate an involvement of Kv channels and may serve to filter out high frequencies as well (Higgs and Spain, 2011; Revah et al., 2015).

Whatever the precise mechanism, measuring the dynamic gain of affected neurons has allowed us to reveal functionally relevant neuronal abnormalities that are not uncovered by the usual electrophysiological measures of excitability. We record from a single neocortical cell, yet we are able to assess its ability to function effectively in the multineuronal circuits to which it belongs. The present study of hypoxia effects on dynamic gain has been limited to layer 5 pyramidal neurons in the mouse. It will be interesting to examine the effects of hypoxic challenge on other neuronal cell types, and especially on the various subtypes of inhibitory interneurons. Ultimately, such studies could provide clues to the link between SD generation and focal cortical epileptogenesis (Winkler et al., 2012; Lippmann et al., 2017). It would also be interesting to repeat these experiments with neurons from human slices, which have been reported to be capable of tracking much higher frequencies than mouse cells (Testa-Silva et al., 2014; Eyal et al., 2014, 2016).