Joint Classification and Regression via Deep Multi-Task Multi-Channel Learning for Alzheimer’s Disease Diagnosis

Abstract

In the field of computer-aided Alzheimer’s disease (AD) diagnosis, jointly identifying brain diseases and predicting clinical scores using magnetic resonance imaging (MRI) have attracted increasing attention since these two tasks are highly correlated. Most of existing joint learning approaches require hand-crafted feature representations for MR images. Since hand-crafted features of MRI and classification/regression models may not coordinate well with each other, conventional methods may lead to sub-optimal learning performance. Also, demographic information (e.g., age, gender, and education) of subjects may also be related to brain status, and thus can help improve the diagnostic performance. However, conventional joint learning methods seldom incorporate such demographic information into the learning models. To this end, we propose a deep multi-task multi-channel learning (DM²L) framework for simultaneous brain disease classification and clinical score regression, using MRI data and demographic information of subjects. Specifically, we first identify the discriminative anatomical landmarks from MR images in a data-driven manner, and then extract multiple image patches around these detected landmarks. We then propose a deep multi-task multi-channel convolutional neural network for joint classification and regression. Our DM²L framework can not only automatically learn discriminative features for MR images, but also explicitly incorporate the demographic information of subjects into the learning process. We evaluate the proposed method on four large multi-center cohorts with 1984 subjects, and the experimental results demonstrate that DM²L is superior to several state-of-the-art joint learning methods in both the tasks of disease classification and clinical score regression.

I. Introduction

BRAIN morphometric pattern analysis has been widely investigated to identify disease-related imaging biomarkers from structural magnetic resonance imaging (MRI) [1]–[8] in the challenging and interesting task of computer-aided diagnosis of Alzheimer’s disease (AD) and its prodromal stage (i.e., mild cognitive impairment, MCI). Compared with other widely used biomarkers (e.g., fluorodeoxyglucose positron emission tomography, and cerebrospinal fluid), MRI provides a non-invasive solution to potentially identify abnormal structural brain changes more sensitively [5], [8]–[10]. While extensive MRI-based studies focus on predicting categorical variables in classification tasks, several pattern regression approaches have been developed to estimate the continuous clinical scores using brain MR images [11]–[13]. Even though it is challenging to accurately predict the conversion from MCI to AD in current studies, this research direction is important because it could help evaluate the stage of AD/MCI pathology and predict the future progression of MCI. Different from the classification task that categorizes an MR image of a subject into binary or multiple classes, the task of regression needs to estimate continuous values (e.g., clinical scores), which is more challenging in practice [14], [15].

More recently, it is reported that the tasks of brain disease classification and clinical score regression are highly interrelated [11], [13], [14]. The joint learning of both tasks can utilize the intrinsic association between categorical and clinical variables, and thus, can further promote the learning performance. Although several MRI-based joint learning approaches have been proposed, most of them first extract hand-crafted features from MR images, and then construct joint models for classification and regression based on these features. However, since the process of feature extraction for MRI is independent of the classification/regression model training, the used features and the learned model may not necessarily be coordinated well with each other, leading to sub-optimal learning performance. Hence, a unified learning framework for simultaneous feature extraction and model training is highly desired.

Besides, the demographic information of subjects may have an impact on the main biomarkers and thus can help improve the classification/regression performance in computer-aided AD/MCI diagnosis [9], [16], [17]. Note that the demographic information denotes the age, gender, and education information of subjects in this study. In previous studies, a commonly used strategy for dealing with demographic information is to partition subjects into different groups based on specific demographic factors. However, it is often impossible to simultaneously match different clinical groups on multiple demographic factors using conventional methods. Another way is to treat the meaningful demographic information as confounding factors [18], [19], in which a regression model is often built using these factors to remove their confounding effects from measured features. However, this method itself is adding up several steps of engineered pre-processing that modify the feature vectors in a directed and engineered way. Intuitively, it could further promote the learning performance by considering demographic information in AD diagnosis systems.

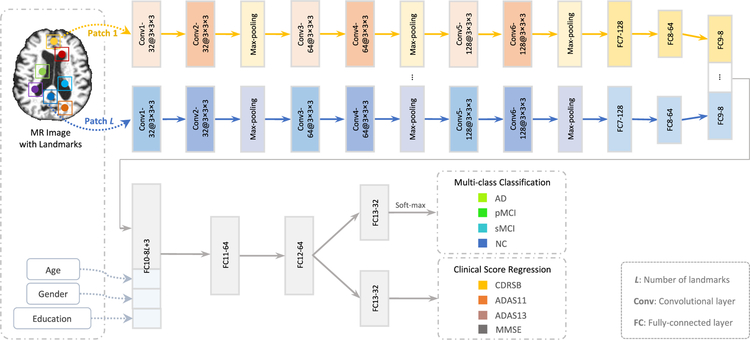
To this end, in this paper, we propose a joint classification and regression framework for AD diagnosis via a deep multi-task multi-channel learning (DM²L) framework. Compared with previous studies, DM²L can automatically learn features from MRI without requiring any expert knowledge for defining features of MRI. Especially, DM²L can explicitly incorporate the demographic information (i.e., age, gender, and education) into the learning model, which can bring more prior information about subjects. Fig. 1 illustrates a schematic diagram of our DM²L framework. Specifically, we first process MR images and identify anatomical landmarks via a data-driven algorithm [20]. We then extract image patches from MR images based on the identified landmarks. Using image patches and demographic factors (i.e., age, gender, and education) as the input data, we further develop a deep multi-task multi-channel convolutional neural network (CNN) to jointly perform both tasks of classification and regression.

Fig. 1.

Illustration of the proposed deep multi-task multi-channel learning (DM²L) framework for joint brain disease classification and clinical score regression. There are four main elements: (a) MR image processing; (b) anatomical landmark identification; (c) landmark-based patch extraction; and (d) deep multi-task multi-channel convolutional neural network for joint classification and regression.

A preliminary version of this work has been reported [21]. In this journal paper, we have offered new contributions in the following aspects: 1) validating the proposed method on two additional datasets, 2) describing the computational cost of our method, 3) analyzing the impact of three demographic factors, 4) studying the influence of two primary parameters, 5) comparing our method with the state-of-the-art learning approaches for joint classification and regression, 6) providing convergence analysis of the proposed CNN model, and 7) performing statistical significance analysis for our method versus the competing methods.

The major contributions of this paper can be summarized as follows. First, we propose to automatically extract discriminative image patches from MR images, based on the anatomical landmarks identified in a data-driven manner. Second, we develop a general joint classification and regression learning framework for MRI-based AD/MCI diagnosis, where both processes of feature extraction and classification/regression model training are incorporated into a unified deep convolutional neural network without using any hand-crafted features of MRI. Finally, we can take advantage of multiple demographic factors of studied subjects via the proposed framework, with the demographic information (i.e., age, gender, and education) embedded into the process of model training.

The rest of this paper is organized as follows. We briefly introduce the most relevant studies in Section II. In Section III, we describe the data used in this study and present our method in detail. We then present the competing methods, experimental settings, and experimental results in Section IV. We further compare our approach with previous studies, analyze the influence of parameters and the computational cost, and present limitations of our method in Section V. Finally, we conclude this paper in Section VI.

II. Related Work

A. MRI-Based AD/MCI Diagnosis

A key component for a MRI-based computer-aided system for AD/MCI diagnosis is determining how to extract informative features from MRI. In general, existing representations of MRI for AD/MCI diagnosis can be roughly categorized into three classes, including 1) voxel-based features, 2) region-of-interest (ROI) based features, and 3) whole-image-based features.

More specifically, in the first category, voxel-based features measure local tissue (e.g., white matter, gray matter, and cerebrospinal fluid) densities of a brain in a voxel-wise manner, and thus are independent of any hypothesis on brain structures [22]–[24]. Since there are usually millions of voxels and very limited (e.g., hundreds) subjects at hand, the major challenge of voxel-based methods is the small-sample-size problem [25]. In the second category, ROI-based representations generally rely on specific hypotheses about abnormal regions of a brain from a structural/functional perspective. For instance, numerous studies employ regional cortical thickness [5], [6], [26], [27], hippocampal volume [3], [4], [28], [29], and gray matter volume [22], [30], [31]) as representations for MR images. However, the hypothesis on ROIs requires expert knowledge in defining disease-related abnormal regions of a brain [32]. In the third category, an MR image is usually treated as a whole [33], without considering the local structural information of the brain. Due to the globally-similar property of brain MR images, these kinds of representations could not identify subtle changes in brain structures caused by dementia. More recently, several studies developed patch-based representations for MR images [34], [35], and some of them rely on deep convolutional neural networks [36], [37] for feature learning. However, it has been remaining a challenging problem to select informative image patches from a 3D MR image (containing tens of thousands of patches).

B. Joint Learning for Classification and Regression

Unlike previous studies that only focus on the task of brain disease classification [12], [31] or the task of clinical score regression [38], there have also been efforts to tackle these two tasks jointly in a unified framework [11], [13]. For instance, Zhang et al. [11] proposed a multi-modal multi-task (M³T) method for both disease diagnosis and clinical score prediction, and showed that the features used for these tasks were highly interrelated. In this work, they computed the gray matter (GM) tissue volumes in pre-defined ROIs as the feature representation for MR images and built a multi-task feature selection model. Following this research line, Jie et al. [12] proposed a manifold regularized multi-task feature (M²TF) learning method, by first performing feature selection and then conducting multitask classification with each task focusing on each data modality. Similarly, they adopted the GM tissue volumes in pre-defined ROIs as representations for MRI. Zhu et al. [13] further developed a matrix-similarity based joint learning (MSJL) method for feature selection across both tasks (i.e., predictions of class labels and clinical scores), where the GM tissue volumes in ROIs are used as representations for MRI. However, these methods highly rely on specific hypotheses about the regions of interest in the brain. In particular, since feature extraction and model training is independently performed, the features and learned models may not be coordinated well with each other. Hence, it is highly desired to develop a unified framework for simultaneous feature extraction and model training.

Besides, the demographic information (i.e., age, gender, and education) of subjects may have an impact on the main biomarkers and thus can affect the classification/regression performance in AD/MCI diagnosis [9], [16], [17]. A straightforward strategy for dealing with the demographic information is matching subjects in different groups. However, it is very challenging to simultaneously match different clinical groups on multiple demographic factors. As another strategy, one can also treat the demographic information as confounding factors [18], [19]. That is, these methods often construct a regression model based on these factors by removing the confounding effects from measured features for subjects. The main disadvantage of such a strategy is that the original representations of subjects will be modified because this strategy adds up several steps of engineered pre-processing in a directed and engineered way. To this end, we propose a joint classification and regression framework, via a deep multi-task multi-channel convolutional neural network based on MR images and three demographic factors (i.e., age, gender, and education). Experimental results on three large-scale cohorts demonstrate that the proposed method out-performs the state-of-the-art methods in both tasks of AD/MCI classification and clinical score regression.

III. Materials and Methods

A. Materials and Image Processing

Four public datasets containing 1,984 subjects are used in this study, including 1) Alzheimer’s Disease Neuroimaging Initiative-1 (ADNI-1) [39], 2) ADNI-2 [39], 3) MIRIAD (Minimal Interval Resonance Imaging in Alzheimer’s Disease) [40], and 4) Australian Imaging, Biomarker & Lifestyle Flagship Study of Ageing (AIBL).¹ It is worth noting that the number of subjects used in this study is larger than that in many previous studies [8], [11]–[13], [20]. Since many subjects participated in both ADNI-1 and ADNI-2, we simply remove these subjects from ADNI-2 for independent testing. Subjects in the baseline ADNI-1 dataset have 1.5 T T1-weighted structural MRI data, while those in the baseline ADNI-2 have 3.0 T T1-weighted structural MRI data. The baseline ADNI-1 dataset contains 181 AD, 226 normal control (NC), 165 progressive MCI (pMCI), and 225 stable MCI (sMCI) subjects. In the baseline ADNI-2 dataset, there are 143 AD, 185 NC, 37 pMCI, and 234 sMCI subjects. Four types of clinical scores are employed for subjects in both ADNI-1 and ADNI-2, including Clinical Dementia Rating Sum of Boxes (CDRSB), classic Alzheimer’s Disease Assessment Scale Cognitive subscale (ADAS-Cog) with 11 items (ADAS11), modified ADAS-Cog with 13 items (ADAS13), and Mini-Mental State Examination (MMSE). The baseline MIRIAD dataset contains 1.5 T T1-weighted structural MRI from 46 AD and 23 NC subjects. Note that in this MIRIAD dataset, only MMSE score, age, and gender information are available for all 69 subjects, while other clinical scores (e.g., CDRSB) are not available for all subjects. Hence, we use only MMSE and two demographic factors (e.g., age, and gender) in the experiments. In the baseline AIBL dataset, there are a total of 519 subjects with 1.5 T or 3.0 T T1-weighted structural MRI data, including 72 AD and 447 NC subjects. Similar to the MIRIAD dataset, two demographic factors (e.g., age, and gender), as well as the MMSE score, are available for all subjects in AIBL. The demographic and clinical information of all studied subjects is listed in Table I.

TABLE I.

Demographic and Clinical Information of Subjects in 3 Datasets. Values are Reported as Mean±Stand Deviation; Edu: Education Years; M/F: Male/Female

Datasets	Class	Age (Years)	Edu (Years)	Gender (M/F)	CDRSB	ADAS11	ADAS13	MMSE
ADNI-1	NC	75.85 ± 5.03	16.05 ± 2.87	118/108	0.03 ± 0.12	6.22 ± 2.92	9.53 ± 4.21	29.11 ± 1.00
	sMCI	74.87 ± 7.64	15.55 ± 3.18	151/74	1.42 ± 0.78	10.35 ± 4.30	16.71 ± 6.14	27.28 ± 1.77
	pMCI	74.82 ± 6.83	15.67 ± 2.85	101/64	1.85 ± 0.94	13.27 ± 4.06	21.50 ± 5.41	26.58 ± 1.71
	AD	75.30 ± 7.50	14.72 ± 3.14	94/87	4.34 ± 1.61	18.58 ± 6.25	29.00 ± 7.64	23.30 ± 1.99
ADNI-2	NC	73.47 ± 6.25	16.51 ± 2.54	88/97	0.05 ± 0.23	5.78 ± 3.08	9.09 ± 4.46	29.03 ± 1.27
	sMCI	71.66 ± 7.56	16.20 ± 2.69	123/111	1.20 ± 0.78	8.22 ± 3.59	12.97 ± 5.73	28.25 ± 1.62
	pMCI	71.27 ± 7.28	16.24 ± 2.67	21/16	2.24 ± 1.26	11.81 ± 4.41	19.30 ± 6.24	26.97 ± 1.66
	AD	74.24 ± 7.99	15.86 ± 2.60	85/58	4.43 ± 1.75	20.73 ± 7.28	30.99 ± 8.67	23.16 ± 2.21
MIRIAD	NC	70.36 ± 7.28	-	12/11	-	-	-	29.39 ± 0.84
	AD	69.95 ± 7.08	-	19/27	-	-	-	19.20 ± 4.01
AIBL	NC	72.79 ± 6.61	-	192/255	-	-	-	28.71 ± 1.22
	AD	71.24 ± 6.37	-	30/42	-	-	-	20.51 ± 5.65

For all studied MR images, we pre-process them using a standard pipeline. Specifically, we first perform anterior commissure (AC)-posterior commissure (PC) correction using the MIPAV software,² and re-sample each image to have the same resolution of 256 × 256 × 256. We then adopt the N3 algorithm [41] to correct the intensity inhomogeneity of those images. We further perform skull stripping to remove both skull and dura. Finally, we remove the cerebellum by warping a labeled template to each skull-stripped image.

B. Anatomical Landmark Identification

To accurately measure early pathological changes, one critical step of MRI-based studies for AD/MCI diagnosis is to locate disease-associated structures in the brain. Most of the existing studies focus only on empirical ROIs [3]–[6], [22], [26]–[31]. However, these ROIs may not cover all possible locations with potential atrophy in brains, due to the limited conclusive knowledge of AD. There are very limited studies reporting biomarkers (e.g., anatomical landmarks) that can model both local (i.e., voxel-level) and global (i.e., whole-image-level) information of brain MR images. One primary reason is due to the great challenge in identifying discriminative anatomical landmarks in 3D MRIs. To this end, we propose a landmark-based patch extraction strategy for AD/MCI diagnosis.

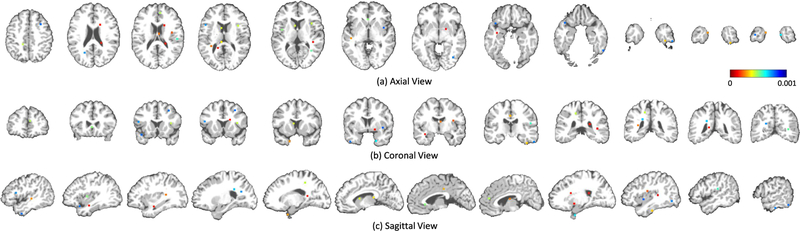
Specifically, to extract informative image patches from MRI, multiple anatomical landmarks are first identified from MRI via a data-driven landmark detection algorithm [20]. This algorithm aims at identifying the landmarks that have statistically significant group differences between AD patients and NC subjects in local brain structures. To be specific, both linear and non-linear registration processes are first performed for all training MR images in the ADNI-1 dataset using the Colin27 template [43]. Based on the deformation field from non-linear registration, the correspondence between voxels in the template and each linearly-aligned image can be constructed. For each voxel in the template, the morphological features (i.e., local energy pattern [44]) are extracted from its corresponding voxels in all linearly-aligned training images that include both AD and NC subjects in ADNI-1. Then, a multivariate statistical test (i.e., Hotelling’s T2 [42]) is used to perform voxel-wise group comparison between AD and NC groups, and thus can obtain a p-value for each voxel in the template space. Finally, the local minima in the obtained p-value map in the template space are defined as locations of discriminative anatomical landmarks. As shown in Fig. 2, there are approximately 1700 anatomical landmarks identified from AD and NC subjects in ADNI-1, and these landmarks are ranked by their corresponding p-values. It is worth noting that a smaller p-value denotes higher discriminative capability of the corresponding landmark in distinguishing AD patients from NC subjects, and vice versa.

Fig. 2.

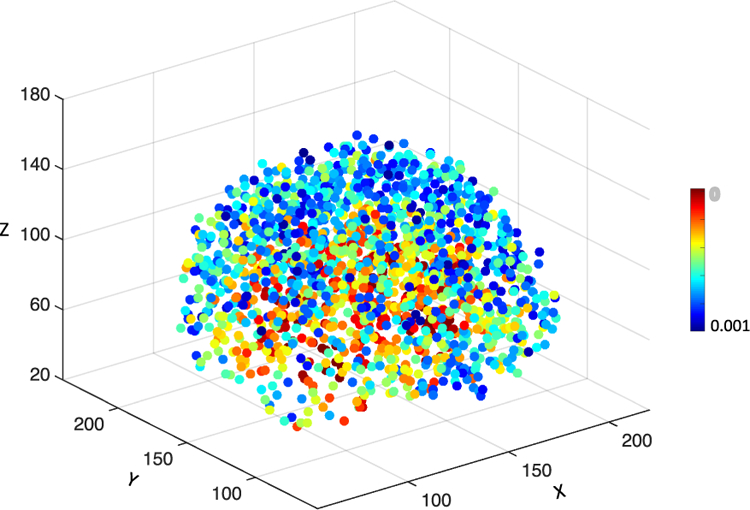
Illustration of all anatomical landmarks identified from AD and NC subjects in ADNI-1. Different colors denote p-values in group comparison between AD and NC subjects [20]. A small p-value indicates that the corresponding landmark has a high discriminative capability and vice versa.

For a new testing MR image, one can first linearly align it to the template space, and then use a pre-trained landmark detector (learned on the training data) to predict the landmark locations in this testing image, with more details given in [20]. In this study, we assume that the anatomical landmarks with group differences between AD and NC subjects would be the potential atrophy locations in brain MR images of MCI subjects, since MCI is the prodromal stage of the AD. That is, both pMCI and sMCI subjects share the same landmarks as those identified from AD and NC groups in ADNI-1.

C. Landmark-Based Patch Extraction

Based on those identified landmarks, we extract multiple patches from each MR image for feature learning and classifier/regressor construction. Since there are approximately 1,700 landmarks identified from AD and NC subjects, it will bring much computational burden if we directly extract image patches from these landmark locations. On the other hand, as shown in Fig. 2, some landmarks are very close to each other, and thus patches extracted from these landmark locations will have large overlaps. In this case, patches with large overlap will provide limited information about the inherent structure of the brain, because they contain a large amount of redundant information. To address this issue, besides considering p-values for those landmarks, we also define a spatial Euclidean distance threshold (i.e., 20 in our experiments) to control the distance between neighboring landmarks, to reduce the overlaps among image patches. More details can be found in Section VI of the Supplementary Materials.

In Fig. 3, we plot those selected top L = 50 landmarks, from which we may see that many landmarks are located in the areas of bilateral hippocampal, bilateral parahippocampal, and bilateral fusiform. In previous studies [29], [45], these areas are reported to be related to AD/MCI. For clarity, we further visually show these landmarks in Fig. S1 and Movie. S1 in the Supplementary Materials. In this study, we extract a 3D image patch centered at a specific landmark location. Given L landmarks, we can obtain L local patches from an MR image to represent a subject. To suppress the impact of registration error and to augment the training set, we further randomly sample different patches centered at each landmark location with displacements within a 5 × 5 × 5 cubic (with the step size of 1). That is, we can generate 125 patches centered at each landmark location. Finally, we treat a combination of L patches as a training sample, with each patch extracted from a particular landmark location. Hence, we can theoretically generate 125^L samples based on different combinations of patches from L landmarks for each MRI. More details can be found in Fig. S2 of the Supplementary Materials.

Fig. 3.

Illustration of selected 50 landmarks identified from AD and NC subjects in ADNI-1 shown in the template space. Different colors denote p-values in group comparison (via Hotelling’s T2 [42]) between AD and NC subjects in the ADNI-1 dataset. A smaller p-value denotes higher discriminative capability of the corresponding landmark in distinguishing AD patients from NC subjects and vice versa.

D. Multi-Task Multi-Channel Convolutional Neural Network

Using image patches extracted from MR images, we jointly perform two types of tasks (i.e., classification, and regression) via a multi-task multi-channel convolutional neural network (CNN). The schematic diagram of the proposed CNN model is given in Fig. 4, which allows the learning model to extract feature representations implicitly for the input image patches. This architecture adopts multi-channel input data, where each channel is corresponding to a local image patch extracted from a specific landmark location. We further incorporate three demographic factors (i.e., age, gender, and education) into the learning model, to investigate the impact of demographic information on the performance of computer-aided disease diagnosis. As shown in Fig. 4, the outputs of the proposed CNN model contain the class label and four clinical scores (i.e., CDRSB, ADAS11, ADAS13, and MMSE).

Fig. 4.

Overview of the proposed deep multi-task multi-channel convolutional neural network. The input data include the MR image and the demographic information (i.e., age, gender, and education) of each subject, while the output includes the class label and four types of clinical scores. Note that the term “a” in “a@b × b × b” denotes the number of kernels, while “b × b × b” represents the size of a 3D convolutional kernel.

Since the appearance of brain MRI is often globally similar but locally different across the population of normal control and diseased subjects, both global and local structural information are important for the learning task. To model the local structural information of MRI, we first develop L-channel parallel sub-CNN architectures. In each channel sub-CNN, there is a sequence of 6 convolutional layers and 2 fully connected (FC) layers (i.e., FC7, and FC8). Each convolutional layer is followed by a rectified linear unit (ReLU) activation function, while Conv2, Conv4, and Conv6 are followed by 2 × 2 × 2 max-pooling operations for down-sampling. Note that each channel contains the same number of convolutional layers and parameters, while their weights are independently optimized and updated. To model the global information of MRI, we concatenate the outputs of L FC8 layers and further add two additional FC layers (i.e., FC9, and FC10) to the network. Moreover, we feed a concatenated representation comprising the output of FC10 and three demographic factors (i.e., age, gender, and education) into two FC layers (i.e., FC11, and FC12). Finally, two FC13 layers are used to predict the class probability (via soft-max) and estimate the clinical scores, respectively. The proposed network can also be mathematically described in the following.

Let $\chi ={\left\{{\text{X}}_n\right\}}_{n=1}^N$ denote the training set, with the element X_n representing the n-th subject. Denote the labels of C categories as ${\text{y}}^c={\left\{y_n^c\right\}}_{n=1}^N\left(c=1,2,\dots ,C\right)$, and S types of clinical scores as ${\text{z}}^s={\left\{z_n^s\right\}}_{n=1}^N\left(s=1,2,\dots ,S\right)$. In this study, the class label and four clinical scores are used in a back-propagation procedure to update the network weights in the convolutional layers and learn the most relevant features in the FC layers. The proposed CNN aims to learn a non-linear mapping $\mathrm{\Psi }:\chi \to ({\left\{{\text{y}}^c\right\}}_{c=1}^C,{\left\{{\text{z}}^s\right\}}_{s=1}^S)$ from the input space to both spaces of the class label and clinical scores. Following [11]–[13], [46], we equally treat the tasks of disease classification and clinical score regression, with the objective function defined as follows:

$$\begin{gathered} \arg \underset{\text{W}}{\min }-\frac{1}{C}\sum _{c=1}^C\frac{1}{N}\sum _{{\text{X}}_n\in \chi }\text{1}\left\{y_n^c=c\right\}\log \left(\text{P}\left(y_n^c=c|{\text{X}}_n;\text{W}\right)\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{S}\sum _{s=1}^S\frac{1}{N}\sum _{{\text{X}}_n\in \chi }{\left(z_n^s-\text{f}\left({\text{X}}_n;\text{W}\right)\right)}^2, \end{gathered}$$ (1)

where the first term is the cross-entropy loss for multi-class classification, and the second one is the mean squared loss for regression to evaluate the difference between the estimated clinical score f (X_n ; W) and the ground truth $z_n^s$. Note that 1 {⋅} is an indicator function, with 1 {⋅} = 1 if {⋅} is true and 0 otherwise. In addition, $\text{P}\left(y_n^c=c|{\text{X}}_n;\text{W}\right)$ indicates the probability of the subject X_n being correctly classified as the category $y_n^c$ using the network coefficients W.

The advantage of the proposed CNN model is that it can not only automatically extract local-to-global feature representations from MR images, but also explicitly incorporate the demographic information into the learning process. We solve this optimization problem via a stochastic gradient descent (SGD) approach [47] combined with the backpropagation algorithm to compute the network gradients. The momentum coefficient and the learning rate for SGD are empirically set to 0.9 and 10⁻² , respectively. The implementation of the proposed CNN model is based on Tensorflow [48], and the computer we used in the experiments contains a single GPU (i.e., NVIDIA GTX TITAN 12 GB).

IV. Experiments

A. Methods for Comparison

We first compare the proposed DM²L method with three conventional feature representation based approaches, including 1) voxel-based morphometry (VBM) method [2], 2) ROI-based (ROI) method, and 3) landmark-based morphometrical feature (LMF) [20]. In these three methods, the tasks of classification and regression are performed separately. We further compare DM²L with three state-of-the-art methods for joint classification and regression, i.e., 1) multi-modal multi-task (M³T) learning method [11], 2) manifold regularized multi-task feature (M²TF) learning method [12], and 3) matrix-similarity based joint learning (MSJL) method [13]. Now we briefly summarize these competing methods as follows.

1). VBM method [2].

In the VBM method, all MR images are first normalized to the anatomical automatic labeling (AAL) template, using a non-linear image registration technique [49], [50]. Then, the local GM tissue density of the brain is extracted in a voxel-wise manner as features of an MR image. Based on the voxel-wise features, a linear support vector machine (SVM) [51] and several linear support vector regressors (SVR) [52] (with C = 1) are constructed for classification and regression tasks, respectively.

2). ROI method.

In the ROI method, the brain MRI is first segmented into three tissue types, i.e., gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). We then align the AAL template (with 90 pre-defined regions-of-interest in cortical and sub-cortical regions) into the native space of each subject using a registration algorithm [50]. Then, the normalized volumes of GM tissue inside 90 ROIs are extracted as the feature representation for an MR image, followed by a linear SVM and several linear SVRs (with C = 1) for classification and regression, respectively.

3). LMF [20] method.

In the LMF method, there are L image patches extracted from L landmark locations, with each patch centered at each landmark. Note that such patch extraction strategy is different from ours as described in Section III-C. Then, the 50-dimensional morphological features (i.e., local energy pattern [44]) are extracted from each patch, followed by a feature concatenation process. Given L landmarks, a 50L-dimensional feature vector is generated for each MR image, followed by a z-score normalization [53] process. Finally, the normalized features are used in both tasks of disease classification (via a linear SVM) and clinical score regression (via several linear SVRs). It is worth noting that, different from our proposed DM²L approach that learns features automatically from MRI, LMF employs hand-crafted features for representing MRI. For a fair comparison, LMF shares the same landmarks and size of patches as that in the proposed DM²L method.

4). M³T method [11].

Specifically, M³T includes two key steps, including (a) multi-task feature selection for determining a common subset of relevant features for multiple tasks and (b) SVM/SVR based classification/regression. Since M³T was designed for multi-modality data, we only apply it to our single modality (i.e., MRI) data in the experiments, and treat the disease classification and the regression for clinical scores as different tasks. In M³T, the feature representation is based on 90 brain regions, which is same as in the ROI method. That is, for each of all 90 regions in the labeled MR image of one subject, we compute the GM tissue volumes in the region by integrating the GM segmentation result of this subject.

5). M²TF method [12].

The manifold regularized multi-task feature (M²TF) learning method first performs feature selection by combining a least square loss function with an l_2,1 -norm regularizer and a graph regularizer, and then perform classification via a multi-task learning framework. This method is originally designed only for conducting classification. In our experiments, we adapt M²TF into a joint learning model, by regarding the disease classification and the regression for clinical scores as different tasks. That is, M²TF can simultaneously perform feature selection and joint classification and regression. Similar to M³T, M²TF shares the same 90-dimensional MRI features as used in VBM.

6). MSJL method [13].

The matrix-similarity based joint learning (MSJL) method is a feature selection model for joint classification and regression tasks. MSJL contains a matrix-similarity based loss function that uses high-level information inherent in the target response matrix. This loss function is combined with a group lasso method [54] for joint feature selection across different tasks, i.e., predictions of class labels and clinical scores. With MSJL, one can use those selected features to predict clinical scores and class labels simultaneously. Similarly, MSJL adopts the 90-dimensional ROI-based features extracted for MR images.

There are two major strategies in DM²L, i.e., 1) joint learning of classification and regression, and 2) using the demographic information of subjects for model training. To investigate the effectiveness of these strategies, we further compare DM²L with its three variants, including 1) deep single-task multi-channel learning (DSML) using the demographic information, 2) deep single-task multi-channel learning without using demographic factors (denoted as DSML-1), and 3) deep multi-task multi-channel learning without using demographic information (denoted as DM²L-1). Note that DSML-1 and DSML employ the similar CNN architecture as shown in Fig. 4, but perform the tasks of classification and regression separately. Also, DM²L-1 and DSML-1 do not use demographic information for model training.

B. Experimental Settings

We conduct two types of tasks, including AD/MCI classification and clinical score regression. To evaluate the generalization ability of a specific model, we use subjects from ADNI-1 as the training data, while subjects from ADNI-2 and MIRIAD as independent testing data. In the first group of experiments, based on MR images and three demographic factors (i.e., age, gender, and education), we train a model for multi-class classification (i.e., AD vs. pMCI vs. sMCI vs. NC) and four clinical scores (i.e., CDRSB, ADAS11, ADAS13, and MMSE) regression on ADNI-1, and test this model on ADNI-2. In the second group of experiments, using MR images and two demographic factors (i.e., age, and gender), we train a model for binary classification (i.e., AD vs. NC) and MMSE score regression on ADNI-1, and test it on MIRIAD. The performance of multi-class classification (i.e., AD vs. pMCI vs. sMCI vs. NC) is evaluated by the overall classification accuracy (ACC) for four categories, as well as the accuracy for each category. The binary classification (i.e., AD vs. NC) performance is evaluated by the accuracy (ACC), sensitivity (SEN), specificity (SPE), and area under the ROC curve (AUC). The regression performance is measured by both correlation coefficient (CC) and the root mean square error (RMSE) between the estimated and real clinical scores.

For VBM, ROI and LMF methods, we adopt the linear SVM with C = 1 as the classifier and the linear SVR with C = 1 as the regressor. Different from our joint learning model (i.e., DM²L), the tasks of classification and regression are performed separately in these three methods. For three joint learning methods (i.e., M³T [11], M²TF [12], and MSJ [13]), we adopt the default parameters given by the authors. For a fair comparison, five landmark-based methods (i.e., LMF, DM²L, DM²L-1, DSML, and DSML-1) employ the same patch size (24 × 24 × 24), and also share the same L = 50 landmarks. The influence of parameters (i.e., the number of landmarks, and the size of image patches) is analyzed in Section V-B.

C. Results on ADNI-2

In this group of experiments, we train a specific model on ADNI-1 and test it on ADNI-2, where both MR images and three demographic factors (i.e., age, gender, and education) are used as the input. The experimental results are reported in Table II and Fig. 5. Note that the clinical scores are normalized to [0, 1] in the procedure of model learning, and we transform the estimated scores back to their original ranges in Fig. 5. We further report the confusion matrices in multi-class classification (i.e., AD vs. pMCI vs. sMCI vs. NC) achieved by different methods in Fig. 6. From Table II and Figs. 5–6, we can make the following observations.

TABLE II.

Results of Multi-Class Disease Classification and Clinical Score Regression (Models Trained on ADNI-1 and Tested on ADNI-2)

	Multi-Class Disease Classification					Clinical Score Regression
Method	AD vs. pMCI vs. sMCI vs. NC					CDRSB		ADAS11		ADAS13		MMSE
	ACC	ACCNC	ACCsMCI	ACCpMCI	ACCAD	CC	RMSE	CC	RMSE	CC	RMSE	CC	RMSE
VBM	0.404	0.557	0.295	0.081	0.469	0.278	2.010	0.290	7.406	0.327	10.322	0.289	2.889
ROI	0.431	0.589	0.269	0.027	0.594	0.380	1.893	0.360	7.358	0.371	10.319	0.325	2.899
DSML-1	0.467	0.784	0.295	0.189	0.413	0.475	1.859	0.497	6.499	0.508	9.195	0.468	2.593
DSML	0.486	0.611	0.419	0.216	0.503	0.522	1.674	0.542	6.268	0.581	8.591	0.538	2.414
DM2L-1	0.487	0.665	0.415	0.297	0.427	0.481	1.817	0.516	6.529	0.554	9.771	0.492	2.643
DM2L	0.518	0.600	0.513	0.243	0.490	0.533	1.666	0.565	6.200	0.590	8.537	0.567	2.373

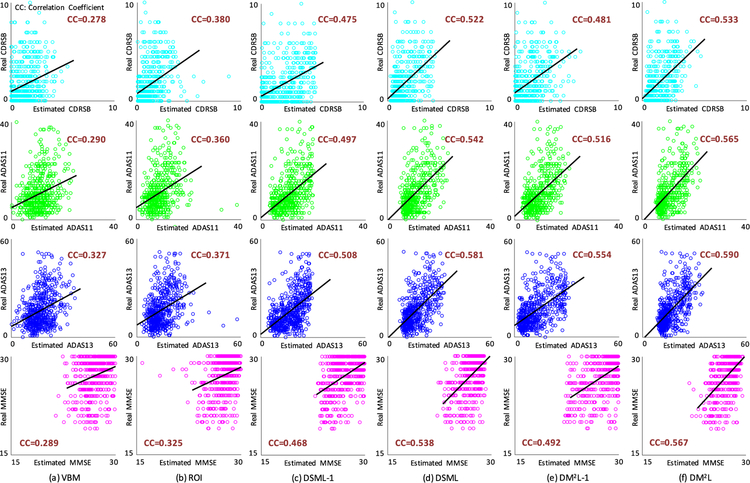
Fig. 5.

Scatter plots of the estimated clinical scores vs. the real clinical scores achieved by six different methods. The corresponding models are trained on ADNI-1 and tested on ADNI-2. CC: Correlation Coefficient.

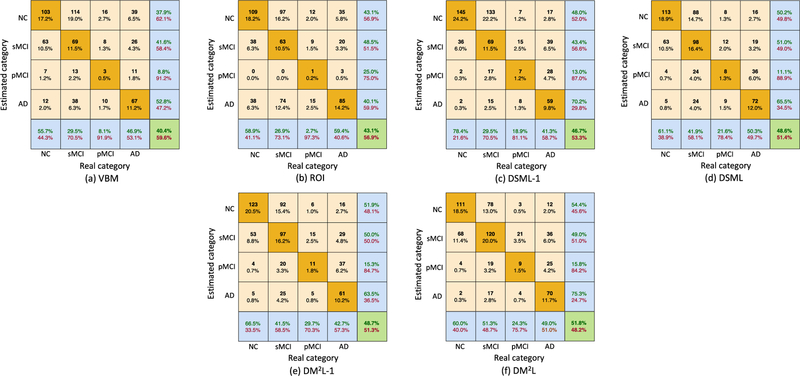
Fig. 6.

Confusion matrices achieved by six different methods in multi-class disease classification (AD vs. pMCI vs. sMCI vs. NC). The corresponding models are trained on ADNI-1 and tested on ADNI-2.

First, compared with conventional methods (i.e., VBM, and ROI), the proposed four deep learning based approaches generally yield better results in both disease classification and clinical score regression. For instance, regarding the overall accuracy, DM²L achieves 11.4% and 8.7% improvements over VBM and ROI, respectively. Besides, VBM and ROI can only achieve the classification accuracies of 0.081 and 0.027 for pMCI subjects, while our DM²L-1 method can achieve an accuracy of 0.297 for pMCI. This implies that the integration of feature extraction into model learning provides a good solution for improving diagnostic performance since feature learning and model training can be optimally coordinated. Second, in both tasks of classification and regression, the proposed joint learning models are usually superior to models that learn different tasks separately. That is, DM²L usually achieves better results than DSML, and DM²L-1 outperforms DSML-1. For instance, in the regression task for the MMSE score, the CC value obtained by DM²L (0.567) is much higher than that obtained by DSML (0.538). In addition, as can be seen from Fig. 5, our DM²L method generally outperforms those five competing methods in the regression of four clinical scores. Considering different signal-to-noise ratios of MRI in the training set (i.e., ADNI-1 with 1.5 T scanners) and MRI in the testing set (i.e., ADNI-2 with 3.0 T scanners), these results imply that the learned model via our DM²L framework has good generalization capability.

D. Results on MIRIAD

Based on MR images and two demographic factors (i.e., age, and gender), we train a model on ADNI-1 and test it on MIRIAD. Since only the MMSE scores are available for subjects in MIRIAD, we perform both tasks of binary classification (AD vs. NC) and MMSE score regression. The experimental results are shown in Table III and Fig. 7. Besides, we further evaluate the proposed method on the baseline AIBL dataset, with experimental results shown in Table S4 of the Supplementary Materials.

TABLE III.

Results of Binary Disease Classification and Clinical Score Regression, With Models Trained on ADNI-1 and Tested on MIRIAD

	Binary Disease Classification				Clinical Score Regression
Method	AD vs. NC				MMSE
	ACC	SEN	SPE	AUC	CC	RMSE
VBM	0.884	0.913	0.826	0.921	0.623	5.271
ROI	0.870	0.913	0.826	0.918	0.699	5.369
DSML-1	0.916	0.954	0.837	0.932	0.708	4.871
DSML	0.918	0.965	0.854	0.959	0.722	4.234
DM2L-1	0.920	0.963	0.898	0.969	0.683	4.295
DM2L	0.937	0.946	0.932	0.986	0.736	4.136

Fig. 7.

Scatter plots of the estimated MMSE scores vs. the real MMSE scores achieved by six different methods. The corresponding models are trained on ADNI-1 and tested on MIRIAD. CC: Correlation Coefficient.

As can be seen from Table III and Fig. 7, our methods (i.e., DM²L, DM²L-1, DSML, and DSML-1) usually outperform VBM and ROI in both tasks of AD vs. NC classification and MMSE score regression. In addition, the use of our proposed joint learning strategy tends to produce better results in the regression task than in the classification task. For instance, the proposed DM²L achieves a CC value of 0.736 in MMSE score regression with an improvement of 15.3% over DM²L-1, while these two methods produce comparable results in AD vs. NC classification. In other words, the joint learning strategy contributes more to the regression task, compared with that to the classification task. Furthermore, DM²L and DSML generally outperform their counterparts (i.e., DM²L-1, and DSML-1) that do not consider demographic information of subjects. It suggests that the use of demographic information helps improve the learning performance of the proposed method. Results using only three demographic factors (via a fully connected neural network) are given in Table S3 and Fig. S6 in the Supplementary Materials.

On the other hand, from Tables II and III, one could observe that the overall accuracy achieved by six different methods in the task of AD vs. pMCI vs. sMCI vs. NC classification is lower than the results of AD vs. NC classification. The similar trend can be found for the regression task. The possible reason could be that the AD-related structural changes of the brain in MRI may be very subtle and not discriminative enough to identify all four categories simultaneously. Furthermore, in the random case, the chances for a subject to be assigned to each class in a 2-class classification problem is roughly 50%, while in 4-class classification problem it is only 25%. As a result, the accuracy results in the 4-class classification problem will degrade, while they are still very far from random assignment.

E. Comparison With State-of-the-Art Approaches

We further compare our DM²L method with a landmark-based method (i.e., LMF [20]), and three state-of-the-art approaches that can perform both tasks of disease classification and clinical score regression, including 1) M³T [11], 2) M²TF [12], and 3) MSJL [13]. Note that LMF, M³T, and MSJL rely on SVM and SVR for separate classification and regression, while M²TF and our DM²L can jointly perform classification and regression. In this group of experiments, we perform multi-class disease classification and clinical score regression, with models trained on the ADNI-1 dataset and tested on the ADNI-2 dataset. In Fig. 8, we report the overall accuracy (ACC) of four categories and the correlation coefficients (CC) between the estimated and real clinical scores.

Fig. 8.

Comparison between our DM²L method and four state-of-the-art approaches (i.e., LMF [20], M³T [11], M²TF [12], and MSJL [13]) in multi-class brain disease classification (i.e., AD vs. pMCI vs. sMCI vs. NC) and regressions for four clinical scores (i.e., CDRSB, ADAS11, ADAS13, and MMSE). The corresponding models are trained on ADNI-1 and tested on ADNI-2. ACC: Accuracy; CC: Correlation Coefficient.

From Fig. 8, we can observe that our DM²L method generally performs better than four competing approaches regarding both ACC and CC. The superiority of our method over those three state-of-the-art methods could be due to the following facts. First, conventional methods rely on either ROI-based feature representations (in M³T, M²TF, and MSJL) or morphological features (in LMF) for MR images, where the feature extraction process is independent of the subsequent classifiers or regressors. In contrast, the proposed DM2L method simultaneously learns the discriminative features of MRI along with the classifier and regressor, and thus those learned features can be more suitable for subsequent classifiers/regressors. Second, DM²L explicitly incorporates three demographic factors (i.e., age, gender, and education) into the model learning, while four competing methods do not use the available demographic information of subjects.

V. Discussion

A. Comparison With Previous Studies

In this paper, we propose a joint learning framework for brain disease classification and clinical score regression. In general, there are at least two major differences between our method and the conventional joint learning models [11]–[13]. First, our method can learn discriminative features automatically from MR images via a deep convolutional neural network, rather than using hand-crafted representations for MRI as in conventional approaches. Second, different from previous studies, we can explicitly incorporate the demographic information (i.e., age, gender, and education) into the model learning process in our method. In this way, more prior information about the studied subjects can be utilized in the model training, which could help improve the robustness of learning models. Experimental results in Table II and Table III suggest that even though we train our model on ADNI-1 and test it on two independent datasets (i.e., ADNI-2, and MIRIAD), our method can still achieve reasonable results in both tasks of classification and regression.

Different from conventional voxel-based and whole-image-based features of MRI that focus on local and global information, respectively, the representations learned in our DM²L method can capture local-to-global structural information of MR images. Specifically, we first learn patch-based local representations via multi-channel sub-CNNs to model the local structural information, and then learn global representations to capture the global information of MR images. That is, DM²L is capable of modeling both local and global characteristics of brain structures. Especially, unlike previous ROI-based approaches, DM²L does not require any pre-defined ROIs for brain MR images. This is particularly useful in practice and can make computeraided diagnosis more straightforward and feasible. Also, different from the conventional patch-based approaches [34], [35], our DM²L framework can automatically learn feature representations for local image patches, without using hand-crafted features of patches [34]. Besides, although there usually exist millions of image patches in a 3D brain MR image, our method can rapidly locate the most informative patches via a data-driven landmark detection algorithm [20].

Currently, there are several studies [55] focusing on the multiclass problem for AD diagnosis. For multi-class AD diagnosis based on MR images, Liu et al. [55] proposed a stacked auto encoders (SAE) based deep feature learning method, and Zhu et al. [56] developed a sparse discriminative feature selection algorithm using GM tissue volumes in 93 ROIs as the representation for MRI. The overall accuracy of the four-class (AD vs. pMCI vs. sMCI vs. NC) classification achieved by our method is 0.518, which is better than that in [55] (i.e., 0.463) but worse than that in [56] (i.e., 0.597). It is worth noting that, in our method, we train a model on ADNI-1 and test it on ADNI-2. And the methods in [55], [56] only used subjects in ADNI-1 via cross-validation for performance evaluation, which often produces over-promising results. On the other hand, these results also indicate that although the data distribution between ADNI-1 and ADNI-2 is different, our proposed model has a high generalization ability.

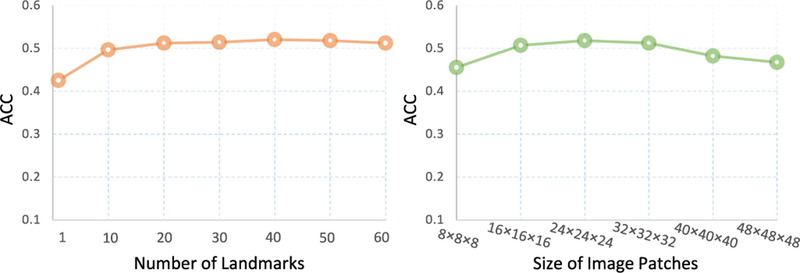
B. Parameter Analysis

We now evaluate the influence of two key parameters (i.e., the number of landmarks and the size of image patches) on the performance of the proposed DM²L method. Specifically, we vary the number of landmarks in the range [1, 10, 20,… , 60] and the size of patches in the range [8 × 8 × 8, × 16 × 16 × 16,…,48 × 48], and record the multi-class classification achieved by DM²L in Fig. 9, with models trained and tested on ADNI-1 and ADNI-2, respectively. From Fig. 9, we can observe that our method achieves good results when the number of landmarks is larger than 20 and the size of image patches is larger than 16 × 16 × 16. Also, using very large (e.g., > 40 × 40 × 40) patches, DM²L cannot yield good results. The possible reason could be that the subtle structural changes caused by AD/MCI will be dominated by a large number of uninformative voxels in a huge patch.

Fig. 9.

Results of the proposed DM²L method in multi-class classification (i.e., AD vs. pMCI vs. sMCI vs. NC) using different number of landmarks (left) and different size of image patches (right).

C. Computational Cost

We now analyze the computational costs of the proposed DM²L method and those competing methods. Since the training process is performed off-line, we only analyze the computational cost of the online testing process for a new testing subject in each method. There are seven significant processes in these methods, including 1) linear alignment, 2) nonlinear registration, 3) landmark prediction, 4) feature extraction, 5) feature selection, 6) classification, and 7) regression. The computational costs of different methods are listed in Table IV. From Table IV, we can observe the conventional voxel-based method (i.e., VBM) and ROI-based methods (i.e., ROI, M³T, M²TF, and MSJL) require about 32 minutes to perform classification and regression for a testing subject. Among two landmark-based methods, DM²L needs only about 15 seconds for joint classification and regression, which is faster than LMF (~20 s). These results imply that our method can perform AD/MCI diagnosis at a speed of close to real-time, which is particularly important in real-world applications.

TABLE IV.

Computational Costs of Different Methods in AD Classification and Clinical Score Regression for a New Testing MR Image

Procedure	VBM	ROI	LMF	M3T	M2TF	MSJL	DM2L
Linear Alignment (C++)	5.00 s	5.00 s	5.00 s	5.00 s	5.00 s	5.00 s	5.00 s
Nonlinear Registration (HAMMER [50])	32.00 min	32.00 min	–	32.00 min	32.00 min	32.00 min	–
Landmark Prediction (Matlab)	–	–	10.00 s	–	–	–	10.00 s
Feature Extraction (Matlab)	4.00 s	3.00 s	5.00 s	3.00 s	3.00 s	3.00 s	–
Feature Selection (Matlab)	–	–	–	0.02 s	0.02 s	0.03 s	–
Classification (Matlab)	0.05 s	0.02 s	0.03 s	0.02 s		0.02 s	0.02 s (Tensorflow [48])
Regression (Matlab)	0.16 s	0.08 s	0.12s	0.08 s		0.08 s
Total Time	~ 32.00 min	~ 32.00 min	~ 20.00 s	~ 32.00 min	~ 32.00 min	~ 32.00 min	~ 15 s

D. Limitations and Future Work

There are still several limitations to be considered in this study, although we obtained good results in classifying AD patients. First, we train a model on ADNI-1 and test it on two independent datasets (i.e., ADNI-2 and MIRIAD). Due to differences in data distributions between the training and the testing data, it may degrade the performance to directly applying the trained model to the independent testing data [57]. It is interesting to study a model adaptation strategy to reduce the negative influence of distribution differences. Second, in the current study, we resort to a landmark identification algorithm [20] to locate informative patches from MR images. Based on these image patches, we then learn representations of MRI for joint classification and regression. The problem here is that the process of landmark detection is independent of the proposed deep feature learning framework. As a future work, one can study how to integrate the landmark detection and landmark-based classification/regression into a unified deep learning framework. Third, the proposed network is trained from scratch in this work. It is interesting to fine-tune the existing convolutional neural networks trained on the other large-scale 3D medical image datasets, to further promote the learning performance, which can also be considered as a direction for future works. Furthermore, we equally treat the tasks of disease classification and clinical score regression in the current work [11]–[13], [46], while these tasks could have different contributions. It is desired to automatically learn weights for these two tasks, which will be our future work.

VI. Conclusion

In this paper, we proposed a deep multi-task multi-channel learning (DM²L) framework for simultaneous Alzheimer’s disease classification and clinical score regression, using both MR imaging data and demographic information (i.e., age, gender, and education) of subjects. Specifically, we first identified discriminative landmarks from MR images in a data-driven manner and extracted multiple image patches around these detected landmarks. We then proposed a deep multi-task multi-channel convolutional neural network for joint classification and regression, in which the demographic information is explicitly incorporated into the learning process. Experimental results on four public datasets demonstrate that our DM²L outperforms several state-of-the-art approaches in both the tasks of disease classification and clinical score regression.