 A predictive approach for driving down machine learning model errors is introduced and demonstrated across discovery for inorganic and organic chemistry.
A predictive approach for driving down machine learning model errors is introduced and demonstrated across discovery for inorganic and organic chemistry.
Abstract
Machine learning (ML) models, such as artificial neural networks, have emerged as a complement to high-throughput screening, enabling characterization of new compounds in seconds instead of hours. The promise of ML models to enable large-scale chemical space exploration can only be realized if it is straightforward to identify when molecules and materials are outside the model's domain of applicability. Established uncertainty metrics for neural network models are either costly to obtain (e.g., ensemble models) or rely on feature engineering (e.g., feature space distances), and each has limitations in estimating prediction errors for chemical space exploration. We introduce the distance to available data in the latent space of a neural network ML model as a low-cost, quantitative uncertainty metric that works for both inorganic and organic chemistry. The calibrated performance of this approach exceeds widely used uncertainty metrics and is readily applied to models of increasing complexity at no additional cost. Tightening latent distance cutoffs systematically drives down predicted model errors below training errors, thus enabling predictive error control in chemical discovery or identification of useful data points for active learning.
1. Introduction
Machine learning (ML) models for property prediction have emerged1–8 as powerful complements to high-throughput computation8–13 and experiment,14–16 enabling the prediction of properties in seconds rather than the hours to days that direct observations would require. Using large data sets, trained interpolative potentials17–21 and property prediction models1–8 have achieved chemical accuracy with respect to the underlying data.22 Predictive models hold great promise in the discovery of new catalysts5,6,23,24 and materials8,25–31 by enabling researchers to overcome combinatorial challenges in chemical space exploration. While application of ML to chemical space exploration is increasingly becoming a reality, a key outstanding challenge remains in knowing in which regions of chemical space a trained ML model may be confidently applied.32
While trained ML models are fast to deploy to large compound spaces, many models (e.g., artificial neural networks or ANNs) are typically trained only after acquisition of thousands33 to millions17,34 of data points. Quantitative uncertainty metrics are most critical in applications of active learning35,36 where the model is improved by acquisition of selected data. Although some models (e.g., Gaussian process regression) inherently provide estimates of model uncertainty,37,38 uncertainty quantification for models suited to handle large data sets (e.g., ANNs) remains an active area of research.39–41
One approach to estimating model uncertainty is to train an ensemble of identical architecture models on distinct partitions of training data to provide both a mean prediction and associated variance (Fig. 1). While widely employed in the chemistry community,19,39,40,42,43 ensembles increase the model training effort in proportion to the number of models used (typically an order of magnitude, ESI Text S1†). Although this additional effort may be practical for some models (e.g., networks with only a few layers), the training effort becomes cost-prohibitive44 during iterative retraining for active learning or for more complex models that are increasingly used in chemical discovery, such as those using many convolutional45,46 or recurrent47,48 layers. Thus, ensemble uncertainty estimates have been most frequently applied19,40 in the context of simpler networks, especially in neural network potentials that are trained in a one-shot manner. A key failing of ensemble metrics is that with sufficient model damping (e.g., by L2 regularization), variance over models can approach zero41 for compounds very distant from training data, leading to over-confidence in model predictions.
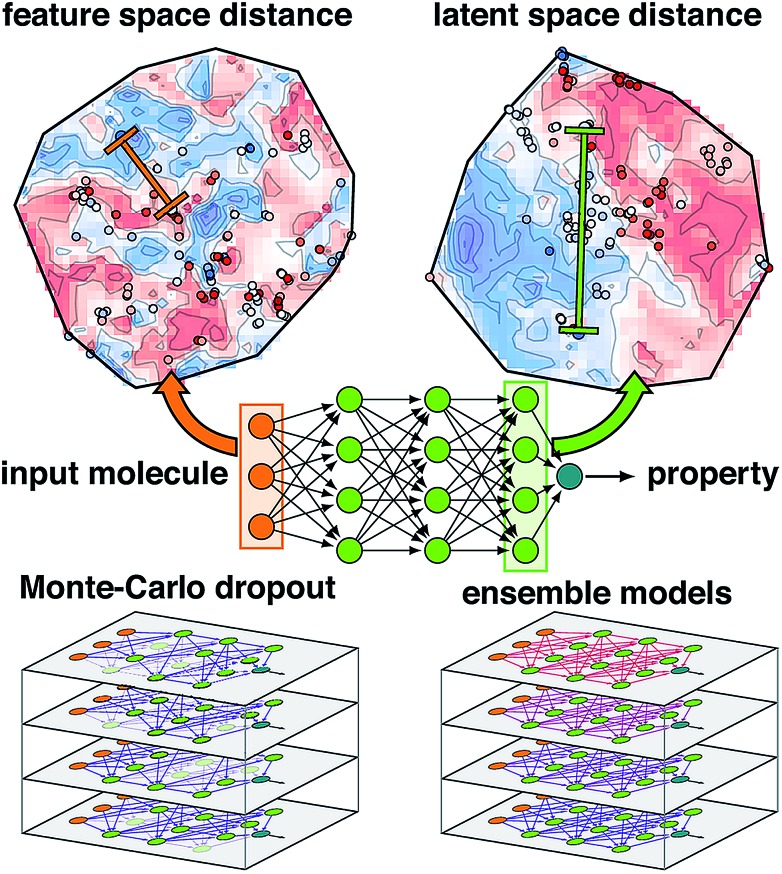
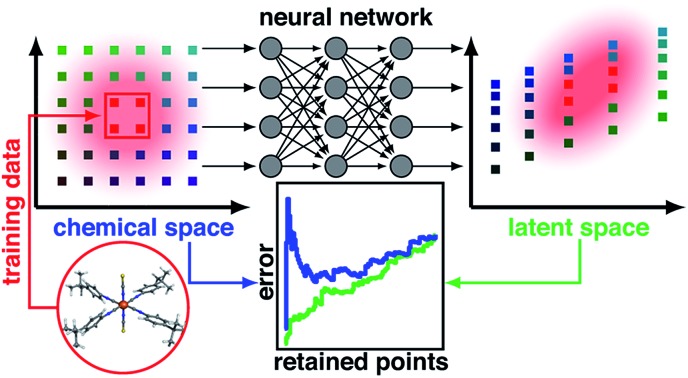
Fig. 1. Schematic of an ANN annotated with the four uncertainty metrics considered in this work. Two points are compared in terms of their feature space distance (i.e., the difference between two points in the molecular representation) on a t-distributed stochastic neighbor embedding map49 (t-SNE) of data in the input layer (top, left, annotations in orange) and the latent space distance (i.e., the difference between two points in the final layer latent space) on a t-SNE of the data in the last layer (top, right, annotations in green). The standard ANN architecture (middle) is compared at bottom for Monte-Carlo dropout (i.e., zeroed out nodes) and ensemble models (i.e., varied model weights) at bottom left and right.
Another approach to obtain model-derived variances in dropout-regularized neural networks is Monte Carlo dropout (mc-dropout)50 (Fig. 1). In mc-dropout, a single trained model is run repeatedly with varied dropout masks, randomly eliminating nodes from the model (ESI Text S1†). The variance over these predictions provides an effective credible interval with the modest cost of running the model multiple times rather than the added cost of model re-training. In transition metal complex discovery, we found that dropout-generated credible intervals provided a good estimate of errors on a set aside test partition but were over-confident when applied to more diverse transition metal complexes.7,8 Consistent with the ensembles and mc-dropout estimates, uncertainty in ANNs can be interpreted by taking a Bayesian view of weight uncertainty where a prior is assumed over the distribution of weights of the ANN and then updated upon observing data, giving a distribution over possible models.51 However, if the distribution of the new test data is distinct from training data, as is expected in chemical discovery, this viewpoint on model uncertainty may be incomplete.
A final class of widely applied uncertainty metrics employs distances in feature space of the test molecule to available training data to provide an estimate of molecular similarity and thus model applicability. The advantages of feature space distances are that they are easily interpreted, may be rapidly computed, and are readily applied regardless of the regression model7,8,41,52 (Fig. 1). We used7,8 high feature space distances to successfully reduce model prediction errors on retained points while still discovering new transition metal complexes. Limitations of this approach are that the molecular representation must be carefully engineered such that distance in feature space is representative of distance in property space, the relationship between distance cutoff and high property uncertainty must be manually chosen, and this metric cannot be applied to message-passing models that learn representations.53,54
A chief advantage of multi-layer neural network models over simpler ML models is that successive layers act to automatically engineer features, limiting the effect of weakly-informative features that otherwise distort distances in the feature space (Fig. 1). Thus, for multi-layer ANNs, feature-based proximity can be very different from the intrinsic relationship between points in the model. Such ideas have been explored in generative modeling where distances in auto-encoded latent representations have informed chemical diversity55,56 and in anomaly detection with separate models57,58 (e.g., autoencoders59–61 or nearest-neighbor classifiers62,63) have enabled identification of ‘poisoned’ input data.64 However, the relationship between latent space properties and feature space properties has not been exploited or understood in the context of error estimation for property prediction (i.e., regression) ML models.
In this work, we propose the distance in latent space, i.e., the distance of a test point to the closest training set point or points in the final layer latent space, as a new uncertainty metric (Fig. 1). The advantages of this approach are that (i) it introduces no overhead into model training or evaluation, (ii) it can work just as easily with both simple and complex ANN models that have been used for chemical property prediction (e.g., hierarchical,65 recurrent,47,48 or convolutional46,66–69), and (iii) it naturally ignores distances corresponding to features to which the model prediction is insensitive, obviating the need for feature engineering to develop an estimate of test point proximity to prior training data. We show that these attributes yield superior performance over other metrics in chemical discovery.
2. Results & discussion
To demonstrate the advantages of the latent space distance metric in a quantitative fashion, we compare to three established uncertainty metrics. This assessment is particularly motivated by the nature of chemical discovery applications,8 where data set sizes are often smaller and have more broadly varying chemistry than typical applications in neural network potentials19,40 or in quantitative structure–property relationships in cheminformatics.41,52 To mimic chemical discovery efforts, we train neural networks to predict transition metal complex spin state energetics7 and test them on diverse transition metal complexes from experimental databases. To confirm the generality of our observations, we also compare uncertainty estimates for neural network models trained on a very small subset (i.e., 5%) of QM9,33 a widely used22,65,70–75 data set in organic chemistry ML.
For open shell transition metal chemistry, we use 1901 equilibrium high (H)/low (L) spin splitting energies (i.e., ΔEH-L) for octahedral first-row transition metal (i.e., M(ii) or M(iii) where M = Cr, Mn, Fe, or Co) complexes generated in prior work7,8 using density functional theory (DFT). We use the previously introduced7 full set of revised autocorrelation (RACs) descriptors (i.e., RAC-155) to train a fully connected ANN with three 200-node hidden layers (see Computational Details and ESI Text S2, Table S1, and Fig. S1†). RACs have been demonstrated for training predictive models of transition metal complex properties,7,8,25,76 including spin splitting, metal–ligand bond length, redox and ionization potentials, and likelihood of simulation success.
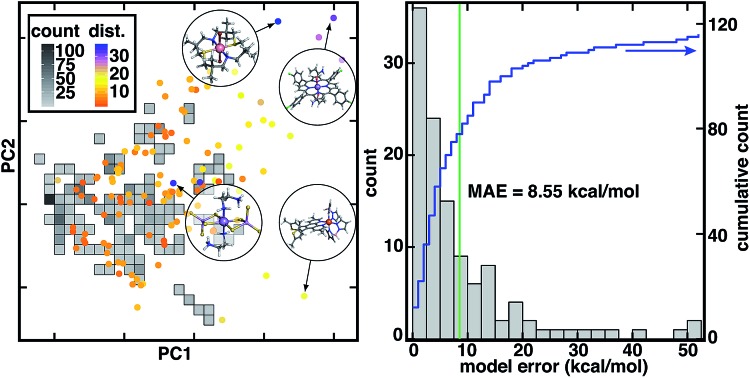
To mimic chemical discovery application of this model, we extracted a set of 116 octahedral, first-row transition metal complexes that have been characterized experimentally (i.e., from the Cambridge Structural Database or CSD77) as an out-of-sample test set (Fig. 2, ESI Text S2 and Fig. S2–S5†). We selected these CSD complexes to be intentionally distinct from training data, as is apparent from principal component analysis (PCA) in the RAC-155 (ref. 7) representation (Fig. 2). Several complexes in the CSD test set fall outside the convex hull of the training data in the first two principal components (ca. 50% of the variance) and are distant from training data, as judged by the Euclidean distance in the full RAC-155 feature space (Fig. 2 and ESI Fig. S6†). High distances are observed for complexes containing elements rarely present (e.g., an S/N macrocycle for a Co(ii) complex, CSD ID: FATJIT) or completely absent from our training data (e.g., B in boronated dipyrazole ligands of the Fe(ii) complex CSD ID: ECODIM and as in thioarsenite ligands in an Mn(ii) complex, CSD ID: CEDTAJ) as well as ligand topologies (e.g., acrylamide axial ligands in an Mn(ii) complex, CSD ID: EYUSUO) not present in training data (Fig. 2).
Fig. 2. (left) Comparison of inorganic training and CSD test data in the dominant two principal components of the RAC-155 representation of the training data set. The density of training data is shown as gray squares shaded as indicated in inset count colorbar. CSD test data points are shown as circles colored by the 10-nearest-neighbor-averaged Euclidean distance in RAC-155 space, as shown in dist. inset color bar. Four representative high-distance structures are shown in circle insets in ball and stick representations: (top left inset, CSD ID: FATJIT) a Co(ii) complex with S/N macrocycle and axial Br– ligands, (top right inset, CSD ID: EYUSUO) Mn(ii) tetra-chlorophenyl-porphyrin with acrylamide axial ligands, (bottom left inset, CSD ID: CEDTAJ) a Mn(ii) complex with thioarsenite ligands, and (bottom right inset, CSD ID: ECODIM) an Fe(ii) complex with boronated dipyrazole and thiolated phenanthrene ligands. (right) Distribution of absolute CSD test set model errors for ΔEH-L (in kcal mol–1, bins: 2.5 kcal mol–1) with the MAE annotated as a green vertical bar and the cumulative count shown in blue according to the axis on the right.
Due to the distinct nature of the CSD test set from the original training data, the 8.6 kcal mol–1 mean absolute error (MAE) of the RAC-155 ANN on the CSD data set is much larger than the 1.5 kcal mol–1 training set MAE (Fig. 2 and ESI Table S2†). Use of ensemble- or mc-dropout-averaged predictions unexpectedly78 worsens or does not improve test MAEs (ensemble: 9.0 kcal mol–1; mc-dropout: 8.5 kcal mol–1), which we attribute to noise in averaging due to the relatively heterogeneous training data (ESI Fig. S7–S9†). The relative error increase on diverse data is consistent with our prior work where we achieved low errors on test set partitions of 1–3 kcal mol–1 (ref. 7) that increased7 to around 10 kcal mol–1 on sets of diverse molecules (e.g., 35 molecules from a prior curation7 of the CSD77). These observations held across feature sets7 (e.g., MCDL-25 vs. RAC-155) and model architectures7,8 (e.g., kernel ridge regression vs. ANNs) for ΔEH-L property prediction.
Despite the increase in MAE, errors are not uniformly high across the 116 molecules in our new CSD data set (Fig. 2). A significant number (24 or 21%) of the complexes have errors within the 1.5 kcal mol–1 training MAE, a substantial fraction are within the 3 kcal mol–1 test set error described in prior work7 (41 or 35%), and a majority (61 or 53%) have errors 5 kcal mol–1 or below (Fig. 2 and ESI†). At the same time, a number of outlier compounds have very large absolute errors with 31 (27%) above 10 kcal mol–1 and 12 (10%) above 20 kcal mol–1 (Fig. 2 and ESI†). Large errors are due to both underestimation of ΔEH-L by the ANN (e.g., Fe(ii) complex CSD ID: CEYSAA, ΔEH-L,ANN = –23.8 kcal mol–1, ΔEH-L,DFT = 26.6 kcal mol–1) and overestimation (CSD ID: Mn(iii) complex CSD ID: EYUSUO, ΔEH-L,ANN = 5.7 kcal mol–1, ΔEH-L,DFT = –46.4 kcal mol–1, see Fig. 2). Given the heterogeneity of observed errors, we apply uncertainty metrics to this data set with the aim to (i) systematically drive down error on predicted data points by only making predictions within the model's domain of applicability and (ii) identify data points that should be characterized and incorporated into the model training set in an active learning setting.
For heavily engineered feature sets (i.e., MCDL-25 (ref. 7)), we showed the Euclidean norm feature space distance to the closest training point could be used to control ANN errors in inorganic complex discovery,7,8 typically limiting discovery MAEs to only slightly larger (i.e., 4–5 kcal mol–1) than the original test MAE. This approach required that we select a cutoff over which distances were deemed too high, a quantity that can be sensitive to the nature of the feature set and the number of nearest neighbors used in the average (ESI Fig. S10 and S11†). Averaging Euclidean norm distances in RAC-155 (ref. 7) or a feature-selected subset7,25 over the nearest (i.e., 1–10) neighbors in the training data and only predicting on points sufficiently close to training data systematically eliminates the highest error points (ESI Fig. S11†). Consistent with prior work,7,8 this approach allows us to achieve sub-6 kcal mol–1 MAE on over half (64 of 116) points in the CSD set, but further improvement of predicted-data MAEs below 5 kcal mol–1 is not possible (ESI Fig. S11†).
In the large, non-engineered feature spaces typically used as input to neural networks, feature space distances may be insufficient for identifying when predictions lack support by data in the model. Thus, we turn to the latent space distance evaluated at the final hidden layer (Fig. 1). Using high distances in latent space as the criterion for prediction uncertainty, we drive down MAEs on predicted data nearly monotonically, well below the 5 kcal mol–1 MAE that could be achieved using feature space distances (ESI Fig. S11†). This difference in performance is motivated by the distinct, higher effective dimensionality of the principal components in the latent space over the feature space (ESI Fig. S6†). With the distance in latent space as our guide, 76 points can be identified as falling within model domain of applicability (i.e., sub-6 kcal mol–1 MAE), and 3 kcal mol–1 MAE can be achieved on over 25% of the data (ca. 30 points), indicating a close relationship between high latent space distance and model error (ESI Fig. S11–S13†). The distance in latent space has the added advantage of being less sensitive to the number of nearest neighbors over which the distance evaluation is carried out than feature space distances (ESI Fig. S11†). Our approach is general and not restricted to the distance in the latent space described here. In future work, we could move beyond potential ambiguities79 in measuring high-dimensional similarity with Euclidean distances and compare to alternatives, including averaged properties55 or those that incorporate other geometric features of the latent data distribution.
Having confirmed that distances in latent space provide significant advantages over feature space distances at no additional cost, we also would like to consider the performance with respect to mc-dropout and ensemble-based uncertainty metrics (ESI Fig. S14 and S15†). To do so, we overcome the key inconvenience that the distance measure itself does not provide an error estimate in the units of the property being predicted. After model training, we calibrate the error estimate by fitting the predictive variance to a simple conditional Gaussian distribution of the error, ε, for a point at latent space distance, d:
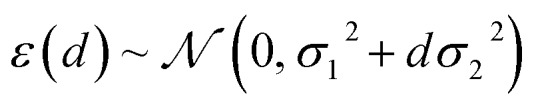 |
1 |
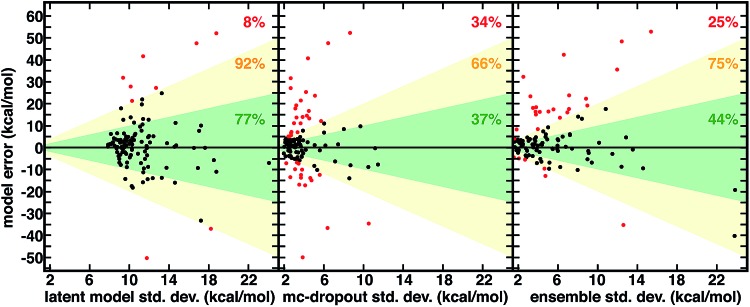
where the error is assumed to be normal with a baseline σ12 term and a growing term σ22. Selection of σ1 and σ2 using a simple maximum likelihood estimator on a small subset (ca. 20 points) of the CSD test set is robust, leading to property-derived uncertainties (Fig. 3, ESI Fig. S16, Tables S3 and S4†). Over the 116-complex CSD test set, this latent space-derived metric spans a large 8–24 kcal mol–1 range and correlates to absolute model errors as strongly as ensemble and mc-dropout standard deviation (std. dev.) metrics (ESI Fig. S13†).
Fig. 3. Relationship between spin-splitting ANN model errors (in kcal mol–1) on a 116 molecule CSD set and three uncertainty metrics all in kcal mol–1: latent model energetic, calibrated std. dev. (left), mc-dropout std. dev. (middle), and 10-model ensemble std. dev. (right). The translucent green region corresponds to one std. dev. and translucent yellow to two std. dev. The points with model errors that lie inside either of these two bounds are shown in black, and the percentage within the green or yellow regions are annotated in each graph in green and yellow, respectively. The points outside two std. dev. are colored red, and the percentage of points in this group is annotated in each graph in red. Three points are omitted from the ensemble plot to allow for a consistent x-axis range.
Although not unique and dependent on the training process of the model, the distance in latent space-derived energetic uncertainties provide a superior bound on high error points (Fig. 3). Observed errors reside within one std. dev. in the majority (77%) of cases, and only a small fraction (8%) exceed two std. dev. ranges (Fig. 3). In comparison, less than half of errors are within one std. dev. evaluated from the ensemble (44%) or mc-dropout (37%), and a significant fraction of errors exceed two std. dev. (23% and 34%, respectively, Fig. 3). When the ensemble or mc-dropout uncertainty metrics are used as cutoffs to decide if predictions should be made, model over-confidence leads to inclusion of more high error (i.e., >12 kcal mol–1) points than when using the latent distance (ESI Fig. S17†). The ability to smoothly transition between high cutoffs where more points are characterized with the ML model (e.g., to achieve 8 kcal mol–1 MAE) vs. conservative where the error is small (e.g., 2 kcal mol–1) but only a minority of predictions are made is important for predictive control; here, the latent distance provides the more robust separation between these two regimes, thus enabling greater distinction between the two (ESI Fig. S15†).
There are numerous cases where both ensemble and mc-dropout are relatively confident on very high error points in comparison to latent distance. For example, an Fe(ii) complex with ethanimine and alkanamine ligands (CSD ID: DOQRAC) is predicted erroneously by the model to be strongly high spin (ΔEH-L,ANN = –34.7 kcal mol–1vs. ΔEH-L,DFT = –1.4 kcal mol–1), but this point has a low std. dev. from the ensemble (4.3 kcal mol–1) in comparison to a relatively high 17.2 kcal mol–1 std. dev. from the latent space distance. Conversely, there are no cases where the latent distance uncertainty is uniquely over-confident, but there are cases where all metrics are overconfident. For example, an Mn(ii) complex with four equatorial water ligands and two axial, oxygen-coordinating 4-pyridinone ligands is expected by all metrics to be reasonably well predicted (std. dev. ensemble = 2.5 kcal mol–1, mc-dropout = 2.7 kcal mol–1, and latent space = 9.4 kcal mol–1), but the DFT preference for the high-spin state is underestimated by the ANN (ΔEH-L,ANN = –45.5 kcal mol–1vs. ΔEH-L,DFT = –77.4 kcal mol–1). Although the latent distance error estimate does not bound all high error points predicted by the model, it provides a high fidelity, no cost uncertainty estimate for >90% of the data.
To assess the generality of our observations on inorganic complexes for other chemical data sets, we briefly consider the approach applied to atomization energies computed with hybrid DFT (i.e., B3LYP80–82/6-31G83) for a set of organic (i.e., C, H, N, O, and F-containing) small molecules. The QM9 data set33 consists of 134k organic molecules with up to 9 heavy atoms and has been widely used as a benchmark for atomistic machine learning model development,22,70–72 with the best models in the literature reporting MAEs well below 1 kcal mol–1.22,65,70,73–75 As in previous work,7 we employ standard autocorrelations (ACs)84 that encode heuristic features85 on the molecular graph and perform well (ca. 6 kcal mol–1 MAE) even on small (<10%) training set partitions for QM9 atomization energies,7 exceeding prior performance from other connectivity-only featurizations.70 For this work, we trained a two-hidden layer residual ANN using AC features and passing the input layer forward in a ResNet-like architecture86 to improve performance over a fully-connected architecture (Computational Details and ESI Fig. S18, Tables S5 and S6†). We use only 5% (6614) of the data points for training, reserving the remaining 127k molecules for our test set to mimic chemical discovery in a single random partition, the choice of which does not influence overall performance (ESI Table S7†).
Baseline model performance for QM9 atomization energies with the ANN is improved over our prior work for both train (4.6 kcal mol–1) and test (6.8 kcal mol–1) MAE, with some further improvement of test MAE with an ensemble model (6.1 kcal mol–1, see ESI Tables S7 and S8†). A wide distribution of errors is observed with some outlier points such as hexafluoropropane (error = 120 kcal mol–1) having very large errors for both the single and ensemble models (ESI Fig. S19†). For the residual ANN, the mc-dropout uncertainty has not been derived, and so we compare only the other three uncertainty metrics. We observe ensemble and latent space distance uncertainty metrics to have similar correlations to model errors and both to outperform feature space distance in this regard (ESI Fig. S20†). Selecting either the distance in latent space or ensemble uncertainty as a cutoff, we systematically drive down MAEs on the predicted data fraction, and latent distance again provides superior control when error tolerance is low (ESI Fig. S21†). For example, setting a tolerance of 3.5 kcal mol–1 for the MAE leads to a pool of over 4200 points retained with the latent space distance metric vs. few points (74) for the ensemble std. dev. (ESI Fig. S21†).
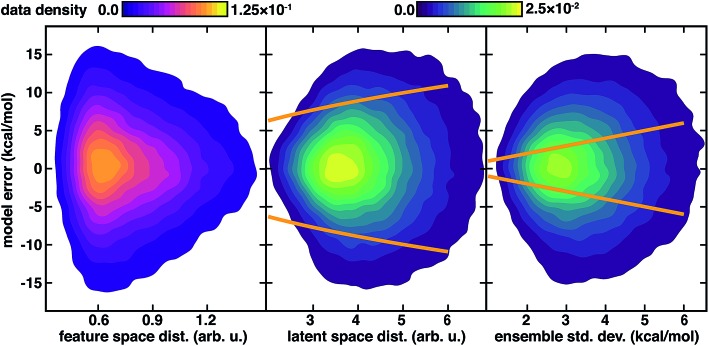
We again observe that the AC feature space distance is a poor indicator of increasing model errors, with as many high error points occurring at low distances as at high distances (Fig. 4). In contrast to feature space distance, ensemble std. dev. and latent distance both grow with increasing error (Fig. 4). Calibration of the latent space distance to the output property enables direct comparison to ensemble uncertainties (ESI Table S9†). As in the inorganic data set, the ensemble std. dev. values are overconfident, capturing a smaller amount (44%) of the errors within a single std. dev. in comparison to the distance in latent space (77%) metric (Fig. 4 and ESI Fig. S22†). For the ensemble uncertainty, a significant fraction (28%) of points have errors larger than twice the std. dev., whereas only a small fraction (5%) do so for the distance in latent space (Fig. 4 and ESI Fig. S22†).
Fig. 4. Model errors (in kcal mol–1) for 127k QM9 atomization energy test points shown as contours as a function of uncertainty metrics. The three uncertainty metrics compared are: feature space distance (in arb. u., left, with top left color bar), latent space distance (in arb. u., middle, with top right color bar), and 10-model ensemble std. dev. (in kcal mol–1, with top right color bar). One standard deviation cutoffs are shown as orange lines for the latent space distance from the calibrated error model (center) and directly from the ensemble (right).
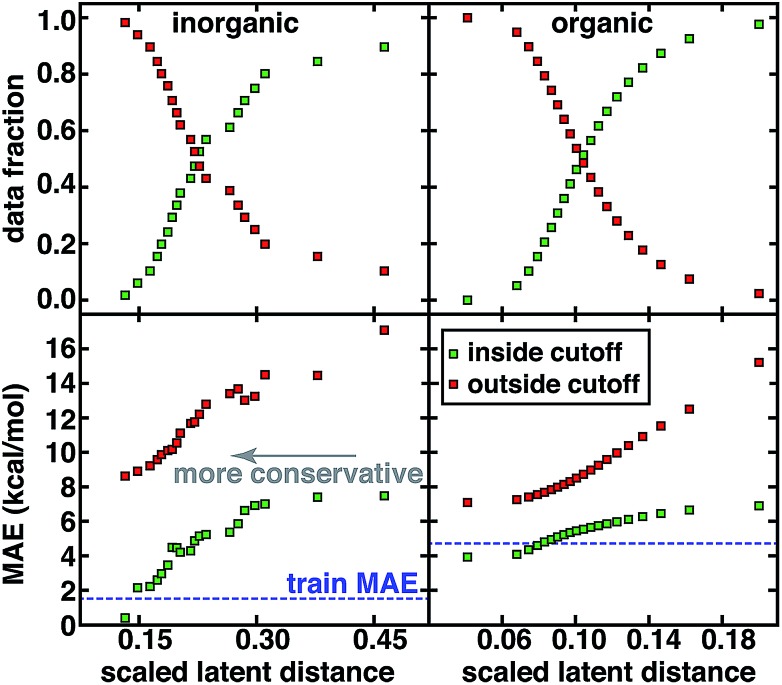
For both the CSD test set and the QM9 set, a systematic reduction in baseline error can be observed in a practical use case where the user adjusts the applied uncertainty metric to become more conservative (Fig. 5). Smooth reductions in MAE on data inside the uncertainty cutoffs can be achieved across a wide range of latent distance cutoffs, with errors nearly monotonically approaching the training data MAE, which may be recognized as a qualitative lower bound on our test set error (Fig. 5). Combining all error metrics to choose the most conservative result does not improve upon the single latent space distance metric (ESI Fig. S23†). PCA or uniform manifold approximation and projection (UMAP)87 analysis of the latent space distance indicates that a large number of the latent space dimensions are needed for error estimation (ESI Fig. S24 and Table S10†). For either data set, at the point on which half of all possible predictions are made, predicted data MAE is less than half of that for the excluded points (Fig. 5).
Fig. 5. MAE for predicted points (inside cutoff, green squares) and those not predicted (outside cutoff, orange squares) compared to the training data MAE (blue horizontal dashed line) along with data fraction in each set for the inorganic CSD test set (left) and organic QM9 set (right). The most distant point in the test set is scaled to have a latent distance of 1.0 for comparison across data sets but the x-axis range is then truncated to focus on the range of latent distance cutoffs that affect most of the data.
The latent distance also shows promise for application in active learning, where a model is trained iteratively by acquiring data in regions of high model uncertainty. To mimic such an application in the context of inorganic chemistry, we returned to the CSD data set and identified the 10 least confident points based on the distance in latent space, retrained the ANN using the same protocol, and re-evaluated model MAE (ESI Table S11†). Incorporating these data points during retraining reduced model errors from 8.6 to 7.1 kcal mol–1, whereas simply removing these points only reduced model MAE to 7.7 kcal mol–1 (ESI Table S11†). This effect is particularly significant considering the relatively small change in the number of data points (i.e., 10 added to 1901 or 0.5%) and an even larger reduction in root mean square error is observed (ESI Table S11†). When compared to an ensemble or mc-dropout cutoff, selection of retraining points based on latent space distance results in the largest reduction in model MAE while also simultaneously only requiring a single model retraining (ESI Table S11†).
Although we have focused on applications in chemical discovery with fully connected neural networks, application to other network architectures is straightforward. We trained convolutional neural networks for image classification tasks on two standard benchmarks, MNIST88 and Fashion-MNIST.89 Incorrectly classified images are observed at higher latent distances in both cases (ESI Text S3, Table S12, and Fig. S25†).
3. Conclusions
We have demonstrated on two diverse chemical data sets that the distance in the latent space of a neural network model provides a measure of model confidence that out-performs the best established metrics (i.e., ensembles) at no additional cost beyond single model training. The distance in latent space provides an improved approach to separating low- and high-confidence points, maximizing the number of retained points for prediction at low error to enable extrapolative application of machine learning models. We introduced a technique to calibrate latent distances that required only a small fraction of out-of-sample data, enabling conversion of this distance-based metric to error estimates in the units of the predicted property. In doing so, >90% of model errors were bounded within 2 std. dev. of latent distance estimates, in significant improvement beyond typically over-confident ensemble estimates. Like ensembles or mc-dropout, the latent space distance could still be challenged by unstable models, such as those trained on highly discontinuous properties. The latent space distance metric is general beyond the examples demonstrated here and is expected to be particularly useful in complex architectures that are normally time-consuming and difficult to train or in active learning approaches where rapid, iterative model retraining may be needed.
4. Computational Details
Neural networks were trained for this work with hyperparameters selected using Hyperopt90 followed by manual fine-tuning in Keras91 with the Tensorflow92 backend (ESI Fig. S17, Tables S5 and S13†). Model weights are provided in the ESI.† The ΔEH-L energy evaluation protocol for inorganic chemistry training data and the curated CSD77 test set used molSimplify8,11 to automate hybrid (i.e., B3LYP80–82) DFT calculations, with more details provided in ESI Text S2.† For the organic chemistry test, the QM9 atomization energy data set was obtained from the literature.33 In all cases, we normalized the representations and properties to make the training data have zero mean and unit variance. For calculating ensemble properties, we employed 10 sub-models trained on 10-fold cross-validation splits of the training data. For mc-dropout, we used the same 8.25% dropout as in training with 100 realizations, and we employed maximum likelihood to optimize the baseline uncertainty parameter, τ (ESI Text S1 and Table S2†). We did not apply mc-dropout to the organic test case because it has not been developed for residual-connectivity networks. For feature space distance, we measured Euclidean distance in the normalized feature space (e.g., RAC-155 (ref. 7)) directly. Featurizations of relevant complexes are provided in the ESI.† For latent distances, we used the latent space after the last hidden layer, which has the dimensionality of the model (i.e., 200 for spin splitting, 120 for the organic model).
Conflicts of interest
The authors declare no competing financial interest.
Supplementary Material
Acknowledgments
The authors acknowledge primary support by DARPA grant D18AP00039 for the generation of the latent space uncertainty metric (for C. D., A. N., and J. P. J). Inorganic complex data set construction (for T. Y.) was supported by the Office of Naval Research under grant number N00014-18-1-2434. This work was also supported in part by an AAAS Marion Milligan Mason Award. H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund. The authors thank Adam H. Steeves for providing a critical reading of the manuscript.
Footnotes
†Electronic supplementary information (ESI) available: Information about ensembles and mc-dropout procedure, information about DFT methods, information about training ligands and structures, information about CSD test cases, PCA decay plots and model performance information for inorganic dataset, comparison between single ANN and ensemble predictions and distribution of CSD errors, error distributions with different distance metrics and numbers of neighbors, correlation between errors and uncertainty metrics, maximum and average retained inorganic errors as function of uncertain metrics, CSD codes used to calibrate latent distance model, variation in uncertainty model calibration parameters for CSD data, type I error rates and with retained errors, architecture and hyperparameters used for QM9 prediction task, performance results for different architectures on QM9 prediction task, variation in QM9 performance with test/train split, performance and error distribution for QM9 for single ANN and ensembles, correlation between QM9 errors and uncertainty metrics, retained mean QM9 errors with different uncertainty metrics, variation in uncertainty model calibration parameters for QM9 data, distribution of predicted and actual errors for QM9 data, results of active learning experiment, hyperparameters for inorganic ANN (PDF). Summary DFT results and information for training and CSD data; model predictions, errors and uncertainties for all tests; DFT-optimized geometries of training and CSD data; model weights, architectures and scaling data for inorganic and QM9 ANNs (ZIP). See DOI: 10.1039/c9sc02298h
References
- Zhuo Y., Mansouri Tehrani A., Brgoch J. J. Phys. Chem. Lett. 2018;9:1668–1673. doi: 10.1021/acs.jpclett.8b00124. [DOI] [PubMed] [Google Scholar]
- De S., Bartok A. P., Csanyi G., Ceriotti M. Phys. Chem. Chem. Phys. 2016;18:13754–13769. doi: 10.1039/c6cp00415f. [DOI] [PubMed] [Google Scholar]
- Ward L., Agrawal A., Choudhary A., Wolverton C. npj Comput. Mater. 2016;2:16028. [Google Scholar]
- Pilania G., Wang C., Jiang X., Rajasekaran S., Ramprasad R. Sci. Rep. 2013;3:2810. doi: 10.1038/srep02810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer B., Sawatlon B., Heinen S., von Lilienfeld O. A., Corminboeuf C. Chem. Sci. 2018;9:7069–7077. doi: 10.1039/c8sc01949e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X., Li Z., Achenie L. E. K., Xin H. J. Phys. Chem. Lett. 2015;6:3528–3533. doi: 10.1021/acs.jpclett.5b01660. [DOI] [PubMed] [Google Scholar]
- Janet J. P., Kulik H. J. J. Phys. Chem. A. 2017;121:8939–8954. doi: 10.1021/acs.jpca.7b08750. [DOI] [PubMed] [Google Scholar]
- Nandy A., Duan C., Janet J. P., Gugler S., Kulik H. J. Ind. Eng. Chem. Res. 2018;57:13973–13986. [Google Scholar]
- Curtarolo S., Setyawan W., Hart G. L., Jahnatek M., Chepulskii R. V., Taylor R. H., Wang S., Xue J., Yang K., Levy O. Comput. Mater. Sci. 2012;58:218–226. [Google Scholar]
- Ong S. P., Richards W. D., Jain A., Hautier G., Kocher M., Cholia S., Gunter D., Chevrier V. L., Persson K. A., Ceder G. Comput. Mater. Sci. 2013;68:314–319. [Google Scholar]
- Ioannidis E. I., Gani T. Z. H., Kulik H. J. J. Comput. Chem. 2016;37:2106–2117. doi: 10.1002/jcc.24437. [DOI] [PubMed] [Google Scholar]
- O'Boyle N. M., Banck M., James C. A., Morley C., Vandermeersch T., Hutchison G. R. J. Cheminf. 2011;3:33. doi: 10.1186/1758-2946-3-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez T. J. Acc. Chem. Res. 2017;50:652–656. doi: 10.1021/acs.accounts.7b00010. [DOI] [PubMed] [Google Scholar]
- Caruthers J., Lauterbach J. A., Thomson K., Venkatasubramanian V., Snively C., Bhan A., Katare S., Oskarsdottir G. J. Catal. 2003;216:98–109. [Google Scholar]
- Katare S., Caruthers J. M., Delgass W. N., Venkatasubramanian V. Ind. Eng. Chem. Res. 2004;43:3484–3512. [Google Scholar]
- Corma A., Díaz-Cabanas M. J., Moliner M., Martínez C. J. Catal. 2006;241:312–318. [Google Scholar]
- Yao K., Herr J. E., Toth D. W., Mckintyre R., Parkhill J. Chem. Sci. 2018;9:2261–2269. doi: 10.1039/c7sc04934j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behler J. J. Chem. Phys. 2016;145:170901. doi: 10.1063/1.4966192. [DOI] [PubMed] [Google Scholar]
- Smith J. S., Isayev O., Roitberg A. E. Chem. Sci. 2017;8:3192–3203. doi: 10.1039/c6sc05720a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Han J., Wang H., Car R., Weinan E. Phys. Rev. Lett. 2018;120:143001. doi: 10.1103/PhysRevLett.120.143001. [DOI] [PubMed] [Google Scholar]
- Chmiela S., Tkatchenko A., Sauceda H. E., Poltavsky I., Schütt K. T., Müller K.-R. Sci. Adv. 2017;3:e1603015. doi: 10.1126/sciadv.1603015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faber F. A., Hutchison L., Huang B., Gilmer J., Schoenholz S. S., Dahl G. E., Vinyals O., Kearnes S., Riley P. F., Von Lilienfeld O. A. J. Chem. Theory Comput. 2017;13:5255–5264. doi: 10.1021/acs.jctc.7b00577. [DOI] [PubMed] [Google Scholar]
- Goldsmith B. R., Esterhuizen J., Liu J. X., Bartel C. J., Sutton C. AIChE J. 2018;64:2311–2323. [Google Scholar]
- Kitchin J. R. Nat. Catal. 2018;1:230. [Google Scholar]
- Janet J. P., Liu F., Nandy A., Duan C., Yang T., Lin S. and Kulik H. J., Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry, Inorganic Chemistry, 2019, ASAP. [DOI] [PubMed] [Google Scholar]
- Lu S., Zhou Q., Ouyang Y., Guo Y., Li Q., Wang J. Nat. Commun. 2018;9:3405. doi: 10.1038/s41467-018-05761-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan R., Liu Z., Balachandran P. V., Xue D., Zhou Y., Ding X., Sun J., Xue D., Lookman T. Adv. Mater. 2018;30:1702884. doi: 10.1002/adma.201702884. [DOI] [PubMed] [Google Scholar]
- Meredig B., Antono E., Church C., Hutchinson M., Ling J., Paradiso S., Blaiszik B., Foster I., Gibbons B., Hattrick-Simpers J. Mol. Syst. Des. Eng. 2018;3:819–825. [Google Scholar]
- Ren F., Ward L., Williams T., Laws K. J., Wolverton C., Hattrick-Simpers J., Mehta A. Sci. Adv. 2018;4:eaaq1566. doi: 10.1126/sciadv.aaq1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Lengeling B., Aspuru-Guzik A. Science. 2018;361:360. doi: 10.1126/science.aat2663. [DOI] [PubMed] [Google Scholar]
- He Y., Cubuk E. D., Allendorf M. D., Reed E. J. J. Phys. Chem. Lett. 2018;9:4562–4569. doi: 10.1021/acs.jpclett.8b01707. [DOI] [PubMed] [Google Scholar]
- Kailkhura B., Gallagher B., Kim S., Hiszpanski A. and Yong-Jin Han T., Reliable and Explainable Machine Learning Methods for Accelerated Material Discovery, arXiv:1901.02717, 2019.
- Ramakrishnan R., Dral P. O., Rupp M., Von Lilienfeld O. A. Sci. Data. 2014;1:140022. doi: 10.1038/sdata.2014.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. S., Isayev O., Roitberg A. E. Sci. Data. 2017;4:170193. doi: 10.1038/sdata.2017.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. S., Nebgen B., Lubbers N., Isayev O., Roitberg A. E. J. Chem. Phys. 2018;148:241733. doi: 10.1063/1.5023802. [DOI] [PubMed] [Google Scholar]
- Butler K. T., Davies D. W., Cartwright H., Isayev O., Walsh A. Nature. 2018;559:547. doi: 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
- Simm G. N., Reiher M. J. Chem. Theory Comput. 2018;14:5238–5248. doi: 10.1021/acs.jctc.8b00504. [DOI] [PubMed] [Google Scholar]
- Ulissi Z. W., Medford A. J., Bligaard T., Nørskov J. K. Nat. Commun. 2017;8:14621. doi: 10.1038/ncomms14621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musil F., Willatt M. J., Langovoy M. A., Ceriotti M. J. Chem. Theory Comput. 2019;15:906–915. doi: 10.1021/acs.jctc.8b00959. [DOI] [PubMed] [Google Scholar]
- Peterson A. A., Christensen R., Khorshidi A. Phys. Chem. Chem. Phys. 2017;19:10978–10985. doi: 10.1039/c7cp00375g. [DOI] [PubMed] [Google Scholar]
- Liu R., Wallqvist A. J. Chem. Inf. Model. 2019;59:181–189. doi: 10.1021/acs.jcim.8b00597. [DOI] [PubMed] [Google Scholar]
- Cortés-Ciriano I., Bender A. J. Chem. Inf. Model. 2018;59:1269–1281. doi: 10.1021/acs.jcim.8b00542. [DOI] [PubMed] [Google Scholar]
- Morais C. L. M., Lima K. M. G., Martin F. L. Anal. Chim. Acta. 2018;1063:40–46. doi: 10.1016/j.aca.2018.09.022. [DOI] [PubMed] [Google Scholar]
- Huang G., Li Y., Pleiss G., Liu Z., Hopcroft J. E. and Weinberger K. Q., Snapshot Ensembles: Train 1, Get M for Free, eprint arXiv:1704.00109, 2017.
- Schütt K., Kindermans P.-J., Felix H. E. S., Chmiela S., Tkatchenko A. and Müller K.-R., SchNet: A Continuous-Filter Convolutional Neural Network for Modeling Quantum Interactions, in Advances in Neural Information Processing Systems, 2017, pp. 991–1001. [Google Scholar]
- Schütt K. T., Sauceda H. E., Kindermans P.-J., Tkatchenko A., Müller K.-R. J. Chem. Phys. 2018;148:241722. doi: 10.1063/1.5019779. [DOI] [PubMed] [Google Scholar]
- Schütt K. T., Arbabzadah F., Chmiela S., Müller K. R., Tkatchenko A. Nat. Commun. 2017;8:13890. doi: 10.1038/ncomms13890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segler M. H., Kogej T., Tyrchan C., Waller M. P. ACS Cent. Sci. 2017;4:120–131. doi: 10.1021/acscentsci.7b00512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Maaten L., Hinton G. J. Mach. Learn. Res. 2008;9:2579–2605. [Google Scholar]
- Gal Y. and Ghahramani Z., in Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning, international conference on machine learning, 2016, pp. 1050–1059. [Google Scholar]
- Neal R. M., Bayesian Learning for Neural Networks, Springer Science & Business Media, 2012, vol. 118. [Google Scholar]
- Liu R., Glover K. P., Feasel M. G., Wallqvist A. J. Chem. Inf. Model. 2018;58:1561–1575. doi: 10.1021/acs.jcim.8b00114. [DOI] [PubMed] [Google Scholar]
- Duvenaud D. K., Maclaurin D., Iparraguirre J., Gömez-Bombarell R., Hirzel T., Aspuru-Guzik A., Adams R. P. Adv. Neural Inf. Process. Syst. 2015:2215–2223. [Google Scholar]
- Gilmer J., Schoenholz S. S., Riley P. F., Vinyals O. and Dahl G. E., Neural Message Passing for Quantum Chemistry, arXiv preprint arXiv:1704.01212, 2017.
- Gómez-Bombarelli R., Wei J. N., Duvenaud D., Hernández-Lobato J. M., Sánchez-Lengeling B., Sheberla D., Aguilera-Iparraguirre J., Hirzel T. D., Adams R. P., Aspuru-Guzik A. ACS Cent. Sci. 2018;4:268–276. doi: 10.1021/acscentsci.7b00572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iovanac N. C., Savoie B. M. J. Phys. Chem. A. 2019;123:4295–4302. doi: 10.1021/acs.jpca.9b01398. [DOI] [PubMed] [Google Scholar]
- Larsen A. H., Mortensen J. J., Blomqvist J., Castelli I. E., Christensen R., Dułak M., Friis J., Groves M. N., Hammer B., Hargus C., Hermes E. D., Jennings P. C., Jensen P. B., Kermode J., Kitchin J. R., Kolsbjerg E. L., Kubal J., Kaasbjerg K., Lysgaard S., Maronsson J. B., Maxson T., Olsen T., Pastewka L., Peterson A., Rostgaard C., Schiøtz J., Schütt O., Strange M., Thygesen K. S., Vegge T., Vilhelmsen L., Walter M., Zeng Z., Jacobsen K. W. J. Phys.: Condens. Matter. 2017;29:273002. doi: 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
- Metzen J. H., Genewein T., Fischer V. and Bischoff B., On Detecting Adversarial Perturbations, in 5th International Conference on Learning Representations, ICLR, 2017. [Google Scholar]
- Gu S. and Rigazio L., Towards Deep Neural Network Architectures Robust to Adversarial Examples, eprint arXiv:1412.5068, 2014.
- Zhou C. and Paffenroth R. C., Anomaly Detection with Robust Deep Autoencoders, in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, Halifax, NS, Canada, 2017, pp. 665–674. [Google Scholar]
- Schlegl T., Seeböck P., Waldstein S. M., Schmidt-Erfurth U. and Langs G., in Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery, Information Processing in Medical Imaging, Springer International Publishing, 2017, pp. 146–157. [Google Scholar]
- Jiang H., Kim B., Guan M. Y. and Gupta M. R., To Trust or Not to Trust a Classifier, 2018, pp. 5546–5557, arxiv:1805.11783. [Google Scholar]
- Papernot N. and McDaniel P. D., Deep K-Nearest Neighbors: Towards Confident, Interpretable and Robust Deep Learning, arXiv:1803.04765.
- Chen B., Carvalho W., Baracaldo N., Ludwig H., Edwards B., Lee T., Molloy I. and Srivastava B., Detecting Backdoor Attacks on Deep Neural Networks by Activation Clustering, eprint arXiv:1811.03728, 2018.
- Lubbers N., Smith J. S., Barros K. J. Chem. Phys. 2018;148:241715. doi: 10.1063/1.5011181. [DOI] [PubMed] [Google Scholar]
- Gomes J., Ramsundar B., Feinberg E. N. and Pande V. S., Atomic convolutional networks for predicting protein-ligand binding affinity, 2017, arXiv preprint arXiv:1703.10603.
- Wu Z. Q., Ramsundar B., Feinberg E. N., Gomes J., Geniesse C., Pappu A. S., Leswing K., Pande V. Chem. Sci. 2018;9:513–530. doi: 10.1039/c7sc02664a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coley C. W., Barzilay R., Green W. H., Jaakkola T. S., Jensen K. F. J. Chem. Inf. Model. 2017;57:1757–1772. doi: 10.1021/acs.jcim.6b00601. [DOI] [PubMed] [Google Scholar]
- Xie T., Grossman J. C. J. Chem. Phys. 2018;149:174111. doi: 10.1063/1.5047803. [DOI] [PubMed] [Google Scholar]
- Collins C. R., Gordon G. J., von Lilienfeld O. A., Yaron D. J. J. Chem. Phys. 2018;148:241718. doi: 10.1063/1.5020441. [DOI] [PubMed] [Google Scholar]
- Huang B., von Lilienfeld O. A. J. Chem. Phys. 2016;145:161102. doi: 10.1063/1.4964627. [DOI] [PubMed] [Google Scholar]
- Yao K., Herr J. E., Brown S. N., Parkhill J. J. Phys. Chem. Lett. 2017;8:2689–2694. doi: 10.1021/acs.jpclett.7b01072. [DOI] [PubMed] [Google Scholar]
- Hansen K., Biegler F., Ramakrishnan R., Pronobis W. J. Phys. Chem. Lett. 2015;6:2326–2331. doi: 10.1021/acs.jpclett.5b00831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gubaev K., Podryabinkin E. V., Shapeev A. V. J. Chem. Phys. 2018;148:241727. doi: 10.1063/1.5005095. [DOI] [PubMed] [Google Scholar]
- Bjørn Jørgensen P., Wedel Jacobsen K. and Schmidt M. N., Neural Message Passing with Edge Updates for Predicting Properties of Molecules and Materials, arXiv e-prints, 2018.
- Duan C., Janet J. P., Liu F., Nandy A., Kulik H. J. J. Chem. Theory Comput. 2019;15:2331–2345. doi: 10.1021/acs.jctc.9b00057. [DOI] [PubMed] [Google Scholar]
- Groom C. R., Bruno I. J., Lightfoot M. P., Ward S. C. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016;72:171–179. doi: 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Mach. Learn. 1996;24:123–140. [Google Scholar]
- Aggarwal C. C., Hinneburg A. and Keim D. A., in On the Surprising Behavior of Distance Metrics in High Dimensional Space, Database Theory—ICDT 2001, ed. J. Van den Bussche and V. Vianu, Springer Berlin Heidelberg, Berlin, Heidelberg, 2001, pp. 420–434. [Google Scholar]
- Lee C., Yang W., Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- Becke A. D. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- Stephens P. J., Devlin F. J., Chabalowski C. F., Frisch M. J. J. Phys. Chem. 1994;98:11623–11627. [Google Scholar]
- Ditchfield R., Hehre W. J., Pople J. A. J. Chem. Phys. 1971;54:724. [Google Scholar]
- Broto P., Moreau G., Vandycke C. Eur. J. Med. Chem. 1984;19:71–78. [Google Scholar]
- Virshup A. M., Contreras-García J., Wipf P., Yang W., Beratan D. N. J. Am. Chem. Soc. 2013;135:7296–7303. doi: 10.1021/ja401184g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K., Zhang X., Ren S. and Sun J., Deep Residual Learning for Image Recognition, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]
- McInnes L. and Healy J., UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv:1802.03426.
- Lecun Y., Bottou L., Bengio Y., Haffner P. Proc. IEEE. 1998;86:2278–2324. [Google Scholar]
- Xiao H., Rasul K. and Vollgraf R., Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms, arXiv:1708.07747.
- Bergstra J. C., Yamins D. and Cox D. D., Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms, Proceedings of the 12th Python in science conference, 2013, pp. 13–20. [Google Scholar]
- Keras, https://keras.io/, accessed Jan 17, 2019.
- Tensorflow, https://www.tensorflow.org, accessed Jan 17, 2019.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.