Differentially Private Distributed Online Learning

Abstract

In the big data era, the generation of data presents some new characteristics, including wide distribution, high velocity, high dimensionality, and privacy concern. To address these challenges for big data analytics, we develop a privacy-preserving distributed online learning framework on the data collected from distributed data sources. Specifically, each node (i.e., data source) has the capacity of learning a model from its local dataset, and exchanges intermediate parameters with a random part of their own neighboring (logically connected) nodes. Hence, the topology of the communications in our distributed computing framework is unfixed in practice. As online learning always performs on the sensitive data, we introduce the notion of differential privacy (DP) into our distributed online learning algorithm (DOLA) to protect the data privacy during the learning, which prevents an adversary from inferring any significant sensitive information. Our model is of general value for big data analytics in the distributed setting, because it can provide rigorous and scalable privacy proof and have much less computational complexity when compared to classic schemes, e.g., secure multiparty computation (SMC). To tackle high-dimensional incoming data entries, we study a sparse version of the DOLA with novel DP techniques to save the computing resources and improve the utility. Furthermore, we present two modified private DOLAs to meet the need of practical applications. One is to convert the DOLA to distributed stochastic optimization in an offline setting, the other is to use the mini-batches approach to reduce the amount of the perturbation noise and improve the utility. We conduct experiments on real datasets in a configured distributed platform. Numerical experiment results validate the feasibility of our private DOLAs.

1. INTRODUCTION

WITH the fast development of the Internet, the data from many application domains are in large scale and distributed. The centralized processing is no longer capable of efficiently computing the internet data nowadays. Moreover, not only the scale of data becomes enormous, but also the velocity of data generating increases dramatically. Hence, the data should be processed in real time (online) to satisfy the need of fast responses to the users. Besides the wide distribution and high velocity, a great deal of data involve personal information which requires privacy protection. Any data mining without guaranteeing the secure computing and data privacy is never permitted. Therefore, a privacy-preserving mechanism needs to be used in the distributed setting. In a word, we intend to study a private and efficient distributed framework for big data related applications. To stimulate our ideas, we provide two reality applications as follows:

Disease prevention and treatment.

Hospitals have a large number of patient cases. A data analysis of these cases helps the doctors to make accurate diagnosis and propose early treatments. However, the information about the patients is extremely private. A hasty survey may reveal sensitive information about the patients. Hence, each hospital cannot share its patient cases with other research institutions and canonicity hospitals. An important challenge is how to conduct medical studies separately, while the privacy of patients are preserved.

Online ads recommendation.

A large number of people engage in online activities by Apps and websites. Advertising revenue is the main part of some IT companies, such as Facebook, Google etc. Such Internet companies recommend personalized advertisements to each user. Since the preferences of the users change over time, the sample data of the users are updated frequently. As a result, they need to handle petabytes of data every day. For solving the problem, some distributed computing systems, e.g., Hadoop and Spark, have been used to process a large scale of data for years by Internet companies. Hadoop and Spark are of the master-slave distributed system, where the raw data are frequently transmitted between the disk and memory. They cost much resources and time. Against this kind of waste, we design an algorithm to optimize the distributed functions by sharing the intermediate parameters. It is also necessary to apply privacy mechanisms to the data transmission in the distributed system.

To solve the above private distributed problems, some methods have been studied. For instance, secure multiparty computation is a preferable method to optimize a function over distributed data resources while keeping these data private. SMC has been studied in many applications (e.g., [1], [2], [3], [4]). Although SMC can solve the distributed computing privately, it costs a large amount of computation resources. As a state-of-the-art privacy notion, differential privacy [5], [6] has been used in some distributed optimization models (e.g., [7], [8], [9]). DP can protect a learning algorithm by using a small amount of noise (generated due to a Gaussian distribution or some else distributions). However, achieving the trade-off between the privacy and utility of a DP-algorithm remains a problem. In this paper, we will propose a much faster and more private distributed learning algorithm, which can be also used in more applications such as high-dimensional data optimizations.

First, we present the distributed online learning model and privacy concerns. Specifically, for the distributed setting, we assume all nodes (i.e., data sources) have the independent online learning ability, which updates the local parameter by one (or a small batch of) data point from the local data source. To achieve the convergence of the DOLA, all nodes must exchange their learnable intermediate parameters to their own neighboring nodes. This approach can save much communication cost. The design of the communication matrices among the nodes poses a great challenge. Our distributed online learning model differs from traditional distributed computing systems (e.g., Hadoop and Spark) that contain a master node and many slave nodes. The master node is in charge of the “MapReduce” scheduling and the slave nodes are responsible for computing data as requested. This kind of distributed system needs much communication cost and easily leads to privacy breaches as a result of transmitting all the computed data to the master. For the privacy mechanism, we present a differentially private framework for the distributed online learning with the sensitive data. Differential privacy is a popular privacy mechanism based on noise perturbation and has been used in a few machine learning applications [10], [11], [12]. In a nutshell, a differentially private machine learning algorithm guarantees its output not to be much different whenever one individual is in the training set or not. Thus, an adversary cannot infer any meaningful information from the output of the algorithm. DP differs from traditional encryption approaches and preserves the privacy of the large and distributed datasets by adding a small amount of noise. How we apply DP to the distributed online learning is an another challenge.

Furthermore, some online data are high-dimensional. For instance, a single person has a variety of social activities in a social network, so the corresponding data vector of his/her social information may be long and complex. When a data miner studies the consumer behavior about one interest, some of the information in the vector may not be relevant. A person’s height and age may not contribute to predicting his taste. Thus, the high-dimensional data could enhance the computational complexity of algorithms and weaken the utility of online learning models. To deal with this problem, we introduce a sparse solution and test it on real datasets. So far, there have been two classical effective methods for sparse online learning [13], [14], [15]. The first method (e.g., [16]) introduced sparsity in the weights of online learning algorithms via truncated gradient. The second method followed the dual averaging algorithm [17]. In this paper, we will exploit online mirror descent [18] and Lasso-L₁ norm [19] to make the learnable parameter sparse for achieving a better learning performance.

Finally, we propose two extensions of the private DOLA for some practice applications. The first extension is that our differentially private DOLA can be converted to the distributed stochastic optimization. Specifically, we show that the regret bound of our private DOLA can be used to obtain good convergence rates for the distributed stochastic optimization algorithm. This application contributes to the offline learning related optimization problem when the data stream is coming in real time. The second one is that we allow a slack in the number of samples computed in each iteration of online learning. Each iteration can process more than one data instant, which is called the mini-batch updates [20], [21]. By using mini-batches in the private DOLA, we not only process the high-velocity data stream much faster, but also reduce the amount of perturbation noise while the algorithm guarantees the same DP level.

Following are the main contributions of this paper:

• We present a distributed framework for online learning. We respectively obtain the classical regret bounds $O(\sqrt{T})$ [22] and O(log T) [23] for convex and strongly convex objective functions for DOLA, which indicates that the utility of our private DOLA achieves almost the same performance with the centralized online learning algorithm.

• We provide ϵ and (ϵ, δ)-differential privacy guarantees for the DOLA. Interestingly, the private regret bounds have the same order of $O(\sqrt{T})$ and O(log T) with the non-private ones, which indicates that guaranteeing differential privacy in the DOLA does not significantly harm the original performance.

• Facing the high-dimensional data, we propose a differentially private sparse DOLA and achieve an $O(\sqrt{T})$ regret bound, which shows that our private sparse DOLA works well.

• We convert our differentially private DOLA to private distributed stochastic optimization and obtain good convergence rates, i.e., $O\left(\frac{1}{\sqrt{T}}\right)$ and $O\left(\frac{\log T}{T}\right)$

• We use mini-batches to improve the performance of our differentially private DOLA. The proposed algorithms using mini-batches guarantees the same level of privacy with less noise, which naturally leads to a better performance than one-batch private DOLA.

The rest of the paper is organized as follows. Section 2 discusses some related works. Section 3 presents the problem statement for our work. We propose ϵ and (ϵ, δ)-differentially private DOLA in Section 4. Section 5 studies the private sparse DOLA aimed at processing the high-dimensional data. In Section 6, we make extensions for our private DOLAs. Section 6.1 discusses the application of the private DOLA to stochastic optimization and Section 6.2 uses mini-batches to improve the privacy and utility performance of our private DOLA. In Section 7, we present simulation results of the proposed algorithms. Section 8 concludes the paper. Some lengthy proofs of this paper are left in the supplement, which can be found on the Computer Society Digital Library at http://doi.ieeecomputersociety.org/10.1109/TKDE.2018.2794384.

2. RELATED WORK

Jain et al. [11] studied the differentially private centralized online learning. They provided a generic differentially private framework for online algorithms. Using their generic framework, Implicit Gradient Descent and Generalized Infinitesimal Gradient Ascent could be transformed into differentially private online learning algorithms. Their work motivates our study on the differentially private online learning in distributed scenarios.

Recently, growing research effort has been devoted to the distributed online learning. Yan et al. [24] has proposed a DOLA to handle the decentralized data. A fixed network topology was used to conduct the communications among the learners in their system. Further, they studied the privacy-preserving problem, and showed that the non-fully connected communication network has intrinsic privacy-preserving properties. Worse than differential privacy, their privacy-preserving method cannot protect the privacy of all learners absolutely. Besides, Huang et al. [7] is closely related to our work. They presented a differentially private distributed optimization algorithm.

The method to solve distributed online learning was pioneered in distributed optimization (DO). Hazan has studied online convex optimization in his book [25]. They proposed that the framework of convex online learning is closely tied to the statistical learning theory and convex optimization. Duchi et al. [26] developed an efficient algorithm for DO based on dual averaging of subgradients. Nedic and Ozdaglar [27] considered a subgradient method for distributed convex optimization, where the functions are convex but not necessarily smooth. They demonstrated that a time-variant communication could ensure the convergence of the DO algorithm. Ram et al. [28] analyzed the influence of stochastic subgradient errors on distributed convex optimization in a time-variant network topology. All these papers have made great contributions to DO, but they did not consider the privacy-preserving issue.

There has been much research effort being devoted to how differential privacy can be used in existing learning algorithms. For example, Chaudhuri et al. [10] presented the output perturbation and objective perturbation ideas about differential privacy in ERM classification. Rajkumar and Agarwal [8] extended the work of [10] to distributed multiparty classification. More importantly, they analyzed the sequential and parallel composability problems while the algorithm guaranteed ϵ-differential privacy. Bassily et al. [29] proposed more efficient algorithms and tighter error bounds for ERM classification on the basis of [10].

For a combination of SMC and DP, Goryczka and Xiong et al. [30] studied existing SMC solutions with differential privacy in distributed setting and compared the complexities and security characteristics of them.

3. PROBLEM STATEMENT

3.1. System Setting

Given a distributed network shown in Fig. 1, where m computing nodes are connected in a non-fully connected graph. Each node is only connected with its neighboring nodes, e.g., node i (the green one in Fig. 1) can communicate with nodes j, k and p, which are located in the light green circular region. The circular regions in Fig. 1 denote the maximum range that the nodes can reach. Note that the lines denoting the links have dotted and solid representations. The dotted line indicates that the link between the neighboring nodes does not work at this time. When this link is connected at one time, its dotted line becomes solid. In a nutshell, each node exchanges information with a random subset of its neighbors in one iteration. This pattern makes further efforts to reduce the communication cost and ensures that each node keeps enough information exchanging with neighbors. Note that since our distributed setting does not consider the delays of the communications, the communication cost of our algorithm is not considered.

Fig. 1.

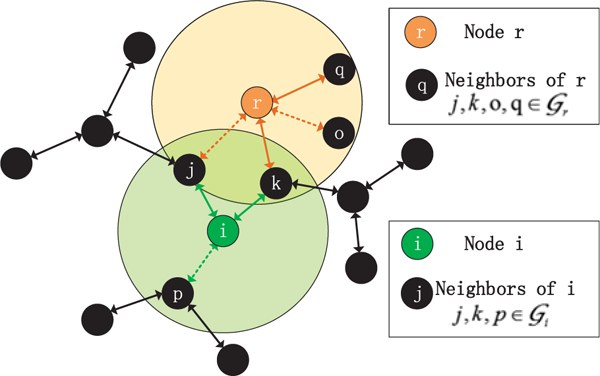
Distributed network where nodes only can communicate with neighbors (localized in their respective circular regions).

Our goal is to train all the nodes to be independent online classifiers fⁱ : $\mathcal{X}$ → $\mathcal{Y}$. For each single node, it receives the “question” $x_t^i$, taken from a convex set $\mathcal{X}$ and should give a prediction (an “answer”) denoted by $p_t^i$ to this question. To measure how “accurate” the prediction is, we compare it with the correct answer $y_t^i\in \mathcal{Y}$, and then compute the loss function $\mathcal{l}\left(w_t^i,x_t^i,y_t^i\right)(\text{e.g.,}\mathcal{l}\left(w_t^i,x_t^i,y_t^i\right)=\left|\langle w^i,x_t^i\rangle -y_t^i\right|)$. We let $f_t^i(w):=\mathcal{l}\left(w^i,x_t^i,y_t^i\right)$ to be a convex function. Different from the ERM optimization, one online node minimizes regret versus best single response in hindsight as follows:

$$Regret=\sum _{t=1}^T{f}_t^i\left(w_t^i,{\xi }_t^i\right)-\underset{w\in W}{\min }\sum _{t=1}^T{f}_t\left(w,{\xi }_t^i\right),$$ (1)

where ${\xi }_t^i$ denotes the sample $\left(x_t^i,y_t^i\right)$ received in the tth iteration, f is the loss function. After T iterations, the regret should be bounded, which indicates that the predictions are more accurate over time. In our distributed online learning, we need to redefine a new regret function.

Definition 1.

In our distributed online learning algorithm, we assume there are m learning nodes. Each node has the independent learning ability. Then, we define the regret of the algorithm as

$$R_D=\sum _{t=1}^T\sum _{i=1}^m{f}_t^i\left(w_t^j\right)-\underset{w\in W}{\min }\sum _{t=1}^T\sum _{i=1}^m{f}_t^i(w).$$ (2)

In a centralized online learning algorithm, N data points need T = N iterations to be finished, while the distributed algorithm can process m × N data points over the same time period. Note that R_D is computed with respect to an arbitrary node’s parameter $w_t^j$. This states that any node of the system can measure the regret of the whole system based on its local parameter (e.g., $w_t^j$), even though the node does not handle the data of other nodes.

In this paper, we bound R_D and use this regret bound to measure the utility of DOLA.

3.2. Distributed Online Learning Model

To solve the problem of minimizing (1), we exploit the distributed convex optimization under the following assumption on the dataset W and the cost function $f_t^i$.

Assumption 1.

The set W and the cost functions $f_t^i$ are such that

1. The set W is closed and convex subset of ${ℝ}^n$. Let $R\triangleq {\text{sup}}_{x,y\in W}\Vert x-y\Vert$ denote the diameter of W.

2. The cost functions $f_t^i$ are strongly convex with modulus λ ≥ 0. For all x, y ∈ W, we have

   $$\langle \nabla f_t^i(x),y-x\rangle \le f_t^i(y)-f_t^i(x)-\frac{\lambda }{2}\Vert y-x{\Vert }^2.$$ (3)
3. The (sub)gradients of $f_t^i$ are uniformly bounded, i.e., there exists L > 0, for all x ∈ W, we have

   $$\Vert \nabla f_t^i(x)\Vert \le L.$$ (4)

In Assumption 1: (1) guarantees that there exists an optimal solution in our algorithm; (2) and (3) help us analyze the convergence of our algorithm.

To achieve the convergence of DOLA, we specify that (i.e., Fig. 2) the ith node (i ∈ [1, m]) updates its local parameter $w_t^i$ based on its local dataset $\left\{\left(x_t^i,y_t^i\right)\in \mathcal{X}\times \mathcal{Y}\right\}$. Since the m nodes are distributed, each node exchanges the learnable parameter w_t with neighbors for a global optimal solution. In this paper, we use a time-variant matrix A_t to conduct the communications among nodes, which makes each node communicate with different subsets of their neighbors in different iterations. Each node first gets the exchanged parameters and computes the weighted average of them, then updates the parameter $w_{t^{\prime }}^i$ finally broadcasts the new learnable parameter to its neighbors.

Fig. 2.

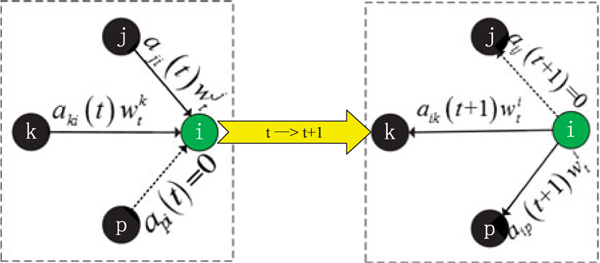
Process of iterations: one node first receives the exchanged parameters, then updates its local parameter and finally broadcasts the new parameter to neighbors.

To recall, the nodes communicate with neighbors based on the matrix A_t. Each node directly or indirectly influences other nodes. For a clear description, we denote the communication graph for a node t in tth iteration by

$${\mathcal{G}}_i(t)=\left\{(i,j):a_{ij}(t)>0\right\}.$$ (5)

In our algorithm, each node computes a weighted average [28] of the m nodes’ parameters. The weighted average should make each node have “equal” influence on other nodes after long iterations.

Besides basic assumptions for datasets and objective functions, how to conduct the communications among the distributed nodes is critical to solve the distributed convex optimization problem in our work. Since the nodes exchange information with neighbors while they update local parameters with subgradients, a time-variant m-by-m doubly stochastic matrix A_t is proposed to conduct the communications. It has a few properties: 1) all elements of A_t are non-negative and the sum of each row or column is one; 2) a_ij(t) > 0 means there exists a communication between the ith and the jth nodes in the tth iteration, while a_ij(t) = 0 means there is no communication between them; 3) there exists a constant η, 0 < η < 1, such that a_ij(t) > 0 implies that a_ij(t) > η.

Then, we make the following assumption on the properties of A_t.

Assumption 2.

For an arbitrary node t, there exists a minimal scalar η, 0 < η < 1, and a scalar N such that

1. $a_{ij}(t)>0\mathit{\text{for}}(i,j)\in C_G(t+1)$,

2. ${\sum }_{j=1}^m{a}_{ij}(t)=1$ and ${\sum }_{i=1}^m{a}_{ij}(t)=1$,

3. $a_{ij}(t)>0$ implies that $a_{ij}(t)\ge \eta$,

4. The graph ${\cup }_{k=1,\dots N}{\mathcal{G}}_i(t+k)$ is strongly connected for all k.

In Assumption 2: (1) and (2) state that each node computes a weighted average of the parameters shown in Algorithm 1; (3) ensures that the influences among the nodes are significant; (2) and (4) ensure that the m nodes are equally influential in a long run. Assumption 2 is crucial to minimize the regret bounds in distributed scenarios.

3.3. Adversary Model and Protection Limits

In recent years, many researchers have made great progress on machine learning and distributed computing. However, some malicious algorithms were proposed for competing the backward-deduction of the machine learning algorithm and inferring the input data by observing the outputs or the intermediate parameters. In order to prevent such “stealing” actions, we must protect every parameter of the algorithms which may be exposed.

In this section, we assume two attack means. The first one is that an adversary can invade any links of the nodes in our network and is free to get the parameters being exchanged between two nodes. In this setting, our algorithm can protect the privacy of all the nodes, since the adversary is not able to infer some sensitive information from the data with perturbation noise. The second one is that an adversary controls one of the nodes and is able to obtain all data in the local source and also can get the parameters from its neighboring nodes. In such a worst case, except for the invaded nodes, the privacy of all the other nodes can be protected. In a word, no matter what kinds of attack means our DP algorithms face, the privacy can be masked as long as the data is differentially private. Note that differential privacy stops the adversary from inferring sensitive information about the data, it cannot resist the invasion of database launched by malicious attackers.

3.4. Differential Privacy Model

Differential Privacy.

Dwork [5] proposed the definition of differential privacy for the first time. Differential privacy makes a data miner be able to release some statistic of its database without revealing sensitive information about a particular value itself. In this paper, we use differential privacy to protect the privacy of the nodes and give the following definition.

Definition 2.

Let $\mathcal{A}$ denote our differentially private DOLA. Let $\mathcal{X}=\langle x_1^i,x_2^i,\dots ,x_T^i\rangle$ be a sequence of questions taken from an arbitrary node’s local data source. Let $\mathcal{W}=\langle w_1^i,w_2^i,\dots ,w_T^i\rangle$ be a sequence of T outputs of the node and $\mathcal{W}=\mathcal{A}\left(\mathcal{X}\right)$. Then, our algorithm $\mathcal{A}$ is ϵ-differentially private if given any two adjacent question sequences $\mathcal{X}$ and $\mathcal{X}$′ that differ in one question entry, the following holds:

$$\mathrm{Pr}[\mathcal{A}(\mathcal{X})\in W]\le e^{ϵ}\mathrm{Pr}\left[\mathcal{A}\left({\mathcal{X}}^{\prime }\right)\in W\right].$$ (6)

This inequality guarantees that whether or not an individual participates in the database, it will not make any significant difference on the output of our algorithm, so the adversary is not able to gain useful information about the individual. Furthermore, $\mathcal{A}$ provides (ϵ, δ)-differential privacy if it satisfies

$$\mathrm{Pr}[\mathcal{A}(\mathcal{X})\in W]\le e^{ϵ}\mathrm{Pr}\left[\mathcal{A}\left({\mathcal{X}}^{\prime }\right)\in W\right]+\delta ,$$

which is a slightly weaker privacy guarantee.

Differential privacy aims at weakening the significantly difference between $\mathcal{A}$(X) and $\mathcal{A}$(X′) by adding random noise to the outputs of learning algorithms. Thus, to ensure differential privacy, we need to know that how “sensitive” the algorithm $\mathcal{A}$ is. Further, according to [5], the magnitude of the noise depends on the largest change that a single entry in data source could have on the output of Algorithm 1; this quantity is referred to as the sensitivity of the algorithm as formally defined below:

Definition 3 (Sensitivity).

Recall in Definition 1, for any $\mathcal{X}$ and $\mathcal{X}$′, which differ in exactly one entry, we define the sensitivity of Algorithm 1 in tth iteration as

$$\text{S}(t)=\underset{\mathcal{X},{\mathcal{X}}^{\prime }}{\sup }{\Vert \mathcal{A}(\mathcal{X})-\mathcal{A}\left({\mathcal{X}}^{\prime }\right)\Vert }_1.$$ (7)

The above norm is L₁-norm. According to the notion of sensitivity, we know that higher sensitivity leads to more noise if the algorithm guarantees the same level of privacy. By bounding the sensitivity S(t), we determine the magnitude of the random noise to guarantee differential privacy. We will provide the bound of S(t) in Lemma 1.

Algorithm 1.

ϵ-Differentially Private DOLA

1:	Input: $f_t^i(w):=\mathcal{l}\left(w,x_t^i,y_t^i\right),i\in [1,m]$ and $t\in [0,T]$; initial points $w_0^1,\dots ,w_0^m$; doubly stochastic matrix $A_t\text{=}\left(a_{ij}(t)\right)\in R^{m\times m}$; maximum iterations T.
2:	for $t=0,\dots ,T$ do
3:	for each node $i=1,\dots ,m$ do
4:	$b_t^i=\sum _{j=1}^m{a}_{ij}(t+1)\left(w_t^i+{\sigma }_t^i\right)$, where ${\sigma }_t^j$ is a Laplace noise vector in ${ℝ}^n$;
5:	$g_t^j\leftarrow \nabla f_t^i\left(b_t^i,{\xi }_t^i\right)$;
6:	$w_{t+1}^i=\text{P}\mathrm{ro}\left[b_t^i-{\alpha }_{t+1}\cdot g_t^i\right]$, where ${\sigma }_t^i~\mathit{Lap}(\mu )$;
	(Projection onto W)  ($Lap(\mu )$ defined in (11))
7:	broadcast the output $\left(w_{t+1}^i+{\sigma }_{t+1}^i\right)\text{to}\mathcal{G}{(t+1)}_i$;
8:	end for
9:	end for

4. DIFFERENTIALLY PRIVATE DOLA

In this section, we first present the ϵ-differentially private DOLA in Algorithm 1, and study the privacy and utility respectively in Sections 4.1 and 4.2. Then, we extend ϵ to (ϵ, δ)-differential privacy in Section 4.3. Handling the composition argument (see more details in [31]) problem of differential privacy, our ϵ-differentially private DOLA behaves different from the related work in [32]. The differences will be specifically described in this section. More importantly, we bound the regret of Algorithm 1 and analyze the tradeoff problem between the privacy and utility.

4.1. ϵ-Differential Privacy Concerns

Lemma 1.

Under Assumption 1, if the L₁-sensitivity of the algorithm is computed as (7), we obtain

$$\text{S}(t)\le 2{\alpha }_t\sqrt{n}L,$$ (8)

where n denotes the dimensionality of vectors and L is the bound of (sub)gradient (see (4)).

Proof.

Recall in Definition 1, $\mathcal{X}$ and $\mathcal{X}$′ are any two data vectors differing in one entry. $w_t^i$ is computed based on the data set $\mathcal{X}$ while $w_t^{i^{\prime }}$ is computed based on the data set $\mathcal{X}$′. Certainly, we have ${\Vert \mathcal{A}(\mathcal{X})-\mathcal{A}\left({\mathcal{X}}^{\prime }\right)\Vert }_1={\Vert w_t^i-w_t^{i^{\prime }}\Vert }_1$.

For datasets $\mathcal{X}$ and $\mathcal{X}$′ we have

$$w_t^i=\mathrm{Pro}\left[b_{t-1}^i-{\alpha }_t{g}_{t-1}^i\right]\text{and}{w}_t^{i^{\prime }}=\mathrm{Pro}\left[b_{t-1}^i-{\alpha }_t{g_{t-1}^i}^{\prime }\right].$$

Then, we have

$$\begin{array}{l}{\Vert w_t^i-w_t^{i^{\prime }}\Vert }_1={\Vert \mathrm{Pro}\left[b_{t-1}^i-{\alpha }_t{g}_{t-1}^i\right]-\mathrm{Pro}\left[b_{t-1}^i-{\alpha }_t{g_{t-1}^i}^{\prime }\right]\Vert }_1\\ \le {\Vert \left(b_{t-1}^i-{\alpha }_t{g}_{t-1}^i\right)-\left(b_{t-1}^i-{\alpha }_t{g_{t-1}^i}^{\prime }\right)\Vert }_1\\ ={\alpha }_t{\Vert g_{t-1}^i-{g_{t-1}^i}^{\prime }\Vert }_1\le {\alpha }_t\left({\Vert g_{t-1}^i\Vert }_1+{\Vert {g_{t-1}^i}^{\prime }\Vert }_1\right)\\ \le {\alpha }_t\sqrt{n}\left({\Vert g_{t-1}^i\Vert }_2+{\Vert {g_{t-1}^i}^{\prime }\Vert }_2\right)\le 2{\alpha }_t\sqrt{n}L.\end{array}$$ (9)

By Definition 3, we know

$$S(t)\le {\Vert w_t^i-w_t^{i^{\prime }}\Vert }_1.$$ (10)

Hence, combining (9) and (10), we obtain (8). □

We next determine the magnitude of the added random noise due to (8). In step 7 of Algorithm 1, we use s to denote the random noise. $\sigma \in {ℝ}^n$ is a Laplace random noise vector drawn independently according to the density function

$$Lap(x|\mu )=\frac{1}{2\mu }\exp \left(-\frac{\left|x\right|}{\mu }\right),$$ (11)

where μ = S(t)/ϵ and Lap(μ) denotes the Laplace distribution. (8) and (11) show that the magnitude of the added random noise depends on the sensitivity parameters: ϵ, the stepsize α_t, the dimensionality of vectors n, and the bounded subgradient L.

Lemma 2.

Under Assumption 1 and 2, at the tth iteration, the output of ith online learner in Algorithm 1, i.e., $\left(w_t^i+{\sigma }_t^i\right)$ is ϵ-differentially private.

Proof.

Let ${\tilde{w}}_t^i=w_t^i+{\sigma }_t^i$ and ${\tilde{w}}_t^{i^{\prime }}=w_t^{i^{\prime }}+{\sigma }_{t^{\prime }}^i$ then by the definition of differential privacy (see Definition 1), ${\tilde{w}}_t^i$ is ϵ-differentially private if

$$\mathrm{Pr}[{\tilde{w}}_t^i\in W]\le e^{ϵ}\mathrm{Pr}[{\tilde{w}}_t^{i^{\prime }}\in W].$$ (12)

For w ∈ W, we obtain

$$\begin{array}{l}\frac{\mathrm{Pr}\left({\tilde{w}}_t^i\right)}{\mathrm{Pr}\left({\tilde{w}}_t^{i^{\prime }}\right)}=\prod _{j=1}^n\left(\frac{\exp \left(-\frac{ϵ|w_t^i[j]-w[j]|}{S(t)}\right)}{\exp \left(-\frac{ϵ|w_t^{i^{\prime }}[j]-w[j\left]\right|}{S(t)}\right)}\right)\\ =\prod _{j=1}^n\exp \left(\frac{ϵ\left(\left|w_t^{i^{\prime }}[j]-w[j]\right|-\left|w_t^i[j]-w[j]\right|\right)}{S(t)}\right)\\ \le \prod _{j=1}^n\exp \left(\frac{ϵ\left|w_t^i{}^{\prime }[j]-w_t^i[j]\right|}{S(t)}\right)=\exp \left(\frac{ϵ{\Vert w_t^{i^{\prime }}-w_t^i\Vert }_1}{S(t)}\right)\\ \le \exp (ϵ),\end{array}$$ (13)

where the first inequality follows from the triangle inequality, and the last inequality follows from (10). □

Composition Theorem.

In Lemma 2, we provide ϵ-differential privacy for each iteration of Algorithm 1. Due to the composition theorem [11], [33], we know that the privacy level of Algorithm 1 will degrade after T-fold adaptive composition. Next, we will study how much privacy is still guaranteed after T iterations. As known, the worst privacy guarantee is at most the “sum” of the differential privacy guarantee of single one iteration.

Theorem 1 ([6], [31], [33]).

For ϵ, δ ≥ 0, the class of (ϵ, δ)-differentially private algorithms provide (Tϵ, Tδ)-differential privacy under T-fold adaptive composition.

The worst privacy happens when an adversary applies many queries to the same database. If our distributed learning algorithm runs in an offline way (i.e., each update depends on the gradients of the all data points over the T iterations), the offline algorithm suffers the “sum” of the differential privacy described in Theorem 1. Dwork et al. (2010) [33] demonstrated that if a slightly larger value of 8 is allowed for, one can have a significantly higher privacy level w.r.t ϵ.

Theorem 2 ([33]).

For ϵ, δ ≥ 0, the class of (ϵ, δ)-differentially private algorithms provide (ϵ^′, Tδ + δ′)-differential privacy under T-fold adaptive composition, for

$${ϵ}^{\prime }=Tϵ\left(e^{ϵ}-1\right)+ϵ\sqrt{2T\log \left(1/{\delta }^{\prime }\right)}.$$ (14)

Furthermore, if the queries are applied to disjoint subsets of the data, the privacy guarantee does not degrade across iterations [32]. This setting is the best solution for the iterative algorithms. However, a learning algorithm never obtain such good privacy guarantees since it is learnt based on the previous sample data and parameters. Hence, we can have the following theorem.

Theorem 3.

The class of our distributed ϵ-differentially private online learning algorithms cannot guarantee ϵ privacy level under T-fold adaptive composition.

Proof.

Due to the composition theorem in [11], [33], we know that the privacy level of the iterative algorithm will degrade after T-fold adaptive composition. □

Our DOLA neither suffers the worst privacy level in Theorem 1, nor achieves the best privacy guarantees. Specifically, in line 4 and 7 of Algorithm 1, we add ${\sigma }_{t+1}^i$ to mask the real value of $w_{t+1}^i$. In other words, we protect the privacy of the data point ${\xi }_t^i$ in the tth iteration. Using the same perturbation, we protect the privacy of the data point ${\xi }_{t+1}^i$ in the (t + 1)th iteration. An important question is that will the privacy level of each data point degrade after several iterations? We give the following theorem to answer: yes, but a little lower. Although every data point is only used in one iteration, it has an effect on the next updates. An adversary may infer some information about the used data points from the later updates. Hence, the privacy level of each data point in the DOLA degrades slightly. Then we obtain the following theorem.

Theorem 4.

Under Assumption 1 and 2, Algorithm 1 can intuitively provide Tϵ-differential privacy, or has a better privacy level (ϵ^′, δ^′) for

$${ϵ}^{\prime }=Tϵ{ϵ}_0+ϵ\sqrt{2T\log \left(1/{\delta }^{\prime }\right)},$$

where ϵ₀ = e^ϵ − 1 and δ^′ ∈ [0,1].

Proof.

This proof will follow from the above analysis, the proof of Theorem 1 in [11] and Theorem III.3. in [33] if we set δ = 0. □

Above all, ϵ-DP is guaranteed for single one node at every iteration of Algorithm 1. And ϵ′-DP is guaranteed for Algorithm 1 after T iterations. To recall the analysis in Section 3.3, the real privacy of Algorithm 1 is tightly associated with the adversary action. If an adversary invades one of the nodes at a certain moment, Algorithm 1 is ϵ-DP at this moment. Furthermore, Algorithm 1 will become ϵ-DP if the adversary keeps observing the node for T iterations. The utility of the Algorithm 1 in Section 4.2 comes from such a situation where Algorithm 1 is invaded in the beginning (at the first iteration). Hence, the utility in Section 4.2 and ϵ-DP are the worst results in our paper.

4.2. Utility of Algorithm 1

In this section, we study the regret bounds of Algorithm 1 for general convex and strongly convex objective functions, respectively. We provide the rigorous formula derivation for final results: $O(\sqrt{T})$ for general convex objective functions and O(log T) for strongly convex objective functions. All proofs in this section are provided in the supplement, available online.

Based on the communication rules shown in Figs. 1 and 2, we have the following lemma.

Lemma 3 ([28]).

We suppose that at each iteration t, the matrix A_t satisfies the description in Assumption 2. Then, we have

1. ${\lim }_{k\to \infty }\varphi (k,s)=\frac{1}{m}e{e}^T$ for all $k,s\in Z$ with $k\ge s$, where

   $$\varphi (k,s)=A(k)A(k-1)A\cdots A(s+1).$$ (15)
2. Further, the convergence is geometric and the rate of convergence is given by

   $$\left|\left[\varphi {(k,s)}_{ij}-\frac{1}{m}\right]\right|\le \theta {\beta }^{k-s},$$ (16)

   where

   $$\theta ={\left(1-\frac{\eta }{4m^2}\right)}^{-2}\beta ={\left(1-\frac{\eta }{4m^2}\right)}^{\frac{1}{N}}.$$

Lemma 3 is repeatedly used in the proofs of the following lemmas. Next, we study the convergence of Algorithm 1 in details. We use subgradient descent method to make $w_t^i$ move forward to the theoretically optimal solution. To estimate the learning rate of the system, computing the norms move forward to the theoretically optimal solution. To estimate the learning rate of the system, computing the norms $\Vert w_t^i-w_t^j\Vert$ does not help. Alternatively we study the behavior of $\Vert {\overline{w}}_t-w_t^i\Vert$, where for all t, ${\overline{w}}_t$ is defined by

$${\overline{w}}_t=\frac{1}{m}\sum _{i=1}^m{w}_t^i.$$ (17)

Lemma 4.

Under Assumption 1 and 2, for all i ∈ {1,...,m} and t ∈ {1,...,T}, we have

$$\Vert {\overline{w}}_t-w_t^i\Vert \le mL\theta \sum _{k=1}^{t-1}{\beta }^{t-k}{\alpha }_k+\theta \sum _{k=1}^{t-1}{\beta }^{t-k}\sum _{i=1}^m\Vert {\sigma }_k^i\Vert +2{\alpha }_{t}L.$$ (18)

Proof.

See Appendix A in the supplement, available online. □

Lemma 5.

Under Assumption 1 and 2, for any w ∈ W and for all t, we have

$$\begin{array}{l}\Vert {\overline{w}}_{t+1}-w\Vert \le (1+2{\alpha }_{t+1}L+2L+\frac{2}{m}\sum _{i=1}^m\Vert {\sigma }_t^i\Vert \\ -2\lambda )\Vert {\overline{w}}_t-w\Vert -\frac{2}{m}\left(f_t\left({\overline{w}}_t\right)-f_t(w)\right)\\ +4L\frac{1}{m}\sum _{i=1}^m\Vert {\overline{w}}_t-w_t^i\Vert \\ +{\Vert \frac{1}{m}\sum _{i=1}^m\left({\sigma }_t^i+d_{t+1}^i\right)\Vert }^2.\end{array}$$ (19)

Proof.

See Appendix B in the supplement, available online. □

Lemma 4 and 5 are used for the proof of Lemma 6. Lemma 6 is the generic regret bound for our private DOLA (see Algorithm 1). More importantly, Lemma 6 indicates that the learnbale parameters w¹, w²,...,w^m approach the w*. In other words, the values of the learnable parameters approach each other over iterations.

Lemma 6.

We let w* denote the optimal solution computed in hindsight. The regret R_D of Algorithm 1 is given by

$$\begin{gathered} \sum _{t=1}^T\left[f_t\left(w_t^i\right)-f_t\left(w^{*}\right)\right] \\ \le \left(mRL+\frac{3\beta \theta m^2{L}^2}{1-\beta }+\frac{13}{2}m{L}^2\right)\sum _{t=1}^T{\alpha }_t \\ +\left(\frac{3\beta \theta mL}{1-\beta }+\frac{2L+1}{2m}\right)\sum _{t=1}^T\sum _{i=1}^m\Vert {\sigma }_t^i\Vert \\ +\frac{mR}{2}. \end{gathered}$$ (20)

Proof.

See Appendix C in the supplement, available online. □

Observing (20), m, R and L directly influence the bound. A faster learning rate α_t can reduce the convergence time, but increases the regret bound. Expectedly, the perturbation noise makes a great contribution to the bound and a higher privacy level increases the regret bound. In short, we have the following observations: 1) the larger scale of distributed online learning (i.e., bigger m, L and R) leads to a higher regret bound; 2) choosing an appropriate α_t is a tradeoff between the convergence rate and the regret bound; 3) the setting of the value of ϵ is also a tradeoff between the privacy level and the regret bound.

Finally, we give two different regret bounds according to the setting of objective functions in the following theorem.

Theorem 5.

Based on Lemma 6, if λ > 0 and we set ${\alpha }_t=\frac{1}{\lambda t^{\prime }}$ then the expected regret of our DOLA satisfies

$$\begin{array}{l}\mathbb{E}\left[\sum _{t=1}^T{f}_t\left(w_t^i\right)\right]-\sum _{t=1}^T{f}_t\left(w^{*}\right)\\ \le \frac{mL}{\lambda }\left(R+\frac{3\beta \theta mL}{1-\beta }+\frac{13}{2}L\right)(1+\log T)\\ +\left(\frac{3\beta \theta mL}{1-\beta }+\frac{2L+1}{2m}\right)\frac{2\sqrt{2}mnL}{\lambda ϵ}(1+\log T)+\frac{mR}{2},\end{array}$$ (21)

and if λ = 0 and set ${\alpha }_t=\frac{1}{2\sqrt{t}}$ then

$$\begin{array}{l}\mathbb{E}\left[\sum _{t=1}^T{f}_t\left(w_t^i\right)\right]-\sum _{t=1}^T{f}_t\left(w^{*}\right)\\ \le \frac{mL}{\lambda }\left(R+\frac{3\beta \theta mL}{1-\beta }+\frac{13}{2}L\right)\left(\sqrt{T}-\frac{1}{2}\right)\\ +\left(\frac{3\beta \theta mL}{1-\beta }+\frac{2L+1}{2m}\right)\frac{2\sqrt{2}mnL}{ϵ}\left(\sqrt{T}-\frac{1}{2}\right)+\frac{mR}{2}.\end{array}$$ (22)

Proof.

See Appendix D in the supplement, available online. □

Remark 1.

Observing (21) and (22), the regret bound is closely related to θ, β, m and ϵ. The higher privacy level (a lower ϵ) makes the bound higher. Interestingly, the parameters θ and β denote the “density” of the network. The more connected the network is, the higher the density is and the lower the regret bound gets. Note that a more connected network leads to a better utility of the DOLA, however it does not mean that the privacy level changes. Since our private DOLA protect every node at each iteration. The privacy level is only determined by the noise and the algorithm updating rules. As shown in Algorithm 1, the Laplace noise is added to w after the projection step, $b_t^i$ may not be in the convex domain so the strongly convexity and boundness of gradient properties may not hold. Indeed, this situation may happen when the privacy level is pretty high. The large noise that provides the high privacy level can get $b_t^i$ out of the convex domain so that the updating parameter w is swallowed up. Hence, we assume that the noise providing differential privacy will not be large enough to get $b_t^i$ out of the convex domain. This assumption is tested in the experiment (see Fig. 3). The experiment shows that the proper privacy level will not destroy the convergence of the DOLA unless ϵ gets too small.

Fig. 3.

(a) and (b) Regret versus Privacy. Average regret is generated by Algorithm 1 and Algorithm 2 that are tested on Diabetes 130-US hospitals dataset and normalized by the number of iterations. (c) and (d) Regret versus Topology. Algorithm 1 and Algorithm 2 are experimented based on three different topologies.

Algorithm 2.

(ϵ, δ)-Differentially Private DOLA

1:	Input: Cost functions $f_t^i(w):=\mathcal{l}\left(w,x_t^i,y_t^i\right),i\in [1,m]$ and $t\in [0,T]$; initial points $w_0^1,\dots ,w_0^m$; doubly stochastic matrix $A_t=\left(a_{ij}(t)\right)\in R^{m\times m}$; maximum iterations T.
2:	$\text{Set}{J}^2\leftarrow \frac{4{\alpha }_t^{2}n{L}^{2}T\log (T/\delta )\log (1/\delta )}{{ϵ}^2}$;
3:	for $t=0,\dots ,T$ do
4:	for each node i = 1,...,m do
5:	$b_t^i=\sum _{j=1}^m{a}_{ij}(t+1){\tilde{w}}_t^i$;
6:	$g_t^i\leftarrow \nabla f_t^i\left(b_t^i,{\xi }_t^i\right)$;
7:	${\tilde{w}}_{t+1}^i=\mathit{Pro}\left[b_t^i-{\alpha }_{t+1}\left(g_t^i+{\sigma }_{t+1}^i\right)\right]$; where ${\sigma }_{t+1}^i~\mathcal{N}\left(0,J^2\right)$; (Projection onto W)
8:	broadcast the output ${\tilde{w}}_{t+1}^i\text{to}\mathcal{G}{(t)}_i$;
9:	end for
10:	end for

4.3. (ϵ, δ)-Differentially Private DOLA

In this section, we use the Gaussian noise to provide (ϵ, δ)-differential privacy guarantees for DOLA instead of using the Laplace noise. Some researches (e.g., [11], [29]) have given very solid approaches to guarantee (ϵ, δ)-differential privacy of their learning algorithms. Using their works for reference, we study to use a Gaussian perturbation in DOLA and analyze the utility. Due to [8], (ϵ, δ)-differential privacy provides a slightly weaker privacy guarantee than ϵ-differential privacy, but is more robust to the number of nodes.

Theorem 6 (Privacy guarantee).

Algorithm 2 guarantees (ϵ, δ)-differential privacy.

Proof.

At any time step t, we have $G_t(X)=\left(g_t^i+{\sigma }_{t+1}^i\right)~\mathcal{N}\left(g_t^i,J^2\right)$, which is a random variable computed over the noise ${\sigma }_{t+1}^i$ and conditioned on ${\tilde{w}}_{t+1}^i$ (combine Line 5, 6 and 7 of Alg .2). Let ${\psi }_{G_t(X)}(v)$ denote the measure of G_t(X) w.r.t a variable v. To measure the privacy loss in the algorithm, we use a random variable $K_t=\left|\log \frac{{\psi }_{G_t(X)}\left(G_t(X)\right)}{{\psi }_{G_t\left(X^{\prime }\right)}\left(G_t(X)\right)}\right|$ (see [29], [33]). Now, according to [34], [35], Gaussian noise perturbation guarantees that with high probability $1-\frac{\delta }{2}$ over the randomness of $\sigma ,K_t\le \frac{ϵ}{\sqrt{\log (1/\delta )}}\le 1$. To conclude this proof, we have to use the composition of differential privacy from [33] which demonstrated that the class of (ϵ, δ)-differential privacy satisfies $\left({ϵ}^{\prime },t\delta +{\delta }^{\prime }\right)$-differential privacy for ${ϵ}^{\prime }=tϵ\left(e^{ϵ}-1\right)+ϵ\sqrt{2t\log \left(1/{\delta }^{\prime }\right)}$. Hence, with probability at least 1 − δ, the privacy loss $K=\sum _{t=1}^t{K}_t$ is at most ϵ, which concludes the proof. □

Theorem 7 (Utility guarantee).

Let $J^2=O\left(\frac{4{\alpha }_t^{2}n{L}^{2}T\log (T/\delta )\log (1/\delta )}{{ϵ}^2}\right)$ our (ϵ, δ)-differentially private DOLA (Algorithm 2) obtains the expected regret as follows:

$$\begin{array}{l}E\left[\sum _{t=1}^T{f}_t\left(w_t^i\right)\right]-\sum _{t=1}^T{f}_t\left(w^{*}\right)\\ \le \left(mRB+\frac{3\beta \theta m^2{B}^2}{1-\beta }+\frac{13}{2}m{B}^2\right)O_T+\frac{mR}{2},\end{array}$$ (23)

where $B=L+\frac{2O_T\sqrt{nT}{\log }^{1/2}(T/\delta )\log (1/\delta )}{ϵ}$. For strongly convex objective functions, λ > 0 and ${\alpha }_t=\frac{1}{\lambda t^{\prime }}$ $O_t=1+\log T$; for general convex objective functions, λ = 0 and ${\alpha }_t=\frac{1}{2\sqrt{t^{\prime }}}$, $O_t=\sqrt{T}-\frac{1}{2}$.

Proof.

Comparing Algorithm 1 and Algorithm 2, we only use different noise distributions. Hence, the analysis of this bound makes no big differences. Due to space limitations, we omit the proof which follows from the proof of Theorem 6. □

Remark 2.

In Algorithm 1 (see Line 7), the noise ${\sigma }_{t+1}^i$ is directly added to the learnable parameter $w_{t+1}^i$ and the Laplace output perturbation $\left(w_{t+1}^i+{\sigma }_{t+1}^i\right)$ is broadcast to neighbors. In Algorithm 2 (see Line 7), we put the Gaussian noise noise ${\sigma }_{t+1}^i$ in the update of w, and obtain the differentially private learnable parameter ${\tilde{w}}_{t+1}^i$. Hence, the parameter w cannot get out of the convex domain. In the proof of guaranteeing differential privacy, Algorithm 1 and Algorithm 2 both exploit the composition theorem. In fact, (ϵ, δ)-DP is a looser privacy requirement than ϵ-DP. However, in this paper we provide totally different methods to guarantee (ϵ, δ) and ϵ private DOLA. It is not very rigorous to compare the utility of Algorithm 1 and Algorithm 2 based on the regret bounds. We only ensure that (ϵ, δ)-DP needs a smaller amount of noise than ϵ-DP at the same privacy level.

Discussion.

In this section, we provide differentially private DOLA in a dynamic and random graph. A fixed communication graph can be also used in distributed online learning (e.g., [24]). Let A denote the fix communication matrix. As with Lemma 3, the limiting behaviors of A^k as k → ∞ is the key point. Since J.S. Liu [36] give the bound in Chapter 12, we directly exploit the following lemma for simplicity.

Lemma 7.

[36]. Let A_ij be (i, j)th element of A, for any j, we have

$$\sum _i\left|A_{ij}^k-\frac{1}{m}\right|\le \gamma C,$$

where C = 2 and γ relates to the minimum nonzero values of A.

In the view of the proofs about the utility of Algorithm 1 (see Appendix A-D, available online.), we are able to rewrite the lemmas and theorems for giving the regret bound in the fixed communication graph. Hence, our distributed differentially private method can be used in a fixed network.

5. SPARSE PRIVATE DOLA

In the big data era, the data is not only large-scale, but also often high-dimensional. Without applying sparse means to the data, the non-sense data contained in some dimensions would have negative effects on the utility of our private DOLA. So we propose a sparse version of the private DOLA in this section.

In this section, we also use the system model and parameters that are defined earlier in the article. Let R_S denote the regret of Algorithm 3, which has the same form with (2) in Definition 1. The proposed private sparse DOLA is shown in Algorithm 3.

Algorithm 3.

Sparse Private Distributed Online Learning

1:	Input: $f_t^i(w):=\mathcal{l}\left(w,x_t^i,y_t^i\right),i\in [1,m]$ and $t\in [1,T]$; doubly stochastic matrix $A_t=\left(a_{ij}(t)\right)\in R^{m\times m}$.
2:	Initiaization: ${\vartheta }_1^i=0,i\in [1,m]$;
3:	for t = 1,...,T do
4:	for each node i = 1,...,m do
5:	receive $x_t^i\in {ℝ}^n$;
6:	$p_t^i=\nabla {\phi }_t^{*}\left({\vartheta }_t^j\right)$;
7:	$w_t^i={\text{arg min}}_w\frac{1}{2}{\Vert p_t^i-w\Vert }_2^2+\rho \Vert w{\Vert }_1$;
8:	predict ${\widehat{y}}_t^i$;
9:	receive $y_t^i$ and obtain $f_t^i\left(w_i^i\right):=\mathcal{l}\left(w_t^i,x_t^i,y_t^i\right)$;
10:	broadcast to neighbors: ${\tilde{\vartheta }}_{t+1}^i={\vartheta }_{t+1}^i+{\delta }_t^i$;
11:	end for
12:	end for

According to line 10 and 11 of Algorithm 3, the differential privacy mechanism of Algorithm 3 follows from Algorithm 1. Hence, the privacy concerns about sparse private DOLA is nearly the same with the analysis in Section 4.1. For Algorithm 3, we mainly study its utility performance and do not give a detailed privacy analysis.

To bound R_S, we first present a special lemma below.

Lemma 8.

Let φ_t be β-strongly convex functions, which have the norms $\Vert \cdot {\Vert }_{{\phi }_t}$ and dual norms $\Vert \cdot {\Vert }_{{\phi }_t}^{*}$. When Algorithm 3 keeps running, we have the following inequality

$$\begin{array}{l}\sum _{t=1}^T\sum _{i=1}^m{\left(w_t-w\right)}^T{g}_t\\ \le m{\phi }_T(w)/{\alpha }_t+\frac{1}{{\alpha }_t}\sum _{t=1}^T\sum _{i=1}^m[{\phi }_t^{*}\left({\vartheta }_t\right)-{\vartheta }_{t+1}^i\left({\vartheta }_t\right)\\ +\frac{{\alpha }_t^2}{2\beta }{\Vert g_t\Vert }_2^2+{\alpha }_t{\Vert {\delta }_t\Vert }_2+{\rho }_t{\Vert g_t\Vert }_1].\end{array}$$ (24)

Proof.

See Appendix E in the supplement, available online. □

Based on Lemma 8, we easily have the regret bound of Algorithm 3.

Theorem 8.

Set ${\phi }_t(w)=\frac{1}{2}\Vert w{\Vert }_2^2$, which is 1-strongly convex. Let ${\rho }_t={\alpha }_t\rho ,$ then the regret bound is

$$R_S\le R\sqrt{(L+\rho )mTL}+\frac{2\sqrt{2}{m}^{2}nTL}{a}\left(\sqrt{T}-\frac{1}{2}\right).$$ (25)

Proof.

See Appendix F in the supplement, available online. □

Remark 3.

According to Theorem 8, Algorithm 3 obtains the classical square root regret $O(\sqrt{T})$. It is a pity that we do not bound the regret to O(log T). Due to the property of the Lasso algorithm, we can set the sparsity of the final result by finetuning ρ_t in Algorithm 3. A proper sparsity is able to improve the utility of a learning model. If the sparsity is too high or too low, the learnable model performs badly in the accuracy of predictions. So the value of ρ_t has a big influence on the utility of Algorithm 3. We will do experiments on the sparsity-accuracy tradeoff and find the sparsity which can lead to the highest accuracy.

6. EXTENSION

We have proposed a private DOLA to solve the real-time learning problem in a distributed setting. Furthermore, our private DOLA can be widely exploited. In this section, we convert our DOLA into a distributed stochastic optimization, and make some improvements on the privacy and utility of the algorithm by the mini-batch updates [20].

6.1. Application to Stochastic Learning Optimization

As known to us, stochastic optimization for machine learning is an important tool in the big data era. The batch learning needs to use a large set of training samples to minimize the empirical risk function $\frac{1}{n}\sum _{i=1}^n{f}_i\left(w,{\xi }_i\right)+r(w)),$ which costs much more time and resources. Stochastic gradient descent (SGD) algorithm updates each iteration by a single sample drawn randomly from the dataset. The out-standing advantage is that SGD substantially reduces the computing resources. Hence, we pay some attention to the stochastic optimization in distributed setting. Recently, Cesa-Bianchi et al. [37] showed that online learning and stochastic optimization are interchangeable.

Theorem 9 ([37]).

One online algorithm with regret guarantee:

$$\frac{1}{T}\sum _{t=1}^T{f}_t^i\left(w_t^i,{\xi }_t^i\right)-\underset{w\in W}{\min }\sum _{t=1}^T{f}_t\left(w,{\xi }_t^i\right)\le \mathcal{R}(T),$$ (26)

can be converted to a stochastic optimization algorithm with high probability, by outputting the average of the iterates:

$$F\left({\widehat{w}}_T\right)-F\left(w^{*}\right)\le \mathcal{R}(T),$$

where ${\widehat{w}}_T=\frac{1}{T}\sum _{t=1}^T{\overline{w}}_t\mathit{\text{and}}F(\widehat{w})=\mathbb{E}[f(\widehat{w},\xi )]$.

Exploiting Theorem 9, our private DOLA regret bounds can be converted into convergence rate and generalization bounds. Following (26), we should compute the bound of $\mathcal{R}(T)=\frac{1}{T}\sum _{t=1}^T{f}_t\left(w_t^i\right)-\frac{1}{T}\sum _{t=1}^T{f}_t\left(w^{*}\right)$, where f_t is short for $\sum _{i=1}^m{f}_t^i$. Recall that our private DOLA achieves O (log T) regret bound for strongly convex functions and $O(\sqrt{T})$ for convex functions. Hence, we have Lemma 9.

Lemma 9.

Based on Theorem 5 and 7, our private DOLA have the following inequalities with high probability of 1 − δ:

if f is general convex,

$$\frac{1}{T}\sum _{t=1}^T{f}_t\left(w_t^i\right)-\frac{1}{T}\sum _{t=1}^T{f}_t\left(w^{*}\right)\le O\left(\sqrt{\frac{\log 1/\delta }{T}}\right);$$

if f is strongly convex,

$$\frac{1}{T}\sum _{t=1}^T{f}_t\left(w_t^i\right)-\frac{1}{T}\sum _{t=1}^T{f}_t\left(w^{*}\right)\le O\left(\frac{\log T\cdot \log 1/\delta }{T}\right).$$

Intuitively, the average regret bound $\mathcal{R}$(T) has an $O\left(\frac{1}{\sqrt{T}}\right)$ or $O\left(\frac{\log T}{T}\right)$ bound. Due to Theorem 9, our private DOLA can be also converted into a distributed stochastic learning algorithm, which also abides by the communication rule (Assumption 2) and the assumption about objective functions (Assumption 1).

Theorem 10.

If the problem defined in Fig. 1 is required to be solved in a stochastic method, our private DOLA can be converted into a corresponding stochastic algorithm and the rate of convergence of this stochastic algorithm satisfies:

$$\mathbb{E}[f(\widehat{w},\xi )]-f\left(w^{*}\right)\le \mathcal{R}(T),$$

where $\mathcal{R}(T)=O\left(\frac{1}{\sqrt{T}}\right)$ general convex function and $\mathcal{R}(T)=O\left(\frac{\log T}{T}\right)$ for strongly convex function.

In the view of some related stochastic optimization researches [38], [39], [40], the stochastic convergence rate obtained by the conversion of our DOLA makes sense. However, the following experiment (see Fig. 6a) shows that this application suffers from some random noise so that does not have a good convergence accuracy.

Fig. 6.

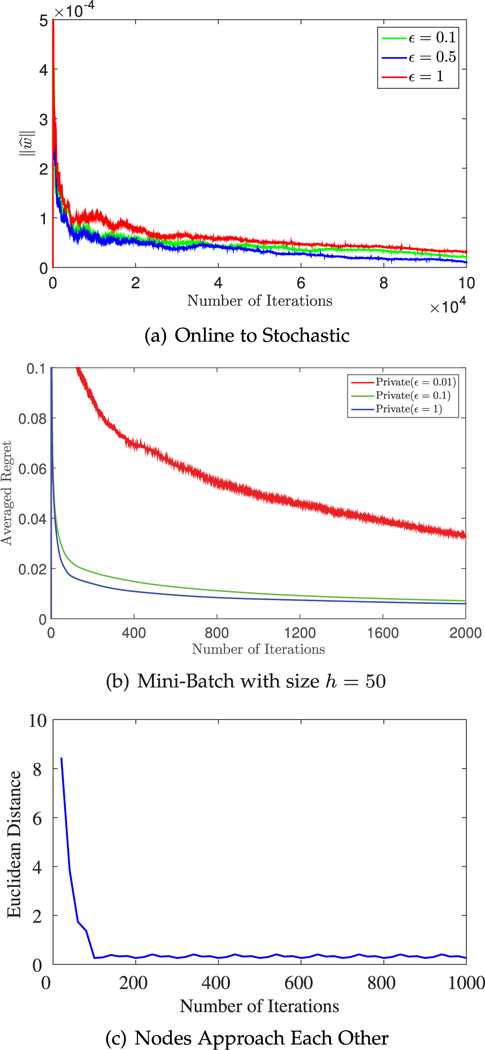
(a) Convergence versus Privacy, $\widehat{w}=\frac{1}{t}{\sum }_{k=1}^t{\overline{w}}_k$. (b) Regret incurred by using Mini-Batches. (c) The euclidean distance is generated by $\sum _{i=1}^m{\Vert w_t^i-{\overline{w}}_t\Vert }_2$, where ${\overline{w}}_t=\frac{1}{m}\sum _{i=1}^m{w}_t^i$.

6.2. Private DOLA Using Mini-Batches

We have provided ϵ and (ϵ, δ)-differential privacy for the DOLA. Although the DOLA handles the data in real time, it may be not fast enough to compute an extremely fastcoming data stream. Motivated by [41], we use the mini-batch method to process multiple samples at the same iteration. Recall that Algorithm 1 and Algorithm 2 compute the (sub) gradient of each iteration over a single sample, $g_t^i\leftarrow \nabla f_t^i\left(b_t^i,{\xi }_t^i\right)$. With mini-batch updates, the learning algorithm at each step computes the (sub)gradient based on a small set H_t of data instead of a single sample. We conclude the details of the improvement in Algorithm 4.

Algorithm 4.

Private DOLA Using Mini-Batches

1:	Input: $f_t^i(w):=\mathcal{l}\left(w,x_t^i,y_t^i\right),i\in [1,m]$ and $t\in [1,T]$; doubly stochastic matrix At = (aij(t)) ∈ Rm×m.
2:	for t = 0,...,T do
3:	for each node i = 1,...,m do
4:	$b_t^i=\sum _{j=1}^m{a}_{ij}(t+1)\left(w_t^j+{\sigma }_t^j\right)$, where ${\sigma }_t^j$ is a Laplace noise vector in ${ℝ}^n$;
5:	$g_k^i\leftarrow \nabla f_k^i\left(b_t^i\right)$, which is computed based on examples $\left(x_k,y_k\right)\in H_t$;
6:	$w_{t+1}^i=\mathrm{Pro}\left[b_t^i-{\alpha }_{t+1}\left(\phi w_t^i+\frac{1}{h}{\sum }_{\left(x_k,y_k\right)\in H_t}{g}_k^i\right)\right]$;  (Projection onto W)
7:	broadcast the output $\left(w_{t+1}^i+{\sigma }_{t+1}^i\right)\text{to}\mathcal{G}{(t)}_i$;
8:	end for
9:	end for

In Line 6 of Algorithm 4, the learnable parameter w is updated on a average of (sub)gradients $\frac{1}{h}\sum g_{k^{\prime }}^i$, where h denotes the number of samples included in H_t. Most importantly, the mini-batch has a great advantage on guaranteeing differential privacy for Algorithm 4. Observing the proof of Lemma 1, we find that the parameter 1/h has reduce the sensitivity of the algorithm, which is shown in the following lemma.

Lemma 10 (Sensitivity of Algorithm 4).

With mini-batch updates, the sensitivity of Algorithm 4 is

$$S_2(t)\le \frac{2{\alpha }_t\sqrt{n}L}{h}.$$ (27)

Proof.

This proof follows from the proof of Lemma 1. □

Intuitively, Algorithm 4 has a much smaller sensitivity than Algorithm 1 and Algorithm 2. According to the analysis of differential privacy, providing the same privacy level for Algorithm 4 needs less noise. The disadvantage of Algorithm 4 is that it takes a little more time to collect h data entries at each iteration in online system. Similar with Algorithm 1 and Algorithm 2, Algorithm 4 can guarantee ϵ or (ϵ, δ)-differential privacy. Hence, we omit the detailed descriptions on the privacy guarantees. As for the utility of Algorithm 4, we will carry out related experiments in next section.

7. EXPERIMENTS

In this section, we conduct numerical experiments to test the theoretical analyses described in Sections 4, 5, and 6. Specifically, we first study the privacy-regret tradeoff of Algorithm 1 and Algorithm 2. Then, we study the influence of the topology of the communication graph on the utility. Further, we test the utilities of Algorithm 1 and Algorithm 2 on three different scales of real world datasets. To verify the feasibility of converting DOLA to distributed stochastic optimization, we output the average (see Fig. 5a) of t online updated parameters, i.e., $\frac{1}{t}{\sum }_{l=1}^t{w}_l^i$. Finally, we study the improvement of the privacy and utility by using mini-batches.

Fig. 5.

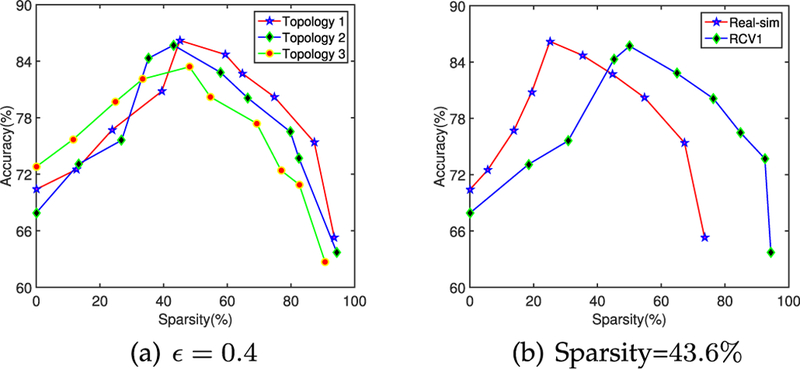
(a) and (b) Regret versus Sparsity on different topologies and datasets.

7.1. Differentially Private Support Vector Machines

In the experiments, we develop a series of differentially private SVM algorithms. We have the hinge loss function $f_t^i(w)=\max \left(1-y_t^i\langle w,x_t^i\rangle \right)$, where $\left\{\left(x_t^i,y_t^i\right)\in {ℝ}^n\times \{\pm 1\}\right\}$ are the data available only to the ith learner. For fast convergence rates, we set the learning rate ${\alpha }_t=\frac{1}{\lambda t}$. The dataset is divided into m subsets. Each node updates the parameter based on its own subset and timely exchanges its parameter to the neighbors. Note that at the iteration t, the ith learner must exchange the parameter $w_t^i$ in strict accordance with Assumption 2. To better evaluate our method, we sum the normalized error bounds (i.e., the “Regret” on y-axis) for the all experiment figures.

7.2. Datasets and Pre-Processing

First, we chose real datasets from UCI machine learning Repository (see Table 2). The main dataset we use for testing is Diabetes 130-US hospitals. This dataset contains 10 years (1999–2008) of clinical care from 130 US hospitals and integrated delivery networks. It includes over 50 features representing patient, which contains such attributes as patient number, race, gender, age, admission type, HbAlc test result, diagnosis and so on. In this dataset, we want to predict whether one patient will experience emergency visits in the year before the hospitalization. If we succeed in predicting this specific condition, medical help can be offered in time when needed. Besides the medical data, Covertype and Adult from UCI are used for comparison. Covertype is used for predicting forest cover type from cartographic variables and the classification task is to predict whether a person makes over 50K per year. Then, we use two high-dimensional datasets Real-sim and RCV1 from LIBSVM, which will be specifically tested on Algorithm 3.

TABLE 2.

Summary of Datasets

Dataset	Number of samples	Dimensionality
Diabetes 130-US hospitals	100,000	55
Covertype	581,012	54
Adult	48,842	14
Real-sim	72,309	20,958
RCV1	20,242	47,236

For pre-processing, we follows from [10]. We remove all entries with missing data points and convert the categorial attributes to a binary vector. For non-numerical attributes such as gender and nationality, we replace the values by their occurrence frequency in their category. More importantly, the maximum value should be first ensured to be 1 by normalizing each column and then the norm of each data example is at most 1.

7.3. Implementation

Many distributed computing platforms such as Hadoop, spark and OpenMPI, are able to deploy the distributed and parallel computing algorithm. Since the nodes of our DOLA need to randomly exchange parameters with some neighboring nodes, we require to conduct the communications among the nodes without any restrictions. So we use Open-MPI to schedule the communications. We run the experiment program in Ubuntu 14.04 equipped with 64 CPU (8 cores) and 128 GB memory. 2 GB memory is assigned to each CPU. The program is implemented in C Language. Specifically, we deploy our experiments as follows:

In step 1, each CPU is regarded as one node in our private DOLA. We equally distribute the dataset to the m nodes. Most importantly, we define the logical neighboring relations among the nodes, which aims at simulating physical neighboring relations. After doing this, we have a topology of this distributed system as shown in Fig. 1. For a solid and simple analysis, we design three different topologies, respectively defined as Topology 1, 2, and 3. The distribution of the nodes in Topology 1 is sparse, which means that each nodes has a small amount of neighbors. The nodes in Topology 2 are more closely linked than that in Topology 1, while Topology 3 has the most intensive nodes.

In step 2, we generate the communication matrix A_t by MATLAB. Although A_t changes with the time t, it must abide by the Assumption 2 and the topology in the current experiment. Generating a series of communication matrices is really a very tedious work. If we look upon A_t as a map for communications. This map is given to all nodes. Because we do not consider the delay in our algorithms, one iteration ends until all the nodes finish computing and exchanging the learnable parameters (i.e., shown in Fig. 2). This process has a high time complexity. Hence, we do not take the communication cost into consideration.

In step 3, when we test one of the proposed algorithms, every output (e.g., $w_t^i$ of the nodes in every iteration shall be recorded. Meanwhile, the regret value (due to (2) in Definition 2) in each iteration is also computed and preserved.

7.4. Results and Analysis

Note that the nodes learn the model from their own data resources, however the final values of the learnable parameters $w_T^1,\dots ,w_T^m$ approach each other after T iterations. This analysis is proved by the experiments. It makes sense that the regret of the DOLA can be measured with respect to an arbitrary node. Therefore, we plot the regret based on the outputs of an arbitrary node.

In Fig. 3a and b show the average regret (normalized by the number of iterations) incurred by our DOLA for ϵ and (ϵ, δ)-different privacy on Diabetes 130-US hospitals dataset. The regret obtained by the non-private algorithm is the lowest as expected. More significantly, the regret gets closer to the non-private regret as its privacy preservation is weaker. However, when we set ϵ = 0.01, the average regret is swallowed up in the noise. Hence, the privacy level cannot be too high. Figs. 3c and d show the average regret on different topologies. In Topology 1, the distribution of the nodes is sparse, where its nodes are not able to conduct effective data interchange. So the DOLA in Topology 1 obtains a bad convergence (see red curves in (c) and (d)). Since Topology 2 and Topology 3 have closer nodes. They achieve better utilities (blue and green curves) than Topology 1.

In Fig. 4, we test Algorithm 1 and Algorithm 2 on three different UCI datasets: Diabetes 130-US hospitals, Covertype and Adult. The three datasets have different scales and dimensions (see Table 2). From Fig. 4, the datasets of the same order of magnitude do not have significant differences in the privacy and utility performance. Based on the results shown in Fig. 4, it is hard to enhance the utility of the private DOLA by merely increasing a small number of the data, unless we can increase the number in several orders of magnitude, which costs too much resource.

Fig. 4.

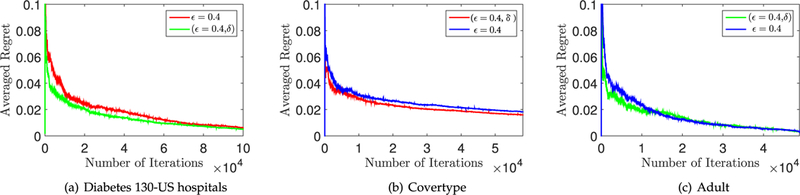
Regret versus Dataset: Regret (normalized by the number of iterations) incurred by Algorithm 1 and Algorithm 2 on three datasets: Diabetes 130-US hospitals, Covertype, and Adult.

In Fig. 5, we show the accuracy-sparsity tradeoff in (a). The three topologies are randomly generated and tested on the same dataset Real-sim, which is of high dimension (see Table 2). This experiment indicates that an appropriate sparsity can yield the best performance (i.e., the three curves achieve the highest accuracy at the sparsity of 43.6%) and other lower or higher sparsity would lead to a worse performance. To be convincing, we test Algorithm 3 on two high-dimensional real datasets in (b). We find that these two datasets have different appropriate sparsity. Therefore, we need to finetune the sparsity parameter ρ due to the features of data.

In Fig. 6, we conduct experiments on Theorem 9 and the mini-batch algorithm (Algorithm 4). Fig. 6a shows that the stochastic algorithm converted to by our DOLA has fast convergence rates, which demonstrates that converting the DOLA to distributed stochastic optimization makes sense. We test the mini-batch algorithm in (b). Comparing Fig. 6b with Figs. 3a and 3b, we find that the curves become relatively smooth in Fig. 6b at the same privacy level, which indicates that the mini-batch weakens the influence of noise on regret. The privacy level can be improved by using mini-batches, because 0.01-DP algorithm converges (red curve in Fig. 6b). That is because mini-batches reduce the sensitivity of the DOLA. See Fig. 6c, we use ${\sum }_{i=1}^m{\Vert w_t^i-{\overline{w}}_t\Vert }_2$ to denote the distance of the all learnable parameters. This experiment shows that the nodes “approach” each other over iterations and is consistent with the theoretical results.

As we know, the hinge loss $\mathcal{l}(w)=\max \left(1-y{w}^{\text{T}}x,0\right)$ leads to the data mining algorithm, SVM. To be more persuasive, we train a differentially private distributed SVM based on Theorem 10 by using RCV1 dataset. Three-quarters of the data are used to train the learnable model and the rest of the data are for testing. Table: 3 shows the accuracy for different level of privacy and different number of nodes of algorithm. Intuitively, the centralized non-private model has the highest accuracy 82.51% while the model of 64 nodes at a high level ϵ = 0.01 of privacy has the lowest accuracy 50.36%. We conclude that the accuracy gets higher as the level of privacy is lower or the number of nodes is smaller.

TABLE 3.

Accuracy for Different Levels of Privacy and Different Numbers of Nodes of an Algorithm

Method		Nodes	Accuracy
Non-private		1	82.51%
		4	74.64%
		64	65.72%
Private	ϵ = 1	1	82.51%
	ϵ = 1	4	74.64%
	ϵ = 1	64	65.72%
	ϵ = 0.1	1	80.17%
	ϵ = 0.1	4	70.86%
	ϵ = 0.1	64	62.34%
	ϵ = 0.01	1	75.69%
	ϵ = 0.01	4	64.81%
	ϵ = 0.01	64	50.36%

8. CONCLUSION AND FUTURE WORK

We have proposed a novel differentially private distributed online learning framework. Both e and (ϵ, δ)-differential privacy are provided for our DOLA. Furthermore, we discussed two extensions of our algorithms. One is the conversion of the differentially private DOLA to distributed stochastic optimization. The other is that we use the mini-batch technique to weaken the influence of added noise. According to [42], the utility if our algorithms can potentially be improved. We will study these improvements in the future.

TABLE 1.

Summary of Main Notations

$w_t^i$	a learnable parameter of the ith node at time t
At	a communication matrix in iteration t
n	the dimensionality of vector parameters
S(t)	the sensitivity of each iteration
$f_t^i$	loss function
m	the number of nodes
αt	learning rate or stepsize
αij(t)	the (i, j)th element of At
$\mathcal{G}$i(t)	the set of neighbors of Node i
L	(sub)gradient bound of $f_t^i$
$g_t^i$	(sub)gradient of $f_t^i$
ϵ	privacy level of DP
RD	regret of the DOLA
${\overline{w}}_t$	$\frac{1}{m}{\sum }_{i=1}^m{w}_t^i$
${\widehat{w}}_T$	$\frac{1}{T}{\sum }_{t=1}^T{\overline{w}}_t$
$\langle \cdot ,\cdot \rangle$	inner product
$\Vert \cdot \Vert$	Euclidean norm unless special remark

Biography

Chencheng Li (S’15) received the BS degree from the Huazhong University of Science and Technology, Wuhan, P. R. China, in 2014, and is currently working toward the PhD degree in the School of Electronic Information and Communications, Huazhong University of Science and Technology, Wuhan, P. R. China. His current research interest includes: online learning in big data analytics and differential privacy. He is a student member of the IEEE.

Pan Zhou (S’07-M’14) received the BS degree in advanced class from the Huazhong University of Science and Technology, the MS degree from the Department of Electronics and Information Engineering, Huazhong University of Science and Technology, and the PhD degree from the School of Electrical and Computer Engineering, Georgia Institute of Technology (Georgia Tech), in 2011, Atlanta. He is currently an associate professor in the School of Electronic Information and Communications, Huazhong University of Science and Technology (HUST), Wuhan, P. R. China. His current research interests include machine learning and big data, security and privacy, and information networks. He is a member of the IEEE.

Li Xiong received the BS degree from the University of Science and Technology of China, the MS degree from Johns Hopkins University, and the PhD degree from the Georgia Institute of Technology, China, all in computer science. She is a Win-ship distinguished research associate professor of mathematics and computer science, Emory University, where she directs the Assured Information Management and Sharing (AIMS) Research Group. Her areas of research are in data privacy and security, distributed and spatio-temporal data management, and biomedical informatics. She is a recent recipient of the Career Enhancement Fellowship by the Woodrow Wilson Foundation.

Qian Wang received the PhD degree in electrical engineering from the Illinois Institute of Technology, in 2012. He is a professor in the School of Computer Science, Wuhan University. His research interests include AI security, cloud security and privacy, wireless systems security, etc. He is an expert under National “1000 Young Talents Program” of China. He is a recipient of the IEEE Asia-Pacific Outstanding Young Researcher Award in 2016. He serves as an associate editor of the IEEE Transactions on Dependable and Secure Computing and the IEEE Transactions on Information Forensics and Security. He is a member of the IEEE and a member of the ACM.

Ting Wang received the PhD degree from the Georgia Institute of Technology. He is an assistant professor with Lehigh University. Prior to joining Lehigh, he was a research staff member with the IBM Thomas J. Watson Research Center. His research interests span both theoretical foundations and real-world applications of large-scale data mining and management. His current work focuses on data analytics for privacy and security.