Abstract
In this scientific report, a new technique of artificial intelligence which is based on k-nearest neighbors (KNN) and particle swarm optimization (PSO), named as PSO-KNN, was developed and proposed for estimating blast-induced ground vibration (PPV). In the proposed PSO-KNN, the hyper-parameters of the KNN were searched and optimized by the PSO. Accordingly, three forms of kernel function of the KNN were used, Quartic (Q), Tri weight (T), and Cosine (C), which result in three models and abbreviated as PSO-KNN-Q, PSO-KNN-T, and PSO-KNN-C models. The valid of the proposed models was surveyed through comparing with those of benchmarks, random forest (RF), support vector regression (SVR), and an empirical technique. A total of 152 blasting events were recorded and analyzed for this aim. Herein, maximum explosive per blast delay (W) and the distance of PPV measurement (R), were used as the two input parameters for predicting PPV. RMSE, R2, and MAE were utilized as performance indicators for evaluating the models’ accuracy. The outcomes instruct that the PSO algorithm significantly improved the efficiency of the PSO-KNN-Q, PSO-KNN-T, and PSO-KNN-C models. Compared to the three benchmarks models (i.e., RF, SVR, and empirical), the PSO-KNN-T model (RMSE = 0.797, R2 = 0.977, and MAE = 0.385) performed better; therefore, it can be introduced as a powerful tool, which can be used in practical blasting for reducing unwanted elements induced by PPV in surface mines.
Subject terms: Environmental impact, Natural hazards
Introduction
Blasting for rock fragmentation is known as one of the most impressive techniques in the fields of mining and civil engineering. However, it is estimated that only about 20% of the total explosive energy was used for rock fragmentation1–4. The remaining of explosive energy is wasted, which cause various undesirable effects to the environment, like, air over-pressure (AOp), flyrock, ground vibration, and back-break5–7. Of these effects, ground vibration, that is calculated using peak particle velocity (PPV), is utilized to be the most adverse parameter due to it can cause structural vibration, demolish structures, include instability of bench and slope, and affects the underground water8–12. Therefore, precise estimation of blast-produced PPV was needed to decrease its influence on our environment.
Until now, experimental and artificial intelligence (AI) commonly utilized for predicting blast-induced PPV13. The first one aims to establish empirical equations based on relationships between explosive charge per blasting delay (W) and the distance of PPV measurement (R)14–23. However, these empirical equations provide poor prediction performance in some cases e.g.24–29; therefore, the latter is considered.
Literature review shows that AI has proven its various efficient fields with promising performance, especially in advanced engineering as well as in mining and measurement30–47,48. In order to estimate blast-induced PPV, Khandelwal and Singh10 have successfully developed an artificial neural network (ANN) utilizing 154 blasting events at a surface coal mine in India with the conclusion that ANN is a powerful tool to estimate blast-induced PPV. Saadat, et al.27 also explored an ANN model to predict blast-induced PPV of an iron mine in Iran (Gol-E-Gohar) has been reported using 69 blasting events, even a proper result. Using other AI technique (i.e., classification and regression tree – CART), Khandelwal, et al.49 also successfully predicted PPV with high accuracy based on 51 datasets. Based on the advantages of the XGBoost model, Nguyen, et al.50 also investigated and predicted PPV with high performance using 136 datasets (i.e., RMSE = 1.742, R2 = 0.952). In another work, Nguyen, et al.51 optimized the Cubist models by a clustering technique (i.e., hierarchical K-means), for predicting PPV with high reliability. They concluded that the clustering technique can be considered as a robust technique in the classification of the dataset, as well as optimization of the Cubist models. In another work, Hasanipanah, et al.52 utilized the PSO algorithm to predict blast-caused PPV, where two forms, power (P) and linear (L) were used. An empirical technique, along with MLR analysis, are also used for comparing with those of the two PSO models. They reported that the PSO-P provides high prediction performance. Armaghani, et al.53 investigated an integration of PSO with ANN in order to estimate blast-induced PPV, namely PSO-ANN model. They utilized the algorithm of PSO for optimizing the network architecture of the ANN model. A series of empirical equations are additionally applied to estimate PPV and compare with those of the PSO-ANN model. Conclusion of their study is that the PSO-ANN model yielded an outstanding result. In another study, Armaghani, et al.54 used the ICA optimization to estimate blast-induced PPV utilizing 73 blasting events and also a suitable result was determined in their work. Based on the ICA, Hasanipanah, et al.55 also introduced a fuzzy system (FS) model for estimating the model of blast-induced PPV, i.e., FS-ICA. For performing comparisons, a variety of empirical models were also calculated in their study, which proved that the model of FS–ICA outperforms the other experimental approaches. By the use of another optimization algorithm (i.e., firefly algorithm-FFA), Shang, et al.56 developed a new technique to predict PPV using FFA-ANN model. Zhang, et al.57 also developed the PSO-XGBoost technique for the aim of PPV prediction with high performance. In addition, PSO-ANFIS and GA-ANFIS were also investigated by Yang, et al.58, for predicting PPV. Table 1 lists some studies concerning the prediction of blast-induced PPV using AI techniques.
Table 1.
Some studies concerning the prediction of blast-induced PPV using AI techniques.
| References | AI technique |
|---|---|
| Singh and Singh8 | ANN |
| Khandelwal and Singh61 | ANN |
| Khandelwal and Singh9 | ANN |
| Iphar, et al.107 | ANFIS |
| Khandelwal and Singh10 | ANN |
| Khandelwal, et al.11 | SVM |
| Monjezi, et al.108 | ANN |
| Monjezi, et al.24 | ANN |
| Khandelwal, et al.62 | ANN |
| Ghasemi, et al.25 | FL |
| Monjezi, et al.26 | ANN |
| Saadat, et al.27 | ANN |
| Armaghani, et al.53 | PSO-ANN |
| Hasanipanah, et al.109 | SVM |
| Dindarloo110 | GA |
| Hajihassani, et al.28 | ICA-ANN |
| Hajihassani, et al.111 | PSO-ANN |
| Amiri, et al.83 | ANN-KNN |
| Monjezi, et al.112 | GEP |
| Hasanipanah, et al.113 | CART |
| Hasanipanah, et al.52 | PSO |
| Taheri, et al.114 | ABC-ANN |
| Ragam and Nimaje115 | GRNN |
| Armaghani, et al.116 | ICA |
| Behzadafshar, et al.117 | ICA |
| Sheykhi, et al.118 | FCM-SVR |
| Arthur, et al.119 | GP |
Note: adaptive neuro-fuzzy inference apparatus (ANFIS); support vector machine (SVM); gene expression programming (GEP); fuzzy logic (FL); genetic algorithm (GA); classification and regression tree (CART); artificial bee colony algorithm (ABC); generalized regression neural network (GRNN); fuzzy C-means clustering (FCM); Gaussian process (GP).
We have found that optimization algorithms are becoming a powerful tool for estimating blast-induced PPV, notably the PSO algorithm. They play a considerable role in the case of enhancing the efficiency of models. However, it was only considered for ANN and XGBoost models. Nevertheless, new hybrid models are needed for knowledge and practical engineering to reduce the undesirable influences of blasting operations. In this work, we expanded the body of knowledge by proposed the PSO optimized k-nearest neighbors (KNN) and named as PSO-KNN for estimating blast-induced PPV. The RF, SVR, and empirical models were also considered and exploited to predict PPV based on the same dataset.
Materials
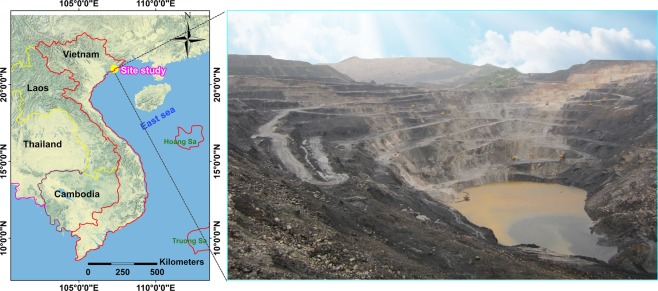
In this study, blasting operations were undertaken at the Deo Nai open-pit coal mine for rock fragmentation. The study site locates in the North of Vietnam, between latitudes 21°01′00″N and 21°20′00″N, and between longitudes 107°18′15″E and 107°19′20″E (Fig. 1). The Arcmap version 10.2 (Link: http://desktop.arcgis.com/en/arcmap/) was used to create the map in Fig. 1. The total area of this mine is ~6.0 km2 with exploitation reserve of 42.5 Mt, and fertility of 2.5 Mt/yr59.
Figure 1.
Location and landscape of the study site.
The geological structure in the mine is very complicated. Many interleaved faults and folds divide the deposit into many different complex blocks. In this mine, the volume of the overburden is 20 to 30 million m3/yr. The main bulk of the overburden includes conglomerate, sandstone, siltstone, claystone, and coal clay. Therefore, in this mine, blasting is considered to be imperative for fragmenting rocks. ANFO explosive (ammonium nitrate–fuel oil) was used as the primary explosive in this mine with the hole diameter in the range of 150 to 250 mm. Note that, the non-electric delay blasting method15,60 is used in this mine in the case of rock breakage.
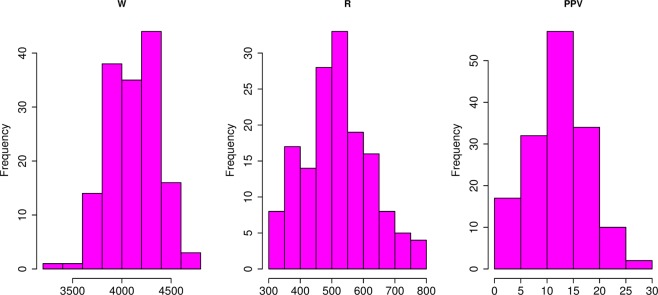
As stated in the literature61–63, W and R have the most impacts on PPV, therefore, in this study, both of the W and R parameters are utilized as the primary input parameters for PPV estimation. The Blastmate III perspective (i.e., Instantel in Canada) is utilized for recording the PPV value. Note that the term R was defined by a handheld GPS where W was extracted from 152 blast patterns. Table 2 summaries the data taken in this work. Also, the histograms of each attribute are illustrated in Fig. 2.
Table 2.
Properties of the data taken.
| Properties | W | R | PPV |
|---|---|---|---|
| Min. | 3200 | 308.2 | 2.050 |
| 1st Qu. | 3952 | 448.0 | 8.545 |
| Median | 4135 | 513.0 | 12.435 |
| Mean | 4120 | 518.3 | 12.400 |
| 3rd Qu. | 4295 | 574.1 | 15.980 |
| Max. | 4643 | 799.2 | 29.180 |
Note: W denotes the explosive charge per delay (in Kg); W indicates the monitoring distance (in m); PPV means the intensity of ground vibration (in mm/s).
Figure 2.
Histogram of the blast-induced ground vibration dataset.
Methods
As mentioned above, the principal purpose of this work is to expand a novel hybrid model for estimating blast-induced PPV (i.e., called PSO-KNN model). Moreover, a practical technique and also two algorithms, (e.g., RF and SVR), are also utilized as benchmarks for estimating blast-induced PPV. However, the description of the RF and the SVR has been well documented, i.e., in64–66; therefore, the background of the RF and the SVR is not provided in this study.
Empirical
From reviewing the lecture, we have shown that empirical equation of the U.S Bureau of Mines (USBM)14 is the most common technique where it has been widely applied to estimate PPV produced by blasting operations. Therefore, for the current research, it was implemented for predicting PPV and is demonstrated as:
| 1 |
W stands for the maximum explosive charge per delay (in Kg);R stands for the monitoring distance (m);where λ and α were the site parameters and were considered using the multivariate regression analysis.
PSO algorithm
In the present work, the algorithm of PSO is utilized for optimizing the KNN model. In the regards of the PSO, more details have been presented in refs.67–71.
The PSO algorithm is one of the most efficient metaheuristic techniques proposed by Eberhart and Kennedy72. This method was adopted from the social animals/particles behavior, like a flock of birds in a swarm and can be used to predict optimization issues with every solution is illustrated as a particle. In order to determine the optimized solution, the algorithm of PSO considers the following steps73:
Step 1: Initialize population of particles as well as its related velocity. After that, predict the fitness of particles and discover the best location as local and global best.
Step 2: Each particle changes about quest zone with a particular velocity. For each iteration, global best and local best are calculated to assess the efficiency of the PSO-KNN models. Global best is considered as the best-gathered particle position, and the local best is regarded as the best solution in the prevalent iteration.
Step 3: Update the location of a particle; After predicting the velocity of particles, the positions of them change about quest zone with the calculated speed and for considered particles, the procedure can calculate and update the new velocity utilizing Eq. 2 as follow:
| 2 |
where denotes the position of particle j at iteration i; means the particle velocity j for iteration i; w stands for the inertial weight coefficient; i stands for the number of iteration; r1 and r2 stand for the numbers in the interval [0,1].
- The global best and the local best can be updated when the new particle becomes to remove. The system was calculated and then updated the location, for each particle, using Eq. 3 as below:
3 Investigate the termination criteria, when the principle of termination has been satisfied, change the global best as the proper and optimized solution for an issue.
k-Nearest Neighbors (KNN)
The KNN is known as one of the non-parametric approaches in term of classification and regression issues74. The most critical parameters of the KNN algorithm are the number of nearest neighbors (k) and the distance metric (d). In regression problems, the parameter k specifies the number of neighbor observations that contribute to the output predictions (i.e., PPV. Instead of considering at the closest reference sample, the algorithm of KNN views at the k instances in the reference collect which is near to the unknown instance as well as performs a vote to make a decision75,76. More details in the case of the algorithm of KNN can be obtained in refs.77–79.
Review of previous works indicate that the KNN algorithms have been applied correctly in many fields80–82; however, it seems to be rarely considered for estimating blast-induced problems. Amiri, et al.83 Amiri et al. proposed the model ANN-KNN for the first time. ANN-KNN is composed of two component models of KNN and ANN. Each model predicts test samples, and the obtained outcome is a weighted combination of the findings. Firstly, they use K means clustering to partition the training sample within identical clusters. In order to predict a testing sample by KNN, the nearest teammate instance has been found utilizing the distance of city for the test sample. Then, the values of the factors of the closest train instance were considered to the test instance. For each cluster, besides KNN, an ANN can be trained to utilize the train instance of that cluster. Once the ANN models trained, they can be used to predict PPV on the same group of the testing dataset. However, optimization problems for the ANN model and the KNN approach for estimating blast-induced PPV in their work have not been implemented. The weights and ascending bias, as well as the hidden node of the ANN model, have been reviewed and calculated according to the experimental formulas. Likewise, the KNN model was also determined by the traditional method. Note that, in the present study, the training dataset is not divided by clustering algorithms. The KNN algorithm was applied to develop the KNN model on the whole of the training dataset with the hyper-parameters (k, d) put to use to tune the performance of KNN model. To define the most optimal values for the KNN model, the PSO method was included in the adjustment process of k and d of the KNN model.
Proposing the PSO-KNN model
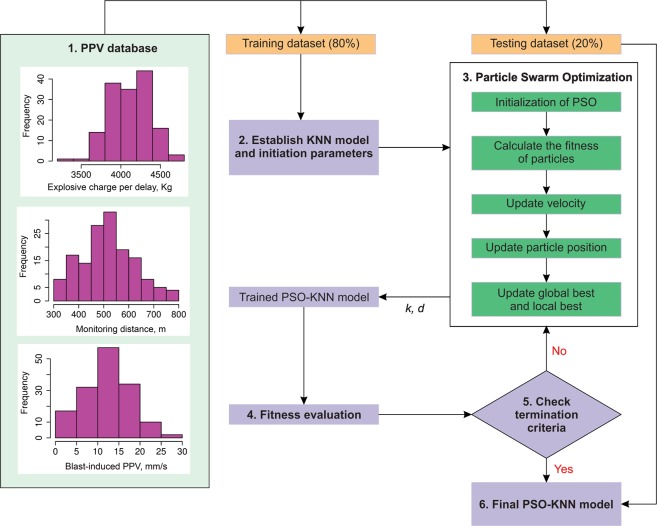
In the present work, the KNN algorithm is the primary algorithm used to estimate blast-induced PPV. The two main hyper-parameters of the KNN model, including k and d, are utilized to adjust the efficiency of the algorithm. For determining the optimal values of k and d, the PSO algorithm was adopted. As shown in Fig. 3, the particles in PSO performed a global search procedure for the best k and d values of the KNN model, called PSO-KNN model. The expanding of the PSO-KNN algorithm has been accomplished through four steps as:
Figure 3.
Scheme of a proposed PSO-KNN model for estimating blast-induced PPV.
- Step 1: Making the PPV data and preparing the training and testing databases.
In this step, 152 blasting events were divided into two phases by randomly; 124 blasting activities in the first phase (~ about 80 percent of the whole dataset) are used for the training process to expand the PSO-KNN models. The rest 28 blasting events (~20%) in the second phase were used to check the efficiency of the constructed approaches.
- Step 2: Configuration of the KNN model.
As a criterion, the KNN model is considered as the dominant model to predict PPV in the present work. It is noted that three shapes of kernel function were applied for KNN, including quartic (Q), triweight (T), and cosine (C). These functions are described as following74,84:
| 4 |
| 5 |
| 6 |
where K is a function that can be integrated with non-negative real values. The primary purpose of using these kernel functions in the present study is to map the data to a higher dimension with the linear relationship. It makes regression of PPV values more accurate in modeling. More details of kernel functions for the KNN model can be found at the following references74,84–87.
- Step 3: Optimization of KNN, evaluation of fitness, and check termination criteria.
This step aimed to find an optimal KNN model with the lowest amount of a fitness function by searching the best amounts for the hyper-factors of KNN (k, d) using PSO algorithm. To perform the most appropriate KNN approaches according to the PSO algorithm, RMSE is computed as a fitness function as described in Eq. 7. The flowchart of the suggested PSO-KNN algorithm for estimating blast-induced PPV was illustrated in Fig. 3.
- Step 4: Final PPV predictive model.
After that, the optimization method by the algorithm of PSO is completed, the best hyper-parameters of the KNN model were derived and used to build the final PPV predictive methods. The goodness of the approaches was evaluated via the training dataset and performance statistical indexes like MAE, RMSE, and R2. The error distribution is provided by RMSE88,89 illustrating the idea of how proper an approach has adjusted the information via R2. In an optimal model, the RMSE, and MAE could be equal to zero whenever the R2 could be equal to 1. The performance indicators are computed as:
| 7 |
| 8 |
| 9 |
n stands for a total number of observations; is the measured PPV, is predicted PPV, and is the mean of .
Establishing the Predictive Models
In order to develop PPV predictive models in this work, the database, including 152 blasting events, was split into two parts. According to Nick90, the most usually utilized train/test ratio was 80:20, which was a proper starting ratio based on Swingler91,92; hence, 80% of the total information (around 124 events of blasting) is used as the training database for the first section; the remaining amount that consists of 28 blasting events was recognized as the testing database in the second section.
Empirical model
For the empirical model, λ and α are the site parameters and are found using an analysis of multivariate regression. In the present work, the SPSS method (version 16.0) is employed to specify λ and α according to 124 blasting events of the training database. We found that λ = 0.051 and α = −2.596 are the optimized amounts for the site parameters. In this work, the empirical equation USBM is illustrated as below:
| 10 |
RF model
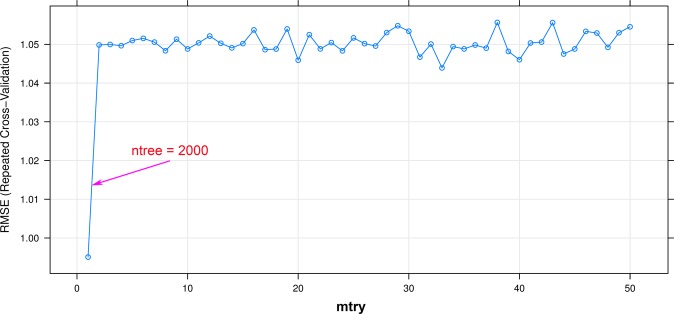
RF is considered as the best decision tree methods suggested by Breiman93. It may predict both classification and regression issues, i.e., predict PPV. For this aim, the number of the tree (ntree) and randomly selected predictor (mtry) are the main hyper-parameters involving to adjust the quality of the RF approach. Theoretically, ntree must be large enough to avouch the wealth and objectivity of the forest94. Each decision tree in the forest acts as a voter. Therefore, ntree was set equal to 2000. To introduce the optimized value of the mtry parameter, the grid search approach95 was applied with mtry in the range of 1 to 50; The 10-fold cross-validation resampling method96 is used to avoid over-fitting for RF model. As a result, ntree = 2000 and mtry = 1 were the best for the RF model (Fig. 4). Its performance was evaluated through RMSE, MAE, and R2 on the training dataset.
Figure 4.
Efficiency of the RF algorithm on the training database.
SVR model
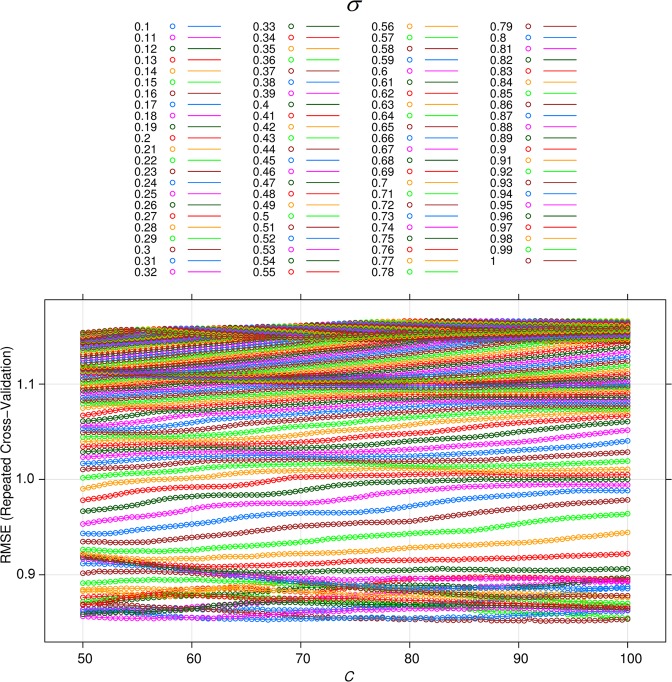
For SVR model, the regression problem of PPV was employed through a kernel function. Many previous scientists recommended that the radial basis function (RBF) should be applied in SVR for regression problems with more high accuracy97–99. Therefore, the function of the RBF kernel is chosen selected for SVR model with σ and C were the RBF’s parameters. The 10-fold cross-validation resampling method is implemented for the SVR model to avoid over-fitting. In the case of expansion of the SVR method, a grid search method for σ and C was established to discover the most proper amounts of the SVR. In this regard, σ was set in the range of 0.1 to around 1; C was adjusted in the range of 50 to 100. Eventually, an optimized SVR method is determined with σ = 0.16 and C = 94.5. Figure 5 indicates the performance of the SVR model for predicting PPV on the training dataset.
Figure 5.
Efficiency of the SVR method on the training dataset.
PSO-KNN model
In this part, the development of the PSO-KNN method for estimating PPV was presented in detail. As stated earlier, this model is developed via a combination of KNN and PSO algorithms, as shown in Fig. 3. The training dataset for the proposed PSO-KNN method is identical with those utilized in the empirical, RF, and SVR models. According to the training dataset, as the first step, a primary KNN model is produced. Then, as the next step, the hyper-factors of the KNN method are improved using the algorithm of PSO. This part aimed to discover a PPV predictive method with the lowest RMSE by finding the best amounts for the hyperparameters by the algorithm of PSO. In this algorithm, maximum particle’s velocity (Vmax), maximum iteration number (mi), the population number (p), individual and group cognitive (ϕ1, ϕ2), as well as inertia weight (w), are the factors utilized for the optimization approach. The sample size should be large enough to ensure the population diversity100,101. Hence, a trial-and-error method is selected, and 50 individuals were the best for the immediate work area (p = 50). For the process of terminating the optimization, mi is adjusted equally to 500102 for checking the particle positions fitness by utilizing the RMSE metric (Eq. 7). For ensuring the balance among global detection and also local search, w is adjusted equal to around 0.9103. Based on previous works, Kennedy104 and Clerc and Kennedy105, ϕ1 can be identical to ϕ2 and ϕ1 + ϕ2 lie in the range of 0 to 4. Hence, in the present work, ϕ1 = ϕ2 = 1.5. In order to ensure convergence along with preventing explosion106, Vmax is adjusted equal to 2.
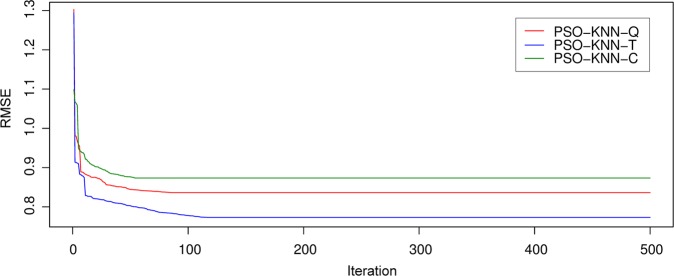
Once the PSO’s factors are adjusted, the compatibility of particle locations is calculated via the RMSE function. For any definition in the process of optimization, considered particles jump in a constrained checking zone and exchange their experiment to discover the best location (i.e., lowest RMSE); 500 iterations were used to determine the best factors of the suggested PSO-KNN model according to the best position (i.e., lowest RMSE) of the swarm of whole repeats. Note that, three forms of the kernel function (Q, T, C) were applied for the PSO-KNN model as described in the previous section. Figure 6 indicates the efficiency of the optimization approach for the PSO-KNN algorithms. Note that, the best amounts of the hyper-factors obtained for the PSO-KNN models (i.e., after the process of optimization) were determined in Table 3.
Figure 6.
Efficiency of the PSO-KNN models in the process of optimization.
Table 3.
The hyper-parameters of PSO-KNN models.
| Model | Optimization values of the hyper-parameters | |
|---|---|---|
| k | d | |
| PSO-KNN-Q | 20 | 0.493 |
| PSO-KNN-T | 10 | 0.503 |
| PSO-KNN-C | 16 | 0.499 |
Results and Discussions
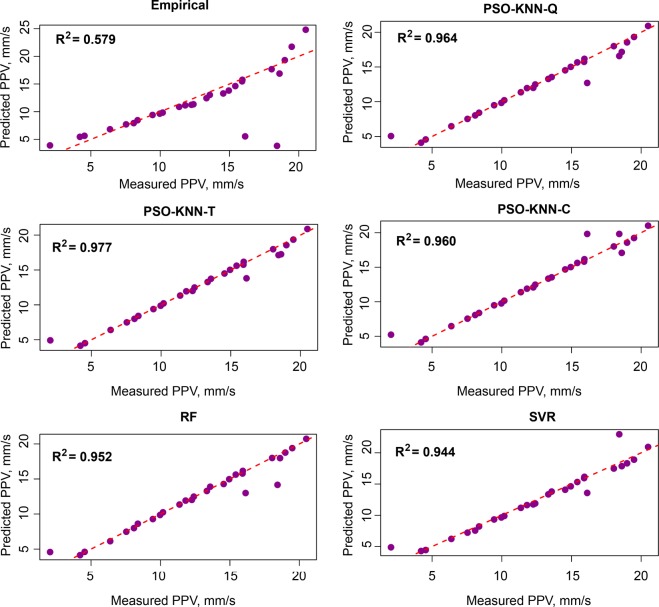
In the present section, the outcomes of the PPV predictive algorithms were highlighted. The efficiency indexes of the empirical, the RF, the SVR, and the three PSO-KNN models were evaluated based on RMSE, R2, and MAE, as illustrated in Table 4. The testing database is utilized as the unseen information to check the quality of the expanded models.
Table 4.
Efficiency indexes of the PPV predictive approaches in this work.
| Model | Training dataset | Testing dataset | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | MAE | RMSE | R2 | MAE | |
| Empirical | 2.525 | 0.822 | 1.306 | 3.615 | 0.579 | 1.727 |
| RF | 0.995 | 0.966 | 0.508 | 1.126 | 0.952 | 0.499 |
| SVR | 0.852 | 0.973 | 0.574 | 1.175 | 0.944 | 0.634 |
| PSO-KNN-Q | 0.836 | 0.977 | 0.417 | 0.982 | 0.964 | 0.454 |
| PSO-KNN-T | 0.773 | 0.982 | 0.403 | 0.797 | 0.977 | 0.385 |
| PSO-KNN-C | 0.873 | 0.975 | 0.430 | 1.014 | 0.960 | 0.455 |
Note: the best model was shown in bold type.
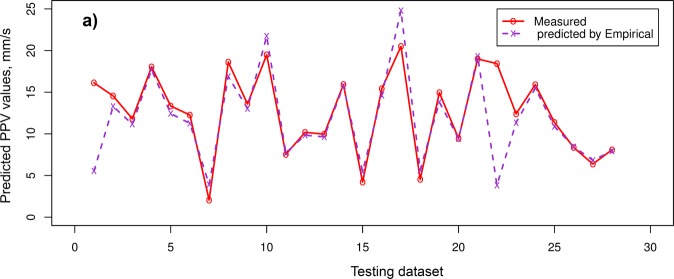
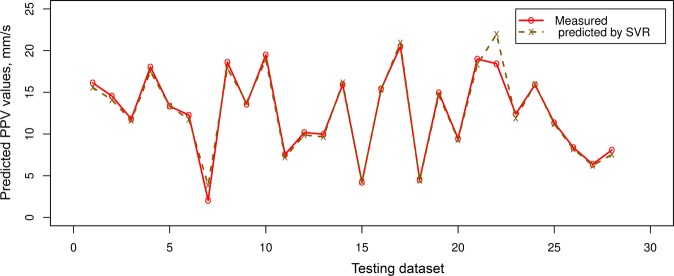
Table 4 indicated that the PSO-KNN models properly performed compared to the empirical, RF, and SVR models in estimating PPV. On the training dataset, the PSO-KNN models obtained robust performance with the RMSE in the range of 0.773 to 0.873; R2 in the range of 0.975 to 0.982; MAE in the field of 0.403 to 0.430. The benchmark models (RF and SVR) were additionally performed quite suitable in this work. But their efficiency was poorer than the PSO-KNN models with an RMSE in the range of 0.852 to 0.995, R2 in the field of 0.966 to 0.973, and MAE in the range of 0.508 to 0.574. In contrast, the empirical model yielded the poorest performance (RMSE = 2.525, R2 = 0.822, and MAE = 1.306). Observing the efficiency of the models on the testing dataset, it may be observed that the PSO-KNN algorithms were also outperformed over the other models (RMSE = 0.797 to 1.014; R2 = 0.960 to 0.977; MAE i = 0.385 to 0.455). Remarkable, the PSO-KNN model with the triweight kernel function (PSO-KNN-T) yielded the most accuracy among the proposed PSO-KNN models (i.e., RMSE = 0.797, R2 = 0.977, and MAE = 0.385). Next are the PSO-KNN-Q, PSO-KNN-C, RF and SVR models with RNSE in the range of 0.982 to 1.175; R2 in the range of 0.944 to 0.964; MAE in the range of 0.454 to 0.634. In contrast, the empirical obtained the poorest performance on the testing dataset (i.e., RMSE = 3.615, R2 = 0.579, and MAE = 1.727). Based on the results in Table 4, all the models are well generalized, especially the PSO-KNN model with triweight kernel function (i.e., PSO-KNN-T) is an outstanding model in term of RMSE, R2, and MAE. Therefore, it was selected as the most appropriate model for estimating PPV produced by bench blasting. Figure 7 shows the efficiency of the models on the testing database. Also, the precision of the expanded models is even compared in Figs 8–11.
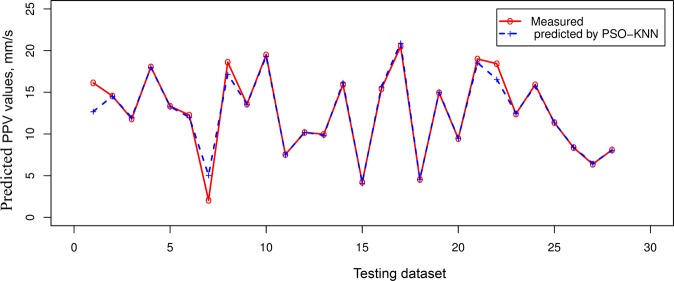
Figure 9.
Comparison among exact and estimated amount using the PSO-KNN-T model.
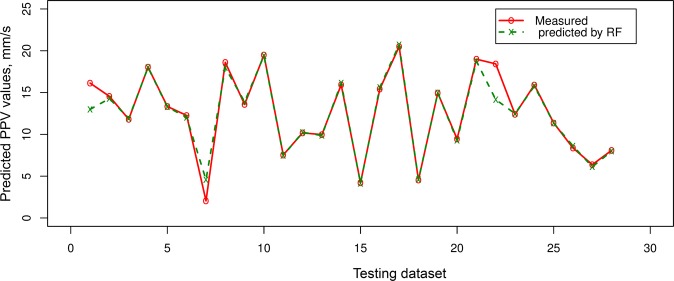
Figure 10.
Comparison among exact and estimated amount using the RF model.
Figure 7.
Measured versus predicted values of the models.
Figure 8.
Comparison among exact and estimated amount using the empirical model.
Figure 11.
Comparison among exact and estimated amount using the SVR model.
Conclusions
Blasting is known as one of the most appropriate and cheapest approaches for the fragmentation of hard-rocks in the case of open-pit mines. Nevertheless, its improper impacts on the surrounding environment, particularly ground vibration (PPV), are unavoidable. Hence, precise blast-induced PPV estimations are essential for decreasing the effects on our environment. The present work proposed a new hybrid technique for estimating PPV according to the KNN and PSO algorithms with high accuracy, namely PSO-KNN. According to the outcomes of this work, authors obtain some results as follows:
Blast-induced PPV is a usual involved and non-linear issue that is hard to investigate and estimate. High accuracy of the proposed PSO-KNN model in this study indicating that AI techniques are reasonable solutions, which solve this problem better than the empirical method.
The PSO algorithm is a suitable optimization tool for estimating purposes of blast-induced PPV. It has a dramatic role in enhancing the precision of the KNN approach, according to RMSE, R2, and MAE, as illustrated in Table 4. However, the integration of PSO and KNN algorithms are often complexity when setting the parameters.
The proposed PSO-KNN model (PSO-KNN-T) is a superior approach in estimating PPV induced by bench blasting; therefore, it is an alternative tool that should be considered for other areas in predicting PPV, as well as the other blasting problems in practical engineering.
This research only considered two parameters of W and R for establishing the blast-induced PPV modes. Therefore, the performance of these models can be enhanced if the other parameters related to the blast pattern and properties of rock mass are to be considered.
Acknowledgements
This research was supported by Hanoi University of Mining and Geology (HUMG), Hanoi Vietnam; Duy Tan University, Da Nang, Vietnam. We also thank the Center for Mining, Electro-Mechanical research of HUMG for supporting the instruments for data collecting.
Author Contributions
Data collection and experimental works: Xuan-Nam Bui, Quang-Hieu Tran and Nguyen Quoc Long; Writing, discussion, analysis: Xuan-Nam Bui, Pirat Jaroonpattanapong and Hoang Nguyen.
Data Availability
All data generated or analyzed during the current study are included.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Khandelwal M, Singh T. Prediction of blast induced air overpressure in opencast mine. Noise & Vibration Worldwide. 2005;36:7–16. doi: 10.1260/0957456053499095. [DOI] [Google Scholar]
- 2.Verma A, Singh T. Intelligent systems for ground vibration measurement: a comparative study. Engineering with Computers. 2011;27:225–233. doi: 10.1007/s00366-010-0193-7. [DOI] [Google Scholar]
- 3.Monjezi M, Khoshalan HA, Varjani AY. Prediction of flyrock and backbreak in open pit blasting operation: a neuro-genetic approach. Arabian Journal of Geosciences. 2012;5:441–448. doi: 10.1007/s12517-010-0185-3. [DOI] [Google Scholar]
- 4.Nguyen, H., Drebenstedt, C., Bui, X.-N. & Bui, D. T. Prediction of Blast-induced Ground Vibration in an Open-pit Mine by a Novel Hybrid Model Based on Clustering and Artificial Neural Network. Natural Resources Research (2019).
- 5.Bui, X. N., Nguyen, H., Le, H. A., Bui, H. B. & Do, N. H. Prediction of Blast-induced Air Over-pressure in Open-Pit Mine: Assessment of Different Artificial Intelligence Techniques. Natural Resources Research, 10.1007/s11053-019-09461-0 (2019).
- 6.Nguyen H. Support vector regression approach with different kernel functions for predicting blast-induced ground vibration: a case study in an open-pit coal mine of Vietnam. SN Applied Sciences. 2019;1:283. doi: 10.1007/s42452-019-0295-9. [DOI] [Google Scholar]
- 7.Nguyen H, et al. Evaluating and predicting blast-induced ground vibration in open-cast mine using ANN: a case study in Vietnam. SN Applied Sciences. 2018;1:125. doi: 10.1007/s42452-018-0136-2. [DOI] [Google Scholar]
- 8.Singh T, Singh V. An intelligent approach to prediction and control ground vibration in mines. Geotechnical & Geological Engineering. 2005;23:249–262. doi: 10.1007/s10706-004-7068-x. [DOI] [Google Scholar]
- 9.Khandelwal M, Singh T. Evaluation of blast-induced ground vibration predictors. Soil Dynamics and Earthquake Engineering. 2007;27:116–125. doi: 10.1016/j.soildyn.2006.06.004. [DOI] [Google Scholar]
- 10.Khandelwal M, Singh T. Prediction of blast-induced ground vibration using artificial neural network. International Journal of Rock Mechanics and Mining Sciences. 2009;46:1214–1222. doi: 10.1016/j.ijrmms.2009.03.004. [DOI] [Google Scholar]
- 11.Khandelwal M, Kankar P, Harsha S. Evaluation and prediction of blast induced ground vibration using support vector machine. Mining Science and Technology (China) 2010;20:64–70. doi: 10.1016/S1674-5264(09)60162-9. [DOI] [Google Scholar]
- 12.Nguyen, H., Bui, X.-N., Tran, Q.-H. & Mai, N.-L. A New Soft Computing Model for Estimating and Controlling Blast-Produced Ground Vibration Based on Hierarchical K-Means Clustering and Cubist Algorithms. Applied Soft Computing, 1–20 (2019).
- 13.Bui, X.-N., Nguyen, H., Le, H.-A., Bui, H.-B. & Do, N.-H. Prediction of Blast-induced Air Over-pressure in Open-Pit Mine: Assessment of Different Artificial Intelligence Techniques. Natural Resources Research, 1–25, 10.1007/s11053-019-09461-0 (2019).
- 14.Duvall, W. I. & Petkof, B. Spherical propagation of explosion-generated strain pulses in rock. (Bureau of Mines, 1958).
- 15.Langefors, U. & Kihlstrom, B. (JohnWiley and Sons Inc., New York, 1963).
- 16.Ambraseys, N. Rock Mechanics in Engineering Practice. (1968).
- 17.Ghosh, A. & Daemen, J. J. In The 24th US Symposium on Rock Mechanics (USRMS). (American Rock Mechanics Association).
- 18.Roy PP. Vibration control in an opencast mine based on improved blast vibration predictors. Mining Science and Technology. 1991;12:157–165. doi: 10.1016/0167-9031(91)91642-U. [DOI] [Google Scholar]
- 19.Hao H, Wu Y, Ma G, Zhou Y. Characteristics of surface ground motions induced by blasts in jointed rock mass. Soil Dynamics and Earthquake Engineering. 2001;21:85–98. doi: 10.1016/S0267-7261(00)00104-4. [DOI] [Google Scholar]
- 20.Venkatesh H. Influence of total charge in a blast on the intensity of ground vibrations—field experiment and computer simulation. Fragblast. 2005;9:127–138. doi: 10.1080/13855140500332260. [DOI] [Google Scholar]
- 21.Kuzu C. The importance of site-specific characters in prediction models for blast-induced ground vibrations. Soil Dynamics and Earthquake Engineering. 2008;28:405–414. doi: 10.1016/j.soildyn.2007.06.013. [DOI] [Google Scholar]
- 22.Ak H, Konuk A. The effect of discontinuity frequency on ground vibrations produced from bench blasting: a case study. Soil Dynamics and Earthquake Engineering. 2008;28:686–694. doi: 10.1016/j.soildyn.2007.11.006. [DOI] [Google Scholar]
- 23.Simangunsong, G. M. & Wahyudi, S. Effect of bedding plane on prediction blast-induced ground vibration in open pit coal mines. International Journal of Rock Mechanics and Mining Sciences, 1–8 (2015).
- 24.Monjezi M, Ghafurikalajahi M, Bahrami A. Prediction of blast-induced ground vibration using artificial neural networks. Tunnelling and Underground Space Technology. 2011;26:46–50. doi: 10.1016/j.tust.2010.05.002. [DOI] [Google Scholar]
- 25.Ghasemi E, Ataei M, Hashemolhosseini H. Development of a fuzzy model for predicting ground vibration caused by rock blasting in surface mining. Journal of Vibration and Control. 2013;19:755–770. doi: 10.1177/1077546312437002. [DOI] [Google Scholar]
- 26.Monjezi M, Hasanipanah M, Khandelwal M. Evaluation and prediction of blast-induced ground vibration at Shur River Dam, Iran, by artificial neural network. Neural Computing and Applications. 2013;22:1637–1643. doi: 10.1007/s00521-012-0856-y. [DOI] [Google Scholar]
- 27.Saadat M, Khandelwal M, Monjezi M. An ANN-based approach to predict blast-induced ground vibration of Gol-E-Gohar iron ore mine, Iran. Journal of Rock Mechanics and Geotechnical Engineering. 2014;6:67–76. doi: 10.1016/j.jrmge.2013.11.001. [DOI] [Google Scholar]
- 28.Hajihassani M, Armaghani DJ, Marto A, Mohamad ET. Ground vibration prediction in quarry blasting through an artificial neural network optimized by imperialist competitive algorithm. Bulletin of Engineering Geology and the Environment. 2015;74:873–886. doi: 10.1007/s10064-014-0657-x. [DOI] [Google Scholar]
- 29.Nguyen, H. & Bui, X.-N. In Mining sciences and technology - XXVI. 177–182 (Industry and trade of the socialist republic of Vietnam).
- 30.Bui DT, Nhu V-H, Hoang N-D. Prediction of soil compression coefficient for urban housing project using novel integration machine learning approach of swarm intelligence and Multi-layer Perceptron Neural Network. Advanced Engineering Informatics. 2018;38:593–604. doi: 10.1016/j.aei.2018.09.005. [DOI] [Google Scholar]
- 31.Zhou Y, Cao R. The artificial neural network prediction algorithm research of rail-gun current and armature speed based on B-dot probes array. Measurement. 2019;133:47–55. doi: 10.1016/j.measurement.2018.09.078. [DOI] [Google Scholar]
- 32.Hoang N-D. Estimating punching shear capacity of steel fibre reinforced concrete slabs using sequential piecewise multiple linear regression and artificial neural network. Measurement. 2019;137:58–70. doi: 10.1016/j.measurement.2019.01.035. [DOI] [Google Scholar]
- 33.Bilski P. Data set preprocessing methods for the artificial intelligence-based diagnostic module. Measurement. 2014;54:180–190. doi: 10.1016/j.measurement.2014.03.023. [DOI] [Google Scholar]
- 34.Di Santo KG, Di Santo SG, Monaro RM, Saidel MA. Active demand side management for households in smart grids using optimization and artificial intelligence. Measurement. 2018;115:152–161. doi: 10.1016/j.measurement.2017.10.010. [DOI] [Google Scholar]
- 35.Ponce H, Gutiérrez S. An indoor predicting climate conditions approach using Internet-of-Things and artificial hydrocarbon networks. Measurement. 2019;135:170–179. doi: 10.1016/j.measurement.2018.11.043. [DOI] [Google Scholar]
- 36.Akhani M, Kashani AR, Mousavi M, Gandomi AH. A hybrid computational intelligence approach to predict spectral acceleration. Measurement. 2019;138:578–589. doi: 10.1016/j.measurement.2019.02.054. [DOI] [Google Scholar]
- 37.Chen S-L, Shu D-Y. Measurement forecast of anomalous threshold voltages in BCD LV submicron n-MOSFETs with two artificial intelligence methods. Measurement. 2017;100:93–98. doi: 10.1016/j.measurement.2016.12.054. [DOI] [Google Scholar]
- 38.Chen, T. Forecasting the yield of a semiconductor product using a hybrid-aggregation and entropy-consensus fuzzy collaborative intelligence approach. Measurement (2019).
- 39.Illias HA, Chai XR. Hybrid modified evolutionary particle swarm optimisation-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis. Measurement. 2016;90:94–102. doi: 10.1016/j.measurement.2016.04.052. [DOI] [Google Scholar]
- 40.Koopialipoor M, Fallah A, Armaghani DJ, Azizi A, Mohamad ET. Three hybrid intelligent models in estimating flyrock distance resulting from blasting. Engineering with Computers. 2019;35:243–256. doi: 10.1007/s00366-018-0596-4. [DOI] [Google Scholar]
- 41.Armaghani DJ, et al. Evaluation and prediction of flyrock resulting from blasting operations using empirical and computational methods. Engineering with Computers. 2016;32:109–121. doi: 10.1007/s00366-015-0402-5. [DOI] [Google Scholar]
- 42.Mohamad ET, Armaghani DJ, Hasanipanah M, Murlidhar BR, Alel MNA. Estimation of air-overpressure produced by blasting operation through a neuro-genetic technique. Environmental Earth Sciences. 2016;75:174. doi: 10.1007/s12665-015-4983-5. [DOI] [Google Scholar]
- 43.Moayedi H, Armaghani DJ. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Engineering with Computers. 2018;34:347–356. doi: 10.1007/s00366-017-0545-7. [DOI] [Google Scholar]
- 44.Moayedi H, Hayati S. Modelling and optimization of ultimate bearing capacity of strip footing near a slope by soft computing methods. Applied Soft Computing. 2018;66:208–219. doi: 10.1016/j.asoc.2018.02.027. [DOI] [Google Scholar]
- 45.Moayedi H, Hayati S. Applicability of a CPT-Based Neural Network Solution in Predicting Load-Settlement Responses of Bored Pile. International Journal of Geomechanics. 2018;18:06018009. doi: 10.1061/(ASCE)GM.1943-5622.0001125. [DOI] [Google Scholar]
- 46.Moayedi, H. & Hayati, S. Artificial intelligence design charts for predicting friction capacity of driven pile in clay. Neural Computing and Applications, 10.1007/s00521-018-3555-5 (2018).
- 47.Moayedi, H. et al. Prediction of ultimate bearing capacity through various novel evolutionary and neural network models. Engineering with Computers, 10.1007/s00366-019-00723-2 (2019).
- 48.Asteris Panagiotis G., Kolovos Konstantinos G. Self-compacting concrete strength prediction using surrogate models. Neural Computing and Applications. 2019;31:409–424. doi: 10.1007/s00521-017-3007-7. [DOI] [Google Scholar]
- 49.Khandelwal M, et al. Classification and regression tree technique in estimating peak particle velocity caused by blasting. Engineering with Computers. 2017;33:45–53. doi: 10.1007/s00366-016-0455-0. [DOI] [Google Scholar]
- 50.Nguyen H, Bui X-N, Bui H-B, Cuong DT. Developing an XGBoost model to predict blast-induced peak particle velocity in an open-pit mine: a case study. Acta Geophysica. 2019;67:477–490. doi: 10.1007/s11600-019-00268-4. [DOI] [Google Scholar]
- 51.Nguyen H, Bui X-N, Tran Q-H, Mai N-L. A new soft computing model for estimating and controlling blast-produced ground vibration based on hierarchical K-means clustering and cubist algorithms. Applied Soft Computing. 2019;77:376–386. doi: 10.1016/j.asoc.2019.01.042. [DOI] [Google Scholar]
- 52.Hasanipanah M, Naderi R, Kashir J, Noorani SA, Qaleh AZA. Prediction of blast-produced ground vibration using particle swarm optimization. Engineering with Computers. 2017;33:173–179. doi: 10.1007/s00366-016-0462-1. [DOI] [Google Scholar]
- 53.Armaghani DJ, Hajihassani M, Mohamad ET, Marto A, Noorani S. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arabian Journal of Geosciences. 2014;7:5383–5396. doi: 10.1007/s12517-013-1174-0. [DOI] [Google Scholar]
- 54.Armaghani DJ, Hasanipanah M, Amnieh HB, Mohamad ET. Feasibility of ICA in approximating ground vibration resulting from mine blasting. Neural Computing and Applications. 2018;29:457–465. doi: 10.1007/s00521-016-2577-0. [DOI] [Google Scholar]
- 55.Hasanipanah M, et al. Prediction of an environmental issue of mine blasting: an imperialistic competitive algorithm-based fuzzy system. International Journal of Environmental Science and Technology. 2018;15:551–560. doi: 10.1007/s13762-017-1395-y. [DOI] [Google Scholar]
- 56.Shang, Y., Nguyen, H., Bui, X.-N., Tran, Q.-H. & Moayedi, H. A Novel Artificial Intelligence Approach to Predict Blast-Induced Ground Vibration in Open-Pit Mines Based on the Firefly Algorithm and Artificial Neural Network. Natural Resources Research, 10.1007/s11053-019-09503-7 (2019).
- 57.Zhang, X. et al. Novel Soft Computing Model for Predicting Blast-Induced Ground Vibration in Open-Pit Mines Based on Particle Swarm Optimization and XGBoost. Natural Resources Research, 10.1007/s11053-019-09492-7 (2019).
- 58.Yang, H., Hasanipanah, M., Tahir, M. M. & Bui, D. T. Intelligent Prediction of Blasting-Induced Ground Vibration Using ANFIS Optimized by GA and PSO. Natural Resources Research, 10.1007/s11053-019-09515-3 (2019).
- 59.Vinacomin. Report on geological exploration of Coc Sau open pit coal mine, Quang Ninh, Vietnam (in Vietnamse-unpublished). (VINACOMIN, Vietnam, 2015).
- 60.Davitt, A. L. & Simon, J. R. (Google Patents, 1983).
- 61.Khandelwal M, Singh T. Prediction of blast induced ground vibrations and frequency in opencast mine: a neural network approach. Journal of sound and vibration. 2006;289:711–725. doi: 10.1016/j.jsv.2005.02.044. [DOI] [Google Scholar]
- 62.Khandelwal M, Kumar DL, Yellishetty M. Application of soft computing to predict blast-induced ground vibration. Engineering with Computers. 2011;27:117–125. doi: 10.1007/s00366-009-0157-y. [DOI] [Google Scholar]
- 63.Nguyen Hoang, Bui Xuan-Nam, Bui Hoang-Bac, Cuong Dao Trong. Developing an XGBoost model to predict blast-induced peak particle velocity in an open-pit mine: a case study. Acta Geophysica. 2019;67(2):477–490. doi: 10.1007/s11600-019-00268-4. [DOI] [Google Scholar]
- 64.Drucker, H., Burges, C. J., Kaufman, L., Smola, A. J. & Vapnik, V. In Advances in neural information processing systems. 155–161.
- 65.Liaw A, Wiener M. Classification and regression by randomForest. R news. 2002;2:18–22. [Google Scholar]
- 66.Gao W, Guirao JL, Basavanagoud B, Wu J. Partial multi-dividing ontology learning algorithm. Information Sciences. 2018;467:35–58. doi: 10.1016/j.ins.2018.07.049. [DOI] [Google Scholar]
- 67.Bansal, J. C. In Evolutionary and Swarm Intelligence Algorithms 11–23 (Springer, 2019).
- 68.Guo H, Li H, Xiong J, Yu M. Indoor positioning system based on particle swarm optimization algorithm. Measurement. 2019;134:908–913. doi: 10.1016/j.measurement.2018.12.038. [DOI] [Google Scholar]
- 69.Bensingh RJ, Machavaram R, Boopathy SR, Jebaraj C. Injection molding process optimization of a bi-aspheric lens using hybrid artificial neural networks (ANNs) and particle swarm optimization (PSO) Measurement. 2019;134:359–374. doi: 10.1016/j.measurement.2018.10.066. [DOI] [Google Scholar]
- 70.Nguyen, H. et al. Optimizing ANN models with PSO for predicting short building seismic response. Engineering with Computers, 10.1007/s00366-019-00733-0 (2019).
- 71.Nguyen, H., Moayedi, H., Jusoh, W. A. W. & Sharifi, A. Proposing a novel predictive technique using M5Rules-PSO model estimating cooling load in energy-efficient building system. Engineering with Computers, 10.1007/s00366-019-00735-y (2019).
- 72.Eberhart, R. C. & Kennedy, J. In MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science. 39–43 (IEEE).
- 73.Kennedy, J. In Encyclopedia of machine learning 760–766 (Springer, 2011).
- 74.Altman NS. An introduction to kernel and nearest-neighbor nonparametric regression. The American Statistician. 1992;46:175–185. [Google Scholar]
- 75.Yu K, Ji L, Zhang X. Kernel nearest-neighbor algorithm. Neural Processing Letters. 2002;15:147–156. doi: 10.1023/A:1015244902967. [DOI] [Google Scholar]
- 76.Gao W, Wu H, Siddiqui MK, Baig AQ. Study of biological networks using graph theory. Saudi journal of biological sciences. 2018;25:1212–1219. doi: 10.1016/j.sjbs.2017.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Zhou J, Li X, Mitri HS. Classification of rockburst in underground projects: Comparison of ten supervised learning methods. Journal of Computing in Civil Engineering. 2016;30:04016003. doi: 10.1061/(ASCE)CP.1943-5487.0000553. [DOI] [Google Scholar]
- 78.Lin, Y., Zhou, K. & Li, J. Application of Cloud Model in Rock Burst Prediction and Performance Comparison with Three Machine Learning Algorithms. IEEE Access (2018).
- 79.Qi C, Tang X. A hybrid ensemble method for improved prediction of slope stability. International Journal for Numerical and Analytical Methods in Geomechanics. 2018;42:1823–1839. doi: 10.1002/nag.2834. [DOI] [Google Scholar]
- 80.Maillo J, Ramírez S, Triguero I, Herrera F. kNN-IS: An Iterative Spark-based design of the k-Nearest Neighbors classifier for big data. Knowledge-Based Systems. 2017;117:3–15. doi: 10.1016/j.knosys.2016.06.012. [DOI] [Google Scholar]
- 81.Ali, L., Kasetkasem, T., Khan, F. G., Chanwimaluang, T. & Nakahara, H. In Information and Communication Technology for Embedded Systems (IC-ICTES), 2017 8th International Conference of. 1–6 (IEEE).
- 82.Wu X, Yang J, Wang S. Tea category identification based on optimal wavelet entropy and weighted k-Nearest Neighbors algorithm. Multimedia Tools and Applications. 2018;77:3745–3759. doi: 10.1007/s11042-016-3931-z. [DOI] [Google Scholar]
- 83.Amiri M, Amnieh HB, Hasanipanah M, Khanli LM. A new combination of artificial neural network and K-nearest neighbors models to predict blast-induced ground vibration and air-overpressure. Engineering with Computers. 2016;32:631–644. doi: 10.1007/s00366-016-0442-5. [DOI] [Google Scholar]
- 84.Cleveland WS, Devlin SJ. Locally weighted regression: an approach to regression analysis by local fitting. Journal of the American statistical association. 1988;83:596–610. doi: 10.1080/01621459.1988.10478639. [DOI] [Google Scholar]
- 85.Epanechnikov VA. Non-parametric estimation of a multivariate probability density. Theory of Probability & Its Applications. 1969;14:153–158. doi: 10.1137/1114019. [DOI] [Google Scholar]
- 86.Silverman, B. W. Density estimation for statistics and data analysis. (Routledge, 2018).
- 87.Li, Q. & Racine, J. S. Nonparametric Econometrics: Theory and Practice Princeton University Press (2007).
- 88.Chai T, Draxler RR. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geoscientific Model Development. 2014;7:1247–1250. doi: 10.5194/gmd-7-1247-2014. [DOI] [Google Scholar]
- 89.Gao, W., Guirao, J. L. G., Abdel-Aty, M. & Xi, W. An independent set degree condition for fractional critical deleted graphs. Discrete & Continuous Dynamical Systems-S (2018).
- 90.Nick N. Joseph Juran, 103, Pioneer in Quality Control, Dies. New York Times. 2008;3:3. [Google Scholar]
- 91.Swingler, K. Applying neural networks: a practical guide. (Morgan Kaufmann, 1996).
- 92.Dou Jie, Yunus Ali P., Tien Bui Dieu, Merghadi Abdelaziz, Sahana Mehebub, Zhu Zhongfan, Chen Chi-Wen, Khosravi Khabat, Yang Yong, Pham Binh Thai. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Science of The Total Environment. 2019;662:332–346. doi: 10.1016/j.scitotenv.2019.01.221. [DOI] [PubMed] [Google Scholar]
- 93.Breiman L. Random forests. Machine learning. 2001;45:5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 94.Nguyen Hoang, Bui Xuan-Nam. Predicting Blast-Induced Air Overpressure: A Robust Artificial Intelligence System Based on Artificial Neural Networks and Random Forest. Natural Resources Research. 2018;28(3):893–907. doi: 10.1007/s11053-018-9424-1. [DOI] [Google Scholar]
- 95.Tsirogiannis G, Perdios E, Markellos V. Improved grid search method: an efficient tool for global computation of periodic orbits. Celestial Mechanics and Dynamical Astronomy. 2009;103:49–78. doi: 10.1007/s10569-008-9165-2. [DOI] [Google Scholar]
- 96.Kohavi, R. In Ijcai. 1137–1145 (Montreal, Canada).
- 97.Scholkopf B, et al. Comparing support vector machines with Gaussian kernels to radial basis function classifiers. IEEE transactions on Signal Processing. 1997;45:2758–2765. doi: 10.1109/78.650102. [DOI] [Google Scholar]
- 98.Ko C-N, Lee C-M. Short-term load forecasting using SVR (support vector regression)-based radial basis function neural network with dual extended Kalman filter. Energy. 2013;49:413–422. doi: 10.1016/j.energy.2012.11.015. [DOI] [Google Scholar]
- 99.Kisi O, Parmar KS. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution. Journal of Hydrology. 2016;534:104–112. doi: 10.1016/j.jhydrol.2015.12.014. [DOI] [Google Scholar]
- 100.Marinakis Y, Migdalas A, Sifaleras A. A hybrid particle swarm optimization–variable neighborhood search algorithm for constrained shortest path problems. European Journal of Operational Research. 2017;261:819–834. doi: 10.1016/j.ejor.2017.03.031. [DOI] [Google Scholar]
- 101.Agrawal, A. P. & Kaur, A. In Data Engineering and Intelligent Computing 397–405 (Springer, 2018).
- 102.Bui DT, et al. Hybrid artificial intelligence approach based on neural fuzzy inference model and metaheuristic optimization for flood susceptibilitgy modeling in a high-frequency tropical cyclone area using GIS. Journal of Hydrology. 2016;540:317–330. doi: 10.1016/j.jhydrol.2016.06.027. [DOI] [Google Scholar]
- 103.Poli R, Kennedy J, Blackwell T. Particle swarm optimization. Swarm intelligence. 2007;1:33–57. doi: 10.1007/s11721-007-0002-0. [DOI] [Google Scholar]
- 104.Kennedy, J. In International Conference on Evolutionary Programming. 579–589 (Springer).
- 105.Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE transactions on Evolutionary Computation. 2002;6:58–73. doi: 10.1109/4235.985692. [DOI] [Google Scholar]
- 106.Eberhart, R. C. & Shi, Y. In Evolutionary Computation, 2000. Proceedings of the 2000 Congress on. 84–88 (IEEE).
- 107.Iphar M, Yavuz M, Ak H. Prediction of ground vibrations resulting from the blasting operations in an open-pit mine by adaptive neuro-fuzzy inference system. Environmental Geology. 2008;56:97–107. doi: 10.1007/s00254-007-1143-6. [DOI] [Google Scholar]
- 108.Monjezi M, Ahmadi M, Sheikhan M, Bahrami A, Salimi A. Predicting blast-induced ground vibration using various types of neural networks. Soil Dynamics and Earthquake Engineering. 2010;30:1233–1236. doi: 10.1016/j.soildyn.2010.05.005. [DOI] [Google Scholar]
- 109.Hasanipanah M, Monjezi M, Shahnazar A, Armaghani DJ, Farazmand A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Measurement. 2015;75:289–297. doi: 10.1016/j.measurement.2015.07.019. [DOI] [Google Scholar]
- 110.Dindarloo SR. Prediction of blast-induced ground vibrations via genetic programming. International Journal of Mining Science and Technology. 2015;25:1011–1015. doi: 10.1016/j.ijmst.2015.09.020. [DOI] [Google Scholar]
- 111.Hajihassani M, Armaghani DJ, Monjezi M, Mohamad ET, Marto A. Blast-induced air and ground vibration prediction: a particle swarm optimization-based artificial neural network approach. Environmental Earth Sciences. 2015;74:2799–2817. doi: 10.1007/s12665-015-4274-1. [DOI] [Google Scholar]
- 112.Monjezi M, Baghestani M, Faradonbeh RS, Saghand MP, Armaghani DJ. Modification and prediction of blast-induced ground vibrations based on both empirical and computational techniques. Engineering with Computers. 2016;32:717–728. doi: 10.1007/s00366-016-0448-z. [DOI] [Google Scholar]
- 113.Hasanipanah M, Faradonbeh RS, Amnieh HB, Armaghani DJ, Monjezi M. Forecasting blast-induced ground vibration developing a CART model. Engineering with Computers. 2017;33:307–316. doi: 10.1007/s00366-016-0475-9. [DOI] [Google Scholar]
- 114.Taheri K, Hasanipanah M, Golzar SB, Majid MZA. A hybrid artificial bee colony algorithm-artificial neural network for forecasting the blast-produced ground vibration. Engineering with Computers. 2017;33:689–700. doi: 10.1007/s00366-016-0497-3. [DOI] [Google Scholar]
- 115.Ragam P, Nimaje D. Assessment of blast-induced ground vibration using different predictor approaches-a comparison. Chemical Engineering Transactions. 2018;66:487–492. [Google Scholar]
- 116.Armaghani DJ, Hasanipanah M, Amnieh HB, Mohamad ET. Feasibility of ICA in approximating ground vibration resulting from mine blasting. Neural Computing and Applications. 2018;29:457–465. doi: 10.1007/s00521-016-2577-0. [DOI] [Google Scholar]
- 117.Behzadafshar K, Mohebbi F, Soltani Tehrani M, Hasanipanah M, Tabrizi O. Predicting the ground vibration induced by mine blasting using imperialist competitive algorithm. Engineering Computations. 2018;35:1774–1787. doi: 10.1108/EC-08-2017-0290. [DOI] [Google Scholar]
- 118.Sheykhi H, Bagherpour R, Ghasemi E, Kalhori H. Forecasting ground vibration due to rock blasting: a hybrid intelligent approach using support vector regression and fuzzy C-means clustering. Engineering with Computers. 2018;34:357–365. doi: 10.1007/s00366-017-0546-6. [DOI] [Google Scholar]
- 119.Arthur, C. K., Temeng, V. A. & Ziggah, Y. Y. Novel approach to predicting blast-induced ground vibration using Gaussian process regression. Engineering with Computers, 1–14 (2019).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed during the current study are included.