LTMG: a novel statistical modeling of transcriptional expression states in single-cell RNA-Seq data

Abstract

A key challenge in modeling single-cell RNA-seq data is to capture the diversity of gene expression states regulated by different transcriptional regulatory inputs across individual cells, which is further complicated by largely observed zero and low expressions. We developed a left truncated mixture Gaussian (LTMG) model, from the kinetic relationships of the transcriptional regulatory inputs, mRNA metabolism and abundance in single cells. LTMG infers the expression multi-modalities across single cells, meanwhile, the dropouts and low expressions are treated as left truncated. We demonstrated that LTMG has significantly better goodness of fitting on an extensive number of scRNA-seq data, comparing to three other state-of-the-art models. Our biological assumption of the low non-zero expressions, rationality of the multimodality setting, and the capability of LTMG in extracting expression states specific to cell types or functions, are validated on independent experimental data sets. A differential gene expression test and a co-regulation module identification method are further developed. We experimentally validated that our differential expression test has higher sensitivity and specificity, compared with other five popular methods. The co-regulation analysis is capable of retrieving gene co-regulation modules corresponding to perturbed transcriptional regulations. A user-friendly R package with all the analysis power is available at https://github.com/zy26/LTMGSCA.

INTRODUCTION

Single-cell RNA sequencing (scRNA-seq) has gained extensive utilities in many fields, among which, the most important one is to investigate the heterogeneity and/or plasticity of cells within a complex tissue micro-environment and/or development process (1–3). This has stimulated the design of a variety of methods specifically for single cells: modeling the expression distribution (4–6), differential expression analysis (7–12), cell clustering (13,14), non-linear embedding based visualization (15,16) and gene co-expression analysis (14,17,18). etc. Gene expression in a single cell is determined by the activation status of the gene's transcriptional regulators and the rate of metabolism of the mRNA molecule. In single cells, owing to the dynamic transcriptional regulatory signals, the observed expressions could span a wider spectrum, and exhibit a more distinct cellular modalities, compared with those observed on bulk cells (14). In addition, the limited experimental resolution often results in a large number of expression values under detected, i.e. zero or lowly observed expressions, which are generally noted as ‘dropout’ events. How to decipher the gene expression multimodality hidden among the cells, and unravel them from the highly noisy background, forms a key challenge in accurate modeling and analyses of scRNA-seq data.

Clearly, all the analysis techniques for single cells RNA-Seq data including differential expression, cell clustering, dimension reduction, and gene co-expression, heavily depend on an accurate characterization of the single cell expression distribution. Currently, multiple statistical distributions have been used to model scRNA-Seq data (4,5,9,10). All the formulations consider a fixed distribution for zero or low expressions disregarding the dynamics of mRNA metabolism, and only the mean of expression level and proportion of the rest is maintained as target of interest. These methods warrant further considerations: (i) the diversity of transcriptional regulatory states among cells, as shown by the single molecular in situ hybridization (smFISH) data (19–21), would be wiped off with a simple mean statistics derived from non-zero expression values; (ii) some of the observed non-zero expressions could be a result of mRNA incompletely degraded, rather than expressions under certain active regulatory input, thus they should not be accounted as true expressions; (iii) zero-inflated unimodal model has an over-simplified assumption for mRNA dynamics, particularly, the error distribution of the zero or low expressions are caused by different reasons, negligence of this may eventually lead to a biased inference for the multi-modality encoded by the expressions on the higher end.

To account for the dynamics of mRNA metabolism, transcriptional regulatory states as well as technology bias contributing to single cell expressions, we developed a novel left truncated mixture Gaussian (LTMG) distribution that can effectively address the challenges above, from a systems biology point of view. The multiple left truncated Gaussian distributions correspond to heterogeneous gene expression states among cells, as an approximation of the gene's varied transcriptional regulation states. Truncation on the left of Gaussian distribution was introduced to specifically handle observed zero and low expressions in scRNA-seq data, caused by true zero expressions, ‘dropout’ events and low expressions resulted from incompletely metabolized mRNAs, respectively. Specifically, LTMG models the normalized expression profile (log CPM, or TPM) of a gene across cells as a mixture Gaussian distribution with K peaks corresponding to suppressed expression (SE) state and active expression (AE) state(s). We introduced a latent cutoff to represent the lowest expression level that can be reliably detected under the current experimental resolution. Any observed expression values below the experimental resolution are modeled as left censored data in fitting the mixture Gaussian model. For each gene, LTMG conveniently assigns each single cell to one expression state by reducing the amount of discretization error to a level considered negligible, while the signal-to-noise ratio and the interpretability of the expression data are largely improved. Based on the LTMG model, a differential expression test, a co-regulation module detection and a cell clustering algorithm were further developed.

A systematic method validation was conducted with the following key results: (i) LTMG achieves the best goodness of fitting in 23 high quality data sets, compared with four commonly utilized multimodal models of scRNA-seq data; (ii) using a set of mRNA kinetic data, we confirmed the validity of treating a significant portion of the low but non-zero expressions as a result of incompletely degraded mRNA in LTMG, which should not be considered as true expressions under active regulations; (iii) on a cancer single cell RNA-seq data, we demonstrated that single cell groups defined by distinct gene expression states captured by LTMG, are in good agreement with known sub cell types, i.e. exhausted CD8+T cell population and subclasses of fibroblast cells, in other words, the multi-modality setting in LTMG uncovers the heterogeneity among single cells; (iv) non-linear embedding and cell clustering based on LTMG discretized expression states produces more informative clusters; (v) we generated a single cell RNA-seq data with perturbed transcriptional regulation and validated the high sensitivity and specificity of the LTMG based differential gene expression and gene co-regulation analysis. A user-friendly R package with all the key features of the LTMG model was released through https://github.com/zy26/LTMGSCA.

METHODS

Mathematical model linking gene expression states in single cells to transcriptional regulation

A gene's expression in a mammalian cell is the result of the interactions between its DNA template and a collection of transcriptional regulatory inputs (TRIs) including: (i) transcriptional regulatory factors (TFs) (cis-regulation); (ii) miRNA or lncRNA; (iii) enhancer and super-enhancer and (iv) epigenetic regulatory signals (22,23). For a gene with P possible transcriptional regulation inputs, 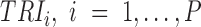, the probability of its promoter being bound by an RNA polymerase, 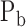, which is proportional to the rate of its transcription, can be modeled by a Michaelis–Menten equation (24,25)

(1)

where 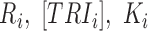denote production rate, concentration and kinetic parameters associated with the ith TRI; 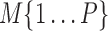is the power set of 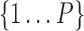, 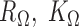denote the production rate and kinetic parameters associated with the interactive effects of TRIs in 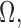where 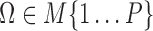. The set of active TRIs in a single cell fully determines the transcription rate of the gene, and thus its transcriptional regulatory state (TRS). Note that in a single cell each TRI can be rationally simplified to have two states: present or absent from the DNA molecule, thus the 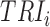is a Boolean variable and Equation (1) becomes a discrete function with at most 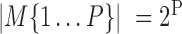values:

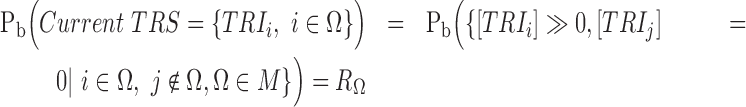(2)

Such discretization of gene's transcriptional rate greatly simplified the kinetic model and has achieved satisfactory performances in deriving the transcriptional regulatory dependency between the gene's expression state and its TRIs, which has been commonly utilized in thermodynamic modeling of transcriptional regulation (26–28). For a mammalian cell, the total number of combinations of TRIs can be substantially large, especially considering the epi-genetic regulators (22). However, the number of TRSs of a gene in a single cell RNA-seq experiment is always much smaller. The reason being: (i) the phenotypic diversity of the cells measured in one experiment is relatively small; (ii) local interactive effects among multiple TRIs are exerted on the same regulatory element (23) and (iii) some master repressors such as chromatin folding or certain TFs can dominate the regulation of the gene's expression (23).

Denote 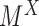as the set of all possible TRS of gene X and 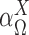as the probability of sampling a cell with TRS 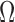, , 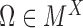from the cell population. By introducing a Gaussian error to the simplified model described in (2), the probability density function of the transcriptional rate of X in a single cell can be modeled as a mixture Gaussian distribution:

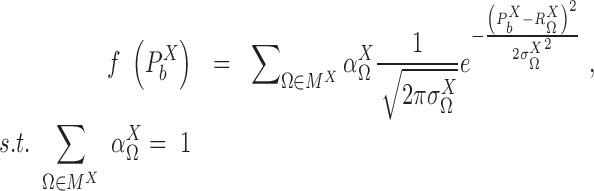(3)

where the mixing probability, mean and standard deviation, 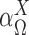, 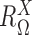and 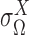correspond to the frequency, transcription rate, and variance of the TRS 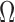. Single cell RNA-seq measures the abundance of mature mRNA in cytosol, which is determined by the transcription and degradation rate of the mRNA. The gene expression pattern we eventually observe is mainly shaped by the (i) cytosol mRNA abundance, compounded with (ii) observation errors and (iii) experimental resolution. Based on several common transcriptional regulation models, including constant transcriptional regulatory input and transcriptional bursting (29), we extend the multimodality of transcription inputs and rates defined in (2) and (3) to the multimodality of observed mRNA abundance (see more details in Supplementary Methods).

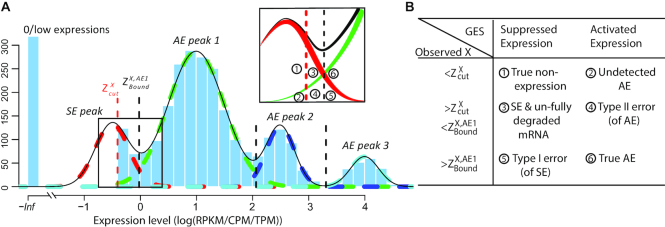
Denote 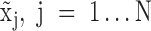as the normalized gene expression (such as log CPM or TPM) of gene X in a scRNA-seq experiment with individual library constructed for N cells and measured with high sequencing depth. Based on the derivations above, we illustrated the relationship between the repertoire of the TRSs of X, multi-modality of mRNA abundance, and its observed gene expression profile in Figure 1A. A mixture Gaussian model is utilized to characterize the distribution of observed normalized gene expression level of X through multiple cells. Gene expressions falling into a same peak are considered to have the same gene expression state (GES), that share the same TRS or different TRS with a similar mean pattern; while the expressions falling into different peaks are more likely to have different TRSs. We index the Gaussian peaks by their means and denote the one with smallest mean as peak 1, and define 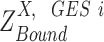as the boundary for the 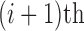and 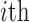peak, which can be easily obtained by maximum likelihood.

Figure 1.

(A, B) The relationship between observed expression level, the gene's SE and AE states, and the experimental resolution threshold 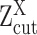. The histogram in light blue illustrates the distribution of the log normalized gene expression (RPKM, CPM or TPM) of one gene in a scRNA-seq data. The four dash curves represent the four fitted mixture components, corresponding to one SE and three AE peaks. 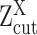is shown as the red dash line. The framed panel on top right is a zooming in of the non-zero low expression distribution, which is divided into six small areas (B) corresponding to the cases -, with detailed definition given in Supplementary Note.

For robust characterization of the single cell expression distribution, a key challenge is to address the observed zero and low expressions. These low expressions could be a result of multiple factors, such as technical errors, incompletely degraded mRNAs and varied experimental resolutions. We introduced a latent threshold 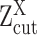where when 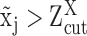, 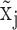is modeled by mixture Gaussian distribution. Otherwise, we conclude that 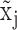cannot be reliably quantified under the current experimental resolution. Correspondingly, peaks with mean smaller or larger than 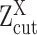were defined as suppressed expression (SE) or active expression (AE) peaks. 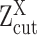differentiates the large expression values that are more likely to be under active expression state, from those low expression values that are not reliably quantifiable. In scRNA-seq data, other than a small number of housekeeping genes, an SE peak generally exists for most genes.

Figure 1A and B illustrates the relationship between the expression states of X, observed expression level 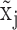, and 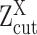. Specifically, when 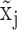is observed to be lower than 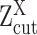, it can be: 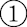true non-expression or expressions under an suppressed expression state and true active expression with low observed values, i.e. ‘drop-outs’; when is larger than 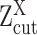and lower than 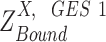, it can be: true non expression but observed to have non-zero expression value, probably due to sequencing error, or a delay in mRNA degradation; and true active expression state but falsely observed to have low expression, called Type II error; when 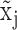is larger than 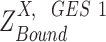, true suppressed expression state but falsely observed to have high expression, called Type I error; and true active expression state.

Based on the derivations above, we could model a single cell's gene expression profile as a multimodal distribution, with observations smaller than 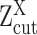left truncated. Hence, active expression states, i.e. the AE peaks, can be robustly inferred as mixture Gaussian is highly sensitive to outliers; and the unquantifiable non-zero low expressions, i.e. the SE peak(s), can be effectively handled.

Left Truncated Mixture Gaussian (LTMG) distribution for gene expression modeling

To accurately and robustly model the gene expression profile of scRNA-seq data, we developed a Left Truncated Mixture Gaussian model, namely LTMG, to fit the log transformed normalized gene expression measures of gene X, such as TPM, CPM or RPKM, over N cells as 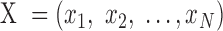. We assume that 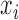follows a mixture Gaussian distribution with K Gaussian peaks corresponding to different SE and AE peaks. We introduce a parameter 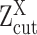and consider the log transformed zero and low expression values smaller than 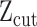as left censored data. With the left truncation assumption, 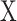is divided into reliably measured expressions (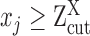) and left-censored gene expressions (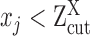). The density function of X can be written as:

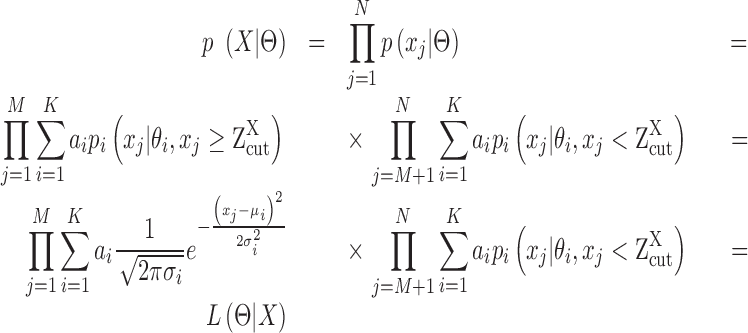(4)

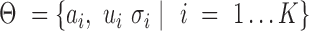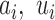where parameters and and 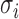are the mixing probability, mean and standard deviation of the K Gaussian distributions, corresponding to K expression states, M is the number of observations 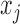that are larger than 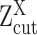, N is the total number of observations. 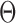can be estimated using EM algorithm with given 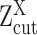and K. The computation of 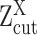for each gene, EM algorithm for estimating 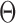, selection of K, and complete algorithm and mathematical derivations are detailed in Supplementary Methods.

Datasets used for model comparison

To conduct a comprehensive evaluation our model, we collected 23 datasets totaling 66 780 human and mouse cells across different cell extraction and sequencing platforms with varied experimental designs. It is noteworthy there are multiple scRNA-seq protocols that differ by cell capture, lysis and sequencing methods. These methods either construct individual libraries for each cell, or an overall library for thousands of cells at once, the latter of which is known as ‘drop-seq’ based method. Recent reviews suggested that the Smart-Seq2 protocols achieve best performance among the methods with individual libraries, and 10× Genomics Chromium is the most utilized commercialized pipeline (30). Our data collection comprehensively covers human and mouse data generated by Smart-seq/Smart-Seq2, 10x Genomics and inDrops platforms from January 2016 to June 2018 in the GEO database. Hence, we consider this collection as unbiased testing data that can represent the general characteristics of the single cell data generated from the two types of protocol. The detailed data information was listed in the Supplementary Table S1. Since each dataset has different levels of complexity, we reorganized the datasets into sub datasets with comparable levels of complexities. The sub datasets were generated to represent three different types of sample complexities: (i) pure condition, where each sub dataset contains cells of one type under a specific experimental condition; (ii) cell cluster, where each sub dataset belongs to a priori computationally clustered cells and (iii) complete data, where each sub dataset contains multiple mixed cell population, such as cells from one cancer tumor tissue (see detail in Supplementary Methods). In total, sub datasets with 51 pure condition, 49 cell cluster and 78 complete data were extracted from the 23 large data sets. It is noteworthy that each sub data set consists of only cells from one of the 23 original data set, to avoid causing batch effect.

Comparing the goodness of fitting of LTMG with other models

We compared LTMG with Zero-inflated mixed Gaussian (ZIMG), MAST[4] and Beta Poisson (BPSC)[5]. We use MAST with default parameters, and for each gene, only non-zero values were used and fitted with Gaussian distribution. For BPSC, to achieve a reliable estimation, only genes with non-zero expressions in at least 25 single cells were kept. ZIMG was used with default parameters. Kolmogorov Statistic (KS) is used to measure gene-wise goodness of fitting. For each gene, the KS score is assessed by using the none zero observations for ZIMG, MAST and BPSC models and normalized by dividing the KS score by the none zero proportions, due to their zero inflation assumption. Only genes kept for all four models are used for downstream evaluations.

For each extracted sub dataset, we defined a goodness fitting score for each method using the mean and standard deviation of gene-wise KS values:

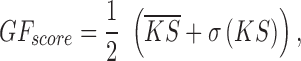where 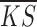is the mean value of gene-wise KS scores from a dataset and 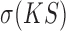is the standard deviation. The GF score evaluates each method on both overall accuracy (lower 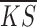value) and stability (lower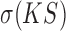), and smaller GF indicates better goodness of fitting. The mean and variance of gene-wise KS values for each sub dataset corresponding to all four methods were all provided in the Supplementary Table S2.

Modeling of mRNA metabolic rate with the LTMG model

We collected experimentally measured kinetics of mouse fibroblast cells, particularly the mRNA half-life, of 5028 mRNAs from Schwanhäusser et al's work (31) and two mouse fibroblast scRNA-Seq datasets (32,33) (GSE99235 and GSE98816). To the best of our knowledge, this is the only cell type with both whole genome level kinetics of mRNA metabolism and scRNA-seq data available in the public domain. In order to pick out the fibroblast cells, we first performed cell clustering using Seurat (34) with default parameters, and each cluster was further annotated with regards to fibroblast cell gene markers (35). In total, we identified 397 fibroblast cells in the GSE99235 and 1100 fibroblast-like cells in GSE98816 datasets. Heatmaps of marker gene expression and t-SNE clustering plots for two datasets were displayed in Supplementary Figure S1.

LTMG attributes certain low expressions to mRNA not fully degraded, and we turn to observe the relationship between the ratio of the observed low expression caused by incompletely degraded mRNA in the SE peak, i.e 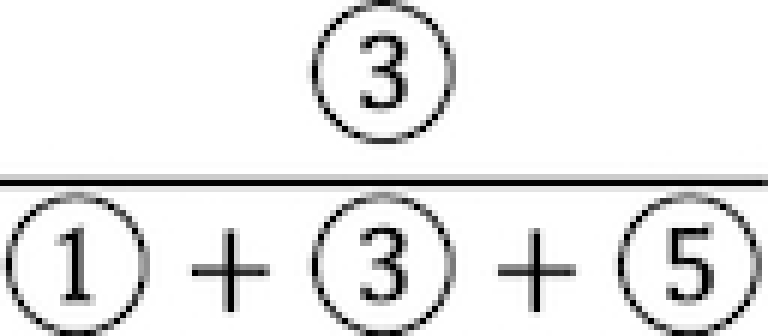in Figure 1, and the mRNA half-life. By applying LTMG on the single fibroblast cell expressions, we calculated the correlation between the mRNA half-life and proportion of uncensored expression in SE peak, i.e. 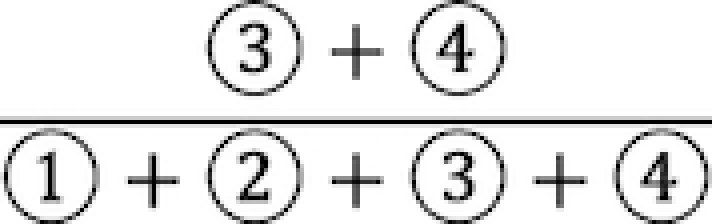an approximation of . To normalize the impact of the parts , and , i.e. different rates of the type I error of SE peak and the type II error of AE peak of each gene, we compute the correlation conditional on the mean of the first AE peak. Specifically, for each dataset, we ordered genes based on the mean values of their first AE peaks from low to high and place every 100 genes into a group, which gave us 21 and 18 groups in GSE99235 and GSE98816, respectively. Within each group, Spearman correlation between the mRNA half-life and proportion of uncensored expressions in the SE peak of genes is calculated, and the significance was assessed by using the Student's t distribution based test. We observed significant correlation between these two, meaning there is a higher probability observed low but non-zero expressions for the genes have longer half-lives.

Calculating cell type enrichment score

Under LTMG, each cell with its cell type identify known a priori, is designated to a peak with largest probability. Then, for a given gene, we define a peak enrichment score of a cell type as the exponential of the proportion of each cell type assigned to the peak. Here we do not differentiate different AE peaks, and treat them as one peak. The enrichment score is calculated for all cell type gene markers, and due to the specificity of these gene markers, a cell type should have a high AE peak enrichment score for a gene if it is indeed its gene markers, but a high SE peak enrichment score if not. The enrichment score is used to evaluate how specific LTMG model is in identifying truly expressed genes.

T-SNE visualization of the head and neck cancer

We clustered GSE103322 (1) datasets by using the Rtsne package with perplexity parameter equal to 30, and max iterations equal to 20 000. We used only the markers genes provided by the original paper for cell clustering. The t-SNE analysis is only for data visualization. Cell type annotated by the original work was used to label the cell types.

LTMG based clustering, visualization, and comparisons with other methods

Cell clustering under the framework of LTMG is performed by converting the continuous expression values to its discrete expression states. In other words, for each gene, we assign a cell to an integer k if it is to be assigned to the kth AE peak with maximum likelihood (k > 0); or 0 for SE peak. The LTMG UMAP and LTMG t-SNE methods were conducted with LTMG inferred gene expression states as input, by using R UMAP package with the default parameters and RTSNE function with perplexity = 30 and max iteration = 20 000. We used original expression data as input (CPM/RPKM) for UMAP and t-SNE with the same parameters. Original expression data was used as input with default parameters for SIMLR (16), and we selected the cluster number ranging from 5 to 15 by using the SIMLR built-in function SIMLR_Estimate_Number_of_Clusters, for SMLR analysis. These five dimension reduction methods namely LTMG UMAP, LTMG t-SNE, UMAP, t-SNE and SIMLR are applied on three datasets: GSE103322, GSE72056 and 10× PBMC data set all with known cell labels.

We evaluated the clustering performance by sum of silhouette width of all the cells (see details in Supplementary Methods). Cell type information are directly retrieved from original works or related sources. Since GSE103322 and GSE72056 provides a comprehensive list of cell marker genes, cell clustering was conducted using only the marker genes.

LTMG based differential expression analysis

Under the framework of LTMG, we define that a gene is differentially expressed between the cells of two conditions, if at least one gene expression state (either SE or AE) of the gene has a significantly different representing level in one condition versus the other. To avoid the bias caused in assessment of mixture components and keep a high rigorousness for the differential gene expression test, we developed a bi-modal distribution namely LTMG-2LR from LTMG model to fit the gene expression data collected from multiple conditions. Specifically, LTMG-2LR simultaneously fit LTMG model of one AE and one SE peak for a series of expression profile of different conditions, with assuming a same mean and variance of the SE peak of each condition and the proportion of SE peak takes value from 0–1 (Supplementary Methods). For a given gene X in a scRNA-seq data under J conditions, denote 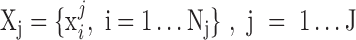as its expression profile in the 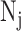cells of the jth condition. Depending on the multi-modality of the gene's expression profile in each condition, LTMG-DGE utilize the following two tests to assess if a gene's expression state is varied through multiple conditions.

LTMG-DGE test 1

If 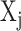is fitted with at most one SE and one AE peak for all conditions, X will be fitted with LTMG-2LR distribution, namely,

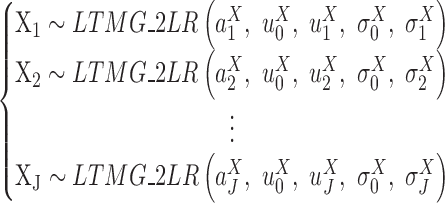Specifically, LTMG-2LR fits LTMG with one AE and one SE peak for pooled expression values of cells from different conditions and assume same mean and variance of the SE peak of each condition and the proportion of SE peak takes value from 0 to 1 (Supplementary Methods). In this case, we assume X shares the same SE state and similar degradation rates through different conditions. Then testing differential expression turns into testing differences in 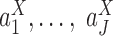and 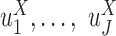. For significance measure, we implemented Generalized Linear Model (GLM) models on randomly generated observations, as detailed below.

For each iteration, we generated N observations such that each falls under an SE or AE peak with probability 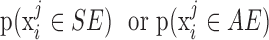, in other words, we assign 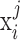to the SE (or AE) state of condition 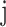with probability 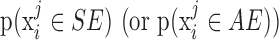. With the randomly generated N observations, we build a logistic regression model between the binary outcome, which equals to 1 if 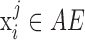, and 0 otherwise, and a design matrix with J columns, where elements in the 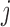th column equal to 1 if the observation comes from the 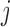th condition, and 0 otherwise. Differences in 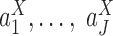could be reflected by the significance of the coefficients of the logistic regression model. Repeat this random generator multiple times, and we take the median of the obtained P-values as the significance measure of the differences in 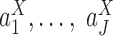. The same procedure is also performed for testing differences in 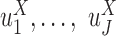, only that linear regression will be used instead of logistic regression.

The advantages of this process include (i) flexibility in allowing complicated experimental design with a rigorously defined GLM model, (ii) high sensitivity to the changes in both frequency and mean expression level of the AE peak and (iii) avoid the errors in separately assessing the SE peak in different conditions. Our comprehensive analysis revealed that on average more than 83.8% genes in the PC and CC groups of small sample size are fitted with one and two peaks, which can be well fitted by the LTMG-2LR model.

LTMG-DGE test 2

If the gene is fitted with more than two AE peaks in at least one condition, we apply the following hypergeometric test based DGE test: (i) fit an LTMG model on pooled data, i.e. 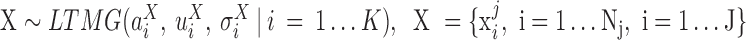, (ii) compute the likelihood that 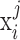belongs to peak 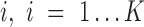and assign 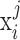to the peak with the maximal likelihood, (iii) compute if the samples of each condition 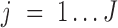enrich a peak 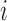via a hypergeometric test.

The difference of the two testing schemes is that the former one assumes a gene has only one AE peak in each condition, which can vary in proportion, mean, or variance through different conditions, and the test is on the proportion and mean of the AE peak, while the later fits one LTMG model over the pooled data through all conditions, and test if one condition is specifically enriched by one expression state. It is noteworthy that the second test may decrease the statistical power, but it is more robust than the test made on separately estimated multimodality of different conditions, which is sensitive to errors in assessment of mixture components of different conditions.

Single cell RNA-sequencing

Pa03C cells were obtained from Dr Anirban Maitra's lab at The Johns Hopkins University (36). All cells were maintained at 37°C in 5% CO₂ and grown in DMEM (Invitrogen; Carlsbad, CA, USA) with 10% Serum (Hyclone; Logan, UT, USA). Cell line identity was confirmed by DNA fingerprint analysis (IDEXX BioResearch, Columbia, MO, USA) for species and baseline short-tandem repeat analysis testing in February 2017. All cell lines were 100% human and a nine-marker short tandem repeat analysis is on file. They were also confirmed to be mycoplasma free.

Cells were transfected with either Scrambled (SCR) (5′ CCAUGAGGUCAGCAUGGUCUG 3′, 5′ GACCAUGCUGACCUCAUGGAA 3′) or siAPE1 (5′ GUCUGGUACGACUGGAGUACC 3′, 5′ UACUCCAGUCGUACCAGACCU 3′ siRNA). Briefly, 1 × 10⁵ cells are plated per well of a six-well plate and allowed to attach overnight. The next day, Lipofectamine RNAiMAX reagent (Invitrogen, Carlsbad, CA) was used to transfect in the APE1 and SCR siRNA at 20 nM following the manufacturer's indicated protocol. Opti-MEM, siRNA, and Lipofectamine was left on the cells for 16 h and then regular DMEM media with 10% serum was added.

Three days post-transfection, SCR/siAPE1 cells were collected and loaded into 96-well microfluidic C1 Fluidigm array (Fluidigm, South San Francisco, CA, USA). All chambers were visually assessed and any chamber containing dead or multiple cells was excluded. The SMARTer system (Clontech, Mountain View, CA, USA) was used to generate cDNA from captured single cells. The dscDNA quantity and quality was assessed using an Agilent Bioanalyzer (Agilent Technologies, Santa Clara, CA, USA) with the High Sensitivity DNA Chip. The Purdue Genomics Facility prepared libraries using a Nextera kit (Illumina, San Diego, CA). Unstrained 2 × 100 bp reads were sequenced using the HiSeq2500 on rapid run mode in one lane.

qRT-PCR

qRT-PCR was used to measure the mRNA expression levels of the various genes identified from the scRNA-seq analysis. Following transfection, total RNA was extracted from cells using the Qiagen RNeasy Mini kit (Qiagen, Valencia, CA) according to the manufacturer's instructions. First-strand cDNA was obtained from RNA using random hexamers and MultiScribe reverse transcriptase (Applied Biosystems, Foster City, CA, USA). Quantitative PCR was performed using SYBR Green Real Time PCR master mix (Applied Biosystems, Foster City, CA, USA) in a CFX96 Real Time detection system (Bio-Rad, Hercules, CA, USA). The relative quantitative mRNA level was determined using the comparative Ct method using ribosomal protein L6 (RPL6) as the reference gene. The primers used for qRT-PCR and qRT-PCR experimental data are detailed in Supplementary Table S3. Experiments were performed in triplicate for each sample. Statistical analysis performed using the 2^−ΔΔCT method and analysis of covariance (ANCOVA) models, as previously published (37).

LTMG based gene coregulation module detection

By the formulation of LTMG, for a gene with one K’ SE peak and K–K’ different AE peaks, its expression profile across different single cells is modeled by a mixture of K Gaussian distributions.

For a gene X’s expression profile through N cells fitted with one SE and K-1 AE peaks, denote 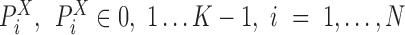as the peak for cell 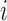with highest likelihood

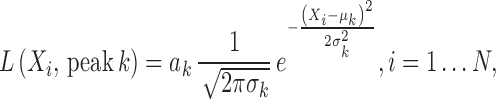in which 0 represents the SE peak and 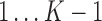represents the AE peaks. Then a 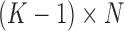binary matrix 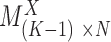can be constructed for those genes with at least one AE peak, by

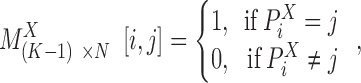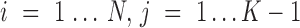. A binary matrix 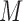is then constructed by merging all such 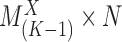row-wise, that contains the expression states regarding each gene for each single cell.

Different from bulk cells, the highly diverse and volatile transcriptional signals in single cell populations makes it challenging for coregulation module detection, as a specific TRS may be functional only in a subset of cells, but not all the single cells. LTMG maps each gene's expression state to a single cell in the binary matrix , allowing us to locate the (subset of) single cells that share the same TRS, i.e. the same expression states over a set of genes. Hence, a gene co-regulation module corresponds to a submatrix enriched by 1s in the binary matrix , called a bi-cluster. A bi-cluster enriched by 1s in corresponds a group of genes and cells, where all the genes are regulated by one specific TRS through the cells, which is potentially a gene co-regulation module.

We applied our in-house bi-clustering method QUBIC (17,38) on the binary matrix constructed as above, to identify gene co-regulation modules, namely LTMG-GCR. Specifically, QUBIC is implemented with the following parameters: -o 3000 -f 0.25 -c 0.95. LTMG-GCR is applied to a scRNA-seq data of APEX/Ref-1 KD experiment. Pathway enrichment analysis of the genes in the identified bi-clusters are computed using hypergeometric test against the 1329 canonical pathway and 658 validated transcriptional regulation pathways in MsigDB database (39), with P <0.001 as a significance cutoff.

RESULTS

LTMG model substantially improved the goodness of fitting and accurately captured multimodality of scRNA-seq data

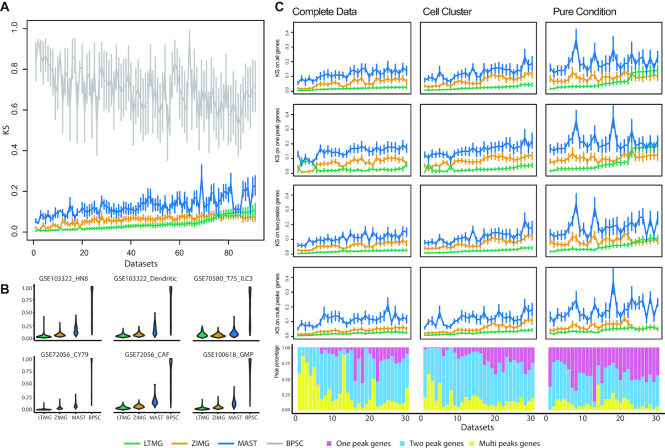
We compared the performances of LTMG versus other methods on 23 data sets totaling 66,780 single cells which was reorganized into: (i) 51 pure condition datasets, (ii) 49 cell cluster datasets and (iii) 78 complete data sets (see Methods). We first applied LTMG, ZIMG, MAST and BPSC to fit the expression profile of each gene in all the 178 sub data sets. Kolmogorov Statistics (KS) (40) was applied to evaluate the goodness of fitting of each gene, and for each dataset using each method. The mean and standard deviation of the KS values over all the genes for each dataset and method was calculated, and the 178 sub datasets were ordered in increasing order by the mean KS values calculated based on LTMG. And the comparisons on the top 91 datasets were shown in Figure 2A, which suggested: (a) LTMG has significantly better goodness of fitting compared with BPSC and MAST in all the analyzed data sets and outperforms ZIMG in most of the datasets (Figure 2A); (b) LTMG generally has a smaller number of outliers with poor fitting through all the datasets (Figure 2B and Supplementary Table S4), suggesting the higher robustness of LTMG comparing to others. Our analysis suggested that the average proportion of genes fitted with one, two, and more than two peaks are 42.5%, 44.9% and 12.6% in pure condition, 16.6%, 65.7% and 17.6% in cell cluster, and 25.4%, 51.5% and 23.1% in complete data sets, respectively.

Figure 2.

Detailed fitting comparison of LTMG and other models. (A) Goodness of fitting of the four models. X-axis represents different data sets, and Y-axis the goodness of fitting evaluation for each method using KS values, where the mean and standard deviations of the KS values are shown. Note smaller KS values indicate better goodness of fitting. (B) Violin plot of KS value of selected example datasets, two for each group. (C) Detailed comparisons of the three models on genes of different peaks and datasets of different groups. The three columns from left to right are the KS values and distribution of peaks in the top 30 complete, cell cluster and pure condition data sets ordered by the KS statistics of LTMG. Horizontal lines in the KS plots represents the mean of KS value fitted in that group of genes and vertical line is the standard deviation accordingly. Stocked histogram illustrates the percentage distribution of genes of different peaks in different datasets.

In addition to investigating the goodness of fitting over all the genes, we focused on a more detailed comparison of gene groups that are fitted with different number of peaks under LTMG. We compared the goodness of fitting between LTMG and ZIMG, MAST, on all the genes, genes fitted with one, two and multiple peaks. Here, BPSC was dropped from the comparison, since it has much lower performance than other models. Figure 2C shows the top 30 sub datasets in each of the three cases: pure condition, cell cluster and complete data, that has the smallest KS values based on LTMG model respectively, and similar analysis results on rest of the datasets was illustrated in Supplementary Figure S2. Within the cell cluster and complete data sets, LTMG consistently outperformed ZIMG (120/127) and MAST (127/127), for genes fitted with different peaks. In the pure condition datasets, LTMG outperformed MAST in all the sub data sets (51/51), outperformed ZIMG (42/51) for the genes fitted with more than two Gaussian peaks, and have comparable performance as ZIMG (23/51) for the genes that are fitted with one or two peaks (Supplementary Table S5). A possible reason for the less significant performance of LTMG on the pure condition datasets could be that the sample size of the PC datasets is generally small (∼115 cells on average) compared to cell cluster (∼388 cells) and complete (∼622 cells) data sets. A consequence is that the half bell shaped SE peak (Figure 1A) is not significantly different from a full Gaussian peak when the sample size is small. Notably, ZIMG tends to overfit, as the non-zero expression caused by incompletely degraded mRNA could inflate the number of AE peaks, while LTMG can effectively handle the non-zero low expressions by the left truncation assumption.

To further investigate the model robustness in casting the true gene expression states, we collected one data set with both scRNA-seq and single molecule fluorescence in situ hybridization (smFISH) conducted over the same cell conditions for 15 genes. SmFISH is so far known as the technology that can most precisely capture the single cell gene expression state and is henceforth used as gold standard in profiling single cell gene expressions. For each gene, we compared the similarity of the probability density functions (pdf) between the ones inferred by LTMG, ZIMG and MAST models using scRNA-seq data, with the one characterized by smFISH data. To the best of our knowledge, this is the only one data set with both scRNA-seq and smFISH available for the same cell population. We evaluated the consistency between the pdf of scRNA-seq data and density of smFISH data by using KL divergence, the lower value of which indicates the better consistency with smFISH data (Supplementary Methods). Specifically, LTMG achieved a smaller KL divergence comparing to MAST in all the genes and achieved a smaller and similar KL divergence in three and 12 genes when compare to ZIMG (Supplementary Figure S3A). In addition, visualizations of the expression profile suggested that the multimodality inferred by LTMG has higher concordance with the observed expression profile, comparing to other two methods (Supplementary Figure S3B).

We also applied the LTMG model to three recent data sets of purified T cells collected from liver, lung and colon cancer tissues (41–43). These data sets all consist of pure T cell with large sample sizes (5063, 11 138, and 12 346 cells). In these data sets, LTMG also achieved the best goodness of fitting comparing to ZIMG and MAST. LTMG identified more than 44.5% (4893/10 874), 69.73% (7093/10 172) and 69.95% (7551/10 794) of significantly expressed genes with at least one SE peak and two AE peaks in the three datasets, respectively (Supplementary Figure S4). We further utilized a stringent criterion to select only the genes with at least two AE peaks, each of which covers significant proportion of the total cells and is distinct to other peaks. (see more details in the Supplementary Method). This results in 26.56% (2888/10 874), 22.67% (2306/10 172) and 24.56% (2651/10 794) of the genes with at least two distinct AE peaks in the three data sets, demonstrating the prevalence of multi-modality in gene expression states in large data sets, and the heterogeneity of single T cell expressions in tumor micro-environment.

A discussion on model comparisons regarding a balance between goodness of fitting and model complexity, by using KS statistics, BIC and likelihood ratio test was provided in the Supplementary Note. Particularly, for fair comparisons, we considered: (i) using BIC to compare LTMG and other zero inflated models and (ii) using KS statistics to compare LTMG and other non-zero inflated models on only those genes fitted the same number of parameters in each case, such that the models being compared have the same complexity level. These two tests also suggested LTMG outperform other zero-inflated models and mixture models (see details in Supplementary Note).

LTMG handles zero and low expressions properly

The observed low expression depicted as and in Figure 1A are generally seen in all the analyzed data sets, which on average take 27.9%, 16.3% and 14.5% of non-zero values in the PC, CC and CD data (Supplementary Table S6). We hypothesized that one major contributor of the low expression is the incompletely degraded mRNA under the regulation of a TRS of suppressed state, which should be distinguished from those TRSs under active states, namely, (Figure 3A). To validate this hypothesis, we collected a data set of experimentally measured mRNA kinetics of mouse fibroblast cells (31), and two scRNA-seq data set (GSE99235 and GSE98816) of mouse fibroblast cells (32,33) (see Methods). We examined the correlations between the mRNA half-lives and the estimated proportion of incompletely degraded mRNA.

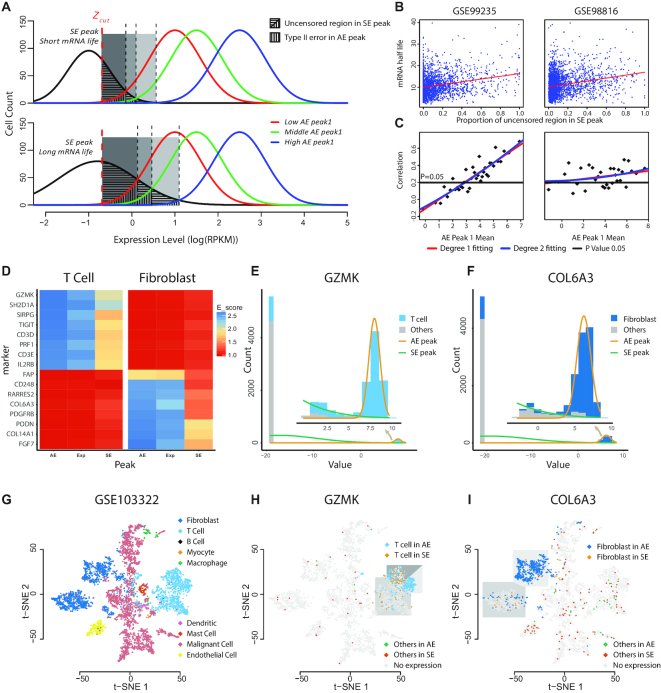
Figure 3.

(A–C) Association between the scRNA-Seq measured expression and mRNA degradation rate. (A) Schematic of the uncensored region of genes with different SE peak and influences from different AE peak1. Genes with longer mRNA life tend to have a larger uncensored region. Lower AE peak1 is more likely to introduce a bigger Type II error. (B) Scatter plot of the uncensored region and mRNA half-life in three different datasets. Red line is the degree 1 fitting. (C) Scatter plot of correlation value in different AE peak1 Mean. Red line is degree 1 fitting, blue line is degree 2 fitting, and black line is the correlation threshold when the P value is equal to 0.05. (D–I) Distribution of AE and uncensored SE expression of cell type markers through different cell types. (D) Heat map of T cell and fibroblast enrichment information across T cell and fibroblast markers, AE, Exp and SE on the x-axis represents AE peak, non-zero expressions, and non-zero expressions in SE peak. (E, F) Cell distributions with respect to the gene expression and peak fittings of GZMK and COL6A3. Light blue region presents T cells, dark blue presents Fibroblast cells and gray represents other cells. (G) t-SNE plot of different cell types in the GSE103322 dataset. (H) Detailed gene expression states of GZMK in three subclasses of T cells and other cells over the t-SNE plot. (I) Detailed gene expression states of COL6A3 in two subclasses of Fibroblast cells and other cells over the t-SNE plot.

Specifically, positive correlations between (i) the proportions of uncensored observations in the SE peak, defined by 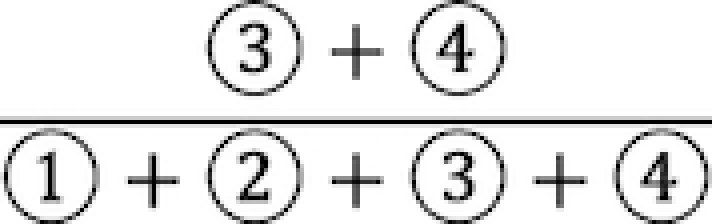in Figure 1A, and (ii) mRNA half-life, were consistently observed in both data sets (Figure 3B), suggesting that genes with more uncensored expressions regulated by suppressing regulators are probably a result of longer mRNA half-life. It is noteworthy the AE peaks for higher mean expression suffer less impact from the non-zero low expressions. To adjust for this bias, we examined the correlations of mRNA half-life with the proportion of uncensored observations conditional on the mean of AE peak (Methods). Significant positive correlations (P < 0.05) were observed for the genes with a relatively larger mean of AE peak, and the correlations tend to be stronger among the genes with larger AE peaks, in both of the analyzed data sets (Figure 3C), further validated the relationship between the observed low expression and incompletely degraded mRNA.

Modeling the transcriptomic heterogeneity among cells

The multi-modality characteristic of LTMG unravels the transcriptomic heterogeneity among a cell population. We then ask how cells behave with respect to our identified SE and AE peaks. For a gene, we denoted the cells with non-zero expression as ‘Exp’, the cells assigned to the AE peaks as ‘AE’ and the cells assigned to the SE peaks as ‘SE’. We tested for cell marker genes, how the cells of known cell type labels are distributed through the ‘AE’, ‘Exp’ and ‘SE’ cell groups, with regards to different marker genes.

Our hypothesis is that for the cells with a certain identity such as cytotoxic T cells, they are expected to overly express specific cell marker genes like granzymes, such that their expression level is more likely to be in an AE peak rather than an SE peak. On the other hand, T cells are more likely to be enriched in certain AE peaks of granzymes but are excluded in SE peaks. In addition, since LTMG identifies certain low non-zero expressions to SE peak, we hypothesize that a cell type will be more strongly enriched to the AE peaks rather than all the cells with non-zero expression value of a marker gene.

We applied LTMG on a head and neck cancer (HNSC) data set (GSE103322) consisting of 5902 cells of nine cell types namely B cell, T cell, Myocyte, Macrophage, Endothelial, Dendritic and Mast cell, with pre-annotated cell labels and uniquely expressed maker genes (1). We defined an enrichment score to evaluate the association between cell type and the cell expression states, namely, ‘AE’, ‘Exp’ and ‘SE’, for each marker gene (see Methods). Not surprisingly, our analysis showed that a cell type always significantly enriches the ‘AE’ expression state if the gene is specific to the cell type, suggesting that the AE state identified by LTMG is a good characterization of the true active expression state, comparing to other methods (Supplementary Table S7). Figure 3D shows the enrichment score of T and fibroblast cells associated with ‘AE’, ‘Exp’ and ‘SE’ states, for eight T cell marker genes (top eight rows) and eight fibroblast marker genes (bottom eight rows). Figure 3E and F illustrate the LTMG fitted curves of GZMK, a cytotoxic T cell marker, and COL6A3, a fibroblast marker. Figure 3G shows on a clustering visualization using 2D-tSNE plot of the nine cell types, the distribution of all the cells with the AE and uncensored SE states of these two genes. We observed that the CD8+ T cells with the AE expressions or uncensored SE expressions of GZMK were clearly separated to high cytotoxic and exhausted CD8+ T cells in the HNSC microenvironment (44–46) (Figure 3H). Similarly, the fibroblast cells with an AE or an uncensored SE expression of COL6A3 were differentially distributed as two sub fibroblast types (Figure 3I). Moreover, cells that expressed in SE peak are scattered outside T cell or Fibroblast cell region, validated that SE peak does not representing cell type identity and should be de-noised for further analysis.

Single-cell clustering based on inferred modality by LTMG

Our analysis suggested that the gene expression states inferred by LTMG can reflect the cell type specific gene expression characteristics by effectively removing the noise of the low but non-zero expressions. Here we show that this denoising approach can largely benefit the cell clustering analysis and visualization of the single cell data collected from complicated microenvironment such as cancer and peripheral blood samples.

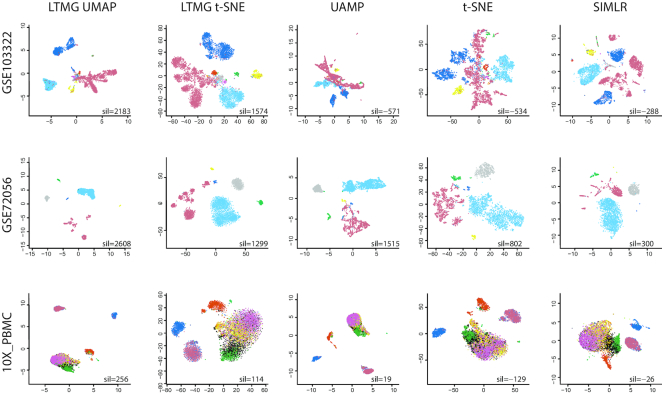
Five dimension reduction and clustering methods including: (i) UMAP; (ii) t-SNE; (iii) UMAP on LTMG denoised data, called LTMG UMAP; (iv) t-SNE on LTMG denoised data, called LTMG t-SNE and (v) SIMLR, were compared on three datasets: GSE103322, GSE72056, and 10× PBMC with annotated cell types (Methods). We compared LTMG UMAP, LTMG t-SNE, UAMP, t-SNE and SIMLR by using the Silhouette width, the higher value of which suggests a better consistency between predicted cell clusters and true cell labels. 2D visualization of cell clustering and the Silhouette width were shown in Figure 4. Our analysis suggested the cell clusters inferred from LTMG denoised data outperform the clusters identified by using original data, for both UMAP and t-SNE. In the GSE72056 and GSE103322 dataset, cell surface markers and predicted copy number variations were used to identify true malignant cells, which were composed by multiple subclasses of cells due to inter-tumor heterogeneity, as illustrated by the red colored cells in Figure 4. We observed the malignant cells, as well as other normal cells, are more spreaded over the 2D UAMP and t-SNE of the original data while the LTMG UMAP and LTMG t-SNE well manage the subclass of malignant cells from different patients (Figure 4 and Supplementary Figure S5). In addition, different types of immune and stromal cells were better distinguished from malignant cells and each other in the LTMG UMAP and LTMG t-SNE based embedding. A possible explanation is that the LTMG based transformation of gene expression states can better characterize the inter-cell type varied expression states via removing the intra-cell type gene expression variations that do not form varied expression states.

Figure 4.

Clustering visualization of three datasets using five methods. 2D visualization of the three datasets GSE103322, GSE72056 and 10X_PBMC embedded by LTMG UMAP, LTMG t-SNE, UMAP, t-SNE and SIMLR. Cells are colored by the cell types annotated in original work. Sil value represent the sum of silhouette width between the predicted cell clusters and known cell labels.

Differential gene expression and co-regulation analysis with experimental validation

Under the formulation of LTMG, a gene is considered as differentially expressed among cells of different conditions if (i) the proportion of the SE or AE peak or the mean of the peak are significantly different among the conditions when all conditions have at most one AE peak, and (ii) the proportion of the SE peak or at least one AE peak is significantly different among the conditions, when there are more than one AE peaks in at least one condition (see Methods). A gene co-regulation module is defined as a group of genes sharing a common GES throughout a subset of cells. LTMG based differential gene expression analysis (LTMG-DGE) is capable of handling complicated designs with a generalized linear model setting; and the gene co-regulation analysis (LTMG-GCR) is empowered by implementing a bi-clustering algorithm to detect co-regulation modules of potential transcriptional heterogeneity (17,18) (Methods).

To experimentally validate the LTMG based DGE and GCR analysis, we generated a scRNA-seq data set consisting of 142 patient-derived pancreatic cancer cells under two crossed experimental conditions: APEX1 knockdown (APE1/Ref-1-KD) or control, and under hypoxia or normoxia conditions.

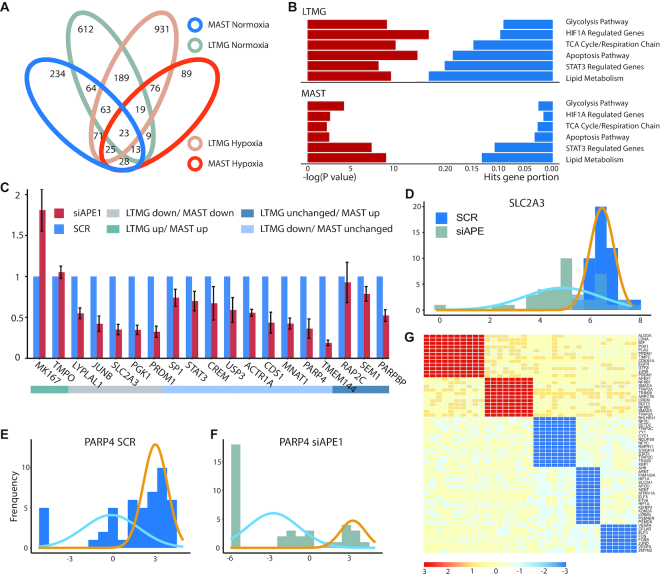
We compared the set of differentially expressed genes and their functional relevance to APE1, identified by LTMG-DGE with MAST, SCDE, SC2P, EdgeR and DESeq. Using LTMG-DGE, we identified 448 up- and 1397 down-regulated genes in APE1/Ref-1-KD vs. control under hypoxia, and 471 up- and 992 down-regulated genes under normoxia (P < 0.01); while MAST identified 282 and 521 up-regulated and 397 and 607 down-regulated genes, under hypoxia and normoxia conditions, respectively (P <0.01). In addition, under the hypoxia condition, 215, 187, 129 and 500 up- and 281, 1528, 188 and 1085 down-regulated genes were identified by SCDE, SC2P, EdgeR and DESeq (P < 0.01), respectively. The differentially expressed genes identified by the methods are given in Supplementary Table S8. Consistency of the differentially expressed genes identified by LTMG-DGE and MAST are shown in Figure 5A and Supplementary Table S8.

Figure 5.

Experimental validation of LTMG-DGE. (A) Overlap of down-regulated genes in APE1/Ref-1-KD vs. SCR control in hypoxia and normoxia, identified by LTMG-DGE and MAST. (B) Enrichment of the genes down-regulated in APE1/Ref-1-KD versus SCR control in key APE1/Ref-1 related pathway, under hypoxic conditions. (C) Expression of selected genes analyzed by qPCR of Pa03C cells transfected with APE1/Ref-1 siRNA and placed under hypoxia for 24 h. (D–F) Expression profile of SLC2A3 and PARP4 in APE1/Ref-1-KD (siAPE) and control (SCR) under hypoxia. Gene expression level is quantified by log(RPKM) and represented on the x-axis. Gold and blue curves represent peaks correspond to different TRSs. (G) Bi-cluster structures of gene coregulation modules enriched by STAT3 and HIF1A regulated genes. The x-axis represents samples and y axis represents genes. AE and SE status of a gene in a sample are colored by red and blue, respectively.

APEX1 is a multifunctional protein that interacts with multiple transcriptional factors (TFs) to regulate the genes involvement in response to DNA damage, hypoxia and oxidative stress (47). Our previous study identified significant roles of APEX1 in the regulation of Pa03c cell's response to microenvironmental stresses (48). Functional enrichment of the differentially expressed genes identified by the methods were examined. Comparing to MAST, SCDE, SC2P, EdgeR and DESeq, the down-regulated genes in APE1/Ref-1-KD versus control under hypoxia conditions identified by LTMG-DGE are more significantly relevant to the pathways such as glycolysis, TCA cycle and respiration chain, apoptosis, and lipid metabolism pathways, as well as genes regulated by HIF1A and STAT3 (Figure 5B and Supplementary Table S8). Note that APE1/Ref-1 directly interacts with HIF1A and STAT3 (48,49), and regulates oxidative stress response, glucose and lipid metabolism, and relevant mitochondrial functions. These results suggest LTMG-DGE method can detect more functionally relevant genes than other methods. Complete pathway enrichment results of the differentially expressed genes identified by the tested methods were given in Supplementary Table S8.

We utilized qPCR to investigate 12 selected differentially expressed genes with highest significances identified by LTMG-DGE and MAST each, and seven genes commonly identified by both methods (Methods). Specifically, comparing APE1/Ref-1-KD versus control under hypoxia, (i) nine genes namely STAT3, CREM, SP1, USP3, CDS1, ACTR1A, PARP4, TMEM144 and MNAT1 were identified as significantly down-regulated by LTMG-DGE, while not by MAST; (ii) three genes namely SEM1, PARPBP and RAP2C were identified as up-regulated by MAST while not by LTMG-DGE; (iii) two genes namely MKI67 and TMPO were identified as up-regulated genes by both methods and (iv) five genes namely JUNB, LYPLAL1, PRDM1, PGK1 and SLC2A3 were identified as down-regulated by both methods. Using qPCR, we demonstrated that eight out of the nine genes identified as significantly down-regulated by LTMG-DGE but not by MAST are confirmed to be down-regulated (P < 1e–3 and fold change < –0.7), while the three genes identified as up-regulated by MAST but unchanged by LTMG-DGE are truly unchanged in the qPCR experiment. In addition, qPCR confirmed the up- and down-regulation for the seven common differentially expressed genes (Figure 5C). These observations clearly suggest a better sensitivity and specificity of LTMG-DGE compared with MAST. To further validate the nine down regulated genes specifically identified by LTMG-DGE, we checked their expression in TCGA pancreatic cancer data and identified eight of the nine are significantly down regulated in the samples with low APEX1 expression comparing to the samples with high APE1 expression (P < 1e–3 by Mann–Whitney test, Supplementary Figure S6). In addition, our analysis suggested the down regulated genes identified by LTMG is highly consistent with the down regulated genes in APEX1 low vs APEX1 high TCGA samples.

With the qPCR experiment, we validated 13 down regulated genes namely JUNB, LYPLAL1, PRDM1, PGK1, SLC2A3, STAT3, CREM, USP3, CDS1, ACTR1A, PARP4, TMEM144 and MNAT1. We further checked the differential expression of these genes given by SCDE, SC2P, EdgeR and DESeq (all with P < 0.01 as the significance cut-off). Down regulation of 0, 11, 0 and 3 out of the 13 genes were also identified by SCDE, SC2P, EdgeR and DESeq, respectively.

We also examined the SE and AE peaks for the genes regulated by different TFs. Specifically, in APE1/Ref-1-KD versus control under hypoxia, LTMG-DGE identified that genes regulated by STAT3 have a higher proportion of SE peaks (Figure 5D and E) while genes regulated by HIF1 have an emerging AE peak with a low-valued mean (Figure 5F). This again implies a regulatory functional loss of STAT3 and attenuation of HIF1 in the APE1/Ref-1-KD cells. Figure 5D-F shows the histograms of the expression profile and LTMG fitted curves of PARP4 (regulated by STAT3) and SLC2A3 (regulated HIF1).

LTMG-GCR was further applied for gene co-regulation analysis. Two co-regulation modules corresponding to the AE of the STAT3 and HIF1A regulated genes and three co-regulation modules corresponding to the SE of the STAT3 and HIF1A regulated genes were identified (Figure 5G and Supplementary Table S9). Further analysis revealed that the 16 out of the 17 cells of the SE modules are APE1/Ref-1-KD samples and 16 out of the 18 cells of the AE modules are the control samples, respectively, suggesting a switch of the TRS of STAT3 and HIF1A in the APE1 knock down cells. More interestingly, the AE module of the HIF1A regulated genes include glycolytic genes ALDOA, PGK1 and LDHA, while the two SE modules are enriched by genes related to DNA methylation, angiogenesis and other transcriptional factors, which are independent to glycolytic genes, suggesting that loss of APE1 results in a suppression of certain HIF1A regulated genes.

We also compared LTMG-GCR with SCENIC (14), a state of the art regulatory network analysis tool designed for single cells. Comparing to LTMG-GCR, SCENIC uses the gene co-expression correlation derived from all cells to identify co-regulation modules in scRNA-seq data, assuming that all single cells should either share the same regulatory module simultaneously or not. In the SCENIC derived gene coregulation modules, no module regulated by STAT3 was found while only seven genes were identified in the HIF1A regulated module, none of which is related to glycolysis, TCA cycle, or angiogenesis. In addition, majority of down regulated genes in the APE1/Ref-1-KD cells under hypoxia condition were identified in the modules of JUNB and JUND, which we identified as the downstream of STAT3 and HIF1A. We believe LTMG-GCR takes into consideration the heterogeneity of transcription signals among the cells, i.e. a transcriptional signal may be active in a certain subset of cells that forming a local low rank submatrix, which can better characterize the ‘locality’ of genes and cells sharing a common transcriptional regulatory signal.

DISCUSSION

We developed LTMG as a statistical model specifically for scRNA-Seq data. LTMG considers the heterogeneity of transcriptional regulatory and gene expression states, and in handling the low expressions, LTMG considers the metabolism rates of mRNA molecules, and experimental resolution in modeling scRNA-seq data, from a systems biology perspective. Our comprehensive model evaluations demonstrated that LTMG can accurately infer the multi-modality of genes expression states, better handle low expressions caused by suppressed regulation and incompletely degraded mRNA, and has a significantly improved goodness of fitting, compared to other existing models. Our experimental validation suggested the differential gene expression tests LTMG-DGE has better sensitivity and specificity compared to five state-of-art methods. In addition, LTMG-DGE is equipped with a generalized linear model that could deal with complex experimental designs.

LTMG is designed for analysis of scRNA-seq with a comparable sequencing depth for each cell. Application of LTMG on drop-seq based data such as 10x Genomics data demonstrated that the model also outperforms other models in goodness of fitting and can successfully infer multimodality from single gene's expression profile. However, in cases where a wide span of total reads among the cells in the drop-seq data exist, the distribution of the normalized gene expression may be severely affected by variations in total sequenced reads. We noticed that, the inference of varied expression states heavily relies on sample size. For the cells collected from a pure condition, on average, LTMG only identified 200–1500 genes with more than one distinct AE peaks when the sample size is several hundreds, while >2000 of such genes can be identified when the sample size is larger than 5000. SC2P introduced a cell wise sequencing resolution to account for the discrepancies in library sizes (50). A possible future direction of LTMG is to incorporate a similar cell wise factor into the current model, so it will improve the characterization of varied expression resolution and SE peak for drop-seq based scRNA-Seq data. LTMG characterize the heterogenous gene expression states via a mixture Gaussian model on log normalized gene expression data. Log-normal assumption has been commonly utilized to model the active expressions, i.e. non-zero expressions, in MAST, scImpute, and SC2P. However, as derived in the supplementary method, gene expression regulated by high frequency transcriptional bursting or highly dynamic regulatory signals, may unnecessarily follow distinct gene expression states that fits the mixture Gaussian assumption. High resolution data such as large scale smFISH data would be needed for inference of the gene expression states in this case, with more sophisticated model.

ScRNA-Seq provides an ideal environment for studying the transcriptional regulatory mechanism, as each gene's expression in a single cell is the end product of all its current transcriptional regulatory inputs. A key challenge here is to identify the data patterns encoded in scRNA-seq data that corresponds to heterogeneous regulatory signals. LTMG delineates the diversity of the expression states for each single cell with regards to each gene, which naturally characterize the regulatory states on single gene and single cell level. This serves as an informative starting point for characterization of gene co-regulation modules. And indeed, application of LTMG-GCR on the APEX1 data demonstrated that modules displaying a bi-clustering structure can be effectively identified with higher specificity comparing to SCENIC in a scRNA-seq data set with transcriptional perturbation. The bi-clustering formulation identifies a submatrix in which each gene has a consistent expression state with regards to the subset of single cells, and overall, the genes are very likely to be co-regulated by a same transcriptional signal specific to these single cells, i.e. a local rank-1 submatrix in the full matrix. We believe that in scRNA-seq data, gene co-regulation modules identified via local low rank submatrix is more rational than via gene co-expression analysis through all cells, where the ‘locality’ of transcriptional regulation is lost. This is easy to understand considering in single cells, the gene regulation signals could be highly heterogeneous, and in most cases, may be activated only in a certain subset of cells.

LTMG based co-regulation module analysis considers a group of genes with constant transcriptional input, however, there are more complicated scenarios. For single cells collected from a highly dynamic biological process, such as cells under fast differentiation, a continuous switch of transcriptional regulatory signals such as phase transitions and delayed effects may result in more complicated expression patterns of genes they regulate. In this case, genes in a co-regulation module no longer have a constant expression states, but rather variable expression states with similar patterns among the genes. We anticipate that our LTMG model and its future synthesis with sophisticated low rank structure detection methods, will effectively identify co-regulation modules, where their genes have more complicated expression patterns caused by incessant switches of all transcriptional regulation inputs.

Our analysis also suggested that the cell clustering conducted on LTMG inferred gene expression states performs better than clustering on the raw expression data, either using the same or different clustering techniques. This indicates that to distinguish cell types, it suffices to use the distinct expression states of the genes, which forms a good characterization of the difference among cell types, and more importantly, the discretized expression states are more robust to noise and outliers. We believe that the cell type specifically expressed genes tend to form distinct gene expression states across a large cell population, compared with those non-specific genes, such as housekeeping genes, which could usually be fitted with one Gaussian peak of large variance. The flexibility in selecting the best number of peaks in LTMG can thus identify the genes with significantly varied expression states, that are more likely to be cell type specific markers. Actually, regulation of the cell type specific genes is more commonly seen through constant regulatory inputs, which best fits the assumption of LTMG model (see Supplementary Methods). Successfully distinguishing the cell type and phenotypic genes not only increase the specificity of cell type clustering analysis, but also helps to extract the low rank structure in scRNA-seq data and provides more biologically meaningful visualization. LTMG model can also fit into cases with transcriptional bursting regulations, when considering the bi-state property observed from transcriptional bursting. A straightforward link between LTMG inferred peaks and the transcriptional bursting model is that the proportion and mean of each peak in LTMG directly corresponds to the frequency and expression level of each input signal (51). Eventually, we hope the LTMG model based inference of gene expression states will shed new light on deducing the mechanisms transcriptional regulation by using scRNA-seq data.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of General Medical Sciences [R01 award 1R01GM131399-01]; National Institute of Cancer of the National Institutes of Health [2R01CA167291-06 to M.L.F.]; The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health; Showalter Young Investigator Award from Indiana CTSI. Funding for open access charge: Foundation for the National Institutes of Health.

Conflict of interest statement. None declared.