Connecting the legs with a spring improves human running economy

ABSTRACT

Human running is inefficient. For every 10 calories burned, less than 1 is needed to maintain a constant forward velocity – the remaining energy is, in a sense, wasted. The majority of this wasted energy is expended to support the bodyweight and redirect the center of mass during the stance phase of gait. An order of magnitude less energy is expended to brake and accelerate the swinging leg. Accordingly, most devices designed to increase running efficiency have targeted the costlier stance phase of gait. An alternative approach is seen in nature: spring-like tissues in some animals and humans are believed to assist leg swing. While it has been assumed that such a spring simply offloads the muscles that swing the legs, thus saving energy, this mechanism has not been experimentally investigated. Here, we show that a spring, or ‘exotendon’, connecting the legs of a human reduces the energy required for running by 6.4±2.8%, and does so through a complex mechanism that produces savings beyond those associated with leg swing. The exotendon applies assistive forces to the swinging legs, increasing the energy optimal stride frequency. Runners then adopt this frequency, taking faster and shorter strides, and reduce the joint mechanical work to redirect their center of mass. Our study shows how a simple spring improves running economy through a complex interaction between the changing dynamics of the body and the adaptive strategies of the runner, highlighting the importance of considering each when designing systems that couple human and machine.

Highlighted Article: Connecting the legs with a spring assists runners in swinging their legs, enabling them to take faster, shorter, more efficient strides.

INTRODUCTION

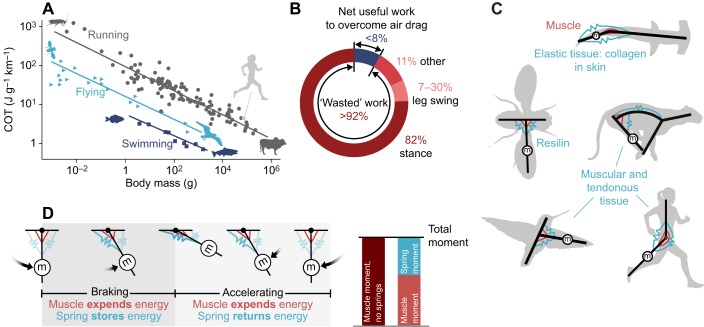
Running expends more energy than any other commonly used form of locomotion, including walking, swimming and flying (Alexander, 2005; Butler, 2016; Schmidt-Nielsen, 1972) (Fig. 1A). In running humans, only a small amount of the metabolic energy expended does net external work on the environment; this energy is used to overcome aerodynamic drag and represents less than 8% of the total energy expended (Fig. 1B) (Davies, 1980; Pugh, 1970). The remaining energy is ‘wasted’ in the sense that it is expended by processes that do no useful external work on the environment. According to studies that attempt to partition the energy expended by these processes, most of the wasted energy (65–82%) is used to brake and accelerate the center of mass, both vertically and fore–aft, a process that occurs during each stance phase (Arellano and Kram, 2014). A smaller portion is used to swing the legs (Arellano and Kram, 2014; Marsh et al., 2004; Modica and Kram, 2005), with the current best estimate at 7% (Arellano and Kram, 2014).

Fig. 1.

Energetics and mechanics in running animals. (A) Cost of transport (COT) as a function of body mass (Full, 1989; Minetti et al., 2013; Schmidt-Nielsen, 1972) shows that running (gray circles) is less efficient than swimming (dark blue squares) and flying (light blue triangles). (B) Only a small fraction of the energy expended in running does useful work on the environment to move against air resistance (Davies, 1980; Pugh, 1970); the remainder is expended primarily to accelerate the center of mass, both vertically and fore–aft, during stance. Much less is used to swing the legs (Arellano and Kram, 2014; Marsh et al., 2004; Modica and Kram, 2005). (C) Elastic tissues are hypothesized to reduce the energy required to swing the mass (m) of the limbs. (D) A pendular model of limb oscillation showing that a parallel spring (elastic tissue) can store energy during braking and return energy during acceleration, reducing required muscle moments.

Given the inefficiency of running, many devices have been designed to reduce a runner's metabolic energy expenditure, with most targeting the largest costs – redirecting the center of mass and supporting the weight during the stance phase of gait. These devices can be either active or passive. Active devices inject energy from an external source to reduce the amount of energy expended by the human, even while the total energy expended by the human-plus-device may increase. For example, exoskeleton robots use motors in parallel with human muscles (Lee et al., 2017; Zhang et al., 2017). However, these active exoskeleton robots usually use offboard motors and power sources, which prevent them from being autonomous. Other examples of active devices include mechanisms with accelerated masses (Sugar et al., 2015) and jet packs (Kerestes and Sugar, 2015). No actively powered device, however, has consistently reduced the energy required for a human to run while carrying the full weight of the device. Passive devices, in contrast, seek to reduce the energy required by the human to run by storing and returning energy to create a more efficient human-plus-device system. An early example is a running surface with stiffness tuned to minimize energy lost during impact (Kerdok et al., 2002; McMahon and Greene, 1979). Another passive assistance strategy involves using springs in parallel with the legs (Dollar and Herr, 2008; Grabowski and Herr, 2009), but this approach has yielded mixed results. Most recently, a shoe with spring-like foam and an assistive carbon fiber plate resulted in a 4% improvement in running economy (Hoogkamer et al., 2017, 2019), the largest saving for a self-contained system across all devices that target costs primarily occurring during stance.

Notably, few devices have been designed that specifically target the metabolic energy expended for leg swing during running, even though numerous researchers hypothesize that passive elastic tissues in animals may reduce the energy required to oscillate limbs. Many quadrupeds have elastic tissues running along the top of the spine and front of the hip that are thought to assist spinal extension and hip flexion (Alexander et al., 1985; Bennett, 1989) (Fig. 1C). Analogous passive elastic tissues are also in the skin of some fishes (Pabst, 2007) and the wings of birds and insects (Alexander and Bennet-Clark, 1977; Wells, 1993). While no such mechanisms have been identified in humans, studies have correlated less flexibility in the legs and lower back with improved running economy (Craib et al., 1996; Gleim et al., 1990; Jones, 2002). This decreased flexibility might result from increased stiffness of passive elastic tissue spanning the relevant joints. For all of these examples, it is thought that the passive elastic tissues store and return energy during the oscillation of a limb, reducing the effort required to actively brake and accelerate the limb with muscles (Fig. 1D) (Alexander and Bennet-Clark, 1977; Alexander et al., 1985; Bennett, 1989; Craib et al., 1996; Dickinson and Lighton, 1995; Pabst, 2007; Wells, 1993). Interestingly, recent work both in simulation (Welker et al., 2017) and in experiments with a hip-mounted metal torsional spring device (Nasiri et al., 2018) suggests that the savings resulting from assisting swing in humans are comparable to those seen when assisting stance. This is despite the fact that the energy expenditure associated with stance is an order of magnitude larger (Arellano and Kram, 2014). Moreover, the savings associated with assisting swing may actually exceed the expected expenditure associated with swing (Arellano and Kram, 2014), suggesting that the mechanism of savings when assisting swing is not understood.

Here, we first tested whether a simple spring, or ‘exotendon’, connecting the legs of a human can reduce whole-body metabolic energy expenditure during running. Next, to elucidate the underlying mechanism of savings, we tested the hypothesis that applying moments to assist moving the legs back and forth during swing may in fact reduce the costs associated with performing work on the center of mass incurred during the stance phase of gait (Fig. 2). This hypothesis can be explained as follows. During natural running, we expect certain costs to increase with increasing stride frequency, such as costs associated with swinging the legs back and forth at rates higher than the natural frequency (Doke et al., 2005; Kuo, 2001). Other costs we expect to decrease as stride frequency increases, such as costs associated with performing mechanical work on the center of mass to redirect the body in both the vertical and fore–aft directions (Kuo, 2001; Kuo et al., 2005; Snyder and Farley, 2011). Therefore, the optimal stride frequency is dictated by a tradeoff between the marginal costs of each. We thus hypothesize that when a device assists leg swing to reduce energy expenditure at a higher stride frequency, the optimal stride frequency will increase. Adopting this new higher stride frequency will reduce costs that decrease at higher stride frequencies, such as redirecting the body during stance.

Fig. 2.

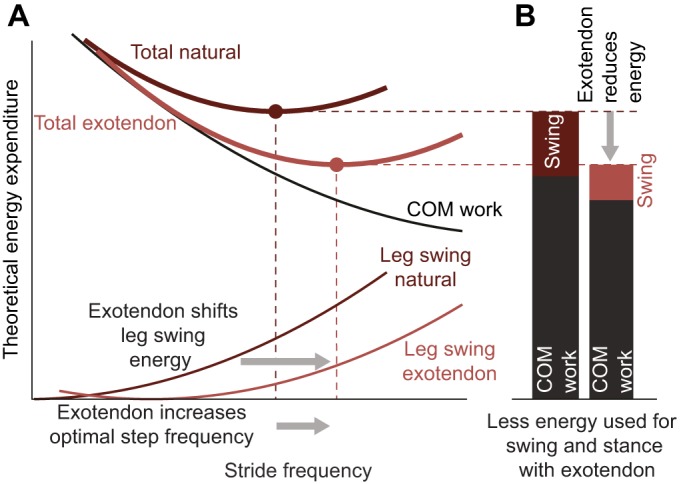
Exotendon hypothesized mechanism of savings. (A) Runners choose an energetically optimal stride frequency (dark red circle), which results from a combination of processes that require more energy with increasing stride frequency, such as leg swing (dark red thin line), and those that require less energy with increasing stride frequency, such as the work performed to redirect the center of mass (COM) during stance (black thin line). We hypothesize that the exotendon shifts the leg swing curve rightward (light red thin line), increasing the optimal stride frequency, and reduces total energy expenditure (including expenditure associated with work on the center of mass). (B) Note that at this new optimal stride frequency, the costs associated with performing work on the center of mass can be reduced by an amount that is comparable to, or even exceeds, reductions associated with swinging the legs.

MATERIALS AND METHODS

Device design

We constructed our exotendons out of natural latex rubber surgical tubing (hollow cylindrical tubing, 0.95 cm outer diameter, 0.64 cm inner diameter). Each exotendon consisted of a single length of tubing with a 1 cm loop at each end for attachment purposes. To make each loop, we folded the tubing, stretched the loop by hand, and wrapped the looped tubing tightly with electrical tape. Once released, the forces provided by Poisson expansion of the tubing supplement the adhesive, forming a secure connection. We then attached each loop to a 1.6×0.5 cm S-shaped stainless-steel carabiner that was clipped to the shoelaces of each participant. The length of each exotendon from end to end of each attachment loop was set to 25% of the participant's leg length, measured as the distance from the top of the anterior superior iliac spine to the medial malleolus of the ankle. Through pilot testing, we found that this length was long enough to avoid breaking and short enough to avoid tripping during running. As this work was our first proof-of-concept for the device, we did not develop a systematic method for determining the optimal stiffness of the device. Instead, we heuristically chose a single stiffness for the device that was stiff enough in piloting to exert noticeable assistive forces, yet compliant enough that it did not highly constrain gait. An exotendon device is shown in Fig. 3 and Movie 1.

Fig. 3.

Time-lapse photographs of a runner using the exotendon. The length of the exotendon is tuned so that the device is long enough that it does not apply forces when the feet cross each other and does not break when the feet are far apart, yet short enough that it does not become entangled when the feet pass each other. Images span one complete gait cycle.

Designing devices that reliably and accurately apply forces to the human body is a challenge. It often requires overcoming a myriad of difficulties including: aligning device and joint axes (Schiele and van der Helm, 2009), limiting added mass and materials to the body, and comfortably transferring force from rigid devices to often soft and deforming body segments (Sengeh and Herr, 2013). While we could have designed our device to attach more proximally, at the knee or hip, for example, we found in piloting that the aforementioned challenges could be largely avoided by affixing our device to the shoes. In addition, attaching more distally on the leg offered two further advantages. First, because of a longer moment arm about the hip, the forces necessary to provide assistive moments to the limb were smaller than if the attachment points were more proximal. Second, more distal placements ensure the line-of-action of the spring is predominantly along the flexion–extension axis of the hip, minimizing adduction moments on the leg. We note Nasiri et al. (2018) have created an effective hip-mounted device, although the current, largely metal, design must contend with the challenges of added mass and comfortably transferring force from the device to the user.

Device characterization

To determine the force–length relationship of our device, we applied six known forces to one end of a 23 cm exotendon 5 times each using a pull-linear scale while the other end was fixed. At the same time, the length was recorded with a motion-capture system at 270 Hz (Impulse X2E, PhaseSpace, San Leandro, CA, USA). We insured that the displacements achieved exceeded 30 cm (that expected during exotendon running at our experimental speeds). We then fitted a linear model to the force–displacement data using least-squares regression and computed the coefficient of determination. Although a Mooney–Rivlin model would provide a higher fidelity representation (Boyce and Arruda, 2000), the linear model was able to account for most of the variance (R²=0.96) and simplified calculations.

To determine how much of the energy stored in a stretched exotendon is returned, we suspended a 2.3 kg mass from one end of a 30 cm exotendon with its other end fixed to a table. We stretched the exotendon to 70 cm (for 40 cm of displacement beyond its free length) and, after releasing, measured displacement. We computed the stored potential energy in the stretched exotendon and the gravitational potential energy at the apex of the motion. Comparing these two values gave an energy return of 97%.

Participants

A total of 19 healthy young adults, with no known musculoskeletal or cardiopulmonary impairment, participated in the study (8 females, 11 males; age: 24.9±2.7 years; height: 174.4±6.9 cm; mass: 67.3±11.0 kg). The study was approved by the Stanford University ethics board and all participants provided written informed consent prior to testing.

Experimental protocols

We conducted four separate experiments to: determine whether the exotendon improves running economy (experiment 1), test for the possibility of a placebo effect (experiment 2), investigate the mechanism of energy savings (experiment 3), and test the safety of the device during over-ground running (experiment 4).

Experiment 1 – running economy

To determine whether the exotendon improves running economy, we conducted an experiment to compare metabolic energy expenditure with and without the exotendon. Twelve participants (5 females, 7 males; age: 24.7±2.9 years; height: 177.0±6.7 cm; mass: 69.3±11.4 kg) completed a 2 day running protocol. On the first day of testing, we measured participants' leg lengths and constructed personalized exotendons (25% of leg length). Participants were told that the exotendon was designed to improve running efficiency and were told to ‘relax into running with the device’ and try to ‘think about something else’ while running. The exotendon was then attached to the participant's shoes (see ‘Device design’, above, for attachment location rationale). To habituate participants to the device, they completed a minimum of four 15 m over-ground walking and running trials until they verbally confirmed they were comfortable walking and running with the exotendon. Participants were then instrumented with indirect calorimetry equipment (Quark CPET, COSMED, Rome, Italy) and completed a 5 min quiet standing trial, during which baseline metabolic energy expenditure was measured. Participants then completed four 10 min runs, with 5 min rests between each, on a treadmill (Woodway, Waukesha, WI, USA) at 2.67 m s⁻¹ (10 min mile⁻¹). Though slow for competitive runners, this pace allowed a larger pool of potential participants than a faster pace and is similar to that used in other studies of assistive devices for running (Lee et al., 2017; Nasiri et al., 2018). This pace is also similar to the pace chosen by healthy recreational runners in previous treadmill studies (Kong et al., 2012; Minetti et al., 2015) and to the 2.74 m s⁻¹ (2.9 m s⁻¹ for men and 2.5 m s⁻¹ for women) average running pace measured across 36 million users who ran 1.5 billion kilometers (Strava, San Francisco, CA, USA; https://blog.strava.com/press/2018-year-in-sport/, accessed 11 July 2019). The runs alternated between ‘natural running’ (without an exotendon) and ‘exotendon running’ (with an exotendon), with the first running condition randomly assigned. The second day of testing was identical to the first for each participant. We define a trial as the comparison between consecutive natural and exotendon runs, resulting in four trials over the 2 day experiment. During runs, we recorded sagittal plane video, which we later used to determine the runners' stride frequencies. However, in 5 of 12 participants, because of equipment availability, we recorded stride frequency using an accelerometer (Trigno IM, Delsys Inc., Natick, MA, USA) mounted on the dorsal surface of the foot.

Experiment 2 – placebo effect

To determine whether a placebo effect could explain the changes in running economy observed in experiment 1, we conducted a separate experiment to compare metabolic energy expenditure during running with and without a placebo exotendon. Four naive participants (2 females; age: 24±2.2 years; height: 168.3±2.5 cm; mass: 60.1±10.8 kg) completed a 2 day running protocol that was identical to experiment 1. The only difference was that participants ran with an exotendon that had a stiffness two orders of magnitude lower than that of the original exotendon (5 versus 120 N m⁻¹, respectively), and therefore provided negligible assistive moments to the limbs. The length of each placebo exotendon was still set to 25% of participant leg length.

Experiment 3 – mechanism

To investigate how the exotendon reduces energy expenditure, we conducted an experiment to test how running mechanics, energetics and muscle activity change during exotendon running. Four participants (2 females, 2 males; age: 25.0±1.6 years; height: 179.5±7.4 cm; mass: 75.3±13.7 kg), randomly selected from the 12 that participated in experiment 1, completed an additional third day of testing. During this testing day, kinematic, kinetic, electromyographical (EMG) and metabolic data were recorded during running with and without the exotendon at a range of stride frequencies.

All runs were completed at 2.67 m s⁻¹ on an instrumented treadmill (Bertec Corporation, Columbus, OH, USA) to allow for collection of ground reaction forces (2000 Hz). Kinematic data were recorded at 100 Hz using a 9-camera optical motion-tracking system (Motion Analysis Corporation, Santa Rosa, CA, USA). Anatomical reflective markers were placed bilaterally on the second and fifth metatarsal heads, calcanei, malleoli, femoral epicondyles, anterior and posterior superior iliac spines, and acromion processes, as well as on the C7 vertebrae. An additional 16 tracking markers, arranged in clusters, were placed on the shanks and thighs of both legs. Markers on the medial malleoli and femoral epicondyles were removed following the static trial. EMG data were recorded (Trigno IM, Delsys Inc., Natick, MA, USA) at 2000 Hz from the following 15 muscles of a single limb: peroneus, soleus, medial and lateral gastrocnemii, tibialis anterior, medial and lateral hamstrings, gluteus medius and maximus, vastus lateralis and medialis, rectus femoris, sartorius, adductor group and iliopsoas. EMG electrodes were placed in accordance with SENIAM (surface electromyography for the non-invasive assessment of muscles) guidelines (Hermens et al., 1999). Metabolic power was measured using indirect calorimetry (Quark CPET, COSMED).

To warm up, participants ran without an exotendon for 5 min on the treadmill. Next, participants completed a series of maximum voluntary contractions (MVCs) for later normalization of EMG signals. These MVCs included five maximum height jumps and five sprints (Suydam et al., 2017), in addition to one isometric and three isokinetic maximum contractions of the hamstrings, adductor group, tibialis anterior, peroneus, hip flexors (with both a flexed knee and an extended knee), and hip abductors. We then recorded motion-capture marker positions and ground reaction forces during a static standing trial for later scaling of a musculoskeletal model. As in experiment 1, participants were habituated to the device through a series of over-ground walking and running trials. Participants were then instrumented with indirect calorimetry equipment and a 5 min quiet standing trial was recorded to capture baseline metabolic energy expenditure.

Participants then completed two 7 min runs, one ‘natural running’ (without an exotendon) and one ‘exotendon running’ (with an exotendon), with a 5 min rest between and the order randomly assigned. Kinematic, kinetic, EMG and metabolic data were recorded. Self-selected stride frequency was computed during the last minute of each run from the instrumented treadmill force signals with a custom-written MATLAB script (Mathworks Inc., Natick, MA, USA). We will refer to these self-selected stride frequencies as natural self-selected stride frequency and exotendon self-selected stride frequency.

To investigate how the relationship between stride frequency and metabolic power changed when running with an exotendon, participants next completed six additional 7 min runs during which step frequency was prescribed using an auditory metronome, along with visual cues provided by a monitor in front of the treadmill. Participants ran at three prescribed stride frequencies during both natural and exotendon running. For the natural running conditions, the following three stride frequencies were prescribed: (i) the participant's natural self-selected stride frequency; (ii) the participant's exotendon self-selected stride frequency, which was higher than the natural self-selected stride frequency; and (iii) a stride frequency lower than the natural self-selected stride frequency. The change from the natural self-selected stride frequency to the lower stride frequency was set to the percentage difference between the natural self-selected stride frequency and the exotendon self-selected stride frequency. For the exotendon running conditions, the following three stride frequencies were prescribed: (i) the participant's exotendon self-selected stride frequency; (ii) the participant's natural self-selected stride frequency; and (iii) a stride frequency higher than the exotendon self-selected stride frequency. The change from exotendon self-selected stride frequency to the higher stride frequency was similarly set to the percentage difference between the natural self-selected stride frequency and the exotendon self-selected stride frequency.

Experiment 4 – over-ground test

To test whether the exotendon can safely be used in the real-world, we conducted an experiment to monitor fall risk during outdoor running. Four participants (2 females, 2 males; age: 27.8±1.3 years; height: 172.6±6.1 cm; mass: 66.7±8.0 kg), who had previous experience with the exotendon through pilot testing or participation in experiment 1, ran with a modified exotendon for 6 km on suburban streets. The modified exotendon, which attached directly to the ankle via a compression brace, was reported to be more comfortable than the original exotendon, which attached directly to the shoelaces. Moving the attachment point off the shoes also reduced wear of the shoelaces caused by sliding of the carabiner. This small change in attachment point was not expected to have a significant effect on running economy. The number of tripping and falling incidents was recorded.

A note on device optimization

In supplementary pilot experiments (not presented here), we did attempt to perform human-in-the-loop optimization to determine the optimal exotendon length and stiffness. Four participants (two who had previously completed experiment 1 and two naive participants) completed a protocol similar to that described in Zhang et al. (2017). We were unable to identify length and stiffness combinations with better performance than our standard device in the four pilot participants. One possible explanation is that our chosen device parameters were indeed near optimal. A more likely explanation is that our optimization protocol did not allow sufficient time for the algorithm to converge on the most efficient set of exotendon parameters. Also, learning effects may have interfered with the optimization as a result of the relatively short exposure to each exotendon. Another possible explanation is that participants were more risk averse in running with our device and thus adopted control strategies that prioritized stability (not falling) over efficiency. Parsing the different effects of human-in-the-loop optimization is left for future work.

Data analysis

The data that support the findings of this study are available from the corresponding authors on request.

Experiment 1 – running economy

Metabolics

We computed the gross metabolic power (energy expenditure) from indirect calorimetry (Brockway, 1987) by averaging data from the last 2 min of each experimental run. Baseline metabolic power, calculated as the average metabolic power during the last 2 min of the rested standing trial, was subtracted from our gross metabolic power measurements to obtain net metabolic power during each run. We then computed the percentage change in net metabolic power, from natural running to exotendon running for each of the four trials. We used two-tailed, one-sample t-tests, with a Holm–Šidák correction, to determine whether percentage changes in net metabolic power were significant.

Stride frequency

We manually determined average stride frequency from video recordings by counting the strides taken and dividing by the time elapsed. When foot-mounted accelerometers were instead used to compute stride frequency, we bandpass filtered accelerometer data (4th order, zero-phase shift Butterworth, 2–20 Hz), summed the X, Y and Z accelerations, identified peak accelerations, and computed stride frequency as one over the average time between peaks. Average stride frequency measures were not statistically different between the two measurement methods.

Experiment 2 – placebo effect

Metabolics

We performed the same metabolic analyses as described in experiment 1.

Experiment 3 – mechanism

Metabolics

We performed the same metabolic analyses as described in experiment 1 to determine the average net metabolic power for each run. To determine the effect of altering stride frequency, we computed the percentage change in average net metabolic power for each enforced stride frequency, both with and without an exotendon, relative to natural running (without an exotendon and with no enforced stride frequency). For each participant, we then used least-squares regression to find the best-fit quadratic curves relating net metabolic power to stride frequency for both exotendon and natural running. We calculated the stride frequencies at the minima of the natural running and exotendon running best-fit curves, which we will refer to as the natural optimal stride frequency and the exotendon optimal stride frequency, respectively. To determine whether the exotendon shifted the optimal stride frequency, we performed two-tailed paired t-tests comparing exotendon optimal stride frequency with natural optimal stride frequency. Using all participant data, we also solved for best-fit quadratic curves relating net metabolic power to stride frequency for both exotendon and natural running, and calculated the 95% bootstrap confidence intervals for these across participant curves. Note that each quadratic curve was fitted to only three data points. While this is an overfit to our data, we have chosen to do so because previous studies have shown that running metabolic cost varies quadratically with stride frequency (Högberg, 1952; Hunter and Smith, 2007; Snyder and Farley, 2011). The curve fits were only used to interpolate the stride frequency associated with the minimum metabolic cost.

Musculoskeletal modeling

Joint-level kinematics, kinetics and mechanical power were computed using a modified musculoskeletal model (Rajagopal et al., 2016) in OpenSim 3.3 (Delp et al., 2007). Of the original 37 model degrees of freedom, we locked 18 including ankle eversion, toe flexion and all those associated with the arms, leaving us with a 19 degree-of-freedom model. We generated subject-specific models by scaling the generic model to match the anthropometry of each subject during a standing static trial. For scaling, ankle and knee joint centers were calculated as the midpoint of the calcanei markers and femoral epicondyle markers, respectively, while the hip joint centers were calculated using a regression model based on the marker positions of the posterior and anterior superior iliac spines (Harrington et al., 2007). After low-pass filtering, the marker positions at 15 Hz (4th order, zero-phase shift Butterworth), we computed joint angles using the OpenSim inverse kinematics tool. This tool uses a weighted least-squares algorithm to pose the model in a way that minimizes the error between model and experimental marker locations. Joint moments were computed using the OpenSim inverse dynamics tool, which uses ground reaction forces and moments, joint angles from inverse kinematics, and classical equations of motion to solve for intersegmental moments. The joint angles used as input were low-pass filtered at 15 Hz (6th order, zero-phase shift Butterworth), and ground reaction forces and moments were low-pass filtered at 15 Hz (4th order, zero-phase shift Butterworth).

We modeled the exotendon in OpenSim as a linear path spring with a deadband range equal to its slack length. Though no real material behaves as a perfect linear spring, we determined in benchtop tests that the stiffness of our device was roughly linear (R²=0.96) and returned 97% of the energy stored in it. The spring forces were applied to the calcaneus body of each foot at the location of the band attachment marker from the static trial. The length and stiffness of the modeled exotendon were scaled for each participant. Inverse dynamics were first computed without the modeled exotendon to determine the total joint moments required to produce the resultant motion and ground reaction forces, referred to as exotendon running total moments. Inverse dynamics were then recomputed with the modeled exotendon for all exotendon runs to determine the moments produced solely by biological muscle and tissue, referred to as the biological moments. The moments applied by the exotendon were computed as the difference between the exotendon running total moments and biological moments, referred to as exotendon moments. We confirmed that the exotendon did approximately zero net work during a gait cycle (−0.04 J) in a representative participant. This value can be non-zero because the gait cycle may not end exactly where it began. Power was then computed at each joint by multiplying moments by angular velocities.

Participants' average joint angles and moments as a function of gait cycle for the hip, knee and ankle were calculated from the last minute of each run. To do this, we averaged across strides after normalizing each stride time to 100% gait cycle, computed as the time from heel strike to subsequent heel strike on a single leg. Strides were excluded from these average trajectories if the value of the measure exceeded 5 s.d. from the mean at any time point in the stride. This resulted in the removal of 3% of strides on average for all runs and participants. Joint power was then computed from the averaged joint angles and moments for each participant. Joint power and moments were then normalized to body mass and across-participant average trajectories were computed.

We next computed the average absolute natural running and exotendon running moments and power (both biological and exotendon) during the stance and swing phases of gait. We note that because these values are time averaged, the relative length of the stride does not affect their magnitude. We tested for differences between natural running and exotendon running (again, both biological and exotendon) using two-tailed paired t-tests with Holm–Šidák corrections.

We performed these analyses, comparing joint moment and power during the swing and stance phases of gait both with and without the exotendon, as a means of estimating effort during each phase. Metabolic power, measured using indirect calorimetry, is our most direct measure of energy expenditure, but cannot be used to distinguish stance and swing expenditures; their effects are intermingled during the long sampling period of indirect calorimetry. Instead, we analyzed the mechanical requirements of the body (joint moments) during each phase of gait. Previous studies have shown strong correlations between metabolic power and joint moment (Doke and Kuo, 2007), but we note that reduced joint moments do not guarantee reduced metabolic rate (Robertson et al., 2014).

Electromyography

Electromyograms from each muscle were bandpass filtered at 30–500 Hz (4th order, zero-phase shift Butterworth), rectified, and then low-pass filtered at 6 Hz (4th order, zero-phase shift Butterworth) to create linear envelopes. Envelopes were then normalized to the peak signal from the MVCs (Suydam et al., 2017) to compute muscle activity. We then averaged muscle activity across strides from the final minute of each run, then normalized to 100% of the gait cycle. Strides in which the muscle activity exceeded 5 s.d. from the mean for any time point were excluded from the average curve. All remaining EMG signals were visually examined and excluded if they appeared corrupted. Overall, 8% were excluded, with no bias towards exotendon or natural running. All processing was performed using custom-written MATLAB scripts. We also computed average muscle activity during the stance and swing phase of gait, for both natural and exotendon running. We used two-tailed paired t-tests with Holm–Šidák correction to compare activity during natural and exotendon running, during both stance and swing.

RESULTS

Experiment 1 – running economy

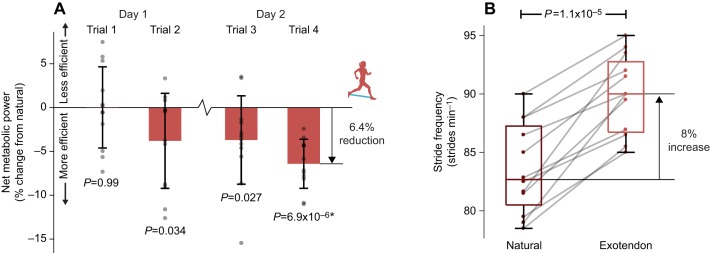
We found that connecting the legs of a running human with a simple spring improved running economy by 6.4±2.8% (n=12, P=6.9×10⁻⁶, one-sample t-test; Fig. 4A). During the first trial of the first day, participants showed no metabolic savings when running with an exotendon compared with natural running. However, by the end of the second trial, participants were expending 3.8±5.4% less energy during exotendon running compared with natural running (n=12, P=0.034, one-sample t-test). Metabolic savings continued to increase on the second testing day, with all participants achieving savings by the end of the second trial of the second testing day. By the end of our protocol, stride frequency increased by an average of 7.7±3.5% when wearing an exotendon (n=12, P=1.1×10⁻⁵, paired t-test; Fig. 4B).

Fig. 4.

Reduced energy expenditure during exotendon running. (A) On day 1, runners initially showed no change in energy expenditure (trial 1), yet showed reductions after running with the exotendon for 15–20 min (trial 2). Runners retained these savings across days (trial 3). After a total of 35–40 min of experience with the exotendon across both days, the greatest reductions in energy expenditure were evident (trial 4), with all runners (n=12) showing improved economy and average savings of 6.4±2.8%. Error bars represent 1 s.d. Asterisks indicate statistical significance after Holm–Šidák correction with confidence level α=0.05. (B) By the final trial, participants took shorter, faster strides with the exotendon, increasing stride frequency by an average of 8% above that measured during natural running (P=1.1×10⁻⁵, two-tailed paired t-test, n=12).

Experiment 2 – placebo effect

The placebo exotendon did not improve running economy (n=4, P=0.88, one-sample t-test; Fig. S1).

Experiment 3 – mechanism

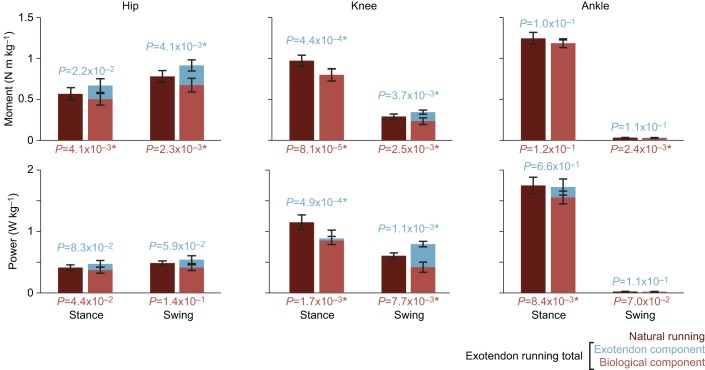
The exotendon significantly increased the optimal stride frequency (+8.1%, P=3.7×10⁻³, n=4, paired t-test; Fig. 5A) and all participants adapted toward the new optimum. The exotendon reduced biological hip and knee moments during swing (P=2.3×10⁻³ and 2.5×10⁻³, respectively, paired t-test) and stance (P=4.1×10⁻³ and 8.1×10⁻⁵, respectively, paired t-test) (Figs 5B and 6; Fig. S2). Interestingly, average knee moments during stance decreased (P=4.4×10⁻⁴, paired t-test), even when the exotendon was applying negligible moments, likely because runners adopted a higher stride frequency, as our hypothesis suggests. In addition, biological joint power at the knee decreased during swing and stance (P=7.7×10⁻³ and 1.7×10⁻³, respectively, paired t-test; Fig. 6), as did ankle joint power during stance (P=8.4×10⁻³, paired t-test; Fig. 6). Corresponding reductions in muscle activity were not significant, possibly due to the low signal-to-noise ratio (Figs S3 and S4).

Fig. 5.

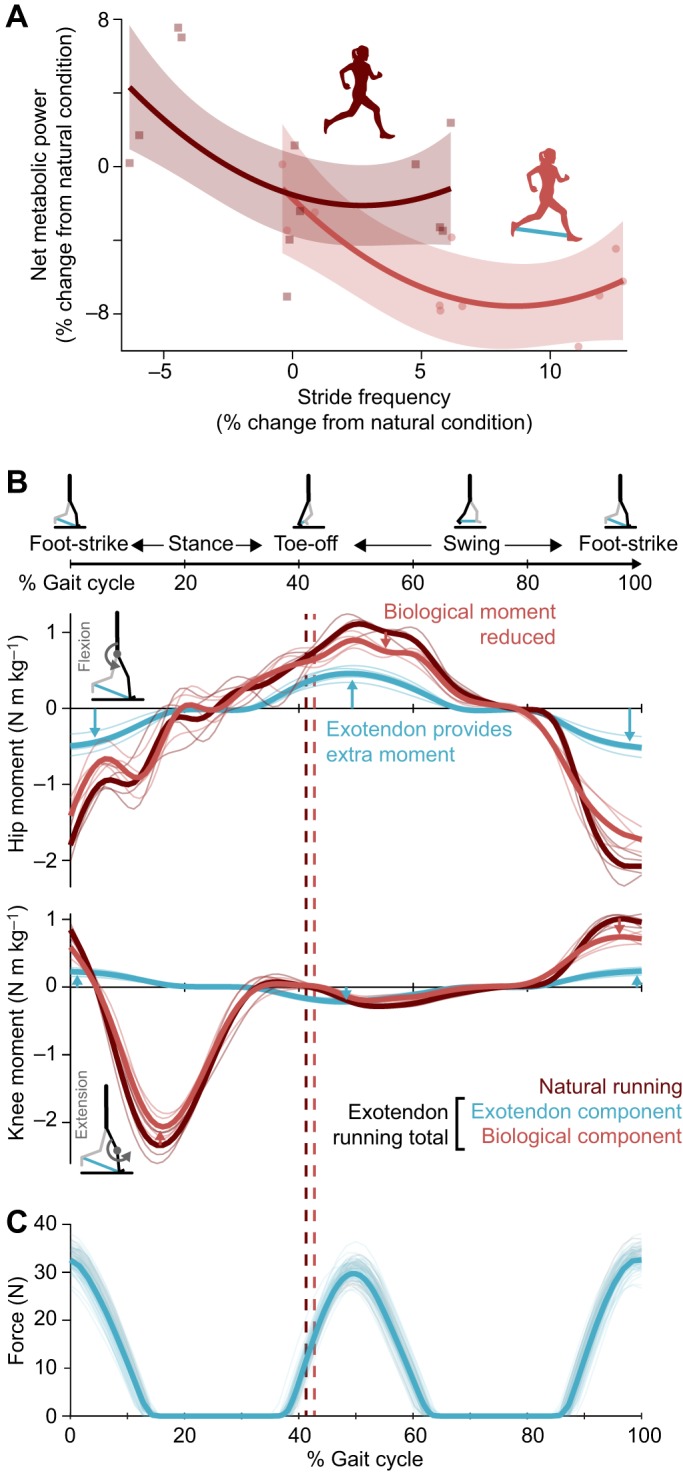
Exotendon mechanism of savings. (A) In experiments, the exotendon increased the energetically optimal stride frequency (8.1%, P=3.7×10⁻³, paired t-test, n=4). Shaded regions show the 95% confidence interval of curve fits. (B) Biological moments during swing were reduced, likely due to the assistance of the exotendon, and biological moments during stance were reduced, possibly due to the increased stride frequency. Note that horizontal forces applied by the exotendon to the stance foot likely do not affect the joint moments of that leg, because they are opposed by frictional forces with the ground. However, the exotendon forces applied to the swing leg may indirectly affect the joint moments of the stance leg through the hips. (C) Force–time plot of the exotendon throughout the stride for one participant (n=1). The tension in the exotendon peaked at around 30 N at the extents of the stride, and was zero whenever the feet were closer together than the slack length of the device.

Fig. 6.

Average joint-level kinetics. Comparisons of average, absolute joint moments and power across stance and swing for the participants from experiment 3 (n=4). We compared moments and power produced during natural running (dark red) with those produced during exotendon running. Average kinetics during exotendon runs were separated into the exotendon contribution (blue) and the biological contribution (light red). We report the P-values resulting from two-tailed paired t-tests comparing biological contributions to kinetics in natural and exotendon running below the axes (light red text) and comparing total kinetics in natural and exotendon runs above the bars (light blue). Asterisks indicate comparisons that were significant after Holm–Šidák correction (α=0.05). When running with the exotendon, during swing, hip, knee and ankle biological moments were reduced compared with natural running, as was knee power. During stance, hip and knee biological moments were reduced, along with knee and ankle power.

Experiment 4 – over-ground test

To test the safety and potential real-world applicability of our exotendon, four participants each ran 6 km on city streets with a modified exotendon (see Materials and Methods, experiment 4); no tripping incidents occurred.

DISCUSSION

We found that a simple spring connecting the legs of a running human can improve overall economy. Moreover, the exotendon appears to not simply reduce the cost of swinging the limbs. Instead, we found that savings are the product of a complex interaction between the mechanics of the simple device and the adaptive strategies of the runner. We show that the exotendon increases the energy optimal stride frequency, which runners then adopt. At this new stride frequency, the mechanical work of redirecting the center of mass during stance is reduced – shorter strides result in a reduction of biological joint moments and power. This suggests that the metabolic cost associated with this mechanical work is reduced, and the overall improvement of economy is not derived solely from reducing the cost of swinging the legs. Our findings help explain why devices designed to assist the low expenditure costs of leg swing (Nasiri et al., 2018) yield greater improvements in overall running economy than those that directly assist the larger costs of redirecting the center of mass and supporting the body weight (Hoogkamer et al., 2017).

Stated more generally, during natural running, low-expenditure components can have high expenditures when a gait parameter (such as stride frequency) is changed outside of the preferred range. These sharp increases in expenditure (the marginal costs) act as a constraint, preventing adjustment to the gait parameter. During assisted running, this constraint is relaxed, freeing the runner to reduce expenditures associated with the high-expenditure components of gait (such as center of mass redirection) and achieve more efficient gait patterns overall. Critically, the associated savings can be large – much larger than would be expected from savings directly associated with a low-expenditure component of gait (Fig. 2).

A primary limitation of our study is the difficulty of disentangling, and quantifying, costs associated with one component of gait from another during human running. In particular, we refer to two costs. One is the cost associated with performing work to redirect the center of mass both vertically and fore–aft, which we expect to primarily occur during the stance phase of gait and to decrease with increasing stride frequency (or decreasing step length). The other is the cost to move the legs back and forth during the swing phase of gait, which we expect to increase with increasing stride frequency. While there is a body of modeling and experimental evidence to broadly support the importance and tradeoff of these two competing costs (Doke and Kuo, 2007; Kuo, 2001; Kuo et al., 2005; Snyder and Farley, 2011), in reality they cannot be measured in isolation. For example, at higher step frequencies we also expect a greater ‘force rate cost’. This cost is associated with more rapidly turning muscles on and off, with the more rapid activation cycling hypothesized to require more costly calcium pumping (Doke and Kuo, 2007; Doke et al., 2005; Pontzer, 2007). This cost would be incurred by muscles involved in center of mass redirection and body weight support, as well as muscles responsible for swing. Although joint moments and power were reduced during both stance and swing, this does not directly map to reductions in cost because of complications like force rate costs, as well as other considerations such as biological tendon energy storage and return, or isometric force production. While we expect force rate costs to increase while wearing the exotendon as a result of the shortened ground contact time, the increased cost is mostly mitigated by changes in the effective moment arms of the joints. Notably, considering these costs does not negate our proposed mechanism of savings; even in their presence, our results are consistent and compatible with our hypothesized mechanism of savings (Fig. S5).

Adding to the challenge of disentangling costs was the limitation that we did not find significant changes in muscle activity, despite reductions in metabolic and mechanical power during exotendon running. A similar study was also unable to verify changes in muscle activity while testing an exosuit that improved running economy by 5% in 8 participants (Lee et al., 2017). This apparent discrepancy in our study is likely due to the distribution of the exotendon's effect on metabolic power consumption across a large number of muscles. This diluted effect might be difficult to verify in EMG signals with relatively high variability. Additionally, recorded muscle activity may not have changed despite decreased joint moments if changes occurred in non-superficial muscles that are unmeasurable with surface electromyography (Bernstein, 1967; Martelli et al., 2015; Simpson et al., 2015). Alternatively, because metabolic power results from a combination of factors including muscle activation, muscle fiber length and velocity (kinematics), and mechanical work done by the muscle fibers (Umberger, 2010; Umberger et al., 2003), muscle activity need not change, though joint moments and metabolic power did.

An open question is whether our device would be more or less effective at higher running speeds. Our current study was conducted at one, relatively slow, speed. At higher running speeds, the amplitude and frequency of leg swing increase (Schache et al., 2014), leading to greater leg swing costs (Doke and Kuo, 2007) that the device may help offset. However, the marginal costs associated with the work to redirect the center of mass and force rate costs would likely change with running speed, making the net effect unclear. To further complicate the situation, other kinematic changes occur at high speeds. For example, during natural running at faster speeds, greater knee flexion is evident at the rearward extent of leg swing, reducing the leg's moment of inertia about the hip and potentially reducing swing costs. The exotendon may in fact hinder this more exaggerated knee flexion at higher speeds, leaving the net effect on leg swing costs uncertain. Although the effect of our device at faster running speeds is somewhat unclear, the improvement in economy at the tested speed does imply that recreational runners may be able to run faster and further with our device. A runner, with a natural pace of 2.7 m s⁻¹ and a marathon finishing time of 4 h 20 min, could expect a 6% improvement in economy with our device, theoretically leading to a decrease in their finishing time to around the 4 h mark (Hoogkamer et al., 2016; Kipp et al., 2019).

Our study shows how a spring designed to assist leg swing can significantly improve human running economy through a complex mechanism of savings. The device changes the relationship between stride frequency and energy expenditure, driving the runner to discover new locomotor strategies. This change in turn reduces the mechanical work the runner does to both swing the legs and redirect the center of mass, resulting in overall greater efficiency than anticipated. Our exotendon could serve as an affordable and low-tech assistive device to improve human running performance, or a simple and robust intervention to further explore the complexities of human gait and human–machine interactions. More broadly, our study shows that a simple device can create unexpected and complex interactions between the dynamics of the body and the adaptive strategies of the individual – an important reminder for all who seek to augment humans.