ABSTRACT
In rapidly growing animals there are numerous selective pressures and developmental constraints underpinning the ontogenetic development of muscle–tendon morphology and mechanical properties. Muscle force generating capacity, tendon stiffness, elastic energy storage capacity and efficiency were calculated from muscle and tendon morphological parameters and in vitro tendon mechanical properties obtained from a growth series of ostrich cadavers. Ontogenetic scaling relationships were established using reduced major axis regression analysis. Ostrich pelvic limb muscle mass and cross-sectional area broadly scaled with positive allometry, indicating maintained or relatively greater capacity for maximum isometric force generation in larger animals. The length of distal limb tendons was found to scale with positive allometry in several tendons associated with antigravity support and elastic energy storage during locomotion. Distal limb tendon stiffness scaled with negative allometry with respect to body mass, with tendons being relatively more compliant in larger birds. Tendon material properties also appeared to be size-dependent, suggesting that the relative increased compliance of tendons in larger ostriches is due in part to compensatory distortions in tendon material properties during maturation and development, not simply from ontogenetic changes in tendon geometry. Our results suggest that the previously reported increase in locomotor economy through ontogeny in the ostrich is due to greater potential for elastic energy storage with increasing body size. In fact, the rate of this increase may be somewhat greater than the conservative predictions of previous studies, thus illustrating the biological importance of elastic tendon structures in adult ostriches.
KEY WORDS: Growth, Ontogeny, Allometry, Biped, Economical locomotion, Locomotor efficiency
Summary: The ontogenetic scaling of muscle–tendon morphology and tendon material properties suggests maintained or relatively increased muscle force generation, increased elastic energy storage and locomotor economy in adult versus juvenile ostriches.
INTRODUCTION
Species over a large size range move in a dynamically similar manner (Alexander and Jayes, 1983; Bullimore and Burn, 2004, 2006). Complete dynamic similarity requires relevant locomotor parameters to scale appropriately with size and requires geometrically similar body morphology; however, animals across species achieve similarity through appropriate scaling of body segments and postural alterations with increasing body mass (Biewener, 1989). Despite these adaptations to increasing body size, there is increasing evidence that interspecific scaling relationships may not reflect those that occur within a species during growth (Carrier, 1983; Young, 2005; Main and Biewener, 2007; Smith et al., 2010; Smith and Wilson, 2013).
As animals grow, their mass increases, and therefore so does the ground reaction force. This is generally considered to be accompanied by an increase in muscle force development (Biewener, 2005), which results in greater stresses experienced by bone, muscle and tendon (Biewener, 2005). As musculoskeletal stresses increase, so does risk of failure or injury (Biewener and Bertram, 1990; Biewener, 2008). Larger animals can reduce these stresses via postural alterations that result in increased effective mechanical advantage (EMA; Biewener, 1983) but at the expense of some locomotor performance (e.g. accelerative ability; Biewener, 1989, 2005). However, studies in growing ostriches (Smith et al., 2010; Smith and Wilson, 2013) suggest that both limb posture and EMA are independent of body size. Conversely, changes to the kinematics and kinetics of ostrich locomotion during ontogeny demonstrate trends similar to those found between species of increasing size, resulting in many gait parameters scaling close to dynamic similarity (Smith et al., 2010). This species hence appears to exhibit a lack of compensatory postural adaptation alongside maintained locomotor performance during growth. This, together with the concomitant increased loading that accompanies a higher body mass, may be expected to result in changes to stresses, and therefore safety factors, within some elements of the musculoskeletal system. It is possible, however, that the anatomical structure or material properties of key musculoskeletal tissues could be altered to ensure that strain levels remain within acceptable limits throughout growth.
Musculoskeletal tissues show considerable ability to respond and adapt to changes in the loading environment (Rubin and Lanyon, 1985; Reeves et al., 2003; Saadat et al., 2006), and adaptive musculoskeletal responses have been reported in previous ontogenetic scaling studies. Positive allometric scaling of long bones has been noted in a range of species during ontogeny (Carrier, 1983; Main and Biewener, 2007; Smith et al., 2010; Doube et al., 2011; Lamas et al., 2014) suggesting that bone stresses may, at least in part, be maintained via structural changes to the skeleton. In terms of muscle adaptations across species of increasing size, there is a relative reduction in muscle force (∝M0.74-0.8, where M is body mass; Alexander et al., 1981; Biewener, 1989). This, coupled with the interspecific scaling of extensor muscle fibre length (∝M0.23) and mass (∝M1.03) (Alexander et al., 1981), suggests a decreased ability of muscles to generate force relative to their size in larger animals. In contrast, through ontogeny, in the ostrich the relative muscle force is conserved throughout growth (∝M1.0; Smith et al., 2010) with positive allometric scaling of muscle mass across ontogeny being demonstrated in ostrich and other avian muscles (Lamas et al., 2014; Picasso, 2010; Paxton et al., 2010; Dial and Carrier, 2012). This suggests that, not only are muscle forces likely to be maintained to support body mass during growth within a species, but that adult limbs may be specifically adapted for enhanced muscle power production over their juvenile counterparts (Lamas et al., 2014).
Trends for scaling of tendon morphology in growing animals are less clear. Interspecific studies indicate isometric scaling of tendon cross-sectional area (Pollock and Shadwick, 1994a; Bullimore and Burn, 2005), implying that tendon stresses are likely to scale ∝M0.33 and elastic energy storage capacity ∝M0.66. The ratio of muscle to tendon cross-sectional area, however, scaled with positive allometry, suggesting greater relative tendon stress (and strain) and proportionally more elastic energy storage in larger mammals (Pollock and Shadwick, 1994a). Other studies have argued that large animals have less opportunity for elastic strain energy storage because they take fewer steps for a given distance, have a more upright posture and smaller joint excursions (Bullimore and Burn, 2005; Taylor, 1994). These latter relationships, however, do not hold true during ontogeny (Smith and Wilson, 2013). Indeed in emu, the morphology (as defined by measurements of length and cross-sectional area) of 50% of tendons scaled with positive allometry during growth, with the rest scaling isometrically (Lamas et al., 2014). This suggests that at least some tendons in adult animals may have enhanced or at least equivalent potential for elastic energy storage compared with their juvenile counterparts. These previous ontogenetic studies have used estimation and simple models to indirectly explore scaling relationships of tendon functional properties such as elastic energy storage capacity (Smith and Wilson, 2013; Lamas et al., 2014). However, to date, ontogenetic variation of directly measured functional tendon properties across a broad size range have not been determined within a species. The distal limb tendons of the ostrich are of interest since the limb design of this species appears optimised for high-speed economical locomotion utilising elastic energy storage in tendons (Smith et al., 2006; Smith and Wilson, 2013).
There are likely to be a variety of selective pressures and developmental constraints underpinning ontogenetic development of muscle and tendon morphology and properties, particularly in species that exhibit extremely rapid growth, such as ratites. Ostriches typically grow to over 100 kg within a year (Cooper, 2005) at rates of up to 455 g day−1 during periods of maximum growth (70–98 days; Degen et al., 1991). As such, further information is needed to elucidate dynamic ontogenetic relationships of muscle and tendon structure and function in these animals. Many studies have used quantitative measures of muscle and tendon anatomy to produce simple but effective estimates of biomechanical function (e.g. Lieber and Blevins, 1989; Payne et al., 2005; Smith et al., 2006; Williams et al., 2008a,b), and collectively these metrics represent major determinants of how muscles produce force and movement (Lieber and Blevins, 1989). Muscle fibre length and ‘physiological cross-sectional area’ (PCSA) respectively provide estimates of the working range and force-generating capacity of muscles. Greater working ranges come at a cost of reduced muscle forces and vice versa; however, muscles that produce high forces over a large working range (i.e. to do large amounts of work) do exist (e.g. iliofibularis in the ostrich; Smith et al., 2006): the muscle volume must be large to allow a large cross section of long fibres. Such muscles are powerful, have large masses and high associated metabolic costs. We aim in this study to explore how quantitative measures of muscle anatomy are associated with body mass to explore the ontogenetic scaling of muscle function. We also aim to experimentally examine tendon loading response to explore the scaling relationships of tendon stiffness, elastic energy storage, and efficiency in growing ostriches. Considering previous studies (both interspecific and ontogenetic), we hypothesise that muscle and tendon morphological parameters will scale in the ostrich with positive allometry. However, since individual muscles and tendons will vary in terms of their functional contribution to body weight support, we hypothesise that specific ontogenetic scaling relationships will depend on the functional specialisation of the muscle–tendon unit within the limb. We further hypothesise that tendon stiffness will scale with negative allometry in an ontogenetic growth series to reflect the theoretical scaling enhancements of elastic energy storage previously reported in adult ostriches (Smith and Wilson, 2013).
MATERIALS AND METHODS
Subjects
The study was approved by the Royal Veterinary College Ethics and Welfare Committee, UK, reference no. 2011 1123. Eighteen ostrich cadavers of ages ranging from hatching to 2 years were obtained opportunistically from a UK ostrich farm (Pathfinder Ostrich Farm, Chesham, UK). A single farm was used to standardise husbandry and feeding practices, in order to minimise the confounding influence of nutrition and exercise variations on the study. All ostriches were kept free range from birth until death and fed standard pelleted lucerne feed. Ostriches used for the study were deemed to be free from obvious musculoskeletal pathology or nutritional deficits and died after a range of incidents unrelated to this study (for example skull fracture, ingestion of foreign objects). Ostriches were collected from the farm within 24 h of death, and immediately frozen at −20°C. Cadavers were stored at 4°C for 24–48 h prior to dissection.
Muscle and tendon parameters
Each bird was dissected in order for muscle and tendon architectural parameters to be measured, and to obtain tendon samples. Left limbs were skinned and systematically dissected in accordance with the methodology in Smith et al. (2006). Fascicles were revealed by making incisions longitudinally from origin to insertion, or parallel with the internal tendon (as appropriate) through the muscle belly until the plane of the muscle fascicles had been obtained (i.e. when the entire fascicle bundle could be seen). The lengths of 10 random fascicles, from different areas of the belly, were measured with a flexible plastic tape measure (accurate to 1 mm). The measurement of muscle fascicles allows an estimate, rather than microscopic measurement of muscle fibre length. The tendon of origin and insertion (if present) were removed, and tendon and muscle belly resting length and mass were measured, with masses recorded using a set of electronic scales (PL1502E, Mettler Toledo, Leicester, UK). After anatomical measurements were taken, tendons were wrapped in moist tissue and cling film, and placed in a sealed plastic bag to maintain hydration. They were then immediately frozen intact at −20°C until mechanical testing took place.
Muscle volume was determined by dividing muscle mass by muscle density (1.06 g cm−3; Mendez and Keys, 1960). PCSA was calculated as muscle volume/fascicle length. Estimated tendon cross-sectional area (CSAA) was determined by dividing tendon volume (tendon mass divided by a published value for tendon density of 1.12 g cm−3; Ker, 1981) by tendon length. For those tendons subject to mechanical testing [extensor digitorum longus (EDL), flexor perforans et perforatus digiti III (FPPD3) and flexor perforatus digiti III (FPD3)], the CSA of the central part of the tendon sample (CSAB) was also measured using an alginate gel mould, as per Goodship and Birch (2005). In short, alginate gel impressions were made of the central portion of the tested portion of tendon using dust-free alginate impression material (Blueprint x-crème, Dentsply Sirona, Weybridge, UK). The cross section of the created mould was photographed with a digital camera and the CSA of the moulded area was measured using freely available image processing software (ImageJ, NIH, Bethesda, MD, USA; Schneider et al., 2012).
Mechanical testing
Tendon samples were defrosted and prepared for testing by wrapping the middle portion of the tendon in moist tissue and cling film (to maintain hydration) and leaving the proximal and distal end sections for 48 h to dry (for ease of clamping; Haut, 1983; Ker et al., 2000; Wang and Ker, 1995). Mechanical testing was carried out at the University of Liverpool using an Instron E3000 Electropuls servo-electric materials testing machine (Instron, UK) at room temperature. Tendons were clamped at the proximal and distal ends using steel serrated face mechanical wedge action clamps. Tendons divided distally for individual digits, and so clamping was 1 cm proximal to the split to ensure even loading across all collagen fibres. The load cell was calibrated to 0 N with the mounted tendon slack. Following this, a dynamic load-controlled cyclic sine wave test (frequency 2 Hz, 1 kHz sampling rate, recording every cycle) was carried out consisting of 40 cycles, of which the 20th to 29th cycles were used for analysis to ensure appropriate preconditioning of the tendon samples. For each tendon sample, the cyclic test was carried out at 2, 3, 4 and 5% strain, in succession, or until tendon failure or slippage in the clamps caused cessation of testing. Tendons were not intentionally tested to failure since the maximum load of the Instron device was not sufficient to rupture the tendons of the largest birds, and due to the large diameters of these bigger tendons, slippage in the clamps was a problem at high strains.
Analysis
Load versus displacement curves were plotted for each tendon for the 3% strain cyclic test in LabVIEW Version 8.6.1 (National Instruments, UK). An example plot is provided in Fig. 1. A second-order polynomial was fitted to the load–displacement data during loading and unloading and analysed as per Vereecke and Channon (2013). The integral of this quadratic with respect to displacement (i.e. the area under the load–displacement curve) provided the amount of energy stored and returned (energy absorption capacity) during loading and unloading, respectively. Hysteresis (the amount of energy lost as heat during a load–unload cycle) was calculated as the difference between the integral of the loading and unloading curves, divided by the integral of the loading curve. When multiplied by 100, hysteresis gives a value for tendon efficiency (%). A linear regression was plotted to every part of the load–displacement curve (for every 10 data point section). The r2 squared value of this fit was determined, and the most linear region (r2 closest to 1) of the curve was chosen as the linear region for determination of tendon stiffness (Fig. 1). The appropriate selection of a consistent linear region was corroborated by eye for every cycle/tendon/individual within the custom written software, and it was apparent from this visual assessment that the most linear region was always towards the upper end of the load-displacement relationship, i.e. between 2.5 and 3% strain. The r2 values of the linear regression equations were consistently above 0.99, supporting a good linearity of the load–displacement relationship for the data. Tendon stiffness was determined as the slope of the linear regression equation. Stress, σ, was calculated by dividing load by the resting pre-load cross-sectional area of the tendon sample (CSAB). Strain, ε, was calculated by dividing tendon elongation during the test by original length of the sample spanning the two test machine grips. In a similar fashion to determination of stiffness, the Young's modulus, E (MPa), was calculated as the slope of the linear regression of the stress–strain data in the linear portion of the loading curve. The r2 of these regression equations was always greater than 0.99.
Fig. 1.
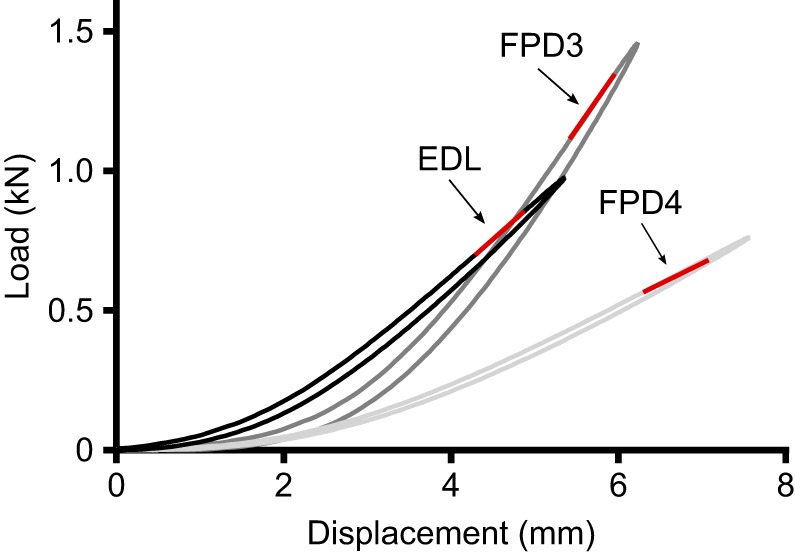
Example tendon load–displacement curves for one ostrich during cyclical loading at 3% strain. EDL, extensor digitorum longus; FPD3, flexor perforatus digiti III; FPD4, flexor perforatus digiti IV. Data from Ostrich 2, which weighed 140 kg. Red lines indicate the linear regions of the load–displacement curve from which tendon stiffness measures were taken using the slope, m, of the linear regression equation (where y=mx+c).
Scaling analysis
Relationships between variables (e.g. muscle physiological cross-sectional area, tendon hysteresis) and body mass were explored. Allometric equations were calculated for each variable by log10 transforming the data and using reduced major axis (RMA) linear regression analysis to define the scaling relationship in the form y=bMa [where y is a variable, b is the proportionality coefficient and a is a scaling exponent (slope of the regression line)]. Analysis was carried out in R version 3.2.2 using the lmodel2 package (https://CRAN.R-project.org/package=lmodel2). An ANCOVA was undertaken to compare the scaling relationships between muscles/tendons with different functional roles. The t-ratio [(best fit slope−hypothetical slope)/standard error of slope] for each relationship was used to identify whether the slope of the regression line differed from zero and from the predicted isometric scaling exponent for that parameter (0.33 for parameters relating to a length; 0.67 for those related to area and 1 for parameters associated with volume/mass). Significance was accepted at α=0.05 for all statistical tests.
RESULTS
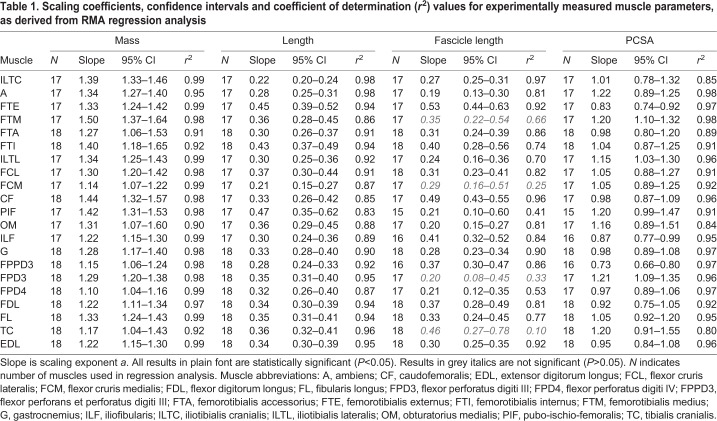
Twenty-one muscles were included for analysis and are considered here (see Figs S1–S6 for plots of each parameter against body mass). Linear regression equations and coefficient of determination (r2) values for linear regressions of each measurement against body mass are given in Table 1. Unless otherwise stated, the scaling relationship for each parameter with body mass differed between muscles (P<0.0001), and all relationships were significantly different from zero (P<0.05).
Table 1.
Scaling coefficients, confidence intervals and coefficient of determination (r2) values for experimentally measured muscle parameters, as derived from RMA regression analysis
Muscle mass
The relationship between muscle mass and body mass exhibited positive allometry (scaling exponent a>1; P<0.05) for all the 21 muscles considered (Table 1 and Fig. 2).
Fig. 2.
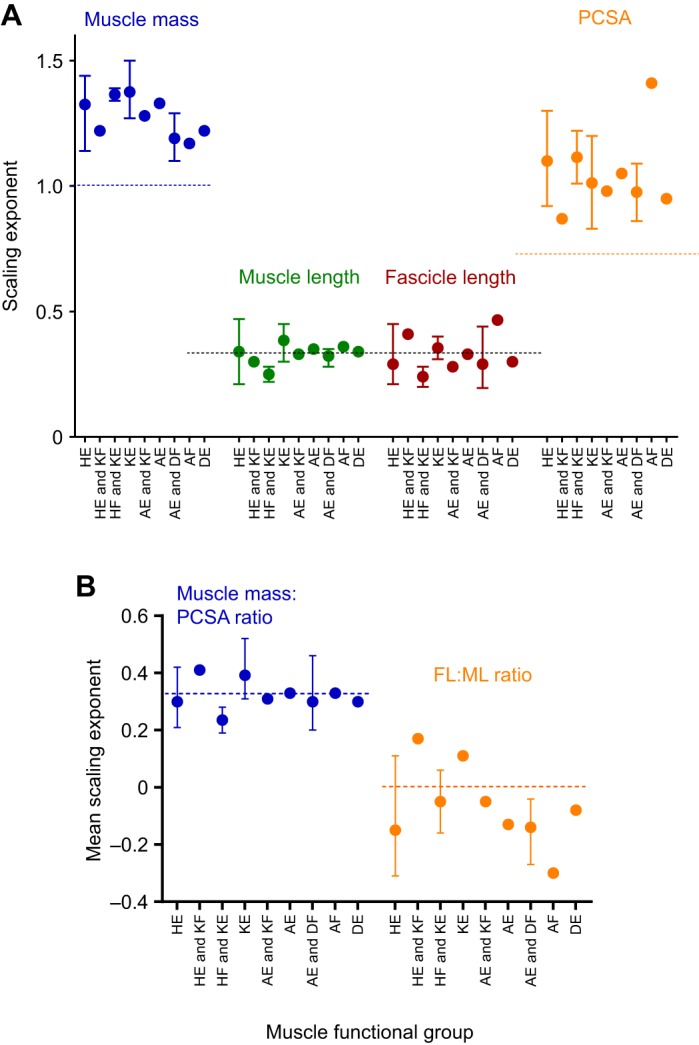
Mean scaling exponents for the scaling of muscle architectural parameters by muscle functional group. (A) Muscle mass, fascicle length, length and muscle physiological cross-sectional area (PCSA). (B) Ratio of muscle fascicle length:muscle length (FL:ML) and ratio of muscle mass:PCSA. Bars represent the range of scaling exponents within each functional category where the number of muscles within that category >1. Horizontal dashed lines represent predicted isometric scaling exponents for each of: (A) mass (M1.0), area (M0.67) and length (M0.33), (B) FL:ML (no scaling relationship) and mass:PCSA (M0.33). Functional groups on horizontal axis: HE, hip extensors; KF, knee flexors; HF, hip flexors; KE, knee extensors; AE, ankle extensors; DF, digital Flexors; AF, ankle flexors; DE, digital extensors.
Muscle length
For 15 muscles, we found insufficient evidence of allometric scaling of muscle length with body mass (a=0.33; P>0.05). There were several exceptions to this (Table 1 and Fig. 2A); three muscles appeared to scale with positive allometry (a>0.33; P<0.05; femorotibialis externus and internus, and pubo-ischio-femoralis) and three muscles appeared to scale with negative allometry (a<0.33; P<0.05; ambiens, iliotibialis cranialis and flexor cruris medialis).
Muscle fascicle lengths
The relationship of muscle fascicle lengths with body mass was not significant for four muscles (Table 1; P>0.05); these relationships also had low r2 values and so were excluded from subsequent analysis and discussion (however data are included in tables and figures in grey italics for information). For 12 muscles, muscle fascicle length did not scale allometrically with body mass (a=0.33; P>0.05). Of the other five muscles, three exhibited negative allometric scaling (a<0.33; P<0.05) and two (femorotibialis externus and caudofemoralis) exhibited positive allometry (a>0.33; P<0.05).
Fascicle length:muscle length (FL:ML) ratio was independent of body mass for 10 muscles (a=0; P<0.05; Fig. 2B). FL: ML ratio scaled positively with body mass for four muscles (a>0; P<0.05; iliotibialis cranialis, femorotibialis externus, FPPD3 and caudofemoralis). The remaining seven muscles had a FL: ML ratio which scaled negatively with body mass (a<0; P<0.05).
Muscle PCSA
All but one muscle showed positive allometric scaling of muscle PCSA with body mass (a>0.67; P<0.05; Fig. 2A). The exception was FPPD3, which showed no evidence of allometric scaling (a=0.67; P>0.05).
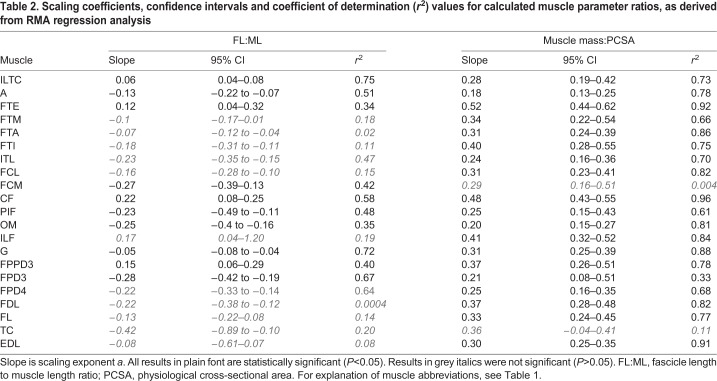
Scaling relationships for muscle mass:PCSA ratio were not significant (Table 2; P>0.05) in two muscles (flexor cruris medialis and tibialis cranialis). The muscle mass:PCSA ratio for the remaining muscles showed no evidence of allometric scaling with body mass in 15 muscles (a=0.33; P>0.05), scaled with negative allometry in two muscles (ambiens and obturatoruis medialis; a<0.33; P<0.05) and with positive allometry (a>0.33; P<0.05) in the two remaining muscles (Table 2).
Table 2.
Scaling coefficients, confidence intervals and coefficient of determination (r2) values for calculated muscle parameter ratios, as derived from RMA regression analysis
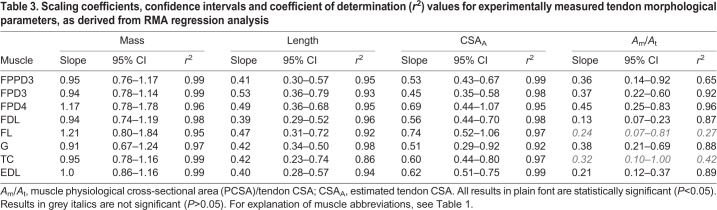
Tendon mass and length
Eight major tendons of insertion were included for analysis. Linear regression equations and r2 values for linear regressions of each measurement against body mass are given in Table 3. The scaling relationship for tendon mass and length with body mass differed for each tendon (P<0.0001). There was no evidence of allometric scaling of tendon mass (a=1.0; P>0.05) for any tendons measured in this study (Fig. 3A). There was no evidence of allometric scaling of tendon length for five tendons (a=0.33; P>0.05). The tendon length of gastrocnemius and two digital flexor muscles (FPD3 and FPD4) scaled with slight positive allometry (a>0.33; P<0.05; Table 3; Fig. 3B).
Table 3.
Scaling coefficients, confidence intervals and coefficient of determination (r2) values for experimentally measured tendon morphological parameters, as derived from RMA regression analysis
Fig. 3.
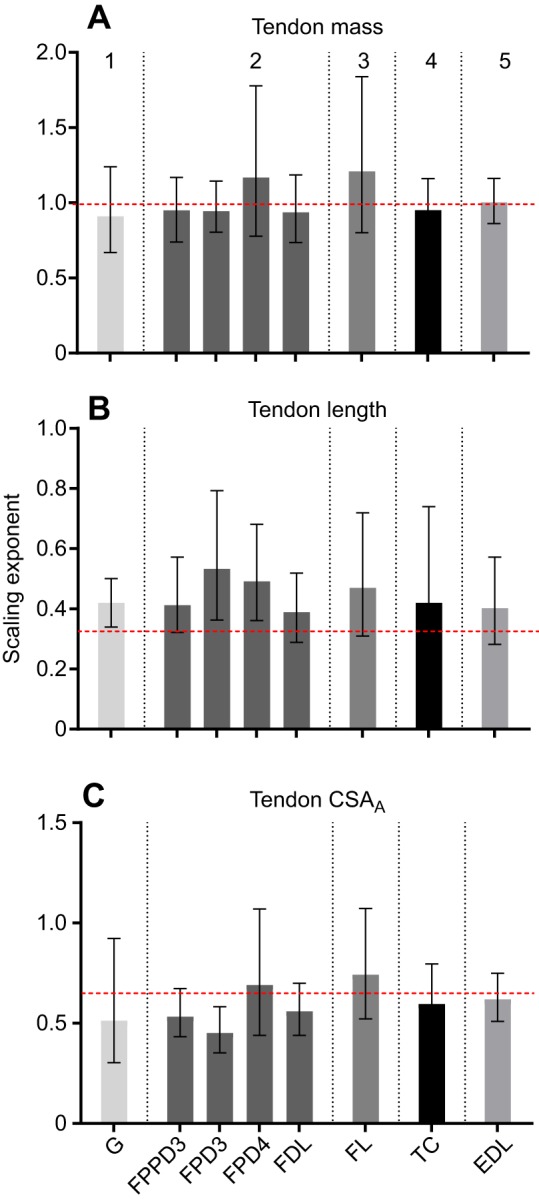
Scaling exponents and 95% confidence intervals for individual pelvic limb tendons. (A) Tendon mass. (B) Tendon length. (C) Tendon CSAA. Vertical dotted lines group tendons by muscle–tendon unit function, which from left to right are: (1) ankle extension and knee flexion; (2) ankle extension and digital flexion; (3) ankle extension; (4) ankle flexion; (5) digital extension. Horizontal dashed lines represent predicted isometric scaling exponents. Muscle abbreviations: G, gastrocnemius; FPPD3, flexor perforans et perforatus digiti III; FPD3, flexor perforatus digiti III; FPD4, flexor perforatus digiti IV; FDL, flexor digitorum longus; FL, fibularis longus; TC, tibialis cranialis; EDL, extensor digitorum longus.
Tendon CSA
The scaling relationship for tendon CSAA with body mass differed for each tendon (P<0.0001; Table 3). There was no evidence of allometric scaling of tendon CSAA for seven tendons (a=0.67; P>0.05); the remaining tendon scaled with negative allometry (FPD3; a<0.67; P<0.05). CSAB showed no evidence of allometric scaling (a=0.67; P>0.05) for all three tendons used for mechanical testing (Table 4; Fig. 3C).
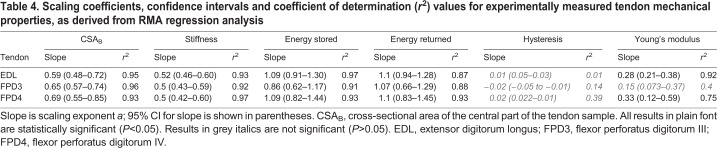
Table 4.
Scaling coefficients, confidence intervals and coefficient of determination (r2) values for experimentally measured tendon mechanical properties, as derived from RMA regression analysis
Tendon material properties
Scaling relationships for tendon material properties are based on mechanical tests at 3% strain. The relationship between tendon energy absorption capacity and body mass was similar for each tendon (P>0.05) and not significantly different from 1 (Table 4; Fig. 4; P>0.05). Tendon efficiency did not scale with body mass, with the scaling exponent for each tendon close to, and not significantly different from, zero (P>0.05; Fig. 4). The scaling relationship of tendon stiffness with body mass was significant and positive (P<0.05) with scaling exponents for each tendon falling between 0.5 and 0.52 (Fig. 4 and Table 4). Young's modulus was found to scale positively with body mass for two out of three tendons, with scaling exponents significantly greater than zero (P<0.05) for EDL (a=0.28) and FPD4 (a=0.33). The scaling exponent for FPD3 (a=0.15) was not significantly different from zero (P>0.05).
Fig. 4.
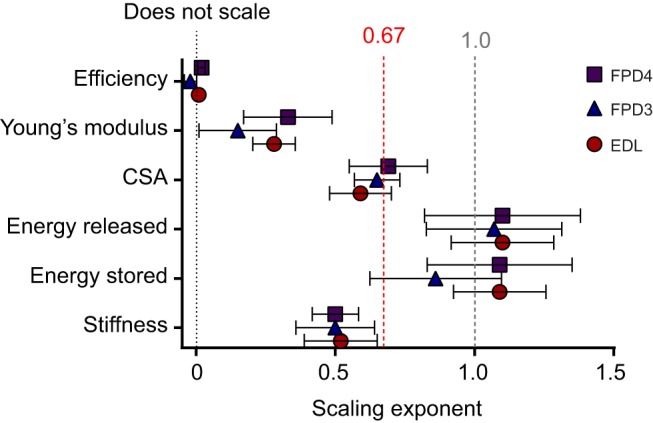
Scaling exponents and 95% confidence intervals for physical and mechanical properties of selected pelvic limb tendons. Black dotted line represents scaling exponent of zero. Red dashed line represents theoretical scaling of tendon stiffness as well as the predicted isometric scaling relationship for tendon CSA. Dashed grey line indicates proportional scaling with body mass. FPD4, flexor perforatus digiti IV, FPD3, flexor perforatus digiti III; EDL, extensor digitorum longus.
Am/At
The relationship between muscle PCSA to tendon CSA ratio (Am/At) and body mass increased with body mass for six of the eight tendons considered (P<0.05) thus scaling with positive allometry (a=0.21 to 0.45; Table 3). The exceptions were fibularis longus and tibialis cranialis, for which there was no significant scaling relationship (P>0.05).
DISCUSSION
Muscle morphology
Ostrich pelvic limb muscle mass broadly scaled with strong positive allometry (M∝1.1–1.5), indicating they have the capacity for relatively greater amounts of work as the animal grows. PCSA also tended to scale with positive allometry (M∝0.73–1.22). Many muscles did not scale significantly differently from M1.0, suggesting that muscle force would be at least maintained in the larger animals, if not enhanced. For three muscles, PCSA scaled greater than M1.0 suggesting, for these muscles at least, force would be relatively increased in larger birds. This is contrary to between species observations where PCSA scales proportionally to M∼0.8 (Alexander et al., 1981), resulting in a relative reduction in peak muscle force with increasing size (∝M0.74–0.8; Alexander et al., 1981; Biewener, 1989) and creates an increasing disparity between muscle force and gravitational loading as animals get bigger (Biewener, 2005). This is accommodated through postural changes and an increase in effective mechanical advantage in order for larger animals to balance rotational moments about their limb joints (Biewener, 1990, 1989; Snelling et al., 2017). Limb posture and ground reaction force vector alignment with the limb do not change significantly with increasing mass in ostriches (Smith and Wilson, 2013). Furthermore, average muscle force requirements during locomotion scale in direct proportion to body mass in ostriches (Smith and Wilson, 2013). This may explain the greater functional requirement for higher peak isometric force generation in bigger ostriches, as illustrated in this study and is seen in other ground dwelling birds (galliform birds and ratites), which exhibit positive allometry of muscle mass and PCSA (Lamas et al., 2014; Paxton et al., 2010, 2014; Picasso, 2010, 2014).
A positive scaling relationship of FL:ML ratio was found for some muscles in the proximal limb. This indicates a developmental emphasis toward increased capacity for muscle work and range of motion at joints and a potential requirement for greater joint range of motion during the swing phase of running of adult ostriches compared to juveniles. In several muscles, the FL:ML ratio scaled negatively with body mass. This indicates optimisation for efficiency of force generation. Many of these are distal limb muscles with a role in body weight support (e.g. gastrocnemius, FPD3, FPD4) and all but obturator medialis have long tendons. The combination of short distal limb muscle fibres with long tendons is well documented (e.g. Biewener, 1998; Wilson et al., 2001), where it provides improved capacity for elastic energy storage and return.
Tendon morphology
The length of ostrich distal limb tendons was found to scale either isometrically, or with positive allometry in the gastrocnemius and two digital flexor tendons (all associated with antigravity support and elastic energy storage during locomotion; Smith et al., 2006; Rubenson et al., 2007). This is in line with both the scaling relationship of segment lengths in the limb regions these tendons cross (foot and tarsometatarsus; Smith et al., 2010) as well as enabling greater elastic energy storage during locomotion. Previous studies of ontogenetic scaling in other ratites have also noted positive allometry of tendon length (Lamas et al., 2014).
Except for FPD3 (which scaled with negative allometry), tendon CSA scaled isometrically with body mass. Two methodologies were used to measure tendon CSA (CSAA and CSAB): these resulted in slightly different scaling relationships. CSAA represents an average cross-sectional area of the entire tendon, based on the tendon volume and using an assumed value for tendon density, including the portion of the tendon after any splitting (e.g. to follow several different paths into individual digits). CSAB represents the directly measured central cross-sectional area of the portion of tendon (thickest region) used for mechanical testing. This indicates that any negative allometry in FPD3 might be restricted to the distal region of this tendon. Using a data set (Smith et al., 2006) across a limited size range, and at a later stage of development when growth had slowed, Smith and Wilson (2013) suggested negative allometric scaling exponents for the CSA of ostrich digital flexor tendons (0.55) and the gastrocnemius tendon (0.54). The general trend towards isometric scaling of tendon CSA in this study, and the negative allometry found by Smith et al. (2006), is striking, and broadly supports the theoretical scaling of elastic energy storage suggested for the ostrich (Smith and Wilson, 2013). Based on an assumption of isometry in tendon cross-sectional area, this predicts that larger ostriches can store proportionally more elastic energy in their tendons than smaller ostriches, with a greater rate of increase with body mass than observed in interspecific studies (Pollock and Shadwick, 1994b). Comparatively, scaling of tendon CSA in the ostrich, which appears largely isometric, differs from the positive allometric relationship in some of the same tendons in emus (FPPD3, FPD3, fibularis longus and FDL; Lamas et al., 2014). The strength of some regression equations appears weaker for comparable tendons in the emu [coefficients of variation: 0.58–0.95 (Lamas et al., 2014), versus 0.92−0.99 in this study]. The discrepancies may also reflect the smaller size of adult emu compared with the ostrich [the largest emu in Lamas et al. (2014) was 64% smaller than the largest ostrich in this study]. Different target sizes and growth rates may lead to differing ontogenetic requirements between the two species. Additionally, the more highly specialised nature of the ostrich as an athletic and cursorial biped, well adapted for high speed running may impact the requirements for tendon development. Other athletic species (bipedal hoppers) also exhibit isometric and negative allometric scaling of pelvic limb tendons (Snelling et al., 2017).
Tendon stiffness and material properties
Tendon stiffness scaled ∝M0.51. For some quadrupedal mammals and macropodidae, dynamic similarity is evident from stiffness scaling with M0.67 (Farley et al., 1993). In contrast, the stiffness of ostrich distal limb tendons consistently scales with negative allometry with body mass. Whole limb stiffness in the ostrich also scales with negative allometry (∝M0.59) implying proportionally greater leg length change during running in larger birds (Smith et al., 2010). These findings are consistent with the supposition that this greater leg length change in adult birds would be facilitated by more compliant distal limb tendons.
Biewener (2005) suggested that ‘maintaining sufficient stiffness may be the overriding design requirement for some tendons’. Indeed, the need for tendons to possess an appropriate stiffness to maintain an adequate safety margin, whilst retaining sufficient ability to store elastic energy, is likely an important trade off and developmental compromise. Stiff tendons require more force to stretch them, are stronger (Matson et al., 2012) and more suited for transfer of muscle power to the skeleton. Compliant tendons are more suited to spring-like behaviour and storage and release of elastic energy. The limb stiffness in large ostriches is comparable with other animals of similar size (25 kN m−1 versus 30 kN m−1; Smith et al., 2010; Farley et al., 1993), suggesting that the scaling relationship could arise out of developmental constraints to reach the required adult properties, and that small and immature ostriches may be, by necessity, ‘overdesigned’.
Changes to tendon stiffness through growth in the ostrich are consistent with studies in pigs and rabbits which found that mature animals have stiffer tendons than their immature counterparts (Shadwick, 1990; Nakagawa et al., 1996). However, whilst we find that tendon stiffness is numerically higher in mature animals (e.g. 15 (youngest) to 433 (mature) N mm−1 in FPD3), the negative allometry means that this disparity is not as large as one might expect. The stiffness (k) of a tendon in its linear region depends on the Young's modulus (E), cross-sectional area (A) and length (l), as follows:
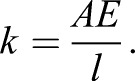 |
(1) |
Eqn 1 illustrates that, in general, stiffness decreases with decreased tendon cross-sectional area and with increases in tendon length. Both of which are suggested by the scaling relationships in this study. Since tendon stiffness also depends on the material properties of a tendon, evaluating Young's modulus is useful. This alternative measure arises from the stress–strain relationship and is independent of geometry. To allow dynamically similar locomotion, Young's modulus should scale ∝M0.33 (Bullimore and Burn, 2004), i.e. to a characteristic length. Contrary to this, interspecific scaling studies indicate that musculoskeletal tissue properties in mammals scale independently of body mass (Weir et al., 1949; Smith and Walmsley, 1959; Currey, 1979; Biewener, 1982; Pollock and Shadwick, 1994b; Medler, 2002). However, ontogenetically within a species, the current study suggests that material properties (Young's modulus) in some tendons do indeed appear to scale as predicted by dynamic similarity. It appears that it cannot be assumed that the inherent material properties of biological tissues are independent of body size (as seen in many interspecific scaling studies, e.g. Pollock and Shadwick, 1994a; Bertram and Biewener, 1992), especially when considering growth. Further research is required to fully explore the dynamic structure–function relationship during this period.
The mechanisms underlying variation in tendon material properties in response to growth and the consequential changes in mechanical behaviour are not entirely clear (Kjaer, 2004). Structural increases in collagen density are associated with increased tendon stiffness (Woo et al., 1980) as are alterations to collagen fibril orientation (Wood et al., 1988). Collagen crimp angle has been implicated in direct modulation of the length of the toe region of the tendon stress–strain curve (Shadwick, 1990; Shearer, 2015). This is the region in which tendons in terrestrial animals tend to operate (Ker et al., 1988). Recent studies in energy-storing tendons suggest that their energy-storing capabilities may be more readily influenced by their helical fibril arrangement (Shearer et al., 2017). The helix angle appears to be able to tune the relative compliance or stiffness of a tendon independently of the crimp angle, influencing the full length of the stress–strain curve. It is possible that such changes impact the elastic modulus of tendon during growth, although there do not appear to be any published studies specifically considering the organisation of collagen fibrils during ontogeny.
Tendon ‘safety’ and energy-storing capacity
For tendons and ligaments, a trade-off exists in terms of design for adequate strength versus achieving high-energy savings (Biewener and Blickhan, 1988). High strength and high ‘safety factor’ minimise the probability of failure, whilst tendons specialised for elastic energy storage tend to operate at much lower safety factors, perhaps at the cost of the maximum locomotor performance (e.g. speed, acceleration) that can be achieved. Whilst most tendons appear to have higher than expected safety factors (Ker et al., 1988), some (particularly in highly specialised cursors such as some ungulates and the ostrich) function close to their safety limit (Biewener, 1998; Birch, 2007). Differential scaling relationships of tendon versus muscle cross-sectional area with size in this study suggest a potential trade off in tendon safety factor in the adult ostrich. Whilst tendon CSA appears to scale with isometry, or in some cases mild negative allometry, muscle PCSA scales consistently with strong positive allometry. This disparity results in Am/At ∝M0.21–0.45 and suggests considerably greater tendon strains in the major digital flexor tendons in adult birds during maximal locomotor activities. Adult ostrich tendons therefore likely operate closer to their safety limit than their juvenile counterparts, reflecting a design for enhanced elastic energy storage in adults and, potentially, a requirement to minimise tendon compliance to improve positional control in juvenile birds (Biewener, 2005).
Enhancement of elastic energy storage in adult ostriches is supported by our measurements of tendon properties: tendon energy storage and return were found to scale to M1.01 (∝M0.89–1.09). A more relevant way to express tendon energy storage is as energy stored per stride. Using the relationship of Bullimore and Burn (2005), this is proportional to the product of body mass and the energy stored per unit volume of tendon, such that:
| (2) |
This greatly exceeds that previously predicted for the scaling of tendon elastic energy storage per stride (∝M1.14; Bullimore and Burn, 2005) but is close to the theoretical scaling based on an ontogenetic series of biomechanical data from running ostriches (∝M1.90; Smith and Wilson, 2013). This suggests that the amount of energy storage in elastic elements increases at a far greater rate than the increase in size: a trend previously observed between species of differing size, although to a lesser degree (Alexander et al., 1981; Bennett and Taylor, 1995; Reilly et al., 2007).
Our values for the total functional elastic energy storage within the ostrich limb during locomotion are estimates: other structures in addition to distal limb tendons, including proximal tendinous structures, ligaments, fascia and aponeuroses may also contribute (Ettema and Huijing, 1989; Lichtwark and Wilson, 2005; Roberts et al., 1997). Similarly, our mechanical tests used only the central portion of the distal limb tendons (neglecting functionally and anatomically more complex tendons within the foot). Our loading protocol was also basic, using a simple cyclic sinusoidal wave, so cannot fully represent tendon behaviour in vivo across the full range of locomotor behaviours. However, despite these limitations, our findings support the theory that ostriches display a significant increase in locomotor economy through ontogeny as a result of greater elastic energy storage with increasing body size (Smith and Wilson, 2013). Furthermore, the rate of this increase may be greater than earlier predictions illustrating the likely biological importance of locomotor economy in adult ostriches.
Statistical power and limitations
Brown and Vavrek (2015) show that for intraspecific scaling studies with sample sizes less than ∼70, the likelihood of ‘false isometry’ (type II error) is reasonably high, and higher than the likelihood of obtaining ‘false allometry’. The current study was restricted in its sample size because of the challenges in accessing cadaver material of an exotic species, reared in controlled conditions and similar husbandry across a wide size range. We, therefore, acknowledge that for some muscles and parameters that exhibit a high degree of natural variation, there is a reasonable possibility of false isometry. However, since the likelihood of false allometry is not closely linked to sample size (Brown and Vavrek, 2015), the positive and negative allometric relationships indicated should not be adversely affected by type II errors associated with low subject numbers.
Measurement errors are always a possibility in anatomical studies: these were minimised by using a standard cadaver storage and dissection protocol for all cadavers carried out by the same two experienced investigators working together. A sensitivity analysis, carried out to investigate the influence of error – due to natural variation or hypothetical measurement errors during data collection – on the scaling relationships shown, indicated that sensitivity to error varied depending on both muscle and measurement parameters. The full analysis for individual muscles/tendons is provided in the Appendix. In summary, the resultant errors introduced into the regression slopes were mostly small, fell within the confidence intervals of the original regression equations and did not alter the main conclusions of this study.
An oblique pennation angle within a muscle may cause it to experience a loss in vector force along its line of pull. PCSA values were not corrected for pennation angle (as per Smith et al., 2006, for example). There is convincing evidence that pennation angle alters substantially during muscle contraction (e.g. Herbert and Gandevia, 1995; Azizi et al., 2008) as well as being influenced by joint position during the storage of frozen cadavers, and so we were not comfortable with its use as a correction factor in this instance. This may therefore result in PCSA being overestimated in some more pennate muscles (by approximately 14% for a pennation of 30 deg) such as the femorotibialis group, flexor cruris medialis and ambiens. Our data for PCSA are also estimated based on previous measures of muscle density in mammals (Mendez and Keys, 1960) and assume that muscle density is similar across all muscles and birds in our study. This may not be correct if muscle density changes with body mass. Muscle density is known to change with tissue hydration and such hydration effects can impact PCSA estimations by 5–10% (Ward and Lieber, 2005). Similarly, our methodology for calculating CSAA used a predetermined value for tendon density (Ker, 1981), which may have introduced error into the values if tendon density changes with body mass. Establishing detailed ontogenetic scaling relationships for muscle and tendon density was, however, beyond the scope of the current study.
Our data are derived from mechanical testing based on loads at 3% strain, a value at the lower end of estimates of in vivo tendon strain during running in birds (Biewener and Roberts, 2000; Buchanan and Marsh, 2001) but which produced reliable and repeatable data across the full size range of our samples. The restriction of our data set to 3% strain was necessary, since some tendons from very small birds were stretched to failure beyond this; additionally, adequate clamping of larger tendons for testing at high strains was problematic. 3% strain reflects the more commonly utilised range of tendon stress and strain during sub-maximal locomotor behaviours but is not representative of maximum in vivo tendon strains during running. Further investigations are required to understand how our findings are relevant to maximal locomotor performance, when tendons operate far closer to their safety limits. Similarly, it is difficult to rule out unequal stress in larger tendons (e.g. reduced stress in the central core); this is a known difficulty with in vitro tendon testing methodologies. However, we were as rigorous as possible in minimising the potential for clamping-induced artefacts and followed standard and previously published protocols (e.g. Vereecke and Channon, 2013). Finally, we mechanically tested tendons based on consistent maximum strain values, and a consistent loading rate across body size; future in vitro or, ideally, in vivo data are required to fully validate the impact of our choice of loading conditions on our conclusions.
Conclusions
In summary, we examined the intraspecific scaling of muscle–tendon morphology and tendon mechanical and material properties in ostriches. We highlight that both muscle mass and cross-sectional area are relatively greater in larger birds, consistent with a requirement for larger birds to maintain or reduce muscle stresses, to compensate for the lack of alteration of limb posture with body mass. Tendon stiffness scaled with negative allometry, most likely a function of the body mass dependence of tendon material properties during maturation and development, as well as changes in tendon geometry. This apparent ‘design’ for enhanced elastic energy storage and release in larger birds is supported by previously published predictions and highlights a likely functional requirement for greater energy savings in elastic elements in adult ostriches.
Supplementary Material
Acknowledgements
The authors would like to thank Dr Carol Hercock and Elizabeth Starkey for assistance with data collection. We would like to thank Anthony Channon for sharing and custom editing scripts for data analysis. Scott Dyason of Pathfinder Ostrich Farm was instrumental in donating cadaver material. We would also like to thank the editor and two anonymous reviewers for their insightful comments which have improved the manuscript considerably.
Appendix
Sensitivity analysis
A sensitivity analysis was carried out to investigate the influence of any measurement error (either caused by individual variation between birds, or due to hypothetical measurement errors during data collection); 10% and 50% changes to measurement values were chosen to represent each of these scenarios. These changes were applied to the smallest birds, which due to their small size would be likely to be most sensitive to measurement error and due to their presence at one extreme of the regression line, most likely to influence the slope of the regression equation.
Sensitivity to error varied depending on both muscle, and measurement parameter. Full analysis for individual muscles/tendons is provided in Figs S1–S6. The average errors for each parameter are provided in Table A1.
Table A1.
Mean error (%) in slope of the regression line for measurement parameters in this study
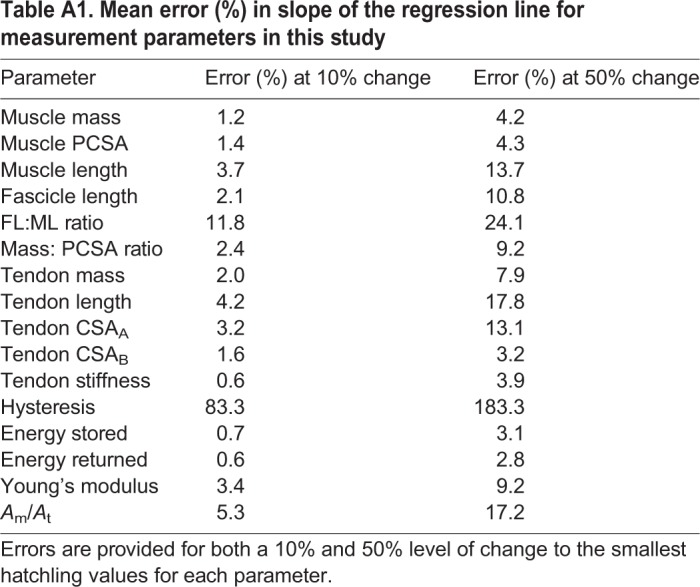
Across most parameters, output errors are small at 10% error (below 5% for all but three parameters). The absolute output values for the slope of the regression lines, following the introduction of error, still fall within the confidence intervals of the original regression analyses, suggesting that individual anatomical variation of the smallest ostriches is unlikely to have influenced the main outcomes of this study. This is also the case at the 50% level where, whilst output errors are higher, absolute measurement values fall comfortably within confidence intervals of the regression lines.
Large output errors were seen for tendon hysteresis; however, the values for this parameter are near zero (this parameter was found not to scale with muscle mass) and small changes inevitably result in a large percentage error. The absolute values of hysteresis following the introduction of 10 and 50% error are still close to zero and the interpretation of the study results does not change on this basis. Average output errors are also relatively high for FL:ML ratio. This reflects large output error for six muscles, which is due to their small numerical values. The absolute values for this parameter following the introduction of both 10 and 50% error still fall within the confidence intervals of the original regression analysis.
Footnotes
Competing interests
The authors declare no competing or financial interests.
Author contributions
Conceptualization: S.B.C., N.S.; Methodology: S.B.C., I.S.Y., N.S.; Formal analysis: S.B.C., B.C.; Investigation: S.B.C., I.S.Y., B.C., N.S.; Resources: S.B.C., I.S.Y.; Data curation: S.B.C., B.C.; Writing - original draft: S.B.C., B.C.; Writing - review & editing: S.B.C., I.S.Y., N.S.; Visualization: S.B.C.; Supervision: S.B.C., N.S.; Project administration: S.B.C.; Funding acquisition: S.B.C., N.S.
Funding
The Wellcome Trust funded undergraduate clinical veterinary research training scholarships for B.C. and Elizabeth Starkey. The project was funded by an internal grant from the Royal Veterinary College to S.B.C. Deposited in PMC for release after 6 months.
Supplementary information
Supplementary information available online at http://jeb.biologists.org/lookup/doi/10.1242/jeb.182741.supplemental
References
- Alexander R. M. N., Jayes A. S., Maloiy G. M. O. and Wathuta E. M. (1981). Allometry of the leg muscles of mammals. J. Zool. 194, 539-552. 10.1111/j.1469-7998.1981.tb04600.x [DOI] [Google Scholar]
- Alexander R. M. N. and Jayes A. S. (1983). A dynamic similarity hypothesis for the gaits of quadrupedal mammals. J. Zool. Lond. 201, 135-152. 10.1111/j.1469-7998.1983.tb04266.x [DOI] [Google Scholar]
- Azizi E., Brainerd E. L. and Roberts T. J. (2008). Variable gearing in pennate muscles. Proc. Natl. Acad. Sci. USA 105, 1745-1750. 10.1073/pnas.0709212105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett M. B. and Taylor G. C. (1995). Scaling of elastic strain energy in kangaroos and the benefits of being big. Nature 378, 56-59. 10.1038/378056a0 [DOI] [PubMed] [Google Scholar]
- Bertram J. and Biewener A. A. (1992). Allometry and curvature in the long bones of quadrupedal mammals. J. Zool. 226, 445-467. 10.1111/j.1469-7998.1992.tb07492.x [DOI] [Google Scholar]
- Biewener A. A. (1982). Bone strength in small mammals and bipedal birds: do safety factors change with body size? J. Exp. Biol. 98, 289-301. [DOI] [PubMed] [Google Scholar]
- Biewener A. A. (1983). Allometry of quadrupedal locomotion: the scaling of duty factor, bone curvature and limb orientation to body size. J. Exp. Biol. 105, 147-171. [DOI] [PubMed] [Google Scholar]
- Biewener A. A. (1989). Scaling body support in mammals: limb posture and muscle mechanics. Science 245, 45-48. 10.1126/science.2740914 [DOI] [PubMed] [Google Scholar]
- Biewener A. A. (1990). Biomechanics of mammalian terrestrial locomotion. Science 250, 1097-1103. 10.1126/science.2251499 [DOI] [PubMed] [Google Scholar]
- Biewener A. A. (1998). Muscle-tendon stresses and elastic energy storage during locomotion in the horse. Comp. Biochem. Physiol. B Biochem. Mol. Biol. 120, 73-87. 10.1016/S0305-0491(98)00024-8 [DOI] [PubMed] [Google Scholar]
- Biewener A. A. (2005). Biomechanical consequences of scaling. J. Exp. Biol. 208, 1665-1676. 10.1242/jeb.01520 [DOI] [PubMed] [Google Scholar]
- Biewener A. A. (2008). Tendons and ligaments: structure, mechanical behavior and biological function. In Collagen: Structure and Mechanics (ed. Fratzl P.), pp. 269-284. New York: Springer Science & Business Media, LLC. [Google Scholar]
- Biewener A. A. and Bertram J. E. A. (1990). Efficiency and optimization in the design of skeletal support systems. In: Concepts of Efficiency in Biological Systems (ed. Blake R. W.), pp. 65-82. Cambridge: Cambridge University Press. [Google Scholar]
- Biewener A. A. and Blickhan R. (1988). Kangaroo rat locomotion: design for elastic energy storage or acceleration? J. Exp. Biol. 140, 243-255. [DOI] [PubMed] [Google Scholar]
- Biewener A. A. and Roberts T. J. (2000). Muscle and tendon contributions to force, work, and elastic energy savings: a comparative perspective. Exerc. Sport Sci. Rev. 28, 99-107. [PubMed] [Google Scholar]
- Birch H. L. (2007). Tendon matrix composition and turnover in relation to functional requirements. Int. J. Exp. Path 88, 241-248. 10.1111/j.1365-2613.2007.00552.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown C. M. and Vavrek M. J. (2015). Small sample sizes in the study of ontogenetic allometry; implications for palaeobiology. Peer J. 3, e818 10.7717/peerj.818 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchanan C. I. and Marsh R. L. (2001). Effects of long-term exercise on the biomechanical properties of the Achilles tendon of guinea fowl. J. Appl. Physiol. 1, 164-171. 10.1152/jappl.2001.90.1.164 [DOI] [PubMed] [Google Scholar]
- Bullimore S. R. and Burn J. F. (2004). Distorting limb design for dynamically similar locomotion. Proc. Biol. Sci. 271, 285-289. 10.1098/rspb.2003.2611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullimore S. R. and Burn J. F. (2005). Scaling of elastic energy storage in mammalian limb tendons: do small mammals really lose out? Biol. Lett. 1, 57-59. 10.1098/rsbl.2004.0243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullimore S. R. and Burn J. F. (2006). Dynamically similar locomotion in horses. J. Exp. Biol. 209, 455-465. 10.1242/jeb.02029 [DOI] [PubMed] [Google Scholar]
- Carrier D. R. (1983). Postnatal ontogeny of the musculoskeletal system in the Black tailed jack-rabbit. J. Zool. Lond. 201, 27-55. 10.1111/j.1469-7998.1983.tb04259.x [DOI] [Google Scholar]
- Cooper R. G. (2005). Growth in the ostrich (Struthio camelus var. domesticus). Anim. Sci. J. 76, 1-4. 10.1111/j.1740-0929.2005.00230.x [DOI] [Google Scholar]
- Currey J. D. (1979). Mechanical properties of bone tissues with greatly differing functions. J. Biomech. 12, 313-319. 10.1016/0021-9290(79)90073-3 [DOI] [PubMed] [Google Scholar]
- Degen A. A., Kam M., Rosentrauch A. and Plavnik I. (1991). Growth rate, total water volume, dry matter intake and water consumption of domesticated ostriches. Animal Production 52, 225-232. 10.1017/S0003356100005870 [DOI] [Google Scholar]
- Dial T. R. and Carrier D. R. (2012). Precocial hindlimbs and altricial forelimbs: partitioning ontogenetic strategies in mallards (Anas platyrhynchos). J. Exp. Biol. 215, 3703-3710. 10.1242/jeb.057380 [DOI] [PubMed] [Google Scholar]
- Doube M., Klosowski M. M., Wiktorowicz-Conroy A. M., Hutchinson J. R. and Shefelbine S. J. (2011). Trabecular bone scales allometrically in mammals and birds. Proc. Biol. Sci. 278, 3067-3073. 10.1098/rspb.2011.0069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ettema G. J. C. and Huijing P. A. (1989). Properties of the tendinous structures and series elastic component of the EDL muscle tendon complex of the rat. J. Biomech. 22, 209-1215. 10.1016/0021-9290(89)90223-6 [DOI] [PubMed] [Google Scholar]
- Farley C. T., Glasheen J. and McMahon T. A. (1993). Running springs: speed and animal size. J. Exp. Biol. 185, 71-86. [DOI] [PubMed] [Google Scholar]
- Goodship A. and Birch H. (2005). Cross sectional area measurement of tendon and ligament in vitro: a simple, rapid, non-destructive technique . J. Biomech. 38, 605-608. 10.1016/j.jbiomech.2004.05.003 [DOI] [PubMed] [Google Scholar]
- Haut R. C. (1983). Age dependent influence of strain rate on the tensile failure of rat-tail tendon. J. Biomech. Eng 105, 296-299. 10.1115/1.3138422 [DOI] [PubMed] [Google Scholar]
- Herbert R. D. and Gandevia S. C. (1995). Changes in pennation with joint angle and muscle torque: in vivo measurements in human brachialis muscle. J. Physiol. 484, 523-532. 10.1113/jphysiol.1995.sp020683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ker R. F. (1981). Dynamic tensile properties of the plantaris tendon of sheep (Ovis aries). J. Exp. Biol. 93, 283-302. [DOI] [PubMed] [Google Scholar]
- Ker R. F., Alexander R. M. N. and Bennett M. B. (1988). Why are mammalian tendons so thick? J.Zool. Lond. 216, 309-324. 10.1111/j.1469-7998.1988.tb02432.x [DOI] [Google Scholar]
- Ker R. F., Wang X. T. and Pike A. V. L. (2000). Fatigue quality of mammalian tendons. J. Exp. Biol. 203, 1317-1327. [DOI] [PubMed] [Google Scholar]
- Kjaer M. (2004). Role of extracellular matrix in adaptation of tendon and skeletal muscle to mechanical loading. Physiol. Rev. 84, 649-698. 10.1152/physrev.00031.2003 [DOI] [PubMed] [Google Scholar]
- Lamas L. P., Main R. P. and Hutchinson J. R. (2014). Ontogenetic scaling patterns and functional anatomy of the pelvic limb musculature in emus (Dromaius novaehollandiae) . PeerJ 2, e.716 10.7287/peerj.preprints.508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichtwark G. A. and Wilson A. M. (2005). Effects of series elasticity and activation conditions on muscle power output and efficiency. J. Exp. Biol. 208, 2845-2853. 10.1242/jeb.01710 [DOI] [PubMed] [Google Scholar]
- Lieber R. L. and Blevins F. T. (1989). Skeletal muscle architecture of the rabbit hindlimb: functional implications of muscle design. J. Morphol. 199, 93-101. 10.1002/jmor.1051990108 [DOI] [PubMed] [Google Scholar]
- Main R. P. and Biewener A. A. (2007). Skeletal strain patterns and growth in the emu hindlimb during ontogeny. J. Exp. Biol. 210, 2676-2690. 10.1242/jeb.004580 [DOI] [PubMed] [Google Scholar]
- Matson A., Konow N., Miller S., Konow P. P. and Roberts T. J. (2012). Tendon material properties vary and are interdependent among turkey hindlimb muscles. J. Exp. Biol. 215, 3552-3558. 10.1242/jeb.072728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medler S. (2002). Comparative trends in shortening velocity and force production in skeletal muscles. Am. J. Physiol. Regul. Integr. Comp. Physiol. 283, R368-R378. 10.1152/ajpregu.00689.2001 [DOI] [PubMed] [Google Scholar]
- Mendez J. and Keys A. (1960). Density and composition of mammalian muscle . Metabolism 9, 184-188. [Google Scholar]
- Nakagawa Y., Hayashi K., Yamamoto N. and Nagashima K. (1996). Age-related changes in biomechanical properties of the Achilles tendon in rabbits. Eur. J. Appl. Physiol. 73, 7-10. 10.1007/BF00262803 [DOI] [PubMed] [Google Scholar]
- Paxton H., Anthony N. B., Corr S. A. and Hutchinson J. R. (2010). The effects of selective breeding on the architectural properties of the pelvic limb in broiler chickens: a comparative study across modern and ancestral populations. J. Anat. 217, 153-166. 10.1111/j.1469-7580.2010.01251.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxton H., Tickle P. G., Rankin J. W., Codd J. R. and Hutchinson J. R. (2014). Anatomical and biomechanical traits of broiler chickens across ontogeny. Part II. Body segment inertial properties and muscle architecture of the pelvic limb. Peer J. 2, e473 10.7287/peerj.preprints.343v1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne R. C., Hutchinson J. R., Robilliard J. J., Smith N. C. and Wilson A. M. (2005). Functional specialisation of pelvic limb anatomy in horses (Equus caballus). J. Anat. 206, 557-574. 10.1111/j.1469-7580.2005.00420.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picasso M. B. J. (2010). The hindlimb muscles of Rhea americana (Aves, Paleognathae, Rheidae). Anat. Histol. Embryol. 39, 462-472. 10.1111/j.1439-0264.2010.01017.x [DOI] [PubMed] [Google Scholar]
- Picasso M. B. J. (2014). Ontogenetic scaling of the hindlimb muscles of the greater rhea (Rhea americana). Anat. Histol. Embryol. 44, 452-459. 10.1111/ahe.12158 [DOI] [PubMed] [Google Scholar]
- Pollock C. M. and Shadwick R. E. (1994a). Allometry of muscle, tendon and elastic energy storage capacity in mammals. Am. J. Physiol. Reg. Integr. Comp. Physiol. 266, 1022-1031. 10.1152/ajpregu.1994.266.3.R1022 [DOI] [PubMed] [Google Scholar]
- Pollock C. M. and Shadwick R. E. (1994b). Relationship between body mass and biomechanical properties of limb tendons in adult mammals. Amer. J. Physiol. Reg. Integr. Comp. Physiol. 266, R1016-R1021. 10.1152/ajpregu.1994.266.3.R1016 [DOI] [PubMed] [Google Scholar]
- Reeves N. D., Maganaris C. N. and Narici M. V. (2003). Effect of strength training on human patella tendon mechanical properties of older individuals. Eur. J. Appl. Physiol. 91, 116-118. 10.1007/s00421-003-0961-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reilly S. M., McElroy E. J. and Biknevicius A. R. (2007). Posture, gait and the ecological relevance of locomotor costs and energy-saving mechanisms in tetrapods. Zoology 110, 271-289. 10.1016/j.zool.2007.01.003 [DOI] [PubMed] [Google Scholar]
- Roberts T. J., Marsh R. L., Weyand P. G. and Taylor C. R. (1997). Muscular force in running turkeys: the economy of minimizing work. Science 275, 1113-1115. 10.1126/science.275.5303.1113 [DOI] [PubMed] [Google Scholar]
- Rubenson J., Lloyd D. G., Besier T. F., Heliams D. B. and Fournier P. A. (2007). Running in ostriches (Struthio camelus): three-dimensional joint axes alignment and joint kinematics . J. Exp. Biol. 210, 2548-2562. 10.1242/jeb.02792 [DOI] [PubMed] [Google Scholar]
- Rubin C. T. and Lanyon L. (1985). Regulation of bone mass by mechanical strain magnitude. CalcTiss Int. 37, 411-417. 10.1007/bf02553711 [DOI] [PubMed] [Google Scholar]
- Saadat E., Lan H., Majumdar S., Rempel D. M. and King K. B. (2006). Long-term cyclical in vivo loading increases cartilage proteoglycan content in a spatially specific manner: an infrared microspectroscopic imaging and polarized light microscopy study. Arthritis Res. Ther. 8, 147 10.1186/ar2040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider C. A., Rasband W. S. and Eliceiri K. W. (2012). NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671-675. 10.1038/nmeth.2089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadwick R. E. (1990). Elastic energy storage in tendons: mechanical differences related to function and age. J. Appl. Physiol. 68, 1033-1040. 10.1152/jappl.1990.68.3.1033 [DOI] [PubMed] [Google Scholar]
- Shearer T. (2015). A new strain energy function for modelling ligaments and tendons whose fascicles have a helical arrangement of fibrils . J. Biomech. 48, 3017-3025. 10.1016/j.jbiomech.2015.07.032 [DOI] [PubMed] [Google Scholar]
- Shearer T., Thorpe C. T. and Screen H. R. C. (2017). The relative compliance of energy storing tendons may be due to the helical fibril arrangement of their fascicles. J. R. Soc. Interface 14, 20170261 10.1098/rsif.2017.0261 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. W. and Walmsley R. (1959). Factors affecting the elasticity of bone. J. Anat. 93, 503-523. [PMC free article] [PubMed] [Google Scholar]
- Smith N. C. and Wilson A. M. (2013). Mechanical and energetic scaling relationships of running gait through ontogeny in the ostrich (Struthio camelus). J. Exp. Biol. 216, 841-849. 10.1242/jeb.064691 [DOI] [PubMed] [Google Scholar]
- Smith N. C., Wilson A. M., Jespers K. J. and Payne R. C. (2006). Muscle architecture and functional anatomy of the pelvic limb of the ostrich (Struthio camelus). J. Anat. 209, 765-779. 10.1111/j.1469-7580.2006.00658.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith N. C., Jespers K. and Wilson A. M. (2010). Ontogenetic scaling of locomotor kinetics and kinematics of the ostrich (Struthio camelus). J. Exp. Biol. 213, 1347-1355. 10.1242/jeb.020271 [DOI] [PubMed] [Google Scholar]
- Snelling E. P., Biewener A. A., Hu Q., Taggart D. A., Fuller A., Mitchell D., Maloney S. K. and Seymour R. S. (2017). Scaling of the ankle extensor muscle-tendon units and the biomechanical implications for bipedal hopping locomotion in the post-pouch kangaroo Macropus fuliginosus. J. Anat. 231, 921-930. 10.1111/joa.12715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor C. R. (1994). Relating mechanics and energetics during exercise. Comparative vertebrate exercise physiology: unifying physiological principles. Adv. Vet. Sci. Comp. Med. 38, 181-215. [PubMed] [Google Scholar]
- Vereecke E. E. and Channon A. J. (2013). The role of hind limb tendons in gibbon locomotion: springs or strings? J. Exp. Biol. 216, 3971-3980. 10.1242/jeb.083527 [DOI] [PubMed] [Google Scholar]
- Wang X. T. and Ker R. F. (1995). Creep rupture of wallaby tail tendons. J. Exp. Biol. 198, 831-845. [DOI] [PubMed] [Google Scholar]
- Ward S. and Lieber R. L. (2005). Density and hydration of fresh and fixed human skeletal muscle. J. Biomech. 38, 2317-2320. 10.1016/j.jbiomech.2004.10.001 [DOI] [PubMed] [Google Scholar]
- Weir J. B. de V., Bell G. H. and Chambers J. W. (1949). The strength and elasticity of bone in rats on a rachitogenic diet. J. Bone Joint Surg. B 31, 444-451. 10.1302/0301-620X.31B3.444 [DOI] [PubMed] [Google Scholar]
- Williams S. B., Rhodes L., Andrews J., Wilson A. M. and Payne R. C. (2008a). Functional anatomy of the pelvic limb of the racing greyhound (Canis familiaris). J. Anat. 213, 361 10.1111/j.1469-7580.2008.00961.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams S. B., Daynes J., Peckham K., Wilson A. M. and Payne R. C. (2008b). Functional anatomy of the thoracic limb of the racing greyhound (Canis familiaris). J. Anat. 213, 373 10.1111/j.1469-7580.2008.00962.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson A. M., McGuigan P. M., Su A. and van den Bogert J. (2001). Horses damp the spring in their step. Nature 414, 895-899. 10.1038/414895a [DOI] [PubMed] [Google Scholar]
- Woo S. L., Ritter M. A., Amiel D., Sanders T. M., Gomez M. A., Kuei S. C., Garfin S. R. and Akeson W. H. (1980). The biomechanical and biochemical properties of swine tendons-long term effects of exercise on the digital extensors. Connect. Tissue Res. 7, 177-183. 10.3109/03008208009152109 [DOI] [PubMed] [Google Scholar]
- Wood T. O., Cooke P. H. and Goodship A. E. (1988). The effect of exercise and anabolic steroids on the mechanical properties and crimp morphology of the rat tendon. Am. J. Sports Med. 16, 153-158. 10.1177/036354658801600211 [DOI] [PubMed] [Google Scholar]
- Young J. W. (2005). Ontogeny of muscle mechanical advantage in capuchin monkeys (Cebus albifrons and Cebus apella). J. Zool. 267, 351-362. 10.1017/S0952836905007521 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.