Three archetypical classes of macromolecular regulators of protein liquid–liquid phase separation

Significance

The assembly/disassembly of membraneless organelles, crucial for cellular functions and linked to human diseases, is delicately regulated by macromolecular components and other signals. To what extent and how macromolecular regulators affect this phase separation process are largely unknown. Here, by measuring the effects on the phase boundary and the levels of partitioning into the condensates of 2 proteins (SH3₅ and PRM₅), we define 3 archetypical classes of macromolecular regulators. Depending on their strengths of attraction with condensate proteins, regulators either promote or suppress phase separation, and can generally be classified as volume-exclusion promotors, weak-attraction suppressors, and strong-attraction promotors. This classification provides a much needed understanding, given the numerous macromolecular species in and around membraneless organelles for exerting regulatory effects.

Abstract

Membraneless organelles, corresponding to the droplet phase upon liquid–liquid phase separation (LLPS) of protein or protein–RNA mixtures, mediate myriad cellular functions. Cells use a variety of biochemical signals such as expression level and posttranslational modification to regulate droplet formation and dissolution, but the physical basis of the regulatory mechanisms remains ill-defined and quantitative assessment of the effects is largely lacking. Our computational study predicted that the strength of attraction by droplet-forming proteins dictates whether and how macromolecular regulators promote or suppress LLPS. We experimentally tested this prediction, using the pentamers of SH3 domains and proline-rich motifs (SH3₅ and PRM₅) as droplet-forming proteins. Determination of the changes in phase boundary and the partition coefficients in the droplet phase over a wide range of regulator concentrations yielded both a quantitative measure and a mechanistic understanding of the regulatory effects. Three archetypical classes of regulatory effects were observed. Ficoll 70 at high concentrations indirectly promoted SH3₅–PRM₅ LLPS, by taking up volume in the bulk phase and thereby displacing SH3₅ and PRM₅ into the droplet phase. Lysozyme had a moderate partition coefficient and suppressed LLPS by substituting weaker attraction with SH3₅ for the stronger SH3₅–PRM₅ attraction in the droplet phase. By forming even stronger attraction with PRM₅, heparin at low concentrations partitioned heavily into the droplet phase and promoted LLPS. These characteristics were recapitulated by computational results of patchy particle models, validating the identification of the 3 classes of macromolecular regulators as volume-exclusion promotors, weak-attraction suppressors, and strong-attraction promotors.

Membraneless organelles, formed by liquid–liquid phase separation (LLPS) of proteins or protein–RNA mixtures, mediate a myriad of cellular functions, including ribosome biogenesis and sequestration of signaling molecules (1, 2). This process has to be delicately regulated, for 2 important reasons. First, the macromolecules involved need to be maintained at conditions near the boundary of the 2 phases, bulk (or dilute) and droplet (or condensate), such that the assembly and disassembly of membraneless organelles can be readily reversed. Second, as macromolecular components become concentrated inside membraneless organelles, they have heightened chances for aggregation, potentially leading to diseases (3–8). Classical means such as temperature, pH, and ionic strength have been reported to induce intracellular phase separation during stress response (9). A number of studies have investigated the roles of posttranslational modifications, by changing intramolecular and intermolecular interactions, in LLPS (6, 8, 10–12). Increasing attention has also been paid to the effects of macromolecular regulators (3, 4, 7, 8, 10, 13–26). A notable example is the control of dissolution/condensation of P granules in a Caenorhabditis elegans embryonic cell by the protein MEX-5 (13). High concentrations of MEX-5 in the anterior of the embryo correlated with dissolution of P granules, while low concentrations of MEX-5 in the posterior allowed continued condensation of P granules. Membraneless organelles contain dozens to hundreds of macromolecular components and are surrounded by many nonconstituent macromolecules. The large number of macromolecular species involved presents ample opportunities to regulate the phase boundary of any membraneless organelle, but establishing the physical rules governing such regulation is a significant challenge. This study aimed to make progress in this direction, by defining 3 archetypical classes of macromolecular regulators of LLPS.

The assembly of membraneless organelles is usually driven by one or a few proteins [known as “scaffolds” (27, 28)], which can form droplets on their own, whereas other “client” macromolecular components (including RNA) potentially play regulatory roles. The effects of regulators can be easily detected by shifts in phase boundary, in particular changes in the critical temperature (T_c) or threshold concentration (C_th) for phase separation. T_c is the upper bound of temperatures at which phase separation occurs (here the interest is specifically on systems with upper critical solution temperature), whereas C_th, often called saturation concentration, is the lowest protein concentration resulting in phase separation at a given temperature. The changes in T_c and C_th are correlated. Regulators that increase T_c or decrease C_th are hence referred to as promotors of phase separation, whereas those with the opposite effects, as suppressors (23). Another property that can provide physical insight into regulatory effects is the extent to which a regulator partitions into the droplet phase, which can be measured by the partition coefficient (PC), i.e., the ratio of the regulator’s concentration in the droplet phase to that in the bulk phase. PC is determined by the equality in chemical potential between the 2 phases and thus dictated by the interactions between the regulator and droplet-forming proteins, which predominantly occur in the droplet phase. Regulator–protein interactions include steric repulsion and possibly additional repulsion (e.g., between like-charged molecules) as well as attraction (e.g., electrostatic, van der Waals, and hydrophobic). Low PCs indicate dominance of repulsion over attraction, whereas high PCs indicate the opposite. Both the regulatory effects (such as an increase or decrease in C_th) and the PC, determined at the same regulator concentrations, are required for a comprehensive, quantitative characterization of the regulator.

Disparate regulatory effects have been reported in experimental studies. Polymeric crowding agents such as Ficoll, dextran, and polyethylene glycol (PEG) were found to promote phase separation in several cases (3, 4, 8, 24–26). In particular, Wegmann et al. (8) found a decrease in C_th for tau phase separation with increasing level of PEG. Given that many driver proteins contain RNA-binding motifs or domains (29, 30), the regulatory effects of RNA have been studied, and the results appeared conflicting (3, 4, 7, 10, 14–20, 22). Whereas most of these studies found RNA to have promotional effects, others found RNA to be promotive only up to a certain concentration and become suppressive at higher concentrations, a behavior known as “reentrant” (7, 14, 15, 20), and yet others found the most significant effect of RNA was in reducing the concentration of the driver protein in the droplet phase (22). The effects of protein regulators were even more mixed, with promotional effects reported for some regulators (3, 10, 21, 24) whereas suppressive effects for other regulators (18, 19, 21, 24). For a given driver protein, one regulator protein can act as a promotor while another regulator protein as a suppressor (21). Likewise, a given regulator protein (e.g., BSA) can be a promotor for one driver protein but a suppressor for another driver protein (24). The latter study also reported a reentrant effect for lysozyme as a protein regulator. These diverse observations, perplexing at first sight, spurred the development toward a unified understanding of macromolecular regulation of LLPS (23).

PCs have been reported for a number of macromolecular regulators in protein droplets, mostly from using fluorescently labeled regulators at low concentrations (28). For example, Lin et al. (3) obtained PCs in the range of 3 to 12 for GFP fusions of disordered protein fragments in droplets formed by a protein–RNA mixture. The PC of GFP alone was 1, and the enhanced recruitment of the fusions was attributed to charge-mediated interactions between the disordered fragments with one of the droplet-forming components. Banani et al. (27) used droplets formed by 2 repeat proteins composed of interaction modules (e.g., polySH3 and polyPRM, where PRM means proline-rich motif) to investigate the partitioning of the single module clients. The stoichiometry of the repeat proteins dictated the PC of a single module, as the latter competed against its repeat version for interacting with the other repeat protein. Schuster et al. (31) expanded the use of interaction modules, showing that a “cargo” protein can be recruited to the droplet phase when fused to an interaction module. Wang et al. (25) found a positive correlation between the PCs of FUS family proteins in FUS droplets and the numbers of arginine and tyrosine residues in the clients. The latter measure also inversely correlated with the threshold concentrations of FUS family proteins and their mutants, suggesting that the same types of interactions mediate both phase separation of scaffolds and recruitment of clients. None of the foregoing studies probed how the clients might affect the phase separation of the scaffolds. Such a study was carried out by Protter et al. (24), who presented fluorescence images showing recruitment of BSA and lysozyme into the droplet phase, and attributed the suppressive effects of these regulator proteins to competition for interactions with driver proteins. However, even in this study, the recruitment experiment was done at regulator concentrations much lower than those at which regulatory effects were observed. At such low concentrations, the regulators were simply spectators, and not much effect on the phase separation of driver proteins would be expected. In this context, we note that Wegmann et al. (8) reported exclusion of dextran from tau droplets by mixing 1% (wt/vol) of a fluorescently labeled species with 9% of an unlabeled species.

Accumulating evidence seemed to suggest that the strength of driver–regulator interactions is a critical determinant for both regulatory effects and partitioning of regulators. To fully investigate this idea, we studied the phase separation behaviors of driver–regulator models by Monte Carlo simulations (23). In these models, drivers and regulators were represented as patchy particles, which experience steric repulsion when the particles get too close to each other but attraction when their patches are in contact. By sweeping the strength (ε_PR) of driver–regulator attraction (at a fixed strength [ε_PP] of driver–driver attraction), the diverse regulatory effects observed in the various experimental systems were qualitatively recapitulated. The regulatory effects could be summarized into 3 classes, distinguished by the strength of driver–regulator attraction. When driver–regulator interactions are dominated by steric repulsion (ε_PR close to 0), regulators promote phase separation by taking up volume in the bulk phase and thereby displacing drivers into the droplet phase. This behavior typifies the effects of crowding agents, and the regulators are referred to as volume-exclusion promotors. When regulators become weakly attractive to the drivers (ε_PR/ε_PP around 0.5), they partition into the droplet phase and replace some of the strong driver–driver interactions by weaker driver–regulator interactions, thereby suppressing phase separation. These regulators are called weak-attraction suppressors. Finally, when driver–regulator attraction becomes as strong as or even stronger than driver–driver attraction (ε_PR/ε_PP ≥ 1), the regulators, named strong-attraction promotors, exhibit a reentrant behavior, i.e., a concentration-dependent transition from promotor to suppressor.

The present study was designed to experimentally test these predictions and provide support for the notion that macromolecular regulators can be universally placed into 3 archetypical classes. For this purpose, we used pentamers of SH3 domains and proline-rich motifs (SH3₅ and PRM₅), extensively studied by Rosen and coworkers (10, 27), as driver proteins. We assumed that the difference between rigid patchy particles and flexible SH3₅ and PRM₅ molecules (with disordered regions or mostly disordered) is, at a qualitative level, nonessential, partly because LLPS of structured (rigid) and disordered proteins have the same physical basis, even though the latter is generally distinguished by higher T_c and lower C_th (30). In this connection, we note that coarse-grained simulations have validated the tenet of patchy particles for explaining the aggregation of the huntingtin exon-1 fragment (32); of course, flexible regions can influence phase transitions of proteins at a quantitative level (33). For regulators, we sought macromolecules that could serve as archetypes of the 3 classes, and found Ficoll 70, lysozyme, and heparin to fit the respective defining features. The conformity between the computational predictions and experimental results testifies to the universal nature of the 3 archetypical classes for macromolecular regulators of LLPS.

Results

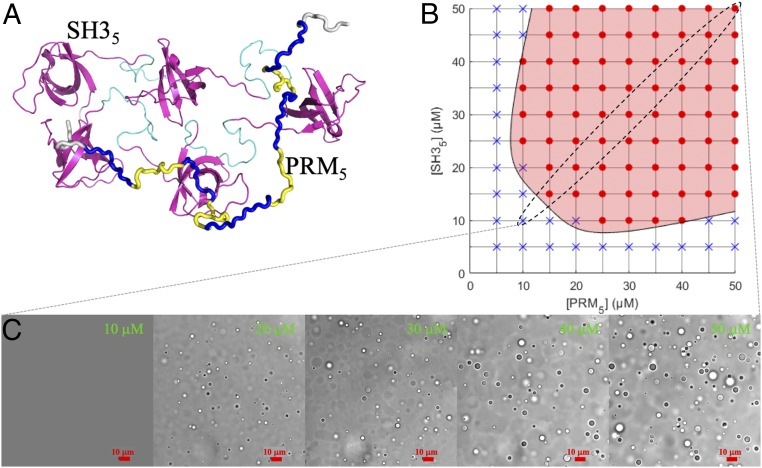
We used SH3₅–PRM₅ mixtures as a model system for LLPS (Fig. 1A). SH3₅ has a significant number of anionic residues and a strong negative electrostatic surface (dotted by a few positive patches); the opposite is true for PRM₅ (SI Appendix, Fig. S1). As for macromolecular regulators, motivated by our computational study (23), we looked for molecules that would cover a range of interaction strengths with the droplet-forming proteins, from sterically repulsive to mildly to strongly (net) attractive. Three macromolecules were selected: the widely used crowding agent Ficoll 70, the cationic protein lysozyme, and the highly anionic polymer heparin. Besides their chemical nature, these molecules also differ in size (ranging from 14 to 70 kDa in molecular weight).

Fig. 1.

SH3₅–PRM₅ mixtures readily phase separate at room temperature and physiological salt concentration. (A) Representative structures of SH3₅ (magenta, SH3 domains; cyan, inter-SH3 linkers) and PRM₅ (blue, proline-rich motifs; yellow, inter-PRM linkers). (B) Phase diagram of SH3₅–PRM₅ mixtures in 10 mM imidazole buffer, pH 7, with 150 mM KCl. The red dots indicate phase separation, and the blue crosses indicate no phase separation. The black curve bordering the pink-shaded region is obtained by fitting the midpoints between phase-separated and non–phase-separated regions to the following set of parametric equations:

$$x=\left(a{\left[1+{\left(\left|t\right|/b\right)}^c\right]}^{1/c}-t\right)/\sqrt{2},$$

$$y=\left(a{\left[1+{\left(\left|t\right|/b\right)}^c\right]}^{1/c}+t\right)/\sqrt{2},$$

with a = 19.3 µM, b = 12.1 µM, and c = 4. For the portion of the boundary curve shown, t runs from −27 to 27 µM. (C) Confocal bright-field images of SH3₅–PRM₅ droplets at different equimolar concentrations of the 2 components.

SH3₅–PRM₅ Droplets Quickly Coalesce and Spread under Gravity.

As was first demonstrated by Li et al. (10), SH3₅–PRM₅ mixtures readily phase separated at room temperature and physiological salt concentration (10 mM imidazole buffer pH 7 with 150 mM KCl). The threshold concentrations of SH3₅ and PRM₅ defined a symmetric phase boundary with respect to the 2 components (Fig. 1B). For equimolar mixing, the threshold concentration was ∼12.5 μM. At increasing concentrations of the 2 component proteins, the volume fraction of the droplet phase increased, as indicated by more abundant and larger droplets (Fig. 1C). Most of the results in this study were obtained with the 2 proteins kept at equimolar mixing, which are reported first.

To assess the SH3₅ concentration in the droplet phase (denoted as [SH3₅]_d), we added 1 μM Alexa 594–SH3₅ to a 40 μM unlabeled SH3₅–PRM₅ mixture. The fluorescence intensity ratio (I_d/I_b) in the droplet and bulk phases was 96 ± 7 (Fig. 2A), consistent with that reported by Li et al. (10). I_d/I_b may at best only give a crude estimate of the SH3₅ concentration ratio between the 2 phases, because standard curves of fluorescently labeled proteins at high concentrations could significantly deviate from linearity (see below). Approximating the concentration ratio by I_d/I_b leads to an SH3₅ concentration of 1.2 mM in the droplet phase (given the SH3₅ concentration, [SH3₅]_b, of 12.5 μM in the bulk phase).

Fig. 2.

Determination of SH3₅ concentration inside droplets and spread of the droplet phase over a coverslip. (A) Confocal fluorescence images of SH3₅–PRM₅ droplets at [SH3₅] = [PRM₅] = 40 µM, with 1 µM Alexa 594–SH3₅ added. Line scans of fluorescence intensity yielded an approximate 100-fold enrichment of Alexa 594–SH3₅ in the droplet phase. (B) Spread of the droplet phase over a coverslip. (Top) Cartoon illustrating a 1.5-µL drop of sample between a slide and the coverslip; red blobs and patches represent floating droplets and the spread droplet phase, respectively. (Bottom) A Z stack of confocal images at the start of a time series.

We also obtained [SH3₅]_d via a different route, based on recording a time series of Z stacks on a confocal microscope (Fig. 2B, SI Appendix, Fig. S2 A and B, and Movie S1). Due to gravity, SH3₅–PRM₅ droplets quickly fell to the base of a drop of sample lying on top of a coverslip (SI Appendix, Fig. S2 B–D). As more and more fallen droplets coalesced onto the droplet phase, it spread into a thin layer over the coverslip by about 15 min (SI Appendix, Fig. S2D). Using the volume of the droplet phase after settling, we estimated a volume fraction of (2.8 ± 0.1)% for the droplet phase in a 1.5-μL sample. We dub this method confocal imaging of gravity-based separation (CIGraBS). By centrifugation of a much larger volume (900 μL) of an equimolar mixture at 170 μM, Li et al. (10) found a volume fraction of 2.2% for the droplet phase. According to mass conservation, we could further estimate [SH3₅]_d in our samples prepared at 40 μM SH3₅ and PRM₅ to be 1.0 mM, corresponding to a concentration ratio of ∼80 between the 2 phases.

Three Macromolecular Regulators Exhibit Disparate Effects.

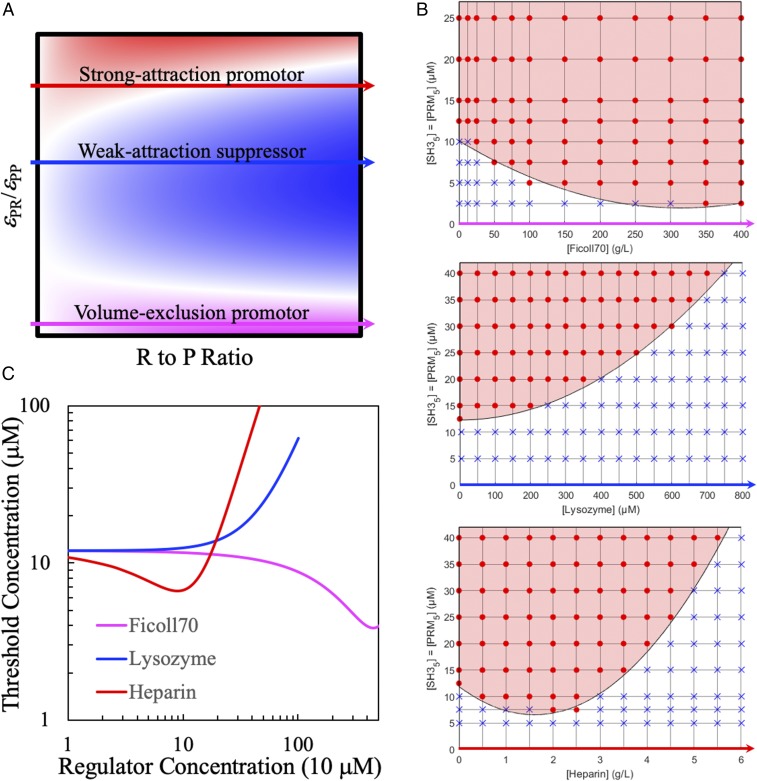
Our computational study of patchy particle models predicted that the strength of attraction between droplet-forming proteins and macromolecular regulators, relative to that between the former themselves, dictate whether the latter promote or suppress LLPS (23). Three characteristic types of regulator behaviors were identified (Fig. 3A). Both regulators that exert steric repulsion but are otherwise inert and regulators that are strongly attractive to driver proteins promote phase separation (magenta and red arrowed lines), but via different mechanisms, whereas weakly attractive regulators suppress phase separation (blue arrowed line). Here, we used the change in threshold concentration for equimolar SH3₅–PRM₅ phase separation to measure effects of 3 regulators, selected to capture the foregoing characteristic behaviors.

Fig. 3.

Disparate effects of 3 macromolecular regulators on the phase boundary of equimolar SH3₅–PRM₅ mixtures. (A) Three characteristic types of regulator behaviors dictated by ε_PR/ε_PP, the strength of driver–regulator attraction relative to the strength of driver–driver attraction, as predicted from patchy particle models (23). The color map displays the ratio of the critical temperature of a driver–regulator mixture to that of the pure driver; blue, white, and magenta (or red) colors mean this ratio is less than 1, 1, and greater than 1, respectively. The regulator-to-driver molar (R-to-P) ratio is a measure of regulator concentration. Volume-exclusion regulators promote LLPS at high concentrations; weak-attraction regulators suppress LLPS at all concentrations; and strong-attraction regulators promote at low concentrations but suppress at high concentrations. (B) Effects of 3 macromolecular regulators on the SH3₅–PRM₅ threshold concentration. The symbols and curves are as explained in Fig. 1B, except that the latter are parabolic fits. (C) Dependences of the threshold concentration on regulator concentrations. The curves are the phase boundary curves shown in B, color matched with the 3 characteristic types of regulators in A. Regulator concentrations are all in units of 10 µM. The factor of 10 accounts for the fact that there are 2 droplet-forming proteins, SH3₅ and PRM₅, and each of them consists of 5 modules.

At 25 g/L (corresponding to 0.36 mM), Ficoll 70 started to promote SH3₅–PRM₅ phase separation, decreasing C_th from 12.5 to 10 μM (Fig. 3 B, Top). C_th further decreased as Ficoll 70 increased, to 5 μM between 100 and 300 g/L Ficoll 70 and 2.5 μM at 350 and 400 g/L Ficoll 70. We anticipate that Ficoll 70 ultimately should suppress LLPS because, at very high concentrations, it would be forced into the droplet phase and disrupt the interaction networks there. We hence fitted the phase boundary (dependence of C_th on Ficoll 70 concentration) to a parabolic function, yielding a minimum C_th of 2 μM at 315 g/L Ficoll 70.

In contrast, lysozyme always suppressed phase separation (Fig. 3 B, Middle). C_th increased with increasing lysozyme concentration, reaching 40 μM at 0.7 mM lysozyme. The phase boundary could be fitted to a one-sided parabola (with minimum at 0 lysozyme). Heparin initially promoted phase separation but then became a suppressor at high concentrations, therefore exhibiting the reentrant behavior (Fig. 3 B, Bottom). C_th decreased from 12.5 to 7.5 μM at 2 and 2.5 g/L heparin. Thereafter, C_th increased gradually, reaching 40 μM at 5.5 g/L heparin. Note that, although both Ficoll 70 and heparin acted as promotors, the concentrations required for reducing C_th to the same level were very different. For example, to reduce C_th to 7.5 μM, it took 50 g/L Ficoll 70 but only 2 g/L heparin. This 25-fold difference in regulator concentration hints at distinct mechanisms for promotion of phase separation.

To highlight the contrasting behaviors of the 3 regulators, their effects on the SH3₅–PRM₅ threshold concentration are compared in Fig. 3C. The magenta curve in Fig. 3C presenting the effect of Ficoll 70 on the SH3₅–PRM₅ phase boundary is similar to the magenta arrowed line in Fig. 3A, which, in our study of patchy particle models (23), is typical of regulators whose interactions with droplet-forming proteins are dominated by steric repulsion. These regulators at high concentrations promote LLPS, by taking up volume in the bulk phase and thereby displacing the proteins into the droplet phase. Likewise, the blue curve in Fig. 3C presenting the effect of lysozyme is similar to the blue arrowed line in Fig. 3A, which exemplifies the behavior of regulators weakly attracted to droplet-forming proteins. These regulators partition moderately into the droplet phase and thereby replace some of the strong attractive interactions between droplet-forming proteins by weak protein–regulator attraction, leading to increasing suppression of LLPS at increasing regulator concentration. Last, the red curve in Fig. 3C presenting the effect of heparin is similar to the red arrowed line in Fig. 3A, which represents the action of regulators strongly attracted to droplet-forming proteins. At low concentrations, these regulators partition heavily into and reinforce the interaction networks in the droplet phase, thereby promoting LLPS. However, at high concentrations, regulators in the droplet phase start to experience repulsion among themselves and hence the initial promotional effect now turns into suppression. This reentrant behavior was also observed for polylysine (SI Appendix, Fig. S3), which should be strongly attracted to the negatively charged SH3₅.

In addition to C_th, the volume fraction of the droplet phase can also be used as an indicator for regulatory effects, with promotors increasing the volume fraction whereas suppressors decrease it. To demonstrate this idea, we used the CIGraBS method to measure the droplet volume fractions formed by 40 μM SH3₅–PRM₅ mixtures in the presence of lysozyme. The volume fractions decreased from (2.8 ± 0.1)% without lysozyme to (1.6 ± 0.2)% at 400 μM lysozyme and further to (0.98 ± 0.01)% at 600 μM lysozyme (SI Appendix, Fig. S4), confirming the suppressive effects of this regulator. Moreover, with the addition of lysozyme, the droplets also became resistant to spreading over the coverslip (SI Appendix, Fig. S5 and Movies S2 and S3), indicating an increase in surface tension.

The volume-exclusion promotors, weak-attraction suppressors, and strong-attraction promotors are predicted to have low, moderate, and high PCs, respectively, in the droplet phase. To further validate that Ficoll 70, lysozyme, and heparin are archetypes for these 3 classes of regulators, next we present their PCs.

PCs of Three Regulators Validate Their Identification as Archetypes for Three Classes.

To measure the extents of partitioning in the droplet phase, we labeled the 3 macromolecular regulators with fluorescein isothiocyanate (FITC). When the labeled regulators were added to a 40 μM SH3₅–PRM₅ mixture to allow for droplet formation, confocal fluorescence images clearly show the exclusion of Ficoll 70 from the droplet phase but moderate and strong recruitment of lysozyme and heparin, respectively, in the droplet phase (Fig. 4 A–C). These observations are precisely those expected of volume-exclusion promotors, weak-attraction suppressors, and strong-attraction promotors. Moreover, the disparate partitions reported by the fluorescence images reflect properties of the macromolecular regulators, not of the label itself, because the free dye molecule shows approximately equal partition between the bulk and droplet phases (Fig. 4D).

Fig. 4.

Confocal images of 3 FITC-labeled regulators, revealing different extents of recruitment into SH3₅–PRM₅ droplets formed by equimolar mixing of the 2 proteins at 40 µM: (A) 5 µM FITC–Ficoll 70 plus 200 g/L Ficoll 70; (B) 2.5 µM FITC–lysozyme; (C) 2.5 µM FITC–heparin; (D) 1 µM Alexa 594–SH3₅ plus 1 µM fluorescein-sodium salt, showing enrichment of SH3₅ in the droplet phase (Left, red channel; similar to Fig. 2A) and nearly equal partitions of free fluorescein label in the 2 phases (Middle, green channel). The merge of the 2 channels is shown on the Right.

We wanted to determine PCs not only for the often-studied situation where regulators are present at sufficiently low concentrations as to not significantly perturb the phase equilibrium, but also at concentrations where effects on phase boundary become significant. To that end, we mixed the labeled regulators with the unlabeled counterparts to reach desired concentrations. To increase the accuracy of the PC measurements, we generated standard curves that maintained constant ratios between the labeled and unlabeled species of each regulator and spanned the full range of observed fluorescence intensities (SI Appendix, Fig. S6). These measures were necessary because the labeled-to-unlabeled ratios affected the standard curves and the standard curves were highly nonlinear in many cases.

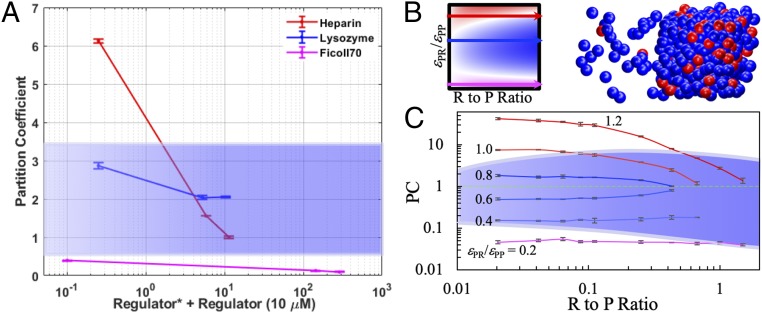
The PCs obtained for Ficoll 70 were small at all concentrations, varying from 0.39 ± 0.01 when 1 μM FITC–Ficoll 70 was added to a 40 μM SH3₅–PRM₅ mixture to 0.10 ± 0.01 when 5 μM FITC–Ficoll 70 and 200 g/L Ficoll 70 were added (Fig. 5A). In comparison, the PCs of lysozyme were 2.87 ± 0.08 at 2.5 μM FITC–lysozyme and reduced to 2.05 ± 0.02 at 2.5 μM FITC–lysozyme plus 100 μM lysozyme. For heparin, the PCs were 6.12 ± 0.05 at 2.5 μM FITC–heparin and reduced to 1.00 ± 0.02 at 2.5 μM FITC–heparin plus 2 g/L heparin. Using fluorescence intensity ratios would have yielded a much higher PC value, 18.6, at 2.5 μM FITC–heparin, highlighting the importance of using appropriate standard curves.

Fig. 5.

PCs of regulators in experimental and computational systems. (A) PC data for Ficoll 70, lysozyme, and heparin spanning wide ranges of regulator concentrations. Error bars reflect SDs of fluorescence intensities determined in multiple (typically a few dozens) regions of interest. The blue band covers PCs (between 0.5 and 3.5) corresponding to suppression of phase separation. Below the band are PCs corresponding to volume-exclusion promotion, and above the band are PCs corresponding to strong-attraction promotion. (B) Patchy particle models. (Left) Miniature version of Fig. 3A; (Right) illustration of partitioning of the driver (blue) and regulator (red) in the 2 phases. (C) PC results for the patchy particle models covering a full range of ε_PR/ε_PP. The curves in magenta, blue, and red represent 3 distinct classes of regulators. PC values and error bars represent averages and SDs determined from 3 replicate simulations. The blue band covers PC values that correspond to suppression of phase separation. These include the entire PC curves of weak-attraction suppressors and the tail portions of the PC curves of strong-attraction promotors.

The decrease of lysozyme and heparin PCs toward 1 are a reflection of the suppressive effects of these regulators at high concentrations. Under the latter conditions, the SH3₅–PRM₅ threshold concentrations steadily increased (Fig. 3 B and C). When C_th exceeded 40 μM, the concentration of SH3₅ and PRM₅ used in the PC measurement, phase separation no longer occurred, and the PC of every component would nominally be 1.

In short, the PCs of the 3 types of regulators start at values in separate ranges and follow distinct dependences on concentration. Without regard for regulator concentration, the PC value by itself provides a rough prediction of regulatory effects. Specifically, PC < 0.5 corresponds to promotion due to volume exclusion while PC > 3.5 corresponds to promotion due to strong attraction. The band in between (blue shading in Fig. 5A) corresponds to suppression, due to either weak attraction or the reentrant behavior of a strong-attraction regulator at high concentrations.

Patchy Particle Models Reinforce the Universal Nature of Three Archetypes.

In our study of patchy particles models, we identified the strength of protein–regulator attraction (ε_PR/ε_PP, relative to the strength of protein–protein attraction) as a critical determinant of regulatory effects (23). Here, we carried out new Monte Carlo simulations (Fig. 5B) to characterize regulator PCs for these models. For a volume-exclusion promotor (ε_PR/ε_PP = 0.2), the PC remained low (at ∼0.05) for the entire range of regulator-to-protein molar (R to P) ratio studied. At ε_PR/ε_PP = 0.4, the regulator became a weak-attraction suppressor and, with increasing regulator concentration, the PC moved gradually upward. With a further increase in ε_PR/ε_PP to 0.6, the upward move in PC was more apparent, and it also became clear that the movement was toward PC = 1. The situation at ε_PR/ε_PP = 0.8 was a mirror image of that at ε_PR/ε_PP = 0.6, with the PC starting above 1 and then moving down to 1 at high regulator concentrations. At ε_PR/ε_PP = 1.0, the regulator changed to a strong-attraction promotor; the PC was high at low regulator concentrations. At increasing concentrations, with the regulator switching from a promotor to a suppressor, the PC declined toward 1. This trend in PC was amplified as ε_PR/ε_PP further increased to 1.2.

The PC trends of the patchy particle models at ε_PR/ε_PP = 0.2, 0.8, and 1.0 are qualitatively similar to those found for Ficoll 70, lysozyme, and heparin, respectively. This similarity is observed despite the obvious differences between the patchy particle models and our experimental protein–regulator systems, therefore indicating that the 3 archetypical classes of regulators exist in general. Fig. 5B further suggests that, for SH3₅–PRM₅ phase separation, lysozyme as a weak-attraction suppressor may have a “twin,” corresponding to the regulator with ε_PR/ε_PP = 0.6 in the patchy particle models. Such a regulator would have slightly weaker attraction with SH3₅ or PRM₅ than the SH3₅–lysozyme attraction and produce a PC that is less than 1 at low concentrations but goes up to 1 at high concentrations.

For the patchy particle models, we could precisely map out 3 distinct bands in the PC vs. R-to-P ratio plane that correspond to promotion or suppression of phase separation. Depending on the R-to-P ratio, the band corresponding to promotion due to volume exclusion has an upper bound in PC ranging from 0.04 to 0.14, and the band corresponding to promotion due to strong attraction has a lower bound in PC ranging from 3.7 to 6.5. Between these bounds is the band of suppression (blue shading in Fig. 5B), due to either weak attraction (covered by blue PC curves) or the reentrant behavior of strong-attraction regulators (covered by the tail portions of red PC curves). The 3-band demarcations of PC are qualitatively similar for the patchy particle models and for our experimental systems.

Not surprisingly, the PC trends of our experimental systems and the patchy particle models do differ in detail. Compared to the patchy particle model for a volume-exclusion regulator, experimentally we were able to probe the promotional effect and measure the PC of Ficoll 70 over a range of R-to-P ratios that was at least an order of magnitude wider, and the PC, although small, was severalfold higher. These discrepancies may be due to the physical differences between the computational and experimental systems: Whereas patchy particles are rigid spheres, SH3₅ or PRM₅ either contains disordered regions or is largely disordered and Ficoll 70 is a cross-linked polymer. In addition, the PC curves of lysozyme and heparin crossed each other, reflecting the fact that these 2 regulators differ not merely in their strengths of attraction with the droplet-forming proteins.

The concept of polyphasic linkage (34) has been used to explain the shift in the threshold concentration for protein aggregation by preferential binding of a regulator (35). In essence, preferential binding to low–molecular-weight species increases C_th but to aggregates decreases C_th. These 2 scenarios, respectively, somewhat parallel weak-attraction suppression and strong-attraction promotion of phase separation. However, polyphasic linkage does not account for either volume-exclusion promotion or the reentrant behavior of strong-attraction regulators.

Why Are There Only Three Archetypical Classes of Regulators?

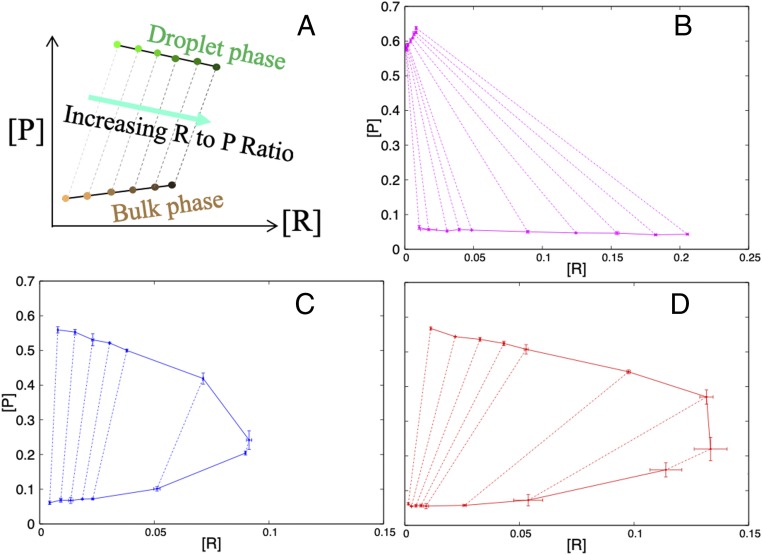
The extensive Monte Carlo simulations reported previously (23) and further expanded here allow us to safely conclude that there are only 3 classes of regulators for patchy particle models. For the experimental protein–regulator systems studied here, we contend that the 3 archetypes of regulators identified here, Ficoll 70, lysozyme, and heparin, provide complete coverage of all regulator behaviors. The observation that polylysine acts similarly to heparin further supports the completeness of the 3 archetypes. We now present yet another justification using tie lines, each of which connects a point representing the regulator and protein concentrations in the bulk phase to the counterpart in the droplet phase (Fig. 6A). With the regulator concentration on the x axis and the protein concentration on the y axis, tie lines follow an upward direction because the protein concentration in the droplet phase must be higher than the counterpart in the bulk phase. As the R-to-P ratio is increased, tie lines move to the right, and lie nearly parallel to each other. A set of tie lines has 3 choices for its general direction: tilting to the left, straight up, and tilting to the right.

Fig. 6.

General behaviors of tie lines. (A) Illustration of tie lines in the plane with regulator concentration on the x axis and driver concentration on the y axis. (B) Tie lines for patchy particle models at ε_PR/ε_PP = 0.2, with a significant tilt to the left. (C) Tie lines at ε_PR/ε_PP = 0.8, pointing nearly straight up. (D) Tie lines at ε_PR/ε_PP = 1.0, with a significant tilt to the right. Densities and error bars represent averages and SDs determined from 3 replicate simulations.

If the tie lines tilt significantly to the left, the PC, which is the ratio of the regulator concentration in the droplet phase to that in the bulk phase, must be very small, as illustrated by the result for the patchy particle models at ε_PR/ε_PP = 0.2 (Fig. 6B). Such a regulator is expected to be a volume-exclusion promotor. On the other hand, if the tie lines go straight up, then the PC is close to 1 (Fig. 6C, with ε_PR/ε_PP = 0.8). Such a regulator is moderately recruited to the droplet phase and is expected to be a weak-attraction suppressor. Last, if the tie lines tilt significantly to the right, then the PC is high (Fig. 6D, with ε_PR/ε_PP = 1.0), and the regulator is expected to be a strong-attraction promotor. In short, 3 distinct classes of regulatory effects can be generally expected, depending on whether a regulator at low concentrations partitions little, moderately, or heavily in the droplet phase.

Unequimolar SH3₅–PRM₅ Mixing Can Tune Effective Strength of Attraction with Regulators.

The patchy particle results reported so far were for binary mixtures between a self-attracting driver and a regulator, while our experimental systems were ternary mixtures between 2 mutually attracting proteins and a regulator. To more closely connect with experiment, we extended our modeling to ternary mixtures, including 2 drivers (with ε₁₂, strength of mutual attraction, fixed at 1.5); driver 1 and driver 2 both interacted with a regulator, but at different strengths (ε_1R twice of ε_2R). We first carried out Monte Carlo simulations at equimolar mixing of the drivers and over a range of values for ε_1R. The same 3 classes of regulatory effects were observed (SI Appendix, Fig. S7). The regulator at ε_1R = 0 behaved as a volume-exclusion promotor, increasing T_c to higher and higher values as the molar fraction, x, increased. At ε_1R = 1.0 the regulator was a weak-attraction suppressor, decreasing T_c with increasing x. At ε_1R = 2.0 the regulator became a strong-attraction promotor, increasing T_c at x up to 0.22 but then decreasing T_c at higher x. The border line between the second and third classes is near ε_1R = 1.5, where T_c was almost flat for x up to 0.41, but then decreases at higher x.

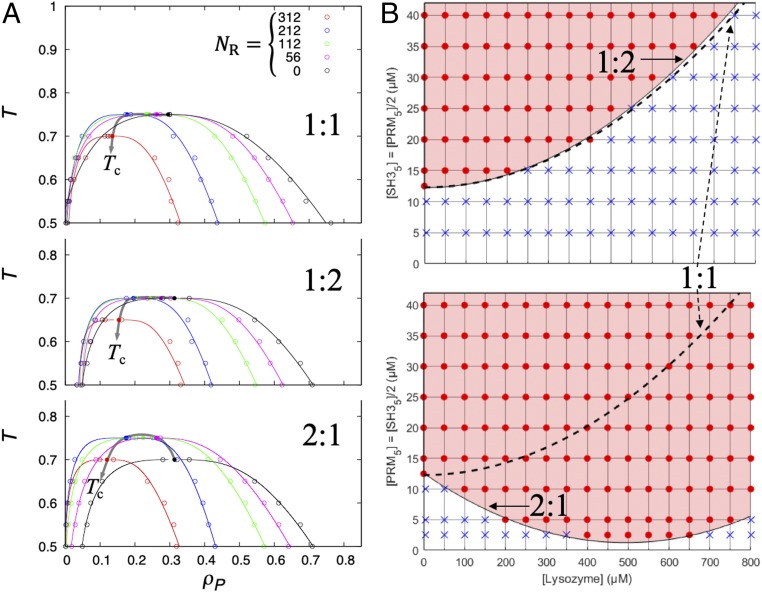
The modeling of ternary mixtures allowed us to investigate regulatory effects at unequimolar driver 1–driver 2 mixing, specifically at 1:2 and 2:1 ratios. The results were unexpected: the regulatory effects on the 1:2 mixtures were largely similar to those on the 1:1 mixtures, but the effects on the 2:1 mixtures had an overall shifted toward the promotion direction (SI Appendix, Fig. S8 and Fig. 7A). For example, the increase in T_c at ε_1R = 2.0 went to greater values, and the decrease in T_c with increasing x at ε_1R = 1.0 was at a slower pace. Most interestingly, at ε_1R = 1.5, while the regulator still acted as a weak-attraction suppressor on 1:2 mixtures as it did on 1:1 mixtures (with monotonic decrease in T_c), it became a strong-attraction promotor, with the signature reentrant behavior (T_c increasing for x up to 0.41 and then decreasing).

Fig. 7.

Tuning of effective strength of driver–regulator attraction by changing molar ratio between driver species. (A) Phase diagrams of patchy particle models of ternary mixtures at ε_1R = 1.5 and 1:1, 1:2, and 2:1 driver–driver molar ratios. The trends of T_c (arrowed curves) at increasing particle number (N_R) of the regulator indicate the regulatory effects as weak-attraction suppression for 1:1 and 1:2 mixing but strong-attraction promotion for 2:1 mixing. (B) Phase boundaries of SH3₅–PRM₅–lysozyme mixtures confirming the computational prediction.

We tested this prediction experimentally (Fig. 7B). Using lysozyme as the regulator, the phase boundary for SH3₅–PRM₅ mixtures at a 1:2 molar ratio was almost unchanged from that for the equimolar mixtures, indicating that lysozyme still acted as a weak-attraction suppressor. However, the phase boundary at a 2:1 molar ratio was markedly different, with C_th having a “reentrant” dependence on lysozyme concentration and therefore indicating lysozyme now acting as a strong-attraction promotor. These data directly confirm the computational prediction.

Why are the regulatory effects of lysozyme asymmetric with respect to a flip in the driver–driver ratio? To answer this question, we note that lysozyme, a cationic protein, interacts much more favorably with the anionic SH3₅ than with the cationic PRM₅. When PRM₅ is in excess, it engages most of the SH3₅ molecules, and so there is not much chance left for SH3₅–lysozyme interactions and lysozyme can only be a weak-attraction suppressor. In contrast, when SH3₅ is in excess, there are ample opportunities for SH3₅–lysozyme interactions, and hence lysozyme becomes a strong-attraction promotor. Changing the molar ratios of driver proteins thus provides a way to tune the effective strength of attraction with regulators.

Discussion

By measuring both the effects on phase boundary and the PCs in the droplet phase for the same regulator concentration range, and with support from computational studies of patchy particle models, we have demonstrated that macromolecular regulators of phase separation can generally be placed into 3 archetypical classes. We have identified the defining features for these classes and named them accordingly as volume-exclusion promotors, weak-attraction suppressors, and strong-attraction promotors. Given that membraneless organelles typically contain dozens to hundreds of macromolecular species and are surrounded by numerous others, each potentially exerting some regulatory effects, the classification of regulators provides a much-needed unifying understanding. For example, at 350 g/L, Ficoll 70 as a volume-exclusion promotor reduces the threshold concentration for SH3₅–PRM₅ phase separation by 5-fold, from 12.5 to 2.5 μM. Such a promotional effect can be anticipated for the numerous nonconstituent macromolecular species present at a high total concentration around any membraneless organelle, and may be necessary for keeping driver protein concentrations needed for phase separation to a minimum.

Moreover, each macromolecular client of a membraneless organelle has a chance to act as a weak-attraction suppressor or strong-attraction promotor of phase separation. The results presented here suggest that changes in expression levels for these regulatory components can have a significant effect on the phase boundary and thereby potentially determine whether the membraneless organelles are assembled or disassembled. Posttranslational modification adds another dimension. While several studies have focused on posttranslational modifications of driver proteins (6, 8, 10–12), the present work suggests that posttranslational modifications of regulator proteins, by changing the strength of interactions with driver proteins, can switch the regulator proteins between suppressor and promotor. Finally, whereas here the regulators were investigated one at a time, regulatory effects of multiple regulators when simultaneously present may well be nonadditive, further enriching the arsenal at a cell’s disposal for delicate control of membraneless organelles.

Such nonadditive effects may be at play in the control of P granule formation/dissolution by the level of MEX-5 (13, 18, 19). Crucial to the precise control may be the strong interaction between MEX-5 and another regulator, i.e., mRNA, instead of just the interactions of the regulators with the driver protein (PGL-3 or MEG-3). Yet another scenario is that, when the levels of macromolecular species change, not only regulators can switch between suppressor and promotor as demonstrated here, even the roles of driver and regulator can be switched. The present work can serve as the foundation for exploring all these complex scenarios.

Although we have emphasized regulatory effects on the threshold concentration, which is the concentration of the driver protein in the bulk phase upon phase separation, regulators also affect the driver protein concentration in the droplet phase (Fig. 6). The latter is a crucial determinant for aggregation. It stands to reason that some of the regulatory species are present to minimize driver protein concentrations in membraneless organelles. A systematic study on the rules for regulating the balance between phase separation and aggregation is thus warranted. Furthermore, material properties of membraneless organelles can be crucial to their cellular functions (16, 36); in line with previous studies (8, 15, 16, 22, 26, 36), we have demonstrated here that regulators also affect both the physical environment and material properties of droplets. In particular, volume-exclusion regulators like Ficoll 70 increase the viscosity of the bulk phase, thereby slowing down the falling of droplets under gravity, whereas regulators that partition into the droplet phase can significantly change its surface tension and viscosity.

Materials and Methods

Protein Expression and Purification.

SH3₅ and PRM₅, each initially fused with an N-terminal TEV-cleavable maltose binding protein tag and a C-terminal TEV-cleavable His6 tag, were expressed in Escherichia coli BL21(DE3) cells and purified as previously described (10), with some modifications. The cells were lysed using a homogenizer (Emulsiflex-C5; Avestin) while containing 40 µg/mL DNase I and 5 mM MgCl₂ to remove any DNA that later may cause aggregation issues. For SH3₅ purification, the lysate was first passed through a HisTrap FF column (GE Healthcare; catalog #17531901). The eluate was then passed through an Amylose column with resin from New England Biolabs (catalog #E8021S). The eluate from this column was dialyzed in a buffer containing high salt (20 mM imidazole, pH 7, 0.01% NaN₃, and 500 mM NaCl) overnight. Following the dialysis, TEV protease was added (at ∼1:20 molar ratio to the fusion protein) for overnight incubation. Postincubation, the solution was diluted 10 times and passed through a HiTrap Q HP column (GE Healthcare; catalog #17115401). The protein was dialyzed in the final buffer containing 10 mM imidazole, pH 7, 0.01% NaN₃, and 150 mM KCl, and concentrated. All experiments were conducted in this buffer. The protocol for PRM₅ purification was the same, except that the second and third columns were HiTrap Q HP and HiTrap SP HP (GE Healthcare; catalog #17115201), respectively.

SH3₅ Labeling.

SH3₅ was labeled using the primary amine reactive Alexa Fluor 594 NHS-ester (Thermo Fisher; catalog #A20004) to obtain Alexa 594–SH3₅. SH3₅ at 20 μM was incubated with 400 µM of the dye overnight. The excess dye was removed using a PD-MiniTrap desalting column (GE Healthcare; catalog #28918007).

Procurement of Macromolecular Regulators.

Ficoll 70, lysozyme, heparin, and poly-l-lysine (molecular weight 15 to 30 kDa) were obtained from GE Healthcare (catalog #17031010), VWR International (catalog #0663-5G), Alfa Aesar (catalog #A1698), and Sigma-Aldrich (catalog #P2658), respectively. FITC–Ficoll 70 and fluorescein sodium salt were from Sigma-Aldrich (catalog #51731-1G and F6377-100G, respectively), and FITC–lysozyme and FITC–heparin were from Nanocs, Inc. (catalog #LS1-FC-1 and HRN1-FC-1, respectively).

Determination of Phase Diagrams.

SH3₅–PRM₅ droplets with or without a regulator molecule were formed by mixing aliquots of the stock solutions to reach desired concentrations. In some cases, whether phase separation occurred was clear from visual inspection of the cloudiness of the sample; for most of the cases, however, the determination was made by observing under an optical microscope (Olympus BX61 or Zeiss Stemi 305). After mapping the phase-separated and non–phase-separated regions on the protein–protein or protein–regulator concentration plane, the midpoints between the 2 regions were fitted to a curve with an approximate hyperbolic shape (Fig. 1B) or a parabola (Fig. 3B).

Confocal Microscopy.

A volume of 1.5 µL of sample was loaded between a slide and a coverslip, and mounted in a flipped orientation to a confocal microscope (37). For visual documentation purposes, fluorescence and bright-field images were acquired on a Zeiss Axio Observer with a Yokogawa spinning disk.

For fluorescence intensity quantification, a Zeiss LSM 710 was used. Z-stack scanning at a step size of 0.48 µm was taken. The Z stacks covered a height of 10 to 20 µm, away from the coverslip or slide, when measuring fluorescence intensities for PCs or standard curves; a height of 40 µm, with the lowest slice positioned within the coverslip, for 4-dimensional scans (i.e., a time series of Z stacks); and the entire height of the sample (with the lowest and highest slices positioned within the coverslip and slide, respectively), for estimating the droplet volume fraction. Each slice covered a 105 × 105-μm² field with 512 × 512 pixels.

Determination of Regulator PCs.

Fluorescence intensities were obtained as the average within a region of interest, located either outside any droplet or inside a selected droplet. Only droplets with clearly defined edges were selected and, for each selected droplet, the largest cross-section within a Z stack was used for region of interest analysis (27). The fluorescence intensities were then converted to regulator concentrations according to standard curves, and the ratio of the concentration in the droplet phase to that in the bulk phase was calculated as the PC.

The standard curves were generated over a wide enough range of labeled-species concentrations, such that the range of fluorescence intensities of the standard samples fully covered the bulk- and droplet-phase fluorescence intensities of the droplet-forming sample. This measure was necessary because the standard curves could be highly nonlinear. In cases where both the labeled and the unlabeled species of a regulator were present in a droplet-forming sample, it was assumed that the 2 species had the same PC. Because the level of the unlabeled species could affect the fluorescence intensity of the labeled species, we added another error-reducing measure. Standard curves were generated using standard samples containing both the labeled and the unlabeled species, at a constant ratio equal to that used in preparing the droplet-forming sample.

Three-Dimensional Rendering and Volume Estimation of Droplet Phase in a Time Series.

The 4-dimensional scans started as soon as a sample containing 1 μM Alexa 594–SH3₅ and 40 μM each of SH3₅ and PRM₅ (without or with 400 or 600 μM lysozyme) was prepared and a 1.5-µL aliquot was mounted on the microscope (no more than 20 s after mixing). The time series lasted 28 min and consisted of 60 Z stacks.

Each stack was analyzed using Imaris 9.2.1, largely as described by Zhang et al. (38). Using the surpass function, the fluorescence intensities of all pixels were collected and auto-adjusted to generate an initial, discretized 3D representation of the droplet phase. The auto-adjustment involved setting a floor of fluorescence intensities (to filter out most of the pixels in the bulk phase) as well as a ceiling (to optimize the contrast between the droplet phase and the bulk phase). Smooth surfaces, with grain size set at 0.415 µm, were then generated, to best match with the boundaries of the initial 3D representation. This was done by adjusting the intensity threshold for the surface representation while applying a default filter of “number of voxels > 10.” The match was based on human judgment and hence the choice of the intensity threshold had a small amount of uncertainty. Last, the number of disconnected surfaces and the total volume enclosed by the surfaces were obtained. The surface representation for each Z stack was exported as a tiff file (SI Appendix, Figs. S2 A and B and S5), and a video was generated at 5 frames per second using MATLAB (Movies S1–S3).

The volume of the droplet phase increased over time as more droplets fell into the 40-µm range of the Z stacks but plateaued near the end of the time series as all of the droplets settled at the base of the 1.5-µL drop of sample (SI Appendix, Fig. S2C). Immediately after the 4-dimensional scans, we took a full scan covering the entire height (h) of the sample. From this scan, we calculated the volume V_d of the droplet phase as just described and measured the height h. The total sample volume V_s, above the same scanned area of A = 105 × 105 μm² was then A × h. Finally, the droplet volume fraction was obtained as the ratio V_d/V_s.

Monte Carlo Simulations of Patchy Particles.

Phase separation of patchy particles representing drivers and regulators was studied by Gibbs-ensemble Monte Carlo simulations (39, 40), as in our previous study (23). Drivers and regulators contained 4 and 2 patches, respectively. For binary mixtures, the total number of particles was 1,000. Simulations were carried out for ε_PR/ε_PP from 0.2 to 1.2 and the R-to-P ratio from 0.02 to 1.5, at a fixed temperature of 0.68. In each simulation, 2 million cycles were collected, with the second half used for data analysis. Each cycle consisted of 1,000 attempts of particle displacement or rotation (with equal probability), 4,000 attempts of particle exchange, and 5 attempts of volume exchange. For each set of conditions, simulations were run in triplicate.

We also extended the modeling to ternary mixtures between 2 drivers and a regulator (labeled as 1, 2, and R, respectively). The following conditions were set for the strengths of attraction between different species: ε₁₂ = 1.5; ε_1R = 2ε_2R; self-attraction absent (e.g., ε₁₁ = 0). Four ε_1R values were studied: 0, 1.0, 1.5, and 2.0. The total number of particles was 512. The molar ratio of the 2 drivers was 1:1, 1:2, or 2:1; the number of regulator particles was 0, 56, 112, 212, or 312 (corresponding to a molar fraction 0, 0.11, 0.22, 0.41, or 0.61).