Intracellular redox potential is correlated with miRNA expression in MCF7 cells under hypoxic conditions

Significance

Cancer is associated with low-oxygen cellular environments. However, a better understanding of the connection between the amount of oxygen in a cell’s microenvironment and its behavior is much needed. By optical measurements, we have characterized how the redox chemistry and the intracellular redox potential of cells respond to changes in oxygen pressure. Through surprisal analysis (a technique based on thermodynamics), we were able to identify changes in cellular signaling molecules (microRNAs [miRNAs]) that correlate with redox changes and found that, at low-oxygen conditions, these miRNAs are associated with tumor spread and survival. The changes in miRNA expression were used to quantify the free-energy variations with oxygen pressure, variations that reflect the changes in the measured intracellular redox potential.

Abstract

Hypoxia is a ubiquitous feature of cancers, encouraging glycolytic metabolism, proliferation, and resistance to therapy. Nonetheless, hypoxia is a poorly defined term with confounding features described in the literature. Redox biology provides an important link between the external cellular microenvironment and the cell’s response to changing oxygen pressures. In this paper, we demonstrate a correlation between intracellular redox potential (measured using optical nanosensors) and the concentrations of microRNAs (miRNAs) involved in the cell’s response to changes in oxygen pressure. The correlations were established using surprisal analysis (an approach derived from thermodynamics and information theory). We found that measured redox potential changes reflect changes in the free energy computed by surprisal analysis of miRNAs. Furthermore, surprisal analysis identified groups of miRNAs, functionally related to changes in proliferation and metastatic potential that played the most significant role in the cell’s response to changing oxygen pressure.

The tumor microenvironment can have a profound effect on the molecular landscape of cells, influencing phenotype at epigenetic, transcriptional, and posttranscriptional levels (1). A better understanding is needed regarding the chemical drivers of these changes and in particular the mechanisms that link microenvironmental changes with changes in molecular phenotypes. Hypoxia, a lack of oxygen, is associated with tumor microenvironments and is thought to drive proliferation and resistance to therapy. Understanding the connection between hypoxia and tumor progression could equip us with the knowledge to improve the efficacy of existing therapies, such as radiotherapy, and to design and screen new therapies (2–4). There is disagreement in the literature regarding hypoxia and its role in the redox chemistry of the cell (5): While some studies indicate that the cellular environment becomes more oxidative as a consequence of hypoxia (5, 6), others claim that hypoxia imposes a reductive stress on cells (7). A possible source of this confusion may be the large range of oxygen pressure quoted in the literature as representing hypoxia; for example, 4 recent publications quote hypoxic oxygen pressures ranging from 5 to 0.2% (8–11). It may be more useful to benchmark hypoxia against in vivo oxygen pressures where tumors typically have oxygen pressures <2%, and healthy tissues have oxygen pressures between 4% and 6% (12). Furthermore, a subtle aspect to this controversy is the question of whether the common measures of “redox status,” e.g., measurements of reactive oxygen species (ROS) or nitroreductase activity report on redox status as a cellular global parameter or on a local concentration of particular analytes. Here, we demonstrate that intracellular redox potential (IRP) is a key parameter through which hypoxic microenvironments affect the expression of signaling molecules that coordinate the cell’s response to hypoxia.

IRP is a function of the concentration of all of the oxidants and reductants in the cell and is a global measure of how oxidative an environment is (13). Where common fluorescent reporters typically give information on a local concentration of, e.g., ROS, our class of surface-enhanced Raman spectroscopy (SERS) nanosensors quantitatively measure a redox potential (14). We have previously used these sensors to measure drug and nanoparticle toxicity in 2D culture (7, 15), to measure the effects of drugs and radiotherapy in 3D culture (4, 16), and have multiplexed pH and redox potential measurements using complementary SERS sensors (16–18). We have characterized the interaction of the sensors with various cell lines (7, 14–18) and with MCF7 cells in particular (17). In these publications, we have shown that the particles localize to the cytoplasm and do not affect cell viability.

The central concept of our investigation is that IRP (E) is a measure of the free energy (ΔG) of a cell (since ΔG = −n F E, where n is the number of electrons transferred and F is the Faraday constant) and a change in this experimentally determined free energy (in response to changing oxygen pressure) should correlate with a free-energy change associated with the cell’s adaptation (e.g., change in the concentrations of signaling molecules such as microRNAs [miRNAs]). Here, we determine how cellular redox potential, E, changes in cells exposed to a range of 21 to 1% oxygen. By using surprisal analysis (SA) (19, 20), a thermodynamic- and information theory-based approach, we identify links between changes in the redox potential and in miRNA expression levels as a consequence of changes in oxygen pressure.

SA is based on the principle that molecular systems are bound by constraints that prevent the system from reaching its maximal possible entropy. In cells, these constraints represent biological pathways that exist as a profile of analyte (metabolite, protein, RNA) abundances and that change in response to (for example) environmental or genetic perturbations. SA takes a matrix of analyte concentrations vs. oxygen pressures and by natural log (ln) transformation converts it to a matrix of chemical potentials vs. oxygen pressures. SA seeks to represent the data in the manner shown in Eq. 1. Using the mathematical tool of singular value decomposition (20), we can analyze this matrix to identify 2 features, the analytes associated with a constraint and the overall importance of that constraint for every oxygen pressure p. The importance of a constraint $\alpha$ is given by a Lagrange multiplier ${\lambda }_{\alpha }\left(p\right)$ [i.e., constraints with ${\lambda }_{\alpha }\left(p\right)$ furthest from zero are those most important in defining the cell’s response to a change in oxygen pressure, p]. The set of analytes associated with a constraint i are represented as a vector with components $G_{i\alpha }$ (i.e., analytes with values of $G_{i\alpha }$ furthest from zero are those that contribute most to the constraint). SA was used here to identify miRNAs that play an important role in determining the cell’s response to changes in oxygen pressure by first determining the thermodynamic reference referred to as “the balanced state,” which is the collection of analyte levels that are invariant with oxygen pressure (Eq. 1):

$$\stackrel{\text{The}\hspace{0.17em}\text{data}}{\overbrace{\begin{array}{c}\ln X_i\left(p\right)\\ \begin{array}{l}\text{Logarithm}\hspace{0.17em}\text{of}\\ \text{abundance}\hspace{0.17em}\text{of}\hspace{0.17em}\text{analyte}\\ \mathit{i}\hspace{0.17em}\text{at}\hspace{0.17em}\text{oxygen}\hspace{0.17em}\text{pressure}\hspace{0.17em}\mathit{p}\end{array}\end{array}}}=\stackrel{\text{The}\hspace{0.17em}\text{Balanced}\hspace{0.17em}\text{State}}{\overbrace{\begin{array}{c}\ln {\mathit{X}}_{\mathit{i}}^{\text{0}}\\ \begin{array}{l}\text{logarithm}\hspace{0.17em}\text{of}\\ \text{abundance}\hspace{0.17em}\text{of}\hspace{0.17em}\text{analyte}\\ \mathit{i}\hspace{0.17em}\text{in}\hspace{0.17em}\text{the}\hspace{0.17em}\text{balanced}\\ \text{state}\end{array}\end{array}}}+\stackrel{\text{Deviations}\hspace{0.17em}\text{from}\hspace{0.17em}\text{the}\hspace{0.17em}\text{Balanced}\hspace{0.17em}\text{State}}{\overbrace{\begin{array}{ccc}{\sum }_{\alpha =\mathrm{1,2},\mathrm{...}}& G_{i\alpha }& {\lambda }_{\alpha }\left(p\right)\\ \begin{array}{l}\text{Sum}\hspace{0.17em}\text{over}\hspace{0.17em}\text{all}\\ \text{constraints}\end{array}& \begin{array}{l}\text{Weight}\hspace{0.17em}\text{of}\\ \text{analyte}\hspace{0.17em}\mathit{i}\hspace{0.17em}\text{in}\\ \text{constraint}\hspace{0.17em}\alpha \end{array}& \begin{array}{l}\text{Multiplier}\hspace{0.17em}\text{of}\\ \text{constraint}\hspace{0.17em}\alpha \hspace{0.17em}\text{at}\\ \text{oxygen}\hspace{0.17em}\text{pressure}\hspace{0.17em}p\end{array}\end{array}}}.$$ [1]

As shown in Eq. 1, there will be separate contributions from the balanced state and from each of the deviations. The minimal work needed to drive the system from the balanced state to an activated state can be written as follows: ${\displaystyle \sum _i{X}_i\left(p\right)\text{ln}\left[X_i\left(p\right)/X_i^0\left(p\right)\right]}$ (21). Thereby, SA enables the free energy of the system to be computed, and this enables a direct comparison with the changes in free energy measured via IRP. Furthermore, SA allows us to identify the analytes that contribute most to the changes in free energy (those with the largest $G_{i\alpha }$ in Eq. 1). By comparison, established techniques for analysis of miRNA expression changes identify pairwise differences between (for example) 1% O₂ and 21% O₂, and do not identify collective behavioral patterns across a set of conditions. Furthermore, a limitation of clustering techniques is that strong signals often dominate the outcome by masking species present in low concentrations that are potentially important in the cell’s behavior.

In this paper, we found that redox potential becomes more reductive as the pressure of oxygen decreases and found an excellent correlation between the computed free energy (on the basis of miRNA concentrations) and the free energy from the directly measured redox potential. This approach defines links between redox potential and miRNA signaling and identifies the miRNAs whose concentration profiles contribute most to the changes in free energy and the cell’s adaptation to hypoxia.

Results

Measurements of the IRP from 21 to 1% O₂.

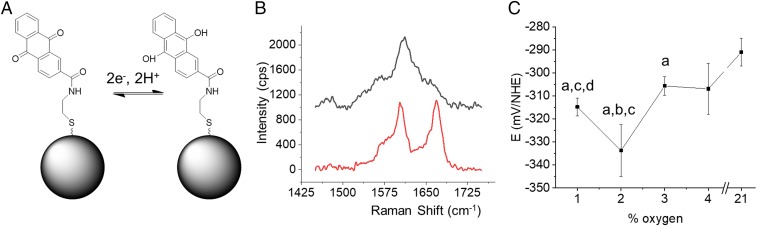
In order to measure IRP in the cytosol of MCF7 cells grown under varying O₂ pressures, we built a homemade device that allowed cells maintained in conditioned media, at a defined O₂ pressure, to be imaged through a MgCl₂ window (with low intrinsic Raman background) (SI Appendix, Fig. S1). We made measurements between 1 and 4% oxygen because they are representative of in vivo concentrations and at 21% because it is the most common choice when culturing cells for biomedical research. Nanoshells (NSs) were functionalized with the redox-active reporter, N-[2-({2-[(9,10-dioxo-9,10-dihydroanthracen-2-yl)formamido]ethyl}disulfanyl)ethyl]-9,10-dioxo-9,10-dihydroanthracene-2-carboxamide (referred to as AQ). AQ undergoes a reversible 2e⁻, 2H⁺ redox reaction (Fig. 1A), resulting in a change in molecular structure and Raman fingerprint. AQ is sensitive to changes in redox potential in the hypoxic range between −250 and −400 mV vs. NHE (7, 17), and redox-sensitive peaks report on the oxidation state through a change in peak intensity. Fig. 1B shows the signals at 1,666 and 1,606 cm⁻¹ that correspond to the (redox-sensitive) quinone C=O stretch and (not redox-sensitive) amide stretch/symmetric ring breathing, respectively. As cellular pH affects the overall redox potential, cells were also incubated with NSs functionalized with the pH-sensitive reporter para-mercaptobenzoic acid (MBA), which has been shown previously to be sensitive to pH changes between 5.5 and 8.5 (16–18, 22). ANOVA analysis revealed no significant difference in pH between different conditions (SI Appendix, Table S1), and we have therefore not adjusted the measured redox potential measurements as a result of pH.

Fig. 1.

SERS nanosensors measure IRP. (A) Schematic showing the change in structure associated with oxidation/reduction. (B) Spectrum of the oxidized (red) and reduced (black) form of the nanosensor. (C) Intracellular redox potentials measured in MCF7 vs. pO₂. Error bars represent the SD of 3 independent measurements. Lowercase letters as labels signify a P value < 0.05 for a paired t test vs. 21% (A), 4% (B), 3% (C), and 2% (D).

As shown in Fig. 1C, the trend in measured IRP is a decrease from 21 to 2% O₂ followed by an increase from 2 to 1% O₂. Pairwise t tests indicated that both the drop in IRP toward 2% O₂ and the increase between 2% and 1% are statistically significant. The overall downward trend in IRP is in line with the expectation that a less oxidative extracellular environment should result in a more reductive intracellular environment. In order to investigate whether IRP changes reflect changes in metabolism, we measured the concentration of ROS and selected metabolites across the same set of O₂ pressures (SI Appendix, Fig. S2). The trend shows that ROS, glucose, taurine, and lactate increase significantly between 21% and 4% before either plateauing or decreasing gradually toward 1%. The opposite trend can be seen in the concentrations of amino acids such as alanine, tyrosine, and phenylalanine, which drop between 21% and 4% and then plateau. As a control, we measured metabolite concentrations of cells grown at 1% O₂, at 21% O₂, and at 21% O₂ treated with rotenone (an inhibitor of oxidative phosphorylation). When rotenone was used to inhibit oxidative phosphorylation at 21% oxygen, the NMR analysis showed a similar increase in metabolites such as lactate and decrease in amino acids such as alanine and glutamine. These results suggest a change in metabolism toward glycolysis since less oxygen is being used to make energy, lactate is being produced, and glucose uptake is increased to feed the less efficient energy requirements of glycolysis. An important point to note is that these data demonstrate not only that IRP and ROS are not equivalent but also that there are significant differences in the manner in which they change in response to changing O₂. While the reasons for the differences between IRP and ROS remain to be fully elucidated, it is worth reiterating that the nature of the measurements is different—IRP is a thermodynamic parameter that is a function of many oxidant and antioxidant concentrations; fluorescent reporters of ROS only measure a single component of the system. In the context of a switch from oxidative phosphorylation to glycolysis at lower O₂ pressures, it is not surprising that a decreased metabolic demand for oxygen leads to higher ROS levels; however, our results also suggest that the switch produces a compensatory increase in antioxidants (e.g., NADPH) that leads to a reduced IRP. Such differences underline the need for caution when using ROS measurements to discuss redox mechanisms and when generalizing on the effects of hypoxia based on measurements made at a single oxygen pressure.

Measurement of miRNA Abundance across a Range of O₂ Pressures.

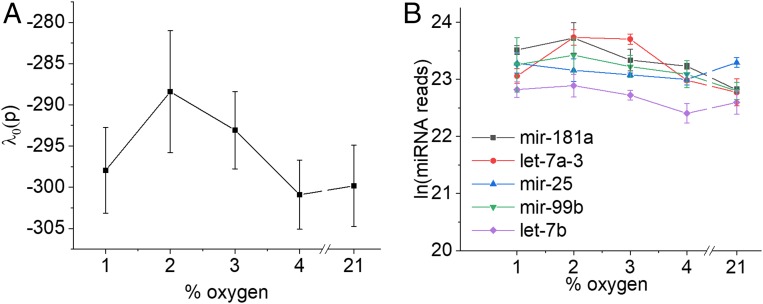
To correlate IRP measurements with cell signaling in response to hypoxia, we measured miRNA expression using Nextgen sequencing. As posttranscriptional gene regulators, miRNAs play important roles in signaling the cell’s response to environmental stresses and several miRNAs have well-documented roles in regulating the response to hypoxia (23). We identified 610 miRNAs with a measurable expression level in MCF7s and used SA to look for patterns of collective activity of the miRNAs across the range of O₂ pressures used in this study. We first used SA to identify the balanced state that should be independent of oxygen pressure (Eq. 1). In a biological context, the molecules most expressed in the balanced state can be considered as having a function unrelated to O₂ pressure. Fig. 2A shows the magnitude of its Lagrange multiplier ${\lambda }_0\left(p\right)$ (which is a measure of its potential) vs. oxygen pressure.

Fig. 2.

The balanced state is independent of the pressure of oxygen. (A) λ₀ vs. pO₂ is essentially constant within the error bars. (B) Expression of the dominant miRNAs in the balanced state vs. pO₂.

${\lambda }_0\left(p\right)$ should be invariant with pO₂ (which within the bounds of the error bars it is), and since its magnitude is higher than for any other ${\lambda }_{\alpha }$ (see below), it is the major contributor to the free energy of the cell. These 2 factors are further illustrated by the fact that the most heavily weighted miRNA members of the balanced state are highly expressed and display very little variation in concentration as a function of oxygen pressure (Fig. 2B).

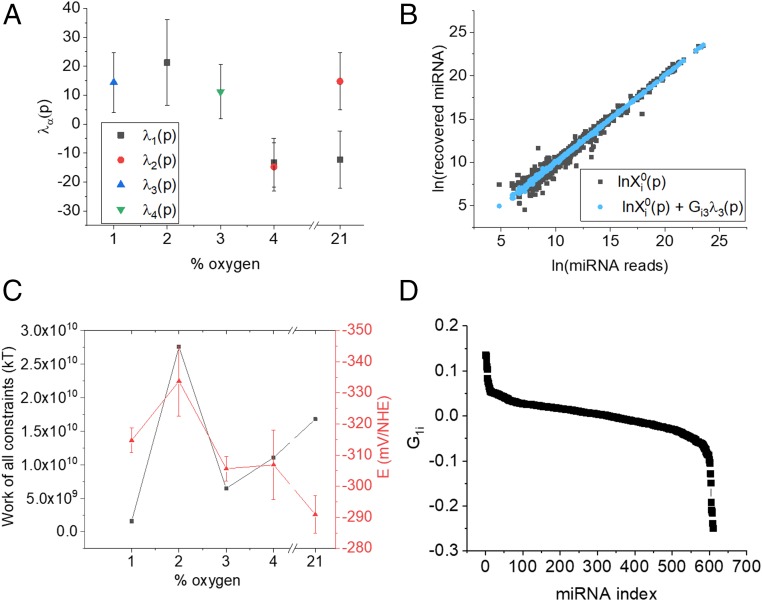
SA also identifies 4 other constraints (λ₁ to λ₄) where the miRNA distribution is deviant from the stable state. The weights of the contributing different constraints are shown in Fig. 3A, and it is clear that each one of ${\lambda }_1$ to ${\lambda }_3$ changes sign as a function of oxygen pressure. It can be seen from Eq. 1 that if ${\lambda }_{\alpha }\left(p\right)$ changes sign between 2 pressures it signifies that a miRNA that was highly expressed has become less expressed and this suggests that within the pO₂ range investigated, there are regimes in which different collections of miRNAs play important roles (rather than, e.g., an even transition from high expressed to low expressed across the range). (For each constraint, only those values where the error bars do not span zero are shown in Fig. 3A.)

Fig. 3.

Measurement of the constraints associated with change in oxygen pressure. (A) The values of λ₁ to λ₄ vs. % O₂. (B) Addition of λ₃ to the stable state improves the fit of the data at 1% O₂. (C, Left ordinate) Work done to deviate the miRNA distribution from its balanced state. Right ordinate: measured IRP, E. Error bars show SDs calculated from 3 biological replicates. (D) Expression level of miRNA i in constraint 1, drawn in descending order for each of the miRNAs.

We can further confirm which constraints are most important at which oxygen pressures by examining the quality of fit to the data. Since adding terms to the right-hand side in Eq. 1 improves the quality of the fit to the data (20), we can determine which ${\lambda }_{\alpha }\left(p\right)$ is most important at a particular oxygen pressure by asking which constraint(s) we should add to get the best fit. For example, at 1% O₂, addition of ${\lambda }_3$ gives the best fit as shown in Fig. 3B. At 2%, the addition of ${\lambda }_1$ gives the best fit, and at 4% and 21%, both ${\lambda }_1$ and ${\lambda }_2$ are needed to give the best fit (SI Appendix, Fig. S3).

Fig. 3C shows the work done by each of the dominant constraints at the relevant oxygen pressure to deviate the distribution of miRNAs from the balanced state and this mirrors the trend in the redox potential (the Pearson correlation coefficient between these datasets is 0.407). Importantly, this shows the direct link between the experimentally measured free energy (based on the measurement of the redox potential E) and the computed free energy (based on the SA of the miRNA concentrations).

We reiterate that, as shown in Fig. 3A, the weights ${\lambda }_{\alpha }\left(p\right)$ of the contribution of different constraints are O₂ dependent, are different for different constraints, and can change sign as the pO₂ is changed. A change of sign between pressures means that if a given miRNA is overexpressed in a particular constraint at one pressure it will be under expressed at the second pressure.

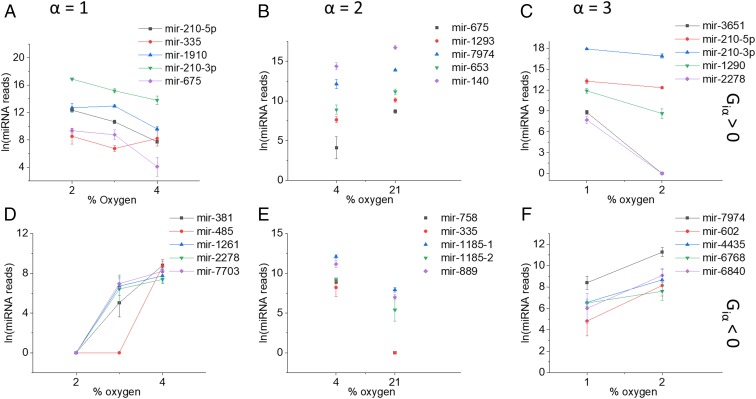
To illustrate what a constraint means in biological terms, Fig. 3D shows a plot of $G_{i1}$ for each of the 610 miRNAs for the constraint $\alpha =1$. The miRNAs that contribute most to this constraint (with G values furthest from zero) are those at the 2 ends of the distribution while those in the flat portion of the graph contribute least. To build upon this view, we now discuss those miRNAs that contribute most to each ${\lambda }_{\alpha }$. The 5 miRNAs with the most positive value of $G_{i\alpha }$ and the 5 miRNAs with the most negative value of $G_{i\alpha }$ are shown in Fig. 4 for λ₁ to λ₃. Each column in Fig. 4 shows the range of oxygen pressures where ${\lambda }_{\alpha }\left(p\right)$ changes sign for $\alpha =\mathrm{1,2,3}$.

Fig. 4.

The miRNAs identified as contributing most to the 3 constraints. Each column is identified by the constraint index α: A and D, α = 1; B and E, α = 2; C and F, α = 3. The Top row (A–C) are expression levels of the 5 miRNAs with the most positive value of their weight, $G_{i\alpha }$ in constraint $\alpha$. The Bottom row (D–F) are the expression levels of the 5 miRNAs with the most negative value of their weight, $G_{i\alpha }$ in constraint $\alpha$. The abscissa is the oxygen pressure range over which ${\lambda }_{\alpha }\left(p\right)$ changes sign. Error bars represent the SD of 3 biological replicates.

The first column in Fig. 4 A and D shows expression levels of miRNAs that contribute most to the first constraint, ${\lambda }_1\left(p\right)$. As seen in Fig. 3A, ${\lambda }_1\left(p\right)$ has a negative sign above 4%, which changes to positive sign at 2%. This change of sign and the corresponding change in the expression levels signify the importance of ${\lambda }_1\left(p\right)$, in the adaptation from 4 to 2% oxygen. This range of oxygen pressures incorporates pressures that are physiologically relevant to tissues as well as being pathologically relevant to tumors (12). Looking at the 2 groups separately, members of the first group ($G_{i,\hspace{0.17em}\alpha =1}>0$; Fig. 4A) have clear functional parallels that correlate an increase in expression with the proliferative phenotype of tumors. The most heavily weighted and well characterized of these are discussed here; in particular, miR-210 has been shown to promote metastasis and invasion in prostate cancer by targeting NF-κB signaling (24). miR-675 has been shown to be up-regulated in hepatocellular carcinoma (HCC) patient samples and cell lines and correlates with high levels of alpha fetoprotein (a superoxide dismutase)—it is thought to play a role in cell cycle regulation and epithelial-to-mesenchymal transition through targeting Twist1 (25). miR-483 has been found to be up-regulated in gastric cancer tissues and in cell cultures has been shown to promote proliferation and invasion, its elevation in pancreatic ductal adenocarcinoma has been correlated with poor prognosis (26).

Members of the group whose expression drops from 4 to 2% oxygen ($G_{i,\hspace{0.17em}\alpha =1}<0$; Fig. 4D) have documented functional characteristics that relate a decrease in expression with a switch toward a more malignant tumor phenotype. For example, miR-381 suppresses growth and proliferation in HCC and osteosarcoma and is thought to target WNT signaling through down-regulation of LRH1 and Hes1 (27, 28). miR-2278 has been reported as having tumor repressor activity through targeting AKT2, STAM2, and STAT5A (29). miR-485 is down-regulated in cancers including HCC and metastatic breast cancer tissue and is thought to inhibit proliferation through targeting PGC-1α (30, 31). Taken together, the 2 groups of miRNAs point toward an increase in proliferative and metastatic phenotype as the oxygen pressure falls from the physiological level (4%) to more pathological level (2%). This very clear thermodynamic-like transition mirrors that previously seen using measurements of phosphorylated proteins at the single-cell level (32).

The second constraint, ${\lambda }_2\left(p\right)$, contributes only at the 2 highest pressures, and it changes sign between pressures of 4% and 21%. It is again clear in this case that the miRNAs most heavily weighted in this constraint have a distinct change in concentration between 4% and 21% (Fig. 4 B and E). While 21% oxygen is commonly used to culture cells in vitro, it is a much higher pressure than experienced by tissues in vivo, and thus these miRNAs may highlight the differences between a physiological oxygen level (4%) and a nonphysiological stress (21%).

These 2 groups identified by the constraint $\alpha =2$, again have documented roles in regulating proliferation or survival. For those where $G_{i,\hspace{0.17em}\alpha =2}>0$ (Fig. 4B), miR-1185 induces apoptosis in endothelial cells by targeting UVRAG and KRIT1, and miR-889 and miR-758 appear to play complementary roles in the regulation of proliferation by targeting DAB2IP and MTOR, respectively. In the group whose concentration drops from 21 to 4% ($G_{i,\hspace{0.17em}\alpha =2}<0$; Fig. 4E), miR-675 is up-regulated in carcinomas (as previously discussed), miR-1293 may promote metastasis through regulation of MMP activity, and miR-653 promotes proliferation through targeting TRIM9 (a ubiquitin ligase). miR-1274 has multiple documented roles including suppression of tumor growth through targeting Wnt and activation of metastasis through activation of tumor-associated macrophages.

The third constraint, ${\lambda }_3\left(p\right)$, contributes only at 1% oxygen, suggesting that it plays a role in adaptation to the more extreme hypoxic conditions found in cancers such as prostate and pancreas. Other than those already discussed (miR-3651, miR-210, miR-2278, miR-381), miR-1290 and miR-4435 are known to promote tumor growth and miR-602 has been shown to inhibit proliferation. For the remainder, their function is less well described in the literature, but our findings may allow predictions to be made regarding their potential role in cancer pathogenesis.

To investigate whether the miRNAs identified by SA also correlate with ROS, we measured the Pearson correlation coefficient between individual miRNA concentrations and ROS concentrations (SI Appendix, Table S2). While the highest ranking miRNAs have no overlap with those discussed above, some of these miRNAs do share characteristics: 2 of the top 6 are from the let-7 family and are thought to act as tumor suppressors and 3 of the top 6 (miR-769, miR-1306, and let-7g) are thought to target TGF-β signaling, suggesting a link between ROS and specific pathways.

The close correlation between the free energy derived from IRP and that calculated from miRNA profiles suggests a mechanistic link. For example, the concentration profile of the miRNAs for which $G_{i,\hspace{0.17em}\alpha =1}<0$ across all pO₂ shows a very strong correlation with redox potential (SI Appendix, Fig. S4 and Table S3). This correlation suggests that redox potential may play a role in regulating transcription of the miRNA loci, perhaps via modulating the oxidation state of amino acids such as cysteine in transcription factors. Indeed, many of the known transcription factors for this group are known to be redox sensitive, including numerous zinc-finger proteins, NRF2 or YAP (detailed in SI Appendix, Table S4), and this idea warrants further investigation, for example using transcriptomic, targeted proteomic, and imaging experiments (33, 34).

Our finding that 3 distinct constraints contribute to the cell’s response to a decrease in oxygen pressure highlights that hypoxia is measurably different depending on the oxygen pressure at which you investigate it. Our finding that the major change in free energy between 4% and 2% oxygen coincides with a change in miRNA expression associated with increased pathogenesis correlates well with previous findings that hypoxia induces a change in kinase signaling networks between these pressures (34), and that hypoxia drives resistance to therapy in some cancers (35, 36).

To summarize, our findings demonstrate that redox potential becomes measurably more reductive as oxygen pressure falls. While this correlates with changes in metabolism, the changes are not well correlated with the changes in ROS (a commonly measured surrogate of redox potential). Through the use of SA, we demonstrate that the measurable free-energy change (from redox potential measurements) directly mirrors the computed free-energy change through analysis of miRNA levels. We also identified groups (as identified by SA) of miRNAs whose free-energy change contributes most to the cell’s adaptation to hypoxia. In particular, we identified groups of miRNAs whose function relates to changes in proliferation and metastatic potential. These findings underline the important role that oxygen and tumor microenvironment play in driving pathogenesis. The correlation between redox potential and miRNA expression underlines the important role that redox reactions play in relaying microenvironmental changes to the genome.

Materials and Methods

Cell Culture.

Human breast adenocarcinoma (MCF7) cells were grown in Dulbecco’s modified Eagle medium (DMEM) supplemented with 10% heat-inactivated FBS, 10,000 units/mL penicillin–streptomycin, and l-glutamine (200 mM). Cells were seeded at a density of 1 × 10⁵ cells per mL and were grown at 37 °C under humidified atmosphere (5% CO₂). All cell culture reagents were purchased from Invitrogen.

Metabolite Extraction.

Cells were incubated at 1%, 2%, 3%, 4%, or 21% O₂ for 24 h before being washed twice with ice-cold PBS (10 mL). MeOH:CHCl₃:H₂O (1:1.5:0.7 mL) was added before vortexing for 60 s. All samples were centrifuged at 1,000 × g for 10 min. The aqueous layer was pipetted into a vial and the solvent was removed under nitrogen. The polar extracts were reconstituted in pH 7.4 sodium phosphate buffer (0.1 M, 600 μL) containing 100% D₂O, to minimize variations in pH, and TSP (50 nM) as a reference. The process was carried out in a hypoxia incubation chamber.

NMR Analysis.

Samples were run on a Bruker Advance 600-MHz spectrometer. Topspin 2.1 was used to acquire spectra using software implementation of digital filters, which produced flat baselines but resulted in the reduction of the signal-to-noise ratio by 25%. Relaxation and acquisition times of 2 and 1.36 s, respectively, and a nuclear Overhauser effect mixing time of 10 ms were used. Pulsed field gradients were set to 50% and −10% of 50 Gauss/cm. A total of 356 scans was accumulated into each spectrum. Each NMR spectrum was normalized to the spectrum with the highest total peak integral in order to correct for slight differences in cell numbers between samples.

Small RNA Library Preparation and Analysis.

Triplicate samples for each O₂ pressure of MCF7 cells were cultured and extracted, once confluent, using the MiRNeasy Mini Kit (Qiagen). The integrity of RNA was determined using a Bioanalyser 2100 Nano LabChip kit (Agilent Technologies) with all samples providing an RNA integrity number of ≥8.8. Small RNA libraries were prepared using the CleanTag kit (Trilink) and libraries pooled prior to sequencing a HiSeq4000 (Illumina). Raw fastq sequences required further preprocessing to remove contaminating primers, etc., which was done using cutadapt software (37). Trimmed sequences were collapsed within each sample to generate a nonredundant set of fasta sequences (singletons were not included). The reference genome used for alignment was the latest version of the human genome (hg19); only full-length perfect-match sequences were kept. Sequences aligning to the human genome were subsequently used as input for a mirDeep2 analysis (38). The analysis used human mature (3p and 5p forms) and precursor sequences obtained from mirBase (release 21; http://mirbase.org/). Raw “tag counts” (i.e., sequences aligning) were obtained for 1,427 different mature miRNAs. miRNAs with an average read count per sample fewer than 5 were discarded, leaving 610 loci. The counts within each sample were normalized by conversion to abundances, which were then multiplied by 1 million to generate a reads set, 1 count added to all to preclude zero counts instances. This dataset was used as input for SA.

NS Functionalization.

For IRP measurements, NSs were incubated overnight in 100 μM AQ (7) dissolved in 1% DMSO. Functionalized AQ–NSs were washed 3 times with water. For pH measurements, NSs were incubated overnight in 100 μM 4-mercaptobenzoic acid (MBA) dissolved in ethanol. Functionalized MBA–NSs were washed 3 times in water. NSs (resonant at 782 nm) were purchased from Nanospectra Biosciences and have a diameter of 150 nm constituting a 25-nm gold shell.

SERS Measurements.

Approximately 75,000 cells were seeded on a MgCl₂ imaging window and incubated overnight at 37 °C and fixed O₂ pressure. Functionalized AQ–NSs (10 fM) or MBA–NSs (10 fM) were added to FCS-free DMEM incubated with cells overnight. Fresh PBS and media were also incubated overnight under same conditions. The following day, cells were then rinsed with preconditioned PBS to remove excess AQ–NSs or MBA–NSs in the medium. The imaging window was assembled into a homemade imaging device into which media, preconditioned at a predetermined O₂ pressure, was injected. The device was designed to keep cells at a fixed O₂ pressure with no air bubbles. A Renishaw inVia Raman microscope and spectrometer equipped with a 785-nm diode laser in-line focus mode was used for obtaining SERS spectra. A large map of a cell was analyzed using a 1-s acquisition, delivering 12.8-mW laser power. The spectra were processed using Origin8.5 and Matlab. Baseline subtraction was performed followed by extraction of peak areas of interest using published Matlab scripts (15). AQ–NS is most sensitive to changes in redox potential between −250 and −400 mV vs. NHE (7, 18). Redox potential was calculated from the SERS spectra using a previously published routine, which measures the ratio of the peaks at 1,666 and 1,606 cm⁻¹ and compares them to calibration data generated using spectroelectrochemistry (spectra whose intensity at 1,606 cm⁻¹ were below 100 counts were discarded) (7, 17). SERS maps were generated, and where multiple pixels within a cell contained SERS spectra (as a result of multiple nanosensors per cell), an average spectrum was used (in the data shown, at least 10 spectra were used to generate an average per cell). At least 3 separate cells were measured to generate an average redox potential at a given oxygen pressure. The same procedure was used to measure pH, the only difference being that the reporter molecule was MBA. MBA–NSs are most sensitive to changes in pH between 5.5 and 8.5 (17, 18). SERS spectra were collected, processed, and baselined as above (15, 17). For the peak at 1,580 cm⁻¹, spectra with <200 counts were rejected. pH was calculated by measuring the peaks 1,400 and 1590 cm⁻¹ and comparing to calibration data as documented previously (15, 17). At least 3 separate cells were measured to generate an average intracellular pH at a given oxygen pressure.

ROS Measurements.

For each O₂ pressure, 5 cell culture flasks were seeded to a total density of 3 × 10⁶ cells. Cells were incubated at 1%, 2%, 3%, 4%, or 21% O₂ for 24 h. Once confluent, cells were washed twice with PBS (10 mL), trypsinized, and centrifuged. Fresh media was added to all flasks. H₂DFFDA (10 µM) was added to 4 of the samples. H₂O₂ (0.03%) was added to one sample (as a positive control), and one was left untreated of both reagents (as a negative control). All samples were covered with foil and incubated for 1 h at 37 °C and a given pressure of O₂. After incubation, the samples were centrifuged for 4 min at 2,000 × g before being washed twice and resuspended in PBS (5 mL). Fluorescence measurements were taken using a Jobin Yvon Spex Fluoromax spectrofluorometer at an excitation of 492 nm. The peak emission of H₂DFFDA at ∼525 nm was monitored.

Surprisal Analysis.

The use of SA in redox chemistry merits discussion of relevant key details. More technical aspects of SA (32, 39), in particular the computation of error bars (32), are discussed together with the experimental methods that we use in the first section of SI Appendix.

Given the logarithmic representation of the abundances as in Eq. 1, one can compute the free energy of the system and compare it to the free-energy changes as measured via the redox potential measurements. There will be 2 contributions, the free energy of the stable state and that of deviations from it. The second contribution can be written as follows: ${\displaystyle \sum _i{X}_i\left(p\right)\text{ln}\left[X_i\left(p\right)/X_i^0\left(p\right)\right]}$. This is the (minimal) work needed to drive the system from the stable state to its actual state (21). Each term in the sum is the contribution of a particular analyte and the work can be written as a sum over the constraints, $\mathrm{\Delta }G\left(p\right)={\displaystyle \sum _{\alpha =\mathrm{1,2},\dots }{\lambda }_{\alpha }\left(p\right)}{\langle G_a\rangle }^p.{\langle G_{\alpha }\rangle }^p$ is the mean value of the $G_{i\alpha }$ values computed over the abundances $X_i$, ${\langle G_{\alpha }\rangle }^p={\displaystyle \sum _i{X}_i\left(p\right)G_{i\alpha }}$. Technically, the ${\lambda }_{\alpha }$ values are Lagrange multipliers. If some ${\lambda }_{\alpha }\left(p\right)$ equals zero, then the constraint is not relevant at this pressure p because it does not change the abundance level as seen in Eq. 1. Due to the unavoidable experimental noise, there is an error in determining the ${\lambda }_{\alpha }$ values from the experimental data. If that error bar spans zero, then, to within experimental accuracy, that ${\lambda }_{\alpha }$ should be taken to equal zero and then that constraint does not contribute to the free energy.

The major term in the free energy is that of the stable state itself. To have a uniform notation, we formally add a zeroth constraint and thereby write $\ln X_i^0\left(p\right)={\lambda }_0\left(p\right)G_{i0}$. Then the free energy of the stable state can be written as for the other constraints, ${\lambda }_0\left(p\right){\langle G_0\rangle }^p$. In much of cell biology, the stable state is the major contributor to the free energy, and this is also the case here (39). This is a reflection of the inherent stability of the cell state even when it is a cancer cell.