Atmosphere–ocean oxygen and productivity dynamics during early animal radiations

Significance

We have discovered 2 major oceanic anoxic events (OAEs) in the early Cambrian at the time when animals markedly diversified. We present a multiproxy constraint on the global biogeochemical cycles to show that these events, in contrast to most younger OAEs, could have been driven by declining atmospheric O₂ levels, plausibly set off by the appearance of bioturbating animals. Pulses of animal appearances may have occurred at different times on different continents, but the last pulse occurred after the OAEs and at a time when we predict higher marine productivity and O₂ levels in the surface oceans suggesting energy supply into the marine food chain was maximal.

Abstract

The proliferation of large, motile animals 540 to 520 Ma has been linked to both rising and declining O₂ levels on Earth. To explore this conundrum, we reconstruct the global extent of seafloor oxygenation at approximately submillion-year resolution based on uranium isotope compositions of 187 marine carbonates samples from China, Siberia, and Morocco, and simulate O₂ levels in the atmosphere and surface oceans using a mass balance model constrained by carbon, sulfur, and strontium isotopes in the same sedimentary successions. Our results point to a dynamically viable and highly variable state of atmosphere–ocean oxygenation with 2 massive expansions of seafloor anoxia in the aftermath of a prolonged interval of declining atmospheric pO₂ levels. Although animals began diversifying beforehand, there were relatively few new appearances during these dramatic fluctuations in seafloor oxygenation. When O₂ levels again rose, it occurred in concert with predicted high rates of photosynthetic production, both of which may have fueled more energy to predators and their armored prey in the evolving marine ecosystem.

The “Cambrian explosion” refers to a relatively short time interval, ca. 540 to 520 Ma, during which nearly every major animal group appeared in the fossil record, mineralized skeletons became widespread, and some large, motile animals began to plow through the sediment surface (1–4). The Cambrian explosion is one of a series of radiations that began in the late Ediacaran and continued through the early Paleozoic, during a time of significant fluctuations in oceanic redox conditions and nutrient supply (4–6). How these fluctuations relate to animal radiations is not well understood (4, 7–11). One hypothesis is that rising O₂ availability in the marine realm allowed the evolution of carnivory, which in turn drove predator–prey “arms races” and concomitant diversification (3, 8). This radiation could result from either higher molar concentrations of O₂ in the surface waters or at the seafloor, which would, in turn, expand oxygenated areas for the benthic animal fauna. With higher molar concentrations of O₂ and/or greater habitats for benthic animals, oxygen could promote animal-driven mixing of sediments. However, as bioturbation ventilates the sediments, less phosphate is released from the sediments back into the water column resulting in decreased nutrients for primary producers and, thus, decreased atmospheric O₂ production (7). In addition to O₂ availability, food availability for prey is another factor that can drive predator–prey evolution toward greater diversity (12), but periods with high nutrient levels also can drive expansive ocean anoxia and limit the animal habitable zone. Therefore, we can envision animal proliferation to be correlated to either rises in surface O₂ availability, increasing productivity, or declining seafloor anoxia. Alternatively, if food and O₂ availability in the marine realm played only a subordinate role in the radiation, we may discover that radiation was not driven by environmental change and could simply result from new biological innovations and styles of interactions (13).

Attempts to test the food and oxygenation hypotheses have given ambiguous results (7, 9, 14, 15), in part due to insufficient spatial and/or temporal resolution of the available paleo-O₂ and paleoproductivity proxies. To fill this gap, we compiled a record of global seafloor oxygenation constrained by high-resolution uranium isotope data in marine carbonates from the Terreneuvian Series of the Cambrian (∼539 to 521 Ma). Furthermore, we model an atmospheric pO₂ curve from carbon, sulfur, and strontium isotope records in the same sedimentary sequences to constrain variations in O₂ availability in the surface oceans through time. We propose to use these records in combination to indirectly constrain O₂ consumption within the ocean interior, which, to a first order, is a function of the size of the global marine nutrient pool that controls new marine biomass production. With global estimates on how net productivity and O₂ availability in the early Cambrian ocean varied through time, we explore potential causal relationships between the availability of food, O₂, and animal radiations by comparing geochemical and paleobiological records from the same sedimentary successions.

The Uranium Isotope Proxy for Global Seafloor Oxygenation

The uranium isotope composition (δ²³⁸U, the permil deviation of the ²³⁸U/²³⁵U ratio relative to the CRM 145 standard) of seawater is a promising global oxygenation proxy because of its sensitivity to ocean oxygenation at a globally integrated scale. This attribute results from the uniform δ²³⁸U distribution in the well-mixed oceans and a strong U isotope fractionation that occurs when sediments are buried in anoxic environments (16–18). Model calculations suggest that oceans still would have been homogeneous in U isotope composition during the Cambrian, despite potentially greater U burial in anoxic settings that were generally more common at the time (19). The δ²³⁸U proxy has been applied to better constrain oceanic anoxic events (OAEs) in the past and reliably recorded negative δ²³⁸U excursions at times when anoxic water masses expanded in the oceans (19–23). The OAEs studied to date are the Cambrian SPICE event (−0.2‰), Late Ordovician extinction (−0.3‰), Frasnian–Famennian extinction (−0.3‰), End Permian extinction (−0.5‰), End Triassic extinction (−0.7‰), and the Cretaceous OAE2 (−0.1‰) (19, 24–28).

The translation of seawater δ²³⁸U into the carbonate rock record has been studied both experimentally and in modern environments (29–32). Uranium exists in the form of uranyl carbonate anions in seawater that are incorporated into primary biogenic carbonate minerals with δ²³⁸U indistinguishable from seawater (−0.39 ± 0.04‰, 2 SD) (16). As carbonate cements form inside the sediments, they tend to adopt a slightly higher and variable δ²³⁸U value. Even in the very oxic oceans today, many of the pore waters in sediment columns are anoxic. In modern Bahamas bank sediments, uranium reduction occurs near the sediment–water interface allowing for nonquantitative U removal that leaves the bulk sediments on average +0.24 ± 0.14‰ (1 SD) heavier than overlying seawater (29–31). The scatter in this offset is not well understood but should be linked to the ability of dissolved U to escape from the sediments. The precursor sediment in the Terreneuvian oceans included both aragonite and calcite phases (33). Today, metastable aragonite and high-Mg calcite are preserved even at several hundred meters of burial depths (34), so U release from these phases would correspondingly occur at these depths. The dissolution process itself causes no U isotope fractionation (32), but the subsequent U(IV) incorporation into secondary and more stable calcite phases does cause U isotope fractionation (35), as may calcite recrystallization under pore water conditions distinct from seawater (36). In all cases, the U isotope fractionation is only expressed in the remaining sediments if U escapes from the system (e.g., in a “fluids-buffered” system as opposed to “rock-buffered” with respect to U). Apart from oxidative weathering in the meteoric vadose zone, where dissolved U(VI) exists, diagenetic alteration at depth appears to induce no systematic changes in δ²³⁸U, presumably because of the low solubility of U(IV) phases that form already at very shallow burial depths (29–31). In this study, we use petrography and various diagenetic proxies (including Mn/Sr, Sr/Ca, Mg/Ca, and δ¹⁸O) that also are affected by the fluid vs. rock-buffered style of diagenesis. This enabled us to identify samples with the smaller diagenetic δ²³⁸U offset from contemporaneous seawater. Furthermore, we also adopt a high-stratigraphic resolution sampling strategy (∼10 per Ma) recommended to correct for stochastic effects in the reconstruction of secular changes in seawater δ²³⁸U from bulk carbonate sedimentary rocks (30).

The Carbon, Sulfur, and Strontium Isotope Proxy for Atmospheric Oxygenation

The combination of carbon, sulfur, and strontium isotope records from shallow carbonate sediments potentially record global changes in the chemical composition of the oceanic reservoir, and if that is the case, these proxies allow us to reconstruct variations in the atmospheric O₂ budget during the Terreneuvian (∼539 to 521 Ma) using a simple mass balance approach for these marine element cycles (37, 38). At this time, 2 of the largest positive carbon isotope excursions of the Phanerozoic are recorded in marine carbonate sediments worldwide (33, 39, 40). We recognize that part of the geochemical signals from shallow carbonates reflects local and/or diagenetic processes, and a major task is to further develop ways to tease apart these local signals from the global. However, in some cases where the inferred seawater isotope trajectories covary over approximately million-year timescales consistent with the respective oceanic residence timescales, we ask what we expect to see, if these signals record global change. The principal atmospheric O₂ sources, organic carbon and pyrite burial in marine sediments, are constrained from the seawater δ¹³C and δ³⁴S records, whereas atmospheric O₂ sinks (mainly reducing gasses emanating from Earth’s interior) and oxidative weathering on land are assumed proportional to changes in weathering fluxes on land, constrained by the ⁸⁷Sr/⁸⁶Sr record (41).

The changes in atmospheric O₂ sourced from the marine carbon cycle are calculated from organic carbon burial flux (J_ORG) in excess of oxidative carbon weathering:

$$\mathrm{d}{\mathrm{M}}_{\mathrm{O}2\left(\mathrm{C}\right)}/\mathrm{dt}={\mathrm{J}}_{\mathrm{ORG}}–{\mathrm{J}}_{\mathrm{W}\left(\mathrm{C}\right)}·{\mathrm{R}}_{\mathrm{ORG}}.$$ [1]

Furthermore, we assume that total oxidative carbon weathering flux is proportional to continental weathering of carbon bearing rocks [J_W(C)] and the organic proportion of carbon undergoing weathering (R_ORG). A similar equation describes the O₂ equivalent released from the marine sulfur cycle (see details in SI Appendix).

If the carbonate δ¹³C record is related to the global dissolved inorganic carbon pool, then the global organic carbon burial flux is calculated from the shallow marine water δ¹³C record (abbreviated δ_C) and its derivative (dδ_C/dt) as a function of average C isotope offset between seawater and buried organic matter (Δ_C), δ¹³C of weathering input [δ_W(C)], and the oceanic C inventory (M_C) (37):

$${\mathrm{J}}_{\mathrm{ORG}}=1/{\mathrm{\Delta }}_{\mathrm{C}}\left[{\mathrm{J}}_{\mathrm{W}\left(\mathrm{C}\right)}\left({\mathrm{\delta }}_{\mathrm{W}\left(\mathrm{C}\right)}–{\mathrm{\delta }}_{\mathrm{C}}\right)–\mathrm{d}{\mathrm{\delta }}_{\mathrm{C}}/\mathrm{dt}\cdot {\mathrm{M}}_{\mathrm{C}}\right].$$ [2]

A similar relationship for the marine sulfur cycle (Eq. 14) constrains total pyrite burial from the seawater δ³⁴S record. The total change in atmospheric pO₂ is modeled by summation of the integrated O₂ flux from the marine cycles of carbon (Eq. 1) and sulfur (Eqs. 15 and 16). In this way, we let the isotope curves drive changes in atmospheric O₂ from the excess O₂ production via sediment burial relative to O₂ destruction via oxidative weathering. Subsequently, we explore the governing feedbacks at play.

The consumption of O₂ through oxidative weathering of organic carbon and pyrite (Eqs. 1 and 16) is allowed to vary in proportion to the global continental weathering rate, which is proportional to the continental Sr runoff [J_W(Sr-R)] obtained from simultaneously fitting the strontium isotope evolution of seawater, R_Sr = (⁸⁷Sr/⁸⁶Sr)_seawater:

$$\mathrm{d}{\mathrm{R}}_{\mathrm{Sr}}/\mathrm{dt}=1/{\mathrm{M}}_{\mathrm{Sr}}\left[\left({\mathrm{R}}_{\mathrm{Sr}-\mathrm{R}}–{\mathrm{R}}_{\mathrm{Sr}}\right)·{\mathrm{J}}_{\mathrm{W}\left(\mathrm{Sr}-\mathrm{R}\right)}+\left({\mathrm{R}}_{\mathrm{Sr}-\mathrm{DC}}–{\mathrm{R}}_{\mathrm{Sr}}\right)·{\mathrm{J}}_{\mathrm{W}\left(\mathrm{Sr}-\mathrm{DC}\right)}+\left({\mathrm{R}}_{\mathrm{Sr}-\mathrm{HT}}–{\mathrm{R}}_{\mathrm{Sr}}\right)·{\mathrm{J}}_{\mathrm{W}\left(\mathrm{Sr}-\mathrm{HT}\right)}\right],$$ [3]

(see derivation in SI Appendix). Although, the Sr isotope constraint depends on boundary conditions, including average isotope compositions (R_x), marine Sr inventory (M_Sr), and fluxes of major sources (J_W,x), including continental rock weathering (Sr-R), diagenetic carbonates (Sr-DC), and hydrothermal Sr input (Sr-HT), this equation tells us that the long-term changes in continental weathering fluxes compared to other oceanic Sr sources were actually quite modest during the Terreneuvian.

Samples

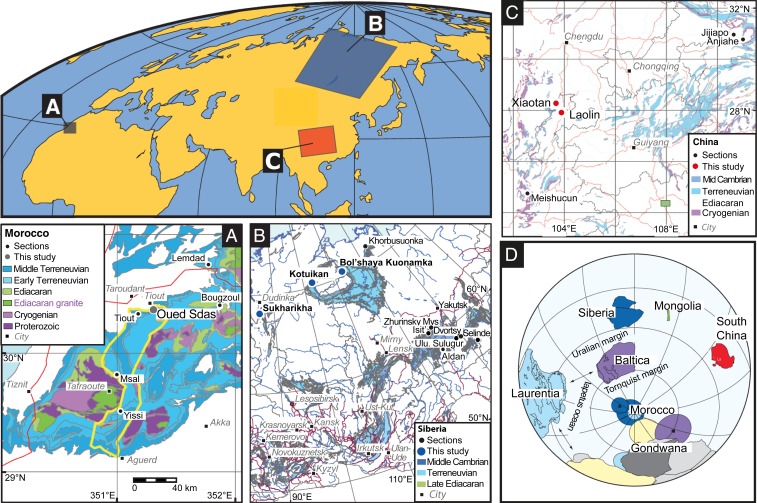
Samples and geological settings are described in Methods. Briefly, we analyzed δ²³⁸U in 187 (and δ³⁴S in 93) marine carbonate rock samples deposited at 6 different localities across 3 paleocontinents during the Terreneuvian when small animals with skeletons and shells diversified in the oceans (Fig. 1). The sections from Xiaotan and Laolin in China, and from the Kotuikan River and the upper part of Sukharikha River in Siberia, mainly consist of limestone with low Mn/Sr, whereas the Kuonamka River section in Siberia displays atypically low U contents, and the Oued Sdas section consists mostly of dolostones. Together, these sections cover most of the Terreneuvian time interval, and specifically record 2 massive perturbations in the marine carbon cycle of hitherto-unknown biogeochemical affinity, manifested as large (>5‰) positive carbon isotope excursions recognized globally in carbonate sediments and in our studied sections (33, 39, 40). The ages of the sediments were approximated using a global age model (33, 40) with minor modifications that combines worldwide chronostratigraphic, biostratigraphic, and chemostratigraphic data worldwide (SI Appendix, Fig. S1).

Fig. 1.

Sample localities and sections in (A) Morocco, (B) Siberia, and (C) South China and (D) paleogeographic reconstruction for ∼525 Ma, modified after ref. 33 (but see alternative reconstruction in ref. 74).

Results

Uranium Isotopes.

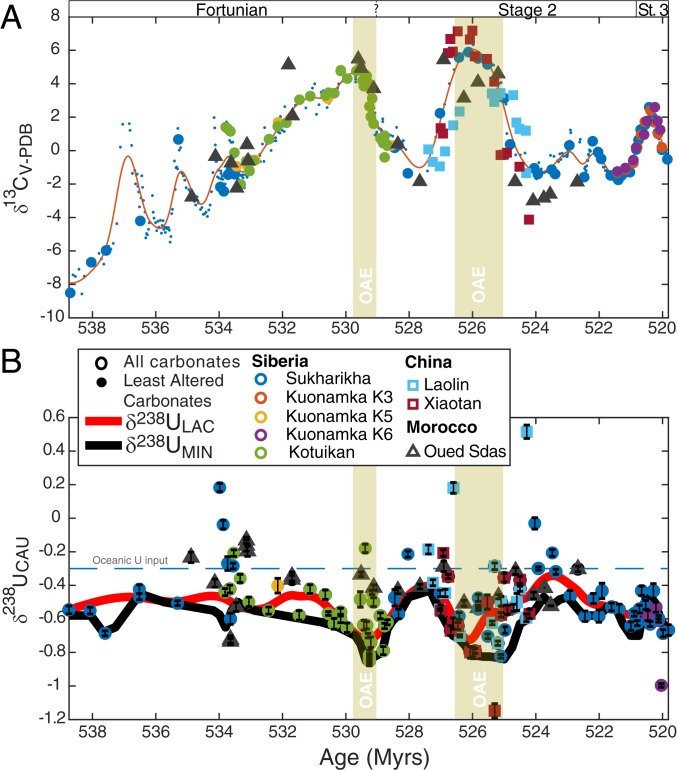
Our U isotope data are plotted as a function of time in Fig. 2, and as a function of stratigraphy at each locality in SI Appendix, Figs. S2–S5 and S7. There is a clear systematic coupling between the marine carbon and uranium isotope records, expressed as large, negative δ²³⁸U excursions (of magnitude −0.4‰) correlated with positive carbon isotope excursions (δ¹³C). This coupling occurs in several sections worldwide and is not expected for any known diagenetic processes. Furthermore, the large isotope oscillations do not correspond to geochemical and petrographic signals of diagenetic alteration. Instead, we suggest these events were associated with global expansions of anoxic water masses in the oceans.

Fig. 2.

(A) Carbon and (B) uranium isotope data of carbonate associated uranium (δ²³⁸U_CAU) during the Terreneuvian (∼539 to 521 Ma). Stratigraphic correlations are obtained at estimated ±1-My relative age resolution using carbon isotope chemostratigraphy, consistent with biostratigraphic records, and tuned to the age-model obtained from chronostratigraphic constraints in Morocco and China (33) (see SI Appendix for details). An interpolated curve through minima (δ²³⁸U_MIN, black curve) represents the best estimate of the composition of Terreneuvian seawater, and it parallels the smoothing spline fit obtained through least altered carbonates (LAC) (δ²³⁸U_LAC, red curve). The δ²³⁸U_LAC and δ²³⁸U_MIN curve carry smaller average offsets from coeval seawater than average marine carbonates (∼0.1 to 0.2‰ and ∼0.0 to 0.1‰, respectively). The composition of the oceanic input is assumed to be similar to modern rivers and continental rocks at −0.30‰ (18).

That said, the δ²³⁸U record shows both systematic oscillations and single outliers reflecting a combination of secular changes in seawater chemistry and isotope variability likely generated locally during diagenetic modifications within the sediments. Although the vast majority of our samples experienced a low degree of diagenetic alteration, recorded as Mn/Sr < 1 and no dolomite (Mg/Ca < 0.1), samples with a more fluid-buffered (open-system) diagenetic alteration signature also are associated with distinctly higher average δ²³⁸U (+0.14‰) compared to the least altered samples (P < 0.01 for both measures; see SI Appendix for details). Accordingly, we also find that samples with Sr/Ca below the median indicative of Sr (and U loss) through open-system diagenesis on average display +0.11‰ higher mean δ²³⁸U value (P < 0.01 for all 3 measures; see SI Appendix for details). This offset is within the range occurring during syndepositional or very early diagenesis on the modern Bahamas banktop (+0.24 ± 0.14‰, 1 SD), suggesting the least altered samples are, on average, ∼0.1‰ closer to contemporaneous seawater than modern carbonates are to modern seawater (29, 31, 36). We use a smoothing spline fit through the least altered carbonate samples and obtain a coherent curve, δ²³⁸U_LAC, and compare this signal to a curve obtained by interpolation between the lowest δ²³⁸U values within 0.4-My intervals, δ²³⁸U_MIN, representing samples with the smallest offset from contemporaneous seawater. The offset between these 2 curves is on average ∼0.1‰, which means that δ²³⁸U_MIN, on average, is even closer to contemporaneous seawater and resembles δ²³⁸U of Terreneuvian seawater with only a small average offset of 0.09‰ (SI Appendix, Fig. S9). In fact, the scatter in Terreneuvian samples matches well with that observed in modern carbonates. Importantly, the δ²³⁸U_MIN and δ²³⁸U_LAC curves are parallel and both capture the major oscillations. Therefore, we infer that δ²³⁸U_MIN best resembles secular variability in Terreneuvian seawater with values between −0.9‰ and −0.4‰, and we adopt a conservative uncertainty estimate of ±0.14‰ at any given time step (1 SD).

Carbon, Sulfur, and Strontium Isotopes.

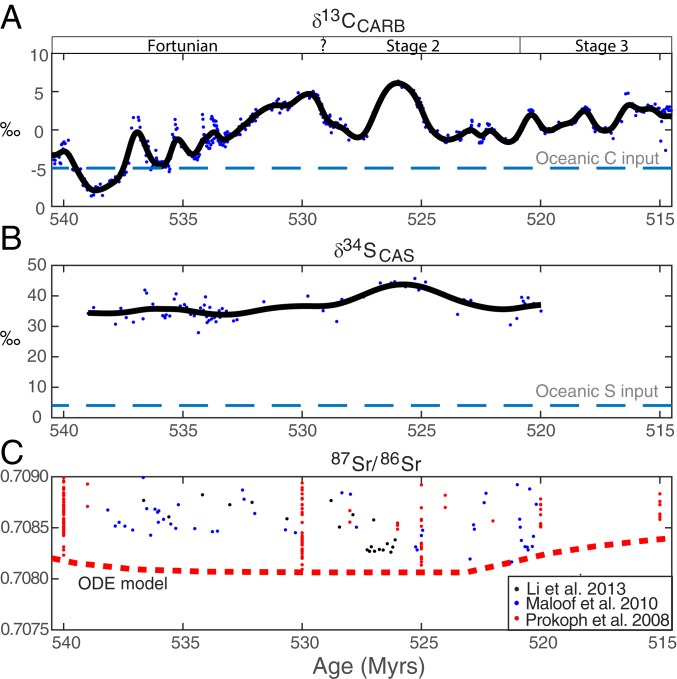
Published carbon isotope records from Mongolia, Siberia, China, and Morocco provide the chemostratigraphic framework for the age model (SI Appendix, Fig. S1) (33, 39, 40, 42). Our uranium isotope data are negatively correlated to the 2 largest positive δ¹³C excursions (>4‰) characteristic of expansions of marine anoxia at the global scale. This correlation is robust, even if the age model is altered.

To constrain changes in the Earth’s atmospheric O₂ budget, we use the carbon isotope data (δ¹³C_CARB) and compiled sulfur isotope data of carbonate-associated sulfur (δ³⁴S_CAS) from the same carbonate rocks where ⁸⁷Sr/⁸⁶Sr, and δ²³⁸U_CAU also are recorded. The δ³⁴S_CAS data (Fig. 3) shows persistently high values (30 to 45‰) in Terreneuvian seawater compared to modern seawater and carbonate banktop sediments (21‰) (43) that are weakly correlated to the δ¹³C_CARB excursions. The δ³⁴S data fills major gaps in the existing sulfur isotope record (44, 45). There is no covariation between δ³⁴S_CAS and diagenetic indicators. If the δ³⁴S_CAS record resembles the isotope composition of overlying seawater sulfate, then the high δ³⁴S_CAS values indicate that pyrite burial accounted for the majority of total marine sulfur burial (∼60 to 100%). This calculation assumes the marine sulfur cycle was at steady state and that the δ³⁴S of oceanic input (4 to 8‰) and average isotope offset of buried pyrite relative to contemporaneous seawater (35‰) were similar to modern day (Dataset S3).

Fig. 3.

Isotope composition of carbonate-associated (A) carbon (δ¹³C_CARB) (39, 46, 75), (B) sulfur (δ³⁴S_CAS; this study), and (C) strontium (⁸⁷Sr/⁸⁶Sr) (33, 46, 76). Smoothing splines were fitted through the data in A and B to represent the chemical evolution of seawater. Diagenetic effects are known to shift ⁸⁷Sr/⁸⁶Sr to higher values than contemporaneous seawater, so the Sr isotope composition of latest Ediacaran to Terreneuvian seawater would evolve through minimum values of available records. The red dotted curve represents the seawater ⁸⁷Sr/⁸⁶Sr calculated from the weathering forcings in Fig. 5 and the ordinary differential equation “ODE model” described in Eq. 3.

Published strontium isotope data from sedimentary carbonates through the Neoproterozoic–Cambrian interval show a long-term ⁸⁷Sr/⁸⁶Sr decline from ∼550 Ma indicative of enhanced basaltic weathering, perhaps by increased seafloor spreading or warming abyssal waters (33, 46) that was finally broken at the inflection point around ∼524 Ma, suggesting the relative amount of continental versus seafloor weathering increased (Fig. 3C). A simple model for the marine Sr budget shows that a 20% increase in continental weathering relative to basaltic weathering alone is sufficient to cause the inflection at ∼524 Ma (see details in SI Appendix).

Discussion

Massive Expansions in the Extent of Seafloor Anoxia.

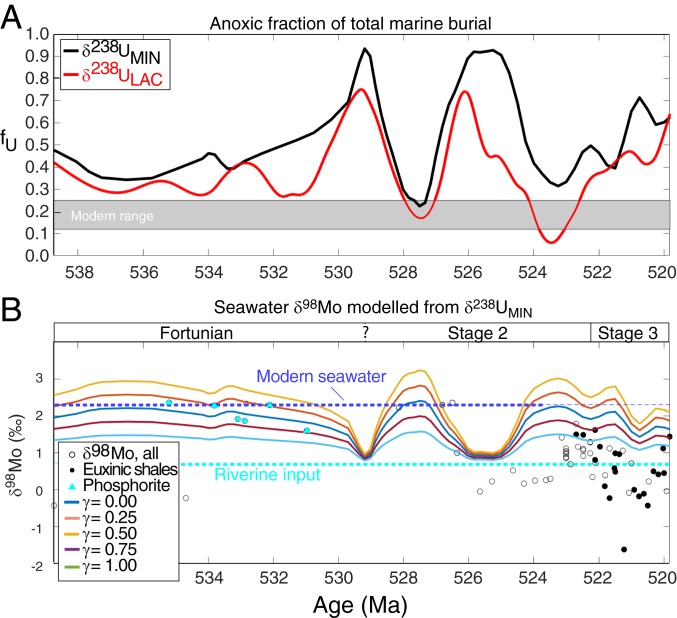
The uranium isotope record indicates that the modeled oxygenation state of the early Cambrian oceans was neither steady nor monotonous (7–9, 47, 48), but rather oscillated dramatically in concert with changes to the global marine carbon cycle as indicated by the δ¹³C curve. Fig. 4A shows the calculated proportion of total marine U burial occurring in anoxic marine settings (f_U) from the estimated seawater δ²³⁸U trends. The calculation assumes a constant U input from rivers and a constant isotope fractionation between seawater and the U sinks. The change in weathering regime favoring more granitic than basaltic rock weathering should not affect the concentration or isotope composition oceanic input (18, 49). The modern oceans have a homogenous δ²³⁸U composition of −0.39 ± 0.04‰ (all errors are 2 SE) slightly below riverine input and crustal rocks (−0.30 ± 0.03‰) due to isotope fractionation occurring when U is buried in reducing sediments (18). Given that 12 to 25% of marine U burial occurs in anoxic sediments with a large positive +0.5 ± 0.1‰ offset from seawater today, all other U sinks (mainly carbonates and reducing sediments below oxic waters) carry an average isotopic offset of −0.01 ± 0.06‰ (18, 45, 50). Applying these constants to the Terreneuvian implies that the early Fortunian (∼539 to 532 Ma) oceans were initially less oxygenated than today (δ²³⁸U = −0.6 ± 0.1‰, f_U = 59 ± 27%). Over millions of years, the modeled oxygenation state of the oceans oscillated between extreme anoxia and extreme oxia with respect to marine U cycling. At peak anoxia, essentially all marine U burial occurred in anoxic settings (δ²³⁸U = −0.80 ± 0.05, f_U = 100 ± 28%) and oceans were as oxygenated as today during peak oxia in the immediate aftermath of the events (f_U ∼ 18 ± 16%, δ²³⁸U = −0.40 ± 0.05‰). In the latest part of the Terreneuvian (“Tommotian,” ∼525 to 521 Ma, f_U = 69 ± 22%, δ²³⁸U = −0.65 ± 0.05‰), oceans returned to an intermediately anoxic state before the major radiation of arthropods, when a brief and dynamically distinct ocean oxygenation episode is inferred from Siberian sections at 521 to 520 Ma, as seen in Figs. 2B and 4A (45).

Fig. 4.

(A) The fraction of total anoxic sediment burial obtained from the δ²³⁸U record (f_U) and (B) predicted δ⁹⁸Mo evolution of Terreneuvian seawater. The best estimated f_U (A, black curve) is obtained from δ²³⁸U_MIN and a conservative underestimate obtained from δ²³⁸U_LAC is shown for comparison in red. (B) Seawater δ⁹⁸Mo curves predicted from the δ²³⁸U_MIN (via f_U) according to Eqs. 8 and 9 for various γ, where γ is the Mn-oxide proportion of all oxic Mo burial. A high γ-value (0.75 to 1.0) is inferred before the OAEs and lower γ (0.25 to 0.5) is acceptable after ∼525 Ma. Since euxinic shales are fractionated to lower δ⁹⁸Mo values than overlying seawater during nonquantitative Mo removal, this U–Mo isotope comparison suggest that δ⁹⁸Mo in ∼90% of the samples must have been fractionated by −2 to −1‰ relative to contemporaneous open oceans. The local fractionation occurs in settings where total hydrogen sulfide levels are either low or only intermittently present (e.g., <100 µM at pH = 8). A few samples (1 phosphorite and 3 shales of unknown redox affinity) plot in the forbidden zone above the predicted curves. However, the uncertainty of the age is large enough (±1 My or more) that this is an artifact of imprecise correlation between the siliciclastics and carbonate sedimentary records, when biostratigraphy is poor.

A first-order estimate for the areal proportion of anoxic seafloor (A_ANOX) can be derived from f_U and the ratio of average U burial rates in anoxic and oxic continental shelf settings (r_ANOX/r_OX = 15 ± 10; SI Appendix):

$${\mathrm{r}}_{\mathrm{ANOX}}{\mathrm{A}}_{\mathrm{ANOX}}/{\mathrm{r}}_{\mathrm{OX}}\left(1–{\mathrm{A}}_{\mathrm{ANOX}}\right)={\mathrm{f}}_{\mathrm{U}}/\left(1–{\mathrm{f}}_{\mathrm{U}}\right).$$ [4]

The estimated seafloor area only includes areas where sedimentation occurs at rates relevant for continental shelves, since anoxia in areas with little or no sediment accumulation will go undetected. The U burial fluxes in oxic and anoxic settings are assumed to scale with seawater uranium concentration in a similar fashion and therefore cancel out in Eq. 4. The resulting anoxic seafloor coverage on a sedimentation-weighted basis is shown in Fig. 6B. During peak anoxia, we find that anoxic water masses might have expanded across 70 to 80% of the continental shelf areas.

Fig. 6.

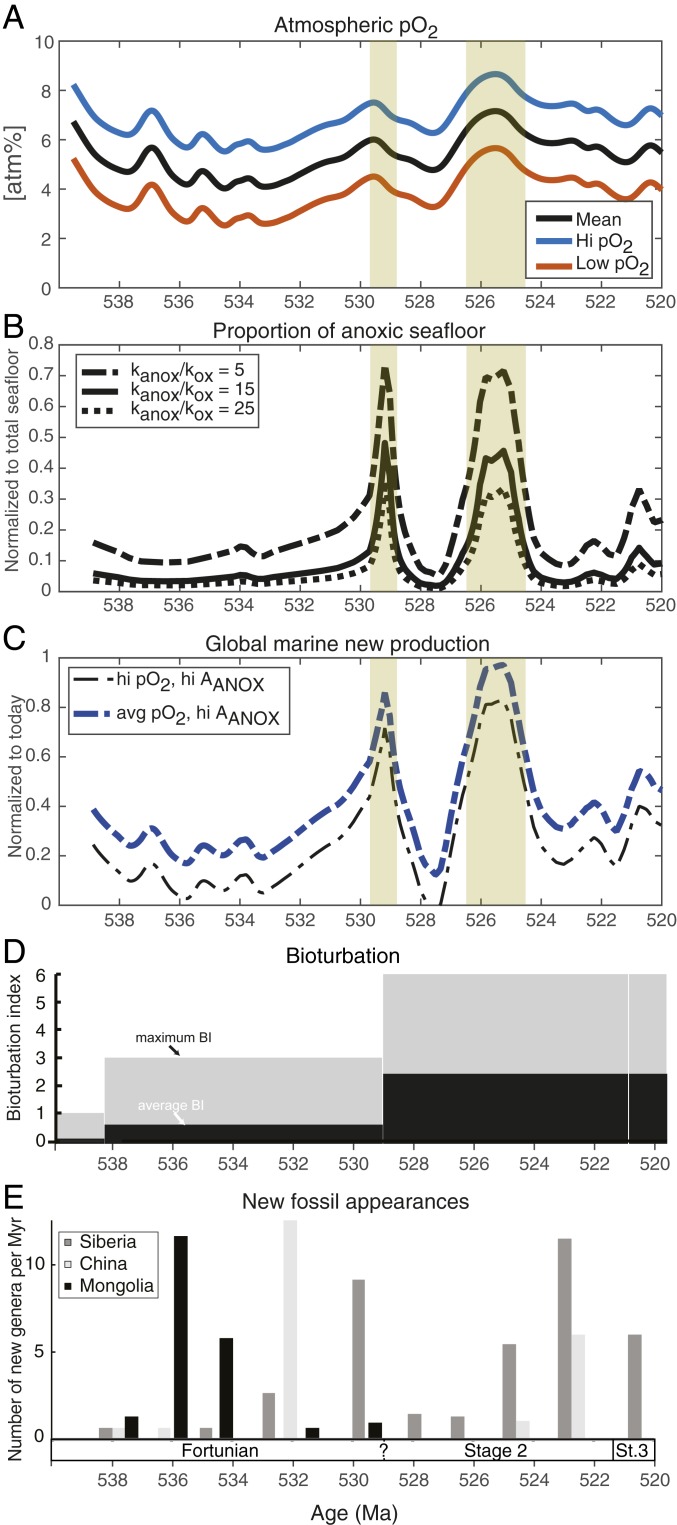
Comparison of O₂ levels on Earth, inferred new productivity, and animal biodiversification. (A) Simulated atmospheric pO₂ (from Fig. 5D) with absolute uncertainty shown in red and green. (B) The proportion of anoxic seafloor (A_ANOX) is calculated from f_U (from Fig. 4A) using a linear relationship between oxic and anoxic burial fluxes and their respective areal coverage, and anoxic U burial rates that are 15 ± 10 times higher than in oxygenated settings (see SI Appendix for details). (C) Estimated global marine new production normalized to modern day using the average and high pO₂ estimate (black and blue curves in A) and the high A_ANOX estimate (dashed curve in B). Other combinations of pO₂ and A_ANOX curves leads to erroneous low productivity at times and have been omitted. (D) Average bioturbation index (scale: 1 to 6) and maximum bioturbation index (59). (E) Number of new animal genera appearing in 2-My time bins during the Terreneuvian (33, 40). After 520 Ma, animal diversity further explodes (>10-fold) (77, 78).

These OAEs in the Terreneuvian would have affected all redox-sensitive metal marine cycles and their isotopes. For example, the oceanic U inventory is predicted to decrease ∼2- to 4-fold during some Phanerozoic OAEs, due to higher U removal rate in anoxic settings relative to oxic settings (19, 23, 51). Interestingly, uranium enrichments in Moroccan carbonates systematically oscillate with about the predicted amplitude in concert with the putative Terreneuvian OAEs (see details in SI Appendix) (33). However, most other sections do not show clear stratigraphic patterns in U contents and U/Th ratios. A dramatic increase in U abundances in shales has been interpreted as evidence for Terreneuvian ocean oxygenation (8). However, the U content in both carbonates and shales predominantly reflect processes in the local depositional environment that affect the U content of sediments more than the subtle variations in the size of the marine U inventory. For example in carbonates, the U content can vary 100-fold depending the relative abundances of primary carbonate minerals and the extent of early diagenetic U loss. U enrichments found in shales are dependent on their total organic carbon content (52). A careful inspection of the U shale record on a total organic carbon-normalized basis and statistical analyses (SI Appendix, Fig. S11) allows us to reject a previous conjecture that the oceanic U inventory steadily increased from the Neoproterozoic into the Cambrian (8).

The changes in global ocean oxygenation state can be independently verified in the molybdenum isotope record, especially if hydrogen sulfide was abundant in the expanding anoxic water masses. This connection appears because both molybdenum and uranium are well-mixed elements in the oceans, and the isotope compositions of seawater (δ⁹⁸Mo, δ²³⁸U) are both positively related to the proportion of global sediment burial in oxygenated settings. Local processes tend to drive the 2 isotope systems in opposite directions, such that the carbonate δ²³⁸U record is equal to or higher than seawater δ²³⁸U, therefore overestimating global ocean oxygenation, whereas the δ⁹⁸Mo record in shales adopt seawater δ⁹⁸Mo or lower values, therefore underestimating global ocean oxygenation. In principle, this relationship means that the combination of the two isotope systems brackets the global ocean oxygenation state. In Fig. 4B, we show the predicted seawater δ⁹⁸Mo curves derived from the δ²³⁸U record if changes in seawater composition were dictated primarily by sediment burial in anoxic marine settings (details in SI Appendix). The comparison of model and data suggests that ∼90% of all shale samples carry a −1 to −2‰ offset of the δ⁹⁸Mo values relative to the predicted seawater δ⁹⁸Mo composition, in good agreement with observations from modern open marine euxinic settings (45). A few samples plot in the forbidden zone above the modeled seawater δ⁹⁸Mo curves. However, this offset can be ascribed to inaccurate age assignment of the shales (up to ∼1 to 2 My), since there is no chemostratigraphic or chronostratigraphic control that can be used to correlate the siliciclastic sediments to the carbonate record at this temporal resolution. Therefore, the δ²³⁸U record from carbonates can be viewed as superior to the existing shale-based Mo isotope record in terms of reliably recording secular changes in global extent of seafloor oxygenation.

Nevertheless, the δ⁹⁸Mo record and model independently verify the large oscillations in marine oxygenation and have low values, similar to the Proterozoic average (∼1.0‰), during peak anoxia and values as high as the modern (up to 2.3‰) during peak oxia, corresponding to the proportion of oxic Mo removal that occurs with marine Mn-oxide burial. The Mo isotope data demand a substantial Mn-oxide sink for Mo before and between the OAEs (25 to 75%) comparable to today (41 ± 3%) and somewhat smaller (0 to 25%) after the OAEs (53). As a large part of this Mo sink occurs in the deep abyssal oxygenated settings in the ocean today, the high Mo isotope values (>1.5‰) before and in between OAEs suggest that oxygenation was a global phenomenon that expanded well beyond the continental shelves and into the deep ocean where Mn-oxide deposition is common in oxygenated areas (14).

Atmospheric pO₂ Decline, Oscillations, and Modest Rise in the Terreneuvian.

We now turn to the question of whether seafloor oxygenation was linked to changes in atmospheric O₂ levels. Although, the C, S, and Sr isotope records do not uniquely determine absolute atmospheric pO₂, and shelfal processes and diagenesis might push these signals in different directions, our point here is to emphasize that a straightforward solution to the observed dynamics exists that consistently fits with all observed isotope records and with our current understanding of the governing feedbacks between atmospheric and oceanic oxygen levels.

Atmospheric O₂ production (Fig. 5E) results from global organic carbon and pyrite burial fluxes that can be calculated from marine carbon and sulfur isotope mass balance (37). Solving for the burial fluxes requires both the isotope records and their first time derivative. To avoid amplification of noise in the derivative curves, we first smoothed the δ¹³C_CARB and δ³⁴S_CAS records using cubic smoothing splines. The splines represent a visual best fit to the data (Fig. 3) and preserve the important timing and magnitudes of observed excursions.

Fig. 5.

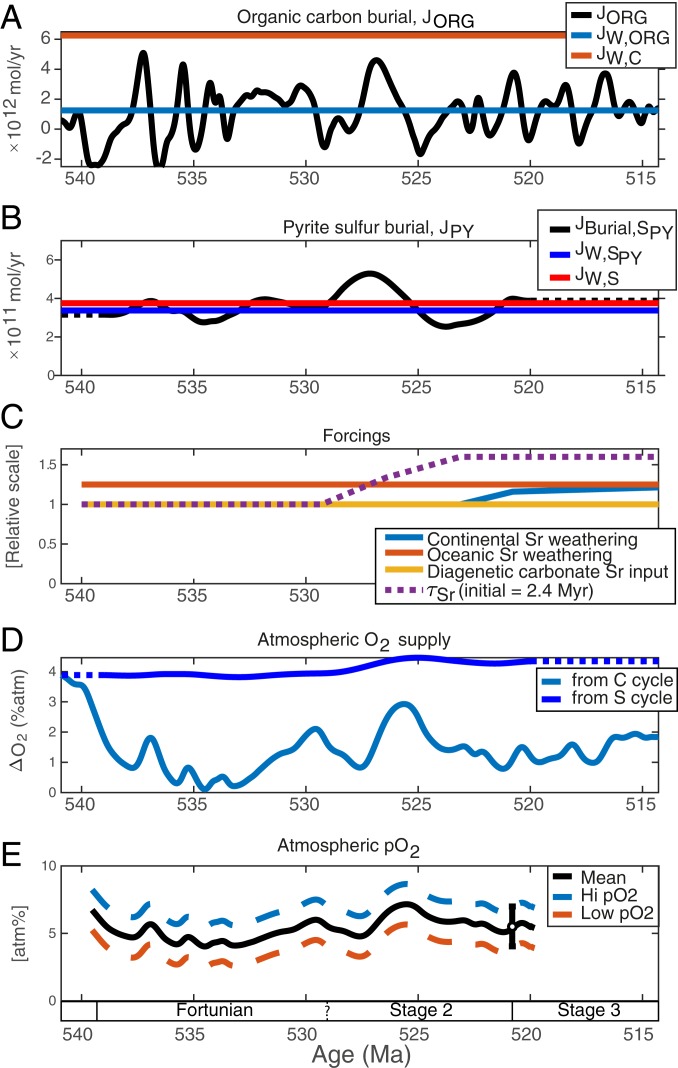
Atmospheric O₂ levels in the Terreneuvian is simulated from (A) organic carbon burial (Eqs. 1 and 2) and (B) pyrite sulfur burial (Eqs. 11 and 12) using typical Cambrian parameter values (Dataset S3) obtained from seawater carbon and sulfur isotope curves and forced by a shift toward more continental weathering 524 to 523 Ma. (C) The weathering fluxes forcings applied to fit the Sr isotope data in Fig. 3 is shown together with the expected oceanic Sr residence time. (D) O₂ release to the atmosphere from organic C burial (light blue) and pyrite S burial (blue) are the principal sources of atmospheric O₂. In combination with global O₂ removal through oxidative weathering (blue curves in A and B), we estimate atmospheric pO₂ change. (E) The absolute atmospheric pO₂ curve (black) is fit to a model-dependent constraint at 521 Ma 4 to 7 atm% (black, dashed curves). A shift from preferential aragonite to calcite precipitation in the ocean ∼525 Ma (here shown a few million years too early to distinguish the effect from enhanced weathering) would have changed the Sr residence time (33), but has no effect on the atmospheric pO₂ curve. Note that enhanced weathering both affects atmospheric O₂ supply through sediment burial and atmospheric O₂ removal through oxidative weathering, and therefore has little effect on atmospheric pO₂ in this model.

Continental weathering of phosphorous (P) modulates global marine productivity, organic carbon burial, and atmospheric O₂ levels on our planet because P is the biolimiting nutrient in the oceans over million-year timescales, where atmospheric O₂ levels change. In the absence of mycorrhizal symbionts that amplify P weathering by plants on the continents today, the Terreneuvian P weathering rate would have been lower than today (54). We fixed P weathering at one-quarter of the modern-day value and explored the O₂ dynamics required by the isotope records. The relative proportion of continental vs. basaltic weathering varied in a fashion that affected the strontium isotope composition of seawater (Fig. 3C, dotted red curve). High rates of seafloor spreading and ocean crust alteration during the early Terreneuvian is suggested to account for the ⁸⁷Sr/⁸⁶Sr decline and arguably lowered seawater Mg/Ca to the extent that calcite rather than aragonite predominantly precipitated in the marine realm from ∼524 Ma and well into the Paleozoic (33, 55). The inflection in the strontium isotope record at this time fits with a modest ∼20% relative increase in continental weathering, and this estimate is unaffected by the higher Sr residence times in calcitic seas (Figs. 3C and 5). The concentrations of dissolved inorganic carbon and sulfate in early Cambrian seawater have been estimated to ∼9 and ∼1 mM, respectively (33, 45, 56), and the organic carbon and pyrite proportions of weathered material are kept constant at characteristic values for marine sediments at this time (R_ORG,W = 0.20, R_PY,W = 0.90). A sensitivity analysis shows that the atmospheric pO₂ trajectory depends strongly on the absolute P weathering rate, the average proportions of organic carbon to total carbon burial and pyrite sulfur to total sulfur burial in weathering products and, to a lesser degree, the oceanic sulfate pool (Dataset S3). Although these parameter values affect the baseline atmospheric pO₂ level and the amplitude of pO₂ change, they cannot drive the observed dynamics. The age model is uncertain, and that also affects the predicted atmospheric pO₂ trajectory, but we suggest that the general features discussed below are robust. The change in continental weathering at ∼524 Ma only had little influence on simulated atmospheric pO₂ because weathering promotes both O₂ consumption by oxidative weathering and O₂ production by organic carbon sediment burial in our model (Fig. 5D). The calculated pyrite burial flux is rather stable and acts as an O₂ source throughout the Terreneuvian. The calculated organic C burial flux varies dramatically through the early Terreneuvian and occasionally yields erroneous, negative values for brief periods when seawater δ¹³C dropped rapidly to values below volcanic input of −5‰. These intervals are attributed to preferential oxidative weathering with excess organic carbon delivering carbon with lower δ¹³C signature into the oceans and acting as an O₂ sink at these times.

The changes in atmospheric pO₂ are reconstructed from the isotope records, but the absolute pO₂ levels are difficult to constrain. We anchored the atmospheric O₂ curve on a recent model-dependent constraint of 4 to 7 atm% at ∼521 Ma (45). Remarkably, in light of the simplicity and uncertainty of the model, this approach readily leads to a physically reasonable (nonzero) atmospheric pO₂ curve. The resulting atmospheric pO₂ trajectory shows a notable decline from ∼7 atm% at the Precambrian–Cambrian boundary to a minimum of ∼4 atm% ∼533 Ma followed by rising O₂ levels during the OAEs before ultimately settling at ∼6 atm% after the second OAE.

Global New Production.

To distinguish between reduced O₂ supply from the atmosphere or O₂ removal within the oceans as the key driver for expanding ocean anoxia, we provide an estimate of global marine photosynthetic production, which consumes O₂ as it sinks into the deeper parts of the oceans. The first-order relationship between global marine new production (newp′), global extent of anoxia (A_ANOX) and atmospheric pO₂ (o′) has been obtained from Earth system ocean–atmosphere models (57):

$${\mathrm{A}}_{\mathrm{anox}}={[1+\exp \left(–{\mathrm{k}}_{\mathrm{anox}}.\left[{\mathrm{k}}_{\mathrm{u}}\ast \mathrm{new}{\mathrm{p}}^{\prime }-{\mathrm{o}}^{\prime }\right]\right)}^{-1}.$$ [5]

The constants k_anox = 12, k_u = 0.5 are determined so that 0.25% of the seafloor is overlain by anoxic water masses similar to modern productivity and oxygen levels (newp′ = o′ = 1) and the formula gives a fairly sharp transition of A_ANOX from 23 to 77% as atmospheric pO₂ declines from 13 to 8 atm%, consistent with biogeochemical models for the spatial distribution of oxygen in the oceans (57, 58). Clearly, this relationship would have changed in concert with changes in organic matter export rates and how ocean circulation ventilated the deeper parts of the oceans. Until values for the Cambrian ocean have been established, we suggest that the marine productivity curve obtained this way is qualitatively correct. This approach consistently shows that the Cambrian oceans were distinctly less oxygenated than today due to lower atmospheric pO₂, and that the overall availability of nutrients oscillated in concert with the OAEs.

We observe 3 key qualitative features of the simulated global net biological productivity during the Terreneuvian that help explain the driving mechanism for early Cambrian OAEs (Fig. 6). First, new photosynthetic production and nutrient availability in the early Fortunian slowly declined from the Precambrian–Cambrian boundary until ∼533 Ma in concert with atmospheric pO₂ levels. Second, both OAEs were associated with high nutrient levels promoting massive blooming of phytoplankton worldwide. Third, a significant, albeit small, increase in marine new production after the OAEs did not drive a third expansion of anoxia. Instead, atmospheric pO₂ rise kept pace with the enhanced biological production reaching slightly higher O₂ levels than the Fortunian and resulting in no further expansion of oceanic anoxia.

Driving Factors for Terreneuvian Atmosphere–Ocean Oxygenation Dynamics.

The combination of the simulated global seafloor oxygenation, atmospheric pO₂, and marine productivity allows us to assess plausible first-order causal feedbacks at play in the Earth system during the Terreneuvian.

First, the mutual decline in new photosynthetic production and atmospheric pO₂ are the key features predicted for nutrient burial in ventilated sediments by bioturbating animals (7). Theory predicts that, as animal activities stir marine sediments, they cause the biolimiting nutrient phosphorous to be retained within organic matter and iron oxyhydroxides in marine sediments. Interestingly, the first widespread motile benthic animal communities, plowing horizontally on the seafloor, emerged near the Ediacaran–Cambrian boundary (59, 60). Therefore, we conclude that benthic animal communities may have limited global ocean phosphorous availability, new marine photosynthetic production, and initiated atmospheric pO₂ decline (7).

Second, an increase in marine productivity hit when atmospheric pO₂ levels were at their lowest in the Terreneuvian (e.g., ∼4 atm% at ∼533 Ma). Marine productivity continued to rise and peaked with the first OAE. The prolonged interval leading into the first OAE appears much longer than most OAEs in the Phanerozoic, and in contrast to younger OAEs triggered by volcanism, there is no evidence of extensive volcanism to trigger expansive anoxia at this time (33, 61). Hence, we suggest that limited O₂ supply from the atmosphere could have initiated the expansion of anoxia in some areas of the continental shelves, and that expanding anoxia ultimately continued via an accelerating feedback loop acting to increase productivity by efficient recycling of P released from expanding seafloor areas covered with anoxic bottom waters (62).

The atmospheric pO₂ decline would have slowly made different parts of the oceans more prone to anoxia depending on the productivity, organic carbon export, water circulation, and O₂ supply into the deeper parts of each basin. When sustained for more than ∼10⁵ to 10⁶ y, excess organic carbon burial acts to increase atmospheric pO₂ to levels where P recycling ultimately collapses and ocean basins again experience higher oceanic O₂ supply from the atmosphere (63). Apparently, our modeled atmospheric pO₂ levels show that O₂ increased from 533 to 529 Ma while the ocean anoxia also continued to expand at the globally integrated scale. Thus, atmospheric O2 had to increase significantly above the levels that initiated expansive anoxia in the first place, before runaway anoxia was ultimately halted.

The second OAE indicates that the system did not immediately stabilize itself. Rather, atmospheric pO₂ again crashed to low levels (∼5 atm%) and triggered a second expansion of marine anoxia lasting for another ∼1 to 2 million years. At least 3 potential triggers for the second event exist. First, the Earth system could have entered a state with natural oscillations, as suggested for the Cretaceous OAEs (63). Second, a change in ocean circulation patterns perhaps linked to slowly rising sea levels may have stratified the oceans and made some parts of the oceans more prone to expanding anoxia even without atmospheric pO₂ decline, once again initiating the positive-feedback loop involving P regeneration in anoxic basins (64). Third, benthic animal communities evolved new infaunal feeding strategies in low-energy offshore deposits and extended the maximum burrowing depth and average bioturbation index at this time [Cambrian stage 2, ∼529 to 521 Ma (59); but see ref. 65 for a different view]. Vertical sediment mixing and enhanced irrigation could have accelerated nutrient removal from the oceans into oxidized sediments and set the system out of balance once again, triggering renewed atmospheric O₂ decline.

Notably, the atmosphere–ocean O₂ oscillations did not produce a third event of similar size. Instead, from ∼525 Ma onward, atmospheric pO₂ levels were higher (∼6 atm%) and above the critical levels where O₂ supply had previously initiated OAEs (∼4 to 5 atm%). From ∼524 to 523 Ma onward, the modest expansion of anoxia, unrelated to atmospheric pO₂ decline, we see evidence for increased marine O₂ consumption either due to external nutrient injection (e.g., from the continents) or enhanced nutrient recycling (e.g., by ocean stratification).

In view of a comparatively modest relative increase in continental weathering at this time consistent with the strontium isotope record, we suggest enhanced physical erosion on the continents is a plausible driver that also would have promoted nutrient loading into the oceans as well as sediment burial in deltaic sediments. Deltaic settings are oxygenated and preferentially affect the marine C and S cycle through organic carbon and pyrite sulfur burial (to a greater degree than deltaic burial affects the marine U cycle) (19). As such, sediment burial in deltas preferentially releases O₂ into the atmosphere and surface oceans that may not have balanced the effect that enhanced weathering had on oceanic nutrient loading and seafloor anoxia. In this view, the change in weathering regime interrupted the anoxic oscillations at ∼524 Ma and both increased O₂ and food availability for marine animals from this time onward.

Implications for Animal Evolution.

Atmospheric pO₂ levels dictate the O₂ availability in the surface oceans. For example, air-saturated water at 25 °C with a salinity of 35‰ would, at equilibrium, have an O₂ concentration of ∼50 μmol·kg⁻¹ at 4 atm% pO₂. Our results show that the dissolved O₂ concentration in the Terreneuvian surface ocean would have varied between ∼40 and ∼110 μmol·kg⁻¹, a range well above the level of severe hypoxia ∼9 μmol·kg⁻¹ where carnivorous taxa disappear (8). Hence, the Terreneuvian surface ocean was sufficiently oxygenated to support both predators and prey living in seawater at all times.

To test hypotheses for the coevolution of animal life and the environmental change, we compare our oxygenation and productivity records to records of fossil first appearances during this time (33, 40). The fossil record show 3 or 4 pulses of animal appearances in the Terreneuvian recorded in distinct parts of the world. A first pulse of skeletal animal appearances is recorded in Mongolia 536 to 534 Ma and was soon followed by 1 or 2 pulses in China and Siberia 532 to 530 Ma. This was followed by an interval ca. 530 to 525 Ma with relatively few first appearances, before a final “Tommotian” pulse of appearances began in the late Terreneuvian ca. 525 Ma (Fig. 6E) (33, 40). Looking for links between biological evolution and environmental change must be considered tentative, since it is still not known to what extent the appearance pulses reflect stratigraphic and preservational biases, or originations of new animal species (40).

The first pulse of animal appearances recorded in Mongolia 536 to 534 Ma occurs at a time when inferred atmospheric O₂ levels declined and marine productivity were rather stable. Although anoxia likely expanded diachronously, enhancing nutrient recycling and productivity in various ocean basins at various times, our records cannot causally link this pulse to a global environmental trigger (66, 67).

The following fossil appearance pulses in China and Siberia at ∼532 and ∼530 Ma occurred during both rising productivity and surface ocean O₂ levels that would have elevated food and O₂ supply to the marine food webs. Experiments show that these factors can promote animal diversification (12). Further investigations on the diachroneity of these events are needed and local paleoredox and/or productivity proxies with high spatial resolution should address whether fossil appearances were correlated to enhanced biological productivity at these times.

After the 2 expansions of seafloor anoxia, animal fossil appearances rose around 524 ± 2 Ma (Tommotian) in both Siberia and China when predicted O₂ levels in the surface oceans were higher and the seafloor was also rather oxygenated, despite slightly higher productivity. A change in weathering regime at this time could have settled atmospheric pO₂ at higher levels than in the earlier Terreneuvian, despite increasing levels of bioturbation. With more food and O₂ available, the carrying capacity for prey and carnivores in the marine ecosystem would have been higher, and this could have promoted further animal radiations (12).

We note that the rate of fossil first appearances was generally lower throughout the intervals with expanded anoxia, although new animal fossils begin to emerge in Siberia during the second OAE, and there are few new fossil taxa recorded in the oxygenated period between the OAEs. We suggest that the Tommotian origination pulse was linked to seafloor oxygenation and the change in weathering regime, similar to later Cambrian bioradiation events (68). We also acknowledge that that the rate of new appearances during the intermediate oxygenated interval has possibly been underestimated either because of sampling or preservational biases or because this particular time interval was shorter than predicted by the age model (40).

Finally, in the greater context of what triggered the emergence of complex animal ecosystems on Earth, our isotope data and models suggest that there were ample amounts of O₂ for animals in the surface ocean at the onset of the Cambrian (69). Our model also shows that atmospheric pO₂ levels declined in concert with global new marine production in the earliest Terreneuvian, which is the predicted result of evolving benthic animal communities that promoted phosphorous burial in bioturbated sediments (7). The first pulse of fossil appearance rates occurred before peak eutrophication and may not have been environmentally triggered. The late Terreneuvian (Tommotian) pulse occurred at a time with both elevated atmospheric O₂ levels and marine productivity likely associated with a change in weathering regime. Ultimately, the trigger for the developing networks of ecological interaction lies in biological innovations (e.g., motility, eyes, armor), but our results suggest that the rate at which animal ecosystems evolved was modulated by O₂ availability as well as chemical energy flow into the marine food web—both of which, in turn, evolving animal ecosystems impacted themselves.

Methods

Carbonate-Associated Elements.

Elemental analyses including U, Th, Mn/Sr, and Mg/Ca were carried out on the mild acetic leachates using Thermo Scientific X-Series 2 quadrupole mass spectrometer at the University of Copenhagen. The leaching procedure utilize a 10% acetic acid with pH >3.6 for <16 h calibrated to maximize the carbonate-associated uranium (CAU) yield, while minimizing the extraction of uranium associated with carbonate fluorapatite, ferric oxyhydroxide-associated P, silicates, and organic-bound U (70). The extraction yield was typically ∼50 to 70%.

Mineralogy.

The bulk mineralogy was characterized by powder X-ray diffraction using a Bruker-AXS D8 Advance diffractometer equipped with the primary beam Ge(111) monochromator, Cu tube (Kα1 wavelength, 1.54059 Å), and silicon strip detector (LynxEye) at the University of Copenhagen. The minerals documented in each sample were identified using the Powder Diffraction File (PDF) database of the International Centre for Diffraction Data.

δ²³⁸U_CAU.

CAU was obtained using a calibrated soft leaching procedure that mainly extracts uranium in calcite and avoids U associated with authigenic carbonate fluorapatite and ferric oxyhydroxide-associated phosphate minerals or any detrital or organic-bound U. The procedure is described in ref. 45.

For the isotope analyses, the concentrations of uranium and thorium were measured on ∼1% of the leachate, and the remaining fraction (99%) or up to 600 ng U was used for isotope analysis. A calibrated ²³³U–²³⁶U double spike (IRMM-3636) was added to the analyte and allowed to equilibrate with the sample to generate a homogeneous mixture with ²³⁵U/²³⁶U ∼ 1 and ²³⁵U/²³³U ∼ 1 (71). Chemical purification was conducted using 4 sequential ion chromatography columns to ensure high U purity of the analyzed solution similar to the reference standard solution (CRM-145) (72). The spike/sample ratio was kept constant for all samples and standards during each analytical session. Each sample solution was measured in 5 replicates at signal intensities matched to the bracketing standard solutions. The long-term reproducibility of a matrix-matched reference material, SRM-1d is better than 0.03‰ (2 SE, n = 5). Therefore, we estimate the long-term reproducibility and accuracy of our ²³⁸U/²³⁵U data to be ±0.03‰ (2 SE). Other reference materials include BCR-2 (whole rock) and IAPSO seawater at δ²³⁸U = −0.271 ± 0.017‰ and −0.372 ± 0.022‰ (2 SE, n = 5), respectively, which are indistinguishable from results obtained in other laboratories (18, 45).

δ³⁴S_CAS.

The isotope composition of carbonate-associated sulfur was obtained using a traditional approach at Virginia Polytechnic Institute and State University (73). Briefly, 3 to 8 g of fine sample powder were treated with a NaCl solution, followed by several distilled water rinses to remove any soluble sulfates that might have been present in the samples. The samples were then dissolved using 4N HCl for less than 1 h. The leachates were centrifuged and vacuum filtered (45 µm) to remove any insoluble portion of the sample, before ∼100 mL of saturated BaCl₂ solution was added to allow sulfate to precipitate as BaSO₄ from the solution. Samples were left for at least 3 d to ensure complete precipitation. Barium sulfate was separated from the remaining solution via filtration. The ³⁴S/³²S isotope ratios were analyzed through on-line combustion using an Elementar Isotope Cube elemental analyzer coupled to Isoprime 100 continuous-flow stable isotope ratio mass spectrometer. Data are reported in standard delta notation (δ³⁴S) as per mil deviations from Vienna Canon Diablo Trolite (VCDT). International isotope standards NBS-127, IAEA SO-5, and IAEA SO-6 were used to convert measured isotope ratios to the VCDT scale. Long-term reproducibility of the international isotope standards was <0.2‰ (1 SD). The external reproducibility of our δ³⁴S data are estimated to be better than 1‰ based on replicate dissolution of samples (45).

Data and Materials Availability.

All data needed to evaluate the conclusions in the paper are present in the paper and/or SI Appendix.