Polymer effects modulate binding affinities in disordered proteins

Significance

The ability to form large interaction networks was one of the driving forces in the evolution of disordered proteins. However, their advantageous flexibility is accompanied by a tremendous solvent sensitivity that does not seem to have detrimental consequences. Our results provide a possible explanation of this conundrum. While individual interactions among 5 disordered proteins are extremely solvent sensitive, their competition for shared ligands in their natural network largely compensates this sensitivity. Recent ideas suggested the presence of a regulatory mechanism that compensates the solvent pliability of disordered proteins. Here, we identified a simple mechanism that achieves this task for networks of homologous disordered proteins.

Abstract

Structural disorder is widespread in regulatory protein networks. Weak and transient interactions render disordered proteins particularly sensitive to fluctuations in solution conditions such as ion and crowder concentrations. How this sensitivity alters folding coupled binding reactions, however, has not been fully understood. Here, we demonstrate that salt jointly modulates polymer properties and binding affinities of 5 disordered proteins from a transcription factor network. A combination of single-molecule Förster resonance energy transfer experiments, polymer theory, and molecular simulations shows that all 5 proteins expand with increasing ionic strengths due to Debye–Hückel charge screening. Simultaneously, pairwise affinities between the proteins increase by an order of magnitude within physiological salt limits. A quantitative analysis shows that 50% of the affinity increase can be explained by changes in the disordered state. Disordered state properties therefore have a functional relevance even if these states are not directly involved in biological functions. Numerical solutions of coupled binding equilibria with our results show that networks of homologous disordered proteins can function surprisingly robustly in fluctuating cellular environments, despite the sensitivity of its individual proteins.

The discovery of protein disorder expanded our view on how proteins interact (1–7). Disordered proteins are extremely flexible (8–11), they are hubs in protein interaction networks (12, 13), and they phase-separate to form liquid droplets (14, 15). However, flexibility has its price and disordered protein ensembles are sensitive to ions, osmolytes, and crowders (16–24) that can vary rapidly in the cellular environment (25). For example, the breakdown of the nuclear envelope during cell division releases large amounts of charged species to the cytoplasm (26). In addition, cells morph during mobility or replication, thus changing volume and internal concentration gradients (27–29). Chromatin is associated with a counterion atmosphere (30, 31), and inhomogeneities in charge density, e.g., due to chromatin condensation, cause spatial ion fluctuations within a nucleus. Even a homogeneous DNA distribution will cause ion gradients in the nucleus. The size distribution of cells and nuclei adds yet another layer of complexity and cell-to-cell differences in ionic strength can amount to ±70 mM in Xenopus oocytes (32). Despite this variability, evolution preferred solution-sensitive disordered proteins for regulatory functions in eukaryotes (12). It remained unclear, however, whether this solution sensitivity is a relevant factor for facilitating or hampering their function (16). Here, we show that an interaction network of 5 disordered transcription factors is robust, i.e., insensitive to solution conditions, not despite but because of their structural disorder.

The 5 proteins MYC, MAX, MAD, MLX, and MONDOA coordinate cellular processes from cell cycle regulation to metabolic control (33). This set of proteins forms a network in which homologous disordered basic helix–loop–helix leucine-zipper (bHLH-LZ) motifs mediate pairwise affinities that lead to folded dimers (34–36) (Fig. 1 A and B and SI Appendix, Tables S1 and S2). However, affinities depend on the free energy difference between bound and unbound states, and changes in the free energy of each can alter affinities (Fig. 1C). Proteins with weak intramolecular interactions such as disordered proteins are expected to be particularly prone to affinity variations. Unfortunately, absolute free energies are extremely difficult to measure such that the impact of intrinsic disorder on binding affinities remained unclear. In this work, we conducted a large set of single-molecule fluorescence experiments to determine the type and strength of interactions in all 5 proteins as a function of a physiological parameter, the ionic strength. The results demonstrate a strong ion sensitivity of affinities in the network that is strongly influenced by the properties of the disordered states, and they show how coupling of many binding reactions in a network of homologous disordered proteins can suppress noise in the concentration of protein complexes under fluctuating solvent conditions. We proceed in 2 steps. First, we demonstrate the extreme ion-sensitive affinities of the 5 proteins and identify their molecular origin. Then we explain the noise-suppression mechanism for 2 limiting network topologies.

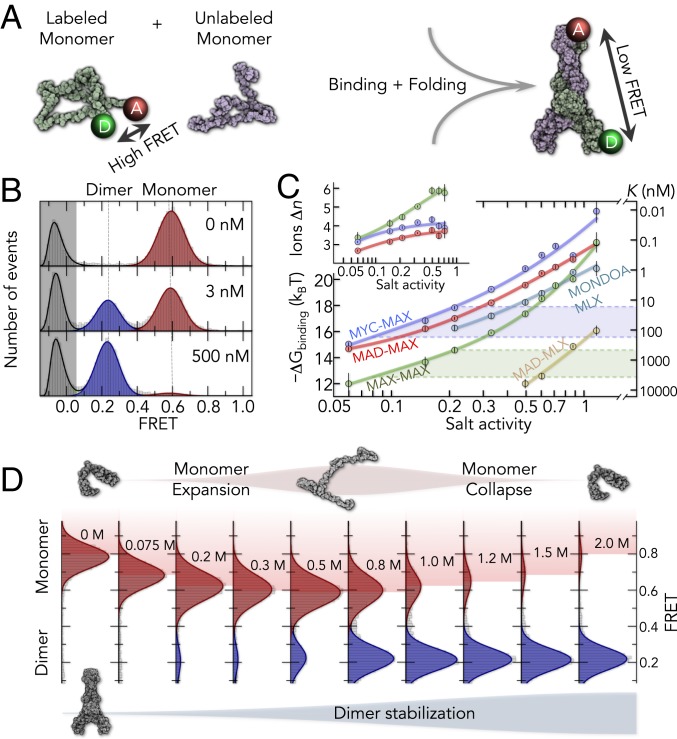
Fig. 1.

smFRET of a disordered protein network. (A) Illustration of interactions among 5 disordered bHLH-LZ proteins. Pairwise interactions allow the formation of 5 dimers. (B) Heat map of pairwise sequence identities (above diagonal) and sequence similarities (below diagonal) of the 5 disordered bHLH-LZ proteins (SI Appendix, Tables S1 and S2). (C) Solvent-driven changes in the free energy of disordered states (red) with respect to that of folded dimers (blue) will alter the affinity. The affinity, expressed by the dissociation constant K, is directly related to the binding free energy via $K\propto \exp \left(-\mathrm{\Delta }{G}_{\mathrm{binding}}\right)$. (D) FRET histograms of the disordered bHLH-LZ proteins at a physiological salt concentration (100 mM KCl).

Results

We use confocal single-molecule Förster resonance energy transfer (smFRET) experiments on freely diffusing proteins labeled terminally with a donor (Alexa Fluor 488) and an acceptor (Alexa Fluor 594) dye (10). In their disordered state, i.e., in the absence of their natural binding partner, all 5 proteins in our study exhibit unimodal FRET histograms with high average FRET (Fig. 1D), suggesting short donor–acceptor distances and hence compact disordered ensembles. The folding of a protein requires its binding partner in the network (37, 38). For instance, the addition of unlabeled MAX to labeled MYC triggers the formation of folded MYC–MAX dimers with an extended coiled-coil structure (Fig. 2A). Since donor and acceptor are placed far apart from each other in the folded dimer, we observe the appearance of a second peak at low FRET with increasing dimerization (Fig. 2B). The fraction of dimer, given by the relative areas of the FRET peaks, directly provides the affinity between the proteins. With dissociation constants in the nanomolar to micromolar range, the absolute affinities vary strongly between the dimer types. However, all affinities exhibit a similar dependence with salt (KCl) (Fig. 2C). The salt-induced changes easily reach up to tenfold within the physiological regime between 100 and 300 mM KCl (Fig. 2C) (39). Classically, salt-triggered affinity increases in binding reactions are explained by the binding of Δn counter ions to the formed complexes, which are the folded dimers in our case. This additional ion binding results in a linear relationship of the type $\ln K\propto -\mathrm{\Delta }\mathit{n}\hspace{0.17em}\ln \hspace{0.17em}\mathit{a}$, with K being the dissociation constant of the dimer equilibrium and a being the salt activity (40, 41). However, our data clearly deviate from this linear dependence, implying that Δn exhibits a salt dependence itself (Fig. 2 C, Inset). Other effects such as hydration (41) and salt-induced conformational changes of the bound or unbound states will have to be taken into account. The latter is particularly relevant for disordered proteins that are known to respond sensitively to a broad spectrum of solution additives (11, 17–19, 23, 42–45).

Fig. 2.

Salt sensitivity of the folding-coupled binding reactions. (A) Disordered proteins labeled with donor (D) and acceptor (A) dyes are mixed with unlabeled proteins (Left) to form the folded dimer (Right). The positions of the terminal labeling sites are indicated in the NMR structure of the MAX homodimer (Right; PDB file 1r05). (B) FRET histograms of MYC at 0.5 M KCl in the presence of unlabeled MAX (concentration is indicated). The gray area indicates molecules without an active acceptor dye. (C) Salt dependence of the binding free energies ΔG_binding (Left) and dissociation constants K (Right) of all dimers. Colored lines are fits with the counterion binding model (colored line) and a hyperbolic salt dependence of Δn. Examples of Δn are shown for clarity (Inset). The change in K within the physiological salt regime (dashed lines) is indicated for MYC–MAX (blue) and MAX–MAX complexes (green). (D) FRET histograms of MYC with 1 nM unlabeled MAX at different KCl concentrations. The expansion and collapse of disordered MYC occur concomitantly with a stabilization of the folded dimer.

Conformational Changes in the Disordered State.

To understand how salt modulates the disordered ensembles of the 5 proteins, we quantify the changes in the FRET peaks of the disordered states. Indeed, we find that salt alters the FRET value of the disordered ensembles substantially (Fig. 2D). Increasing ionic strengths first shift the FRET peak to lower values and then back to high values, indicating an expansion followed by a collapse. Apparently, ions modulate the free energy of the disordered state. However, identifying the origin of this change requires information about chain entropies, charge interactions, van der Waals contacts, and solvation effects, i.e., quantities that are not directly accessible in our experiments. We therefore parameterized a theory for polyampholytes (46–49) with the dataset generated by our smFRET experiments, which, with ∼100 experimental conditions per protein, constitutes the largest dataset to date on disordered polypeptide chains. The theory quantifies residue contacts and solvation effects with 2- and 3-body interaction parameters (ω₂, ω₃) that are essentially virial coefficients, analogously to the van der Waals gas model (Fig. 3A and SI Appendix). In addition, electrostatic interactions between charged residues are explicitly included without any free fitting parameter (46). Since charged amino acids are well mixed along the sequence of the 5 proteins, we do not explicitly account for charge patterning effects (50, 51). The Hamiltonian for a chain with N amino acids contains 4 terms, elastic entropy, 2- and 3-body interactions, and electrostatic interactions:

$$H=\frac{3}{2b^2}{\displaystyle {\int }_0^{N}d\mathit{n}{\left(\frac{\partial {\mathbf{r}}_{\mathit{n}}}{\partial \mathit{n}}\right)}^2}+{\omega }_2{b}^3{\displaystyle {\int }_0^{N}d\mathit{m}}\hspace{0.17em}{\displaystyle {\int }_0^{\mathit{m}}d}\mathit{n}\delta \left({\mathbf{r}}_{\mathit{m}}-{\mathbf{r}}_{\mathit{n}}\right)+{\omega }_3{b}^6{\displaystyle {\int }_0^{N}d\mathit{m}}{\displaystyle {\int }_0^{\mathit{m}}d}\mathit{l}{\displaystyle {\int }_0^{\mathit{l}}d}\mathit{n}\hspace{0.17em}\delta \left({\mathbf{r}}_m-{\mathbf{r}}_{\mathit{l}}\right)\delta \left({\mathbf{r}}_{\mathit{l}}-{\mathbf{r}}_{\mathit{n}}\right)+{\displaystyle {\int }_0^{N}d\mathit{m}}\hspace{0.17em}{\displaystyle {\int }_0^{\mathit{m}}d}\mathit{n}\frac{q_{\mathit{n}}{q}_{\mathit{m}}}{\left|{\mathbf{r}}_{\mathit{m}}-{\mathbf{r}}_{\mathit{n}}\right|}{\mathit{l}}_B\exp \left(-\mathrm{\kappa }\left|{\mathbf{r}}_{\mathit{m}}-{\mathbf{r}}_{\mathit{n}}\right|\right),$$

where the indices (m, n, l) indicate the sequence position of an amino acid, δ is the Dirac delta function, r is the spatial position of an amino acid, b is the Cα–Cα distance between neighboring residues (0.38 nm), q is the charge of an amino acid, l_B is the Bjerrum length, and κ is the inverse Debye screening length (46, 47, 52). The donor–acceptor distance measured in our experiments is then given by averaging the Boltzmann weight $\exp \left(-H\right)$ over all chain conformations (SI Appendix). The theory provides an excellent fit of the full dataset and explains the expansion at low salt (Fig. 3 B and C and SI Appendix, Figs. S1 and S2): The high percentage of basic and acidic residues (30 to 40%) causes strong attractions between oppositely charged groups, which results in a compact ensemble at low salt concentrations. Screening these attractions with salt then causes the chains to expand, an effect that is invariant to the type of cation as expected for Debye–Hückel screening (Fig. 3C, Inset). Due to the long-range nature of charge interactions, we also find the screening effect in proteins that we expanded with the neutral denaturant urea (Fig. 3B). Notably, charge interactions in disordered proteins have often found to be repulsive (17, 23, 44) with only a few reported examples in which charge attractions cause a further collapse (17, 53). For MYC and its homologs, however, charge-driven compaction seems to be the rule rather than an exception. However, as salt concentrations are increased toward rather unphysiological regimes, the chains recollapse (Fig. 3 B and C). A description of the data with polyampholyte theory (Eq. 1) requires a nearly linear strengthening of 2-body interactions (ω₂) with salt (Fig. 3E), suggesting that the effect of salt goes beyond a simple screening of charge–charge interactions. What is the origin of this collapse at high salt concentrations?

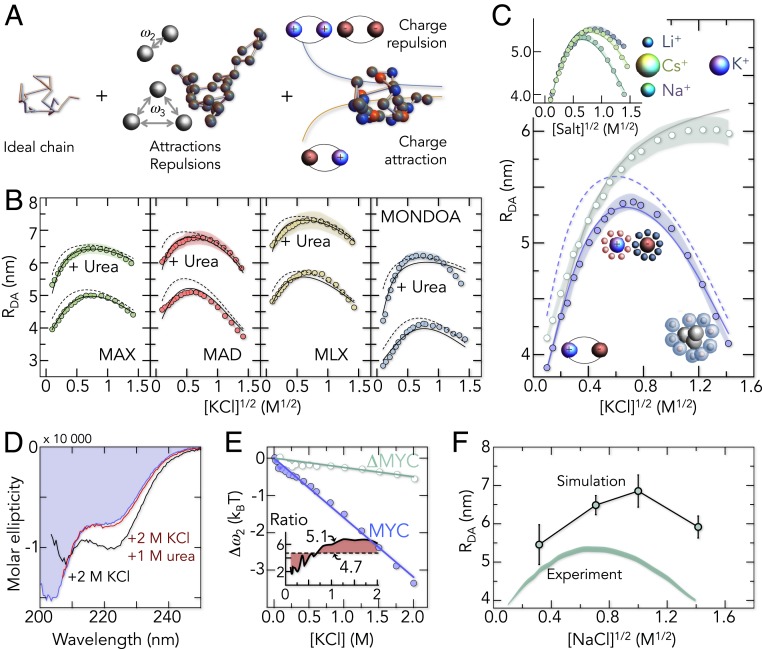
Fig. 3.

Polymer behavior of the disordered proteins. (A) Contributions to the polyampholyte model. Interactions are treated as perturbation of an ideal chain without volume. (B) Donor-acceptor distances (R_DA) of the disordered proteins as a function of KCl with and without 2.5 M urea. Bands are the uncertainty (±2 SD) in the FRET–R_DA conversion (SI Appendix). Black lines are global fits with the polyampholyte theory. Dashed lines are predictions for chains without dye-charges (−4). (C) R_DA for MYC (blue circles) and the modified ΔMYC sequence with less hydrophobicity (green circles). The prediction for a salt-independent hydrophobic effect is shown as a solid gray line. (Inset) R_DA of MYC as function of 3 salts: LiCl, NaCl, and CsCl. The relative ion radius is shown for comparison. (D) CD spectra of MYC at low salt (0 M KCl, blue) and high salt (2 M KCl) with (red) and without (black) urea. (E) Changes in Δω₂ = ω₂(c) – ω₂(0), with c being the KCl concentration for MYC (blue circles) and ΔMYC (green circles). Solid lines are linear fits. (Inset) Ratio of hydrophobic surface area of MYC vs. ΔMYC (dashed line) in comparison to the ratio of Δω₂ (solid line). (F) Molecular simulations of unlabeled MYC at 4 concentrations of NaCl. The root-mean-squared end-to-end distances (R_ee) from the simulation (circles) are compared with the average donor–acceptor distance from the experiment (shaded band).

Solvation Effects at High Ionic Strength.

We first checked whether the addition of high concentrations of KCl induces the formation of secondary structure. Indeed, circular dichroism (CD) spectra show helical signatures in the high-salt limit (Fig. 3D). However, experimentally suppressing the formation of helical segments with urea does not inhibit the high-salt collapse (Fig. 3B, SI Appendix, Fig. S2), suggesting that transient secondary structure formation cannot explain the compaction at high salt concentrations. Importantly, the collapse depends on the cation type (Fig. 3C, Inset), an effect that is reminiscent to the salting-out effect characterized by the Hofmeister series (54–58). Typically, salting-out phenomena are explained by unfavorable interactions of ions with their image charges that form in nonpolar media (59), thus depleting ions around hydrophobic groups (59–61). Burying hydrophobic surfaces lowers this depletion force and may therefore cause the collapse at high salt concentrations. To check this possibility, we replaced bulky hydrophobic amino acids in MYC (V, L, I, F) by serine and glycine, thereby lowering the relative hydrophobicity by 40% while preserving the charge positions of the wild-type sequence (ΔMYC variant). Indeed, the decreased hydrophobicity nearly abolished the collapse at high salt concentrations (Fig. 3C). This is also reflected in the 2-body interaction energy that decreases strongly with KCl for MYC but that exhibits only a weak salt dependence for ΔMYC (Fig. 3E). In fact, we would expect a correlation between the interaction energy change Δω₂ and the salting-out work (59). Zhou (59) found that the salting-out work scales with the surface area of a hydrophobic cavity, i.e., $w_{\mathrm{out}}\propto r^2$ with r being the cavity radius, and we would therefore expect a similar scaling for Δω₂. To check this possibility, we calculated the surface area of hydrophobic side chains (A, V, I, L, M, P, F, Y, W) (62) for MYC and ΔMYC and find a ratio of 4.7, i.e., the surface area is nearly 5-fold larger in MYC compared to ΔMYC. Notably, this number is in good accord with the average value of 5.1 found for the ratio of Δω₂ (Fig. 3E, Inset). We would also like to note that the salting-out work as calculated from Poisson–Boltzmann mean-field theory depends nearly linearly on the salt concentration (59), which also agrees with our experiments that only show a marginal curvature of the salt dependence of Δω₂ (Fig. 3E). In summary, our results together with scaling arguments from theory fully support the idea that salting-out effects are responsible for the observed collapse at high salt concentrations.

All-Atom Simulation of Disordered MYC.

Our findings so far indicate that MYC and its homologs expand at low ionic strength due to charge screening while the chains recollapse at high salt due to a depletion of ions around hydrophobic residues (salting-out). Both effects are rather unspecific and should be well captured by molecular simulations. We therefore simulated disordered MYC in explicit water with unbiased replica-exchange sampling using a specifically optimized force field for disordered proteins (Amber03ws) (63). Simulations of MYC were run for 2 μs at 4 NaCl concentrations after equilibration (SI Appendix, Table S5, see SI Appendix for details). At a qualitative level, we find that the end-to-end distances recapitulate the major trends, i.e., the salt-induced expansion at low salt concentration and the collapse at high salt concentrations (Fig. 3F). This also includes the preferential interaction coefficients between ions and amino acids (SI Appendix, Fig. S4). In the simulation, hydrophobic amino acids indeed exhibit less favorable salt interaction coefficients than polar and charged residues.

However, compared to previous results on other disordered proteins (44), the absolute dimensions of MYC in the simulations differ from the experimental values with increasing ionic strength. While a deviation of 13% is found at 0.1 M NaCl, which is close to previous errors (64), the deviation increases to 33% at high salt concentrations (2 M). To rule out that the charges of our FRET dyes (−2 per dye), which were not included in the simulations, cause an additional compaction due to a strengthening of attractive charge interactions, we used polyampholyte theory to estimate the impact of the attached dyes. With the parameters obtained from fits of our data we computed the donor–acceptor distances for chains in which the dye charges are removed. However, we only find a minor impact on the overall dimensions of the chains (∼0.5 nm) (Fig. 3 B and C) and the screening effect, i.e., the chain expansion with increasing ionic strength, is still preserved. Hence, the quantitative discrepancy between experiment and simulation is likely based on suboptimal interaction parameters between amino acids, water, and salt. In fact, the interaction coefficients of polar amino acids are negative, i.e., repulsive, in our simulation (SI Appendix, Fig. S4), indicating that current force fields are still suboptimal to precisely capture the dimensions of polyampholytes such as MYC over a broad range of experimental salt conditions.

Relation between Disordered States and Binding Affinity.

After characterizing the molecular forces that control the dimensions of disordered MYC and its homologs, the question remains of how we can reconcile the phenomena found in the disordered states with the salt-induced increase in binding affinity among the 5 proteins? Obviously, salt influences the free energy of the disordered ensembles substantially and we need to directly quantify the impact of chain expansion on the affinity change of the dimers. However, binding experiments only report on the difference in free energy between disordered proteins and folded dimers, not on the free energy of the 2 states. Nevertheless, we can provide estimates for the change in free energy in the disordered state based on the experimental FRET values in combination with the donor–acceptor distance distributions that we compute from polyampholyte theory (SI Appendix). Since thermodynamic quantities are path independent, the free binding energy can be divided into 3 contributions: 1) stretching 2 compact disordered proteins to their dimensions in the dimer $\mathrm{\Delta }{G}_1$, 2) folding the stretched proteins $\mathrm{\Delta }{G}_2$, and 3) their association $\mathrm{\Delta }{G}_3$ (Fig. 4A). The sum of these 3 contributions then provides the measured free energy of binding, i.e.,$\mathrm{\Delta }{G}_{\text{binding}}=\mathrm{\Delta }{G}_1+\mathrm{\Delta }{G}_2+\mathrm{\Delta }{G}_3$. While we have no information about $\mathrm{\Delta }{G}_2$ and $\mathrm{\Delta }{G}_3$, the free energy change of stretching ($\mathrm{\Delta }{G}_1$) is a quantity that can be computed from the donor–acceptor distance distribution (Fig. 4A and SI Appendix). Interestingly, $\mathrm{\Delta }{G}_1$ correlates well with $\mathrm{\Delta }{G}_{\text{binding}}$ over a broad range of salt concentrations (Fig. 4B). In particular, within the physiological salt regime (75 to 300 mM), the free energy of stretching 2 disordered proteins becomes more favorable by $\mathrm{\Delta }\mathrm{\Delta }{G}_1$= −1.4 k_BT for MAX (Fig. 4 B and C). In comparison, the binding free energy, i.e., the difference between folded and disordered proteins, increases by $\mathrm{\Delta \Delta }{G}_{\text{binding}}$= −2.6 k_BT within the same range of salt. Although the free energy changes for steps 2 (folding) and 3 (association) cannot be obtained independently, their sum $\mathrm{\Delta }{G}_2+\mathrm{\Delta }{G}_3$ is given by $\mathrm{\Delta }{G}_{\text{binding}}-\hspace{0.17em}\mathrm{\Delta }{G}_1$. While this term renders binding favorable ($\mathrm{\Delta }{G}_2+\mathrm{\Delta }{G}_3\mathrm{<}\mathrm{<}0$) (Fig. 4B), its change with salt within physiological limits is about the same as that of $\mathrm{\Delta \Delta }{G}_1$. Hence stretching a disordered monomer contributes 50% to the affinity increase. We therefore conclude that the disordered state can have a functional relevance even if it is not directly involved in active biological processes. The same calculation for 2 other complexes shows a similar result (Fig. 4C) since similar sequence compositions of the disordered proteins are likely to cause similar salt-induced expansions and hence similar free energy changes in the disordered state ($\mathrm{\Delta }{G}_1$). These changes affect binding affinities by increasing the free energy difference between unbound and bound states. For MYC and its homologs, the binding affinities increase in a synchronized (Syn) manner with salt (Fig. 2C). This similarity is explained, at least in part, by the concordant behavior of their disordered states. Notably, this picture does not capture the unphysiological high-salt limit (Fig. 4B). Although the stretched disordered states become less favorable due to the hydrophobic collapse at high salt concentrations, the affinities do not drop since the hydrophobic interfaces of the dimers themselves are stabilized, a salting-out effect that is reflected by the change of $\mathrm{\Delta }{G}_2+\mathrm{\Delta }{G}_3$ at high salt concentrations (Fig. 4B).

Fig. 4.

Linking disordered state properties to binding affinities. (A) Thermodynamic cycle that dissects the binding process into 3 contributions: 1) stretching of the disordered proteins to the distance in a folded dimer (ΔG₁), 2) folding of the 2 stretched proteins (ΔG₂), and 3) association of the folded proteins (ΔG₃). The contribution of stretching (ΔG₁) is calculated from the distance distributions obtained from polyampholyte theory (Top). ΔG₁ is the free energy of stretching the disordered chains to at least the distance in a folded dimer (dashed line). (B) Results of the calculations schematically depicted in A. The 3 contributions: ΔG₁ obtained from smFRET and polyampholyte theory (blue), ΔG_binding obtained from the determined affinities (Fig. 2C) (green), and the joint contribution of folding and association (ΔG₂ + ΔG₃) calculated from ΔG_binding − ΔG₁ (black dashed line) are shown as function of the KCl concentration for MAX. The arrows indicate the salt-induced changes within the physiological limits of 75 and 300 mM. (C) Comparison of the free energy changes between 75 and 300 mM KCl for the stretching of the disordered state (Bottom, ΔΔG₁) and dimer formation (Top, ΔΔG_binding).

Impact of the Disordered State on the Robustness of the Network.

What is the consequence of this sensitivity for the active network in which all binding partners are present? We start with an isolated binding reaction under the influence of random salt variations and compute the resulting fluctuations (noise) in the fraction of dimer. Not surprisingly, this quantity is most sensitive to perturbations close to half-saturation as shown for MYC–MAX dimers (Fig. 5A). However, the situation is different for networks in which 2 or more binding reactions couple. The simplest scenario is a 3-node network in which proteins i and j compete for the protein k (Fig. 5A). In this case, the fluctuations in the concentration of i–k and j–k dimers are tunable, i.e., the competitor j changes the fluctuations of the i–k dimer. Strikingly, the effect depends on whether the affinities of both reactions respond to salt changes in a synchronized manner (Syn) or in an anticorrelated manner (Anti). If the affinity of one reaction increases with salt while that of the other decreases (Anti), the i–k dimer concentrations are hypersensitive, resulting in a noise enhancement with increasing competitor concentrations (Fig. 5A, Left). In the opposite case, i.e., both affinities respond in Syn with salt, the fluctuations of the dimer concentration (noise) decrease with increasing amounts of competing ligands (Fig. 5A, Right). Competition for a shared ligand explains this effect. If the i–k and j–k affinities increase synchronously, they cause a strong competition for the central protein k, a battle that neither of the 2 reactions wins if the affinities of both reactions are similar. As a result, the dimer concentrations remain nearly constant despite the variations in affinity.

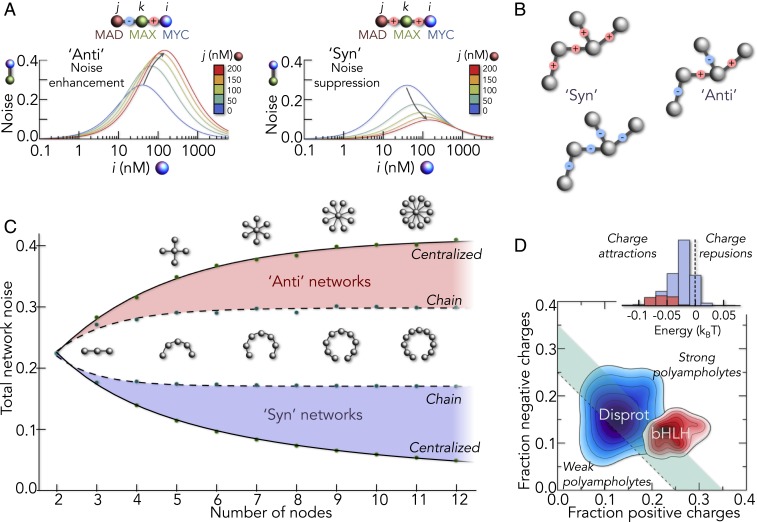
Fig. 5.

Global network behavior. (A) Fluctuation amplitude of an i–k complex (computed for MYC–MAX) in the presence of different concentrations of competitor j (MAD) in the hypothetical Anti (Left) and the experimentally found Syn (Right) case. The signs indicate the direction of affinity changes in the schemes (Top). The salt variation was 0.2 ± 0.1 M. (B) Illustration of networks in Syn (Left) and Anti (Right) configuration. The signs indicate positive (red) or negative (blue) values for the affinity change with salt, i.e., for the gradient. (C) Relative variation of dimer concentrations in linear and centralized networks for the Syn (blue) and Anti (red) scenarios when sampling 1,100 different salt concentrations Δs from a Gaussian with a width of 0.05 M. (D) Comparison of charge fractions of IDPs in the Disprot database (blue) with those of 119 bHLH sequences (red). (Inset) Distribution of electrostatic interaction energies per amino acid for proteins from the Disprot database (blue) and for bHLH sequences (red), computed with polyampholyte theory assuming the donor–acceptor distance of an ideal chain.

Natural networks of course include hundreds of nodes. For example, the network of bHLH domains includes 119 proteins (65) and it will be important to determine how Syn and Anti scenarios depend on the size and architecture of protein interaction networks. We therefore solved the laws of mass action for networks with a simplified salt dependence of the type $\ln K=\ln \overline{K}-m\mathrm{\Delta }s$ for the affinities between all protein pairs. Here, $\overline{K}$ is the dissociation constant at the average salt concentration, Δs is the salt variation, and m is the salt sensitivity of the reaction. Our experiments indicate a value of $\left|m\right|$∼10 k_BT/M (Fig. 2C). If the proteins in the network are unrelated in terms of sequence composition, their disordered states may respond very differently to salt variations, thus also causing unrelated affinity changes. This scenario is modeled by allowing m to take values of −10 or +10 with equal probability for binding reactions in the network. We term this type Anti networks (Fig. 5B). The alternatives are Syn networks. As in the case of MYC and its homologs, all binding reactions in the network exhibit similar responses to salt changes, i.e., the binding affinities change in a synchronized manner with salt. Relative to a control with Δs = 0, the SD of dimer concentrations for random values of Δs, averaged over all dimer types, then provides a measure for the total noise in the network (SI Appendix). We tested 2 limiting network architectures: chain networks and centralized hub-like networks. In the result, we find the total network noise always less pronounced in the Syn scenario, irrespective of the architecture (Fig. 5C). Strikingly, noise suppression increases with the size of Syn networks, which is most pronounced for centralized networks due to the higher number of competitors compared to chain-like networks. Since any real network is a combination of chain-like and centralized architectures, we conjecture that Syn networks will always be more robust than Anti networks. Importantly, for disordered proteins, a substantial part of this robustness comes from the similarity in interaction types and strengths in the disordered state, which is a result of their similar sequence compositions (23, 50). Concordant sequence compositions are expected for homologous proteins with similar patterns of charged and hydrophobic residues. For instance, human bHLH domains (n = 119) show a significantly higher fraction of positive and negative amino acids than unrelated intrinsically disordered protein (IDP) sequences from the Disprot database (n = 632) (66) (Fig. 5D). As a result, bHLH domains have stronger charge–charge attractions (Fig. 5D, Inset), and the effects found for the 5 bHLH domains in this study are likely to be transferable to the whole bHLH network.

Conclusions

Changes in residual structures (67–69) and posttranslational modifications (70, 71) are known to affect the function of disordered proteins. In contrast, the global effects of solvent conditions have often been overlooked, despite the known solution sensitivity of disordered proteins (11, 17–20, 23, 42). A recent study on 2 disordered protein complexes discovered affinity modulations by orders of magnitudes within 1 M of salt, suggesting that the ion sensitivity of disordered proteins may be of biological significance (16). Our results show that even within physiological salt limits of 100 to 300 mM, the affinities among 5 disordered proteins change 10-fold (Fig. 2C). In parallel, our smFRET experiments demonstrate that ions modulate the dimensions of the disordered proteins both by screening and solvation effects (Fig. 3 B and C). The force-balance in the disordered states, as quantified with a polymer theory, indicates that half of the affinity changes can solely be explained by changes in the disordered state (Fig. 4C). Thus, the properties of disordered states, which are mainly dictated by sequence composition, can have pronounced impacts on affinities in folding-coupled binding reactions. In cells, however, protein–protein interactions are rarely isolated. Since a protein can have more than one binding partner, a myriad of binding reactions are connected by shared ligands (72). This is particularly the case for the helix–loop–helix proteins investigated here (Fig. 1A). If we take this connectivity into account, we find that environmentally sensitive affinities must not necessarily be detrimental. In fact, such effects can either be amplified or suppressed, depending on how uniform the environment alters affinities in an interaction network. Notably, this result is general and not restricted to salt as the external variable. The cellular environment is highly diverse and prone to rapid changes in the concentrations of many types of solutes (25). The effect of any change in solution properties on cell regulatory networks—including pH, osmolytes, and crowding—can be dampened as long as affinities change uniformly in a network, i.e., if the network is of Syn type. In fact, protein networks that consist of homologous disordered proteins such as those of bHLH and bHLH-LZ type are not exceptional. Nearly 2,500 functional dimers in humans are composed of homologous proteins (65). One example are disordered bZIPs, i.e., basic zipper proteins (73), with 51 genes in human (65). However, the opposite, i.e., the hypersensitivity of Anti networks, could also be advantageous in certain scenarios, e.g., for rapid sensing and signaling during osmotic shock.

In summary, our results show that disordered proteins encode global network features such as robustness or hypersensitivity already at the level of individual proteins. The structural flexibility of disordered proteins provides previously unanticipated ways to design biological networks at the systems level based on simple sequence parameters such as fraction of positive and negative charges. Evolution may have chosen disordered proteins in regulatory networks not just for their binding versatility but also to tune their sensitivity toward environmental solution variations via fundamental polymer principles.

Materials and Methods

All proteins in this study were expressed, purified, and labeled as described previously (74). An extended description of the methods, theory, and additional data that support the findings of this study are provided in SI Appendix. Unless stated otherwise, all experiments were performed in 20 mM Tris⋅HCl, pH 8.2, containing 0.001% Tween 20 to prevent surface adhesion of the proteins and 100 mM β-mercaptoethanol to maximize photon emission.