Molecular Dynamics of Ion Conduction Through the Selectivity Filter of the NavAb Sodium Channel

Abstract

The determination of the atomic structures of voltage-gated bacterial sodium channels using X-ray crystallography has provided a first view of this family of membrane proteins. Functional measurements indicate that the members of this family display only slight selectivity for sodium over potassium. Molecular dynamics simulations offer one approach to clarify the underlying mechanism of permeation and selectivity in these channels. However, it appears that the intracellular gate of the pore domain is either closed or only open partially in the available X-ray structures. The lack of structure with a fully open intracellular gate poses a special challenge to computational studies aimed at simulating ion conduction. To circumvent this problem, we simulated a model of the NavAb channel in which the transmembrane S5 and S6 helices of the pore domain have been truncated to provide direct open access to the intracellular entryway to the pore. Molecular dynamics simulations were carried out over a range of membrane potential and ion concentration of sodium and potassium. The simulations show that the NavAb selectivity filter is essentially a cationic pore supporting the conduction of ions at a rate comparable to aqueous diffusion with no significant selectivity for sodium. Conductance and selectivity vary as a function of ion concentration for both cations. Permeation occurs primarily via a knock-on mechanism for both sodium and potassium, although the ion ordering in single file along the pore is not strictly maintained. However, at high concentrations, there is an increase in the time it takes individual sodium ions to traverse the selectivity filter toward the intracellular side, with more double occupancy of the pore region near leucine 176. The character of the outward current appears quite different from the inward current, with a build up on ions in the selectivity filter prior to escape toward the extracellular side, indicating the presence of a rectification effect that is overcome by non-physiological applied voltages.

Graphical Abstract

I. INTRODUCTION

In recent years, crystallographic X-ray structures of bacterial voltage-activated sodium (Na_V) channels have tremendously increased our knowledge of this crucially important membrane protein family.^1–13 Of particular interest are the structural features underlying the mechanism of ion selectivity and conduction. Unlike the asymmetric DEKA collar their eukaryotic counterparts,¹⁴ bacterial Na_V channels present a four-fold symmetric pore selectivity filter. The latter differs significant from the selectivity filter of tetrameric potassium channels,^15–16 being wider and allowing direct coordination of the permeant ions by various side chains in addition to backbone carbonyls. The extracellular end of the pore is lined by serine and glutamic acid side chains. However, while the available X-ray structures have provided a wealth of information, they leave a number of issues about the conformation of a fully open and active channel unresolved. The first crystal structure of the NavAb channel from Arcobacter butzleri showed a closed interacellular gate despite the four voltage sensing domains in a putatively activated conformation.¹ Subsequently, a crystal structure of the pore domain NavMs of Magnetococcus sp. was also published, for which the inner gate was at least partially open.² In the intervening time, additional structures of NavAb, NavMs, and few related channels have become available.^3–13 Very recently, an open structure of NavAb was published, with an intracellular gate slightly open, just enough to permit sodium to pass with an almost intact first solvation shell, a similar diameter to structures of NavMs.¹² The structure of the selectivity filter, and the radius of its opening is generally similar across the structures assigned as non-inactivated bacterial sodium channels, whether they are in an open or closed state, differing by only tenths of an angstrom across species (or perhaps across methodology).⁸ In structures of NavMs, three sodium ion binding sites are seen in the selectivity filter: one at the level of the carboxylic acid groups of glutamate, one between there and the carbonyl of leucine, and a third at the carbonyl of leucine. However similar sodium binding sites have not yet been observed in structures of NavAb.^{1, 3, 6–7, 9, 11–13} This brings up the question of whether the absence of sodium results from some difference of protocol, or if NavMs could actually differ in some subtle and yet profound way.

Ion selectivity has been measured through reversal potentials for full channel and pore-only constructs of bacterial Na_V channels. NaChBac from Bacillus halodurans is the most selective of the Na_V channels studied, with a permeability ratio P_Na/P_K between 24 and 171, although Finol-Urdaneta et al. found that selectivity was greater when sodium was on the intracellular side and potassium was on the extracellular side.^17–18 NavMs has a similar, high, selectivity with a permeability ratio P_Na/P_K larger than 24.^{9, 19} The pore-only construct of NavSp1p from Salicibacter pomeroyi has lower permeability ratio P_Na/P_K of 3.7–4.5, and only 1.7 if determined from the conductance of sodium and potassium rather than the direct competition of reversal potentials.^20–21 The full channel of NavAb has a similar, relatively low selectivity, with a permeability ratio P_Na/P_K of about 6.¹ In comparison to the other channels mentioned, the selectivity filter of NaChBac has a second ring of serine above the selectivity filter. This is thought to contribute an additional cation-binding site. The potential for an additional binding site may increase the selectivity of NaChBac relative to the others. Differences in selectivity between NavMs, NavSp1p, and NavAb are more astounding, as the selectivity filter sequence (TLESWSM) is identical and the RMSDs of their crystal structures differ so little. While reversal potential of NavSp1p was obtained from bilayers of 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC), that of NavMs and NavAb were both determined in cells derived from human kidney. Therefore, differences in NavMs and NavAb may be significant.

Variation in ion selectivity also implies variation in the conductance of sodium and potassium. However, the conductance of an ion channel can vary as a function of environmental conditions. The bacteria of interest live in a variety of habitats. While Bacillus halodurans, isolated from soil, can grow under warm (30–60°C), basic (pH 9–12), and saline (up to ~2 M NaCl) conditions, Magnetococcus sp. and Arcobacter butzleri are found in freshwater, brackish water, and marine environments, pH 7, and survives temperatures ranging roughly from 5–35°C, with variation among strains.^22–25 Magnetococcus sp. was found in an estuary with ~0.3 M NaCl and some strains of A. butzleri can survive in up to ~0.7 M NaCl.^23–24 In addition, Arcobacter butzleri is a pathogen of humans and animals, while Magnetococcus has no known pathogenicity and is actually used to deliver drugs to tumors.^{23, 26–28} Because the bacteria survive in a variety of environments, particularly in terms of salinity, the behavior of bacterial Na_V channels as a function of salt concentration becomes of interest. Experimentally reported conductance values of sodium through Na_V channels mostly vary from 10–40 pS over a range of extracellular concentrations from 100 – 500 mM Na⁺, for both asymmetric ion conditions in cells or symmetric ion conditions in bilayer experiments.^{1, 17, 19–21, 29} The conductance of NaChBac rises from 12 pS to ~40 pS as concentration increases from 140 mM to 500 mM [Na⁺]_external.^{17, 29} The conductance of NavMs, which is 33 pS at 150 mM NaCl, approaches its concentration of maximum conductance at 445 mM NaCl.¹⁹ Two notable exceptions to this are in bilayer experiments, where both NaChBac and the NavSp1p pore are reported to have conductances of 120 pS and 106 pS respectively.^30–31 However, this isn’t simply a feature of all bilayer experiments, as other measurements exist of NavSp1p conductance in bilayers give a more comparable conductance of ~30 pS (200 mM [Na⁺]_external).^20–21 The unitary conductance of NavAb has been reported only once (37 pS), this was not only on the high end of the conductance range, but was obtained at the low end of the concentration range at 100 mM [NaCl]_external.¹ The conductance of potassium through NavSp1p was reported to be 18.4 +/− 2.1 pS (110 mM KCl). While the values for selectivity would suggest that conductance of potassium in the other channels may be less than this, direct measurements of single channel conductance for potassium have not been reported in the other channels and there is no study of potassium concentration dependence on conductance.²¹

In addition to concentration, mixtures of ions or asymmetric conditions can affect conductance. In NaChBac, it was observed that extracellular solutions of sodium and potassium had a greater conductance than solutions of just one or the other, when the intracellular solution contained either sodium or potassium, but this effect was removed when the intracellular solution contained primarily cesium, which is impermeant.¹⁸ In contrast, no anomalous mole fraction effect was observed in NavMs.^{9, 19} The selectivity filter of NaChBac does differ from NavMs and NavAb, because of a ring of serine three residues above the top of the TLES motif that may play a role in the anomalous mole fraction effect of NaChBac which potentially adds a binding site.²⁹ No experimental study has been published exploring potential anomalous mole fraction effects in NavAb, although recent advances may make this more possible.¹³

An additional variable which varies from human cells is the resting membrane potential of bacteria. The alkalophilic bacteria Bacillus has a resting membrane potential of −170 mV.³² While the resting membrane potentials may not be known for the other bacteria from which channels are well-characterized by crystallography or electrophysiology, the voltages at which bacterial Na_V channels activate and inactivate give a general indication of relevant membrane potentials. Na_V channels activate upon cell depolarization. The voltage of half-maximal activation of NavAb is −97.8 +/− 1.3 mV at pH 7.4 and ~25°C in Hi5 cells and NavMs it is ~−90 mV near pH 7 and 22°C in HEK293T cells.^{11–12, 19} The V_1/2 of activation is much more depolarized for NaChBac (~ −43 +/− 2 at pH 7.4 and ~20°C in HEK293T cells), but it increases dramatically with both temperature and pH, to reach −102 mV at pH 9.4 and 37°C.^{19, 33–34} The voltage dependence of inactivation occurs at similarly more polarized potentials for NavMs (~125 mV at pH ~7.5 and 22°C in HEK293T cells) and NavAb (−119.3 +/− 0.8 mV at pH 7.4 and 25–27°C in Hi5 cells), than for NaChBac (−60 +/− 3 at pH 7.5 and 22°C in HEK293T cells).^{11–12, 17, 19}

One feature of NavAb that is not observed in NaChBac, NavMs, or pore-only constructs of bacterial sodium channels, is use-dependent rundown of the current resulting from incomplete recovery from inactivation even at holding potentials of −180 mV.^{3, 19, 35–37} This is an inactivation involving residue-residue interactions in the voltage sensor, and can be removed with a single point mutation.³⁵ Recovery from this inactivation in wild-type NavAb has been achieved using a prepulse at −240 mV.¹³ However, it serves as a reminder that the physiological conditions of human cells are not those of bacteria, which when considered individually, may be viewed as relatively extreme in terms of salt concentrations, pH, and even membrane potential.^{32–33, 38} While the observed inactivation is attributed to the voltage sensor, the membrane potential may also affect charged residues in the selectivity filter.

The mechanism of selective ion conduction in bacterial Na_V channels is unresolved. While physiological concentrations of NaCl in humans are approximately ~100 mM, many of the crystallized bacterial Na_V channels originate from halophiles, living in salt concentrations potentially reaching 0.5–2 M NaCl. Individual molecular dynamics studies of ion conduction in bacterial Na_V channels have been performed using concentrations ranging from 100mM to 500 mM NaCl.^{19, 39–44} However, there has been no individual concerted study of the effect of concentration on conduction and the conditions of existing studies in the existing literature are too varied (different force fields, different channels, etc) to provide insight into the concentration dependence of the conduction of sodium and potassium in these channels, and through this the concentration dependence of the selectivity of the NavAb channel. To simulate a sustained flux of ions with an applied membrane potential is only possible with an atomic channel structure that is in an open conductive state. Most of the available structures of sodium channel have an intracellular gate in the closed state. Even the crystallographic structure reported by Lenaeus et al.¹² displays a partially open intracellular hydrophobic gate that may limit the overall rate of ion permeation. One possible strategy is to construct a model of the channel with an open inner gate from the crystallographic structure. However, the details of the modeled inner gate may have an impact on the access resistance and affect the ion conduction properties of the channel, which would undermine the significance of the simulation results. A different strategy, adopted here, is to simply truncate the TM helices forming the inner gate to expose the selectivity filter directly to the bulk solution. Aside from its conceptual simplicity, the main advantage of the truncated model is that it eliminates any effect from the access resistance though the inner gate, exposing the “bare” filter to the bulk solution.

In the following, we establish the general features of a truncated model of the pore based on the crystal structure 3RVY. Then, using potential of mean force calculations of one and two sodium ions penetrating the system, we show that truncation does not alter the properties of the selectivity filter. Using this truncated model of NavAb, we then explore ion conduction of sodium and potassium as a function of concentration, separately and in direct competition.

II. COMPUTATIONAL METHODS

a). Simulations of a truncated model of the NavAb pore domain

The pore domain of the 3RVY structure of NavAb, obtained from the RBSC PDB databank and oriented using the orientations of proteins in membranes (OPM) method, was truncated to residue 143 to 199, in order to form an open pore without perturbing the selectivity filter.^{1, 45} The backbone, heavy atoms of the remaining portions of the S5 and S6 helices (residues 143 to 152 and 193 to 199) were harmonically restrained with a force constant of 10 (kcal/mol/Ų). The membrane was represented by a 14 Å-thick planar slab of Lennard-Jones (LJ) particles that were weakly restrained in place by harmonic potentials. The side chain of glutamate 177 of all four monomer were deprotonated, consistent with pKas calculated using PROPKA on the basis of the 3RVY crystal structure, and with previous analysis by Chakrabarti et al. using a Poisson-Boltzmann continuum-electrostatics approximation.^{44, 46} A number of computational studies have directly probed the effect of Glu77 protonation.^{39, 43, 47} It was observed that protonation of a single glutamate may greatly reduce, but perhaps not prevent, conduction^{39, 43, 47}, protonation of three or more glutamates leads to a barrier in the region above Glu77 side-chains called the high field site (HFS), rendering the filter non-conductive.^{43, 47}

The matrix and protein were solvated in aqueous solutions of 1 M NaCl, 1 M KCl, 0.5 M NaCl + 0.5 M KCl, 0.15 M NaCl, 0.15 M KCl, or 0.15 M NaCl + 0.15 M KCl and equilibrated using the CHARMM program version c36a6.⁴⁸ Simulations contained roughly 25,000 atoms, 1 M corresponding to 140 cations, 128 chlorides and ~6,800 water molecules, 0.15 M corresponding to 28 cations, 16 chlorides and ~7,100 water molecules. The force field used were CHARMM27 for the protein,^49–50 CHARMM36 for the lipid,⁵¹ TIP3 for the water,⁴⁹ the potassium and chloride LJ parameters from Beglov and Roux,⁵² and the sodium LJ parameters from Noskov et al.⁵³ with pair-specific parameters (NBFIX) for the carboxylic acid – sodium interactions to reproduce osmotic pressure data.⁵⁴ MD simulations were carried out in the absence of any applied electric field for at least 100 ns using the NAMD program (version 2.9) to first equilibrate the different systems.⁵⁵ The resulting systems were then used to generate for non-equilibrium MD simulations of the truncated model channel in the NVT ensemble in the presence of a membrane potential via a constant applied electric field applied across the Z-dimension of the simulation cell, the value in kcal/(mol Å e), determined by the desired voltage and the box length along Z (Table S1). Pressure perpendicular to the plane of the bilayer was controlled using the Langevin piston of Feller et al. during equilibration, but constant volume simulations were applied in the presence of the external electric field.⁵⁶ A time step of 2 fs was used. The length of bonds involving hydrogen atoms was kept fixed by SHAKE.⁵⁷ The van der Waals cutoff was 12.0 Å, and the switching distance was 10 Å, and the pairlist distance was 16 Å. Particle-mesh-Ewald (PME) was used to calculate electrostatic interactions.⁵⁸ Temperature was controlled with the Langevin thermostat. More than a microsecond of continuous data was produced for seventeen of the voltage/concentration conditions. All analysis was performed using codes written by KMC in VMD/TCL, python, or perl, except for WHAM. Figures were plotted using gnuplot or matplotlib in python. Visualization of the coordinates was performed with VMD.

b). Potential of mean force calculation

The potentials of mean force (PMFs) of ions in the selectivity filter of the truncated channel model were calculated using umbrella sampling MD simulations. The umbrella sampling simulations were carried out with CHARMM (version c36b1)⁴⁸ using the Hamiltonian replica-exchange (US/H-REMD) method.⁵⁹ The on-dimensional (1D) and two-dimensional (2D) PMF follow the movement of one or two tagged sodium ions inside the selectivity filter, respectively. Thus, these 1D and 2D-PMF calculations correspond to 1-ion and 2-ion occupying the filter. To insure a well-defined number of ions in the pore during the PMF calculations, additional (untagged) sodium ions not involved with the US window biasing were excluded from the pore region; a half-harmonic repulsive spherical region of 10.25 Å radius with a force constant of 10 kcal/mol/Ų centered at the center-of-mass of the Cα of residues 175 to 180 was used. No membrane potential was applied during the umbrella sampling simulations. Because of the harmonic restraints holding the LJ membrane slab in place, these simulations were carried out under constant volume conditions. Hoover temperature control was employed with a reference temperature of 303.15 K.⁶⁰ For the calculation of the PMFs with 1 M and 0.15 M NaCl, the harmonic restraints on the LJ membrane slab and outer helices was 20 kcal/mol/Ų. Initial coordinates were taken from the end of approximately 1-microsecond ion conduction simulation for 1 M NaCl (0 mV), and 0.15 M NaCl (−200 mV). As appropriate, ion and water coordinates were swapped in the selectivity filter to create a series of starting coordinates along the z-axis for one and two ions. The 1D-PMF covers the movement of one tagged sodium ion from Z_SOD = −10.25 Å to 10.25 Å, for a total of 42 US windows each spaced at 0.5 Å. The 2D-PMF of the truncated pore covers the displacement of two tagged sodium ions, Z_SOD1 ranged from −10.25 Å to 10.25 Å and Z_SOD2 = −6.25 Å to 2.25 Å. A harmonic restraint forming a cylinder of radius 8 Å is additionally imposed on the tagged sodium permeating the truncated channel to avoid unbound lateral displacements of the tagged ion in the bulk region. To adapt to the number of available compute nodes used for the US/H-REMD calculation, the area of the reaction coordinates was divided into two regions for the 2D-PMFs, the first region extending from Z_SOD2 = −6.25 Å to −1.75 Å, and the second region extending from Z_SOD2 = −2.25 Å to 2.25 Å. Z_SOD1 ranged from −10.25 Å to 10.25 Å and all replicas were spaced at 0.5 Å for a total of 420 replicas in each region, for a total of 840 replicas. The overlap of two windows along the Z_SOD2 axis between the two set of US/H-REMD simulations allowed us to omit the windows along the inner edges when calculating the PMF to avoid any potential effects of having uneven ability for replicas to exchange along an edge. The 2D-PMF calculation comprises 756 windows (42 across Z_SOD1 × 18 across Z_SOD2). To obtain the PMFs, the US windows were unbiased using the weighted histogram analysis method (WHAM).^61–63

For comparison, the PMFs of the full-length NavAb pore domain in a lipid membrane were also calculated, although for these calculations the NBFIX parameters for carboxylic acid - sodium interaction were not used, the effect of this interaction is visible in an increase in the barrier at Z_SOD1 = Z_SOD2 = 0 – 2 Å, but it doesn’t affect the basic characteristics of the conduction pathway. These are the subsets of a larger 1D and 2D-PMF calculation, where umbrella windows along Z_SOD1 and Z_SOD2 ranged from −12.25 Å to 13.25 Å for the 2D-PMF, and Z_SOD1 ranged from −10.75 to 12.75 for the 1D-PMF. The pore domain of the 3RVY crystal structure was hydrated using CHARMM, and then the channel was embedded in a POPC bilayer surrounded by a 0.15 M NaCl aqueous solution using the CHARMM-GUI.⁶⁴ The atomic system contained 6707 water molecules, 27 sodium ions, and 11 chloride ions and the volume of the dimensions of the periodic cell are 68.5 Å × 68.5 Å × 78.4 Å. US windows were created along the pore axis (z) at an interval of 0.5 Å, for a total of 2704 replicas. The umbrella potential had a force constant of 10 kcal/mol/Ų. As in the PMF of the truncated channel, sodium ions not involved with the US window biasing were excluded from the pore region via a half-harmonic repulsive spherical region. Constant pressure along the z direction was controlled by the extended system algorithm with a Langevin piston.⁵⁶ Hoover temperature control was employed with a reference temperature of 303.15 K.⁶⁰

III. RESULTS AND DISCUSSION

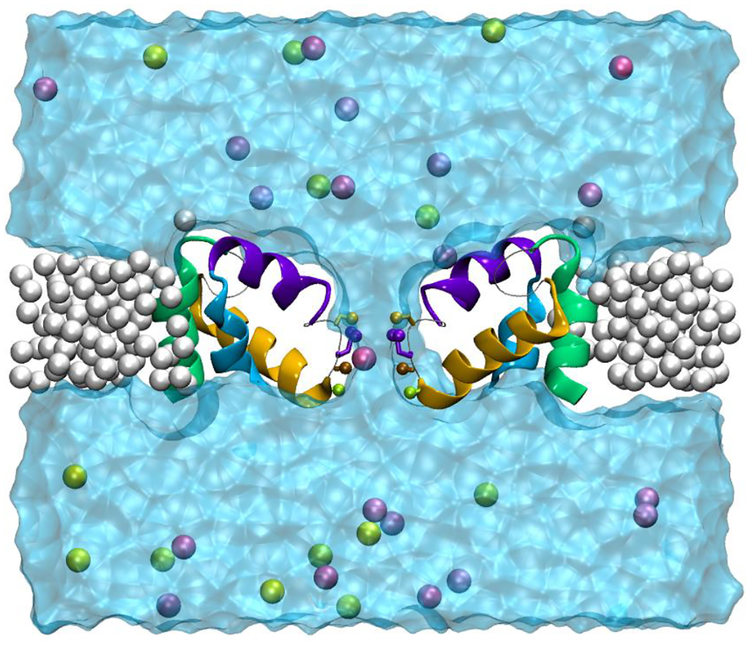
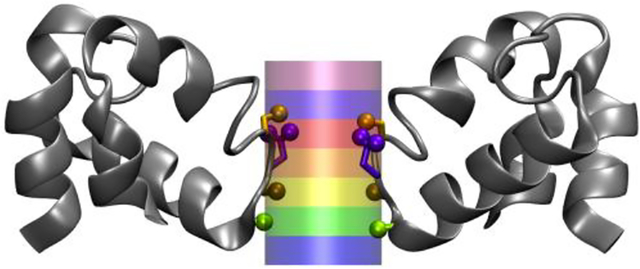
Most previous MD simulations were carried out on the basis of the available crystal structures of NavAb with a closed intracellular gate. These studies focused on the features of the selectivity filter and the binding sites experienced by ions moving in and out of the pore from the extracellular side, since net ion conduction through the entire pore cannot occur.^{39, 42–44, 47, 65–69} While the intracellular gate is closed, it has generally been assumed that the selectivity filter corresponds to a representative ion conductive conformation. More recently, a channel structure with a partially open gate allowing the passage of a sodium with minimal dehydration was reported by Lenaeus et al.¹² Simulations based on the partially open structure indicated the selectivity filter is unaffected by the conformation of the intracellular gate.¹² Simulations were also carried out on the basis of the bacterial sodium channel NavMs, with a partially open intracellular gate. However, the gate would close spontaneously during the simulations and harmonic restraints applied to the protein were necessary to keep the gate open.^{19, 41} For the sake of simplicity, a truncated model of the pore domain in which the S5 and S6 helices were truncated below the level of the pore helix was simulated in the present study. This allows for unhindered ion conduction through the selectivity filter directly into the solvent, removing the influence of the aqueous cavity and intracellular gate. An alternative strategy would be to try to model the conformation of the intracellular helical bundle region in an open state. Even though the crystal structures of some other channels could have served as templates to create an open NavAb channel model, such an exercise remains generally fraught with uncertainty. Amaral et al.⁷⁰ attempted to activate the voltage sensors to open the intracellular gate of NavAb using steered MD (SMD). In these SMD simulations, the pore did not spontaneously open, though it would remain open if the VSDs were fully activated. This “fully-activated open” model of Amaral et al. was further used by Stock et al. to investigate conduction of sodium.⁴² In a similar study, Barber et al. used homology modeling of NaChBac onto the NavAb crystal structure and found that kinking at two glycine residues commonly conserved in the S6 helix (only the upper one is present in NavAb and NavMs) were behind opening of the intracellular gate, suggesting different opening mechanisms are possible within the NaChBac family of channels.⁷¹ The simple truncation adopted here allows the narrowest part of the pore, the “selectivity filter”, to directly experience the environment of the bulk solutions without the additional risk of inducing unwanted structural modification in this sensitive region of the channel via allosteric coupling with an arbitrarily open gate. Our reduced model, based on the crystal structure of NavAb (3RVY) maintains as much of the protein as possible, truncating the S5 and S6 helices beneath the selectivity filter to create an open-like pore directly exposed to the bulk solution (Figure 1). The residues of the S5 and S6 helices that block the intracellular entryway were deleted. The reduced model was then embedded in a support planar slab of harmonically restrained LJ particles, exposing the selectivity filter directly to the two bulk solutions. The model does not possess the typical water cavity seen in tetrameric channel pore domains made of four identical “TM-loop-TM” subunits disposed symmetrically around a common axis.^{15, 72} However, such a water cavity is really well defined only when the intracellular gate is closed. Channels with a widely open intracellular gate present a wide aqueous vestibular entrance rather than an enclosed water cavity.⁷³ The reduced model bears some similarity with a previous study,⁴⁰ with the notable difference that the truncated model also includes part of S5 and S6 is embedded in a membrane to simulate ion conduction. Assuming that the bulk region, the intracellular entry, and the selectivity filter act as a set of resistor in series, the model has retained only that of the selectivity filter. In that sense, the MD simulations simply report on the ionic conductance of the most distinctive ion-conducting region of the NavAb pore, which is its narrow selectivity filter. Thus, while the present truncated model may appear to be somewhat artificial, it has the obvious virtue of probing directly the ionic conduction through the narrowest part of the channel, unimpeded by the diffusional access resistance through the intracellular gate.

FIGURE 1.

Image of the model of NavAb with the S5 (green) and S6 (cyan) helices truncated to form an open pore and harmonically restrained within a supporting lattice made from inert particles (neon, white). The selectivity filter and pore helices (purple and gold) are free to move, as are water (transparent, cyan), chloride ions (yellow spheres), and cations (mauve). The front and rear subunits of the protein are removed for clarity. A cross region of the support and water and the ions in and behind it are presented for clarity. The image was taken from a simulation with 0.15 M KCl.

Simulations were carried out in two concentration regimes. Simulations with 1 M salt are designed to approach maximal conductance. The reported saturating concentration was 445 mM for full-length NavMs.¹⁹ The concentration dependence of the NavAb conductance has not been reported. The high concentration regime is relevant to the highly alkaline conditions of related channels,⁷⁴ and conceptually comparable to some lipid bilayer experiments.^{30–31, 75} Additional simulations, at concentrations approaching the physiological regime (0.15M-0.3M), are relevant to other electrophysiological studies of prokaryotic sodium channels expressed heterologously in cells, as well as some studies in lipid bilayers and giant unilamellar vesicles.^{1, 18–21} Experimental measurements of selectivity are typically performed under asymmetric concentration conditions. However, it is also imperative to point out that the conductance of sodium through NaChBac and NavSp, including their pore-only constructs, has a strong dependence on sodium concentration in the mM range.^30–31 No comparable measurements have been published for potassium. Lipid dependence of conductance also exists in prokaryotic sodium channels, however the presence of channel-specific, negatively-charged lipids affects the conductance of full channels more strongly than the pore-only constructs.⁷⁶

a). Free energy landscape of ions in the selectivity filter

Characterizing the potential of mean force (PMF) or free energy landscape of ions in the selectivity filter provide important information about the energetics associated with the dominant states underlying ion permeation. For the sake of clarity, we consider situations with either one or two ions located within the pore region. Additionally, by comparing the PMFs of the full pore and the truncated pore system the effects of truncation, if any, on the free energy surface of ion permeation is visible.

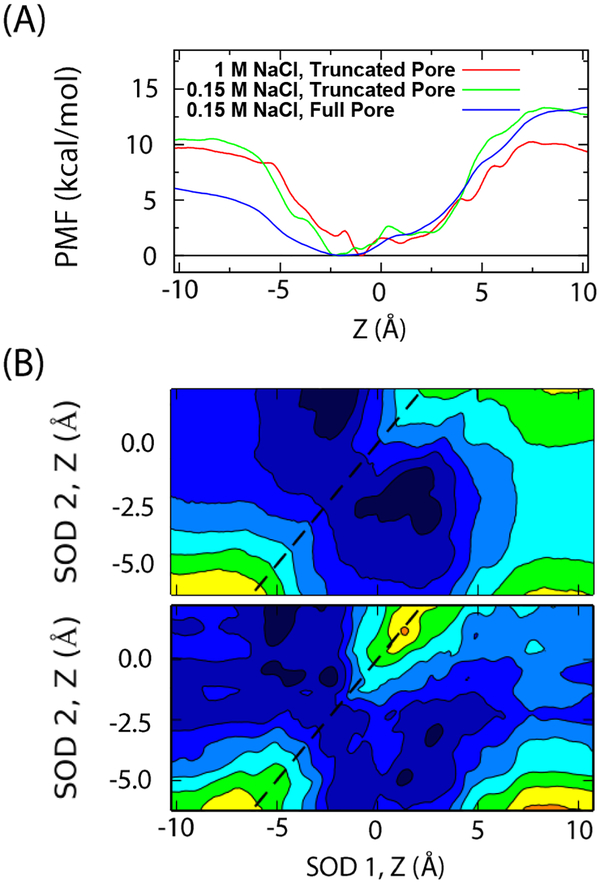
The 1D-PMF of a single tagged sodium ion entering the selectivity filter of the full-length pore domain NavAb at 0.15 M and of the truncated open model at both 0.15 M and 1 M computed from US/H-REMD simulations is shown in Fig. 2 (top). The PMF covers the pathway of an ion traversing from the extracellular funnel (Z =5 Å) to the intracellular side (Z = −5 Å). In the case of the full-length pore domain, the lowest value at Z = −10 Å corresponds to the aqueous intracellular cavity; in the reduced model, this corresponds to the aqueous intracellular solution. The different environments account for differences in the two PMFs in the region Z < 0 Å. Ion concentration also appears to have some effect on the value of the barrier on the extracellular side (+Z), potentially owing to ionic screening of charged residues in the extracellular funnel above the region sampled in the PMFs. The PMFs of the open truncated-pore model are more featured than that of the closed full-length pore. The absolute minimum of the 1D-PMF of a sodium in the truncated pore in 1M NaCl is at Z ≈ −1 Å, where it is coordinated by Leu176 and sometimes Glu177; this minimum is near −2.5 Å for 0.15 M where the ion is coordinated by Leu176. In contrast, the broad minimum of the PMF of the full-length pore domain encompasses both. The predominant feature is the remarkable depth of each of these PMFs, suggesting that a single cation occupying the selectivity filter would be at the bottom of a well of 5–10 kcal/mol deep. A number of single-ion PMFs calculations have been reported for sodium entering NavAb, displaying some considerable variability.^{18, 39, 47, 65–68} In contrast with the previous calculations, it is important to note that the present 1D-PMF purely reflects a 1-ion situation, as all other ions in the bulk are prevented from entering the filter region. In spite of this important difference, the strong binding of sodium to the filter of the present 1D-PMFs most resemble the previous results by Furini et al.,⁶⁵ Qui et al.,⁶⁷ and Finol-Urdaneta et al.,¹⁸ though some like Ke et al.⁶⁸ might look similar if they were extended to a broader range of the range of the reaction coordinate.^{18, 47, 65, 67–68, 77}

FIGURE 2.

Potential of mean force of sodium in the NavAb channel. (A) PMFs of a single sodium ion through the truncated-open and full pore (closed) domain models of NavAb. (B) 2D-PMF of two sodium ions entering the selectivity filter of the full pore NavAb (top) and open truncated-pore model (bottom), both at 0.15 M. Z = 10 Å is above the selectivity filter and can be near Glu¹⁶⁵. Each colored level corresponds to 2 kcal/mol. A dashed line in the bottom two plots is drawn to indicate the plane of symmetry.

The 2D-PMFs show the free energy surface as a function of the movement of two sodium ions along the z-axis in the filter. The center panel of Figure 2 shows a PMF of the full-length pore domain of NavAb (intracellular gate closed). The bottom panel of Figure 2 shows the 2D-PMF of two ions passing through the truncated open model of NavAb that is used for the conduction simulations. The two-sodium PMFs share general structural features. The binding of the second sodium ion is also quite energetically favorable, suggesting that more than one ion is involved in conduction. In particular, two sodium ions are able to pass each other within the selectivity filter near Leu176 (Z ~ −2.5 Å) in both 2D-PMFs, consistent with previous PMFs and MD trajectories.^{18, 42, 47} This suggests that an ordering of the ions in single file—a necessary feature to support a knock-on mechanism—may not be strictly enforced by the NavAb pore. Some published 2-ion PMFs show sodium ions passing each other around and above Glu177 (Z = 2.5 – 7.5 Å) in NavAb rather than near Leu176. This is energetically prohibitive in our calculations, particularly in the PMFs of the truncated model.^{39, 66} The binding of the second sodium to the selectivity filter appears to be slightly more favorable in the full pore than the truncated-pore model. This is likely due to the differences in the electrostatic and dielectric environments. While an aqueous salt solution is in direct contact with the bottom of the truncated-pore model, a small aqueous cavity devoid of ions abuts to the selectivity filter of the full pore domain. This reasoning is supported by comparing the PMF of a sodium moving through the selectivity filter when a second sodium is at Z = 10 Å or Z = - 10 Å, per the left and right edge of the 2-ion PMFs. The difference between the PMF of an ion traveling these two paths for the PMF of the full channel shows that the presence/absence of an ion in the intracellular cavity (Z=−10 Å) influences the free energy surface felt by a permeating ion. However, this observation may be unique to the closed pore. For a channel in a true open state, cations could enter and leave the aqueous intracellular cavity through the intracellular gate resulting in a free energy surface resembling that of the truncated pore. The 1- and 2-ion PMFs of the full channel and the truncated pore suggest that truncating the pore above the intracellular gate does not drastically change the local free energy surface of ions passing through the selectivity filter, and that the truncated model is valid for exploring ion conduction in NavAb. It is possible that there are some long-range electrostatic effects due the dielectric environments in the truncated pore model compared to the “true” NavAb channel with open intracellular gate. However, differences in dielectric environment would be expected to equally affect ions with the same charge such as Na⁺ and K⁺. In that sense, it seems unlikely that the relative free energy of Na⁺ versus K⁺ in the selectivity filter could be altered by the reduced truncated pore model.

b). Current voltage relationship and selectivity for sodium and potassium

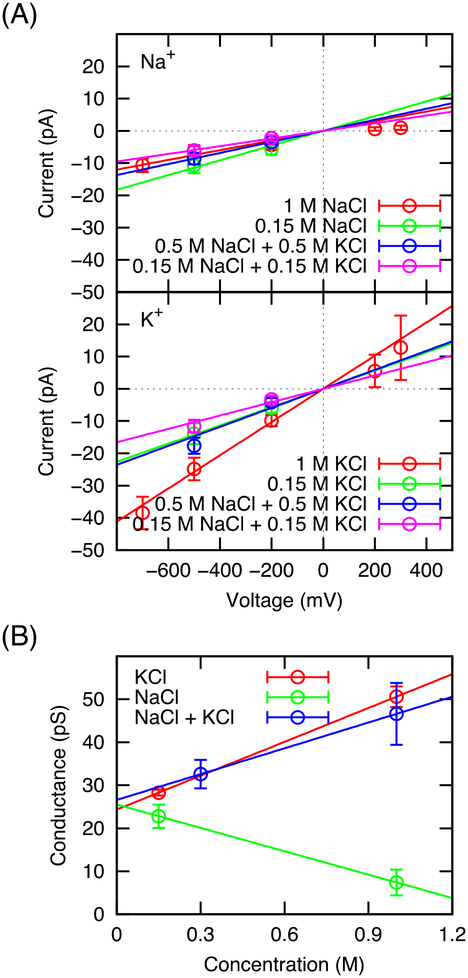
Non-equilibrium MD simulations were used to study the conduction of cations through the selectivity filter of the truncated NavAb selectivity filter under an applied membrane potential. Simulations were carried out in two concentration regimes, high concentrations to approach the give maximal conductance (1 M), and lower concentrations relevant to the physiological regime (0.15M-0.3M). Membrane potentials ranging from +700 mV to −700mV were examined (negative voltage is defined such that the net movement of the cations is inward toward the intracellular side of the pore). Figure 3 shows the current-voltage curves determined from continuous trajectories lasting hundreds of nanoseconds to microseconds in timescale, in the presence of NaCl, KCl, or both. The sodium current (top) is plotted separately from the potassium current (center) for solutions of one salt or both. Conductance was computed for sodium and potassium in each concentration condition from the slope of a line fit by linear least squares fit of the data in the current-voltage plot from Figure 3, these values are plotted in Figure 3 (bottom) and reported in Table 1 (error bars are the standard deviations from the linear fit).

FIGURE 3.

Ion conduction through a model of NavAb from nonequilibrium MD simulations. (A) Current-voltage curves; (B) Slope conductances and their associated error bars. Data from neat solutions of 1 M and 0.15 M of either salt are provided, as are data from solutions containing 0.15 M of each salt (total 0.3 M salt) or 0.5 M of each salt (total 1 M salt). Each data point is determined from 1.3–1.8 microseconds of simulation, since symmetric ion conditions are employed, the Nernst potential is zero and the data points correspond to chord conductances. The error bars are obtained by using the method of blocking transforms on the time series of instances of conduction. The fit lines are obtained from a linear least squares fit of the current of a system at multiple voltages and the y-intercept was set to 0. The slopes of the lines correspond to the slope conductance and errors for the slope conductance are determined from both the fit and the error bars of chord conductances. Slope conductances and their associated error bars are presented in the bottom graph as well as in Table 1. Chord conductances and their associated error bars are provided in the supplement (Table S1). Error bars on the conductance of individual simulations are 2σ determined using the method of blocking transforms to remove time correlation and reported along with the average values in Table S1.⁸⁴

Table 1.

Values of slope conductance of sodium and potassium through model NavAb pore.

Ion concentration	Na+ Conductance (pS)	Simulation	K+ Conductance (pS)	Na+/K+
0.15 M NaCl	22.8 +/− 2.7	0.15 M KCl	28.3 +/− 0.7	0.81
1 M NaCl	7.4 +/− 3.0	1 M KCl	50.6 +/− 2.4	0.15
0.15 M NaCl + 0.15 M KCl	11.9 +/− 0.3	0.15 M NaCl + 0.15 M KCl	20.7 +/− 3.3	0.57
0.5 M NaCl + 0.5 M KCl	17.1 +/− 0.04	0.5 M NaCl + 0.5 M KCl	29.5 +/− 7.2	0.58

Slopes are taken from data in the range of −700 mV to 300 mV, where available

The most striking observation from the ion conduction data reported in Figure 3 and Table 1 is the lack of any significant sodium selectivity in nonequilibrium conduction through the NavAb selectivity filter itself. In fact, the sodium to potassium conductance ratio is systematically smaller than 1.0 for all the conditions simulated here. The ratio is closest to unity (0.81) when the conductance of 0.15 M of NaCl and KCl are compared, although the ratio falls back to ~0.6 when simulating a combined mixture of ions. According to the data in Table 2, such a conductance ratio is very close to the ratio of the coefficient of self-diffusion for sodium and potassium in water. While these computational results may appear surprising, they appear to be generally consistent with the limited available experimental data on the selectivity of the NavAb channel. In fact, both the NavAb and the NavMs channels are less selective than the NaChBac channel according to experiment. Furthermore, the apparent lack of selectivity observed in the current simulations is unlikely to be related to the truncation of the intracellular gate. The latter is certainly expected to have some long-range effects on the global energetics of cations in the pore, as reflected in the PMF shown in Figure 2. But the conformation of the selectivity filter remains very close to the original X-ray structure in the current simulations, and it seems unlikely that the truncation of the TM helices and the removal of the aqueous cavity on the intracellular side could affect the ion selectivity in the narrowest part of the pore.

Table 2.

Coefficient of self-diffusion for sodium and potassium in NaCl and KCl solutions

Concentration	DNa+ (Å2/ps)	DK+ (Å2/ps)	DNa+/DK+
0.1 M	0.236	0.301	0.78
0.5 M	0.190	0.300	0.63
1.0 M	0.186	0.288	0.65

MD results no salt solutions taken from Wonpil Im.⁸³ All the simulated systems consist of 2750 water molecules in a periodic cubic box of ~44 Å with different number of ions according to different concentrations; 5 ion pairs (0.1M), 25 (0.5M), 50 (1M). The MD simulations were performed using the CHARMM program⁴⁸ with the TIP3 water model⁴⁹ and LJ parameters for the ions from Beglov and Roux.⁵² Water geometry was kept fixed with SHAKE.⁵⁷ MD trajectories were generated with a time step of 2 fs at constant pressure (1 atm) and temperature (300 K) in the CPT ensemble using PME.⁵⁸

Thus, the implication is that the NavAb selectivity filter is essentially a cationic pore supporting the conduction of ions at a rate comparable to aqueous diffusion, though the blockage effect displayed by sodium at high concentration appears to be more pronounced than the concentration-dependent change in diffusion. For a concentration of 0.15 M, the calculated conductance of the channel in sodium chloride and in potassium chloride is on the order of 23 and 28 pS, respectively. There is no significant difference in the chord conductance of sodium versus potassium at the nearest approximation of human physiological conditions, 0.15 M NaCl or 0.15 M KCl and −200 mV. These values are on the order of magnitude of experimental values reported for the conductance of prokaryotic channels under asymmetric concentration conditions: NavSp1p 31.1 pS,²¹ NaChBac 12 pS,¹⁷, NavAb 37pS.¹ However, a conductance of 106 pS has been reported for the pore construct of NavSp1p at 0.5 M NaCl, and 120 pS for NaChBac in 150 mM NaCl under symmetric conditions in lipid bilayers.^30–31

An intriguing observation is the difference in concentration dependence for sodium and potassium. While potassium current increases with concentration, sodium current decreases, indicative of some type of self-blocking mechanism. One may note, however, that the coefficient of self-diffusion of sodium also drops by 20% from 0.1 to 1M (Table 2) for the same potential function. The decrease as a function of concentration contrasts with experimental observations for the NavMs channel, which increases with sodium concentration for concentrations up to 0.445M.¹⁹ However, mixing sodium and potassium in equal proportion appears to recover the conductance of the potassium solution over the range of concentrations. When the cations are in direct competition, the potassium/sodium selectivity from slope conductance is similar at both concentrations. In general, the conductance of potassium varies more with the concentration and co-dissolved species than that of sodium, which is always small.

c). Voltage, concentration, and cation alter the behavior of NavAb

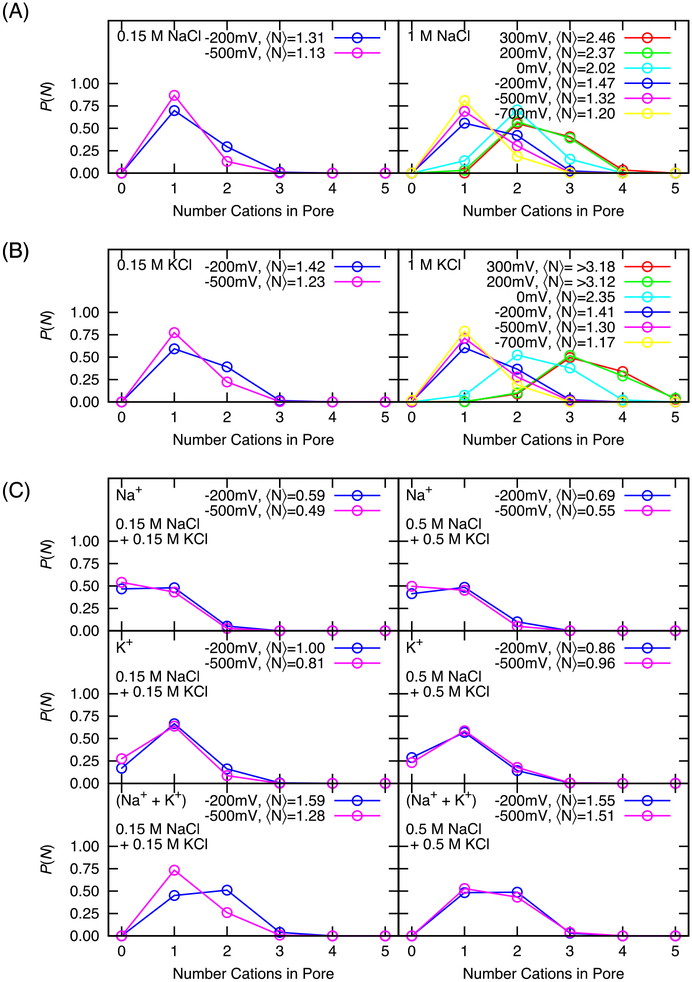
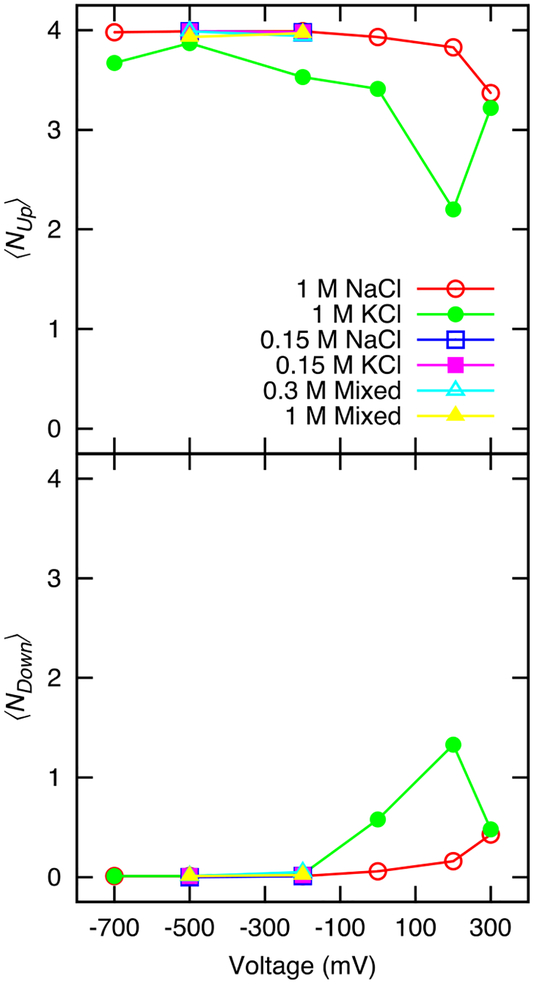
The difference in concentration dependence of conduction of sodium and potassium ions through NavAb suggests that they may not be conducted through the selectivity filter according to the same mechanism. To examine the permeation mechanism, a comparison is made of several time-averaged features of the selectivity filter. For this purpose, the pore region is defined as a cylinder of 5 Å radius, extending from −7.5 Å below to 10 Å above the center-of-mass of the Cαs of residues 175 to 178. The probability of finding the pore occupied by n ions, P(n), is plotted in Figure 4. The mean and sigma of these distributions is reported in table S2. Few values exist for selectivity filter occupancy of NavAb by Na⁺ (2.09 +/− 0.5 by Chakrabarti et al.⁴⁴ and 2.3 by Boiteux et al.⁴³, both in agreement with our value at 0 mV), and none have been reported for K⁺.⁷⁸ To demonstrate the significance of results, two-tailed t-tests of the hypothesis that pairs of distributions have the same mean (or different) are reported in table S3 for concentration dependence, S4 for voltage dependence, and S5 and S6 to compare occupancy of sodium with potassium in single species and mixed cation simulations.⁷⁹ Hypotheses are tested with a 95% confidence interval and 100 degrees of freedom (N −1) and means were accepted as “Same” if t < t_critical = 1.984, and “Different” otherwise. An increase in sodium concentration correlates with an increased average number of sodium in the selectivity filter (Figure 4 and Table S2 and S3). However, the potassium concentration has no significant effect on the number of potassium in the selectivity filter. Similarly, for simulations containing both cations, most concentration-dependent differences are not significant. The average number of cations in the pore is between 1.1 and 1.6 for all conditions of negative applied potential (Figure 4 and Table S2), and for NaCl simulations, is slightly larger for −200 mV than for more negative potentials (Table S4). However, the number of cations in the pore increases when a positive voltage is applied. In addition, at 0 mV and positive voltages, differences in occupancy between Na⁺ and K⁺ occupancy are significant (Table S5, S6). This correlates to conformational changes of the Glu177 side chains, however the degree to which either aspect is the cause and symptom of the other is difficult to separate. There is more glutamate flipping at positive voltage, but higher ion occupancy may also contribute to stabilize the dunked conformation. The pore is readily occupied by up to three sodium ions or four potassium ions. The average occupation of the pore at 0 mV and positive voltages is in agreement with previous MD studies.^43–44 However, at negative voltages, the occupation of the truncated model is slightly lower than that observed in MD studies based on the complete NavMs or NavAb pore.^{19, 41–44} The lower average occupation of the truncated selectivity filter at negative potentials than of open models and structures of the full pore could originate in the hydrophobic cavity which has a lower barrier to enter (for one ion) than the aqueous solution, per the region between −5 and −10 Å in the one and two ion PMFs, although the full pore domain in this calculation was closed. In 0.15 M NaCl + 0.15 M KCl solutions, when there is only one cation in the filter, it is more likely to be potassium and when two cations are present, it is most likely to be one sodium and one potassium.

FIGURE 4.

Probability of the number of ions occupying the selectivity filter as a function of concentration and voltage. (A) in NaCl, (B) in KCl, and(C) in simulations containing a mixture of NaCl and KCl. (Lines are meant as a guide to the eye.)

The voltage-sensitivity of ion occupancy observed in the present simulations is intriguing. Generally, voltage-sensitive occupancy of a pore can occur if, as a function of applied voltage, the entry rate of ions is accelerated while the exit rate is slowed down. The truncated pore mode presents no energy barrier to an ion moving from the solution all the way to the edge of the selectivity filter. Nonetheless, it is possible that some barrier would oppose the entry of ions through the intracellular gate in the case of the “true” open state of the full-length channel. However, these differences would be unlikely to greatly affect ion occupancy, as continuum electrostatic calculations show that the membrane potential across the intracellular gate of similar tetrameric potassium channels is fairly small.^80–81 It is difficult to compare the voltage-dependent ion occupancy observed in the present simulations from previous MD results on the NavAb channel. Ngo et al. previously reported a self-blocking mechanism observed during steered MD simulations driving the ions in the inward direction. There was no actual membrane potential and no steady state ion conduction. In contrast, the voltage-dependent occupancy properties describe here are deduced from genuine non-equilibrium steady state conditions with sustained ion conduction. Therefore, we think that the voltage-sensitive ion occupancy is a genuine feature of the selectivity filter of the NavAb channel.

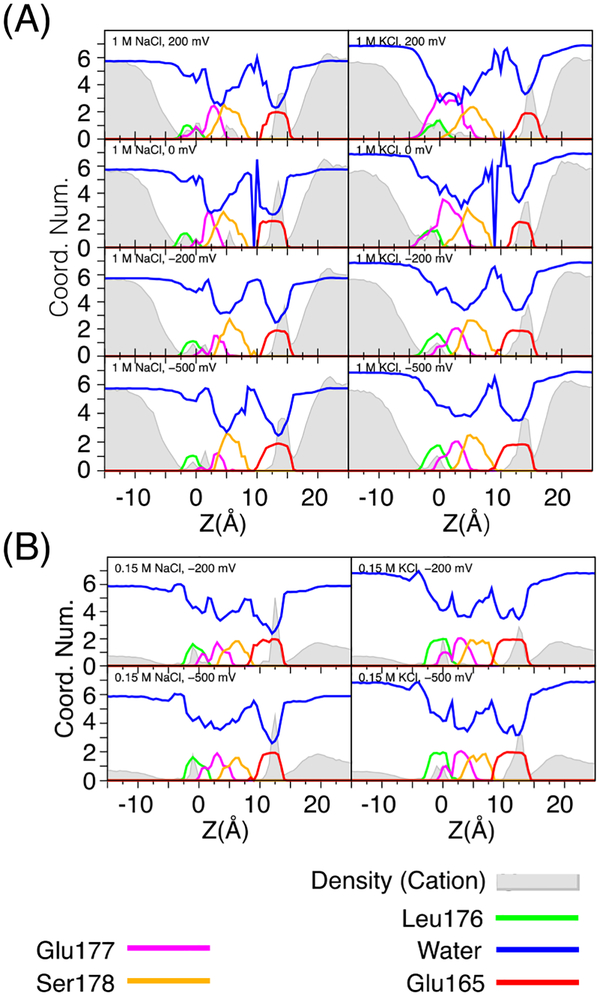
The average density profiles from the non-equilibrium trajectories with applied membrane potential projected onto the Z-axis for sodium and potassium (grey solid) and the average coordination number water and channel oxygen atoms with cations (colored lines) are plotted in Figure 5. Sodium and potassium are both coordinated by Ser178, Glu177, and Leu176 in the selectivity filter. In the extracellular funnel, coordination of the cations is also strongly affected by Glu165 (red line, Z = 10 – 15 Å).

Figure 5.

Density profiles and ion coordination numbers in the pore. Filled lines are the density profiles of sodium and potassium in the truncated model of NavAb for solutions of 1 M (A) and 0.15 M (B). Units are arbitrary, but comparable between subfigures. Colored lines are the coordination number of water and protein oxygen atoms solvating sodium and potassium where cutoff distances have been determined from the first minimum of the radial distribution function. Each of the oxygen atoms of the glutamate carboxylic acid side chain are counted separately. Glu165 is located in the wide extracellular funnel above the selectivity filter. The side chains of Ser178 and Glu177 line the selectivity filter along with the carbonyl of Leu leucine. Minimal coordination of sodium and potassium to the carbonyl of Thr175 occurs and it is not shown.

The density profiles projected in grey onto the Z-axis in Figure 5 (and directly compared in Figure S1) were extracted from the nonequilibrium trajectories with applied membrane potential and the profiles for the 0 mV simulations can be compared to PMFs in the literature created from the inverse density of sodium projected onto the pore axis (1D or 2D, with an unrestricted number of cations in the pore region).⁴³ The PMFs show weaker binding to the selectivity filter than PMFs from biased simulations with strictly 1 or 2 ions in the SF. Comparable PMFs have also been computed from ion density for NavMs.^{19, 41} Boiteux et al.⁴³ and Finol-Urdaneta et al.¹⁸ performed related calculations of the 1D-PMFs based upon sampling of the selectivity filter with two ions in the selectivity filter. To compute a 1D-PMF along the pore axis of NavAb truncated to include only the p-loop, Domene et al.⁴⁰ use a bias-exchange method that considered different numbers of ions in the pore. Densities profiles of sodium and potassium taken radially and along the pore axis are plotted in supplemental Figure S2 and S3. Binding sites are apparent, and their numbers grow with the number of ions in the pore. For a single cation there are two binding sites in nearly each simulation one at approximately Z = 0–2 Å and r = ~ 0 – 1 Å, and one slightly beneath this near r = 1 – 2 Å. When two sodium or potassium ions are present in the pore, there are 3 to 4 distinct binding locations, as well as a continuum of density along the pore axis. The binding sites for sodium and potassium are generally similar, although the frequency of their occupation may differ between simulation conditions.

Glu165 appears to coordinate sodium and potassium to a similar degree independent of concentration and voltage, although it is mobile. It strongly influences the concentration of ions above the selectivity filter. This residue is not conserved in NavMs, NavSp, or NaChBac. This glutamate is offset from the selectivity filter, but beneath Glu165 the cation is fully hydrated, although the density in this region is very low. The cation is partially coordinated by two Ser178 near Z = 5 Å, which gives way to Glu177 as it moves into the selectivity filter. The coordination of both sodium and potassium to Ser178 is greater at 1 M than at 0.15 M in solutions of NaCl or KCl. Ion coordination by Glu177 is voltage dependent, as well as cation dependent. Glutamate coordinates potassium more than sodium under all conditions, but this is particularly evident at 0 mV and +200 mV and 1 M, where potassium is strongly coordinated by the side chain of Glu177 including the entire region where potassium is coordinated by Leu176 as well as above it. In contrast, sodium is consistently coordinated by a single carbonyl of Leu176 in 1 M NaCl between Z = −1.5 – 0 Å. at all voltages. At 0.15 M NaCl there is a region near Z = −1 Å where sodium is coordinated by ~1.5 Leu176. In general, potassium is coordinated more by Leu176 and Ser178 than sodium, in agreement with previous studies of NavAb.^{18, 39} The most populated binding sites are coordination to Leu176 or simultaneously Leu176 and Glu177 in all of the simulations of NaCl or KCl. At 0 mV and +200 mV in 1 M NaCl, another binding site at Z = 5 – 7 Å is populated with much higher probability than at the other conditions. The coordination of sodium and potassium agree best with the results from the simulation studies on NavAb at 0 mV by Chakrabarti et al.⁴⁴ and Finol-Urdaneta et al.¹⁸. However, a direct comparison of coordination numbers reported in other studies is complicated by differences in concentration and applied voltage.^{19, 39, 41, 66, 68} Furthermore, it is possible that ion coordination differs in NavMs and NavAb. The regions of near full hydration between Leu176 and Glu177 as well as at and above Ser178 in Figure 5 are not analogous to the positions of hydrated sodium determined from the crystal structure of NavMs.⁹

The side chain of Glu177 located in in the selectivity filter has been observed in previous MD studies to dynamically flip its orientation.⁴⁴ The majority of states occupied by individual side chains at any given time can be described as: upward and downward (or dunked), corresponding to side chain dihedral χ₁ = 50°−180°, χ₂ = 0°−100° and χ₁ = 150°−210°, χ₂ = 290°−330°, respectively. In Figure 6, the average number of glutamate in the upward and downward conformations are plotted as a function of applied voltage for each of the concentration conditions. We note that other conformations are possible, including, but not exclusively, the moments during the transition between these two states, however they are less frequent, less well-defined, and presented here only as the disparity between the sum of the average number of glutamates in the up and down states and the number of glutamates in the selectivity filter (four). All four glutamate side chains are usually in the upward position under all simulation conditions with negative potential except 1 M KCl. The Glu177 side-chains are anions, and move in the opposite direction to the permeating cations. When there is a large positive voltage, the negative Glu177 move down and adopt a so-called “dunked” conformation. A strong positive potential can induce transitions of the side chain toward the downward position independent of which cation is in the simulation. However, 1 M KCl correlates with an increased variability of the glutamate side chain positions over the range from −700 mV to 200 mV, including positions that are not defined as either the upward or downward states. Figure 5 shows that relative to negative voltages, both sodium and potassium are coordinated by Glu177 over a longer region (−2.5 Å < Z < 5 Å) and are coordinated by more Glu177 at positive voltages. Ke et al. had observed a similarly small propensity of the glutamate side chains to enter the “dunked” conformation at negative voltages in molecular dynamics simulations of NavAb at 100 mM NaCl and NavMs in 500 mM NaCl, although at positive voltages our model shows fewer side chains in the dunked conformation, but also fewer in the up conformation.^{41, 68} At positive voltages the number of cations in the pore increases, occupation of the selectivity filter by three cations has been correlated to an increase in glutamate flipping by Domene et al.⁴⁰ Comparison with Figure 4 confirms this correlation. In the present simulations, we see less downward conformation of the glutamate side chains 0 mV and 1 M NaCl than observed by Chakrabarti et al. in the full NavAb pore at 0 mV and 150 mM NaCl using either the CHARMM or OPLS force fields.⁴⁴ Ke et al. have hypothesized that they may have seen less glutamate flipping in simulations of NavMs because of the presence of an ion in the hydrophobic cavity of NavAb in the study of Chakrabarti et al.⁴¹ Alternatively, it is possible that the open state is correlated with less conformational variability of the glutamate.

FIGURE 6.

The probability of observing N Glu77 sidechain in the defined upward (Up) or downward (Down) conformation. Note that with the exception of 1 M KCl, the points at −500 mV and −200 mV overlie each other.

d). Sodium and potassium conduction through the NavAb selectivity filter

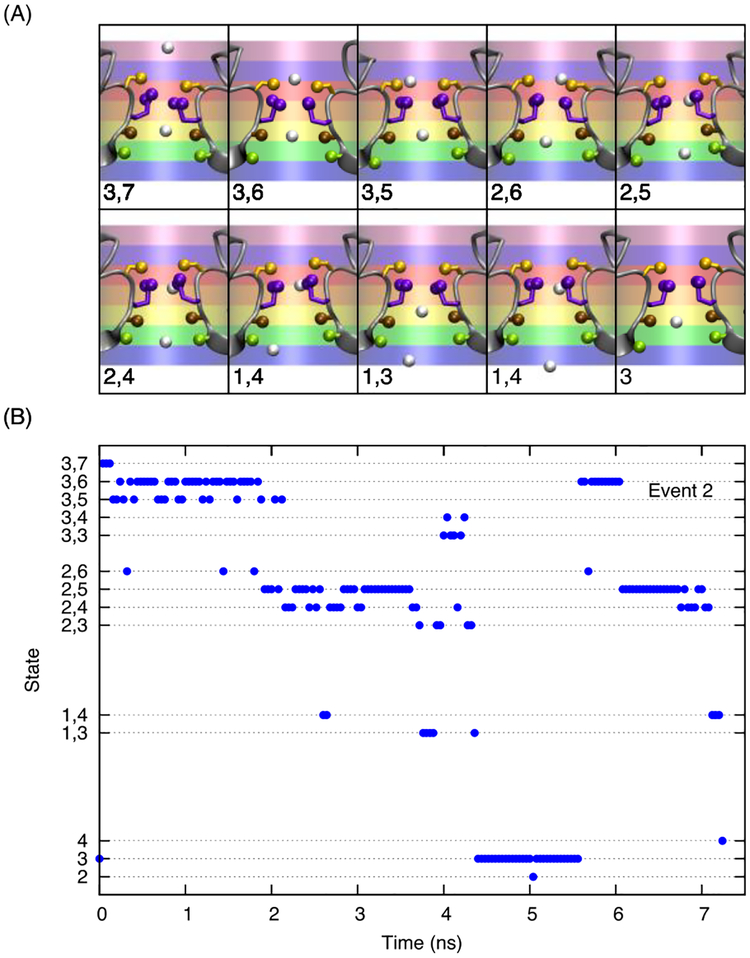
In order to draw statistically relevant conclusions about the mechanism of ion conduction, only successful and productive permeation events were analyzed in terms of their duration and sequence of ion positions in the selectivity filter. For the sake of simplicity, the analysis was limited to the inward conduction, which corresponds to the physiological function of sodium channels in excitable membranes. A conduction event was defined to occur from the moment an ion entered a cylindrical region 10 Å above the center of mass of the Cα of residues 175–178, until it exited the cylinder 7.5 Å below it. This is the same region used to define the number of ions in the selectivity filter in Figure 4. For the purpose of this analysis, the cylinder defining the selectivity filter was subdivided into 7 equal region of 2.5 Å thick along the Z-axis, as illustrated in the top panel of Figure 7. Region 1 is just beneath threonine and is the lowest region of structured sodium density, leading to the intracellular vestibule of the channel (truncated in the present model). Region 2 is the threonine-binding site (inner site). Region 3 is the leucine-binding site (central site). Region 4 corresponds to site S2, a local minimum on the barrier, in NavMs.^{19, 41} However, in studies of NavAb this region seems to be lumped into either the central site or the high field site (Glu77). Furthermore, in some published PMFs of NavAb but not others, a barrier is present in the region of state 4 (0 Å < Z < 2.5 Å).^{18, 42} With its long flexible side chain, Glu177 can reach both regions 5 and 6 along the pore. Region 7 marks the uppermost region of the narrow constriction of sodium density, opened to the external bulk solution. The extracellular funnel continues above this, but is considerably wider than the cylinder used to demarcate the selectivity filter. One ion may only be in one region of the pore as defined by its center of mass at that instant in time. However multiple ions can occupy the pore simultaneously. Occupancy states of the pore are defined by the presence of cations in one or more of these regions. For example, in state 3,7 a first ion is in region 3 and a second ion is in region 7. Furthermore, multiple ions can be present in a single region (e.g., in state 3,3,4 there would be two ions in region 3 and a third in region 4). While the ion crossing the pore from one side to the other is tagged for determining the duration of a conduction event, the sequence of states during the permeation event was recorded by treating the ions as indistinguishable such that information about the actual identity and order of the ions inside the selectivity filter was not preserved. For the sake of simplicity, a single state was defined for the infrequent situations where 4 ions were present in the selectivity filter, and another state for 5 ions. These rare situations are sometimes observed under positive voltage conditions (supplemental Figure S4).

FIGURE 7.

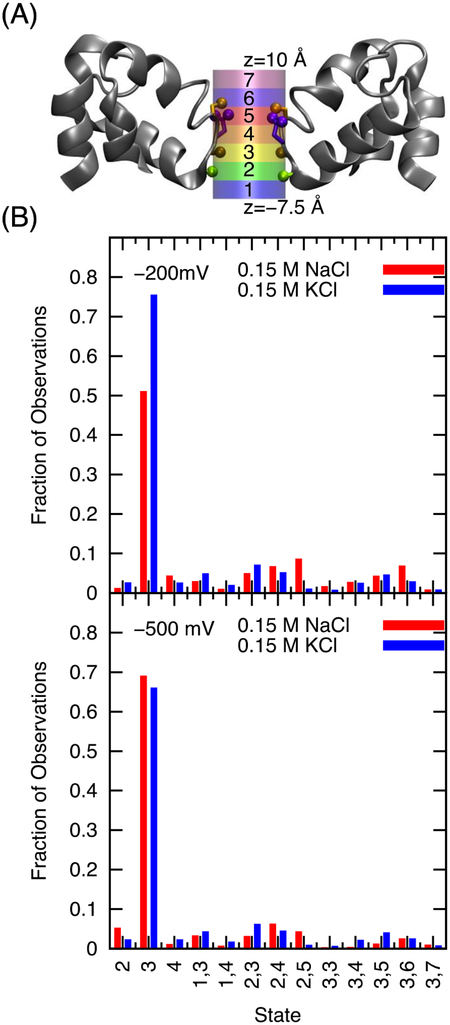
Discrete region in the selectivity filter and their probability. (A) Depiction of the selectivity filter divided into 7 regions used to define the states. The protein backbone is illustrated in gray, while the serine side chain is orange, the glutamate side chain is purple and the carbonyl groups of leucine 176 and threonine 175 are brown and green respectively. The ions are treated as interchangeable. A single ion in region 3 would be denoted as state 3, while two ions in region 3 would be denoted as the state 33, and a configuration of one ion in region 2 and two in region 3 would be state 233. 4444 and 55555 are an exception to this, these states are defined by 4 and 5 ions in the pore respectively, independent of their positions. (B) Density of states, for 0.15 M NaCl and 0.15 M KCl in the presence of an applied electric field of −200mV and −500mV, respectively. Only states that account for >0.6% of states sampled in a system are included in this chart. (13 states remain).

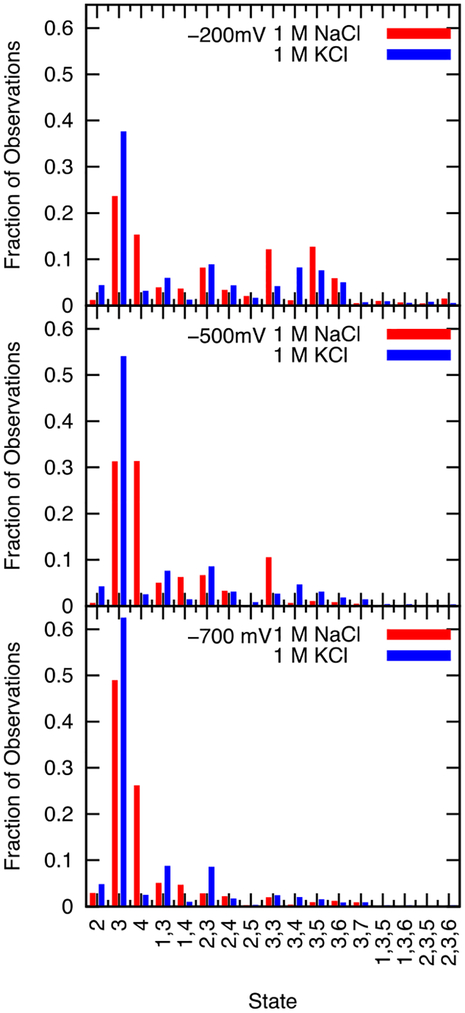
The state of the selectivity filter defined by the coordinates of all the ions in the pore was recorded every 40 ps from the time an ion enters to when it leaves (from the top to the bottom for negative potentials and from the bottom to the top for positive potentials). Multiple cations present in the selectivity filter results in conduction events that overlap in whole or in part, but the series of states of the selectivity filter experienced by each individual ion being conducted is the important quantity for describing the mechanism. So the normalized distribution of states experienced over the course of each conduction event for the simulations under physiological concentrations of NaCl and KCl (0.15 M) is reported in Figure 7. All states observed with a probability of 0.6% or more are reported. Similar plots for 1 M NaCl and 1 M KCl under applied voltages ranging from −700 mV to −200 mV are provided in Figure 8, while data for non-negative voltages is given in the Supplementary Information (supplemental Figure S4).

FIGURE 8.

Density of states, for 1M NaCl (red) and 1M KCl (blue) at negative voltages. The top, center and bottom graphs show data from simulations with an applied voltage of −200 mV, −500 mV, and −700 mV, respectively. Only states that account for >0.6% of states sampled during the conduction events of at least one of these systems are included in this chart. 17 states are shown, but not all are sampled by all voltages. The ions are treated as interchangeable for the determination of the state but not for keeping track of the conduction events. Because the distribution of states is summed from each conduction event, and multiple ions are frequently in the pore, states with more than one ion are counted from the perspective of each ion.

Figure 7 shows that at 0.15 M under voltages of −200 mV and −500 mV, the most commonly occupied state of both sodium and potassium is a single cation in site 3, the leucine-binding site. The remainder of the time the systems are in a series of singly and doubly occupied sites. Figure 8 shows that at 1 M KCl, state 3 has the highest occupation, although in 1 M NaCl state 4 also figures prominently consistent with the single and double peaks near Z = 0 Å in Figure 5 for sodium and potassium at 1 M, respectively. Most of the states sampled involve one or two ions in the pore, but at −200 mV three ions are occasionally observed in the selectivity filter in both NaCl and KCl at 1 M. Also notable, the 1 M NaCl system samples the state 33 at −200 mV and −500 mV more than 10% of the observed time. This state is sampled much less frequently in 1 M KCl and at lower concentrations. Figure S4 shows that several ions in the selectivity filter are observed at 200 mV, although the number is greater for potassium than sodium. This is consistent with the pore occupancies reported in Figure 4.

An example of the time-course of an ion being conducted through the pore under conditions of 0.15 M NaCl and an applied voltage of −200 mV, described in terms of the states as defined, is provided in Figure 9 and an additional example is provided in the SI (Figure S5). Images of the trajectory are used to illustrate examples of the position of sodium ions (white spheres) and protein side chains (threonine carbonyl oxygen green, leucine carbonyl oxygen brown, glutamate carboxylate oxygens purple, and serine hydroxyl carbons orange) and their corresponding defined states. When an ion enters the uppermost region of the pore, there is frequently already one cation in the pore in the leucine-binding site (region 3). The upper ion moves into the high field site and the lower ion moves lower, into region 2. Both ions may end up near leucine, but one ion will later leave out the bottom of the selectivity filter while the other ion remains either in region 3 or 4. At this point a new cation could enter region 7, restarting the process.

FIGURE 9.

Analysis of a complete conduction event of a sodium cation in the system with 0.15 M NaCl and a voltage of −200 mV. (A) Sequence of configuration in the pore. Sodium ions are represented by white spheres, the side chains of the selectivity filter are represented by balls on sticks, serine is orange, glutamate is purple, and the leucine carbonyls are brown spheres, and the threonine carbonyls are green spheres. The cylinder of seven equal regions used to define the states is drawn and the state defined by the center of sodium ions for each image is marked on the graphic. (B) The trajectory of the particular conduction event the images are taken from. Occupational states are reported at 40 ps intervals. Note that additional ions leave or enter the SF during the time a particular ion takes to traverse the SF. Horizontal gridlines are meant to guide the eye.

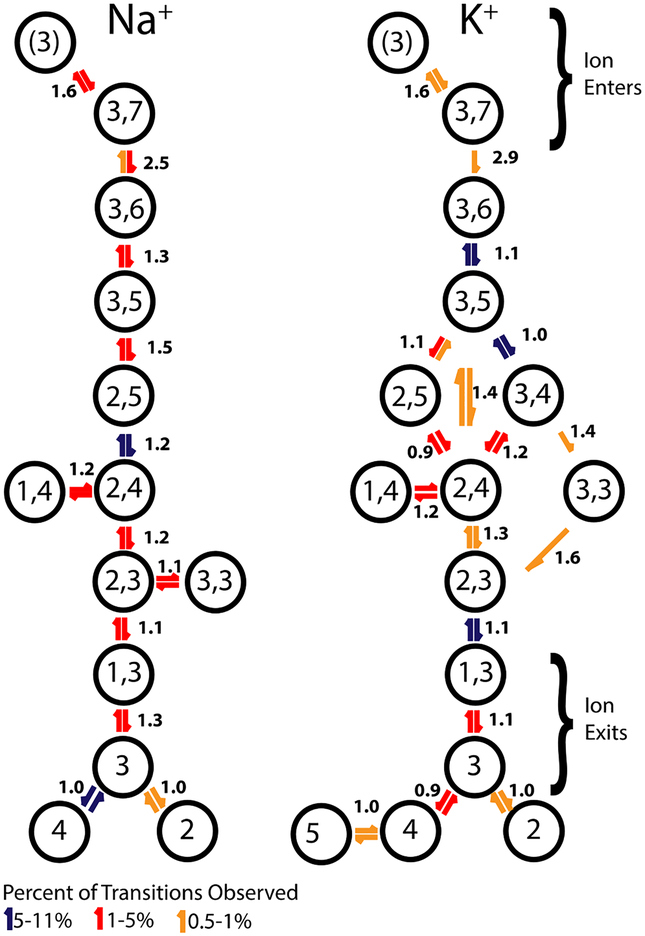
The dominant ion conducting process for sodium and potassium is depicted in Scheme 1 in terms of discrete states. The scheme was built from MD permeation data collected at 0.15 M and −200 mV. These conditions offer a limited number of states compared to the simulations at 1 M, but are closest to the conditions in electrophysiological experiments. Defining a small set of discrete states allows the relative frequency of transitions between these states to be determined from the simulations. All transitions between states for all productive conduction events of a simulation were collected and sorted in terms of which occurred most frequently. (e.g, what part of the transitions 100% total was an individual transition). The ratio between the frequency of the forward (downwards/outwards on the scheme) and reverse (upwards/inwards) transition is reported as the number to the side of the arrows. This is a measure that takes into account the movement between states but not the length of time spent in any state. A large number of transitions originating between two states would suggest that there is little energy barrier between them (compared to the applied potential of −200 mV), and perhaps these would not be distinct states in a less arbitrary scheme. Considerable asymmetry in the forwards and back transitions would imply one state to be favored over another.

SCHEME 1.

The most common transitions between states (those responsible for 99.5% of observed transitions), their relative frequency, and the asymmetry between the forwards and backwards transitions are mapped for simulations of 0.15 M NaCl (left scheme) or 0.15 M KCl (right scheme) under an applied voltage of −200 mV.

On the basis of Scheme 1, the ion conduction process may be summarized by the following sequence of events. Initially, a single sodium or potassium occupies the leucine-binding site (state 3). A second cation enters the selectivity filter from the extracellular side (state 3,7), and then starts to progress inward along the pore (states 3,6 → 3,5) until it “knocks” the lower sodium into the second region (3,5 →2,5), and proceeds to the release of the ion toward the intracellular side (2,4 → 2,3 → 1,3 → 3). The knock-on mechanism is not strictly enforced however, as there can be some jostling around Leu176 corresponding to states 2,3 and 3,3, allowing the possibility of switching the order of the two ions along this region of the pore. This observation is also consistent with the 2D-PMF of Figure 2, which shows that the free energy surface corresponding to the state 3,3 (−2.5 Å < Z < 0.0 Å for both ions) does not strictly prohibit such ion-ion exchange.

Potassium conduction covers a somewhat larger variety of states, but for both sodium and potassium, the state 1,3 is typically visited just before the ejection of the lowest cation. The system then returns to state 3. This mechanism is not consistent with that proposed for NavMs, which allows for occupation of the high field site (region 5 and 6) by two cations, and in the case of potassium requires it.¹⁹ The same mechanism predicted for NavMs has been proposed from PMFs of NavAb^{39, 42}; however, it was not actually observed in simulations of conduction of an artificially opened NavAb pore in NaCl. The traces of actual conduction events reported by Stock et al. resemble the mechanism described here, which allows for double occupancy near leucine, but not in the high field site.⁴² The only time we observe a state that could potentially be described as containing two cations in the high field site is at +200 mV and 1 M (NaCl or KCl), when region 4 can be occupied along with 5 or 6. There is always at least a third cation in the pore in these instances.

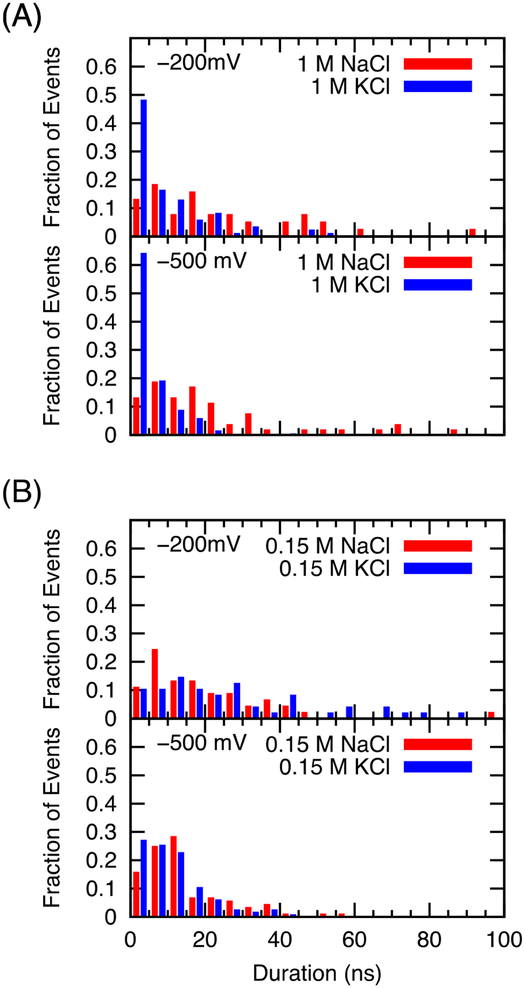
Figure 10 shows the distribution of durations of the individual conduction events for solutions of NaCl and of KCl both at 1M and 0.15 M in nanoseconds at two voltages. Only conduction of cations that did not begin the simulation in the selectivity filter was considered. Dwell times for sodium in the SF are roughly consistent with values obtained by Ke et al. for NavMs under charge a displacement protocol of ~−565 mV (13.5 +/− 0.6 ns).⁴¹ However, the comparison of full-pore NavMs dwell times in the work of Ke et al.⁴¹ to that of Ulmschneider et al.¹⁹ using applied electric fields to drive conduction suggest differences in the average dwell time between the two works is on the order of the difference observed for sodium versus potassium in the later. We do note that average conductance and occupation of the selectivity filter were in agreement in those two works, suggesting that the definition of dwell time may differ in some unspecified way.^{19, 41} At both −200 mV and −500 mV, 1 M KCl has a much greater proportion of conduction events that occur within 5 ns than 0.15 M KCl, or NaCl at either concentration, correlating with the larger conductance of NavAb in 1 M KCl. At 0.15 M, the distribution of duration of conduction events for simulations with sodium and with potassium are much more similar.

FIGURE 10.

Distribution of time taken by individual (identifiable/non-interchangeable) ions to pass from 10 Å above the COM of the selectivity filter to 7.5 Å beneath it, binned in 5 ns increments.

IV. CONCLUSION

The conduction of sodium and potassium through the selectivity filter of the NavAb channel was studied using computational methods based on truncated model of the pore domain embedded in planar nonpolar membrane. The simplified model enabled us to probe directly the ionic conduction through the narrowest part of the channel, unimpeded by the diffusional access resistance through the intracellular gate. The most striking observation from nonequilibrium simulations over a range of ion concentrations with an applied membrane potential is the lack of any significant sodium selectivity. The sodium to potassium conductance ratio is systematically smaller than 1.0 for all the simulations. The results indicate that the NavAb selectivity filter is essentially a cationic pore supporting the conduction of ions at a rate comparable to aqueous diffusion. The mechanism dominating the productive ion conduction events was analyzed.

There has been considerable disagreement as to the mechanisms of sodium selectivity of prokaryotic Nav channels. The discrepancies have been attributed to differences in force fields, but could also be due to differences in ion concentration and applied membrane potential. An example of unresolved issues is whether two cations can reside in the region just above Glu177 or at the level of Leu176. Under conditions of 1 M NaCl, two sodium ions visit the region #3 simultaneously far more frequently than in any of the other conditions examined (state 3,3). This situation allows an ion to pass-by another, an action previously observed in several simulation studies.^{42–44, 82} This is often described as a mechanism by which one ion can pass-by another to exit the selectivity filter first. However, because these events are energetically equivalent, repeated ion-ion passing are unproductive, or “redundant”, in contrast with the progressive movements of ions through the pore according to a single file knock-on mechanism. Under high concentration, the increased sodium occupancy and particularly the increased occupancy of the state 3,3 may indicate that the sodium ions spend time making the aforementioned redundant motions, which are more infrequent in the case of potassium (or at low sodium concentration)s. Conduction in the outward direction, particularly of sodium, may exhibit some rectification. The lower conductance in the outward direction correlates with larger numbers of cations in the selectivity filter, and may also be attributed to the effects of a positive voltage on the conformational distribution of Glu177, which can be pulled down by voltage.

The mechanisms of conduction through the NavAb selectivity filter, and models of it are likely complex and depending on multiple factors. Both membrane potential and concentration and identity of cations influence the orientation of Glu177 as well as the average number of cations in the pore. Under conditions of 0.15 M NaCl or KCl, and biologically relevant applied voltages of −200 mV, negligible sodium/potassium selectivity is observed. Permeation occurs primarily via a loose knock-on mechanism for both sodium and potassium, although a single file ordering of the ion is not strictly enforced along the NavAb pore. Weak potassium selectivity even in the lower concentration range is seen at −500 mV. The effect of voltage on occupancy of the pore is more dramatic. The average number of cations in the selectivity filter is greater in the absence of an electric field than in the presence of a negatively applied voltage, and much greater at positive voltages, consistent with asymmetric conductance or rectification. Higher concentrations of sodium, frequently corresponds to slightly larger average number of cations in the pore, but this is not unanimous. Higher concentrations of sodium also correspond to increased sampling of a state where two sodium ions simultaneously occupy the region of the Leu176 carbonyl, which is implicated in a bypass mechanism, but can also work as a rotary, potentially contributing to the low conductance observed for simulations of NavAb at 1 M NaCl. Occupancy of this state in solutions of KCl is far more rare. Further, the presence of potassium in mixed solutions (NaCl/KCl) allows NavAb to retain the conductance of the same concentration of KCl, predicting an unusual anomalous mole fraction effect.