Abstract
This article describes the modeling of the compaction/consolidation behavior of thermoplastic composite prepregs during the thermoforming process. The proposed model is principally based on a generalized Maxwell approach. Within a hyperelastic framework, viscoelasticity is introduced for the compaction mode in addition to the in-plane shearing mode by taking into account the influence of the resin and its flow during consolidation. To reveal the evolution of the consolidation level, which reflects the number of voids in the composite, an intimate contact model was used during the process. The model was characterized by a compaction test at a high temperature. It was implemented into a recently developed prismatic solid-shell finite element. The analysis of the thermoforming of a double dome demonstrated the relevance of the consolidation computation in determining the process parameters leading to a composite part free of voids.
Keywords: forming, thermoplastic, prepreg, consolidation, process simulation, finite element method
1. Introduction
Continuous fiber-reinforced prepreg thermoplastic composites are of interest to the automotive industry [1,2,3] and by using thermoforming, short cycle times are made possible. This manufacturing technique can be easily automated and can be achieved thanks to technologies that are close to those of metal sheet forming. Furthermore, the higher impact resistance and ductility of thermoplastic prepregs, as well as their reparability and recyclability, offer great competitiveness over composites with thermosetting matrices.
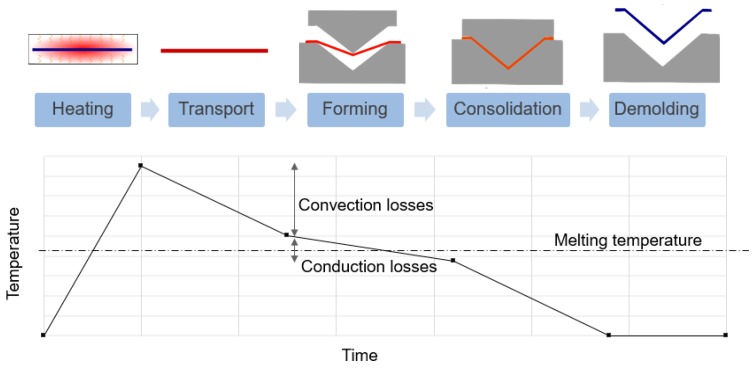
As illustrated in Figure 1, the complete thermoforming process consists of five stages. The thermoplastic prepreg blank is preliminarily heated slightly over the fusion temperature of the matrix, then quickly transported to a mold. After shaping of the part, a pressure is applied and maintained to consolidate the composite, and the temperature is lowered for crystallization. Subsequently, the final part is obtained by demolding. The thermoforming process is complex considering the multidisciplinary problems, such as the thermal, mechanical and physical aspects [4,5,6,7]. For the purpose of producing a finished product with a determined cost and quality, the manufacturing process must be carefully optimized with appropriate processing conditions. Virtual manufacturing by numerical simulations has become an essential approach to replace the traditional (and costly) trial and error processes [8,9,10]. In view of this, some investigators have created their proper models by considering the processing parameters (temperature, pressure), the architecture of the composite structure (stacking, multiple plies, etc.), and the defects (wrinkles, porosity, distortion, micro fractures, etc.) during the thermoforming process. Simulation methods have thus been developed for the forming stage (draping) [5,8,10,11,12,13,14,15,16,17,18].
Figure 1.
Principal steps of the thermoplastic thermoforming process.
The consolidation phase is very important for the quality of the composite part. During this step, pressure is applied to the formed part that leads to compaction to ensure a good cohesion of the matrix by removing the inter- and intra-ply porosities. Modeling of the consolidation step thus helps to predict the time consumption and defect content under the given process parameters, i.e., temperature, pressure, etc. The objective of this article is to propose a simulation of the prepreg thermoforming process including the consolidation phase in order to determine the time and pressure required for consolidation of a composite part of any geometry.
In the recent past, different aspects of consolidation for thermoplastic and thermosetting composites during manufacturing have been addressed. These include automated lay-up [19,20,21], VARTM process (Vacuum Assisted Resin Transfer Molding) [22], autoclave [23], and compression flow molding [24,25], all of which focused on experimental investigations. Furthermore, Helmus et al. proposed both a stochastic approach [26] and an air evacuation-coupled impregnation model [27] for out-of-autoclave prepreg consolidation. In the framework of the finite element method, a two-dimensional thermal model [28] and a constitutive model [29] have been developed for composite consolidation during a filament winding process. Wrinkling is one of the major failure mechanisms [30] and can be induced by consolidation. Some authors have analyzed the generation of wrinkling during consolidation both in experimental studies and finite element simulations [31,32].
This resin flow is governed by Darcy’s law [33,34], coupled with fiber bed compaction behavior, which is assumed to be an elastic porous medium with incompressible and inextensible fibers. The compaction behavior is described by the fiber volume fracture as a function of the pressure [35,36,37,38,39,40]. Another typical resin flow is transverse squeeze flow to describe the viscous incompressible thermoplastic fluid moving transversely together with the fibers. The fluid is modeled according to either a Newtonian [41,42,43] or non-Newtonian [44] behavior or both [45]. Taking into account the two flow types, Belnoue et al. [46] recently proposed a viscoelastic model in terms of strain- and strain rate-dependent behaviors for uncured toughened prepreg systems. Besides the resin flow model, many authors have combined other models to reveal the consolidation or compaction behavior. These include a fiber bed elastic model [35,36,38,39,47,48,49], an impregnation model [49,50,51,52], and an interply cohesion model [51,52,53].
Based on the aforementioned issues, the present work concerns both the matrix’s viscosity, the elasticity of the fiber bed and the interply cohesion. Based on the experimental and analytical studies of [37,46,54,55], Section 2 proposes a viscoelastic model combining the elastic behavior of dry fiber reinforcements and the viscous behavior of the resin. For the purpose of evaluating the consolidation level, an intimate contact model is introduced in Section 3 by considering the uneven ply surface of thermoplastic prepregs. This model makes it possible to compute the evolution of the consolidation (porosity closure) level and the thickness as a function of the pressure and temperature during manufacturing. Section 4 presents a simple experimental compaction test at a high temperature to identify the parameters of the proposed models. Finally, the compaction test and a double dome thermoforming process were simulated by the models. A list of symbols is given in Appendix B.
2. Viscoelastic Characterization for Compaction Behavior
Accurate prediction models for unique and complex material behaviors remain a key challenge of process simulation. In many cases, both elastic and viscous responses are outlined to describe fiber-reinforced epoxy composites, especially for intra-ply mechanisms [11,17,18,56,57,58]. When 3D states of stress are applied during processing, such as the consolidation investigated in the current work, a through-the-thickness mechanical behavior needs to be considered. Based on a previous visco-hyperelastic model for shells [11], the transverse compaction behavior within the viscoelastic response is addressed by taking into account the rheology of the composites, including the fiber bed and resin flow.
The definition of a hyperelastic constitutive model is derived from the Clausius–Duhem inequality equation with an assumption of no dissipated energy. The constitutive equation of the model gives the 2nd Piola–Kirchoff stress tensor derived from an internal potential energy w (per undeformed unit volume) that depends on the right Cauchy–Green strain tensor [59]:
| (1) |
For hyperelastic materials with an anisotropic response, the anisotropy is simply embodied in the potential w, providing a natural framework for a frame-invariant formulation [60].
| (2) |
The hyperelastic laws for a 2D fabric [56] and 3D interlock [61,62,63] were recently developed. This approach, inspired by the work of Criscione [64], involves a multiplicative decomposition of the deformation gradient . Each term of this decomposition linking to the classical invariants are characterized by a “physical” invariant . The advantage consists in decoupling the deformation modes, after which they are investigated separately.
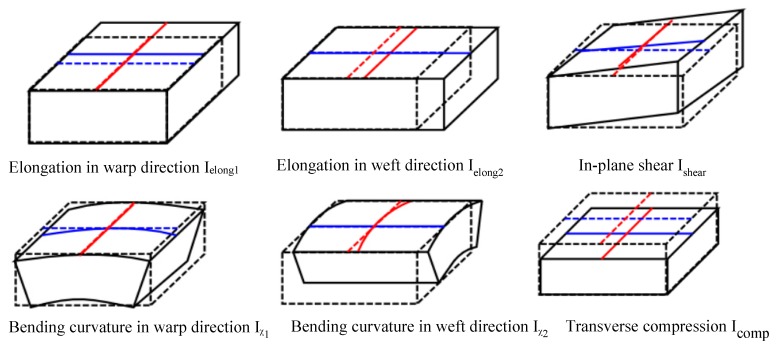
A thin shell structure is usually assumed for the thermoplastic prepreg composites. The considered deformation modes are membrane (including elongation and in-plane shear) and bending. When the through-the-thickness behavior becomes predominant during forming, the transverse compression deformation mode is considered. Figure 2 presents all of the considered deformation modes with their respective physical invariants.
Figure 2.
Deformation modes for woven reinforcement within a hyperelastic framework.
The volume strain energy is the sum of the different strain energies that are assumed to depend only on the corresponding physical invariants [11,62].
| (3) |
In the present study on thermoplastic prepregs, only the in-plane shear and compaction viscosities were taken into account. The tension and bending behavior were assumed to be elastic [65]. The viscoelastic model for compaction is detailed in Section 2.1. All the other strain potential energies, taking the thermal and viscous behaviors into account or not, are provided in Appendix A.
2.1. Viscoelastic Model for Compaction Behavior
As discussed previously, some authors have described a viscoelastic response for the compaction behavior for both dry and wet fibrous materials [36,54,55]. During the forming process, the presence of the molten matrix and its flow phenomena, especially the resin percolation and the transverse squeezing flow, highlight the viscous proportion for the mechanical consolidation behavior. In view of the viscous description for the matrix flow and the fiber bed’s elastic behavior, a viscoelastic model for the consolidation behavior was proposed in the framework of Guzman’s thermo-hyper-viscoelastic constitutive law [11,12] for thin thermoplastic prepreg composites. In this model (shown in Figure 3), a single spring element is placed in parallel with N Maxwell elements, and the elastic stiffness for all the springs is represented by the Young modulus and . These viscous effects are modeled by N dashpots with a constant viscosity , a set of stress-like internal variables are completed for the free energy function of the compaction deformation mode (the comp index is relative to compaction) [11,66]:
| (4) |
Figure 3.
Viscoelastic model with springs and dashpots.
The first elastic part indicates the compaction behavior of dry reinforcement, whose potential energy is formulated with a fifth-order polynomial function:
| (5) |
Clausius Duhem’s inequality introduced into Equation (4) derives the compression deformation-related stress tensor by the following expression [11,66]:
| (6) |
For a generalized-Maxwell model, Simo and Hughes [66] provided detailed evolution equations for the internal variables in the present work) and their algorithmic solutions at current time tn+1:
| (7) |
Here, is the stress tensor attributed by the pure elastic part (superscript 0) at the time tn+1 (subscript n+1). τi denotes the relaxation time.
Hence, the stress tensor from Equation (6) is consequently computed as a function of the internal variables:
| (8) |
Within the relative weights .The viscoelastic model to describe transverse compression behavior is eventually established. The related model parameters such as Dk, τi, and γi, could be calibrated by compaction tests at a high temperature. This is presented in Section 4.
3. Prediction of the Consolidation Level
3.1. Intimate Contact Model
Consolidation induces complex phenomena during thermoplastic composite thermoforming. These phenomena have been investigated at three levels. Most of the studies were focused on intimate contact between layers, interlaminar bonding (autohesion), impregnation of the fibers, as well as molecular diffusion at microscopic and molecular levels [52,53,67,68]. Moreover, macroscopic analysis involves the laminate properties, such as fiber volume fraction, mechanical properties and void content, related to the processing parameters. In this work, the macro level was considered for the purpose of predicting the consolidation level through the global composite part during thermoforming.
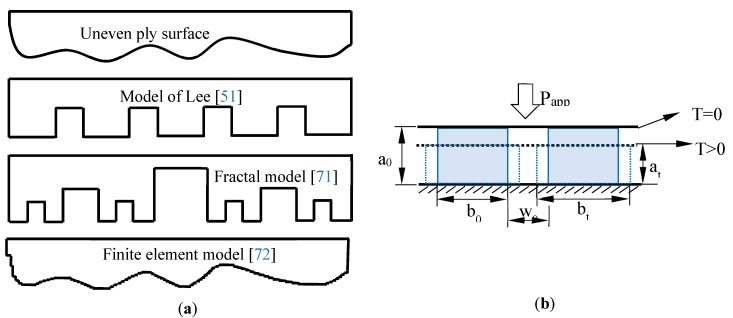
The intimate contact model has been widely described in the literature due to its simplicity when it comes to representing the coalescence between two adjacent ply surfaces during the manufacturing of thermoplastic composites. In this model, a degree of intimate contact, corresponding to the coalescence level, is defined geometrically from the initial roughness of the ply surface. In view of the description of the surface, several related models have been developed. The most popular model is the approach proposed by Lee et al. [51]. In their work, the roughness of the ply surface was modeled by a series of periodic rectangular asperities (Figure 4a). Several authors have used this model for their investigations [52,53,68,69,70] and assumed constant pressure and temperature during the intimate contact process. With the aim of getting closer to reality, other options like the fractal model [71] and the finite element model [72] show good correlation with the original model and experimental results.
Figure 4.
Intimate contact model: (a) Different approaches; (b) Discretization by regular rectangular elements.
3.2. A Time Discrete Approach
Following the investigation of Lee and Springer [51], a series of identical rectangles were employed to signify the initial ply surfaces with irregularities (Figure 4b). Here, the matrix was represented by blue solid rectangles of dimension (0 refers to the initial state), and the remaining elements denoted the void defects in the composite part. As the processing force or pressure was applied, the resin rectangles spread over the interface with b0 extending to b (at an actual time state t). Simultaneously, the void width dwindled to w. During the rheology of this mechanism, the degree of intimate contact D was defined as [51]:
| (9) |
During processing, hypotheses were made. The width of the smallest repeated volume unit (one matrix element + one void element) b+w was assumed to be constant, and the matrix was considered as an incompressible material. Hence:
| (10) |
Next, the law of conservation of mass was taken into account. A laminar Newtonian flow was assumed for the resin elements, and the velocity field could be described by Poiseuille’s law [73]. Based on these assumptions, Lee and Springer [51] finally obtained an ordinary differential equation governing the ply height a with the process parameters:
| (11) |
Here, the viscosity η was assumed constant in the isothermal case. C3 was a constant related to the initial condition.
As the pressure P is a function of the time t, the evolution of the pressure is discretized with n increments of time Δt (small enough). The time returns to 0 at the beginning of each time increment. Meanwhile, the applied pressure papp n is presumed constant, and the following relations are assumed:
| t = 0, a = an, t = Δt, a = an+1 | (12) |
At time t = 0, . The width after the nth time increment is
| (13) |
Substituting Equation (10) into Equation (9), the actual degree of intimate contact is rewritten as:
| (14) |
For simplification, k1 and k2 are introduced with
Combining the previous equations yields:
| (15) |
Hence, with the time discrete approach, the intimate contact model is expressed under non-constant pressure. The degree of intimate contact evolves instantaneously as a function of pressure Papp, temperature T, consolidation time t, and material parameters, such as fiber-matrix mixture viscosity η, and the geometric ratios k1 and k2, which can be also identified from a compaction test. It should be noticed that the developed approach is equal to the Lee-Springer model when the pressure is assumed constant during processing.
3.3. Remark on Consolidation and Crystallisation
After the forming process at a high temperature, the composite is cooled and undergoes crystallisation of the resin to obtain the hardened composite. Consolidation and crystallization are two important aspects that are related but nevertheless different. Consolidation is achieved if the composite has no voids. This is the purpose of this study. At the end of a thermoforming process, this absence of voids (or a sufficiently low void fraction) is necessary to obtain good mechanical properties of the composite part. This consolidation is analyzed here using Lee and Springer’s [51] model, which determines the degree of intimate contact.
The crystallization of the semi-crystalline thermoplastic matrix is essential for the properties of the final composite [74,75]. Cooling conditions (cooling rate and pressure) affect the crystallization and quality of the composite [76,77,78,79,80]. This cooling phase is of great importance, but is not directly addressed in this work. This one proposes a method of simulation of the thermoforming process and the calculation of a consolidation indicator (degree of intimate contact).
4. Compaction Tests at a High Temperature
Compaction can be used to identify these models [37,46,47,81]. Based on the method presented in [47], the compaction test at a high temperature is carried out to identify the parameters both for the proposed viscoelastic compaction model and the time-discretized intimate contact model. Furthermore, the obtained experimental results are compared to those of the simulations during the final validation.
4.1. Material
The material analyzed in this paper was composed of a 2 × 2 woven twill reinforcement and a thermoplastic resin (polyamide 6-6, PA 6-6). The material plates containing four layers were pre-impregnated and produced by Solvay. The melting temperature was set at 262 °C. The principal material properties are detailed in Table 1.
Table 1.
Main material properties.
| Matrix | PA 6-6 |
|---|---|
| Fibers | Carbon |
| Weaving pattern | 2 × 2 twill |
| Number of layers | 4 |
| Thickness (mm) | 2.05 |
| Surface density (g.mm-2) | 2600 |
| Fiber volume content | 0.6 |
4.2. Experimental Set-up
Figure 5 shows the schematic of the compaction test device (Tensile machine RSA 250, Schenck, Darmstadt, Germany) at a high temperature for thermoplastic prepregs. Two metallic plates linked to a tensile test machine were used to compress the specimen with dimensions of 60 mm × 60 mm. The device was caged in an isothermal oven. Besides the internal thermocouple in the oven, three additional thermocouples were employed in order to precisely follow the evolution of the temperature over time: one was inserted in the cross-section of the material (through a small hole with a 0.5-mm diameter and 2-mm depth), and the other two were fixed in the two metallic plates. Prior to the compaction step, the system was heated to the desired temperature. The thermal gradient was assumed to be negligible inside the specimen during the tests. As the mechanical system of the tensile machine was equipped with damping, its own transverse displacement sensor seemed insufficiently precise. Instead, a digital image correlation (DIC) system was used to correctly determine the compression displacement through the images taken by a CCD camera (Camera Mega+, Kodak, Rochester, NY, USA).Furthermore, compression measurements were provided by an extra load sensor placed at the bottom of the support.
Figure 5.
High-temperature compaction test device.
4.3. Experimental Conditions
It should be noted that the exposition time of the material must be controlled and limited because of the risk of matrix oxidation at a high temperature. Before introducing the specimen, the system was rapidly heated to about 300 °C. Subsequently, the sample was placed in the machine, causing the temperature to decrease below 300 °C. For this reason, another 5 min of heating was needed to obtain a more homogenous temperature field (about 300 °C in accordance with the thermoforming process) for the whole equipment, especially for the sample. Then, cooling was performed gradually to the desired test temperature, and followed by the start-up system to activate the compression and camera recording. In order to model the compression behavior during the process at different temperature levels, a series of tests were performed over the range of 260–300 °C, while the compaction speed was fixed at 0.2 mm/min. A maximum load value was set to 8000 N as the test limit. Once this value was achieved, the loading and image recording system became deactivated. Finally, the system was cooled by opening the mesh and resetting the top plate to its initial position.
4.4. Experimental Results
Figure 6 shows the load versus displacement curves at different temperatures. One can notice that the compaction stiffness decreased when the temperature increased. Based on the experimental results, an inverse method (the Levenberg-Marquardt method) [82] was employed to optimize the parameters of the proposed model over the temperature range 260–300 °C. The calibrated parameters are given in Table 2 and Table 3. Here, their optimal loads at different temperatures are compared with the experimental loads demonstrated in Figure 6.
Figure 6.
Comparison between experimental and optimal results for a 2 × 2 twill in carbon/PA 6-6 prepregs.
Table 2.
Optimized parameters related to consolidation deformation at different temperatures.
| 260 °C | 270 °C | 280 °C | 300 °C | Units | |
|---|---|---|---|---|---|
| D1 | 2.274 × 10−2 | 6.814 × 10−2 | 2.177× 10−2 | 8.793 × 10−2 | [J mm−2] |
| D2 | 4.113 × 10−1 | 5.870× 10−1 | 3.607× 10−1 | 6.889× 10−1 | [J mm−2] |
| D3 | 2.478 | 1.080 | 1.279 | 1.466 | [J mm−2] |
| D4 | 5.386 | 3.434 × 10-1 | 1.974 | -3.411 | [J mm−2] |
| D5 | 4.170 | 1.383 | −9.312 × 10−1 | 6.299 × 10−1 | [J mm−2] |
| γ1 | 7.293 | 1.043 | 5.236 × 10−1 | 8.024 × 10−1 | - |
| γ2 | 4.499 × 10−1 | 5.754 × 10−1 | 9.420 × 10−2 | 4.443 × 10−1 | - |
| τ1 | 35.87 | 8.473 × 10−1 | 5.787 × 10−2 | 3.638 × 10−1 | [s] |
| τ2 | 20.37 | 6.724 × 10−1 | 3.262 × 10−1 | 3.881 × 10−1 | [s] |
Table 3.
Optimized parameters related to the intimate contact model for a 2 × 2 twill in carbon/PA 6-6 prepregs at different temperatures.
| 260 °C | 270 °C | 280 °C | 300 °C | Units | |
|---|---|---|---|---|---|
| k1 | 1.85 | - | |||
| k2 | 0.82 | - | |||
| η | [MPa·s] | ||||
5. F.E. Simulations of Thermoforming
5.1. Prismatic Solid Shell Finite Element Model
Many mechanical approaches exist for modeling of textile composite forming at the macroscopic scale [83,84], including discrete approaches [85,86], continuous methods [5,8,11,12,18,46], and semi-discrete techniques [87,88,89]. All of them focus on the in-plane and bending behaviors during the forming step, whereas the through-the-thickness behavior is ignored with the assumption of a thin plate theory. For the purpose of thin/thick shell analysis by considering the evolution of the consolidation effect during the thermoforming process of the prepreg composites, a new seven-node prismatic solid-shell finite element approach was recently developed [90]. As shown in Figure 7, the new prismatic finite element possesses seven nodes: six (i,j,k,l,m,n) apical nodes and an extra one at the center, and 19 degrees of freedom (DOF) of translation: three for each apex, one along the thickness at the seventh center node.
Figure 7.
Seven-node prismatic solid-shell element for the consolidation simulation.
Equation (16) shows the virtual work theorem for any virtual displacement field , in which each virtual work (external, internal and inertial) is denoted by , respectively. Three deformation components, i.e., bending, membrane, and pinching, are described separately for the internal virtual work.
| (16) |
with
| (17) |
The virtual work theorem equation can be expressed by finite element interpolation, which leads to [91]:
| (18) |
where the mass matrix is represented by , is the nodal acceleration vector, and is the single column matrix of the exterior load. The single column matrix for each internal load, , , and , can be simply written by [91]:
| (19) |
Here, refers to three considered deformation modes (bending, membrane, and pinching), and is the related Cauchy stress. For each attributed mode in the introduced prismatic solid shell element, the conventional DKT6 shell element offers the bending part, while the formulation of the CST shell element provides membrane formulations. In the aspect of pinching, the enhanced assumed strain (EAS) method is carried out within the extra displacement DOF imported by the seventh node. As a result, a linear variation of stresses in thickness is obtained and the thickness locking is avoided. Because a reduced integration (RI) scheme is used, an hourglass stabilization (HS) procedure is performed to correct the element’s rank deficiency for pinching, while transverse shear deformations are calculated by the assumed strain (AS) method to prevent specific zero energy modes. Based on the above ideas, the strain interpolation matrix related to mode was formulated in the work of Xiong et al. [90]. This solid shell element has the same efficiency as the shell elements for thin parts, but also allows the use of a complete 3D constitutive law (Section 2) within the through-the-thickness behavior.
The presented 3D visco-hyperelastic constitutive model for thermoplastic prepreg composites and the time discrete intimate contact model described above was implanted in the finite element code Plasfib [92] based on an explicit dynamic approach. The prismatic solid shell element presented in Section 5.1 is used in this simulation. The flowchart of the finite element analysis of the degree of consolidation is carried out according to Figure 8.
Figure 8.
Flowchart of the finite element analysis of the degree of consolidation Dn.
5.2. Simulation of Compaction Tests
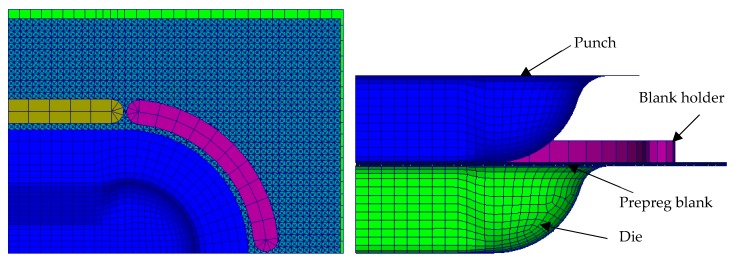
Figure 9a demonstrates the meshed geometry of the compaction test, conforming to the experimental set-up. The metallic compression plates were modeled by two rigid plates, within the squared plate (60 mm × 60 mm × 2.5 mm) placed inside. The mechanical properties for the studied thermoplastic composites calibrated at 300 °C were used during this numerical compaction test. The bottom plate was fixed, while the top one was subject to a displacement of 1.4 mm in the downward vertical direction. The speed of the displacement loading was 2 mm/min, which corresponds to the experimental loading speed.
Figure 9.
Simulation of a compaction test at 300 °C. (a) Meshed structure (composite blank in the middle); (b) Simulated and experimental load versus displacement curves; (c) Evolution of the degree of intimate contact during the simulation.
Figure 9b depicts the comparison between the simulated load and the experimental load as a function of displacement. It was shown that the simulation results were in good agreement with the experiment. In addition, the evolution of the degree of intimate contact D during the compaction test is represented in Figure 9c, where the degree of intimate contact equated 0.8 at about 40 s as the maximum load was achieved, and by keeping this maximum value within approx. 10 s, the complete consolidation (D = 1) could take place.
5.3. Thermoforming Simulation of a Double Dome
As a forming benchmark example owing to its double-curved structure, the double dome test enables comparative investigations of the existing models both for continuous dry and pre-impregnated reinforcements at room temperature or high temperatures [14,93,94,95,96,97,98]. It is also conducted to investigate various relevant aspects such as the effect of fiber orientations due to the process on the in-service behavior properties of the composite [96].
Figure 10 only shows one quarter of the process structure for symmetric reasons. The rectangular pre-impregnated blank, with dimensions of 270 mm × 190 mm × 2 mm, was placed between the punch and the die. Moreover, six blank holders were added to maintain the blank in contact. Within the related properties identified at different temperatures, the material of the studied carbon-twill/PA 6-6 thermoplastic prepregs was applied and orientated in 0/90° directions. Isothermal and homogeneous distribution assumptions were made during the simulations, and the temperature was fixed at 300 °C, which corresponds to the manufacturing temperature. The objective of this simulation was to investigate the evolution of consolidation during the manufacturing process including the thermoforming and consolidation steps.
Figure 10.
Double dome structure (geometry and mesh).
Firstly, simulation of the forming stage was launched subject to a vertical displacement of the punch. The total displacement was 60 mm and its rate was set to 240 mm/min. The through-the-thickness behavior could be simultaneously analyzed all along the simulation, and Figure 11a–c give the final distributions of the transverse stress σ33 in the bottom, top and middle faces at the end of this step. Moreover, the degree of intimate contact Dn, which represents the consolidation level, is depicted in Figure 11d–f for the bottom, top and middle faces, respectively.
Figure 11.
Simulation results during the forming step of a double dome test. Normal stress σ33 in (a–c) and intimate contact Dn in (d–f).
As most of the deformed piece did not achieve the completed consolidation level (Dn = 1) after the forming step, additional time consumption or extra pressure was required. Due to the cost of time, a reasonable pressure was first considered. In the finite element simulation case, extra compression displacement on the punch was applied, while the equivalent load integrated through the internal forces of each element was obtained. In order to investigate the influence of compaction, a set of simulations was performed within two compressed displacements: Δu = 0.2 mm and 0.5 mm. Consequently, the equivalent loads Fn were increased from 2.85 kN (at the end of the forming step) to Fn = 4.95 kN and 10.44 kN, respectively. Their distributions of transverse stress σ33 in the middle face are shown in Figure 12.
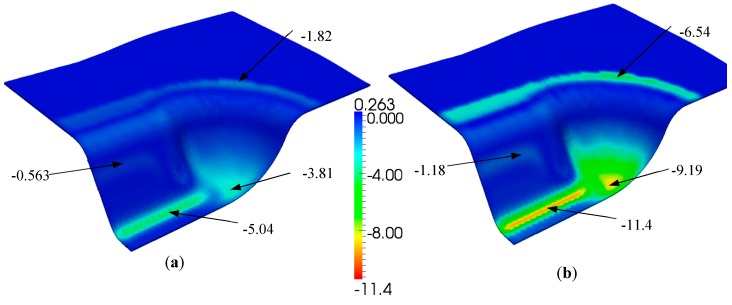
Figure 12.
Distribution of transverse stress σ33 (middle face) during the consolidation process: (a) σ33 (MPa) for Δu = 0.2 mm; (b) σ33 (MPa) for Δu = 0.5 mm.
Finally, the consolidation evolved within the final compaction load that was maintained. The developments over time in the middle face of the part are displayed in Figure 13 and Figure 14, according to the two compaction levels. The figures reveal that increased time leads to higher consolidation levels. The test with a compaction displacement of 0.5 mm required about 3 min of consolidation to obtain a relatively complete consolidation level through the active region of the part. However, more than 5 min were needed when the consolidated displacement was 0.2 mm. Furthermore, designers could obtain more guidance for industrial manufacturing by assessing the consolidation level through the part, which would make it possible to optimize the processing parameters and thereby the geometry design.
Figure 13.
Comparison between two simulation results under a compaction displacement of Δu = 0.2 mm (left) and Δu = 0.5 mm (right) during the first 30 s.
Figure 14.
Comparison between two simulation results under a compaction displacement of Δu = 0.2 mm (left) and Δu = 0.5 mm (right) after 30 s up to 5 min.
5.4. Remark Concerning the Type of Element and The Finite Element Software
Solid-shell elements show a good performance in the case of both thin parts (equivalent to that of standard shell finite elements) and deformation/stress in thickness calculations. The 7-node prismatic element briefly presented in Section 5.1 provides thickness stresses that verify the load boundary conditions on the upper and lower surfaces, and is essential for the analysis of the consolidation. The viscoelastic law and the calculation of the intimate contact are implemented in this prismatic element. This would not be possible in standard shell finite elements that are classically based on a plane stress assumption.
The viscoelastic constitutive law and the calculation of the intimate contact can be implemented in 3D elements of finite element codes using user subroutines such as UMAT/VUMAT for the ABAQUS software [99]. However, this approach will only be numerically effective in the case of composites that are thick enough, otherwise 3D finite elements are not efficient.
Another possibility for using the approach proposed for the consolidation calculation in a commercial finite element code is to implement a solid-shell element that performs an efficient calculation of the stress in the thickness (such as the prism that has been presented). This can be done in the ABAQUS software by creating a UELEM/VUELEM user subroutine that makes it possible to develop a specific element.
6. Conclusions
In summary, modeling of the consolidation behavior is crucial to assess void defects during thermoforming of thermoplastic composite prepregs. In this context, a viscoelastic model based on the generalized Maxwell approach was proposed by considering the elastic fiber bed and the viscosity of the thermoplastic matrix. The 3D constitutive behavior was accounted for in a hyperelastic framework. Five major deformation modes, i.e., two elongations in the warp and weft directions, in-plane shearing deformation, bending deformation, and transverse compression deformation, were highlighted separately. Among them, the viscous response was not only addressed for the in-plane shearing behavior but also for the compaction. As a result, the hyperelastic potential was decomposed by characterizing each physical invariant related to its deformation mode. Moreover, a time-discretized approach was realized for the intimate contact model, which makes the evolution of the consolidation level evident, and helps optimize the process conditions (pressure, temperature and time), which leads to better control of the process. In order to calibrate the parameters of the studied material associated with the considered models, a compaction test at a high temperature was performed. The proposed models were integrated into a finite element software, and the recently developed solid-shell finite element approach was used to simulate the compaction test and the thermoforming processing of a double dome within the consolidation part. The simulation results revealed that a good agreement was found with experimental data. Consequently, the evolution of the consolidation during simulation of the consolidation step made it feasible to achieve a complete consolidation level though the final product by controlling the processing parameters.
The cooling phase at the end of the process is of great importance. Crystallization was not directly addressed in this work. We proposed a method of simulation of the thermoforming process and the calculation of a consolidation indicator (degree of intimate contact). In this study, we focused on the simulation of the consolidation, it will be important to add additional software to analyze and simulate the crystallization during the cooling phase.
Appendix A. Strain Energy Functions Associated with Each Deformation Mode
A.1. Elongation Strain Energy
The studied reinforcement of a prepreg material is balanced: the mechanical behavior during tension is identical in both the warp and weft directions. For the sake of simplicity, a second-order polynomial function is defined for the strain potential energy:
| (A1) |
where is the tensile stiffness in the direction of the yarn i. Identification of the parameters can be obtained both by an approximate analytical homogenization approach and a tensile test at a high temperature.
A.2. Bending Strain Energy
For thermoplastic prepregs, a bending behavior with a strong temperature dependence is used, while the viscosity of the bending behavior is ignored. The strain energy linked to the bending invariant is written as follows:
| (A2) |
where the two thermo-dependent coefficients B1 and B2 are identical on account of the balance of the material. They can be obtained from experimental results by cantilever tests at a high temperature.
A.3. In-plane Shear Strain Energy
The strain energy density expression is usually described by a polynomial, piecewise of its physical invariant related to the shear angle. By considering the presence of the matrix for thermoplastic prepreg composites, the viscoelastic model with thermo-dependence is introduced here. This model is based on the generalized Maxwell model, a free energy function is completed by the effect of viscoelastic internal variables :
| (A3) |
where the first part is the in-plane shear energy, also called the free energy at equilibrium, i.e., the energy stored after all viscous effects have ended. The second term characterizes the non-equilibrium state.
For the equilibrium part, a polynomial function with thermo-dependence is introduced as:
| (A4) |
All of the coefficients for an elastic equilibrium part and the internal variables for the viscous relaxation part can be identified by a bias-extension test at a high temperature [100].
Appendix B. List of Symbols
| Nomenclature | |||
| List of definition | |||
| /S | Second Piola-Kirchoff stress tensor | Papp | Applied pressure |
| /C | Right Cauchy-Green strain tensor | a, b, w | Dimension parameters |
| w | Internal potential energy | D | Degree of intimate contact |
| /F | Deformation gradient tensor | η | Matrix viscosity |
| I1, I2, I3… In | Invariants | k1, k2 | Geometric ratios |
| Aelong1, Aelong2 | Parameter A related to elongation mode in warp, weft direction | A0, An, An+1 | Parameter A at initial state, before, after nth time increment |
| Aχ1, Aχ2 | Parameter A related to bending mode in warp, weft direction | Ashear, Acomp | Parameter A related to in-plane shearing mode, and compression mode |
| T | Temperature | External, internal and inertial work | |
| Ei | Young’s modulus of spring element i | Virtual displacement vector | |
| Viscosity of dashpot i | u, | Displacement and acceleration vectors | |
| τi | Relaxation time | Exterior and interior load vectors | |
| γi | Relative weight | Superscript α | Index related to bending, membrane, or pinching deformation |
| Stress-like internal variable | σ | Cauchy stress tensor | |
| Algorithmic solution of Q | B | Strain interpolation matrix | |
| Dk, Ci | Polynomial parameters | Ωe | Volume of element |
| ψ | Free energy function | T1, T2 | Tensile stiffness in two directions of yarn |
| tn, tn+1 | Times at the beginning and end of the nth time increment | Mχ1, Mχ2 | Bending moments in two directions of yarn |
| Δtn | nth time increment | B1, B2 | Material parameters related to bending |
| α, β | Thermo-dependent parameters | ||
Author Contributions
Software, H.X. and N.H.; validation, H.X.; investigation, H.X., N.H. and P.B.; writing—original draft preparation H.X., P.B.; project administration P.B., writing—review and editing H.X., P.B.
Funding
This research was funded by the Agence de l’environnement et de la maitrise de l’energie (ADEME), as part of the project STIICPA.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Fuchs E.R.H., Field F.R., Roth R., Kirchain R.E. Strategic materials selection in the automobile body: Economic opportunities for polymer composite design. Compos. Sci. Technol. 2008;68:1989–2002. doi: 10.1016/j.compscitech.2008.01.015. [DOI] [Google Scholar]
- 2.Mallick P.K. Materials, Design and Manufacturing for Lightweight Vehicles. Woodhead Publishing; Cambridge, UK: 2010. Thermoplastics and thermoplastic-matrix composites for lightweight automotive structures; pp. 174–207. [Google Scholar]
- 3.Friedrich K., Almajid A.A. Manufacturing aspects of advanced polymer composites for automotive applications. Appl. Compos. Mater. 2013;20:107–128. doi: 10.1007/s10443-012-9258-7. [DOI] [Google Scholar]
- 4.Friedrich K., Hou M., Krebs J. Thermoforming of continuous fibre/thermoplastic composite sheets. Compos. Mater. Ser. 1997;11:91–162. [Google Scholar]
- 5.Haanappel S.P., Ten Thije R.H.W., Sachs U., Rietman B., Akkerman R. Formability analyses of uni-directional and textile reinforced thermoplastics. Compos. Part A Appl. Sci. Manuf. 2014;56:80–92. doi: 10.1016/j.compositesa.2013.09.009. [DOI] [Google Scholar]
- 6.Lessard H., Lebrun G., Benkaddour A., Pham X.T. Influence of process parameters on the thermostamping of a [0/90] 12 carbon/polyether ether ketone laminate. Compos. Part A Appl. Sci. Manuf. 2015;70:59–68. doi: 10.1016/j.compositesa.2014.12.009. [DOI] [Google Scholar]
- 7.Gnaba I., Wang P., Soulat D., Omrani F., Ferreira M., Vroman P. Investigation about the effect of manufacturing parameters on the mechanical behaviour of natural fibre nonwovens reinforced thermoplastic composites. Materials. 2019;12:2560. doi: 10.3390/ma12162560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.De Luca P., Lefébure P., Pickett A.K. Numerical and experimental investigation of some press forming parameters of two fibre reinforced thermoplastics: APC2-AS4 and PEI-CETEX. Compos. Part A Appl. Sci. Manuf. 1998;29:101–110. doi: 10.1016/S1359-835X(97)00060-2. [DOI] [Google Scholar]
- 9.Boisse P. Composites Forming Technologies. Woodhead Publishing; Cambridge, UK: 2007. Finite element analysis of composite forming; pp. 46–79. [Google Scholar]
- 10.Hsiao S.W., Kikuchi N. Numerical analysis and optimal design of composite thermoforming process. Comput. Methods Appl. Mech. Eng. 1999;177:1–34. doi: 10.1016/S0045-7825(98)00273-4. [DOI] [Google Scholar]
- 11.Guzman-Maldonado E., Hamila N., Boisse P., Bikard J. Thermomechanical analysis, modelling and simulation of the forming of pre-impregnated thermoplastics composites. Compos. Part A Appl. Sci. Manuf. 2015;78:211–222. doi: 10.1016/j.compositesa.2015.08.017. [DOI] [Google Scholar]
- 12.Guzman-Maldonado E., Hamila N., Naouar N., Moulin G., Boisse P. Simulation of thermoplastic prepreg thermoforming based on a visco-hyperelastic model and a thermal homogenization. Mater. Des. 2016;93:431–442. doi: 10.1016/j.matdes.2015.12.166. [DOI] [Google Scholar]
- 13.Jauffrès D., Morris C.D., Sherwood J.A., Chen J. Simulation of the thermostamping of woven composites: Mesoscopic modelling using explicit FEA codes. Int. J. Mater. Form. 2009;2:173–176. doi: 10.1007/s12289-009-0519-4. [DOI] [Google Scholar]
- 14.Harrison P., Gomes R., Curado-Correia N. Press forming a 0/90 cross-ply advanced thermoplastic composite using the double-dome benchmark geometry. Compos. Part A Appl. Sci. Manuf. 2013;54:56–69. doi: 10.1016/j.compositesa.2013.06.014. [DOI] [Google Scholar]
- 15.Sherwood J.A., Fetfatsidis K.A., Gorczyca J.L., Berger L. Manufacturing Techniques for Polymer Matrix Composites (PMCs) Woodhead Publishing; Cambridge, UK: 2012. Fabric thermostamping in polymer matrix composites; pp. 139–181. [Google Scholar]
- 16.Gong Y., Peng X., Yao Y., Guo Z. An anisotropic hyperelastic constitutive model for thermoplastic woven composite prepregs. Compos. Sci. Technol. 2016;128:17–24. doi: 10.1016/j.compscitech.2016.03.005. [DOI] [Google Scholar]
- 17.Machado M., Fischlschweiger M., Major Z. A rate-dependent non-orthogonal constitutive model for describing shear behaviour of woven reinforced thermoplastic composites. Compos. Part A Appl. Sci. Manuf. 2016;80:194–203. doi: 10.1016/j.compositesa.2015.10.028. [DOI] [Google Scholar]
- 18.Dörr D., Henning F., Kärger L. Nonlinear hyperviscoelastic modelling of intra-ply deformation behaviour in finite element forming simulation of continuously fibre-reinforced thermoplastics. Compos. Part A Appl. Sci. Manuf. 2018;109:585–596. doi: 10.1016/j.compositesa.2018.03.037. [DOI] [Google Scholar]
- 19.Slange T.K., Grouve W.J.B., Warnet L.L., Wijskamp S., Akkerman R. Towards the combination of automated lay-up and stamp forming for consolidation of tailored composite components. Compos. Part A Appl. Sci. Manuf. 2019;119:165–175. doi: 10.1016/j.compositesa.2019.01.016. [DOI] [Google Scholar]
- 20.Nixon-Pearson O.J., Belnoue J.P.H., Ivanov D.S., Potter K.D., Hallett S.R. An experimental investigation of the consolidation behaviour of uncured prepregs under processing conditions. J. Compos. Mater. 2017;51:1911–1924. doi: 10.1177/0021998316665681. [DOI] [Google Scholar]
- 21.Dell’Anna R., Lionetto F., Montagna F., Maffezzoli A. Lay-Up and Consolidation of a Composite Pipe by In Situ Ultrasonic Welding of a Thermoplastic Matrix Composite Tape. Materials. 2018;11:786. doi: 10.3390/ma11050786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Amirkhosravi M., Pishvar M., Cengiz Altan M. Fabricating high-quality VARTM laminates by magnetic consolidation: Experiments and process model. Compos. Part A Appl. Sci. Manuf. 2018;114:398–406. doi: 10.1016/j.compositesa.2018.09.003. [DOI] [Google Scholar]
- 23.Patou J., Bonnaire R., De Luycker E., Bernhart G. Influence of consolidation process on voids and mechanical properties of powdered and commingled carbon/PPS laminates. Compos. Part A Appl. Sci. Manuf. 2019;117:260–275. doi: 10.1016/j.compositesa.2018.11.012. [DOI] [Google Scholar]
- 24.Michaud V., Tornqvist R., Manson J.-A.E. Impregnation of Compressible Fiber Mats with a Thermoplastic Resin. Part II: Experiments. J. Compos. Mater. 2001;35:1174–1200. doi: 10.1177/002199801772662280. [DOI] [Google Scholar]
- 25.Long A.C., Wilks C.E., Rudd C.D. Experimental characterisation of the consolidation of a commingled glass/polypropylene composite. Compos. Sci. Technol. 2001;61:1591–1603. doi: 10.1016/S0266-3538(01)00059-8. [DOI] [Google Scholar]
- 26.Helmus R., Hinterhölzl R., Hubert P. A stochastic approach to model material variation determining tow impregnation in out-of-autoclave prepreg consolidation. Compos. Part A Appl. Sci. Manuf. 2015;77:293–300. doi: 10.1016/j.compositesa.2015.03.021. [DOI] [Google Scholar]
- 27.Helmus R., Centea T., Hubert P., Hinterhölzl R. Out-of-autoclave prepreg consolidation: Coupled air evacuation and prepreg impregnation modeling. J. Compos. Mater. 2016;50:1403–1413. doi: 10.1177/0021998315592005. [DOI] [Google Scholar]
- 28.Lionetto F., Dell’Anna R., Montagna F., Maffezzoli A. Modeling of continuous ultrasonic impregnation and consolidation of thermoplastic matrix composites. Compos. Part A Appl. Sci. Manuf. 2016;82:119–129. doi: 10.1016/j.compositesa.2015.12.004. [DOI] [Google Scholar]
- 29.Wysocki M., Toll S., Larsson R., Asp L.E. Anisotropic and tension-compression asymmetric model for composites consolidation. Compos. Part A Appl. Sci. Manuf. 2010;41:284–294. doi: 10.1016/j.compositesa.2009.10.016. [DOI] [Google Scholar]
- 30.Gutowski T.G., Dillon G., Chey S., Li H. Laminate wrinkling scaling laws for ideal composites. Compos. Manuf. 1995;6:123–134. doi: 10.1016/0956-7143(95)95003-H. [DOI] [Google Scholar]
- 31.Dodwell T.J., Butler R., Hunt G.W. Out-of-plane ply wrinkling defects during consolidation over an external radius. Compos. Sci. Technol. 2014;105:151–159. doi: 10.1016/j.compscitech.2014.10.007. [DOI] [Google Scholar]
- 32.Belnoue J.P.-H., Nixon-Pearson O.J., Thompson A.J., Ivanov D.S., Potter K.D., Hallett S.R. Consolidation-Driven Defect Generation in Thick Composite Parts. J. Manuf. Sci. Eng. 2018;140:071006. doi: 10.1115/1.4039555. [DOI] [Google Scholar]
- 33.Springer G.S. Resin Flow During the Cure of Fiber Reinforced Composites. J. Compos. Mater. 1982;16:400–410. doi: 10.1177/002199838201600505. [DOI] [Google Scholar]
- 34.Loos A.C., Springer G.S. Curing of Epoxy Matrix Composites. J. Compos. Mater. 1983;17:135–169. doi: 10.1177/002199838301700204. [DOI] [Google Scholar]
- 35.Dave R., Kardos J.L., Duduković M.P. A model for resin flow during composite processing: Part 1—General mathematical development. Polym. Compos. 1987;8:29–38. doi: 10.1002/pc.750080106. [DOI] [Google Scholar]
- 36.Kelly P.A., Umer R., Bickerton S. Viscoelastic response of dry and wet fibrous materials during infusion processes. Compos. Part A Appl. Sci. Manuf. 2006;37:868–873. doi: 10.1016/j.compositesa.2005.02.008. [DOI] [Google Scholar]
- 37.Kelly P.A. A viscoelastic model for the compaction of fibrous materials. J. Text. Inst. 2011;102:689–699. doi: 10.1080/00405000.2010.515103. [DOI] [Google Scholar]
- 38.Gutowski T.G., Cai Z., Bauer S., Boucher D., Kingery J., Wineman S. Consolidation Experiments for Laminate Composites. J. Compos. Mater. 1987;21:650–669. doi: 10.1177/002199838702100705. [DOI] [Google Scholar]
- 39.Gu Y., Li M., Zhang Z., Sun Z. Numerical simulation and experimental study on consolidation of toughened epoxy resin composite laminates. J. Compos. Mater. 2006;40:2257–2277. doi: 10.1177/0021998306062319. [DOI] [Google Scholar]
- 40.Hagège B., Boisse P., Billoët J.-L. Finite element analyses of knitted composite reinforcement at large strain. Rev. Eur. Éléments Finis. 2005;14:767–776. doi: 10.3166/reef.14.767-776. [DOI] [Google Scholar]
- 41.Rogers T.G. Squeezing flow of fibre-reinforced viscous fluids. J. Eng. Math. 1989;23:81–89. doi: 10.1007/BF00058434. [DOI] [Google Scholar]
- 42.Kaprielian P.V., O’Neill J.M. Shearing flow of highly anisotropic laminated composites. Composites. 1989;20:43–47. doi: 10.1016/0010-4361(89)90681-2. [DOI] [Google Scholar]
- 43.Balasubramanyam R., Jones R.S., Wheeler A.B. Modelling transverse flows of reinforced thermoplastic materials. Composites. 1989;20:33–37. doi: 10.1016/0010-4361(89)90679-4. [DOI] [Google Scholar]
- 44.Wang E.L., Gutowski T.G. Laps and gaps in thermoplastic composites processing. Compos. Manuf. 1991;2:69–78. doi: 10.1016/0956-7143(91)90182-G. [DOI] [Google Scholar]
- 45.Shuler S.F., Advani S.G. Transverse squeeze flow of concentrated aligned fibers in viscous fluids. J. Nonnewton Fluid Mech. 1996;65:47–74. doi: 10.1016/0377-0257(96)01440-1. [DOI] [Google Scholar]
- 46.Belnoue J.P.H., Nixon-Pearson O.J., Ivanov D., Hallett S.R. A novel hyper-viscoelastic model for consolidation of toughened prepregs under processing conditions. Mech. Mater. 2016;97:118–134. doi: 10.1016/j.mechmat.2016.02.019. [DOI] [Google Scholar]
- 47.Nguyen Q.T., Vidal-Sallé E., Boisse P., Park C.H., Saouab A., Bréard J., Hivet G. Mesoscopic scale analyses of textile composite reinforcement compaction. Compos. Part B Eng. 2013;44:231–241. doi: 10.1016/j.compositesb.2012.05.028. [DOI] [Google Scholar]
- 48.Zou H., Yin W., Cai C., Wang B., Liu A., Yang Z., Li Y., He X. The Out-of-Plane Compression Behavior of Cross-Ply AS4/PEEK Thermoplastic Composite Laminates at High Strain Rates. Materials. 2018;11:2312. doi: 10.3390/ma11112312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Van West B.P., Pipes R.B., Advani S.G. The consolidation of commingled thermoplastic fabrics. Polym. Compos. 1991;12:417–427. doi: 10.1002/pc.750120607. [DOI] [Google Scholar]
- 50.Bernet N., Michaud V., Bourban P.E., Manson J.A.E. Impregnation model for the consolidation of thermoplastic composites made from commingled yarns. J. Compos. Mater. 1999;33:751–772. doi: 10.1177/002199839903300806. [DOI] [Google Scholar]
- 51.Lee W.I., Springer G.S. A Model of the Manufacturing Process of Thermoplastic Matrix Composites. J. Compos. Mater. 1987;21:1017–1055. doi: 10.1177/002199838702101103. [DOI] [Google Scholar]
- 52.Phillips R., Akyüz D.A., Månson J.A.E. Prediction of the consolidation of woven fibre-reinforced thermoplastic composites. Part I. Isothermal case. Compos. Part A Appl. Sci. Manuf. 1998;29:395–402. doi: 10.1016/S1359-835X(97)00099-7. [DOI] [Google Scholar]
- 53.Mantell S.C., Springer G.S. Manufacturing Process Models for Thermoplastic Composites. J. Compos. Mater. 1992;26:2348–2377. doi: 10.1177/002199839202601602. [DOI] [Google Scholar]
- 54.Bickerton S., Buntain M.J., Somashekar A.A. The viscoelastic compression behavior of liquid composite molding preforms. Compos. Part A Appl. Sci. Manuf. 2003;34:431–444. doi: 10.1016/S1359-835X(03)00088-5. [DOI] [Google Scholar]
- 55.Hubert P., Poursartip A. Method for the direct measurement of the fibre bed compaction curve of composite prepregs. Compos. Part A Appl. Sci. Manuf. 2001;32:179–187. doi: 10.1016/S1359-835X(00)00143-3. [DOI] [Google Scholar]
- 56.Dörr D., Schirmaier F.J., Henning F., Kärger L. A viscoelastic approach for modeling bending behavior in finite element forming simulation of continuously fiber reinforced composites. Compos. Part A Appl. Sci. Manuf. 2017;94:113–123. doi: 10.1016/j.compositesa.2016.11.027. [DOI] [Google Scholar]
- 57.Harrison P., Yu W.R., Long A.C. Rate dependent modelling of the forming behaviour of viscous textile composites. Compos. Part A Appl. Sci. Manuf. 2011;42:1717–1726. doi: 10.1016/j.compositesa.2011.07.026. [DOI] [Google Scholar]
- 58.Boisse P., Hamila N., Helenon F., Hagège B., Cao J. Different approaches for woven composite reinforcement forming simulation. Int. J. Mater. Form. 2008;1:21–29. doi: 10.1007/s12289-008-0002-7. [DOI] [Google Scholar]
- 59.Ciarlet P. Mechanical Elasticity: Three Dimensional Elasticity. Elsevier; Amsterdam, The Netherlands: 1988. [Google Scholar]
- 60.Zhang J.M., Rychlewski J. Structural tensors for anisotropic solids. Arch. Mech. 1990;42:267–277. [Google Scholar]
- 61.Charmetant A., Orliac J.G., Vidal-Sallé E., Boisse P. Hyperelastic model for large deformation analyses of 3D interlock composite preforms. Compos. Sci. Technol. 2012;72:1352–1360. doi: 10.1016/j.compscitech.2012.05.006. [DOI] [Google Scholar]
- 62.Mathieu S., Hamila N., Bouillon F., Boisse P. Enhanced modeling of 3D composite preform deformations taking into account local fiber bending stiffness. Compos. Sci. Technol. 2015;117:322–333. doi: 10.1016/j.compscitech.2015.07.005. [DOI] [Google Scholar]
- 63.Naouar N., Vidal-Salle E., Schneider J., Maire E., Boisse P. 3D composite reinforcement meso FE analyses based on X-ray computed tomography. Compos. Struct. 2015;132:1094–1104. doi: 10.1016/j.compstruct.2015.07.005. [DOI] [Google Scholar]
- 64.Criscione C.J., Douglas A.S., Hunter W.C. Physically based strain invariant set for materials exhibiting transversely isotropic behavior. J. Mech. Phys. Solids. 2001;49:871–897. doi: 10.1016/S0022-5096(00)00047-8. [DOI] [Google Scholar]
- 65.Liang B., Hamila N., Peillon M., Boisse P. Analysis of thermoplastic prepreg bending stiffness during manufacturing and of its influence on wrinkling simulations. Compos. Part A Appl. Sci. Manuf. 2014;67:111–122. doi: 10.1016/j.compositesa.2014.08.020. [DOI] [Google Scholar]
- 66.Simo J., Hughes T. Computational Inelasticity. Springer; New York, NY, USA: 1998. [Google Scholar]
- 67.Dara P.H., Loos A.C. Thermoplastic Matrix Composite Processing Model. Center for Composite Materials and Structures, Virginia Polytechnic Institute and State University; Blacksburg, VA, USA: 1985. Report CCMS-85-10, VPI-E-85-21. [Google Scholar]
- 68.Bersee H.E.N., Beukers A. Consolidation of thermoplastic composites. J. Thermoplast. Compos. Mater. 2003;16:433–455. doi: 10.1177/0892705703031862. [DOI] [Google Scholar]
- 69.Levy A., Heider D., Tierney J., Gillespie J.W. Inter-layer thermal contact resistance evolution with the degree of intimate contact in the processing of thermoplastic composite laminates. J. Compos. Mater. 2014;48:491–503. doi: 10.1177/0021998313476318. [DOI] [Google Scholar]
- 70.Sonmez F.O., Hahn H.T. Modeling of heat transfer and crystallization in thermoplastic composite tape placement process. J. Thermoplast. Compos. Mater. 1997;10:198–240. doi: 10.1177/089270579701000301. [DOI] [Google Scholar]
- 71.Yang F., Pitchumani R. A fractal Cantor set based description of interlaminar contact evolution during thermoplastic composites processing. J. Mater. Sci. 2001;36:4661–4671. doi: 10.1023/A:1017950215945. [DOI] [Google Scholar]
- 72.Gruber M.B., Lockwood I.Z., Dolan T.L., Funck S.B., Tierney J.J., Simacek P., Gillespie J.W., Jr., Advani S.G., Jensen B.J., Cano R.J., et al. Thermoplastic in situ placement requires better impregnated tapes and tows; Proceedings of the International SAMPE Technical Conference; North Charleston, SC, USA. 22–25 October 2012. [Google Scholar]
- 73.Streeter V.L., Wylie E.B. Fluid Mechanics. McGraw-Hill; New York, NY, USA: 1975. [Google Scholar]
- 74.Cartledge H.C.Y., Baillie C.A. Studies of microstructural and mechanical properties of nylon/glass composite—Part II—The effect of microstructures on mechanical and interfacial properties. J. Mater. Sci. 1999;34:5113–5126. doi: 10.1023/A:1004765201803. [DOI] [Google Scholar]
- 75.Quan H., Li Z.M., Yang M.B., Huang R. On transcrystallinity in semi-crystalline polymer composites. Compos. Sci. Technol. 2005;65:999–1021. doi: 10.1016/j.compscitech.2004.11.015. [DOI] [Google Scholar]
- 76.Nakamura K., Watanabe T., Katayama K., Amano T. Some aspects of nonisothermal crystallization of polymers. I. Relationship between crystallization temperature, crystallinity and cooling conditions. J. Appl. Polym. Sci. 1972;6:1077–1092. doi: 10.1002/app.1972.070160503. [DOI] [Google Scholar]
- 77.Sonmez F.O., Eyol E. Optimal post-manufacturing cooling paths for thermoplastic composites. Compos. Part A Appl. Sci. Manuf. 2002;33:301–314. doi: 10.1016/S1359-835X(01)00133-6. [DOI] [Google Scholar]
- 78.Di Lorenzo M.L., Silvestre C. Non-isothermal crystallization of polymers. Prog. Polym. Sci. 1999;24:917–950. doi: 10.1016/S0079-6700(99)00019-2. [DOI] [Google Scholar]
- 79.Ijaz M., Robinson M., Gibson A.G. Cooling and crystallisation behaviour during vacuum-consolidation of commingled thermoplastic composites. Compos. Part A Appl. Sci. Manuf. 2007;38:828–842. doi: 10.1016/j.compositesa.2006.08.007. [DOI] [Google Scholar]
- 80.Kim K.J., Yu W.R., Harrison P. Optimum consolidation of self-reinforced polypropylene composite and its time-dependent deformation behavior. Compos. Part A Appl. Sci. Manuf. 2008;39:1597–1605. doi: 10.1016/j.compositesa.2008.06.005. [DOI] [Google Scholar]
- 81.Robitaille F., Gauvin R. Compaction of textile reinforcements for composites manufacturing. I: Review of experimental results. Polym. Compos. 1998;19:198–216. doi: 10.1002/pc.10091. [DOI] [Google Scholar]
- 82.Marquardt D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963;11:431–441. doi: 10.1137/0111030. [DOI] [Google Scholar]
- 83.Gereke T., Döbrich O., Hübner M., Cherif C. Experimental and computational composite textile reinforcement forming: A review. Compos. Part A Appl. Sci. Manuf. 2013;46:1–10. doi: 10.1016/j.compositesa.2012.10.004. [DOI] [Google Scholar]
- 84.Bussetta P., Correia N. Numerical forming of continuous fibre reinforced composite material: A review. Compos. Part A Appl. Sci. Manuf. 2018;113:12–31. doi: 10.1016/j.compositesa.2018.07.010. [DOI] [Google Scholar]
- 85.Skordos A.A., Monroy Aceves C., Sutcliffe M.P.F. A simplified rate dependent model of forming and wrinkling of pre-impregnated woven composites. Compos. Part A Appl. Sci. Manuf. 2007;38:1318–1330. doi: 10.1016/j.compositesa.2006.11.005. [DOI] [Google Scholar]
- 86.D’Agostino M.V., Giorgio I., Greco L., Madeo A., Boisse P. Continuum and discrete models for structures including (quasi-) inextensible elasticae with a view to the design and modeling of composite reinforcements. Int. J. Solids Struct. 2015;59:1–17. doi: 10.1016/j.ijsolstr.2014.12.014. [DOI] [Google Scholar]
- 87.Zouari B., Daniel J.L., Boisse P. A woven reinforcement forming simulation method. Influence of the shear stiffness. Comput. Struct. 2006;84:351–363. doi: 10.1016/j.compstruc.2005.09.031. [DOI] [Google Scholar]
- 88.Hamila N., Boisse P. A meso-macro three node finite element for draping of textile composite preforms. Appl. Compos. Mater. 2007;14:235–250. doi: 10.1007/s10443-007-9043-1. [DOI] [Google Scholar]
- 89.Hamila N., Boisse P., Sabourin F., Brunet M. A semi-discrete shell finite element for textile composite reinforcement forming simulation. Int. J. Numer. Methods Eng. 2009;79:1443–1466. doi: 10.1002/nme.2625. [DOI] [Google Scholar]
- 90.Xiong H., Guzman Maldonado E., Hamila N., Boisse P. A prismatic solid-shell finite element based on a DKT approach with efficient calculation of through the thickness deformation. Finite Elem. Anal. Des. 2018;151:18–33. doi: 10.1016/j.finel.2018.08.003. [DOI] [Google Scholar]
- 91.Belytschko T., Liu W.K., Moran B., Elkhodary K. Nonlinear Finite Elements for Continua and Structures. John Wiley & Sons; Hoboken, NJ, USA: 2013. [Google Scholar]
- 92.Software PLASFIB . Inter Deposit Certification. Agence pour la Protection des Programmes; Paris, France: 2011. [Google Scholar]
- 93.Khan M.A., Mabrouki T., Vidal-Sallé E., Boisse P. Numerical and experimental analyses of woven composite reinforcement forming using a hypoelastic behaviour. Application to the double dome benchmark. J. Mater. Process. Technol. 2010;201:378–388. doi: 10.1016/j.jmatprotec.2009.09.027. [DOI] [Google Scholar]
- 94.Sargent J., Chen J., Sherwood J., Cao J., Boisse P., Willem A., Vanclooster K., Lomov S.V., Khan M., Mabrouki T., et al. Benchmark study of finite element models for simulating the thermostamping of woven-fabric reinforced composites. Int. J. Mater. Form. 2010;3:683–686. doi: 10.1007/s12289-010-0862-5. [DOI] [Google Scholar]
- 95.Lee W., Um M.K., Byun J.H., Boisse P., Cao J. Numerical study on thermo-stamping of woven fabric composites based on double-dome stretch forming. Int. J. Mater. Form. 2010;3:1217–1227. doi: 10.1007/s12289-009-0668-5. [DOI] [Google Scholar]
- 96.Aridhi A., Arfaoui M., Mabrouki T., Naouar N., Denis Y., Zarroug M., Boisse P. Textile composite structural analysis taking into account the forming process. Compos. Part B Eng. 2019;166:773–784. doi: 10.1016/j.compositesb.2019.02.047. [DOI] [Google Scholar]
- 97.Peng X., Rehman Z.U. Textile composite double dome stamping simulation using a non-orthogonal constitutive model. Compos. Sci. Technol. 2011;7:1075–1081. doi: 10.1016/j.compscitech.2011.03.010. [DOI] [Google Scholar]
- 98.Willems A., Lomov S.V., Verpoest I., Vandepitte D., Harrison P., Yu W.R. Forming simulation of a thermoplastic commingled woven textile on a double dome. Int. J. Mater. Form. 2008;1:965–968. doi: 10.1007/s12289-008-0218-6. [DOI] [Google Scholar]
- 99.Abaqus 6.14 Theory Manual. Dassault Systèmes Simulia Corp.; Johnston, RI, USA: 2014. [(accessed on 3 September 2019)]. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ [Google Scholar]
- 100.Boisse P., Hamila N., Guzman-Maldonado E., Madeo A., Hivet G., Dell’Isola F. The bias-extension test for the analysis of in-plane shear properties of textile composite reinforcements and prepregs: A review. Int. J. Mater. Form. 2017;10:473–492. doi: 10.1007/s12289-016-1294-7. [DOI] [Google Scholar]