Abstract
Organic cation transporter 2 (OCT2) clears the blood of cationic drugs. Efforts to understand OCT2 selectivity as a means to predict the potential of new molecular entities (NMEs) to produce unwanted drug-drug interactions typically assess the influence of the NMEs on inhibition of transport. However, the identity of the substrate used to assess transport activity can influence the quantitative profile of inhibition. Metformin and 1-methyl-4-phenylpyridinium (MPP), in particular, display markedly different inhibitory profiles, with IC50 values for inhibition of MPP transport often being more than fivefold greater than IC50 values for the inhibition of metformin transport by the same compound, suggesting that interaction of metformin and MPP with OCT2 cannot be restricted to competition for a single binding site. Here, we determined the kinetic basis for the mutual inhibitory interaction of metformin and MPP with OCT2 expressed in Chinese hamster ovary cells. Although metformin did produce simple competitive inhibition of MPP transport, MPP was a mixed-type inhibitor of metformin transport, decreasing the maximum rate of mediated substrate transport and increasing the apparent Michaelis constant (Ktapp) for OCT2-mediated metformin transport. Furthermore, whereas the IC50 value for metformin’s inhibition of MPP transport did not differ from the Ktapp value for metformin transport, the IC50 value for MPP’s inhibition of metformin transport was less than its Ktapp value for transport. The simplest model to account for these observations required the influence of a distinct inhibitory site for MPP that, when occupied, decreases the translocation of substrate. These observations underscore the complexity of ligand interaction with OCT2 and argue for use of multiple substrates to obtain the needed kinetic assessment of NME interactions with OCT2.
Keywords: kinetics, 1-methyl-4-phenylpyridinium, organic cation, proximal tubule, transport
INTRODUCTION
The renal proximal tubule plays a significant role in the elimination of many small, positively charged organic electrolytes (12). Whereas many of these “organic cations” (OCs) are produced endogenously (e.g., choline, N1-methylnicotinamide, and thiamine), exogenous (xenobiotic) OCs are often introduced to the body through either the consumption of plant products or as prescription drugs (30). The transepithelial secretion of xenobiotic OCs by renal proximal tubule (RPT) cells limits the accumulation of these compounds in the blood and, as a result, reduces their toxic potential. The first step in renal OC secretion involves the entry of OCs into RPT cells from the blood across the basolateral membrane; in humans, this step is mediated by organic cation transporter 2 (OCT2) (25, 26). OCT2 is an electrogenic uniporter that depends on the inside negative membrane potential to passively accumulate OCs in the cell by allowing them to move down their electrochemical gradient (3). A defining characteristic of multidrug transporters, including OCT2, is their broad substrate selectivity, referred to as “multisubstrate specificity” in the seminal work of Ullrich et al. (43, 44) on renal OC transport using in vivo stopped-flow capillary perfusion and extended through studies of OCT2-mediated transport in heterologous expression systems (17, 28, 40, 50).
The broad selectivity of OCT2 results in its service as a common pathway for a wide array of clinically relevant drugs, thereby setting the stage for unwanted, and potentially adverse, drug-drug interactions (DDIs) (6). The simultaneous presence of two or more compounds that interact with OCT2, as either substrates for or inhibitors of transport activity, can influence the pharmacokinetics of elimination of one or both compounds and increase the potential of tissue-specific toxicity associated with elevated concentrations of some compounds. One approach to preemptively identifying potential perpetrators of unwanted DDIs is a decision tree-based assay that compares the test agent’s IC50 for inhibition of OCT2 transport activity, determined in vitro, to its maximum (unbound) plasma concentration. The initial recommended protocol for an OCT2 decision tree suggested measurement of transport of either 1-methyl-4-phenylpyridinium (MPP) or metformin to provide the in vitro indicator of OCT2 activity (6). Subsequent work, however, showed that OCT2-mediated MPP transport is less sensitive to inhibition than metformin transport (1, 11), with IC50 values for inhibition of MPP transport that exceed those for metformin by 5- to 10-fold (1). Other pairs of OCT2 substrates also show differential sensitivity to inhibition as well (11, 41, 47). We recently screened the inhibitory influence of >400 compounds against OCT2-mediated transport of 6 structurally distinct substrates, including MPP and metformin (34). Although modest differences (<2-fold) of inhibitory interaction were noted between metformin and several other OCT2 substrates {including cimetidine, tetraethylammonium, and the fluorescent OC 4-[4-(dimethylamino)styryl]-N-methylpyridinium (i.e., ASP)}, the results confirmed that MPP transport is typically >5-fold less sensitive to inhibition than is metformin transport (based on IC50 values). Consequently, conclusions concerning the DDI risk of a new molecular entity (NME) can be markedly influenced by the choice of substrate to serve as a marker of OCT2 activity. Indeed, the marked substrate dependence of ligand interaction with OCTs and other multidrug transporters (4, 5, 33, 46) is cited as reason for substantial modification of in vitro testing protocols (18) and was a causative factor in the recent modification of the United States Food and Drug Administration’s (FDA) Guidance for Industry (45a) with respect to the design of decision tree-based assays for assessing DDI risks for NMEs.
The discrepancy between the inhibitory profiles for MPP and metformin with OCT2 implies that interaction of these substrates with the transporter involves two or more distinct binding sites (13, 34). This conclusion is supported by evidence obtained in site-directed structural studies for both OCT2 and OCT1 (8, 9, 49), observations of biphasic inhibitory interactions of selected compounds (including MPP) with OCTs (10, 24), substrate dependency of ligand-induced substrate counterflow by OCT1 (2), and recent evidence for the presence of multiple binding sites for MPP on purified OCT1 protein (16). However, the kinetic mechanism for the differential interaction of MPP and metformin with OCT2 is not clear. To address this issue, we examined the kinetics of OCT2-mediated transport of both of these substrates, applying an analytic approach that uses the time course of net substrate accumulation at different substrate concentrations to determine initial rates of transport, thereby reducing the influence on kinetic analyses of both unstirred water layers and mediated back flux of substrate. This method was used to determine the kinetics of transport of each substrate measured in the presence of the other. A theoretical model was used to test whether the observed transport kinetics were consistent with the effects of MPP binding to a second site, distinct from the site(s) associated with MPP and metformin transport. The results support the conclusion that an inhibitory binding site for MPP is present on OCT2, distinct from the transport site(s) associated with MPP and metformin transport, that can influence the binding and translocation of metformin and that the observed differences in sensitivity of MPP and metformin transport to inhibition by other substrates can be accounted for by the binding of such substrates to the inhibitory site.
METHODS
Chemicals.
[3H]MPP [specific activity (SA): 80 Ci/mmol] was purchased from Perkin-Elmer, and [14C]metformin (SA: 90 mCi/mmol) was purchased from Moravek Biochemicals (Brea, CA). Unlabeled metformin was purchased from AK Scientific (Union City, CA), and unlabeled MPP (purity > 99.5%) was synthesized by the Department of Chemistry and Biochemistry, University of Arizona. Ham’s F-12 Kaighn’s modified medium was obtained from Sigma-Aldrich (St. Louis, MO). Other reagents were of analytic grade and were commercially obtained.
Cell culture.
Chinese hamster ovary (CHO) cells with a single integrated Flp-in recombination site were obtained from Invitrogen (Carlsbad, CA). Methods for the generation of cell lines that stably express human OCT2 were as previously described (31). Cells were passaged every 3–4 days and maintained at 37°C in a humidified environment with 5% CO2. Expression of human OCT2 was maintained through hygromycin (200 µg/ml, Invitrogen, Carlsbad, CA)-selective pressure; wild-type (WT; non-OCT2-expressing) CHO cells were maintained through Zeocin (100 µg/ml, Invitrogen)-selective pressure. When seeded into 96-well plates (Greiner, VWR, Arlington Heights, IL) for transport assays, cells were grown to confluence in antibiotic-free medium.
Transport experiments.
Cells were seeded in 96-well plates with 200 µl cell media containing 550,000 cells/ml or 275,000 cells/ml, and experiments were performed 24 or 48 h later, respectively. To begin an experiment, media were aspirated and the wells were washed for three cycles over 12 s with 300 µl of room temperature (23°C) Waymouth buffer [WB; containing (in mM) 135 NaCl, 13 HEPES, 2.5 CaCl2·2H2O, 1.2 MgCl2, 0.8 MgSO4·7H2O, 5 KCl, and 28 D-glucose, at pH 7.4] using an automatic microplate washer (model 405, BioTek, Winooski, VT). Transport was then initiated by the addition of 60 µl WB containing radiolabeled substrate and other compounds as needed. For all experiments, transport buffer was added using a VIAFLO 96-well multichannel pipet (Integra Biosciences, Hudson, NH). After selected time intervals, transport was terminated by rinsing with three cycles of cold WB (300 µl). After a rinse and final aspiration, 200 µl scintillation cocktail (Microscint 20, Perkin-Elmer, Waltham, MA) was added to each well. The plates were sealed (Topseal-A, Perkin-Elmer), and, after plates were allowed to sit for at least 2 h, accumulated radioactivity was determined in a 12-channel multiwell scintillation counter (Wallac Trilux 1450 Microbeta, Perkin-Elmer, Waltham, MA).
Data analysis.
In some cases, uptake in OCT2-expressing cells was corrected for transport measured in WT CHO cells determined under the same experimental conditions and reported as means with SDs. The significance of observed differences was determined using paired one- or two-tailed t-tests or one-way ANOVA (with the Tukey multiple-comparisons test) as appropriate. Observed differences were deemed significant when P < 0.05. Analyses used either Excel 2010 (Microsoft, Redmond, WA) or Prism 6 (GraphPad, La Jolla, CA).
Kinetic transport models.
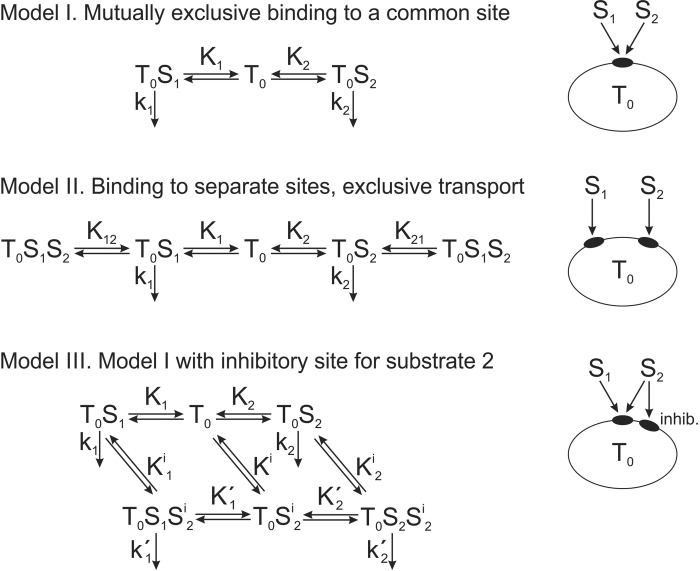
Three theoretical models were developed to allow quantitative analysis of potential OCT2 competitive binding and transport mechanisms for MPP and metformin. In model I, both substrates are assumed to bind reversibly to a single binding site, with mutually exclusive binding. In model II, each substrate binds reversibly to a separate site on the transporter, with the possibility of simultaneous binding but with a mutually exclusive transport step. In model III, both substrates are assumed to bind reversibly and exclusively to a single binding site (or mutually exclusive sites), as in model I, but with an additional binding site for MPP that, when occupied, exerts an allosteric inhibition of metformin transport without supporting transport of the occupying MPP molecule. In all three models, the transitions between different states of binding are governed by standard mass action kinetics, which are assumed to reach equilibrium very rapidly relative to timescales of transport experiments. The governing equations for the models are provided in the appendix. Fitting of unknown parameters to experimental data for these models was performed using the “lsqnonlin” routine of MATLAB (MathWorks, Natick, MA). These models were then used to predict the inhibitory effects on metformin and MPP transport of a third substrate with OCT2 binding characteristics similar to those of MPP.
RESULTS
Estimating initial rates of transport from the time course of net uptake.
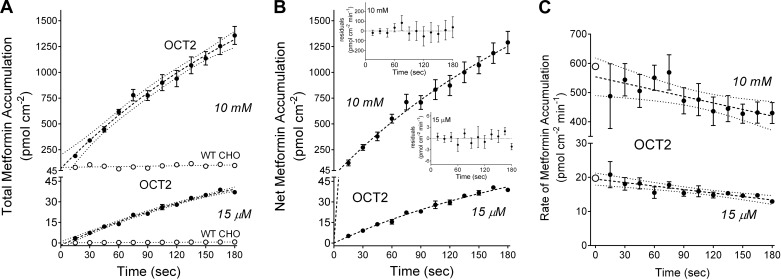
Although the rates of transport required for determining kinetics are typically estimated from the amount of substrate accumulated at a single time point selected from within the “linear phase” of net accumulation, achieving a true initial rate of transport is challenging. The need to obtain adequate precision in the signal for transport activity, usually through the accumulation of a radioactively or fluorescently labeled substrate, often requires the use of time points that lie outside of an unambiguously linear phase of uptake. Frequently exacerbating the issue is the comparatively high level of transport activity that can be achieved with heterologous expression systems, and, when combined with the small volume of cultured cells, the result can be a rapid rise in intracellular substrate concentration that amplifies backflux (mediated or passive) of accumulated substrate. Figure 1A shows time courses of net accumulation of [14C]metformin into OCT2-expressing (OCT2) and nonexpressing (WT CHO) CHO cells determined for two concentrations of substrate that were well below (15 µM) or well above (10 mM) the apparent Michaelis constant for OCT2-mediated metformin transport [Ktapp; ~300 µM (37); supported by upcoming results]. While the modest rate of metformin accumulation by WT CHO cells was effectively linear for the 3-min time course, net uptake into OCT2-expressing cells was not, for either substrate concentration. However, for each concentration, extrapolation of the time courses of substrate accumulation by OCT2 and WT CHO cells to time 0 [as described by a simple exponential rise to a constant (15)] revealed intercepts that did not differ significantly from one another. Consequently, total net accumulation of substrate by OCT2-expressing cells, corrected for this “background,” was determined by subtracting the time 0 intercept from substrate accumulation at each time point. Figure 1B shows the resulting time courses of total net accumulation of 15 µM and 10 mM metformin by OCT2-expressing cells. Although not linear, these time courses were adequately described by a hyperbolic rise to an extrapolated maximum, as follows:
| (1) |
where Ut is net substrate accumulation at time t, Umax is the extrapolated maximum accumulation (including carrier-mediated uptake and any additional accumulation arising from diffusion, nonspecific binding, and/or incomplete rinsing of the test solution), and KU is a fitted constant. In our preliminary work, we compared several classes of equation to describe the time course of net substrate accumulation, including one phase exponential association, a second-order polynomial expansion (see Ref. 15), and the rectangular hyperbola that we ultimately selected. Although the polynomial expansion proved inadequate to the task, the exponential and hyperbolic fits produced similar results, with hyperbolic analysis generally providing fits that most closely matched simulated time courses derived from the integrated Michaelis-Menten equation (data not shown). These fits generally underestimated the “true” rates of transport (and, therefore, the kinetic parameters calculated from these estimates) for simulated time courses of net substrate accumulation, but these errors were typically <10%, and we used this method to establish the kinetic parameters for OCT2-mediated transport of metformin and MPP.
Fig. 1.
A: time course of net accumulation of two concentrations of [14C]metformin (15 µM and 10 mM) into organic cation transporter 2 (OCT2)-expressing Chinese hamster ovary (CHO) cells (solid symbols) and wild-type (WT; nonexpressing) CHO cells (open symbols). Each point is the mean ± SE of uptakes determined sequentially in three 96-well plates (n = 3) and represents a single experiment. The dashed lines were fit to the OCT2 data using an exponential rise to a constant (showing 95% confidence intervals); the dotted lines were fit to the WT CHO cell data using simple linear regression. B: time course of net accumulation of 15 µM and 10 mM metformin into OCT2 cells, corrected for plate background as discussed in the text. Dashed lines were fit to the data using Eq. 1. The residuals for each time course are shown in the insets. C: calculated rates (per minute) of OCT2-dependent metformin transport, determined from net accumulation at each measured point of the time courses shown in B. Each solid point is the mean transport rate ± SE calculated from uptakes measured in three wells. The dashed lines represent simple linear regressions of the data as plotted. The open symbols at time 0 represent the rates of metformin transport at time 0 calculated using extrapolated maximum accumulation (Umax) and fitted constant (KU) values determined with Eq. 1.
The ratio of Umax to KU (Umax/KU) provided an empirical estimate of the rate at time 0, i.e., “the initial rate” of total substrate accumulation. Figure 1C shows these calculated time 0 rates (open circles) of metformin accumulation at 15 µM and 10 mM (19.8 and 589 pmol·cm−2·min−1) as well as the rates estimated from the accumulation of substrate at each point along the time courses of net uptake. As the time point increased, the calculated rate of substrate accumulation decreased, presumably reflecting the growing influence of 1) mediated substrate backflux (21) and 2) the decrease in substrate concentration at the membrane due to the diffusion-limited impact of unstirred water layers (39). The systematic shift was larger at the lower substrate concentration, with the 15-s-based rate being ~30% higher than that based on the 2-min uptake for 15-µM MPP time course compared with ~10% for the 10-mM time course. Also evident, the errors associated with rates calculated from early time points were generally larger than those associated with rates based on later time points, reflecting the error associated with measuring the smaller amount of substrate accumulated in 15 s compared with 120 s. We suggest that the initial rate estimated using Eq. 1, reflecting as it does the analysis of a detailed time course of uptake, results in smaller random error of measurement with less bias and a more accurate estimate of the true initial rate of substrate accumulation (see Ref. 15).
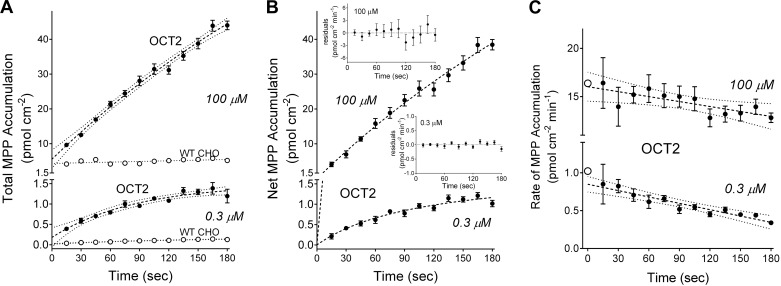
Similar profiles were also evident for time courses of MPP accumulation by OCT2-expressing cells. Figure 2A shows time courses of net accumulation of [3H]MPP by OCT2-expressing and nonexpressing cells determined for two concentrations of the labeled substrate, 0.3 µM and 100 µM, that were well below and well above the nominal Ktapp for OCT2-mediated MPP transport [~5 µM (37); supported by upcoming data]. As with metformin, accumulation of MPP by WT CHO cells was effectively linear for 3 min, whereas net uptake into OCT2-expressing cells was not, for either substrate concentration. These profiles were also adequately described by Eq. 1, and Fig. 2B shows the resulting time courses of total net accumulation for 0.3 and 100 µM MPP by OCT2-expressing cells. Figure 2C shows the calculated time 0 rates of MPP uptake at these two concentrations (open symbols) and the rates estimated from the accumulation of substrate at each point along the time courses of net uptake. As with metformin, there was a systematic decrease in the calculated rate of transport as the time point used for estimating initial rate increased; again, the difference was larger at the lower substrate concentration (~50%) compared with the higher substrate concentration (~30%), and, again, the errors associated with early time points were generally larger than those associated with later time points.
Fig. 2.
A: time course of net accumulation of two concentrations of [3H]1-methyl-4-phenylpyridinium (MPP; 0.3 µM and 100 µM) into organic cation transporter 2 (OCT2)-expressing Chinese hamster ovary (CHO) cells (solid symbols) and wild-type (WT; nonexpressing) CHO cells (open symbols). Each point is the mean ± SE of uptakes determined sequentially in three 96-well plates (n = 3) and represents a single experiment. The dashed lines were fit to the OCT2 data using an exponential rise to a constant (showing 95% confidence intervals); the dotted lines were fit to the WT CHO cell data using simple linear regression. B: time course of net accumulation of 0.3 µM and 100 µM MPP into OCT2 cells, corrected for plate background as discussed in the text. Dashed lines were fit to the data using Eq. 1. The residuals for each time course are shown in the insets. C: calculated rates (per minute) of OCT2-dependent MPP transport, determined from net accumulation at each measured point of the time courses shown B. Each solid point is the mean transport rate ± SE calculated from uptakes measured in three wells. The dashed lines represent simple linear regressions of the data as plotted. The open symbols at time 0 represent the rate of MPP transport at time 0 calculated using extrapolated maximum accumulation (Umax) and fitted constant (KU) values determined with Eq. 1.
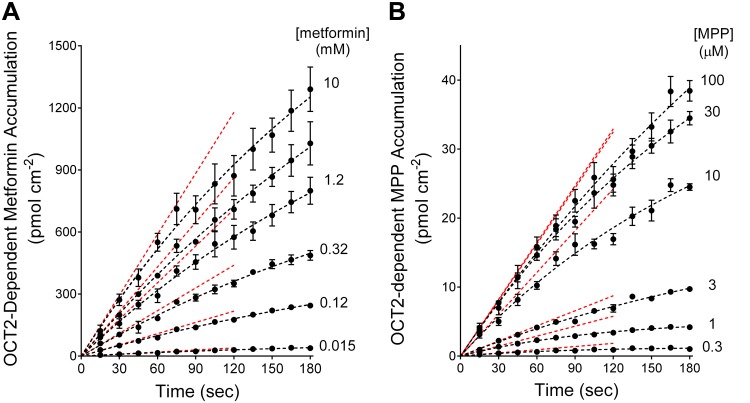
Figure 3 shows the 3-min time courses for net accumulation of metformin (Fig. 3A) and MPP (Fig. 3B) by OCT2-expressing cells for six concentrations of radiolabeled substrate (in the single experiments from which the data shown in Figs. 1 and 2 were taken) and the calculated time 0 rates of net accumulation (dashed red lines).
Fig. 3.
Time courses of net accumulation of six concentrations of [14C]metformin (A) or [3H]1-methyl-4-phenylpyridinium (MPP; B) into organic cation transporter 2 (OCT2)-expressing Chinese hamster ovary cells. Each time course was corrected for background uptake, as described in the text and in Figs. 1 and 2. Each point is the mean ± SE of uptakes determined sequentially in three 96-well plates (n = 3) and reflects results of single representative experiments. The dashed black lines were fit to these data using Eq. 1. The dashed red lines indicate the slopes at time 0 (initial rate) calculated using the extrapolated maximum accumulation (Umax) and fitted constant (KU) values obtained with Eq. 1.
Kinetics of OCT2-mediated transport of metformin and MPP.
Figure 4A shows the relationship between increasing substrate concentration and the initial rate (calculated as described above) of total accumulation of metformin into OCT2-expressing or WT CHO cells. The kinetic profile reflected the sum of two processes: 1) OCT2-mediated uptake that was described by Michaelis-Menten kinetics and 2) a nonsaturable, first-order component that reflected residual extracellular substrate left after the rapid rinsing procedure (transmembrane diffusion and nonspecific binding of these hydrophilic compounds were minimal; unpublished observations). Although the nonsaturable component was evident in parallel measurements of transport in WT (non-OCT2 expressing) CHO cells (Figs. 1 and 2), we found that subtracting WT accumulation from total accumulation measured in OCT2-expressing cells to correct for this noncarrier-mediated component of transport frequently introduced errors, particularly at the millimolar range of metformin concentrations required to establish full saturation of the transporter. This discrepancy reflected modest differences in the efficiency of rinsing extracellular substrate from the OCT2 and WT CHO cell lines, which were also evident in differences in retention of an extracellular space marker after a rinse (data not shown). However, a longer rinse, even with an ice-cold stop solution, introduced greater problems due to the loss of accumulated substrate from cells (e.g., Ref. 32). Consequently, we elected not to use substrate accumulation by WT CHO cells to “correct” that by OCT2 cells; instead, kinetic parameters were determined from total substrate accumulation by OCT2-expressing CHO cells (i.e., mediated plus nonsaturable) using the following relationship:
| (2) |
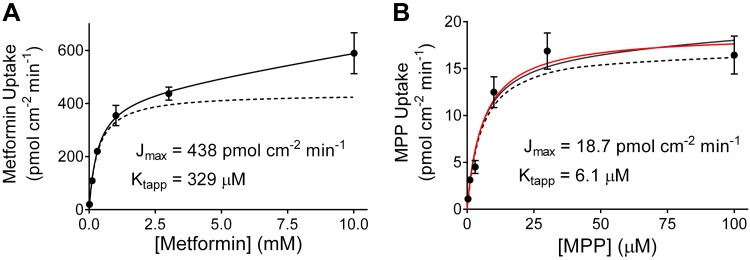
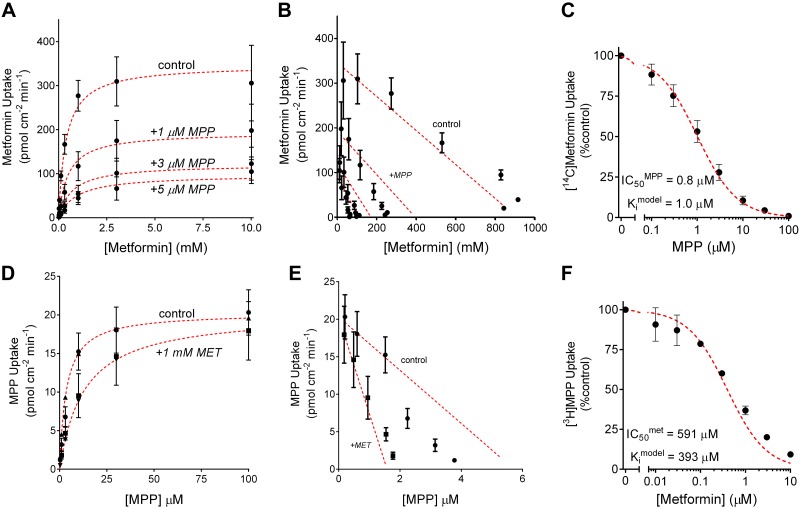
where J is the initial rate of mediated transport from a given substrate concentration ([S]), Jmax is the maximum rate of mediated substrate transport, and kaccum is a constant that describes the nonsaturable (nonmediated) component of total net substrate accumulation. The analysis of the metformin data shown in Fig. 4A resulted in a Jmax of 438 pmol·cm−2·min−1 and Ktapp of 329 µM (and kaccum of 0.016 µl·cm−2·min−1). Jmax for metformin transport determined from five separate experiments (each performed in triplicate) was 339 (SD 159) pmol·cm−2·min−1, with a Ktapp of 278 (SD 90) (Table 1).
Fig. 4.
A: kinetics of organic cation transporter 2 (OCT2)-mediated metformin transport. Solid symbols represent mean ± SE rates of total metformin uptake by OCT2-expressing Chinese hamster ovary (CHO) cells calculated using the data shown in Fig. 3A. The solid line was fit to these data using Eq. 2 and reflects the combined influence of OCT2 and a nonsaturable (first-order) process (dominated by extracellular substrate not removed by the rinsing procedure). The dashed line was calculated using maximum rate of mediated substrate transport (Jmax) and apparent Michaelis constant (Ktapp) values determined from Eq. 2. B: kinetics of OCT2-mediated 1-methyl-4-phenylpyridinium (MPP) transport. Solid symbols represent mean ± SE rates of total MPP uptake by OCT2-expressing CHO cells calculated using the data shown in Fig. 3B. The solid black line was fit to these data using Eq. 2 and reflects the combined influence of OCT2 and a nonsaturable (first-order) process. Note that the nonsaturable (nonmediated) component of total net substrate accumulation (kaccum) value used in this analysis was set equal to the kaccum value calculated from the metformin data in Fig. 4A, and the dashed black line was calculated using Jmax and Ktapp values determined from this analysis. The solid red line was fit to the data using just the Michaelis-Menten equation (i.e., with no first-order component). The resulting kinetic values (listed in the figure) were not statistically different from those obtained with Eq. 2 (using the metformin kaccum value).
Table 1.
Kinetics of organic cation transporter 2-mediated transport of metformin and MPP and the kinetics of their mutual inhibition
| Metformin |
MPP |
|||
|---|---|---|---|---|
| Condition | Jmax, pmol·cm−2·min−1 | Ktapp, µM | Jmax, pmol·cm−2·min−1 | Ktapp, µM |
| Control | 339 (SD 159) (n = 5) | 278 (SD 90) | 21.7 (SD 6.3) (n = 4) | 5.6 (SD 0.7) |
| +3 µM MPP | 176 (SD 126) (n = 5; P = 0.0005) | 790 (SD 256) (P = 0.003) | ||
| +1 mM metformin | 23.1 (SD 8.6) (n = 4) | 20.1 (SD 12.8) (P = 0.05) | ||
MPP, 1-methyl-4-phenylpyridinium; Jmax, maximum rate of mediated substrate transport; Ktapp, apparent Michaelis constant.
The relationship between increasing MPP concentration and the time course-based rates of MPP transport shown in Fig. 3B is presented in Fig. 4B. When these data were analyzed using Eq. 2, the resulting kaccum value was not significantly different from zero and the calculated Jmax and Ktapp values were the same as those obtained by simply using the Michaelis-Menten equation: a Jmax of 18.7 pmol·cm−2·min−1 and Ktapp of 6.1 µM (that fit is shown by the solid red line in Fig. 4B). The impact of the first-order component over the concentration range used to assess the kinetics of MPP transport (highest concentration typically 100 µM) was sufficiently modest that it could generally be ignored. This is evident in the solid black line fit to the MPP data that shows the impact of the kaccum value obtained in the analysis of the metformin data shown in Fig. 4A; the MPP kinetic constants, resulting from that analysis (dashed black line; Jmax and Ktapp values of 17.3 pmol·cm−2·min−1 and 4.7 µM, respectively) did not differ significantly from those obtained for MPP transport using only the Michaelis-Menten relationship. This was not always the case for MPP; some experiments did reveal a nonsaturable component. It is notable that the average kaccum values for uptake of metformin and MPP in all experiments did not differ significantly (0.025 and 0.024 µl·cm−2·min−1, n = 4 or 5, P = 0.027), which is consistent with our interpretation that these values are independent of the substrate used and largely reflect inadequate rinsing of substrate in spatially complex extracellular compartments. Consequently, we routinely analyzed kinetic data using both the simple Michaelis-Menten relationship and the Eq. 2 relationship and used the fit that resulted in a superior residual profile. Jmax for MPP transport determined from four separate experiments (each performed in triplicate) was 21.7 (SD 6.3) pmol·cm−2·min−1, with a Ktapp of 5.6 (SD 0.7) µM (Table 1).
Inhibition of MPP transport by metformin and of metformin transport by MPP.
Metformin produced a monophasic inhibition of the OCT2-mediated 30-s accumulation of ~10 nM [3H]MPP (Fig. 5A). This inhibitory profile was adequately described by the following relationship:
| (3) |
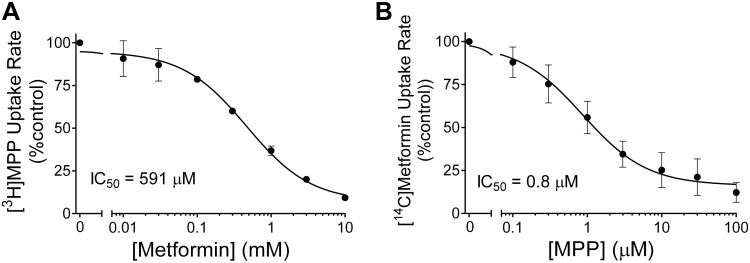
where [I] is the concentration of inhibitor (in this case, metformin), J* is the rate of OCT2-mediated transport of radiolabeled substrate (in this case, [3H]MPP) from a concentration equal to [S*] (in this case, ~10 nM), IC50 is the concentration of inhibitor that reduces mediated (i.e., inhibitable) substrate transport by 50%, is a constant that includes the maximal rate of substrate transport times the ratio of the inhibitor IC50 and the Ktapp for transport of the substrate, and kaccum is the constant introduced in Eq. 2 that accounts for the nonsaturable component of net substrate accumulation. In three separate experiments, the IC50 value for metformin’s inhibition of ~8 nM [3H]MPP was 591 (SD 112) µM, which did not differ significantly from the Ktapp for OCT2-mediated metformin transport (P > 0.05). MPP also produced a simple monophasic inhibition of the OCT2-mediated 30-s net accumulation of ~9 µM [14C]metformin (Fig. 5B). In five separate experiments, the IC50 value for MPP’s inhibition of net metformin uptake was 0.84 (SD 0.62) µM, which was significantly less than the Ktapp for OCT2-mediated MPP transport (P < 0.00001).
Fig. 5.
A: effect of increasing metformin concentration on the rate of organic cation transporter 2 (OCT2)-mediated [3H]1-methyl-4-phenylpyridinium (MPP; 6 nM) transport. MPP uptakes were based on 30-s net accumulation [uncorrected for accumulation in wild-type (WT) Chinese hamster ovary (CHO) cells). Each point is the mean ± SE of uptakes (normalized to accumulation measured in the absence of metformin) determined in three separate experiments (each the average of 6 wells in a 96-well plate). The line was fit to the data using Eq. 3. B: effect of increasing MPP concentration on the rate of OCT2-mediated [14C]metformin (12 µM) transport. Metformin uptakes were based on 30-s net accumulation (uncorrected for accumulation in WT CHO cells). Each point is mean ± SE of uptakes (normalized to accumulation measured in the absence of MPP) determined in five separate experiments (each the average of 6 wells in a 96-well plate). The line was fit to the data using Eq. 3.
Kinetic basis of metformin inhibition of MPP transport and of MPP inhibition of metformin transport.
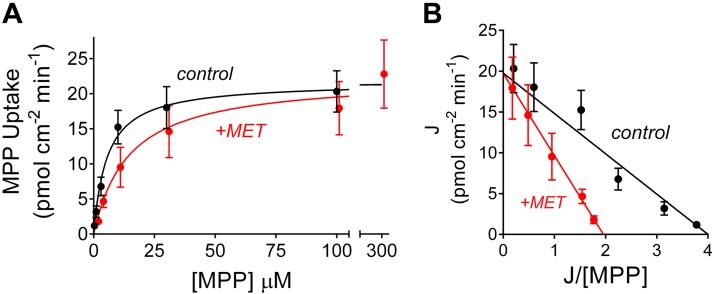
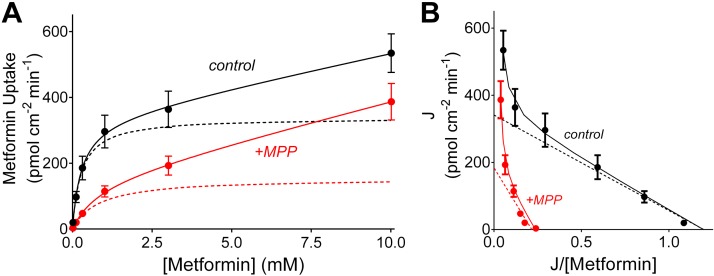
The kinetics of interacting substrates are often considered to involve competitive binding of the substrates to a single binding site on the surface of the transporter. However, we have previously shown that OCT2-mediated MPP transport is typically less sensitive to inhibition than is transport of metformin, i.e., IC50 values for other substrates are typically >5-fold larger for inhibition of MPP transport than are those for inhibition of metformin transport (1, 34). This observation is not consistent with the assumption of a single binding site for all substrates. Furthermore, our present observations show that the IC50 value for inhibition of metformin transport by MPP (~1 µm) was significantly less than the Ktapp for MPP transport (~5 µm). The two constants would be expected to be equal when both substrates bind only to a single site (36). A potential explanation for both of these observed behaviors is the presence of two or more, potentially interacting, substrate-binding sites on OCT that may be occupied simultaneously. To probe these aspects of OCT2 transport kinetics, we performed further experiments to characterize the competitive interactions between metformin and MPP transport. Figure 6A shows the relationship between increasing MPP concentration on the initial rates of OCT2-mediated MPP transport (calculated as described above), determined in four separate experiments, in the absence (control) and presence of 1-mM unlabeled metformin. Figure 6B shows the Eadie-Hofstee transformation of these data. The data revealed that the presence of 1 mM metformin had no effect on the Jmax for MPP transport (21.7 vs. 23.1 pmol·cm−2·min−1; Table 1) but did significantly increase the value for Ktapp (5.6 vs. 20.1 µM; Table 1). In those four separate experiments, the calculated apparent inhibitory constant (Kiapp) for metformin’s inhibition of MPP transport was 555 (SD 282) µM, which did not differ significantly from either the Ktapp of 278 µM for metformin’s transport or the IC50 value for metformin’s inhibition of MPP transport. Together, these observations support the conclusion that metformin’s interaction with OCT2-mediated MPP transport is adequately described as competitive. However, MPP’s inhibition of metformin transport revealed a different kinetic profile. As shown in Fig. 7A, which summarizes the results of five separate experiments, and as highlighted in the Eadie-Hofstee transformation in Fig. 7B, with the dashed lines showing the data corrected for the influence of the first-order component of substrate accumulation, elevated concentrations of metformin did not relieve the inhibition produced by MPP; the presence of 3 µM unlabeled MPP resulted in a reduction of Jmax (from 339 to 176 pmol·cm−2·min−1; Table 1) and an increase in Ktapp (from 278 to 790 µM; Table 1), a profile consistent with mixed-type inhibition (36).
Fig. 6.
Kinetics of organic cation transporter 2 (OCT2)-mediated 1-methyl-4-phenylpyridinium (MPP) transport determined in the absence (black symbols and line) and presence (red symbols and line) of 1 mM of unlabeled metformin. Rates of transport were determined from the time courses of net MPP accumulation (see Figs. 2 and 3). Each point is the average of OCT2-mediated transport (uncorrected the first-order component of substrate accumulation; see Fig. 4) determined in four separate experiments. B: Eadie-Hofstee transformation of the data shown in A.
Fig. 7.
Kinetics of organic cation transporter 2 (OCT2)-mediated metformin transport determined in the absence (black circles with line) and presence (red circles with line) of 3 μM of unlabeled 1-methyl-4-phenylpyridinium (MPP). Rates of transport were determined from the time courses of net metformin accumulation (see Figs. 1 and 3). Each point is the average of OCT2-mediated transport (uncorrected the first-order component of substrate accumulation; see Fig. 4) determined in five separate experiments. Dashed lines show the OCT2-mediated kinetic profiles determined using Eq. 2. B: Eadie-Hofstee transformation of the data shown in A.
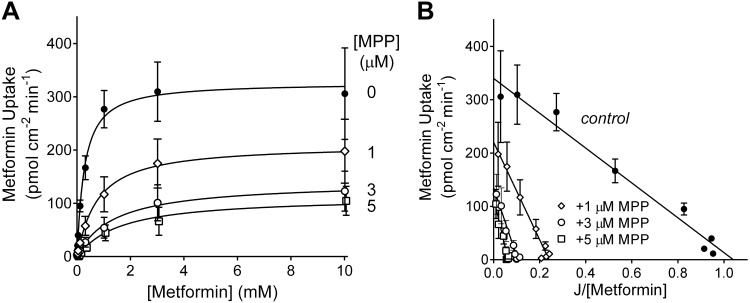
We expanded our examination of the kinetic basis of MPP’s inhibition of metformin transport by determining the impact of increasing the concentration of MPP from 1 to 3 to 5 µM on Jmax and Ktapp values for OCT2-mediated metformin uptake (Fig. 8A and Table 2). In light of the number of paired samples in this study, we used the “two-step” approach to the assessment of transport kinetics and estimated the initial rate of metformin transport from 60-s net uptakes, recognizing that the calculated rates represented 10−30% underestimates of rates at time 0 (see Fig. 1C). Figure 8B shows Eadie-Hofstee transformations of the resulting kinetic profiles. As the concentration of unlabeled MPP increased, Jmax consistently decreased and Ktapp consistently increased, indicative of a mixed-type mechanism of inhibition.
Fig. 8.
Effect of increasing 1-methyl-4-phenylpyridinium (MPP) concentration on the kinetics of organic cation transporter 2 (OCT2)-mediated metformin transport. A: relationship between increasing metformin concentration and the rate of metformin transport, determined in the absence (0 µM; solid circles) and presence of unlabeled MPP (1, 3, and 5 µM; open symbols). Each point is the average ± SE of rates (calculated from 60-s net uptakes) of transport measured in three separate experiments, each performed in triplicate. Each rate was corrected for the influence of a first-order component of metformin accumulation (see Fig. 7), and the resulting profiles described by the Michaelis-Menten equation (solid black lines). B: Eadie-Hofstee transformations of the kinetic profiles for metformin transport shown in A.
Table 2.
Effect of single concentrations of MPP on the kinetics of organic cation transporter 2-mediated metformin transport
| Metformin |
||
|---|---|---|
| Condition | Jmax pmol·cm−2·min−1 | Ktapp µM |
| Control | 342 ± 30 (n = 3) | 331 ± 43 |
| +1 µM MPP | 224 ± 45 (n = 3) | 939 ± 250 |
| +3 µM MPP | 139 ± 38 (n = 3) | 1327 ± 466 |
| +5 µM MPP | 121 ± 39 (n = 3) | 1935 ± 774 |
Maximum rate of mediated substrate transport (Jmax) and apparent Michaelis constant (Ktapp) values as well as their associated SEs were calculated by Prism (GraphPad, La Jolla, CA) based on the pooled data from three separate experiments that included all experimental conditions (total of 24 data points analyzed for each data set). MPP, 1-methyl-4-phenylpyridinium.
We have previously suggested that the observation of mixed-type profiles for inhibition of OCT2-mediated transport was consistent with a “linear mixed-type” (LM-T) kinetic mechanism of ligand interaction and the presence of multiple binding sites on a ligand binding surface (13). However, the overall profile of mutual inhibitory interaction between metformin and MPP with OCT2 is inconsistent with the predictions inherent in a LM-T inhibitory mechanism. Although appropriate parameter selection in a LM-T model can produce apparently distinct inhibitory interactions between two substrates (i.e., competitive versus mixed type), the LM-T model should result in an IC50/Ki value for an inhibitor that is equal to (or greater than) the Kt for that compound’s transport (36). While this was the case for metformin’s inhibition of MPP transport (Fig. 5A), the IC50 value for MPP’s inhibition of metformin transport was consistently less than its Ktapp for transport (Fig. 5B).
We considered three possible models, of increasing complexity, to account for the mutual inhibitory interactions observed between metformin and MPP with OCT2 (Fig. A1; see the appendix). Models I and II were rejected as being unable to reproduce the full profile of mutual metformin MPP interactions; model I resulted in mutual competitive interactions between the two substrates, and model II reflected the standard LM-T model described above. Model III proved to be the simplest model that could account for the mutual inhibitory interactions observed for metformin and MPP transport. It includes a common (or mutually exclusive) binding site(s) for metformin and MPP that is associated with substrate transport and a second, nontransporting site that causes inhibition of metformin transport when MPP is bound to it. With the assumption that the allosteric influence of MPP bound to the inhibitory site is largely restricted to a decrease in turnover rate constant for metformin transport, (i.e., < k1), model III can explain the mixed-type interaction of MPP on metformin transport (Fig. A2, A and B) and the competitive interaction of metformin on MPP transport (Fig. A2, D and E). Importantly, it also provides a basis for an IC50 value for MPP inhibition of metformin transport that is significantly lower than the Ktapp value for MPP transport (Fig. A2C) while also supporting an IC50 value for metformin inhibition of MPP that is similar to the Ktapp value for metformin (Fig. A2F). Table 3 shows a comparison of the experimentally determined kinetic parameters for the mutual interactions of metformin and MPP with OCT2 to those obtained by optimizing the fit of model III to these data.
Table 3.
Comparison of measured kinetic parameters for organic cation transporter 2-mediated transport to those predicted by model III (Fig. A1)
| Inhibitor | Ktapp, µM | , µM | Jmax, pmol·cm−2·min−1 | , pmol·cm−2·min−1 | IC50, µM | , µM |
|---|---|---|---|---|---|---|
| Metformin substate | ||||||
| 0 | 331 | 381 | 342 | 347 | 591 | 393 |
| 1 µM MPP | 939 | 489 | 224 | 194 | ||
| 3 µM MPP | 1327 | 703 | 139 | 121 | ||
| 5 µM MPP | 1935 | 917 | 121 | 97 | ||
| MPP substrate | ||||||
| 0 | 5.6 | 3.5 | 21.7 | 20.3 | 0.8 | 1.0 |
| 10 mM metformin | 20.1 | 12.9 | 23.1 | 20.3 | ||
DISCUSSION
OCT2 mediates the initial step in the renal secretion of organic cations in humans (30). Because these compounds include as many as 40% of prescribed drugs (27), the potential for disadvantageous DDIs made OCT2 the focus of studies assessing its selectivity (20, 28, 40, 50), and a current “FDA Guidance for Industry” outlines guidelines for determining the DDI potential of new compounds (45a). The new guidelines reflect observations showing that the inhibitory profile of novel ligands can be influenced by the identity of the substrate used as a marker of OCT2 activity. In particular, OCT2-mediated MPP transport is markedly less sensitive to inhibition than is metformin transport (1, 11, 34, 50). This observation is ironic in light of the initial recommendation by the International Transport Consortium that suggested using these two substrates for decision tree-based assessments of potential DDIs with OCTs (6). The choice of those substrates was not, however, arbitrary. Metformin’s inclusion reflected its widespread clinical importance and the strong evidence that OCT2 plays a quantitatively significant role in mediating its clearance (6), and MPP’s inclusion reflected the simple fact that it has long been recognized (19) as an efficiently transported substrate by organic cation transporters (35), so its use can provide strong transport signals amenable to precise quantitative analysis. However, precision is not accuracy, and a review of the literature (29, 39) revealed a 5- to 10-fold range of reported Kt/Km values for OCT2-mediated transport of both MPP and metformin. As the focus of the present study was to determine the kinetic basis of the mutual inhibitory interaction of MPP and metformin with OCT2, we first reexamined the methods used to establish the kinetics of OCT2-mediated transport.
The approach used to determine the rates of OCT-mediated transport for kinetic analyses typically uses measurements of uptake at a single time point, generally 30 s (37, 39), 1 min (45), 2 min (14, 50), or longer (22, 38). The presumption is that these measures of net substrate accumulation reflect the initial rate of transport. Although frequently supported by a representative time course of transport, inspection of the time courses of OCT-mediated transport generally shows that the time points selected for kinetic analyses seldom lie unambiguously within a “linear” phase of substrate accumulation. In fact, the semiautomated method described here to determine the time course of OCT2-mediated MPP and metformin transport into cultured cells revealed that even 15-s net uptakes are unlikely to represent the true initial rate of influx. Indeed, studies by Koepsell et al. (7, 24) and our own work suggest that rates of OCT-mediated MPP transport into cultured cells cease to be linear within a few seconds. This is not surprising in light of the fact that typical rates of substrate accumulation should produce nominal intracellular concentrations that exceed that of the surrounding medium within a few seconds, at least from substrate concentrations <Kt (see, e.g., Ref. 32 and unpublished observations). Others have documented some of the problems of the so-called “two-step” method of analysis [i.e., 1) measure rates at single time points and 2) subsequent analysis of these rates using the Michaelis-Menten equation (48)] can introduce into the assessment of transport kinetics and suggested use of extended time course data as an alternative approach to kinetic analysis (32, 48). The method proposed by Poirier et al. (32) used a mechanistic model that solves for the kinetic parameters of transport, including the influence of parallel passive diffusion (both into and back out of the cells), which best describe the measured time courses of net substrate accumulation. However, although this approach addresses some of the problems associated with the two-step method, it did not consider the influence of either time-dependent mediated back flux through the transporter (21) or the impact of unstirred water layers on the concentration of substrate at the membrane (39). In the present study, we elected to estimate the unidirectional rate of influx at time 0 (due to both saturable and unsaturable processes) by fitting the time course of metformin and MPP net uptake to a simple hyperbolic relationship (Figs. 1 and 2) and used the resulting initial rate estimates to examine in detail the kinetics of OCT2-mediated metformin and MPP transport.
As noted earlier, IC50 values for inhibition of OCT2-mediated metformin transport are routinely higher (5-fold to >10-fold) than are IC50 values for inhibition of MPP transport (1, 34). The distinct nature of the MPP interaction with OCT2 is also evident in the results of studies that used site-directed modifications of OCTs. While replacement of glutamate at position 447 in rabbit OCT2 (E448 in human OCT2) with leucine reduced transport of cimetidine and tetraethylammonium (TEA) by >90%, MPP transport was unaffected (49). The differential interaction with MPP extends to OCT1 as well; replacement of aspartate at position 475 with glutamate in rat OCT1 had no effect on Ktapp for MPP transport but produced marked changes in the apparent affinity for choline, TEA, and N1-methylnicotinamide (9). It is also noteworthy that human OCT1 and human OCT2 both display the presence of at least two kinetically distinct sites for the inhibition of MPP transport. The nucleoside reverse transcriptase inhibitor lamivudine produces a markedly biphasic inhibition of MPP transport, with high- and low-affinity IC50 values of ~10 pM and ~2 µM (24). Importantly, substrate translocation appears to be associated with the low-affinity site, whereas interaction with the high-affinity site, which is accessible from the external face of the transporter (10), appears to be restricted to producing a partial inhibition of OCT activity.
These observations suggest that the interaction between OCT2 and MPP, metformin, and other inhibitory ligands cannot be restricted to simple competition for a common binding site (36). Nevertheless, the inhibition of MPP transport by metformin was adequately described by simple competition (Fig. 6); the kinetic consequence of 1 mM metformin on MPP transport was an increase in Ktapp with no change in Jmax. In other words, MPP appeared to have access to the site (or sites) accessible to metformin. The fact that neither the calculated Kiapp nor the IC50 value for metformin’s inhibition of MPP transport differed significantly from metformin’s Ktapp is also consistent with simple competition between MPP (as substrate) and metformin (as inhibitor). However, the interaction of metformin as substrate and MPP as inhibitor was different; increasing the metformin concentration did not completely relieve MPP’s inhibition of metformin transport. Instead, the kinetic consequence of the presence of MPP on metformin transport was an increase in Ktapp and a decrease in Jmax (Figs. 7 and 8). In other words, metformin did not appear to have (complete) access to the site (or sites) accessible to MPP. Consequently, whereas metformin’s inhibition of MPP transport appeared to be competitive, MPP exerted a mixed-type inhibition of OCT2-mediated metformin transport. The complexity of this interaction was also evident in the observation that the IC50 for MPP’s inhibition of metformin transport was significantly less than the Ktapp value for MPP transport (Figs. 4 and 5). We have previously suggested that two different substrates can bind simultaneously to OCT2 and that a transporter bound to two ligands cannot undergo the conformational changes required for translocation, consistent with LM-T inhibition (13, 36). However, the profile of MPP’s inhibition of metformin transport noted above implies a more complex mechanism of kinetic interaction.
In attempting to understand the kinetic basis for the interactions of metformin and MPP with OCT2, we considered three schemes of increasing complexity (Fig. A1). Simple competition for a common binding site (model I in Fig. A1) could not account for the mixed-type inhibition of metformin transport produced by MPP (Fig. 8). Although the LM-T scheme of model II could, with appropriate selection of interaction constants, produce both competitive and mixed-type inhibitory profiles, the LM-T model was inconsistent with an IC50 value for MPP’s inhibition of metformin transport that was significantly less than the Ktapp value for MPP transport. Model III introduced a distinct inhibitory site for MPP that, although not capable of supporting translocation, could exert an allosteric inhibition of metformin transport. This site, combined with a single site (or mutually exclusive sites) for MPP and metformin binding (that is associated with transport) could account for the full suite of inhibitory interactions we observed (Fig. A2).
Of particular relevance to the evidence reported here for a kinetically distinct inhibitory influence of MPP on OCT2-mediated metformin transport are recent observations by Koepsell and colleagues (16) showing the presence of multiple binding sites for MPP on purified preparations of rat OCT1 protein. Binding assays using OCT1 protein inserted into synthetic nanodisc phospholipid bilayers revealed three spatially distinct MPP binding sites. Two of these displayed a comparatively low affinity for MPP, with a common apparent dissociation constant (KD) value of ~30 µM. That these interactions involved spatially distinct locations was evident in results using site-directed mutants. Mutations to either of the spatial neighbors, W218 and D475, or to the spatially distinct R440 residue (based on a three-dimensional homology model of rat OCT1) reduced the stoichiometry of maximal binding from ~2 to ~1 MPP molecule per protein monomer. The third MPP-binding site was revealed in experiments that examined the influence of phospholipid composition on MPP binding; nanodisks composed of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine bound three MPP molecules per OCT1 monomer, two to the low-affinity sites and the third to a site of substantially higher affinity (apparent KD value of 0.2 µM). Importantly, while the previously mentioned site-directed mutations eliminated transport activity (in reconstituted proteoliposomes), they had no effect on binding to the high-affinity site, suggesting that interaction with the high-affinity site may be associated with the high-affinity inhibition observed in previous studies (e.g., Ref. 24) and in the current work (Figs. 5 and A2).
The observation of three distinct sites for MPP lends support for the inclusion of an additional site to model III. However, although an in silico docking study with an outwardly facing three-dimensional homology model of rat OCT1 suggested that both low-affinity MPP-binding sites may be accessible to the external medium (16), we cannot reject the possibility that only one low-affinity site, plus the high-affinity site, is accessible from the external aspect of the transporter. Moreover, if the spatially distinct sites share a common affinity for MPP, and if binding to these sites displays no cooperativity [as indicated by the hyperbolic saturation curve for MPP kinetics and as noted by Keller et al. (16)], the two sites will behave as one kinetically. Consequently, model III, with its key inclusion of a distinct inhibitory site for MPP interaction, is capable of describing the kinetics of the mutual inhibition between metformin and MPP. Furthermore, model III predicts that other ligands that interact with the inhibitory site result in more effective inhibition of metformin transport than of MPP transport (see appendix), consistent with the lower IC50 values for inhibition of metformin transport than MPP transport reported by us (1) and others (11). It is worth emphasizing that ligand binding to OCT2 could entail more complex interactions than those described in model III, but support for that added complexity will likely require detailed site-directed examination of potential binding sites.
Koepsell (18) recently collated the evidence obtained with human and rat OCT orthologs and showed the complexity of MPP interaction with these transporters. Those observations, together with the evidence presented here for the mechanistic basis of metformin-MPP interactions with OCT2, argue strongly against use of MPP as a model substrate for the purpose of predicting the potential of NMEs to produce unwanted interactions with OCTs. The new United States FDA Guidance notes that “Inhibition can be substrate dependent; therefore, the sponsor should determine the inhibition constant of the test drug with a probe substrate that may also be used in later clinical studies. Alternatively, the sponsor may use a probe substrate that usually generates a lower IC50 for known inhibitors to avoid underestimating the interaction potential of the investigational drug” (45a). Koepsell (18) suggested that, in addition, inhibitory interactions should be determined using multiple concentrations of substrate, owing to observations of differential inhibition profiles for some compounds when tested against low (<<Kt) versus high (~Kt) concentration of substrate. Although we have not observed that to be the case with the substrate-inhibitors pairs that we have studied (34), the evidence for this effect for at least some substrate-inhibitor pairs (23, 24) underscores the care that must be taken when designing and interpreting in vitro DDI experiments.
In conclusion, the present study describes a method for increasing the accuracy of initial transport rate estimates for use in kinetic analyses. The method, which uses an extended time course of net substrate accumulation to estimate the rate at time 0, was used to determine the kinetics of mutual inhibition of OCT-mediated transport of metformin and MPP. Modeling the markedly different inhibitory profiles observed for these interactions required introduction of a distinct inhibitory site for MPP, thereby providing kinetic evidence consistent with recent observations of a distinct high-affinity site for binding of MPP to purified OCT protein (16). The kinetic complexity of MPP’s interaction with OCT2 argues against its use in studies designed to assess the inhibitory potential of new drugs and supports recommendations to use multiple substrates, at both high and low concentrations, to maximize the likelihood of identifying potential unwanted DDIs.
GRANTS
This work was supported by National Institutes of Health Grants GM-129777 and T32-HL-07249.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
PJS and SHW conceived and designed research; PJS and MM performed experiments; PJS, MM and SHW analyzed data; PJS, TWS and SHW interpreted results of experiments; PJS and SHW prepared figures; PJS and SHW drafted manuscript; PJS, TWS and SHW edited the manuscript; PJS, MM, TWS and SHW approved final version of manuscript.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the comments and suggestions about this project provided by Dr. Irwin Segel (who never forgets a former student of his biochemistry class).
APPENDIX
Theoretical Models for Transport Kinetics.
The three theoretical models for OCT2 binding and transport of metformin and MPP are shown schematically in Fig. A1, including definitions of the kinetic parameters. Here, the governing equations and their solutions are specified. All reversible transitions between binding states are assumed to be governed by standard mass action kinetics. For example, the binding has a forward rate kf[T0][S1] and a reverse rate kb[T0S1]. We assumed that the reaction is at equilibrium, and so these rates are equal, implying that [T0S1] = [T0][S1]/K1, where K1 = kb/kf. For each model, the amount of transporter in each binding state is obtained by solving the resulting set of algebraic equations, and the corresponding substrate transport rates are expressed in terms of the kinetic parameters. Below, S1 refers to metformin and S2 refers to MPP.
Model I.
In model I, the two substrates are assumed to bind reversibly to a single binding site, with mutually exclusive binding. The assumption of equilibrium implies that [T0S1] = [T0][S1]/K1 and [T0S2] = [T0][S2]/K2. The total concentration of transporter () satisfies and, therefore, . The fluxes of the two solutes are as follows:
| (A1) |
| (A2) |
These equations show that transport of each substrate separately is governed by Michaelis-Menten kinetics with Michaelis constants and , respectively. Furthermore, the IC50 value for inhibition by substrate 2 of transport of substrate 1 at low concentrations is , and similarly for the inhibition by substrate 1 of transport of substrate 2. Thus, the IC50 values are equal to the Michaelis constants for each substrate.
Model II.
In model II, each substrate binds reversibly to a separate site on the transporter, with the possibility of simultaneous binding. For simplicity, the solute transport is assumed to be mutually exclusive, i.e., no transport occurs when both substrates are bound. At equilibrium of binding, the following equations apply: [T0S1] = [T0][S1]/K1, [T0S2] = [T0][S2]/K2, and [T0S1S2] = [T0][S1][S2]/(K1K2). As a condition for the consistency of the equilibrium equations, the relationship K1K12 = K2K21 must also hold. The total concentration of transporter is as follows:
The fluxes of the two solutes are as follows:
| (A3) |
| (A4) |
As in model I, transport of each substrate separately is governed by Michaelis-Menten kinetics with Michaelis constants K1 and K2, respectively, and IC50 values are equal to the Michaelis constants for each substrate.
Model III.
In model III, both substrates are assumed to bind reversibly and exclusively to a single binding site, as in model I, but with an additional binding site for MPP that, when occupied, exerts an allosteric inhibition of metformin transport, without supporting transport of the occupying MPP molecule. represents MPP binding to this inhibitory site. The conditions of binding equilibrium yield the following: [T0S1] = [T0][S1]/K1, [T0S2] = [T0][S2]/K2, /, /, and .
As conditions for the consistency of the equilibrium equations, the relationships and must also hold. The total concentration of transporter is as follows:
where
The solute fluxes are as follows:
| (A5) |
| (A6) |
In the absence of MPP, the transport of metformin is seen to follow Michaelis-Menten uptake kinetics. However, the uptake of MPP alone may not follow Michaelis-Menten kinetics because of the presence of quadratic terms in . In particular, if is smaller than , the transport rate may rise and then fall with increasing , because of the increasing effect of the inhibitory binding site. When is small, its transport is halved when , i.e., the IC50 value of metformin for MPP transport is equal to the Michaelis constant of metformin as before. For MPP, however, its IC50 for inhibition of metformin transport may be less than its Michaelis constant, as discussed in the text.
Parameter estimation for model III.
The model described above contains too many unknown parameters to be reliably estimated from the available data. To reduce the number of independent parameters, we made some physically plausible assumptions. First, we assumed that the binding of S2 to the inhibitory site is independent of binding of S1 and S2 to the transport site, i.e., . According to the consistency conditions stated above, this assumption implies that the binding of S1 and S2 to the transport site is independent of binding of S2 to the inhibitory site, i.e., and . Second, we assumed that the transport rate of S2 is independent of binding of S2 to the inhibitory site, i.e., . Thus, MPP binding to the inhibitory site may inhibit metformin transport but not MPP transport. The results shown in Fig. A2 were obtained by optimizing the remaining free parameters to minimize the sum of squared deviations between experimental data and mode, using the MATAB “lsqnonlin” routine. The resulting parameter values are shown in Table A1.
Relaxing the assumptions stated above leads to a slight reduction of the deviation between model and experiments but at the expense of less reliable parameter estimation.
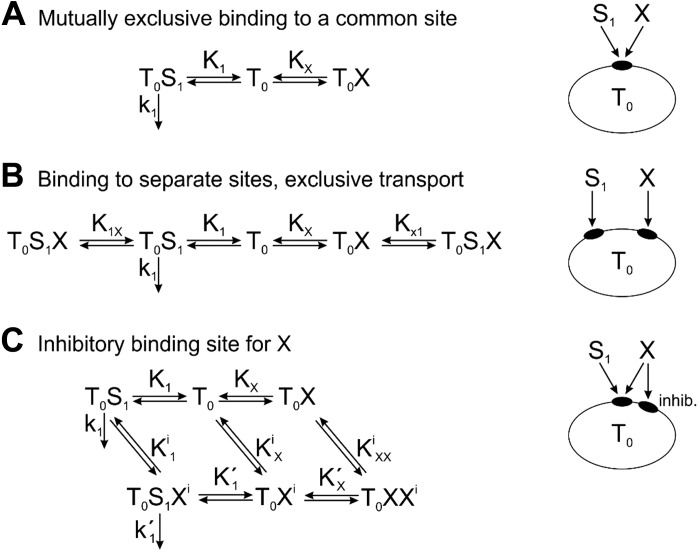
Inhibitory Effects of a Third Substrate on the Transport of Metformin and MPP
The observed IC50 values for inhibition of MPP transport by a third substrate (here labeled X) are often more than fivefold greater than IC50 values for inhibition of metformin transport by the same substrate. Here, we examine the ability of the models described above to account for this phenomenon. To analyze the inhibitory effects of X, we assumed small concentrations of metformin (S1) and MPP (S2), such that their transport rates are proportional to their concentrations, and determine IC50X under this assumption. The relevant reactions are shown schematically in Fig. A3.
Model I.
This system is shown in Fig. A3A. The analysis is as before for model I, with X replacing S2, giving
| (A7) |
assuming [S1] << K1. The transport rate is reduced by 50% when [X] = KX, and so IC50X = KX. The same result applies for substrate S2, implying that this model cannot account for different IC50X values for metformin and MPP.
Model II.
This system is shown in Fig. A3B. The analysis is as before for model II, with X replacing S2, and gave the same result, Eq. A7, assuming [S1] << K1. Hence, IC50X = KX. The same result applies for substrate S2, and this model cannot account for differing IC50X values.
Model III.
Here, two cases can arise. First, if X does not interact with the inhibitory site, the system is as shown in Fig. A3A, and the IC50X values are the same for substrates S1 and S2. This result is not affected by binding of substrate S1 or S2 to the inhibitory site, because their concentrations are assumed to be small so that the amount of binding is negligible. Second, if X does interact with the inhibitory site, the system is as shown in Fig. A3C. The analysis is analogous to that for model III above. Again, the result is not affected by binding of substrate S1 or S2 to the inhibitory site. The conditions of binding equilibrium yield the following: [T0S1] = [T0][S1]/K1, [T0X] = [T0][X]/KX, , , and .
The total concentration of transporter is , where .
Under the assumption that [S1] << K1 and [S1] << , this reduces to . The solute flux is as follows:
| (A8) |
To simplify the notation, we define x = [X]/KX, , and . Then, and . The transport rate is reduced by 50% when . This leads to the following quadratic equation: x2 = (αβ + α − 2αβγ)x − αβ = 0, with as the unique positive solution and IC50X = x50KX. With this model, IC50X values can differ for substrates S1 and S2 because the value of γ depends on the substrate.
To illustrate this effect, we assumed that the transport parameters for substrate X are the same as those estimated above for substrate S2 (MPP), since this serves as a prototype for substrates that can interact with the inhibitory site. Using the values shown in Table A1, we obtained and . For transport of S2 (MPP), , and the solution is x50 = 1, i.e., IC50X = KX as expected, because X acts purely as a competitive inhibitor of MPP transport. However, for transport of S1 (metformin), , and the solution is x50 = 0.22, i.e., IC50X = 0.22KX. By binding to the inhibitory site, substrate X causes inhibition of metformin transport at lower concentrations than would be the case for purely competitive inhibition.
Fig. A1.
Potential kinetic schemes to explain the mutual interactions of metformin and 1-methyl-4-phenylpyridinium (MPP) with organic cation transporter 2 (OCT2). For each scheme, the configuration of binding sites on the transporter T0 and their binding to substrate 1 (S1; metformin) and substrate 2 (S2; MPP) is shown in the diagrams on the right. In model III, “inhib” represents the inhibitory MPP-binding site. In the diagrams on the left, the available binding states are represented. For example, T0S1S2 denotes the two substrates S1 and S2 simultaneously bound to the transporter T0, as in model II. The reversible transitions between the binding states are represented by double arrows. The associated constants (K1, K2, etc.) represent the ratios of the backward to the forward rate constants for each binding step. The available transport steps for substrate uptake are indicated by single arrows. The associated constants (k1, k2, etc.) represent the rate constants for the corresponding uptake. Since initial uptake rates are considered, cellular release of substrate is not considered. In model II, the state T0S1S2 is replicated to simplify the layout.
Fig. A2.
Model III-based descriptions of the kinetic interactions of metformin and 1-methyl-4-phenylpyridinium (MPP) with organic cation transporter 2 (OCT2). The solid points (with associated error bars) show experimental data previously presented: data from Fig. 8A (A), data from Fig. 8B (B), data from Fig. 5B (C), data from Fig. 6A (D), data from Fig. 6B (E), and data from Fig. 5A (F). The red dashed lines show the predicted kinetic profiles derived from optimizing model III to the transport profiles shown in A and D.
Fig. A3.
Potential kinetic schemes to explain the inhibitory effects of a third substrate (X) on the transport of metformin or 1-methyl-4-phenylpyridinium (MPP) by organic cation transporter 2 (OCT2): mutually exclusive binding to a common site (A), binding to separate sites, exclusive transport (B), and inhibitory binding site for X (C). See Fig. A1 for an explanation of symbols. Here, S1 represents either metformin or MPP.
Table A1.
Values for K and k
| Parameter | Value |
|---|---|
| K1 | 0.380493 mM |
| K2 | 3.545 μM |
| Ki | 0.9285 μM |
| 0.9285 μM | |
| 0.9285 μM | |
| 0.380493 mM | |
| 3.545 μM | |
| 347.072 pmol·cm−2·min−1 | |
| 50.9 pmol·cm−2·min−1 | |
| 20.2851 pmol·m−2·min−1 | |
| 20.2851 pmol·cm−2·min−1 |
REFERENCES
- 1.Belzer M, Morales M, Jagadish B, Mash EA, Wright SH. Substrate-dependent ligand inhibition of the human organic cation transporter OCT2. J Pharmacol Exp Ther 346: 300–310, 2013. doi: 10.1124/jpet.113.203257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boxberger KH, Hagenbuch B, Lampe JN. Ligand-dependent modulation of hOCT1 transport reveals discrete ligand binding sites within the substrate translocation channel. Biochem Pharmacol 156: 371–384, 2018. doi: 10.1016/j.bcp.2018.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Budiman T, Bamberg E, Koepsell H, Nagel G. Mechanism of electrogenic cation transport by the cloned organic cation transporter 2 from rat. J Biol Chem 275: 29413–29420, 2000. doi: 10.1074/jbc.M004645200. [DOI] [PubMed] [Google Scholar]
- 4.Ekins S, Kim RB, Leake BF, Dantzig AH, Schuetz EG, Lan LB, Yasuda K, Shepard RL, Winter MA, Schuetz JD, Wikel JH, Wrighton SA. Application of three-dimensional quantitative structure-activity relationships of P-glycoprotein inhibitors and substrates. Mol Pharmacol 61: 974–981, 2002. doi: 10.1124/mol.61.5.974. [DOI] [PubMed] [Google Scholar]
- 5.Garrigues A, Loiseau N, Delaforge M, Ferté J, Garrigos M, André F, Orlowski S. Characterization of two pharmacophores on the multidrug transporter P-glycoprotein. Mol Pharmacol 62: 1288–1298, 2002. doi: 10.1124/mol.62.6.1288. [DOI] [PubMed] [Google Scholar]
- 6.Giacomini KM, Huang SM, Tweedie DJ, Benet LZ, Brouwer KL, Chu X, Dahlin A, Evers R, Fischer V, Hillgren KM, Hoffmaster KA, Ishikawa T, Keppler D, Kim RB, Lee CA, Niemi M, Polli JW, Sugiyama Y, Swaan PW, Ware JA, Wright SH, Yee SW, Zamek-Gliszczynski MJ, Zhang L; International Transporter Consortium . Membrane transporters in drug development. Nat Rev Drug Discov 9: 215–236, 2010. doi: 10.1038/nrd3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gorboulev V, Rehman S, Albert CM, Roth U, Meyer MJ, Tzvetkov MV, Mueller TD, Koepsell H. Assay conditions influence affinities of rat organic cation transporter 1: analysis of mutagenesis in the modeled outward-facing cleft by measuring effects of substrates and inhibitors on initial uptake. Mol Pharmacol 93: 402–415, 2018. doi: 10.1124/mol.117.110767. [DOI] [PubMed] [Google Scholar]
- 8.Gorboulev V, Shatskaya N, Volk C, Koepsell H. Subtype-specific affinity for corticosterone of rat organic cation transporters rOCT1 and rOCT2 depends on three amino acids within the substrate binding region. Mol Pharmacol 67: 1612–1619, 2005. doi: 10.1124/mol.104.008821. [DOI] [PubMed] [Google Scholar]
- 9.Gorboulev V, Volk C, Arndt P, Akhoundova A, Koepsell H. Selectivity of the polyspecific cation transporter rOCT1 is changed by mutation of aspartate 475 to glutamate. Mol Pharmacol 56: 1254–1261, 1999. doi: 10.1124/mol.56.6.1254. [DOI] [PubMed] [Google Scholar]
- 10.Gorbunov D, Gorboulev V, Shatskaya N, Mueller T, Bamberg E, Friedrich T, Koepsell H. High-affinity cation binding to organic cation transporter 1 induces movement of helix 11 and blocks transport after mutations in a modelled interaction domain between two helices. Mol Pharmacol 73: 50–61, 2007. doi: 10.1124/mol.107.040170. [DOI] [PubMed] [Google Scholar]
- 11.Hacker K, Maas R, Kornhuber J, Fromm MF, Zolk O. Substrate-dependent inhibition of the human Organic Cation Transporter OCT2: a comparison of metformin with experimental substrates. PLoS One 10: e0136451, 2015. doi: 10.1371/journal.pone.0136451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hagenbuch B. Drug uptake systems in liver and kidney: a historic perspective. Clin Pharmacol Ther 87: 39–47, 2010. doi: 10.1038/clpt.2009.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Harper JN, Wright SH. Multiple mechanisms of ligand interaction with the human organic cation transporter, OCT2. Am J Physiol Renal Physiol 304: F56–F67, 2013. doi: 10.1152/ajprenal.00486.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ito S, Kusuhara H, Yokochi M, Toyoshima J, Inoue K, Yuasa H, Sugiyama Y. Competitive inhibition of the luminal efflux by multidrug and toxin extrusions, but not basolateral uptake by organic cation transporter 2, is the likely mechanism underlying the pharmacokinetic drug-drug interactions caused by cimetidine in the kidney. J Pharmacol Exp Ther 340: 393–403, 2012. doi: 10.1124/jpet.111.184986. [DOI] [PubMed] [Google Scholar]
- 15.Jacquez JA. Tracers in the study of membrane processes. In: Physiology of Membrane Disorders, edited by Andreoli TE, Hoffman JF, Fanestil DD. New York: Plenum, 1978, p. 147–164. [Google Scholar]
- 16.Keller T, Gorboulev V, Mueller T, Dotsch V, Bernhard F, Koepsell H. Rat organic cation transporter 1 contains three binding sites for substrate 1-methyl-4-phenylpyridinium per monomer. Mol Pharmacol 95: 169–182, 2019. doi: 10.1124/mol.118.113498. [DOI] [PubMed] [Google Scholar]
- 17.Kido Y, Matsson P, Giacomini KM. Profiling of a prescription drug library for potential renal drug-drug interactions mediated by the organic cation transporter 2. J Med Chem 54: 4548–4558, 2011. doi: 10.1021/jm2001629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Koepsell H. Multiple binding sites in organic cation transporters require sophisticated procedures to identify interactions of novel drugs. Biol Chem 400: 195–207, 2019. doi: 10.1515/hsz-2018-0191. [DOI] [PubMed] [Google Scholar]
- 19.Lazaruk KDA, Wright SH. MPP+ is transported by the TEA+-H+ exchanger of renal brush-border membrane vesicles. Am J Physiol Renal Physiol 258: F597–F605, 1990. doi: 10.1152/ajprenal.1990.258.3.F597. [DOI] [PubMed] [Google Scholar]
- 20.Liu HC, Goldenberg A, Chen Y, Lun C, Wu W, Bush KT, Balac N, Rodriguez P, Abagyan R, Nigam SK. Molecular properties of drugs interacting with SLC22 transporters OAT1, OAT3, OCT1, and OCT2: a machine-learning approach. J Pharmacol Exp Ther 359: 215–229, 2016. doi: 10.1124/jpet.116.232660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Martínez-Guerrero LJ, Evans KK, Dantzler WH, Wright SH. The multidrug transporter MATE1 sequesters OCs within an intracellular compartment that has no influence on OC secretion in renal proximal tubules. Am J Physiol Renal Physiol 310: F57–F67, 2016. doi: 10.1152/ajprenal.00318.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ming X, Ju W, Wu H, Tidwell RR, Hall JE, Thakker DR. Transport of dicationic drugs pentamidine and furamidine by human organic cation transporters. Drug Metab Dispos 37: 424–430, 2009. doi: 10.1124/dmd.108.024083. [DOI] [PubMed] [Google Scholar]
- 23.Minuesa G, Albert C, Pastor-Anglada M, Martinez-Picado J, Koepsell H. Response to “Tenofovir disoproxil fumarate is not an inhibitor of human organic cation transporter 1”. J Pharmacol Exp Ther 360: 343–345, 2017. doi: 10.1124/jpet.116.239004. [DOI] [PubMed] [Google Scholar]
- 24.Minuesa G, Volk C, Molina-Arcas M, Gorboulev V, Erkizia I, Arndt P, Clotet B, Pastor-Anglada M, Koepsell H, Martinez-Picado J. Transport of lamivudine [(−)-β-l-2′,3′-dideoxy-3′-thiacytidine] and high-affinity interaction of nucleoside reverse transcriptase inhibitors with human organic cation transporters 1, 2, and 3. J Pharmacol Exp Ther 329: 252–261, 2009. doi: 10.1124/jpet.108.146225. [DOI] [PubMed] [Google Scholar]
- 25.Motohashi H, Nakao Y, Masuda S, Katsura T, Kamba T, Ogawa O, Inui K-I. Precise comparison of protein localization among OCT, OAT, and MATE in human kidney. J Pharm Sci 102: 3302–3308, 2013. doi: 10.1002/jps.23567. [DOI] [PubMed] [Google Scholar]
- 26.Motohashi H, Sakurai Y, Saito H, Masuda S, Urakami Y, Goto M, Fukatsu A, Ogawa O, and Inui K. Gene expression levels and immunolocalization of organic ion transporters in the human kidney. J Am Soc Nephrol 13: 866–874, 2002. [DOI] [PubMed] [Google Scholar]
- 27.Neuhoff S, Ungell AL, Zamora I, Artursson P. pH-dependent bidirectional transport of weakly basic drugs across Caco-2 monolayers: implications for drug-drug interactions. Pharm Res 20: 1141–1148, 2003. doi: 10.1023/A:1025032511040. [DOI] [PubMed] [Google Scholar]
- 28.Nies AT, Hofmann U, Resch C, Schaeffeler E, Rius M, Schwab M. Proton pump inhibitors inhibit metformin uptake by organic cation transporters (OCTs). PLoS One 6: e22163, 2011. doi: 10.1371/journal.pone.0022163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nies AT, Koepsell H, Damme K, Schwab M. Organic cation transporters (OCTs, MATEs), in vitro and in vivo evidence for the importance in drug therapy. Handb Exp Pharmacol 201: 105–167, 2011. doi: 10.1007/978-3-642-14541-4_3. [DOI] [PubMed] [Google Scholar]
- 30.Pelis RM, Wright SH. Renal transport of organic anions and cations. Compr Physiol 1: 1795–1835, 2011. doi: 10.1002/cphy.c100084. [DOI] [PubMed] [Google Scholar]
- 31.Pelis RM, Zhang X, Dangprapai Y, Wright SH. Cysteine accessibility in the hydrophilic cleft of human organic cation transporter 2. J Biol Chem 281: 35272–35280, 2006. doi: 10.1074/jbc.M606561200. [DOI] [PubMed] [Google Scholar]
- 32.Poirier A, Lavé T, Portmann R, Brun ME, Senner F, Kansy M, Grimm HP, Funk C. Design, data analysis, and simulation of in vitro drug transport kinetic experiments using a mechanistic in vitro model. Drug Metab Dispos 36: 2434–2444, 2008. doi: 10.1124/dmd.108.020750. [DOI] [PubMed] [Google Scholar]
- 33.Roth M, Timmermann BN, Hagenbuch B. Interactions of green tea catechins with organic anion-transporting polypeptides. Drug Metab Dispos 39: 920–926, 2011. doi: 10.1124/dmd.110.036640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sandoval PJ, Zorn KM, Clark AM, Ekins S, Wright SH. Assessment of substrate-dependent ligand interactions at the organic cation transporter OCT2 using six model substrates. Mol Pharmacol 94: 1057–1068, 2018. doi: 10.1124/mol.117.111443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schömig E, Lazar A, Gründemann D. Extraneuronal monoamine transporter and organic cation transporters 1 and 2: a review of transport efficiency. Handb Exp Pharmacol 175: 151–180, 2006. doi: 10.1007/3-540-29784-7_8. [DOI] [PubMed] [Google Scholar]
- 36.Segel IH. Enzyme Kinetics. New York: Wiley, 1975, p. 1–957. [Google Scholar]
- 37.Severance AC, Sandoval PJ, Wright SH. Correlation between apparent substrate affinity and OCT2 transporter turnover. J Pharmacol Exp Ther 362: 405–412, 2017. doi: 10.1124/jpet.117.242552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shen H, Yang Z, Zhao W, Zhang Y, Rodrigues AD. Assessment of vandetanib as an inhibitor of various human renal transporters: inhibition of multidrug and toxin extrusion as a possible mechanism leading to decreased cisplatin and creatinine clearance. Drug Metab Dispos 41: 2095–2103, 2013. doi: 10.1124/dmd.113.053215. [DOI] [PubMed] [Google Scholar]
- 39.Shibayama T, Morales M, Zhang X, Martínez-Guerrero LJ, Berteloot A, Secomb TW, Wright SH. Unstirred water layers and the kinetics of organic cation transport. Pharm Res 32: 2937–2949, 2015. doi: 10.1007/s11095-015-1675-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Suhre WM, Ekins S, Chang C, Swaan PW, Wright SH. Molecular determinants of substrate/inhibitor binding to the human and rabbit renal organic cation transporters hOCT2 and rbOCT2. Mol Pharmacol 67: 1067–1077, 2005. doi: 10.1124/mol.104.004713. [DOI] [PubMed] [Google Scholar]
- 41.Thévenod F, Ciarimboli G, Leistner M, Wolff NA, Lee WK, Schatz I, Keller T, Al-Monajjed R, Gorboulev V, Koepsell H. Substrate- and cell contact-dependent inhibitor affinity of human organic cation transporter 2: studies with two classical organic cation substrates and the novel substrate cd2+. Mol Pharm 10: 3045–3056, 2013. doi: 10.1021/mp400113d. [DOI] [PubMed] [Google Scholar]
- 43.Ullrich KJ, Papavassiliou F, David C, Rumrich G, Fritzsch G. Contraluminal transport of organic cations in the proximal tubule of the rat kidney. I. Kinetics of N1-methylnicotinamide and tetraethylammonium, influence of K+, , pH; inhibition by aliphatic primary, secondary and tertiary amines and mono- and bisquaternary compounds. Pflügers Arch 419: 84–92, 1991. doi: 10.1007/BF00373751. [DOI] [PubMed] [Google Scholar]
- 44.Ullrich KJ, Rumrich G, Neiteler K, Fritzsch G. Contraluminal transport of organic cations in the proximal tubule of the rat kidney. II. Specificity: anilines, phenylalkylamines (catecholamines), heterocyclic compounds (pyridines, quinolines, acridines). Pflugers Arch 420: 29–38, 1992. doi: 10.1007/BF00378638. [DOI] [PubMed] [Google Scholar]
- 45.Umehara KI, Iwatsubo T, Noguchi K, Kamimura H. Comparison of the kinetic characteristics of inhibitory effects exerted by biguanides and H2-blockers on human and rat organic cation transporter-mediated transport: Insight into the development of drug candidates. Xenobiotica 37: 618–634, 2007. doi: 10.1080/00498250701397705. [DOI] [PubMed] [Google Scholar]
- 45a.United Food and Drug Administration In Vitro Metabolism- and Transporter- Mediated Drug-Drug Interaction Studies Guidance for Industry. Rockville, MD: Center for Drug Evaluation and Research, 2017. [Google Scholar]
- 46.Westholm DE, Salo DR, Viken KJ, Rumbley JN, Anderson GW. The blood-brain barrier thyroxine transporter organic anion-transporting polypeptide 1c1 displays atypical transport kinetics. Endocrinology 150: 5153–5162, 2009. doi: 10.1210/en.2009-0769. [DOI] [PubMed] [Google Scholar]
- 47.Yin J, Duan H, Wang J. Impact of substrate-dependent inhibition on renal organic cation transporters hOCT2 and hMATE1/2-K-mediated drug transport and intracellular accumulation. J Pharmacol Exp Ther 359: 401–410, 2016. doi: 10.1124/jpet.116.236158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zamek-Gliszczynski MJ, Lee CA, Poirier A, Bentz J, Chu X, Ellens H, Ishikawa T, Jamei M, Kalvass JC, Nagar S, Pang KS, Korzekwa K, Swaan PW, Taub ME, Zhao P, Galetin A; International Transporter Consortium . ITC recommendations for transporter kinetic parameter estimation and translational modeling of transport-mediated PK and DDIs in humans. Clin Pharmacol Ther 94: 64–79, 2013. doi: 10.1038/clpt.2013.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhang X, Shirahatti NV, Mahadevan D, Wright SH. A conserved glutamate residue in transmembrane helix 10 influences substrate specificity of rabbit OCT2 (SLC22A2). J Biol Chem 280: 34813–34822, 2005. doi: 10.1074/jbc.M506342200. [DOI] [PubMed] [Google Scholar]
- 50.Zolk O, Solbach TF, König J, Fromm MF. Structural determinants of inhibitor interaction with the human organic cation transporter OCT2 (SLC22A2). Naunyn Schmiedebergs Arch Pharmacol 379: 337–348, 2009. doi: 10.1007/s00210-008-0369-5. [DOI] [PubMed] [Google Scholar]