Crosshatch nanofiber networks of tunable interfiber spacing induce plasticity in cell migration and cytoskeletal response

Abstract

Biomechanical cues within tissue microenvironments are critical for maintaining homeostasis, and their disruption can contribute to malignant transformation and metastasis. Once transformed, metastatic cancer cells can migrate persistently by adapting (plasticity) to changes in the local fibrous extracellular matrix, and current strategies to recapitulate persistent migration rely exclusively on the use of aligned geometries. Here, the controlled interfiber spacing in suspended crosshatch networks of nanofibers induces cells to exhibit plasticity in migratory behavior (persistent and random) and the associated cytoskeletal arrangement. At dense spacing (3 and 6 µm), unexpectedly, elongated cells migrate persistently (in 1 dimension) at high speeds in 3-dimensional shapes with thick nuclei, and short focal adhesion cluster (FAC) lengths. With increased spacing (18 and 36 µm), cells attain 2-dimensional morphologies, have flattened nuclei and longer FACs, and migrate randomly by rapidly detaching their trailing edges that strain the nuclei by ∼35%. At 54-µm spacing, kite-shaped cells become near stationary. Poorly developed filamentous actin stress fibers are found only in cells on 3-µm networks. Gene-expression profiling shows a decrease in transcriptional potential and a differential up-regulation of metabolic pathways. The consistency in observed phenotypes across cell lines supports using this platform to dissect hallmarks of plasticity in migration in vitro.—Jana, A., Nookaew, I., Singh, J., Behkam, B., Franco, A. T., Nain, A. S. Crosshatch nanofiber networks of tunable interfiber spacing induce plasticity in cell migration and cytoskeletal response.

Cell migration plays a critical role in development, repair, and disease biology. Notably, in cancer, cell metastasis from tumors often portends unfortunate life-ending outcomes (1, 2). Migratory metastatic cells take advantage of both biophysical and biochemical cues present in the surrounding extracellular matrix (ECM) to achieve persistent migration. Although it is easy to visualize how the aligned (parallel) arrangement of ECM individual strands or groups of strands favor cells to invade neighboring stroma followed by persistent migration, we inquired as to whether alignment was the only fiber configuration capable of promoting and sustaining persistent migration that is observed along the metastatic journey. This seemingly straightforward question has been difficult to resolve because of challenges in imaging deep inside the body over long periods (3, 4) and recapitulation of structures in vitro (5). Thus, it is not uncommon to find illustrations of fibrous ECM interfacing with tumors depicting the existence of both aligned fibers and nonaligned configurations of varying pore sizes and lengths that are able to support persistent migration (2, 6–12).

In vivo, cells migrate through fibrous ECM or on top of the dense basement membrane of varying porosities (13–18). Currently, a large number of in vitro strategies exist to investigate cell migration. Perhaps the most widely used method involves culturing cells on featureless flat 2-dimensional (2D) substrates that describe cell migration to occur in short phases of cell motion interspersed with random changes in the migration direction and periods of cell inactivity. These steps collectively are described by the classical random walk (19, 20). To achieve persistent cell migration, a number of strategies (micropatterned stripes, microchannels, microgrooves, micropillars, etc.) (21–29) have been devised that mechanically confine cells to have aligned 1-dimensional (1D) morphologies. To investigate cell migration in a 3-dimensional (3D) environment, cells are embedded in a 2.5- or 3D gel system, and gels with built-in anisotropy recapitulate persistent migration (30–34). The given complexity and the interconnectivity of ECM biophysical parameters (stiffness, fiber size and alignment, pore size, and architecture) (34–46) make it exceedingly difficult to elucidate the role of individual parameters in persistent cell migration. Thus, it is not surprising that, in a recent commentary, it was noted that there are generally no accepted methods to cross-validate in vitro findings and to compare them with in vivo behavior (5).

Although many in vitro strategies (including by us) have demonstrated anisotropic migration using aligned geometries, the contributions of other configurations, including cross-linked networks of varied interfiber spacing, remain unclear. Here, using our previously reported nonelectrospinning spinneret-based tunable engineered parameters (STEP) technique (47–50), we use suspended nanofiber crosshatch networks of tunable interfiber spacing to interrogate the plasticity of single-cell migratory behavior and cytoskeleton arrangement in the Hras1 murine cell line. We chose Hras1 because it is derived from aggressive follicular thyroid cancer, a tumor with highly invasive capacity and propensity to metastasize to distant sites, primarily the lungs (51). This tumor has increased levels of lysyl oxidase enzyme, which crosslinks the collagenous ECM, thus imparting collagen fibers to increase stability and stiffness: known promoters of tumor progression (52). Using cross-linked nanofibers in a 2-layer fiber system, we show that, contrary to intuition, dense (low interfiber spacing) crosshatch networks that resemble 2D flat surfaces cause cells to migrate persistently (in 1 D) in 3D shapes, whereas increasing interfiber spacing recapitulates 2D shapes and random walk migration. Furthermore, through high spatiotemporal resolution microscopy and genome sequencing, we show that interfiber spacing is a modulator of focal adhesion clustering, nucleus thickness and strain, filamentous actin (f-actin) stress-fiber organization, and differential up-regulation of metabolic pathways. Using multiple migratory cell lines {mouse 3T3 fibroblasts [National Institutes of Health (NIH), Bethesda, MD, USA], human smooth muscle cells, mesenchymal stem cells, and cancerous MDA-MB-231 cells}, we find similarities in the migratory phenotype and show that alignment is not the only requisite biophysical configuration for achieving high-speed persistent migration.

MATERIALS AND METHODS

Fiber network fabrication and characterization

Preparation of nanofiber networks

Polystyrene (MW: 2,000,000 g/mol; Category No. 829; Scientific Polymer Products, Ontario, NY, USA) was dissolved in xylene (X5-500; Thermo Fisher Scientific, Waltham, MA, USA) to form a 10 wt% solution. Isotropic crosshatch networks of nanofibers with tunable interfiber spacing and a uniform fiber diameter of ∼500 nm were then fabricated using the STEP technique. Briefly, polystyrene was dissolved in para-xylene for at least 1 week to prepare a polymeric solution for fiber spinning. The solution was extruded through a micropipette (inside diameter, ∼100 µm; Jensen Global, Santa Barbara, CA, USA) to deposit suspended and aligned fibers in parallel and crosshatch patterns (48). Fused-fiber networks were created using a custom fusing chamber (53).

Atomic force microscopy characterization of fiber networks

Fused-fiber networks on hollow stainless-steel scaffolds (3 mm × 3 mm hollow square region) were mounted on a plastic wedge with a 12° incline that was subsequently placed in the substrate holder of an atomic force microscope (Veeco, Plainview, NY, USA). A tipless SiN atomic force microscopy cantilever (FORTA-TL-10; AppNano, Mountain View, CA, USA) was used to measure the stiffness in contact mode. Cantilever stiffness (2 N/m) was measured by thermal tuning (mean value from 8 independent tests). Deflection sensitivity (nanometers per volt) was obtained using the standard approach of probing a hard surface (stainless-steel surface used) in contact mode. Using the above 2 parameters, force-distance curves were directly obtained from the deflection error (V) vs. z (distance) plots generated in contact mode atomic force microscopy. The bending stiffness of the fiber networks was then evaluated from the slope of the linear region in the force-distance curves.

Cell culture, imaging, and RNA extraction

Cell seeding

The nanofiber networks were mounted in individual wells of a 6-well plate and sterilized with 70% ethanol for 10 min, followed by rinsing twice with PBS. Subsequently, the networks and flat glass were functionalized by coating with 4 µg/ml of fibronectin (F1141-1MG; MilliporeSigma, Burlington, MA, USA) for 1 h at 37°C. Hras1 cells were obtained from an Hras^G12V/Pten knockout murine thyroid tumor (51). Cells were confirmed to be mycoplasma negative by PCR, and the cell line was authenticated using short tandem repeat DNA profiling (DDC Medical, Thermo Fisher Scientific). Cells were cultured in F12 medium (Thermo Fisher Scientific) supplemented with 10% fetal bovine serum in T25 flasks (Corning, Corning, NY, USA) kept at 37°C and 5% CO₂ in a humidified incubator. 3T3 fibroblasts [CRL-1658; American Type Culture Collection (ATCC), Manassas, VA, USA] were cultured in DMEM supplemented with 10% fetal calf serum at 37°C and 5% CO₂ in a humidified incubator. MDA-MB-231 cells (HTB-26; ATCC) were cultured in Leibovitz (L15) medium supplemented with 10% fetal calf serum at 37°C in a CO₂-free environment. Smooth muscle cells (a gift from the University of Pittsburgh, Pittsburgh, PA, USA) (54) were cultured in smooth muscle basal cell medium (Cell Applications, San Diego, CA, USA) at 37°C and 5% CO₂ in a humidified incubator. Bone marrow–derived human mesenchymal stem cells (Lonza, Basel, Switzerland) were cultured in supplemented growth medium (Lonza) at 37°C and 5% CO₂. The functionalized nanofiber networks were seeded with a low concentration (∼7 × 10⁴ cells/ml, 50 µl added to each well) of cells and allowed to attach and spread on the fiber networks for 1 h, followed by addition of 2 ml of medium and 2% penicillin-streptomycin to each well to prevent contamination during the experiments. Time-lapse optical microscopy for migration characterization was subsequently performed for at least 8 h with an interval of either 5 or 10 min using a ×20 [Plan-Apochromat 0.8 numerical aperture (NA)] objective.

Fluorescent imaging

Fixed immunofluorescent staining was performed on the cells for f-actin, focal adhesion protein paxillin, and nucleus. Cells were fixed with 4% paraformaldehyde for 15 min, followed by permeabilization in 0.1% Triton X-100 in PBS solution for 15 min and blocking in anti-goat blocking buffer (Thermo Fisher Scientific) for 30 min. Rabbit anti-paxillin primary antibody (Tyr31, 44-720G; Research Resource Identifier, AB_843415; Thermo Fisher Scientific) was diluted in antibody dilution buffer in a 1:200 dilution ratio and was added to the substrates containing the fixed cells and refrigerated for 1 h. Afterward, goat anti-rabbit secondary antibody (Alexa Fluor 488, A-11008; Research Resource Identifier, AB_143165; Thermo Fisher Scientific) diluted in a 1:200 ratio was added with the rhodamine-conjugated phalloidin (sc-301530; Santa Cruz Biotechnology, Dallas, TX, USA) diluted in a 1:80 ratio. Samples were stored in a dark place for 45 min, followed by 3 PBS washes. Subsequently, DAPI (D1306; Thermo Fisher Scientific) was added for 5 min to stain the cell nuclei. Images were taken with an inverted Zeiss microscope (Axio Observer.Z1; Zarl Zeiss, Oberkochen, Germany) using either a ×40 (0.75 NA) or ×63 (1.2 NA water immersion) objective. Confocal microscopy was performed using a laser scanning confocal microscope (LSM 880; Carl Zeiss), and images were obtained using a ×63, 1.15 NA water immersion objective.

RNA-extraction protocol

The total RNA was extracted (from 3 independent experiments) from the cells using the Ambion RNAqueous-Micro Kit (AM1931; Thermo Fisher Scientific), and the manufacturer’s recommended protocol was followed. Briefly, cells were seeded on the fiber networks (3, 6, 18, 36, and 54 µm) attached to individual wells of a glass-bottom 6-well plate (MatTek Corporation, Ashland, MA, USA). The sixth well acted as the control well, in which cells were seeded on the flat glass. Cells were cultured until 40–50% confluency. Afterwards, cell medium was aspirated from the wells, and fiber networks were transferred quickly (∼5 s transfer time) to a new sterile 6-well plate using a pair of tweezers (UV sterilized, RNase free) and immediately lysed with the lysis solution from the kit. Control cells were lysed directly in the wells. Following RNA isolation with the kit, extracted RNA was eluted with a total volume of 50 µl of eluate. The RNA in the elution solution was then transferred to an RNase-free microcentrifuge tube and stored at −80°C for further processing.

Quantification and statistical analysis

Analysis of aspect ratios, cell shapes, and areas

The aspect ratio was defined as the ratio of the maximum and minimum dimensions of the cell and was intended to quantify the degree of polarization of the cell body in a certain direction. Cells stained for actin were manually outlined in ImageJ (NIH; https://imagej.nih.gov/ij/). The Bounding Rectangle function in ImageJ was subsequently used to evaluate the maximum horizontal and vertical dimensions of the outlined cell. Widths of individual cells were measured at ∼25 positions along the cell length, and mean width vs. length profiles (corresponding to each fiber network category were generated by averaging (using a bin size of 5 µm) the individual profiles. Cell areas and perimeters were measured by manually outlining the cells in ImageJ.

Analysis of cell profiles and slope of leading edge

Cells were not of the same lengths. To calculate the mean cell shape profile representing each interfiber spacing, we first calculated the mean cell length for each interfiber spacing category. Then, the individual cell profiles in each interfiber spacing category were normalized (stretched or shortened) with respect to the respective mean length. Finally, the mean profile for each interfiber spacing was obtained by averaging the individual normalized profiles. To calculate the slopes of leading edges, mean profiles of each interfiber spacing were superimposed to coincide at x = 0 µm.

Analysis of focal adhesion clusters and actin stress fibers

We report focal adhesion cluster (FAC) lengths as the longest continuous length of paxillin clustering. These lengths were generated from manual measurements of the fluorescently labeled paxillin FACs in Axiovision (Carl Zeiss) software. Straight lines were drawn from end to end of the major stress fibers in ImageJ, and the orientation of such lines with respect to the net cell orientation were considered as the stress-fiber orientations.

Analysis of cell migration

Single (not in contact with neighboring cells) motile cells were chosen randomly from the time-lapse videos, and their centroids were tracked using the Centroid function in ImageJ every 10 min for 8 h. The centroid data were subsequently processed using a custom MATLAB (https://www.mathworks.com/) code to evaluate the migration rate, angular displacement, and mean squared displacements (MSDs) over each 10-min interval. The migration rate for a cell was calculated every 10 min over an 8-h experiment (48 measurements), and the measurements were then averaged for each cell to obtain the final migration rate. Migration persistence is defined as (net cell displacement)/(length of total path of cell motion), and angular displacement is defined as the change in migration direction after each time interval. It is evaluated from the following equation:

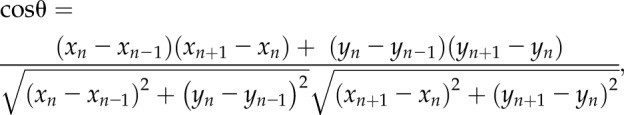where (x_n-1,y_n-1), (x_n,y_n), and (x_n+1,y_n+1) represent the x and y coordinates of the cell centroid at the (n − 1)^th, n^th, and (n + 1)^th time points (n = 2, 3,…, 48) and θ represents the angular displacement. MSD for a time interval (τ) is defined by the equation

where x and y are the coordinates of the cell centroid and t denotes time. Experimental MSD values were fitted against the exponential function 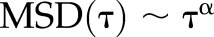, where α denotes the scaling exponent to describe cell’s diffusive motion. Cell migration was also evaluated using the persistent random walk model. (19, 55) MSD for a time interval (τ) is defined by the equation

where D is the diffusion coefficient, P is the persistence time, and the last term denotes the noise in the cell-position detection. Persistence length is calculated as persistence time (P) multiplied by the mean speed.

Analysis of leading and trailing edges

For individual cells, we chose the most active leading and trailing-edge regions and tracked their positions over time using the Manual Tracking plugin of ImageJ. Displacements for each of the leading and the trailing edges are normalized to their individual starting positions, respectively.

Nuclear movement, nuclear shape, area, eccentricity, and thickness

To investigate the movement of the cell nucleus, the cell nucleus was stained using the CellLight Nucleus-GFP BacMam 2.0 reagent (C10602; Thermo Fisher Scientific). Cells were incubated with the reagent overnight for at least 16 h, and time-lapse imaging was performed afterwards with either 5- or 10-min intervals for 4 h. Throughout our analysis, we approximated the nucleus to be an elliptical body, and specifications of the nuclear shape were calculated using the Fit ellipse function of ImageJ. The nucleus eccentricity was defined as

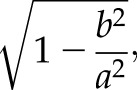where 2a and 2b denote the lengths of the major and minor axes of the ellipse, respectively. The nucleus areas and perimeters were recorded by manually outlining the nuclei in ImageJ. Z-stack images of the cell nucleus were taken using a confocal microscope, with a slice thickness of 0.36 µm, and the nucleus thickness was measured from the orthogonal cross section (x-z or y-z section) images.

Genome-wide analysis of gene expression

The RNA was extracted from cells grown at each condition as described in the RNA-extraction protocol. Libraries were prepared using the standard Illumina RNA sequencing (RNA-seq) protocol, and the sequencing was performed using a Hiseq 3000 system. The sequencing data for the RNA-seq analysis are deposited in the National Center for Biotechnology Information Sequence Read Archive (https://www.ncbi.nlm.nih.gov/sra) database under SRP131388. RNA-seq data were handled and processed following the basis of our previous work (56). The statistical analysis for differential gene expression compares the different interfiber spacing size with flat using the DESeq2 method (57). The functional enrichment analysis over Gene Ontology gen-set were performed, and the selected results were plotted in a heatmap using the platform for integrative analysis of omics data (Piano) package (58).

Statistical analysis and data fitting

Statistical analysis for the microscopy data was performed using the GraphPad Prism (GraphPad Software, La Jolla, CA, USA) software. Typically, the D’Agostino and Pearson omnibus normality test was utilized to test the normality of the data. Based on the normality of the data, either ANOVA (along with Tukey’s honestly significant difference test for multiple comparisons) or the nonparametric Kruskal-Wallis test (along with the Dunn’s multiple comparison test) was used to test the statistical significance between groups. For comparisons between only 2 groups, Student’s t tests were utilized. Data fits were performed in either MATLAB (for nonlinear fits) or Microsoft Excel (linear fits). Standard values for reporting significance were used. Unless otherwise mentioned, error bars represent standard error of measurement.

RESULTS

Crosshatch interfiber spacing modulates cell morphology

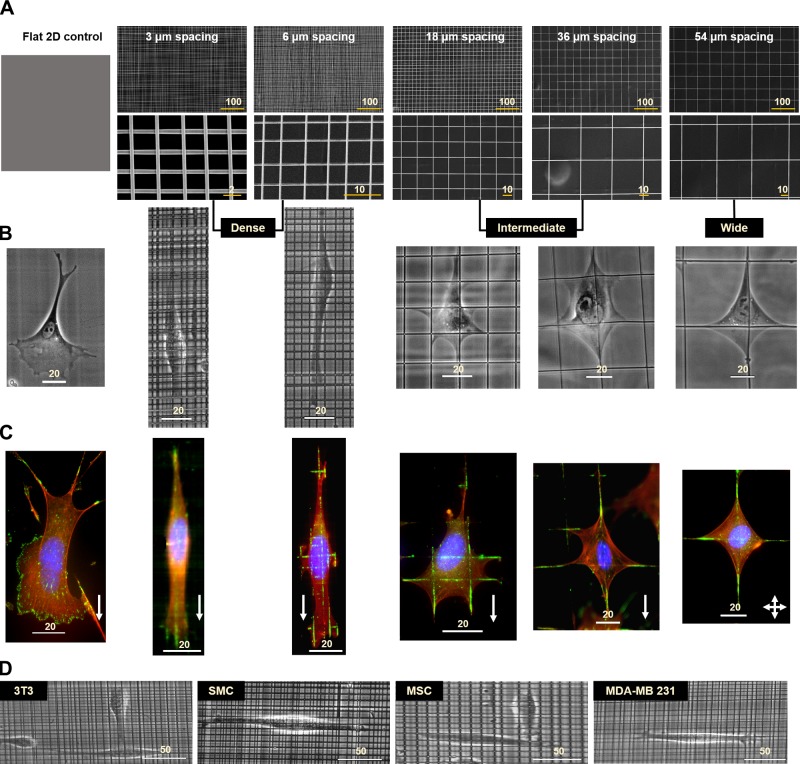
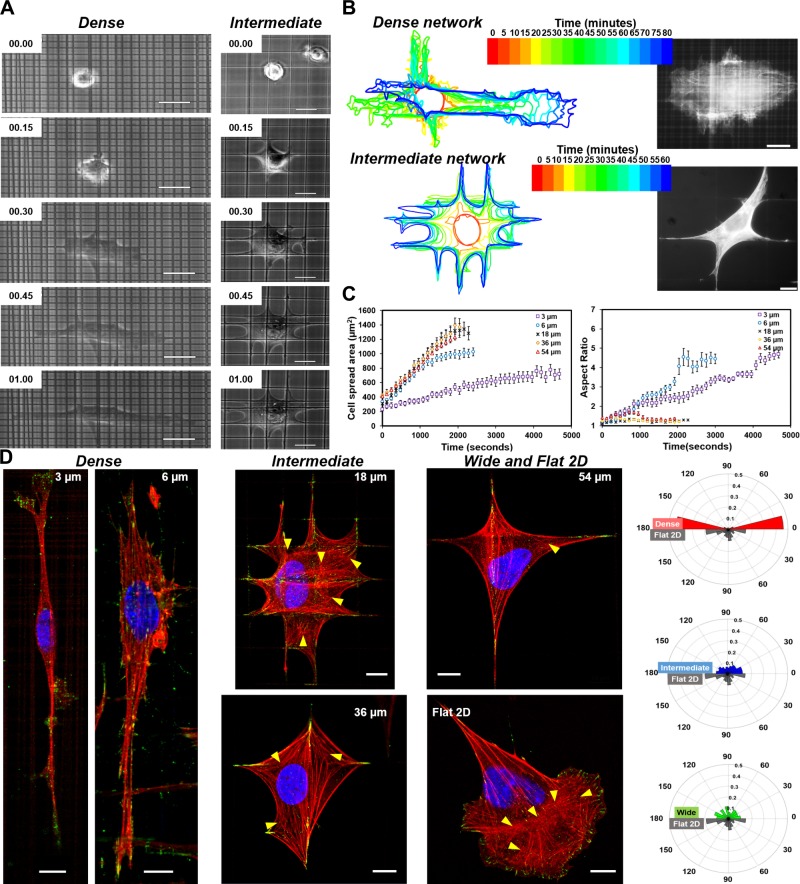
We wanted to determine the role of network interfiber spacing in modulating cell morphology (cell and nucleus size and shape). We generated 5 different categories of crosshatch fiber networks with interfiber dimensions: 3, 6, 18, 36, and 54 µm (means ± se; n = 100 per category); 2.6 ± 0.09, 6.0 ± 0.26; 17.8 ± 0.3, 35.6 ± 0.48; and 53.5 ± 0.42 µm, respectively Supplemental Fig. S1), with flat 2D culture serving as the control (Fig. 1A). For interpretation of statistical differences, we categorized the fiber networks into 3 major characteristically similar groups: dense (3 and 6 µm), intermediate (18 and 36 µm), and wide (54 µm). Although cells on wide fiber networks (∼54 µm) attained a symmetric kite shape characterized by well-defined branching of the cell body along each fiber axis, on intermediate networks, we observed cells with increased branching at multiple fiber intersections (Fig. 1B). Interestingly, on the 18-µm networks, we observed that cells had a broad leading and a narrow trailing edge, which strikingly resembled the flat 2D morphology (Supplemental Fig. S2). With a further decrease in unit-cell size (dense networks), unexpectedly, we found the cells to have elongated shapes similar to those observed in cells moving through dense collagen gels or cell-derived matrices (59). For all interfiber spacing networks, cells were found to interact with both fiber layers as observed by time-lapse imaging (Supplemental Fig. S3 and Supplemental Movies S1–S3). To visualize the cell-fiber adhesion areas, we performed immunostaining for paxillin (60), a major focal adhesion marker. Although paxillin adhesions were distributed throughout the cells on the 2D flat substrata, on fibers, they were observed to be concentrated in FACs (Fig. 1C), consistent with our previous observations (61, 62). The observed migratory phenotype was not unique to Hras1 because other commonly used cell lines with migratory potential [NIH 3T3 fibroblasts, human smooth muscle cells, human bone mesenchymal stem cells, and human breast adenocarcinoma MDA-MB-231 cells (Fig. 1D)] also exhibited similar behavior, thus generalizing our findings.

Figure 1.

Nanofiber networks and the corresponding cell morphologies. A) Scanning electron microscopy images of 500-nm diameter fiber networks with bottom panel showing high-magnification images. Also shown is a schematic of the flat control substratum. B) Representative phase contrast images of cell morphologies obtained on the different substrata. C) Assembly of focal adhesions visualized by staining for the focal adhesion protein, paxillin (shown in green), and f-actin stress fibers in red and nucleus in blue. White arrows denote cell migration direction. In the case of the 54-µm fiber networks, cells exhibit no bias in direction of migration. Characteristically similar fiber categories are grouped as dense (3 and 6 µm) and intermediate (18 and 36 µm), whereas the 54-µm network is designated as wide. D) Cells of different migratory lineages behave similarly on fiber networks (example shown for dense network). All scale bars shown in µm. MSC, mesenchymal stem cell; SMC, smooth muscle cell.

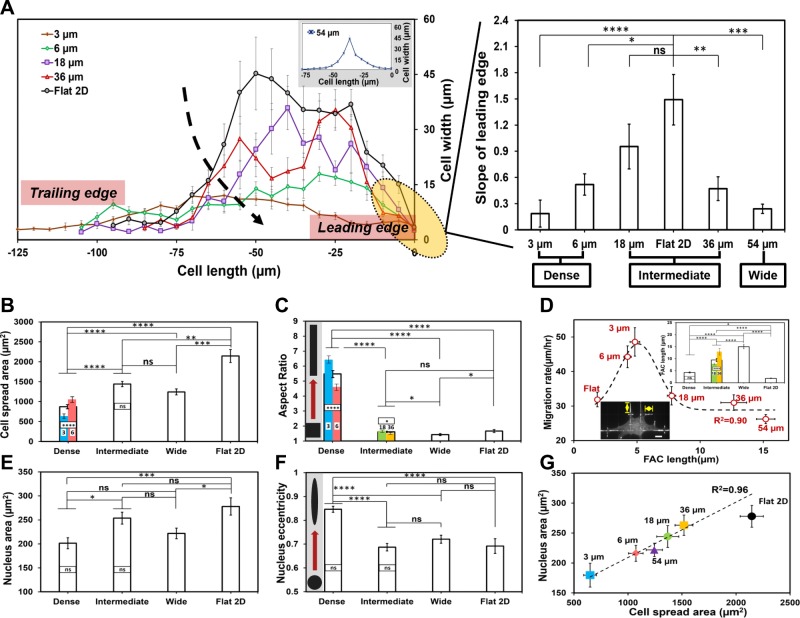
Next, we biophysically phenotyped cell shape on fiber networks using metrics of area, aspect ratio, and eccentricity. First, a comparison of the mean slope of the leading edge of cell shape showed a close match between the 18-µm unit-cell spacing and the flat 2D substrate (Fig. 2A). Lower slope values indicate elongated cell bodies, whereas the higher slopes, associated with cells on intermediate and 2D flat substrata, indicate spread cell shapes. Cells on dense networks had lower cell spread areas and higher aspect ratios (Fig. 2B, C). Cells cultured on the 3-µm interfiber spacing had the most elongated cell bodies and the lowest spread area, a morphology often associated with invasive cells and resembling cells undergoing the epithelial-mesenchymal transition. Next, quantitating the FAC-migratory behavior revealed that increasing length of FACs with interfiber spacing (inset, Fig. 2D) resulted in a biphasic migratory response (R² = 0.90, Fig. 2D). Cells on flat substrate had the shortest FAC, but their high-number density compared with cells on 3 and 6 µm likely caused the drop in migration rate. On the other hand, longer FACs at higher spacing contributed to the slowing of cells due to the line arrangement of adhesion sites that needed to be disengaged during migration. We also observed that cells on dense networks had the lowest nucleus areas (Fig. 2E) and highest eccentricity (Fig. 2F). Altogether, we found cell and nucleus areas linearly correlated across all fiber network spacing (R² = 0.96, Fig. 2G). Although previous studies have relied on printing adhesion proteins and patterned surfaces to achieve control on cell shape (63–66), here, we demonstrate that varying the geometric interfiber spacing alone is sufficient to control cell morphology.

Figure 2.

Interfiber spacing modulates cell and nucleus morphologies and FAC lengths. A) Cell width vs. cell-length profiles (top: profile of cell, shown only half because of symmetry) for each category along with the measured slopes of the profiles at the leading edges (n = 13, 7, 8, 10, 9, and 9 for 3, 6, 18, 36, and 54 µm and flat 2D, respectively). Cells on dense networks have lower slopes, indicating elongated cell bodies. B) Cell spread areas on networks of increasing interfiber spacing (n = 107, 101, 84, and 50 for dense, intermediate, and wide networks and flat 2D, respectively). C) Aspect ratios of the cells on varying fiber networks show cells to be highly elongated on dense networks (n = 107, 101, 84, and 50 for dense, intermediate, and wide networks and flat 2D, respectively). Inset in gray box shows schematic of geometry change (square to elongated rectangle) with increase in aspect ratio. D) Paxillin FAC lengths increase with interfiber spacing leading to a biphasic migratory response (n = 11, 17, 20, 10, 13, and 12 for 3, 6, 18, 36, and 54 µm and flat 2D, respectively). Inset shows FAC data for different cateogries and a representative image with yellow arrows depicting FAC measurement (scale bar, 10 µm). E, F) Nucleus area (E) and nucleus eccentricity (F) are modulated by the underlying interfiber spacing with smallest size and highest eccentricity found in dense networks (n ≥ 40 per category). Inset in gray box shows schematic of geometry change (circle to elongated oval) with increase in eccentricity. G) Cell and nucleus areas are positively correlated. Linear fit to data corresponding to fiber networks with flat 2D data shown as reference. Error bars represent sem. Statistical differences between individual interfiber spacing categories are superimposed on the data for their respective groups; ns, not significant. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.

Network interfiber spacing modulates cell motility

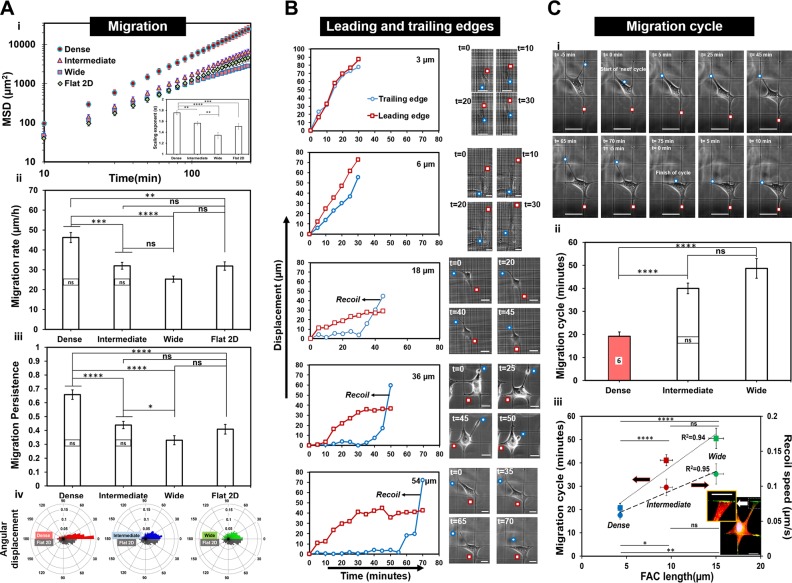
We next sought to determine whether the dynamics of cell migration (speed, persistence, angular displacements, and cell-body movement) were driven by spacing of the fiber networks. We determined the MSD (Fig. 3A) exponents and found a scaling exponent of ∼1.4 for cells on intermediate and wide spacing, indicative of migratory behavior resembling a diffusive random walk similar to that observed on flat 2D substrate. (67–70) However, on dense networks (3 and 6 µm), we obtained a scaling exponent of ∼1.8, signifying a persistent migratory behavior similar to migratory behavior observed in the presence of physical constraints such as microchannels, grooves, 1D stripes, or fibrillar tracks (22, 24, 29). Migration rate (Fig. 3A) and persistence (Fig. 3A) were inversely related to interfiber spacing. Cells on dense networks not only moved faster but with higher persistence, demonstrating smaller angular displacement during migration (Fig. 3A). Interestingly, we observed that the migratory behavior of cells on flat 2D substrate matched closely with the cells migrating on networks with intermediate (18 and 36 µm) spacing. This is consistent with our finding that cell shapes in these categories (especially in the 18-µm category) resembled cell shapes on 2D flat substrata. Altogether, we report that crosshatch fiber networks of varying interfiber spacing are able to achieve precise control on migratory behavior (1D highly persistent to a diffusive 2D random walk).

Figure 3.

Interfiber spacing modulates cell migration. A) MSD vs. time (t) plots corresponding to dense, intermediate, and wide fiber network categories and flat 2D (i). Inset shows the scaling relation MSD ∼ t^α, where α is the scaling exponent that is used to fit the data. Aii) Migration rate of single cells (n = 59, 40, 44, and 29 for dense, intermediate, wide, and flat 2D, respectively). Aiii) Persistence of single cells (n = 49, 40, 36, and 20 for dense, intermediate and wide networks and flat 2D, respectively) for the different substrates. Aiv) Polar plots showing angular displacements for cells on varying fiber network porosities and compared with flat 2D (n = 40, 40, 20, and 20 for dense, intermediate, and wide networks and flat 2D, respectively). Data demonstrate cells moving fastest and with highest persistence on dense crosshatch pattern of fibers. B) Representative displacement profiles of the leading and trailing edge for the different fiber network categories. Leading and trailing edges are shown in red squares and blue circles, respectively, in associated time-lapse images (scale bars, 20 µm; time shown in minutes). C) Recoil-to-recoil analysis method to calculate migration cycle time (i). Cii) Migration cycle time over the different fiber network categories (n = 29, 50, and 25 for dense, intermediate, and wide networks, respectively). Note for the dense group: data are only shown for 6-µm fiber spacing because the recoil-to-recoil migration cycle for the 3-µm fiber spacing was not discernable optically. Ciii) Migration cycle and retraction recoil speeds plotted as function of FAC length showing both metrics to linearly scale with FAC lengths. Inset image shows a fluorescently labeled cell attached to a 54-µm interfiber spacing network and the magnified image of retracting edge showing f-actin stress-fiber distribution (red: f-actin stress fiber; blue: nucleus; green: paxillin. Scale bars, 20 µm). Statistical differences between individual interfiber spacing categories are superimposed on the data for their respective groups; ns, not significant. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.

Next, to understand the mechanics of how cells migrated on fiber networks of varying spacing, we investigated the dynamics of trailing and leading edges (shown by blue and red circles, respectively, in Fig. 3B). We observed that the trailing edge served as an anchor point for the advancing leading edge. Thus, as the leading edge advanced, the trailing edge elongated over time, and subsequently, it was observed to detach and retract in a recoil manner at the rate of 10⁻²–10⁻¹ µm/s. These rates are equivalent to those observed for the fast phase of fibroblast trailing-edge retractions cultured on 2D glass substrates (71). This mechanism, a well-documented aspect of 2D cell migration, matched well with the cells migrating on the intermediate and wide fiber network categories. However, on the dense networks, the motion of the trailing edge was much smoother compared with intermediate and wide spacing. We quantified the time taken between successive trailing-edge retractions to determine migration cycle (Fig. 3C). Migration cycle time increased with increased interfiber spacing (Fig. 3C) and increased FAC lengths (R² = 0.94, Fig. 3C). Similarly, the recoil speed was found to increase with FAC length (R² = 0.95), thus suggesting that the longer FAC lengths associated with well-defined f-actin stress fibers originating from the adhesion sites (inset in Fig. 3C) were causing stronger recoils.

Nucleus dynamics response to network porosity

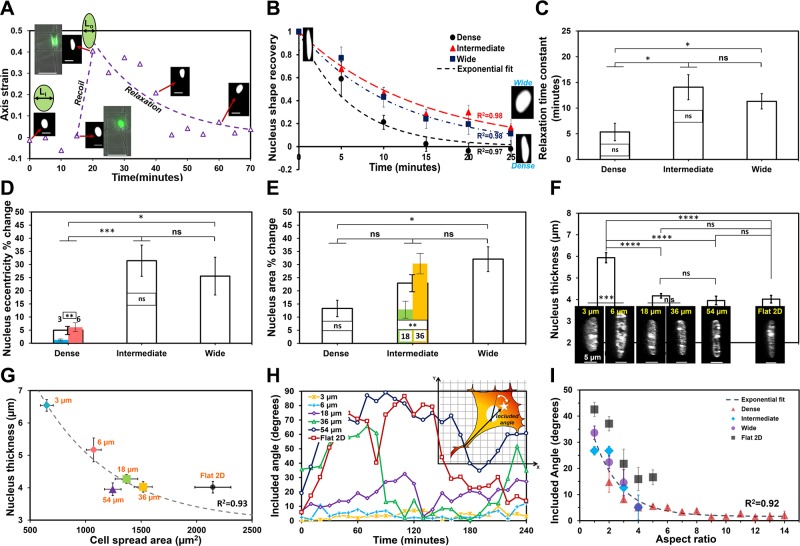
We next sought to determine the dynamics of nucleus shape change in response to fiber network spacing. Nuclei underwent distinct and rapid deformation (Supplemental Movie S4) with the recoil of the trailing edge. We quantitated the changes in nucleus shape (major and minor axes, projected area) within a migration cycle and found nucleus shape changes to be pronounced on intermediate and wide interfiber spacing networks. On these networks, at the start of the migration cycle, the nucleus was observed to be rounded (low eccentricity), which transitioned to an elongated shape (high eccentricity) during recoil of the trailing edge and returned to rounded morphology as the trailing edge reattached [Fig. 4A, B (R² = 0.98 for both wide and intermediate networks)]. This is in contrast to cells on dense networks that maintain high eccentricity (elongated nuclei) at all times. In general, the recovery time constant (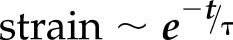where τ is the recovery time constant) for nucleus shape dynamics was found to increase with the interfiber spacing, thus signifying a larger deformation with stronger trailing-edge recoil (Fig. 4C). The extent of the nucleus shape change was estimated in terms of the percent change of the nucleus eccentricity, and it was found that trailing-edge retractions in intermediate and wide networks involved up to ∼35% eccentricity change of the nucleus (Fig. 4D), whereas, on dense networks, it was significantly reduced (∼5%). Similarly, the change in nucleus area increased with network interfiber spacing (Fig. 4E). We observed large (∼30%) changes in areas only on the 36- and 54-µm fiber categories, presumably due to high forces generated during recoil to compress the nucleus. Next, we interrogated the thickness of nuclei on different fiber network categories using confocal microscopy. Reconstruction of nucleus height using z-stack images showed the nuclei to be significantly thicker in dense networks (Fig. 4F). Furthermore, nucleus thickness was found to decrease with the increase in cell spread area (R² = 0.93, Fig. 4G). Because intermediate and wide fiber spacing were causing nuclei to undergo shape changes, we interrogated the angular coupling between nucleus and cell-body vector [defined as included angle (inset in Fig. 4H) signifying the extent of coalignment between nucleus and cell body during migration]. We found that increasing interfiber spacing resulted in larger nucleus angular spins (Fig. 4H), similar to the results from studies previously described by Kim et al. (72), on flat substrates, whereas, with increasing aspect ratio of cells (signifying persistent migration on denser networks), the extent of nucleus–cell body coordination increased (included angle decreases, R² = 0.92, Fig. 4I) (Supplemental Movie S4). Altogether, our data shows that nucleus thickness, shape, deformation, and the degree of change in angular orientation during migration cycle are controllable through the choice of interfiber spacing.

Figure 4.

Interfiber spacing modulates nucleus dynamics. A) Representative profile of the deformation of nucleus during retraction of a trailing edge demonstrating that rounded nucleus is strained to elongated shape, and, after recoil, the nucleus relaxes to its original shape. Axis strain is defined as ε = [L_i – L(t)] ÷ L_i, where L_i is the minor axis length of the nucleus prerecoil and L(t) represents the minor axis length of the nucleus at time (t) (scale bars, 20 µm). Immediately postrecoil, minor axis length; L(t) = L₀. B) Post-recoil normalized nucleus shape recovery data is defined as ε/ε₀, where ε₀ = (L_i – L₀) ÷ L_i is the initial nucleus axis strain immediately postrecoil. Exponential fits to data show that cells on dense networks recover their original shape faster after recoil. Inset shows representative images of the nucleus postrecoil and after relaxation (rounded is for wide and elongated for dense networks). C) Relaxation time constants calculated on basis of an exponential decay of nucleus deformation showing stronger recoil in intermediate and wide networks. D, E) Percentage change in nucleus shape [eccentricity (D)] and size [projected area (E)] during trailing-edge recoil. F) Nucleus height measured by confocal microscopy quantitates cell nuclei to be thicker in dense regions. Inset shows representative images of nucleus (projected side view from confocal microscopy; scale bars, 5 µm). G) Nucleus thickness decreases with increase in cell spread area. H) Representative temporal plots of nucleus–cell body angular coupling (included angle) for the different interfiber spacing with inset illustration showing that the included angle is defined by the coordination between cell-body vector (trailing edge to centroid shown by white star) and nucleus major axis. I) Data show the influence of cell shape (aspect ratio) on the extent of nucleus–cell body coordination. For G and I, exponential fit to data corresponding to fiber networks with flat 2D data shown as reference. Sample size for B–E (n = 11, 23, and 10: dense, intermediate, and wide networks, respectively); for F and G (n = 25, 32, 14, and 13: dense, intermediate, wide, and flat 2D, respectively) and for I (n = 13, 15, 9, and 9: dense, intermediate, wide, and flat 2D, respectively). Included angle and aspect ratios are calculated every 10 min over the 4-h experimental time (25 measurements) and then averaged across cells of similar aspect ratios. Statistical differences between individual interfiber spacing categories are superimposed on the data for their respective groups; ns, not significant. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.

Cell spreading and symmetry breaking dynamics

Next, we wanted to investigate how cells adopted highly elongated geometries on dense fiber networks. We monitored the cell spreading behavior from the moment the cells first started interacting with the fibrous networks (Fig. 5A). Cells cultured on dense networks formed transient, short-lived protrusions resulting in delayed spreading (Fig. 5B). We calculated the temporal evolution of the projected spread area of the cells (Fig. 5C) and found that all interfiber spacings demonstrated an almost linear growth of the projected area (with slowest on the 3-µm category), which is in accordance with cell spreading on flat substrata and in gel systems (73–75). Furthermore, we observed that, on dense networks, spreading occurred with continuous growth in aspect ratio, signifying anisotropic shapes, whereas cells on intermediate and wide categories continually protrude along all fiber axes and spread mostly in an isotropic fashion (aspect ratio, ∼1). Next, we looked at the organization of f-actin stress fibers once cells had completely stretched. We observed stress fibers to be aligned along the cell-body axis in dense networks and isotropically distributed as meshwork (shown by yellow arrows) in intermediate and wide networks similar to those observed on flat 2D substrata (Fig. 5D and Supplemental Fig. S4). Interestingly, on the 3-µm network of fibers, we did not observe a large number of dominant stress fibers, similar to reported observations of cells in 3D morphologies (29). Altogether, our data suggest that the interfiber spacing of crosshatch networks of fibers is a modulator of cell spreading dynamics and actin cytoskeleton organization.

Figure 5.

Interfiber spacing modulates cell spreading and f-actin stress-fiber organization. A) Phase contrast time-lapse images showing anisotropic and isotropic cell spreading on 6 and 18 µm representing dense and intermediate fiber networks, respectively. B) Transient profiles outlining cell spreading on dense and intermediate networks. On dense networks, cells form multiple short-lived protrusions in all directions (inset image) before elongating in a primary direction, whereas, on intermediate networks, cells protrude and extend isotropically. C) Analysis of cell spread area and associated aspect ratio (length to width) of cells spreading on fibers of varying network porosities (n = 8–11 per category). D) Immunostained images of f-actin stress fibers (red), focal adhesion paxillin (green), and nucleus (blue) on all fiber categories and the flat 2D substratum. Cells cultured on the 3-µm porosity networks lack dominant stress fibers. Yellow arrows indicate clustering (meshwork) of stress fibers, with intermediate spacing matching the stress-fiber distribution found in cells on flat 2D substrata. Polar plots of f-actin stress-fiber distribution demonstrating highly aligned stress fibers in dense networks and isotropic distribution of stress fibers in intermediate and wide categories resembling those on flat substrates (n = 25, 24, 11, and 10 for dense, intermediate, wide, and flat 2D, respectively; 15–20 stress fibers analyzed for each cell). Scale bars, 20 µm.

Gene-expression analysis

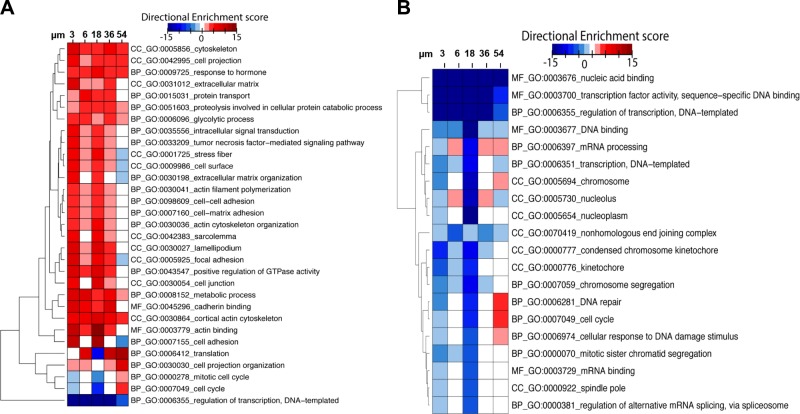
To determine whether growth on different fiber networks could drive transcriptional reprogramming, we performed RNA-seq analysis on independent replicates grown on the different fiber networks. The up-regulation of genes related to cytoskeletal rearrangement and cell-cell adhesion were concordant with the observed phenotypes described (Fig. 6A). Interestingly, we observed a generalized decrease in transcriptional activity compared with flat control (Fig. 6B). Previous studies have shown that nuclear shape and size can influence gene transcription and access of transcriptional machinery to DNA (76–78). Surprisingly, gene families associated with the transcriptional activity are suppressed, and we do not observe dynamic changes concordant with changes in nucleus shape and size observed between cells on the different fiber networks. However, we observed up-regulation of multiple genes in pathways regulating translation and protein expression, suggesting functional changes in cell behavior may be due to post-transcriptional modifications. Furthermore, up-regulation of genes involved in metabolic processes (BP-GO: 0008152) was observed in cells grown on all fibers compared with a flat surface. These data suggest that interfiber spacing is sufficient to induce changes in gene expression, which may be independent of changes in nuclear morphology. The resulting gene-expression changes appear to be primarily involved with driving post-transcriptional alterations related to translation and protein modifications, whereas generalized transcriptional up-regulation is not altered. Together, all these data suggest that biophysical alterations within the tumor microenvironment (TME) may be sufficient to modulate transcriptional programming that could increase the expression of genes implicated in enhanced pathogenic and tumorigenic potential in transformed cells.

Figure 6.

Interfiber spacing modulates gene expression. A) Hierarchical clustering and gene ontology (GO) enrichment analysis of gene families related to cellular phenotypes in cells cultured on fiber networks of different interfiber spacing. B) Hierarchical clustering and GO enrichment analysis of gene families primarily down-regulated during growth on fiber networks. Down-regulated networks are primarily associated with transcription. Directional enrichment scores are reported with respect to flat 2D control. BP, biological process; CC, cellular component; MF, molecular function.

DISCUSSION

The immediate environment surrounding a cell offers a variety of biophysical cues of confinement, rigidity, topography (isotropic and anisotropic), and porosity (79). Here, we have explored how in the context of in vivo crosshatch network of fibrous environments found in dermis (11), basement membrane (15), muscular hydrostats (37), and the loose connective tissue (17), different levels of interfiber spacing can result in different morphologies and associated migration dynamics. Firstly, we observed that, at a very high interfiber spacing (wide: ∼54 × 54 µm), cells form symmetric kite shapes and have reduced migration rates and persistence due to the formation of significantly large FACs. With the decrease in interfiber spacing to intermediate (18 and 36 µm), we observed that the cell morphologies and migratory behavior were very similar to those obtained on traditional flat 2D substrata (Figs. 2 and 3). Encouraged by our ability to recapitulate 2D migratory behavior on a suspended network of fibers, we inquired as to whether making the fiber networks denser would still maintain this behavior because we presumed that decreased interfiber spacing would translate to the increased number of contact points similar to those available on a featureless 2D substratum. Unexpectedly, we found that the increased contact points caused multiple transient short protrusions, leading to elongated cell bodies and anisotropic migration. We found that cell elongation occurred much earlier during the cell spreading process (Fig. 5B), and because cells were probing both directions, we observed polarized cells in both principal directions. Once polarized, the cells maintained symmetry on dense networks and migrated in the direction of polarization. However, with increasing interfiber spacing, cells were able to more readily change direction, resembling random walks.

3D persistent migration can be obtained using cell-derived matrices, 1D microprinted fibrillar lines, or mechanically confining cells using microgrooves or microposts, whereas 2D random migration is typically obtained using flat, featureless substrates with no confinement. Here, we demonstrate that our method recapitulates random 2D and persistent 3D migration by simply varying the interfiber spacing in a suspended crosshatch network of fibers. Our method of achieving persistent migration is independent of the requirement of aligned topographical cues. Cells on networks of suspended crosshatch fibers make contact with both layers (shown by paxillin adhesions on both layers: Supplemental Fig. S3). On dense networks, cells maintain elongated shapes that have significantly longer persistence lengths [dense: 92.5 μm; intermediate: 29.8 μm; wide: 12.16 μm; flat 2D: 19.95 μm; calculated using persistent random walk model, Supplemental Fig. S5 (19, 55)]. Interestingly, cells on dense networks align along both principal axes of crosshatch networks (Supplemental Movies S1–S3) and can make right-angle turns, thus changing their migratory direction (Supplemental Movie S5). Our quantitation of leading trailing-edge displacements (Fig. 3B) of cells migrating in dense networks matches the 3D migration profiles and cell shapes reported in the literature using cell-derived matrices and narrow 1D microprinted fibrillar lines (29). Furthermore, cell migratory behavior on dense networks in 3D shapes matches the reported migration speed patterns and cell shapes obtained in narrow microgrooves (27). However, our findings diverge from cell behavior observed on 2D crosshatch microprinted patterns, which report similarities in cell shapes across dense, sparse, and smooth 2D substrates, whereas the migration rates across dense and sparse remain similar (80, 81). We speculate the differences from our method arise because of the absence of curvature in microprinted lines and cells presumably making contact with the underlying flat substrate. Suspended fibers not only provide curvature as a cue to cells but also ensure that cells interact only with fibers. Supporting this, we have previously shown that suspended flat 2D ribbons do not capture the protrusive sensitivity to suspended round fibers (49).

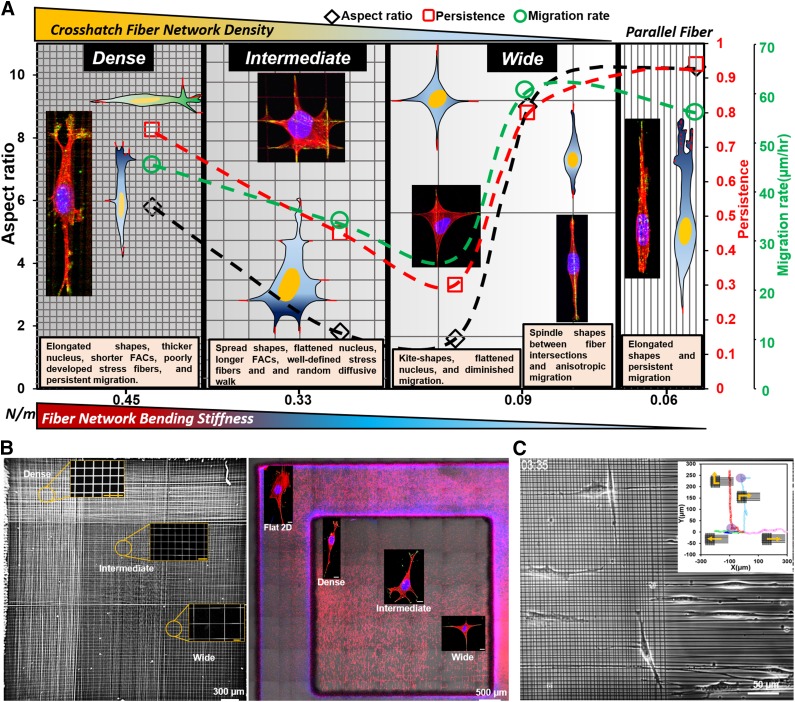
Our observation of cells of multiple lineages (fibroblasts, cancer cells, smooth muscle cells, and mesenchymal stem cells) having high aspect ratios and 3D shapes moving persistently (in 1 dimension) on dense networks (Fig. 1) compares well with the reported morphology and behavior of cells in 3D collagen gels and cell-derived matrices (29, 59, 82). Coalignment between the nucleus and cell-body vectors, a hallmark of persistent migration, is recapitulated in vitro using anisotropic topographical cues of varying widths (83, 84), whereas here, in contrast, we show that dense crosshatch fiber environments can achieve similar behavior. With the increase in interfiber spacing, cells on intermediate and wide network categories have a loss of the coalignment that leads to random migration as observed in cells on 2D flat substrata. Furthermore, cells on dense networks had thicker nuclei (Fig. 5F), exhibited lower time constants during shape recovery after recoil (Fig. 5C), and lacked well-defined f-actin stress fibers (Fig. 6D). These findings suggest that dense networks induce 3D morphologies of compliant (soft) cells that migrate anisotropically: a mechanical signature that is often associated with higher invasive potential (85, 86) Interestingly, plotting the migratory behavior across the bending stiffness (newtons per meter, Supplemental Fig. S6) of crosshatch networks shows that cells in elongated shapes having thicker 3D bodies migrate faster at high stiffness values (dense networks) and slower on lower stiffness values (intermediate and wide networks, Fig. 7A). Contrastingly, cells having elongated shapes similar to dense networks but cultured on multiple parallel fibers or on single parallel fibers in spindle shapes move faster at lower stiffness (43, 62). Thus, we emphasize the need to conjointly examine geometric arrangement of fibers and their stiffness for a comprehensive description of the migratory phenotype.

Figure 7.

Fiber network–based migration platform. A) Migration phase diagram based upon interfiber spacing and bending stiffness (N/m) modulates single-cell migratory phenotype in 1D, 2D, and 3D cell shapes. Data are plotted for various interfiber spacings against parallel arrangement of fibers (shown on extreme right). On average, cells were found to engage with 3 parallel fibers, resulting in estimation of equivalent stiffness by summation of stiffness of individual fibers (43, 62) (springs in parallel). B) Scanning electron microscopy image (left) of a single scaffold with 3 fiber network categories along with fluorescence microscopy images showing images of the cells seeded on fibers of varying crosshatch densities and the flat 2D control. Scale bars in inset images in scanning electron microscopy panel are 20 µm, and stained images are 10 µm. C) Custom suspended fiber networks to study cell shape and migration changes as cells transition between aligned and crosshatch networks [pattern adapted from Doyle et al. (29)]. Inset shows representative migration trajectories demonstrating cells maintaining elongated shapes and persistent migration on both networks along with cases in which cells can turn directions shown by purple circles (Supplemental Movie S7).

Surprisingly, we found that isotropic environments not only induce plasticity in migration but also lead to transcriptional modifications that may enhance transformation. We report the up-regulation of multiple metabolic pathways in response to growth on fibers and report that the observed transcriptional changes were primarily in gene ontologies related to post-transcriptional modifications and modulation of metabolic capacity. Furthermore, we did not observe general transcriptional up-regulation that correlated with nuclear size and shape, presumably because of similarities in morphology across the different substrates (Fig. 2E, F). Instead, we observed more specific up-regulation of pathways related to translation and post-translational modification of proteins, including up-regulation of metabolic pathways. These data support that physical cues in the microenvironment can alter transcriptional output seemingly independent of nuclear shape changes and modulate the metabolic capacity of tumor cells. These observations support targeting the TME through therapeutic intervention to decrease tumor-cell growth and motility (87, 88). A dense TME has been shown in previous studies to limit therapeutic efficacy, and many dense tumors are resistant to chemotherapy (87–90). It has been proposed that this is because of decreased delivery of drug to the tumor site due to transport barriers to drug delivery. However, our data reveals a potential additional mechanism of resistance whereby metabolic programming within the tumor cells is changed based on the TME and may contribute to therapeutic resistance. Our current and future studies are aimed at discerning the mechanisms of drug resistance in our in vitro models of thyroid cancer and determining whether growth on varying interfiber spacing changes the sensitivity of tumor cells to molecular inhibitors. Finally, although we did not identify transcriptional and metabolic changes that have been previously reported in regards to nuclear shape changes (76–78), we cannot exclude the possibility that chronic stresses and strain to nuclear shape associated with repeated cycles of attachment and recoil that were observed may have contributed to some of the transcriptional reprogramming and expression changes observed. We believe short- to long-term future studies using our platform provide novel quantifiable metrics to dissect whether acute nuclear shape changes vs. chronic stresses to nuclear shape associated with motility and recoil forces lead to distinct transcriptional responses.

In summary, we report the development of a new ECM mimicking crosshatch nanofibrous platform for studying 1D, 2D, and 3D cell migration. Our method of using crosshatch suspended fibrous environments of tunable interfiber spacing modulates plasticity in cell migration and cytoskeletal arrangement, thus allowing us to identify crosshatch fiber density–driven rules in cell migration. Notably, we show that dense crosshatch spacing, much like aligned fibers, is a fertile environment that induces fast, persistent migration in 3D shapes, which is a known signature of softer invasive cancer cells, whereas wider crosshatches induce random migration in 2D shapes of cells with higher contractility. We demonstrate that aligned geometries are not the only requisite biophysical configuration that can elicit elongated cell shapes and sustain persistent migration. The flexibility of our approach permits using a single scaffold with tunable crosshatch interfiber spacing, thus allowing simultaneous recovery of 1D, 2D, and 3D cell morphologies and migratory patterns at desired locations (Fig. 7B) that are currently recapitulated using a wide variety of in vitro methods. The nonelectrospinning STEP platform can also generate custom fibrous networks matching patterns reported in the literature (29) to compare cell shape and migration-mode changes (Fig. 7C). In doing so, we overcome the well-noted current challenges of cross-validating migratory phenotypes across platforms, quantitative microscopy at high spatiotemporal resolutions, and easy access to desired cells for detailed molecular profiling (5). We envision that extending the platform to include cocultures and biochemical cues along with the ability to estimate the physical forces exerted by cells (nanonet force microscopy) (53, 91) will yield new mechanotransduction knowledge in metastatic invasion, regenerative wound repair, and stem cell migrational homing.

Supplementary Material

This article includes supplemental data. Please visit http://www.fasebj.org to obtain this information.

Glossary

1D

1 dimensional

2D

2 dimensional

3D

3 dimensional

ECM

extracellular matrix

f-actin

filamentous actin

FAC

focal adhesion cluster

MSD

mean squared displacement

NA

numerical aperture

RNA-seq

RNA sequencing

STEP

spinneret-based tunable engineered parameters

TME

tumor microenvironment

AUTHOR CONTRIBUTIONS

B. Behkam, A. T. Franco, and A. S. Nain designed research; A. S. Nain supervised overall research; A. Jana and A. S. Nain performed research; A. Jana, J. Singh, B. Behkam, A. T. Franco, and A. S. Nain analyzed data; I. Nookaew and A. T. Franco performed gene-expression analysis; and A. Jana, B. Behkam, A. T. Franco, and A. S. Nain wrote the manuscript.