The 24-h savings of adaptation to novel movement dynamics initially reflects the recall of previous performance

Abstract

Humans rapidly adapt reaching movements in response to perturbations (e.g., manipulations of movement dynamics or visual feedback). Following a break, when reexposed to the same perturbation, subjects demonstrate savings, a faster learning rate compared with the time course of initial training. Although this has been well studied, there are open questions on the extent early savings reflects the rapid recall of previous performance. To address this question, we examined how the properties of initial training (duration and final adaptive state) influence initial single-trial adaptation to force-field perturbations when training sessions were separated by 24 h. There were two main groups that were distinct based on the presence or absence of a washout period at the end of day 1 (with washout vs. without washout). We also varied the training duration on day 1 (15, 30, 90, or 160 training trials), resulting in 8 subgroups of subjects. We show that single-trial adaptation on day 2 scaled with training duration, even for similar asymptotic levels of learning on day 1 of training. Interestingly, the temporal force profile following the first perturbation on day 2 matched that at the end of day 1 for the longest training duration group that did not complete the washout. This correspondence persisted but was significantly lower for shorter training durations and the washout subject groups. Collectively, the results suggest that the adaptation observed very early in reexposure results from the rapid recall of the previously learned motor recalibration but is highly dependent on the initial training duration and final adaptive state.

NEW & NOTEWORTHY The extent initial readaptation reflects the recall of previous motor performance is largely unknown. We examined early single-trial force-field adaptation on the second day of training and distinguished initial retention from recall. We found that the single-trial adaptation following the 24-h break matched that at the end of the first day, but this recall was modified by the training duration and final level of learning on the first day of training.

INTRODUCTION

Adaptation is a simple form of motor learning in which subjects compensate for an imposed perturbation that disrupts movement (Krakauer and Mazzoni 2011). Adaptation savings refers to the phenomenon where relearning to compensate for a previously experienced perturbation occurs at a faster rate on reexposure. This faster learning rate has been demonstrated for different movement adaptations: rotations of movement visual feedback (Bédard and Sanes 2011; Cassady et al. 2018; Haith et al. 2015; Herzfeld et al. 2014; Huang et al. 2011; Huberdeau et al. 2015; Jiang et al. 2018; Krakauer et al. 1999, 2005; Leow et al. 2012, 2013, 2014, 2016; Miall et al. 2004; Morehead et al. 2015; Orban de Xivry and Lefèvre 2015; Tong et al. 2002; Villalta et al. 2015; Wigmore et al. 2002; Yin et al. 2016; Zarahn et al. 2008), saccade target displacements (Kojima et al. 2004; Robinson et al. 2006), prism displacements (Goedert and Willingham 2002; Seidler et al. 2017; Welch et al. 1993), novel gait patterns (Day et al. 2018; Malone et al. 2011; Mawase et al. 2014; Roemmich and Bastian 2015), and novel arm reaching dynamics (Caithness et al. 2004; Coltman et al. 2019; Overduin et al. 2006; Richardson et al. 2006; Sarwary et al. 2013; Shadmehr and Brashers-Krug 1997). Recently, Huberdeau and colleagues (2015) varied the length of the first exposure to a rotation of visual feedback and demonstrated that a brief training period is sufficient to induce savings 24 h later. In addition, Roemmich and Bastian (2015) varied the length of the first exposure in a gait pattern paradigm and found that a longer first exposure increased the savings observed during the second training period. Together, the results suggest that adaptation savings can be induced from a brief exposure but strengthened with extended experience. However, the exact relationships between the initial training duration and subsequent savings for adaptation to novel arm reaching dynamics are largely unknown.

In addition to training duration, savings is also influenced by the formation of different, competing motor memories. For example, savings is subject to interference by opposing perturbations, which suggests that the training structure, and subsequently, the final learning state at the end of initial training, can influence the amount of savings with reexposure (Bock et al. 2001; Caithness et al. 2004; Kojima et al. 2004; Krakauer et al. 1999, 2005; Overduin et al. 2006; Pekny et al. 2011; Shadmehr and Brashers-Krug 1997; Sing and Smith 2010; Wigmore et al. 2002; Zarahn et al. 2008). This also suggests that although the magnitude of the motor recalibration can be reduced (a final learning state that returns to baseline), the motor memory may not be forgotten (Criscimagna-Hemminger and Shadmehr 2008; Kitago et al. 2013; Pekny et al. 2011; Smith et al. 2006). Although washout of adaptation has been shown to reduce the amount of savings (Caithness et al. 2004; Krakauer et al. 2005; Villalta et al. 2015), only a few studies have (mostly indirectly) examined the influence of washout in combination with the initial training duration (Krakauer et al. 2005; Orban de Xivry and Lefèvre 2015; Roemmich and Bastian 2015). Thus there are open questions on how these two parameters of initial training collectively influence adaptation savings.

In the present study, we examined the effects of training duration and washout on 24-h motor adaptation savings using a force-field paradigm. We were interested in the earliest possible expression of savings, that following a single trial of exposure. Thus we structured the start of each training session with a perturbation trial flanked by two trials that measured the temporal force patterns before and after the perturbation (Gonzalez Castro et al. 2014; Joiner et al. 2017; Sing et al. 2009, 2013; Wu et al. 2014). Two main subject groups were studied, one that did not complete washout trials at the end of day 1 (without washout) and one that did complete washout (with washout). Within each of these main groups there were four subgroups based on the duration of training on the first day (15, 30, 90, or 160 training trials). After training on day 1, all subjects experienced a 24-h break and returned to complete the same second training session on day 2. Utilizing the structured initial training sequence described above, we compared initial single-trial adaptation on day 1 with initial single-trial adaptation on day 2. We found that single-trial adaptation scaled with training duration for both the without-washout and with-washout groups. However, completing the washout at the end of day 1 significantly decreased the magnitude of savings for all training durations. Importantly, by examining the temporal force patterns, we quantified how closely the force profiles after a single exposure on day 2 matched those at the end of training on day 1. Interestingly, we observed that the force pattern of without-washout subjects trained at the longest duration (160 trials) completely matched the previously applied force pattern after a single perturbation exposure on day 2. However, this memory was reduced when 1) the training duration was decreased and 2) subjects completed a washout session on day 1, suggesting that these two features of initial training significantly influenced the rapid recall of the previously acquired motor memory.

MATERIALS AND METHODS

Participants.

One hundred twelve healthy subjects (75 men and 37 women, 26 ± 0.46 yr of age) with no known neurological disorders or impairments were recruited for this study. All participants were right-hand dominant and used this hand to perform the task throughout the entirety of the experiment. Each participant only performed a single experimental paradigm and was naive to the task. The study protocol was reviewed and approved by the George Mason University Institutional Review Board, and all participants provided written informed consent.

Experimental design.

Participants were seated in an adjustable chair directly in front of the robotic manipulandum (KINARM End-Point Lab; BKIN Technologies) at a height where their forehead could rest comfortably on the system’s headrest. A horizontal mirror display occluded the subject’s view of the right forearm to limit feedback of the upper limb and hand position to only what was observed on the screen. Visual feedback from the task was projected onto the mirror from a downward-facing LCD monitor positioned directly above. Participants gripped the right handle of the robotic manipulandum and made point-to-point reaching movements to two red circular targets 0.6 cm in diameter, placed 10 cm apart on the sagittal axis of the body. During movements, the manipulandum continuously measured hand position, velocity, and forces applied by subjects while simultaneously exerting external forces at a sampling rate of 1,000 Hz.

The centers of the two targets were positioned at 20 and 30 cm from the body, lying in the same x-position (Fig. 1A). Movement from the 20- to 30-cm target is considered to be in the 90° direction, whereas movement from 30 to 20 cm is 270°. Continuous position of the hand was indicated by a solid white circular cursor 0.1 cm in diameter. During each trial, participants were given visual and auditory feedback of their performance. Trials were marked successful if 1) movements had a maximum velocity within a range of 0.25–0.35 m/s, 2) movement duration was <750 ms, and 3) the final position was maintained inside the goal target for at least 500 ms. When each target was reached, the color changed to red, green, or yellow to indicate whether the movement speed was too fast, within the limit, or too slow, respectively. Additionally, trials in which movements accomplished the successful criteria were reinforced with a brief tone. This feedback allowed participants to adjust their movements to obtain as many successful trials as possible (i.e., green targets accompanied by the tone). The end point of each movement subsequently became the starting point of the next movement in such a way that the back and forth movements were made almost consecutively, with a 500-ms pause between the time the target was reached and the next target appeared. Once the new target appeared, subjects were allowed 75–2,000 ms to start the movement. Otherwise, the screen reset and the trial was repeated. Finally, at the end of each block of movements, a performance score, the percentage of successful trials only for 270° movement direction, was displayed. Subjects were not aware of how this calculation was made and were only informed to make as many successful movements in both reaching directions as possible. All subjects were instructed to achieve a value of at least 50% by the end of the baseline period to proceed with the study.

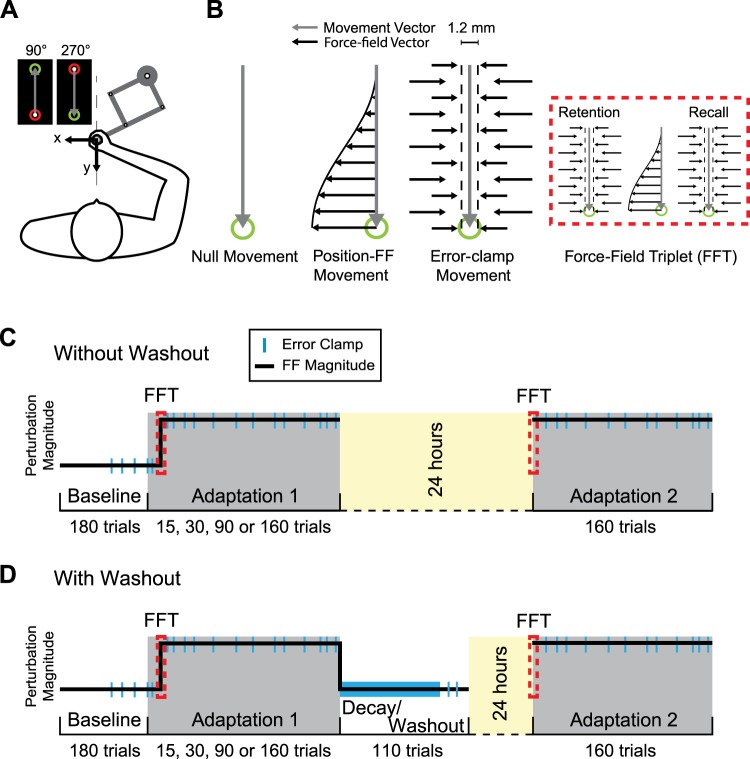
Fig. 1.

Experimental setup and protocol. A: subjects made reaching movements from midline in the forward (90°) and backward (270°) directions while holding the handle of a robotic manipulandum. The location of the hand was represented by a filled white circle. Subjects made reaching movements to move the cursor between 2 targets, the red and green circles. B: there were 3 types of movements studied. Null movements were made in the absence of any force from the robot. On position force-field (pFF) movements, the robot applied lateral forces (horizontal small black arrows) that scaled with hand position with respect to the start position. During error-clamp (EC) movements, the manipulandum constrained the movement trajectory between the 2 targets by countering any lateral motions. The force-field triplet (FTT) consisted of a single pFF flanked by 2 EC to assess single-trial adaptation. On day 2, the first EC was a measure of retention whereas the second was a measure of recall following the single exposure to the pFF. C and D: experimental protocol for the without-washout (C) and with-washout (D) groups. The main difference between groups was the completion of a washout period following adaptation on the first day of training. All subjects first completed a baseline period, during which they experienced null movements with sparse instances of EC movements (blue bars). Within the 2 main groups (without washout and with washout), there were 4 subgroups based on the duration of initial training (15, 30, 90, or 160 adaptation trials). On the first and second day of training, subjects experienced the FFT at the start of training (within the red dashed box). Unlike subjects in the without-washout group that ended day 1 after the adaptation period, subjects in the with-washout group completed a series of EC (thick blue bar) and null trials to washout the motor adaptation before the 24-h break. On day 2, all subjects completed the same training period that started with a FFT.

Experiments were divided into three main periods: baseline, adaptation, and washout (if appropriate). These different periods are described below. Throughout the experiment there were three trial types (Fig. 1B). First, in null trials, the motors of the robotic arm were turned off, allowing participants to move freely to each target. Second, during force-field (FF) trials, the robot applied a force that was perpendicular and proportional in magnitude to the position of the hand movement (position-dependent force field, pFF). [Previous work has shown that the initial learning in response to a pFF is more rapid compared with that in response to a velocity-dependent perturbation (Hosseini et al. 2017; Sing et al. 2009). We elected to use pFFs in the current study because we wanted to have comparable levels of learning after only a few trials of training (15). This also allowed us to rule out differences in initial learning levels on day 1 when examining relearning on day 2.] Full compensation to the imposed perturbation required participants to apply a force that was equal and opposite in magnitude to the force applied by the robot. The relationship between the amount of force applied to the hand and the participant’s instantaneous hand position, in regard to the start and end points, was determined by Eq. 1:

$$\begin{array}{cc}\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=c_K.\left[\begin{array}{cc}0& -K\\ K& 0\end{array}\right].\left[\begin{array}{c}x\\ y\end{array}\right],& \hspace{0.17em}K=45\frac{N\cdot s}{m}.\end{array}$$ (1)

In Eq. 1, c_K = ±1, where c_K = +1 and c_K = −1 correspond to the clockwise and counterclockwise directions of the force field, respectively (an example of a clockwise force field is shown in Fig. 1B). The force field was only applied in the 270° movement direction. The last trial type was error-clamp (EC) trials, where the robot constrained movements in a straight line between the two targets (Fig. 1B). Horizontal displacement from the straight path was limited to 1.2 mm by applying a stiff one-dimensional spring (6 kN/m) and a damper (150 Ns/m) in the axis perpendicular to the hand movement (Joiner and Smith 2008). EC trials were dispersed pseudorandomly to probe and measure the level of adaptation throughout the experiment.

Importantly, the ability to measure the initial adaptation and subsequent recall after a single force-field trial was integrated into the paradigm. We used the sequence EC-pFF-EC to measure the response to a single pFF trial (Fig. 1B, inset); this pattern is hereafter referred to as a force-field triplet (FFT; Gonzalez Castro et al. 2014; Joiner et al. 2017; Sing et al. 2009, 2013; Wu et al. 2014). Through this task structure, lateral forces applied immediately before and after the introduction of one pFF trial were carefully measured on the first (initial adaptation) and second (recall) day of training. Specifically, on the second day of training, the first EC measured retention whereas the second EC assessed recall of the motor learning (Fig. 1B).

Experimental task.

We trained participants to make point-to-point reaching movements in the 90° and 270° directions over 2 consecutive days, with a 24-h break period in between. There were eight groups of subjects, with 14 subjects per group. Each subject experienced the same basic experimental paradigm shown in Fig. 1, C or D. The major differences in the paradigm between subject groups were the duration of initial training on day 1 (15, 30, 90, or 160, trials) and whether this training was followed by a decay and washout period before the 24-h break (with washout or without washout). Thus each group was defined by the duration of training and the presence or absence of a washout period on day 1 (e.g., 30 trials, without washout). The structure of the experimental paradigm on day 2 was the same for all subjects, and subjects were only trained in the 270° movement direction. Thus “trial” refers only to movements in the 270° movement direction. Although the sign (direction) of the pFF remained constant for each subject, the pFF direction was counterbalanced between subjects; each group had seven subjects that experienced the counterclockwise pFF and seven subjects that experienced the clockwise pFF. Subjects were free to take a break or continue with the experiment between blocks during the baseline period. However, once the adaptation and (if experienced) decay periods started, we limited breaks between blocks to a maximum of 2 min.

On day 1, all subjects first completed 180 trials divided into four baseline blocks. The first two blocks consisted of 40 trials each, and the last two blocks contained 50 trials. In each of the last two blocks of trials, five EC trials were pseudorandomly interspersed to measure the baseline levels of forces for each subject. The average lateral forces during these 10 EC trials were then subtracted from the forces applied on EC trials during the adaptation and (if experienced) decay periods.

Following the baseline period, all subjects experienced the first adaptation period (Adaptation 1 in Fig. 1, C and D) during which the force-field environment was suddenly introduced after an initial 14 null and EC trials (only the 10th trial was an EC trial). We designed this initial adaptation block to capture the single-trial adaptation with the FFT. In this case, the 15th trial of the block was the first EC trial of the FFT, the 16th trial was a pFF trial, and the 17th trial was the second EC trial of the FFT. Depending on the group, subjects then completed 15, 30, 90, or 160 trials of training (note that once the perturbation was introduced, all 90° movements were made under the EC condition). For all subjects, for the first 9 training trials, the ratio of force-field (pFF) to error-clamp (EC) trials was 2 pFF:1 EC and then 5 pFF:1 EC. The ratio for the training for the longer duration subject groups was reduced to 5 pFF:1 EC for the remaining trials to measure the adaptation level at different points in training.

The above details apply for the four subject groups without washout (Fig. 1C). The four subject groups that did complete a washout on day 1 (Fig. 1D) experienced a final decay transition block of 73 trials. This block started with 13 training trials. For the first 6 trials, there was a ratio of 5 FF:1 EC, which increased to 4 FF:3 EC for the last 7 trials to obtain an accurate measure of final adaptation levels. These 13 trials were then followed by 60 consecutive EC trials. We refer to these 60 EC as decay in Fig. 2B, during which the adaptation decayed to the baseline levels before the force field was experienced. We used 60 consecutive EC trials to measure adaptation decay to keep this experimental block within a reasonable duration and to avoid breaks and possible cognitive influences during the transition to the decay period. To further ensure performance returned to baseline levels, an additional 50 trials (a combination of null and EC trials; washout in Fig. 2B) were presented before the conclusion of the experiment on day 1 (Fig. 1D). Throughout these 50 trials, we pseudorandomly interspersed 5 EC trials (a ratio of 9 null:1 EC) to measure the final adaptation levels toward the end of these null trials.

Fig. 2.

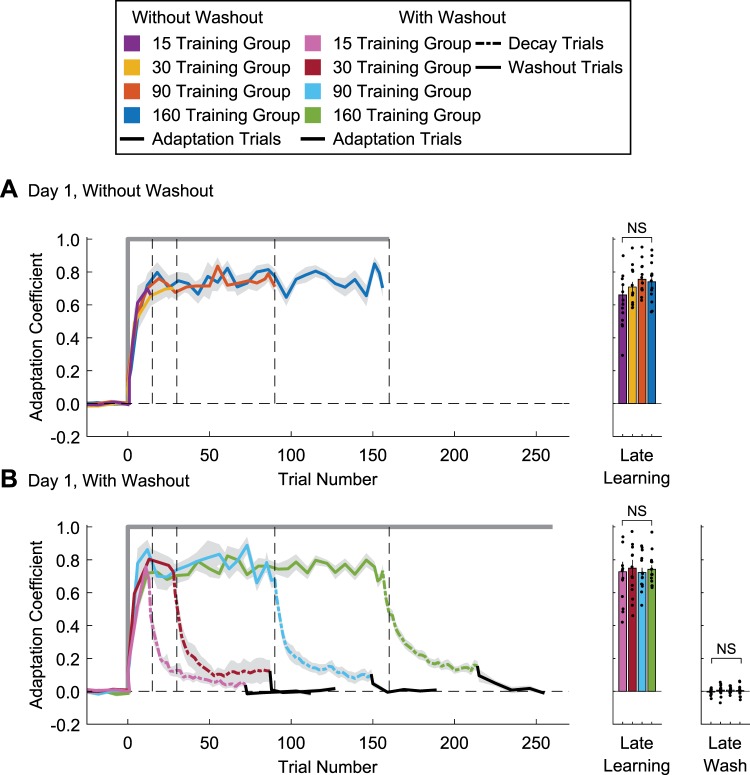
Adaptation on day 1 of training. The adaptation coefficient is plotted as a function of trial number for the without-washout (A) and with-washout (B) groups. Solid traces represent mean adaptation levels during training, dashed lines are mean adaptation levels during the consecutive error-clamp (EC)/decay trials, and black traces are mean adaptation levels during the null/washout trials. The level of adaptation for late learning (asymptotic values, last 10% of training) and at the end of the washout period (final 3 interspersed EC trials) are shown for the respective groups in the bar graphs. Shaded areas for the learning curves and vertical lines for the bar graphs represent SE. Black circles represent individual data points. NS, no significant difference.

All participants returned to complete the second day of the experiment after 24 h. As stated above, all subjects experienced the same task structure on day 2. Importantly, subjects did not receive baseline null trials before exposure to the perturbation on day 2 of training. Instead, the training schedule immediately began with an FFT (Fig. 1, C and D), to measure single-trial adaptation and possible recall, before proceeding to the remainder of the training blocks. Following the FFT, subjects completed 160 training trials (Adaptation 2 in Fig. 1, C and D). Note that the direction of the perturbation (clockwise vs. counterclockwise) remained the same for each subject over the 2 days.

Analysis of force profiles.

Throughout all parts of the experiment, EC trials were dispersed to measure the lateral forces participants applied to compensate for the position-dependent robotic perturbation. Here, only EC trials in the 270° direction were used for analysis. We assumed that the lateral force profile exerted during EC trials gave predictive feedforward measurements of the adaptation to the perturbation. To fully compensate for the applied perturbation, a lateral force that is proportionally equal and opposite in magnitude to the movement position has to be applied. The ideal force pattern was computed by the position movement kinematics during EC trials. Each individual trial was then centered, based on the peak velocity, with a temporal window of 1,200 ms (±600 ms); this window ensured the complete movement was captured. The linear regression coefficient of the force applied laterally by subjects to the ideal force was determined to quantify an adaptation coefficient value on any given trial (Hosseini et al. 2017; Joiner and Smith 2008; Joiner et al. 2011, 2013, 2017; McKenna et al. 2017; Sing et al. 2009; Wagner and Smith 2008). To counter any initial biases (measured from preadaptation ECs placed throughout baseline blocks), mean baseline force profiles were subtracted from subsequent force profiles recorded on an individual basis (Gonzalez Castro et al. 2014; Hosseini et al. 2017; Joiner and Smith 2008; Joiner et al. 2011, 2013, 2017; McKenna et al. 2017; Sing et al. 2009). We computed the adaptation coefficient for each subject during both the adaptation and (if experienced) decay periods and averaged the values over all subjects. We operationally defined late adaptation on day 1 as the last 10% of training trials. For example, we examined all EC trials within the last 16 trials for the 160 training groups and within the last 2 trials for the 15 training groups.

Statistical analysis.

Offline statistical data analysis was done in MATLAB and R using the statistical packages lmerTest (Kuznetsova et al. 2017) and lsmeans (Lenth 2016) on trials that met the speed, duration, and position criteria listed above. (Note that discarded trials that did not meet the criteria above affected the degrees of freedom listed for some of the statistical tests.) To compare adaptation levels at various stages of training on day 1 and day 2, we used different statistical methods. For example, when differences in adaptation levels in the same experiment session (e.g., day 1) were examined, a two-way ANOVA with two between-subject factors (duration: 15, 30, 90, 160 trials; washout condition: with or without) was used to report main effects and interactions. If significant results were found, we further investigated significance and corrected for multiple comparisons using a Bonferroni post hoc test. When adaptation was compared over 2 consecutive days, a linear mixed model was used because of the repeated measurements of the same subjects and exclusion of discarded (based on the exclusion criteria) movement data. We assumed that the main effects (training duration, washout group, testing day) were fixed, and random effects were added for subjects and the interaction with testing days, which takes into account the variability of the subjects across the 2 testing days [model in MATLAB/R syntax: single-trial adaptation ~duration × washout group × day + (1|subject) + (1|day:subject)]. The model was estimated using the restricted maximum likelihood method (REML), and significance was determined for fixed effects using Kenward-Roger methods for approximations for degrees of freedom for F-tests (R package lmerTest). The percent recall on day 2 (see Fig. 6) was quantified by determining the slope of the regression (linear mixed-effects model) between the late-adaptation force profile on day 1 and the force profile on the second EC trial of the FFT on day 2. In this case, the model took the form FP day2 ~FP day1 + (1 + FP day1|subject). The random effects of the subjects for the recall were taken into consideration in the model. Note that similar results were also obtained through a principle component analysis of the two force profiles. The regression slope was computed for each subject and scaled by 100 to obtain a percentage of recall. Finally, to compare the recall across training duration and washout group, we fit two linear mixed effects models for the force profile for all subjects on day 1 and day 2 [FP day2 ~FP day1 + (1 + FP day1 | subject) and FP day2 ~FP day1 × duration × washout group + (1 + FP day1 | subject)]. We then compared the two models and determined the effects of training duration and washout group on the recall using likelihood ratio tests. Pairwise comparisons were performed with Bonferroni correction using R package lsmeans. For all tests, the significance level was 0.05 and data are means ± SE.

Fig. 6.

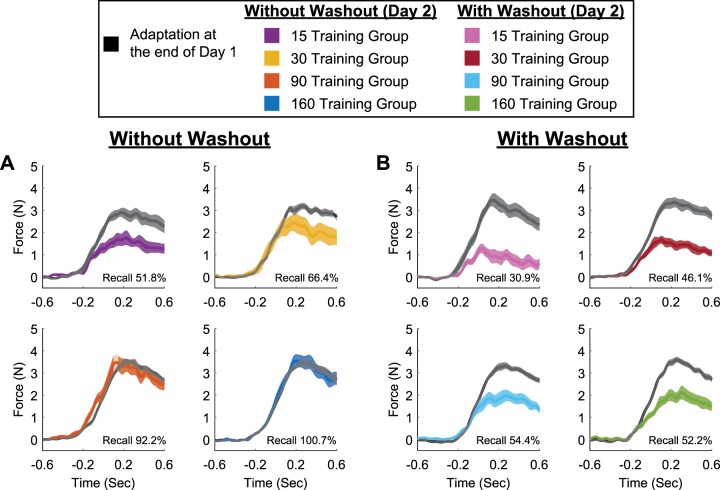
Recall of novel movement dynamics following a single perturbation. Temporal force profiles are shown on day 1 and day 2 of training for the without-washout (A) and with-washout (B) groups. Black traces represent asymptotic performance on day 1, whereas colored traces represent the initial single-trial performance on day 2. Background shading represents SE. Percentages represent the recall by comparison of the temporal force profiles on days 1 and 2.

RESULTS

In this study, our aim was to probe how two features of the initial adaptation to novel movement dynamics influenced the early readaptation rate following a 24-h break period. We were specifically interested in how the training duration and final adaptive state on the first day (day 1) of training affected early motor adaptation on the subsequent second day (day 2) of reexposure. There were two main groups, one that did not complete washout trials at the end of day 1 (without washout; see Fig. 1C) and one that did complete washout trials to return performance to baseline levels before day 2 (with washout; see Fig. 1D). The subjects in both groups experienced pFF perturbations, but the duration of training on day 1 varied (15, 30, 90, or 160 training trials), resulting in four subgroups within each of the main with-washout and without-washout groups. Importantly, following the 24-h break, all subjects returned to complete the same experimental session on day 2. Similar to the initial training on day 1, the session on day 2 immediately began with an FFT (see materials and methods and Fig. 1B), which allowed the quantification of the earliest effects on readaptation after a single perturbation (i.e., the recall).

Final adaptive state at the end of initial day 1 training.

On day 1 we trained subjects to make arm movements when pFF perturbations were applied during the reaching motion (Fig. 1, A and B). EC trials were used to quantify the lateral forces participants applied to compensate for the pFF (see materials and methods). Based on the data from these trials, we were able to determine the adaptation coefficient (see materials and methods) to quantify the time course of motor learning. As described above, there were two main groups (trials without washout and trials with washout on day 1) and four subgroups based on the training duration on day 1 (15, 30, 90, or 160 training trials). A two-way ANOVA examining two between-subject factors of training duration and presence of washout showed that the average ACs within both without-washout and with-washout groups during baseline on day 1 were not significantly different from each other [training duration: F(3,104) = 0.42, P = 0.74, ${\eta }_p^2$ = 0.012; presence of washout: F(1,104) = 0.51, P = 0.48, ${\eta }_p^2$ = 0.005; interaction of the two factors: F(3,104) = 0.64, P = 0.59, ${\eta }_p^2$ = 0.018]. These baseline values were also not significantly different from zero [without washout: 15 trials: −0.004 ± 0.004, 95% confidence interval (CI) (−0.013, 0.004); 30 trials: −0.004 ± 0.006, 95% CI (−0.018, 0.009); 90 trials: −0.002 ± 0.006, 95% CI (−0.016, 0.012); 160 trials: −0.004 ± 0.004, 95% CI (−0.012, 0.005); with washout: 15 trials: 0.002 ± 0.004, 95% CI (−0.007, 0.010); 30 trials: 0.004 ± 0.005, 95% CI (−0.006, 0.014); 90 trials: −0.003 ± 0.005, 95% CI (−0.013, 0.007); 160 trials: −0.007 ± 0.004, 95% CI (−0.015, 0.002)]. Similar to previous studies (Hosseini et al. 2017), for all groups we observed a fast progression of adaptation to the pFF within the first 15 trials (Fig. 2). A two-way ANOVA was used to examine the effect of training duration and presence of washout on late adaptation levels (average of the last 10% of the respective training trials; see materials and methods). The main effects of training duration or washout on late adaptation were not significant [F(3,103) = 0.53, P = 0.66, ${\eta }_p^2$ = 0.016 and F(1,103) = 0.40, P = 0.53, ${\eta }_p^2$ = 0.004, respectively]. Furthermore, there was no significant interaction between the two main effects [F(3,103) = 0.54, P = 0.66, ${\eta }_p^2$ = 0.016]. Despite the wide range of exposure durations, the adaptation levels during late training were similar across all groups (without washout: 15 trials: 0.66 ± 0.06; 30 trials: 0.71 ± 0.03; 90 trials: 0.76 ± 0.03; 160 trials: 0.74 ± 0.03; with washout: 15 trials: 0.73 ± 0.06; 30 trials: 0.75 ± 0.05; 90 trials: 0.72 ± 0.03; 160 trials: 0.74 ± 0.03).

Subjects in the with-washout group completed a series of EC/decay (dashed lines in Fig. 2B) and null/washout trials (black traces in Fig. 2B) to return performance to baseline levels before the second day of training. The final three interspersed EC trials during the washout period showed that adaptation levels were not significantly different between training durations [1-way ANOVA: F(3,52) = 0.64, P = 0.59, ${\eta }_p^2$ = 0.036] nor significantly different from zero [with washout: 15 trials: −0.005 ± 0.005, 95% CI (−0.016, 0.006); 30 trials: 0.007 ± 0.008, 95% CI (−0.011, 0.025); 90 trials: 0.007 ± 0.005, 95% CI (−0.003, 0.018); 160 trials: 0.004 ± 0.009, 95% CI (−0.014, 0.023)]. Thus, at the end of day 1, subjects in the without-washout group reached comparable levels of adaptation, whereas subjects in the with-washout group returned to similar initial baseline levels before the 24-h break.

Single-trial adaptation on day 2 is dependent on the initial training duration and the final adaptive state on day 1.

Figure 3 plots the first 15 trials subjects completed on day 2 of training to closely examine the time course of readaptation (A, without washout; B, with washout). Subjects first completed an FFT (see materials and methods and Fig. 1B), which consisted of a single pFF trial flanked by two EC trials. The first EC trial (trial 1 in Fig. 3, A and B) assessed initial retention of the adaptation from day 1. The second EC trial (trial 3 in Fig. 3, A and B), when compared with the first, quantified the single-trial adaptation, the earliest assessment of savings. A two-way ANOVA was used to investigate the impact of the two between-subject factors on retention levels. We found a significant difference in the adaptation coefficient between the without-washout and with-washout groups [F(1,92) = 12.24, P < 0.001, ${\eta }_p^2$ = 0.117], whereas no main effect or interaction with training duration was found [F(3,92) = 1.49, P < 0.23, ${\eta }_p^2$ = 0.046 for main effect of training duration; F(3,92) = 0.98, P = 0.41, ${\eta }_p^2$ = 0.031 for the interaction]. In addition, the Bonferroni post hoc method was used to further investigate the significant impact of the presence of the washout. Although, in general, we observed a greater retention in the without-washout groups (15 trials: 0.06 ± 0.02; 30 trials: 0.11 ± 0.06; 90 trials: 0.19 ± 0.05; 160 trials: 0.14 ± 0.07) compared with the with-washout groups (15 trials: −0.001 ± 0.03; 30 trials: 0.02 ± 0.02; 90 trials: 0.004 ± 0.01; 160 trials: 0.08 ± 0.02), we only found a significant difference in the adaptation coefficient between the two washout conditions for training at the 90-trial duration (P = 0.04).

Fig. 3.

Comparison of single-trial adaptation across consecutive days of training. Learning curves are shown over the first 15 trials on day 2 for the without-washout (A) and with-washout (B) groups. The first and second data points represent the first and second error-clamp (EC) trials of the force-field triplet (FFT). Bar graphs summarize adaptation retention (first EC trial of the FFT), single-trial adaptation (second EC trial of the FFT), and adaptation level over trials 11–15. Vertical lines are SE. Black circles represent individual data points.

Immediately following the first experienced pFF trial, we observed a rapid increase in the adaptation coefficient for both groups. Similar to the retention results, the adaptation coefficient on this trial was greater for the without-washout group. Additionally, for both the without-washout and with-washout groups, we did find a significant difference in the adaptation coefficient following the perturbation across the different training durations [without washout: 15 trials: 0.37 ± 0.06; 30 trials: 0.52 ± 0.10; 90 trials: 0.73 ± 0.07; 160 trials: 0.75 ± 0.07; with washout: 15 trials: 0.21 ± 0.06; 30 trials: 0.34 ± 0.04; 90 trials: 0.44 ± 0.05; 160 trials: 0.44 ± 0.05; 2-way ANOVA: F(1,102) = 26.2, P < 0.001, ${\eta }_p^2$ = 0.204 for the main effect of washout group; F(3,102) = 9.66, P < 0.001, ${\eta }_p^2$ = 0.221 for the main effect of training duration], but there was no interaction between the two factors [F(3,102) = 0.72, P = 0.54, ${\eta }_p^2$ = 0.021]. Bonferroni post hoc results showed that for the main effect of training duration, longer training duration (90 and 160 trials) lead to significantly greater retraining levels compared with shorter training duration (15 trials) in the without-washout group (P < 0.007 and P < 0.002, respectively). For the main effect of washout, longer training duration (90 and 160 trials) showed greater retraining in the without-washout group compared with the with-washout group (P = 0.048 and P = 0.017, respectively).

Soon after the FFT, the adaptation levels across the four training duration groups merged (Fig. 3, A and B). By trials 11–15 there was no significant difference in the adaptation levels between the without-washout and with-washout groups or across the different training durations [2-way ANOVA: F(1,103) = 0.77, P = 0.38, ${\eta }_p^2$ = 0.074 for the main effect of washout group, F(3,103) = 0.42, P = 0.74, ${\eta }_p^2$ = 0.012 for the main effect of training duration, F(3,103) = 1.01, P = 0.39, ${\eta }_p^2$ = 0.029 for the interaction]. [Note that we use the trials 11–15 window due to the EC trials occurring randomly following the FFT (see materials and methods). The fourth value reported in the day 2 learning curve (Fig. 3, A and B) is the mean adaptation coefficient for EC trials within this window.] Thus the majority of the influence of training duration and final adaptive state on 24-h motor adaptation savings occurs very early into the training, after the first trial of exposure.

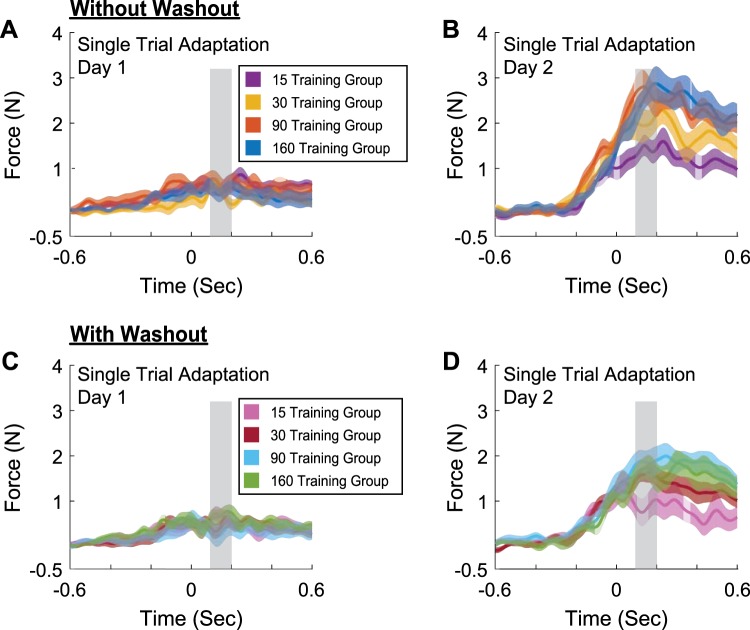
The temporal force profiles on day 1 and day 2 following the initial single pFF exposure are shown for the without-washout (Fig. 4, A and B) and with-washout groups (Fig. 4, C and D). Note that 0 ms corresponds to the midpoint of the movement (when the position profile crossed the 5-cm point of the 10-cm-long movement). Not surprisingly, the peak force levels of the adaptive response on day 1 was similar across the two groups and training durations. To quantify any potential differences between the temporal structures of the single-trial adaptive response, we analyzed the force data within a 100-ms window centered at 150 ms after the mid-movement point. We based this analysis on our previous study, which found that 150 ms after the mid-movement point provided a good measure of the adaptation specific to a pFF (Joiner et al. 2017). Analysis of the adaptive response within this window revealed no significant difference between the two groups and training durations [without washout: 15 trials: 0.58 ± 0.11 N; 30 trials: 0.46 ± 0.10 N; 90 trials: 0.65 ± 0.18 N; 160 trials: 0.50 ± 0.15 N; with washout: 15 trials: 0.66 ± 0.14 N; 30 trials: 0.45 ± 0.14 N; 90 trials: 0.33 ± 0.22 N; 160 trials: 0.70 ± 0.14 N; 2-way ANOVA: F(1,103) = 0.02, P = 0.89, ${\eta }_p^2$ = 0.0002 for the main effect of washout group, F(3,103) = 0.59, P = 0.62, ${\eta }_p^2$ = 0.017 for the main effect of training duration, F(3,103) = 1.07, P = 0.37, ${\eta }_p^2$ = 0.030 for the interaction). This was not the case following the single pFF on day 2. In this case there was a significant difference in the force magnitude between the two groups and across training durations [without washout: 15 trials: 1.42 ± 0.21 N; 30 trials: 2.00 ± 0.30 N; 90 trials: 2.68 ± 0.32 N; 160 trials: 2.62 ± 0.28 N; with washout: 15 trials: 0.87 ± 0.28 N; 30 trials: 1.59 ± 0.16 N; 90 trials: 1.86 ± 0.26 N; 160 trials: 1.66 ± 0.25 N; 2-way ANOVA: F(1,90) = 12.21, P = 0.007, ${\eta }_p^2$ = 0.120 for the main effect of washout group, F(3,90) = 0.79, P = 0.003, ${\eta }_p^2$ = 0.185 for the main effect of training duration]. No interaction between the two factors was found [F(3,90) = 0.4, P = 0.76, ${\eta }_p^2$ = 0.013]. The Bonferroni post hoc tests showed the force magnitude of the longer training durations (90 and 160 trials) in the without-washout group were significantly greater than the magnitude of the 15-trial training durations in the without-washout group (P < 0.044) and the with-washout group (P < 0.005). These data again indicate that the time course of the adaptive response on day 2 is influenced by the training duration and the completion of a washout period on day 1.

Fig. 4.

Initial force patterns following a single perturbation on days 1 and 2. Force profiles show the average temporal structure of the single-trial adaptive response on day 1 (A and C) and day 2 (B and D) for the without-washout (A and B) and with-washout (C and D) groups, where 0 ms corresponds to the midpoint of the movement (when the position profile crossed the 5-cm point of the 10-cm-long movement). The average force data within the shaded box (a 100-ms window centered at 150 ms after the mid-movement point) was used to compare differences in applied force. Background shading represents SE.

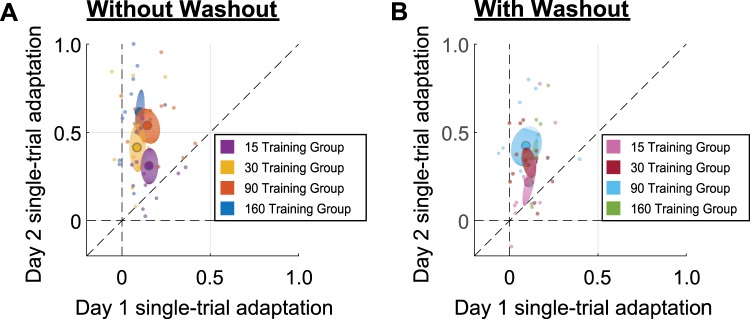
Figure 5, A and B, plots the single-trial adaptation on day 2 as a function of the single-trial adaptation on day 1. In this case we determined the difference between the second and first EC trials in Fig. 3, A and B, to quantify single-trial learning (day 1 without washout: 15 trials: 0.16 ± 0.03; 30 trials: 0.09 ± 0.02; 90 trials: 0.15 ± 0.04; 160 trials: 0.10 ± 0.03; day 1 with washout: 15 trials: 0.11 ± 0.02; 30 trials: 0.11 ± 0.02; 90 trials: 0.09 ± 0.04; 160 trials: 0.13 ± 0.02; day 2 without washout: 15 trials: 0.31 ± 0.05; 30 trials: 0.45 ± 0.07; 90 trials: 0.56 ± 0.05; 160 trials: 0.59 ± 0.06; day 2 with washout: 15 trials: 0.20 ± 0.06; 30 trials: 0.33 ± 0.04; 90 trials: 0.43 ± 0.05; 160 trials: 0.37 ± 0.06). Plots depict the results of individual subjects and the mean and SE across subjects. For both groups the majority of the data are above the unity line, signifying that the single-trial adaptation on day 2 is greater than on day1 and demonstrating the savings of adaptation. Thus, even though subjects in the with-washout group 1) ended training on day 1 at an adaptation level that was not significantly different from initial baseline and 2) showed little retention at the start of day 2, these subjects still demonstrated savings in the adaptation when the perturbation was briefly presented for one trial.

Fig. 5.

Comparison of single-trial adaptation on days 1 and 2. The initial single-trial adaptation coefficient on day 2 is plotted as a function of that on day 1 for the without-washout (A) and with-washout (B) groups. Each small circle is the data for a single subject, and larger circles represent the mean across subjects for each subgroup. The dashed diagonal line represents the unity line, and shaded ellipses represent SE.

Next, we examined differences in single-trial adaption between the successive days of training using a linear mixed-effects model (see materials and methods). The analysis of variance for the model is summarized in Table 1. There was a significant difference in the single-trial adaptation between testing days (P = 0.012). The interaction between the testing day and training duration was also significant (P = 0.001). The post hoc test with Bonferroni correction showed that the single-trial adaptation was significantly different between 30, 90, and 160 training trials on the 2 testing days (P < 0.001).

Table 1.

Results from the linear mixed-effects model analysis

Predictor	F Statistic	P Value
Intercept	F(1, 189) = 12.219	0.0006*
Day	F(1, 189) = 6.314	0.012*
Group	F(1, 189) = 0.417	0.519
Duration	F(3, 189) = 0.548	0.650
Day × group	F(1, 189) = 0.298	0.586
Day × duration	F(3, 189) = 5.561	0.001*
Group × duration	F(3, 189) = 0.458	0.712
Day × group × duration	F(3, 189) = 0.821	0.484

Data are results of linear mixed-model analysis predicting single-trial adaptation from testing day and training duration, and the interaction between the two fixed effects. *P < 0.05, significant effects.

Reexposure to the perturbation prompts the recall of the learned movement dynamics.

The results described above, specifically, the final adaptive state near baseline on day 1 and low retention on day 2 for the with-washout group, suggest that the first trial of exposure on day 2 facilitated the rapid recall of the learned movement dynamics from day 1. To assess this directly, we compared the temporal force profiles at the end of day 1 (the last 10% of total training trials; see materials and methods) to the applied force profiles following the single-trial exposure on day 2. Figure 6A shows the respective mean force profiles for the without-washout group, and Fig. 6B shows the average force profiles for the with-washout group. As the training duration increases, the applied force patterns on day 2 closely match the temporal force profiles on day 1. For example, following the single-trial reexposure on day 2, the subjects in the without-washout group with 160 training trials applied a force pattern that is almost identical to that observed at the end of day 1, revealing near-perfect recall of the previously learned force pattern (Fig. 6A, bottom right). (Note that this was also the case on a subject-by-subject basis; a qualitative comparison showed that 11 of the 14 subjects in the without-washout group with 160 training trials displayed a temporal pattern of force on day 2 that approximately matched the magnitude of the force profile on day 1. However, subject-specific recall was difficult to distinguish in this task because of similarity in the force profiles across subjects. That is, due to the motion state dependence of the movement perturbation, the motor responses were similar in shape across subjects. Nevertheless, in terms of the response magnitude, we do see motor output on day 2 that is qualitatively similar to that on day 1 for subjects that demonstrated the largest recall, the without-washout 160-trials group.) To quantify the amount of recall on day 2, we determined the slope of the regression between the force profile on day 1 and the force profile on day 2 using a linear mixed-effects model (see materials and methods). The estimated recall across subjects is shown in each subpanel of Fig. 6, A and B. [Note that the adaptation coefficient results presented in Figs. 2, 3, and 5 are a comparison of the compensatory pattern of force and the ideal force pattern based on changes in limb position (see materials and methods). The comparisons in Fig. 6 are between the compensatory patterns of force on day 1 and day 2 for each training duration and washout group.] As with the adaptation coefficients, the percent recall for the without-washout group was significantly greater than that for the with-washout group (P < 0.001) and also increased with training duration (without washout: 15 trials: 51.8 ± 8.3%; 30 trials: 66.4 ± 9.7%; 90 trials: 92.2 ± 9.3%; 160 trials: 100.7 ± 8.8%; with washout: 15 trials: 30.9 ± 6.7%; 30 trials: 46.1 ± 7.2%; 90 trials: 54.4 ± 5.8%; 160 trials: 52.2 ± 6.2%). To compare the recall across training duration and washout group, we fit two linear mixed-effects models for the force profile for all subjects on day 1 and day 2 (see materials and methods). There was significant interaction between recall and training duration (P < 0.001). The interaction between recall and washout group was also significant (P < 0.001). The results showed that in the without-washout group, recall for longer training durations (90 and 160 trials) was significantly greater than recall for shorter training durations (15 and 30 trials; P < 0.04), and recall for the longer training durations (90 and 160 trials) was significantly different across the two washout groups (P < 0.03). Thus the results suggest that the rapid increase in adaptation following the single perturbation on day 2 (Fig. 3) is due to implementation of the same force pattern that was learned at the end of day 1 training, but this is modified by training duration and the washout of adaptation.

DISCUSSION

In this study we were interested in the extent the properties of the initial training (duration and the final level of learning) influenced the early savings of adaption to novel movement dynamics following a 24-h break. We specifically examined the earliest possible time point during relearning, the motor output following a single trial of reexposure, which we operationally defined as the recall of previous performance. In the experiment, subjects adapted reaching arm movements in response to a pFF on day 1 and then were retrained on the same perturbation following a 24-h break, on day 2. There were two main groups of subjects that differed in the presence or absence of a washout period at the end of day 1 (with washout vs. without washout). Within these two groups there were four subgroups of subjects based on the day 1 training duration (15, 30, 90, or 160 training trials). We assessed single-trial adaptation at the beginning of training on days 1 and 2 and show that this early assessment of savings scales with training duration. This duration-based modulation was observed 1) for similar asymptotic levels of learning at the end of day 1 adaptation (without-washout group) and 2) when learning levels were reduced back to initial baseline levels at the end of day 1 training (with-washout group). Interestingly, the temporal force profiles following the first perturbation experienced on day 2 matched the asymptotic performance at the end of day 1 for the longest training duration (160 trials, without washout). Additionally, the magnitude of the force profile systematically decreased with the training duration for the without-washout group and, surprisingly, also for the with-washout group. In fact, the washout period negated the benefit of extended day 1 training; recall for the longest duration training in the with-washout group (160 trials, 52.2 ± 6.2%) was approximately the same as for the shortest duration training in the without-washout group (15 trials, 51.8 ± 8.3%). Overall, the results suggest that 1) the rapid recall of the motor recalibration in response to novel movement dynamics largely accounts for the early increase in learning rate during readaptation, and 2) this recall is influenced by the initial training duration and final adaptive state of the prior training.

Separating adaptation retention from recall.

Although previous studies have examined the savings of motor adaptation to novel movement dynamics (Caithness et al. 2004; Coltman et al. 2019; Overduin et al. 2006; Richardson et al. 2006; Sarwary et al. 2013; Shadmehr and Brashers-Krug 1997), there is little known about the earliest stages of the relearning and the extent the temporal pattern of force during readaptation resembles previous performance. This is likely due to previous assessments of learning largely 1) relying on the analysis of the movement trajectories (e.g., perpendicular displacement) rather than the temporal force profile, 2) measuring adaptation over multiple movement directions, and 3) examining relearning over a window of the initial trials, likely confounding the retention of previous performance and the recall and readaptation to the perturbation. In the present study, we have shown that after 15 trials of reexposure to the pFF, adaptation levels were statistically indistinguishable between the different training durations and washout groups (Fig. 3, A and B, right). The fast convergence of the learning curves across the different subject groups reveals that the separation of retention and recall, and the ability to quantify initial differences in relearning rates, is difficult without the proper task structure. To address these issues, the arrangement of trials on day 2 was specifically designed to measure initial retention of the adaptation from day 1 (Joiner and Smith 2008) and to distinguish this from the earliest possible expression of savings, that following a single trial of exposure (see materials and methods; Gonzalez Castro et al. 2014; Joiner et al. 2017; Sing et al. 2009, 2013; Wu et al. 2014). This task structure is similar to a study by Malone and colleagues (2011) that investigated how different training schedules (a series of adaptation and washout periods vs. a prolonged training period) affected the memory of an adapted gait pattern. The authors defined the difference in the first stride across days of training as the recall of previous performance and distinguished this from the early readaptation period (strides 2–30). On the basis of this distinction, Malone et al. (2011) showed that the different training schedules influenced the readaptation of the gait pattern, but not the recall. These results, similar to those of the current study, demonstrate that the task structure can reveal interesting relationships within initial adaptation savings that may have previously been obscured.

Implications for computational modeling.

As described above, the majority of studies that examined the savings of motor adaptation for reaching arm movements have utilized tasks that manipulated movement visual feedback (Bédard and Sanes 2011; Cassady et al. 2018; Haith et al. 2015; Herzfeld et al. 2014; Huang et al. 2011; Huberdeau et al. 2015; Jiang et al. 2018; Krakauer et al. 1999, 2005; Leow et al. 2012, 2013, 2014, 2016; Miall et al. 2004; Morehead et al. 2015; Orban de Xivry and Lefèvre 2015; Tong et al. 2002; Villalta et al. 2015; Wigmore et al. 2002; Yin et al. 2016; Zarahn et al. 2008). Recent evidence suggests that there are concurrent explicit (e.g., based on aiming strategy) and implicit learning mechanisms (e.g., based on sensory prediction errors) that contribute to this type of motor recalibration (Bond and Taylor 2015; Mazzoni and Krakauer 2006; Taylor et al. 2014). Interestingly, recent studies suggest that the former is largely responsible for the savings for this type of motor recalibration (Haith et al. 2015; Morehead et al. 2015). Not surprisingly, state-space models that are centered on implicit, error-based learning mechanisms fail to capture some aspects of this type of motor recalibration, namely, findings for adaptation savings (Zarahn et al. 2008).

The interaction of these learning mechanisms during the adaptation to novel dynamics is likely different than that utilized to adjust for rotations of the visual feedback, complicating the interpretation of adaptation savings for physical dynamics within the context of the above-described studies. For example, there is evidence that adaptation to physical vs. visual perturbations involve at least partially distinct neural mechanisms (Krakauer et al. 1999; Rabe et al. 2009; Tanaka et al. 2009). In addition, previous indirect findings suggest initial recalibration to perturbations of movement dynamics is likely a more implicit process than adaptation to manipulated visual feedback (however, see also McDougle et al. 2015). First, previous work has shown that single-trial adaptation to novel dynamics is specific to the temporal pattern of the movement perturbation (Joiner et al. 2017), suggesting the briefly experienced movement error is used to determine an initial, likely implicit, state-dependent compensation. Note that the temporal specificity of this immediate response following a single perturbation [randomized in both type (velocity or position dependent) and direction] is likely too fast to reflect the formation of a cognitive strategy. Second, explicit cue-associated learning (e.g., color association with perturbation direction) is largely not effective for adaptation to physical dynamics unless the prompt itself is motion associated (e.g., motion direction or the motion of the other limb; Gupta and Ashe 2007; Hirashima and Nozaki 2012; Howard et al. 2012, 2013; Nozaki et al. 2006). This is very different from visuomotor learning, where cue-driven cognitive strategies can be very effective in reducing the movement error (Mazzoni and Krakauer 2006; Taylor et al. 2014).

Based on the evidence above, the adaptation to the physical perturbations used in the current study is likely the result of a more implicit driven adjustment in motor output compared with recalibration in response to manipulated visual feedback. However, based on current results, the retention and recall of this type of motor recalibration appear more complex. Largely consistent with previous work, the retention of adaptation to novel dynamics (Fig. 3, A and B) can be largely explained as the result of a two-state model, with retention following the predictions of a slow learning component (Joiner and Smith 2008). [Note that the relationship between retention and training duration was not exactly the same as that in Joiner and Smith (2008). Specifically, the retention for the longest training (160 trials) was less than that for the 90-training trial group. In addition to using different state-dependent perturbations (velocity vs. position), one important difference is that retention in the current study was determined over a single EC trial, whereas the result presented in Joiner and Smith (2008) was an average, likely reducing the noise associated with the small signal.] In addition, consistent with the two-state model, when washout was experienced at the end of day 1, there was little to no retention on day 2. However, contrary to the model prediction, after a single perturbation trial, both the with-washout and without-washout groups showed rapid savings. Although adaptation retention patterns are largely accounted for, the recall following a single perturbation trial is not easily captured by previous error-based models.

The results shown in this study suggest it is possible that both explicit and implicit learning mechanisms contribute to the savings of this type of short-term motor learning. As described above, the retention of adaptation is likely based on the previous implicit learning from day 1. In contrast, the recall may be based on more explicit mechanisms, relying on a stored memory of previous successful performance that is reexpressed when the error is again experienced. The recall results (Fig. 6) provide insight into the strength of this motor memory and the factors that modulate its magnitude (training duration and washout). Future computational work could take these relationships into account in formulating the strength of the contextual relevance of errors (Berniker and Kording 2011) or memory of errors (Herzfeld et al. 2014) to explain the recall results presented here. For example, one possibility is that the sensitivity to the movement perturbation on day 2 increases as a function of exposure (i.e., training duration) but decreases with both passive (i.e., the passage of time) and active unlearning (null trials). The results of Kitago et al. (2013) suggest that there is a complex interaction between active, movement-based decay and the passive reduction of the motor memory. Specifically, the slowest decrease in adaptation level occurred with the passage of time, but when subjects made consecutive movements within the same time frame, there was an additional decrease in the stability of the motor memory. Thus, if error sensitivity is indeed altered, recall of the adaptation could be differentially affected by the manner the adaptation is unlearned on day 1 (e.g., inactivity for a period of time or completing consecutive null trials over the same time duration). In the first case (passage of time), there could be a reduction in the neural connectivity changes that accompany learning. However, in the second case (completing consecutive null trials), a new association between motor action and sensory outcomes may be formed, and this may significantly interfere with the previous learning (Rescorla 2004). Therefore, additional studies are required to develop a computational framework that fully captures the current behavioral results (see below).

Dissociating the learning mechanisms involved in movement adaptation recall.

Despite the differences noted above, there are aspects of the previous findings for visual feedback adaptation paradigms that could assist in distinguishing the various learning mechanisms involved in the recall of adaptation to novel dynamics. First, Huang et al. (2011) demonstrated that savings for a visuomotor adaptation task can be explained by the recall of successful movements (see also Orban de Xivry and Lefèvre 2015). Specifically, the authors arranged the target locations for initial training and subsequent retraining such that opposite perturbation directions were countered by the same movement trajectory. That is, when subjects were retrained, the movement trajectory that brought the rotated cursor to the movement goal was the same as that during the initial training in the opposite perturbation direction. Interestingly, subjects demonstrated savings despite executing the movements in the opposite visuomotor rotation during retraining. The authors suggested that this savings of motor adaptation resulted from the rapid recall of the reinforced action, the recall of the repeated prior movement that led to success. These findings for visuomotor rotation could be relevant to the current results; it is possible that the early recall of the motor recalibration reflects the memory of repeated successful actions from day 1 training. In the current study we cannot address this possibility because we always used the same perturbation experienced on day 1 to test recall on day 2. In future studies it would be of interest to determine the extent the single-trial recall we have shown for adaptation to novel dynamics can be induced or modified with a nonexperienced/nonspecific movement perturbation, for example, one that is opposite the initially trained disturbance or one that contains no temporal information (e.g., a force pulse; Fine and Thoroughman 2006; Sing et al. 2013). As mentioned above, if recall is influenced by the contextual relevance of experienced errors (Berniker and Kording 2011), this study, in combination with modulation of the training duration and unlearning process (passage of time or completing consecutive null movements), would provide valuable insight into how this relevance is established and its stability.

Second, there is recent evidence that the time available for movement preparation influences adaptation savings, essentially dissociating the underlying mechanisms. Haith and colleagues (2015) examined the adaptation to rotated visual feedback when the movement preparation time (i.e., the time between the presentation of the movement goal and initiation of the reach) was high (1.5 s) or low (less than ~0.6 s). The paradigm intermixed these two trial types (high and low preparation time), allowing the authors to examine within each subject the initial adaptation and subsequent relearning under the two movement conditions. Interestingly, subjects demonstrated faster initial learning and adaptation savings under the high preparation time condition. The authors suggested that this difference in behavior reflects concurrent implicit and explicit learning mechanisms, which are revealed by the low- and high-preparation time conditions, respectively. [Note that the conclusion that savings in this task is due to an explicit aiming strategy is consistent with recent results by Morehead et al. (2015) that directly tested this hypothesis.] Thus the results of Haith et al. (2015) demonstrate that the time allowed to prepare movement differentially influences some learning components and suggest that implicit contributions can be observed by limiting the time available to prepare the reach. This temporal manipulation could be applied to the adaptation to novel dynamics to determine the extent this type of learning and memory formation is dependent on cognitive strategy vs. the utilization of sensory prediction errors.

Third is a clear definition of the role of the washout session on the recall of adaptation. As stated above, the washout period countered the effects of extended day 1 training; recall for 160 training trials in the with-washout group (52.2 ± 6.2%) was approximately the same as 15 training trials in the without-washout group (51.8 ± 8.3%). Consistent with previous studies, the completion of a series of nonperturbation trials (washout) following training influences the amount of savings during reexposure to the perturbation (Caithness et al. 2004; Krakauer et al. 2005; Villalta et al. 2015; Zarahn et al. 2008). Recently, Villalta and colleagues (2015) trained subjects in a visuomotor rotation task over several days. In the first condition, a washout session occurred on the same day as retraining, immediately before the 24-h reexposure to the perturbation. In the second condition, the washout session and retraining were on separate days, with the washout occurring 24 h before the reexposure. The authors found that increasing the time between the washout and retraining (from immediately to 24 h) significantly increased the savings of adaptation, suggesting that the washout immediately before retraining interfered with the relearning. To further examine these effects, Villalta et al. (2015) used a paradigm structure similar to the first condition and applied transcranial magnetic stimulation (TMS) to the sensorimotor cortex before the washout period. The authors showed that adaptation savings was increased by the stimulation, suggesting that TMS disrupted the possible interference of the motor memory retrieval caused by the completion of the washout trials. Given the role of the sensorimotor cortex in the formation and recall of motor memories (Galea and Celnik 2009; Hadipour-Niktarash et al. 2007; Li et al. 2001; Orban de Xivry et al. 2011; Richardson et al. 2006), it is possible that stimulation following training with novel dynamics but immediately before washout (with-washout condition, Fig. 1D) may disrupt the potential learning during this period. That is, the learning of a new association between motor action and sensory outcome during washout may be reduced by the stimulation and subsequently increase the magnitude of the recall on day 2. Furthermore, it is possible that TMS over the sensorimotor cortex before initial adaptation on day 1 will not impair learning, but will reduce recall 24 h later due to the TMS-induced instability during initial training (Richardson et al. 2006). Thus the application of stimulation before the initial training and washout periods on day 1 could assist in determining the influence of the washout period on the various learning mechanisms, and subsequently, the recall of adaptation to novel movement dynamics.

GRANTS

This work was supported by National Eye Institute Grant R00 EY021252 and National Science Foundation Grant 1553895 (to W. M. Joiner).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

L.C.J.B. and W.M.J. conceived and designed research; K.P.N., E.M., K.C.-C., L.C.J.B., E.A.H., L.A., and M.R. performed experiments; K.P.N., W.Z., K.C.-C., L.C.J.B., E.A.H., L.A., and W.M.J. analyzed data; W.Z., E.A.H., L.A., and W.M.J. interpreted results of experiments; K.P.N., W.Z., L.A., M.R., and W.M.J. prepared figures; K.P.N., W.Z., and W.M.J. drafted manuscript; K.P.N., W.Z., E.M., L.C.J.B., and L.A. edited and revised manuscript; K.P.N., E.A.H., L.A., and W.M.J. approved final version of manuscript.