A model-based reassessment of the three-dimensional tuning of head direction cells in rats

Abstract

In a recent study, Shinder and Taube (Shinder ME, Taube JS. J Neurophysiol 121: 4–37, 2019) concluded that head direction cells in the anterior thalamus of rats are tuned to one-dimensional (1D, yaw-only) motion, in contrast to recent findings in bats, mice, and rats. Here we reinterpret the author’s experimental results using model comparison and demonstrate that, contrary to their conclusions, experimental data actually supports the dual-axis rule (lson JJ, Jeffery KJ. J Neurophysiol 119: 192–208, 2018) and tilted azimuth model (Laurens J, Angelaki DE. Neuron 97: 275–289, 2018), where head direction cells use gravity to integrate 3D rotation signals about all cardinal axes of the head. We further show that the Shinder and Taube study is inconclusive regarding the presence of vertical orientation tuning; i.e., whether head direction cells encode 3D orientation in the horizontal and vertical planes conjunctively. Using model simulations, we demonstrate that, even if 3D tuning existed, the experimental protocol and data analyses used by Shinder and Taube would not have revealed it. We conclude that the actual experimental data of Shinder and Taube are compatible with the 3D properties of head direction cells discovered by other groups, yet incorrect conclusions were reached because of incomplete and qualitative analyses.

NEW & NOTEWORTHY We conducted a model-based analysis previously published data where rat head direction cells were recorded during three-dimensional motion (Shinder ME, Taube JS. J Neurophysiol 121: 4–37, 2019). We found that these data corroborate previous models (“dual-axis rule,” Page HJI, Wilson JJ, Jeffery KJ. J Neurophysiol 119: 192–208, 2018; and “tilted azimuth model,” Laurens J, Angelaki DE. Neuron 97: 275–289, 2018) where head direction cells integrate rotations along all three head axes to encode head orientation in a gravity-anchored reference frame.

INTRODUCTION

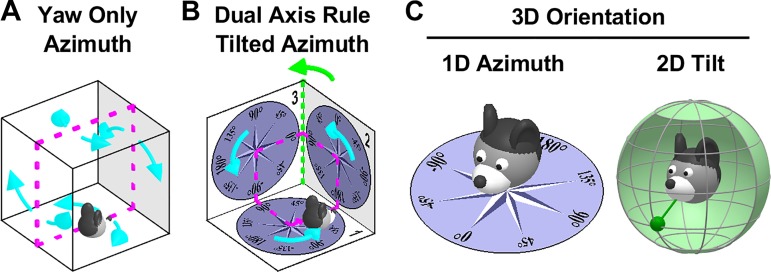
Head direction cells (HDC) track allocentric head orientation, similar to a “neuronal compass.” Since their discovery (Taube et al. 1990a, 1990b), most studies have focused on how HDC encode head orientation in the horizontal plane (azimuth) when animals explore horizontal surfaces. Initial studies during 2D motion concluded that HDC treat vertical walls as an extension of the floor (Fig. 1A) and postulated that the HDC system tracks head orientation by integrating yaw rotations (i.e., left/right rotations in the egocentric head-horizontal plane) exclusively (“Yaw-only,” YO, model; Fig. 1A; Calton and Taube 2005; Stackman et al. 2000). Furthermore, these studies observed that HDC lose their tuning when animals walk in an inverted orientation, e.g., on the ceiling in Fig. 1A.

Fig. 1.

Fundamental differences between the Yaw-only (YO) and tilted azimuth (TA) models. A: the YO azimuth model (Calton and Taube 2005; Shinder and Taube 2019) assumes that vertical surfaces are treated as extension of the floor. Azimuth is computed by integrating yaw (i.e., left/right, cyan) rotations only, irrespective of the allocentric orientation of the locomotion surface. This model is sufficient to track head orientation when walking on the floor, ceiling, and opposite walls of a cage (magenta). B: the difference between the YO and TA (Laurens and Angelaki 2018)/dual-axis rule (Page et al. 2018) model arises when movement is not restricted to 2D. In this example, the animal completes a closed-loop trajectory (magenta) that includes three left-hand yaw turns (cyan). The YO model cannot maintain allocentric consistency, as it will only register a total azimuth rotation angle of 270°, in contradiction with the fact that the animal has returned to its initial orientation. The “missing” rotation not registered by the YO model occurs when the animal transitions from surface 2 to 3 (green). This is the 2nd axis of the dual-axis rule: Tracking 3D orientation correctly requires updating azimuth also when the locomotion surface (or the head-horizontal plane) crosses vertical surfaces, i.e., during rotations about an earth-vertical axis. The equivalent TA model (Laurens and Angelaki 2018; see Fig. 3A for definition) assumes that azimuth is measured in the compasses drawn on the three surfaces and yields a correct total rotation of 360°. Thus, the YO model of Shinder and Taube (2019) and the TA/dual-axis model of Page et al. (2018) and Laurens and Angelaki (2018) are consistent with each other only when movement is restricted to 2D (e.g., magenta trajectory in A). The YO model would fail to track azimuth during 3D movements (as shown in B; see also Laurens and Angelaki 2018). Thus, by supporting the YO model, Shinder and Taube (2019) imply that the HD system will fail during 3D movements on the surfaces of a cube, which is inconsistent with experimental results (Page et al. 2018). C: decomposition of 3D orientation into 1D tilted azimuth and 2D tilt, as proposed by Laurens et al. (2016) and Laurens and Angelaki (2018). Azimuth measures 1D orientation relative to allocentric horizontal landmarks and has a circular topology. Tilt measures 2D orientation of the head relative to gravity, or equivalently the egocentric orientation of the gravity vector (left: green pendulum) and has a spherical topology. This model generalizes Finkelstein's toroidal (Yaw-Pitch) model (Finkelstein et al. 2015) to 3D.

Recent studies by several other groups, however, have shed additional insight about the 3D properties of HDC. Experimental (Angelaki et al. 2019; Page et al. 2018) and theoretical (Jeffery et al. 2013; Laurens and Angelaki 2018) studies have shown that HDC track azimuth by combining egocentric rotations about the head’s three cardinal axes, not only yaw, with gravity signals. This process, which has been called “dual-axis rule” in Page et al. (2018) and Fig. 1B and tilted azimuth (TA) model in Laurens and Angelaki (2018), was confirmed experimentally by HDC recordings in the anterior thalamus of rats (Page et al. 2018) and mice (Angelaki et al. 2019). Furthermore, a series of studies have shown that HDC in bats (Finkelstein et al. 2016), mice (Angelaki et al. 2019) and likely macaques (Laurens et al. 2016) can also represent head tilt, i.e., 2D head orientation in vertical planes (pitch and roll). By encoding 1D azimuth and 2D tilt conjunctively, the HDC system can thus represent 3D orientation (Fig. 1C).

Yet, a recent study of HDC in rats (Shinder and Taube (2019) has challenged the recent evidence for a 3D organization of the HDC system by resurrecting the YO model. Based on a series of 3D passive rotation protocols, the authors have reiterated the conclusions from previous studies, i.e., that HDC 1) are only efficiently updated by yaw rotations; 2) cease to encode azimuth when the head tilts more than 90° from upright; and 3) don’t exhibit any conjunctive response to azimuth and pitch or roll tilt (vertical orientation). These conclusions were made without quantitative analyses and model comparison.

Why do Shinder and Taube’s conclusions differ from recent findings in an array of mammalian species (Angelaki et al. 2019; Finkelstein et al. 2015; Page et al. 2018)? We have reexamined their data quantitatively using comparisons with model simulations and reached entirely different conclusions. Specifically, we find that 1) the HDC responses of Shinder and Taube (2019) cannot be predicted by the YO model, in direct conflict with their conclusion. On the contrary, we show that their experimental data are in fact supportive of the dual axis/TA model. Importantly, the YO and dual axis/TA models are mutually exclusive. The dual-axis rule, by definition, implies that 3D, not just yaw, rotation signals processed by gravity are necessary to update and maintain the azimuth tuning of HDC. We also find that 2) HDC measured by Shinder and Taube don’t cease abruptly to encode azimuth when head tilt exceeds 90°, but rather progressively, similar to our findings in mice (Angelaki et al. 2019).

Regarding their last conclusion, we also demonstrate that 3) the experimental protocol and data analyses used by Shinder and Taube (2019) entangle the tilt dependence of azimuth tuning and putative 2D tilt tuning in a way that would conceal the existence of tilt tuning, thus making their study essentially inconclusive in this regard.

Here we present this analysis, first focusing on azimuth coding by providing a quantitative comparison between predictions of the two azimuth (TA and YO) models (which Shinder and Taube never did). We next present model simulations demonstrating that, even if tilt tuning existed, it would not have been obvious using the authors’ experimental protocol and data analyses.

METHODS

In this study, we use a model-based approach to analyze the data in Shinder and Taube (2019) and test distinct hypotheses about how the HD system encodes 3D head orientation.

In this section, we first define various hypotheses of how HDC may encode azimuth during 3D motion. Next, we present a mathematical model of how azimuth-tuned HDC respond during 3D motion. Finally, we present a model of how conjunctive (azimuth + tilt) HDC tuning can be defined.

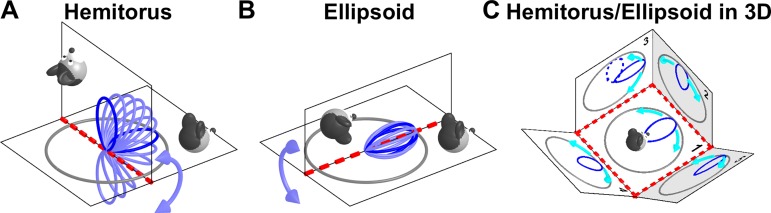
Shinder and Taube: HDC are tuned to azimuth only based on a YO model that leads to a hemitorus/ellipsoidal tuning scheme.

Shinder and Taube’s hypothesis (see also Stackman et al. 2000) is that:

• Property 1: Azimuth is computed by always integrating “primarily yaw” (head-fixed left-right) rotations (Fig. 1A, cyan; referred to as the “YO model”).

• Property 2: On sloped surfaces, a HD cell fires as if the surfaces were extensions of the floor.

• Property 3: Azimuth tuning is lost when animals are tilted more than 90° away from vertical in any direction, pitch or roll. Note that this property is not a form of 2D tilt tuning as meant by Angelaki et al. (2019), Finkelstein et al. (2015), Laurens et al. (2016), where individual HD cells respond preferentially to orientations scattered in 2D tilt space; but instead a global effect whereby all HDC cease to function when the animal is tilted more than 90° from upright.

To conceptualize the second and third properties, Shinder and Taube (2019) refer to a “hemitorus” [which, should be noted, is unrelated to Finkelstein et al.’s (2015) toroidal model] and “ellipsoid,” both illustrated graphically in Fig. 2. The hemitorus is produced by plotting the cell’s tuning curve in a polar plot on the head’s yaw plane (Fig. 2A, dark blue: response on the earth-horizontal and earth-vertical planes) as the head tilts ± 90° about an axis perpendicular to the preferred direction (PD) (Fig. 2A, red). Note that the hemitorus restricts head tilt to 90°, such as to imply the loss of tuning when the head is inverted [allowing the head’s horizontal plane to rotate fully (±180°) would form a full torus]. The ellipsoidal model follows a similar rationale (Fig. 2B), now describing tilts about an axis parallel to the PD (red line).

Fig. 2.

Hemitorus and ellipsoid schematics corresponding to the Yaw-only (YO) model. A: head direction cell (HDC) tuning curves at different head orientations between nose-up and nose-down (light blue) form a hemitorus when the tilt axis (red) is perpendicular to the cell’s preferred direction (PD). Dark blue: tuning curves when animal oriented as in the drawing. B: HDC tuning curves form an ellipsoid when the tilt axis (red) is now parallel to the cell’s PD. The orientations shown in A and B do not cover the full 3D space; therefore the YO model is incomplete and inadequate to maintain 3D orientation consistently, as shown in C. C: predicted tuning curves on multiple planes spanning 3D space. The plane marked “1” is earth-horizontal. The tuning curves shown on earth-vertical planes 2 and 3 are predicted by the hemitorus and ellipsoid YO model, respectively. The tuning curves on planes 4 and 5, which are tilted by 45°, are also predicted by same YO model (where azimuth is updated by yaw rotations only, cyan arrow) during transitions from plane 1. In fact, the YO model allows tracking azimuth accurately when the head stays in one plane or transitions between plane 1 and any other plane (a “null” rotation; see Fig. 3A). However, the YO model fails whenever the animal’s movement is such that updating azimuth requires use of the 2nd updating rule (rotation about an earth-vertical axis). The broken line on plane 3 shows the tuning curve that would result from transitioning from plane 2 to plane 3 based on the YO model. Note that the same physical orientation on plane 3 would be registered differently by the YO model depending on whether the animal originated from plane 1 or plane 2. Thus, the YO model would not maintain allocentric invariance when animals move in 3D.

Thus, Shinder and Taube make two arguments, which are related, but not equivalent: that HDC are only updated efficiently by yaw rotations (YO model; properties 1 and 2 above) and that the response of HDC follows the hemitorus/ellipsoidal model, which does not make explicit assumptions about how HDC cells are updated but encompasses properties 2 and 3.

An important point is that the YO model of Shinder and Taube (2019) would completely lose allocentric invariance for any movement that would bring the animal’s head outside these two planes (e.g., between planes 2 and 3 in Fig. 1B; Fig. 2C; see Laurens and Angelaki 2018 for details). This problem is illustrated by plotting the predicted firing rate of a HDC when the animal walks on a variety of planes (Fig. 2C). In this figure, the hemitorus is used to predict the tuning curves when the animal transitions between planes 1, 2, and 4 and the ellipsoid is used to predict the tuning curves when the animal transitions between planes 1, 3, and 5 (both movements within a combination of two planes). What would happen if the animal transitions between other pairs of surfaces that truly span 3D space? For example, when moving from plane 2 (where the tuning curve peaks when the animal faces “upward”) to plane 3, the YO model would not update; thus, the resulting tuning curve (Fig. 2C, broken blue line) would still point “upward.” But this would directly contradict the prediction of the ellipsoid model (solid line). Here lies exactly the problem with the YO model: it only works when transitioning between the earth-horizontal to an earth-vertical plane but cannot handle truly 3D reorientations and is not inherently consistent when movements are not restricted to rotations about axes either parallel (ellipsoid) or perpendicular (hemitorus) to HDC PDs.

Note also that the hemitorus and ellipsoid models are entirely incomplete in terms of 3D orientation: each covers a 2D range of movements (the hemitorus model deals with movements that can be expressed as pitch followed by yaw and the ellipsoid model deals with roll + yaw), and together the two models cover only two planar subspaces of the ensemble of 3D head rotations, leaving out most 3D orientations.

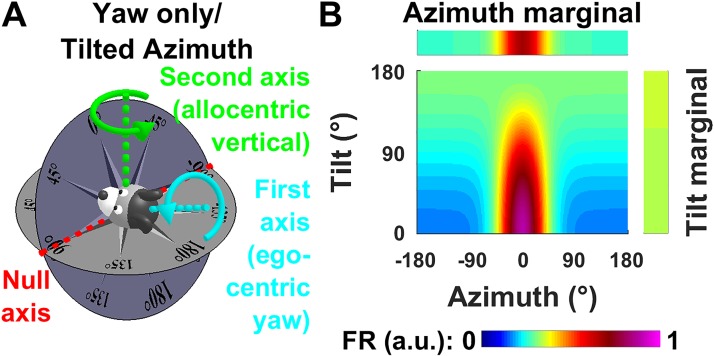
Tilted azimuth and the dual-axis rule.

Recent studies (Angelaki et al. 2019; Laurens and Angelaki 2018; Page et al. 2018) have proposed a “tilted azimuth” model (TA) defined at any 3D head orientation by placing a compass on the head-horizontal plane and orienting it such that it matches the earth-horizontal compass at the level of the line where the head-horizontal and earth-horizontal planes intersect (Fig. 3A, red, also called null axis, see below; see also animations in Supplemental Movies S1–S4, available at https://github.com/JeanLaurens/Modelling-3D-HD-Cell-Tuning). For instance, in Fig. 3A, both compasses read ±90° along this line. Further details about the TA and dual-axis rule models can be found in Laurens and Angelaki (2018) and Page et al. (2018). Note that the TA model also assumes that HD cells treat sloped surface as an extension of the floor but integrates 3D rotation signals when this surface moves to maintain allocentric consistency.

Fig. 3.

Tilted azimuth (TA)/dual-axis rule model and dependence of azimuth tuning on tilt angle. A: definition of the TA model. Azimuth is measured in a compass affixed to the head-horizontal plane (dark blue), oriented so that it matches the earth-horizontal compass (gray) along the intersection of both planes (null axis; red line). In this model, azimuth is updated both during head-fixed yaw rotations (cyan arrow) and by rotations around an allocentric vertical axis (green). This 2nd updating rule is necessary for the TA compass to maintain allocentric invariance (i.e., consistency with the earth-horizontal compass). Rotations about the null axis (red) don’t affect TA. Note that the TA and YO models are entirely distinct when considering 3D orientation, because the latter does not include the dual-axis rule and only updates during yaw rotations. B: model tilt-dependent azimuth tuning curve, with a preferred direction (PD) at 0° azimuth (magenta), illustrating tilt-dependent azimuth tuning strength. The marginal distributions indicate the average firing across all tilt angles (azimuth marginal) and across all azimuth (tilt marginal; which is uniform). Note that a tilt angle-dependent azimuth tuning results in an untuned tilt marginal (i.e., the model cell is not tuned to tilt). a.u., Arbitrary units; FR, firing rate.

In contrast to the YO model, azimuth in the TA model is updated using a dual-axis updating rule: 1) rotations about the head-vertical yaw axis (common with the YO model), as well as 2) rotations about the earth-vertical axis (Page et al. 2018; Fig. 3A). To maintain spatial consistency during 3D trajectories, both types of rotation should update azimuth orientation. One can formalize this rule by expressing rotation velocity in a frame formed by three axes:

• The first axis (Fig. 3A, cyan) is the egocentric yaw (head-vertical) axis.

• The second axis (Fig. 3A, green) is the allocentric yaw (earth-vertical) axis. Depending on 3D head orientation, this axis may coincide with the egocentric pitch axis (when the animal is tilted 90° ear-down), egocentric roll axis (e.g., when the head faces upward) or yaw axis (in the special cases when the head is upright or upside down, discussed in the last paragraph of this section), or in general may correspond to any combination of these axes.

• The third axis (Fig. 3A, red), called “null axis” (rotations about this axis do not change azimuth), is also defined in an allocentric frame. This axis is not described in the original formulation of the dual-axis rule and is introduced here as a useful concept for describing 3D trajectories. The null axis is orthogonal to the first and second axes (which are themselves not necessarily orthogonal) and therefore lies at the intersection of the head-horizontal and earth-horizontal planes.

In general, the three axes form a (nonorthogonal) reference frame. The dual-axis rule states that angular velocity must be expressed in this frame. The sum of rotation components along the first two axes (egocentric yaw and allocentric yaw) update TA (in contrast to YO azimuth, which is updated only with the first component). Only rotations about the null axis do not update TA.

Of course, when the head is upright, head-fixed yaw and earth-fixed yaw axes are identical, and a yaw rotation may be indifferently considered as a rotation along the first or second axes. Furthermore, neither pitch nor roll rotations update TA in this orientation (i.e., the null axis is replaced by a null plane). When the head is upside-down, the first two axes are opposite, the dual-axis rule breaks down, and TA is undefined.

Comparison between azimuth tuning models.

To summarize, the YO + hemitorus/ellipsoid and dual-axis rule + TA models have in common that azimuth is measured on a compass affixed to the head-horizontal plane, or in other words that HDC treat inclined surfaces as extensions of the floor. In fact, all these models are equivalent for a restricted range of 2D movements (i.e., those in Fig. 2, A and B with less than 90° tilt).

Beyond these similarities, the YO + hemitorus/ellipsoid and dual-axis rule + TA models differ in many respects:

• Since the YO model lacks the second axis updating rule, it predicts that HD responses will lose consistency during 3D rotations. The TA model can handle any 3D reorientation, but the YO model fails saliently.

• The hemitorus/ellipsoidal model is restricted to a narrow range of 2D movements and therefore can generally not be used to predict HDC responses during 3D motion. On the other hand, the TA model accounts for azimuth tuning throughout the 3D orientation space, other than upside-down.

• The hemitorus/ellipsoidal model incorporates the assumption that HD tuning vanishes abruptly when the head tilts more than 90° from upright. In contrast, in mice (Angelaki et al. 2019), we observed that the modulation depth of azimuth tuning curves decreases progressively and gradually when the head tilts away from upright. As will be shown here, quantitative analysis also reveals a similar result for the Shinder and Taube data in rats.

• Note, nevertheless, that the tilt-dependent attenuation of azimuth tuning is not a consequence of the TA model, but rather an independent property. This contrasts with the formulation of the hemitorus/ellipsoidal model, which is based on this assumption of abrupt transition from azimuth tuning to no tuning.

Thus, the two conclusions of Shinder and Taube (2019), i.e., that HD cells integrate primarily head-fixed, egocentric yaw rotation signals (YO model) and that they follow the hemitorus/ellipsoid model, raise distinct questions: do HD cells encode azimuth computed according to the YO or TA model, and does HD tuning decrease abruptly or progressively? We address these questions by modeling HDC that encode either YO azimuth or TA, and where tuning amplitude decreases either abruptly or progressively.

Model of azimuth-tuned HDC.

Mathematically, we model the azimuth tuning curve when the head is upright by a von Mises function. For simplicity, we set the cell’s preferred azimuth to 0°:

$$F{R}_{Az}\left(Az\right)=K\cdot exp\left[\kappa \cdot cos\left(Az\right)\right]$$ (1)

where Az is the azimuth angle (in a YO or TA reference frame), κ is the von Mises function’s parameter and K is a gain factor adjusted such that the peak value of FR_Az(Az) is 1.

To model the decrease of azimuth tuning when the head tilts away from upright, we introduce a tilt-dependent gain function G(α) which decreases from a peak value of k_G (maximum tuning gain) when the head is upright to 0 (no tuning) when the head is inverted.

For the hemitorus/ellipsoid model:

$$G\left(\alpha \right)=k_G\text{\hspace{0.17em}if\hspace{0.17em}}\alpha \le 90,G\left(\alpha \right)=0\text{\hspace{0.17em}otherwise}$$ (2a)

For a smooth tilt dependence (observed in Angelaki et al. 2019):

$$G(\alpha )=k_G\cdot \left[1-si{n}^2(\alpha /2)\right]$$ (2b)

In these equations, α is the angle between the head’s yaw axis and upright. Note that head tilt relative to vertical is 2D in general (e.g., pitch or roll). However, the modulation of tuning curves modeled here depends only on tilt angle and is identical for pitch and roll tilt.

Thus, the firing rate of a model azimuth-tuned HDC during 3D motion can thus be expressed as a function of (1D) azimuth (Az, in YO or TA frame) and (1D) tilt angle (α) relative to upright:

$$F{R}_{Az}\left(Az,\alpha \right)=K\cdot \left\{G\left(\alpha \right)\cdot exp\left[\kappa \cdot cos\left(Az\right)\right]/k+\left[1-G\left(\alpha \right)\right]\right\}$$ (3)

In this equation k is the average of exp[κ·cos(Az)] across all values of Az, such that the average of FR_Az(Az,α) across all Az is equal to 1 independently of α. Note also that, in upside-down position (α = 180°), G(α) is equal to zero and the cell’s firing rate is set to K. Thus, even though TA is not defined in upside-down position, the cell’s firing rate can still be computed continuously.

Model simulations using the gradual gain function are shown as a function of azimuth (Fig. 3B, abscissa) and tilt angle (Fig. 3B, ordinate) as a color map. On average across all tilt angles (upper marginal distribution), the model cell is tuned to azimuth. Note, however, that the average firing rate across all azimuth angles is uniform when plotted as a function of tilt (right marginal distribution). Thus, the tilt-dependent modulation of azimuth does not result in tilt tuning (i.e., it does not affect the average firing rate across all azimuth angles). How this is altered for cells with actual tilt tuning will be presented next.

Tilt tuning.

We define tilt tuning as a modulation of firing rate, averaged across all azimuth angles, as a function of tilt angle (Fig. 4, tilt marginal). Thus, a cell whose firing rate is sampled uniformly, and, when averaged across azimuth, is independent of tilt, would be classified as azimuth tuned, but not tilt tuned (Fig. 4A). In contrast, tilt tuning should manifest itself as an increase in the cell’s firing at a certain tilt angle, regardless of azimuth (Fig. 4B). To analyze Shinder and Taube (2019)’s results, we only need to simulate tilt tuning during rotations in a single vertical plane, i.e., pitch or roll. For simplicity, we model tuning curves in a single plane using a von Mises function:

$$F{R}_{\text{Tilt}}\left(\alpha \right)=L\cdot \left\{k_{\text{Tilt}}\cdot exp\left[\lambda \cdot cos\left(\alpha -P\alpha \right)\right]/l+\left(1-k_{\text{Tilt}}\right)\right\}$$ (4)

where λ is the coefficient of the von Mises distribution, l is the average of exp[λ·cos(α-Pα)],k_Tilt a gain factor, and α is the tilt angle, equal to 0 or 360° in upright position and 180° when upside-down. The parameter L is a scaling factor adjusted such that the peak value of FR_Tilt(α) is 1.

Fig. 4.

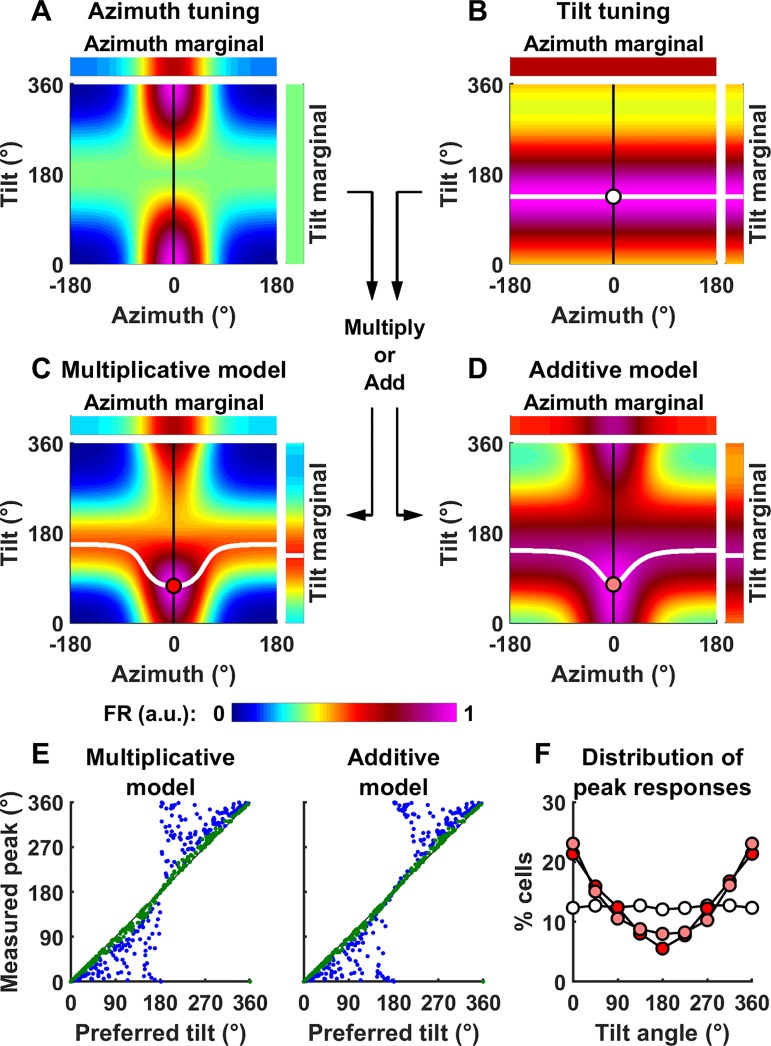
Definition of tilt tuning and generalization to conjunctive azimuth and tilt tuning. A: model cell tuned to azimuth only. Top: azimuth tuning curve of the model cell when upright (κ = 3.7 and k_G = 0.51 where κ is the von Mises function’s parameter and k_G is maximum tuning gain). Bottom: tilt-dependent azimuth tuning curve of a model cell tuned to azimuth only as in Fig. 3A, with the tilt axis ranging from 0° to 360°). B: model cell tuned to tilt only. Top: tilt tuning curve. In this example, the baseline and peak firing as well as the cell’s tuning width are identical as in A (λ = 3.7, k_Tilt = 0.51, where λ is the coefficient of the von Mises distribution and k_Tilt a gain factor). Bottom: simulated response as a function of azimuth and tilt angle. Tilt tuning is independent of azimuth and peaks at 135°. C and D: model cell tuned conjunctively to both azimuth and tilt. Conjunctive tuning curve, assuming that tilt and azimuth tuning interact either multiplicatively (C) or additively (D). Note that, for simplicity, we express tilt along one axis only here (e.g., pitch or roll). For better readability, all two-dimensional firing rate maps have been scaled to a peak value of 1. a.u., Arbitrary units; FR, firing rate.

To simulate the response of a cell that encodes both azimuth and tilt conjunctively, we consider two alternatives where tilt and azimuth interact multiplicatively or additively:

$$F{R}_{Multiplicative}(Az,\alpha )=F{R}_{Az}(Az,\alpha )/m\cdot F{R}_{Tilt}(\alpha )$$ (5a)

$$F{R}_{Additive}(Az,\alpha )=F{R}_{Az}(Az,\alpha )-m+F{R}_{Tilt}(\alpha )$$ (5b)

In both equations, m is equal to the average of FR_Az(Az,α) across all azimuth angles (which is independent of α). It is introduced in both equations to ensure that the average values of FR_{Multiplicative}(Az,α) and FR_Additive(Az,α) across all azimuths are equal to FR_Tilt(α), in agreement with the definition of the tilt tuning curve.

Example conjunctive tuning curves, assuming multiplicative or additive interaction, are shown in Fig. 4, C and D. In these examples, we have assumed that azimuth and tilt tuning have identical strength. In this case, the resulting 2D tuning curve adopts a “cross” shape, with a horizontal band corresponding to an increased firing at the preferred tilt angle and a vertical band corresponding to an increased firing at the preferred azimuth.

Experimental data.

Our analysis is based on the average normalized firing rate data published in Fig. 2, column 5 of Shinder and Taube (2019). Each panel in this figure represents the average firing rate across all recorded cells at nine different positions (from 0 to 360° by increments of 45°). Data was extracted directly from the published figure by importing each panel as an image file. Within each image, we measured the coordinates (in pixels) of each data point and converted them into normalized firing rate based on the pixel coordinates of the panel’s axes.

Simulations of TA and YO models.

To determine whether Shinder and Taube’s data support the dual-axis rule/TA model or the YO model, we used Eq. 3 to simulate the responses of HDC encoding either YO azimuth or TA during the whole range of manipulations performed in Shinder and Taube (2019). To ensure a uniform analysis, where each manipulation spans nine positions (from 0 to 360°), we exclude manipulation 25, which spans more than 360° rotation and is redundant with manipulation 24.

In these models, κ and k_G were treated as free parameters and K was set to 1. We used a gradient ascent procedure (MATLAB function lsqcurvefit) to fit these parameters to the cells’ responses reported by Shinder and Taube (2019) (i.e., averaged normalized firing rate across all cells) over the whole range of manipulations, for each model. We found that the best fitting parameters were κ = 3.7 and k_G = 0.5 for the TA model and κ = 6.6 and k_G = 0.35 for the YO model.

We compared the model’s correlations by using a bootstrap procedure. Bootstrap samples were created by randomly selecting 234 data points out of the 234 data points in the original data set (26 manipulations × 9 data points each), with replacement. The YO and TA models were fitted for each bootstrap sample and their correlations were computed. The P value of the hypothesis H₀ (both models fit the data equally well) is equal to m × 2, where m is the mean number of bootstrap samples where the best model’s correlation is lower than the other model’s correlation (m is multiplied by two to implement a double-tailed test).

RESULTS

Model overview.

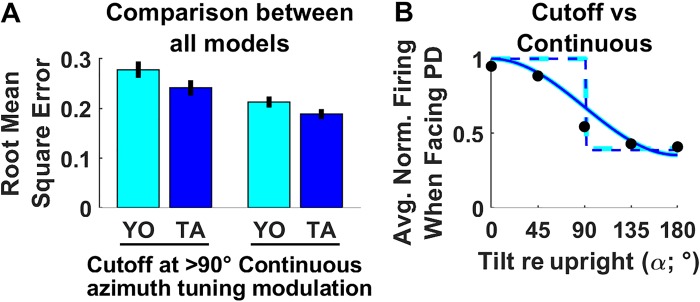
We used a modeling approach to test whether published rat HDC data encodes azimuth in a YO (Fig. 1A) or TA (Fig. 3A) reference frame. We also tested whether tilting the head away from upright cuts off rat HDC azimuth tuning abruptly at 90°, as assumed by the hemitorus/ellipsoid model (Shinder and Taube 2019; Fig. 2) or continuously (Fig. 3B), as found by Angelaki et al. (2019) in mice.

We thus fitted models that incorporate all four possibilities (Fig. 5A: cutoff+YO; cutoff+TA; continuous+YO; continuous + TA). In a nutshell, we found that the rat HDC data across all manipulations reported by Shinder and Taube (2019) was best fitted by the continuous+TA model, as measured by the mean square error (MSE) (Fig. 5A; MSE = 0.19 ± 0.02 confidence interval). In contrast, models that incorporated a cutoff yielded significantly (bootstrap test: P < 10⁻³/P < 10⁻³; YO/TA models) higher error. Likewise, the YO models yielded lower goodness of fit (P = 0.01/P = 0.003; cutoff/continuous models). Thus, the model where HDC follow the hemitorus/ellipsoid model (cutoff at 90°) and are updated in a YO frame, as argued by Shinder and Taube (2019), produced the highest errors fitting their own data (MSE: 0.28 ± 0.03 confidence interval).

Fig. 5.

Model comparison. A: overall goodness of fits of all models considered in this study. Error bars indicate the standard error, based on a bootstrap procedure. B: modulation of head direction (HD) responses as a function of tilt angle when facing the cell’s preferred direction (PD). Dots: median firing rate in Shinder and Taube’s (2019) study as a function of tilt angle, when facing the cell PD, and across all manipulations. Solid/broken cyan/blue lines: firing rate predicted by models during manipulations 4, 6, and 7 where the head tilts when facing the PD, assuming that 1) azimuth is encoded in a yaw-only (YO; cyan) or tilted azimuth (TA; blue) frame and 2) HD firing decreases continuously (solid line) or abruptly at 90° tilt (i.e., hemitorus/ellipsoid model, broken line). Note that the TA and YO (cyan versus blue) models yield identical predictions during this motion. Avg. Norm., average normalized.

The hemitorus/ellipsoid model assumes that HD tuning doesn’t change when the head tilts 90° or less from upright and then abruptly disappears. To illustrate directly why this assumption doesn’t account for the experimental findings of Shinder and Taube (2019), we pooled all data points where the head faces the cells’ PD and computed the median firing at tilt angles ranging from 0 to 180° (Fig. 5B; black). We compare it to simulations of manipulations 5, 6, and 7, where the head tilts while facing the PD. Note that the YO and TA models predict the same responses during these motions (see Fig. 8, A and B below), which allows us to compare the cutoff or continuous models directly. We found that the firing rate decreases continuously, in a manner that was very well predicted by the continuous+YO (solid cyan) or continuous+TA (solid blue) model. In contrast, the hemitorus/ellipsoid model predicts an abrupt decrease in firing rate (broken cyan/blue lines) that doesn’t match their data.

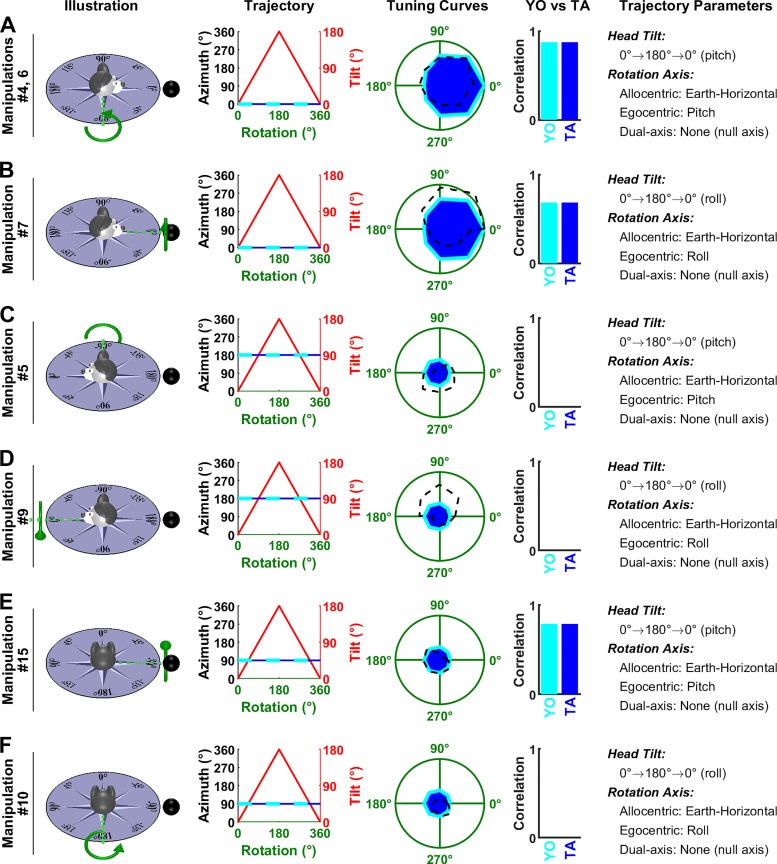
Fig. 8.

Analysis of Shinder and Taube’s (2019) manipulations: pitch/roll rotations in the earth-vertical plane. Same format as in Fig. 6. Note that, strictly speaking, tilted azimuth (TA; Trajectory panels, blue) is not defined when the tilt angle (red) is 180°. However, it is defined in the immediate vicinity of this point, such that the blue curve appears uninterrupted. Manipulations 4 and 6 (A), 7 (B), 5 (C), 9 (D), 15 (E), and 10 (F) are animated in Supplemental Movie S3, available at https://github.com/JeanLaurens/Modelling-3D-HD-Cell-Tuning. YO, yaw only.

Note also that, taken literally, this model posits that the firing rate at 90° should be identical as the firing rate when upright (which is clearly not the case). However, Shinder and Taube (2019)’s discussion also suggest that the firing rate at this boundary may be “difficult to predict.” Thus, the hemitorus/ellipsoid, arguably, is not unambiguously defined at 90° tilt, and how well it fits the data in general would depend on this definition. We tested various alternatives (setting the cutoff just before or after 90° tilt, or ignoring data at 90° tilt altogether) but found that the hemitorus/ellipsoid always yielded higher errors. Therefore, we conclude that the hemitorus/ellipsoid is a rough qualitative approximation of how tilting away from upright modulates HDC responses that poorly accounts for experimental data. In the rest of our analysis, we compared the YO and TA frame of reference based on models that assume a continuous modulation.

HDC integrate 3D rotation signals, and not only yaw.

As illustrated in Figs. 6–9 that simulate model predictions for the experimental manipulations performed by Shinder and Taube (2019) (illustrated by animated movies: Supplemental Movies S1–S4, available at https://github.com/JeanLaurens/Modelling-3D-HD-Cell-Tuning), the TA model (Angelaki et al. 2019; Laurens and Angelaki 2018; Page et al. 2018) fits Shinder and Taube’s (2019) data better than the YO model.

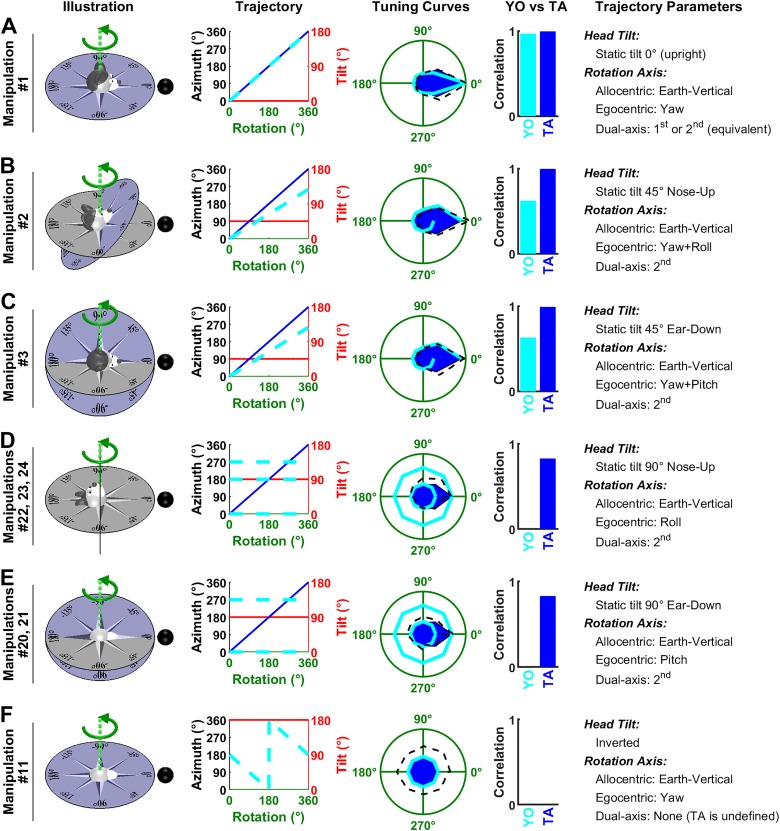
Fig. 6.

Analysis of Shinder and Taube’s (2019) manipulations: rotations around an earth-vertical axis. Experimental conditions in Shinder and Taube (2019) are named “manipulations” here, numbered 1 to 27 (see their Fig. 3). Each line corresponds to one manipulation, or to multiple manipulations that follow the same trajectory (with different starting positions). Illustration: representation of the motion trajectories with the head at 0°. The gray and blue azimuth frames represent an earth-fixed and tilted azimuth (TA) compass, respectively. Green, rotation axis. Black sphere, cell’s preferred direction (PD) when the animal is upright. Trajectory: head azimuth [in TA and yaw-only (YO) frames: blue and cyan, respectively] and tilt (red) resulting from a rotation of ± 180° relative to the 0° position. Tuning Curves: simulations of each model are compared with experimental results. Firing rate is represented in polar coordinate for consistency with Shinder and Taube (2019) and normalized to 1 (green circle) when facing the PD in upright orientation. Blue: simulated firing of a cell encoding TA; Cyan: simulated firing rate of a cell encoding YO azimuth; black, experimental results of Shinder and Taube (2019). When the trajectory corresponds to multiple manipulations, the corresponding results are averaged. YO versus TA: correlation between the tuning curves predicted by the YO and TA models and the average head direction cell (HDC) response. Correlations were computed independently for each manipulation and averaged across manipulations. Trajectory Parameters: description of the trajectory, including head tilt, the position of the rotation axis in allocentric and egocentric coordinates, and decomposition of the rotation axis based on the dual-axis rule. Manipulations 1 (A), 2 (B), 3 (C), 22–24 (D), 20 and 21 (E), and 11 (F) are animated in Supplemental Movie S1, available at https://github.com/JeanLaurens/Modelling-3D-HD-Cell-Tuning.

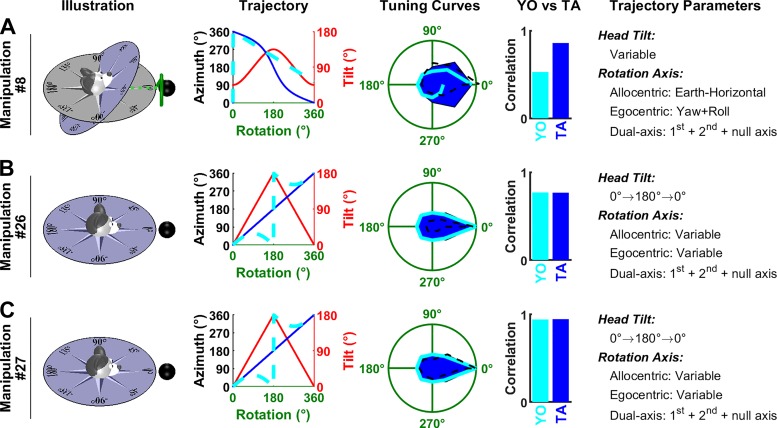
Fig. 9.

Analysis of Shinder and Taube’s (2019) manipulations: complex rotations. Same format as in Fig. 6. As in Fig. 8, tilted azimuth (TA) is not defined at 180° tilt in B and C, but the corresponding curve (Trajectory panels, blue) appears uninterrupted since TA is defined in the vicinity of this point. Manipulations 8 (A), 26 (B), and 27 (C) are animated in Supplemental Movie S4, available at https://github.com/JeanLaurens/Modelling-3D-HD-Cell-Tuning. YO, yaw only.

In the first manipulation (Fig. 6A), the head is upright and the rotation axis coincides with the head’s yaw axis. Therefore, the trajectories are the same in both YO and TA models (Trajectory panel, TA: blue; Yaw-only: cyan) and the predicted tuning curves (Tuning Curves panel) are similar (although the parameters of both models differ slightly, this difference is negligible in practice). Both predictions are highly correlated (TA: ρ = 0.99; YO: ρ = 0.97) with the average response measured across cells (Tuning Curves panel, black).

In the next two manipulations, the head is tilted 45° in pitch (Fig. 6B) or roll (Fig. 6C), such that the rotation axis now falls between the head’s yaw and roll (Fig. 6B, manipulation 2) or pitch (Fig. 6C, manipulation 3) axes. According to the TA model, this rotation corresponds to the second updating rule (rotation axis parallel to gravity), and the brain integrates 3D (yaw, pitch, roll) rotation signals to update azimuth accurately (Trajectory panels, blue). Because the head is tilted, HD azimuth tuning is reduced (Fig. 3B), although to a minimal extent since tilt angle is small (45°). Thus, the TA model predicts that cells should exhibit a clear tuning (Tuning Curves panels, blue), in agreement with experimental results (ρ = 0.99 in both Fig. 6B and Fig. 6C). In contrast, the YO model predicts that azimuth is not tracked accurately since the rotation is not aligned with the head-fixed yaw axis. Specifically, yaw velocity is equal to 71% of the total velocity (i.e., the cosine of 45°) and therefore the YO model predicts that the rotation is underestimated: after a rotation of 360°, the estimated azimuth is 255° (Trajectory and Tuning Curves panels, cyan), and therefore the simulated firing doesn’t return to the peak value that is expected when facing the PD. This prediction doesn’t correlate well (ρ = 0.62 in Fig. 6B and ρ = 0.63 in Fig. 6C) with the average tuning curves reported by Shinder and Taube (2019).

In the subsequent manipulations 20–24 (Fig. 6, D and E), head tilt increases to 90° such that the rotation occurs in the pitch or roll plane. According to the TA model, these pitch and roll rotations correspond to the 2nd updating rule and are thus integrated to generate a veridical azimuth signal (Trajectory panels, blue), although the cell’s response tuning is now significantly attenuated due to the large head tilt (Tuning Curves panels, blue). In contrast, the YO model predicts that HDC do not detect any change in azimuth (Trajectory panels, cyan). Note that, in these manipulations, head azimuth computed by the YO model is identical to the initial head orientation throughout the whole manipulation. In manipulation 24, the head faces the cell’s PD initially (0° Azimuth, Trajectory panel in Fig. 6D), whereas it faces 270° and 180° at the beginning of manipulations 22 and 23. Therefore, the YO model predicts that the cell should respond strongly during the entire manipulation 24, and less during manipulations 22 and 23 (the predicted firing in these two manipulations is similar). The corresponding predictions are shown as two distinct cyan curves in Fig. 6D, Tuning Curves panel. Similarly, the YO model predicts different responses during manipulations 20 and 21 in Fig. 6E. The HDC responses measured by Shinder and Taube exhibited a weak modulation that matched the TA model’s simulation (ρ = 0.83 in both Fig. 6D and Fig. 6E). In contrast, Shinder and Taube’s YO model predicts that HDC should not be modulated at all during these manipulations, in contradiction with their own results (in this case, the correlation is undefined). Remarkably, although these manipulations provide strong experimental support for the TA model, the authors reached the opposite conclusion without any simulations or quantification.

In a final manipulation (Fig. 6F), the head is placed upside down. In this simulation, both models predict that the neuron is unmodulated.

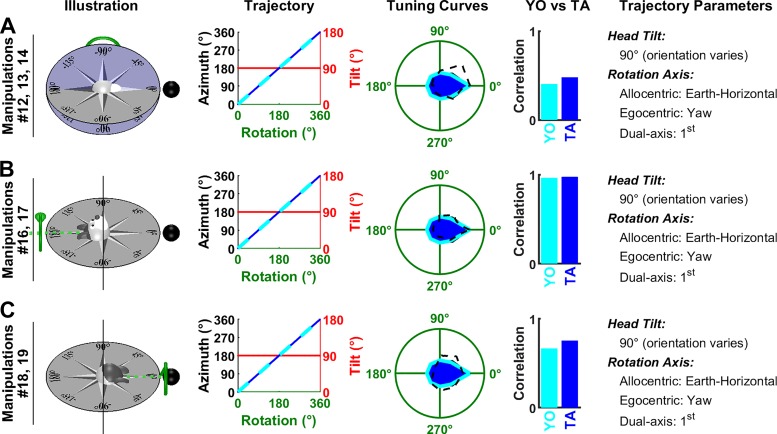
HDC responses during yaw rotations in an earth-vertical plane.

Next we consider a series of manipulations where the animal rotates in yaw about an earth-horizontal axis. These manipulations cannot distinguish between the TA and YO models, because predictions are identical: both models predict that azimuth is updated by the rotation, although the predicted firing is attenuated since the head is tilted by 90° (Fig. 7, A–C, Trajectory panels). The predicted tuning curves match equally well the experimental data (TA model: ρ = 0.48/0.98/0.75; YO model: ρ = 0.41/0.96/0.67).

Fig. 7.

Analysis of Shinder and Taube’s (2019) manipulations: yaw rotations in the earth-vertical plane. A: the top of the head faces away from the reader. B and C: the top of the head faces left/right. In all panels, the head rotates in yaw. Same format as in Fig. 6. Manipulations 12–14 (A), 16 and 17 (B), and 18 and 19 (C) are animated in Supplemental Movie S2, available at https://github.com/JeanLaurens/Modelling-3D-HD-Cell-Tuning. TA, tilted azimuth; YO, yaw only.

HDC responses during pitch and roll rotations in an earth-vertical plane.

Shinder and Taube (2019) also performed a series of manipulations where animals rotated in pitch or roll in the earth-vertical plane. According to the TA model, these rotations are about the null axis and should therefore not affect azimuth. According to the YO model, these rotations are about an axis orthogonal to the yaw axis and shouldn’t affect azimuth either. Thus, these manipulations don’t distinguish these models. Yet, they provide additional support to our modeling framework, and in particular to the gradual tilt-dependent gain function used here (Fig. 3B).

In Fig. 8, A and B, the animal faces the cell’s PD at the beginning of rotation. Since azimuth doesn’t change during the whole rotation cycle, the animal faces the PD during the entire manipulation (Trajectory panels, blue and cyan curves have a constant value of 0). However, the models predict that the cell’s response is modulated by tilt angle (Fig. 3B; Fig. 4B), resulting in a broad tuning curve (“Tuning curves” panels, blue and cyan) that matches the average responses reported by Shinder and Taube (2019) (TA model: ρ = 0.87 and ρ = 0.68 in Fig. 7A and B; YO model: ρ = 0.87 and ρ = 0.68).

In Fig. 8, C–F, the animal initially faces 90° or 180° away from the cell’s PD. As in previous manipulations, both models predict that the rotation doesn’t change azimuth (Trajectory panels, blue and cyan curves). The cell’s predicted response corresponds to its firing at 90° or 180° azimuth in Fig. 3B and is affected to a small extent by tilt angle. Shinder and Taube (2019) observed a weak modulation in Fig. 8, C and D, that wasn’t predicted by either the TA or YO model (but might be attributable to tilt tuning; see Tilt responses shown in Shinder and Taube are biased by azimuth tuning). In Fig. 8, E and F, the average firing was weak, as predicted by both models. In Fig. 8E, it correlated with the predicted tuning curve, although this correlation may not be very meaningful due to the weakness of the predicted modulation.

Other manipulations.

Shinder and Taube (2019) also performed complex rotation protocols (Fig. 9). For example, the head starting from 45° nose-up tilt was rotated around an earth-horizontal axis (Fig. 9A). In this situation, TA follows a nonlinear trajectory (Trajectory panel, blue) while the YO model predicts that rotation velocity is underestimated (Trajectory panel, cyan), similar to Fig. 6, B and C. The average measured firing rate measured correlates better with the TA than YO model (ρ = 0.86 versus 0.53).

The manipulations in Fig. 9, B and C are combinations of yaw and roll or yaw and pitch (that can’t be represented using a single rotation axis as in other panels). The TA and YO models predict that azimuth follows different trajectories (Trajectory panels, blue versus cyan). However, in both trajectories, the head is inverted after 180° of rotation, resulting in a low firing rate, and the head returns to facing the PD after 360° of rotation, resulting in a high firing rate. Therefore, the predicted responses are very similar (“Tuning curves” panel, blue versus cyan), despite the trajectories being different. Both models predict that HDC should be strongly modulated during these simulations, in agreement with simulation results (TA model: ρ = 0.77 and 0.77 in Fig. 9B and C; YO model: ρ = 0.95 and 0.94 in Fig. 9, B and C).

Conclusions: Shinder and Taube’s experimental results support the TA and not the YO model.

One of the two main conclusions of Shinder and Taube (2019) is that azimuth is updated primarily by yaw rotations, using qualitative arguments, rather than model-based analyses. In contrast, here we have simulated each of the two (TA and YO) models and compared them with their experimental data. Strikingly, this comparison demonstrates that the experimental data is rather supportive of the TA/dual-axis rule model, where HDC encode TA and, thus, by definition, integrate rotations about all three head axes. We may also point out that, while the attenuation of HDC tuning is a complicating factor, both the TA and YO models need the independent incorporation of its existence. Thus, this factor doesn’t affect the comparison between the two models.

The critical manipulations for distinguishing between the YO versus TA models are rotations about an earth-vertical axis (which represents the second axis of the dual-axis rule) with the animal at different static orientations, as shown in Fig. 6. Shinder and Taube (2019)’s YO model predicts that HDC should not be updated correctly in Fig. 6, B and C, when the head is tilted by 45° and the rotation is misaligned with the yaw axis, and that tuning should vanish altogether in Fig. 6, D and E, when the head is tilted by 90° and the rotation occurs along the pitch or roll axis. However, their data indicate that the average HD tuning is maintained in Fig. 6, B and C as well as in Fig. 6, D and E although it is attenuated in the later conditions because the head is tilted. In their study, Shinder and Taube don’t discuss the fact that HDC tuning is maintained when the head is tilted 45° (Fig. 6, B and C), a fact that contradicts the model they promote. Furthermore, they conclude from the manipulation in Fig. 6, D and E that HDC aren’t updated during rotations in the head’s vertical planes, without appreciating that the response attenuation may be due to head tilt and not to the fact that the head rotates in pitch and roll.

To explore this matter further, we note that another veridical comparison among TA and YO model predictions without the possible contamination of tilt attenuation is provided by considering the manipulations in Fig. 6, D and E and Fig. 7, where head tilt is identical. Based on the TA model, each of these rotations spans the whole azimuth compass, and, since head tilt is identical, the attenuation of the cell’s response should be identical. In contrast, the YO model predicts that HD cells should be tuned in Fig. 7 but not at all in Fig. 6, D and E. We averaged the experimental tuning curves in Fig. 6, D and E and Fig. 7 and found that the average tuning curves are similar (Fig. 10) and highly correlated (ρ = 0.9), thus confirming the TA/dual-axis model.

Fig. 10.

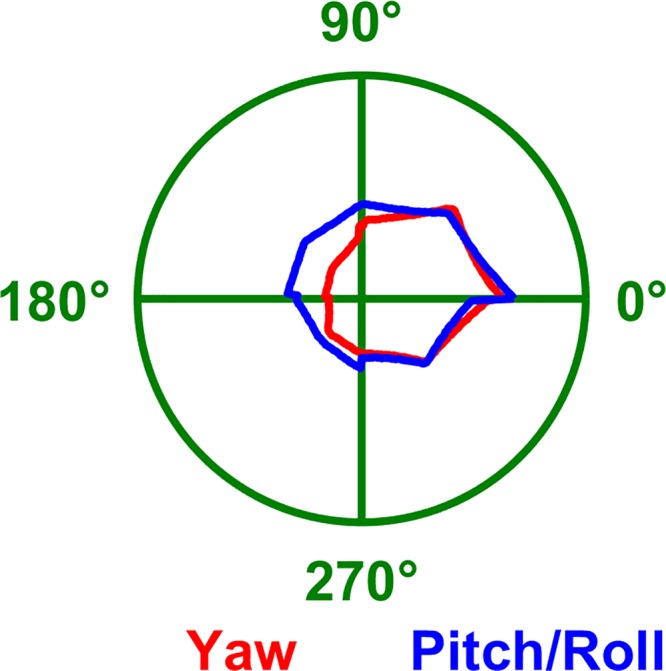
Average azimuth tuning curves measured by Shinder and Taube (2019) with the head tilted 90°. Red: tuning curve during yaw rotations in the earth-vertical plane (average of all manipulations in Fig. 7). This tuning is based on the 1st-axis rule. Blue: tuning curve during pitch and roll rotations in the earth-horizontal plane (average of all manipulations in Fig. 6, D and E). This tuning is based on the 2nd-axis rule. As predicted by the TA/dual-axis model, the two curves are highly correlated (ρ = 0.9). In contrast, the yaw-only (YO) model would predict no tuning during pitch/roll (blue).

Shinder and Taube (2019) performed additional manipulations that resulted in elimination of directional tuning. For example, in manipulations 12, 20, 24, and 25, they observed that cells fired maximally at the beginning of the trajectory, when animals faced the PD, but that this firing didn’t recover after an entire 360° rotation when the animal returned to the PD. The authors emphasized that these occurred during rotations in pitch and roll (manipulations 20, 24, and 25), and actually used this point to support the YO model. However, they ignored the fact that a similar phenomenon also occurs in manipulation 12, which is a yaw rotation. Since loss of directional tuning may occur during rotations about all three head axes (yaw, pitch, and roll), it doesn’t support any particular model (TA versus YO). Instead, it likely reflects a decrease in the reproducibility of neuronal responses when the head tilts away from vertical. The absence of tuning in conditions 6 and 21 may be interpreted in a similar manner.

Shinder and Taube (2019) further reported that the average HDC responses may vary between different manipulations that follow the same trajectory but with different initial positions or directions (e.g., manipulations 12, 13, and 14, Fig. 7A). However, this occurred only in trajectories where both models yielded identical predictions. Therefore, the variability of the responses across manipulations may involve neuronal response variability, alertness, or other factors but doesn’t weight in favor of a particular model.

Overall, although HD responses appear to be less consistent when the head tilts, responses that clearly support the TA frame and dual-axis rule were observed at least in one manipulation for each trajectory. Furthermore, Shinder and Taube (2019) never observed a strong directional tuning in a direction that was not predicted by the TA model. Therefore, there is absolutely no evidence in their experimental results in favor of the YO model.

Note that Shinder and Taube (2019)’s experiment rule out a third possibility, called “Earth-Horizontal (EH)” model (Angelaki et al. 2019; Laurens and Angelaki 2018), where head orientation is projected and measured on the earth-horizontal plane. Indeed, based on such a model, azimuth would be unaffected by static head roll and therefore span the full 0–360° range in Fig. 6E but would be undefined when the head is facing upward in Fig. 6D or would alternate between ±90° in Fig. 7, B and C. Yet, HDC exhibit identical tuning curves in all these conditions. The EH model is also refuted by Finkelstein et al. (2015), Page et al. (2018), and Angelaki et al. (2019).

Note that, in our model-based analysis, we reproduced the average tuning curve, across all recorded cells, by simulating a HD cell that was tuned to azimuth, but not to tilt. This doesn’t imply that individual cells recorded by Shinder and Taube (2019) were not tuned to tilt, but rather that tilt tuning would generally average itself out when data from multiple cells, that would likely prefer different tilt, are pooled. We discuss tilt tuning in detail next.

Tilt responses shown in Shinder and Taube are biased by azimuth tuning.

A second conclusion of Shinder and Taube (2019) is that HDC don’t encode head tilt in vertical planes. This conclusion is based on the analysis of pitch and roll responses recorded when the head initially faced the PD (Figs. 7 and 8 in their study; i.e., manipulations 4 and 7; Fig. 8, A and B in the present paper). Specifically, the authors found that neuronal responses were systematically higher when the animals are upright, compared with responses at tilts larger than 90°, and concluded that HDC don’t exhibit any preference for any tilt position other than upright.

Here we show that this observation is biased because the cells’ azimuth tuning decreases as a function of tilt. We base our reasoning on a mathematical model of conjunctive cells that are tuned to both azimuth and head tilt (see methods). We first use an example cell to illustrate how azimuth tuning biases the measurement of tilt tuning. Next, we simulate a population of conjunctive HDC where preferred tilt angles are distributed uniformly across the whole range of possible head tilt. We show that, using Shinder and Taube (2019)’s experimental manipulation, the preferred tilt angles of these cells appear largely biased toward upright.

Example cell.

We first describe an example model conjunctive cell, where the parameters of azimuth and tilt tuning have been chosen to illustrate how azimuth tuning may bias tilt tuning identification. In this example, azimuth tuning (simulated with κ = 2 and k_G = 1; Fig. 11A) is stronger than tilt tuning (simulated with λ = 0.5 and k_Tilt = 1; Fig. 11B). We also assume that tilt tuning peaks at 135° (Fig. 11B, white line), i.e., closer to upside-down (180°) than upright (0°). We will show how, under the influence of azimuth tuning, tilt tuning may appear to peak at an angle lower than 90°, i.e., closer to upright. A population analysis, including a discussion of these parameters, is shown in the next section.

Fig. 11.

Why the pitch/roll rotations when facing the cell’s preferred direction (used by Shinder and Taube) are inappropriate to test for tilt tuning. A–D: simulation of a model conjunctive cell, as in Fig. 4, but with different parameters such that azimuth tuning (κ = 2 and k_G = 1, where κ is the von Mises function’s parameter and k_G is maximum tuning gain) is now stronger than tilt tuning (λ = 0.5 and k_Tilt = 1, where λ is the coefficient of the von Mises distribution and k_Tilt a gain factor). The solid white lines in B–D indicate the tilt angle at which firing peaks, as a function of azimuth. The tilt tuning function in B, where tilt tuning is independent of azimuth and peaks at 135°, is multiplied by or added to the azimuth tuning function (A) to produce the tuning curves in C and D. The white (B), red (C), or pink (D) markers indicate the tilt angle at which firing peaks when facing 0° azimuth, i.e., the cell’s PD: note the bias toward upright. E: peak response measured during pitch or roll, as a function of the cell’s preferred tilt angle, in 500 simulated cells (k_G and are k_Tilt set to 1, κ and λ are drawn randomly such that the Rayleigh vector length of azimuth and tilt tuning curves are distributed uniformly). Green/blue dots: cells where tilt tuning is higher/lower than azimuth tuning. F: distribution of the preferred tilt angle (white markers) and of the angle at which the peak response occurs (red/pink: multiplicative/additive model). a.u., Arbitrary units; FR, firing rate.

Under these conditions, azimuth and tilt tuning interact to form a response peak at 0° azimuth and, importantly, at a smaller tilt angle than 135° (specifically at a tilt angle of α = 74° and α = 77° in Fig. 11, C and D, red/pink circle, respectively). This is because the tilt-dependent azimuth tuning (Fig. 11A), which is maximal when upright, leads to higher firing rates for small tilt angles. Thus, the fact that azimuth tuning strength is tilt dependent results in biases of response peak toward upright, even though tilt PD is at 135°. Note that this “pulling” of response peak toward upright is maximal for tilts along the azimuth PD (0° in the present simulations) (Fig. 11, C and D, white lines)—and these are exactly the conditions tested by Shinder and Taube (2019).

The extent to which azimuth tuning biases the response to tilt tuning depends on the relative strength of azimuth versus tilt tuning (Rayleigh vector length of the corresponding marginals: 0.79 versus 0.25 in Fig. 11, A and B). We modeled a population of neurons where the tuning strength of tilt and azimuth (measured by their Rayleigh vector length) are independent and distributed uniformly between 0 and 1, and where the preferred tilt is distributed uniformly between 0 and 360° (Fig. 11E, abscissae). We repeated the simulations in Fig. 11, C and D and computed the tilt angle at which firing rate would be maximum (Fig. 11E, ordinate axis), when facing 0° azimuth, and assuming a multiplicative or additive interaction. Furthermore, we color coded neurons where tilt tuning was stronger than azimuth tuning in green. These neurons appear close to the diagonal, indicating that pitch tuning was weakly biased in these neurons. In contrast, the peak response of neurons where azimuth tuning is larger than tilt tuning (blue) appeared away from the diagonal and close to 0 or 360° on the ordinate axis, indicating that it is strongly biased toward upright. Note that Shinder and Taube (2019) only recorded from cells with strong azimuth tuning, thus inherently biasing their data in the direction of the blue symbols.

To summarize the population responses, we plotted the distribution of preferred pitch orientation in the absence of azimuth tuning (Fig. 11F, white symbols) and the distribution of peak firing during pitch rotation assuming a multiplicative (red) or additive (pink) model. The later distributions are biased toward 0°, i.e., upright.

Furthermore, additional sources of bias should be considered:

• First, Shinder and Taube recorded only azimuth-tuned HDC with a Rayleigh vector length higher than 0.5. Therefore, cells were preselected to have a high azimuth response but were not selected to have a large tilt response, implying that most cells would have a stronger azimuth tuning than tilt tuning (i.e., blue symbols in Fig. 11E). Since HDC with a larger azimuth tuning compared with tilt tuning are biased toward responding maximally in upright, this preselection would have biased their results further.

• We simulated rotations in a single plane (e.g., pitch) and assumed that the tuning strength of tilt tuning is uniformly distributed, similar to azimuth tuning. However, tilt-tuned cells may in fact respond preferentially in a different plane, e.g., roll. Because of this, the distribution of tilt tuning strength should be biased toward lower values and the population response should be biased even further toward upright.

Given these multiple sources of bias, and considering the limited set of cells analyzed [only 11 and 13 cells in manipulations 4 (pitch rotation) and 7 (roll rotations), respectively], it is not surprising that Shinder and Taube didn’t observe any cells firing maximally in the range of 135–215° tilt, i.e., within ± 45° of being upside-down (although some of their cells fired maximally at 90° or 270° tilt, i.e., half-way between upright and upside-down).

Conclusion: Tilt tuning.

We conclude that the manipulations shown and analyzed in Shinder and Taube (2019) are insufficient to characterize the presence or absence of tilt tuning. Our simulations indicate that they would have observed a clear tilt tuning (characterized by an increase in firing rate at tilt angles larger than 90°), only in cells where 1) tilt tuning is stronger compared with azimuth tuning, which would likely represent a minority of the population since recordings were performed in cells where azimuth tuning was strong in the first place, 2) the preferred tilt angle is larger than 90°, and 3) tilt tuning occurs in the plane in which recordings were performed. Considering the limited sample shown by Shinder and Taube (Figs. 7 and 8 in their study: 11 and 13 cells, respectively), it is not surprising that no such cells were found.

Tilt responses would be better characterized by measuring pitch and roll responses when the head faces 90° or 180° away from the preferred azimuth (Fig. 9, C–F in the present paper). Although this data was collected by Shinder and Taube (2019), it was not used to assess the presence or absence of tilt tuning and individual cell responses were not shown. Alternatively, tilt tuning may be revealed as in Angelaki et al. (2019), by averaging 3D responses across all azimuths.

DISCUSSION

Shinder and Taube (2019) have drawn three conclusions from their data set:

The first conclusion is that HDC response may be described by a hemitorus/ellipsoid model, where HD tuning subsides abruptly when the head tilts more than 90° from upright. Based on our analyses, tilting the head away from upright has a modulatory effect on rat HDC, which is better described as a continuous decrease in azimuth tuning, similar to our finding in mice (Angelaki et al. 2019). This observation, together with the fact that the hemitorus and ellipsoid models are restricted to a limited range of 2D orientation, severely questions their usefulness for describing HDC response during 3D motions.

The second conclusion is that the azimuth tuning of HDC is primarily updated by yaw rotations, as opposed to 3D rotations (Fig. 1A), as stated in their discussion: “Because the system could not effectively utilize nonhorizontal information to determine rotation in the horizontal plane, this result challenges the viability of the internal model, which postulates that the brain uses all available sensory data in combination with gravity information to derive a directional heading vector. […] Instead, our findings suggest that the horizontal canals and its associated pathways are hard-wired and designed to specifically extract azimuthal heading information—most likely in the form of angular head velocity information.” Although not acknowledged by the authors, this conclusion directly refutes the TA and dual-axis rule models, which by definition are updated by 3D rotation. Here, we have shown that this conclusion is not supported by their data. In fact, a model-based analysis of their experimental protocols and neural responses shows the exact opposite: HDC responses are inconsistent with a YO model that integrates only yaw rotations but instead support the TA/dual-axis model (Angelaki et al. 2019; Laurens and Angelaki 2018; Page et al. 2018), where 3D (yaw, pitch, roll) rotation information originating from all semicircular canals are integrated with gravity signals to track azimuthal heading.

More specifically, our model-based analysis reveals two shortcomings in Shinder and Taube’s reasoning. First, they didn’t consider the fact that pitch and roll rotations performed in most experimental manipulations are not expected to update azimuth in the first place, based on either the TA or YO model (Fig. 8). Second, they didn’t appreciate that, in those manipulations where pitch and roll should update azimuth according to the dual-axis rule (e.g., Fig. 6, B–E), they do it just as effectively as yaw rotations (see Fig. 10).

The TA model accounts for the responses of azimuth-tuned HDC reported in three independent studies conducted by separate groups and using radically different protocols (Angelaki et al. 2019; Page et al. 2018, Shinder and Taube 2019). It is also compatible with the toroidal model proposed to account for HDC tuning in bats (Finkelstein et al. 2015), except for one point. Azimuth is undefined in a TA frame when the head is placed upside-down, and yet Finkelstein et al. (2015) observed HDC responses for approximately half of their neurons in this orientation. It is currently unknown how these responses should be modeled. Future studies should establish whether animals rely on a different frame of reference in this situation.

The third conclusion is that HDC don’t encode head tilt, as stated in their discussion: “HD cells increased their firing rates when the animal faced into the recorded cell’s preferred firing direction in the horizontal plane, independent of the tilt or roll position of the head, as long as the head did not become inverted by tilt or roll beyond 90°.” We agree with their conclusion that azimuth signals carried by HDC decrease with head tilt, but we showed that their data is inconclusive regarding whether HDC are tuned to tilt. Note that, in a recent study (Angelaki et al. 2019), we have shown that about two-thirds of cells in the anterodorsal thalamus of mice are tuned to tilt, and that their preferred tilt orientation is distributed uniformly between upright and upside-down (with a slight preference for forward, i.e., nose-down tilt). We also reproduced the analysis in Fig. 11 based on a direct analysis of our experimental data, instead of simulations (Angelaki et al. 2019, supplemental materials).

The YO model originally proposed and recently resurrected by Shinder and Taube implies that HDC encode exclusively 1D information. Ironically, the authors state that gravity plays a role in HDC (“Both of these models [hemitorus and ellipsoid] predict that HD cell firing ceases once the animal’s orientation enters a plane that is >90° away from the horizontal (x-y) plane (inversion). There are two ways to consider how these models might relate to the reference frame(s) used by HD cells. These models [hemitorus and ellipsoid] could be referenced to the animal and rotate with it as the animal moves across different planar surfaces or they could be fixed and referenced to the global environment and thus dependent on gravity. Our results are more consistent with the latter possibility because directional firing is disrupted during inversion.”)

However, throughout these statements, Shinder and Taube consider that the sole effect of gravity is to “switch off” HDC responses when the head tilts more than 90° from upright. Furthermore, the authors never describe how gravity would contribute to computing or encoding any navigation or behavioral variable and clearly state that HDC do not, in their view, encode pitch or roll tilt: “whereas a sizeable percentage of HD cells in bats (30%) were found to have conjunctive properties with pitch and roll, where the cells were best tuned to a particular orientation in 3D space and not just in the azimuthal plane (Finkelstein et al. 2015, their Fig. 2G), there was limited evidence to support this same occurrence in the rat anterodorsal thalamus.” Therefore, we find it surprising that the authors would state, in their study’s abstract and title, that “the HD signal is a 3D gravity-referenced signal,” in what seems in blatant contradiction with their own conclusions.

Shinder and Taube (2019)’s argument that HD cells use a gravity-anchored reference frame also suffers from logical mistakes. For instance, the authors reject an “alternative hypothesis” where the hemitorus/ellipsoid would be anchored to the animal instead of gravity, i.e., “These models could be referenced to the animal and rotate with it as the animal moves across different planar surfaces […]” Thus, their “alternative model” is literally built on the assumption that HD cell firing would cease when the animal is oriented >90° relative to itself, which is illogical to begin with.

The authors’ conclusion regarding the dual-axis rule model are also highly misleading; e.g., “In this regard [referring to the fact that directional firing is disrupted during inversion], the hemitorus and ellipsoid models when considered fixed to gravity are similar to the dual-axis model (Page et al. 2018), which postulates that the reference frame for HD cells is defined by two parameters: the animal’s head position relative to its dorsal-ventral axis and the relationship of the animal’s dorsal-ventral axis to gravity.” This statement implies that the hemitorus/ellipsoid and TA models are identical because both somehow depend on gravity, although the way gravity contributes to each model is entirely different. As illustrated here, the gravity-dependent attenuation of azimuth tuning is independent from the reference frame used to define and update azimuth tuning. Furthermore, the authors never mention the crucial point that the dual-axis model requires integration of 3D rotation signals and is therefore refuted (incorrectly) by their own conclusion that HD cells integrate yaw rotations only. Thus, the authors misrepresent the TA/dual-axis rule model and succeed in refuting it while not refuting it at the same time.

We have proposed (Laurens and Angelaki 2018) that the HD system combines visual landmark signals with self-motion information provided by a multisensory 3D internal model (Laurens and Angelaki 2011, 2017; Laurens and Droulez 2007; Laurens et al. 2013; Merfeld et al. 1999). The fact that HDC responded as predicted (Figs. 6–9) along all three rotation axes supports the 3D internal model theory. Note that all manipulations in the Shinder and Taube (2019) study were performed in light and likely involve a combination of vestibular self-motion signals, visual self-motion signals, and visual landmarks. Therefore, HDC responses didn’t reflect how the brain processes vestibular signals specifically, but rather how it maintains a 3D representation of head orientation based on multisensory signals.

In summary, for nearly two decades (Calton and Taube 2005, Shinder and Taube 2019, Stackman et al. 2000) the group’s conclusion that HDC integrate yaw rotations exclusively to encode 1D azimuth has remained unchanged, at the expense of contradicting their own experimental findings. Several groups (Angelaki et al. 2019; Finkelstein et al. 2015; Laurens et al. 2016; Page et al. 2018) have recently discovered that HDC encode 3D head orientation and derive orientation from 3D rotation signals. Here we have shown that the experimental results in Shinder and Taube (2019) are entirely consistent with the conclusions of these other studies in bats, monkeys, and mice, although the authors failed to assimilate recent developments to interpret their data in a more model-driven, quantitative way.

GRANTS

This work was supported by the Simons Collaboration on the Global Brain, grants 542949 and R01-AT010459, and NIH grant DC004260.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.L. conceived and designed research; J.L. analyzed data; J.L. interpreted results of experiments; J.L. prepared figures; J.L. and D.E.A. drafted manuscript; J.L. and D.E.A. edited and revised manuscript; J.L. and D.E.A. approved final version of manuscript.