Probing vibrational coupling via a grid‐based quantum approach—an efficient strategy for accurate calculations of localized normal modes in solid‐state systems

Abstract

In this work an approach to investigate the properties of strongly localized vibrational modes of functional groups in bulk material and on solid‐state surfaces is presented. The associated normal mode vectors are approximated solely on the basis of structural information and obtained via diagonalization of a reduced Hessian. The grid‐based Numerov procedure in one and two dimensions is then applied to an adequate scan of the respective potential surface yielding the associated vibrational wave functions and energy eigenvalues. This not only provides a detailed description of anharmonic effects but also an accurate inclusion of the coupling between the investigated vibrational states on a quantum mechanical level. All results obtained for the constructed normal modes are benchmarked against their analytical counterparts obtained from the diagonalization of the total Hessian of the entire system. Three increasingly complex systems treated at quantum chemical level of theory have been considered, namely the symmetric and asymmetric stretch vibrations of an isolated water molecule, hydroxyl groups bound to the surface of GeO₂ (001), α‐quartz(001) and Rutil (001) as well as crystalline Li₂NH serving as an example for a bulk material. While the data obtained for the individual systems verify the applicability of the proposed methodology, comparison to experimental data demonstrates the accuracy of this methodology despite the restriction to limit this methodology to a few selected vibrational modes.

The possibility to investigate vibrational phenomena of localized normal modes without the requirement of executing costly harmonic frequency calculations of the entire system enables the application of this method to cases in which the determination of normal modes is prohibitively expensive or not available for a particular level of theory. © 2018 Wiley Periodicals, Inc.

Introduction

Infrared (IR)‐spectroscopy1 is a particularly widespread and frequently used method for the investigation and characterization of chemical systems. As a non‐invasive method it enables the measurements to be performed without damaging the sample, while at the same time the required instruments are comparatively cost‐efficient and straightforward in their application. Because of these properties IR‐spectroscopy became one of the main methods for analysis in industrial and scientific applications. As a consequence theoretical approaches to study and predict IR spectroscopic properties are of special interest and thus highly regarded. Especially the distinction of overtones and combination bands gained increasing demand resulting from limitations to unambiguously assign experimentally observed wave numbers to the respective vibrational modes in certain cases. To achieve an accurate prediction of vibrational wave numbers of chemical systems the influence of anharmonicity, inter‐mode coupling as well as other quantum mechanical phenomena such as the influence of tunneling into the classically forbidden region has to be accurately taken into account, while at the same time a computationally efficient implementation is to be preferred.

However, the most common method for the calculation of vibrational frequencies based on the harmonic approximation of the potential neglects these important effects2 and is known to overestimate predicted frequencies due to the severe oversimplification of the problem.

An improved framework to take the anharmonicity of the underlying potential into account is Vibrational Perturbation Theory (VPT2).3, 4, 5 This method has a rather high computational effort (6N‐5 harmonic frequency evaluations with N being the number of atoms in the system) but at the same time considers only local curvature information close to the minimum. For this reason VPT2 approaches are known to be of limited accuracy in case of strongly anharmonic potentials (e.g., OH bonds) which have been recently confirmed in joint experimental and theoretical investigations.6, 7 A further widely employed method is the so‐called Vibrational Self Consisting Field (VSCF)8, 9, 10, 11 approach. This method uses, in analogy to Hartree‐Fock SCF, an ansatz which by definition strongly approximates coupling of different modes. Various improved VSCF approaches have been formulated focusing on higher accuracy12, 13, 14, 15 and a computational efficient procedure.16, 17, 18, 19, 20, 21 While VSCF and its extensions are based on grid data that is typically interpolated to obtain a continuous representation of the potential energy surface, there exist different families of grid‐based methods evaluating the wave functions only on the provided data‐points. These methods lead to reliable results with comparably small computational effort.6, 7, 22, 23, 24, 25 The latter are not limited to problems in vibrational spectroscopy, but have also been applied in approaches to describe the electronic density in atoms and small molecules.26, 27, 28, 29, 30, 31, 32, 33 Among these is the so‐called Numerov method,34, 35 which was shown to predict the experimentally determined vibrational frequencies of H₂ and H₂O within 1 cm⁻¹ (≤0.1)% using correlated ab initio based potential energy information.36 Also density functional theory (DFT) at hybrid level37, 38 combined with the Numerov scheme proved highly accurate in predicting the IR fundamental and first overtone of the OH‐vibrational modes of methanol and phenol, especially under gas‐phase conditions where a deviation of <0.5% was achieved.6, 7, 39 The employed potential energy grids were created via single point energy calculations along the vibrational normal modes obtained from an evaluation of harmonic normal modes of the entire system.

This preparatory step may quickly become a bottleneck even if approximate gradient‐based approaches are employed. In addition to the dramatically increased execution times the high demand in memory may exceed the capacities of available computational equipment (for instance in periodic quantum chemical methods). Therefore, an approach restricting the vibrational analysis to the modes of interest avoiding the costly calculation of harmonic modes for the entire system would greatly extend the capabilities of grid‐based approaches. Since the latter requires the execution of individual, less‐demanding single point computations, the creation of the potential energy grid is in principle perfectly parallelizable. This strategy is particularly suitable if vibrational modes with strongly local character are the focus of interest. In this case the vibration is concentrated on a small number of atoms of the chemical system. A typical example are hydroxy (OH) groups in molecules or on the surface of a bulk material, which concentrate more than 99% of the associated vector norm to the respective oxygen and hydrogen atoms.39 It has been shown that the frequencies of localized modes like the OH‐vibration of organic molecules can be approximated exploiting the local character of the vibration by considering only the motion of the involved O and H atoms, assuming the rest of the molecule to remain rigid. Besley and Bryan presented a similar approach based on a partial Hessian for the determination of harmonic frequencies that only considers atoms of interest while neglecting the motion of all other atoms.40 This approach resulted in a reasonable prediction of wave numbers with small deviations compared to a full normal mode analysis employing the Hessian of the entire system.

The concept to reduce the computational demand by focusing only on a reduced set of vibrational modes has also been employed in a number of investigations. Bowman and co‐workers proposed a local monomer model41, 42 to investigate clusters of small molecules.43, 44, 45, 46 Jacob, Reiher, and Neugebauer proposed an approach to calculate vibrational normal modes of quantum mechanical (QM)‐systems and combined quantum mechanica/molecular mechanical (QM/MM) simulations.47, 48 Kjaergaard et al. employed local mode descriptions to describe XH stretching systems.49, 50, 51, 52, 53, 54, 55, 56 Another local‐mode coordinate model was proposed by Steele and co‐workers57 for the calculation of vibrational frequencies of large molecules. Recently the FALCON framework was proposed by Christiansen and co‐workers,58 a method for flexible adaptation of local coordinates of nuclei.

The main focus of these methods are applications in molecular clusters composed of small molecules or single large molecules, whereas the method presented in this paper is aimed at the characterization of vibrational properties of solid‐state systems considering also the associated surface chemistry. For this purpose, the strategy to employ constructed normal mode vectors39 is adapted to higher dimensions by combining it with the idea of a partial Hessian.40 Comparison of the results obtained via a one‐dimensional and two‐dimensional treatment provides detailed information on the contributions arising by just considering anharmonic effects and alternatively the inclusion of both anharmonicity and coupling of the investigated vibrational modes. First, the theoretical basis and the presented test systems are introduced, followed by the discussion of the obtained results and concluding remarks.

Methods

Previous applications of the Numerov method to vibrational spectroscopy have demonstrated that the wave numbers of the strongly localized OH modes in methanol, phenol, and thymol can be calculated within 0.5% of the experimental value employing artificial normal modes.39 The latter are constructed employing only the structural information of the OH bond at the respective minimum geometry. In this work the approach was extended to higher dimensions as discussed in “Numerov's approach to solve Schrödingers equation” Section and tested with chemical systems containing two XH bonds (X = O,N). The vibrational frequencies are evaluated using the Numerov method, a grid‐based approach to numerically solve the Schrödinger equation of the vibrational quantum system. The employed Numerov approach has been derived earlier36 and is summarized in “Constructed normal modes” Section. It has been shown that the respective accuracy mainly depends on the spacing h of the potential energy grid.36 To guarantee an accurate prediction the individual grid points have to be computed using at least DFT on generalized gradient approximation level37, 38 with suitable basis sets. In the example of water coupled cluster theory was employed.

The direction of the potential energy scan and the respective effective mass is usually determined via a harmonic normal mode calculation. This may become a computational bottleneck, especially for large chemical systems. However, in most cases only a small part of the gained information is subsequently used to create the potential energy grid considering only a small number of relevant modes. Thus, the idea of the presented approach is to avoid the costly computation of harmonic normal modes and to approximate the scan direction only for the vibrations of interest via constructed displacement vectors requiring only the knowledge of the minimum configuration. While in case of all test systems presented in this work the results obtained by applying constructed normal modes are critically compared to those obtained from modes evaluated via the full Hessian for the purpose of validation, future investigations of large systems (e.g., large surface structures) will strongly benefit from the possibility to construct normal modes solely on the basis of the respective minimum configuration. In the following normal modes determined via the harmonic calculation of the entire system Q_i are referred to as analytical in the sense that the entire Hessian matrix ℍ of the system is evaluated and all respective normal modes are calculated via diagonalization. This consideration also applies if the individual elements of ℍ are computed via finite difference of gradient contributions as it is done in the program Crystal14.59

Constructed normal modes

In this section the formalism to construct approximated normal mode vectors $\overline{{\mathbf{Q}}_i}$ from the minimum geometry is presented. For better clarity the discussion is split into two parts, namely the one‐ and higher‐dimensional case.

One dimension

Starting with the minimum geometry the localized normal modes of XH bonds (X = N,O in this work) can be approximated.39 As discussed up to 99% of the vector norm of the respective localized normal mode is concentrated on a small number of atoms of the chemical system, while the remaining part of the molecule effectively remains rigid. The associated atomic displacement vectors Δr_X and Δr_H are obtained via weighting based on the respective atomic masses m_X and m_H according to

$$\mathrm{\Delta }{\mathbf{r}}_X={\mathbf{r}}_{\mathit{XH}}\frac{m_H}{m_X+m_H}$$ (1)

$$\mathrm{\Delta }{\mathbf{r}}_H=-{\mathbf{r}}_{\mathit{XH}}\frac{m_X}{m_X+m_H},$$ (2)

with r_XH corresponding to the associated bond vector at the equilibrium configuration. The displacement of all other N‐2 atoms is assumed to be negligible and set to zero. Finally, all atomic contributions are collected in a single displacement vector Δr ∈ ℝ^3N followed by normalization yielding the approximated normal mode $\overline{\mathbf{Q}}$. The quality of the constructed displacement vector ${\overline{\mathbf{Q}}}_i$ can be validated via the scalar product p_i with the associated, analytical normal mode vector Q_i obtained via diagonalisation of the total Hessian.

$$p_i={\mathbf{Q}}_i^{\mathrm{T}}{\overline{\mathbf{Q}}}_i$$ (3)

thereby assuming the vectors to be properly normalized. Here, the superscript T denotes the vector transpose. The smaller the corresponding angle obtained via the inverse cosine the better the approximation, with 0^∘ corresponding to an ideal agreement. A second mean of validation is the difference in the reduced masses μ_i 2 obtained via

$${\mu }_i=\sqrt{{\sum }_{j=1}^{3N}\hspace{0.17em}{\mathbf{Q}}_{i,j}^2·m_{\left(\lfloor \left(j-1\right)/3\rfloor \right)+1}},$$ (4)

with the elements of Q_i representing either an analytical or constructed normal mode, respectively, while the expression ⌊...⌋ corresponds to the floor function.

Higher dimensions

Since the approach in one dimension considering just a single XH bond proved viable, an extension to several XH bonds is envisaged, to explicitly consider the respective mode‐mode interactions at quantum mechanical level. In order to achieve a higher dimensional framework, a reduced Hessian ℍ_red considering only the vibrations of interest is introduced. This idea was already successfully applied in case of purely harmonic frequency calculation as shown by Besley and Bryan.40 Comparison between an 1d treatment and the corresponding higher dimensional investigation provides detailed information about influence of anharmonicity compared to anharmonicity plus mode coupling.

Given a chemical system with N atoms, the respective positions can be described using Cartesian coordinates, denoted (x₁, y₁, z₁, …, x_N, y_N, z_N). After choosing a basis in this 3N‐dimensional vector space the positions and movements of all atoms are uniquely described. In this case it is convenient to express the degrees of freedom by mass‐weighted coordinates2:

$$q_1=\sqrt{m_1}\mathrm{\Delta }{x}_1,q_2=\sqrt{m_1}\mathrm{\Delta }{y}_1,q_3=\sqrt{m_1}\mathrm{\Delta }{z}_1,q_4=\sqrt{m_2}\mathrm{\Delta }{x}_2,\dots ,q_{3N}=\sqrt{m_N}\mathrm{\Delta }{z}_N.$$

This enables a simultaneous treatment of XH bonds with different effective masses (e.g., an NH bond and an OH bond). In the next step the Hessian matrix is introduced containing all second derivatives with respect to {q_i}³ⁿ:

$$ℍ=\left(\begin{array}{llll}\frac{{\partial }^{2}V}{\partial q_1^2}& \frac{{\partial }^{2}V}{\partial q_1\partial q_2}& \dots & \frac{{\partial }^{2}V}{\partial q_1\partial q_{3N}}\\ \frac{{\partial }^{2}V}{\partial q_2\partial q_1}& \frac{{\partial }^{2}V}{{\partial }^2{q}_2}& \dots & \frac{{\partial }^{2}V}{\partial q_2\partial q_{3N}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}V}{\partial q_{3N}\partial q_1}& \frac{{\partial }^{2}V}{\partial q_{3N}\partial q_1}& \dots & \frac{{\partial }^{2}V}{\partial q_{3N}^2}\\ & & & \end{array}\right).$$ (5)

To derive vibrational data the Hessian matrix is always considered in a minimum of the potential hyper‐surface at which point the gradient of the potential energy is vanishing. By determining a proper basis in the 3N‐dimensional vector space it is possible to reduce the Hessian to a diagonal matrix. This basis corresponds to all 3N normal modes and is obtained by calculating the eigenvalues and respective eigenvectors of the Hessian matrix. If the translational and rotational normal modes are neglected 3N − 6 vibrational normal modes exist (3N − 5 in case of linear molecules, 3N − 3 for periodic systems). An exhaustive theoretical evaluation including the justifications for this step is given by Wilson.2

For the presented purpose this step is not required because the size of the Hessian matrix will be significantly reduced. Similar to the ansatz in one dimension all atoms except the considered XH bonds remain fixed. The respective Hessian containing a large number of zero entries leads to a small sub matrix with non‐zero entries. Using the coordinates q_i defined above the investigation of m XH bonds leads to 2m movable atoms and therefore to a 2m · 3 × 2m · 3 sub matrix with non‐zero entries. The remainder of the Hessian is zero by definition because the respective atoms are considered fixed. Without loss of generality the non‐zero entries are assumed to have the indices 1, …, 6m.

$${ℍ}_{\mathit{red}}=\left(\begin{array}{lllllll}\frac{{\partial }^{2}V}{\partial q_1^2}& \frac{{\partial }^{2}V}{\partial q_1\partial q_2}& \dots & \frac{{\partial }^{2}V}{\partial q_1\partial q_{6m}}& 0& \dots & 0\\ \frac{{\partial }^{2}V}{\partial q_2\partial q_1}& \frac{{\partial }^{2}V}{{\partial }^2{q}_2}& \dots & \frac{{\partial }^{2}V}{\partial q_2\partial q_{6m}}& 0& \dots & 0\\ ⋮& ⋮& \ddots & \ddots & ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}V}{\partial q_{6m}\partial q_1}& \frac{{\partial }^{2}V}{\partial q_{6m}\partial q_1}& \dots & \frac{{\partial }^{2}V}{\partial q_{6m}^2}& 0& \dots & 0\\ 0& 0& 0& 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & \ddots & \ddots & 0\\ 0& 0& 0& 0& \dots & \dots & 0\\ & & & & & & \end{array}\right).$$ (6)

The movement of all XH bonds is limited to the predefined direction given by the respective XH‐distance vector. This enables to represent the displacement of the atoms in internal coordinates as presented in Ref.2 , which can be used to further reduce the size of the sub matrix. By describing the displacement of each atom pair using only a single internal coordinate per XH bond, the size of the reduced Hessian matrix is only of the dimension m × m. Here, each XH bond is considered separately as an arbitrary vibrational mode and each bond to be investigated is represented by a single normalized coordinate Δr_i corresponding to the displacement vectors discussed in the one‐dimensional case.

While the latter yields the constructed normal mode ${\overline{\mathbf{Q}}}_i$ in the one‐dimensional case, a diagonalization of the reduced Hessian matrix is required, yielding the eigenvalues λ_i and the associated eigenvectors v_i. The elements of v_i are then employed as coefficients in a linear combination of the displacement vectors Δr_i leading to the approximated normal modes ${\overline{\mathbf{Q}}}_i$ for the higher dimensional system.

$${\overline{\mathbf{Q}}}_i=\sum _{j=1}^m\hspace{0.17em}{v}_{i,j}·\mathrm{\Delta }{r}_j\text{for}i=1,\dots ,m,$$ (7)

where v_{i, j} denotes the j‐th entry of v_i. If the displacement and eigenvectors Δr_i and v_i have been properly normalized the same applies to the constructed normal modes ${\overline{\mathbf{Q}}}_i$. The associated reduced mass of the mode μ_i is then evaluated via the components of ${\overline{\mathbf{Q}}}_i$ according to eq. (4).

In this work the elements of the reduced Hessian have been numerically approximated in mass‐weighted coordinates using finite differences.60 Assuming an n‐point approximation to the second derivative (i.e., an n‐point stencil) and m XH bonds to be considered, then n^m single point energy calculations have to be executed to approximate the reduced Hessian matrix. This approach can be used for an arbitrary number of XH bonds. Especially in case of large systems containing only a few vibrations of interest with local character this approach may dramatically improve hardware requirements as well as execution times.

The equispaced, multi‐dimensional potential grid obtained from the subsequent scanning of the energy landscape may then serve as input to solve the Schrödinger equation of the respective vibrational subsystem. Because of the properties of eigenvectors the respective sign is undetermined: It is thus possible that the potential energy scan yields a dependence opposite to the general chemical consensus (i.e., the repulsive branch is found in positive direction while the attractive dispersion interaction is in the negative region). Looking at chemical systems with multiple XH bonds of interest two possibilities can be envisaged: either the procedure presented above can be extended to an arbitrary dimension or each combination of modes is investigated in a pair‐wise fashion. Although looking only at two vibrations at a time may not fully represent the coupling between all vibrational modes, this approach provides detailed information about the mutual influence of each coupling pair. Moreover, it has been pointed out in the literature that a three‐dimensional description of the potential energy is not always required to achieve accurate predictions of vibrational wave numbers.16

Numerov approach to solve Schrödinger's equation

Numerov's method34, 35 can be applied to numerically solve all ordinary differential equations (ODEs) of the form

$$\mathrm{\Delta }\psi \left(x\right)=f\left(x\right)\psi \left(x\right),$$ (8)

with the Laplace operator Δ, the discretised vector x and a known function f. The eigenfunction ψ(x) is to be determined. The grid {x₁, x₂, …} has to be equidistant with a spacing h = x_{i + 1} − x_i. In this approach the differential equation is solved numerically on a grid, implying that the solution of the ODE is approximated only at the grid points.

Schrödinger's equation can be rearranged into a form compatible with the Numerov framework:

$$\mathrm{\Delta }\psi \left(x\right)=\frac{2m}{{\mathrm{\hslash }}^2}\left(E-V\left(x\right)\right)\psi \left(x\right)=f\left(x\right)\psi \left(x\right),$$ (9)

with the potential V(x), the effective mass m and the energy eigenvalue E. In the following an adapted Numerov method36 presented earlier is outlined, which has the advantage that the sparse character of the matrix formulation is fully exploited leading to a dramatic reduction of memory demand and execution time while at the same time real eigenvalues and orthogonal eigenvectors are guaranteed. As in the previous study36 the employed algorithms to solve the sparse eigenvalue problem is based on the Armadillo61 library and uses the sparse eigenvalue routine of the ARPACK62 package.

One dimension

As mentioned the Numerov method is a grid‐based method employing K equispaced points x_i,  i = 1, …, K, following the short notation ψ(x_i) = ψ_i and ψ(x_i ± k · h) = ψ_{i ± k}.

Here, k denotes a natural number and all ψ_i with i < 1 and i > K are considered zero, implying a Dirichlet (zero) boundary condition. In the one‐dimensional case the Laplace operator Δ simplifies to the second derivative ∂²/∂x². Summation of the two Taylor series for x + h and x − h and using the identity eq. (8) yields the numerical expression

$${\psi }_{i+1}-2{\psi }_i+{\psi }_{i-1}=h^2{f}_i{\psi }_i+2\sum _{k=2}^n\hspace{0.17em}\frac{h^{2k}}{\left(2k\right)!}{\psi }_i^{\left(2k\right)}+\mathcal{O}\left(h^{2n+2}\right).$$ (10)

In eq. (10) the desired accuracy n can be chosen via the number of terms included in the sum specified by the parameter n. Next, all occurring derivatives have to be approximated using the respective finite difference expressions.60 As an example the equation for n = 3 is shown:

$$f_i{\psi }_i=\frac{1}{h^2}\left(\frac{1}{90}{\psi }_{i+3}-\frac{3}{20}{\psi }_{i+2}+\frac{3}{2}{\psi }_{i+1}-\frac{49}{18}{\psi }_i+\frac{3}{2}{\psi }_{i-1}-\frac{3}{20}{\psi }_{i-2}+\frac{1}{90}{\psi }_{i-3}\right)+\mathcal{O}\left(h^6\right).$$ (11)

Thus, the more neighboring points ψ_{i ± n} are included the better the approximation of the second derivative. Considering ψ_i as entries of a vector, the equations for all ψ_i can be combined to a matrix equation

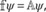(12)

with $\mathbb{A}$ being a matrix filled with the respective coefficients near the diagonal and being a diagonal matrix. Next, eq. (12) is applied to the Schrödinger equation according to eq. (9) which leads to the eigenvalue equation in matrix form given as

$$\left(\mathbb{A}+\mathbb{V}\right)\psi =ℍ\psi =\mathit{E\psi }.$$ (13)

Since the potential matrix $\mathbb{V}$ is diagonal, the Hamiltonian ℍ is sparse filled and symmetric. It has been shown that this property not only leads to a substantial improvement in the computational demand, but also guarantees the respective eigenvalues to be real. In contrast the original formulation of the matrix Numerov procedure34, 35, 63 requires additional steps in the computation (one matrix inversion, one matrix multiplication, and the diagonalization of a dense matrix). Since the product of two symmetric matrices is not guaranteed to result in a symmetric matrix, the original matrix Numerov formulation does not guarantee real eigenvectors. Furthermore, comparing the performance of the adapted version against the original formulation showed that effectively the same results are obtained while a substantial reduction of the computational effort could be achieved.36

Two dimensions

In this part the higher dimensional approaches are outlined shortly. Exemplarily, the derivation of the two‐dimensional approach is shown. Analogously to the one‐dimensional case a shortened notation is used: ψ(x_i, y_j) = ψ_i,j and ψ(x_i ± k · h, y_j ± l · h) = ψ_{i ± k, j ± l}. In two dimensions the differential equation to be solved is

$$\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)\psi \left(x,y\right)=f\left(x,y\right)\psi \left(x,y\right).$$ (14)

The respective spacing h in both dimensions of the grid has to be equal which in case of vibrational spectroscopy is ensured by using mass‐weighted coordinates.2 Analogous to the one‐dimensional case the method is derived using a sum of four individual Taylor series:

$$\begin{array}{l}{\psi }_{i+1,j+1}+{\psi }_{i+1,j-1}+{\psi }_{i-1,j+1}+{\psi }_{i-1,j-1}-4{\psi }_{i,j}=2h^2{f}_{i,j}{\psi }_{i,j}+\\ +4\sum _{k=2}^n\hspace{0.17em}\frac{h^{2k}}{\left(2k\right)!}\left(\sum _{l=0}^k\hspace{0.17em}\frac{\left(2k!\right)}{\left(2k-2l\right)!2l!}\frac{{\partial }^{\left(2k\right)}\psi }{\partial x^{2k-2l}\partial y^{2l}}\right)+\mathcal{O}\left(h^{2n+2}\right),\end{array}$$ (15)

in which the second derivatives were substituted using eq. (14). After choosing the desired accuracy n all derivatives on the right‐hand side of the equation have to be approximated using finite difference expressions60 followed by a separation of terms containing $\psi$. Next, the derivatives in eq. (15) are applied to Schrödinger's equation leading again to a matrix eigenvalue problem as shown in eq. (13). In this formulation the two‐dimensional wave function is represented in vector form ψ. Diagonalisation of the resulting Hamiltonian matrix ℍ yields the eigenvalues E_i and the associated two‐dimensional wave functions. It has been demonstrated that this concept can be analogously adapted to higher dimensions.36

Target systems

As mentioned the presented approach is focused on problems in solid‐state chemistry, in which the definition of local monomers is not as straightforward as it is in case of clusters composed of small molecules. Moreover, in case of X‐H vibrational groups located at the solid‐state interface, the vibrational features inside the solid are of minor importance due to the comparably higher reduced masses and the associated low wave numbers. On the other hand since a substantial amount of atoms should be included to properly represent the bulk of the solid, the calculation of all vibrational modes via the diagonalization of the full Hessian provides a large number of redundant information while at the same time the computational effort is unnecessarily increased.

To demonstrate the applicability of this strategy four increasingly complex solid‐state systems were investigated. The predicted wave numbers obtained using the constructed vibrational vectors $\overline{{\mathbf{Q}}_i}$ are then compared to those resulting from application of the analytically derived normal modes Q_i. For this purpose a GeO₂ (001) with two adsorbed hydrogen atoms, bulk Li₂NH containing two NH bonds in the unit cell, the complex H bond pattern on hydroxylated SiO₂ (001) reported by Catlow et al.64 and a TiO₂ (001) bulk with a chemisorbed H₂O molecule on the surface were considered. Finally, an isolated water molecule was used to test the performance of the approach in case two O‐H bonds are assigned to the same oxygen atom. Furthermore, it was investigated if the presented approach is also applicable to deuterated water.

If not explicitly mentioned the number of grid points was chosen in between 41 and 61, corresponding to a grid size h in between 0.025 an 0.03 Å. In all examples the calculations were performed in one and two dimensions, so that the influence of mode–mode coupling can be observed in comparison to the uncoupled 1d‐case. The results are then compared to the harmonic frequency calculation and to experimental data. For the approximation of the Hessian matrix a 9‐point‐stencil was applied in all examples, combined with a grid size of h = 0.025 Å, leading to 81 single point energy calculations. The grid size h was chosen low to ensure the accuracy of the numerical second derivative.

Germanium dioxide—(001)‐surface

The first example is the (001)‐surface of tetragonal GeO₂ with two hydrogen atoms adsorbed to different oxygen atoms, forming two surface hydroxy groups. The number of atom layers of the GeO₂ surface was chosen sufficiently high to ensure that a surface model consistent with the bulk material is retained, resulting in a system containing 20 atoms subject to two‐dimensional periodic boundary conditions. A depiction of the unit cell and its periodic images are shown in Figure 1. To determine the minimum geometry of the system two different variations with and without relaxation of the unit cell were carried out. In the following these two variations are referred to as configurations A and B, corresponding to models without and with relaxation of the unit cell, respectively.

Figure 1.

GeO(001) surface with adsorbed hydrogen atoms in front (left) and top view (right). The unit cell of the 2d‐periodic system is outlined via the gray box which has been periodically enlarged for clarity (represented by the transparent atoms). The z‐dimension is not considered as periodic. [Color figure can be viewed at wileyonlinelibrary.com]

The calculations were performed with the program Crystal1459 at DFT level using the PBESOL65 functional. The 8‐51G,66 LC‐31d,67 and POB‐TZVP68 basis sets have been applied in case of O, Ge, and H, respectively. The layer group was set to P1 in all cases to ensure each atom in the system is irreducible, which is a requirement for the associated normal mode scan moving the atoms away from the respective minimum positions.

Lithium imide

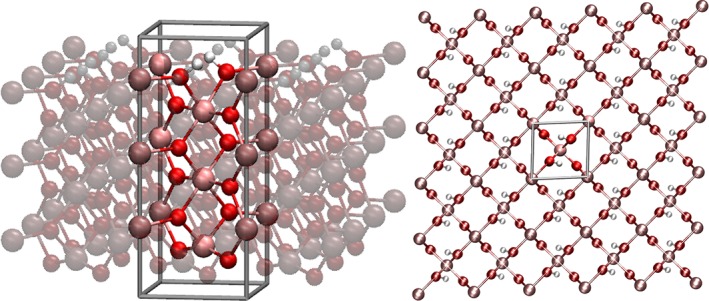
In addition a bulk material was investigated to analyze the performance of the artificial normal mode calculation in a material. For this purpose lithium imide (Li₂NH) was chosen, the respective structural data have been obtained from Ohoyama et al.69 Since the positions of the hydrogen atoms are only reported via fractional occupation (1/4 to 1/24 for different structural models), two idealized configurations with parallel (P) and opposing (O) orientation of the NH‐groups based on the data provided by Magyary‐Köpe et al.70 and Mueller et al.71 have been constructed to ensure a manageable computational demand. The respective unit cells are depicted in Figure 2a.

Figure 2.

Lithium imide cells shown prior to energy minimizations: a) Unit cell of lithium imide and its periodic propagation. Due to the large number of possible arrangements of the hydrogen atoms resulting from the fractional occupation, two idealized systems have been constructed based on the discussion provided in literature70, 71: b) Conf. P of the investigated lithium imide, both NH bond are oriented in the parallel direction c) Conf. O of the investigated lithium imide, the NH bond are oriented in opposite directions. [Color figure can be viewed at wileyonlinelibrary.com]

Again two different variations of geometry optimization strategies A and B as described in “Germanium dioxide—(001)‐surface” Section were performed. The calculations were executed using Crystal1459 on hybrid DFT‐level37, 38 using the functional B3LYP.72 For H and N the POB‐TZVP68 basis set was applied, in case of Li the 6‐11G73 basis was chosen. Similar as in the case of GeO₂ (001) the space group was set to P1 for all systems ensuring irreducibility of all atoms in the systems which is required during the potential energy scanning along the direction of the vibrational mode vectors.

α‐quartz (SiO₂)—(001)‐surface

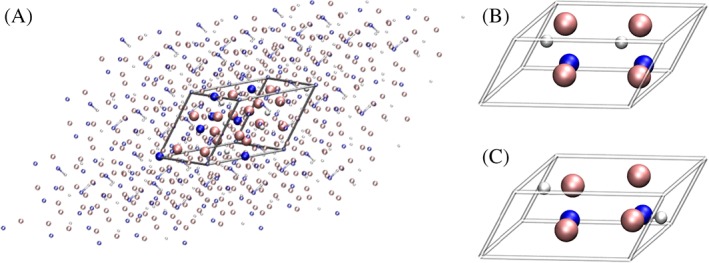
The third target system is a hydroxylated α‐quartz (001)‐surface. The investigated system was inspired by the results of Catlow et al.64 , being composed of an 18 layer two‐dimensional‐periodic (001)‐surface containing 21 atoms. The number of layers was chosen sufficiently high to encompass the full properties of the surfaces. Following the notation in Ref.64 , the target system was constructed by the reconstructed configuration on the lower surface and the hydroxylated configuration on the upper side. For the hydroxylation a water molecule was adsorbed to the so‐called cleaved surface as an OH ⁻‐group and a proton. A depiction of the unit cell and its periodic images are shown in Figure 3. The interesting and at the same time challenging property of this surface is, that the OH‐groups of interest are connected to each other via subsequent hydrogen bonding. Looking at the target system it has the effect, that the hydrogen atom of one hydroxy group is hydrogen‐bonded to the oxygen of a periodic image of the other OH group and vice versa. This configuration is shown in Figure 4. The calculations were executed using the program Crystal1459 at DFT level employing the PBESOL65 functional. The O6‐31d174 basis set was applied for oxygen and hydrogen, while for silicium the Si88‐31G(*)75 basis set was used. The box parameters are a = b = 5.01035882Å with γ = 120^∘.

Figure 3.

Hydroxylated α‐quartz (001) surface with two hydrogen bonded, OH groups in front (left) and top view (right). The unit cell of the 2d‐periodic system is outlined via the gray box which has been periodically enlarged for clarity (represented by the transparent atoms). The z‐dimension is not considered as periodic. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 4.

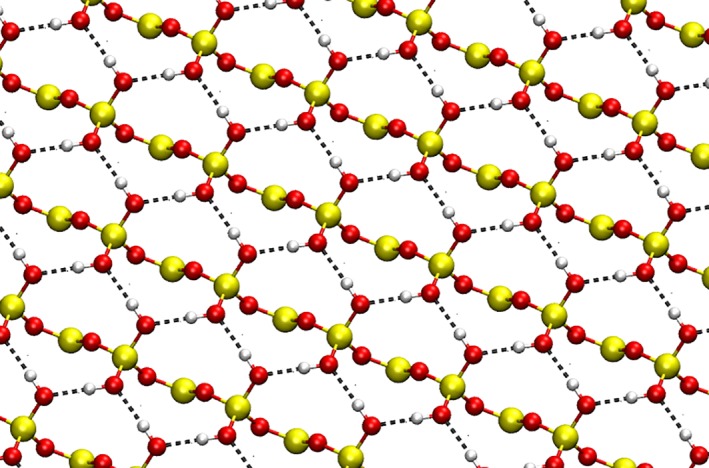
Top five layers of the hydroxylated α‐quartz (001)‐surface showing the hydrogen bonded OH groups. Due to the periodicity of the surface the OH groups subsequently act as hydrogen bond donor and acceptor, forming a unique H bond wire motif. The associated hydrogen bonds are represented by the dashed black lines. [Color figure can be viewed at wileyonlinelibrary.com]

TiO₂—Rutil (001) surface

As fourth example a 10 layer system of a rectangular, 2d‐periodic 2 × 2 supercell (sidelength 9.187 Å) of TiO₂ was investigated. It contains 120 atoms plus an chemisorbed, dissociated H₂O molecule forming two OH‐groups on the surface, leading to a total number of 123 atoms and 1530 electrons. The 10 layers are necessary to achieve an adequate representation of the bulk structure thus avoiding interactions between the top and the bottom surfaces. All calculations were executed applying the PBESOL functional65 with the basis sets 86‐51(3d)G for titan76, 77 and the O6‐31d174 basis set for oxygen and hydrogen. The gridspacing h of the 31 ×31 point grid was chosen as 0.05Å before mass weighted coordinates were applied.

Water

As last example the two OH‐modes of an isolated water molecule were chosen. In this system both OH bonds share the same oxygen atom leading to a strong coupling of the symmetric and asymmetric stretching modes. Water thus comprises a further critical test for the suggested approach. In the other examples the XH bonds of interest do not originate at the same atom, thus being simpler examples compared to H₂O. Moreover, since the performance of the Numerov method in three dimensions has already been demonstrated,36 the influence of the coupling between the symmetric and asymmetric OH stretch modes can be highlighted by comparing the results of the 2d‐problem to that of the individual one‐dimensional predictions. Additionally the vibrational frequencies of heavy water (D₂O) were calculated to verify the performance of the approach if the hydrogen atom is replaced with deuterium.

All computations were executed with the ab initio program Gaussian0978 at CCSD(T)/aug‐cc‐pvqz79, 80 level without frozen core approximation using tight settings for energy and gradient convergence criteria.

Results

In this section the predicted wave numbers for the different systems are discussed. The main focus of this work is the comparison of the wave numbers obtained via the use of the constructed and analytical normal mode vectors $\overline{{\mathbf{Q}}_i}$ and Q_i, respectively. Although the experimental data (if available) is not 100% comparable to the executed calculations, the comparison gives an impression of the general quality of the applied procedure and level of theory. In general only the fully optimized geometries (Conf. A) were compared to the experiment, while the geometry with fixed box dimensions (Conf. B) was considered only to compare constructed and analytical vibrational frequencies.

Germanium dioxide

The first example is comprised of a germanium dioxide (001) surface with two adsorbed hydrogen atoms. Since the system contains 20 atoms the number of vibrational degrees of freedom amounts to 57 resulting already in a cumbersome, time‐consuming evaluation of the analytical normal modes in addition to the rather costly requirements in terms of system memory as well as hard disk capacity imposed by the periodic quantum chemical treatment.59

The possibility to avoid the harmonic frequency calculation proved to be a substantial improvement in the general applicability as well as the computational effort. While in this work the chosen system still enables the comparison of the different strategies (i.e., constructed vs analytical normal modes), a further enlargement of the system would lead to a prohibitively expensive computing time, thus rendering the approach based on constructed modes the only option. As outlined above two different minimum geometries have been considered. First the unit cell dimension and the atom positions were optimized simultaneously (Conf A) while in the second case only the atom positions have been subject to minimization (Conf B). The dimensions of the optimized 2d‐periodic unit cells are shown in Table 1. It can be seen that the optimization of the entire system (Conf A) leads to a notable relaxation of the surface structure. Therefore, the vibrational properties of conformer A are expected to provide a more reliable representation of the surface. For both configurations the vicinity of the OH groups on the surface may induce inter‐mode coupling and a two‐dimensional Numerov treatment appears mandatory.

Table 1.

Unit cell parameters of the two considered GeO₂(001) minimum geometries under 2d‐periodic boundary conditions optimizing the entire system (Conf A, cell dimension plus atom positions) and only the atom positions (Conf B), respectively. The cell dimensions a and b are given in Angstrom, the respective angles γ in degree.

	Conf A	Conf B
a	4.508	4.364
b	4.525	4.364
γ	93.584	90.0

The wave numbers of the OH vibrational modes of both conformers are presented in Table 2. Since the one‐dimensional case does not account for any coupling between the modes, large deviations between the analytical and constructed modes are observed. In the two‐dimensional case the differences vanish with a consistent deviation of 3 cm⁻¹ corresponding to 0.1%. Considering the typical accuracy of experimental setups being in the range of approx. 2–8 cm⁻¹, the observed deviations between the analytical and constructed normal modes are within the same range of precision.

Table 2.

Predicted wave numbers of the OH modes on the GeO₂ (001) surface in cm⁻¹ obtained at PBEsol level and the angle α between the analytical and constructed normal modes in degree. Conf A and B correspond to different minimum configurations with and without surface relaxation, respectively.

Conf A
		Analytical		Constructed
	harm	1D	2D	1D	2D	α
asym	3547	3361	3215	3547	3212	3.05
sym	3556	3310	3243	3362	3240	0.09
Conf B
		Analytical		Constructed
	harm	1D	2D	1D	2D	α
asym	3453	3558	3334	3604	3337	0.35
sym	3479	3437	3349	3446	3352	0.34

The angle between the respective normal mode vectors α obtained via the associated scalar products remain in the range of 0.09°–3.05°, respectively. Comparing the angle to the respective results no correlation between angle and accuracy of the predicted wave numbers can be identified.

The vibrational frequencies of Conf. A show a good agreement with the experimental spectrum.81 Although experiment and calculation are not 100% comparable this shows that the calculations lead to reasonable results.

Lithium imide

As a second example lithium imide (Li₂NH) was chosen in order to investigate the performance of the approach in a bulk material. The respective unit cell parameters have been taken from the article of Ohoyama and co‐workers69 and Noritake and co‐workers.82 Due to the fact that the occupancy of the hydrogen atoms is reported in the range of 1/4 to 1/24 for different structural models, a selection of systems had to be made to achieve a manageable system size. The unit cells employed in this study are composed of two NH‐groups surrounded by four lithium ions. Two conformers with parallel (P) and opposing (O) alignment of the N‐H groups as suggested by Magyari‐Köpe et al.70 and Mueller et al.71 have been employed, both being subject to energy minimization optimizing both cell dimension and atom positions (Conf P_A and O_A) as well as considering only the atomic positions (Conf P_B and O_B). The respective structural parameters of the unit cell are summarized in Table 3. It can be seen that the unit cell obtained for the P_A conformer remains close to the constrained geometry (P_B, O_B) whereas a significant alteration is observed for the O_A case. This implies that the anti‐parallel configuration of the NH bonds appears to be of minor relevance.

Table 3.

Primitive cell parameters of the configuration with parallel (P) and opposing (O) orientation of the NH groups considered in the test calculations for Li₂NH considering the cell plus atom positions (A) as well as only the atomic positions (B) in the energy minimization. The cell dimensions a, b, and c are given in Angstrom, the respective angles α, β, and γ in degree.

	a	b	c	α	β	γ
P A	3.467	3.641	6.912	58.202	62.769	58.321
O A	3.491	3.512	7.419	61.772	73.168	59.802
P B,O B	3.590	3.590	7.080	60.000	60.000	60.000
4real	3.590	3.590	7.080	60.000	60.000	60.000

The predicted wave numbers obtained from the respective one‐dimensional and two‐dimensional Numerov treatment for the different Li₂NH model systems are listed in Table 4. Again a substantial decrease in wave numbers from the harmonic approximation to the two‐dimensional analysis of the vibrational quantum system is observed in line with the simultaneous consideration of anharmonicity and mode–mode coupling discussed earlier. Similar as in the case of the water molecule, anharmonicity may result in a blue‐shift of the respective wave numbers resulting from higher order contributions to the potential.

Table 4.

Wave number in cm⁻¹ obtained for the N‐H stretch vibration for different configurations of Li₂NH. P and O refers to configurations with parallel and opposite orientation of the N‐H bonds, while A and B denote energy minimization with and without consideration of the unit cell parameters.

	Conf. P A					Conf. P B
		Analytic		Constructed			Analytic		Constructed
	harm	1D	2D	1D	2D	harm	1D	2D	1D	2D
NH1(sym)	3274	3189	3159	3169	3160	3301	3223	3129	3221	3130
NH2(asym)	3276	3391	3161	3167	3161	3307	3408	3135	3398	3136
	Conf. O A					Conf. O B
		Analytic		Constructed			Analytic		Constructed
	harm	1D	2D	1D	2D	harm	1D	2D	1D	2D
NH1a	3288	3177	3127	3283	3127	3445	3432	3312	3522	3311
NH2a	3322	3168	3146	3205	3146	3495	3396	3354	3419	3353

^aIn Configuration O the different vibrations cannot be categorized as symmetric and asymmetric stretch modes.

Comparison to experimental measurements reporting a dominant peak at 3180 cm⁻¹ 83 in very good agreement with the prediction obtained for the P‐conformers (N‐H bonds in parallel orientation), in particular the case considering the relaxation of atoms and the unit cell (P_A). Again, this shows that the Numerov treatment with both, analytical and constructed normal modes, leads to reasonable results.

Comparison of the prediction obtained via the constructed normal modes yields wave numbers within 1% of the values obtained using the analytical mode vectors. In the two‐dimensional case all conformers showed deviations of 1 cm⁻¹ and less. Nevertheless, the angle between the analytical and constructed normal vectors remained within a range of 2.29°–2.92^° in all cases, the deviation in the associated reduced masses are in the range of 0.102–4.67 mg/mol.

The results clearly demonstrate that although the employed model configurations do not fully reflect the variation of all possible structural motifs in the crystal the obtained results provide an excellent evidence in favor of the presented strategy to study vibrational phenomena. The selected system lithium imide is a particularly well‐suited example to demonstrate the allocation of IR‐peaks, providing substantial insight into the underlying chemical structure. Since the presented model system contains only 8 atoms corresponding to 21 vibrational modes, a benchmark of the constructed normal modes against their analytical counterpart was feasible. Extending the system to larger unit cells soon results in an overwhelming computational demand, especially in case of advanced approaches (such as VSCF and VPT2). The possibility to focus exclusively on the experimentally most visible N‐H vibrations (relevant for instance in case of purity determination, quality assurance, etc.) and avoiding the requirement to analyze the harmonic frequencies of the entire system is thus of great advantage and enables the application of the outlined approach to more complex systems.

α‐quartz—(001)‐surface

The third example is the hydroxylated α‐quartz (001)‐surface reported by Catlow et al.64 The 21 atoms of the system result in a total of 60 normal modes, whereas only the two O‐H modes are of main interest, for instance in spectroscopic measurements of surface wetting. The investigated chemical system is a 18‐layer α‐quartz (001)‐surface. Following the notation of Catlow, the top layer of the solid is hydroxylated whereas the opposite side features the reconstructed configuration.64 The minimum structure obtained at PBESOL‐level is shown in Figure 3, the associated hydrogen bonds are marked by dashed lines. These hydrogen bonds in between the individual OH groups make the system challenging and highly complex: Due to the periodic extension of the surface OH group act as each acceptor for its respective counterpart, forming a unique H bond wire motif along the surface which is depicted in Figure 4.

The potential obtained from the respective 2d‐normal mode scan is shown in Figure 5. The unique structural features of the H bond wire leads to a double well potential. The second minimum of the potential is at 4.3 kcal/mol compared to the global minimum of this potential energy surface. This local minimum can be seen as evidence for the possibility of a concerted proton transfer (PT) reaction of both H‐atoms. The higher value of the potential can be explained by the missing surface relaxation of the oxygen atoms and the underlying structure of the solid. This concerted PT leads to a mirror image of the hydrogen bond structure, with a comparably high reaction barrier of approximately 40 kcal/mol.

Figure 5.

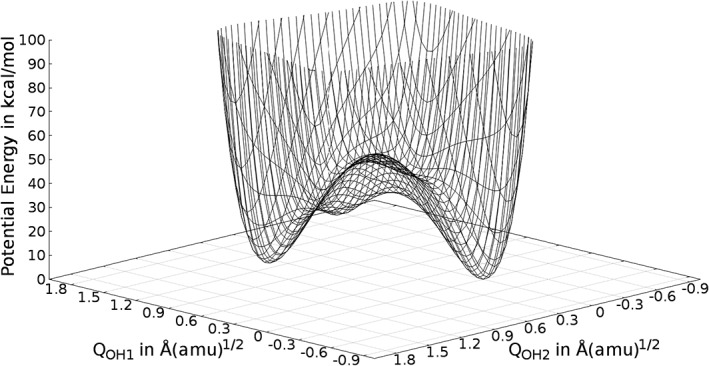
Potential energy surface of the two hydroxy groups on the α‐quartz surface. The potential is plotted up to 100 kcal/mol. Values above are ignored.

While the missing surface relaxation may appear as a potential limitation of this approach, one should keep in mind that PT reactions may occur spontaneously and are often aided by quantum tunneling. As such the transfer of the protons may occur on a faster time scale as the relaxation of the heavier O and Si atoms of the solid and hence, the quantification of the unrelaxed minimum is of particular interest. Interestingly, the 2d‐Numerov procedure yields two separated sets of vibrational wave functions that can be unambiguously assigned to either of the two minima. Two of the wave functions resulting from the Numerov procedure now act as ground states for the individual minima (cf. Figure 6). Since the associated energy difference between these states amounts to 4.3 kcal/mol (≈1120 cm⁻¹), the associated wave functions are clearly separate. No superposition of these eigenstates occur, implying that tunneling is not relevant on this potential energy surface.

Figure 6.

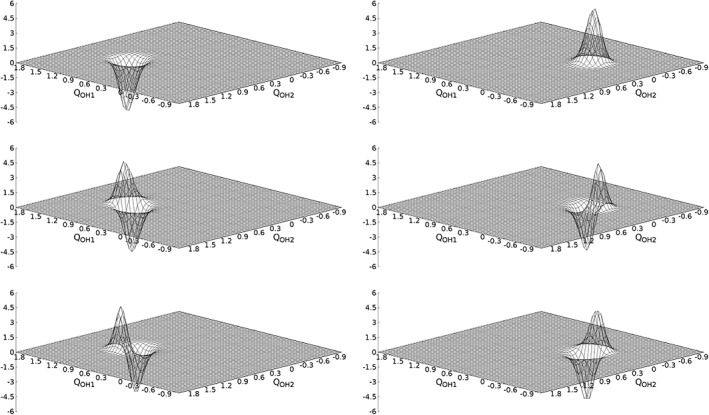
Due to the double‐well potential and the large reaction barrier of approx. 40 kcal/mol two separate sets of vibrational wave functions are obtained for the global (right) and local minimum (left). The associated excited vibrational states show the expected orthonormality, i.e., a local rotation by approx. 90 ^∘. The displacement of the modes Q _OH1 and Q _OH2 is given in Å$\sqrt{\mathrm{amu}}$.

Similarly as the two separate ground states associated excited wave functions are observed, that show the expected orthonormal features visible by a local rotation close to 90^° (see Fig. 6). The resulting vibrational frequencies obtained via analytical and constructed normal modes are listed in Table 5. Comparison of the two sets shows that the vibrational frequencies in the global minima show a maximum deviation of 4 cm⁻¹. This agreement is in line with the observation of the GeO₂ and Li₂NH systems presented above. However, in case of the local minimum a larger deviation of 8 and 44 cm⁻¹ is observed. This large deviation highlights a potential limitation of this strategy to obtain normal modes, namely the constructed normal modes are only valid close to the associated minimum of the potential energy surface.

Table 5.

Wave number in cm⁻¹ obtained for the O‐H stretch vibrations of hydroxylated α‐quartz according to Catlow et al.64 The global minimum data refers to the vibrational frequencies of the OH‐vibrations of the minimum structure, while the local minimum refers to the OH‐vibrational frequencies for the second minimum obtained after a concerted proton transfer without relaxation of the oxygen atoms. Harmonic and one‐dimensional calculations do not provide data for the local minimum.

	Global minimum					Local minimum
		Analytic		Constructed		Analytic	Constructed
	harm	1D	2D	1D	2D	2D	2D
OH1a	3243	3096	3044	3112	3041	2810	2818
OH2a	3372	3277	3204	3314	3200	2994	3038

^aThe different vibrations cannot be categorized as symmetric and asymmetric stretch modes.

Due to the complexity of the H bonded structure no experimental data addressing this particular surface motif could be found in the literature. In Ref.84 three different types of α‐quartz powder were investigated. All IR‐spectra showing a small band in the range of 2800–3000 cm⁻¹ that could be the result of a concerted PT reaction. Furthermore two of the three samples showed a distinct band at ≈3300 cm⁻¹, which corresponds to a deviation of ≈3% of the results in the global minima. However, also in this case the experimental data shows that the Numerov treatment combined with constructed normal modes leads to reasonable results.

In case of both O‐H vibrations the angle between analytical and constructed modes is below 0.084^° and the difference of the effective mass is 5.56 and 1.55 mg/mol, respectively. These results show that the constructed modes are in good agreement with the analytical normal modes (deviations below 1%). Looking at this system with 21 atoms and only 2 vibrational modes of interest the approach using constructed normal modes showed to be a promising alternative to save computational time with a minimal loss of accuracy for the vibrations associated to the global minimum.

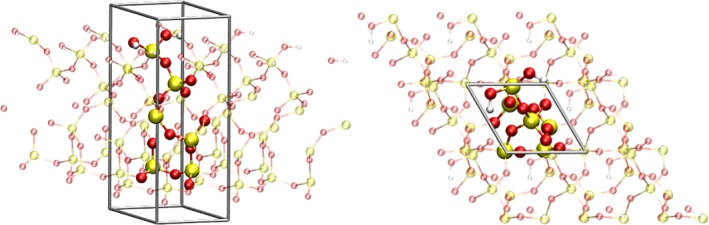
Titan dioxide—(001) surface

As fourth example the (001)‐surface of rutil‐structured titan dioxide was investigated. Due to the large number of atoms and at the same time the large number of electrons amounting to 123 and 1530, respectively, the computational effort to execute a frequency analysis is massively increased, especially since no use of symmetry considerations can be employed to accelerate the calculation. Moreover, 362 out of the 366 expected normal modes can be expected to represent vibrations linked to the lattice of the solid‐state system, which due to the high reduced masses occur at comparably low frequencies. Two modes are the associated Ti‐O‐H frequencies which too can be expected to be about factor of 2 smaller than the O‐H stretching vibration. Thus, since the OH vibration occur at a distinct range of wave numbers, an approach to focus only on the vibrational modes of interest is of particular benefit. The determination of the harmonic frequencies required approximately 10–15 days using 32 computing nodes (Intel Xeon X5650), which appears rather high considering the at most 0.5% of the computed normal modes are relevant for the following investigations. Although a harmonic frequency analysis was done in crystal for up to 1000 atoms,85 such an approach greatly reducing the required execution time to just determine the normal vectors of the two OH stretch vibrations would enable multiple studies within the same time frame for instance the impact of different OH configurations on the surface. Figure 7 depicts the minimum configuration of the TiO₂ (OH)₂ system considered in this example. During the energy minimization of the system dissociation of the H₂O molecule took place forming an isolated OH‐group pointing away from the surface. The transferred proton is accepted by a surface oxygen atom, which forms a hydrogen bond to the water oxygen atom. As a consequence the latter can be expected to have a significantly reduced wave number. However, due to the similar frequency range and the spatial proximity of these OH bonds an explicit consideration of inter‐mode coupling in addition to anharmonic contributions appears necessary. The harmonic frequencies calculated using Crystal14 are 3153 and 3597 cm⁻¹. Application of Numerov's procedure in 2 dimensions yields 2890 and 3445 cm⁻¹, compared to 2898 and 3452 cm⁻¹ in the one‐dimensional case. While the considered anharmonicity leads to strong deviations of 263 and 152 cm⁻¹, respectively.

Figure 7.

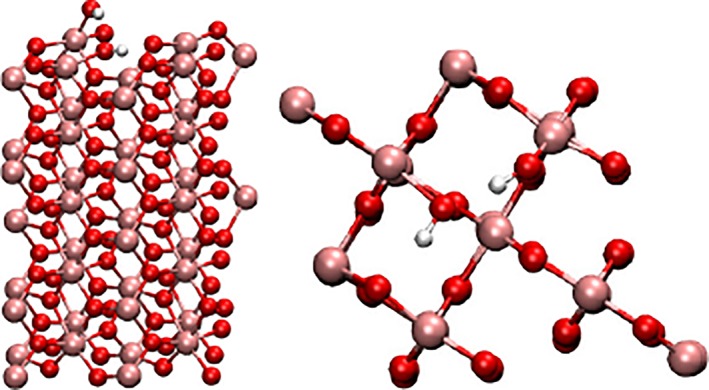
TiO₂ (001) surface with chemisorbed H₂O forming two OH‐groups on the surface in front (left) and top view (right). [Color figure can be viewed at wileyonlinelibrary.com]

Water

The water molecule was chosen to provide evidence that the approach can be applied to two H‐atoms binding to the same oxygen, thus leading to a particular strong coupling between the vibrational modes. The benefit of avoiding the harmonic frequency analysis is negligible in case of small molecules like water, however the respective potential energy surface has been extracted from the three‐dimensional Numerov investigation presented earlier.36

The one‐dimensional and two‐dimensional results using the constructed normal modes $\overline{\mathbf{Q}}$ obtained via the reduced Hessian yields wave numbers in good agreement with the analytical result (see Table 6), the respective deviations being 8 (sym) and 4 cm⁻¹ (asym), respectively. The angle between $\overline{\mathbf{Q}}$ and Q representing the agreement of the constructed and analytical normal mode vectors was found as 1.6^° (sym) and 3. 1^∘ (asym), respectively. The associated difference in reduced mass amounts to 4.09 (sym) and 7.33 mg/mol (asym). Also for D₂O the constructed normal modes lead to a good agreement compared to the two‐dimensional analytical Numerov treatment with deviations of 4 (sym) and 9 (asym) cm⁻¹.

Table 6.

Wave numbers in cm⁻¹ for the symmetric and asymmetric stretch vibration of H₂O and D₂O obtained via a 1d‐, 2d‐, and 3d‐ Numerov approach at CCSD(T)/aug‐cc‐pVQZ level and a grid‐spacing of h = 0.025 A. The prediction obtained via the constructed normal modes are in very good agreement with those employing the analytical ones.

H 2O		Analytical			Constructed
	harm	1D	2D	3Da	1D	2D	exp.b
sym	3842	3757	3678	3668	3751	3670	3657
asym	3951	4037	3778	3744	4045	3782	3756
D 2O		Analytical			Constructed
	harm	1D	2D	3Da	1D	2D	exp.b
sym	2769	2725	2683	2679	2730	2687	2672
asym	2895	2942	2801	2784	2954	2810	2788

^aRef. 36.

^bRef. 86.

These results can be seen as a proof of concept for the adequate representation of the vibrational properties by the constructed modes and demonstrate that the vibrational frequencies of two OH bonds originating from the same oxygen atom can be accurately calculated using this approach, leading to a dramatic improvement over a simple one‐dimensional treatment. At the same time it shows that the approach of the constructed normal modes is applicable also to deuterated bonds.

Conclusions

In this work a strategy for the approximation of strongly localized vibrational modes such as O‐H and N‐H bonds was investigated. In the presented approach the normal modes of interest are approximated via a reduced Hessian in order to reproduce the interactions between selected XH bonds, while considering the remaining part of the chemical system as rigid. The underlying vibrational degrees of freedom can be constructed solely on the basis of the minimum geometry of the system, thus avoiding the often costly harmonic normal mode analysis. Although in this manuscript the approach is demonstrated only for systems containing two XH bonds at a time, the number of considered bonds can be in principle chosen arbitrarily.

Benchmark computations comparing the result using these constructed modes against their analytical analogues yield deviations of just a few wave numbers in case of the four different test systems, being two hydroxy groups on GeO₂ (001), two N‐H bonds in the Li₂NH bulk material, and two hydroxy groups on α‐quartz(001) and Rutil(001). The water molecule was only considered to demonstrate that the vibrational frequencies of two OH bonds originating from the same oxygen atom can be accurately calculated using this approach. Furthermore, the investigation of heavy water showed that the constructed normal modes treatment is also applicable in case of deuterated bonds.

The extension to 2d‐periodic and 3d‐periodic solid‐state systems demonstrates the advantage in exploiting the local character of vibrational modes, thus greatly reducing the associated computational effort. This is of particular interest in those cases, in which the determination of analytical normal modes is prohibitively expensive or not implemented in a particular quantum chemical program. The angle between the analytical and constructed normal modes as well as the deviation of the reduced masses provide another means to measure the accuracy of the procedure. The largest registered angle amounts to approx. 3.5^°, the highest observed deviation of the reduced mass was 7.33 mg/mol.

Since the potential energy surface required for the Numerov procedure needs only single point information along the involved normal mode vectors the approach is in principle perfectly parallelizable. Due to the sparsity of the respective matrix problem, the Numerov procedure itself does not provide any bottleneck even if large grids and stencil sizes are employed. A big advantage of the applied Numerov method is that once the potential is given no additional assumptions about the form of the wave function have to be introduced. The accuracy of the resulting eigenenergies and respective wave functions depend solely on the quality of the grid (i.e., the applied level of theory and the grid‐spacing) and the chosen stencil size to approximate the second derivative in Schrödinger's equation.

The presented general strategy for the investigation of strongly localized vibrational phenomena provides access to a broad variety of chemical systems including solid‐state structures and has the potential to provide detailed insight into the anharmonic and coupling properties in various chemical environments. Future investigations will focus on the possibility to construct the normal mode vectors of more complex vibrations such as angle bending and dihedral rotation, which will further enhance the spectrum of the outlined methodology.

How to cite this article: Kuenzer U., Klotz M., Hofer T. S.. J. Comput. Chem. 2018, 39, 2196–2209. DOI: 10.1002/jcc.25533