Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2019 Feb 5;50(3):816–823. doi: 10.1002/jmri.26679

Paraspinal Muscle DTI Metrics Predict Muscle Strength

Elisabeth Klupp 1,2,✉, Barbara Cervantes 2, Sarah Schlaeger 1,2, Stephanie Inhuber 3, Florian Kreuzpointer 3, Ansgar Schwirtz 3, Alexander Rohrmeier 1, Michael Dieckmeyer 2, Dennis M Hedderich 1, Maximilian N Diefenbach 2, Friedemann Freitag 2, Ernst J Rummeny 2, Claus Zimmer 1, Jan S Kirschke 1, Dimitrios C Karampinos 2, Thomas Baum 1
PMCID: PMC6767405  PMID: 30723976

Abstract

Background

The paraspinal muscles play an important role in the onset and progression of lower back pain. It would be of clinical interest to identify imaging biomarkers of the paraspinal musculature that are related to muscle function and strength. Diffusion tensor imaging (DTI) enables the microstructural examination of muscle tissue and its pathological changes.

Purpose

To investigate associations of DTI parameters of the lumbar paraspinal muscles with isometric strength measurements in healthy volunteers.

Study Type

Prospective.

Subjects

Twenty‐one healthy subjects (12 male, 9 female; age = 30.1 ± 5.6 years; body mass index [BMI] = 27.5 ± 2.6 kg/m2) were recruited.

Field Strength/Sequence

3 T/single‐shot echo planar imaging (ss‐EPI) DTI in 24 directions; six‐echo 3D spoiled gradient echo sequence for chemical shift encoding‐based water–fat separation.

Assessment

Paraspinal muscles at the lumbar spine were examined. Erector spinae muscles were segmented bilaterally; cross‐sectional area (CSA), proton density fat fraction (PDFF), and DTI parameters were calculated. Muscle flexion and extension maximum isometric torque values [Nm] at the back were measured with an isokinetic dynamometer and the ratio of extension to flexion strength (E/F) calculated.

Statistical Tests

Pearson correlation coefficients; multivariate regression models.

Results

Significant positive correlations were found between the ratio of extension to flexion (E/F) strength and mean diffusivity (MD) (P = 0.019), RD (P = 0.02) and the eigenvalues (λ1: P = 0.026, λ2: P = 0.033, λ3: P = 0.014). In multivariate regression models λ3 of the erector spinae muscle λ3 and gender remained statistically significant predictors of E/F (R2 adj = 0.42, P = 0.003).

Data Conclusion

DTI allowed the identification of muscle microstructure differences related to back muscle function that were not reflected by CSA and PDFF. DTI may potentially track subtle changes of back muscle tissue composition.

Level of Evidence: 3

Technical Efficacy: Stage 2

J. Magn. Reson. Imaging 2019;50:816–823.

Keywords: diffusion tensor imaging, lumbar spine, muscle microstructure, muscle strength, paraspinal musculature

CHRONIC BACK PAIN is a multifactorial disease; besides physical and biomechanical problems, also psychological and psychosocial factors have important roles in the development and continuance of pain.1 By means of conventional imaging methods, causes of back pain often cannot be identified.2 Besides the alignment and bone structure of the spine, changes of the paraspinal musculature have an important influence on the stability and therefore the development of back pain and other back muscle‐related diseases.3 It would be of clinical interest to identify imaging biomarkers of the musculature that are related to muscle function and strength and therefore useful in the early diagnosis of back muscle‐related diseases.

Quantitative magnetic resonance imaging (MRI) enables the noninvasive assessment of muscle tissue composition. Chemical shift encoding‐based water–fat MRI is a frequently used quantitative MRI technique, which enables a quantification of inter‐ and intramuscular proton density fat fraction (PDFF).4 MR‐based assessment of the fat composition of paraspinal muscles has been proposed as a surrogate marker in subjects with intervertebral disc disease, osteoporosis, sarcopenia, and neuromuscular disorders.3, 5 Previously published studies demonstrated that PDFF of muscle tissue significantly correlates with strength measurements.6, 7, 8 Furthermore, PDFF seems to predict muscle strength better than the assessment of the cross‐sectional area (CSA) of the musculature, which was shown in a previously published study.9

Diffusion tensor imaging (DTI) is an MRI method enabling the microstructural examination of biological tissues by quantifying the diffusion of water molecules and its directional anisotropy noninvasively.10 The DTI‐derived parameters (eigenvalues [λ1, λ2, λ3], mean diffusivity [MD], radial diffusivity [RD], apparent diffusion coefficient [ADC] and fractional anisotropy [FA]) are sensitive to changes in microstructure, so that pathological and stress‐dependent changes in tissue composition can be identified. Recent studies have demonstrated the feasibility of DTI in skeletal muscle and its capability for noninvasive characterization of muscle tissue architecture at a microstructural level.11, 12, 13, 14, 15, 16, 17, 18, 19, 20 Recently, this method has also been used to examine the influence of different diseases21, 22 or injuries.11, 23 Also, discrete and subclinical changes of the musculature caused by strenuous exercise can be identified with DTI that can remain undetected by using conventional T2‐weighted fat‐suppressed MRI sequences, as shown in a longitudinal study examining athletes before and after running a marathon.24

Little is known about the associations between muscular DTI parameters and physiological characteristics of musculature. Deux et al showed in different muscles of the calf that contraction and passive elongation leads to significant changes in DTI parameters.25 Muscular shortening leads to an increased fiber radius with a decrease in muscle length, allowing a facilitated diffusion of water molecules in the radial direction, resulting in increased λ2, λ3, and MD and decreased FA. Consistently, passive muscular stretching causes increased FA and decreased MD values.26 A general influence of physical training on the diffusion properties of the leg musculature was demonstrated by Okamato et al.27 Associations between DTI‐parameters and maximal muscle power were found for the soleus muscle, more specifically, significant negative correlations with FA and significant positive correlations with RD.28 To our best knowledge, all of these DTI studies have been performed in leg muscles and there are no studies existing that have examined relations between DTI parameters and muscle strength in the paraspinal musculature.

The purpose of this work was to investigate the associations of DTI parameters of the lumbar paraspinal muscles with isometric strength measurements in young and healthy volunteers. We hypothesized that DTI parameters would improve the prediction of muscle strength beyond muscular PDFF and muscle CSA.

Materials and Methods

Twenty‐one young healthy subjects (12 male, 9 female; age = 30.1 ± 5.6 years (range 22–41 years); body mass index (BMI) = 27.5 ± 2.6 kg/m2) were recruited for this study. Exclusion criteria were history of lower back pain, vertebral fractures, neuromuscular diseases, and general MRI contraindications. The height and body weight of each subject were noted and the BMI was calculated dividing body weight (kg) by height squared (m2). All subjects gave written informed consent for MRI examinations and biometrical strength measurements before participation in the study. The study was approved by the local institutional Committee for Human Research.

MRI Acquisition Protocol

The lumbar spine of all subjects was scanned with a 3 T whole‐body system (Ingenia, Philips Healthcare, Best, Netherlands) using the built‐in‐the‐table posterior coil elements (12‐channel array) and an anterior coil (16‐channel array to ensure best signal quality. Subjects were positioned head‐first in a supine position.

DTI was performed at the lumbar spine (L4 to L5) using a reduced‐field of view (FOV) single‐shot echo planar imaging (ss‐EPI) sequence employing a combination of non‐coplanar excitation and refocusing pulses combined with outer volume suppression29 to reduce geometric distortions and to minimize motion and off‐resonance effects from the abdominal organs (phase‐encoding direction was anterior/posterior). To reduce chemical shift artifacts and minimize the effect of fat on the muscle DTI metrics, the following fat suppression techniques were combined: Suppression of the main aliphatic fat peak at 440 Hz from the water peak was performed using spectrally adiabatic inversion recovery (SPAIR) with inversion time = 220ms in conjunction with slice‐selection gradient reversal (SSGR). Suppression of the olefinic fat peak was performed using an 18 msec spectrally selective Gaussian‐windowed sinc pulse30 with frequency offset = 200 Hz. The other sequence parameters were as follows: FOV = 220 × 147 × 80 mm3; acquisition voxel = 3 × 3 mm2; slice thickness = 8 mm; repetition time / echo time (TR/TE) = 2457/65 msec; partial‐Fourier reduction factor = 0.75; b‐values = 0, 400 with 2 and 3 averages, respectively; 24 diffusion directions; scan duration = 6 min and 8 sec. A small FOV in the feet–head direction was especially selected to minimize B0 inhomogeneity effects on the performance of the olefinic fat peak suppression pulse.

An axially prescribed six‐echo 3D spoiled gradient echo sequence was used for chemical shift‐encoding‐based water–fat separation covering the lumbar spine. The sequence acquired the six echoes in a single TR using non‐flyback (bipolar) readout gradients and the following imaging parameters: TR/TEmin/ΔTE = 6.4/1.1/0.8 msec, FOV = 220 × 401 × 252 m3, acquisition matrix = 68 × 150, voxel size = 3.2 × 2.0 × 4.0 mm3, frequency encoding direction = L/R, no sensitivity encoding (SENSE), scan time = 1 min and 25 sec. A flip angle of 3° was used to minimize T1‐bias effects.31

Generation of Quantitative MR maps

The b = 400 diffusion‐weighted ss‐EPI data were registered to b = 0 ss‐EPI data using an affine transformation to minimize geometric distortions produced by eddy currents. Diffusion tensors were estimated from DTI data using nonlinear least‐squares fitting in diffusion imaging in Python (DIPY) and DTI parameters were computed from the derived eigenvalues.

The gradient echo imaging data were processed online using the fat quantification routine of the vendor. The multiecho mDIXON algorithm performs a phase error correction followed by a complex‐based water–fat decomposition using a precalibrated seven‐peak fat spectrum and a single T2* to model the signal variation with echo time. The imaging‐based PDFF maps were computed as the ratio of the fat signal over the sum of fat and water signals.

MR Image Segmentation

Segmentation of the paraspinal muscles was performed manually by using the free open‐source software "Medical Imaging Interaction Toolkit" (MITK, developed by the Division of Medical and Biological Informatics, German Cancer Research Center, Heidelberg, Germany; www.mitk.org) on the "average of diffusion‐weighted" images. Due to an expected different fiber orientation, the medial and lateral region of the erector spinae muscles on both sides were separately segmented, resulting in four analyzable muscle regions. Round‐shaped regions of interest (ROIs) were drawn manually in the interior two‐thirds of these muscles compartment on the "average of diffusion‐weighted" images avoiding the inclusion of vessels, fasciae, and surrounding intermuscular fat tissue. The exclusion of intermuscular fat was achieved by visual inspection of the "average of diffusion‐weighted" images by a radiologist (E.K.; with 3 years of experience in musculoskeletal radiology).

The first and last slice were excluded from analyses due to increased B0 inhomogeneity effects, resulting in eight analyzable slices. Eigenvalues, FA, MD, and RD values were calculated from the DTI maps32 in each muscle region separately. Mean values of the left and right side were averaged. Furthermore, the values of the medial and lateral muscle regions were analyzed separated and averaged, respectively.

To assess CSA and PDFF of the lumbar erector spinae muscle, left and right muscles were segmented separately from the upper endplate level of L2 to the lower endplate level of L5. To allow the determination of muscle CSA, ROIs were placed at the contour of the muscle (see Fig. 1). CSA and PDFF of each muscle were extracted and the mean values of left and right side were averaged, respectively.

Figure 1.

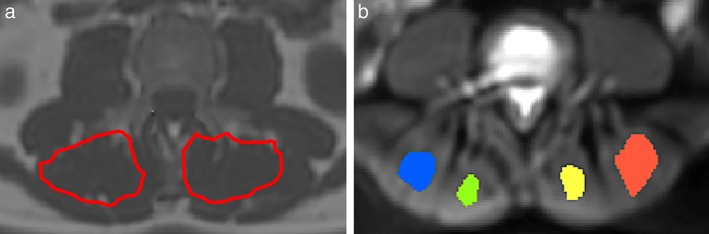
Figure 1

Open in a new tab

(a) Representative PDFF map with manually segmented muscle compartments. Segmentation for CSA and PDFF was performed from the upper endplate level of L2 to the lower endplate level of L5. (b) Exemplary "average of diffusion‐weighted image" with representative intramuscular ROIs for extraction of values.

Isometric Strength Measurement

Muscle flexion and extension maximum isometric torque [Nm] at the back was measured with a rotational dynamometer (Isomed 2000, D&R Fertsl, Hemau, Germany), which was calibrated exactly on each individual body dimension. The subjects were seated in an upright position. The setup for isometric muscle strength measurements is shown exemplarily for one volunteer in Fig. 2 and described in detail previously.9 To ensure the reproducibility of strength measurement, each subject performed between five and eight repetitions with maximum voluntary isometric contraction with breaks in between. Reproducibility measurements for paraspinal muscle strength measurements were reported by Roth et al.33

Figure 2.

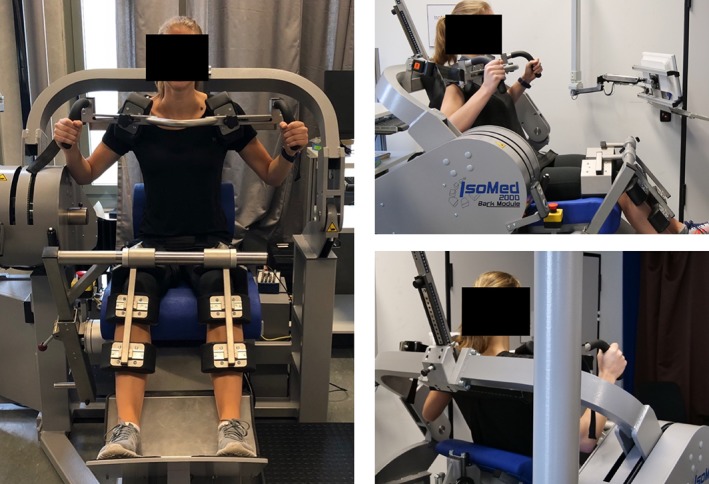
Figure 2

Open in a new tab

Setup for isometric muscle strength measurements.

The ratio between extension and flexion muscle strength (E/F) was computed to obtain normalized values.

Statistical Analysis

Statistical analyses were performed with SPSS v. 23.0 (Chicago, IL). All tests were done using a two‐sided P < 0.05 level of significance. Parameters were presented as mean ± standard deviation (SD). Strength measurements, CSA, and PDFF were compared between males and females using t‐tests. Differences in DTI parameters of the medial and lateral region of the erector spinae muscle were assessed using paired t‐tests.

Pearson correlation coefficients were calculated between MRI‐derived diffusivity parameters (λ1, λ2, λ3, MD, RD, and FA, CSA, PDFF, age, BMI, and the ratio between extension and flexion strength, E/F). Bonferroni correction was applied for multiple comparison testing.

Stepwise multivariate regression models were used to determine significant predictors of the ratio between extension and flexion muscle strength. A forward selection approach was applied starting with no variables in the model, testing the addition of each variable using and adding the variables whose inclusion give statistically significant improvement of the fit.

Potential predictors (eigenvalues, MD, RD, FA, PDFF, CSA) and confounding variables (age, BMI, gender) were tested as covariates and included in the regression models if the level of significance was P < 0.05.

Results

A gender difference was found when comparing the ratio between extension and flexion with a significantly higher percentage value in females compared with males (178.53 ± 41.87% vs. 140.43 ± 35.09%; P = 0.035).

CSA of the erector spinae muscle was significantly greater in males compared with females (3.41 ± 0.77 cm2 vs. 2.32 ± 0.71 cm2; P = 0.004). No gender differences were found comparing PDFF of the erector spinae muscle (9.73 ± 2.68% in females vs. 11.32 ± 3.36% in males; P = 0.387). The values of the strength measurements, CSA, and PDFF are shown in Table 1.

Table 1.

Mean Values (± Standard Deviations) of Ratio Between Extension to Flexion Strength, Cross‐Sectional Area (CSA), and Proton Density Fat Fraction (PDFF) Compared Between Female and Male Subjects

Female (n = 9) Male (n = 12) P
Ratio
extension to flexion strength (%)		 178.53 ± 41.87 140.43 ± 35.09 0.035
CSA (cm2) 3.41 ± 0.77 2.32 ± 0.71 0.004
PDFF (%) 11.32 ± 3.36 9.73 ± 2.68 0.387
Open in a new tab

P‐values refer to the results of t‐tests.

Representative MD and RD maps of two different subjects are demonstrated in Fig. 3; the diffusivity and FA values of the medial and lateral region of the erector spinae muscle are shown in Table 2. No significant differences were found between the values of either region (MD: P = 0.744; FA: P = 0.699; λ1: P = 0.402; λ2: P = 0.14; λ3: P = 0.054; RD: P = 0.782). Furthermore, no significant gender differences were observed (MD: P = 0.901; FA: P = 0.571; λ1: P = 0.874; λ2: P = 0.633; λ3: P = 0.888; RD: P = 0.866).

Figure 3.

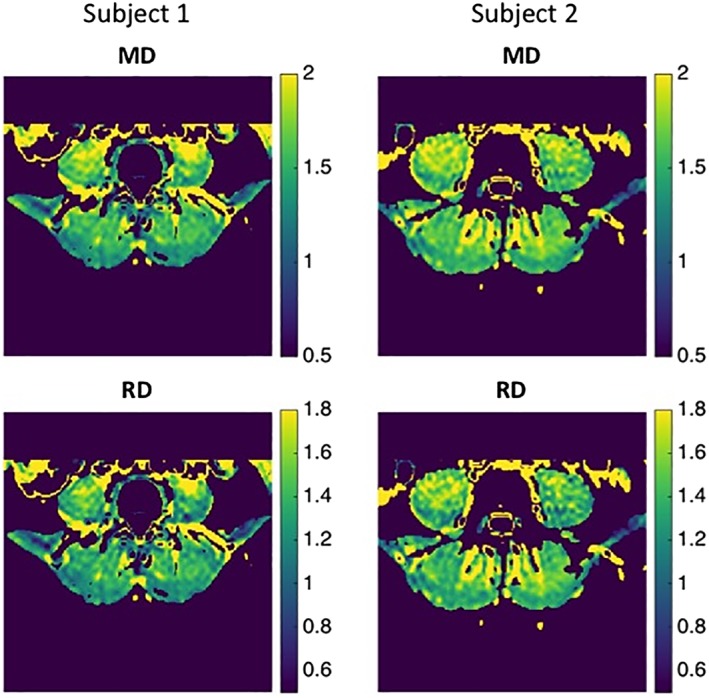
Figure 3

Open in a new tab

Representative MD‐ and RD‐maps of two subjects. Subject 1 (female, 22 years, BMI: 27.3) and Subject 2 (male, 33 years, BMI: 27.1) were observed to have the lowest (1) and highest (2) relative extension strength values among the examined cohort, respectively. MD and RD maps are shown in units of 10‐9 m2/s.

Table 2.

DTI Parameters of the Medial and Lateral Region of Erector Spinae Muscle (10‐9 mm2/s)

Erector spinae muscle medial region Erector spinae muscle lateral region P
MD 1.68 ± 0.10 1.68 ± 0.09 0.744
FA 0.19 ± 0.02 0.19 ± 0.01 0.699
λ1 2.03 ± 0.13 2.05 ± 0.11 0.402
λ2 1.61 ± 0.10 1.59 ± 0.08 0.140
λ3 1.39 ± 0.09 1.42 ± 0.08 0.054
RD 1.50 ± 0.09 1.50 ± 0.08 0.782
Open in a new tab

P‐values refer to the results of paired t‐tests comparing DTI parameters of these two muscle groups.

The DTI values of the erector spinae muscle showed no significant correlations with BMI (MD: P = 0.91; FA: P = 0.518; λ1: P = 0.843; λ2: P = 0.786; λ3: P = 0.956; RD: P = 0.913). Pearson correlation coefficients r for DTI values of the erector spinae muscle vs. strength measurements are shown in Table 3.

Table 3.

Pearson Correlation Coefficients r for Muscle Strength Measurements vs. DTI Parameters of the Erector Spinae Muscle

MD FA λ1 λ2 λ3 RD
Ratio Extension to Flexion Medial r = 0.527 (P = 0.014*) r = 0.042
(P = 0.855)		 r = 0.523 (P = 0.015*) r = 0.431 (P = 0.051) r = 0.518 (P = 0.016*) r = 0.483 (P = 0.026*)
Lateral r = 0.441 (P = 0.045*) r = –0.118
(P = 0.610)		 r = 0.393 (P = 0.078) r = 0.446 (P = 0.043*) r = 0.461 (P = 0.036*) r = 0.458 (P = 0.037*)
Average Medial
Lateral		 r = 0.507
(P = 0.019*)		 r = –0.040
(P = 0.863)		 r = 0.486
(P = 0.026*)		 r = 0.468
(P = 0.033*)		 r = 0.528
(P = 0.014*)		 r = 0.502
(P = 0.020*)
Open in a new tab
*

P < 0.05 (statistical significance); no statistical significance after applying the Bonferroni correction (P < 0.0028).

In the medial region of the erector spinae muscle, significant positive correlations were found between MD, λ1, λ3, and RD and the ratio of extension to flexion strength (MD: r = 0.527, P = 0.015; λ1: r = 0.523, P = 0.015; λ3: r = 0.518, P = 0.016; RD: r = 0.483, P = 0.026). In the lateral region, significant correlations were found between the ratio of extension to flexion strength and MD (r = 0.441, P = 0.045), λ2 (r = 0.446; P = 0.043), λ3 (r = 0.461, P = 0.036), and RD (P = 0.458; P = 0.037).

Figure 4 shows the plots of MD and λ3 with the ratio of extension to flexion strength for the medial and the lateral regions of the erector spinae muscle, respectively.

Figure 4.

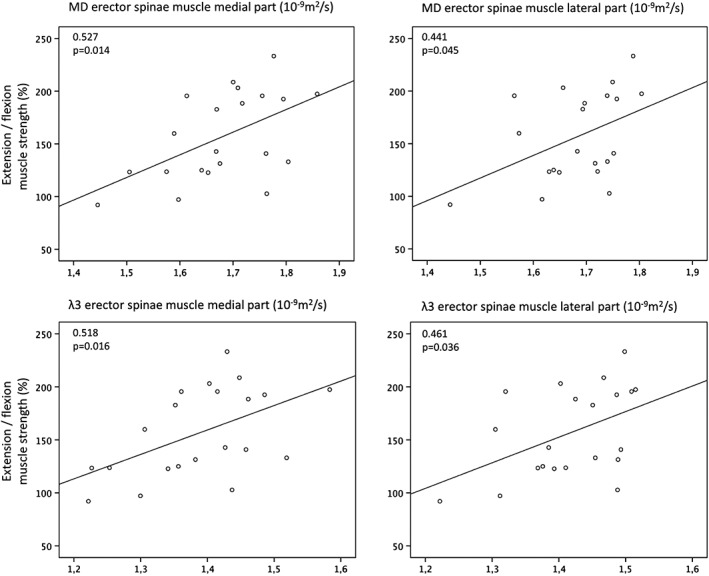
Figure 4

Open in a new tab

Top diagrams: Plots of erector spinae muscle MD values (left: medial region; right: lateral region) as a function of the ratio between extension to flexion muscle strength. Bottom diagrams: Plots of erector spinae muscle λ3 values (left: medial region; right: lateral region) as a function of the ratio between extension to flexion muscle strength.

Analyzing the averaged values of medial and lateral regions of the erector spinae muscle, significant positive correlations were found between the ratio of extension to flexion strength and MD, RD, and the three (MD: r = 0.507, P = 0.019; RD: r = 0.502, P = 0.020; λ1: r = 0.486, P = 0.026; λ2: r = 0.468, P = 0.033; λ3: r = 0.528, P = 0.014).

No significant correlations were found between erector spinae muscle PDFF and CSA vs. the ratio of extension to flexion strength, respectively (PDFF: r = 0,181; P = 0.431; CSA: r = –0.237, P = 0.300).

In multivariate regression models, MD and gender remained the only statistically significant predictors of the ratio of extension to flexion strength in the medial region of the erector spinae muscle (R2 adj = 0.24, P = 0.014; R2 adj = 0.42, P = 0.003). In the lateral region, MD and gender were included at a statistically significant level in the multivariate regression model for the prediction of the ratio of extension to flexion strength (R2 adj = 0.39, P = 0.004). Analyzing the averaged values of the medial and lateral regions, λ3 and gender remained the only statistically significant predictors of and the ratio of extension to flexion strength (R2 adj = 0.42, P = 0.003).

Discussion

The present study demonstrates an association between DTI parameters and isometric strength measurements in the clinically important lumbar muscle region in young healthy subjects. DTI performed better than PDFF and CSA in predicting muscle strength.

Significant positive correlations were found between relative muscle strength and diffusivity parameters, whereby MD, λ3, and RD—as measures of diffusion restriction—showed the strongest correlations. A plausible explanation of this result is the fact that stronger muscles have larger myofibers, which should reduce restriction effects, leading to higher RD and λ3 values. In a previous study Galban et al hypothesized that particularly λ3 correlates with the CSA of single fiber units.34 The study of the differences between λ2 and λ3 was outside the scope of the present work.35

Mazzoli et al36 investigated associations between diffusion parameters and changes in muscle fiber CSA of the calf muscles caused by passive lengthening and shortening and observed significant positive correlations between CSA and changes in RD in the dorsiflexed and plantarflexed positions. We did not observe significant correlations between diffusion parameters and CSA of the lumbar erector spinae muscle. This discrepancy can be explained by the different methodological approaches used to measure the muscle CSA. Mazzoli et al estimated the CSA of single muscle heads, whereas we used the CSA of the whole erector spinae muscle assessed in a large ROI. Furthermore, they investigated only RD values, rather than eigenvalues separately. In a recently published study, Berry et al demonstrated strong relationships between fiber size, MD, and λ3 and reported fiber size as the strongest predictor of diffusivity parameters; RD, however, was not analyzed separately in that study.37 They systematically simulated key microstructural features of skeletal muscle (eg, fiber size, fibrosis, edema, and permeability) and used stepwise multiple regression analyses to identify which microstructural features of skeletal muscle significantly predict diffusion parameters.

Our multivariate regression analyses revealed MD, λ3, and gender as statistically significant predictors of the ratio of extension to flexion muscle strength, whereas CSA and PDFF did not significantly contribute to the statistical model. Thus, DTI allows the characterization of back muscle fiber microstructure, which is related to muscle function and strength and may therefore be useful in the early diagnosis of back muscle‐related diseases and back pain.

Relationships between muscle DTI metrics and strength measurements have been previously reported only in the musculature of the lower extremities.25, 28 Deux et al demonstrated a significant influence of active dorsal and plantar flexion of the foot on the eigenvalues and ADC25 of the medial gastrocnemius and the tibialis anterior muscle; Scheel et al found significant associations of maximal muscle power of the soleus muscle with FA and RD.28 The present study analyzed associations between diffusion parameters and isometric strength measurements in the clinically important lumbar muscle region. However, the observed R2 adj is still relatively low. This finding points out that imaging biomarkers including CSA, PDFF, and DTI parameters reflect only partly the rather complex muscle functionality at the lumbar spine.

To obtain unbiased quantitative measurements of diffusion parameters, complete fat suppression is essential, especially in conditions where a significant fat content within the interesting tissue is expected.30, 38, 39 In this study we applied a rather conservative approach for fat suppression using SPAIR in conjunction with SSGR. SPAIR can achieve good suppression of the main methylene (‐CH2) and methyl (‐CH3) peaks, whereas the olefinic fat peak is suppressed with a second spectral fat saturation method. As described by Williams et al, this method leads to a good suppression for most of the fat spectrum, although it is sensitive to B0 inhomogeneities and causes the loss of ~10% of the water signal due to the spectral proximity of the olefinic fat and water peaks.30 However, the FOV in the head/feet direction had to be restricted in order to reduce the range of B0 inhomogeneities affecting the olefinic fat peak suppression pulse. Water–fat separation has also been previously proposed for olefinic fat suppression in muscle diffusion measurements,38, 39 but were not used in the present work.

The present study has some limitations. First, a rather small sample of young healthy subjects with relatively low fat fractions were examined in this pilot study. Future studies should examine patients with neuromuscular diseases or older patients suffering from back pain to investigate the association of muscle strength and DTI parameters in muscles with higher fat fractions. Second, different ROIs were used to extract intramuscular diffusion parameters in contrast to CSA and PDFF. CSA and PDFF were assessed within nearly the whole lumbar erector spinae muscle starting from the upper endplate level of L2 to the lower endplate level of L5, whereas the DTI parameters were extracted from smaller ROIs covering only a part of the lower lumbar erector spinae muscle in order to ensure the exclusion of vessels, fasciae, and surrounding intermuscular fat tissue. Because of the torsions of the DTI images, a coregistration of these images and the PDFF maps would be technically very demanding and was not performed in the context of this study.

In conclusion, DTI enables not only the characterization of back muscle fiber architecture, but also of muscle microstructure differences, which are related to back muscle function and are not reflected by CSA and PDFF. DTI may thus potentially track subtle changes of back muscle tissue composition that relate to muscle strength.

Contract grant sponsor: Philips Healthcare (to D.K.); Contract grant sponsor: European Union; Contract grant numbers: 637164 ‐ iBack (to J.K;) and 677661 ‐ ProFatMRI (to D.K.); Contract grant sponsor: TUM Faculty of Medicine KKF; Contract grant number: H01 (to T.B.).

References

  • 1. Fehlings MG, Tetreault L, Nater A, et al. The aging of the global population: The changing epidemiology of disease and spinal disorders. Neurosurgery 2015;77(Suppl 4):S1–5. [DOI] [PubMed] [Google Scholar]
  • 2. Lotz JC, Haughton V, Boden SD, et al. New treatments and imaging strategies in degenerative disease of the intervertebral disks. Radiology 2012;264:6–19. [DOI] [PubMed] [Google Scholar]
  • 3. Teichtahl AJ, Urquhart DM, Wang Y, et al. Lumbar disc degeneration is associated with Modic change and high paraspinal fat content — A 3.0T magnetic resonance imaging study. BMC Musculoskel Disord 2016;17:439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4. Hu HH, Kan HE. Quantitative proton MR techniques for measuring fat. NMR Biomed 2013;26:1609–1629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5. Dahlqvist JR, Vissing CR, Thomsen C, Vissing J. Severe paraspinal muscle involvement in facioscapulohumeral muscular dystrophy. Neurology 2014;83:1178–1183. [DOI] [PubMed] [Google Scholar]
  • 6. Baum T, Inhuber S, Dieckmeyer M, et al. Association of quadriceps muscle fat with isometric strength measurements in healthy males using chemical shift encoding‐based water‐fat magnetic resonance imaging. J Comput Assist Tomogr 2016;40:447–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7. Horvath JJ, Austin SL, Case LE, et al. Correlation between quantitative whole‐body muscle magnetic resonance imaging and clinical muscle weakness in pompe disease. Muscle Nerve 2015;51:722–730. [DOI] [PubMed] [Google Scholar]
  • 8. Willis TA, Hollingsworth KG, Coombs A, et al. Quantitative muscle MRI as an assessment tool for monitoring disease progression in LGMD2I: A multicentre longitudinal study. PLoS One 2013;8:e70993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9. Schlaeger S, Inhuber S, Rohrmeier A, et al. Association of paraspinal muscle water‐fat MRI‐based measurements with isometric strength measurements. Eur Radiol 2018. [Epub ahead of print]. [DOI] [PubMed] [Google Scholar]
  • 10. Pierpaoli C, Basser PJ. Toward a quantitative assessment of diffusion anisotropy. Magn Reson Med 1996;36:893–906. [DOI] [PubMed] [Google Scholar]
  • 11. Zaraiskaya T, Kumbhare D, Noseworthy MD. Diffusion tensor imaging in evaluation of human skeletal muscle injury. J Magn Reson Imaging 2006;24:402–408. [DOI] [PubMed] [Google Scholar]
  • 12. Heemskerk AM, Strijkers GJ, Vilanova A, Drost MR, Nicolay K. Determination of mouse skeletal muscle architecture using three‐dimensional diffusion tensor imaging. Magn Reson Med 2005;53:1333–1340. [DOI] [PubMed] [Google Scholar]
  • 13. Oudeman J, Nederveen AJ, Strijkers GJ, Maas M, Luijten PR, Froeling M. Techniques and applications of skeletal muscle diffusion tensor imaging: A review. J Magn Reson Imaging 2016;43:773–788. [DOI] [PubMed] [Google Scholar]
  • 14. Damon BM, Froeling M, Buck AK, et al. Skeletal muscle diffusion tensor‐MRI fiber tracking: Rationale, data acquisition and analysis methods, applications and future directions. NMR Biomed 2017;30(3). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Budzik JF, Le Thuc V, Demondion X, Morel M, Chechin D, Cotten A. In vivo MR tractography of thigh muscles using diffusion imaging: Initial results. Eur Radiol 2007;17:3079–3085. [DOI] [PubMed] [Google Scholar]
  • 16. Froeling M, Nederveen AJ, Heijtel DF, et al. Diffusion‐tensor MRI reveals the complex muscle architecture of the human forearm. J Magn Reson Imaging 2012;36:237–248. [DOI] [PubMed] [Google Scholar]
  • 17. Heemskerk AM, Sinha TK, Wilson KJ, Ding Z, Damon BM. Repeatability of DTI‐based skeletal muscle fiber tracking. NMR Biomed 2010;23:294–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18. Kan JH, Heemskerk AM, Ding Z, et al. DTI‐based muscle fiber tracking of the quadriceps mechanism in lateral patellar dislocation. J Magn Reson Imaging 2009;29:663–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19. Zijta FM, Froeling M, van der Paardt MP, et al. Feasibility of diffusion tensor imaging (DTI) with fibre tractography of the normal female pelvic floor. Eur Radiol 2011;21:1243–1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Karampinos DC, Banerjee S, King KF, Link TM, Majumdar S. Considerations in high‐resolution skeletal muscle diffusion tensor imaging using single‐shot echo planar imaging with stimulated‐echo preparation and sensitivity encoding. NMR Biomed 2012;25:766–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21. Heemskerk AM, Damon BM. Diffusion tensor MRI assessment of skeletal muscle architecture. Curr Med Imaging Rev 2007;3:152–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22. McMillan AB, Shi D, Pratt SJ, Lovering RM. Diffusion tensor MRI to assess damage in healthy and dystrophic skeletal muscle after lengthening contractions. J Biomed Biotechnol 2011;2011:970726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23. Yanagisawa O, Kurihara T, Kobayashi N, Fukubayashi T. Strenuous resistance exercise effects on magnetic resonance diffusion parameters and muscle‐tendon function in human skeletal muscle. J Magn Reson Imaging 2011;34:887–894. [DOI] [PubMed] [Google Scholar]
  • 24. Froeling M, Oudeman J, Strijkers GJ, et al. Muscle changes detected with diffusion‐tensor imaging after long‐distance running. Radiology 2015;274:548–562. [DOI] [PubMed] [Google Scholar]
  • 25. Deux JF, Malzy P, Paragios N, et al. Assessment of calf muscle contraction by diffusion tensor imaging. Eur Radiol 2008;18:2303–2310. [DOI] [PubMed] [Google Scholar]
  • 26. Schwenzer NF, Steidle G, Martirosian P, et al. Diffusion tensor imaging of the human calf muscle: Distinct changes in fractional anisotropy and mean diffusion due to passive muscle shortening and stretching. NMR Biomed 2009;22:1047–1053. [DOI] [PubMed] [Google Scholar]
  • 27. Okamoto Y, Mori S, Kujiraoka Y, Nasu K, Hirano Y, Minami M. Diffusion property differences of the lower leg musculature between athletes and non‐athletes using 1.5T MRI. MAGMA 2012;25:277–284. [DOI] [PubMed] [Google Scholar]
  • 28. Scheel M, Prokscha T, von Roth P, et al. Diffusion tensor imaging of skeletal muscle—correlation of fractional anisotropy to muscle power. Rofo 2013;185:857–861. [DOI] [PubMed] [Google Scholar]
  • 29. Wilm BJ, Gamper U, Henning A, Pruessmann KP, Kollias SS, Boesiger P. Diffusion‐weighted imaging of the entire spinal cord. NMR Biomed 2009;22:174–181. [DOI] [PubMed] [Google Scholar]
  • 30. Williams SE, Heemskerk AM, Welch EB, Li K, Damon BM, Park JH. Quantitative effects of inclusion of fat on muscle diffusion tensor MRI measurements. J Magn Reson Imaging 2013;38:1292–1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31. Karampinos DC, Yu H, Shimakawa A, Link TM, Majumdar S. T (1)‐corrected fat quantification using chemical shift‐based water/fat separation: Application to skeletal muscle. Magn Reson Med 2011;66:1312–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32. Le Bihan D, Mangin JF, Poupon C, et al. Diffusion tensor imaging: Concepts and applications. J Magn Reson Imaging 2001;13:534–546. [DOI] [PubMed] [Google Scholar]
  • 33. Roth R, Donath L, Kurz E, Zahner L, Faude O. Absolute and relative reliability of isokinetic and isometric trunk strength testing using the IsoMed‐2000 dynamometer. Phys Ther Sport 2017;24:26–31. [DOI] [PubMed] [Google Scholar]
  • 34. Galban CJ, Maderwald S, Uffmann K, de Greiff A, Ladd ME. Diffusive sensitivity to muscle architecture: A magnetic resonance diffusion tensor imaging study of the human calf. Eur J Appl Physiol 2004;93:253–262. [DOI] [PubMed] [Google Scholar]
  • 35. Karampinos DC, King KF, Sutton BP, Georgiadis JG. Myofiber ellipticity as an explanation for transverse asymmetry of skeletal muscle diffusion MRI in vivo signal. Ann Biomed Eng 2009;37:2532–2546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36. Mazzoli V, Oudeman J, Nicolay K, et al. Assessment of passive muscle elongation using diffusion tensor MRI: Correlation between fiber length and diffusion coefficients. NMR Biomed 2016;29:1813–1824. [DOI] [PubMed] [Google Scholar]
  • 37. Berry DB, Regner B, Galinsky V, Ward SR, Frank LR. Relationships between tissue microstructure and the diffusion tensor in simulated skeletal muscle. Magn Reson Med 2018;80:317–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38. Hernando D, Karampinos DC, King KF, et al. Removal of olefinic fat chemical shift artifact in diffusion MRI. Magn Reson Med 2011;65:692–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39. Burakiewicz J, Hooijmans MT, Webb AG, Verschuuren J, Niks EH, Kan HE. Improved olefinic fat suppression in skeletal muscle DTI using a magnitude‐based dixon method. Magn Reson Med 2018;79:152–159. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Magnetic Resonance Imaging are provided here courtesy of Wiley

RESOURCES