Accuracy of blood flow assessment in cerebral arteries with 4D flow MRI: Evaluation with three segmentation methods

Abstract

Background

Accelerated 4D flow MRI allows for high‐resolution velocity measurements with whole‐brain coverage. Such scans are increasingly used to calculate flow rates of individual arteries in the vascular tree, but detailed information about the accuracy and precision in relation to different postprocessing options is lacking.

Purpose

To evaluate and optimize three proposed segmentation methods and determine the accuracy of in vivo 4D flow MRI blood flow rate assessments in major cerebral arteries, with high‐resolution 2D PCMRI as a reference.

Study Type

Prospective.

Subjects

Thirty‐five subjects (20 women, 79 ± 5 years, range 70–91 years).

Field Strength/Sequence

4D flow MRI with PC‐VIPR and 2D PCMRI acquired with a 3 T scanner.

Assessment

We compared blood flow rates measured with 4D flow MRI, to the reference, in nine main cerebral arteries. Lumen segmentation in the 4D flow MRI was performed with k‐means clustering using four different input datasets, and with two types of thresholding methods. The threshold was defined as a percentage of the maximum intensity value in the complex difference image. Local and global thresholding approaches were used, with evaluated thresholds from 6–26%.

Statistical Tests

Paired t‐test, F‐test, linear correlation (P < 0.05 was considered significant) along with intraclass correlation (ICC).

Results

With the thresholding methods, the lowest average flow difference was obtained for 20% local (0.02 ± 15.0 ml/min, ICC = 0.97, n = 310) or 10% global (0.08 ± 17.3 ml/min, ICC = 0.97, n = 310) thresholding with a significant lower standard deviation for local (F‐test, P = 0.01). For all clustering methods, we found a large systematic underestimation of flow compared with 2D PCMRI (16.1–22.3 ml/min).

Data Conclusion

A locally adapted threshold value gives a more stable result compared with a globally fixed threshold. 4D flow with the proposed segmentation method has the potential to become a useful reliable clinical tool for assessment of blood flow in the major cerebral arteries.

Level of Evidence: 2

Technical Efficacy: Stage 2

J. Magn. Reson. Imaging 2019;50:511–518.

THE PRESERVATION of a balanced and sufficient cerebral circulation is vital for the brain. When studying vascular diseases such as stroke, accurate and efficient assessment of the cerebral blood flow distribution is therefore important. Blood flow rate in cerebral arteries can be assessed with higher‐resolution 2D phase contrast magnetic resonance imaging (2D PCMRI).1, 2, 3 With 2D PCMRI, each artery is measured individually, increasing the length of the investigation by ~3 minutes for each additional artery being measured. The results are also dependent on operator experience, since measurement planes are placed during acquisition.

An upcoming alternative for quantitative measurements is 4D flow MRI, where the arterial flow is acquired simultaneously in the multiple brain arteries, with a total acquisition time of less than 10 minutes. In a single scan, this technique thus makes it possible to investigate the entire vascular tree of the brain. However, validated postprocessing tools are lacking, making it difficult to introduce this new technique to the clinic.

Postprocessing algorithms and software for 4D flow MRI, with the purpose of segmenting the vascular cross‐section, have so far only been developed for research purposes. These methods generally use manual or semimanual outlining of single vascular cross‐sections.4, 5 To be able to implement a standardized, user‐friendly, and efficient postprocessing tool,6, 7 the segmentation method should not require manual outlining of the vessel. Previous studies have suggested segmentation methods based on clustering or global thresholding,7, 8 but there is no consensus on the algorithms for artery flow assessment. In addition, the accuracy and reliability of in vivo 4D flow measurements against a reference method has not been fully established. In this study we investigated k‐means clustering,8 global thresholding,9 and propose a local thresholding method for segmentation.

The aim of this study was to optimize the three proposed segmentation methods and determine the accuracy of in vivo 4D flow MRI blood flow rate assessments in major cerebral arteries, with 2D PCMRI as a reference.

Materials and Methods

Subjects

We recruited 37 elderly volunteers in the fall of 2017. Subjects who belonged to a cohort previously investigated at our department10 were invited. Apart from this, there was no relationship with respect to the purpose of this study. Two subjects were excluded due to incomplete MR investigations, leaving a total of 35 subjects (20 women, 79 ± 5 years, range 70–91 years). Written informed consent was obtained from all participants and the study was approved by the ethical review board at Umeå University, Sweden.

MRI

The protocol was performed with a 3 T scanner (GE Discovery MR 750, Milwaukee, WI) with a 32‐channel head coil, including 4D flow MRI and 2D PCMRI acquisitions. No contrast agent was used for any of the acquisitions. The 4D flow MRI data were collected using a balanced 5‐point phase contrast vastly undersampled isotropic projection reconstruction (PC‐VIPR) sequence,11 covering the full brain in ~9 minutes. Scan parameters: repetition time / echo time (TR/TE) 6.5/2.7 msec, velocity‐encoding (Venc) 110 cm/s, flip angle 8°, 16,000 radial projections, acquisition resolution 300 × 300 × 300, imaging volume 22 × 22 × 22 cm, reconstructed resolution 320 × 320 × 320 mm (zero padded interpolation), and isotropic voxel size of 0.7 mm³. From these data, an angiographic complex difference image (CD), a T₁‐weighted magnitude image (Mag) and velocity images in three directions were reconstructed.

The 4D flow MRI sequence was followed by eight 2D PCMRI acquisitions (TR/TE 7.6–10.7/4.1–4.7 msec, Venc 60–100 cm/s, flip angle 15°, in‐plane resolution 0.35 × 0.35 mm², slice thickness 3 mm, matrix size 512 × 512 voxels, 32 time‐resolved images reconstructed). Each 2D PCMRI measurement plane was placed perpendicular to the selected artery. First, the left (L) and right (R) internal carotid artery (ICA), covered in one plane just below the scull base, followed by the basilar artery (BA), the left and right middle cerebral artery (MCA) at the M1 level, the left and right anterior cerebral artery (ACA) at the A1 level, and finally the left and right posterior cerebral artery (PCA) at the P2 level. In two subjects, the first branch of the MCA bifurcated immediately, and the plane was therefore placed to cover the two distal branches of MCA. The flow rates of these two branches were summed in postprocessing to get the total MCA flow.

2D PCMRI Segmentation

The 2D PCMRI data were processed using the software Segment v2.1 R5960 (http://medviso.com/products/segment).12 A region of interest (ROI) covering the vessel was manually outlined in the image, considering both the magnitude and the phase image. The ROI size was kept constant through all timeframes, with a strategy to segment with a slightly oversized ROI13 that included all pixels that had a flow signal during any of the timeframes. For each artery, flow rates from the 2D PCMRI were determined as the mean flow over the 32 timeframes. Both 2D and 4D data were eddy current‐corrected.

Matching of 4D and 2D Measurement Locations

To ensure that the flow rates were measured at the same spatial location in the two sets of measurements, scanner coordinates from the centerpoint of the segmented 2D PCMRI ROIs were extracted and matched to the 4D flow data. To identify the branches in the 4D flow data, vessels were separated from background by thresholding, creating a binary image that was gradually thinned until a one‐voxel thick centerline remained.14 The centerline was divided into branches, connected by junction points, and each branch was assigned a unique identification number.15 This centerline approach has previously been implemented on in vivo 4D flow MRI data, both for flow assessment8 and vessel identification.6, 7 In order to match the 4D and the 2D measurement locations, the centerline‐point closest to each of the 2D center‐points was identified and used as the seed points for the 4D flow segmentation methods. Only branches with a length of at least five voxels were used, and seed points were placed with a minimum of three voxels from a bifurcation (junction point). The identified points were visually inspected, and in cases of coordinate mismatch, the position was adjusted by manually selecting the correct branch. Seed points were adjusted in three ICA, one BA, two MCA, five ACA, and five PCA. In Fig. 1, an example of the agreement of 2D and 4D locations is shown, together with the binary vessel image.

Figure 1.

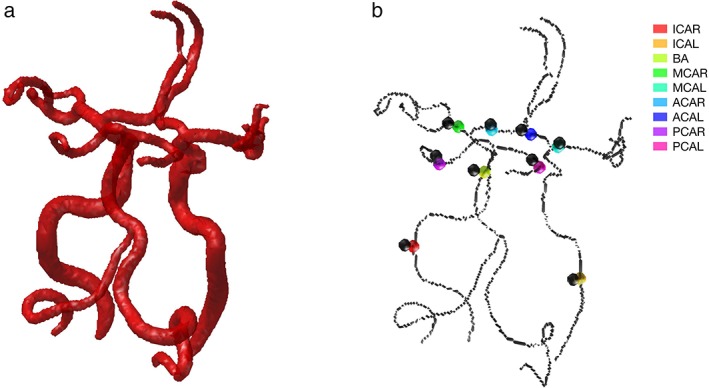
(a) Binary image of the cerebral arterial tree, used to construct the one‐voxel thick centerline representation. (b) Centerline representation of the cerebral arterial tree, with 2D coordinates in black and positions of 4D seed points in color.

Proposed Segmentation Methods for 4D Flow MRI

A region around the selected seed point was resampled in the direction of the artery, and a cut‐plane perpendicular to the artery was extracted and used for segmentation and flow calculations. The normal direction of the plane was defined based on the local direction of the artery. This was approximated as the centerline direction in a region around the seed point, extending three voxels in each direction, or to the end of the centerline branch. The local cut‐planes had a thickness of one voxel, and a size of 17 × 17 voxels in the plane. Before segmentation, the resampled voxels in the plane were linearly interpolated with a factor four in each direction.

For identifying an appropriate method for segmentation of 4D flow MRI data, with the purpose of separating the vessel lumen from the surrounding tissue, we investigated both k‐means clustering and two threshold algorithms. K‐means clustering offers different combinations of reconstructed input data, where CD together with velocity previously has been proposed in combination with the centerline processing.8 The threshold algorithms are divided into global or local thresholding, where the global is previously investigated but without the centerline processing,9 while the local thresholding was developed and presented in this study.

Methods based on k‐means clustering were evaluated with four different input datasets, dividing the data into two clusters in a way that minimizes the within‐cluster sum of squares. The z‐score of each dataset was used as input to remove the impact of scaling. The first of the four datasets used only the CD as input, the second added the T₁‐weighed magnitude image (CD + Mag), the third included the velocity norm (CD + Vel),8 and the fourth used all three images (CD + Vel + Mag).

The global and local thresholding was done on the CD, expressed as a percentage of the maximum intensity value. The threshold value for the global method was calculated as:

$$T_{\mathit{\text{global}}}=\frac{\mathit{\text{percentage threshold}}}{100}·\max \left({\mathit{CD}}_{\mathit{\text{full}}}\right),$$

and the local as:

$$T_{\mathit{\text{local}}}=\frac{\mathit{\text{percentage thre}}\mathrm{s}\mathit{\text{hold}}}{100}·\max \left({\mathit{CD}}_{\mathit{cut}}\right),$$

where CD _full is the whole‐brain CD volume and CD _cut is the cut‐plane through the artery. Both thresholding methods were evaluated for percentage thresholds ranging from 6–26.

T _global was calculated as a percentage of the maximum CD‐value in the whole brain and will therefore be the same for all arteries, while the T _local was related to the maximum velocity in each of the local cut‐planes.

After completing the segmentation, blood flow through each voxel was calculated by multiplying the voxel area with the velocity vector projected on the direction vector of the artery. The projection adjusts for potential deviations between the flow direction and the normal of the cut‐plane. Total blood flow through the artery was then calculated by summing the flow through all voxels within the segmented area.

Statistics and Analysis

To evaluate the segmentation and the accuracy of the 4D flow MRI, we compared the 4D flow MRI estimate for each vessel with the corresponding 2D PCMRI measurement. All differences in mean flow rates and standard deviations (SDs) were compared with a paired t‐test and an F‐test, respectively. For all statistical tests, P < 0.05 was considered significant. Agreement was evaluated with respect to the mean difference in flow rate between 4D flow and 2D PCMRI. Threshold analysis was performed to identify thresholds that produced the mean flow difference closest to zero. Additionally, we calculated the SD of the flow difference, and the intraclass correlation ICC(2,1).16 The presence of an undesirable dependency between flow rate deviations and mean flow rates was investigated using the slope of the linear regression between them, which we define as flow dependency. In practice, a significant value of the slope indicates that the flow error depends on the size of the artery.

For each of the two thresholding methods for which optimization was possible, the optimal threshold level in percentage was determined by minimizing the mean flow difference. The ratio between T _local and T _global was calculated to study how the choice of local or global thresholding affected the actual threshold value in the segmentation and how this varied between type of artery.

To assess how generalizable the optimized threshold was, we used a leave‐one‐out analysis for each subject. Accordingly, for each subject the 4D flow rates were calculated using a threshold determined in an optimization performed on the other 34 subjects.

We selected the minimum slice thickness of one voxel. Potentially, increasing the cross‐section thickness improves the signal‐to‐noise ratio (SNR) in the flow calculations. Therefore, to access the impact of segment length we analyzed the effect of multiple cut‐planes in the evaluation. Flow rates were calculated in both a single cut‐plane and averaged over three or five cut‐planes around the seed voxel.

Interrater Reliability in 2D PCMRI

Interrater reliability of the 2D PCMRI segmentations was assessed in 10 randomly selected subjects, by comparing measurements performed by two operators (M.H. and A.W.), in five arteries for each subject. The arteries used in the evaluation were the BA and the ICA, MCA, ACA, and the PCA on the left side. ICC(2,1) was used to assess the interrater reliability, where an ICC >0.9 indicated an excellent reliability.

Interscan Variation in 4D Flow MRI

We constructed a phantom to assess the interscan variation in 4D flow MRI. Three plastic tubes with different diameters were fixed in a glass container filled with agar (37 g/l). Water was pumped through the phantom by a peristaltic pump, Ismatec BVK (Cole‐Parmer, Wertheim, Germany), and pulsatile flow was added, creating a pulsatile index of approximately one,17 by an in‐house‐developed syringe pump, programmable and controlled by the software LabView (National Instruments, Austin, TX). To simulate arterial blood flow, we pumped water at three approximate average flow rates: 56 ± 0.9 ml/min (2.4 mm tube), 166 ± 0.9 ml/min (3.2 mm tube), and 262 ± 0.9 ml/min (4.6 mm tube) for five consecutive measurements each. The flow rate for each measurement was assessed, during the MRI scan, by simultaneously collecting the returning water to a container placed on a balance and thus measuring the water weight per minutes. The 4D flow MRI data were acquired and reconstructed in the same way as for the subjects.

Flow was analyzed at four positions along each tube. The interscan variation in 4D flow MRI, in each position, was found by dividing the SD of the five repeated measurements, with the mean flow rate of these.

Results

Out of 315 potential arteries, four arteries were missing or hypoplastic, and one artery was excluded because of incomplete 2D PCMRI data. Thus, 310 arteries had a complete set of data.

By selecting local thresholding as the segmentation method and using the optimized threshold value, 20% of CD maximum, a Bland–Altman analysis of the difference between flow of 2D PCMRI and 4D flow MRI showed 95% limits of agreements of [–29.4, 29.4] ml/min with an average of 0.02 ml/min (P = 0.98, n = 310) (Fig. 2a). The linear correlation between 2D PCMRI and 4D flow MRI was r = 0.97 (P < 0.001) (Fig. 2b). Below is the analysis of the proposed segmentation methods that led to these optimized results.

Figure 2.

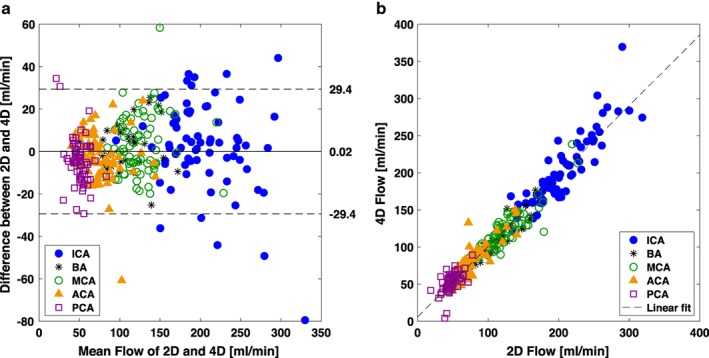
Bland–Altman analysis and linear correlation between the 2D PCMRI and 4D flow MRI measurements of flow rate for the optimized local thresholding method at 20%. (a) Solid line represents the mean difference between methods and dashed lines represent the 95% limits of agreements. (b) The linear correlation was r = 0.97 (P < 0.001) and the linear model Flow4D = 0.95 Flow2D + 5.76.

The comparisons between 2D PCMRI and 4D flow MRI for all proposed segmentation methods are summarized in Fig. 3. The optimization procedure identified a mean flow difference for local and global thresholding at thresholds of 20% (0.02 ± 15.0 ml/min) and 10% (0.08 ± 17.3 ml/min), respectively (Fig. 3a). Subsequent analysis with thresholding was performed with these optimized thresholds. Further, Table 1 shows the results divided by artery for these two methods. The flow differences from the local thresholding ranged from –7.3 to 7.0 ml/min, while the same values for global thresholding were –15.3 to 9.1 ml/min, showing that local thresholding was more stable for measurements in arteries with varying size and flow rate (Table 1). This was also supported by the SD at the group level, which was significantly lower (15.0 ml/min) for the local threshold compared with the global (17.3 ml/min) (F‐test, P = 0.01) (Fig. 3b). For local thresholding, flow rates averaged over three (–0.05 ± 14.9 ml/min) and five (0.04 ± 14.8 ml/min) cut‐planes showed that there was no reduction in SD by averaging flow values over multiple cut‐planes when compared with the single plane (F‐test, P = 0.92 and P = 0.84, respectively). The mean flow difference after the leave‐one‐out analysis with the local thresholding was –0.04 ± 15.1 ml/min (P = 0.97).

Figure 3.

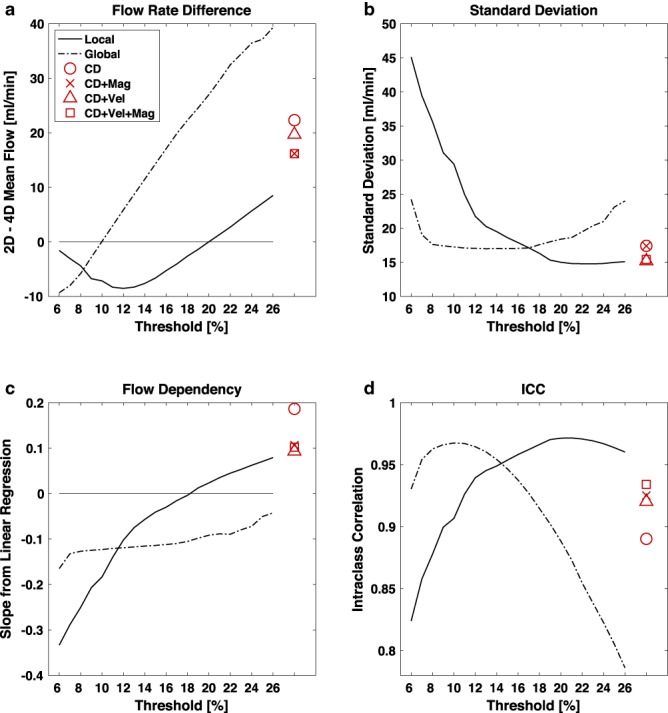
Comparing 4D flow MRI against the 2D PCMRI measurements. Thresholding; Effects of different thresholds with the local (solid line) and the global (dash‐dot line) thresholding method. Clustering; Results from clustering in red with CD (○), CD + Mag (×), CD + Vel (Δ) and CD + Vel + Mag (□) as input data. (a) Difference between 2D and 4D flow rate measurements [ml/min]. (b) Standard deviation of flow rate difference [ml/min]. (c) Slope of a linear regression on flow difference vs. flow. (d) Intraclass correlation (ICC).

Table 1.

Flow Results for Thresholding Methods

Artery	Local threshold (20%)			Global threshold (10%)				2D PCMRI
	Flow diff ± SD	P	ICC	Flow diff ± SD	P	ICC	N	Flow ± SD
ICAR	5.3 ± 22.5	0.17	0.88	–11.4 ± 23.6	0.007	0.86	35	212.5 ± 43.9
ICAL	0.2 ± 19.4	0.96	0.90	–15.3 ± 22.0	<0.001	0.84	35	198.2 ± 39.9
BA	3.0 ± 11.0	0.12	0.93	6.6 ± 13.3	0.006	0.90	34	108.7 ± 30.4
MCAR	–1.3 ± 13.0	0.54	0.88	–2.1 ± 14.0	0.39	0.87	35	126.6 ± 25.8
MCAL	7.0 ± 14.1	0.006	0.84	6.3 ± 14.6	0.016	0.85	35	127.3 ± 29.6
ACAR	0.0 ± 10.3	0.99	0.91	2.7 ± 9.5	0.10	0.93	34	78.3 ± 24.3
ACAL	–5.3 ± 13.8	0.03	0.76	–1.5 ± 15.0	0.57	0.76	33	72.4 ± 18.1
PCAR	–7.3 ± 9.1	<0.001	0.41	6.7 ± 9.1	<0.001	0.52	35	46.3 ± 8.9
PCAL	–1.7 ± 11.9	0.41	0.58	9.1 ± 10.2	<0.001	0.47	34	49.7 ± 9.8

Flow rate difference (Flow diff) [ml/min], standard deviation (SD) [ml/min] and ICC between 2D PCMRI and 4D flow MRI for each artery presented separately for two methods; local thresholding (20%) and global thresholding (10%). Mean flow for each artery is presented as 2D PCMRI flow [ml/min].

ICA, internal carotid artery; BA, basilar artery; MCA, middle cerebral artery; ACA, anterior cerebral artery; PCA, posterior cerebral artery; R, right; L, left.

Local thresholding showed a nonsignificant flow dependency for threshold 16% (P = 0.06), 17% (P = 0.32), 18% (P = 0.80), 19% (P = 0.37), and 20% (P = 0.09), while global thresholding showed a negative flow dependency (overestimating flow rates in large arteries and underestimating in small arteries) for all thresholds (Fig. 3c).

There was no correlation in flow differences between 2D PCMRI and 4D flow MRI with respect to the age of the subjects, for neither local (r = 0.04, P = 0.49) nor global (r = 0.08, P = 0.15) thresholding.

The ratio between T _local and T _global showed that in ICA the local threshold value was higher than the global (P < 0.001), while the opposite was true for PCA (P < 0.001). For all other arteries, T _local and could be both higher and lower than T _global (Fig. 4).

Figure 4.

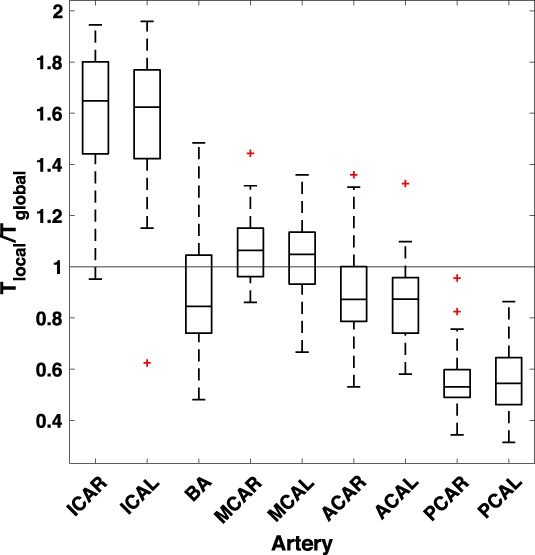
Boxplot of ratio between local, T _local, and global threshold value, T _global, for the local and global threshold methods at 20% and 10%, respectively. The bottom and top edge of the box represent the 1^st and the 3^rd quartile, respectively, and the red + sign the outliers.

Clustering methods produced a good flow agreement with 2D PCMRI with respect to SD and ICC (Fig. 3b,d), but they all measured systematically lower flow. The mean differences were 22.3 ± 17.4, 16.2 ± 17.4, 19.7 ± 15.2, and 16.1 ± 15.2 ml/min for clustering on the CD, CD + Mag, CD + Vel, and CD + Vel + Mag datasets, respectively (P < 0.001) (Fig. 3a), all with positive flow dependencies (P < 0.001) (Fig. 3c).

For 2D PCMRI, assessment of data reliability was evaluated using interrater reliability, which revealed an ICC of 0.99. For 4D flow MRI, the interscan variation in the phantom showed that the SD of the repeated measurements divided by mean flow rate was 3.3% (range 1.1–6.8%) for the 12 measurement positions, segmented with the local thresholding (20%).

Discussion

In vivo validation of 4D flow MRI including the postprocessing algorithms is needed. In this study we present a straightforward local thresholding approach for segmentation of 4D flow MRI. It could be optimized to give a zero mean difference compared with 2D PCMRI, and precision on the same level as repeated 2D PCMRI measurements.18 Furthermore, it was consistent over arteries with different diameters, flow rates, and anatomical locations. The precision of the new algorithm was promising and suggests that local thresholding of 4D flow MRI could be the basis for the development of a new clinical method to be used for efficient and comprehensive assessment of blood flow distribution in the main brain arteries.

Generally, our data suggest the robustness of 4D flow MRI in estimating blood flow rates in cerebral arteries. This result adds to a growing body of literature that have begun exploring the agreement between 4D flow MRI and conventional 2D phase contrast techniques.19, 20 Importantly, such measurements have also been shown consistent across sites.21

We investigated the agreement between 2D PCMRI and 4D flow MRI segmentation using k‐means clustering, global thresholding, or local thresholding. The clustering methods, regardless of input data, were robust in terms of producing flow values with good precision, but with a systematic underestimation of 4D flow MRI compared with 2D PCMRI. Combining the CD in the clustering method with velocity data and the magnitude image improved the agreement, but the systematic difference, which was similar to previous k‐means clustering results in ICA,8 must still be considered too large to be accepted for clinical use. In addition, we included a larger set of arteries that revealed a flow dependency in the clustering methods, reducing its generalizability.

The bias in k‐means clustering results indicated that a more generous voxel inclusion is appropriate, specifically for larger vessels, but the clustering methods does not give us any straightforward option to tune the inclusion limits. Tuning was on the other hand possible with the thresholding methods, where a threshold could be chosen to minimize the mean difference between the 2D reference and the 4D flow method. Flow rate dependency analysis showed that the optimized threshold value for the global thresholding was too generous in larger arteries such as the ICA, but too restrictive in smaller arteries like the PCA, producing an artery size‐dependent deviation. For local thresholding, with its adaptive nature, this effect could be reduced. We note that zero slope for the flow dependency was found at a threshold of 18%, but we prioritized the zero‐mean bias accomplished with the 20% threshold, which still produced a nonsignificant flow dependency. Local thresholding thus fulfills both the criteria of zero‐mean bias and the arterial size independency, supporting its generalizability for flow assessment of cerebral arteries.

The temporal physiological variations within subjects are always a remaining factor when comparing flow rate measurements separated in time.18, 22 Heart rate, blood pressure, and autoregulation can vary during the investigation, which affects the flow rate in each artery, creating an unavoidable random variation between two repeated flow assessments.23, 24, 25, 26 In addition, there is a contribution to the variability that comes from the nonnegligible 4D flow MRI interscan variation revealed in the well‐controlled flow conditions in the phantom measurements. A previous study show that within‐subject variation of repeated 2D PCMRI measurement is about 20 ml/min in ICA,18 which is similar to the variation found between 2D and 4D in our study. This emphasizes the advantage of using 4D flow MRI, with simultaneously measured flow, in the analysis of the cerebral blood flow distribution.

In previous studies, flow values were either averaged over several cross‐sections to mimic the slice thickness of 2D PCMRI,8, 23 or spatially lowpass‐filtered to remove noise.5 The effect of this averaging on accuracy and stability of the measurements has not yet been evaluated. We showed that averaging flow values over several cut‐planes did not improve the results, again indicating that the deviations between 2D and 4D estimates primarily were due to a physiological variability between the acquisitions.

There was a variability in ICC between arteries. This can be explained by considering the physiology of the Circle of Willis. It has a function of reducing a potential pressure difference on the left and right sides of the brain and to maintain the flow distribution to the different arteries.3 Proximal arteries (BA and ICA) on the feeding side of the Circle of Willis generally have larger between‐subject variations in flow values, and the larger range of values gives a higher ICC. Distal arteries such as PCA, which are more directly supplying tissue, need a steadier flow, and any deviations earlier in the circulation have already been compensated. This gives a lower interindividual variation for the distal arteries, and hence partly explains their lower ICC.

Limitations in this study include that 4D flow data were acquired exclusively with Venc 110 cm/s and that 2D PCMRI with manual segmentation was chosen as the reference method. In addition, all MRI measurements were performed on a single 3 T scanner. This must be considered when interpreting the generalizability of the results. The optimal threshold was chosen as the one giving the lowest systematic difference for the whole group of arteries, and therefore optimized with respect to the segmentation strategy used for 2D PCMRI. Our strategy and priority were to use a slightly oversized ROI that included all flow. With an oversized ROI the results are affected by partial volume effects,27 Gibbs ringing, and eddy currents.28, 29 The error in flow quantification should, however, be smaller and less vessel area‐dependent with an oversized ROI compared with an undersized one.13 Therefore, although subjective variability is always present in manual segmentations, we believe that our approach minimized the impact of unwanted subjectivity on the result. This robustness was further supported by our high interrater agreement. Regarding generalizability, even if the threshold level possibly is scanner‐dependent and expected to vary with respect to selection of the reference method, the approach with local thresholding has, by construction, potential to be stable, specifically across Venc selections. Partial volume problems in smaller arteries becomes relevant when the artery is fewer than four voxels in diameter,13, 18, 30 which could be of importance in PCA. Another limitation of the present study design is that ground truth for in vivo cerebral blood flow was not available and that the 4D flow MRI and the reference measurements cannot be performed simultaneously in human participants. The alternative approach, with phantom measurements, also has its limitations, since the segmentation challenge is different compared with in vivo.

In conclusion, we describe the performance of three segmentation methods where the one based on local thresholding was superior. Using such thresholding it was possible to obtain 4D flow quantification in cerebral arteries with good precision and agreement with 2D PCMRI. A local threshold of 20% of the CD maximum intensity value eliminated the systematic difference and the correlation between flow difference and flow, and revealed a remaining variability probably dominated by true physiological variability between measurements separated in time. Implemented together with an automatic arterial vessel identification method, this standardized and user‐independent segmentation algorithm has the potential to advance 4D flow MRI into a reliable clinical tool for assessment of blood flow in the major cerebral arteries.