Large particle penetration through N95 respirator filters and facepiece leaks with cyclic flow

Abstract

The aim of this study was to investigate respirator filter and faceseal penetration of particles representing bacterial and fungal spore size ranges (0.7 – 4 µm). First, field experiments were conducted to determine workplace protection factors (WPFs) for a typical N95 filtering facepiece respirator (FFR). This data (average WPF = 515) was then used to position the FFR on a manikin to simulate realistic donning conditions for laboratory experiments. Filter penetration was also measured after the FFR was fully sealed on the manikin face. This value was deducted from the total penetration (obtained from tests with the partially sealed FFR) to determine the faceseal penetration. All manikin experiments were repeated using three sinusoidal breathing flow patterns corresponding to mean inspiratory flow rates of 15, 30, and 85 L/min. The faceseal penetration varied from 0.1 to 1.1 % and decreased with increasing particle size (p<0.001) and breathing rate (p<0.001). The fractions of aerosols penetrating through the faceseal leakage varied from 0.66 to 0.94. In conclusion, even for a well-fitting FFR respirator, most particle penetration occurs through faceseal leakage, which varies with breathing flow rate and particle size.

Introduction

Respirators protect wearers from non-biological and biological aerosols which may potentially cause human health problems. One of the respirators extensively used in a variety of workplaces is a filtering facepiece respirator (FFR) because of its low price, comfort and efficiency (Chen and Huang, 1998). A degree of protection provided by a respirator can be expressed as a workplace protection factor (WPF), which is defined as a ratio of the concentration of airborne contaminant (e.g., particulates) outside the respirator to the concentration inside the respirator when measured under the workplace condition with a properly selected, fit tested and functioning respirator while it is correctly worn (OSHA, 2006). In some cases, WPF studies are not feasible. In these situations the workplace environment may be simulated in the laboratory. Protection factors determined in this manner are designated simulated workplace protection factors (SWPFs). Several investigators have conducted WPF or SWPF studies with N95 elastomeric respirators and N95 FFRs (Myers and Zhuang, 1998; Lawrence et al., 2006; Duling et al., 2007; Janssen et al., 2007). While these studies provided WPF information they did not quantitatively characterize the factors, which may cause variation in the WPF, e.g., particle size. Lee et al. (2005) investigated the effect of particle size on the WPF by simultaneously measuring concentration and size distribution of particles in the size range of 0.8 – 10 μm inside and outside of an FFR. This study showed that WPF increases with increased particle size.

Measurement of penetration into the respirator (determined as the inverse of PF) can be used to characterize respirator performance. Total penetration represents two different pathways, through the filter media and through faceseal leaks (Grinshpun et al., 2009). Respirators certified by NIOSH (1995), have well-defined penetrations through their filter media for particles with mass median aerodynamic diameter of 0.3 µm as measured at a constant flow rate of 85 L/min. NIOSH certified N95 respirator filters have at least 95% efficiency under the conditions of the certification test. Likewise, an N99 filter is at least 99% efficient. Studies have shown that the filter penetration of nanosized particles through N95 FFRs can be higher than 5% because the peak penetration in electret filters may occur at smaller particle sizes than those used in the certification tests (Balazy et al., 2006; Eninger et al., 2008). Generally, the most penetrating particle size (MPPS) ranges from 0.04 to 0.3 μm depending on the filter properties and face velocity (Balazy et al., 2006; Huang et al., 2007). At the MPPS, the combined effect of diffusion, electrostatic attraction, impaction, and interception on the particle collection is at its minimum. Below this size range, diffusion and electrostatic attraction are the primary mechanisms for particle collection, whereas above this size range, impaction and interception usually dominate (Huang et al., 2007)

Much less is known about faceseal penetration into respirators, especially with cyclic flow. Chen et al. (1990) compared total penetration and faceseal penetration of 0.8 – 4 μm particles into a FFR under constant inhalation flow rates ranging from 5 to 95 L/min. Faceseal leakage was simulated by circular tubes varying in diameter. The investigators reported that both filter and faceseal penetration decreased with increased particle size and this dependence was stronger with higher air flow rates. This was explained by increased effect of impaction losses on the filter and faceseal penetrations at higher air flows. For supermicrometer particles (2 – 4 μm), both filter and faceseal penetrations were lowest at the highest air flow, and this difference was more clearly seen for faceseal penetration. For submicrometer sized particles, this was reversed because the effect of electrostatic attraction decreases with increased air velocity. They also showed that for fixed leak dimensions, the fraction of aerosols penetrating through the leak relative to the aerosol penetrating through the filter material increases with decreased flow rate. Thus, at flow rates of 5 – 10 L/min, which represent the initial and final phases of an inhalation cycle, a relatively higher proportion of particles penetrate through the leak than through the filter material (Chen et al., 1990). Coffey et al investigated total penetration through 21 N95 respirators worn by 25 human subjects during fit-test exercises (Coffey et al., 1998). They separately measured filter penetration of the 21 respirators using a protocol developed earlier (Zhuang et al., 1998). Fit factors were measured by PortaCount Plus using ambient aerosols and then converted to total penetration. Filter penetration was also measured by PortaCount Plus under conditions corresponding to respiration flow rate of 31.4 L/min,. Faceseal leakage was calculated by subtracting filter penetration from total penetration. They reported that total penetration had a geometric mean of 2.8 %, and corresponding values for faceseal leakage and filter penetration were 2.4 % and 0.16 %, respectively. The investigators also illustrated that faceseal leakage was highly correlated with total penetration while filter penetration was not (Coffey et al., 1998).

The pattern of human breathing consists of inhalation and exhalation flows that are much closer to a sinusoidal than constant flow pattern (Johnson, 1993). Several studies have reported that filter penetration of particles in the size range of 0.02 – 3 µm is higher under cyclic flow than under constant inhalation flow (Stafford et al., 1973; Brosseau et al., 1990; Eshbaugh et al., 2009). However, a recent study by Haruta et al. (Haruta et al., 2009)) showed that the effect of cyclic flow rate may be more complex. In the latter paper, the filter penetration of ultrafine particles (25, 65, and 99 nm) was compared under four constant and cyclic air flows (15, 30, 85, and 135 L/min (Silverman et al., 1951)). At 15 and 30 L/min, the filter penetration under cyclic flow was higher than that under corresponding constant flow. In contrast, no difference was found at 85 L/min, and an opposite trend was identified at 135 L/min (penetration under cyclic flow was lower than under constant flow). The finding was attributed to a complex interaction of diffusion, electrostatic interaction, impaction, and interception, which exhibit different effects on penetration as the flow rate increases.

Recently, Grinshpun et al. (2009) investigated the penetrations through filter media and faceseal leakage for fine particles (size range 0.04 – 1 µm) using a combination of human and manikin-based experiments. The investigators reported that both penetration pathways decreased significantly as particle size increased from approximately 0.1 to 1 µm.

In summary, several studies have investigated the effect of particle size, breathing flow rate and respiration pattern (cyclic vs. constant) on filter penetration. Only a few studies have characterized faceseal leakage and even fewer have conducted tests under realistic faceseal leakage conditions. In this manikin-based study, an experimental set-up was developed to investigate the penetration of particles through faceseal leakage under cyclic air flow. Penetrations through filter and faceseal leakage into filtering facepiece respirators was determined at three different cyclic breathing rates [mean inspiration flow (MIF) = 15, 30, and 85 L/min] using challenge aerosol particles in the size range of 0.7 – 4 µm. This size range was selected because of special interest on respiratory protection in agricultural environments, which typically have high concentrations of supermicrometer particles, including airborne bacteria and fungi.

Methods

Pilot-scale field experiment

Before starting the manikin-based study, a pilot-scale field study was conducted in order to collect data on particle size distributions and concentrations that occur in agricultural environments. The pilot study also provided information regarding the level of protection (WPF) offered by the specific respirator to be used in the subsequent manikin study. N95 FFR used for the experiment was a pleated respirator with adjustable nose band without any additional sealing material. In the field experiment, the WPF of an N95 FFR was determined for 13 human subjects on three different agricultural farms (horse farm, swine confinement and corn farm). All subjects were medically cleared, were trained to wear the tested respirator according to the manufacturer’s instruction and passed both a user seal check and a fit testing prior to the start of field experiments. Subjects wore a commonly used NIOSH-approved N95 FFR while performing their daily activities, such as spreading hay, feeding livestock, and handling corn.

Particle concentrations inside and outside the respirator were measured by a sampling system that was developed earlier (Lee et al., 2005b). Briefly, the personal sampling system consists of two identical sampling lines, each one including a sampling probe, a sampling chamber, an optical particle counter (HHPC-6, ARTI Inc., USA) and a pump (Leland Legacy, SKC Inc., USA). The optical particle counter has five channels to measure particle concentration: 0.7 – 1, 1 – 2, 2 – 3, 3 – 5, and 5 – 10 µm. The corresponding mean sizes of these channels are 0.85, 1.5, 2.5, 4, and 7.5 µm. Using a DryCal DC-Lite calibrator (Bios International Corporation, USA), the flow rate for the pump was adjusted to maintain the total sampling flow of 10 L/min. Each field experiment lasted for 1 hr, and particle concentrations were determined simultaneously inside and outside of the respirator during 15 min in the beginning and 15 min at the end of the experiment to avoid moisture condensation inside sampling tubing. For every subject, size-selective WPFs were calculated in one-minute intervals and then averaged.

Experimental set-up for manikin study

The manikin experiments were conducted using an experimental set-up shown in Figure 1. A breathing manikin wearing the same type of N95 FFR as in the field study was placed in a walk-in test chamber (volume = 24.3 m³). The manikin used for the study is commercially available (Allen Display^SM) and is made of hard plastic with smooth facial surfaces. The manikin breathed at three different MIF cyclic breathing rates of 15, 30 and 85 L/min, which simulate the human breathing rate during rest, medium work load, and strenuous work load, respectively. MIF is defined as a ratio of the tidal inspiratory volume to the inspiratory duration. Cyclic flow was produced by an electromechanical breathing simulator described in detail by Haruta et al. (2009) (Koken Ltd, Japan). Briefly, an electromechanical drive-cylinder connected to two air cylinders is the primary mechanical component of the breathing simulator. As the electromechanical cylinder moves back and forth, a sinusoidal air flow is generated. A HEPA-filter was placed between the manikin and the breathing simulator to prevent re-entry of particles into the respirator cavity by the exhalation air.

Figure 1.

Experimental set-up for manikin-based testing of particle penetration through filter and face seal leakage.

Particle concentrations inside and outside the respirator were measured by the same personal sampling system used in the field study. In each experiment, particle concentrations were determined over a period of 15 min and the measurement was repeated three times. The particle penetration (P, %) was calculated by dividing the particle concentration inside the respirator (C_in) by that outside the respirator (C_out) and expressed in percent:

$$\text{P}\left(\%\right)=100·{\text{C}}_{\text{in}}/{\text{C}}_{\text{out}}$$ (1)

Penetration through respirator filter (P_filter) was determined by a similar testing conducted with a fully sealed respirator (glued to the manikin face with silicon). The seal was verified using a bubbling solution that was applied to the interface between a manikin and the respirator. The total penetration (P_total) was determined with the respirator only partially sealed on the manikin face as described below.

For this study, one objective was to simulate faceseal leakage that results in similar PF as measured in the field. Several different sealing configurations on the manikin were tested in order to select the configuration that showed protection factors closest to the WPF measured in the workplace-based pilot study. Table 1 presents the sealing configuration on a manikin that resulted in similar total penetration to the one measured under the field conditions. The length of sealing from the cheekbone towards the chin was 11 cm on both left and right sides of the respirator. This configuration was selected for further manikin experiments to simulate faceseal leakage. P_total was determined for the partially sealed respirator. For comparison with the WPF data obtained in the field, P_total was converted to Protection Factor (PF):

$$\text{PF}=100/{\text{P}}_{\text{total}}$$ (2)

P_filter and P_total were determined particle size selectively and separately for the three respiration flow rates. The experiments under the three flow rates were conducted in random order. Penetration through the faceseal leakage (P_faceseal) was calculated as follows (Grinshpun et al., 2009):

$${\text{P}}_{\text{faceseal}}={\text{P}}_{\text{total}}-{\text{P}}_{\text{filter}}$$ (3)

Table 1.

Sealing configuration selected to simulate faceseal leakage on a manikin.

Partially sealed condition
Sealed length	11 cm × 2
Unsealed length	16 cm
Sealed: solid line Unsealed: dash line

Particle generation

A Collison nebulizer with NaCl solution has been widely used to generate challenge aerosols in previous studies related to filter performance (Eninger et al., 2008; Lee et al., 2008). Most of the particles aerosolized by this method are in the size range of 0.01 to 1 µm (Balazy et al., 2006), which is low relative to the bacterial and fungal size ranges. Thus, we needed larger test particles and consequently a different aerosolization methodology. Since particles in the field experiment were well distributed from 0.7 to 10 µm, we chose a Koken-manufactured nebulizer to generate test dust (ISO 12103–1 A1, Powder Technology Inc., USA) ranging from 1 to 20 µm. This nebulizer was originally used to generate 2-µm silica particles for the filter testing program at Koken Ltd. Due to the high water-solubility of the test dust, it was mixed with 2-propanol instead of water. The challenge aerosol was mixed with filtered-dry air of 100 L/min and passed through a ⁸⁵Kr charge neutralizer (3054, TSI Inc, USA) to attain the Boltzmann charge distribution. An air blower with a capacity of approximately 25.5 m³/min was utilized for air mixing in the chamber. The challenge particles were continuously produced for about 15 min in the beginning of the experiment to attain airborne particle concentration of 70,000 particles/L and then, intermittently atomized to maintain the desired concentration. The coefficient of variation for the concentration generated during entire experiment was 0.04. A concentration of 10 particles/L per size channel was set as the minimum acceptable level inside the respirator and is referred from this point on, as the detection limit. The maximum concentration that can be measured with the HHPC-6 optical particle counter is 70,000 particles/L. Thus, the minimum theoretical penetration that could be measured with this set-up was 0.01 %.

It has been reported that electret respirator filters loose their electrostatic charge if treated by isopropanol. A treatment consisting of dipping a FFR in 2-propanol for 15 sec and air-drying overnight resulted in 30% higher penetration compared to untreated respirators (Martin and Moyer, 2000). To assure that atomized 2-propanol did not affect particle penetration in our experiments, an additional manikin experiment was conducted to examine filter penetration with and without aerosolizing isopropanol. Monodisperse polystyrene latex spheres (PSL) of 2.03 µm were used to challenge an N95 FFR that was completely sealed on the manikin face for the measurement of filter penetration. Completely sealed condition was expected to provide the worst-case scenario on the possible effect of 2-propanol in reducing the electrostatic forces in the filter material. First, PSL particles were atomized by a Collison nebulizer (BGI Inc., USA), mixed with filtered-dry air of 100 L/min and passed through the ⁸⁵Kr charge neutralizer. PSL particles were generated continuously for 2 hrs to attain sufficient particle concentration in the chamber. Then, filter penetration was measured for 15 min and repeated with three different manikins. After assuring that the concentration of PSL particles continued to be sufficiently high for further testing, the Collison nebulizer was replaced by the Koken nebulizer containing 2-propanol. Continuously atomized 2-propanol was mixed with filtered-dry air of 100 L/min and passed through the charge neutralizer. After 30 min, while continuing the generation of 2-propanol, filter penetration was measured for 15 min and repeated using the three manikins. The filter penetrations of PSL alone and of PSL with 2-propanol were 0.025% and 0.029%, respectively. The difference between these two values was not significant (t-test: p=0.82). Therefore, it was concluded that aerosolized 2-propanol was unlikely to affect the filter penetrations measured in this study.

Statistical analysis

All statistical analyses were performed using SAS 9.1.3 software (SAS Institute Inc., Cary, NC). Analyses of variance were performed with penetration as the dependent variable separately for P_filter and P_faceseal and for the fraction of particles penetrating though the faceseal vs through the filter (P_faceseal/P_filter). The P_filter and P_faceseal values were square-root transformed and P_faceseal/P_filter-fractions were log-transformed to approximate normality. General linear model (PROC GLM) was used to construct two-factor models with interaction to relate penetrations and P_faceseal/P_filter –fractions with breathing rate and particle size. Adjusted mean penetrations of all levels of breathing rate and particle size were obtained through a Least Squares MEANS statement in PROC GLM. These predicted (adjusted) penetration values are listed for one factor (breathing flow rate) adjusted for the other factor (particle size) and vice versa in Tables. Paired t-test was conducted to study the difference in particle concentration measured in the field vs. in the laboratory.

Results

Figure 2 shows the laboratory and field aerosol concentrations and size distributions measured outside the respirator. In the largest particle size range (5 – 10 µm, mean diameter = 7.5 µm), the ambient concentration generated in the laboratory was approximately 250 particles/L (normalized value, ΔC_N/ΔLog(D_p) = 5.2 × 10⁶ #/m³ as shown in Fig. 2). This resulted in concentrations below the detection limit for all in-facepiece measurements. Therefore, results obtained for particles larger than 5 µm were excluded from this study. Results for filter penetration from the previous particle size range (mean diameter = 4 µm) were also excluded from the analysis because, the inside concentration was below the detection limit when the respirator was sealed to the manikin, despite an outside concentration of approximately 1000 particles/L. Because filter penetration was negligible, it was assumed that the faceseal penetration was equal to the total penetration for 4-µm particles. The size distribution of the challenge aerosol generated in the laboratory was close to that in the field in the size range from 0.7 to 5 µm (paired t-test: p=0.977).

Figure 2.

Mean of outside concentration in four field experiments and in all laboratory experiments. The concentration in the laboratory was averaged over all laboratory experiments (completely sealed and partially sealed respirator tested under three respiration flow rates), and the concentration in the field was averaged from four agricultural farms where WPF was measured for 13 human subjects. The symbols present means, and error bars present 95% confidence intervals.

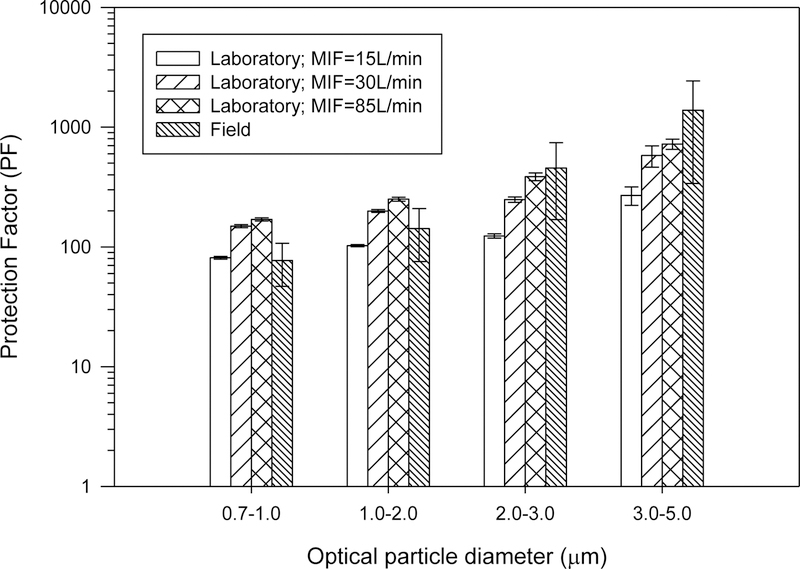
Figure 3 compares PF-values measured under the partially sealed condition in the laboratory at different MIF cyclic breathing rates with WPF-values obtained in the field study. Generally, WPF in the field and PF in the laboratory showed particle size dependence, increasing with the increase in the particle size. PF also consistently increased within each size range with the increase in the cyclic breathing flow. These trends are expected given that the test particles are relatively large so that their motion and collection is governed primarily by impaction and interception mechanisms. The unadjusted WPF-values (not adjusted for size and breathing flow) ranged from 12 to 9,531 and had a mean value of 515 when averaged over all particle sizes for all subjects. The unadjusted PF-values measured in the laboratory varied from 71 to 1,161 and most were within 95% confidence interval of WPF-values measured in the field.

Figure 3.

WPF measured in the field for 13 agricultural workers and in the laboratory for three different Mean Inspiration Flow (MIF) cyclic breathing rates under partially sealed condition. The histograms present means, and error bars present 95% confidence intervals.

Total penetration, filter penetration and faceseal penetration measured in the manikin experiments at three different MIF cyclic breathing rates at different particle sizes are shown in Figure 4, and the results obtained by the general linear model are summarized in Tables 2 and 3. The unadjusted values for the faceseal penetration varied from 0.11 to 1.07 % and those for the filter penetration were between 0.04 and 0.19%. Within each breathing flow rate, the faceseal penetration and the filter penetration decreased with the increase in the particle size. This decrease was statistically significant (p<0.001; Table 2). Also, the faceseal penetration significantly decreased with the increase in the MIF cyclic breathing rate (p<0.001; Table 3). In contrast, the filter penetration slightly increased with the increase in the breathing rate (p=0.02; Table 3). Maximum faceseal and filter penetration were observed at the particle size of 0.85 µm, which was the smallest particle size included in this study. The aerosol fraction penetrating through the faceseal leak relative to the fraction penetrating through the filter material increased significantly with the increase in particle size (p<0.001) and with the decrease in the breathing rate (p<0.001), varying from 6.2 to 16.1 at MIF = 15 L/min, from 2.9 to 6.2 at MIF = 30 L/min, and from 1.9 to 4.1 at MIF = 85 L/min.

Figure 4.

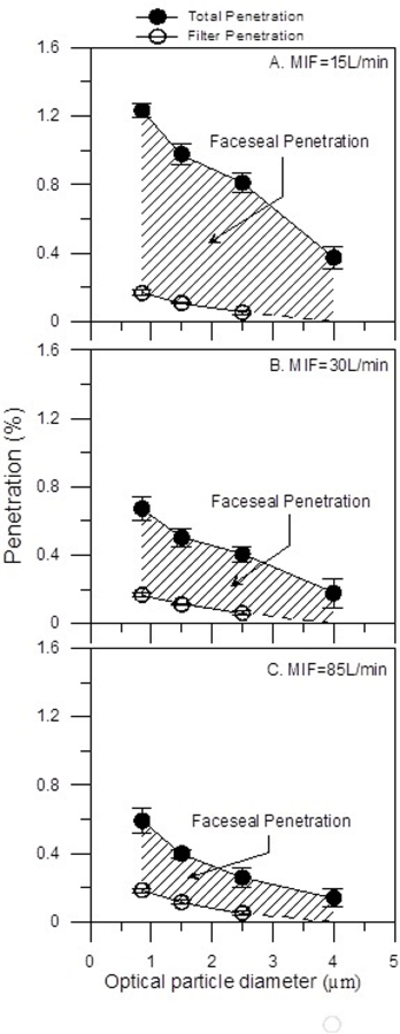
Comparison of total penetration, filter penetration and face seal penetration at three different Mean Inspiratory Flow (MIF) breathing rates. The symbols present means, and error bars present 95% confidence intervals.

Table 2.

Penetration at different particle sizes adjusted for breathing rate.

Particle size (µm)	Faceseal penetration (%)	Filter penetration (%)
0.85	0.62	0.17
1.50	0.48	0.11
2.50	0.40	0.05
4.00	0.21	Below detection limit
p-value	< 0.001	<0.001

Table 3.

Penetration at different MIF cyclic breathing rates adjusted for particle size.

MIF	Faceseal penetration (%)	Filter penetration (%)
15 L/min	0.74	0.10
30 L/min	0.34	0.10
85 L/min	0.25	0.11
p-value	< 0.001	0.02

Figure 5 demonstrates how the faceseal penetration correlated with the total penetration and the filter penetration. Significant correlation was demonstrated between the faceseal penetration and the total penetration (R² = 0.97). However, no correlation was found between the faceseal penetration and the filter penetration when all data were included in the analysis (R² = 0.07). When data were analyzed separately for each respiration flow rate, significant correlations were found between faceseal and filter penetration: R²=0.96 at MIF=15 L/min, R²=0.90 at MIF=30 L/min, and R²=0.91 at MIF=85 L/min.

Figure 5.

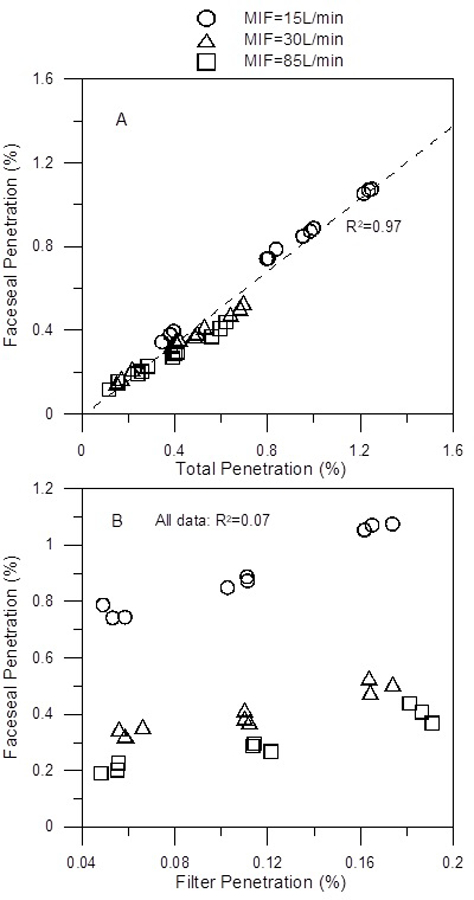
Correlation between faceseal penetration and total penetration (A) and between faceseal penetration and filter penetration (B).

Discussion and Conclusions

Most of the laboratory protection factors (PF) were within the 95% confidence interval of the WPFs measured in the field evaluation. This demonstrates that the positioning of the respirator on the manikin closely simulated the size of faceseal leakage in the field study. In both cases, the WPF and laboratory PF increased with increasing particle size. This is consistent with previous laboratory and field studies (Chen et al., 1990; Lee et al., 2005b). The laboratory PF also increased with flow rate. This also agrees with previous studies and can be explained by greater effect of impaction and interception that occurs at higher air velocities (Chen et al., 1990; Huang et al., 2007). It should be noted that we studied a relatively well-fitting respirator having a mean PF of 660 and a minimum PF of 71 (measured at particle size of 0.85 µm and flow rate of 15 L/min). As pointed out by Chen et al. (1990), the effect of particle size on the faceseal penetration may be enhanced for well-fitting respirators; the smaller the leak and the larger the particle size, the greater the effect of impaction in removing particles during their passage through the leak.

Similar to total penetration, faceseal penetration decreased with an increase in particle size and breathing rate. Although dynamic change of the fitting of the respirator to the dummy head could potentially contribute to our observation, no visual deformation of the respirator was observed even at MIF of 85L/min. Furthermore, our finding agrees with the results reported by Chen et al. (1990), who used fixed leaks (circular tubes varying in diameter) and reported that faceseal penetration decreased with an increase in particle size and breathing rate. This trend should be expected as impaction and interception mechanisms dominate with increasing particle size and air velocity, particularly in the supermicrometer size range (Huang et al., 2007). We conclude that change of fitting of the respirator to the dummy head due to flow rate appears to be negligible.

Filter penetration also decreased with increasing particle size, consistent with classic filtration theory. However, the slight increase in filter penetration with increased breathing rate was not expected (Table 3) and appears to be opposite to the findings reported by Chen and Willeke (1990), especially for particles larger than 2 µm. This discrepancy may be partially explained by the fact that Chen and Willeke compared constant inhalation flows whereas we used sinusoidal breathing pattern, which more closely simulates the human breathing. Even though the unadjusted values of filter penetration did not considerably differ and are relatively low (varied between 0.05 and 0.2 %), filter penetration was significantly affected by particle size and breathing rate. Low filter penetration was expected as the challenge particles were large, 0.7 – 10 µm. Esbaugh et al. (2009) reported that when the penetration approaches zero, the influence of flow rate has less of an effect on penetration.

The ratio of particles penetrating through the faceseal leak relative to those penetrating through the filter varied from 1.9 to 16.1. This suggests that faceseal penetration accounted for most of the total penetration and consequently, affects the level of protection more than the filter penetration. The results are in accordance with the findings of Coffey et al. (1998) who reported that faceseal leakage was the largest component of total penetration for a given respirator (Coffey et al., 1998).

The fraction of faceseal penetration relative to total penetration decreased with decreasing particle size and an increase in cyclic MIF. This appears to be similar to what was reported by Chen and Willeke (1990). Furthermore, Grinshpun et al. (2009) found a similar trend for smaller particles (0.04 – 1 µm). The faceseal penetration correlated highly with the total penetration. This was anticipated as the faceseal penetration accounted for most of the total penetration. It was also accordance with the findings by Coffey et al. (1998) who reported that total penetration was significantly correlated with faceseal leakage. However, they did not measure breathing flow rates of human subjects when total penetration was determined and measured filter penetration at one flow rate of 31.4 L/min. As a consequence, no correlation between filter penetration and faceseal leakage was observed because, as shown in our study, this correlation is dependent upon flow rate. In our study, the faceseal penetration correlated with the filter penetration only when analyzed separately for each breathing flow. For example, the faceseal penetration at 30 L/min correlated with the filter penetration at 30 L/min but not with the filter penetration at 15 L/min. This was because the faceseal penetration was affected by the respiration flow more strongly than the filter penetration.

This study has a limitation associated with a relatively high sampling flow rate. Penetration through filter media and faceseal leakage is expected to be affected by high sampling flow rate especially under respiration flow rates that are comparable to the sampling flow rate. However, high sampling flow rate decreases the detection limit when measuring particles during a specific sampling period, which is important especially for measuring bioaerosols presented at low concentration. Higher sampling rate also reduces respirator purge time and significantly declines potential sampling bias especially for non homogeneous particles (Myers et al., 1986; Myers et al., 1988). The largest particle size range (mean diameter = 7.5 µm) was excluded from the analysis of this study due to low particle concentration outside the respirator. Consequently, it was not possible to compare experimental data with field data for this particle size. Another limitation is that the experiments were conducted using a breathing manikin with fixed faceseal leakage. Even though no visual deformation of the respirator was observed during the experiment, shape and size for faceseal leakage are unknown. Faceseal leakage likely fluctuates when a worker is wearing a respirator. Additional limitation is that unlike WPF, PFs determined using the manikin set-up did not account for particles returning to the respirator cavity during human exhalation. According to the findings of Lee et al., total deposition in human respiratory tract ranges from 39 % to 96% in the particle size range from 0.7 to 5 µm for adult males under medium work load (Lee et al., 2005a). This means that 4 to 61 % of particles return to respirator cavity in human experiments versus 0% in our manikin experiments. This could cause up to 1.6 times higher PF in manikin experiments even if the leakage is the same as in the human experiments. The manikin-based set-up used in this study has the advantage of investigating factors affecting faceseal and filter penetrations of hazardous substances that cannot be studied in human subjects. In the future, the set-up and testing protocol utilized in this study can be used to investigate the faceseal penetration of hazardous substances, such as allergens or toxic fungal spores.

In conclusion, an experimental set-up and procedure was developed to study realistic faceseal leakage in conditions that simulate human breathing patterns. Results with a well-fitted N95 FFR indicate that most of the particles penetrate into the respirator through the faceseal leakage, which decreases with an increase in the respiration flow rate and with an increase in the particle size.