Laser phase plate for transmission electron microscopy

Abstract

Transmission electron microscopy (TEM) of rapidly frozen biological specimens, or cryo-EM, would benefit from the development of a phase plate for in-focus phase contrast imaging. Several types of phase plates have been investigated, but rapid electrostatic charging of all such devices has hindered these efforts. Here, we demonstrate electron phase manipulation with a high-intensity continuous-wave laser beam, and utilize it as a phase plate for TEM. We demonstrate the laser phase plate by imaging an amorphous carbon film. The laser phase plate provides a stable and tunable phase shift without charging or unwanted electron scattering. These results suggest the possibility for dose-efficient imaging of unstained biological macromolecules and cells.

Introduction

Radiation-sensitive specimens, such as biological macromolecules¹ or thin lamellae milled from frozen cells² can only tolerate a limited electron exposure, making it necessary to extract the maximum information from each transmitted electron. At the same time, such specimens typically imprint a weak, position-dependent phase modulation on the electron wave function but create almost no amplitude contrast. Similarly to optical microscopy, maximum contrast in TEM of weak phase objects can be achieved with Zernike phase contrast^3,4, which allows for imaging at the limit set by electron shot-noise⁵. To realize maximum contrast, the phase of the electron wave scattered by the specimen must be shifted by 90° relative to the unscattered wave, thereby converting the phase modulation imprinted by the specimen into detectable amplitude modulation in the image.

Since the initial proposal⁶ in 1947, a series of research efforts aimed at the development of phase plates for TEM have only met partial success due to electrostatic potentials caused by surface or volume charge accumulation in the phase plates³. These potentials perturb the electron waves, scrambling the image. Recently, phase contrast imaging and protein reconstruction have been demonstrated with the Volta phase plate⁷, which is based on electron retardation caused by the beam-induced surface potential of a carbon film. Even this method, however, inherently leads to a time-varying phase shift⁸.

Electron-light interactions have been proposed as an alternative approach to coherent electron manipulation in free space⁹. Here, we demonstrate a phase plate for TEM based on the electron phase shift in the ponderomotive potential of a standing laser wave resonantly enhanced in an optical cavity^10,11. Unlike thin-membrane electron optics^3,12, the laser phase plate is a nearly ideal electron-optical element: it can withstand indefinite exposure to the electron beam, provides a stable, continuously tunable phase shift, and is free of charging and unwanted electron scattering.

Electrons interact with light via the repulsive ponderomotive potential arising from stimulated Compton scattering, given by U = e²E ²λ_L²/(16π²mc²), where e is the elementary charge, m is the electron mass, c is the speed of light, and λ_L and E are the wavelength and electric field amplitude of the light wave, respectively¹⁰. Due to the short electron-light interaction time in a micron-scale laser focus, retardation of the relativistic electrons used in TEM requires an intensity of tens of GW/cm². Such intensities have so far only been attained with pulsed lasers, which have been used in previous experiments on free-space electron-light interactions^13,14. Here, we use instead a CW laser system¹¹ that allows for operation in a state-of-the-art, continuously operating TEM. While more technically challenging, a CW system has no limitations associated with the laser duty cycle or synchronization jitter and intensity variation due to the temporal envelope of a pulse. In addition, the cavity mode provides a precise, speckle-free spatial distribution of the laser field, which allows for well-defined electron manipulation.

Results [CE: please query the authors to add callouts to Supplementary Notes 4 and 5]

Electron-laser interaction

The requisite laser intensity is generated by 4000-fold resonant power enhancement in a near-concentric Fabry-Perot optical cavity¹¹ with a mode waist of w₀ = 13 µm. A laser system consisting of a fiber amplifier seeded by a low-power master laser supplies an input laser beam at a wavelength of λ_L = 1064 nm. The laser is frequency-stabilized to the cavity resonance using the Pound-Drever-Hall scheme. The experiments are carried out with 80 keV electrons, in a custom-modified TEM (FEI Titan) equipped with additional electron optics that magnify the diffraction pattern to an effective focal length of f = 20 mm. The cavity is suspended in the TEM column, with its axis orthogonal to the electron beam direction and with the mode waist positioned close to the center of the magnified electron diffraction plane, as shown in Fig. 1 and described in the Online Methods.

Fig. 1. Laser-based control of the electron phase in a TEM.

Schematic of the experimental setup: a high-power standing laser wave, resonantly enhanced in an optical cavity, is introduced into the path of the electron beam in a custom TEM. The electron diffraction pattern, formed in the back focal plane of the objective lens, is magnified and relayed into the section of the TEM column containing the optical cavity. The configuration shown in the schematic illustrates the laser wave used as a Zernike phase plate for phase contrast imaging. The unscattered electron beam is focused in the center of the diffraction pattern, where it passes through a single antinode of the standing laser wave. The phase-shifted unscattered electron beam and the scattered electron beams are then recombined in the image plane.

To demonstrate spatial control of the electron phase with a laser beam, we position the electron beam focus downstream of the cavity axis (Fig. 2a). These studies were performed with an input laser power of 7.4 W, with no specimen inserted. The standing light wave diffracts the converging electron wave via the Kapitza-Dirac effect^13,15, producing a series of spatially separated focal points, with the 0th and ±1st diffraction orders accounting for most of the electron density. Diverging again, the diffraction orders overlap and interfere, forming an image of the laser-induced phase profile in the far field (Fig. 2b–d). These far-field images, also known as Ronchigrams¹⁶, are electron micrographs of the standing light wave. The transverse (y) and the longitudinal (x) profiles (Fig. 2e) of the standing wave image (Fig. 2c) are in excellent agreement with the fitted model. The fits of Fig. 2e correspond to a peak phase shift of 38° and an intensity of 43 GW/cm² at the antinode, which are the lower bounds for the corresponding experimental values (see Supplementary Note 1). Capturing the standing light wave images at varying laser power, we found that the phase shift at the antinode scales linearly with the input laser power, as expected (Fig. 2f, left). It is stable as a function of time, showing a root-mean-square variation of 0.36° over 1 hour (Fig. 2f, right).

Fig. 2. Electron micrographs of a standing laser wave.

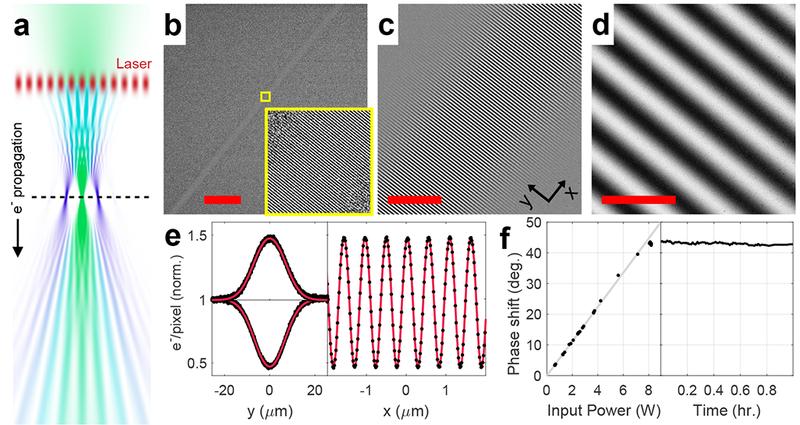
(a) Simulation of the electron beam propagation in the experimental setup for imaging light waves. The horizontal scale is exaggerated relative to the vertical scale. Top to bottom: a converging Gaussian electron beam (green) is diffracted by the laser standing wave acting as a phase grating (red), which generates density modulation in the electron beam (teal) as it propagates downstream from the laser wave. At the focal plane of the unscattered electron beam (dashed line), the diffraction orders spatially separate, each forming an isolated focal point. As the diffraction orders expand beyond their focal points, they overlap again and their interference pattern forms a Ronchigram image of the light wave in the far-field. The hue of the electron beam represents the fraction of diffracted (blue) or undiffracted (green) wave function amplitudes. (b-d) Electron micrographs of the intra-cavity standing laser wave at different magnifications. Scale bars: (b), 100 µm; (c), 10 µm; (d), 1 µm. The inset in (b) shows a magnified view of the region indicated by the yellow square. The coordinate axes annotation in (c) shows the axes used in (e). (e) Averaged transverse (left) and longitudinal (right) profiles of the standing wave image shown in (d) (black dots) with the fitted model (red lines). The transverse profile is shown for both the positive fringe in the image (upper curve) and the negative fringe (lower curve). The longitudinal profile is averaged over a narrow region along the central axis of the laser wave (see Supplementary Note 1). (f) The phase shift at the antinode of the light wave as a function of the input power (left) and time (right). The gray line in the left graph shows a linear least squares fit to the data.

We note that we have captured TEM images of light waves in free space, unlike previous work on TEM of evanescent electromagnetic fields near nanostructures^17–20. Evanescent fields can be imaged at much lower intensity via single-photon processes that are disallowed in free space due to energy and momentum conservation²¹.

Contrast enhancement

Next, we utilize the laser-induced retardation of electron waves for contrast enhancement in TEM images. The Fourier transform I(s) of a TEM image of a weak phase object can be expressed as I(s)=δ(s)–2φ(s)∙CTF(s), where s is spatial frequency, δ(s) is the Dirac delta function, φ(s) is the Fourier transform of the phase modulation imprinted by the specimen, and CTF(s) is the contrast transfer function²⁸. The theoretical CTF, including the effect of the laser phase plate, is

$$\text{CTF}\left(\mathbf{s}\right)=\text{sin}\left[\eta \left(\mathbf{s}\right)-\eta \left(0\right)+\gamma \left(\mathbf{s}\right)\right]·E\left(\mathbf{s}\right),$$ (1)

where η(s) is the spatial-frequency dependent phase shift applied to the scattered wave by the laser beam (see Supplementary Note 2), η(0) is the phase shift applied to the unscattered wave, γ(s) = π/2 (−2 ΔZ λ_e s² + C_s λ_e³s⁴) is the wave aberration function, λ_e is the electron wavelength, ΔZ is the defocus, C_s is the spherical aberration coefficient, and E(s) is an envelope function arising from the finite coherence of the electron beam. Conventionally, phase contrast is achieved by defocusing the TEM, which gives a CTF that oscillates with the spatial frequency. Ideal Zernike phase contrast is achieved with a phase plate that retards the unscattered beam by η(0) = 90°, which extends phase contrast to low spatial frequencies and potentially enables in-focus imaging with a uniform CTF²².

The laser phase plate provides phase contrast for almost all spatial frequencies, with reduced contrast in the limited areas where the intensity of the standing light wave is high. The CTF thus features a broad high-contrast plateau at low spatial frequencies, with a dark stripe along the cavity axis composed of alternating dark and bright transverse stripes. The width of the dark stripe s₀ is set by the laser beam waist at s₀ = w₀/(f λ_e) = (6.4 nm)⁻¹. Spatial frequencies down to s₀ are transmitted with virtually full contrast (Supplementary Note 2). Even larger features, up to a few hundred nanometers, are transmitted with a CTF > 0.6 on average due to the nodes in the standing wave. The standing laser wave has previously been shown in numerical simulations to function as a nearly ideal phase plate for TEM imaging of individual biological macromolecules in vitreous ice¹¹. If the phase shift of the unscattered wave is less than 90°, as is the case here, the low-frequency contrast is decreased by a factor of sin(η(0)).

To demonstrate phase contrast with a laser phase plate, we must focus the electron diffraction pattern at the plane of the laser cavity, so that the unscattered electron beam passes through a single antinode of the laser standing wave. As we approach this condition, the magnification of the light-wave Ronchigram image increases until the entire image covers a small region of a single antinode of the standing wave, and the image background becomes uniform (see Supplementary Note 6). We then align the center of the electron diffraction pattern relative to the laser standing wave by tuning appropriate electron-deflector coils in the TEM. We chose a thin (3 nm) amorphous carbon film as a test specimen, as its structure contains a broad range of spatial frequencies and thus allows for CTF characterization. The real-time Fourier transform of the image of the carbon film is used to guide the alignment, as described in Supplementary Note 6. The input laser power in this case was reduced to 4.4 W as a precaution against possible thermal damage to the cavity output-coupling optics.

With the laser phase plate enabled, phase contrast is evident in a typical close-to-focus image (Fig. 3a), showing the structure of the carbon film. The Fourier transform of the image (Fig. 3c) has a broad plateau at low spatial frequencies, with a dark stripe across the center, characteristic of the CTF with the laser phase plate (see Supplementary Note 2). For comparison, an image of the carbon film with the laser turned off, at a substantially higher defocus of ΔZ = 880 nm (Fig. 3b), has a Fourier transform with multiple concentric fringes, known as Thon rings, and a dark center (Fig. 3d). An angular average of the absolute value squared of the Fourier transform with the dark stripe excluded (Fig. 3e) demonstrates laser-induced phase contrast by showing a much higher amplitude at low spatial frequency.

Fig. 3. Phase-contrast imaging with a laser-based phase plate.

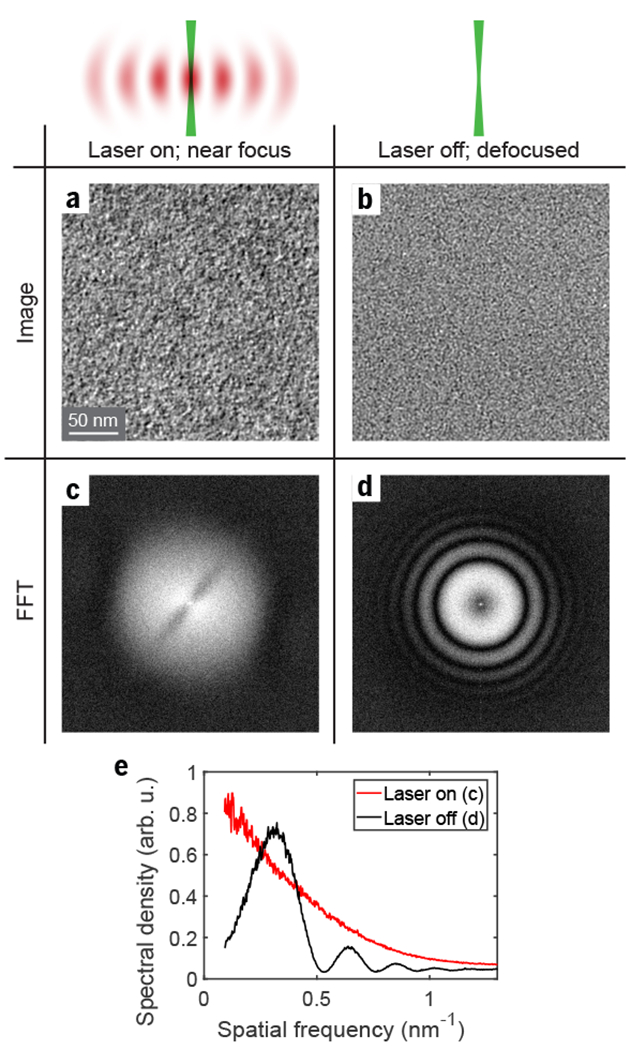
(a) A close-to-focus image of a 3 nm-thick amorphous carbon film with the laser phase plate enabled. (b) For comparison, a defocus-based phase-contrast image with the laser off, at a defocus of 880 nm, at the same magnification and using the same gray scale as in (a). (c,d) Absolute value squared of the Fourier transforms of the images in (a,b), in logarithmic scale, shown in the spatial frequency range from −1.5 nm⁻¹ to 1.5 nm⁻¹ along both axes. (e) Angular averages of the Fourier transforms in (c) (red) and (d) (black), showing increased low-frequency contrast with the laser phase plate enabled. Note that that the peak values of the (d) curve exceeds the monotonically decreasing (c) curve because the phase shift at an antinode was less than 90°.

Finally, to show that the phase of the unscattered beam can be continuously tuned by varying the local laser intensity along its path, we translate the electron diffraction pattern along the axis of the cavity. The phase shift changes periodically from a maximum at the standing wave antinode to zero at the node. Representative carbon film images at the antinode and at the node, and their respective Fourier transforms, are shown in Figs. 4a–d. The images were taken at a defocus of ΔZ = −500 nm. The angular averages of these Fourier transforms (Fig. 4e) demonstrate a substantial increase in low-frequency contrast and reveal the shift in the CTF zero crossings, seen as minima in the image spectral density.

Fig. 4. Continuous variation of the unscattered beam retardation.

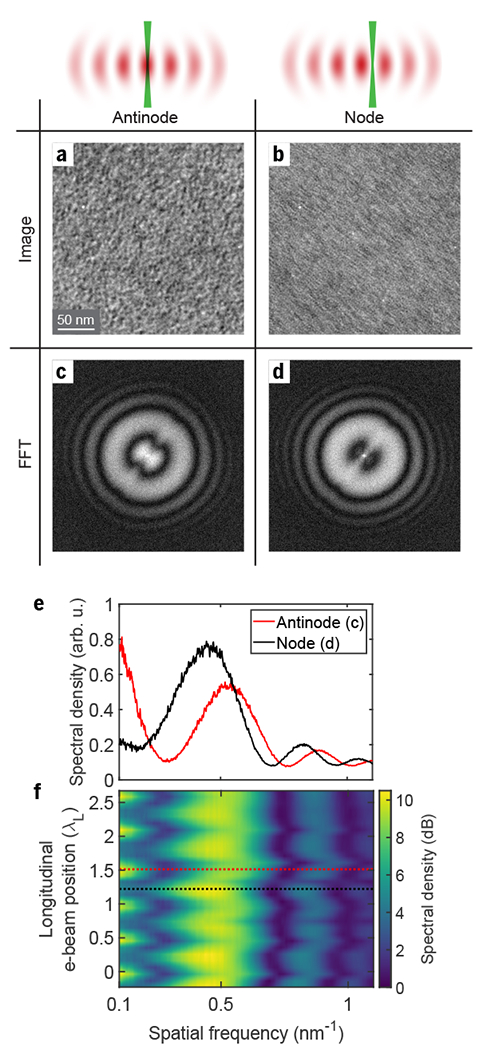
The electron diffraction pattern is translated along the axis of the cavity, with the unscattered beam experiencing maximum phase shift in the antinodes and no phase shift in the nodes of the laser wave. (a,b) Images of the carbon film with the unscattered electron beam passing through an antinode (a) and a node (b) of the standing wave. The images are recorded at a −500 nm defocus (overfocus). (c,d) Absolute value squared of the Fourier transforms of the images in (a,b), in logarithmic scale, shown in the spatial frequency range from −1.5 nm⁻¹ to 1.5 nm⁻¹ along both axes. The streaking in (b) is due to selective enhancement of contrast for spatial frequencies coincident with the standing wave antinodes; note that this is not the condition under which the phase plate is intended to be used. (e) Angular averages of the Fourier transforms in (c) and (d), showing a radial shift of the interference pattern (Thon rings) and an increase of contrast at low spatial frequencies when the unscattered electron beam passes through the laser wave antinode. (f) Angularly averaged Fourier transform of the image as a function of the electron beam position along the laser propagation direction, demonstrating a periodic shift in the fringe pattern as the unscattered electron beam moves between subsequent laser standing wave nodes and antinodes. The red and black dashed lines indicate the positions corresponding to the images shown in (a) and (b), respectively.

The color map plotted in Fig. 4f shows the angularly averaged image Fourier transforms as a function of the unscattered electron beam position. Fitting the CTF zero crossing frequencies as a function of the unscattered electron beam position, we find an 18° phase shift at the antinode, corresponding to a contrast transfer of sin(18°) = 0.31 at low spatial frequencies (see Suplpementary Note 3).

Discussion

We have thus shown that a high-intensity CW laser field generates phase contrast in a TEM and significantly increases the image contrast at low spatial frequencies. The laser phase plate thus has the potential to enable dose-efficient data collection in single-particle analysis of biological macromolecules^22–24, electron tomography of vitrified cells², and imaging of sensitive materials science specimens²⁵. This may allow for reconstruction of macromolecules that are currently too small for cryo-EM analysis, and will improve the resolution in assemblies with movable domains. In tomography, the application of the laser phase plate may enable discerning finer details of cellular structure.

Further work is underway to double the laser power and halve the focus size, which will allow for the optimal 90° phase shift at an electron energy of 300 keV, preferred for cryo-EM. These goals are attainable by improving the cavity stability at high power through the use of custom-designed cavity mirrors with low thermal expansion coefficient and advanced low-absorption coatings²⁶. Although the resolution of our TEM images is currently limited to 0.8 nm, preliminary studies indicate that engineering improvements such as a more rigid cavity suspension will restore the higher resolution information (see Supplementary Note 7). The laser phase plate is in principle compatible with aberration correction and should not affect attainable imaging resolution. The phase plate is highly transparent, with less than one in 10⁷ electrons passing through the antinode of the laser wave undergoing Compton scattering.

These results establish a technological platform for further development of the laser-based electron optics for TEM⁹, such as diffraction gratings¹³, beam splitters and reflectors²⁷, and temporal modulators^14,21. Such optics can be used to introduce new electron-based imaging modalities^18,28, including multi-pass schemes that increase the signal to noise ratio (at a given degree of radiation damage) beyond the standard quantum limit^29,30. Laser control of electron waves thus offers a path towards dose-efficient interrogation of radiation-sensitive specimens.

Online Methods

Experimental setup of laser phase plate

The experimental setup consists of a continuous-wave laser which sends light into a Fabry-Pérot optical cavity. The laser system is of the master oscillator fiber amplifier (MOFA) design, where the light from a narrow linewidth seed laser is amplified in a fiber amplifier. The seed laser is an NKT Photonics ADJUSTIK Y10 operating at a wavelength of 1064 nm with 15 mW of output power. The linewidth of the seed laser is specified to be 3 kHz. A fiber-based acousto-optic modulator (AOM) installed at the input of the fiber amplifier provides fast control of the laser frequency. The fiber amplifier is a Nufern NUA-1064-PD-0030-D1 capable of providing up to 30 W of output power in a single-mode, polarization-maintaining fiber.

The light from the amplifier is collimated into a free-space Gaussian beam by an aspheric lens and then sent through a Faraday optical isolator to prevent back-reflections from entering the amplifier. A pair of mirrors on standard manually adjustable optomechanical mounts are used to direct the beam into the cavity. A focusing lens couples the collimated input beam to the cavity mode.

The laser frequency is locked to the cavity resonance frequency using the Pound-Drever-Hall (PDH) technique³¹. The AOM provides fast feedback (overall bandwidth of approximately 200 kHz), as well as the PDH frequency modulation sidebands. Thermal and mechanical control of the seed laser frequency provides a large mode hop free tuning range of 169.5 GHz. The large tuning range is desired because the cavity length changes due to thermal expansion at high laser power and the laser frequency must be able to follow the concomitant change in cavity resonance frequency.

The effect of the PDH sidebands on the laser field inside the cavity is negligible. We used weak sidebands (less than 1 percent of the laser power), which are outside of the width of the cavity resonance and thus almost entirely rejected (reflected) by the cavity. The sideband detuning from the main beam was f = 5 MHz, while the cavity linewidth was ν = 120 kHz. The sidebands inside the cavity were therefore attenuated by a factor of (ν/f)² ≈ 0.5·10⁻³. Thus, the resulting laser power in the sidebands was less than 10⁻⁵ of the total power, which had no noticeable effect on our experiment.

The Fabry-Pérot cavity consists of two mirrors installed in a monolithic aluminum flexure mount. Aspheric lenses couple input light into the cavity and collimate the output beam. The tip/tilt angle and distance between the mirrors is controlled by adjusting the position of the flexure stage with micrometer screws for coarse adjustment, and with piezoelectric actuators for fine adjustment and active feedback.

The tip and tilt angles determine the orientation of the cavity mode, the axis of which passes through the centers of curvature of each mirror. The mirror-to-mirror distance (cavity length) determines the numerical aperture (NA) of the cavity mode. Both the orientation and NA of the cavity mode become extremely sensitive to the mirror alignment in the near-concentric regime.

When operating the cavity at high power, thermoelastic deformation of the cavity mount and mirrors changes the mirror alignment. This deformation is large enough to cause the cavity mode to become misaligned with the input beam, preventing the cavity power from being increased further. Even at low power, the alignment of the cavity drifts slowly over time. Consequently, the cavity mode orientation must be actively stabilized. To stabilize the orientation of the cavity mode, the transverse position of the laser beam after exiting the cavity output coupling lens is monitored using a position-sensitive detector (PSD). The position on the PSD (and therefore the orientation of the mode within the cavity) is held constant by applying a feedback signal to control the two axes of tip/tilt adjustment provided by the cavity alignment piezos.

The finesse of the cavity was periodically measured between high power experiments using the rapidly-swept continuous-wave cavity ringdown technique^11,32.

The amorphous carbon film samples, prepared by carbon evaporation onto freshly cleaved mica and transfer onto holey carbon films on EM grids, were generously provided by Dr. B.G. Han.

Statistics and reproducibility

For all representative micrographs obtained with the laser phase plate, at least 10 similar TEM images of the same type have been collected.

Data and materials availability

The raw TEM images collected over the course of this study are available from the corresponding author upon request.

Code availability

The code for fitting the light wave micrographs is available from the corresponding author upon request.