Abstract
The intensity of the light scattered from individual dielectric spheres was measured as a function of the scattering angle, for light polarized parallel and perpendicular to the scattering plane. These sets of data were used to determine the radius and refractive index of the spheres by fitting the data to the scattering function obtained from Mie theory. The light was produced by a He-Cd laser (λ=441.6 nm). Measurements were performed on particles of six discrete sizes with radii in the range 117–1175 nm. Several different measures of the quality of fit were examined, and the least-squares fit, unweighted or weighted with a factor sin2(θ/2), was found to be the best. The values obtained for the index of refraction were found to be within 1% of the published bulk value 1.615. The measured radii differed by several percent from those specified by the manufacturer. Several sources of error were analyzed, and their effects were simulated in numerical experiments. The largest source of error in the instrument was a discrepancy between the actual scattering angle and the reading provided by the instrument. Less significant was the noise introduced by the motion of the particle within the laser beam. A calibration eliminated most of the error in the scattering angle. The precision and accuracy of this technique are estimated to be 0.2% and 0.9%, respectively, of the particle size for particles of a nominal radius of 457 nm.
Keywords: dielectric spheres, inverse electromagnetic scattering, light scattering, Mie scattering, particle size, polystyrene latex, refractive index
1. Introduction
Recently developed instrumentation has the capability of recording the intensity of the light scattered from a single micrometer-size particle as a function of angle. One such instrument has as its key component an electrostatic particle levitator with automatic servocontrol and a periscope detector that moves in a horizontal arc of nearly 180° [1]1. Phillips et al. [2] reported the determination of particle radius r and refractive index n of a single polystyrene sphere with a diameter of 1099 nm. Subsequent studies of polystyrene spheres with this type of instrument include analysis of the size distribution of spheres of diameter of 796 nm [3], and measurements of size and refractive index for spheres of diameters of 1011, 794, and 600 nm [4].
Our study represents an extension of these investigations and includes the following improvements: the spectra for both vertically and horizontally polarized light are recorded, an accurate angle calibration is performed, the output is automatically converted to digital form by a high-precision A/D converter, and several sizes in a wide range—six groups of particles with radii between 117 and 1175 nm—were studied. A major effort of our study was a detailed error analysis, enabling us to make a quantitative statement regarding the accuracy of the technique. Our analysis applies specifically to the Differential II light scattering photometer2, which was designed by Wyatt and Phillips, but the principles apply to such other single-particle instruments as the Gucker photometer for rapid measurement of angular scattering patterns for individual particles [5].
We describe the instrument used to measure the scattered light, the procedure used to collect the data, and the preliminary manipulation of the data to prepare it for analysis in section 2. Of special importance is the calibration of the readings of the scattering angles, which greatly affects the results of the analysis.
We discuss the data analysis procedure in section 3. Although the principle is straightforward, the effect of noise and other errors introduce a number of complications familiar in inverse scattering problems. The choice of the measure of fit, resulting in different weights being assigned to errors, influences the results significantly, especially for smaller particles that show more noise in the data.
To understand the sensitivity of the results to different errors, we conducted several numerical experiments in which theoretically computed intensities are altered with simulated errors to generate the “data” that are analyzed by the same procedures as the real data. The results of the sensitivity analysis are presented in section 4.
The experiments were performed on particles with radii between 117 and 1175 nm. We took data for a number of particles in each nominal size sample, both for horizontal and vertical light polarizations, with several repeat scans for the same particle and polarization. In section 5 we discuss the different sources of errors and compare our results to those obtained by other authors.
2. Experimental Method
2.1. General Characteristics
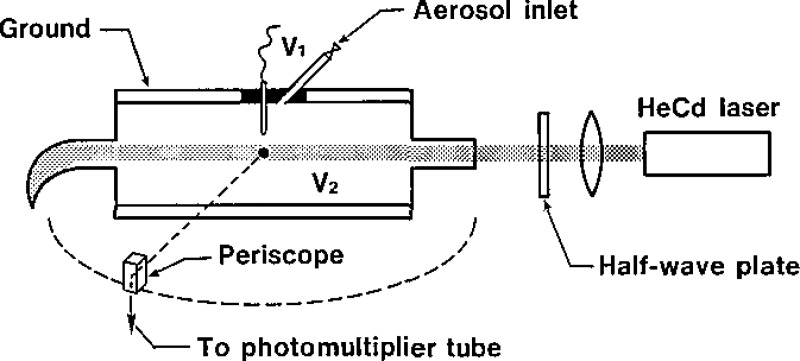
We use a Differential II light scattering photometer, manufactured by Science Spectrum, to measure the intensity of scattered light versus angle for a single particle. An aerosol made up of polystyrene spheres is generated by nebulizing a suspension of the spheres in distilled water; the water evaporates rapidly leaving charged spheres. The spheres are passed into the optical cell, which has two plate electrodes and a pin electrode as shown in figure 1. The pin electrode is located just above the laser beam. We move a sphere into the field of view by use of a hydrostatic bellows, turn on the voltage to the pin electrode, and “walk” the particle to the center of the laser beam by adjusting the differential voltage between the pin and base plate. Catching a particle turns out to be analogous to playing a pinball game in terms of the required manipulations and, especially, in regard to the psychological mood that evolves. Once the particle is in the center of the laser beam, we engage the servo-control that keeps the particle at a fixed location by comparing the intensity of the acattered light reflected by a mirror edge with that transmitted above; the two intensities differ when the particle is at the edge of the beam. A more detailed account of the instrument design can be found in the literature, see ref. [1].
Figure 1–
Single particle scattering instrument (Differential II). The pillbox-shaped scattering cell has a pin electrode (V1) separated by an insulator from the ground plate electrode and opposite to the base plate electrode (V2).
The scattered light reaches the photomultiplier with an S-21 response via a traversing periscope, which has an acceptance angle of about 2°. Data are typically recorded over the range of 20° to 160°. The stepping motor is operated at the highest scanning speed, which corresponds to about 1 scan in 50 s. The output of the angle encoder and the photomultiplier tube is displayed on an x-y recorder and is also processed by a Hewlett-Packard scanner, A/D converter, and an HP 9845T desktop calculator. The switching rate of a scanner used to feed the intensity and angle data to a single A/D converter limits the data acquisition rate to a pair of readings every 0.3 degrees. The data pair closest to each integer angle is stored on magnetic tape.
A He-Cd laser (λ=441.6 nm) is used as the light source. The short wavelength is an advantage when scattering experiments from submicron particles are performed, because the scattered intensity is a function of r/λ and higher values of r/λ increase the structure in the scattering pattern. We find that inserting a 15-cm focal length coated achromat 20 cm from the pin electrode increases the scattered light intensity and reduces the stray light reflection from the entrance tube to the scattering cell and from the light trap. This choice of lens is actually a compromise between ease of catching the particle (no lens at all is best) and optimum signal-to-noise ratio (the laser beam should be focused near the particle). We have also inserted a half-wave plate to allow measurements of the scattering intensity with the plane of polarization of the light perpendicular to the scattering plane as well as in the same plane (vertical and horizontal polarizations, respectively). The availability of both polarizations helps in the accurate determination of the values of n and r, described in section 3.
A typical sequence of measurements begins with a scan, with no particle in the beam, to determine the background intensity versus angle. After catching a particle, the voltage is adjusted to minimize noise due to the particle motion in the laser beam (the lowest noise is obtained for highly charged particles and low electric fields). We then take one or more scans with a particle in the beam, rotate the half-wave plate by 45° to change the polarization of the incident beam, and take one or more scans for this configuration. Finally, we remove the particle and take another background scan with the second polarization state. We subtract the appropriate background scan IB from the particle scan IP by setting
| (1) |
The angles θi and at which measurements are made are close to each other but not equal. Due to the flatness of the background scan from 20° to 160°, the difference between these angles is of no consequence.
Scattering measurements were made for six discrete particle sizes spanning a range of 117 to 1175 nm in radius. The largest particles were polyvinyltoluene; the others were polystyrene. The material was obtained from Dow Diagnostics. The nominal particle size and lot number, as stated on the labels, are given in table 1. A few drops of the packaged material, which is nominally 10% particles by volume suspended in water, were diluted with filtered distilled water to a convenient concentration for catching the particle in the scattering cell. For nominal particle size of 551 nm radius, a volume concentration of 100 ppm, corresponding to a number concentration of about 2×l06 particles/cm3, provided an adequate concentration for ease in catching the particle. For other particle sizes, the material was diluted so that the number concentration was constant at about 2 × 106 particles/cm3.
Table 1.
Comparison of our results for particle size with electron microscope results of Dow Chemical Company.
| Samplea | No, of Particles | NBS Light Scattering r ± σ, nm | C.I.b, nm | Dow Electron Microscopy r ± σc, nm | % Diff. |
|---|---|---|---|---|---|
| PVT, 8C2J | 6 | 1129 ± 2 | ± 10.4 | 1175 ± 9.7 | +4 |
| PSL, 7G3L | 7 | 587 ± 4 | ± 2.6 | 551 ± 2.8 | −7 |
| PSL, 1A74 | 8 | 450 ± 5 | ± 2.5 | 457 ± 3.0 | +2 |
| PSL, 2F8E | 10 | 295 ± 4 | ± 1.1 | 300 ± 1.5 | +2 |
| PSL, 4N1A | 9 | 236 ± 4 | ± 1.8 | 230 ± 2.4 | −3 |
| PSL, 4N6H | 6 | 108 ± 3 | ± 1.5 | 117 ± 1.4 | +8 |
The abbreviations PVT and PSL are used for poly vinyltoluene and polystyrene. The four character designation is the Dow Diagnostics lot number.
The confidence interval, C.I., is calculated for the 95% confidence level using the relation, , where m refers to the number of runs, σ is the standard deviation as measured by Dow, and tm-1(0.95) is Student’s t-value corresponding to a 95% confidence level.
This is the nominal radius as specified on the label on the sample.
An effort was made to estimate the amount of impurities in the distilled water, which can affect the measured particle size and index of refraction. We determined by a gravimetric technique that the nonvolatile impurities in the filtered distilled water were of the order of 1 to 2 ppm. The effect of these impurities as well as impurities coming from the packaged material are discussed below.
2.2. Calibration
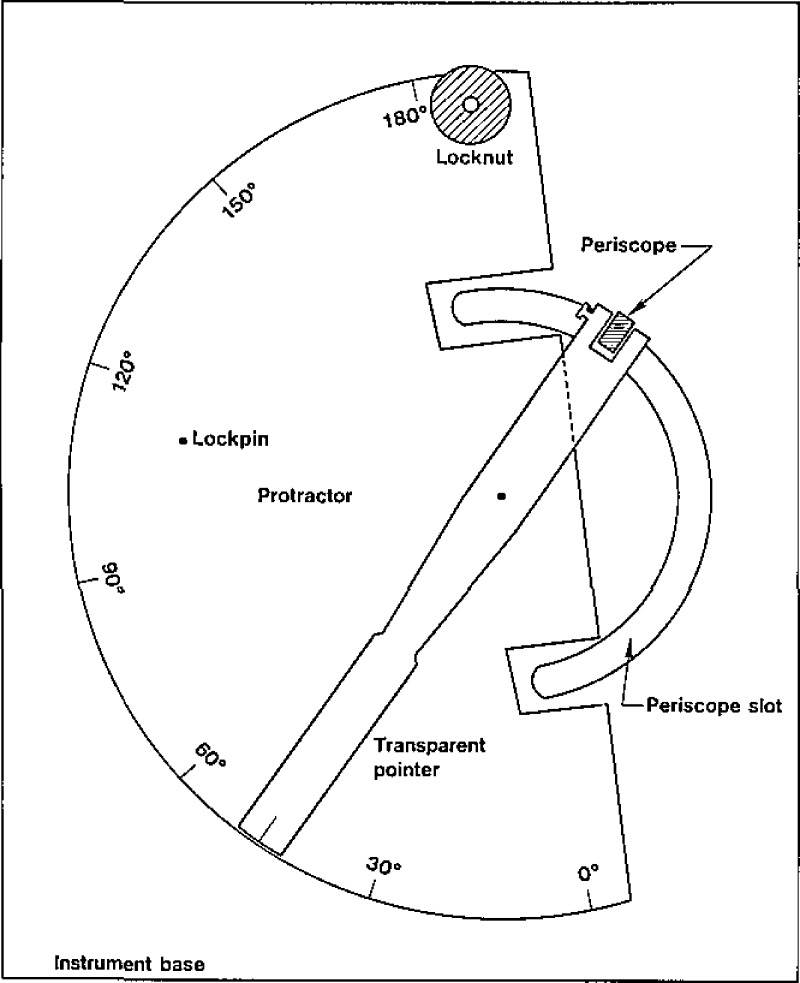
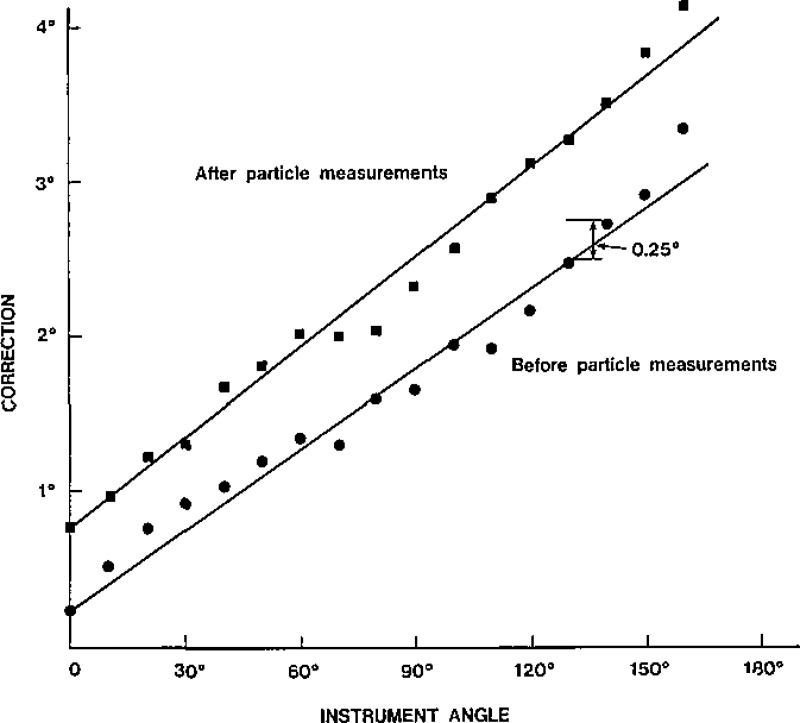
We found that the angle reading, θinst, deviates from the true angle, θt, by as much as 3°. We performed an angular calibration using an accurately indexed protractor 20 cm in diameter with a pointer connected to the traversing periscope, as shown in Figure 2. The protractor agreed within 0.09° with an indexing table. Instrument readings and protractor readings were made every 10°. As shown in figure 3, the angle θc defined by
| (2) |
is essentially linear with respect to the instrument angle. From a linear least square fit of the data, we obtain
| (3) |
A small correction, 0.18°, must be added to the constant term on the right-hand side of eq (3) to account for the change in angle due to the scanner time delay in going from an angle reading to an intensity reading. We found that the angle correction given by eq (3) changed after performing experiments on 50 particles. We think that this drift is primarily a result of electronic instability in the encoder.
Figure 2–
Angle calibration device. Marks are etched every half degree.
Figure 3–
Correction to the angle read by the instrument as a function of that angle before and after measurements done on 50 particles.
In addition to the scattering angle calibration, we also checked the polarization of the light relative to the scattering plane by using an accurately oriented polarizer mounted in a rotator. The ratio of the intensities of the vertically and (unwanted) horizontally polarized components of the light was about 200:1. This ratio was reversed when the light passed through a half-wave plate to change the polarization. In section 4.2, we estimate the effects of the polarization mixture and the scattering angle correction on the fitted value of size and refractive index via numerical experiments.
One other slight misalignment results from the elevation of the periscope above the plane where the scattering angle is measured, defining a new scattering plane. This offset is most apparent when the periscope is rotated to the zero scattering angle, because the laser impinges on the lower portion of the periscope slit. The offset is about 1 mm, which corresponds to a 1.3° inclination from the intended scattering plane. This offset leads to both a correction Δθ in the scattering angle and a small angle α between the direction of polarization and the perpendicular to the physical scattering plane for vertical polarization. These angles are given by
| (4) |
| (5) |
where θ is the scattering angle measured by the instrument and ϕ is the elevation angle of the periscope. The change in the polarization direction is the same for both horizontal and vertical polarizations. These equations give Δθ=ϕ, α=90° for θ=0°; Δθ=0°, α=ϕ, for θ=90°; and Δθ =−ϕ, α=90° for θ = 180°. We can see that the corrections are largest for the endpoints of the angle range; for θ = 20° and ϕ=1.3°, we obtain Δθ=0.04° and α = 3.8 °. The correction in the scattering angle is negligible, and the polarization effect is comparable to that produced by the laser beam (about 200:1).
3. Data Analysis
After the light scattering data are collected, they are transmitted to an Interdata 7/32 minicomputer for processing. We adapted the program supplied with the Differential II instrument to our needs, and wrote a number of ancillary FORTRAN programs to facilitate the preparation of the input files and the presentation of the results.
We can specify a range of values of the refractive index n and the radius r, and a number of points for each range; the computer finds a quality of fit Q for each of the points in the corresponding rectangular grid. The quality of fit can be defined in a number of ways, as discussed in section 3.3, The values of n and r that correspond to the minimum value of Q give us the best estimates of n and r for that particle. When data are taken for the horizontal and vertical polarizations, a separate best fit is provided for both. Usually we obtain plots showing the theoretical and experimental curves for both polarizations for each best fit, allowing visual evaluation of the data and the fit. We also used three dimensional plots of Q as a function of n and r to get a better understanding of the results. To obtain information about the sensitivity of the results to different types of errors, we also carried out the same procedure with simulated data generated from a theoretical curve by addition of random noise and other errors.
3.1. Mie Theory
The theory originally developed by G. Mie [6–8] allows us to express the intensity of the electromagnetic field scattered by a uniform sphere when a monochromatic plane wave falls on it.
Due to the symmetry of the configuration, the scattered intensity depends only on the angle θ between the incident and scattered directions and the direction of polarization. It suffices to consider separately two polarizations, with the incident field either perpendicular or parallel to the scattering plane defined by the incident and scattered light directions of propagation.
The intensity of the scattered field at a large distance R from the sphere (R large compared to the wavelength λ) is given by
| (6) |
| (7) |
where I0 is the intensity of the incoming beam, is an associated Legendre function, the wave number is k=2π/λ, and the scattering coefficients eBl and mBl are given by
| (8) |
| (9) |
with ψl and ζl related to Bessel and Hankel functions by
| (10) |
| (11) |
We see that the coefficients eBl and mBl have an intricate dependence on n and r. The fact that at least in some cases the shape of the scattering curves changes little if the product nr remains constant is not apparent from the equations. The effects of this dependence on the data analysis are discussed in section 4.
3.2. Procedure
The data from the experiment are stored on the HP microcomputer, formatted as required for the input to the analysis program, and transmitted to the Interdata minicomputer. We then add the remaining input information required by the program, choose a range of values for n and r and the number of grid points for each variable, and compute the corresponding values of the quality of fit. In most cases we also eliminate some of the readings that are obviously incorrect, especially at the beginning and at the end of the curves; we attribute these errors to saturation of the photomultiplier or to uncertainties due to a large background intensity and a small signal. Normally we plot the theoretical and experimental curves for the best fits (both polarizations for each best fit), and decide whether it is necessary to shift or refine the grid. Another helpful tool is the production of three-dimensional plots of Q as a function of n and r to represent and understand the shape of this surface better. Actually, we plot 1/Q and −logQ and look for a maximum, because the resulting plots are more easily visualized.
In most cases, this procedure is repeated for one or more other measures of the quality of fit, as discussed below.
3.3. Quality of Fit
Although often the quality of the fit of a theoretical curve to the experimental data can be evaluated visually from the plots, a numerical value of the quality of fit is of great help and can be used for automated computer searches for a minimum.
A simple least-squares fit is based on the expression
| (12) |
where N is the number of data points, Ei, is the experimental value, Ti is the theoretical value for the same angle, and α is an overall scaling factor required because we do not measure absolute intensities. The theoretical value is computed for each degree, and then averaged over three consecutive values to take into account the two-degree acceptance angle of the detector. We carry out a further interpolation to find a better approximation to the theoretical value at the precise angle where the intensity was measured. The original program uses integer values for the angles, and this correction becomes important if the angles are entered digitally and then corrected.
We compute the value of α by finding the value that minimizes the corresponding Q, which is
| (13) |
Originally we used the expression for Q as given in the program supplied with the instrument, which differs from eq (12) in that the experimental values of the intensities are scaled to the theoretical ones, not the other way around. This choice proved to be troublesome because the normalization of the theoretical values can change abruptly as peaks in the curve appear or disappear; that is, the normalization becomes strongly dependent on n and r. Although in most cases the values of n and r for the best fit change little if at all, spurious minima may appear when the normalization changes abruptly near those values, as described in section 4.2 for a numerical experiment. Also the sensitivity analysis can be affected by this difficulty.
Alternatively, the value of α can be chosen by matching a particular value of the measured intensity to the theoretical value at the same angle. This least-squares fit gives much weight to errors in the measured intensity in the region where these values are large and the slope of the curve is steep; a small error in the measured value for the scattering angle leads to a large deviation between Ei and αTi, which is then squared.
We tried several other methods to define the quality of fit. The most interesting alternative resulted from weighting the intensities by a function of the angle. Specifically, we considered
| (14) |
which reduces the contributions to the quality of fit from the large peaks at small angles; conversely, it overemphasizes the error at angles close to 180°, where the amplitudes are small and the relative errors are large. The factor sin2(θ/2) was chosen because it tends to equalize the size of the peaks.
We also tried a least-squares fit to the function
| (15) |
where u is a unit step function we introduced to avoid problems with values of the intensity smaller than a selected minimum value Imin.
For the previous functions, we can find a value of α that minimizes Q. This is not the case for Q defined as the area between the experimental and theoretical scattering curves, which is approximately equal to the sum of the absolute values of the differences of the intensities at each angle. The value of α was selected by matching the first peak or, preferably, by setting
| (16) |
which makes the average deviation between the curves vanish; these choices do not necessarily minimize Q.
For good quality data, all methods naturally lead to the same or very similar values for n and r. For noisy data, there were examples where the least-squares fit would not lead to the best value for n and r as seen from the curves. Other methods also failed in particular examples, so that no overall recommendation can be made other than to try several methods in difficult cases, and always check the plots of the curves for the selected best fits.
4. Results
4.1. Actual Experiments
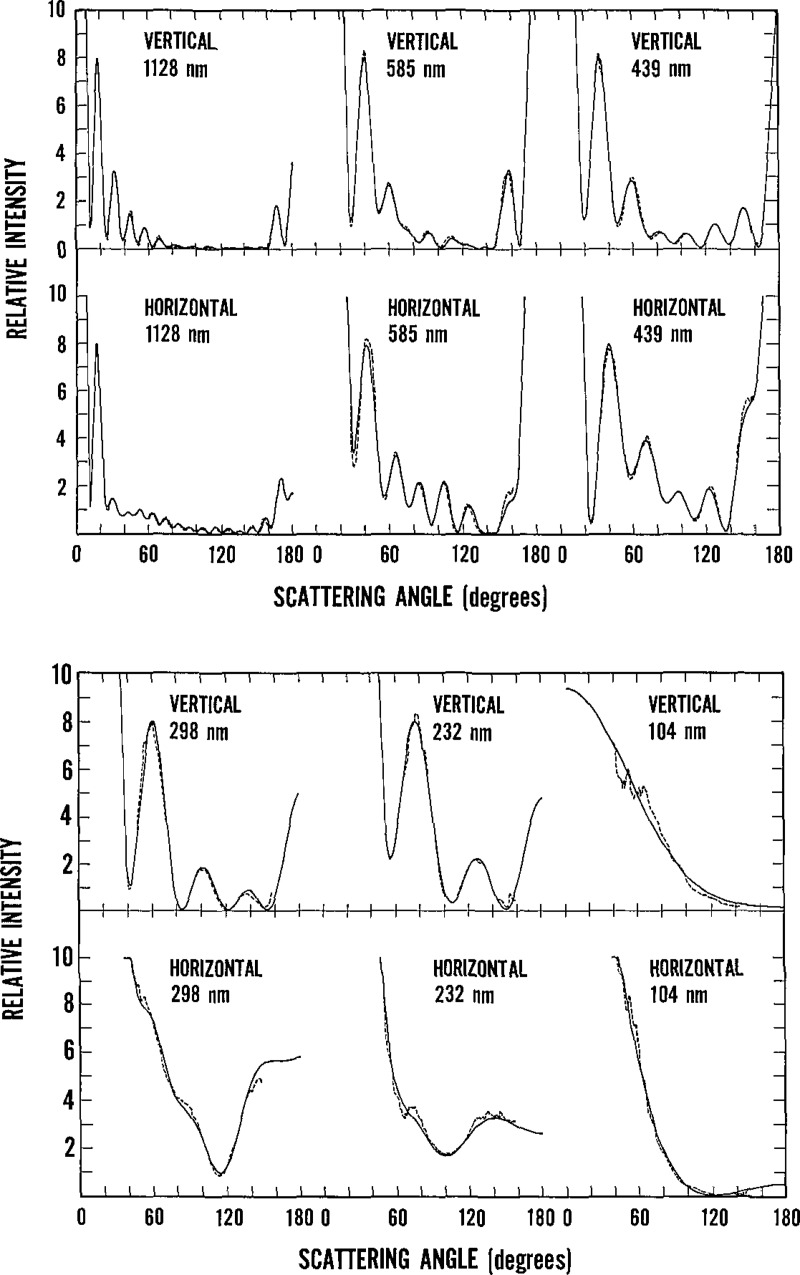
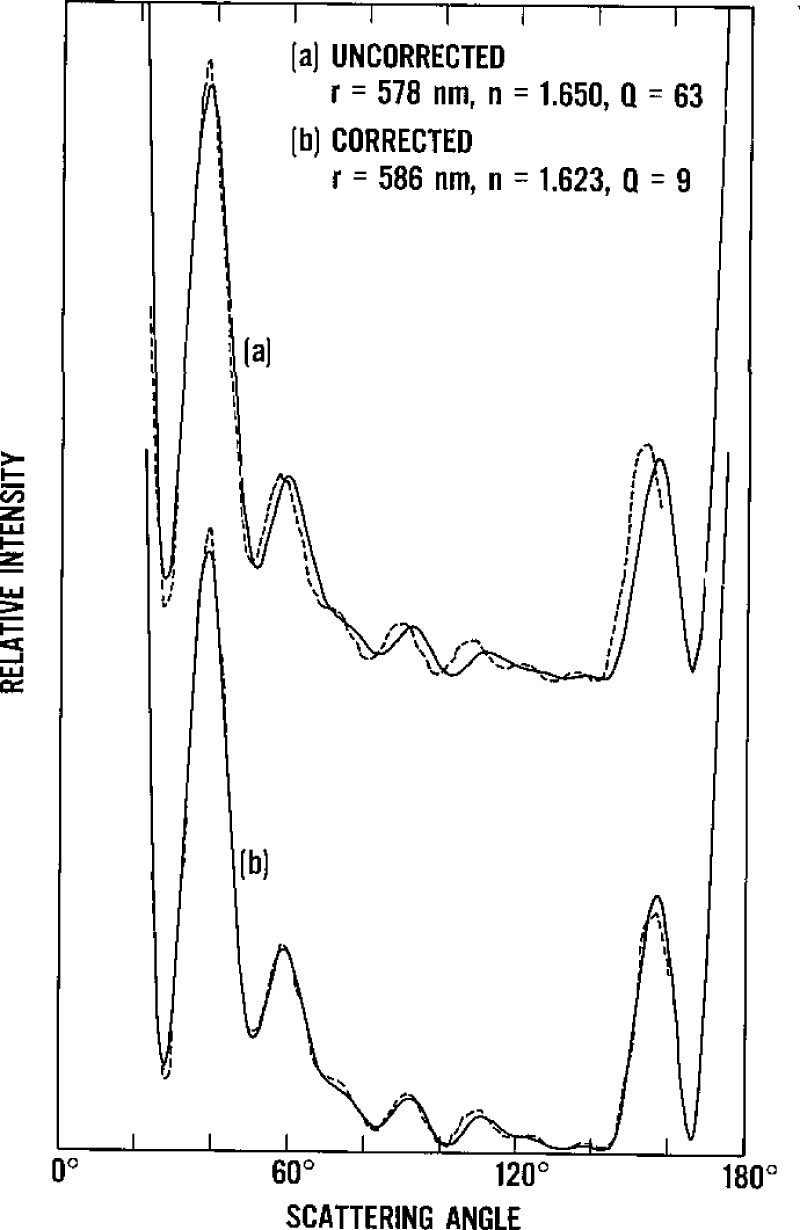
The primary results that we obtained from this series of experiments were the size and refractive index of the particles. In table 1 we present the average values and standard deviations for the radius obtained from a number of particles of each nominal size. In table 2 we give our results for the index of refraction together with values found by other authors. For each particle, the chosen values are those that provide the best fit for both polarizations (as reflected in the harmonic mean of the values of Q for vertical and horizontal polarizations); we chose the scan with the lowest Q if we repeated scans of the same particle. The nature of the theoretical curves and the quality of the data vary considerably with the size of the particles. One sample curve for each size and polarization is shown in figure 4. The number of features (peaks and valleys) increases with the radius of the sphere, while the observed noise, due mainly to the particle motion in the laser beam, is larger for the small particles. In figure 5 we use actual data to illustrate the difference in the quality of fit before and after the angle correction. The errors in n and r are almost 2% if the angle correction is not made.
Table 2.
Comparison of our results for the refractive index with those obtained by others
| Refractive Index | |||
|---|---|---|---|
| Material | Nominal Radius, nm | This study n ± σ | Literaturea n ± σ |
| PSL | bulk | 1.615b | |
| PSL | 66–148 | 1.620 ± 0.008c | |
| PSL | 117 | 1.66 ± 0.05 | |
| PSL | 230 | 1.603 ± 0.029 | |
| PSL | 279 | 1.610 ± 0.002d | |
| PSL | 300 | 1.599 ± 0.013 | 1.64 ± 0.019c |
| PSL | 457 | 1.612 ± 0.004 | |
| PSL | 505 | 1.58 ± 0.012e | |
| PSL | 551 | 1.619 ± 0.002 | |
| PVT | 23–190 | 1.603 ± 0.009d | |
| PVT | 1175 | 1.613 ± 0.002 | |
Bateman’s dispersion relation used to obtain refractive indices for λ = 441.6 nm
Boundy and Boyer
Heller and Pugh
Smart and Willis
McRae
Figure 4–
Typical curves of the scattered intensity as a function of angle for both polarizations and for each particle size. The computed curve (solid line) is a best fit to the data (dashed line).
Figure 5–
Best fit to experimental data (a) before and (b) after angle correction.
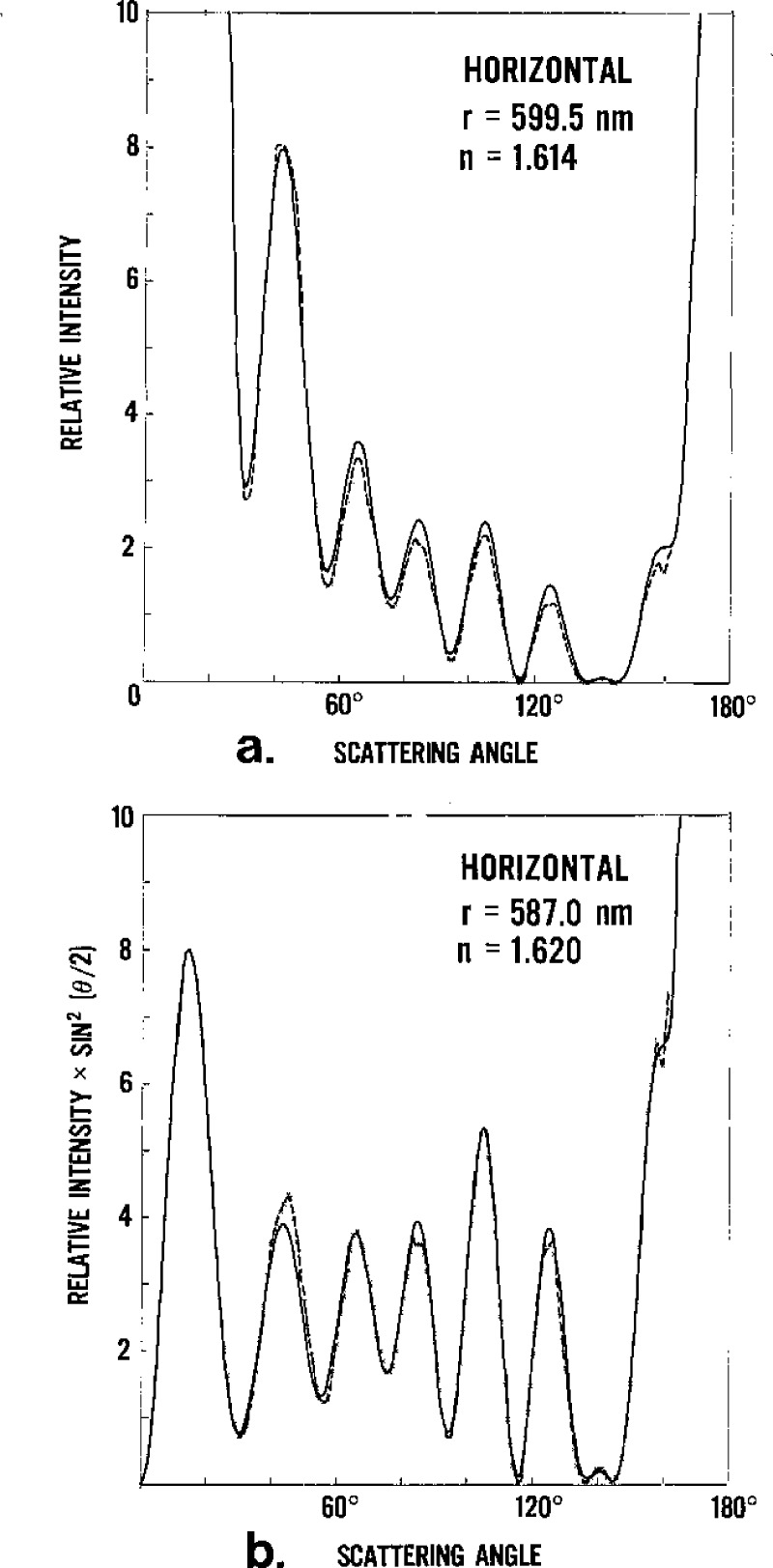
When the same data are analyzed with the weight function sin2(θ/2), the results vary slightly for the different particles; a comparison of the averages for both types of fit is shown in table 3. In figure 6 we compare a curve obtained with this weight factor to the unweighted curve.
Table 3.
Comparison of radius and refractive index obtained by unweighted and weighted least-squares fits.
| Nominal radius, nm | Radius, nm (unweighted) | Radius, nm (weighted) | Refractive index (unweighted) | Refractive Index (weighted) |
|---|---|---|---|---|
| 117 | 108 | 108 | 1.664 | 1.669 |
| 230 | 236 | 237 | 1.603 | 1.607 |
| 300 | 295 | 293 | 1.599 | 1.616 |
| 457 | 450 | 451 | 1.612 | 1.609 |
| 551 | 587 | 587 | 1.619 | 1.622 |
| 1175 | 1129 | 1118 | 1.613 | 1.627 |
Figure 6–
Best fits for curves of intensity of the light scattered by a 551-nm particle as a function of angle by the least squares method (a) without, and (b) with a weighting factor.
To show the variability of the results within a group of particles, we present in table 4 the best values of the radius and the index of refraction for those particles of nominal radius of 457 nm, including the best scans for each polarization when multiple scans were made. The particle size is not perfectly uniform in each sample, and we expect to see a spread in the measured radii. On the other hand, the refractive index should be the same for all particles of equal composition, and we attribute the variations to experimental error.
Table 4.
Radius and index of refraction for eight particles of 457 nm nominal radius.
| Harmonic meana | Vertical polarization | Horizontal polarization | ||||
|---|---|---|---|---|---|---|
| Radius | Refractive Index | Radius | Refractive index | Radius | Refractive index | |
| 454.5 | 1.614 | 455.0 | 1.614 | 453.5 | 1.610 | |
| 457.0 | 1.613 | 457.0 | 1.613 | 453.0 | 1.623 | |
| 449.0 | 1.618 | 453.0 | 1.605 | 449.0 | 1.618 | |
| 446.5 | 1.612 | 451.0 | 1.600 | 446.0 | 1.614 | |
| 448.0 | 1.613 | 451.5 | 1.610 | 448.0 | 1.613 | |
| 450.5 | 1.613 | 453.5 | 1.610 | 450.5 | 1.613 | |
| 453.5 | 1.608 | 453.5 | 1.608 | 453.5 | 1.610 | |
| 439.4 | 1.606 | 440.2 | 1.603 | 439.4 | 1.610 | |
| Average | 449.8 | 1.612 | 451.8 | 1.608 | 449.1 | 1.614 |
| σ | 5.1 | 0.004 | 4.8 | 0.005 | 4.5 | 0.004 |
Harmonic mean refers to the determination of the best fit radius and refractive index by taking the harmonic mean of the Q’s for the cases of vertically and horizontally polarized light.
For one particle we took nine scans with vertically polarized light and three more for horizontal polarization. The results of the analysis of these data are shown in table 5. The standard deviation for the radius is smaller than the one previously calculated for groups of particles, but that for the refractive index is about the same, suggesting that this parameter does not change at least for particles of the same size.
Table 5.
Results for repeated scans for one particle of 457 nm nominal radius.
| Unweighted fit | Weighted fit | |||||
|---|---|---|---|---|---|---|
| Run | Radius | Refractive index | Radius | Refractive index | n = 1.608a Radius | n = 1.615 Radius |
| 1-V | 440.2 | 1.601 | 438.0 | 1.612 | 438.4 | 436.6 |
| 2-V | 436.4 | 1.620 | 437.6 | 1.614 | 439.8 | 437.8 |
| 3-V | 439.2 | 1.606 | 436.6 | 1.618 | 438.6 | 437.2 |
| 4-V | 440.2 | 1.603 | 439.8 | 1.605 | 438.8 | 437.2 |
| 5-V | 439.4 | 1.606 | 441.0 | 1.601 | 439.0 | 437.2 |
| 6-V | 438.0 | 1.610 | 439.8 | 1.604 | 438.6 | 436.8 |
| 7-V | 439.8 | 1.604 | 438.6 | 1.610 | 438.8 | 437.0 |
| 8-V | 439.4 | 1.606 | 438.8 | 1.609 | 439.0 | 437.2 |
| 9-V | 439.4 | 1.607 | 440.0 | 1.604 | 439.2 | 437.4 |
| 1-H | 439.4 | 1.610 | 440.2 | 1.601 | 439.8 | 438.4 |
| 2-H | 438.0 | 1.612 | 440.2 | 1.612 | 438.6 | 437.4 |
| 3-H | 438.4 | 1.614 | 436.4 | 1.620 | 439.4 | 438.2 |
| Average | 439.0 | 1.608 | 438.9 | 1.609 | 439.0 | 437.4 |
| σ | 1.10 | 0.0053 | 1.50 | 0.0063 | 0.47 | 0.53 |
The last two columns correspond to values of the radii obtained for a fixed value of the refractive index (unweighted fit). The first value is obtained for the best fit to all particles of this size, and the second one is the published bulk value.
If we choose the value of r that gives the best fit for a fixed value of the refractive index, for instance the best-fit value 1.608, we find that the standard deviation σ of the radius is lowered to a value of 0.47 nm. The quantity σ provides a measure of the random component of the uncertainty in the single-particle measurements. If we choose instead the value 1.615 obtained from bulk measurements, we obtain a radius of 437.4 nm with a σ of 0.53 nm. Cook and Kerker [3] reported results from nine repeated scans for a single particle of radius 398 nm; they obtain a σ of the radius equal to 1.6 nm. Our smaller value of σ is probably in part a result of the automatic conversion of data to the digital form; Cook and Kerker point out that the component of σ resulting from reading the data off the chart recordings is approximately 0.8 nm.
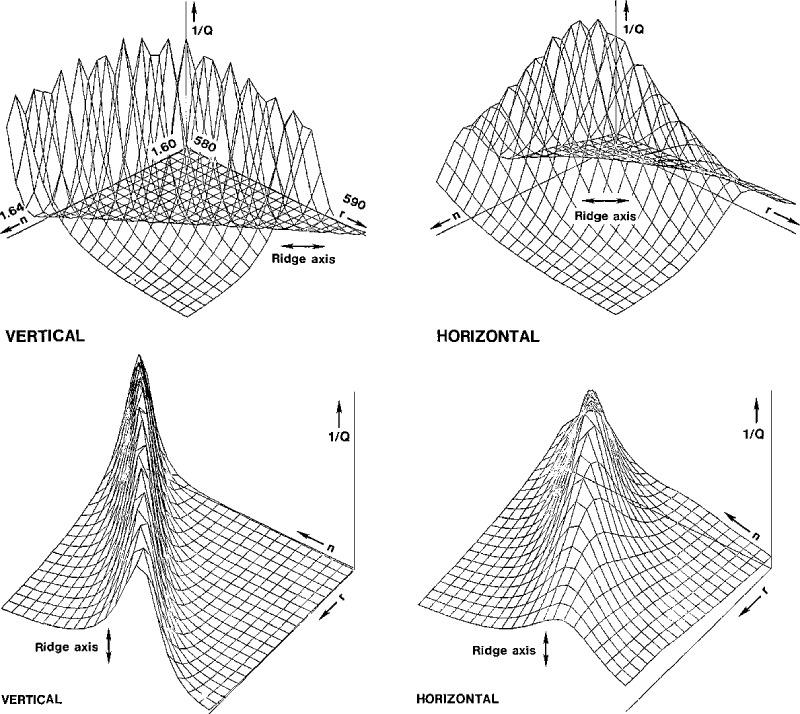
To obtain the parameters of the best fit, we examined a table of values of Q(n,r) for a rectangular grid to find the minimum. The nature of the surfaces representing 1/Q and −logeQ as functions of n and r vary mainly with the size of the particle and the polarization. Some of these surfaces are rather flat, while others show a ridge that cuts diagonally across the surface in such a way that Q varies little when we increase the radius and decrease the index of refraction simultaneously. We show part of such a table near the minimum of Q for a particle of nominal radius of 551 nm in table 6, and we show three-dimensional plots of the surface in figure 7 for both polarizations.
Table 6.
Normalized values of Q near the minimum for a particle of 551 nm nominal radius.
| Vertical polarization | Horizontal polarization | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 1.618 | 1.622 | 1.626 | 1.630 | 1.634 | n | 1.614 | 1.618 | 1.622 | 1.626 | 1.630 | |
| r | r | |||||||||||
| 582.5 | 384 | 147 | 28 | 4.8 | 1.1a | 581.5 | 6.3 | 5.0 | 3.5 | 2.1 | 1.5 | |
| 583.5 | 204 | 40 | 7.3 | 1.3 | 1.8 | 582.5 | 5.3 | 3.6 | 2.1 | 1.3 | 1.6 | |
| 584.5 | 57 | 11.1 | 1.8 | 1.2 | 3.4 | 583.5 | 4.0 | 2.4 | 1.3 | 1.1 | 2.2 | |
| 585.5 | 16.6 | 3.0 | 1.0 | 2.4 | 5.4 | 584.5 | 3.0 | 1.7 | 1.0 | 1.5 | 3.2 | |
| 586.5 | 4.7 | 1.1 | 1.8 | 4.3 | 7.9 | 585.5 | 2.3 | 1.3 | 1.2 | 2.3 | 4.5 | |
| 587.5 | 1.5 | 1.4 | 3.3 | 6.4 | 10.5 | 586.5 | 1.9 | 1.3 | 1.9 | 3.5 | 6.2 | |
| 588.5 | 1.3 | 2.6 | 5.1 | 8.8 | 13.5 | 587.5 | 1.9 | 1.8 | 2.9 | 5.1 | 8.1 | |
The minimum values of Q in each column are underlined to illustrate the slow variation of Q on a diagonal.
Figure 7–
Two views of the three-dimensional surface of the inverse of the quality of fit, 1/Q, as a function of the index of refraction n and the radius r, over a range of a few percent from the best values. The ridges cause difficulties in accurately determining the correct values of n and r.
4.2. Numerical Experiments and Sensitivity Analysis
To study the effects of experimental errors on the best fit parameters, we modified the program that produces the theoretical values of the scattered intensities to add simulated errors and generate a file or “data” to be processed by the same procedure described above. Noise obtained using a random number generator with a maximum amplitude of from 1 to 3% of the intensity at each angle was added to all curves.
The error in the angle calibrations was simulated by computing an “experimental” angle
| (17) |
the errors is of the order of 2%, and the relative error in the refractive index is comparable in magnitude to where θ is the true angle used in the computation of the scattered intensity. The results of the analysis of these “data” are shown in table 7. The magnitude of that in the radius, and they are of opposite signs. In this table we also show the results obtained by minimizing the average instead of the harmonic mean of the Q’s for the vertical and horizontal polarizations. In a number of cases we obtain a better result when we use the average value. The reason for this behavior is that the quality of the “data” is essentially the same for both polarizations, so that larger values of Q reflect a greater variability of Q with n and r; thus, a mean that emphasizes the larger set of Q’s leads to a better result. This property is even more evident in the second group of results, which simulate the drift in the angle correction between the beginning and the end of a series of runs made over a period of a month. The formula we used here is
| (18) |
and the resulting errors in n and r can be as large as 1.5% when we use the harmonic mean, and 0.5% when we use the average of the Q’s.
Table 7.
Results of numerical experimentsa.
| Angle error (θ′ = 0.98θ–0.5), Harmonic mean Q | ||||
|---|---|---|---|---|
| Assumed radius, nm | Best | Best (weighted) | ||
| Radius, nm | Refractive index | Radius, nm | Refractive index | |
| 1150 | 1114(−3.1%) | 1.660(+3.1%) | 1098(−4.5%) | 1.695(+5.2%) |
| 580 | 560(−3.4%) | 1.660(+3.1%) | 576(−0.7%) | 1.600(−0.6%) |
| 450 | 434(−3.6%) | 1.655(+2.8%) | 438(−2.7%) | 1.660(+3.1%) |
| 300 | 288(−4.0%) | 1.635(+1.6%) | 292(+2.7%) | 1.615(+0.3%) |
| 230 | 228(−0.9%) | 1.640(+1.9%) | 226(−1.7%) | 1.645(+2.2%) |
| 115 | 119(+3.5%) | 1.560(−3.1%) | 119(+3.5%) | 1.560(−3.1%) |
| Angle error, average Q | ||||
| Assumed radius, nm | Best | Best (weighted) | ||
| Radius, nm | Refractive index | Radius, nm | Refractive index | |
| 1150 | 1114(−3.1 %) | 1.665(+3.4%) | 1134(+1.4%) | 1.635(−1.6%) |
| 580 | 572(−1.4%) | 1.635(+1.6%) | 580 - | 1.610 - |
| 450 | 442(−1.8%) | 1.630(+1.2%) | 446(−0.9%) | 1.610 - |
| 300 | 292(−2.7%) | 1.645(+2.2%) | 300 - | 1.625(+0.9%) |
| 230 | 228(−0.9%) | 1.640(+1.9%) | 226(−1.7%) | 1.645(+1.2%) |
| 115 | 119(+3.5%) | 1.560(−3.1%) | 119(+3.5%) | 1.560(−3.t%) |
| Angle calibration drift (θ′ = 0.998θ–0.5), Harmonic mean Q | ||||
| Assumed radius, nm | Best | Best (weighted) | ||
| Radius, nm | Refractive index | Radius, nm | Refractive index | |
| 1150 | 1132(−1.6%) | 1.634(+1.5%) | 1148(−0.2%) | 1.608(−0.1%) |
| 580 | 570(−1.7%) | 1.632(+1.4%) | 578(—0.3%) | 1.608(−0.1%) |
| 450 | 444(−1.3%) | 1.626(+1.0%) | 444(−1.3%) | 1.630(+1.2%) |
| 300 | 300 - | 1.620(+0.6%) | 300 - | 1.618(+0.5%) |
| 230 | 228(−0.8%) | 1.630(+1.2%) | 228(−0.9%) | 1.626(+1.0%) |
| 115 | 117(+1.7%) | 1.590(−1.2%) | 115 - | 1.606(−0.2%) |
| Angle calibration drift, average Q | ||||
| Assumed radius, nm | Best | Best (weighted) | ||
| Radius, nm | Refractive index | Radius, nm | Refractive index | |
| 1150 | 1140(−0.7%) | 1.626(+1.0%) | 1150 - | 1.60S(−0.1%) |
| 580 | 578(−0.3%) | 1.616(+0.4%) | 582(+0.3%) | 1.604(−0.4%) |
| 450 | 448(−0.4%) | 1.616(+0.4%) | 446(−0.9%) | 1.620(+0.6%) |
| 300 | 296(−1.3%) | 1.628(+1.1%) | 300 - | 1.614(+0.2%) |
| 230 | 230 - | 1.616(+0.4%) | 228(−0.9%) | 1.628(+1.1%) |
| 115 | 117(+1.7%) | 1.586(−1.5%) | 115 - | 1.612(+0.1%) |
| Random noiseb, Harmonic mean Q | ||||
| Assumed radius, nm | Best | Best (weighted) | ||
| Radius, nm | Refractive index | Radius, nm | Refractive index | |
| 1150 | 1150 - | 1.610 - | 1150 - | 1.610 - |
| 580 | 582(+0.3%) | 1.604(−0.4%) | 580 - | 1.610 - |
| 450 | 450 - | 1.610 - | 450 - | 1.610 |
| 300 | 300 - | 1.616(+0.4%) | 300 - | 1.612(+0.1%) |
| 230 | 230 - | 1.608(−0.1%) | 230 - | 1.610 - |
| 115 | 115 - | 1.594(−1.0%) | 115 - | 1.614(+0.2%) |
| Random noise, average Q | ||||
| Assumed radius, nm | Best | Best (weighted) | ||
| Radius, nm | Refractive index | Radius, nm | Refractive index | |
| 1150 | 1150. - | 1.610 - | 1150. - | 1.610 |
| 580 | 582.(+0.3%) | 1.604(−0.4%) | 580. - | 1.610 - |
| 450 | 450. - | 1.610 - | 450. - | 1.610 - |
| 300 | 300. - | 1.618(+0.5%) | 300. - | 1.614(+0.2%) |
| 230 | 232.(+0.9%) | 1.596(−0.9%) | 230. - | 1.608(−0.1%) |
| 115 | 115. - | 1.592(−1.1%) | 115. - | 1.614(+0.2%) |
Refractive index is 1.610 in all cases. The numbers in parentheses are the deviations from the assumed values.
Random noise of maximum amplitude of 2% every degree plus a larger noise of maximum amplitude 5% that remain constant for 10° is used. For the smallest two particle sizes the corresponding numbers are 3% and 10% respectively.
We simulated the noise in the values of the scattered light intensities by superimposing: (1) a random noise of maximum amplitude of 2% computed independently at each degree, and, (2) a larger noise of maximum amplitude of 5% that remains constant over periods of 10° in the scattering angle. For the two smallest particles, which are less stable in the beam than the larger ones, we increased the amplitudes of the noise to 3 and 10% respectively. For particles of a radius of 450 nm and larger, the error in the results was at most 0.3%, while for the smallest particles the error can reach 1%.
We also added 1% of the intensity for the horizontal polarization to the intensity for the vertical polarization and vice versa to simulate the detector displacement and the imperfection of the half-wave plate. The effect on the results was less than 0.2%, and we do not show them in table 7.
We also processed all these simulated experiments using the program that includes a weighting factor of sin2(θ/2). The results obtained this way were better than those obtained with a straight least-squares fit in many cases, and worse in some.
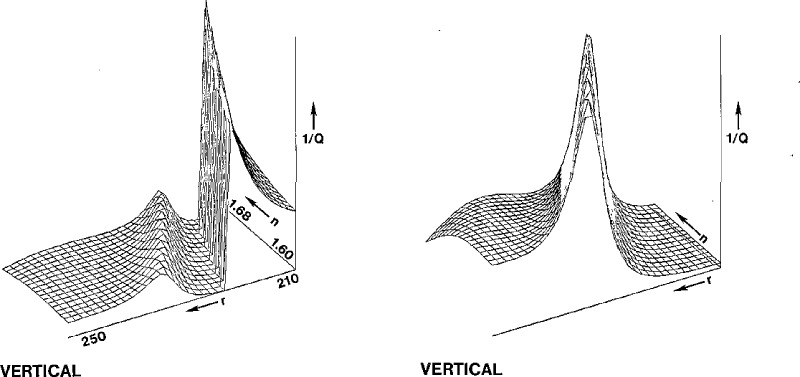
A numerical experiment with simulated noise illustrates the problem that can arise when the experimental intensities are the ones to be scaled. The high sharp ridge in the first graph of figure 8 is a consequence of a sudden change in the normalization of the theoretical intensities as a peak in the curve disappears; the corresponding values for n and r lead to a poor fit of the curves. The accompanying figure obtained by scaling the theoretical intensities shows only the physically meaningful ridge.
Figure 8–
Plots of 1/Q as a function of n and r that show a ridge of spurious “best” fits for vertical polarization when the experimental intensities are scaled, a ridge that is absent when the theoretical intensities are scaled instead. Simulated data obtained by adding random noise to the calculated intensity.
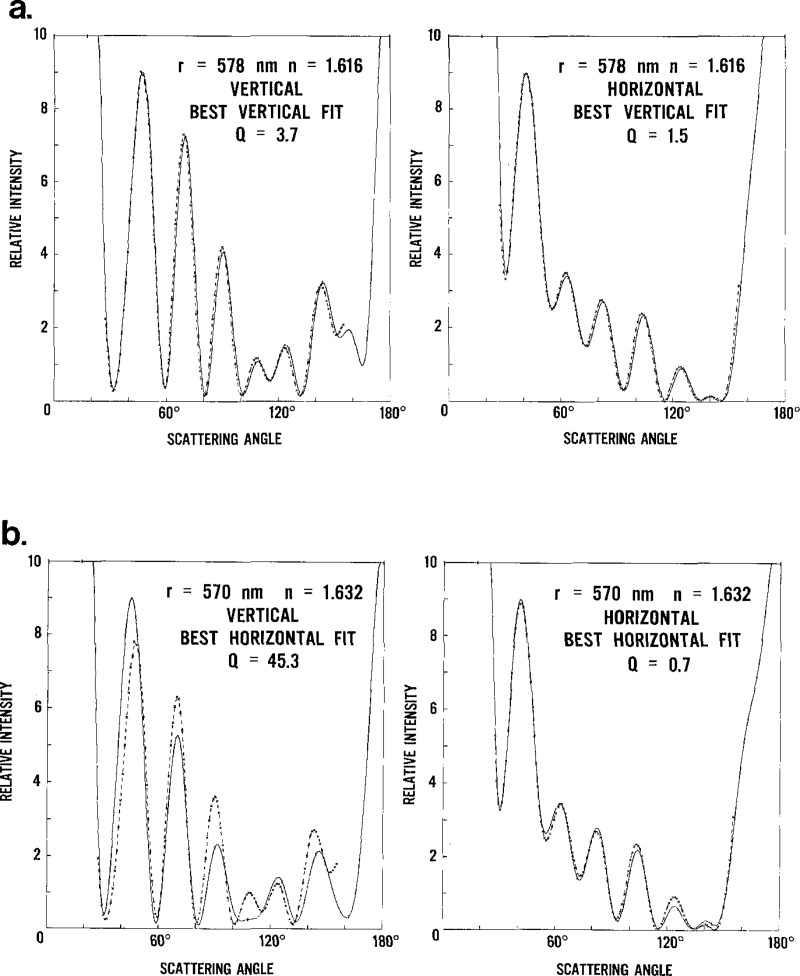
We also show an example of the pitfalls of an uncritical use of the value assigned to the quality of fit. In figure 9 we show two curves that correspond to the horizontal and vertical polarizations for the parameters that give the best fit for the vertical polarization (a), and two more that do so for the best fit for the horizontal polarization (b). If we choose the pair (b) with the lowest harmonic mean between Qv and QH, that is, the one that has Qv = 45.3 and QH = 0.7, we obtain a very poor fit to the data for vertical polarization. The other pair (a), with Qv = 3.7 and QH = 1.5, which has the lowest average of Qv and QH, is a much better compromise. In this case, the larger values of Qv relative to QH are not due to lower quality data, but to the presence of more variation in the intensity curve. A third method to choose between different pairs of Qv and QH is to normalize both to the corresponding minimum value and then take the average. In numerical experiments, each of these methods gave the best values of n and r in comparable numbers of instances, so that no clear choice of method was evident.
Figure 9–
Overall best fit using (a) the average of Qv and QH, which emphasizes the larger of the two, and (b) the harmonic mean, which emphasizes the smaller Q.
5. Discussion
5.1. Error Analysis
We obtained information about the magnitude of the errors both from numerical experiments and from the actual data.
The size of the error in the index of refraction and in the radius when the angle errors are not corrected, a decrease of about 2% in the r and an increase of the same magnitude in n, indicate that the calibration of the angle readout is a necessity. We found an additional problem of a drift in this calibration, as the correcting factors came out somewhat different at the beginning and at the end of a run of experiments. The effect of this drift, a relative error of about 1%, has to be included in the uncertainty of our results.
The noise in the intensity of the scattered light can be observed better by fixing the angle and recording a trace of the intensity versus time. The general characteristics of such a trace show that there are two components of this noise. The smaller component, of about 2–3% of the intensity, affects each angle reading independently; the larger component, which we think comes from the motion of the particle within the laser beam when the servocontrol is activated, varies between 5% for the larger particle to 10% for the smaller ones and has a lower frequency so that it affects intensity readings in groups of about 10° for the data collection speed that we used.
Errors in the polarization of the laser beam come mainly from two sources, imperfections in optical components and misalignment of the periscope. The imperfections in the half-wave plate and other optical components allow the introduction of some light of the wrong polarization into the incident beam at a 200:1 intensity ratio. The error from the inclination of the periscope with respect to the assumed scattering plane varies with the scattering angle, as shown in section 2, and it remains within about 0.2% for the range of angles that we used. The effects of these errors on the size and refractive index are small compared to those introduced by the angle errors and the noise discussed above. A combined estimate of the effects of these errors on n and r comes to less than 0.2%.
Variability in the experimental results can be found in the analysis of the data for different particles within the same sample, and also from repeated scans of the same particle.
Within a group of particles from the same sample, we expect the index of refraction to have a common value, while the radius can vary significantly. (For instance, we excluded a particle of radius 417 nm from the statistics for the particles of nominal radius of 457 nm.)
When we take a fixed value for the index of refraction for all particles from a sample, the best values for the radius under this restriction show a smaller variation but the value of this radius depends on which value is chosen from the index of refraction. We can see this from the results shown in table 5.
Tables 4 and 5 show that the values of the standard deviations for the index of refraction are similar in the particle group and for repeated scans of the same particle, which confirms that the index of refraction does not vary significantly within particles of a given nominal size. For particles of different sizes we find a variation of the index of refraction from 1.599 to 1.619, with the exception of the smallest particle. For this particle of nominal radius of 117 nm, the data are too noisy to find a reliable value of the refractive index; also the curves show very little structure and the quality of fit varies slowly with the radius and index of refraction.
The magnitudes of the various errors affecting the overall uncertainty in the measurement of the radius of a single particle are summarized in table 8. The quantity σ obtained for the 12 repeat measurements of one particle with nominal radius of 457 nm is a measure of the random error. The numerical experiments simulating the noise in the scattered light intensity yield similar values of σ. Sources of systematic errors associated with the instrument include the error in particle size due to the angle drift, δθ, to the polarization misalignment, δP, and to the uncertainty in the laser wavelength, δλ. Results in table 7 indicate that the percentage change in r and n are comparable in magnitude. Consequently, our observed variation in n of 1 % leads to a δθ of 1 % also. The minimum value of δθ, estimated to be 1.4 nm, was obtained for the 457 nm particle for which an angle calibration was performed at the beginning and at the end of 2 days of measurements. Numerical experiments give a magnitude of 0.2% for δP. The least important error is the uncertainty in the wavelength of the He-Cd laser, δλ=0.07 nm. An overall estimate of the instrument uncertainty for five measurements on a single particle, us, can be obtained from
| (19) |
where t4(0.95) is the value of the limit obtained from Student’s t-distribution for four degrees of freedom. For the case above we find us equal to 3.8 nm. As indicated in table 8, for all other sizes there is a greater error associated with the angle drift and a correspondingly larger value of us.
Table 8.
Uncertainty in the particle radius.
| Nominal radius, nm | Precision σa, nm | δθa, nm | δPa, nm | δIa, nm | usb, nm | uTc, nm |
|---|---|---|---|---|---|---|
| 1175 | 1.1 | +11.0 | 2.0 | −1.0 | 14.4 | 24.4 |
| 551 | 1.1 | +6.0 | 1.0 | −0.5 | 8.4 | 10.1 |
| 457 | 1.1 | +1.4d | 1.0 | −0.4 | 3.8 | 5.3 |
| 300 | 1.2 | +3.0 | 0.5 | −0.3 | 5.0 | 4.9 |
| 230 | 2.0 | +2.0 | 0.3 | −0.9 | 4.8 | 5.0 |
| 117 | 2.0 | −1.0 | 0.2 | −0.6 | 3.7 | 3.5 |
σ was estimated from repeat measurements of a single 457 nm particle. The quantities δθ, δP, and δI represent systematic errors resulting from angle calibration drift, polarization misalignment, and impurities in the water, respectively.
The total uncertainty for a single particle based on five experiments is , where t4(0.95) is the Student t-value for four degrees of freedom and for 95% confidence level.
The total uncertainty for the mean particle size is given by , where σP is the size distribution determined by Dow Chemical Company.
For this particle size, the uncertainty resulting from angle calibration drift is small, because an angle calibration was performed before and after the experiment.
For comparison with other studies of particle size, it is of interest to obtain the uncertainty associated with the determination of the average particle size. In eq (19) the quantity is replaced by the standard error, , where σP is the standard deviation of the m particles measured. The formula for the standard error assumes the particle to be randomly selected. The use of the Differential II for an aerosol with a broad distribution will probably lead to a biased result because of the operator’s tendency to choose inadvertently, say, the particle with the brightest appearance. In our case we expect little bias because the size distribution is narrow.
In addition to instrumental errors and statistical uncertainty due to the small sample size, there are uncertainties associated with the nature of the particle. While the polystyrene spheres are often considered to be spherical and homogeneous, we expect that slight imperfections might exist. One source of nonuniformity of the particle can be the residual (nonvolatile) impurities in the distilled water. If the 2 ppm of impurities coat the particle when the water droplet containing the particle evaporates, the thickness of this coat would vary between 0.4% of the radius for the smallest particles and 0.003% for the largest one, based on the average droplet diameter of 4.2 μm. This calculation also includes the impurities coming from the liquid in the undiluted sample. If we assume, on the other hand, that all the emulsion stays on the particle instead of being diluted, we find that another coating of between 0.4% for the smallest particles and 0.09% for the largest one is produced. The measured index of refraction can also be affected by such a coating, but visual observation of the residue indicates that these coats are translucent and not likely to change the results significantly. Table 8 includes the uncertainty associated with the impurity, δI, and an estimate of the overall uncertainty in the mean particle size, uT, which is given by
| (20) |
The relative error in n is similar in magnitude to that in r.
Another imperfection of the particle is the slight deviation from spherical shape. Careful measurements by transmission electron microscope of the particles of nominal radius of 457 nm indicated a deviation of 0.6% from sphericity at a precision of about 0.3%. If the particles were nonspherical, then over the course of our measurements the particle would have undergone extensive rotation as a result of Brownian motion. We conclude from Yeh’s treatment of light scattering from spheroids with a slight deviation from sphericity [9] that the effective radius measured by light scattering will satisfy the inequality rmin<r<rmax, where the corresponding Dmin and Dmax are the length of the minor and major axes of an ellipsoid of revolution. So we expect that our measurement r would be within 0.6% of the average of rmin and rmax, probably closer to 0.3 or 0.4%. This possible error is not included in eq (20). There may also be inhomogeneity of the particle resulting from strain as the water evaporates from the particle, but we have no estimate of this effect.
5.2. Comparison With Other Experiments
In table 1 we compare our results with the information provided by Dow Chemical Co. on the samples. The size and standard deviation they provide are obtained by transmission electron microscopy on a population of the order of 100 particles [10]. We find a difference that is outside the limits of the statistical variation within a lot.
Particles of the same sample of nominal radius 457 nm were examined at the National Bureau of Standards by other methods to determine the size distribution of the particles. Preliminary results obtained by light scattering from a suspension give a mean radius of 448 nm; array sizing by optical microscopy gives 450 nm, and transmission electron microscopy gives between 441 to 466 nm depending on the diffraction grating replica used to determine the magnification.
McRae [4] obtained a radius of 288 nm for the same lot of particles of nominal radius of 300 nm, for which we determined a radius of 295 nm.
In table 2 we compare our results for the refractive index to those reported in the literature. We used Bateman’s dispersion relation [11].
| (21) |
where a and b are constants and λ is the wavelength of the light, to reduce results obtained with light of other wavelengths to a common wavelength, namely the one we used. The value of b is determined in Bateman’s article [11] to be 1.0087 × 10−10 when λ is in centimeters. The constant a is found from the original pair of values of n and λ. Our results are fairly close to the bulk value of 1.615 and not too different from the results obtained in other experiments.
McRae [4] used the same type of instrument that we used and found a stronger size dependence of the refractive index than we did. Before performing the correction of the angle readings, we also found that the values of the refractive index that we obtained varied more with the size of the particle. Heller and Pugh [12] used an interferometer to measure the refractive index of a suspension of polystyrene spheres in water. Their results were most reliable for particle sizes up to 200 nm radius. They also determined the refractive index of polyvinyltoluene spheres.
Smart and Willis [13] made refractive index measurements of different mixtures of glycerol and water and then used a suspension of polystyrene spheres in these liquids to determine the transmission of light through this medium. Then they extrapolated to 100% transmission in a liquid that would have the same refractive index of the polystyrene spheres. The extrapolation method depends on the particle size, and it is simplest for small particles.
6. Concluding Remarks
We have demonstrated that both the size and the refractive index of a single polystyrene sphere with a nominal radius in the neighborhood of 500 nm, comparable to the wavelength of light, can be determined with an error of less than 1% with the Differential II light scattering photometer. The accuracy of this method is better than that achieved by electron microscopy and other procedures.
To obtain accurate results, we find that the angle calibration of the instrument must be made to an accuracy of 0.2° to 0.3°. Using the instrument readout without correction can lead to errors as large as 3 or 4% in the determination of size and refractive index of polystyrene spheres. Furthermore, the magnitude of the errors varies with particle size, so that the refractive index can appear to be size dependent.
The determination of the best estimates of the particle size and refractive index requires a considerable amount of care when the quality of fit surface Q(n,r) has a deep and narrow valley in a diagonal direction (see fig. 7), where correlated changes in both n and r lead to very small changes in Q. This problem occurs frequently in nonlinear least-squares fit procedures. The measurement of the scattered light intensities for both polarizations for the same particle allows for a more reliable estimate of the size and refractive index.
For the smaller values of the radius the surface of fit is rather flat with a shallow trough, a situation that also leads to difficulties in the determination of n and r, especially with noisy data.
If we establish that the true index of refraction obtained by this method is independent of the particle size, this quantity could be determined accurately from data for a large number of particles or from bulk measurements. We can then use the data from light scattering to make a much faster and more accurate determination of the radius of a particle, especially when a deep valley exists.
Rapid data collection and processing are essential for obtaining the large amount of data necessary for an accurate determination of the size and refractive index of dielectric spheres. Even with the instrument operated at its maximum scan speed, it takes about 10 min to obtain the vertical and horizontal polarization scans and the associated background scans, to do some minor processing on the data, and to store it on tape. The data reduction using a minicomputer (Interdata 7/32) requires about 30 min per particle when Q is computed over a rectangular grid of values of n and r. We have tried a Marquardt-Levenberg algorithm to speed up the search for the minimum value of Q, but preliminary results indicate that this method is difficult to apply and sometimes fails to find the minimum when the surface of fit has a deep narrow valley or when this surface is almost flat. We found it best to perform first a grid search and start a more efficient algorithm from the best fit to refine the results. In any case, it is always best to inspect the resulting curves for the actual fit between the theoretical and measured values.
Noise in the intensity of the scattered light limits the accuracy of the determination of size and refractive index, especially for the smaller particles. The noise might be reduced by filtering out the high-frequency structure in the laser beam to obtain a smooth Gaussian profile. If the noise is a result of the motion of the particle within the laser beam, the ratio of the intensity to that at a fixed angle would be insensitive to this noise. To obtain this ratio, one must add a detector system at a fixed angle to measure this intensity for each pair of intensity-angle readings.
If the Differential II is calibrated to measure absolute intensity by means of monodisperse spheres of known size, the additional information might alleviate the difficulties related to the valleys in the surface of fit. Measurements of absolute intensities may also be helpful to characterize particles with an additional parameter such as a nonnegligible imaginary component of the refractive index or a layered structure.
Acknowledgments
The authors acknowledge R. Bukowski and E. Braun for their assistance in interfacing the Differential II to a data acquisition system, and R. Young for his advice in designing an angle calibration device.
Biography
About the Authors: Egon Marx is a physicist with the Micro and Optical Metrology Group in the NBS Center for Manufacturing Engineering. George W. Mulholland is a chemist with the Smoke and Toxic Gas Group in the NBS Center for Fire Research.
Footnotes
Figures in brackets indicate the literature references at the end of this paper.
Certain commercial equipment, instruments, and materials are identified in this paper to specify adequately the experimental procedure. In no case does such identification imply recommendation or endorsement by the National Bureau of Standards, nor does it imply that the material or equipment identified is necessarily the best available for the purpose.
References
- [1].Wyatt P. J.; Phillips D. Q. J. Colloid Interface Sci. 39: 125–135; 1972. [Google Scholar]
- [2].Phillips D. Q.; Wyatt P. J.; Bergman R. M. J. Colloid Interface Sci. 34: 159–162; 1970. [Google Scholar]
- [3].Cooke D. D.; Kerker M. J. Colloid Interface Sci. 42: 150–155; 1973. [Google Scholar]
- [4].McRae D. D. J. Colloid Interface Sci. 87: 117–123; 1982. [Google Scholar]
- [5].Marshall Q, R.; Parmenter C. S.; Seaver M. J. Colloid Interface Sci. 55: 624–636; 1976. [Google Scholar]
- [6].Mie G. Ann. Physik 25: 337–445; 1908. [Google Scholar]
- [7].Born M.; Wolf E. Principles of Optics, 1980; Oxford: Pergamon Press. [Google Scholar]
- [8].Kerker M. The Scattering of Light and Other Electromagnetic Radiation, New York: Academic Press; 1969. [Google Scholar]
- [9].Yeh C. Physical Rev. 135: A1193–1201; 1969. [Google Scholar]
- [10].Bradford E. B.; Vanderhoff J. W. J. Appl. Phys. 26: 864–871; 1955. [Google Scholar]
- [11].Bateman J. B.; Weneck E. J.; Eshler D. C. J. Colloid Sci. 14: 308–329; 1959. [Google Scholar]
- [12].Heller W.; Pugh L. L. J. Colloid Sci. 12: 294–307; 1957. [Google Scholar]
- [13].Smart C.; Willis E. J. Colloid Interface Sci. 25: 577–583; 1967. [Google Scholar]