Circulants and the Characterization of Vertex-Transitive Graphs

Abstract

In this paper, we extend the notion of a circulant to a broader class of vertex-transitive graphs, which we call multidimensional circulants. This new class of graphs is shown to consist precisely of those Vertex-Transitive graphs with an automorphism group containing a regular abelian subgroup. The result is proved using a theorem of Sabidussi which shows how to recover any Vertex-Transitive graph from any transitive subgroup of its automorphism group. The approach also allows a short proof of Turner’s theorem that every Vertex-Transitive graph on a prime number of nodes is a circulant

1. Introduction

Following the graph-theoretic notation of [10]¹ and the group-theoretic notation of [14], we denote the set of nodes of a finite simple graph X by V(X), the set of edges by E(X), and the automorphism group of X by G(X). Throughout, we regard G(X) as a finite permutation group on the nodes, and sometimes the edges, of X. In particular, a subgroup J of G(X) is said to be transitive if for every pair of nodes u,v ∈ V(X), J contains an automorphism mapping u to v. If, in addition to being transitive, o(J)=o(V(X)), then J is a regular subgroup of G(X). We are interested primarily in those graphs which have a transitive automorphism group. Such graphs are called vertex-transitive or, equivalently, point-symmetric.

A topic of recent interest in the literature involves the characterization of vertex-transitive graphs [2,3,5,6,8–11,13]. In section 2, we present two such characterizations. The first is elementary and perhaps known to many but we have not found it in the literature. The second is due to Sabidussi [10] and is more substantial. In fact, we present a very slight generalization of his result, which he stated so as to apply only to connected vertex-transitive graphs.

Though Sabidussi’s characterization is useful, it involves significant conditions on the automorphism groups of the associated graphs. Indeed, the problem of characterizing vertex-transitive graphs in a more graph-theoretical manner appears to be very difficult. In [13], Turner provided a partial solution to the problem by showing that a graph with a prime number of nodes is vertex-transitive if and only if it is a circulant (or, equivalently, a starred polygon). Unfortunately, if the number of nodes is not a prime, then a vertex-transitive graph need not be a circulant. In section 3, we define a circulant graph and use the extension of Sabidussi’s result to show that a graph X is a circulant if and only if G(X) contains a regular cyclic subgroup. As a corollary, we prove Turner’s result mentioned above.

In section 4, we extend the notion of a circulant to a broader class of vertex-transitive graphs, which we call multidimensional circulants. In doing so, we broaden the class of vertex-transitive graphs for which a nice graph-theoretical characterization is known. Moreover, we then give a group-theoretical characterization of what is special about these graphs in relation to the class of all vertex-transitive graphs. In particular, we prove that a graph X is a multidimensional circulant if and only if G(X) contains a regular abelian subgroup. In addition, we derive a simple upper bound on the dimension of a multidimensional circulant and, as an example, prove that the n-cube is an ⌊(n + 1)/2⌋-dimensional circulant for n ⩾ 1.

2. Characterizations

We now present the characterizations discussed in the introduction. Given any graph X with nodes V(X)={v₀,..., v_n-1,}, define the graph X_i for 0⩽i<n to be the subgraph of X induced by V(X)-{v_i}.

Theorem 1²: A graph X with n nodes is vertex-transitive if and only if X₀≃X₁≃…≃X_n-1.

Proof: Assume that X is an n-node graph such that X₀≃X₁≃…≃X_n-1 From the definition, we know that o(E(X_i))=o(E(X ))-deg_X (v_i) for 0⩽i<n, where o(E(X_i)) is the number of edges in X_i and deg_x(v_i) is the degree of node v_i, in X. Since X₀≃X₁≃…≃X_n-1, we know that o(E(X₀)) = o(E(X₁)) = … =o(E(X_n-1) and thus that deg_x(v_o)=deg_x(v_i)= … =deg_x(v_n-1). Thus X is k-regular where k=deg_x(v_o). This means that each node in X_i, has degree k or k-1 depending on whether or not the node is adjacent to v₁, in X. Let σ_ij be an isomorphism from X_i, onto X_j. Clearly, σ_ij maps the k nodes of degree k-1 in X_i (those adjacent to v_i in X) onto the k nodes of degree k-1 in X_j (those adjacent to v_j, in X). Define the extension of σ_ij to X by ${\sigma }_{ij}^{\prime }\left(v_m\right)={\sigma }_{ij}\left(v_m\right)$ for m≠i and ${\sigma }_{ij}^{\prime }\left(v_i\right)=v_j$. It is clear that for all 0⩽i,j<n, ${\sigma }_{ij}^{\prime }$ is an automorphism of X mapping v_i, onto v_j, and thus X is vertex-transitive.

Conversely, if X is vertex-transitive, then for all i and j, there is a σ ∈ G(X) such that σ(v_i) = v_j and thus σ(X_i) = X_j which implies that X_i≃X_j.□

In Theorem 2 of [10], Sabidussi characterizes connected vertex-transitive graphs. We now state a slight generalization of this result to include all vertex-transitive graphs. Given any group G, subgroup J of G and subset H of G-J, define X_G,H/J to be the graph

$$\begin{gathered} V\left(X_{G,H}/J\right)=\left\{\alpha J\right|\alpha \in G\}\text{and} \\ E\left(X_{G,H}/J\right)=\{(\alpha J,\beta J)|\alpha J\cap \beta J\overline{H}\ne \varnothing \},\text{where} \\ \overline{H}=H\cup H^{-1}\text{and}{H}^{-1}\text{is}\text{the}\text{set}\text{of}\text{inverses}\text{of}\text{elements}\text{of}H. \end{gathered}$$

Theorem 2: If X is a vertex-transitive graph and G is a transitive subgroup of G(X), then there is a subgroup J of G and a subset H of G-J such that X≃X_G,H/J. Conversely, if G is a group, J a subgroup of G and H a subset of G–J, then X_G,H/J is a vertex-transitive graph with G homomorphic to a transitive subgroup of its automorphism group.

The proof of Theorem 2 is lengthy but not difficult and is essentially that found in [10]. We mention here one key step. Given X and G as in the first part of the theorem, choose J to be the subgroup of all automorphisms which fix a given node v₀ and H to be the subset of all automorphisms which move v₀ to an adjacent node.

3. Circulants

A circulant (or equivalently, a starred polygon) is a graph whose nodes can be labeled so that there exists a set S⊂Z, where Z is the set of integers, such that V(X)={v₀,…,v_n-1} and E(X)={(v_i,v_j)|0⩽i,j<n and mod(i-j,n)∈S}. (By mod(x,y) we mean the remainder of x upon division by y.) For such a graph, the pair (n,S) is called a symbol for X. Note that 0∉S since we are only concerned with simple graphs. Since edges are unordered, we may restrict S so that d∈S if and only if n-d∈S for all values of d. For example, consider the graph in figure 1. Contrary to the claim of Turner [13], this graph is, in fact, a circulant with symbol (6,{2,3,4}).

Figure 1.

We now determine those vertex-transitive graphs which are circulants. In ([1], Proposition 2), Alspach proves a similar result for tournaments. Henceforth, we assume all subscript arithmetic is done modulo n=o(V(X)).

Theorem 3: A graph X is a circulant if and only if G(X) contains a regular cyclic subgroup.

Proof: Let X be a circulant with symbol (n,S). Define α to be the permutation (v₀v₁ … v_n-1) where V(X)={v₀,…,v_n-1} In other words, α(v_i)=v_i+1 for 0⩽i<n. Thus α(E(X))=E(X), which means that α∈G(X) and G(X) contains the regular cyclic subgroup {1,α,…, αⁿ⁻¹}.

Now assume that X is an n-node graph and that G(X) contains a regular cyclic subgroup. Let G={1,α,…, αⁿ⁻¹} be this subgroup. By Theorem 2, we know that there exist disjoint H and J such that X≃X_G,H/J. Since o(G)=n=o(V(X))=o(V(X_G,H/J))=o(G)/o(J), we must have o(J)=l and thus J={1}. This means that we may relabel V(X)={αⁱ|0⩽i<n} and E(X)={(αⁱ,α^j)|αⁱ=α^jα^k for some ${\alpha }^k\subset \overline{H}=H\cup H^{-1}$}. Note that αⁱ=α^jα^k if and only if mod(i-j,n)=k. Define $S=\left\{k|{\alpha }^k\subset \overline{H}\right\}$. Relabeling the nodes of X once more, we have V(X)={v₀, … v_n-1} and E(X)={(v_i, v_j) | mod(i-j,n)∈S}. Thus X is a circulant with symbol (n,S).□

It is now easy to prove Theorem 1 of [13].

Theorem 4: A graph with a prime number of nodes is vertex-transitive if and only if it is a circulant.

Proof: Let X be vertex-transitive with a prime number p of nodes. Since the subgroup of automorphisms of X which fix a particular node has index p in G(X), p|o(G(X)). By Sylow’s theorem on groups, G(X) contains an element of order p. Without loss of generality, this element must be α=(v₀, … v_p-1) where V(X)={v₀, … v_p-1}, since no permutation on p elements with more than one orbit has order p. Thus R={l,α, …, α^p−1} is an order p transitive subgroup of G(X). Equivalently, R is a regular cyclic subgroup of G(X) so by Theorem 3, X is a circulant. Since every circulant is vertex-transitive, the converse follows trivially.□

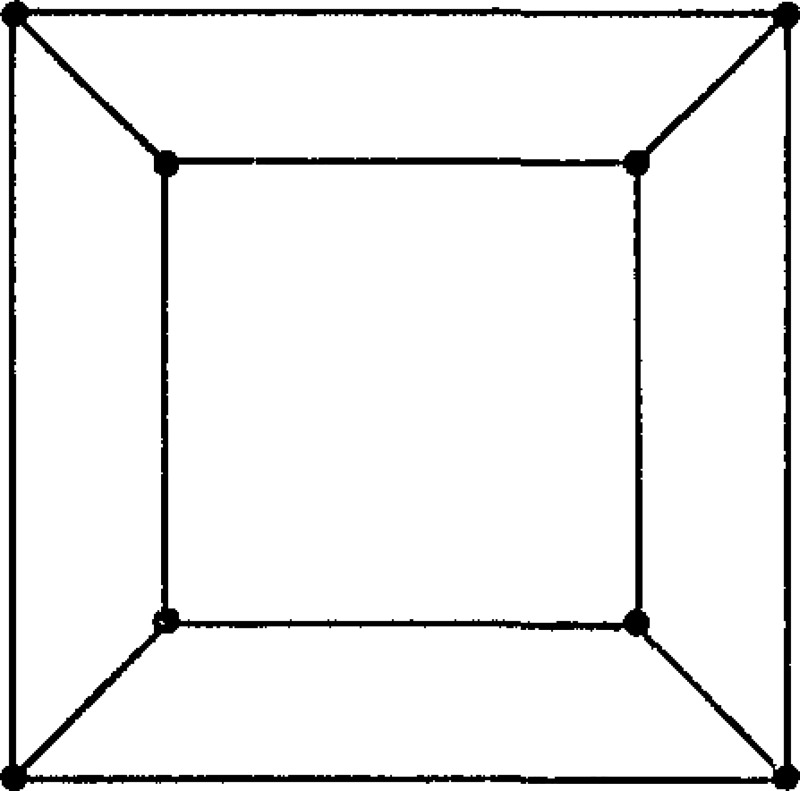
Not every vertex-transitive graph has an automorphism group containing a regular cyclic subgroup. For example, consider the graph in figure 2. This graph is vertex-transitive but has no automorphism of order eight and thus cannot be a circulant.

Figure 2.

4. Multidimensional Circulants

Define a multidimensional circulant to be a graph X whose nodes can be labeled so that there exist positive integers k, a₁ a₂,…, a_k and a set S⊂Z^k such that

$$\begin{gathered} V(X)=\left\{v_{i_1},\dots {,}_{i_k}|0⩽i_l<a_l\text{for}1⩽l⩽k\right\}\text{and} \\ E(X)=\left\{\left(v_{i_1},\dots {,}_{i_k},v_{j_1},\dots {,}_{j_k}\right)|\left(\mathrm{mod}\left(i_1-j_1,a_1\right),\dots ,\mathrm{mod}\left(i_k-j_k,a_k\right)\right)\in S\right\}. \end{gathered}$$

In order to simplify the notation when dealing with multidimensional circulants, we will henceforth employ vector notation. For example, we use the k-vector a to represent (a₁,…,a_k), i to represent (i₁,…,i_k), j to represent (j₁…,j_k), and so on. In particular, we represent the zero vector (0,…,0) by 0 and the unit vector (0,…,0,1,0,…,0) with a one in the ith position and zeros elsewhere by e_i. In addition, it will be convenient to use mod(i-j,a) to represent the k-vector (mod(i₁-j₁,a₁),…, mod(i_k-j_k,a_k)), σ^t to represent the product $\prod _{l=1}^k{\sigma }_l^{i_l}$, and 0⩽i<j to denote the fact that for 0⩽i_l<j_l for i⩽l⩽k. Thus a multidimensional circulant is a graph X whose nodes can be labeled so that there exists an integer k, a k-vector a, and a set S⊂Z^k such that

$$\begin{gathered} V(X)=\left\{v_{\text{i}}|0⩽\mathrm{i}<\mathrm{a}\right\}\text{and} \\ E(X)=\left\{\left(v_{\mathrm{i}},v_{\mathrm{j}}\right)|\mathrm{mod}(\mathbf{i}-\mathbf{j},\mathbf{a})\in S\right\}. \end{gathered}$$

Generalizing the concept of a symbol, we define the pair (a,S) to be a k-symbol of X. As was true in the definition of a circulant (where k = 1), it is clear that the symbol can be restricted so that $\prod _{i=1}^k{a}_i=n=\mathrm{o}(V(X))$, 0∉S, S⊂{i|0⩽i<a}, and that i∈S if and only if mod(−i,a)∈S. For example, consider the graph displayed in figure 2. Whereas this graph is not a circulant, it is a multidimensional circulant. In figure 3a, we display the labeling of this graph which corresponds to the 2-symbol ((2,4),{(0,1),(0,3), (1,0)}), and in figure 3b, we display the labeling which corresponds to the 3-symbol ((2,2,2), {(0,0,1), (0,1,0), (1,0,0)}).

Figure 3.

As is evidenced by this example, multidimensional circulants may have k-symbols for several differing values of k. We call the smallest value of k for which a k-symbol exists the dimension of the graph. In particular, a graph is said to be a k-dimensional circulant if it is a multidimensional circulant and k is the smallest integer for which the graph has a k-symbol. In this notation, the class of circulants is precisely the class of 1-dimensional circulants.

We now generalize Theorem 3.

Theorem 5: A graph X is a multidimensional circulant if and only if G(X) contains a regular abelian subgroup.

Proof: Assume that X is a multidimensional circulant with a k-symbol (a,S). Define the permutation σ_l, on X for 1⩽l⩽k by σ_l(v_i)=v_mod(i+el,a) for all v_i∈V(X). Since mod(mod(i+e_l,a)–mod(j+e_l,a),a)=mod(i-j,a), we know that σ_l(E(X))=E(X). Thus, σ_l∈G(X) for 1⩽l⩽k. Further, σ_lσ_m = σ_mσ_l for 1⩽l,m⩽k and, thus, the subgroup of G(X) generated by {σ₁,…,σ_k} is abelian. It is not difficult to show that this subgroup is also transitive and has $\prod _{i=1}^k{a}_i=\mathrm{o}(V(X))$ elements. Thus it is regular and we have shown that G(X) contains a regular abelian subgroup.

Now assume that we are given a graph X such that G(X) contains a regular abelian subgroup R. By a well-known result concerning finitely generated abelian groups ([4], p. 101–3), we know that we can express R as the direct product of cyclic groups. Thus we can write $\text{R}=\underset{i=1}{\overset{k}{✕}}$ R where each R_i is cyclic, has order a_i, and is generated by σ_i. Replacing G with R in Theorem 2, we know that there exist H⊆R−{1} and a subgroup J of R such that X≃X_R,H/J. Since R is regular, we must have that J={1}. Thus we may label the nodes of X so that

$$\begin{gathered} V(X)=\left\{{\sigma }^{\mathbf{i}}|\mathbf{0}⩽\mathbf{i}⩽\mathbf{a}\right\}\text{and} \\ E(X)=\left\{({\sigma }^{\mathbf{i}},{\sigma }^{\mathbf{j}})|{\sigma }^{\mathbf{i}}={\sigma }^{\mathbf{j}}{\sigma }^{\mathbf{h}}\mathrm{for}\mathrm{some}{\sigma }^{\mathbf{h}}\in \overline{H}\right\}. \end{gathered}$$

Since R is abelian, σⁱ=σ^jσ^h if and only if σ^i-j=σ^h and thus if and only if mod(i-j,a)=h. Further simplifying, it is possible to relabel the nodes of X so that

$$\begin{gathered} V(X)=\left\{v_{\mathrm{i}}|\mathbf{0}⩽\mathbf{i}⩽\mathbf{a}\right\}\text{and} \\ E(X)=\left\{\left(v_{\text{i}},v_{\text{j}}\right)|\mathrm{mod}(\mathbf{i}-\mathbf{j},\mathbf{a})\in S\right\} \end{gathered}$$

where $S=\left\{\mathbf{h}|{\mathit{\sigma }}^{\mathbf{h}}\in \overline{H}\right\}$. Thus X is a multidimensional circulant with k-symbol (a,S).□

Corollary 1: Every multidimensional circulant is vertex-transitive.

The arguments in the preceding proof make it clear that, in principle, it is possible to determine the dimension of a multidimensional circulant through examination of the structure of its automorphism group. In practice, however, this may be quite difficult to accomplish. The following theorem provides an upper bound on the dimension based solely on the number of nodes in the graph.

Theorem 6: If X is a multidimensional circulant with $\text{n}=\prod _{\mathrm{i}=1}^{\mathrm{t}}{\text{p}}_{\text{i}}^{{\mathrm{b}}_{\mathrm{i}}}$ nodes (primes p_i≠p_j for i≠j), then X has dimension k for some k<max_1<i<t(b_i).

Proof: Given a multidimensional circulant X, we know from Theorem 5 that G(X) contains a regular abelian subgroup R. Decomposing R into cyclic subgroups, we have $R=\underset{i=1}{\overset{t}{✕}}\underset{j=1}{\overset{d_i}{✕}}{R}_{ij}$ where R_ij is a cyclic subgroup of R with order $p_i^{c_{ij}}$. Recomposing cyclic subgroups with differing prime power orders, we can write $R=\stackrel{\max d_i}{\underset{j=1}{✕}}{R}_j^{\prime }$ where $R_j^{\prime }$ is cyclic with order $\prod _{i=1}^t{p}_i^{c_{ij}}$ (c_ij is defined to be zero if j>d_i) and is the product (with as many terms as exist) R_1,j✕…✕R_i,j. Thus R is the direct product of $\underset{1<i<t}{\max }(d_i)$ cyclic subgroups. The result now follows from the arguments in the proof of Theorem 5 and the fact that d_i⩽b_i for 1⩽i⩽t.□

Corollary 2: The class of n-node multidimensional circulants is precisely the class of n-node circulants whenever n is the product of disjoint primes.

We now demonstrate the existence of k-dimensional circulants for every k⩾1. This is accomplished by showing that the n-cube is an ⌊(n+1)/2]-dimensional circulant for every n⩾1. The n-cube is the graph X with nodes V(X)={v_i|0⩽i<2ⁿ} and edges E(X)={(v_i,v_j)| the n-bit binary representation of i differs from the n-bit binary representation of j in exactly one bit}. The 3-cube, for example, is displayed in figures 2 and 3. Our result requires the following lemma, the proof of which was suggested by Lawrence [7].

Lemma 1: If α is an element of a regular abelian subgroup of automorphisms of the n-cube, then α has order 1, 2, or 4.

Proof: Let R be any regular abelian subgroup of automorphisms of the n-cube X. View R as an automorphism subgroup of the facets of X. The facets of X are the (n-1)-cubes contained in X. There are 2n such (n-1)-cubes, one corresponding to each set of 2ⁿ⁻¹ nodes whose labels have identical ith bits for some fixed i, 1⩽i⩽n, in the n-bit binary representation of the labels. It is not difficult to show that the action of an automorphism on the facets of X completely determines its action on the nodes, and vice-versa.

Let F₁,…,F_k be the facet orbits of R and define R_i for 1⩽i⩽k to be the restriction of R to F_i with duplicates eliminated. Then, each R_i is a group of automorphisms of F_i and $R\subseteq \underset{i=1}{\overset{k}{✕}}{R}_i$. Thus $\text{o}(R)⩽\prod _{i=1}^k\text{o}\left(R_i\right)$ and, since o(R)=2ⁿ,

$$\prod _{i=1}^k\mathrm{o}\left(R_i\right)⩾2^n.$$ (1)

In addition, each R_i is regular on F_i. If not, then we could find s,t∈F_i and α,β∈R_i such that α(s)=s, α(t)≠t and β(s)=t. By the commutativity of R, this implies t=β(s)=αβα⁻¹(s)=α(t)≠t which is a contradiction. Thus o(R_i)=o(F_i) for 1⩽i⩽k. By definition, we must have $\sum _{i=1}^k\mathrm{o}\left(F_i\right)=2n$ and thus

$$\sum _{i=1}^k\text{o}\left(R_i\right)=2n.$$ (2)

It is well known that the order of an orbit is a divisor of the order of the permutation group [14]. Thus o(R_i)|o(R) for 1⩽i⩽k. Since o(R)=2ⁿ, we can define nonnegative integers r_i such that o(R_i)=2^r_i for 1⩽i⩽k. Rewriting (1) and (2), we have

$$\sum _{i=1}^k{r}_i⩾n\text{and}\sum _{i=1}^k{2}^{r_i}=2n.$$

Thus $\sum _{i=1}^{k}2r_i⩾2n=\sum _{i=1}^k{2}^{r_i}$. Since $2r_i<2^{r_i}$ for r_i = 0 and r_i>2 and $2r_i=2^{r_i}$ for 1⩽r_i⩽2, it is clear that 1⩽r_i⩽2 for 1⩽i⩽k. Thus o(R_i)=2 or 4 for 1⩽i⩽k. Thus for each α∈R, α⁴ leaves each facet of X fixed and α⁴ = 1. Thus o(α) = 1, 2, or 4.□

We are now ready to prove:

Theorem 7: The n-cube is an ⌊(n+1)/2⌋-dimensional circulant.

Proof: We first show that the n-cube X is a k-dimensional circulant for some k⩽⌊(n+1)/2⌋. It follows from the definition of X that we may label the nodes so that X has symbol (a,S) where a=(2,2,…,2) and S={e_i|1⩽i⩽n}. By relabeling node v_i, with index j so that

$$j_l=\left\{\begin{array}{l}0\text{if}\left(i_{2l-1},i_{2l}\right)=(0,0)\\ 1\text{if}\left(i_{2l-1},i_{2l}\right)=(0,1)\\ 2\text{if}\left(i_{2l-1},i_{2l}\right)=(1,1)\\ 3\text{if}\left(i_{2l-1},i_{2l}\right)=(1,0)\\ i_n\text{if}2\nmid n\text{and}l=\lfloor (n+1)/2\rfloor \end{array}\right\}\text{for}1⩽l⩽\lfloor (n+1)/2\rfloor ,$$

it is easy to show that X has ⌊(n+1)/2⌋-symbol (a,S) where

$$\begin{gathered} \mathbf{a}=\left\{\begin{array}{l}(4,4,\dots ,4)\text{if}2|n\hfill \\ (4,\dots ,4,2)\text{if}2\nmid n\hfill \end{array}\right\}\text{and} \\ S=\left\{\pm {\mathrm{e}}_i|1⩽i⩽\lfloor (n+1)/2\rfloor \right\}. \end{gathered}$$

Thus X is a k-dimensional circulant for some k⩽⌊(n+1)/2⌋.

Assume now that X has dimension k<⌊(n+1)/2⌋. Then X has a k-symbol (a,S) such that $\prod _{i=1}^k{a}_i=2^n$. But this means that a_i⩾8 for at least one value of i. Otherwise, $\prod _{i=1}^k{a}_i⩽4^k⩽4^{(n+1)/2-1}⩽2^{n-1}<2^n$. By the arguments in the proof of Theorem 5, G(X) must contain a regular abelian subgroup with an element of order a_i⩾8. But this contradicts the result of Lemma 1. Thus X has dimension ⌊(n+1)/2⌋.□

Not every vertex-transitive graph is a multidimensional circulant. Indeed, there are examples of vertex-transitive graphs which do not have a regular subgroup of automorphisms. For instance, the smallest transitive subgroup of automorphisms of the 10-node Petersen graph, shown in figure 4, has 20 elements.

Figure 4.

5. Concluding Remarks

With the introduction of multidimensional circulants, we have moderately broadened the class of vertex-transitive graphs for which a nice graph-theoretical characterization is known. The notational complexity, however, has increased substantially. Indeed, the problem of characterizing graph-theoretically the entire class of vertex-transitive graphs has been unsolved for quite some time. Maybe some of the following subclasses are easier to characterize: those with an automorphism group containing a regular subgroup (the Cayley graphs), those with an automorphism group containing an order o(V(X)) transitive subset, or those with twice a prime number of nodes. The last subclass has received much attention in the literature of late [3,8,9,11], but even so, a complete characterization has yet to be found.

Biography

About the Author, Papers: F.T. Leighton is an assistant professor of mathematics at MIT and a member of the Laboratory for Computer Science. This paper and the paper following were written while he served as a summer intern at NBS and in part while he was an undergraduate at Princeton University working under the guidance of Professor Stephen B. Maurer.