The Efficiency of the Biweight as a Robust Estimator of Location

Abstract

The biweight is one member of the family of M-estimators used to estimate location. The variance of this estimator is calculated via Monte Carlo simulation for samples of sizes 5, 10, and 20. The scale factors and tuning constants used in the definition of the biweight are varied to determine their effects on the variance. A measure of efficiency for three distributional situations (Gaussian and two stretched-tailed distributions) is determined. Using a biweight scale and a tuning constant of c = 6, the biweight attains an efficiency of 98.2% for samples of size 20 from the Gaussian distribution. The minimum efficiency at n = 20 using the biweight scale and c = 4 is 84.7%, revealing that the biweight performs well even when the underlying distibution of the samples has abnormally stretched tails.

1. Introduction

Robust estimation of location has become an important tool of the data analyst, due to the recognition among statisticians that parametric models are rarely absolutely precise. Much discussion has taken place to determine the “best” estimators (“best” in a certain sense, such as low variance across several distributional situations). Estimators which were designed to be robust against departures from the Gaussian distribution in a symmetric, long-tailed fashion were investigated indepth by Andrews et al. in 1970–1971 [1].¹ Subsequent to this, Gross and Tukey compared several other estimators in the same fashion, one of which they called the biweight [2]. It was designed to be highly efficient in the Gaussian situation as well as in other symmetric, long-tailed situations. The first reference of its practical use appears two years later [3]. Gross showed that the biweight proves useful in the “t”-like confidence interval for the one-sample problem [4] and for estimating regression coefficients [5]; Kafadar showed that it is efficient for the two-sample problem also [6].

Many scientists collect data and perform elementary statistical analyses but seldom use summary statistics other than the sample mean and sample standard deviation. This paper is therefore addressed to two audiences. It provides a brief introduction to the field of robust estimation of location to explain the biweight in particular (section 2). Those who are familiar with the basic concepts may wish to proceed directly to section 3 which raises the specific questions about the biweight’s computation and efficiency that are answered in this paper. Section 4 describes the results of a Monte Carlo evaluation of the biweight. An example to illustrate the biweight calculation is presented in section 5, followed by a summary in section 6.

2. Robust Estimation of Location; M-Estimates

Given a random sample of n observations, X₁,…,X_n, typically one assumes that they are distributed independently according to some probability distribution with a finite mean and variance. For convenience, the Gaussian distribution is the most popular candidate; representing its mean and variance by μ and 𝜎², it is well known that the ordinary sample mean and sample variance are “good” estimates, in that, on the average, they estimate μ and 𝜎² unbiasedly and with minimum variance. Often, however, this Gaussian assumption is not exactly true, owing to a variety of reasons (e.g., measurement errors, outliers). Ideally, such departures from the assumed model should cause only small errors in the final conclusions. Such is not the case with the sample mean and sample variance; even one misspecified observation can throw these estimates far from the true μ and σ² (e.g., see Tukey’s example in [7]).

It is important, then, to find alternative estimators of location and scale. Huber [8, p. 5] lists three desirable features of a statistical procedure:

1. reasonably efficient at the assumed model;

2. large changes in a small part of the data or small changes in a large part of the data should cause only small changes in the result (resistant);

3. gross deviations from the model should not severely decrease its efficiency (robust).

A class of estimators, called M-estimators, was proposed by Huber [9] to satisfy these three criteria. This class includes the sample mean in the following way. Let T be the estimate which minimizes

$$\sum _{i=1}^n\varrho \left(X_{\mathrm{i}}-T\right)$$ (1)

where ϱ is an arbitrary function. If Ψ(x−μ) = (∂/∂μ)ϱ(x−μ), then T may also be defined implicitly by the equation

$$\sum _{i=1}^n\mathrm{\Psi }\left(X_{\mathrm{i}}-T\right)=0.$$ (1′)

(There may be more solutions to (1′), however, corresponding to local minima of (1).)

If ϱ(u) = u², then (1) defines the sample mean $\overline{X}$ (and $\overline{X}$ is therefore called least squares estimate). It can be shown that M-estimates are maximum likelihood estimates (MLE) when X₁,…,X_n have a density proportional to exp{-∫Ψ(u)du} (e.g., $\overline{X}$ is MLE for the Gaussian distribution), but their real virtue is determined by their robustness in the face of possible departures from an assumed Gaussian model. Many suggestions for Ψ have been offered, one of which is the biweight Ψ-function:

$$\begin{array}{lll}\mathrm{\Psi }(\mathrm{u})& =\mathrm{u}{\left(1-{\mathrm{u}}^2\right)}^2& \left|\mathrm{u}\right|⩽1\\ & =0& \text{otherwise.}\end{array}$$ (2)

Using (2), T as defined by (1′) is called the biweight. Actually, the solution in this form is not scale invariant. We therefore define the biweight as the solution to the scale-invariant equation

$$\sum _{\mathrm{i}=1}^n\mathrm{\Psi }\left[\left({\mathrm{X}}_{\mathrm{i}}-T\right)/(c\mathrm{s})\right]=0,$$ (3)

where s is a measure of scale of the sample and c is any positive constant, commonly called the “tuning constant.” A graph of the biweight Ψ function (2) is shown in figure 1.

FIGURE 1.

The lack of monotonicity in the biweight Ψ-function leads to its inclusion in the class of the so-called “redescending M-estimates,” a term first introduced by Hampel [1, p. 14]. Typically, the defining Ψ-functions have finite support (i.e., are 0 outside a finite interval); hence, redescending M-estimates have the property that the calculation assigns zero weight to any observation which is more than c multiples of the width from the estimated location. To see this, we define the weight function corresponding to any M-estimate, w(⋅), by the following equation:

$$w(\text{u})=\mathrm{\Psi }(\text{u})/\text{u.}$$

Hence, (3) becomes

$$0=\mathrm{\Sigma }\left[\left(X_{\text{i}}-T\right)/(c\text{s})\right]\cdot w\left[\left(X_{\text{i}}-T\right)/(c\text{s})\right]$$

which implies

$$T=\mathrm{\Sigma }{X}_{\text{i}}w\left({\text{u}}_{\text{i}}\right)/\mathrm{\Sigma }w\left({\text{u}}_{\text{i}}\right)$$ (4)

where

$${\mathrm{u}}_{\mathrm{i}}=\left(X_{\mathrm{i}}-T\right)/(c\mathrm{s}).$$

Equation (4) reveals that the calculation of T may be viewed as an iteratively reweighted average of the observations. A graph of the weight function used for the biweight,

$$\begin{array}{lll}w(\mathrm{u})& ={\left(1-{\mathrm{u}}^2\right)}^2& \left|\mathrm{u}\right|⩽1\\ & =0& \text{otherwise,}\end{array}$$

also known as the bisquare weight function, is shown in figure 2, where it is clear that zero weight is assigned to any value outside (T − cs, T + cs). Henceforth, Ψ and w will always refer to the biweight M-estimator.

FIGURE 2.

Because of the non-monotonicity of the biweight Ψ-function, multiple solutions to (3) are possible. It has been argued that an iteration based on (4) will not converge to all of the solutions to (3) and therefore will not get trapped by local minima of (1) [10]. In addition, the iteration suggested by eq (4) is more stable than a root finding search suggested by (3). These two facts encourage the use of (4), called the w-iteration, in calculating T.

3. Use of the Biweight in Practice

There has been considerable discussion on the practical usefulness of the biweight, and of redescending M-estimates in general. Huber points out that they are more sensitive to scaling (i.e., prior estimation of s in (4)), and warns of possible problems in convergence [8, pp. 102–103]. In addition, unlike the monotone Ψ-functions, an estimate defined by a redescending Ψ-function is not a maximum likelihood estimate for any density function, for it is constant outside a finite interval and hence does not integrate to 1. The central (non-constant) part of what would be the corresponding density (exp(−∫Ψ(u)du)), scaled to have the same density at 0 as the unit Gaussian, reveals “shoulders” (Fig. 3), which may or may not correspond to realistic applications.Nonetheless, the popularization of the biweight demands a careful assessment of its performance. This paper, therefore, documents its efficiency in three distributional situations using small- to moderate-sized samples.

FIGURE 3.

The study reported below involved a Monte Carlo simulation of three situations, and three sample sizes, in order to determine the variance of the biweight using four different scalings and seven different values of the tuning constant. This section provides details on the calculation of the biweight, a description of the underlying situations in the Monte Carlo study, and the efficiency criterion on which it was evaluated.

3.1. Calculation and Scalings

Taking (3) as the definition of T for this study, we calculate the biweight iteratively: after the k^th iteration,

$$T^{(\mathrm{k}+1)}=\frac{\sum {\mathrm{X}}_{i}w\left[\left({\mathrm{X}}_{\mathrm{i}}-T^{(\mathrm{k})}\right)/(c\mathrm{s})\right]}{\sum w\left[\left({\mathrm{X}}_{\mathrm{i}}-T^{(\mathrm{k})}\right)/(c\mathrm{s})\right]},\mathrm{k}=0,1,2\dots .$$ (5)

One may begin the iteration with any robust estimate of location. For this study, T⁽⁰⁾ is the median for reasons of convenience and computational ease. In this form, the scale estimate remains fixed throughout the iteration. One may also consider updates on the scale:

$$T^{(\mathrm{k}+1)}=\frac{\sum {\mathrm{X}}_{\mathrm{i}}w\left[\left({\mathrm{X}}_{\mathrm{i}}-T^{(\mathrm{k})}\right)/\left(c{\mathrm{s}}^{(\mathrm{k})}\right)\right]}{\sum w\left[\left({\mathrm{X}}_{\mathrm{i}}-T^{(\mathrm{k})}\right)/\left(c{\mathrm{s}}^{(\mathrm{k})}\right)\right]},\mathrm{k}=0,1,2\dots .$$ (6)

Two forms of scale functions were considered in connection with iterations (5) and (6). The median absolute deviation about the current estimate

$${{\mathrm{s}}_{MAD}}^{(k+1)}=\underset{1⩽\text{i}⩽\text{n}}{\mathrm{med}}\left|{\mathrm{X}}_{\mathrm{i}}-T^{(\mathrm{k})}\right|,T^{(0)}=\underset{1⩽\text{i}⩽\text{n}}{\mathrm{med}}{\mathrm{X}}_{\mathrm{i}}$$ (7)

or “MAD,” has been used frequently in many robustness studies, including Andrews et al. [1]. In the Gaussian situation, the average value of the MAD is roughly two thirds of the standard deviation, so we really use 1.5 × MAD. The second scale is based on a finite sample version of the theoretical asymptotic variance of T [8, p. 45]:

$$\begin{gathered} {s_{bi}}^{(\mathrm{k}+1)}={\left(\frac{\mathrm{n}{\left(c{s_{bi}}^{(\mathrm{k})}\right)}^2\mathrm{\Sigma }{\mathrm{\Psi }}^{\prime }\left({\mathrm{u}}_{\mathrm{i}}\right)}{\left[\mathrm{\Sigma }{\mathrm{\Psi }}^{\prime }\left({\mathrm{u}}_{\mathrm{i}}\right)\right]\max [1,-1+\mathrm{\Sigma }{\mathrm{\Psi }}^{\prime }\left({\mathrm{u}}_{\mathrm{i}}\right)]}\right)}^{1/2} \\ {\text{u}}_{\text{i}}=\left({\text{X}}_{\text{i}}-T^{(\text{k})}\right)/\left(c{s_{bi}}^{(\text{k})}\right). \end{gathered}$$ (8)

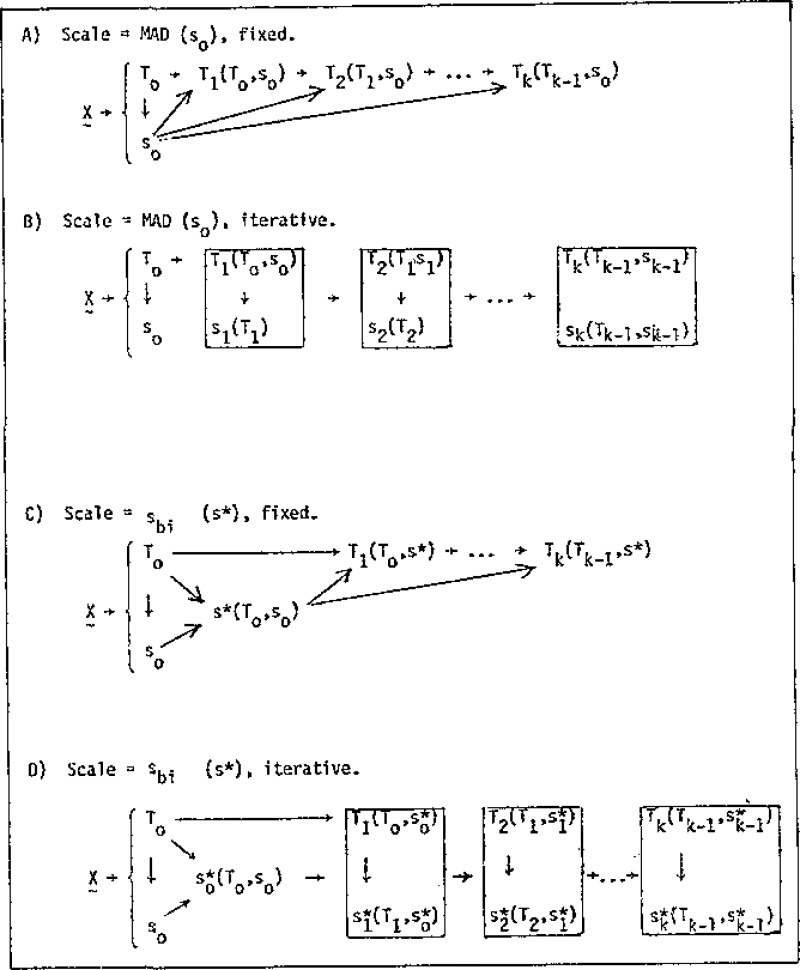
The subscript refers to the fact that s_bi uses the bisquare weight function in its computation. The initial s_bi⁽⁰⁾, again for reasons of convenience, is taken here as 1.5 × MAD. Equation (8) is designed to yield the ordinary sample variance when the Ψ-function is the identity (least squares); hence the use of the “−1” in the denominator. Other values besides −1 have been investigated [11] but have proved less satisfactory. Equation (5) may also proceed without any scale updates (i.e., (7) and (8) calculated once and used throughout the iteration). Figure 4 illustrates four possibilities for scale evaluated in this study.

FIGURE 4.

Four possible methods of iteration in the calculation of the biweight and associated scale from a sample $\underset{˜}{\mathrm{X}}=({\mathrm{X}}_1,\dots ,{\mathrm{X}}_{\text{n}})$ of n observations.

For purposes of notational clarity, the following notation is used:

T = biweight location estimate

s = MAD scale estimate (equation 7)

s* = biweight scale estimate (equation 8)

and the subscript on each refers to the iteration at which the estimate is calculated.

3.2. Distributional Situations

The variance of the biweight was calculated on three distributional situations:

• Gaussian (n observations from N(0,1));

• One Wild (n−1 observations from N(0,1); 1 unidentified observation from N(0,100));

• Slash (n observations from N(0,l)/independent uniform on [0,1]).

The general term “situation” is applied particularly for the One-Wild, as the observations are not independent (n−1 “reasonable-looking” observations suggest that the next is almost sure to be “wild”). The Slash distribution is a very stretched-tailed distribution like the Cauchy, but is less peaked in the center, making it a more realistic situation.

These three situations were chosen for two reasons. First, characteristics of sampling distributions of the various statistics may be estimated efficiently through a Monte Carlo swindle described by Simon [12] when the underlying distribution is of the form Gaussian/( symmetric positive distribution). Second, the three situations represent extreme types of situations for real-world applications (“utopian,” outliers, and stretched tails); if an estimator performs well on these three, it is likely to perform well on almost any symmetric distribution arising in practice [13]. Additional characteristics about these distributions may be found in [14].

3.3. Efficiency Comparisons

In assessing the performance of a location estimator, one typically hopes for (i) unbiasedness, and (ii) minimal variance. It is simple to see that any M-estimate defined with an antisymmetric Ψ function will be unbiased in symmetric situations. Furthermore, Huber has shown that under some regularity conditions, an M-estimator has an asymptotically Gaussian distribution with a finite variance, even for underlying distributions having infinite mean and variance [8, pp. 49–50]. Thus, it is reasonable to compare the variance of the biweight with the variance of the unbiased location estimator having minimal variance, if it exists, for a given situation.

It is known that the minimal variance that is attainable for an unbiased location estimator in the Gaussian situation is simply 1/n, or

$$\mathrm{Var}(\sqrt{\mathrm{n}}\overline{\mathrm{X}})={\mathrm{V}}_{\mathrm{G}}=1.$$

Minimal variances for the One-Wild and Slash, however, are not so simple. Theoretically, one might determine the variance of the maximum likelihood estimate for the One-Wild density but the derivation is not straightforward. A simple remedy is to pretend that one knows an observation is wild, which one it is, and eliminate it from the sample. Then the “near-optimal” variance would be

$${\mathrm{V}}_{\mathrm{w}}=n/(n-1).$$

A “near-optimal” variance for the Slash density

$$\begin{array}{llll}(1/\sigma )\mathrm{f}(z)& =& \left[1-\exp \left(-z^2/2\right)\right]/\left(\sqrt{2\pi }\sigma z^2\right)& z\ne 0\\ & & {\left(2\sigma \sqrt{2\pi }\right)}^{-1}& z=0\end{array}$$

where

$$z=(\mathrm{X}-\mu )/\sigma ,$$

may be obtained through a maximum likelihood procedure. Details of this derivation may be examined in [15]. The variance of the Slash MLE, V₈, was determined within the Monte Carlo. For all three situations, the efficiency of the biweight is then calculated as

$$\text{efficiency}=\frac{“\text{minimum}”\text{attainable}\text{variance}}{\text{variance}(\text{biweight})}.$$

Efficiency as close to 1 (or 100%) as possible is desirable. So, sometimes it is more useful to calculate the complement, i.e., to examine how far

$$\text{deficiency}=1-\text{efficiency}$$

is from zero (see [1, p. 121]).

4. Results

All computations were performed on a Univac 1108. One thousand samples of sizes 5, 10, and 20 were generated. Uniform deviates were obtained using a congruential generator [16]; the Box-Muller transform was applied to these to obtain Gaussian deviates [17]. The iteration in (4) was terminated when the relative change was less than 0.0005, or if the number of iterations exceeded 15 (in which case, T⁽¹⁵⁾ became the estimate of location).

Tables 1, 2, and 3 provide the variances, their sampling errors (SE) and deficiencies of the biweight for the Gaussian, One-Wild, and Slash situations. The most immediate observation is the low deficiency of the biweight in the Gaussian situation: using c = 4, as recommended in Mosteller and Tukey [18], the biweight is never more than 10% less efficient than the optimal sample mean for any of the scalings here (except n=5, where it loses 15% for fixed s_bi). As c increases, the deficiency is even lower. At c = 6, even for n = 5, the deficiency is less than 6%. As noted by Mosteller and Tukey, relative differences in deficiency of less than 10% are essentially indistinguishable in practice [18, p. 206].

Table 1.

Biweight variances and deficiencies: n =5.

Tuning Constant	1.5xMAD — Fixed			1.5xMAD — Iterative			sbi — Fixed			sbi — Iterative
	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)
Gaussian (optimal = 1.0)
3	1.2114	0.0172	17.5	1.1959	0.0171	16.4	1.2652	0.0203	21.0	1.2475	0.0201	21.1
4	1299	0134	11.5	1065	0130	9.6	1694	0163	14.5	1294	0149	12.6
5	0879	0109	8.1	0702	0106	6.6	1068	0132	9.6	0816	0126	8.6
6	0611	0088	5.8	0398	0082	3.8	0693	0106	6.5	0550	0104	6.1
7	0438	0072	4.2	0200	0053	2.0	0487	0090	4.6	0371	0086	4.4
8	0326	0061	3.2	0155	0045	1.5	0387	0084	3.7	0311	0082	3.8
9	0264	0057	2.6	0124	0043	1.2	0262	0070	2.6	0204	0068	2.6
One-Wild (optimal = 1.2)
3	1.7377	0.0314	30.9	1.7064	0.0302	29.7	1.6946	0.0282	29.2	1.6979	0.0281	30.5
4	2.0164	0461	40.4	2.1890	0658	45.2	1.8322	0366	34.5	1.9621	0447	40.2
5	2.4523	0709	51.1	3.0922	1281	61.2	2.1110	0540	43.2	2.5201	0835	53.9
6	2.9642	0977	59.5	4.2740	1933	71.9	2.6146	0850	54.1	3.3286	1302	65.3
7	3.5080	1235	65.8	5.6037	2657	78.6	3.2118	1199	62.6	4.2358	1748	72.8
8	4.0822	1481	70.6	6.9447	3101	82.7	3.9072	1537	69.3	5.0837	2163	77.4
9	4.6817	1725	74.4	8.3881	3705	85.7	4.5843	1877	73.8	5.9725	2561	80.7
Slash (optimal = 10.375)
3	22.291	5.787	53.4	21.964	6.008	52.8	22.497	6.346	53.9	22.312	5.976	63.3
4	23.470	6.034	55.8	33.974	11.664	69.5	22.618	6.006	54.1	30.965	10.533	75.0
5	25.218	6.331	58.8	37.209	12.131	72.1	26.191	7.061	60.4	33.872	11.295	77.0
6	28.207	6.981	63.2	42.045	12.466	75.3	31.643	9.610	67.2	37.952	11.764	79.1
7	31.873	3.205	67.4	45.744	12.647	77.3	34.461	10.723	69.9	39.713	12.034	80.0
8	34.778	9.289	70.2	47.387	12.743	78.1	37.223	11.570	72.1	42.677	12.312	81.1
9	36.791	10.073	71.8	52.963	13.121	80.4	39.923	12.188	74.0	45.549	12.470	82.1

Table 2.

Biweight variances and deficiencies: n = 10.

Tuning Constant	l.5xMAD — Fixed			1.5xMAD — Iterative			sbi — Fixed			sbi — Iterative
	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)
Gaussian (optimal — 1.0)
3	1.1250	0.0109	11.1	1.1083	0.0115	9.8	1.1937	0.0146	16.2	1.1930	0.0156	16.2
4	.0578	0075	5.5	0469	0069	4.5	0961	0099	8.8	0800	0083	7.4
5	0319	0056	3.1	0236	0051	2.3	0479	0068	4.6	0335	0048	3.2
6	0198	0043	1.9	0133	0035	1.3	0259	0048	2.5	0145	0032	1.4
7	0126	0031	1.2	0074	0026	0.7	0145	0034	1.4	0056	0013	0.6
8	0084	0024	0.8	0039	0017	0.4	0078	0023	0.8	0037	0013	0.4
9	0059	0019	0.6	0029	0019	0.3	0042	0015	0.4	0027	0013	0.3
One-Wild (optimal = 1.1111)
3	1.2785	0.0116	13.1	1.2781	0.0114	13.1	1.3414	0.0161	17.2	1.3413	0.0168	17.2
4	1.2946	0109	14.1	1.3105	0117	15.2	2709	0112	12.6	1.2630	0105	12.0
5	1.3714	0137	19.0	1.4125	0159	21.3	2775	0104	13.0	1.2828	0102	13.4
6	1.4990	0189	25.9	1.5948	0246	30.3	3257	0115	16.2	1.3794	0141	19.4
7	1.6793	0253	33.8	1.8333	0332	39.4	4196	0163	21.7	1.5757	0242	29.5
8	1.9034	0331	41.6	2.1332	0445	47.9	5621	0223	28.9	1.9037	0397	41.6
9	2.1590	0420	48.5	2.4703	0580	55.0	7562	0301	36.1	2.3703	0591	53.1
Slash (optimal = 5.9843)
3	7.0895	0.2795	15.6	7.4991	0.3348	20.2	6.4815	0.2422	7.7	6.5367	0.2465	8.5
4	7.9896	3382	25.1	8.6854	0.4129	31.1	7.1538	.2796	16.3	7.6037	0.3339	21.3
5	8.9977	4355	33.5	10.819	0.9005	44.7	8.0679	3586	25.8	9.2930	0.7666	35.6
6	10.261	5815	41.7	14.567	1.4310	58.9	8.9836	4739	33.4	11.167	0.8863	46.4
7	11.487	7135	47.9	25.156	8.6783	76.2	10.555	7319	43.3	22.739	7.8504	73.7
8	12.692	8214	52.8	28.036	9.0950	78.6	11.705	5120	51.6	28.258	8.5066	78.8
9	13.999	9294	57.3	33.752	9.4908	82.3	12.908	6051	58.4	31.727	8.9310	81.1

Table 3.

Biweight variances and deficiencies: n = 20.

Tuning Constant	l.5xMAD — Fixed			1.5xMAD — Iterative			sbi — Fixed			sbi — Iterative
	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)	Variance	SE	Deficiency (%)
Gaussian (optimal = 1.0)
3	1.0973	0.0076	8.8	1.0841	0.0069	7.8	1.2111	0.0147	17.4	1.2159	0.0154	17.8
4	0369	0039	3.6	0299	0034	2.9	.0842	0064	7.8	0769	0051	7.1
5	0172	0026	1.7	0117	0013	1.2	0387	0036	3.7	0331	0024	3.2
6	0087	0015	0.9	0056	0007	0.6	0187	0019	1.8	0163	0015	1.6
7	0047	0008	0.5	0030	0004	0.3	0096	0010	0.9	0084	0008	0.8
8	0027	0005	0.3	0018	0002	0.2	0052	0005	0.5	0045	0004	0.4
9	0017	0003	0.2	0011	0001	0.1	0030	0003	0.3	0027	0002	0.3
One-Wild (optimal = 1.0526)
3	1.1597	0.0077	9.2	1.1494	0.0055	8.4	1.2663	0.0148	16.9	1.2561	0.0139	16.2
4	1313	0040	7.0	1298	0037	6.8	1517	0066	8.6	1421	0053	7.8
5	1572	0049	9.0	1594	0050	9.2	1198	0034	6.0	1185	0034	5.9
6	2082	0069	12.9	2145	0071	13.3	1273	0037	6.6	1289	0037	6.8
7	2745	0094	17.4	2848	0097	18.1	1522	0047	8.6	1578	0050	9.1
8	3532	0122	22.2	3721	0127	23.2	1905	0062	11.6	2019	0067	12.4
9	4439	0151	27.1	4690	0159	28.3	2431	0081	15.3	2700	0092	17.1
Slash (optimal — 5.2666)
3	6.2724	0.2046	16.0	6.4046	0.2284	17.8	5.6057	0.1410	6.1	6.7146	0.1541	7.8
4	7.5085	3189	29.9	8.1706	0.4386	35.5	6.2212	1976	15.3	6.4293	0.2137	18.1
5	8.8490	4364	40.5	10.255	0.6849	48.6	7.3065	2822	27.9	8.3053	0.4552	36.6
6	10.157	5377	48.1	12.260	0.8502	57.0	8.6312	4237	39.0	10.434	0.6585	49.5
7	11.453	6307	54.0	13.964	1.0004	62.3	10.116	5670	47.9	12.580	0.8205	58.1
8	12.733	7235	58.6	15.762	1.1107	66.6	11.832	7166	55.4	15.324	1.0068	65.7
9	13.996	8083	62.3	17.100	1.1866	69.2	13.442	8405	60.8	18.235	1.1790	71.1

Comparing the scalings, s_bi typically provides lower variances than does 1.5 × MAD. The only exception to this is in some of the values computed for the Gaussian, where the differences are so small as to be unimportant (at c = 4, largest difference = 4.9%; at c = 6, 2.7%). The differences in deficiency can be quite sizeable for the One-Wild and Slash situations (e.g., at c = 4, a difference of almost 20% for Slash, n = 20).

In addition, one notes that the additional computation in updating the scale estimate with each iteration is not terribly worthwhile, as deficiencies are only trivially higher in most cases. In fact, such updating can cause considerable deficiency. As a check on the convergence of the iteration, table 4 shows the number of samples, out of 1000, that did not satisfy the convergence criterion. Most of the non-convergences occurred with the iterative scales, particularly the iterative MAD.

Table 4.

Number of samples (out of 1000 samples of size n =5/n = l0/n =20) that did not converge k > 15 and |T^(k+1)| > .0005 × scale).

(Tuning Constant)	1.5xMAD FIXED	l.5xMAD ITERATIVE	sbi FIXED	sbi ITERATIVE
Gaussian
3	6/0/0	106/44/9	1/0/0	34/13/0
4	9/0/0	92/ 5/1	1/0/0	0/ 6/1
5	1/0/0	68/ 8/2	1/0/0	0/ 2/0
6	5/0/0	50/ 4/0	0/0/0	0/ 2/0
7	3/0/0	33/ 2/0	1/0/0	0/ 0/0
8	2/0/0	29/ 2/0	0/0/0	0/ 0/0
9	0/0/0	20/ 2/0	0/0/0	0/ 0/0
One-Wild
3	3/0/0	120/ 11/ 6	0/0/0	18/13/ 0
4	1/0/0	168/ 14/ 3	0/0/0	0/10/ 3
5	1/0/0	170/ 42/ 0	0/0/0	0/ 9/ 0
6	0/0/0	159/ 70/ 3	0/0/0	0/47/ 0
7	1/0/0	138/ 91/6	0/0/0	0/46/ 0
8	0/0/0	121/113/20	0/0/0	0/36/ 0
9	0/0/0	92/120/37	0/0/0	0/22/32
Slash
3	4/0/0	119/3½0	1/0/0	0/ 0/15
4	5/0/0	156/33/16	0/0/0	1/ 3/15
5	1/0/0	138/5½4	0/0/0	0/ 0/41
6	8/0/0	121/81/36	1/0/0	0/ 0/94
7	1/0/0	99/65/39	1/0/0	0/ 0/56
8	0/0/0	79/64/48	0/0/0	0/ 0/76
9	0/0/0	67/53/53	0/0/0	0/32/74

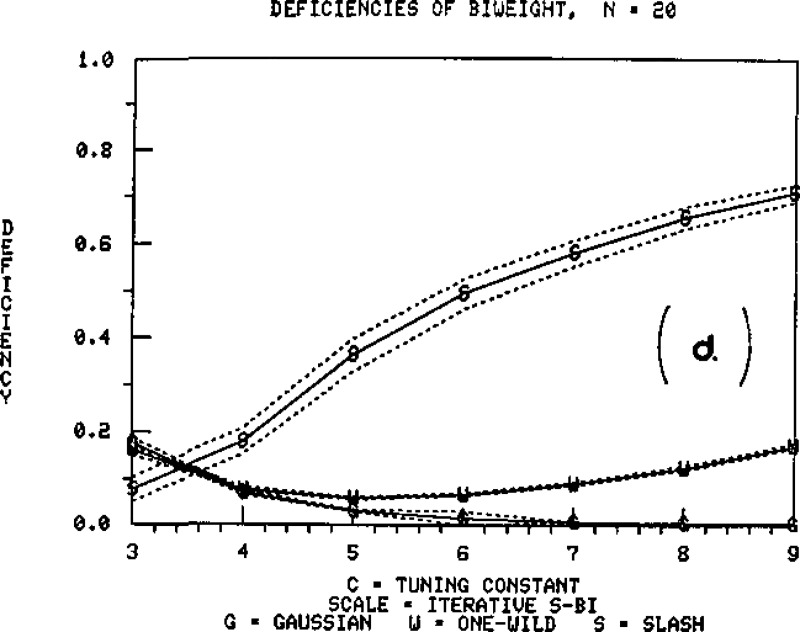
Figures 5, 6, and 7 provide graphs of deficiency as a function of the tuning constant, for sample sizes n = 5, 10, and 20. The uncertainty limits on these graphs, plotted with dotted lines, are given by

$$1-[“\text{minimum}”\text{variance}]/[\text{var}(\text{biweight})\pm \text{SE}],$$

where SE refers to the Monte Carlo sampling error in the calculation of the biweight variances. These reveal that, across these three situations, c = 4 to c = 6 is a practical value of the tuning constant, for larger values tend to yield extremely high deficiencies for the Slash.

Figure 5.

Figure 6.

Figure 7.

The biweight deficiencies computed here scaled by 1.5 × MAD (fixed) differ from those computed by Holland and Welsch [19] in part because of the difference in starting value (they took T⁽⁰⁾ = least absolute deviations estimate), and in convergence criterion (they took T⁽⁵⁾ as their solution). Asymptotically, c = 4.685 yields 95% asymptotic efficiency at the Gaussian [i.e., $\sqrt{n}T$ converges in distribution to N(0,1.0526)]; within two sampling errors, the results in tables 1, 2, and 3 are consistent with this value.

As noted earlier, T⁽¹⁵⁾ became the estimate of location in cases of non-convergence in the study. This only increases the variance of the biweight that we are likely to see in practice, because this situation occurred typically when the iteration alternated between two equally distant values from μ. In practice, one should examine the sample to determine the cause of non-convergence, and possibly settle on the median and 1.5 × MAD as expedient location and scale estimates.

5. An Example

To illustrate the calculation of the biweight, we use some chemical measurements collected at the National Bureau of Standards. These data were taken from several ampoules of n-Heptane material at NBS between May 22 and June 17, 1981. The ampoules were filled from two lots in several sets. Lot A includes 20 sets of ampoules; lot B includes six sets; only the data from 10 ampoules in sets from lot A will be used here. Panel A of table 5 shows the mean percent purity from 10 ampoules, where the mean was calculated as an average of anywhere between 5 and 10 measurements. To eliminate the big numbers and decimal points, we subtract 99.9900 and multiply by 10⁴ in the third column.

Table 5.

Measurements on ampoules of n-Heptane.

A) The data
Set No.—
Ampoule		% purity		(% purity-99.99)·104
2–05		99.9880		−20
3–04		99.9909		9
20–20		99.9956		56
7–07		99.9908		8
20–03		99.9901		1
14–10		99.9928		28
2–15		99.9915		15
8–14		99.9899		− 1
14–20		99.9906		6
7–17		99.9894		− 6
B) Biweight iterations: c =5, T(0)=7.0, s(0)=12.0, sbi=17.2
Columns give weights $w_i^{(k)}$ corresponding to each observation yi at kth iteration. $T^{\left(k\right)}={\displaystyle \sum w_i^{\left(k\right)}{y}_i/}{\displaystyle \sum w_i^{\left(k\right)}}$
obsv’n	(1)		(2)		(3)	(4)		(5)
−20	.8120		.8082		.8075	.8074		.8074
9	.9989		.9992		.9992	.9993		.9993
56	.4546		.4597		.4606	.4607		.4608
8	.9997		.9999		.9999	.9999		.9999
1	.9903		.9893		.9891	.9891		.9891
28	.8839		.8869		.8875	.8876		.8876
15	.9827		.9839		.9841	.9842		.9842
− 1	.9827		.9815		.9812	.9812		.9812
6	.9997		.9996		.9995	.9995		.9995
− 6	.9547		.9527		.9523	.9523		.9523
T(1)=7.283 T(2)=7.334 T(3)=7.344 T(4)=7.345 T(5)=7.346 sbi=18.648
Final location and scale estimates (original scale):
$\widehat{\mu }$ = 99.9900 + 7.346/104 = 99.9907
$\widehat{\sigma }$ = 18.648/104 = .0019

Notice that, by virtue of the central limit theorem, one would expect that these averages would be approximately normally distributed and a higher value for the tuning constant, say c =5, would be reasonable. The third column of Panel A reveals three somewhat anomolous values: −20, 56, and 28. Notice that the low value corresponds to ampoules in set 2, and the high value to those in set 20. Since the sets were filled sequentially, there may have been some aspect of the filling procedure which caused these odd values. Also, the data are listed in the order in which they were measured, so the low value for the first ampoule may have resulted from some problem in the measuring equipment on the first day.

The iteration initiates with the median, T⁽⁰⁾ = 7, and s_bi is calculated from the median and 1.5 × MAD (= 12.0), yielding a scale estimate of 17.2. The convergence criterion in this calculation is relative to the estimated scale; i.e., the iteration ceases when either k ≥ 15 or |T^(k) – T^(k−1)|/s_bi ≤ .0005.

Panel B gives the bisquare weights associated with each observation and the biweight at each iteration. Notice that the three “suspect” values all receive lower weight than the other seven. The final scale estimate, 0.0019, is computed from the final location estimate, 99.9907, and the s_bi used throughout the iteration (.0017). These estimates compare favorably with the sample mean and standard deviation, 99.9910 and 0.0021.

In this case, there is little difference between the two procedures, and either may be reported. Had there been a substantial difference, one would want to examine the data more closely to understand the reason. This is an important step in data analysis, and robust methods offer easy, objective procedures for making this comparison and illustrating possible anomolies in the data.

6. Conclusions

This paper establishes the variance of the biweight as a location estimator across three distributional situations, for small to moderate sample sizes. In terms of scaling, s_bi performs more satisfactorily than does 1.5 × MAD, and need not be recalculated with subsequent iterations. Three to six iterations of the w-iteration are typically required to attain satisfactory convergence (< .0005 × s_bi). The minimum efficiencies of the biweight across the three situations for sample sizes, 5, 10, and 20 at c = 4 are 46%, 83%, and 85% respectively; at c = 6 they are 33%, 67%, and 61% respectively. Gaussian efficiencies are considerably higher: at c = 4, 86%, 91%, and 92%; at c = 6, 94%, 97%, and 98%.

A final comment concerns the results on n = 5. For such a small sample size, it is encouraging that the biweight (c = 4) is only 14% less efficient than the optimal sample mean if the underlying population is really Gaussian. In fact, s_bi can be very misleading in a small (between 2% and 5% for the situations listed here) but influential proportion of the time. Conditioning on some ancillary statistic, such as the average value of the weights, would undoubtedly increase the efficiency for all three situations when n = 5.