Abstract
This paper describes the design, construction, and testing of a probe for the measurement of electric current in a circuit. This measurement is performed by using Faraday rotation produced in a beam of polarized light that encircles the current-carrying conductor. Such a probe is an absolute instrument whose calibration only depends upon the Verdet constant of the rotative medium and is independent of the dimensions or positions of the light path relative to the current. The time resolution of the probe is the optical transit time about the closed path and can in practice be reduced to a few nanoseconds.
Keywords: absolute instrument, electric current, Faraday effect, measurement, polarized light, Verdet constant
1. Introduction
The Faraday effect, known for over a century, has been applied extensively in the measurement of magnetic fields and, more recently, in the measurement of electric current. A Faraday effect current probe offers several advantages, especially for the current measurements in high-voltage circuits. Since measurement information is conveyed by variations in the intensity of an optical signal, the probe can be perfectly insulated electrically from the measurement and recording circuitry either by the free space propagation of a light beam or the transmission of the signal via fiber optics. Indeed the probe need not interrupt the circuit in which the current is being measured; it need only be close enough to be affected in a controlled way by the magnetic field produced by the current. A second advantage of the Faraday effect current probe is the possibility of its being an absolute instrument because calibration can be made to depend solely upon the Verdet constant of the rotative medium. For diamagnetic media, the Verdet constant is determined by the dispersion curve of the medium and does not depend upon temperature.
A great deal of work has been done to develop Faraday effect current probes. Hebner et al. summarized this work up to 1977 [1]1. The difficulties with the current probes can be summarized as owing to 1) calibration errors and, 2) limited dynamic range, signal-to-noise ratio, and the effects of optical detector sensitivity variations.
The principal source of the first set of difficulties lies in the fact that the magnetic field arising from the current flow in an arbitrary circuit, in general, has a spatial variation. Hence, the calibration of the probe involves geometric factors such as the shape and dimensions of the probe and its position relative to the circuit. The second set of difficulties stems from the relatively small value of the Verdet constant for most media and the concomitant small value of the rotation for currents of the magnitudes encountered in electric utility transmission lines. The schemes [1] proposed to improve this situation, such as null-seeking feedback devices, etc., generally lead to expensive, complicated, and less than satisfactory devices. In spite of these problems, satisfactory Faraday probes for use on utility transmission lines have been realized [2,3,4].
The geometric factors in the probe calibration can be eliminated by designing the optical path in the rotative medium so that it encircles the current. Since the Faraday rotation angle θ is proportional to the line integral of the magnetic induction B along the path l, we can write for a closed light path
| (1) |
where V, the constant proportionality, the so-called Verdet constant, is characteristic of the rotative medium and is usually expressed in the units of minutes of arc per gauss-centimeter. From the circuital statement of Ampere’s law, we replace the circuital integral by where i is the current in amperes that is enclosed by the path of integration. The resulting Faraday rotation is thus
| (2) |
The Faraday rotation in such a current probe depends only on the Verdet constant of the rotative medium; geometric factors do not enter. Current probes based on this principle have been developed [3,4], using optical fibers as the rotative medium. Unfortunately, optical fibers which rigorously preserve the state of polarization transversing them are at present beyond the state of the art.2 Since the Verdet constant of the fiber core material (essentially fused quartz) is very small, a large number of turns of the fiber around the conductor is needed to obtain a measureable rotation which greatly increases the stray birefringence due to fiber strain and curvature. To minimize these effects, the radius of curvature of the fiber turns is kept as large as possible which increases the overall size of the probe. As the optical transit time of the fiber coil gives the time resolution of the current variations such a fiber optic probe would be unsuitable for measuring fast-rising currents. In spite of these problems, however, Faraday effect current monitors have been developed for use on high voltage utility transmission lines and offer a cost-effective alternative to conventional current transformers. At the relative low frequencies present in these lines, the decreased time resolution of these fiber optic probes poses no problem.
The second set of problems, dynamic range, signal-to-noise ratio etc., can be addressed by designing the probe so that the number of complete Faraday rotations at the maximum value of current is large. In our work this required no particular effort as the peak current was in the mega-ampere range. The advantage of this mode of operation can be seen from the following discussion.
The light entering the Faraday probe is rendered plane polarized by use of a suitable device (unless a laser emitting plane polarized light is used as a source) and the emerging light passes through a second polarizer or analyzer before entering the detector.
The intensity of light on the detector for an incident intensity of I0 is given by
| (3) |
where χ is the angle between the transmission axes of the polarizer and analyzer.
Two different methods of handling Faraday effect signals can be used depending upon whether the value θ(i) at peak current is very much less than π.
In the latter case, the usual practice is to make use of a differential analyzer such as a Wollaston prism which separates the entering light into two beams of intensity I1 and I2 which are polarized orthogonally to each other [4,5]. The analyzer is oriented at 45° with respect to the transmission axis of the polarizer. The intensities of the transmitted beams for a Faraday rotation angle of the θ are
| (4) |
The sum and difference of these two intensities and their quotient are computed giving
| (5) |
or using eq (2) we have for θ⪡π
| (6) |
Note that the result is independent of the intensity of the light or the sensitivities of the two detectors provided that the latter are equal.
An alternative method of measurement useful when θ(imax)⪢π is to use crossed or parallel analyzers (X=0 or π/2). The signal is then
| (7) |
or
| (7a) |
The upper sign is for crossed polarizers which, using eq (2), gives
| (8) |
The signal given by eq (8) can be inverted numerically to obtain i as a function of t.
The accuracy is determined by the precision with which the phase of the cosine can be determined from the record of θ(t) which depends upon the signal-to-noise ratio. If we call this phase uncertainty Δϕ, then the relative error ϵ is
| (9) |
where N is the total number of cycles of Faraday rotation. Thus even though a relatively large value of Δϕ is obtained due to a poor signal-to-noise ratio, the error in the current measurements can be made small by making N large. It is assumed, however, that Δϕ is not so large that a change of sign of the time derivative of the phase cannot be detected. Such a reversal in occurs when i attains an extremum.
Variations in peak amplitudes of the Faraday signal due to noise, source intensity, detector sensitivity, or transmission fluctuations can be averaged out by normalizing all maxima except those associated with the excess fraction of a cycle. These effects will thus only affect the accuracy with which the excess fraction can be measured.
If the value of iπ can be made sufficiently small so that iπ=Δi the allowable current error, then the signals can be handled purely by digital techniques. The value of the current can thus be evaluated by simple pulse counting. The reversal in sign of can be detected by using a Wollaston prism or similar analyzer crossed with the input polarization direction to obtain the two outputs given by eq (7) thus providing a phase reference. Such digital processing would eliminate most of the second class of problems in the use of Faraday probes. The problem is now that of reducing iπ to a sufficiently low value to obtain a probe of required accuracy for currents of the magnitude encountered in electric power transmission. This in turn requires the development of polarization preserving optical fibers of high Verdet constant (see footnote 2).
2. Design of a Faraday Current Probe
We have designed and tested a Faraday current probe based on the principle of the preceding section. It is designed to measure currents of up to 4 MA rising to their maximum value in times of the order of 50 ns.
Even if polarization preserving fibers were available their use in this application would be impossible since the low Verdet constant of these fibers would require many turns. The resulting long optical transit time and poor time resolution would obscure completely the details of the current waveform. In addition, only a few cycles of Faraday rotation would be obtained so the relative error given by eq (9) would be large.
We selected as the Faraday rotative medium a high density flint glass, Schott type SF-58. This glass has a Verdet constant of 0.082 min/gauss-cm and a refractive index of 1.907 at the wavelength of the helium-neon laser, 6328 Å. This glass has a very low residual birefringence and a high transmission for the He-Ne laser wavelength. An alternative choice considered was one of the terbium-doped glasses. These glasses have a large Verdet constant of the order of 0.2 min/gauss-cm. We decided against using one of these glasses, because 1) they are very costly and, 2) their Verdet constants vary with temperature since the glasses are paramagnetic. While the diamagnetic glasses such as SF-58 have lower Verdet constants, the values of these constants are approximately constant, independent of temperature variations. As the current required to produce a rotation of 180°, iπ is ~ 105 A for SF-58, the number of cycles of Faraday rotation at the expected peak currents of 2-to 4 MA will be 20 or more. Thus a larger value of Verdet constant, while useful for reducing the relative error, was really not needed for this application.
The closed light path within the rotative medium was realized by multiple total internal reflection (TIR) within the rotative medium. As is well known, a TIR introduces a phase shift between the components of polarization parallel and perpendicular to the plane of incidence. Hence, if the incident light is plane-polarized, the reflected light becomes elliptically polarized. This ellipticity would lead to a Faraday signal in which the amplitude as well as the phase varied with time unlike the simple expression, eq (8). The numerical inversion of the Faraday signal would thus be more complicated and the effects of noise more severe.
A very simple solution to this problem has been found by Kard [6]. He showed that a quarter-wave coating (corrected for angle of incidence) on the TIR interface whose refractive index was the geometric mean of that of the substrate and the external medium (usually air or vacuum) would compensate the phase shift and the reflected light would remain plane polarized if the incident light was polarized. This solution is applicable only to cases for which the angle of incidence on the interface is less than the critical angle, i.e., some of the light must enter the coating and be totally reflected from the coating-vacuum interface. For the SF-58 glass of refractive index 1.907, a magnesium fluoride coating of refractive index 1.38 is almost a perfect match and is a very satisfactory material for making a durable optical coating of very precisely controlled thickness. The critical angle of the coating-substrate interface is arcsin (1.38)−1 or 46.4°. Thus a coat of MgF2 will effectively compensate the ellipticity for TIR at an angle of incidence of 45°. We have tested such coatings and found that a very good null of the reflected light can be obtained with an analyzer for any arbitrary azimuth of the incident polarization.
Another fundamental problem in the design of a closed-optical-path Faraday rotator is that of mirror reversion. As is well known, the rotation sense of light reflected in a mirror is changed. Thus a magnetic field in the same direction will produce rotation in the opposite sense after mirror reflection. Indeed it was just this property that enabled Faraday to discover the very small effect that bears his name with the relatively feeble magnetic fields available to him in 1845. The sense of the rotation of the plane of polarization induced by a magnetic field changes sign when the relative direction of the field and the light propagation is changed. Thus if the light after traversing the rotative medium is reflected from .a mirror back along the field direction, the change of sense of rotation due to mirror reversion is compensated by the reversed sense of the Faraday effect and the two rotations add rather than cancel as happens in the case of ordinary optical activity. Thus Faraday was able to amplify the effect by multiple passes between mirrors and obtain a measurable rotation with a field of only several hundred gauss.
In our probe, however, the relative direction of the field and the light propagation remains unchanged, Thus if we number the segments of the light path between reflections in order, we can write for the total rotation
| (10) |
Hence, in order to realize the Faraday rotation appropriate to the current linking the light path, it is necessary to design the probe so that the even-numbered segments of the light path are as short as possible and oriented as nearly as possible normal to the magnetic field direction. The contribution of the second integral in eq (10) can then be neglected.
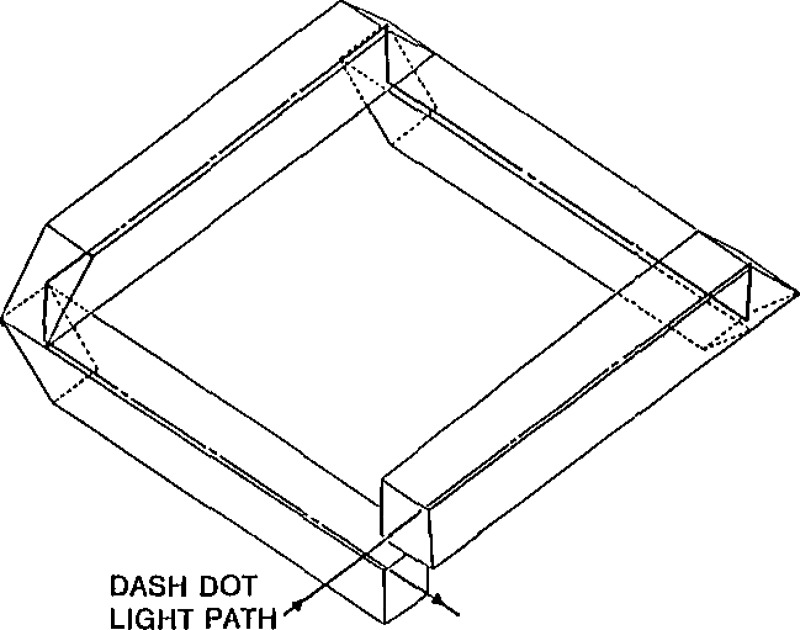
Figure 1 is an isometric projection of the Faraday rotation probe design that meets these requirements. It consists of four rectangular parallelepipeds of SF-58 glass; two of which have surfaces at each end at 45° to the direction of the edges, and two have 90° faces at one end and 45° inclined faces at the opposite end. The latter pieces form the initial and final segments of the optical path, the 90° faces being the entrance and exit windows. The four pieces are cemented or clamped together as shown. The odd-numbered segments form a closed path in the form of a square when projected into a common plane. The even-numbered segments are the short segments normal to the plane of the ring between successive 45° faces. These segments are much shorter than the odd-numbered segments forming the projected closed square. Furthermore, if the path of the current is rigorously perpendicular to the plane of the ring, the magnetic field will be normal to the short even-numbered segments, and the contribution of the second integral in eq (10) will be zero.
Figure 1 –
Optical path of Faraday effect current probe.
When dealing with rapidly varying currents, the contribution of the even-numbered segments can also be reduced to zero by enclosing the ring in a conducting shell with an equatorial slit insulated against the voltage developed by the flow of skin currents in the shell. Provided this insulation requirement can be met and the skin depth of surface currents is less than the shell thickness, only equatorial components of magnetic field can penetrate the shell, and the condition of zero contribution of the even-numbered segments can be maintained for any orientation of the plane of the ring. The situation is quite similar to that encountered in the use of a Rogowski coil; an error in the current measurement results from the inclination of the plane of an unshielded Rogowski coil with respect to the current. This error can likewise be eliminated by shielding the coil by a conducting shell with an equatorial slit.
The 45° inclined faces are all coated with quarter-wave MgF2 coatings to compensate for the ellipticity induced by total internal reflection. It is noted that these coatings are unnecessary if there is no Faraday rotation in the short sections as would be the case of a shielded rotator. The double reflections interchange the perpendicular and parallel components so that the phase shift is compensated provided no rotation occurs between reflections. This is a well-known property of an Abbé prism formed by two 45° faces whose azimuthal directions differ by 90°.
Figure 2, the assembled probe, shows the glass ring, the conducting shield, the Banning type polarizers, and the lenses for coupling the input and output beams into optical fibers. The entire cavity can be pressurized with SF6 for insulation in high voltage applications.
Figure 2 –
Drawing of assembled probe showing the glass rotator, input and output lenses and polarizers and positioners for input and output fibers.
Optical fibers bring the light from the He-Ne source to the ring and return the Faraday rotation signal to the detector, both of which can be located in a screened room remote from the high current being measured. Note that since the ring is placed between crossed polarizers, residual birefringence in the fibers and Faraday effect in the fibers due to stray fields do not affect the measurement. The optical fibers thus function solely as a convenient means for conveying the light to and from the ring.
3. Experimental Results
The Faraday probe was tested by use of the discharge of a capacitor bank through a straight conductor, the shield furnishing a coaxial return circuit. The bank, which consists of 15 2.25 μF capacitors in parallel, is connected to the current probe through a parallel plate transmission line with a shorting bar linking the rotator ring. The bank could be charged to 40 kV maximum.
The discharge current waveform of such a circuit is a damped sine wave. We obtain this waveform by integrating the voltage signal from a small magnetic pickup coil located in a hole in one plate of the transmission line close to the thin mylar dielectric layer that separates the two plates of the transmission line. Unfortunately this coil was inaccessible and the area and number of turns are not known so the absolute value of current could not be measured directly. We can obtain a relatively crude estimate of this value, however, by measuring the period and logarithmic decrement of the waveform. Knowing the value of capacitance C, and the charging voltage, V0, of the bank, we can compute the total inductance L =0.0523 μH and the circuit resistance R = 17 mΩ. From the elementary relationships for a simple LRC circuit
| (11a) |
| (11b) |
we can determine the peak discharge current at the first maximum for a given initial charging voltage. The accuracy of this determination is poor because of errors in the measurement of the period and especially the logarithmic decrement from the waveform.
Using the value of the Verdet constant V=0.082 min/gauss-cm at 632 Å given by the supplier of the glass we can use eq (2) to compute iπ the current increment required for a complete cycle of Faraday rotation i.e., a complete fringe. The value of iπ = 1.035 × 105 amps/fringe. We can obtain the number of half cycles of Faraday rotation N plus the excess fringe fraction ΔN from the waveform of the Faraday rotation signal. If A be the normalized amplitude of the Faraday rotation signal at time t the excess fringe fraction is given by
| (12a) |
| (12b) |
taking the principal value of the arcsin function. Note that N is either an integer or one-half times an odd integer and that ΔN varies from zero to one-half.
The corresponding current at time t is then just
| (13) |
The above treatment is valid provided the current has not reached an extremum prior to t. An extremum is characterized by the failure of the Faraday rotation signal to complete a cycle, i.e., the signal reaches an extremum at an intermediate amplitude and by a marked reduction in frequency. Following such an extremum, the number of half-cycles N2 following the extremum should be subtracted from the number of half-cycles N1, prior to the extremum to obtain
| (14) |
or generalizing to several extrema
| (15) |
The sign of the excess fractional fringe ΔN is taken positive for an even number of extrema and negative for an odd number. Note that the excess fractional fringe immediately before and after an extremum just cancel each other.
We can thus calculate the fringe number to the first current maximum at various charging voltages and the value of current at the first maximum using the value of iπ given above. These are compared in table 1 with those using eq (11) and the bank parameters. As one might expect the agreement is rather poor due mainly to the inaccuracy of the current determination from the oscillogram using eq (11) as mentioned before. What is more significant is the value of the current per fringe obtained by dividing the calculated current by the fringe number. The resulting values differ by less than 2%. Furthermore, if only the last three values are considered, the deviation from the mean is less than 1%. This might be expected from eq (9) since only the excess fraction depends upon the amplitude of the Faraday rotation signal and this makes an increasingly small contribution to the total current as the number of half fringes increases.
Table 1.
| Bank Voltage | No. of Faraday Fringes to First Current Maximum | Maximum Current Calculated from Circuit Parameters | Maximum Current from Faraday Effect Nx1.035×105 | Current per Fringe, Iπ Using Calculated Current kA |
|---|---|---|---|---|
| KV | N | kA | kA | kA |
| 15 | 3.41 | 322 | 353 | 94.4 |
| 20 | 4.63 | 429 | 479 | 92.7 |
| 25 | 5.83 | 537 | 603 | 92.1 |
| 30 | 7.00 | 644 | 667 | 92.0 |
Figures 3, 4, and 5 respectively show the Faraday rotation signal for a charging voltage of 20 kV, the corresponding magnetic pickup coil signal after integration, and the waveform obtained by numerical inversion of the Faraday signal. This latter waveform is virtually identical to that of the integrated magnetic pick-up coil signal.
Figure 3 –
Faraday rotation signal.
Figure 4 –
Bank discharge waveform corresponding to Faraday rotation signal in figure 3 obtained with a magnetic pickup coil and integrated.
Figure 5 –
Numerical inversion of Faraday signal in figure 3.
4. Conclusions
We have designed, constructed, and tested a current probe based upon the Faraday rotation angle of polarized light produced by propagation of the light along a light path encircling the current to be measured. Such a probe is an absolute instrument whose calibration depends upon the Verdet constant of the rotative medium independent of the dimensions or position of the light path.
The claim for an absolute instrument is not based upon our rather limited experimental work. This work had to be curtailed because of a lack of funding and really constitutes only a proof of principle. This claim rests upon the elimination of positional and geometric factors in the calibration of the probe and the fact that the Verdet constant of a diamagnetic medium depends only upon the dispersion curve of the medium and is not affected appreciably by mechanical or temperature effects [8].
It is true that the subtractive contribution of the even-ordered light path segments does complicate the claim of insensitivity to positional and geometric factors. Our design of the probe addresses this question by 1) ensuring that the odd-ordered segments alone make up the complete circuital path, 2) making the even-ordered segments as short as possible and orienting them as nearly as possible normal to the magnetic field direction, and 3) using a suitable conducting shell to shield out the poloidal magnetic field components which alone can contribute to the line integral of the field along these even-ordered segments.
As mentioned before, we rejected the use of the rare-earth doped glasses for use in the probe even though their Verdet constants are three times those of the diamagnetic glasses employed. This was on account of the temperature dependence of their Verdet constants.
This probe is intended for measurement of very fast transient currents in the mega-ampere range for which it is well suited. For slower varying currents of smaller magnitude, this type of probe can still be used by increasing the number of circuital paths either by multiple light transits or the use of multi-turn optical fibers [2,3]. Since the time resolution is limited to the light transit time between polarizers, the increase in current sensitivity is realized at the price of a longer resolution time.
Acknowledgments
We wish to acknowledge John Shannon, Mark Wilkinson, and Norman Rostoker of Maxwell Laboratories, Inc., for their many valuable discussions; Leslie Vargady of Metrooptics Company, Glendora, CA, for the skillful and dedicated design and fabrication of the rotator ring; Lawrence Houghton and David Lischer of Maxwell for their devoted assistance with the experimental work; and Clifford Fowler, also of Maxwell, for developing the algorithm for the numerical inversion of the Faraday signal.
Biography
About the Authors, Paper: While W. Caton remains associated with Maxwell Laboratories, J. Katzenstein is now with the University of California at Irvine. The work on which they report, performed while both were at Maxwell, was carried out for the Defense Nuclear Agency, U.S. Department of Defense, under contract DNA001-79-C-0019.
Footnotes
Figures in brackets indicate literature references at the end of this paper.
Presently single mode optical fibers have been produced with different propagation velocities for right- and left-hand polarized light. [9] Since these two modes of propagation have different phase velocities, there is no intermixing of the modes due to fiber imperfections and the relative phase of the two circular modes of propagation is preserved. If such fibers could be made with cores of high Verdet constant glass which should in principle pose no difficulty, then a Faraday rotation current probe making use of only a few turns could be produced with a concomitant low transit time and short time resolution.
References
- [1].Hebner R. E.; Malewski R. A. and Cassidy E. C., Proc. IEEE 65, part 2, p. 1524 (1977). [Google Scholar]
- [2].Massey O. A.; Erickson D. C. and Kadlec R. A., Applied Optics 14, 2712 (1975). [DOI] [PubMed] [Google Scholar]
- [3].Smith A. M. Applied Optics 17, 52 (1978). [DOI] [PubMed] [Google Scholar]
- [4].Papp A. and Harms H., Applied Optics 19, 3729 (1980). [DOI] [PubMed] [Google Scholar]
- [5].Aulich H.; Beck W., Douklias N., Harms H., Papp A, and Schneider H., Applied Optics 19, 3735 (1980). [DOI] [PubMed] [Google Scholar]
- [6].Harms H., and Papp A., Applied Optics 19, 3741 (1980). [DOI] [PubMed] [Google Scholar]
- [7].Kard P. G. Optics and Spectroscopy 6, 339 (1959). [Google Scholar]
- [8].Becker R. Theorie der Elektrizitat, Vol. II, p. 142–150, [Google Scholar]; Teubner B. G., Leipzig and Berlin 1933. [Google Scholar]
- [9].Barlow A. J.; Ramskov-Hansen J. J. and Payne D. N., Applied Optics 20, 2962 (1981). [DOI] [PubMed] [Google Scholar]