Nuclear Orientation Thermometry

Abstract

Low temperature nuclear orientation thermometry, in particular γ-ray anisotropy thermometry, is discussed both from a theoretical and practical point of view. Detailed information is given on the most often used γ-ray anisotropy thermometers, along with a comprehensive description of the γ-ray anisotropy technique. The ⁶⁰Co in (hcp) cobalt single crystal γ-ray anisotropy thermometer is discussed in considerable detail since it is used more frequently in comparison experiments with other primary thermometers. Recent experimental results using γ-ray anisotropy thermometers are also reviewed.

1. Introduction

One of the fundamental problems recurring in Low temperature physics is the accurate determination of the temperature of the sample. Fortunately the nuclear orientation (NO) technique offers us one of the most direct and accurate means of measuring temperatures below 1 K. In the NO method, which is essentially a measurement of the degree of ordering of a nuclear spin system in thermodynamic equilibrium, the temperature is derived from the Boltzmann factor and, in principle, is absolute (thermodynamic). Thus a measurement of the anisotropic emission of γ-rays or β- or α-particles from an assembly of oriented radioactive nuclei has the same potential of yielding the absolute temperature as does the scattering or absorption of photons or particles by an oriented nuclear target. An obvious restriction is, of course, that the nuclei must have a nonvanishing spin. In addition, it should be kept in mind that the temperature obtained with a NO thermometer is that of the nuclear spin system and not that of the lattice. If the lattice temperature is to be measured, then the spin-lattice relaxation time must be relatively short.

Most of the work in NO thermometry has been done using γ-ray anisotropy (γ-RA) thermometers. In addition to being primary thermometers, these types of NO thermometers have many advantages over conventional thermometers: they are usually physically small and metallic, and thus can be easily attached (soldered) to the experimental package with good thermal contact; for some the self-heating due to the radioactivity is quite small (~ 0.02 erg/min); no wires are attached to it; the readout is digital, and the (counting) equipment needed can be relatively inexpensive. Moreover, some can operate in zero magnetic field as well as in a magnetic field. Although γ-RA thermometers have been used in many different types of low temperature experiments, e.g., studies of nuclear properties (spins, moments, multipolarities, etc.), calibration of secondary thermometers (paramagnetic salts, resistance thermometers, etc.) and development of a low temperature scale, and, have been the subject of several reviews [1–3]¹, their use is still not as extensive as it could be. This perhaps stems from the nonuser’s having to learn a new technique foreign to his own Field of research. One of the objectives here is to provide sufficient information to those unfamiliar with this technique so that they too can use it. Thus, details are given which would normally not be given.

A general discussion of NO thermometry is given in the next section, thereafter we will deal almost entirely with γ-RA thermometry. In section 2 the theory of γ-RA thermometry is given along with some general remarks. This is followed by a discussion of practical γ-RA thermometry which is divided into two sections, section 3 dealing with the general problem, and section 4, with specific γ-RA thermometers. Section 5 contains recent experimental results. The conclusions are included in the last section.

2. Theory of Nuclear Orientation Thermometry

2.1. Basic Concepts

The degree of orientation of an ensemble of nuclei of spin I can be specified in various ways. The most general description is given in terms of a spin-density matrix ρ with (2I+1)² matrix elements. For an ensemble of nuclear spins with cylindrical symmetry the description is considerably simplified. In this case the symmetry axis is the axis of quantization of the nuclear spin system and ρ is a diagonal matrix with (2I+1) matrix elements. These diagonal matrix elements, ρ_mm, are just the relative populations, a_m, of the nuclear spin substates m(m = I, I −1, …, −I). Since it is convenient to normalize the populations a_m such that Σa_m= 1, we are left with only 2I independent values of a_m.

In the theoretical interpretation of the nuclear process studied, it is usually more convenient to work with the [(2I+l)²−l] independent quantities, $B_{\lambda }^q(I)$, called statistical tensors, which are defined in terms of the density matrix. For a spin ensemble with cylindrical symmetry the number of statistical tensors, or orientation parameters, is reduced to 2I, The explicit expression for these orientation parameters is given by

$$\begin{gathered} B_{\lambda }(I)={\left(2I+1\right)}^{1/2}{\rho }_0^{\lambda }(I)=\sum _{m=-I}^I{(-1)}^{I-m}{[(2\lambda +1)(2I+1)]}^{1/2} \\ \left(\begin{array}{ccc}I& I& \lambda \\ m& -m& 0\end{array}\right)a_m \end{gathered}$$ (1)

where a_m and m have already been defined and λ goes from 0 to 2I, with B₀(I) = 1. A system of nuclear spins is said to be aligned if all the B_λ values with λ odd are zero. If at least one value for λ odd is not zero, then the spin system is said to be polarized.

Although there are different methods for producing ensembles of oriented nuclear spins (i.e., changing the populations of the m-states), here we will only be concerned with those methods where the spin ensemble is in thermodynamic equilibrium. In this case, the populations are governed by the Boltzmann distribution and are given by

$$a_m=\frac{e^{-E_m/kT}}{\sum _m{e}^{-E_m/kT}}$$ (2)

where E_m are the energies of the nuclear m-states, k the Boltzmann constant and T the absolute temperature. At temperatures T≫E_m/k the populations are essentially equal and are given by (2I+1)⁻¹ (only at T= ∞ are the populations exactly equal). For temperatures T≲E_m/k the populations are unequal, resulting in nuclear orientation. The lower the temperature, the greater is the degree of nuclear orientation. In figure 1 we show some population distributions for a nuclear spin system with I=3 and E_m/k =(0.013 K)_m, which are the values for the ⁵⁴MnNi, -γ-RA thermometer. The first three, (a), (b), and (c) are Boltzmann distributions at temperatures of 1.0, 0.1, and 0.02 K respectively. As one can see, there are hardly any differences between the populations at 1.0 K, the ratio of the populations for the lowest and highest m-states being 1.07. At 0.1 and 0.02 K the distributions are skewed to favor the lower states with the ratios now being approximately 2 and 50 respectively. In the distribution shown in (d), the Boltzmann distribution (c) was perturbed so that the lowest two m-states were equally populated, thus yielding a non-Boltzmann distribution. For all four distributions, values of B_λ(I) can be calculated; however, only the first three can be associated with meaningful values of the absolute temperature. We will designate these, i.e., nuclear orientation parameters for a system of nuclear spins in thermodynamic equilibrium by B_λ(I,T) rather than by B_λ(I). If the perturbation is turned off in (d) and the spins can relax (by interacting among themselves or with their environment, e.g., the lattice) so that thermal equilibrium is achieved, then the populations will again by governed by a Boltzmann distribution reflecting this new equilibrium temperature.

Figure 1.

Thus, we see that the entire theoretical basis for NO thermometry is contained in eqs (1) and (2): one determines the value of any nonzero B_λ(I,T) for a nuclear spin system in thermodynamic equilibrium where E_m is known, and from this a unique value of the absolute temperature is obtained. How well one can determine the value of the temperature depends upon the accuracy with which one knows E_m and how accurately B_λ(I,T) can be measured. The latter will contain all the statistical and almost all the systematic errors of the measurement. As we shall see later on, a complete understanding of all the systematic errors associated with deducing a temperature from an ensemble of oriented nuclear spins is nontrivial and will cause us the greatest concern about how well one can measure the absolute temperature.

In figure 2 we show the six B_λ(I,T) plotted as a function of temperature for the nuclear spin system that was used in calculating the populations for (a), (b), and (c) of figure 1, namely, I=3 and E_m/k= (0.013 K)m. AS one can see each B_λ(I,T) is a single-valued function of the temperature.

Figure 2.

It is often the case that the measurement made on an ensemble of nuclear spins will depend upon more than one B_λ(I,T) value; however, as we mentioned previously, once E_m is known, any one of the nonzero B_λ(I,T) will yield the temperature. Once the temperature is known, all the other B_λ(I,T) are uniquely determined. This follows directly from eq (2), i.e., once E_m and T are known, all of the a_m can be calculated and hence each B_λ(I,T). Thus, we see that the condition that the populations be governed by the Boltzmann distribution is very restrictive. Whereas in the general case of an ensemble of oriented nuclear spins with cylindrical symmetry the a_m were independent (except for normalization), now they are dependent such that if any one a_m is known along with E_m, then the remaining a_m can be obtained. For the general case above where we do not have a Boltzmann distribution, each of the B_λ(I) would have to be measured in order to obtain all the a_m.

It is important to realize that having the populations follow a Boltzmann distribution does not necessarily imply that the spin system is in thermal equilibrium. A spin system can be prepared with the a_m being the same as those given by a Boltzmann distribution; however, if there are no spin-spin or spin-lattice interactions (the latter being important for very dilute systems, e.g., γ-RA thermometers) to achieve thermal equilibrium a spin temperature cannot be defined. The most obvious example of this is a nuclear spin system with I= ½. In this case every distribution (of the two states) corresponds to a Boltzmann distribution; however, the spin system need not be in thermal equilibrium.

Although the concept of spin temperature is fundamental to NO thermometry, and leads to some interesting properties (e.g., negative temperatures) not found in other thermodynamic systems, we will not be concerned with those here since many excellent articles have been written on this subject [4–6].

2.2. Gamma Ray Anisotropy Thermometry

The normalized directional distribution of γ-radiation emitted from an axially symmetric oriented nuclear spin system is given by

$$W(\theta )=\sum _{\lambda =0}^{{\lambda }_{\max }}{B}_{\lambda }(I)U_{\lambda }{A}_{\lambda }{Q}_{\lambda }{P}_{\lambda }(\cos \theta )$$ (3)

where θ is the angle between the direction of emission of the γ-ray and the orientation axis. The quantities U_λ and A_λ, which are called angular momentum deorientation coefficients and angular distribution coefficients respectively, only depend upon the decay scheme (spins and multipole amplitudes) of the radioactive nuclei. The Legendre polynomials, P_λ(cos θ), contain all of the angular dependence of the radiation pattern. However, for a detector which subtends a finite solid angle the pattern is “smeared out” and the P_λ(cos θ) must be corrected. These corrections, called solid angle correction factors, are given by the Q_λ coefficients. Since we are only concerned with the directional distribution of the radiation and not the state of polarization, only even values of λ enter into the summation. The maximum value of λ is equal to the lesser of the two values 2I′ or 2L, with I′ being the lowest nuclear spin in the decay sequence preceding the observed γ-ray and L being the highest multipolarity of the observed γ-ray. As we mentioned in the previous section, we will only be dealing with nuclear spin ensembles that are in thermal equilibrium—thus, the nuclear orientation parameters B_λ(I) in eq (3) are replaced by B_λ(I,T).

As their name implies, the U_λ coefficients take into account the “effective” deorientation of the initial orientation (m-states) caused by all the intermediate transitions feeding the observed γ-ray. If the decay scheme is completely known, then the deorientation coefficients (which are always less than 1) can be calculated exactly. This is true as long as the lifetimes of the intermediate states are sufficiently short (<10⁻¹⁰ s) so that the nucleus cannot reorient itself before a transition takes place. If there are reorientation effects due to long-lived intermediate states then eq (3) has to be modified (by including the attenuation coefficients G_λ to take this into account. For the present, we will assume that the lifetimes of the intermediate states that we are dealing with are all short enough so that the U_λ properly account for all the deorientation of the initial orientation.

The explicit expression for U_λ between two states of spin I₁, and I₂ being linked by a transition of angular momentum L is given by

$$\begin{gathered} U_{\lambda }\left(I_1{I}_{2}L\right)={\left(-1\right)}^{I_1+I_2+L+\lambda }{\left[\left(2I_1+1\right)\left(2I_2+1\right)\right]}^{1/2} \\ \left\{\begin{array}{l}{I}_1{I}_1\lambda \hfill \\ I_2{I}_{2}L\hfill \end{array}\right\} \end{gathered}$$ (4)

In case the transition linking the two states is of mixed multipolarity with mixing ratio δ then

$$U_{\lambda }\left(I_1,I_2,L,L^{\prime }\right)=\frac{U_{\lambda }\left(I_1,I_2,L\right)+{\mathrm{\delta }}^2{U}_{\lambda }\left(I_1,I_2,L^{\prime }\right)}{1+{\mathrm{\delta }}^2}$$ (5)

where L = L′ + 1. For the case where there are several transitions in series between the initial oriented state and the γ-ray of interest, the total deorientation coefficient is simply the product of separate U_λ’s. For the case where there is more than one branch, i.e., parallel decay modes, then each mode has to be weighted by its branching fraction. In general, one starts at the initial oriented state and calculates the total deorientation coefficient by accounting for all the unobserved transitions using both the series and parallel rules where applicable.

The angular distribution coefficient A_λ is given by

$$A_{\lambda }=\frac{F_{\lambda }\left(LL{I}_2{I}_1\right)+2\mathrm{\delta }{F}_{\lambda }\left(L{L}^{\prime }{I}_2{I}_2\right)+{\mathrm{\delta }}^2{F}_{\lambda }\left(L^{\prime }{L}^{\prime }{I}_2{I}_1\right)}{1+{\mathrm{\delta }}^2}$$ (6)

where L and L′ have been defined previously, I₁ and I₂ are the spins of the initial and final states linking the observed γ-ray whose mixing ratio is δ. The F_λ coefficients are defined by

$$\begin{gathered} F_{\lambda }\left(L{L}^{\prime }{I}_2{I}_1\right)={\left(-1\right)}^{I_1+I_2+1}[(2L+1)\left(2L^{\prime }+1\right)\left(2I_1+1\right) \\ \left(2\lambda +1\right){]}^{1/2}\left(\begin{array}{ccc}L& L^{\prime }& \lambda \\ 1& -0& 0\end{array}\right)\left\{\begin{array}{lll}L\hfill & L^{\prime }\hfill & \lambda \hfill \\ I_1\hfill & I_1\hfill & I_2\hfill \end{array}\right\} \end{gathered}$$ (7)

For the case where the observed transition is a pure multipole of order L or L′, the A_λ coefficients reduce to

$$A_{\lambda }=F_{\lambda }\left(LL{I}_2{I}_1\right),\text{or}{F}_{\lambda }\left(L^{\prime }{L}^{\prime }{I}_2{I}_1\right)$$ (8)

When the multipolarity of the observed γ-ray is known (or if it is a pure transition) and if the spins of the initial and final states are also known, the A_λ coefficients can be calculated exactly.

In general, the decay schemes for the radioactive nuclei that are used in γ-RA thermometry are sufficiently well known (e.g., ⁵⁴Mn, ⁵⁷Co, ⁶⁰Co) that the uncertainties in the U_λ and A_λ coefficients are usually small when compared to some of the other errors encountered in deducing the temperature.

As mentioned earlier, the solid angle correction factors Q_λ were included in eq (3) to take into account that the detectors used to measure W(θ) are not points, but subtend Finite solid angles. One usually employs NaI(T1) and Ge(Li-drifted and intrinsic) detectors in these measurements. Fortunately, both types of detectors are available with cylindrical symmetry, which simplifies the calculation of the Q_λ. However, owing to the statistical nature of the photon energy - loss process, Monte Carlo calculations are required to obtain accurate values for the Q_λ coefficients. Results of these calculations for detectors of different sizes and for different source-to-detector distances can be found in the literature [7,8]. Although these are usually given to four significant figures, it should be remembered that the calculations were done assuming ideal experimental conditions, i.e., uniformity of detector efficiency and exact detector-to-source distances. In general, NaI(T1) detectors satisfy these assumptions better then Ge detectors. For a well-defined geometry using NaI(T1) detectors, one can expect the Monte Carlo calculated Q_λ values to be accurate to about 0.1%. For Ge detectors the accuracy would be somewhat worse. It is also possible, when necessary, to experimentally determine the Q_λ values for a particular geometry and detector.

In writing the expression for W(θ) we assumed that the radioactive sample was a point source. Although in principle this is not the case, in practice it can be approximated quite well, i.e., the source can usually be made relatively small when compared to the distance to the detector.

A good discussion of the Q_λ coefficients and finite source size corrections is given by Hamilton [9].

The nuclear orientation parameters B_λ(I,T) for our ensemble of radioactive nuclei are given by combining eqs (1) and (2):

$$\begin{gathered} B_{\lambda }(I,T)={\left(\sum _m{e}^{-E_m/kT}\right)}^{-1}\sum _m{(-1)}^{I-m}[(2\lambda +1)2I+1){]}^{1/2} \\ \left(\begin{array}{ccc}I& I& \lambda \\ m& -m& 0\end{array}\right)e^{-E_m/kT} \end{gathered}$$ (9)

Once the energies E_m of the m-states are known (and, of course, I), the B_λ(I,T) can be calculated as a function of temperature. Thus, for any particular γ-ray in the decay, if all the quantities in eq (3) are known, namely U_λ, A_λ, Q_λ and θ, then usually a single measurement of W(θ) will result in a unique value of the temperature for the radioactive nuclei. For most radiations the largest changes in W(θ) as a function of temperature occur at θ=0 or π/2, thus W(0) or W(π/2) are usually measured. In figure 3 we show W(0) as a function of temperature along with some W(θ) distributions (for various temperatures) for the 835 keV γ-ray of the ⁵⁴MnNi thermometer. It is possible under certain conditions, e.g., when the λ= 2 and λ=4 terms have opposite signs, that a measurement of W(θ) at only one angle does not result in a unique value of the temperature—in which case measurements must be made at a second angle. However, for the γ-RA thermometers that we will discuss here W(θ) is a single-valued function of the temperature at either θ=0 or π/2.

Figure 3.

The energy levels E_m for the γ-RA thermometers that we will be discussing can be calculated assuming that the hyperfine interaction Hamiltonian has the form

$$\mathcal{H}=-\mathit{\mu }\cdot {\mathbf{B}}_{\text{eff}}+P[I_z^2-\frac{1}{3}I(I+1)]$$ (10)

where μ is the nuclear magnetic dipole moment, B_eff is the effective field at the nucleus, and P the quadrupole coupling constant. The first term is the magnetic hyperfine interaction. The effective field at the nucleus includes the hyperfine field, the applied field (Knight-shift corrected) and the demagnetizing field, the last depending upon both the magnetization and shape of the sample. The second term in eq (10) is the nuclear electric quadrupole interaction. For the case where both interactions are co-axial, the quadrupole coupling constant P is given by

$$P=\frac{3e^{2}qQ}{4I(2I-1)}$$ (11)

where eq is the electric field gradient and Q the electric quadrupole moment of the nucleus.

The energy levels for the above Hamiltonian are given by

$$E_m=-(\begin{array}{c}\mu \\ I\end{array}{B}_{\mathrm{eff}})m+P[m^2-\frac{1}{3}I(I+1)].$$ (12)

For those systems where only a magnetic dipole (Zeeman) interaction is present, e.g., as in the case of ⁵⁴MnNi that we discussed in the previous section, there are 2I+1 equally spaced levels (see fig. 1) separated in energy by μB_eff/I. The lowest energy level is m= +I when μB_eff is positive and −I when μB_eff is negative. When there is only a quadrupole interaction present (usually noncubic single crystals), the degeneracy of the ± m-states is not removed and we effectively only have I+1 levels for I integer and I+1/2 levels when I is half-integer. The energy separation of these levels is given by |P|(2|m|−1), where m goes from I to 1 or 3/2 depending upon whether I is integer or half-integer. The lowest energy levels are m=0 and m = ± 1/2 for integer and half-integer spins, respectively, when P is positive, and m±I when P is negative.

For the case where both interactions are present (with μB_eff/I≫P) there are 2I+1 unequally spaced levels. The ordering of the levels is still determined by the sign of μB_eff as in the Zeeman case. The energy separations are given by |μB_eff/I| +P(2m−1), where m goes from I to −(I−1). For positive P the largest separation occurs between the top two levels and decreases monotonically down to the two lowest levels, regardless of the ordering of the levels. When P is negative the relative spacing is inverted; the largest separation is now between the two lowest levels.

The most accurate means of measuring hyperfine splittings for dilute radioactive systems, e.g., γ-RA thermometers, is by nuclear resonance techniques. When the Zeeman, or Zeeman plus quadrupole, interaction is present the NMR/ON (nuclear magnetic resonance of oriented nuclei) technique can be used. In favorable cases, e.g., ⁵⁴MnNi and ⁶⁰CoCo(hcp) (by this notation we mean hcp single crystal), Zeeman splittings have been determined by NMR/ON with an uncertainty of less than 1/1000 [10]. For a system with only a quadrupole interaction, the NQR/ON (nuclear quadrupole resonance of oriented nuclei) technique would be ideally suited; however it has not yet been realized experimentally. Although it is possible to determine hyperfine splittings by other techniques, the uncertainties are usually no better than about 1/100.

The ultimate accuracy of the temperature measurements made using γ-RA thermometers not only depends upon how accurately E_m, U_λ, A_λ and Q_λ are known, and on how accurately γ-ray intensity ratios can be measured, but on how well θ is known for the entire nuclear spin system, i.e., whether or not one axis of quantization exists for all the radioactive nuclear spins. Uncertainties in θ due to incomplete magnetic saturation can be caused by insufficient applied field, shape of the sample (demagnetization correction) and strained or contaminated samples. For single crystal thermometers, in particular ⁶⁰CoCo(hcp). closure domains, crystal imperfections (mosaic substructures) and sample-detector misalignment, all affect how well θ is known. These, as well as other problems, will be discussed in the next section. In general, for most γ-RA thermometers, absolute temperature measurements can be made with an inaccuracy of ~1%. For some γ-RA thermometers the level of inaccuracy can be reduced to 0.5% [11] and perhaps (in a limited temperature range) to 0.1%.

Before proceeding to the next section, on experimental techniques, it is worthwhile to discuss two other general properties of γ-RA thermometers. The first is the useful life of a γ-ray thermometer. Assuming that a thermometer is not physically damaged, its useful life should be about 2–3 times the half-life (t_1/2) of the radioactive nucleus. Thus for thermometers using ⁵⁴Mn(t_1/2 = 312 d), their useful life is 1.7–2.6 y, for those using ⁶⁰Co(t_1/2=5.27 y) 10.5–17.6 y, and for those using ^166mHo(t_1/2= 1200 y) 2400–3600 y! A second general property is the useful temperature range of a γ-RA thermometer. Assuming that B_λ(I,T), U_λ and A_λ are known for a particular thermometer, one can then calculate its useful temperature range and its sensitivity (or response) function. In this way one γ-RA thermometer can be compared directly against another. The sensitivity function is defined to be

$$\partial W(\theta ,T)/(\partial T/T)$$ (13)

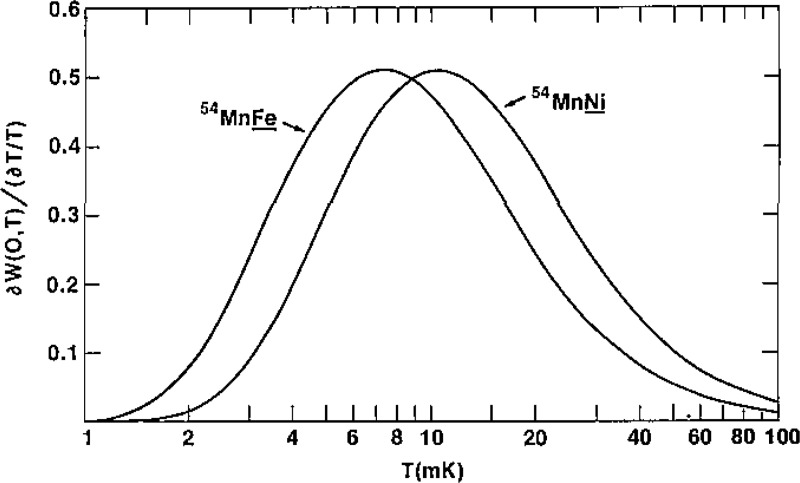
i.e., the change in W(θ,T) per fractional change in the temperature. In figure 4 we show the sensitivity functions for three different γ-RA thermometers: ⁵⁴MnNi, ⁶⁰CoCo(hcp) and ^166mHoHo(hcp). The values used for the U_λA_λ coefficients and E_m are given in the next section. For simplicity, these plots will always be given for B_app=0 and Q_λ= 1, which is clearly not the case for most γ-RA thermometer experiments. However, the effect of B_app≠0 and Q_λ≠1 on the sensitivity plots is usually quite small. In the case of the ⁵⁴MnNi thermometer there is only one sensitivity curve since there is only γ-ray (835 keV) in its decay. For ⁶⁰CoCo(hcp), which has two prominent γ-rays (1173 and 1332 keV) we still have only one curve since they both have essentially the same U_λA_λ coefficients. However, for the ^166mHoHo(hcp) thermometer, ^166mHo has a very complicated decay scheme with numerous γ-rays. In general, for each γ-ray there is a different sensitivity curve since its U_λA_λ coefficients will be different from the others. The results for two of the more intense γ-rays (712 and 810 keV) are shown in figure 4. Sensitivity curves should actually be normalized to take into account relative intensities and detector efficiencies. However, no effort was made to do this here since the latter depends both on the energy of the γ-ray and on the type of detector used. In the case of the two γ-rays shown for ^166mHo, both have about the same energy and relative intensity.

Figure 4.

As can be seen in figure 4, both the ⁵⁴MnNi and ⁶⁰CoCo(hcp) thermometers have about the same sensitivity over almost the same temperature range, with ⁵⁴MnNi shifted to slightly higher temperatures. The curves for the ^166mHoHo(hcp) thermometer are shifted to much higher temperatures since the magnetic hyperfine interaction is so much larger in this system than in the two previous ones. In addition, both the magnitude and position of the two curves for ^166mHoHo(hcp) are considerably different; the peak for the 810 keV γ-ray is at 137 mK and its magnitude is about twice that for the 712 keV γ-ray whose peak is at 300 mK. This large difference in the position and magnitudes of the peaks comes about because the contribution of the B₂(I,T) and B₄(I,T) terms (which determine the position of the peaks, see fig. 2) are considerably different for each γ-ray; the 712 keV γ-ray only has a λ = 2 term (U₄A₄≅0), whereas the 810 keV γ-ray has a small U₂A₂ coefficient compared to its U₂A₂ coefficient.

Assuming that a thermometer’s useful temperature range is given when ∂W(θ,T)≥0.05, then the ⁵⁴MnNi thermometer covers a range of 2.6 to 74 mK with its greatest sensitivity being at 10.4 mK, the ⁶⁰CoCo(hcp) thermometer covers a range of 1.3 to 50 mK with its greatest sensitivity being at 6.9 mK, and the ^166mHoHo(hcp) thermometer (using both the 712 keV and 810 keV sensitivity curves) covers a range of 32 to 1250 mK. Thus we see that by having more than one γ-ray in the decay with different U_λA_λ coefficients, the range and sensitivity of a thermometer can be extended over that for one which has (effectively) only one γ-ray present in its decay. However, if there is more than one γ-ray in the decay, other factors can degrade the usefulness of the thermometer. For decays with more than one γ-ray, the relative intensity (and detector efficiency) normalization mentioned previously must be taken into account since it determines the counting time required to obtain a certain precision. In some cases, where the radioactive heating is not a problem, the activity can be increased (to a certain extent) to compensate for using weaker γ-rays. In addition, the U_λA_λ coefficients are usually better known for simple decays like ⁵⁴Mn and ⁶⁰Co than they are for complex decays like ^166mHo.

Thus, although sensitivity curves, such as those shown in figure 4, do not “tell the whole story,” they are the starting point for deciding which γ-RA thermometer to choose for a particular experiment.

3. Practical Gamma-Ray Anisotropy Thermometry

3.1. General Considerations

In the previous sections we discussed the theoretical basis of NO thermometry, in particular γ-RA thermometry, and showed that in principle a measurement of the normalized directional intensity of a system of oriented radioactive nuclear spins can yield the absolute temperature. We now turn to the practical aspects of γ-RA thermometry and start by listing all the features that an ideal γ-RA thermometer should have. Although some effort has been made to list these in order of descending importance, it should be kept in mind that their relative importance will depend to a certain extent on their use in any one particular experiment,

1. Radioactivity easily incorporated into substitutional sites in the host lattice.

2. Hyperfine splitting suitable for the intended temperature range has been accurately measured by NMR/ON.

3. Spin-lattice relaxation time is relatively short over the entire useful range of the thermometer.

4. Single γ-ray so that a NaI(T1) can be used in most experimental situations.

5. Pure transition (e.g., E2) with the decay scheme completely known and no reorientation effects, so that the U_λA_λ can be calculated exactly.

6. Should operate both in zero magnetic field and in an applied field.

7. Atomic magnetic properties are well characterized (e.g., magnetization, Knight shift, domain structure, etc.)

8. Very little radiative heating from both the initial decay β-decay) and from the emitted γ-ray. The latter should be penetrating enough to be easily detected in most experimental situations.

9. Easily connected (e.g., with solder) to the experimental package.

In this section we will first treat the practical aspects of γ-RA thermometry in a general way, touching upon the items in the above list in some detail. The remainder of this section will include a discussion of experimental details and information on specific thermometers.

3.2. Measuring W(θ) and Determining T

The basis for γ-RA thermometry is contained in eqs (3) and (9). If we assume that all the parameters, E_m, U_λ, A_λ, Q_λ and θ, are precisely known, a measurement of W(θ)±ΔW(θ) yields T±ΔT, Since the greatest changes in W(θ) versus T usually occur at 0° or 90°, measurements are made at either angle. Assuming that the greatest change occurs at 0°, W(0) ± ΔW(0) is measured. In general, it is very difficult to solve for T explicitly because of all the exponential functions involved. Instead a “look-up” table is generated of W(0) versus T, with the latter being incremented in steps small enough so that values of W(0)+ΔW(0) and W(0)−ΔW(0) can be easily resolved. The advantage in writing a computer program to generate this table is that if there are any uncertainties in E_m, O_λ, A_λ, Q_λ or θ, a new table can be quickly generated showing their effect on the deduced temperature.

3.3. Measuring W(0)

Experimentally the quantity W(0) is determined by

$$W(0)=\frac{C_c}{C_w}$$ (14)

where C_c are the “cold” γ-ray counts obtained at a temperature T for a predetermined count time T_ct. The “warm” counts C_w are obtained for an identical time interval, but at a temperature sufficiently high that there is essentially no anisotropy. In most measurements t_ct is the order of several minutes. The quantity ΔW(0), as used above, represents the measured standard deviation of the mean of W(0). This uncertainty not only depends upon counting statistics (for the particular γ-ray involved), but also on how accurately the background counts can be determined and how stable T is during the measurement period. Assuming that T can be held constant, the counting statistics should theoretically follow a Poisson distribution. Deviations do occur, however, due to such things as gain shifts in the counting system, physical movement of the source or detector, and fluctuations in the background. If T can be held constant for a long period of time, i.e., for times much greater than t_ct, many cycles of cold (and warm) counts can be obtained and the data can be tested to see if they do fit a Poisson distribution. The assumption, too often made, that $\mathrm{\Delta }{C}_c=\sqrt{C_{{}_c}}$ is only true for a Poisson distribution.

In general, the problems associated with accurate γ-ray counting are quite extensive and often complex. The ultimate accuracy will depend upon the complexity of the spectrum, the type of detector and associated electronics used, data reduction techniques, and the experimental and environmental conditions. Since a comprehensive discussion of this subject is outside the scope of this paper, we will only touch upon the most important aspects that are relevant to γ-ray anisotropy thermometry.

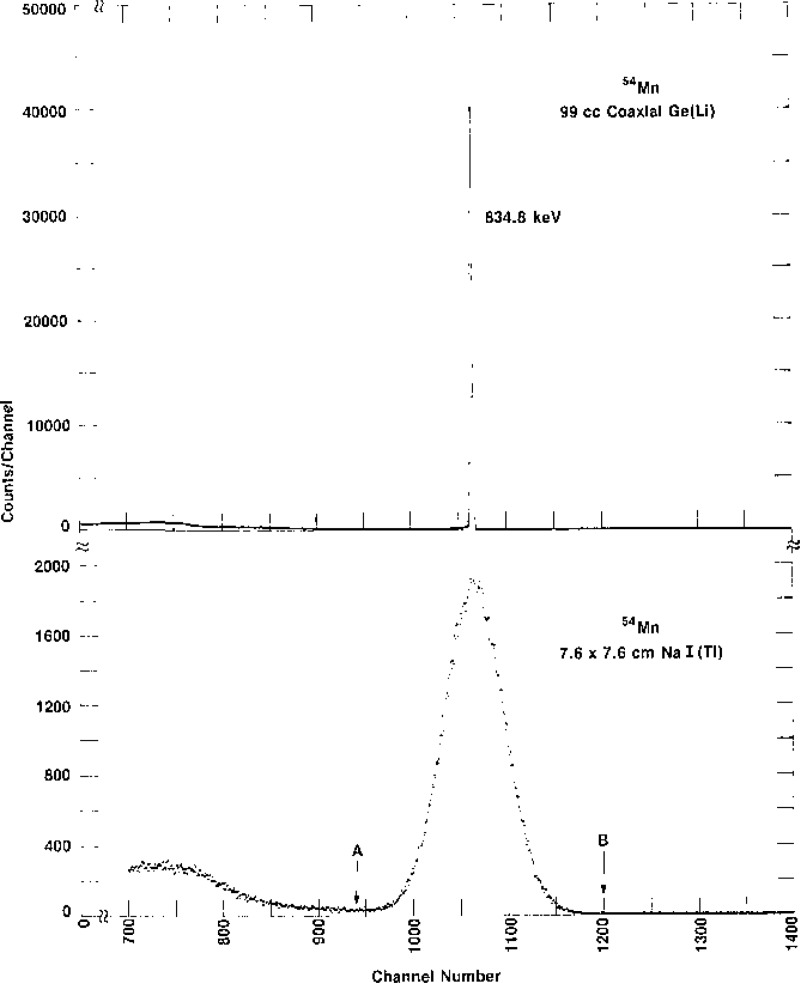
The two types of detectors most often used for γ-ray anisotropy thermometry measurements are NaI(T1) and Ge(Li). Figure 5 shows the associated electronics typically used with each detector. For simple decay schemes (e.g., ⁵⁴Mn and ⁶⁰Co) the relatively inexpensive NaI(T1) counting system shown can be used. In the case of complex spectra (e.g., ^166mHo) where good energy resolution is needed, a Ge(Li) detector must be used. Although NaI(T1) detectors have much poorer energy resolution (~100 keV for 1.33 MeV γ-rays) than Ge(Li) detectors (~2 keV for 1.33 MeV γ-rays), their higher full energy peak efficiencies enables one to obtain better counting statistics in a given geometry. For example, the full energy peak efficiency (for a 1.33 MeV γ-ray) for a 7.6×7.6 cm NaI(T1) detector at 25 cm from a source is about five times greater than a fairly large size (~100 cc) Ge(Li) detector. Typical γ-ray spectra of ⁵⁴Mn taken in clean geometry (very little scattering material near the source or detector) with NaI(T1) and Ge(Li) detectors are shown in figure 6.

Figure 5.

Figure 6.

The NaI(T1) counting system, figure 5, consists of a scintillation detector (TI doped NaI crystal plus photomultiplier), high voltage (HV) supply, preamplifier, amplifier, single channel analyzer (SCA), scalar and timer. In brief, scintillation pulses produced in the NaI(T1) crystal by the γ-rays are converted to electrical pulses (and amplified) by the photomultiplier. A charge-sensitive preamplifier presents the pulse to the linear amplifier for pulse shaping and amplification. It is then presented to the SCA, where only those pulses that lie between a predetermined lower and upper (positions A and B, fig. 6) discriminator level produce fixed output pulses to the scalar. The counting interval (clock time) is set by the timer which gates the scalar. The output of the scalar can either be recorded by hand (visual) or with a printer. This rather simple NaI(T1) counting system is capable of high statistical precision under favorable experimental conditions. The problem most often encountered with such systems is gain instability (mostly in the detector) due to fluctuations in the room (environmental) temperature. If the room temperature cannot be held constant to ≤0.5 °C, a gain stabilization system must be used. This usually consists of either a second radioactive source (single γ-ray source) or a light pulser (placed on the face of the photomultiplier) coupled to a feedback system. In addition to the gain changes caused by temperature fluctuations, large gain changes can also be caused by magnetic field fluctuations. Photomultiplier tubes are extremely sensitive to magnetic fields and should always be used with ja-metal shields. If the magnetic field changes during the measurement period, either intentionally or unintentionally (e.g., a decaying superconducting magnet), the gain of the system should be checked.

Another problem often encountered when striving for high statistical precision is counting changes due to relative displacement of the thermometer and the detector. This is very important when tight geometry (small thermometer-detector separation) is required. Rigid mounting of the detector can be achieved quite easily with a clamping arrangement using a low-Z nonmagnetic material, e.g., Al. Rigid mounting of the γ-ray thermometer is usually more difficult to achieve, and depends on the particular low temperature apparatus. Thermometer movement caused by thermal expansion and contraction of the upper parts of the cryostat due to changes in the liquid helium level can be important—especially in tight geometry situations.

After stable counting is achieved, the major problem facing the experimenter when using the NaI(T1) counting system described above is the treatment of the background counts, i.e., obtaining the actual γ-ray counts C_c and C_w, from the measured counts C_c′ and C_w′. Since this problem is better understood after the Ge(Li) counting system is described, we will postpone it until later. In some cases, depending upon the counting rate, dead-time losses will have to be compensated.

The Ge(Li) counting system (fig. 5) consists of a semiconductor detector (Li-drifted Ge crystal plus liquid nitrogen dewar), bias voltage supply, preamplifier, amplifier, analog-to-digital converter (ADC), and a computer based multichannel analyzer (MCA). In brief, the γ-ray deposits its energy mostly by Compton scattering in the electrons in the crystal; these in turn expend their energy in the production of electron-hole pairs which are collected (at the electrodes of the device) to form a pulse. This pulse is then presented by means of a charge-sensitive preamplifier to a linear amplifier for pulse shaping and amplification. The ADC takes the 0–10 V analog pulse and digitizes it so that it falls in one of the channels of the MCA. Depending upon the particular spectrum being investigated, 2048, 4096, or 8192 channels are usually used with a Ge(Li) detector. The counting interval can either be live time (that time when the ADC is “alive” to accept a pulse) or clock time: the former is convenient when high counting rates are encountered. Although it is possible, at least in the case of a simple spectrum, e.g., the Ge(Li) spectrum of ⁵⁴Mn in figure 6, to accept only those counts in the peak defined by a lower and upper channel on either side of the peak (as was done with the SC A), it is seldom done. Instead, a peak fitting routine is used which fits, for example, a Gaussian function to the peak along with an analytical (linear, quadratic, cubic, etc.) function to the background. By using a computer based MCA the fitting can be done on-line. The output, usually in the form of peak position, peak counts, background counts and other useful information, can be recorded with a printer. If further analysis is warranted, e.g., a more complicated peak fitting routine than can be handled by the computer of the MCA, the spectrum can be recorded on magnetic tape or disk.

In figure 7 we show part of a 4096 channel spectrum of ^166mHo taken with a Ge(Li) system similar to that shown in figure 5. The data are from an actual warm run (4.2 K) of the ^166mHoHo(hcp) single crystal thermometer [12]. The large Compton background, due to scattering in the Ge(Li) crystal as well as from the components of the cryostat, is quite evident.

Figure 7.

In contrast to the situation with the NaI(T1) system, gain instability in the Ge(Li) system due to room temperature fluctuations is quite small. Using relatively high quality electronic components, and good room temperature regulation (±1 °C), gain stability of 1 part in 10⁴/24 h can be achieved. When possible, a pulser should be included in the Ge(Li) system; this can be used to monitor the gain and aid in making pile-up corrections when necessary. Since Ge(Li) detectors do not use photomultiplier tubes, the large gain shifts seen with NaI(T1) detectors, due to magnetic field changes, are not present; however, magnetic fields do affect Ge(Li) detectors. Although some work has been reported by Ganner and Rauch [13] on the effect of magnetic fields on Ge(Li) detectors, the detector used was quite small (~2 cc). No recent systematic study has been reported using a larger detector. Evidence [14] indicates that for low fields (≾0.01 T) there seems to be little, if any, effect, whereas for high fields (≿0.1 T), some detectors lose resolution or cease to operate. The mechanism thought to be responsible for this behavior is the Penning Effect (principle of the Philips cold-cathode ionization gauge). If it is known beforehand that a Ge(Li) detector must be operated in a high field, this can be put in the specifications to the manufacturer, since certain precautions can be taken to minimize this effect.

The problem of physical movement of the thermometer or the detector, mentioned previously, is usually quite important when using a Ge(Li) detector, as tight geometry is often required. The problem of background subtraction is fairly straightforward with the Ge(Li) system described above. Assuming that stable counting has been achieved, the ultimate accuracy in determining C_c and C_w will depend upon the particular spectrum being viewed and its treatment (peak fitting routine, pile-up correction, summing correction, etc.). An excellent review of γ-ray intensity (and energy) measurements using Ge(Li) detectors has been given by Helmer and coworkers [15]. It is important to remember that absolute γ-ray intensity measurements are not required to obtain accurate values of W(0) since the latter is determined by the ratio of C_c to C_w. For this same reason, errors made in underestimating or overestimating the size of the background, if made consistently, tend to be diminished, In conclusion, whereas absolute γ-ray intensity measurements with an inaccuracy of 0.1% are very rare, W(0) measurements of 0.1 % are not.

In the case of the NaI(T1) system, background subtraction is not as straightforward, nor as accurate, as it is in the Ge(Li) system. By counting all the pulses between the lower level discriminator (LLD) and the upper level discriminator (ULD) of the SCA (i.e., positions A and B in fig. 6) all the background pulses are also included. These, of course, must be subtracted out to get the actual counts. Rewriting eq (14) to include the background counts explicitly

$$W(0)=\frac{C_c}{C_w}=\frac{C_c^{\prime }-B_c}{C_w^{\prime }-B_w}$$ (15)

where C_c, C_w, $C_c^{\prime }$ and $C_w^{\prime }$ have been defined previously, and B_c and B_w are the cold and warm background counts respectively. The NaI(T1) spectrum shown in figure 6 is not a good example of the problem at hand because it is not from an actual low temperature experiment (it is a clean geometry spectrum), A more realistic view of the background problem is shown in figure 8. These data (4.2 K) are from an experiment by Soulen and Marshak [11] using the ⁶⁰CoCo(hcp) thermometer. For ⁶⁰Co the LLD is usually set at A to include both γ-rays since they essentially have the same anisotropy, (For Nal systems with very good gain stability the LLD can be set at A′ to count only the higher energy peak and thus reduce the Compton background; however, the counting rate is then reduced by about a factor of two.) As can be seen in this figure the background contribution is significant: not only must the Compton background be subtracted out, but the environmental background, see figure 8 (taken for an identical counting time with the source removed), must also be subtracted. Thus, we have

$$B_c=B_{cc}+B_e\text{and}{B}_w=B_{wc}+B_e$$ (16)

where B_cc and B_wc are the Compton background counts cold and warm respectively, and B_e is the environmental background count, which is the same whether the sample is cold or warm. The environmental background, although it can be determined quite easily, is particularly important if a peak in the background accidently falls under or near a peak in the thermometer source as it does for ⁶⁰Co (the small peak to the right of the ULD, B in fig. 8, is due to the 1460 keV γ-ray of ⁴⁰K which is found in the concrete walls and floors of the laboratory). In order to determine the Compton background under the peaks, spectrum fitting techniques specifically developed for NaI(T1) detectors (see e.g., [16]) have to be used. However, in order to use these, the SCA in the NaI(T1) system shown in figure 5 must be replaced with a MCA to obtain the spectrum. In this way fairly accurate (~0.1%) values of W(0) can be obtained using NaI(T1).

Figure 8.

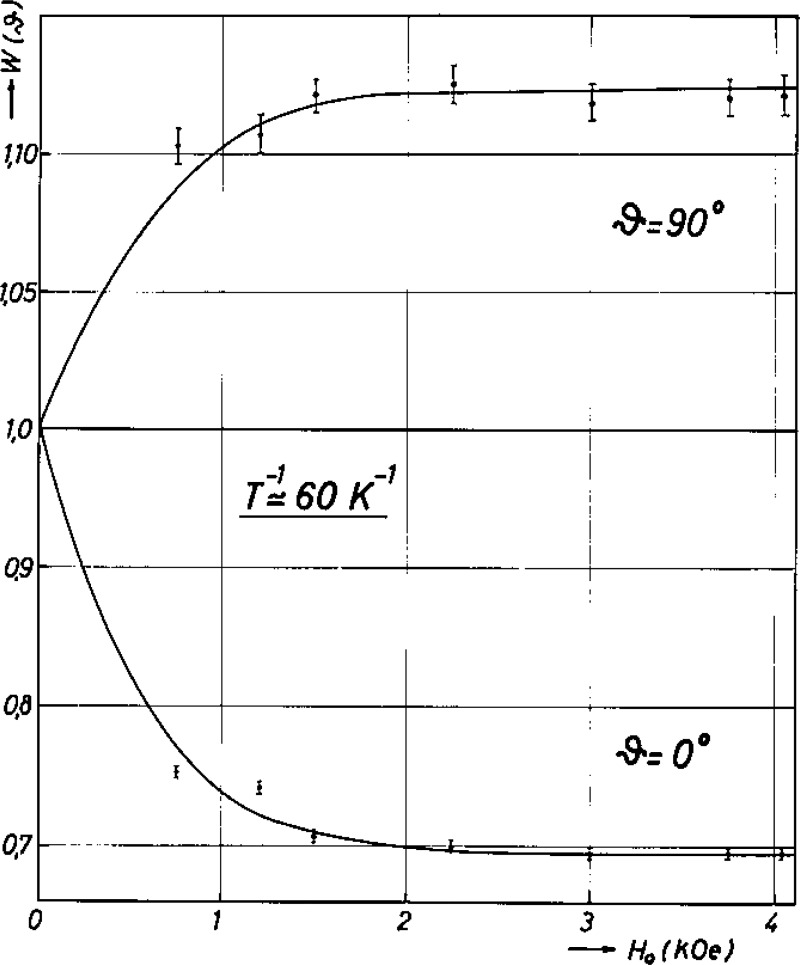
It is also possible to experimentally correct for the Compton background when using a NaI(T1) system if a Ge(Li) system is available (even for a short time). Measurements can be made with both detectors simultaneously, one set at 0° and the other at 180°. Since both detectors have different solid angle factors, this correction is usually generated in terms of temperature rather than W(0). That is, from the measured values of W(0) for each system, W(0)_Ge and W(0)_Na, temperatures, T_Ge and T_Na, are obtained with T_Na being in error because the Compton background was ignored. If the environmental background was also ignored, T_Na would reflect this as well. This background temperature correction (Compton, or Compton plus environmental), ΔT_B(=T_Na–T_Ge), can be generated as a function of temperature and used for subsequent measurements with the NaI(T1) system as long as the overall experimental geometry and source strength remains the same. The effect of ignoring the background when using a NaI(T1) system always results in the deduced temperature being higher than the actual temperature, i.e., ΔT_B is always positive. The magnitude of this correction depends upon each particular experimental setup (i.e., the type of source, source strength, source-to-detector distance and the environmental background) and can be quite large. This technique of using a Ge(Li) detector set at 180° to the NaI(T1) detector to correct for the Compton background was actually carried out for the data shown in figure 8. The 180° Ge(Li) spectrum is shown in figure 9. In this particular experiment the background temperature correction for the NaI(T1) system was about 0.8%.

Figure 9.

One final correction which may have to be made to C_c′ and C_w′ is that which is due to the decay of the thermometer source. This correction, called the lifetime correction, can be made quite easily and can be important, depending upon the times involved in the measurements and the half-life of the radioactive nucleus involved.

In summary, with some effort and reasonably good equipment, measurements of W(0) can be made with an inaccuracy of 0.1%.

3.4. Determining T

As we have mentioned previously, if all of the parameters in eqs (3) and (9) are precisely known, then T±ΔT can be easily obtained from the measured value of W(0)±ΔW(0). In this ideal case the uncertainty in T will, of course, only depend upon the uncertainty in W(0). Unfortunately, as we alluded to in section 2.2, even for the most favorable γ-RA thermometers, e.g., ⁵⁴MnNi. and ⁶⁰CoCo(hcp). uncertainties exist in some of the parameters which also contribute to the uncertainty in T. The effect of any uncertainties in U_λ and A_λ, along with the uncertainty in Q_λ can be easily included in ΔT. Uncertainties in E_m, and in particular θ are more difficult to characterize because they depend upon many things. In the case of E_m even when a very precise NMR/ON measurement of the hyperfine has been made, its value is given for zero applied field, which is seldom the case in γ-RA thermometry. The quantity needed, see eq (10), is the effective field at the nucleus. In a ferromagnetic domain, B_eff is given by

$${\mathbf{B}}_{\text{eff}}={\mathbf{B}}_{\text{hf}}+{\mathbf{B}}_{\text{app}}(1+K)-\mathcal{D}\mathbf{M}$$ (17)

where B_hf is the hyperfine field (which includes the Lorentz field, (4/3)πM, plus the field arising from dipoles in the Lorentz cavity), B_app is the applied field, K is the Knight shift, $\mathcal{D}$is the demagnetizing factor (which depends upon the shape of the sample) and M is the electronic magnetization. Assuming that all the fields are colinear, the energy splitting in Kelvin Δ_eff (= μB_eff/kI) is given by

$${\mathrm{\Delta }}_{\text{eff}}={\mathrm{\Delta }}_{\text{hf}}+\frac{\mu }{kI}\left[B_{\text{app}}(1+K)-\mathcal{D}M\right]$$ (18)

where Δ_hf (= μB_hf/kI) is the measured hyperfine splitting. Accurate values (determined by NMR/ON) of Δ_hf for most of the γ-RA thermometers can be found in the very useful compilation of Herzog [10]. Unfortunately, no similar compilation of ferromagnetic Knight shifts exists for γ-RA thermometers since very few have been measured. Some values have been reported in the literature, e.g., for ⁶⁰CoFe, K= 1.5(4)% [17]. In general, ferromagnetic Knight shifts are expected to be quite small (the order of a few percent or less) and can be ignored as long as B_hf≫B_app, which is usually the case.

The shape of the γ-RA thermometer is usually chosen so that the demagnetizing factor is relatively small. However, even small demagnetizing factors can substantially reduce marginal values of B_app (those just sufficient for magnetic saturation), so that magnetic saturation is no longer achieved. For example, for a rectangular foil 1.0 × 0.4 × 0.025 cm³ magnetized along the 1.0 cm dimension, $\mathcal{D}/4\pi =0.012$. If the foil were polycrystalline Fe with B_app=0.075 T, then $B_{\text{app}}-\mathcal{D}M\simeq 0.05$ T. For a similar shaped foil of cobalt single crystal magnetized along the c-axis (1.0 cm dimension) with B_app =0.1 T, then $B_{\text{app}}-\mathcal{D}M\simeq 0.08$ T. In both cases magnetic saturation would no longer be achieved. When thick foils or disks are used, the demagnetizing field can be quite large. A very useful table of demagnetization factors for rods, disks and slabs has been prepared by Jones [18]. For very anisotropic magnetic materials (e.g., Ho) the demagnetization correction is more complicated, but can still be carried out using the method developed by Osborn [19]. This has been applied to holmium (single crystal) by Wagner and coworkers [20].

The uncertainties in θ are the most difficult to evaluate and usually cause the greatest uncertainty in T, In writing eq (18) it was assumed that all the magnetic fields were colinear; however, if magnetic saturation is not achieved this is no longer true. Instead of having one axis of quantization for the entire nuclear spin system, there is a distribution of spin axes. When the distribution has axial symmetry with respect to the applied field direction, eq (3) can be modified accordingly. This has been done by Berglund and coworkers [1] and applied to polycrystalline Fe, Ni and Co. It has also been done by Shelley [21] and Marshak and coworkers [22] for polycrystalline holmium. Since incomplete magnetic saturation is often sample-dependent (i.e., the method used, purity, strains etc.), such calculations, which assume ideal magnetization properties, should be viewed with some skepticism when precise γ-RA thermometry must be done.

The problem of incomplete magnetic saturation for ⁵⁴Mn, ⁵⁷Co, ¹⁸²Ta, and ^19lmIr in Fe hosts has been investigated by Krane and coworkers [23], Their results showed that much larger fields (>5 kG) than expected (~1 kG) were needed to achieve saturation. Brewer [24] has also investigated this problem for ⁵⁴MnNi and found somewhat similar results. These will be discussed in section 5.

The problem of closure domains, e.g., for the ⁶⁰CoCo(hcp) thermometer, is similar to that of incomplete magnetic saturation, except that the mechanism is better understood. If the closure domain structure is known, its effect on W(0) can be calculated quite easily. However, by proper sample choice, its effect can be minimized or even eliminated completely. We will discuss the problem of closure domains in more detail when we discuss the ⁶⁰CoCo(hcp) thermometer in section 4.3.

The uncertainty in θ due to sample-detector misalignment can usually be kept quite small by reasonably careful experimental techniques. For very accurate γ-RA thermometry the angular distribution can always be measured to determine θ=0.

In conclusion, although the largest source of uncertainty in determining T is usually that due to the uncertainty in θ (with incomplete magnetic saturation being the major problem), some precautions can be taken to minimize it. When possible, large applied fields should be used. For the temperature region below 5 mK, two different γ-RA thermometers can be used simultaneously as a check against each other. Finally, if all the other parameters in eq (3) are known, measurements of W(0) and W(π/2) at a fixed temperature should agree with the theoretical values for magnetic saturation.

3.5. Sample (Thermometer) Preparation

One of the least discussed aspects of γ-ray anisotropy thermometry is in “obtaining” the thermometer. Unfortunately, out of the dozen or so γ-RA thermometers, only one, ⁶⁰CoCo(hcp), is available commercially. Thus the experimenter is often left to prepare the thermometer himself. Although preparation procedures for each thermometer may be different, there are some general rules which apply to most of them. We give these here, with specific details for each thermometer (when available) given in the individual discussions later on.

In all cases the procedure for incorporating the radioactivity (which is usually from ~0.1 to ~ 10 μCi/thermometer) into the host lattice is either by thermal diffusion (including remelting), nuclear reaction, or crystal growing. The goal, of course, is to put the radioactivity into substitutional sites in the lattice. One starts with as pure a host as is available—when possible 5- to 6–9’s purity. In the case of single crystals, only very high quality (minimum mosaic spread) and well defined (axis measured accurately) crystals should be used. The activity, if possible, should be carrier free. A minimum of operations should be done, since each step usually introduces some new contaminant into the sample. For example, one should always question whether an annealing step or a remelting (along with its subsequent rolling and annealing) is necessary after a high temperature diffusion. Although some of the extra steps cited in the literature may in fact be necessary, unfortunately very few systematic studies have been done, and when they have been done they are at best hidden in a thesis or an internal report. When making a thermometer it is wise to make more than one at a time—especially if the radioactivity has a fairly long half-life. Finally, the thermometers should be handled as little as possible after preparation and stored in an inert atmosphere when not being used.

3.6. Thermometer Response Time

The response time of a γ-RA thermometer depends primarily on the spin-lattice relaxation (SLR) time, τ₁, of the dilute radioactive nucleus in the host lattice, the later being at a temperature T_L. At high temperatures, T≫μB_eff/Ik, SLR times for nuclei in metals obey the familiar Korringa relation τ₁T_L=C_K, where C_K is the Korringa constant. At very low temperatures τ₁ deviates from this simple linear relationship and tends toward a constant value. This constant value is not simply the T=0 limit, viz., τ₁(lim)= 2kIC_K/μB_eff, of the full Korringa equation

$${\tau }_1=\frac{2kI{C}_K}{\mu B_{\text{eff}}}\tanh \left(\frac{\mu B_{\text{eff}}}{2kI{T}_L}\right)$$ (19)

but depends upon whether or not a spin temperature, T_S, can be defined for the system. For those systems where a T_S can be defined (either I = 1/2 systems or those with large spin-spin interactions), the low temperature limit is given by the Korringa limit above. For these systems where a T_S cannot be defined, the limiting SLR time, τ₁′(lim) is much shorter than the τ₁(lim) given above. As expected, τ₁′(lim) depends upon the initial distribution of m-states. It can be shown that the worst case, i.e., that distribution which gives the longest τ′(lim), is given by τ₁′(lim) = τ₁(lim)/2I. Thus for a γ-RA thermometer, where the spin-spin interaction is extremely weak (because of the dilution), and where I is usually greater than 1/2, its SLR time at very low temperatures is given by τ₁′(lim) rather than the Korringa limit τ₁(lim).

For ferromagnetic γ-RA thermometers (e.g., ⁶⁰CoFe) the situation is further complicated since τ₁ also increases with the applied field. A good discussion of SLR in ferromagnetic metals has been given by Turrell [25].

In general, since the counting intervals used in most γ-RA thermometry measurements are the order of several minutes, the response time of the thermometer does not seem to be limited by the SLR time of the system as most τ₁′(lim) are less than 100 s. When measurements have to be done using short counting intervals (e.g., τ₁ measurements), a thermometer should be chosen which is known to have a short τ₁′(lim). The values of τ₁′(lim) given in this section for a particular γ-ray anisotropy thermometer are those reported in the literature. In most cases these should be viewed with caution as they could be in error by as much as a factor of two—depending upon how they were measured (initial m-state population). When no value is given for τ₁′(lim), an estimate can be obtained using the Korringa constant for the system, viz., τ₁′(lim) = τ₁(lim)/2I = kC_K/μB_eff.

3.7. Radioactive Heating

There are two sources of radioactive heating that have to be considered when using a γ-RA thermometer. The first, ${\dot{Q}}_{\beta }$, is that due to the β-decay (this includes electron and positron emission, and electron capture) and can be calculated quite easily since most of the heating is in the thermometer itself, i.e., it self-heats. The second source of heating, ${\dot{Q}}_{\gamma }$, is that due to the γ-rays and is more difficult to calculate since it depends upon both the experimental configuration and materials near the thermometer, especially that on which it is mounted. Although the γ-ray heating in the sample is small for thin (<0.1 mm) foil thermometers, it can be important when more massive (e.g., a disk 1 cm in dia by 1 mm thick) thermometers are used. The self-heating in the thermometer (most of ${\dot{Q}}_{\beta }$ and perhaps some${\dot{Q}}_{\gamma }$) can be a problem if there is poor thermal contact between it and the experiment (i.e., the sample, the cold finger or the thermometer mount). Fortunately, when metallic thermometers are used they can usually be soldered quite easily, ensuring good thermal contact as long as the solder is not superconducting. The self-heating should always be calculated, especially when using high activity thermometers. In table 1 we give ${\dot{Q}}_{\beta }$-values (per μCi) for the radioactive nuclei most often used in γ-RA thermometry. As expected, the ${\dot{Q}}_{\beta }$-values for those nuclei decaying by β-particle emission (⁶⁰Co and ^166mHo) are much greater than those decaying by electron capture (⁵⁴Mn and ⁵⁷Co). Values of ${\dot{Q}}_{\beta }$ for other nuclei can easily be calculated using the “Table of Nuclear Decay Data” in NCRP Report No. 58 [16].

Table 1.

Summary of some of the more often used γ-RA thermometers. The useful temperature range of a thermometer is defined by the sensitivity function ∂W(0)/(∂T/T) ≥ 0.05. The low and high temperature limits are given by T_L and T_H, respectively. The maximum of the sensitivity function is given by T_MAX. All values for T_L, T_H, and T_MAX are for B_app = 0, Q_λ = 1. See text for further details.

γ-RA thermometer	Δhf (mK)	P/k (mK)	Eγ(keV)	Multipolarity	δ	Probability/decay	U2	U4	A2	A4	TL(mK)	TH(mK)	TMAX (mK)	${\dot{\mathit{Q}}}_{\mathit{\beta }}/\mathbf{\mu }\mathbf{Ci}$ (erg/min)
54MnFe	−9.119(14)	0	834.8	E2	-	1.00	0.828079	0.417856	−0.597615	−1.069046	1.8	51.	7.2	0.019
54MnNi	−13.112(5)	0	834.8								2.6	74.	10.4
57CoFe	−14.178(3)	0	122.1	E2/M1	+ 0.120(2)a	0.86	0.874818	0.580289	0.141692	0.010013	6.5[4.0]b	40.[76]b	16.3	0.061
			136.5	E2	-	0.11	0.874818	0.580289	−0.534523	−0.617214	2.9	90.	12.4
57CoNi	−5.922(19)	0	122.1								2.8[1.7]b	17.[32]b	6.8
			136.5								1.2	37.	5.2
60CoFe	−7.967(2)	0	1173.2	M3/E2	−0.0008(1 l)c	1.00	0.939374	0.797724	−0.446855	−0.305820	1.8	66.	9.0	0.34
			1332.5	E2	-	1.00	0.703731	0.227128	−0.597614	−1.069046	1.8	66.	9.0
60CoNi	−3.315(2)	0	1173.2								0.8	27.	3.7
			1332.5								0.8	27.	3.7
60CoCo(hcp)	−6.0725(24)	−0.0022(4)	1173.2								1.3	50.	6.9
			1332.5								1.3	50.	6.9
100mHoHo(hcp)	137.(5)	−0.6(6)	711.7	M2/E1	−0.001(3)	0.59	0.969228	0.897406	0.283(2)	0.001(3)	57.	1250.	300.	0.15
			810.3	E2/M1	−22.3(7)	0.64	0.925{2}d	0.767{2}d	0.084(3)	0.563(5)	32.	750.	137.

^aThe effect of the uncertainty in δ is given in table 2.

^bWith intensity normalization, see text.

^cThe effect of the uncertainly in δ is given in table 4.

^dThese errors should not be used in calculating U_λA_λ for thermometry. see text.

The heating due to the γ-rays, which is often ignored by the experimenter, should be calculated, as it can be quite large. Since each experimental configuration is different, no universal set of ${\dot{Q}}_{\gamma }$-values can be given. In addition, due to the nature of the photon interaction in matter, accurate values of ${\dot{Q}}_{\gamma }$ are difficult to obtain, as the Monte Carlo technique must be used. However, in most experimental situations ${\dot{Q}}_{\gamma }$-values accurate to 10–20% are all that are needed. Such accuracy is easy to obtain by making certain approximations; namely, that the material under consideration has circular geometry, the thermometer is a point source (on-axis), and only single photon interactions take place. Under these conditions the heating due to a photon of energy E_γ is given by

$${\dot{Q}}_{\gamma }\left(E_{\gamma }\right)=E_{\gamma }f\left(E_{\gamma }\right){\int }_0^{\pi /2}F(\theta )[1-e^{-\mu (E_{\gamma })t(\theta )}]\sin \theta d\theta$$ (20)

where f_γ(E_γ) is the fraction of photon energy transferred to the material as a result of the interaction, F(θ) is the photon intensity, μ(E_γ) is the total linear attenuation coefficient for the material and t(θ) is the path length through it. Since copper is often used, we give results for this material in figure 10. These curves were calculated for a 1 μCi (isotropic) source mounted on a copper disk of diameter D and thickness τ. The intensity through the disk is only 0.5 μCi. We show results only for D=1.0 and 2.0 cm, and τ = 0.1, 0.2, 0.3, 0.5, and 1.0 cm. Similar calculations can be done for other materials using NSRDS-NBS 29 [26], The assumption of single photon interaction breaks down when the path length gets too long in the medium, e.g., the mean free paths for 0.5 and 1.0 MeV photons in copper are 1.3 and 1.9 cm respectively. The reason for the increase in ${\dot{Q}}_{\gamma }\left(E_{\gamma }\right)$ at low energies is the dominance of the photoelectric cross section. As can be seen from these curves, the γ-ray heating can be quite large, even for a small disk. For example, for a 1 μCi ⁵⁴Mn thermometer mounted on a copper disk of D=1.0 cm and τ=0.5 cm, ${\dot{Q}}_{\gamma }(835\text{keV})=0.18$ erg/min, which is about a factor of ten larger than its ${\dot{Q}}_{\beta }\left(=1.9\times {10}^{-2}\text{erg}/\min \right)$.

Figure 10.

The problem of thermal equilibrium between the γ-RA thermometer and the experiment not only depends upon the radioactive heating and the thermal contact between the two, but also on the thermal conductivity of the materials used. Other aspects (e.g., heat capacities, Kapitza resistance, etc.) may also have to be considered, depending upon the complexity of the experiment. An excellent discussion of the problem of heat transfer and thermal equilibrium in the temperature region below 1 K has been given by Lounasmaa [27].

4. Specific γ-RA Thermometers

4.1. Manganese-54

Manganese-54 is perhaps the most useful nucleus for γ-RA thermometry. It has been used in ferromagnetic hosts Fe and Ni, and in nonmagnetic hosts Al, Cu, and Zn; the latter three forming Kondo systems. The main advantages in using ⁵⁴Mn lie in its very favorable decay properties and in the relative ease with which it can be incorporated into the above hosts. Its simple and well-established decay scheme is shown in figure 11. Manganese-54 $({\stackrel{.}{I}}^{\pi }=3^{+})$ has a half-life of 312 days and decays by electron capture to the 2⁺ state of ⁵⁴Cr, which emits a 834.8 keV, pure E2 γ-ray to the 0⁺ ground state. Since it decays by electron capture rather than β-particle emission, there is very little self-heating associated with this part of the decay. The 5.2 keV of energy (x-rays and Auger electrons) released during the electron capture process, produces a self-heating of 1.9 × 10⁻² erg/min for a 1 μCi source. In addition, since the 835 keV γ-rays are very penetrating, very few will lose any energy in the thermometer itself. However, some energy will be deposited in the thermometer mount, cold finger, mixing chamber, etc. depending upon the experimental configuration. This heating can be minimized by careful geometric (solid angle) design and by using low-Z material where possible. An estimate of this heating for copper can be obtained using figure 10 as explained in section 3.7.

Figure 11.

Since the electron capture is pure Gamow-Teller and the γ-transition is pure E2, exact values for U and A_λ can be calculated: these are given in table 1. In addition, the lifetime of the 2⁺ state is short enough (8.9×10⁻¹²) so that reorientation effects can be neglected. The advantage of having only one γ-ray in the decay is that the more efficient NaI(T1) detectors, with their more accurate Q_λ-values, can be used in the measurement of W(0). The only slight disadvantage in using ⁵⁴Mn for γ-RA thermometry is that lifetime corrections may have to be made to the data if counts are taken for more than 1 or 2 days, e.g., after 1 day the source will have decayed by 0.222%, after 2 days by 0.443% and so on. Thus, we see that as far as the nuclear aspects of ⁵⁴MnX thermometers are concerned, ⁵⁴Mn is almost the perfect nucleus for γ-RA thermometry.

⁵⁴MnFe

The hyperfine splitting for ⁵⁴MnFe has been measured by NMR/ON [28] with v_hf= 190.0(3) MHz. This gives Δ_hf (= h v_hf/k)=−9.119(14) mK, the sign being determined by the sign of μB_hf. The hyperfine field is −22.697 T. Since this is negative, the applied field makes the effective splitting smaller, i.e., Δ_eff< Δ_hf for B_app> 0, In figure 12 we show the sensitivity function for this thermometer. (As mentioned previously, all sensitivity plots are given for B_app=0 and Q_λ=1.) Using the criterion ∂W(0,T)/(∂T/T)≽0.05, its useful range extends from 1.8 to 51 mK with its greatest sensitivity occurring at 7.2 mK. The spin-lattice relaxation time has been measured for the ⁵⁴MnFe system [28] and τ₁′(lim)≃10 s.

Figure 12.

To prepare a ⁵⁴MnFe thermometer one starts with 5- to 6–9’s pure iron foil about 0.05 to 0.1 mm thick and carrier free ⁵⁴Mn, usually in the form of a chloride solution. After the foil is cleaned, small drops of ⁵⁴MnCl₂ are deposited uniformly on it and then dried using a heat lamp. The foil is then placed in a quartz “boat” and heated to 1100–1200 °C in a hydrogen atmosphere for 12–24 h. Next the sample is cooled down relatively slowly by turning the oven off: this is done using either a hydrogen or inert gas atmosphere. The foil is then etched to remove any surface activity. The total activity of the foil is measured and a piece is cut out of the right size and shape, depending upon the particular experiment. The thermometer is usually attached by soldering with indium or some other low melting solder.

A different procedure employed by some (e.g., [29]) is to melt the iron after it has been coated with the ⁵⁴Mn. It is then cleaned, rolled and annealed. In addition, some replace the coating process explained in the previous paragraph with electroplating on the premise of obtaining a more uniform distribution of activity on the foil.

A problem often encountered in sample preparation is evaporation of the manganese during the diffusion process.

Some typical examples of the use of the ⁵⁴MnFe thermometer can be found in [23,29,30] and the pioneering NMR/ON measurements of Templeton and Shirley [28].

⁵⁴MnNi

The ⁵⁴MnNi. thermometer, like ⁵⁴MnFe, has been used quite frequently in γ-RA thermometry. Three independent measurements of the hyperfine splitting have been made on this system by NMR/ON and are in excellent agreement. The value for v_hf is 273.2(1) MHz [31], which corresponds to Δ_hf= −13.112(5) mK. The hyperfine field is −32.56(5) T, thus B_app reduces the splitting. The sensitivity function has already been given in figure 4 and discussed in section 2.2; however, for comparison with the ⁵⁴MnFe thermometer we have included it again in figure 12. As can be seen in this figure, its useful range is shifted to higher temperatures relative to ⁵⁴MnFe (by the ratio of the hyperfine splittings, i.e., 273.2/190.0). Turrell [32] has measured SLR times for the ⁵⁴MnNi system in fields of from 0.02 to 0.8 T. His largest value for the Korringa constant (0.8 T) was 0.15 sK. This corresponds to a τ₁(lim)=22 s and a τ₁′(lim)=3.7 s (see sec. 3.6).

Preparation of the ⁵⁴MnNi thermometer is essentially the same as that for the ⁵⁴MnFe thermometer. The exact procedure followed by the Bonn NO Group [33] is to deposit carrier-free ⁵⁴MnCl₂ on a piece of 25 μm thick nickel foil (99.99+% purity), and dry it slowly with a heat lamp. The foil is placed in an Al₂O₃ “boat” and heated to 900 °C in a hydrogen atmosphere for at least 24 h. It is slowly (~15 h) cooled to room temperature. The thermometer is attached using Bakers flux and Woods metal.

The ⁵⁴MnNi thermometer has been described in considerable detail by Berglund and coworkers [1], and typical examples of its use are available [34,35].

⁵⁴MnAI. Cu and Zn

Manganese-54 in Al, Cu, or Zn forms Kondo systems and has been used for γ-RA thermometry. The advantage of using such Kondo alloys is that at temperatures far below the Kondo temperature, T_K, the hyperfine field is strongly dependent upon the applied field and independent of the temperature. Thus, in effect, we have a tunable γ-RA thermometer. At low fields, μ_effB_app≪KT_K, the hyperfine field is linearly proportional to the applied field, as the field is increased, B_hf approaches a saturation value, B_sat. This was quite clearly shown for ⁵⁴MnCu by Pratt and coworkers [36]. They found that very small changes (~0.01 T) in B_app result in large changes (~5 T) in B_hf. Similar results have been obtained for ⁵⁴MnZn by Marsh [37] and more recently by Hunik [38]. The relationship between B_sat and T_K is such that the higher the value of T_K the lower the value of B_sat. For ⁵⁴MnCu. T_K~0.06 K and B_sat~30 T, whereas for ⁵⁴MnZn. T_K~0.26 K and B_sat~19 T. However, in the case of ⁵⁴MnAl the Kondo temperature is very high, T_K~500 K, resulting in B_sat being very small. Thus, at very low temperatures and moderately high fields, Mn acts like a nonmagnetic impurity in AI, i.e., it just “sees” the applied field. In effect we have a brute force γ-RA thermometer using ⁵⁴Mn. This, along with the fact that ⁵⁴Mn generates only a small amount of radioactive self-heating, is quite fortunate since it can then be used to do thermometry in the μK region. Ono and coworkers [39] have actually used a ⁵⁴MnAl thermometer to measure temperatures as low as 10 μK!

Since the hyperfine field can be varied so easily in a Kondo thermometer, its useful range is much larger than in a fixed hyperfine field thermometer (neglecting the small change in the latter due to the addition or subtraction of the applied field). Instead of having just one sensitivity function we now have many, with the useful range being determined by the highest and lowest ones. Whereas the upper limit can be defined to be that temperature at which the hyperfine field is no longer independent of temperature, defining the lower limit is quite difficult. Theoretically Kondo thermometers should operate far below 1 mK; however, the limit is actually set by the B_hf versus B_app relation (see e.g., fig. 2 in [36]) and by concentration and impurity effects.

Although much more work has to be done with Kondo thermometers, they should play an even more important role in γ-RA thermometry in the future because of their ability to operate at much lower temperatures. In addition, Kondo thermometers have very short SLR times which make them particularly useful for SLR measurements on other systems (see, e.g., [40]). Further information on Kondo thermometers can be found in [41] and [42] as well as the references already cited.

4.2. Cobalt-56, 57, and 58

Although all of the four long-lived isotopes of cobalt, ⁵⁶Co (78.8 d), ⁵⁷Co (270.9 d), ⁵³Co (70.8 d), and ⁶⁰Co (5.27 y), have been used in γ-RA thermometry, only ⁵⁷Co and ⁶⁰Co have had extensive use, with the latter being used most frequently. The ⁶⁰Co γ-RA thermometers will be discussed separately in section 4.3. Cobalt-56 has only been used in an Fe host, ⁵⁷Co both in Fe and Ni hosts, and ⁵⁸Co in an Fe host and in a Tutton salt. The latter use of ⁵⁸Co by Griffing and Wheatley [43] was the first demonstration of the γ-RA thermometry technique. Since both ⁵⁶Co and ⁵⁸Co have been used rather infrequently, only ⁵⁷Co will be discussed in this section. Some information on the use of the ⁵⁶CoFe and ⁵⁸CoFe thermometers can be found in [44] and [45], respectively. More recent work using the ⁵⁸CoFe thermometer has been done by Spanhoff and coworkers [46,47].

The decay scheme for ⁵⁷Co is shown in figure 13. Cobalt-57 (I^π=7/2⁻) decays by electron capture with 0.998 branching to the 136.5 keV level in ⁵⁷Fe. Although both the ground state E2 transition and the more intense M1+E2 122.1 keV transition have been used for γ-RA thermometry, the small uncertainty in the mixing ratio of the latter makes it less useful as an absolute thermometer. The values of the U_λ and A_λ coefficients for each γ-ray are given in table 1. Since they both originate from the same level, their U_λ coefficients are the same. These can be calculated quite accurately since the electron capture can only go by spin change 1 for an allowed transition. The A_λ coefficients for the 136.5 keV γ-ray can also be calculated quite accurately since it is known to be an E2 transition. The mixing ratio for the 122.1 keV γ-ray has been measured by different methods and the accepted value [48] is δ(E2/M1)= + 0.120, with an uncertainty of ±0.002. Using this value for δ, the calculated values for A_λ (see table 1) are substantially smaller in magnitude than those for the 136.5 keV transition resulting in a considerable reduction in the anisotropy. However, as was pointed out earlier, the usefulness of a γ-RA thermometer not only depends upon the magnitude of its W(0) versus T relation, but also on the γ-ray intensity. As will be seen later in the sensitivity plots for the ⁵⁷Co thermometer, when the intensities are taken into account the 136.5 keV γ-ray is still quite a bit more sensitive then the 122.1 keV γ-ray. In addition, there is a considerable uncertainty in the deduced temperature when using the 122.1 keV γ-ray due to the uncertainty in its mixing ratio. In table 2 we give the calculated temperatures for δ = + 0.120(2) for the ^S7CoFe thermometer. These were done for temperatures from 4.0 to 76 mK, which is the useful range of the thermometer (see next section) for δ=+0.120. As can be seen in this table, the resulting temperature errors are very large at the lower end of the thermometer’s range. Thus, we see that although the more intense 122.1 keV transition can be used for γ-RA thermometry, its reduced anisotropy along with “its” temperature uncertainty make it less desirable than the 136.5 keV transition.

Figure 13.

Table 2.

Temperature errors due to the uncertainty in δ for the 122.1 keV γ-ray of the ⁵⁷CoFe thermometer. The temperatures were calculated for δ = +0.120(2) using the values of W(0) shown. The latter were chosen to give values of T for δ = +0.120 which cover the thermometers useful temperature range (4.0 to 76 mK). These calculations were done using B_app = 0 and Q_λ = 1.

W(0)	T	T′	(T′−T)/T	T′	(T′−T)/T
	δ = +0.120	δ = +0.122		δ = +0.118
	A2 = 0.141692	A2 = 0.137795		A2 = 0.145591
	A4 = 0.010013	A4 = 0.010345		A4 = 0.009687
1.18882	4.00 mK	1.91 mK	−52.27%	4.89 mK	22.25%
1.14490	10.00	9.50	−4.97	10.48	4.78
1.10064	16.30	15.83	−2.85	16.75	2.78
1.08108	20.00	19.52	−2.39	20.47	2.34
1.04728	30.00	29.45	−1.84	30.54	1.81
1.02990	40.00	39.34	−1.65	40.65	1.62
1.02032	50.00	49.22	−1.55	50.77	1.53
1.01460	60.00	59.10	−1.50	60.89	1.48
1.01096	70.00	68.97	−1.47	71.02	1.45
1.00938	76.00	74.89	−1.46	77.09	1.44

The lifetime of the 136.5 keV level in ⁵⁷Fe is sufficiently long, 8.6 ns, that reorientation of the nuclear spins (see sec. 2.2) are possible. The mechanism responsible for this reorientation is the perturbing fields at the nucleus caused by the electron capture process. In the first part of this process the electron capture creates a hole in the K-shell, which propagates to the outer shells creating additional holes (mainly by Auger effects) and finally to the valence shell. The time required for this part to take place is quite short, being of the order of 10⁻¹⁴ s for cobalt. The second part is the filling of the holes in the valence shell and, as expected, depends upon the type of material that the radioactive atom is embedded in. In metals these holes are filled fairly rapidly, < 10⁻¹² s, with electrons from the conduction band. Thus in metallic samples, e.g., ⁵⁷CoFe and ⁵⁷CoNi, reorientation effects for the 136.5 keV level should not be present since a stable electronic configuration will be achieved in a time which is short compared to the 8.6 ns lifetime of this state. This has been verified both by Mössbauer [49] and γ-RA measurements [50]. In the case of insulators, e.g., ionic crystals, these high valency states live much longer, >10⁻⁸ s, resulting in unstable electronic configuration during the lifetime of the 136.5 keV level and reorientation of the nuclear spins. The latter, which results in an attenuation of the γ-RA can be quite large, e.g., Niesen [51] has measured the attenuation coefficients G₂ and G₄ for ⁵⁷Co in lanthanum magnesium nitrate and found them to be 0.41(2) and 0.32(4) respectively. Further details on reorientation effects can be found in [52], In conclusion, whereas reorientation of the nuclear spins for the 136.5 keV level does occur when it is in an insulator, it does not occur when ⁱ⁷Co is embedded in a metallic host.

Since the 122.1 and 136.5 keV γ-rays are not very penetrating, care must be taken to minimize scattering and absorption in the sample mount as well as in the radiation shields and walls of the cryostat. In addition, low energy γ-rays can undergo large angle scattering without losing much energy. However, the problem is not as severe as it may seem to be since Ge(Li) detectors must be used; their better energy resolution (~1 keV at 100 keV) enhances the rejection of scattered radiation. The low energies of the two γ-rays are particularly useful when higher energy γ-rays are present, e.g., in decay scheme studies or when using two γ-RA thermometers (such as the measurement of temperature gradients), since they can be resolved easily.

The self-heating due to the electron capture, as in the case of ⁵⁴Mn, is quite small being only 6.0 ×10⁻² erg/min for a 1 μCi source. Although the energies of the two prominent γ-rays are low and their heating thereby reduced (see fig. 10), more activity is needed to compensate for the reduced intensity of the 136.5 keV γ-ray. For example, if both a ⁵⁷Co and a ⁵⁴Mn thermometer were mounted on a similar copper disk with D=1.0 cm and τ=0.5 cm (see fig. 10), and it was required that both the 136.5 and 834.8 keV γ-rays be of equal intensity, then the ⁵⁷Co source would produce about eight times more heat.

Since the half-life of ^S7Co is somewhat the same as ⁵⁴Mn (a ^S7Co source will have decayed by 0.255% after 1 day), lifetime corrections may have to be applied to the data if counts are taken for more than 1 or 2 days.

⁵⁷CoFe

The large hyperfme splitting of ³⁷CoFe, Δ_hf= −14.178(3) mK, measured by NMR/ON, v_hf= 295.42(6) MHz [53], with B_hf being −28.81 T, along with its favorable decay properties (for the 136.5 keV γ-ray), make it a particularly useful γ-RA thermometer. The only problem with it, as mentioned in the previous section, is the low energy of the γ-rays. The sensitivity function for both the 136,5 and 122.1 keV γ-rays are shown in figure 14 (the two solid curves on the right). The useful temperature range of the 136.5 keV γ-ray is quite large, from 2.9 to 90 mK, with its greatest sensitivity at 12.4 mK. In contrast, the useful range of the 122.1 keV γ-ray is considerably less, from 6.5 to 40 mK (peak at 16.3 mK); however, when intensity normalization, $\sqrt{.86/.11}=2.8$, is taken into account (dashed curve in fig. 14) the range is improved to 4.0 to 76 mK. This is still about 20% less than that for the 136.5 keV γ-ray. This reduced anisotropy, along with the uncertainty in its mixing ratio, which causes a rather large temperature uncertainty (see table 2 and the discussion in the previous section) makes it less favorable for thermometry. However, it can be useful in some experimental situations if it is “calibrated” since its anisotropy is opposite to that of the 136.5 keV γ-ray. Although no value of τ₁′(lim) for ⁵⁷CoFe has been reported in the literature, a rough estimate can be made based on the measured value of τ₁′(lim)~25 s for ⁵⁶CoFe by Bacon and coworkers [44]. Using this value, along with the v_hf and I-values for both ⁵⁶CoFe and ⁵⁷CoFe, a value of τ₁′(lim)~10 s is obtained for the latter.

Figure 14.

The technique used to prepare a ⁵⁷CoFe thermometer is the same as that used for ⁵⁴MnFe and ⁵⁴MnNi, namely high temperature diffusion. Essentially the same preparation procedure is used for ⁵⁷CoFe, ⁶⁰CoFe, ⁵⁷CoNi, and ⁶⁰CoNi. The following procedure is that used by the Leuven NO Group [54]. Starting with 5- to 6–9’s pure Fe or Ni foil 50 μm thick, a piece 2.5 × 2.5 cm² is cut out and degreased using trichloroethylene or acetone. Carrier free ⁵⁷CoCl₂ or ⁶⁰CoCl₂ (in 0.1 M HCl solution) is deposited uniformly on the foil using a pipette. It is then dried with a heat lamp. The foil is placed in a quartz “boat” located in a quartz tube of an induction furnace. The air is purged from the tube using either pure argon or helium gas for about 10 minutes. With pure hydrogen gas flowing through the tube the oven is heated to 900–1000 °C. After about 8 hours the oven is turned off and the hydrogen gas is replaced by argon or helium gas, which flows through the tube while the oven cools down overnight. The foil is then removed and stored in a desiccator until needed. At that time a piece is cut and attached to the experiment using Bakers flux and Woods metal. If a foil oxidizes it can be cleaned by putting it back in the oven and heating it to 700 °C in a hydrogen atmosphere.

Cobalt-57, as well as ⁵⁶Co and ⁵⁸Co, can also be incorporated into Fe by nuclear reactions (e.g., a-particle or proton bombardment), which is convenient in some experimental situations, see [55] and [46,47].

Although the ⁵⁷CoFe thermometer has many advantages, it has been used rather infrequently when compared to other γ-RA thermometers. This is due no doubt to the low energy of the γ-rays which makes detection difficult in most experimental situations. For those cryostats which have relatively thin walls (or windows), ^S7CoFe should be one of the prime γ-RA thermometers considered for temperature measurements in the range of 2.9 to 90 mK (and when magnetic fields can be used). Some examples of its use can be found in [56,23] and more recently in [57].

⁵⁷CoNi

The hyperfine splitting of ⁵⁷CoNi is Δ_hf=−5.922(19) mK, which is less than half (0.418) that of ⁵⁷CoFe. Thus, although it can be used for lower temperature measurements, its useful range is much smaller than that of ⁵⁷CoFe. In figure 14 we show the sensitivity function for the 136.5 keV γ-ray. Its useful range extends from 1.2 to 37 mK, with its peak sensitivity at 5.2 mK. The hyperfine splitting has been measured by NMR/ON [58] with v_hf= 123.4(4) MHz with B_hf being −12.01(4) T, This rather “low” and negative value of B_hf is an advantage (especially in the case of ⁵⁷Co as its self-heating is quite small) if thermometry must be done below ~1 mK in large B_app, since the latter can substantially reduce Δ_eff. In fact, Brewer [34] has pointed out that for B_app=6 T, ⁵⁷CoNi is essentially a “reverse” brute force γ-RA thermometer. As in the case of ⁵⁷CoFe, no value of τ₁′(lim) has been reported; however, Bacon and coworkers [44] have measured a value of τ₁′(lim)~15 s for ⁶⁰CoNi Using this value (see last section), a value of τ₁′(lim)~4 s is obtained for ⁵⁷CoNi.

The method used to prepare a ⁵⁷CoNi thermometer is the same as that used for ⁵⁷CoFe (see last section). It, like ⁵⁷CoFe, has been used rather infrequently in γ-RA thermometry measurements. Some examples of its use can be found in [50,30,and 59], The latter two used it along with a second γ-RA thermometer to check for temperature gradients in their experiments.

4.3. Cobalt-60

Cobalt-60, like ⁵⁴Mn, has had considerable use in γ-RA thermometry. It has been used in Fe, Co, and Ni hosts, in a Au host and in the rare-earth salts neodymium zinc nitrate and lanthanum magnesium nitrate. In addition, since cobalt is monisotopic (⁵⁹Co),⁶⁰Co can easily be produced in-situ in cobalt single crystals by neutron activation. One of the main advantages of the ⁶⁰CoCo(hcp) single crystal γ-RA thermometer is that no magnetic field is needed to orient the electronic moments because of the large uniaxial magnetic anisotropy. This is particularly useful for those experiments where thermometry must be done in a field-free region. It can, of course, also be used in a magnetic field. Because of its many favorable properties, i.e., being able to operate with or without a magnetic field, ease of preparation, accurate values for the hyperfine splittings, etc., ⁶⁰CoCo(hcp) is one of the most useful γ-RA thermometers. We will discuss this thermometer in considerable detail later on.

The decay scheme for ⁶⁰Co is shown in figure 15. Cobalt-60 (I^π=5⁺) has a half-life of 5.27 y and decays by β⁻ emission with 0.9992 branching to the 4⁺ level at 2505.8 keV in ⁶⁰Ni. From this level the familiar 4⁺(l 173.2 keV)2⁺(1332.5 keV)0⁺ gamma cascade completes the decay to the ⁶⁰Ni ground state. A much less intense β⁻ branch (0.0008) populates the 1332.5 keV level directly. Although the 1332.5 keV transition must be pure E2, the 1173.2 keV transition could have a small M3 admixture. If the latter were pure E2, i.e., δ(M3/E2)=0, then both γ-rays would have the same anisotropy. This would be very favorable for γ-RA thermometry since the inexpensive and more efficient NaI(T1) counting system could be used where both γ-rays are counted together (see sec. 3.3). If δ≠0, the NaI(T1) system could still be used; however, the accuracy of the deduced temperatures will depend upon how accurately δ is known. Using a ⁶⁰CoCo(hcp) thermometer along with a Ge(Li) detector, Marshak [14] has measured the M3/E2 mixing ratio for the 1173.2 keV transition and obtained δ=−0.0008(11). This value results in a temperature difference for the ⁶⁰CoCo(hcp) thermometer (operating between 1.3 and 50 mK) of no more than −0.04 to +0.28% from that if δ=0 (this is discussed in more detail later on). When both γ-rays are counted together the temperature uncertainty is, of course, only about one-half of this amount. The small admixture in the 1173.2 keV transition also shows up in the U_λ coefficients for the 1332.5 keV transition; however, this goes as δ² (see eq (5)) and amounts to a very small change in its temperature—the order of μK for the ⁶⁰CoCo(hcp) thermometer, from that if δ=0.

Figure 15.

The values for the U_λ and A_λ coefficients for both γ-rays are given in table 1. The U_λ coefficients for the intense β⁻ transition, i.e., U_λ(5⁺ → 4⁺,β), can be calculated quite accurately since it can only go by spin change 1 for an allowed transition. The A_λ coefficients for the 1173.2 keV transition were calculated using the M3/E2 mixing ratio value given above. In the case of the pure E2 1332.5 keV transition, its U_λ from the y-feeding, viz., U_λ(5⁺→4⁺,β) U_λ(4⁺→2⁺,γ), can also be calculated quite accurately since the effect of the small value of δ in U_λ(4⁺→2⁺,γ) can, as mentioned previously, be ignored. The small direct β-feeding of this level is a unique second forbidden transition and its U_λ(5⁺→2⁺,β) is just equal to U_λ(5⁺→4⁺,β) U_λ(4⁺→2⁺,γ), thus it has the same effect on the angular distribution of the 1332.5 keV γ-ray.

Since ⁶⁰Co decays by β-particle emission, its self-heating is quite large in comparison to either ⁵⁴Mn or ⁵⁷Co. The average β⁻ energy is 95.8 keV and results in a ${\dot{Q}}_{\beta }=0.34\text{arg}/\text{min}$ for a 1 μCi source. This heating can be important when doing thermometry below ~3 mK. The heating due to the two γ-rays should also be considered (especially at lower temperatures) as it can be quite large, e.g., a 1 μCi ⁶⁰Co thermometer mounted on a copper disk with D=1.0 cm and τ=0.5 cm (see fig. 10) produces 0.5 erg/min; which is even more then the β-heating.

Due to the relatively long half-life of ⁶⁰Co, 5.27 y, the lifetime correction is quite small (after 1 day the source will have decayed by 0.036%).

⁶⁰CoFe

Cobalt-60 in Fe has been used more often than any other system in nuclear orientation studies. It was used by Matthias and Holliday [60] in the first successful demonstration of the NMR/ON technique. Templeton and Shirley [28] used it (along with ⁵⁴MnFe) in the first SLR-time measurements by NMR/ON. It was used for thermometry more than 20 years ago by Stone and Turrell [61], and has been used more frequently than any other y-RA thermometer.

The hyperfine splitting for ⁶⁰CoFe is 166.00(5) MHz [28], which gives a Δ_hf of −7.967(2) mK. The hyperfine field is −29.01(1) T. Its sensitivity function is shown in figure 16 and, as can be seen, its useful range (1.8 to 66 mK, with maximum sensitivity at 9.0 mK) is higher then either the ⁶⁰CoCo(hcp) or ⁶⁰CoNi thermometers. The value of τ₁^′(lim) is ~65 s [62], Information on the effect of magnetic fields on the SLR-time for ⁶⁰CoFe can be found in [63,25].

Figure 16.

The procedure used to prepare a ⁶⁰CoFe thermometer is the same as that described for ⁵⁷CoFe. Information on different methods of preparation can be found in [63,64], the latter also describing the use of both the ⁶⁰CoFe and ⁶⁰CoNi thermometers in considerable detail. In addition, some other examples on the use of the ⁶⁰CoFe. thermometer can be found in [65,66,34, and 59].

⁶⁰CoNi

Barclay [67] has measured the hyperfine splitting for ⁶⁰CoNi by NMR/ON and obtained v_hf= 69.08(5) MHz, which corresponds to Δ_hf=−3.315(2) mK. This is only 0.416 that of ⁶⁰CoFe (similar to the situation for ^S7Co in the same hosts), thus its useful temperature range is reduced proportionately, i.e., from the 1.8–66 mK for ⁶⁰CoFe to 0.8–27 mK (see ⁶⁰CoNi sensitivity function, fig. 16). Although the hyperfine field of ⁶⁰CoNi. B_hf=−12.09(1) T is essentially the same as that of ⁵⁷CoNi (the difference being the hyperfine anomaly), ⁶⁰CoNi, in contrast to ⁵⁷CoNi, is much more difficult to use for thermometry ≲1 mK (by using large B_app, see discussion on ⁵⁷CoNi) because of the large self-heating of the ⁶⁰Co. The SLR-time for ⁶⁰CoNi has been measured by Bacon and coworkers [44] and they obtained a τ₁^′(lim)=15 s. Sample preparation is the same as that described for ⁵⁷CoFe. A different method of sample preparation has been used by Andres and coworkers [64].

In spite of the limited temperature range of the ⁶⁰CoNi thermometer and its self-heating problem, it has been used quite frequently in γ-RA thermometry—the reason being that the temperature region around its greatest sensitivity (3.7 mK) is presently important in low temperature research (e.g., nuclear magnetic ordering studies and properties of ³He). No doubt it will also be used more often in the future since it complements the temperature region where present-day ³He/⁴He dilution refrigerators “bottom out,” i.e., ~3 mK. Some examples of the use of the ⁶⁰CoNi thermometer can be found in [64,68–70].

⁶⁰CoCo(hcp) Single Crystal

Cobalt-60 in hcp cobalt single crystal, because of its many favorable properties, has proven to be a very useful γ-RA thermometer. As previously mentioned, its ability to operate without any magnetic field is very important for many experiments at low temperatures where magnetic fields must be avoided, e.g., superconductivity studies, noise thermometer measurements and paramagnetic salt investigations.

The hyperfine splitting, v_hf, for ⁶⁰CoCo(hcp) contains a small electric quadrupole interaction, v_Q, along with the magnetic dipole interaction, v_M. This is in contrast to the other γ-RA thermometers that were discussed so far where v_hf = v_M. The most accurate values for the hyperfine parameters for ⁶⁰CoCo(hcp) can be obtained from the recent NMR/ON measurements of Hagn and Zech [71]. Hagn [72] has shown that the differential resonance displacement, $\overline{\mathrm{\Delta }v}$, between the centers of the NMR/ON resonances measured at 0° and 90° to the axis of quantization of the nuclear spin system (c-axis of the crystal) can yield both the sign and magnitude of the quadrupole interaction, i.e.,

$$\overline{\mathrm{\Delta }\nu }=\overline{v(0)}-\overline{\nu (90)}=\overline{\mathrm{\Delta }C}\mathrm{\Delta }{v}_Q$$ (21)

where ΔC is a constant which depends upon the temperature and Δv_Q=3v_Q/2I(2I−1) is the quadruple subresonance separation. He also shows that once Δv_Q is known, the magnetic interaction can be obtained from

$$\overline{\nu (0)}=v_M+\overline{C(0)}\mathrm{\Delta }{v}_Q$$ (22)

where $\overline{C(0)}$ is another constant, also depending upon the temperature. Hagn and Zech have measured $\overline{\mathrm{\Delta }v}=57(6)\text{kHz}$ and $\overline{\nu (0)}=126.82(2)\text{MH}\mathrm{z}$ and have calculated that ΔC=−0.61(7) and C(0)=−3.1(l) for the temperature (10 mK) of their measurements. From (21) they obtain Δv_Q=−93(16) kHz, which gives v_Q=−2.8(5) MHz. In terms of the quadrupole coupling constant P in eq (11), this corresponds to P/k=−2.2(4) μK. Using the above value for Δv_Q, a value of v_M=126.53(5) MHz is obtained using eq (22). This gives a dipole splitting Δ_M=−6.0725(24) mK, The value for the hyperfine field is −21.90(5) T.

The values of v_M and v_Q given above are slightly different from those quoted by Hagn and Zech, namely v_M=126.38(7) MHz and v_Q=−3.1(4) MHz. The reason for this is that they obtained v_M for ⁶⁰CoCo(hcp) by using the value of v_M for ⁵⁹CoCo(hcp), measured by Kawakami and coworkers [73], along with the ratio of the g_I-factors, g_I(⁶⁰Co)/g_I(⁵⁹Co) measured by Niesen and Huiskamp [74], viz., v_M=[219.9(1) MHz][0.5747(2)]=126.38(7) MHz. The latter was then used along with the values of $\overline{\nu (0)}$ and $\overline{C(0)}$ in eq (22) to obtain a second value for Δv_Q =− 142(29) kHz. This was averaged with the first value, −93(16) kHz, to yield Δv_Q = − 104(14) kHz, which gives v_Q = −3.1(4) MHz. Their values for v_M and v_Q correspond to Δ_M = −6.0653(34) mK and P/k = −2.5(3) μK.

In table 3 we give the calculated temperatures and temperature differences for both sets of parameters (Δ_M and P/k) for various values of W(0). The latter were chosen to give the values of T shown in column 2 (which cover the useful range of the thermometer, see table 1) using the parameters Δ_M = −6.0725 mK, P/k = −2.2 μK, U₂A₂ = −0.420560, U₄A₄=0.242810, Q₂=0.9965 and Q₄=0.9886. The values for U_λA_λ are those for the 1332.5 keV transition from table 1. The values for the solid angle correction factors are those from the work of Marshak and Soulen [75] and will be useful in calculations which will be presented later on. In addition, a third set of parameters (Δ_M=−6.0668 mK and P/k=−2.9 μK) is included in table 3. These are the values used by Soulen and Marshak [11] in their latest measurements comparing a Josephson junction noise (JJN) thermometer to a ⁶⁰CoCo(hcp) thermometer. As can be seen in table 3, the differences between the parameters deduced solely on the basis of the Hagn and Zech measurements (Δ_M=−6.0725 mK, P/k=−2.2 μK) and their quoted values (Δ_M=−6.0653 mK, P/k=−2.5 μK) are ⩽0.088%, whereas the differences between the former and those used by Soulen and Marshak are ⩽0.023%. In either case the differences are quite small and would only become important for very precise thermometry (⩽0.1%), and if the temperature uncertainty, due to the uncertainties in the parameters Δ_M, P/k, U_λ, A_λ, Q_λ, and θ, was negligible in comparison to these differences. We will show later that this temperature uncertainty is not negligible in comparison to the differences in table 3.

Table 3.

Temperature differences for three different sets of values of Δ_M and P/k for the ⁶⁰CoCo thermometer. All the temperatures were calculated using the values of W(0) shown. The latter were chosen to give values of T for Δ_M = −6.0725 mK and P/k = −2.2 μK which cover the thermometers useful temperature range (1.3-50 mK). The values used for U₂A₂ and U_λA_λ are those given in table 1 for the 1332.5 keV transition. Solid angle correction factors were Q₂ = 0.9965 and Q₄ = 0.9886. See text for further details.

W(0)	T	T′	(T′−T)/T	T′	(T′−T)/T
	ΔM = −6.0725 mK	ΔM = −6.0653 mK		ΔM = −6.0668 mK
	P/k = −2.2 μK	P/k = −2.5 μK		P/k = −2.9 μK
0.014932	1.30000 mK	1.29904 mK	−0.074%	1.30012 mK	+0.010%
0.327535	5.00000	4.99606	−0.079	4.99993	−0.001
0.470108	6.90000	6.89437	−0.082	6.89945	−0.008
0.633327	10.00000	9.99147	−0.085	9.99835	−0.016
0.783152	15.00000	14.98679	−0.088	14.99656	−0.023
0.860948	20.00000	19.98236	−0.088	19.99537	−0.023
0.931038	30.00000	29.97466	−0.084	29.99561	−0.015
0.959508	40.00000	39.96856	−0.079	39.99951	−0.001
0.973528	50.00000	49.96406	−0.072	50.00723	+0.014

The sensitivity function for the ⁶⁰CoCo thermometer (using Δ_M =−6.0725 mK and P/k=−2.2 μK) has already been shown in figure 4 and discussed in section 2.2; however, for comparison with the ⁶⁰CoFe and ⁶⁰CoNi thermometers we have also included it in figure 16. Although no value for τ₁^′(lim) for ⁶⁰CoCo/hcp) has been reported in the literature, its value is not expected to be much different from that reported for ⁶⁰CoCo(cubic) [76] which is approximately 23 s.

The method used to prepare a ⁶⁰CoCo(hcp) thermometer is quite different from those described previously. In all the previous thermometers most of the effort was spent in incorporating the radioactivity into the host, the latter usually being a high purity thin foil which was readily available. In contrast, for the ⁶⁰CoCo(hcp) thermometer most of the effort is spent in preparing a good single crystal sample of the desired shape and size; the radioactivity is produced in-situ in the crystal by neutron activation and is accomplished quite easily. Since the ⁶⁰CoCo(hcp) thermometer is usually used in zero magnetic field, the shape of the sample is such to minimize the effect of closure domains. Due to the large magnetic anisotropy (the magnetization is directed along the c-axis of the crystal) the shape of the sample should be that of a long rectangular parallelepiped (e.g., 10×1×1 mm³), with the long dimension being parallel to the c-axis of the crystal. Such shaped samples are also advantageous when using the ⁶⁰CoCo(hcp) thermometer in a magnetic field since the demagnetizing factor will also be smaller.

The following sample preparation procedure is that used by Marshak and coworkers [14]. Starting with a large high-quality (purity 99.99+% with mosaic spread ⩽1°) cobalt single crystal whose c-axis has been accurately determined, a slab 10.3 mm thick is cut out with the c-axis being perpendicular to the cut sides. (All cutting operations are done using a spark cutter.) Both cut faces are then spark planed and mechanically polished (using 2μ, A1 oxide abrasive) to minimize surface damage. Since ~0.15 mm is needed for each spark planing operation, the slab is now 10 mm thick (very little is lost in the polishing operation). These polished surfaces will be the ends of the 10×1×1 mm³ rectangular parallelepiped samples. A slice, parallel to the c-axis, 1.3 mm thick is cut from this slab. As before, both cut surfaces are spark planed and polished, thus the slice is now 1 mm thick. This is then cut, again parallel to the c-axis, into pieces 10×1×1 mm³. The cut surfaces of each of these are spark planed and polished, resulting in 10×1×1 mm³ samples with the c-axis parallel to the long dimension. These samples are then etched in a solution of 20 cc H₂O, 20 cc HCl, 10 cc HNO₃, 0.5 g FeCl₃ for approximately 20 min at room temperature to remove the surface damage due to the polishing operation. While the samples are in the etching solution they are wiped periodically with a cotton swab to remove the surface reaction products. After the etching operation, they are cleaned in distilled water and then in ethyl alcohol. If possible, x-ray diffraction patterns should be made after some of the important steps, e.g., after the slab is polished and after the samples are finished, to both check on the orientation of the c-axis and to study surface damage. The samples are activated in a reactor, either individually or in groups, to the desired ⁶⁰Co activity (usually 1–10 μCi), depending upon the experimenter’s need. Finally, they are annealed at 300 °C for 24 h in a hydrogen atmosphere. (There is some evidence indicating that this annealing step may not be necessary.) The samples should never be heated above 390 °C since they undergo an irreversible phase change from hcp to fcc.

When a ⁶⁰CoCo(hcp) thermometer is used in a magnetic field, thermal contact is usually made using a soft-solder, e.g., indium. Such soft-solder joints, in which the trapped flux keeps the solder normal, have been successfully used with a ⁶⁰CoCo(hcp) thermometer down to about 2 mK by Hunik [38]. When a ⁶⁰CoCo(hcp) thermometer is used in zero field, which is often the case, soft-solder joints are usually avoided and thermal contact is made by other means. Thorp and coworkers [77] used copper plating to attach their ⁶⁰CoCo(hcp) thermometer to the experiment and encountered no problems down to 3.5 mK. Marshak and Soulen [75] have used gold plating in a similar fashion. More recently they [11] have used an 80 Au-20 Sn solder (m.p.=280 °C), which is known to be a normal conductor, down to the lowest temperature (10 mK) used in their measurements. However, there is some evidence that indicates that indium can also be used to make thermal contact to a ⁶⁰CoCo(hcp) thermometer for zero field measurements. The mechanism thought to be responsible for keeping the indium in the normal state is the magnetic field at the surface of the cobalt crystal—especially one which has been magnetized previously (the ferromagnetic Curie temperature for cobalt is 1400 K).

We will now return to the problem of the temperature uncertainty caused by the uncertainties in the parameters that we previously mentioned. In what follows we will assume that the ⁶⁰CoCo(hcp) thermometer is used in zero field. In table 4 we give the temperature errors due to the uncertainties in the values of the dipole splitting and the quadrupole coupling constant. The values used for these quantities were: Δ_M=−6.0725(24) mK and P/k=−2.2(4) μK. The values used for U_λA_λ and Q_λ are the same as those used in table 3. Table 4 was prepared in a similar fashion to table 3, i.e., we fix the values of all the parameters and generate W(0) versus T (column 1 and 2); these values of W(0) are then used to obtain new temperatures, T′, when a parameter is changed. In order to simplify the presentation of the data we no longer give the T′ values (as in tables 2 and 3), but only give ΔT/T=(T′-T)/T in percent. Columns 1 and 2 of table 4 are the same as those in table 3 since the same set of parameters was used. As can be seen in table 4 a dipole uncertainty of ±2.4 μK results in a constant temperature error of 0.039% over the thermometer’s useful temperature range. The ±0.4 μK quadrupole uncertainty results in a temperature error of between ∓0.040 to ∓0.062%, depending upon the temperature. The temperature error due to both, assuming that they are independent, is ⩽| ±0.073%|.

Table 4.

Temperature errors due to the uncertainties in the values of Δ_M and P/k for the ⁶⁰CoCo(hcp) thermometer. The same parameters were used to determine W(0) and T as those used in table 3. The quantity ΔT/T = (T′-T)/T is given in percent. See text for further details.

W(0)	T	ΔT/T	ΔT/T
	ΔM = −6.0725 mK	Dipole error	Quadrupole error
	P̅/k = −2.2 μK	δΔM = ±2.4 μK	δ(P/k) = ±0.4 μK
0.014932	1.3 mK	±0.039%	±0.059%
0.327535	5.0	±0.039	±0.053
0.470108	6.9	±0.039	±0.049
0.633327	10.0	±0.039	±0.044
0.783152	15.0	±0.039	±0.040
0.860948	20.0	±0.039	±0.040
0.931038	30.0	±0.039	±0.045
0.959508	40.0	±0.039	±0.053
0.973528	50.0	±0.039	±0.062

Turning now to the parameters U_λ, A_λand Q_λ we will assume that the 1173.2 and 1332.5 keV γ-rays are counted together using a 7.6×7.6 cm² NaI(T1) detector as explained in section 3.2, i.e., with the LLD and ULD set at positions A and B as shown in figure 8. Since the values of U_λA_λ for the 1332.5 keV transition are known very accurately (see discussion on ⁶⁰Co in sec. 4.3), we only have to consider the temperature difference and its uncertainty due to δ(M3/E2=−0.0008)(11) for the 1173.2 keV transition. In table 5, ΔT/T is given for δ=0.0003, −0.0008, and −0.0019. These temperature differences are given relative to δ=0, since then both γ-rays would have the same anisotropy. The A_λ, coefficients for each δ are also given. The values used for Δ_M, P/k, and Q_λ are the same as those used in table 4. As can be seen for δ=−0.0008, ΔT/T≃% over most of the thermometer’s useful range. Since both γ-rays are counted together, and assuming equal counting efficiency, the deduced temperatures would be ~0.05% too high if the δ=0 values are used, e.g., for a measured W(0)=0.470103 the 1332.5 keV γ-ray(δ=0 values in table 5) gives 6.900 mK, whereas the 1173.2 keV γ-ray gives (for δ=−0.0008) 6.892 mK, the average being 6.896 mK. The uncertainty in this temperature correction is about half again as big as the correlation itself (see ΔT/T values for δ=0.0003 and δ=−0.0019). Thus, although this temperature correction and its uncertainty are quite small and can be ignored in most applications, we will include its uncertainty when calculating the total temperature uncertainty (due to all the parameters).

Table 5.

Temperature differences due to δ(M3/E2) = −0.0008(11) for the 1173.2 keV γ-ray of the ⁶⁰CoCo(hcp) thermometer. The values used for Δ_M, P/k and Q_λ are the same as those used in table 3. The differences, ΔT/T, were calculated relative to δ = 0 (thus relative to the 1332.5 keV γ-ray), see text for further details.

W(0)	T	ΔT/T	ΔT/T	ΔT/T
	δ = 0	δ = 0.0003	δ = −0.0008	δ = −0.0019
	A2 = −0.447702	A2 = −0.448020	A2 = −0.446855	A2 = −0.445690
	A4 = −0.304379	A4 = −0.303839	A4 = −0.305820	A4 = −0.307800
0.014932	1.3 mK	0.024%	−0.064%	−0.154%
0.327535	5.0	0.040	−0.107	−0.255
0.470108	6.9	0.043	−0.116	−0.276
0.633327	10.0	0.044	−0.116	−0.277
0.783152	15.0	0.041	−0.110	−0.261
0.860948	20.0	0.039	−0.105	−0.249
0.931038	30.0	0.037	−0.100	−0.238
0.959508	40.0	0.037	−0.098	−0.233
0.973528	50.0	0.036	−0.097	−0.231

As mentioned earlier, the values used for Q_λ (Q₂=0.9965 and Q₄=0.9886) are those used by Marshak and Soulen [75], and are for a 7.6×7.6 cm² NaI(T1) detector 50.8 cm (20 in) from the center of a 10×1×1 mm^{3 60}CoCo(hcp) thermometer. They were obtained by averaging the Q_λ(photopeak)-values for 1.17 and 1.33 MeV γ-rays, which were determined by Monte Carlo calculations, The effect of the source geometry was also investigated and found to be quite small (<1×10⁻⁵ for Q₂, and <3×10⁻⁵ for Q₄) for this distance. The uncertainties in Q₂ and Q₄ were estimated to be δQ₂=±5×10⁻⁴ and δQ₄=±×10⁻⁴. The effect of these uncertainties on the deduced temperature is given in table 6 for the worst case, i.e., treating δQ₂ and δQ₄ as being correlated with both being positive or negative. All the other parameters are the same as those used in table 3 to generate W(0) and T. As can be seen in table 6 the temperature errors are quite large, −2.063/+2.192%, at the lowest temperature (1.3 mK) and decrease fairly rapidly to ∓ 0.027% at the highest temperature (50 mK).

Table 6.

Temperature errors due to the uncertainties in the solid angle correction factors Q₂ and Q₄ for the ⁶⁰CoCo(hcp) thermometer. The same parameters were used to determine W(0) and T as those used in table 3. See text for further details.

W(0)	T	ΔT/Ta
	Q2 = 0.9965	δQ2 = ±5 X 10−3
	Q4 = 0.9886	δQ4 = ±20 X 10−3
0.014932	1.3	+2.063%
		−2.192
0.327535	5.0	±0.124
0.470108	6.9	±0.083
0.633327	10.0	±0.056
0.783152	15.0	±0.039
0.860948	20.0	±0.033
0.931038	30.0	±0.029
0.959508	40.0	±0.027
0.973528	50.0	±0.027

^aThe largest errors are given, when δQ₂ and δQ₄ are both positive or negative.

The last parameter that we have to investigate is θ. There are three sources of error that enter into the angular term. First, there is the misalignment of the c-axis of the crystal with respect to the detector. Second, there is the mosaic spread of the crystal. Finally, there are the closure domains which are perpendicular to the c-axis. The effect of each of these always results in a positive temperature error, i.e., the “true” temperature is always lower than that deduced from the measured W(0). The uncertainty in the alignment between the c-axis and the detector is usually about 1–2° when mechanical means (jigs) are used. For very precise thermometry, W(θ) can be measured and the uncertainty can be reduced to less than 1°. In table 7 we give the temperature errors for various values of Δθ. Since P_λ(cosθ) is an even function of θ, +Δθ and −Δθ errors yield the same values. As can be seen in this table, as long as Δθ<2° the temperature errors are quite small except for the lowest temperature values.

Table 7.

Temperature errors for various values of Δθ for the ⁶⁰CoCo(hcp) thermometer. The same parameters were used to determine W(0) and T as those used in table 3. See text for further details.

W(0)	T	ΔT/T	ΔT/T	ΔT/T	ΔT/T
		Δθ = ±0.5°	Δθ = ±1.0°	Δθ = ±2.0°	δθ = ±5.0°
0.014932	1.3 mK	0.427%	1.689%	6.358%	30.626%
0.327535	5.0	0.026	0.103	0.413	2.589
0.470108	6.9	0.108	0.071	0.283	1.775
0.633327	10.0	0.012	0.048	0.193	1.213
0.783152	15.0	0.009	0.035	0.140	0.878
0.860948	20.0	0.007	0.030	0.119	0.749
0.931038	30.0	0.006	0.026	0.104	0.654
0.959508	40.0	0.006	0.025	0.099	0.620
0.973528	50.0	0.006	0.024	0.096	0.605

The mosaic spread of a crystal, which is an indication of the crystal’s imperfection, is determined by x-ray diffraction. Its magnitude is given by the FWHM (full width at half maximum) of the distribution of local c-axes about the principal direction. For computational purposes we will assume that this distribution can be approximated by a Gaussian. Since cobalt single crystals with mosaic spreads of between 1–2° are readily available, we give the results for only these two values in table 8. Except for the 1.3 mK values, these temperature errors are all quite small.

Table 8.

Temperature errors due to the mosaic spread for the ⁶⁰CoCo(hcp) thermometer. Calculations were done for mosaic spreads (FWHM) of 1° and 2°. The distribution of local c-axes was assumed to be Gaussian. The same parameters were used to determine W(0) and T as those used in table 3. See text for further details.

W(0)	T	ΔT/T	ΔT/T
		FWHM = 1°	FWHM = 2°
0.014932	1.3 mK	0.305%	1.210%
0.327535	5.0	0.018	0.073
0.470108	6.9	0.013	0.050
0.633327	10.0	0.009	0.034
0.783152	15.0	0.006	0.025
0.860948	20.0	0.005	0.021
0.931038	30.0	0.005	0.018
0.959508	40.0	0.004	0.018
0.973528	50.0	0.004	0.017

The third contribution to the angular error, that due to closure domains, is the most difficult to calculate. In figure 17a we show the configuration of normal (0° and 180°) and closure (90°) domains that is usually depicted for uniaxial crystals. Although such a domain configuration is observed in iron, it is not observed in cobalt. In bcc single crystal iron the easy directions of magnetization are parallel to the edges of the cube and energetically favor such a configuration. In the case of hep single crystal cobalt with a unique direction (c-axis) of easy magnetization, closure domain formation perpendicular to the c-axis is energetically less favorable since these are the hard directions of magnetization. In figure 17b we show a closure domain structure which is more applicable to cobalt [78]. Since the exact closure structure is expected to be even more complicated than that shown, especially for large cobalt crystals (i.e., those containing many magnetic domains) like our thermometer, no accurate calculation can be carried out of their effect on the deduced temperature. However, their contribution, i.e., the volume of closure domains to the volume of the crystal, will always be less than that shown in figure 17a. Thus, we will calculate the effect of the closure domains for figure 17a, keeping in mind that these results will be larger than the actual situation.

Figure 17.

The effect of the closure domains is given by

$$W{(0)}^{\prime }=W(0)f+W(\pi /2)(1-f)$$ (23)

where W(0) and W(π/2) are the values of W(θ) when there are no closure domains present, and f and (1–f) are respectively the ratios of the volumes of the normal and closure domains to the volume of the crystal. It can easily be seen in figure 17a that (1–f)=d/2L, where d is the domain width and L the length of the crystal. The domain width for cobalt (in zero magnetic field and at rotsm temperature} has been measured by Elmore [79] and was found to vary from a few jam to slightly more than 60 μm, depending upon the crystal The domain width is proportions, to K₁^−1/2 where K. is the anisotropy energy. Since the latter changes from ~ 4 × l erg/cm³ at 300 K. to ~7×10⁶ erg/cm³ at low temperatures, the values measured by Elmore should be reduced by$\sqrt{4/7}=0.75$. In addition to those measured values, d can also be calculated following the method of Landau and Lifshitz [80]. These calculations yield a d of about 15 μm for cobalt: thus we see that <f can vary from a few pm to about 50 /cm at low temperatures. Using eq (23), calculations were carried out for two values of d, 10 and 50 μm, with L=1 cm, which is the length of our thermometer. These results are given in table 9. The same parameters were used to determine W(0), W(π/2) and T as chose used in table 3. As can be seen in this table, the effect of the closure domains on the deduced temperature is fairly small for d = 10 μm. For d=50 μm, the temperature error is about five times greater. Since these calculations, as mentioned earlier, give larger temperature errors than are actually the case for the ⁶⁰CoCo(hcp) thermometer, we will assume that the d=10 μm results are mere representative of the true situation.

Table 9.

Temperature errors due to closure domains for the ⁶⁰CoCo(hcp) thermometer. These calculations were done for the closure domain structure shown in figure 17a. The same parameters were used to calculate W(0), W(π/2), and T as those used in table 3. See text for further details.

W(0)	W(π/2)	T	W(0)′	ΔT/T	W(0)′	ΔT/T
			f = 0.9995		f = 0.9975
			D = 10 μ, L = 1 cm		D = 50 μ, L = 1 cm
0.014932	1.249941	1.3 mK	0.015549	1.405%	0.018049	6.630%
0.327535	1.228283	5.0	0.327986	0.106	0.329787	0.531
0.470108	1.201600	6.9	0.470473	0.081	0.471936	0.406
0.633327	1.155682	10.0	0.633588	0.063	0.634633	0.314
0.783152	1.099698	15.0	0.783310	0.050	0.783943	0.253
0.860948	1.066134	20.0	0.851051	0.045	0.861461	0.227
0.931038	1.033636	50.0	0.931090	0.041	0.931295	0.206
0.959508	1.019977	40.0	0.959538	2.040	0.959653	0.199
0.97 3528	1.013122	50.0	0.973548	0.039	0.973627	0.199

The effect of the closure domains can be completely avoided by following a suggestion of Shirley [81]; namely, to activate only the center part of the sample. This can easily be carried out by making small cadmium “boots” to cover the ends of the sample during the irradiation. Such thermometers have been made by Marshak [14] and compared to fully activated 5/1 and 10/1 (5×l×l mm³ and 10×1×1 mm³) thermometers. The results of these measurements showed that the fully activated 5/1 and 10/1 thermometers yielded essentially the same temperatures, whereas a 5/1 center activated thermometer yielded slightly lower temperatures. Unfortunately, the comparison was only done at a few temperatures and the imprecision (−1%) was not adequate to discern any significant trend. On the basis of table 9, more precise measurements(~0.1%) are needed.

Disk-shaped ⁶⁰CoCo(hcp) thermometers should be avoided since the contribution from the closure domains is quite large. Chandra and Radhakrishnan [82] have compared a 3 mm dia × 0.2 mm thick disk-shaped ⁶⁰CoCo(hcp) thermometer with one which was 5×1×0.3 mm³. By measuring W(0)′ and W(π/2)′ for both thermometers and comparing them to the calculated values for W(0) and W(π/2) they were able to deduce that (l–f) was 0.18 for the disk-shaped thermometer and essentially zero for the other.

The total temperature uncertainty, (ΔT/T), is given in table 10 for three different cases. In the First case we included all the errors discussed in tables 4 through 9. The values used for the c-axis misalignment (table 7) and for the mosaic spread (table 8) were Δθ= ± 1° and FWHM= 1° respectively. Case I corresponds to the experimental situation of Soulen and Marshak [11] where they used a NaI(T1) detector to count both γ-rays. The second case is for the experimental situation where only the 1332.5 keV γ-ray is detected; thus we can ignore the mixing ratio uncertainties given in table 5. This case would also correspond to the experimental situation in Case I if the value of δ(M3/E2) for the 1173.2 keV transition were actually equal to zero. Case III is the same as Case II except we did not include the uncertainties due to the closure domains (table 9), since, as mentioned previously, they can be avoided.

Table 10.

Total temperature uncertainty, (ΔT/T), for the ⁶⁰CoCo(hcp) thermometer. Case I includes all the errors given in tables 4–6, and those for Δθ = ±1° (table 7), FWHM = 1° (table 8), and f = 0.9995 (table 9). Case II does not include the errors due to the mixing ratio (table 5). Case III does not include the errors due to the mixing ratio (table 5), or those due to the closure domains (table 9). See text for further details.

T	(ΔT/T), Case I	(ΔT/T), Case II	(ΔT/T), Case III
1.3	+3.075%	+3.074%	+2.734%
	−2.129	−2.129	−2.129
5.0	−0.218	+0.205	−0.175
	−0.159	−0.140	−0.140
6.9	+0.170	+0.150	+0.127
	−0.131	−0.104	−0.104
10.0	+0.141	+0.114	+0.095
	−0.116	−0.081	−0.081
15.0	+0.119	+0.092	+0.077
	−0.102	−0.068	−0.068
20.0	+0.111	+0.085	+0.072
	−0.097	−0.065	−0.065
30.0	+0.107	+0.082	+0.071
	−0.095	−0.066	−0.066
40.0	+0.109	+0.085	+0.075
	−0.098	−0.071	−0.071
50.0	+0.113	+0.091	+0.082
	−0.103	−0.078	−0.078

The total uncertainty was calculated assuming that all the errors are independent. The asymmetry Ln each (ΔT/T), value is due to the angular contributions which yield only positive errors. With the exception of 1.3 mK, all the values of (ΔT/T), in table 10 lie between +0.218 and −0.159%. The values for 1.3 mK are quite large for all three cases; this is mainly due to the uncertainties in Q_λ and those from the angular terms. As can be seen, all the (ΔT/T), values for Case I are larger than those in table 3, which were calculated using slightly different values for the parameters Δ_M, and P/k (see discussion on table 3). Even when the uncertainties due to the mixing ratio and closure domains are eliminated (Case II and III), the values of (ΔT/T), are still not negligible in comparison to the differences given in table 3. Thus, in order to do very precise thermometry (⩽0.1%) using the ⁶⁰CoCO(hcp) thermometer, not only are more accurate values of Δ_M and P/k needed, but also those for Q_λ and Δθ.

In section 5 we will review the experimental results of Soulen and Marshak [11], making use of the (ΔT/T)_t values for Case I.

In addition to the references already cited, some examples of the use of ⁶⁰CoCo(hcp) thermometers can be found in [77 and 83–86].

4.4. Holmium-166m

The useful temperature ranges of all the γ-RA thermometers that have been discussed in this section so far have been limited to the region below ~ 100 mK. In order for a thermometer to operate at higher temperatures, Δ_hf must be larger. It is known that Δ_hf for some of the rare earth metals and their alloys are quite large. Although there are many possibilities for developing γ-RA thermometers using the rare earths, only two systems have been investigated to date, both using the long-lived (1200 y) isotope ^166mHo. The first system, ^166mHo in gold, has been studied by Barclay and coworkers [88]. The second system, ^166mHo in hep holmium single crystal, has been studied by Marshak [12,87]. Since holmium, like cobalt, is monoisotopic (¹⁶⁵Ho), ^166mHo can be easily produced in-situ in holmium single crystals by neutron activation. This method of sample preparation, which leads to quite uniform and reproducible samples because the radioactivity is incorporated into substitutional sites without any clustering, is particularly advantageous for γ-RA thermometry. Since the ^166mHoAu thermometer has been described in considerable detail by Barclay et al. [88], and as some sample problems do exist (e.g., clustering), we will only discuss the ^166mHoHo(hcp) thermometer.

The first indication that ^166mHo could be a useful nucleus for thermometry was obtained by Postma [89] in his work on holmium ethyl sulfate. Unfortunately, this work was done before Ge(Li) detectors were in use so that the anisotropies from the individual γ-rays could not be fully resolved.

In comparison to the other radioactive nuclei that have been discussed, ^166mHo has a rather complicated decay scheme. In figure 7 we showed part of a 4096 channel spectrum of ^166mHo taken with a Ge(Li) detector. As one can see in this figure, there are numerous γ-rays which could be used for thermometry. In figure 18 we show part of the decay scheme of ^166mHo, indicating only the nine most intense transitions. Holmium-166m (I^π=7⁻) decays by β⁻ emission via two branches, both going to 6⁻ levels in ¹⁶⁶Er. The U_λ coefficients are the same for both branches and can be calculated exactly since they can only go by spin change 1 for an allowed transition. The energy levels of ¹⁶⁶Er have been studied extensively because they provide a good test of the collective model. Most of the spins and parities of the levels are known; however, until very recently [12,14,90,91] very few precise multipole mixing ratio measurements have been made. Although all of the γ-rays shown in figure 18 can be used for thermometry (see fig. 4 of [12]), the energy, intensity and U_λA_λ values for the 712 and 810 keV transitions make them the most useful, therefore we will limit our discussion to these two. The values for the U_λ and A_λ coefficients for both γ-rays are given in table 1. The 712 keV transition goes from one of the β⁻ fed 6⁻ levels to the 5⁺ level of the gamma vibrational band (K=2) and is expected to be almost pure El. The 810 keV transition, which goes from the 5⁺ level of the K=2 band to the 4⁺ level of the ground state band (K=0), should be mostly E2. The U_λ coefficients for the 712 keV transition can be calculated exactly since only the β⁻ feeding is involved. In contrast, the U_λ coefficients for the 810 keV transition cannot be calculated as accurately since they also involve all the γ-rays feeding the 5⁺ level. The values given in table 1 for the A_λ coefficients and multipole mixing ratios were determined using the measured values of U_λA_λ [12,14] and the calculated values for the U_λ coefficients. Since only the measured values of U_λA_λ and their uncertainties are needed for thermometry, these are obtained from table 1 by ignoring the calculated uncertainties, { }, in the U_λ coefficients for the 810 keV transition, i.e., the measured uncertainties in U_λA_λ are all placed with the A_λ coefficients. The uncertainties in the calculated U_λ coefficients for the 810 keV transition were, of course, included in calculating the uncertainty in its mixing ratio.

Figure 18.

Although the values for the U_λA_λ coefficients for both γ-rays have rather large uncertainties (compared to most of the other γ-rays in table 1), at the present time they are not the major source of the temperature uncertainty for the ^166mHoHo(hcp) thermometer.

The average β⁻ energy for ^166mHo is 41 keV and results in a ${\dot{Q}}_{\beta }=0.15$ erg/min for a 1 μCi source. Depending upon the size of a ^166mHoHo(hcp) thermometer, fairly large ${\dot{Q}}_{\gamma }$ self-heating can occur, especially from some of the lower energy γ-rays which are highly converted. However, as we will see in the next section, since the thermometer is usually used at temperatures >32 mK, and almost always in a magnetic field (a superconducting solder must be used to attach it), the self-heating (due to both ${\dot{Q}}_{\beta }$ and${\dot{Q}}_{\gamma }$) is usually no problem.

Since the half-life of ^l66mHo is 1200 y, no lifetime correction need be made to the data.

^166mHoHo(hcp) Single Crystal

One of the most interesting γ-RA thermometers is ^l66mHo in hcp holmium single crystal. The hyperfine interaction for monoisotopic (¹⁶⁵Ho) holmium metal (Δ_hf=310 mK) is the largest of all the rare earth metals. The hyperfine field, which is mainly due to the unpaired 4f electrons, is 740 T. As mentioned earlier, substitutional replacement of ¹⁶⁵Ho with ^166mHo can be accomplished quite easily by neutron activation. Since the ratio of the g_I-factors, g_I(^l66mHo)/g_I(^166mHo)≃0.45, the resulting hyperfine interaction for ^166mHoHo should be about 140 mK. Although this is considerably less than that for ^lwHo, it is still quite large in comparison to all the other Δ_hf in table 1. The low temperature atomic magnetic properties of holmium metal have been determined both by neutron diffraction [92,93] and magnetization [94] studies. Whereas cobalt is a fairly simple uniaxial (c-axis) ferromagnet with a linear atomic magnetic spin structure, holmium is a very complicated uniaxial (also c-axis) ferromagnet with a helical atomic magnetic spin structure (B_app=0). Specifically, the atomic moments in holmium are canted at an angle of about 10° out of the basal plane of the hep lattice, and, although parallel in any one basal plane layer, are rotated through a fixed angle from layer to layer. The latter angle is called the turn angle of the helix and for holmium it is 30°. Thus the atomic moments define 12 different axes. Since the hyperfine field directions follow the atomic moment directions, the hyperfine fields in holmium form an identical helical spin structure. In essence we have a multiaxial (12) nuclear spin system with the axes lying on a cone of half-angle 80°, whose symmetry axis is the c-axis.

Marshak and Turrell [95,96] have studied the spatial distribution of the γ-rays emitted from ^166mHo incorporated into hcp holmium single crystal by neutron activation. Their results show that the nuclear spin axis of ^166mHo do lie on a cone of semi-angle 80°, thus confirming that the neutron activation does lead to substitutional replacement of ¹⁶⁵Ho.

As expected, the atomic magnetization of holmium metal is very anisotropic. The c-axis is the hard axis of magnetization, requiring fields of the order of 25 to 30 T to destroy the helical spin structure and achieve magnetic saturation. In contrast, the helical spin structure is destroyed very easily when a field (~0.5 T) is applied in the basal plane along one of the b-axes (easy axes). Thus, in order for a ^166mHo thermometer to operate at the highest possible temperature it should be a single crystal, i.e., ^166mHoHo(hcp), with at least 0.5 T applied along an easy axis. Although the ^166mHoHo(hcp) thermometer can operate in zero field, the multiaxial nature of the distribution of hyperfine fields substantially reduces the γ-ray anisotropy over that for a single-axis system.

Unfortunately, no NMR/ON measurement of Δ_hf for ^166mHoHo(hcp) has yet been made. This is mainly due to the difficulties in preparing a usable NMR/ON sample. Such a sample would have to have all the ^166mHo located in a surface thickness of about 0.1 μm. The reason for this is that the expected resonance frequency is very high (v_h≃3 GHz) resulting in a very shallow skin depth (~0.1 μm). One possible way to prepare such a sample would be by ion implantation using an isotope separator.

Although no direct measurement of the hyperfine parameters has been made for ^166mHoHo(hcp), indirect measurements have been carried out using the thermal method. In this method experimental values for the nuclear orientation parameters, B_λ(I,T)_exp, are obtained by measuring W(0) and W(π/2) as a function of temperature for a “known” γ-ray (i.e., one for which the U_λA_λ coefficients are known). The temperature is determined using either a primary or secondary thermometer. For most radioactive decays, usually only the λ=2 and λ=4 terms are necessary. The explicit expressions for B₂(I,T)_exp and B₄(I,T)_exp are

$$\begin{gathered} B_2{\left(I,T\right)}_{\exp }=\frac{3W(0)-8W(\pi /2)+5}{7U_2{A}_2{Q}_2} \\ {B}_4{\left(I,T\right)}_{\text{exp}}=\frac{4W(0)+8W(\pi /2)-12}{7U_4{A}_4{Q}_4} \end{gathered}$$ (24)

Assuming a certain form for the interaction Hamiltonian, e.g., eq (10), theoretical values for B(I,T) can be calculated using eq (9) and least-square-fitted to the experiment values to obtain the hyperfine parameters. Using this method to fit eight of the γ-rays simultaneously, Marshak [12] has obtained Δ_M= 137(5) mK and P/k=−0.6(6) mK for ¹⁶⁶HoHo(hcp). The errors in the parameters are quite large and are mostly due to the uncertainty in determining the temperature. Although more accurate thermometry can be done to reduce the uncertainties in Δ_M and P/k, the temperature scale defined by the ^l66mHoHo(hcp) thermometer still will be a secondary scale, since it is based on another thermometer. Only when the energy splittings are measured directly (e.g., by NMR/ON) can the ^166mHoHo(hcp) thermometer be used to realize absolute temperatures directly.

The sensitivity functions for the 712 and 810 keV γ-rays for the ^166mHoHo(hcp) thermometer have been shown in figure 4, and discussed in section 2.2. The useful temperature range for each γ-ray is given in table 1. As can be seen in figure 4, the 810 keV γ-ray should be used for temperature measurements below ~300 mK, whereas the 712 keV γ-ray should be used above ~300 mK.

Although no SLR-time measurements have been reported for the ^166mHoHo(hcp) system, estimates [88] indicate that the τ₁′(lim) should be rather short—the order of seconds or less. Marshak [14] has made some measurements of the thermal response time of a ^166mHoHo(hcp) thermometer and found it to be less than ~60 s. These results are not inconsistent with the τ₁′(lim) estimate above, since a substantial fraction of the thermal response time is due to the large nuclear specific heat of the ¹⁶⁵Ho in the thermometer. This large nuclear specific heat can be particularly bothersome in some experiments when temperature measurements are made at widely spaced intervals (ΔT~50 to ~100 mK).

The method used to prepare a ^166mHoHo(hcp) thermometer is essentially the same as that used for a ⁶⁰CoCo(hcp) thermometer, i.e., spark cutting, spark planing, polishing and etching a small single crystal from a larger one, and then activating it in a reactor, The long dimension should now be a b-axis, as these are the easy axes of magnetization. The activation is slightly more complicated than that for cobalt, as a short-lived (27 h) isomer is also produced along with the 1200 y isomer. Before the thermometer can be used the short-lived activity has to decay away.

Further information on the ^166mHoHo thermometer can be found in the next section, and in the references already cited.

5. Recent Experimental Results

In this section we will review some of the recent experimental results using γ-RA thermometers. Since Hudson and coworkers’ [3] review of NO thermometry covered the period up to 1974, we will concentrate on the work after 1974. The γ-RA thermometers will be discussed (where possible) in the same order as that used in the last section.

In many experimental situations, thermometry must be done in the presence of large magnetic fields. Although γ-RA thermometers would seem to be ideally suited for such measurements, problems could arise which would lead to erroneous results. Brewer [34] has investigated this problem for the ⁵⁴MnNi and ⁶⁰CoFe thermometers. In figure 19 we show his results comparing the temperatures derived from both thermometers in fields up to 7 T. The solid line indicates exact agreement. At low fields (1.56 T) and for temperatures down to 8 mK, the agreement was found to be better than 0.5%. The high field data (4,6 and 7.1 T), taken at temperatures from 12 to 20 mK, showed the ⁶⁰CoFe thermometer yielding 3.8% higher temperatures (dashed line in fig. 19) than the ⁵⁴MnNi thermometer. This difference is thought [24] to be due to either higher eddy-current heating in the Fe foil (caused by sample vibration), or more likely, the bending of the ⁶⁰Co β-particles back into the foil giving increased heating (compared to the electron capture decay of ⁵⁴Mn) at high fields.

Figure 19.

Brewer [24] has also recently compared the ⁵⁴MnNi and ⁶⁰CoNi thermometers down to 3 mK in low magnetic fields (less than 1.2 T). His results are shown in figure 20. (A piece of the same ⁶⁰CoNi foil was tested by the Oxford NO Group and found to be reliable down to 2.5 mK), As can be seen, at 0.33 T the ⁵⁴MnNi thermometer indicates ~ 100% higher temperatures than those from the ⁶⁰CoNi thermometer; at 0.78 T, the agreement is good down to 5 mK, where the ⁵⁴MnNi thermometer saturates; at 1.2 T, it agrees down to 4 mK, and then saturates again. This saturation, which looks just like the saturation one sees when a thermometer loses thermal contact, is clearly a function of the applied field. Brewer suggests that it is caused by a deviation (angle) between the local quantization axis and the applied field, which gets smaller as the field increases (Aharoni effect). Because of the shape of the anisotropy curve, ΔT/T is more pronounced at low temperatures (see table 7). As the field is increased, resulting in a smaller angle, the saturation occurs at lower temperatures. Brewer has seen this magnetic “hardness” in every ⁵⁴MnNi thermometer he has made, regardless of whether it was melted or diffused, cold-rolled or annealed. In addition, he has not seen it in ⁵⁷CoNi or ⁶⁰CoNi thermometers, i.e., both thermometers seem to be completely saturated (magnetically) at 0.2 T. Clearly, these very interesting results should be kept in mind when using the ⁵⁴MnNi thermometer at low temperatures.

Figure 20.

The Oxford NO Group [97] has compared the ⁵⁴MnNi thermometer to ⁶⁰CoFe, ⁶⁰CoNi and ⁶⁰CoCo(hcp) thermometers. These measurements, covered the temperature range ~12.5 to ~42 mK, and were done in magnetic fields of 0.5 to 1.0 T. Both axial and equatorial detectors were used. Within the imprecision of their measurements (typically ±1 and ±2% at 20 mK for the axial and equatorial detectors, respectively) the results showed that each of the three “Co thermometers agreed with the ⁵⁴MnNi thermometers, and that no problems were encountered with saturation of the ferromagnetic domains. In figure 21 we show their results for a 4.5×1×1 mm^{3 60}CoCo(hcp) thermometer and a ⁵⁴MnNi thermometer (supplied by the Bonn NO Group), This group also compared a second, more needle-like, ⁶⁰CoCo(hcp) thermometer (supplied by the Berlin NO Group) to the ⁵⁴MnNi thermometer and obtained similar results, Thus, within the imprecision of their measurements, they do not see any effect of the- closure domains in their 4.5×1×1 mm^{3 60}CoCo(hcp) thermometer. However, since both ⁶⁰CoCo(hcp) thermometers were used in a magnetic field, the contribution from the closure domains will be reduced over that in zero field. In addition, on the basis of table 9, the effect of the closure domains for a ~5/1 ⁶⁰CoCo(hcp) thermometer, used even in zero field, will only be a few tenths of a percent for temperatures greater than 10 mK.

Figure 21.

Comparison experiments between γ-RA thermometers can be particularly useful in “weeding out” bad thermometers. In figure 22 we show the results of a comparison (dashed line) between a ⁶⁰CoCo(hcp) thermometer and a ⁵⁴MnNi thermometer, in a field of 0.54 T, by the Bonn NO Group [33]. The solid line would indicate exact agreement between the thermometers. As can be seen, the ⁶⁰CoCo(hcp) yields too high (~3%) a temperature and is clearly suspect.

Figure 22.

A good example of the use of γ-RA thermometers as calibration thermometers can be found in the work of Babcock and coworkers [69,35], In figures 23 and 24 we show their calibration of a tin nuclear magnetic susceptibility thermometer using both ⁵⁴MnNi and ⁶⁰CoNi thermometers. By utilizing these two γ-RA thermometers, with overlapping sensitivity functions (see figs. 12 and 16 and table 1), they were able to cover a fairly wide temperature range (2 to 40 mK) with good sensitivity. The applied field used for the γ-RA thermometers was 0.55 T. The susceptibility of the tin (¹¹⁹Sn) nuclei was measured using a flux transformer-superconducting quantum interference device (SQUID) magnetometer. The results showed that susceptibility followed a T⁻¹ behavior from 2 to 15 mK (see fig. 24). Above 15 mK, the temperature dependence is no longer T⁻¹ (see fig. 23); the deviation is thought to be due to either iron impurities in the tin or paramagnetic impurities in the magnetometer itself [35,98]. The calibrated tin thermometer was used to study nuclear magnetic ordering in PrCu₆ [69]. The advantage in using the calibrated tin thermometer for these measurements, rather than the γ-RA thermometers themselves, is its very fast response time.

Figure 23.

Figure 24.

Turning now to the ⁵⁷Co thermometers, because of the low energy of the γ-rays, their major use has been in experiments where two γ-RA thermometers must be used simultaneously (e.g., to measure temperature gradients). Ernst and coworkers [99] have used ⁵⁷CoNi and ⁶⁰CoNi thermometers to check for temperature gradients in a rhenium single crystal used in a nuclear quadrupole alignment experiment. They have also used ⁵⁷CoNi and ⁵⁴MnFe thermometers in similar measurements involving a lutetium single crystal [30], Heidari-Dehkordi and coworkers [59] have used ⁵⁷CoNi and ⁶⁰CoFe similarly for measuring the hyperfine fields at ⁵⁴Mn and ⁵¹Cr nuclei incorporated into the intermetallic compound ZnFe₂. In figure 25 we show their experimental arrangement. A comparison of the temperatures of the two thermometers for various applied fields is shown in figure 26. With the exception of the 1.07 T data, the agreement (no temperature gradient) is quite good in the temperature range 6 to 11 mK. The discrepancy above 11 mK is due to the thermal lag between the two thermometers during the cooling down and warming up procedures for the adiabatic demagnetization cryostat. The discrepancy in the 1.07 T data, which shows that the ⁵⁷CoNi. thermometer (mounted directly on the cold finger) is colder than the ⁶⁰CoFe thermometer (mounted directly on the ZnFe₂ sample), is thought to be due to incomplete magnetization of the ⁶⁰CoFe thermometer caused by its being directly coupled to the incompletely magnetized ZnFe₂ sample. Brewer [100] has also used ⁵⁴MnNi along with either ⁶⁰CoCo(hcp) or ⁶⁰CoFe thermometers in a similar fashion to detect temperature gradients.

Figure 25.

Figure 26.

We will now review the ⁶⁰Co thermometers. Andres and coworkers [64] have carried out a careful investigation of the reliability of both the ⁶⁰CoFe and the ⁶⁰CoNi thermometers prior to using them in separate experiments to evaluate the performance of their PrCu₆ demagnetization cryostat. In addition to discussing both thermometers in considerable detail, they also give other information which can be quite useful in similar low temperature experiments employing γ-RA thermometers. After preparing their thermometers very carefully, they performed NMR/ON measurements on the thermometers themselves to check that the resonance occurred at the predicted frequency and with the expected linewidth. These results demonstrated that most of the ⁶⁰Co nuclei were subjected to the same hyperfine field. In order to ensure that the 0.3 T field used for the thermometers was sufficient to achieve magnetic saturation, they measured W(0) and W(π/2) as a function of applied field at a fixed temperature. In figure 27 we show their results for the 1.33 MeV γ-ray of the ⁶⁰CoFe thermometer. These measurements were made at a temperature of 16.7 mK. As can be clearly seen, saturation is reached at about 0.2 T. Using their calculated values for Q_λ, they found that the saturation values of W(0) and W(π/2) were consistent with each other, thus indicating that the axis of quantization of the nuclear spin system is colinear with the applied magnetic field. As a check on their Q_λ values, they measured the asymptotic value (T→0) of W(π/2) for the ⁶⁰CoFe thermometer and compared it to the theoretical value. The agreement was within 1 %. In figure 28 we show their results (for the 1.33 MeV γ-ray of the ⁶⁰CoFe thermometer) comparing the temperatures deduced from the W(0) data with those from the W(π/2) data. Although W(π/2) becomes insensitive to T at low temperatures (as indicated by the large error bars), both sets of data give consistent temperatures. They also investigated the effect of the background radiation and found it to be negligible. As a check, they compared the temperatures deduced from both the 1.17 and 1.33 MeV γ-rays. As can be seen in figure 29, the agreement is excellent. Finally, both ⁶⁰CoFe and ⁶⁰CoNi thermometers were used to monitor the performance of the PrCu₆ stage of their demagnetization cryostat. In figure 30 we show a typical warm-up curve of the PrCu₆ stage taken with a ⁶⁰CoNi thermometer. The demagnetization was done from about 25 mK and 2.4 T to zero field. Typical end temperatures, as determined by the ⁶⁰CoNi thermometer, for identical demagnetizations were 2.76 and 2.68 mK. When a similar demagnetization was done using a ⁶⁰CoFe thermometer, the end temperature was 2.78 mK. Their results show that both thermometers give essentially the same temperatures, so that either one can be used to monitor the performance of such refrigerators.

Figure 27.

Figure 28.

Figure 29.

Figure 30.

Considerable use has been made of this PrCu₆ demagnetization cryostat by the Munich NO Group. Another example of the use of the ⁶⁰CoNi by this group is that made by Eska and coworkers [68] in their study of recoil-implanted ⁵²Mn in pure Au. The measurements of the ⁵²MnAu foil were made in fields of from 0.005 to 0.3 T. Since the ⁶⁰CoNi thermometer was exposed to the same fields, magnetic saturation was not achieved. Thus, the magnetization of the ⁶⁰CoNi thermometer had to be measured in order to correct the measured anisotropies to saturation magnetization values, before any meaningful temperatures could be obtained. In figure 31 we show the magnetization results. These measurements were made at a temperature of about 3.2 mK using both the W(0) and W(π/2) anisotropies, viz., ϵ = [W(0)/W(π/2)–1. As can be seen, saturation magnetization occurs above 0.35 T. Both the 1.17 and 1.33 MeV γ-rays were used for thermometry after first establishing that they gave the same anisotropy. This comparison is shown in figure 32, Eska and coworkers found that the systematic deviation from exact agreement (solid line) was much smaller than the error from the counting statistics. In using the ⁶⁰CoNi thermometer in this fashion (correcting the low field anisotropies to saturation values), they were able to measure the anisotropies of the three most intense γ-rays from the ⁵²MnAu sample as a function of both the magnetic field and the temperature. These data, along with SLR measurements, enabled them to conclude that the behavior of the ⁵²MnAu system at low temperatures was due to both Kondo and relaxation effects.

Figure 31.

Figure 32.

Going on to the ⁶⁰CoCo(hcp) thermometer, we note that Hunik [38] has made extensive use of this thermometer to measure the performance of his two-stage (PrCu₆ plus an indium stage) nuclear demagnetization cryostat, and also to calibrate both a Pt NMR thermometer and a brute force ⁹⁵NbPt γ-RA thermometer. In figure 33 we show his results for the SLR time of Pt as a function of the inverse temperature of the ⁶⁰CoCo(hcp) thermometer. The temperature range covered in the calibration was 2.4 to 6 mK. A Korringa constant of 30.1 ms-K (solid line) fitted the data. The calibrated Pt NMR thermometer was then used to measure temperatures down to 0.88 mK.

Figure 33.

The final ⁶⁰CoCo(hcp) thermometer work that we will review is that by Soulen and Marshak [11]. Their use of this thermometer is unique in that it was directly compared to another primary thermometer, a Josephson junction noise (JJN) thermometer. The ⁶⁰CoCo(hcp) thermometer is ideally suited for these measurements since it can operate in zero field, a condition imposed by the JJN thermometer. The temperature range covered in this comparison experiment was 10.2 to 50.3 mK. The results of these measurements, along with noise thermometer measurements from 50 to 500 mK, form the basis for the National Bureau of Standards–Cryogenic Temperature Scale-1 (NBS-CTS-1).

In order to achieve high statistical precision, these comparison measurements were done in a different fashion than most of the comparison experiments previously described; data were accumulated at constant temperature for long periods of time. In particular, the following routine was used to compare the thermometers which were mounted on a cold finger attached to the mixing chamber of a ³He-⁴He dilution refrigerator: on the morning of a given day, a predetermined resistance value for a carbon thermometer mounted on the mixing chamber was set on a resistance bridge and a temperature controller activated. Both noise and γ-ray data were taken “cold” simultaneously for a period of 10–13 h at constant temperature (fluctuations were less than 7 μK). The refrigerator was then warmed to, and maintained at, 205 mK, where “warm” data were taken overnight (about 8–10 h) by both thermometers (the warm data are actually only needed by the γ-ray thermometer). The next morning the refrigerator was cooled to a different predetermined resistance value and cold data taken again by both thermometers for another 10–13 h. Then another set of warm data at 205 mK was taken overnight. This routine was followed for 51 days during which the refrigerator was never warmed above 205 mK. Fourteen different resistance values were chosen covering the temperature range of ~10 to ~50 mK. At least two, and as many as four, measurements were made at each of the 14 resistance values.

Although both a NaI(T1) detector (placed at 0°) and a Ge(Li) detector (placed at 180°) were used in the measurements, only the Nal data were used for the comparison. This was primarily due to the poor counting statistics obtained as a result of the low efficiency of the small (~10 cc) Ge(Li) detector used in these measurements. The Nal data were taken in the manner described in section 3.3, i.e., by setting a window to accept all pulses from A to B in figure 8. Counts for a typical run (either cold or warm) from the NaI(T1) detector were accumulated automatically in 400 s intervals with a 6 s dead time between each interval for printout. From these data, 70 to 120 intervals of 400 s counts, the mean and its standard deviation were calculated. Various statistical tests were made to check out each set of data. In calculating W(0) for any one cold run, the average of the two bracketing warm runs was used. Values for the environmental background were obtained before the ⁶⁰CoCo(hcp) thermometer was attached to the cold finger and after it was removed (at the end of a 51-day period). No effort was made to subtract the Compton background under the peaks (see sec. 3.3). The W(0) and its statistical uncertainty from each day’s cold run was converted to T_γ±δT_γ. Finally, all the data were averaged for identical resistance values to give${\overline{T}}_{\gamma }\pm \mathrm{\delta }{\overline{T}}_{\gamma }$. The noise thermometer data were analyzed [11] for the same set of cold runs (identical resistance values) and yielded ${\overline{T}}_{\mathrm{N}}\pm \mathrm{\delta }{\overline{T}}_{\mathrm{N}}$. In table 11 we give the results of these measurements. The average temperature as determined by both thermometers for the same set of cold runs is defined by$\overline{T}=\left({\overline{T}}_{\text{N}}+{\overline{T}}_{\gamma }\right)/2$. The temperature difference between the two thermometers is given by$\mathrm{\Delta }\overline{T}={\overline{T}}_{\text{N}}-{\overline{T}}_{\gamma }$. The quantity $\mathrm{\delta }\mathrm{\Delta }\overline{T}$ represents the combined statistical uncertainty, $\sqrt{{\left(\mathrm{\delta }{\overline{T}}_{\mathrm{N}}\right)}^2}+{\left(\mathrm{\delta }{\overline{T}}_{\gamma }\right)}^2$, of the temperature difference. The percentage difference, $\mathrm{\Delta }\overline{T}/\overline{T}$, is also given in table 11. As can be seen, the differences are quite small, averaging about 0.5%, with the ⁶⁰CoCo(hcp) thermometer reading higher. These results are also shown in figure 34 along with the ±0.5% guidelines.

Table 11.

Results of a comparison experiment between a Josephson junction noise thermometer and a ⁶⁰CoCo(hcp) γ-RA thermometer [11]. The noise temperatures and their statistical uncertainties are designated by ${\overline{T}}_{\text{N}}$ and $\mathrm{\delta }{\overline{T}}_{\text{N}}$ respectively, whereas those for the γ-ray thermometer by ${\overline{T}}_{\gamma }$ and$\mathrm{\delta }{\overline{T}}_{\gamma }$. The quantity δΔT is the combined statistical uncertainty due to both thermometers. See text for further details.

${\overline{\mathit{T}}}_{\mathbf{N}}$ (mK)	$\mathit{\delta }{\overline{\mathit{T}}}_{\mathrm{N}}$ (mK)	$\mathit{\delta }{\overline{\mathit{T}}}_{\mathbf{N}}/{\overline{\mathit{T}}}_{\mathbf{N}}$ (%)	${\overline{\mathit{T}}}_{\mathit{\gamma }}$ (mK)	$\mathit{\delta }{\overline{\mathit{T}}}_{\mathit{\gamma }}$ (mK)	$\mathit{\delta }{\overline{\mathit{T}}}_{\mathit{\gamma }}/{\overline{\mathit{T}}}_{\mathit{\gamma }}$ (%)	$\overline{\mathit{T}}=\left({\overline{\mathit{T}}}_{\mathbf{N}}+{\overline{\mathit{T}}}_{\mathit{\gamma }}\right)/\mathbf{2}$ (mK)	$\mathrm{\Delta }\overline{\mathit{T}}=\left({\overline{\mathit{T}}}_{\mathbf{N}}-{\overline{\mathit{T}}}_{\mathit{\gamma }}\right)$ (mK)	$\mathit{\delta }\mathrm{\Delta }\overline{\mathit{T}}$ (mK)	$\mathrm{\Delta }\overline{\mathit{T}}/\overline{\mathit{T}}$ (%)
10.178	±0.039	±0.383	10.196	±0.010	±0.098	10.187	−0.018	±0.040	−0.177
10.956	±0.057	±0.520	10.989	±0.016	±0.146	10.972	−0.033	±0.059	−0.301
11.712	±0.042	±0.359	11.864	±0.012	±0.101	11.788	−0.152	±0.044	−1.290
15,411	±0.077	±0.500	15.518	±0.029	±0.189	15.464	−0.107	±0.082	−0.692
19.635	±0.072	±0.367	19.753	±0.038	±0.192	19.694	−0.118	±0.081	−0.599
23.335	±0.116	±0.497	23.425	±0.080	±0.342	23.380	−0.090	±0.141	−0.384
27.034	±0.133	±0.492	27.252	±0.117	±0.429	27.143	−0.218	±0.177	−0.803
30.209	±0.126	±0.417	30.417	±0.126	±0.414	30.313	−0.208	±0.178	−0.686
34.043	±0.172	±0.505	34.152	±0.215	±0.630	34.098	−0.109	±0.275	−0.312
36.522	±0.136	±0.372	36.978	±0.189	±0.511	36.750	−0.456	±0.233	−1.241
40.431	±0.197	±0.487	40.743	±0.342	±0.839	40.587	−0.312	±0.395	−0.769
45.622	±0.218	±0.478	45.573	±0.486	±1.066	45.598	+0.049	±0.532	+0.107
50.254	±0.244	±0.486	50.421	±0.641	±1.271	50.338	−0.167	±0.686	−0.332

Figure 34.

This systematic difference between these two primary thermometers is thought to be mainly due to the ⁶⁰CoCo(hcp) thermometer. When the Ge(Li) data are used to determine the temperatures, the results are slightly lower than those determined by the Nal data. This difference is probably due to ignoring the Compton background in the treatment of the Nal data (see sec. 3.3). If the Ge(Li) data were to be plotted in figure 34 instead of the Nal data, the overall agreement would be somewhat better. In this case $\mathrm{\Delta }\overline{T}/\overline{T}$ would average about −0.3% instead of the +0.5% for the Nal data. However, the statistical imprecision of the Ge(Li) data is not sufficient to warrant a clear choice.

The 0.5% difference between the two thermometers is clearly larger than the Case I total uncertainty, (ΔT/T)_t given in table 10 for the temperature region covered in this comparison. In order to be affected by the uncertainties in some of the parameters (e.g., Q_λ and Δθ), the comparison would have to been done to better than ~0.1%, or else at much lower temperatures. Since constant temperature measurements below the “bottoming out” temperature (~3 mK) of present day ³He-³He dilution refrigerators are difficult to achieve, improvements must be made in the measurement of W(0) at higher temperatures. As can be seen in table 11, the statistical imprecision in the measurement of${\overline{T}}_{\gamma }$, i.e., $\mathrm{\delta }{\overline{T}}_{\gamma }/{\overline{T}}_{\gamma }$, is quite good (~±0.1%) for the lower temperature values. Thus, probably all that is needed at the present time is better treatment of the Nal data or the use of more efficient Ge(Li) detectors. The statistical imprecision in the measurement of the noise temperatures, $\mathrm{\delta }{\overline{T}}_{\mathrm{N}}/{\overline{T}}_{\mathrm{N}}$, is not quite as good as the ⁶⁰CoCo(hcp) thermometer for the lower temperature values (see table 11). Thus, improvements must be made in the noise thermometer before a comparison can be made at the 0.1% level. Since the ⁶⁰CoCo(hcp) thermometer’s sensitivity function peaks at 6.9 mK, the greatest precision can be obtained at this temperature.

In figure 35 we show some of the recent results of Marshak [12,87] on the ^166mHoHo thermometer. Here measured values of W(0) are shown as a function of temperature for the 712 and 810 keV γ-rays. The measurements were made at 17 temperatures covering the range 24 to 670 mK, and in an applied field of 2 T. Although only 0.5 T is required for magnetic saturation along an easy axis (for a needle-like sample), the excess field was necessary to compensate for the demagnetizing field in the disk-shaped sample used in these measurements (the applied field was in the plane along an easy axis). The theoretical curves for W(0) for both γ-rays are also shown in this figure. These were calculated using Δ_M= 137(5) mK and P/k= −0.6(6) mK, and the values of U_λA_λ given in table 1. The uncertainty in the measured values of W(0) due to the counting statistics is less than or equal to the diameter of the circles. As can be seen, the overall agreement is quite good, except for the higher-temperature region of the 810 keV γ-ray where the experimental values are systematically low. However, as explained in the last section, the values of the parameters Δ_M and P/k were determined by fitting the measured values of W(0) and W(π/2) for eight γ-rays simultaneously (including the 712 and 810 keV γ-rays), thus the theoretical curves shown are not completely independent of the measured values of W(0). Further work is being done [14] on the ^166mHoHo(hcp) system which should make it a more useful γ-RA thermometer.

Figure 35.

Turning now to new developments, a quadrupole orientation (alignment) γ-RA thermometer has been used by the Oxford NO Group. The advantages of such thermometers are that they do not require any magnetic field, and that their useful temperature range is lower than the dipole (or dipole plus small quadrupole) γ-RA thermometers that have already been discussed. The lower temperature range is due to the magnitude of electric quadrupole interactions, which are usually quite small (P/k~0.01 to 1.0 mK). To illustrate a quadrupole γ-RA thermometer, we consider the system consisting of ⁵⁴Mn incorporated into a metallic (hcp) single crystal host X such that P/k = −0.1 mK, (v_Q=−42 MHz). A plot of the sensitivity function for this fictitious ⁵⁴MnX(hcp) quadrupole orientation thermometer is shown in figure 36, The useful temperature range is 0. L to 4.0 mK, with its greatest sensitivity at 0.32 mK. Because of the uneven spacing of the energy levels for a quadrupole interaction (see discussion in sec. 2.2), the sensitivity function is skewed to favor the higher temperature region (above 0.32 mK), Although the useful range of this fictitious quadrupole thermometer (which depends upon the value chosen for v_Q) is quite low in comparison to the dipole thermometers in table 1, the value used for v_Q (−42 MHz) is not unreasonably small for such ⁵⁴MnX(hcp) systems. In fact, for the system ⁵⁴MnZn(hcp), the quadrupole interaction is about an order of magnitude less [101] than that chosen for our fictitious thermometer!

Figure 36.

Returning to real thermometers, the quadrupole orientation γ-RA thermometer used by the Oxford NO Group was ^l90IrRe(hcp). Murray and coworkers [102] have determined v_Q for ^{186,188−190}Ir in single crystal rhenium by measuring W(0) as a function of temperature for some of the more intense γ-rays. For thermometry, they used a ⁶⁰CoCo(hcp) thermometer since the measurements had to be made in zero field (actually a small magnetic field was used to keep both the Re single crystal, and the indium solder used to attach it, in the normal state). A PrNi₅ demagnetization cryostat was used in these measurements to cool the sample to 2 mK. The ¹⁹⁰Ir (I=4⁺), along with the other iridium isotopes were produced in-situ in the single crystal by α-particle irradiation. Two γ-rays can be used for thermometry with this isotope; one is the 518.4 keV transition which is pure El, and the other is the 294,6 keV transition which is predominantly E2. Their result for v_Q was −245(15) MHz (this is the weighted average of the two values given, one for each γ-ray). Using this value for v_Q (which corresponds to P/k=−0.32 mK) and their U_λA_λ values, the sensitivity function for each γ-ray was calculated and is shown in figure 36. As expected, the 294.6 keV (E2) transition has greater sensitivity than the 518.4 keV (El) transition. The useful temperature range for the former is 0.6 to 19 mK, with its greatest sensitivity at 2,0 mK, whereas for the latter it is 0.8 to 13.0 mK, with its greatest sensitivity at 2.3 mK. Although the 294.6 keV γ-ray is more useful for thermometry, the 518.4 keV γ-ray can be useful in some experimental situations since the anisotropy is reversed to that of the 294.6 keV γ-ray.

The major disadvantages of the ¹⁹⁰IrRe(hcp) quadrupole orientation γ-RA thermometer are the relatively short half-life of ^I90Ir (T_1/2= 12.1 d), the need to use a small magnetic field to keep it in the normal state, and, most important, that v_Q has not been directly measured (e.g., by NQR/ON), but has been determined by the thermal method. However, in contrast to the situation for the ^166mHoHo(hcp) thermometer, a primary thermometer, ⁶⁰CoCo(hcp), was used to “calibrate” it.

The ¹⁹⁰IrRe(hcp) has been used by Allsop and coworkers [101] in their study of the ⁵⁴MnZn(hcp) system.

The last thermometer that we will discuss is not a γ-RA thermometer, hut one which makes use of the transmission of unpolarized neutrons through a polarized cobalt-59 single crystal. This thermometer, which has been proposed by Fasoli and coworkers [103], uses the nuclear deformation effect, Δ_def, to measure the temperature of the cobalt spin system. The nuclear deformation effect is defined by

$${\mathrm{\Delta }}_{\text{def}}={\sigma }_t(\text{oriented})-{\sigma }_i(\text{unoriented})$$ (25)

where σ_t (oriented) is the total neutron cross section when the nuclei are oriented, and σ_t, (unoriented) is the unoriented total neutron cross section. This effect, which depends upon the mass shape of the nucleus, was first measured by Marshak and coworkers [22] using a polarized ¹⁶⁵Ho target. As for all NO thermometers, the temperature dependence of this effect is contained in the B_λ(I,T) for the nuclear spin system under consideration. Because of the symmetry of the mass shape of the nucleus, only the even λ-values are needed, with the cutoff in λ-values being essentially determined by the shape of the nucleus (i.e., quadrupole, octopole, etc.). Since both ⁵⁹Co and ¹⁶⁵Ho are almost pure quadrupole-shaped nuclei, the effect is mainly dependent on B₂(I,T) see figure 8 of [22]. In addition, Δ_def also depends upon the neutron energy, and oscillates both positive and negative for some nuclei; see figure 6 of [22], In the case of ⁵⁹Co, Δ_def is a maximum at a neutron energy of ~2 MeV [104,105]. Fasoli and coworkers [103] have proposed that a measurement of Δ_def for ⁵⁹Co using 2 MeV neutrons could be used for thermometry. They point out that such a thermometer could be useful for experiments where high γ-ray backgrounds are encountered (thus making it difficult to use γ-RA thermometers). Information concerning heat input, statistical accuracy, and apparatus needed for this thermometer can be found in their paper.

6. Conclusions

We have discussed NO thermometry, in particular γ-RA thermometry, in considerable detail. Sufficient information has been given on both the theoretical and practical aspects of γ-RA thermometry to enable the experimenter to use this technique with ease and confidence. The latter stems partially from the knowledge that, in principle, the temperatures derived from NO thermometers are absolute. Depending upon the measurements to be done, the experimenter can choose from among the 10 or so γ-RA thermometers reviewed the one which meets his specific needs (i.e., temperature range, magnetic field or no field, heating that can be tolerated, and γ-ray detectors and equipment available). For particularly complex thermometric investigations one might want to employ two or even three (e.g., ⁵⁷CoNi, ⁵⁴MnFe and ⁶⁰CoNi) thermometers simultaneously. The ultimate precision of his thermometry will, to a great extent, depend upon his own effort. He will find that absolute temperature measurements with an imprecision of 1–2% will be fairly easy to make, whereas those of 0.1–0.5% are quite difficult. He will also find that the latter are impossible to achieve without first obtaining constant-temperature operation of his refrigerator. For ³He-⁴He dilution refrigerators, constant-temperature operation is quite easy and inexpensive to achieve. For demagnetization refrigerators (both electronic and nuclear), constant-temperature operation is more difficult to achieve.

Turning now to the γ-RA thermometers themselves, we have seen that they are fairly easy to make and are usually quite compatible (i.e., being small, metallic and easily attached) with the experimenters’ needs. However, their temperature range is rather limited in that most of them are only useful from ~ 1 to ~ 100 mK. Although the ^166mHoHo(hcp) thermometer looks promising for higher temperatures (~ 100 mK to ~ 1 K), more work is necessary before it can be used with confidence. In addition, other rare earths should be investigated for the region above ~ 100 mK. For temperatures below ~ 1 mK, neglecting brute force γ-RA thermometers, the quadrupole orientation thermometer looks very promising; however, more work is also necessary before it Too can be used with confidence.

Finally, what can we expect in the future from γ-RA thermometry? Besides the obvious extensions mentioned above, we can expect that they will he used more frequently by the low temperature community—both as general purpose thermometers and to calibrate secondary thermometers (e.g., Pt NMR and nuclear susceptibility thermometers), the latter use being particularly important when accurate and fast thermometry must be done. We will also see two or more γ-RA thermometers being used simultaneously more often (e.g., to cover a wider temperature range and to measure temperature gradients). And last, they will be used more often in precise comparison experiments with other primary thermometers.

Biography

About the Author: H. Marshak is with NBS’ Center for Absolute Physical Quantities.