Estimation of Parameters in Models for Cesium Beam Atomic Clocks

Abstract

This paper is intended to serve as an introduction to the use of the Kalman filter in modeling atomic clocks and obtaining maximum likelihood estimates of the model paramaters from data on an ensemble of clocks. Tests for the validity of the model and confidence intervals for the parameter estimates are discussed. Techniques for dealing with unequally spaced and partially or completely missing multivariate data are described. The existence of deterministic frequency drifts in clocks is established and estimates of the drifts are obtained.

1. Introduction

The recursive updating of least squares estimates that would later become a special case of the Kalman, “filter” was apparently known to Gauss [1],¹ and published in the modern statistical literature by Plackett [2]. Kalman’s contribution [3] was the generalization to dynamic systems. Kalman’s filter has found immense application in diverse areas of engineering. In classical applications, recursive estimates are obtained of the “state” of the system but parameters appearing elsewhere in the state space representation for the system and the mathematical model for the system must be considered known.

In our application, Kalman’s recursive equations allow us to compute the likelihood function for given values of parameters occurring anywhere in the state space representation. Nonlinear optimization techniques can then be used to find the maximum likelihood estimates. The recursive residuals, or innovations, may be examined to judge the adequacy-of-fit of the model, and generalized likelihood ratio tests may be used to test the significance of model parameters such as frequency drifts and obtain confidence intervals for the estimated parameters. Kalman filter techniques make it quite easy to deal with unequally spaced and completely or partially missing multivariate data. We describe these methods in this paper.

The next article in this issue, “Estimating Time from Atomic Clocks,” by Jones and Tryon [4] describes statistical procedures for detecting clock errors and allowing for the insertion or deletion of clocks in the ensemble during the parameter estimation process. It also describes the development of a time scale algorithm based on the model developed in this paper.

2. Models For Atomic Clocks

A cesium atomic clock is a feedback control device whose frequency locks onto the fundamental resonance of the cesium atom at (ideally) 9,192,631,770 Hz, which defines the second. Frequency bias due to fundamental instrumentation limitations and environmental effects are determined by calibration against primary frequency standards. Stochastic fluctuations arise from shot noise in the cesium beam and the probabilistic nature of quantum mechanical transition rates which cause white noise in the frequency of the clock which is integrated into a random walk in time. In addition, empirical studies have demonstrated that frequency wanders independently as a random walk, introducing the integral of a random walk into time.

Finally, there is considerable international debate over the inclusion of linear drift in frequency to account for break-in and aging. Such drifts could be strictly constant over a long time period, or allowed to change slowly as a third random walk. The methods developed in this paper provide, for the first time, valid statistical tests of these hypotheses.

The proposed stochastic model for a clock’s behavior is

$$\begin{gathered} x(t)=x(t-1)+\delta (t)y(t-1)+\frac{1}{2}{\delta }^2(t)w(t-1)+\epsilon (t) \\ y(t)=y(t-1)+\delta (t)w(t-1)+\eta (t) \\ w(t)=w(t-1)+\alpha (t) \end{gathered}$$ (2.1)

where

x(t) is the clock’s deviation from “perfect” time at sample point t in nanoseconds;

δ(t) is the time interval in days between sample points t and t−1;

y(t) is the clock’s frequency deviation from perfect frequency at sample point t in nanoseconds/day;

w(t) is the drift in frequency in nanoseconds/day²;

ε(t), η(t), and α(t) are mutually independent white zero mean Gaussian random variables with standard deviations $\surd \delta (t){\sigma }_{ϵ}$, $\surd \delta (\tau ){\sigma }_{\eta }$, and $\surd \delta (t){\sigma }_{\alpha }$, respectively, in nanoseconds, nanoseconds/day, and nanoseconds/day². The $\surd \delta (t)$ arises because the variance of a random walk is proportional to the time interval.

If σ_α = 0, w(t) is a constant, w, representing a deterministic linear trend. If both σ_α = 0 and w = 0, the model is drift-free. The purpose of this study is to evaluate the validity of these models, and to obtain generalized likelihood ratio tests for the significance of the drift parameters and maximum likelihood estimates of the parameters σ_ϵ, σ_η, and w (or σ_α, if appropriate), for each clock in the ensemble.

3. The Kalman State Space Model for a Clock Ensemble

The combination of clocks into a Kalman state space model will be explained by considering the special case of a three-clock model. The state transition equation is

$$\left[\begin{array}{l}{x}_1(t)\hfill \\ y_1(t)\hfill \\ w_1(t)\hfill \\ x_2(t)\hfill \\ y_2(t)\hfill \\ w_2(t)\hfill \\ x_3(t)\hfill \\ y_3(t)\hfill \\ w_3(t)\hfill \end{array}\right]=\left[\begin{array}{ccccccccc}1& \delta (t)& \frac{1}{2}{\delta }^2(t)& 0& 0& 0& 0& 0& 0\\ 0& 1& \delta (t)& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& \delta (t)& \frac{1}{2}{\delta }^2(t)& 0& 0& 0\\ 0& 0& 0& 0& 1& \delta (t)& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& \delta (t)& \frac{1}{2}{\delta }^2(t)\\ 0& 0& 0& 0& 0& 0& 0& 1& \delta (t)\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1(t-1)\\ y_1(t-1)\\ w_1(t-1)\\ x_2(t-1)\\ y_2(t-1)\\ w_2(t-1)\\ x_3(t-1)\\ y_3(t-1)\\ w_3(t-1)\end{array}\right]+\left[\begin{array}{c}{\epsilon }_1(t)\\ {\eta }_1(t)\\ {\alpha }_1(t)\\ {\epsilon }_2(t)\\ {\eta }_2(t)\\ {\alpha }_2(t)\\ {\epsilon }_3(t)\\ {\eta }_3(t)\\ {\alpha }_3(t)\end{array}\right]$$

where subscripts indicate the clocks.

In more compact form this is

$$X(t)=\mathrm{\Phi }(t)X(t-1)+U(t),t=1,2,\dots ,$$ (3.1)

where X(t) is the state vector and ϕ(t) is the state transition matrix. The stochastic elements of the transition from one state to the next are contained in U(t).

The clocks are never read directly, but, using sophisticated electronics, the time differences between clocks can be read with a precision of less than a nanosecond. “Perfect” time, which we can never observe, cancels out, leaving an observation of the clock error differences. z₁(t) = x₁(t) – x₂(t) and z₂(t) = x₁(t) – x₃(t). We write the observation equation in matrix form as

$$\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]=\left[\begin{array}{ccccccccc}1& 0& 0& -1& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& -1& 0& 0\end{array}\right]\left[\begin{array}{l}{x}_1(t)\hfill \\ y_1(t)\hfill \\ w_1(t)\hfill \\ x_2(t)\hfill \\ y_2(t)\hfill \\ w_2(t)\hfill \\ x_3(t)\hfill \\ y_3(t)\hfill \\ w_3(t)\hfill \end{array}\right]+\left[\begin{array}{c}{v}_1(t)\\ v_2(t)\end{array}\right]$$

$$Z(t)=H(t)X(t)+V(t),t=1,2,\dots .$$ (3.2)

Z(t) is the vector of observed clock time differences and H(t) is the observation matrix. V(t) is a vector of observational errors. We write H(t) as a time-varying matrix because, in the multivariate case, partially missing data is represented by deleting rows from H(t) thus changing the dimension of Z(t), H(t), and V(t). In some cases it is possible to recover from a problem with the reference clock by defining a new (temporary) reference and changing the patterns of ± 1 and zeros in H(t). This is described in detail in Jones and Tryon [4].

For small δ(t) the covariance matrix of the transition errors, U(t), is of the diagonal form δ(t)Q where Q is

$$Q=\left[\begin{array}{ccccccccc}{{\sigma }_{\epsilon 1}}^2& & & & & & & & \\ & {{\sigma }_{\eta 1}}^2& & & & & & & \\ & & {{\sigma }_{\alpha 1}}^2& & & & & 0& \\ & & & {{\sigma }_{\epsilon 2}}^2& & & & & \\ & & & & {{\sigma }_{\eta 2}}^2& & & & \\ & & & & & {{\sigma }_{\alpha 2}}^2& & & \\ & & & & & & {{\sigma }_{\epsilon 3}}^2& & \\ & 0& & & & & & {{\sigma }_{\eta 3}}^2& \\ & & & & & & & & {{\sigma }_{\alpha 3}}^2\end{array}\right]$$ (3.3)

Note that the matrix Q contains all the parameters to be estimated except w.

If the time offset of each clock is measured to the nearest nanosecond and is otherwise error free, the observational error vector V(t) has covariance matrix

$$R(t)=\left[\begin{array}{cc}1/12& 0\\ 0& 1/12\end{array}\right],$$ (3.4)

since the variance of a uniformly distributed random variable from −0.5 to 0.5 is 1/12. The dimension of R(t) will also vary with time if there are partially missing data.

4. The Kalman Recursion

First, we adopt some notation. By X(t|s), s ⩽ t we denote the best estimate of the state vector at sample time t, based on all the data up to and including sample time s. We define P(t|s) to be the covariance matrix of X(t|s). Similarly, Z(t|s) will be the predicted observation at time t based on all the data up to time s.

The recursion proceeds through the following steps (Kalman [3]).

1. Given the state vector and its covariance matrix at any sample time, say t, we can predict the state vector one observation interval into the future using the transition eq (3.1). The prediction is

   $$X(t+1|t)=\mathrm{\Phi }(t+1)X(t|t)$$ (4.1)

   since the expected value of the stochastic component of the transition is zero. The covariance matrix of the prediction is

   $$P(t+1|t)=\mathrm{\Phi }(t+1)P(t|t){\mathrm{\Phi }}^{\prime }(t+1)+\delta (t+1)\mathrm{Q},$$ (4.2)

   where the first term on the right is the covariance matrix of the linear operation in the state transition and the second term is the covariance of the additive stochastic component.
2. From the observation matrix and the predicted state we can predict the next observation.

   $$Z(t+1|t)=H(t+1\left)X\right(t+1\left|t\right).$$ (4.3)
3. We next compare the prediction with the actual data (when it becomes available in a real-time application). The difference is the recursive residual, or innovation,

   $$I(t+1)=Z(t+1)-Z(t+1|t),$$ (4.4)

   which has covariance matrix

   $$C(t+1)=H(t+1)P(t+1|t)H^{\prime }(t+1)+R(t+1).$$ (4.5)

   The residuals are critically important. Later, they will be used for checking the fit of the model and estimating the parameters. For now, we will use the information in the residual to complete the recursion.

4. Let

   $$\mathrm{\Delta }(t+1)=P(t+1|t)H^{\prime }(t+1)C^{-1}(t+1).$$ (4.6)

   This is sometimes called the Kalman gain.
   Using the Kalman gain we can update the predicted state and its covariance

   $$X(t+1|t+1)=X(t+1|t)+\mathrm{\Delta }(t+1)I(t+1)$$ (4.7)

   and

   $$P(t+1|t+1)=P(t+1|t)-\mathrm{\Delta }(t+1)H(t+1)P(t+1|t).$$ (4.8)

   This completes the recursion.

5. Maximum Likelihood Modeling and Estimation

In this section we will compare the classic use of the Kalman filter with our method of application. In the classical application, unknown parameters to be estimated can appear only in the state vector. All other quantities which appear in the recursion must be known. A single pass of the recursion through the data (often in real time) provides the latest estimate of the state vector and its covariance at each point in time. This is exactly how the Kalman filter is applied to forming a time scale. Given the model and estimates of the parameters, the recursion gives the updated state vector after each new observation. The first, fourth, and seventh, etc., elements of the state vector are estimates of the clock errors, from which, along with their uncertainties from the state covariance matrix, we can estimate time.

Our interest, however, is in evaluating how well the clock model fits; real data, and in estimating the parameters. To do this, we make use of two facts concerning the residuals, I(t), t = 1, 2, …, N.

1. If the model is correct, and the recursion is run through the data with the correct values of the unknown parameters, the residuals will form Gaussian white noise series. Standard statistical tests can then be used to determine if the residuals are in fact Guassian white noise. If not, the structure of the residuals can often give some clues as to the defects in the model.

2. From the residuals and their covariance matrix, obtained by running the recursion with any fixed values of the unknown parameters, the likelihood function for those parameter values can be computed. Specifically, the −2 ln likelihood function (ignoring the additive constant) is

   $$L=\sum _t\left[\ln |C(t)|+I^{\prime }(t)C^{-1}(t)I(t)\right].$$ (5.1)

   The maximum likelihood estimates of the parameters are those for which L is minimized. Starting from initial guesses, we can use iterative nonlinear function minimization methods to find the estimates. Evaluating the function L for new trial values of the parameters requires one pass of the Kalman recursion through the data. Note that the parameters to be estimated may appear anywhere in the structure of the Kalman recursion.

6. Computational Procedures

It is not necessary to invert the residual covariance matrix, C(t), when computing the likelihood function or updating the predicted state vector and its covariance. If the upper triangular portion of C(t+1) is augmented by H(t+1)P(t+1|t), and I(t+1) to form the partitioned matrix

$$\left[C\right(t+1\left)\right|H(t+1)P(t+1|t\left)\right|I(t+1)],$$ (6.1)

a single call to a Choleskey factorization routine (Graybill [5], p. 232) which factors

$$C(t+1)=T^{\prime }(t+1)T(t+1),$$ (6.2)

where T(t+1) is upper triangular, will replace the partitioned matrix by

$$\left[T(t+1)\left|{\left[T^{\prime }(t+1)\right]}^{-1}H(t+1)P(t+1|t)\right|{\left[T^{\prime }(t+1)\right]}^{-1}I(t+1)\right].$$ (6.3)

If we call the parts of the new partitioned matrix

$$\left[T\right(t+1\left)\right|B(t+1)\left|D\right(t+1\left)\right],$$ (6.4)

the updated state and state covariance matrices become

$$X(t+1|t+1)=X(t+1|t)+B^{\prime }(t+1)D(t+1)$$ (6.5)

and

$$P(t+1|t+1)=P(t+1|t)-B^{\prime }(t+1)B(t+1).$$ (6.6)

The −2 ln likelihood function becomes

$$L=\sum _t\left(\sum _i\ln {t^2}_{ii}(t)+D^{\prime }(t)D(t)\right)$$ (6.7)

where t_ii(t) are the diagonal elements of T(t).

Missing data are easily handled by the Kalman filter procedure. However, there are two distinct situations. First, all the data may be missing at one or several successive observation times, and second, occurring only in multivariate data, only part of the data may be available on a given occasion. For example, one or more, but not all, of the clock differences are missing on that occasion.

The first case is most easily dealt with. In the present model, the unequal spacing feature can account for any size gap in the data by proper choice of δ(t). This, however, is a feature of random walk based models and may not apply to other models. A more general procedure for missing data is the following: Suppose k ⩾ 1 successive observations are missing. Simply repeat step one in the recursion k additional times to obtain the predicted state, X(t+k+1|t), and its covariance, P(t+k+1|t), for the next observation time for which there is data. Then proceed with the remainder of the recursion. There is no residual and no contribution to the likelihood function when there is no data (Jones [6]).

In the second case, partial loss of data, i.e., missing elements of the data vector Z(t), can be represented by eliminating the corresponding rows of the observation matrix, H(t). Similarly, rows of the observational error vector V(t) and rows and columns of the error covariance matrix R(t) causes no problem with the remaining steps of the recursion, which proceed normally. The information available in the data is propagated through the recursion to correctly update the state vector prediction and its estimated covariance matrix.

The matrix operations in the recursion are, for reasons of efficiency, best coded to take advantage of the specific structure (many zeros) of each matrix. Using available general purpose subroutines to perform the required matrix operations would increase the cost of computer resources enormously. These calculations can be adapted to a time-varying H(t). One approach is to use indicator variables for missing data to form the various reduced matrices directly. Another approach is to note that pre- and/or post-multiplying by H(t) with rows missing is equivalent to performing the operation with the original H matrix and then eliminating the appropriate rows and/or columns of the product matrix and closing it up. For example, the residual covariance matrix

$$C(t+1)=H(t+1)P(t+1|t)H^{\prime }(t+1)+R(t+1)$$

with, say, the second and fourth elements of the data vector missing can be obtained by using the original H and R but then eliminating the second and fourth rows and columns from C(t+1). It is straightforward to write general purpose subroutines to eliminate rows and/or columns of a matrix and close up the spaces. Again, this can be done in response to indicator variables denoting missing observations.

To start the recursion the initial state X(0|0) and its covariance P(0|0) are needed. Both depend on the application. The time states could be set to zero and the clocks set to agree with International Atomic Time as defined by the BIH. The corresponding variances on the diagonal of P(0|0) would be determined by the accuracy of the intercomparison. If a strictly internal application such as parameter estimation or a time interval measurement was desired, the time states could be set to agree with the difference readings at t = 0, with observational error variances set to the appropriate value for roundoff error. The frequency states might be measured by intercomparison with the frequency standards and the variance determined from the measurement uncertainty. When a measurement is not possible a best guess at the frequency offset can be used with a corresponding guess at its uncertainty used for the variance.

7. Data Analysis

The data used for this analysis were collected over a period of 333 days beginning on February 16, 1979, during which seven clocks listed below were in essentially uninterrupted normal operation. Clock differences were recorded daily to the nearest nanosecond.

Clock Number	Identification
601 (Reference)	HP model 5061A option 004 serial #601
167	HP model 5060A serial #167
137	HP model 5060A serial #137
1316	HP model 5061A option 004 serial #1316
323	HP model 5061A 004 serial #323
324	HP model 5061A 004 serial #324
8	Frequency and Time System model 400 serial #8

In addition to occasional variability in the time of data collection, two successive days were missing entirely. On three other occasions, single clocks had obvious read errors which when discarded resulted in partially missing data. Several dozen other observations which had been flagged as possible errors by the ad hoc procedure then in use were examined visually, judged to be not serious, and retained in the analysis.

Table 1 gives the results of the computations. First we note that the inclusion of deterministic trends (model II) results in a drop of 41 in the −2 ln likelihood function value over the no-trend model (model I). The reduction is distributed as X²(6) under the hypothesis of model I, so this is highly significant. There is less than one chance in a thousand that this is a spurious result. Three of the seven clocks had significant trends. The inclusion of random walk drifts (model III), however, makes no improvement. Furthermore, the estimated values for the σ_α’s are all approximately zero and the estimated initial values of the drift, ω(0), are about the same as the deterministic drifts. The conclusion is that several frequency trends are present in this data and that they are constant over the year, rather than wandering as a random walk. It should be noted that one of the drifting clocks had just begun operation while the remaining two were nearing their end of life and failed shortly after the test period. The remaining clocks were in their “middle years.” The standard errors of the parameter estimates given in the table are obtained from the estimated covariance matrix as approximated by twice the inverse of the Hessian of the −2 ln likelihood function, L.

Table 1.

Results of data analysis.

	Model I No Trend		Model II Deterministic Trend		Model III Random Walk Drift
	L = 10609.1		L = 10567.8		L = 10567.7
Clock Number	Param. Est.*	S.E	Param. Est.*	S.E.	Param. Est.*
601	${\widehat{\sigma }}_{ϵ}$ = 7.42	.32	${\widehat{\sigma }}_{ϵ}$ = 7.46	.32	${\widehat{\sigma }}_{ϵ}$ = 7.47
	${\widehat{\sigma }}_{\eta }$ = .86	.24	${\widehat{\sigma }}_{\eta }$ = .44	.26	${\widehat{\sigma }}_{\eta }$ = .48
			$\widehat{\omega }$ = .152	.038	$\widehat{\omega }(0)$ = .152
					${\widehat{\alpha }}_{\alpha }$ = 4.1×10−5
167	${\widehat{\sigma }}_{ϵ}$ = 13.45	.56	${\widehat{\sigma }}_{ϵ}$ = 13.45	.56	${\widehat{\sigma }}_{ϵ}$ = 13.46
	${\widehat{\sigma }}_{\eta }$ = 1.15	.39	${\widehat{\sigma }}_{\eta }$ = 1.11	.36	${\widehat{\sigma }}_{\eta }$ = 1.07
			$\widehat{\omega }$ .052	.061	$\widehat{\omega }(0)$ = .054
					${\widehat{\sigma }}_{\alpha }$ = 3.7×10−5
137	${\widehat{\sigma }}_{ϵ}$ = 10.03	.45	${\widehat{\sigma }}_{ϵ}$ = 10.04	.45	${\widehat{\sigma }}_{ϵ}$ = 10.06
	${\widehat{\sigma }}_{\eta }$ = 1.71	.36	${\widehat{\sigma }}_{\eta }$ = 1.60	.36	${\widehat{\sigma }}_{\eta }$ = 1.57
			$\widehat{\omega }$ = .179	.081	$\widehat{\omega }(0)$ = .178
					${\widehat{\sigma }}_{\alpha }$ = 2.2×10−4
1316	${\widehat{\sigma }}_{ϵ}$ = 3.61	.24	${\widehat{\sigma }}_{ϵ}$ = 3.62	.25	${\widehat{\sigma }}_{ϵ}$ = 3.59
	${\widehat{\sigma }}_{\eta }$ = 1.29	.24	${\widehat{\sigma }}_{\eta }$ = 1.36	.24	${\widehat{\sigma }}_{\eta }$ = 1.38
			$\widehat{\omega }$ = -.017	.070	$\widehat{\omega }(0)$ = -.015
					${\widehat{\sigma }}_{\alpha }$ = 1.3×10−4
323	${\widehat{\sigma }}_{ϵ}$ = 3.27	.24	${\widehat{\sigma }}_{ϵ}$ = 3.53	.22	${\widehat{\sigma }}_{ϵ}$ = 3.52
	${\widehat{\sigma }}_{\eta }$ = 1.54	.21	${\widehat{\sigma }}_{\eta }$ = .73	.20	${\widehat{\sigma }}_{\eta }$ = .70
			$\widehat{\omega }$ = -.313	.046	$\widehat{\omega }$ = -.314
					${\widehat{\sigma }}_{ϵ}$ = 4.9×10−5
324	${\widehat{\sigma }}_{ϵ}$ = 3.30	.25	${\widehat{\sigma }}_{ϵ}$ = 3.30	.25	${\widehat{\sigma }}_{ϵ}$ = 3.30
	${\widehat{\sigma }}_{\eta }$ = 1.42	.23	${\widehat{\sigma }}_{\eta }$ = 1.40	.22	${\widehat{\sigma }}_{\eta }$ = 1.41
			$\widehat{\omega }$ = .035	.072	$\widehat{\omega }(0)$ = .035
					${\widehat{\sigma }}_{ϵ}$ = 7.9×10−5
8	${\widehat{\sigma }}_{ϵ}$ = 9.08	.43	${\widehat{\sigma }}_{ϵ}$ = 9.09	.43	${\widehat{\sigma }}_{ϵ}$ = 9.09
	${\widehat{\sigma }}_{\eta }$ = 2.68	.39	${\widehat{\sigma }}_{\eta }$ = 2.65	.39	${\widehat{\sigma }}_{\eta }$ = 2.66
			$\widehat{\omega }$ = -.088	-	$\widehat{\omega }(0)$ = -.090
					${\widehat{\sigma }}_{\alpha }$ = 3.9×10−5

^*Units are in nanoseconds.

In model II it is necessary to constrain the solution so that the sum of the drifts is zero. This means that we cannot detect a common drift from clock difference readings. Because of this constraint, a standard error for clock #8 is not available. Due to the large cost of computing the 28 × 28 Hessian for model III, which we have rejected anyway, the standard errors of the estimates have not been computed.

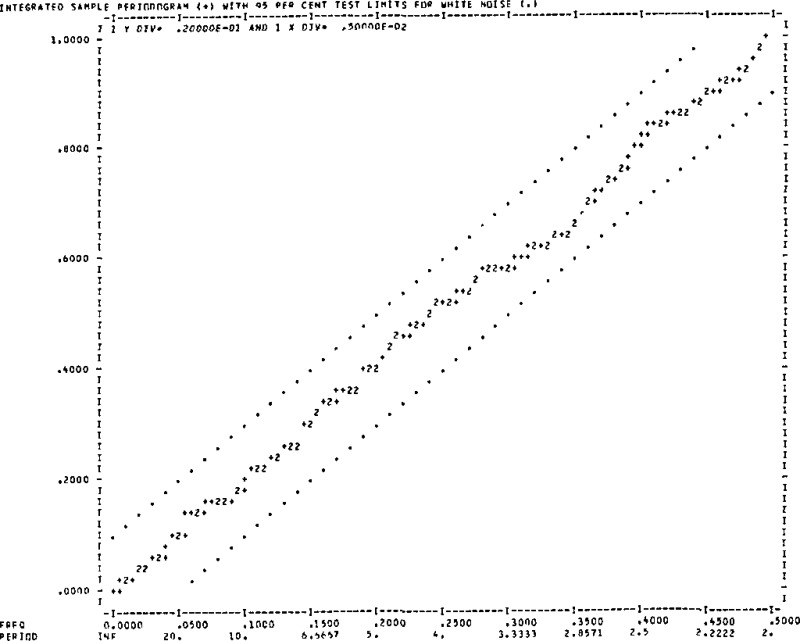
Figures 1a–f are integrated periodograms of the six series of residuals. The parallel lines represent five percent significance test limits for white noise. That is, only five percent of actual white noise series so tested will wander outside the lines. In this data set, only one pair of clocks (601 minus 167) two) show a slight deviation from white noise. We conclude that this model fits very well. Figures 2a–f are histograms of the six residual series. Also given are three different tests for normality. All the series are well approximated by the normal (Gaussian) distribution which verifies that the assumed likelihood function was reasonable.

Figure 1a.

Residuals from clock 601 minus clock 167.

Figure 1f.

Residuals from clock 601 minus clock 8.

Figure 2a.

Histogram—residuals from clock 601 minus clock 167.

Figure 2f.

Histogram—residuals from clock 601 minus clock 8.

Figure 1b.

Residuals from clock 601 minus clock 137.

Figure 1c.

Residuals from clock 601 minus clock 1316.

Figure 1d.

Residuals from clock 601 minus clock 323.

Figure 1e.

Residuals from clock 601 minus clock 324.

Figure 2b.

Histogram—residuals from clock 601 minus clock 137.

Figure 2c.

Histogram—residuals from clock 601 minus clock 1316.

Figure 2d.

Histogram—residuals from clock 601 minus clock 323.

Figure 2e.

Histogram—residuals from clock 601 minus clock 324.

We note in conclusion that, having selected the constant drift model, we could reduce the dimension of the state space model by one-third by rewriting the clock model as

$$\left[\begin{array}{l}x(t)\hfill \\ y(t)\hfill \end{array}\right]=\left[\begin{array}{cc}1& \delta (t)\\ 0& 1\end{array}\right]\left[\begin{array}{l}x(t-1)\hfill \\ y(t-1)\hfill \end{array}\right]+\left[\begin{array}{c}{\delta }^2(t)/2\\ \delta (t)\end{array}\right]w+\left[\begin{array}{l}\epsilon (t)\hfill \\ \eta (t)\hfill \end{array}\right]$$

The state prediction in the first step of the recursion then becomes

$$X(t+1|t)=\mathrm{\Phi }(t+1)X(t|t)+A(t+1)$$

where

$$A(t)=\left[\begin{array}{c}\frac{{\delta }^2(t)}{2}{w}_1\\ \delta (t)w_1\\ \frac{{\delta }^2(t)}{2}{w}_2,\\ \delta (t)w_2\\ \cdot \\ \cdot \\ \cdot \end{array}\right]$$

and X(t) and ϕ(t) are redefined from the clock model in the obvious way. This model would be suitable for estimation purposes but not for a time scale algorithm. With the drift in the state vector we can enter the uncertainty of its estimation in the initial state covariance matrix. It is then propagated through to the uncertainty in time. The simplified model above assumes ω is known without error.

8. Conclusion

The Kalman filter is a powerful tool for maximum likelihood model fitting and parameter estimation in time series analysis. We have established the validity of the proposed models for clock behavior and obtained precise estimates of clock parameters. The existence of deterministic frequency drifts over a period of a year has been demonstrated in clocks at the beginning and end of their life span.

The primary disadvantage of these methods is the cost of function evaluation in the nonlinear optimization process. The analysis of a year of data on seven clocks takes 10 minutes on a CDC Cyber 170/750 computer and 10 hours on the DEC 11/70. Use of state-of-the-art optimization codes is essential. We use an optimization package especially designed for maximum likelihood applications. It is adapted from the package written by Weiss [7], based on algorithms by Dennis and Schnabel [8]. The code used on the CDC Cyber 170/750 is part of a preliminary version of the National Bureau of Standard’s STARPAC library [9].