Relaxed ordered subset preconditioned alternating projection algorithm for PET reconstruction with automated penalty weight selection

Abstract

Purpose

Performance of the preconditioned alternating projection algorithm (PAPA) using relaxed ordered subsets (ROS) with a non‐smooth penalty function was investigated in positron emission tomography (PET). A higher order total variation (HOTV) regularizer was applied and a method for unsupervised selection of penalty weights based on the measured data is introduced.

Methods

A ROS version of PAPA with HOTV penalty (ROS‐HOTV‐PAPA) for PET image reconstruction was developed and implemented. Two‐dimensional PET data were simulated using two synthetic phantoms (geometric and brain) in geometry similar to GE D690/710 PET/CT with uniform attenuation, and realistic scatter (25%) and randoms (25%). Three count levels (high/medium/low) corresponding to mean information densities ($\overline{ID}$s) of 125, 25, and 5 noise equivalent counts (NEC) per support voxel were reconstructed using ROS‐HOTV‐PAPA. The patients’ brain and whole body PET data were acquired at similar $\overline{ID}$s on GE D690 PET/CT with time‐of‐fight and were reconstructed using ROS‐HOTV‐PAPA and available clinical ordered‐subset expectation‐maximization (OSEM) algorithms.

A power‐law model of the penalty weights’ dependence on $\overline{ID}$ was semi‐empirically derived. Its parameters were elucidated from the data and used for unsupervised selection of the penalty weights within a reduced search space. The resulting image quality was evaluated qualitatively, including reduction of staircase artifacts, image noise, spatial resolution and contrast, and quantitatively using root mean squared error (RMSE) as a global metric. The convergence rates were also investigated.

Results

ROS‐HOTV‐PAPA converged rapidly, in comparison to non‐ROS‐HOTV‐PAPA, with no evidence of limit cycle behavior. The reconstructed image quality was superior to optimally post‐filtered OSEM reconstruction in terms of noise, spatial resolution, and contrast. Staircase artifacts were not observed. Images of the measured phantom reconstructed using ROS‐HOTV‐PAPA showed reductions in RMSE of 5%–44% as compared with optimized OSEM. The greatest improvement occurred in the lowest count images. Further, ROS‐HOTV‐PAPA reconstructions produced images with RMSE similar to images reconstructed using optimally post‐filtered OSEM but at one‐quarter the NEC.

Conclusion

Acceleration of HOTV‐PAPA was achieved using ROS. This was accompanied by an improved RMSE metric and perceptual image quality that were both superior to that obtained with either clinical or optimized OSEM. This may allow up to a four‐fold reduction of the radiation dose to the patients in a PET study, as compared with current clinical practice. The proposed unsupervised parameter selection method provided useful estimates of the penalty weights for the selected phantoms’ and patients’ PET studies. In sum, the outcomes of this research indicate that ROS‐HOTV‐PAPA is an appropriate candidate for clinical applications and warrants further research.

1. Introduction

Total variation (TV) regularization via the gradient favors images with sparse gradients,^{1, 2} which tends to remove noise while preserving edges. As such, it has been very successful in image denoising because it preserves details. This has made it an interesting candidate for emission tomography. However, in images without sparse gradients, TV regularization can create piecewise constant artifacts, often referred to as “staircase” artifacts. Unfortunately, images reconstructed from positron emission tomography (PET) and single photon emission computed tomography (SPECT) often have nonsparse gradients, due to a number of factors, including large point spread functions, and partial volume effects from coarse reconstruction grids. To deal with this problem, a number of researchers^{3, 4, 5} have shown that using higher order gradients can reduce or remove these “staircase" artifacts. In particular, Li & Zhang et al.⁵ applied it to penalized‐likelihood SPECT image reconstruction. The TV regularizer creates several other challenges, including not being differentiable everywhere, slow reconstruction convergence, and sensitivity of resulting images to regularization weights.

The problem of nondifferentiability is especially acute because it takes place where the penalty is active, making it difficult to avoid and making convergence slow when using conventional gradient descent schemes. A number of algorithms have been proposed to address this, including those derived from the augmented Lagrangian framework, e.g., Alternating Direction Method of Multipliers (ADMM),^{6, 7, 8} others derived from a primal‐dual framework, e.g., Chambolle–Pock,^{9, 10, 11} and those derived from a fixed‐point proximity framework,^{12, 13} e.g., Preconditioned Alternating Projection Algorithm (PAPA).^{5, 14, 15}

PAPA, in particular, is suitable for optimization problems with three convex terms.¹ Furthermore, PAPA's explicit form is easily derived, unlike ADMM, where the minimizations of the alternating directions are unspecified and must be implemented by the user. It is noted that a well implemented version of ADMM, which allows the use of the PAPA preconditioner, can be derived via fixed‐point methods and has similar convergence properties with PAPA. In the context of PET and SPECT imaging, this includes a convex and differentiable Kullback–Leibler (KL) divergence fidelity term, along with convex nondifferentiable functions (first‐ and second‐order TV in this case), and a non‐negativity constraint.

Algorithm convergence can be accelerated through the use of data subsets. Examples include ordered‐subset expectation‐maximization (OSEM)¹⁶ and sequential frame subsets used in list‐mode EM,^{17, 18, 19} both of which use disjoint subsets of the data to update images. Unfortunately, after initial improved convergence, these methods almost always become “stuck” at a limit cycle and fail to converge to the minima of the objective function.²⁰ Bertsekas²¹ introduced a convergent class of incremental gradient methods to address this. These incremental gradient methods can use ordered subsets (OS) or other data subsets to produce convergent algorithms. In particular, a number of convergent algorithms for gradient descent have been developed.^{22, 23, 24, 25, 26, 27} Of these, block sequential regularized expectation maximization (BSREM)^{23, 24} has been used in a recent clinical implementation. However, even using data subsets, it still requires a large dedicated computer in order to make the computing time clinically viable.

It is also known that the convergence of these algorithms is both data‐ and penalty weight‐dependent, making their assessment complex. Further until recently, given a particular class of imaging problem (i.e., a typical image for a particular patient size, disease, region, etc.), data from that class member, and a particular image quality metric, there were no simple theoretical means with which to choose the optimal penalty weights. At present, several researchers have developed theoretical frameworks based on the discrepancy principle (DP) given Gaussian and Poisson noise for estimating the penalty weights of single parameters.^{28, 29, 30, 31}

The DP is the idea that the uncertainty of the data should match the variability of the object or penalty function. However, it has been pointed out by several researchers that this match does not necessarily result in a minimum mean squared error (MMSE) image,^{32, 33} nor if MMSE is necessarily the right goal.³⁴ Nevertheless in estimating MMSE penalty weights, Eldar³² has developed a generalized framework that does not require knowledge of the true distribution. However, it is computationally intensive, and optimal penalty selection remains a difficult task, making the adoption of regularized algorithms even more challenging.

In this paper, these problems are addressed together and the resulting algorithm is applied to both simulation and clinical data. That is, we demonstrate the performance of a relaxed ordered subsets (ROS) version of PAPA (KL‐divergence) using optimized penalty weights at three realistic count levels, first by simulation and then using patient data are demonstrated. In each case, the optimized penalties are first determined using an empirical methodology, with connections to the DP, for a simple image quality metric for quantitative tasks: root‐mean‐squared error (RMSE). The results are then used with ROS‐PAPA to demonstrate convergence acceleration and show improved image quality relative to conventional unpenalized image reconstruction. In this way, the simulations provide support and insight for the clinical results.

2. Methodology

2.A. Objective function description

Let $f\in {\mathbb{R}}^d$ denote the true activity distribution in d volume elements of the reconstruction space, $g\in {\mathbb{R}}^N$ the detected coincidence events at N pairs of detector elements, $\mathit{\gamma }\in {\mathbb{R}}^N$ the additive background counts (i.e., random, scatter, and cascade counts that are independently estimated), and $A\in {\mathbb{R}}^{N}d$ the system matrix modeling the geometrical mapping, attenuation, and detector blurring. Following the notation used by Krol et al.,¹⁴ the penalized Poisson‐likelihood optimization model for PET reconstruction is as follows

$$\underset{f\in {\mathbb{R}}_{+}^d}{\text{arg min}}\left\{⟨Af,\mathbf{1}⟩-⟨\text{ln}\left(Af+\mathit{\gamma }\right),g⟩+\mathit{\lambda }R(f)\right\}.$$ (1)

The KL data fidelity 〈A·,1〉−〈 ln (A·+γ),g〉, denoted by f in subsequent sections, measures the discrepancy between the estimated and the observed data. The penalty term λR is introduced to regularize the estimate to our prior knowledge. Here, λ is a positive penalty weight; its selection is of practical importance.

The TV regularizer often introduces undesirable “staircase” artifacts when reconstructing images without sparse gradients. However, the first‐order discontinuity of TV can be relaxed by including higher order discontinuity penalties. This can be achieved by using higher‐order gradients of the image, leading to the higher order total variation (HOTV) regularization method.⁵ This work uses the HOTV regularization method, where a second‐order TV penalty is added to the TV regularizer. This results in the penalty term λR(f) in (1) being given by

$$R(f)={\mathit{\lambda }}_1{\mathit{\phi }}_1(B_{1}f)+{\mathit{\lambda }}_2{\mathit{\phi }}_2(B_{2}f),$$ (2)

where $B_1$ and $B_2$ are the first‐ and second‐order difference matrices, respectively, and ${\mathit{\phi }}_1$, ${\mathit{\phi }}_2$ are both sums of isotropic vector norms (see⁵ or Appendix A for their precise definitions).

Because the minimization of both first‐ and second‐order gradients of an image forces a compromise between the piecewise constant and the piecewise linearly varying solutions it results in solutions with substantially reduced “staircase” artifacts, as compared with only first‐order TV regularization.

2.B. Relaxed ordered‐subset high‐order total variation PAPA (ROS‐HOTV‐PAPA)

The nondifferentiable optimization model in Eq. (1) can be solved by the PAPA. Because the details of PAPA and its extension to a HOTV‐regularized reconstruction problem have been previously discussed in,^{5, 14} only a selection of interesting and useful features of PAPA have been given here. First, it allows us to deal with the functions involved in the optimization model, either through their proximity operators¹² or through their gradients. In fact, for nondifferentiable functions, the proximity operator can be a very powerful tool (for smooth functions the gradient may be simpler to implement). Second, PAPA does not require matrix inversion, which is an advantage when solving large‐scale reconstruction problems that can be quite expensive. Finally, PAPA suggests the search direction for the solution to follow the classical EM algorithm, and thus speeds up the convergence. Using the notation in Li & Zhang et al.,⁵ and the HOTV‐PAPA iterative scheme reads

$$\left\{\begin{array}{cc}{h}^{(k)}& =\text{max}\left\{f^{(k)}-\mathit{\beta }{S}^{(k)}\left(\mathrm{\nabla }F\left(f^{(k)}\right)\right.\right.\\ & \left.\left.+B_1^{\top }{b}^{(k)}+B_2^{\top }{c}^{(k)}\right),\mathbf{0}\right\}\\ b^{(k+1)}& ={\mathit{\rho }}_1\left(I-{\text{prox}}_{\frac{{\mathit{\lambda }}_1}{{\mathit{\rho }}_1}{\mathit{\phi }}_1}\right)\left(\frac{1}{{\mathit{\rho }}_1}{b}^{(k)}+B_1{h}^{(k)}\right)\\ c^{(k+1)}& ={\mathit{\rho }}_2\left(I-{\text{prox}}_{\frac{{\mathit{\lambda }}_2}{{\mathit{\rho }}_2}{\mathit{\phi }}_2}\right)\left(\frac{1}{{\mathit{\rho }}_2}{c}^{(k)}+B_2{h}^{(k)}\right)\\ f^{(k+1)}& =\text{max}\left\{f^{(k)}-\mathit{\beta }{S}^{(k)}\left(\mathrm{\nabla }F\left(f^{(k)}\right)\right.\right.\\ & \left.\left.+B_1^{\top }{b}^{(k+1)}+B_2^{\top }{c}^{(k+1)}\right),\mathbf{0}\right\}.\end{array}\right.$$ (3)

In scheme (3), b and c are dual variables, β is the step size, and S denotes a preconditioning matrix. The operator max{·,0} is a projection onto the first octant that is calculated component‐wise. The gradient of the data fidelity term has the form $\mathrm{\nabla }F(f)=A^{\top }(\mathbf{1}-\frac{g}{Af+\mathit{\gamma }})$, and the proximity operators of ${\mathit{\phi }}_1$ and ${\mathit{\phi }}_2$ have closed forms that are described in Appendix A.

To meet the time constraints due to tight clinical work‐flow, an (OS) version of PAPA is proposed. The assumption is made that the data fidelity term F can be decomposed into M smaller KL divergences $F_1,\dots ,F_M$, which satisfies the subset balance condition: $\mathrm{\nabla }F(f)\approx M\mathrm{\nabla }{F}_1(f)\approx \cdots \approx M\mathrm{\nabla }{F}_M(f)$. For OS acceleration, ∇F is replaced in (3) by $M\mathrm{\nabla }{F}_m$ and the updates in (3) are incrementally performed M times to obtain a complete outer iteration,²⁴ leading to a ROS‐PAPA,

$$\left\{\begin{array}{cc}{h}^{(k,m)}& =\text{max}\left\{f^{(k,m-1)}-{\mathit{\beta }}_k{S}^{(k,m-1)}\left(\mathrm{\nabla }{F}_m(f^{(k,m-1)})\right.\right.\\ & \left.\left.+B_1^{\top }{b}^{(k,m-1)}+B_2^{\top }{c}^{(k,m-1)}\right),\mathbf{0}\right\}\\ b^{(k,m)}& ={\mathit{\rho }}_1\left(I-{\text{prox}}_{\frac{{\mathit{\lambda }}_1}{M{\mathit{\rho }}_1}{\mathit{\phi }}_1}\right)\left(\frac{1}{{\mathit{\rho }}_1}{b}^{(k,m-1)}+B_1{h}^{(k,m)}\right)\\ c^{(k,m)}& ={\mathit{\rho }}_2\left(I-{\text{prox}}_{\frac{{\mathit{\lambda }}_2}{M{\mathit{\rho }}_2}{\mathit{\phi }}_2}\right)\left(\frac{1}{{\mathit{\rho }}_2}{c}^{(k,m-1)}+B_2{h}^{(k,m)}\right)\\ f^{(k,m)}& =\text{max}\left\{f^{(k,m-1)}-{\mathit{\beta }}_k{S}^{(k,m-1)}\left(\mathrm{\nabla }{F}_m(f^{(k,m-1)})\right.\right.\\ & \left.\left.+B_1^{\top }{b}^{(k,m)}+B_2^{\top }{c}^{(k,m)}\right),\mathbf{0}\right\}\end{array}\right.$$ (4)

with $f^{(k,0)}=f^{(k)}$ and $f^{(k+1)}=f^{(k,M)}$. The subset gradients are computed by $\mathrm{\nabla }{F}_m(f)=A_m^{\top }(\mathbf{1}-\frac{g_m}{A_{m}f+{\mathit{\gamma }}_m})$ with $A_m$, $g_m$, and ${\mathit{\gamma }}_m$ the $m^{th}$ subsets of the system matrix A, detected coincidence events g, and background counts γ, respectively. The diagonal elements of EM‐induced preconditioning matrix are given by

$$S_{jj}^{(k,m-1)}=\left\{\begin{array}{cc}M{f}_j^{(k,m-1)}/{\left(A^{\top }\mathbf{1}\right)}_j,\hfill & {\left(A^{\top }\mathbf{1}\right)}_j>0\hfill \\ M{f}_j^{(k,m-1)}.\hfill & {\left(A^{\top }\mathbf{1}\right)}_j\le 0\hfill \end{array}\right.$$ (5)

OS techniques can greatly speed up the algorithm convergence. However, they generally exhibit limit cycle behavior when using a constant step size β. Following the relaxation strategy proposed previously,²⁴ a diminishing step size is adapted,

$${\mathit{\beta }}_k=\frac{{\mathit{\beta }}_0}{\mathit{\zeta }k+1}$$ (6)

to suppress the limit cycle and push updates to further approach the minimizer. In the relaxation parameter, ${\mathit{\beta }}_k$, ζ is a constant that depends on the number of subsets, and ${\mathit{\beta }}_0$ is usually set to 1. Recalling the sufficient condition of algorithm convergence for PAPA,¹⁴

$${\mathit{\rho }}_j=\frac{1}{2\Vert B_j{\Vert }_2^2\text{max}\{S^{(k,m-1)}\}},j=1,2,$$ (7)

is set. A more detailed description of the parameters is located in Appendix A.

2.C. Image quality assessment

RMSE was used as the image quality metric due to its relationship to the goals of the DP (i.e., achieving an MMSE image) and PET's quantitative nature. This metric is appropriate for quantitative tasks, balancing the reconstructed image's bias and variance. Further, it is simple to compute and is in the same units as the image, making its interpretation clear. In all image quality comparisons, unpenalized images were postfiltered using RMSE‐optimal filtering parameters after being iterated to convergence (i.e., relative change of the objective function $<\sim {10}^{-5}-{10}^{-8}$ for patient and simulated images, respectively).

2.D. Penalty weight selection and the discrepancy principle

2.D.1. Relation to the discrepancy principle

Several researchers have shown that the DP can be used to guide penalty weight selection. In particular, Guerit et al.³¹ have shown via KL‐divergence that a penalty sub‐update can be added to Poisson denoising algorithms. However, this method relies on the Poisson discrepancy metric for image quality, which may not be optimal in the MMSE sense, and its extension to a two parameter model is unclear.

To avoid these problems, an empirical model based on fitted data whose functional form is consistent with the DP was chosen. This model's connection to the DP is illustrated using a simple minimization problem for sparse representation shown by Elad.³³ Consider the denoising problem:

$$\text{min}{\Vert x\Vert }_1\text{subject to}{\Vert y-Dx\Vert }_2^2\le \mathit{ϵ},$$ (8)

where the noisy image $y\in {\mathbb{R}}^N$ is contaminated with independent and identically distributed Gaussian noise ${\overline{\mathit{\sigma }}}_y$. This problem seeks to represent y with a unitary matrix $D\in {\mathbb{R}}^{N\times M}$ and sparse coefficient vector $x\in {\mathbb{R}}^M$. A natural choice for the error threshold is $\mathit{ϵ}=N{\overline{\mathit{\sigma }}}_y^2$, where N is the number of voxels in y. This problem can also be represented as

$$\text{min}\frac{1}{2}{\Vert y-Dx\Vert }_2^2+\mathit{\lambda }{\Vert x\Vert }_1,$$ (9)

where a particular penalty weight, λ, will produce the same result as Eq. (8).

In the original form of the problem, the interpretation of $\mathit{ϵ}$ was clear and setting its value was straight forward. In the new problem, the parameter λ is more difficult to interpret, but as suggested by the DP, it can be set as $\mathit{\lambda }={\mathit{\sigma }}_y/{\mathit{\sigma }}_x$, where ${\mathit{\sigma }}_x$ is the variability (ensemble standard deviation) of the coefficient vector x. This is motivated by thinking of the penalty weight as balancing between the energy of the residual and the regularization term.

The problem here is to match the discrepancy of KL‐divergence with HOTV penalties in Eq. (1). The standard deviation of our data from this equation is given by $\sqrt{g}$, but it is complicated by the additive noise γ. Likewise, the variability of the image is complicated by the HOTV penalty. As a result, we use a functional form that is consistent with the ratio of data noise to image variability.

Noise equivalent counts (NEC),^{35, 36, 37} defined by NEC $=\frac{T^2}{T+S+R}$ (T+R+S, true, random, and scatter), is good candidate function for data variance. For scale independence, the mean information density in a patient image is defined as the NEC per total voxels within the patient

$$\overline{ID}\triangleq \frac{NEC}{{\sum }_{j=1}^d{\left({\ell }_f\right)}_j},$$ (10)

where ${\ell }_f$, is the indicator vector of voxels within the patient (0 or 1) that can be estimated from a suitability scaled and thresholded CT image set. From this it is observed that ${\mathit{\sigma }}_y^2\propto \overline{ID}$.

Thus, given the definition in Eq. (10), projection data (g = T+R+S), and an estimate of the randoms and scatter counts (γ = R + S , necessary for reconstruction), the ID can be estimated by

$$\overline{ID}\approx \frac{1}{{\sum }_{j=1}^d{\left({\ell }_f\right)}_j}\frac{{\left[{\sum }_{i=1}^N\left(g_i-{\mathit{\gamma }}_i\right){\left({\ell }_{\mathit{\mu }}\right)}_i\right]}^2}{{\sum }_{i=1}^N{g}_i{\left({\ell }_{\mathit{\mu }}\right)}_i},$$ (11)

where ${({\ell }_{\mathit{\mu }})}_i$ is the $i^{th}$ component of the indicator vector of projection attenuation (lines of response that pass through the object).

For the image variability component, ${\mathit{\sigma }}_x$, it is noted that its scale is related to the NEC (or here ID ), and can be thought of as ${\mathit{\sigma }}_x$ being a function of ID for some particular activity distribution. Using a power‐law approximation for ${\mathit{\sigma }}_x$, the penalty weight is given as

$$\mathit{\lambda }=a{\overline{ID}}^b,$$ (12)

with free parameters a and b. Also, the use of a power‐law allows for the absorption of ${\mathit{\sigma }}_y$ into the overall functional form, and the object's variability and choice of penalty function to be accounted for by the free parameters. Furthermore, although the DP does not necessarily guarantee MMSE, the fits using Eq. (12) will use it as the optimization criterion.

2.D.2. Multiparameter penalty weight selection

Using Eq. (12), penalty weights were chosen using a two‐part optimization strategy. This strategy both reduced the search space to 1D and suppressed “staircase” artifacts from the first‐order TV term. It is noted that the first‐order term is slightly more effective in achieving MMSE and will otherwise dominate a two‐term minimization.

In the first step, at several different count levels, the first‐ and second‐order penalties were independently optimized for RMSE using a golden search. These single MMSE penalty fits for $a_1$, $a_2$ and $b_1$, $b_2$ can be written as

$$\begin{array}{cc}& {\mathit{\lambda }}_1^{*}=a_1{\overline{ID}}^{b_1},\text{and}\hfill \\ & {\mathit{\lambda }}_2^{*}=a_2{\overline{ID}}^{b_2},\hfill \end{array}$$ (13)

Next, using these relations to constrain the scale between the penalty weights, a combined MMSE penalty weight correction fit for $a^{*}$ and $b^{*}$ is performed using

$$\begin{array}{cc}& {\mathit{\lambda }}_{1,2}^{*}=a_1{\overline{ID}}^{b_1}{a}^{*}{\overline{ID}}^{b^{*}}={\mathit{\lambda }}_1^{*}{a}^{*}{\overline{ID}}^{b^{*}},\text{and}\hfill \\ & {\mathit{\lambda }}_{2,2}^{*}=a_2{\overline{ID}}^{b_2}{a}^{*}{\overline{ID}}^{b^{*}}={\mathit{\lambda }}_2^{*}{a}^{*}{\overline{ID}}^{b^{*}},\hfill \end{array}$$ (14)

where $a^{*}$ rescales the magnitude and $b^{*}$ alters the slope of the two individual MMSE penalties. This process was repeated at several count levels, and regression uncertainties were computed using a linear approximation via Taylor's expansion.

2.D.3. Optimization surrogate for patient scans

In the case of patient images, the true activity distribution is unknown. Because of this, the cold rod region of the ACR phantom (Flangeless Esser PET Phantom, Data Spectrum Corp.) was used as a surrogate. This region has the largest amount of variability of any commonly used PET phantom and includes cold structures which are well known to have poor contrast and slow convergence in reconstructed images.

The ACR phantom was filled in accordance with the ACR guidelines³⁸ and scanned at one dwell position for 30 minutes with the cold rod (solid plastic rods) section centered in the camera. Projection data with differing ID were generated by replaying the scans for different acquisition durations (3, 6, 10, and 30 min). For each replay, the ID were calculated from the projection data using Eq. (11).

The CT‐derived reference activity distribution of the cold rod section was generated using the accompanying CT images (coregistered by default), where threshold segmentation of the air, water, and plastic defined the activity distribution. These reference images, for both 300 and 700 mm FOV, are shown in the results section. The water portion of the phantom was assigned an activity concentration value from the reconstructions of the uniform region of the phantom (the high contrast cylinders were ignored). Calibration bias, the use of under converged images in clinical calibration, was avoided by individually normalizing to the mean of the activity distribution for each reconstruction.

The calibration of the ACR phantom proceeded in a manner similar to that of the simulations. Using the CT‐derived reference activity distribution, the minimum RMSE penalty weights were determined individually for both the first‐ and second‐order penalties. These results were fitted using Eq. (13). Next, the combined minimum RMSE penalty images were found, and fitted using Eq. (14). This procedure was used for each reconstructed field of view size.

2.E. Simulated PET images and phantoms

Initially 2D PET‐like data were generated to characterize the performance of the PAPA/OS‐PAPA algorithms³⁹ using Matlab (Version 2014b) in an “inverse crime” study. Simple 2D images with variable intensity were created and forward‐projected via a projection matrix built with a ray‐driven model using 32 rays per detector pair. This was based on a similar geometry to the GE D690/710 PET/CT, e.g., 6.3 mm detectors on a 256 × 256 matrix interleaved with 288 views over a 300 mm FOV. Uniform water attenuation was simulated using the PET image support. Scatter was added by forward‐projecting a highly smoothed version of the images. This was added to the attenuated image sinograms scaled by an assumed scatter fraction $SF=\frac{S}{T+S}$.³⁹ Random counts were simulated by adding a uniform uptake to these sinograms scaled by the random fraction $RF=\frac{R}{T+S+R}$.³⁹ The subsequent image was scaled to a number of total counts and Poisson noise realizations were performed at each count level.

Three count levels (high/medium/low) were used based on observed count data from patient studies in the clinic. For high, medium, and low counts¹⁸ FDG‐brain (370 MBq injected, 10‐minute acquisition 1‐hour postinjection),¹⁸ FDG‐whole body (444 MBq injected, 3‐minute per bed position acquisition 1‐hour postinjection), and antibody, (185 MBq of ${}^{89}$Zr injected, 5‐minute per bed position acquisition 3‐days postinjection), respectively, were used. These scans roughly corresponded to ID s of 125, 25, and 5 counts per support voxel. The counts, using scatter and random fractions of 25%, for the scans were scaled to match these ID s using the 2D phantom described below.

Two phantoms were simulated for the study. For the first, referred to hereafter as the Sinc+ phantom, a 2D sinc function with some uniform and constant slope inserts were used (see Figs. 1(a) and 1(b)). The sinc portion of the phantom provided a variable background, whereas the inserts provided edges and regions where staircase artifacts would likely manifest. The inserts were spread radially and azimuthally to aid the analysis. These simulations were performed using penalty weights optimized for RMSE. The second phantom, Fig. 1(c), was taken from a slice of a PET Brain scan and was subsequently denoised using the Rudin–Osher–Fatemi model¹ with HOTV.

Figure 1.

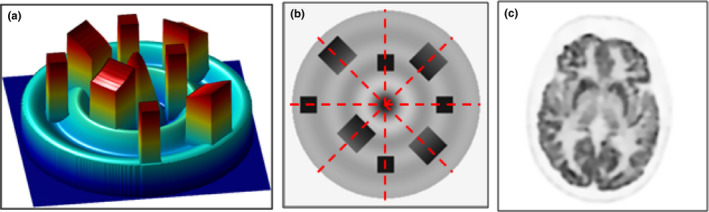
Two simulation phantoms are shown. (a) The Sinc+ phantom with four uniform square inserts and four larger sloped square inserts. (b) The intensity image of the Sinc+ phantom. Dashed lines show where intensity profiles are measured. (c) The denoised brain phantom (shown cropped from the simulated 300 mm FOV). [Color figure can be viewed at wileyonlinelibrary.com]

The simulated data were reconstructed using TV(1)‐OS‐PAPA (first‐order only), TV(2)‐OS‐PAPA (second‐order only), and HOTV‐OS‐PAPA using a modified version of the PETSTEP platform³⁹ described above. Additive noise was included in the loop. Both projectors included attenuation, and back‐projection was performed using the matrix transpose of the forward‐projection to ensure it being the adjoint forward‐projection operator. Simulations were stopped after 50 to 100 iterations.

2.F. Patient brain and whole body scans

All patients were acquired with a GE D690 PET/CT with time‐of‐flight information and reconstructed on a 256 × 256 matrix with point spread function information. The PET brain and whole body patients were injected with 370 and 444 MBq (nominal) of ¹⁸FDG and scanned ∼1 hr postinjection for 10 and 3 min, respectively. The antibody patient was injected with 176 MBq of ${}^{89}$Zr‐Df‐IAB2M (ImagineAb)⁴⁰ scanned ∼3 days postinjection for 5 min per bed position. The patient data were additionally reconstructed using conventional OSEM. For the brain patient, 3 × 32 (iterations × subsets) with a field of view of 300 mm with “standard” z‐axis (3‐point smoothing, [1 4 1]/6) and 2.6 mm FWHM Gaussian transaxial postfilters was used. For whole body and antibody patients, 2 × 16 (iterations × subsets) with a field of view of 700 mm with “heavy” z‐axis (3‐point smoothing, [1 2 1]/4) and 6.4 mm FWHM Gaussian transaxial postfilters was used.

The ROS‐HOTV‐PAPA reconstructions were performed using a modified version of the GE PET Toolbox release 2.0.⁴¹ Similar to GE's Q.Clear reconstruction 25 × 24 iterations and subsets were used.

3. Results

3.A. Simulation penalty weight selection

Figure 2 shows the RMSE‐optimal penalty weights as a function of ID (see Table 1 for the ID values). The solid red and blue lines represent the individual first‐ and second‐order TV penalty fits, which show excellent agreement with the suggested power‐law relationship with correlation coefficients greater than 0.98.

Figure 2.

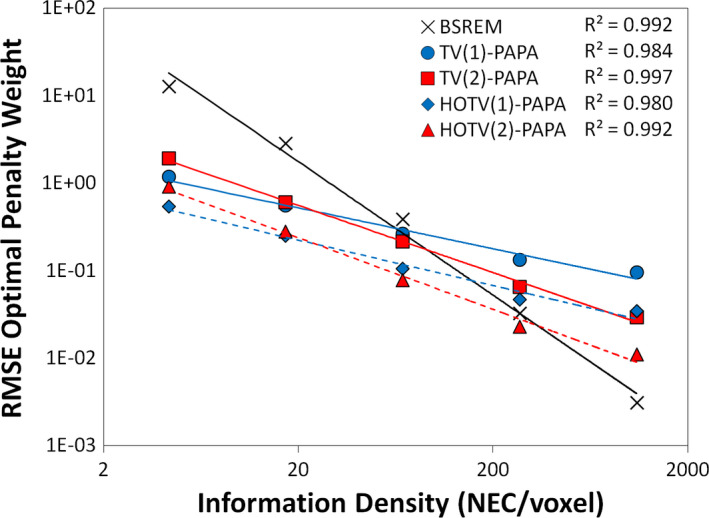
Minimum RMSE penalty weights as a function of information density for the simulated Sinc+ phantom are shown. The lines show the power‐law fits of the individual penalties with RMSE‐optimal penalty weights as a function of ID for the Sinc+ phantom. The first‐ and second‐order individual penalties use the TV(1) and TV(2) prefixes, respectively (and similarly for the combined penalty using the HOTV prefixes). The dashed lines show the minimum RMSE fit for the combined penalties using the same ID ‐dependent scaling term, where the individual penalty fits provide the relative penalty weight scaling. Ten realizations over a wide range of values (see Table 1) were used (error bars smaller than marker size) for each penalty weight estimate. [Color figure can be viewed at wileyonlinelibrary.com]

Table 1.

Percent improvement in RMSE of PAPA with TV(1), TV(2), and HOTV penalties using minimum RMSE fit penalty weights when compared to optimally Gaussian postfiltered fully converged ML‐EM is shown for a wide range of information densities for both the Sinc+ and brain phantoms

ID	Sinc+
	4.3	17.1	68.4	273.3	1093
$\mathrm{\Delta }RMS{E}_{TV(1)}$	13.9%	21.7%	28.2%	31.5%	28.3%
$\mathrm{\Delta }RMS{E}_{TV(2)}$	0.5%	9.4%	11.3%	12.2%	9.9%
$\mathrm{\Delta }RMS{E}_{HOTV}$	15.1%	20.0%	21.3%	24.4%	22.2%

ID	Brain phantom
	4.4	17.5	69.8	279.2	1116
$\mathrm{\Delta }RMS{E}_{TV(1)}$	5.3%	7.7%	9.3%	9.1%	9.7%
$\mathrm{\Delta }RMS{E}_{TV(2)}$	6.9%	9.1%	10.2%	10.4%	10.2%
$\mathrm{\Delta }RMS{E}_{HOTV}$	9.0%	10.8%	14.5%	14.3%	13.8%

In Figure 2, the dashed red and blue lines represent the penalty weights for the combined HOTV penalties. These fits result from a combined second optimization process where the ratio of the individual fits is fixed as described by Eq. (14). The resulting fits again show correlation coefficients near or greater than 0.98. This suggests that the resulting penalty weights are a reasonable estimate for minimum RMSE.

The BSREM algorithm (the blue line in Fig. 2) was added using a simple quadratic difference penalty to show that this methodology works for that type of penalty as well.

3.B. Staircase artifact reduction

TV‐penalties are known to produce “staircase” artifacts that are dependent on the ratio of the penalty weights. As shown in Fig. 3, the addition of a TV second‐order gradient can reduce these artifacts while preserving edges using the minimum RMSE penalty weights derived from the fixed‐ratio fits in Fig. 2.

Figure 3.

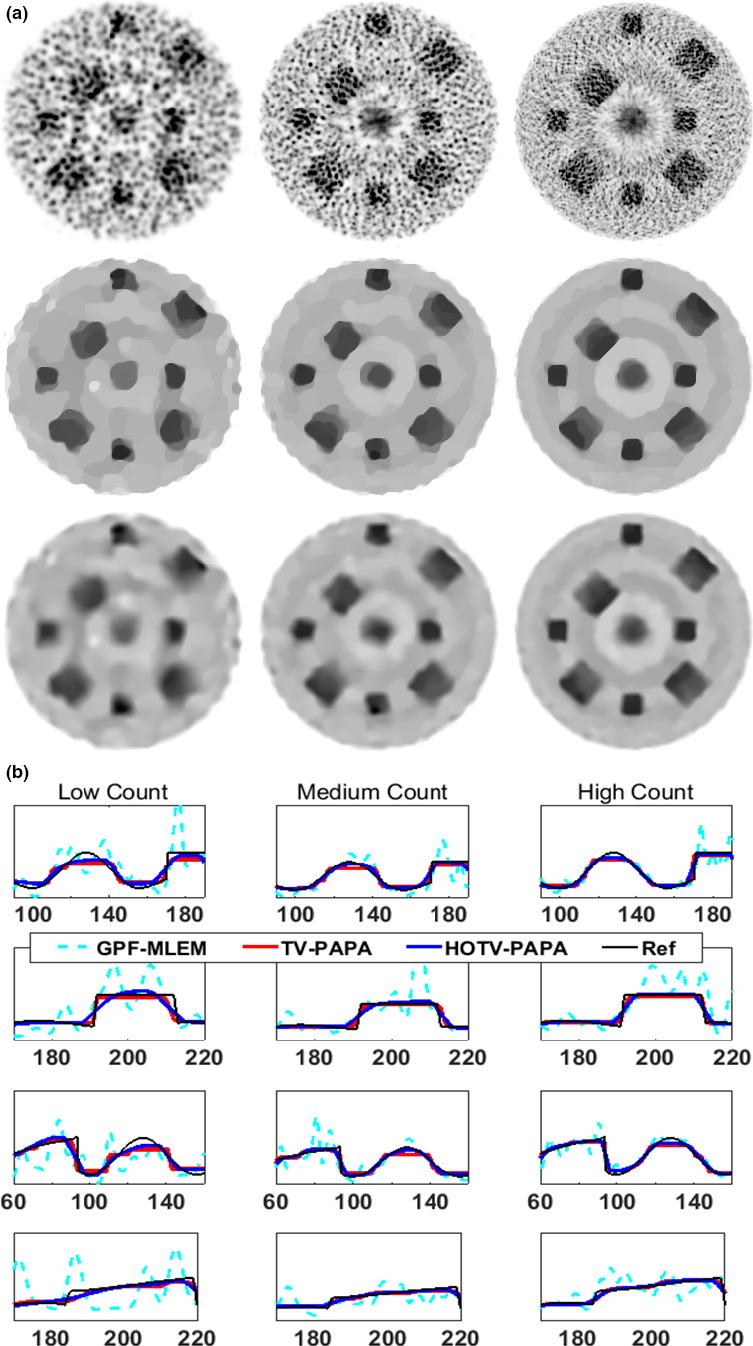
Images (top) and profiles (bottom) from the simulated Sinc+ phantom for (left to right) low, medium, and high count data are shown. The columns from left to right represent the low, medium and high count data of the Sinc+ phantom. The top three image rows are optimal Gaussian postfiltered (GPF‐)MLEM, TV(1)‐PAPA, and HOTV‐PAPA reconstructions. Each column of plots on the remaining rows represents segments of the four profiles shown in dashed lines in Fig. 1(b). [Color figure can be viewed at wileyonlinelibrary.com]

3.C. Comparison of relative penalty performance

The fitted penalty weights for TV(1), TV(2), and HOTV image reconstructions exceeded the performance of optimally postfiltered, fully converged OSEM reconstruction (in the RMSE sense). This is shown in Table 1 for both the Sinc+ phantom and the brain phantom for a wide range of ID s where each increment represents a factor of four over increase of the prior value.

Figure 4 shows the normalized RMSE improvement for HOTV compared with optimally postfiltered maximum‐likelihood expectation‐maximization (ML‐EM). For each of these phantoms, HOTV‐PAPA outperforms, in the RMSE sense, postfiltered OSEM, suggesting that HOTV‐PAPA can reconstruct equivalent image quality at almost one‐quarter of the counts as conventional ML‐EM.

Figure 4.

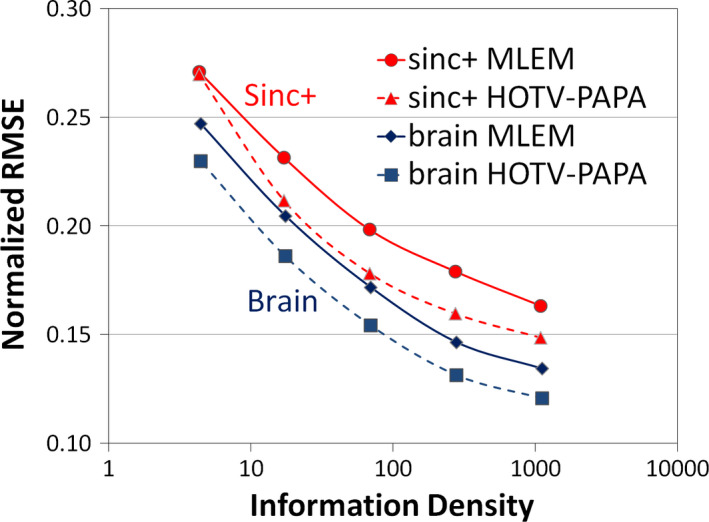
Normalized RMSE as a function of information density is shown for the simulated phantoms. The improvement in RMSE of HOTV‐PAPA compared with optimally Gaussian postfiltered ML‐EM for both the Sinc+ and brain phantoms. The ID is increased by a factor of four for each sequential marker. [Color figure can be viewed at wileyonlinelibrary.com]

3.D. Performance of OS‐PAPA without relaxation

Using the previously determined optimal penalty weights, we show the convergence behavior of the various algorithms for the low‐, medium‐, and high‐ ID images (Fig. 5). Overall, using the normalized difference of the objective function $\frac{{\mathrm{\Phi }}_{\infty }-{\mathrm{\Phi }}_n}{{\mathrm{\Phi }}_{\infty }-{\mathrm{\Phi }}_1}$ where ${\mathrm{\Phi }}_{\infty }\triangleq {\mathrm{\Phi }}_{2000\times 1}$ (iterationsindicating limit cycle behavior × subsets), the behavior is as expected; images converge more quickly and then stop (indicating limit cycle behavior), with higher count studies initially converging more quickly and lower count studies stopping sooner, showing that large subsets do accelerate TV‐OS‐PAPA and HOTV‐OS‐PAPA in a similar way to more conventional algorithms. Larger subsets showed limit‐cycle behavior with fewer iterations. In all cases, when subsets were used, limit cycle behavior was eventually observed.

Figure 5.

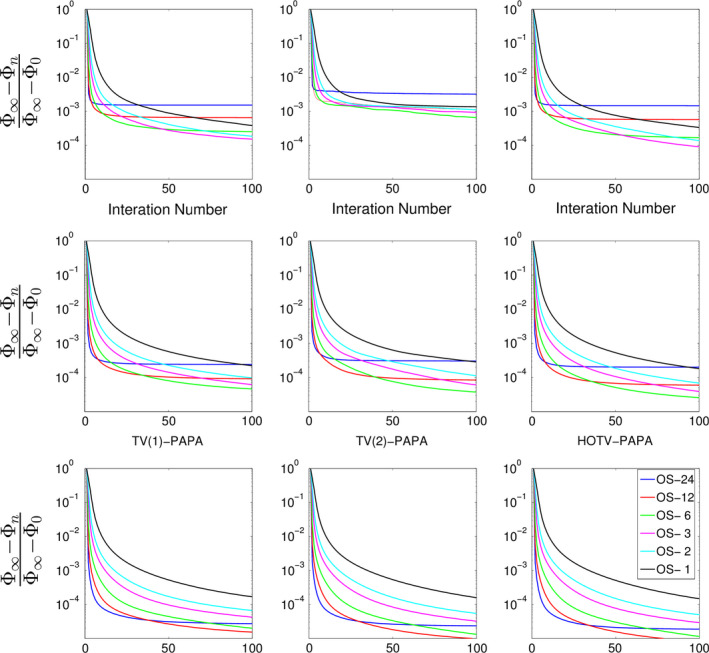
Normalized difference of the objective function as a function of iteration for different numbers of subsets for the simulated Sinc+ phantom are shown. Ordered subset convergence rates are shown for top: low‐ ID ( ID = 5, antibody imaging) convergence rates, middle: medium‐ ID ( ID = 25, whole body imaging) convergence rates, bottom: high‐ ID ( ID = 125, brain imaging) convergence rates. Left to right the figure shows first‐ and second‐order TV and HOTV‐PAPA for each count number. [Color figure can be viewed at wileyonlinelibrary.com]

3.E. Convergence of relaxed (R)OS‐PAPA

The relative convergence rates of OS‐PAPA with and without relaxation are shown, using the normalized difference of the objective function, in Fig. 6. Notice that for the medium‐ and low‐count images the number of subsets were reduced to 12 and 6, respectively. These reductions were based on the observation in Fig. 5 that for lower count data the smaller subset division converged almost as rapidly as the larger subset division. Note that, even with small subset division, very low‐count images showed some convergence instability, which is most evident when the second‐order TV penalty was used alone (not shown). No limit‐cycle behavior was observed when subset relaxation was used (Fig. 6).

Figure 6.

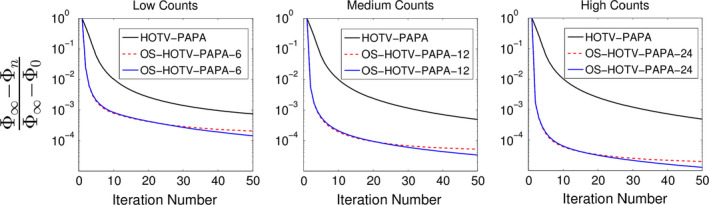
Normalized difference of the objective function as a function of iteration for relaxed and unrelaxed reconstructions of the simulated Sinc+ phantom are shown with 50 iterations. The relative convergence for low‐, medium‐, and high‐counts is shown left to right for HOTV‐PAPA using single subset, unrelaxed, and relaxed ordered subsets reconstruction. The appended numbers in the legends (24, 12, and 6) represent the number of subsets used. [Color figure can be viewed at wileyonlinelibrary.com]

3.F. Patient images using OS‐HOTV‐PAPA

For the clinical images, the penalties were set using the methodology described in section II II.D, where the cold rod region of the ACR phantom was used as a surrogate for the patients. These results are shown in Fig. 7. Power‐law fits of the cold rod region of the ACR phantom were performed using the 300 and 700 mm FOVs that are used for brain and whole body patients. The overall range of these fits covered most of the typical clinical range ( ID = 15−100) where extrapolation was used for ID outside the ranges of the fits.

Figure 7.

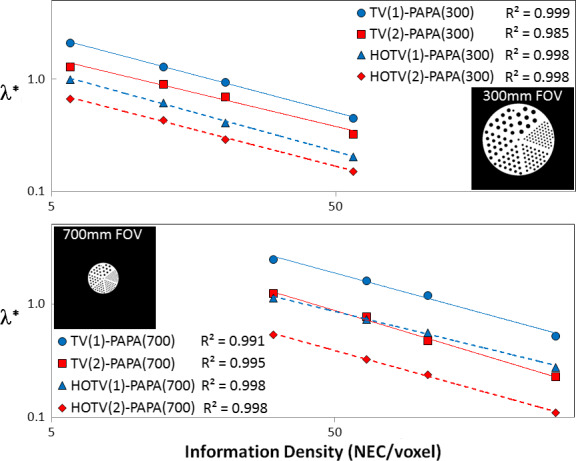
RMSE‐optimal penalty weights curve fits as a function of information density for the cold rod section of the ACR phantom are shown. The upper plot shows the fits for 300 mm FOV, while the lower plot shows those of the 700 mm FOV. In addition, to emphasize the inverse effect the FOV has on concentrating counts, the uncropped CT‐derived PET images of the ACR phantom, which were used as the reference distributions, are shown for each plot. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 8 shows patient images generated with ROS‐HOTV‐PAPA and the clinical algorithm, postfiltered OSEM. The improved image sharpness and reduced noise are readily apparent. These used 25 × 24 (iterations × subsets) with a relaxation constant of one twenty‐fourth on a 256 × 256 matrix and a field of view of 300 mm for brain images, and 700 mm for whole body images, time‐of‐flight and point spread function correction were also used. The mean measured ID and its [minimum to maximum] was: brain‐102,¹⁸ F‐FDG whole body (8 frames)‐17.4 [12.7 to 28.6], and ${}^{89}$Zr‐antibody (9 frames)‐12.3 [4.73 to 23.9] NEC per voxel. The convergence, using OS with several different relaxation constants along with images normalized relative error, is shown in Fig. 9.

Figure 8.

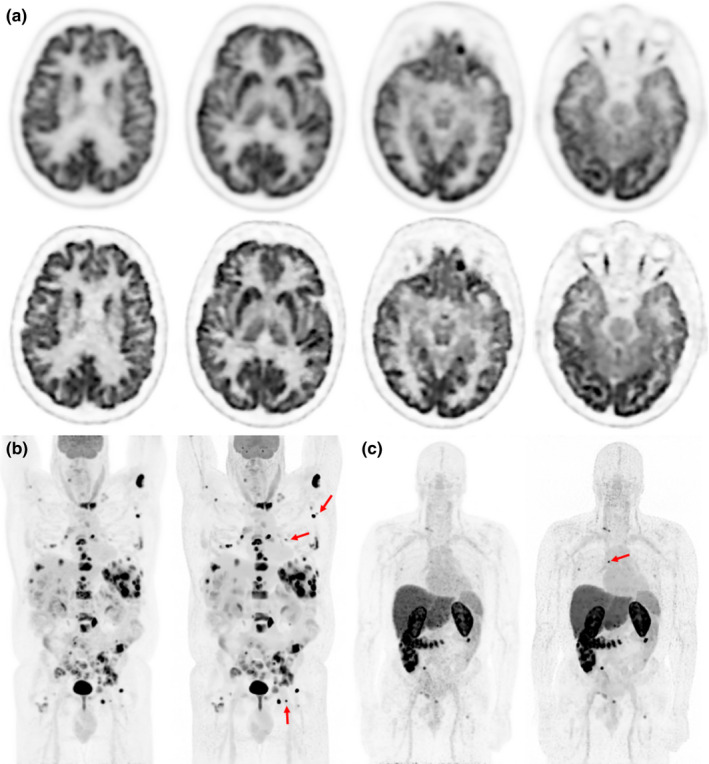
PET Images for three patients are shown. (a) The top two rows show a ¹⁸F‐FDG PET brain scan of 52‐yr‐old male with brain metastases. The upper row was reconstructed with our clinical brain reconstruction protocol (postfiltered OSEM) and the lower with ROS‐HOTV‐PAPA. The bottom row show maximum intensity projection images of two different patients, (b) an ¹⁸F‐FDG whole body scan of a 59‐yr‐old male with non‐Hodgkin's lymphoma, and C) an ${}^{89}$Zr‐antibody whole body scan of a 62‐yr‐old male with metastatic prostate cancer, both patients were reconstructed with clinical whole body (postfiltered OSEM) and ROS‐HOTV‐PAPA reconstructions (left and right, respectively). Note the improved sharpness and detail of the brain, and the improved contrast in the whole body and antibody patients’ images. The red arrows indicate lesions that are especially conspicuous in the ROS‐HOTV‐PAPA images. Intrapatient images were identically windowed and leveled. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 9.

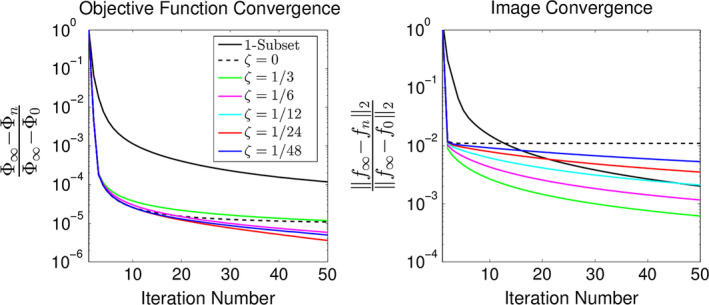
The convergence of the brain patient shown in Fig. 1(a) using 24 subsets using the normalized relative difference of both the objective function (left plot) and images (right plot) are compared using different amounts of relaxation. The left plot (${\mathrm{\Phi }}_{\infty }\triangleq {\mathrm{\Phi }}_{100\times 24}$) shows that objective function convergence is fastest using a relaxation constant between one twenty‐fourth and one‐twelfth. This plot also shows the convergence of the non‐OS reconstruction. The right plot ($f_{\infty }\triangleq f_{100\times 24}$) shows that unrelaxed OS causes the images to stop converging despite the objective function continuing to decrease (see left plot). For assured convergence, it is necessary for both normalized relative differences to continue to decrease. [Color figure can be viewed at wileyonlinelibrary.com]

Four other brain PET patients were reconstructed with similar results. Perturbations of the penalty weights from the determined values by altering the scaling parameter ($c^{*}{a}_{1,2}$ from (14) by small factors (± 20%) showed a consistent detail/variance trade‐off for each patient (results not shown).

Finally, with respect to the surrogate ACR phantom data the resulting RMSE values show that the HOTV penalty improves image quality when compared with optimally (in the RMSE sense) Gaussian postfiltered, fully converged, images. The results are shown in Table 2.

Table 2.

Percent improvement in RMSE of PAPA with an HOTV penalty using near optimal weights compared with optimal Gaussian postfiltered (GPF) fully converged ML‐EM is shown for a series of information densities for cold rod region of ACR Phantom

ID	Cold Rod Region (300 mm FOV)
	5.8	12.4	20.4	57.6
$RMS{E}_{GPF}^{*}$	0.340	0.279	0.250	0.215
$RMS{E}_{HOTV}^{*}$	0.236	0.223	0.213	0.199
%Improvement	44.1%	25.2%	17.5%	8.4%

ID	Cold Rod Region (700 mm FOV)
	30.2	64.3	106.0	299.2
$RMS{E}_{GPF}^{*}$	0.326	0.257	0.230	0.190
$RMS{E}_{HOTV}^{*}$	0.239	0.217	0.204	0.184
%Improvement	36.4%	18.7%	12.6%	3.5%

4. Discussion

The main purpose of this paper was to demonstrate the improved performance of image reconstruction using nonsmooth penalties with parameters optimized using simple image quality metrics (RMSE) under clinically realistic conditions. In this case, ROS‐HOTV‐PAPA is used. This necessitated that realistic simulation over a wide count and noise range be performed to show that similar results hold for clinical data. For noise control, the HOTV penalty that suppresses a well‐known problem referred to as “staircase” artifacts was used and a methodology for selecting fixed‐ratio minimum RMSE penalty weights, which uses information available in the scan data, was presented. Finally, after these pieces were combined ROS‐HOTV‐PAPA was compared with optimally postfiltered ML‐reconstruction (in the RMSE sense).

What is striking is that the net combination of these pieces leads to such large improvements in image quality when compared with the unpenalized reconstruction that is typically used in the clinic. It is noted that TV‐denoising has been around for ∼30 yr,¹ which implies that the use of more recent penalty methods will likely allow for even larger improvements.

The comparison to unpenalized reconstruction was limited because, at present only one vendor offers penalized‐likelihood image reconstruction, and it is not the purpose of this study to make a more specific or detailed comparison. To make such a comparison fair, an equivalent means of penalty optimization should be available for the other algorithm. To our knowledge, this is not the case. However, Fig. 2 suggests that the technique described in this study should be applicable to other types of penalties.

The incremental subgradient extension, via ROS‐HOTV‐PAPA is quite straight forward and follows the methodology described by Ahn and Fessler.²⁴ Here we have shown that our results are consistent with the asymptotic approach to the minima of the objective function and a unique image (i.e., convergence), which is absent when relaxation is not used. Though not shown, we have also noted that the convergence rates of HOTV‐PAPA, ROS‐HOTV‐PAPA are very similar to those of row‐action maximum likelihood algorithm (RAMLA) and BSREM (quadratic penalty), which is easily verifiable with a simple simulation. Further, although in this study was focused on a HOTV penalty, any matrix parameter product that is a proper lower semicontinuous convex function can be used, including $l_1$‐norm minimization problems with sparse coefficients.

To optimize the algorithms performance, a heuristic method based on a power‐law, which uses the data's NEC divided by the image's computation support, was used. This quantity is referred to as ID because counts can be considered bits of information and the NEC, which is known to correlate with image quality,³⁷ can be considered a measure of the total information recovered from the scan. The normalization to voxel support results in less dependence on patient size. Furthermore, this heuristic is consistent with the observation in a related problem (DP) that the optimal penalty weight, in an MMSE sense, is given by the ratio of the data noise to the object variability.³³

The use of the HOTV penalty function requires setting two penalty weights, which is an additional complication. Rather than attempt a direct 2D minimization, we decided to individually optimize each weight and then optimize the combined individually optimized power‐law relations. This second optimization adds a scale and slope factor to the initial optimized power‐law relations. Given this power‐law representation, the results show that as few as two acquisitions (for a particular class of patient), with differing ID s, can be used to estimate minimum RMSE penalty weights for similar patients, thus automating the penalty selection process. In practice, the combined fixed‐ratio penalty weights were very close to simply dividing the individual ones by two, which is consistent with the DP (i.e., the penalty weight serves to balance the tradeoffs between the data uncertainty and object variability).

The decision to forgo a 2D direct search was based on two observations. The first is that a 2D search requires much more computational effort compared with a simpler 1D search, whereas the second observation is that individual penalty searches establish a relative scale between the penalty weights that avoids artifacts. This is due to a weakness in the MMSE optimization goal that the MMSE image may be perceptually inferior despite having the same or smaller RMSE.³⁴ This is the case with first‐ and second‐order TV, where first‐order TV is more effective at achieving MMSE despite poorer perceptual image quality. These improvements are consistent with the results of Li & Zheng et al.,⁵ but now using minimum RMSE penalty weights.

As the results show, this relationship holds over a large range of ID that encompass most clinical situations. However, if two objects have sufficiently different activity variability or distributions (like the Sinc+ and Brain simulation phantoms), then different power‐law parameters are likely necessary. Thus, the parameters can be learned for several patient classes (based on size, location, tracer, etc.) and used thereafter for similar patients. However, how sufficiently different the patient distributions can be is an open question, although initial evidence shows some robustness with respect to visual perception, as seen when using the surrogate phantom for patient images in Fig. 8 (although we cannot claim the resulting images as having lowest RMSE). This result is consistent with what has been seen previously:^{42, 43} the power‐law relationship for HOTV penalty weights with brain patients held for both RMSE and visual assessment (two experienced nuclear medicine physicians) using the ACR phantom as a surrogate for patient data. The confidence from the visual assessment, our simulation experience, the excellent correlation coefficients of the ACR phantom penalty weight fits supports our use of extrapolation with respect to the brain images. The incorporation of object variability into the power‐law is under investigation.

Only RMSE was used for assessing image quality because this simple metric represents the overall quantitative accuracy of the images. Although it is a good place to start, clearly it is insufficient for task‐based assessment.³⁴ In the future we intend to test the penalty selection scheme with more advance structural metrics³⁴ or model‐observers.^{44, 45} However, because these results held for visual assessment of human brain patients,^{42, 43} it is possible that it will work for more sophisticated observer models.

Finally, when compared with conventional maximum likelihood imaging, even using an optimal postfilter, the reduction of noise, improved conspicuity, and apparent improvement in resolution are consistent with the simulation results, indicating that equivalent image quality should be possible with fewer NEC. Both simulation and clinical results showed that RMSE equivalent images could be achieved with almost one‐quarter the NEC used with conventional maximum‐likelihood reconstruction. In addition, the cold rod region of the ACR phantom shows improved quantitative accuracy (RMSE) of up to 44% (Table 2) when compared with optimally postfiltered MLEM. These results are especially interesting for very low count rates, such as late imaging with long half‐lives in antibody studies, and in dose reduction. However, at very low counts ( ID = 4), the second‐order penalty term, when used alone, had some instability, which slowed convergence and achieved poor RMSE (Table 1). This is not surprising where the mean relative uncertainty of the counts is ∼50%. First‐order TV did not show this problem and seemed to regularize the second‐order term when used together (bottom‐right Fig. 6).

At the end of this study several questions have been left unanswered. At present, there is no convergence proof for subset relaxation. The results show that this appears to be the case (or at least it is in any practical sense), but its rate is relaxation parameter‐dependent, which is also an open question. Also, there is no theoretical guidance on how to select the “best” relaxation rate. However, the clinical and simulation results show that a value of ζ between 1/12 and 1/24 work over a wide range of counts. With respect to penalty weight selection, we note that the power‐law's dependence on local image characteristics, such as contrast heterogeneity, remains to be studied. Thus, observations indicate that for similar patients the power‐law parameters are similar enough that they can be ignored, but we have not investigated which differing patient characteristics have important image quality implications. In addition, we have only tested our penalty calibration procedures on one type of scanner (GE Discovery 690/710) and expect that due to differing resolution, sensitivity, and time‐of‐flight that this procedure will need to be performed at least once for each type of scanner and class of image.

5. Conclusion

This study presents a combination of several advances in penalized likelihood image reconstruction, namely the development of relaxation for a convergent OS version of PAPA with nonsmooth convex penalties (HOTV in this case) and a simple empirical automatic means for selecting penalty weights. This combination resulted in improved RMSE‐image quality and showed that equivalent image quality when compared with conventional postfiltered OSEM, was possible with reduced NEC. In fact, low‐count phantom data suggest that similar image quality is achievable with only one‐quarter the counts when compared with optimal postfiltered, unpenalized image reconstruction, which indicates that it may be possible to reduce the injected dose by a similar factor. Furthermore, by first demonstrating these results through simulation, and then with patients, we showed that this combination has the potential for clinical use.

With respect to the use of ROS with PAPA, the results of both simulated and patient reconstructions showed that ROS‐HOTV‐PAPA greatly accelerated convergence, without which the algorithm would be clinically infeasible. The algorithm PAPA that was used is a special case of a fixed‐point framework for minimizing nondifferentiable convex functions. It is our hope that it and other algorithms developed from the fixed‐point framework will allow further improved performance using other advanced sparse representations.

To emphasize clinical relevance a promising methodology for automatically estimating RMSE penalty weights for TV‐type and quadratic penalties was demonstrated. It was further illustrated that this methodology requires as few as two baseline scans for a particular class of image (i.e., uptake variability) and is a very promising candidate for automatically choosing optimal penalty weights for improved image quality metrics.

These advances represent a step toward the clinical adoption of advanced nonsmooth penalties and algorithms that are feasible for the current generation of scanners with existing penalized likelihood computing platforms. In future work, both of these advances will be applied to more sophisticated image quality metrics, penalty types, and improved fixed‐point algorithms for faster image reconstruction using new sparse representation penalties.

Conflicts of interest

The authors have no conflicts of interest to report

Appendix A.

Higher order total variation

In this appendix, the definitions of 3D higher order isotropic total variation as well as the proximity operator are given.⁵

In Section II II.A, it was mentioned that first‐order and second‐order TV semi‐norm can be written as convex functions ${\mathit{\phi }}_1$ composed with matrix $B_1$ and ${\mathit{\phi }}_2$ composed with matrix $B_2$, respectively. To write these explicitly $D_n$ is first defined as the n × n first‐order difference matrix as

$$D_n\triangleq \left[\begin{array}{cccc}0& & & \\ -1& 1& & \\ & \ddots & \ddots & \\ & & -1& 1\end{array}\right].$$ (A1)

It is assumed that an image considered in this paper has a size of p × p × q. The image is treated as a vector in ${\mathbb{R}}^{p^{2}q}$, and its $ij{k}^{th}$ voxel corresponds to the ${(i+(j-1)p+(k-1)p^2)}^{th}$ element of the vector. Setting $d=p^{2}q$ and denoting $I_n$ as the n × n identity matrix, the 3d × d matrix $B_1$ and 9d × d matrix $B_2$, are defined through the matrix Kronecker product ⊗, by

$$B_1\triangleq \left[\begin{array}{c}{I}_q\otimes I_p\otimes D_p\\ I_q\otimes D_p\otimes I_p\\ D_q\otimes I_p\otimes I_p\end{array}\right],\text{and}$$ (A2)

$$B_2\triangleq \left[D_{xx};D_{xy};D_{xz};D_{yx};D_{yy};D_{yz};D_{zx};D_{zy};D_{zz}\right],$$ (A3)

where

$$\begin{array}{c}\hfill \begin{array}{cc}& D_{xx}\triangleq I_q\otimes I_p\otimes (-D_p^{\top })D_p,\\ & D_{xy}\triangleq I_q\otimes (-D_p^{\top })\otimes D_p,\\ & D_{xz}\triangleq (-D_q^{\top })\otimes I_p\otimes D_p,\\ & D_{yx}\triangleq I_q\otimes D_p\otimes (-D_p^{\top }),\\ & D_{yy}\triangleq I_q\otimes (-D_p^{\top })D_p\otimes I_p,\\ & D_{yz}\triangleq (-D_q^{\top })\otimes D_p\otimes I_p,\\ & D_{zx}\triangleq D_q\otimes I_p\otimes (-D_p^{\top }),\\ & D_{zy}\triangleq D_q\otimes (-D_p^{\top })\otimes I_p,\\ & D_{zz}\triangleq (-D_q^{\top })D_q\otimes I_p\otimes I_p.\end{array}\end{array}$$ (A4)

Note that $\Vert B_1{\Vert }_2\le 2\sqrt{3}$ and $\Vert B_2{\Vert }_2\le 12$ (and $\Vert B_1{\Vert }_2\le 2\sqrt{2}$, $\Vert B_2{\Vert }_2\le 8$ for 2D).

The first‐order isotropic TV (FOITV) and second‐order isotropic TV (SOITV) of a vectorized image $f\in {\mathbb{R}}^d$ can now be defined by

$$\begin{array}{cc}& {\Vert f\Vert }_{\text{FOITV}}\triangleq \sum _{i=1}^d\sqrt{{(B_{1}f)}_i^2+{(B_{1}f)}_{i+d}^2+{(B_{1}f)}_{i+2d}^2},\hfill \\ & {\text{and}\Vert f\Vert }_{\text{SOITV}}\triangleq \sum _{i=1}^d\sqrt{\sum _{j=0}^8{(B_{2}f)}_{i+jd}^2}\hfill \end{array},$$ (A5)

respectively. This implies that for $x\in {\mathbb{R}}^{3d}$ and $y\in {\mathbb{R}}^{9d}$, ${\mathit{\phi }}_1:{\mathbb{R}}^{3d}\to {\mathbb{R}}^d$ and ${\mathit{\phi }}_2:{\mathbb{R}}^{9d}\to {\mathbb{R}}^d$ are defined by

$${\mathit{\phi }}_1(x)\triangleq \sum _{i=1}^d\sqrt{\sum _{j=0}^2{x}_{i+jd}^2},\text{and}{\mathit{\phi }}_2(y)\triangleq \sum _{i=1}^d\sqrt{\sum _{j=0}^8{y}_{i+jd}^2},$$ (A6)

for FOITV and SOITV, respectively.⁵

Krol et al.¹⁴ used the closed form of proximity operator of ${\mathit{\phi }}_1$ and ${\mathit{\phi }}_2$ to address the nondifferentiability of TV semi‐norm. For a convex function $\mathit{\psi }:{\mathbb{R}}^n\to \mathbb{R}$, its proximity operator is defined by

$${\text{prox}}_{\mathit{\psi }}(x)\triangleq \text{arg min}\left\{\frac{1}{2}{\Vert u-x\Vert }_2^2+\mathit{\psi }(u):u\in {\mathbb{R}}^n\right\}.$$ (A7)

Using the above definitions, by letting $u={\text{prox}}_{{\mathit{\omega }}_1{\mathit{\phi }}_1}(x)$, $v={\text{prox}}_{{\mathit{\omega }}_2{\mathit{\phi }}_2}(y)$, as shown in,¹² their closed form solution is written as

$$\begin{array}{cc}\hfill {[u_i,u_{i+d},u_{i+2d}]}^{\top }=& \text{max}\left\{\sqrt{\sum _{j=0}^2{x}_{i+jd}^2}-{\mathit{\omega }}_1,0\right\}\times \hfill \\ & \frac{{[x_i,x_{i+d},x_{i+2d}]}^{\top }}{\sqrt{\sum _{j=0}^2{x}_{i+jd}^2}},\text{and}\hfill \end{array}$$

$$\begin{array}{cc}\hfill {[v_i,v_{i+d},\dots ,v_{8d+i}]}^{\top }=& \text{max}\left\{\sqrt{\sum _{j=0}^8{y}_{i+jd}^2}-{\mathit{\omega }}_2,0\right\}\times \hfill \\ & \frac{{[y_i,y_{i+d},\dots ,y_{i+8d}]}^{\top }}{\sqrt{\sum _{j=0}^8{y}_{i+jd}^2}},\hfill \end{array}$$ (A8)

for i = 1,2, …, d.