Revealing quantum mechanical effects in enzyme catalysis with large-scale electronic structure simulation

Abstract

Enzymes have evolved to facilitate challenging reactions at ambient conditions with specificity seldom matched by other catalysts. Computational modeling provides valuable insight into catalytic mechanism, and the large size of enzymes mandates multi-scale, quantum mechanical-molecular mechanical (QM/MM) simulations. Although QM/MM plays an essential role in balancing simulation cost to enable sampling with full QM treatment needed to understand electronic structure in enzyme active sites, the relative importance of these two strategies for understanding enzyme mechanism is not well known. We explore challenges in QM/MM for studying the reactivity and stability of three diverse enzymes: i) Mg²⁺-dependent catechol O-methyltransferase (COMT), ii) radical enzyme choline trimethylamine lyase (CutC), and iii) DNA methyltransferase (DNMT1), which has structural Zn²⁺ binding sites. In COMT, strong non-covalent interactions lead to long range coupling of electronic structure properties across the active site, but the more isolated nature of the metallocofactor in DNMT1 leads to faster convergence of some properties. We quantify these effects in COMT by computing covariance matrices of by-residue electronic structure properties during dynamics and along the reaction coordinate. In CutC, we observe spontaneous bond cleavage following initiation events, highlighting the importance of sampling and dynamics. We use electronic structure analysis to quantify the relative importance of CHO and OHO non-covalent interactions in imparting reactivity. These three diverse cases enable us to provide some general recommendations regarding QM/MM simulation of enzymes.

Graphical Abstract

Large scale quantum mechanical simulation systematically reveals length scales over which electronically driven interactions occur at enzyme active sites.

1. Introduction

Enzymes have evolved to facilitate challenging reactions at ambient temperature and pressure often with exquisite specificity seldom matched in industrial synthesis.^1–2 Nevertheless, the role of the enzyme environment in either statically or dynamically promoting these characteristics remains challenging to understand. Although protein crystallography and spectroscopy provide foundational knowledge of protein structure, atomistic simulation of enzymes³ represents a crucial component in our understanding of how the protein environment contributes to rate enhancement and reaction specificity. Unlike their molecular catalyst counterparts or the unit cells of heterogeneous catalysts, enzymes are usually thousands of atoms in size. Low computational cost, e.g., with molecular mechanics (MM) force fields, is required to enable sampling, whereas quantum mechanical (QM) treatment is needed to describe bond rearrangement, polarization, and charge transfer. These complementary strengths have motivated the development of a multilevel approach known as QM/MM^4–12.

In QM/MM, the region of primary interest is treated with QM and the remainder is treated at the MM level of theory, making the computationally demanding QM simulation the bottleneck. As a result, typical QM region sizes were until recently on the order of tens of atoms (i.e. ligands and a few direct residues).^12–14 The use of small QM regions has motivated method development^{10, 15–24} to minimize QM/MM boundary effects and to evaluate²⁵ how moving beyond conventional electrostatic embedding to advanced, polarizable,^{18, 25–30} force field treatments may improve QM/MM descriptions. Even with these advances, larger QM region sizes may be necessary in order to describe charge transfer between MM residues and the QM active site.^31–32

A key question in QM/MM modeling is how to best choose residues to include in the QM region. When small QM regions or clusters are employed, it is possible to predict physically reasonable mechanisms³³, but one may also not be aware of missing critical residues needed to describe the essential enzyme action^34–35. Despite the successes of force fields in capturing much of globular protein structure, there are notable cases where even fundamental properties of loop structure³⁶ or disordered proteins³⁷ are qualitatively described incorrectly, casting doubt on the ability of present MM force fields to reveal the mechanistic significance of residues in these contexts. Although conventional QM methods employed, e.g., semi-local or hybrid density functional theory (DFT) have their own shortcomings³⁸, treating more of the enzyme with DFT implicitly imparts more physics and makes fewer assumptions than a conventional fixed point charge force field³⁹. Significant advances^{31, 36, 40–46} in computational efficiency over the past decade have made it possible to carry out fully ab initio, quantum chemical simulation of polypeptides^{36, 47} as well as QM/MM treatments of enzymes with large (> 100 atoms) QM regions.

Numerous researchers^{35, 48–56} have leveraged these advances to identify how sensitive mechanistic predictions are to QM region size in QM/MM calculation. The majority of resulting studies have revealed an exceptionally slow approach to asymptotic limits (ca. 500–1000 atoms) for radial convergence: NMR shieldings,^48–49 proton transfer,⁵⁷ solvation effects,⁵⁰ barrier heights,^{35, 51–52} forces⁵³, excitation energies,^{54, 58–59} partial charges,⁵⁵ bond critical points⁶⁰, and redox potentials⁵⁶. There are cases where smaller QM regions have been motivated (e.g., in DNA models⁶¹ and the cytochrome P450cam metalloenzyme⁶²), so there is increasing consensus that it is important to determine the extent to which a given property is sensitive to the QM region size.

Over the years, numerous systematic approaches have been developed for QM region construction based on perturbation or evaluation of properties at the MM^{51, 63} or QM^{35, 62, 64–65} level. Incorporating essential residues in this way can reveal fundamental, quantum mechanical aspects of enzyme mechanism, such as environment-mediated charge separation of neutralizing substrates or essential charge-assisted, low-barrier hydrogen bonds that would be impossible to accurately describe with only MM or across the QM/MM boundary³⁴. In this work we use the phrase “quantum mechanical effects” to focus on classical treatment of nuclei but explicit modeling of the quantum mechanical wavefunction. Furthermore, such interactions can change as a function of the reaction coordinate. Although efficient sampling methods are under development⁶⁶, challenges remain in how to pair large QM regions from systematic QM/MM region construction with the sampling needed to understand the role of protein conformational dynamics in enzyme mechanism. Indeed, although static QM/MM simulations with over 1,000 QM atoms have become increasingly routine, hundreds of thousands of such energy evaluations are required to compute a potential of mean force. Thus, identification of the relationship of dynamical and free energy properties to QM region size has primarily been studied with semi-empirical methods^{53, 67–71}, and this effort has only recently been extended to fully-first principles DFT³⁴.

Given this tension between the need for sampling and for first-principles understanding of the electronic structure of the active site in order to develop mechanistic understanding of enzyme action, it is important to continue to develop an understanding of when large scale electronic structure simulation is essential and what insight it can bring. The rest of this article is outlined as follows. In section 2, we provide the computational details of the calculations employed in this work. In section 3, we show how QM region selection impacts the insights obtained from QM/MM simulation of three representative enzymes with diverse structures: Mg²⁺-dependent catechol O-methyltransferase⁷² (COMT), the metal-free glycyl radical enzyme choline trimethylamine lyase (CutC)^73–75, and a structural Zn-metal binding site in the DNA methyltransferase DNMT1⁷⁶. Finally, in section 4, we provide our conclusions.

2. Computational Details

Protein structure and preparation.

CutC holoenzyme with choline substrate (PDB ID: 5FAU⁷³) and DNMT1 with a 19 base-pair DNA strand and S-adenosyl homocysteine (SAH) inhibitor (3PTA⁷⁶) were obtained from the PDB. SAH in DNMT1 was modified to the S-adenosyl methionine (SAM) cofactor with Avogadro⁷⁷, and 54 missing residues were added and refined using loop refinement with Modeller⁷⁸ (ESI, Table S1). Protonation states of apoenzyme residues were assigned using the H++ webserver^79–82 assuming a pH of 7.0 with all other defaults applied. Protonation states of residues adjacent to cofactors or substrates were manually assigned (ESI, Tables S2-S3). The two resulting holoenzymes (CutC −19 net charge, DNMT −22 net charge) were used as starting points for subsequent force field file preparation with the tleap utility in AMBER⁸³ prior to simulation (ESI, Tables S4-S5). All standard residues were simulated with the AMBER ff14SB⁸⁴ force field. The zinc Amber force field (ZAFF)⁸⁵ was employed for Zn²⁺ and coordinating residues in DNMT, and DNMT DNA base pairs were described by the parmBSC1⁸⁶ force field (ESI, Table S6). Due to our focus on fixed tetrahedral coordination of Zn²⁺ with protein residues, we used the original ZAFF rather than newer forms^87–88 that have improved descriptions of variable coordination, e.g., in aqueous solvent. Force fields for remaining organic non-standard residues were generated using the generalized AMBER force field (GAFF)⁸⁹ with partial charges assigned from restrained electrostatic potential (RESP) charges⁹⁰ obtained with GAMESS-US⁹¹ at the Hartree-Fock/6–31G*⁹² level, as implemented by the R.E.D.S. web server^93–95. The proteins were solvated with 10–15 Å of TIP3P⁹⁶ water in a periodic rectangular prism box and neutralized with Na⁺ counterions. Starting AMBER topology and coordinate files for the 151,473-atom DNMT1 and 111,741-atom CutC systems are provided in the ESI.

MM Equilibration and Dynamics.

Protein molecular dynamics (MD) equilibration and production steps in AMBER were as follows: i) restrained (1000 steps) and unrestrained (2000 steps) minimizations were carried out, ii) 10-ps NVT heating to 300 K with a Langevin thermostat with collision frequency of 1.0 ps⁻¹ and a random seed, iii) 1-ns NPT equilibration using the Berendsen barostat with a pressure relaxation time of 2 ps, and iv) 250 ns (100 ns for CutC) of production dynamics. All MD employed SHAKE⁹⁷ with a 2-fs timestep and a 10-Å electrostatic cutoff.

QM/MM Calculations.

In QM/MM simulations, TeraChem^{42, 98} was used for the QM portion, and OpenMM⁹⁹ was used for DNMT1 whereas AMBER⁸³ was used for CutC. In all cases, we employ electrostatic embedding and hydrogen link atoms for passivating covalent bonds that cross the QM to MM border, i. e.:

$$E_{\text{QM}/\text{MM}}=E_{\text{QM}}+E_{\text{QM}-\text{MM}}+E_{\text{MM}}$$ (1)

QM regions were selected systematically for CutC resulting in a QM region containing 281 atoms (0 net charge) for use in QM/MM, and larger 1043 atom snapshots (+2 net charge) were used for electronic structure analysis (ESI, Table S7). Radial QM regions up to 417 atoms and 0 net charge were studied for Zn2 in DNMT1 as described in the main text. MD snapshots selected for QM/MM were post-processed using the center of mass utility in PyMOL¹⁰⁰ to generate the largest possible spherical droplet centered around each protein that was circumscribed by the original rectangular prism periodic box. These snapshots are simulated without electrostatic cutoff and only spherical cap boundary conditions enforced with a restraining potential of 1.5 kcal/mol^.Ų. This lack of electrostatic cutoff combined with the use of electrostatic embedding means that the point charges of all MM atoms in the systems are explicitly included as one-electron nuclear-electron attraction terms in the QM calculation. For both CutC and DNMT1, the QM region is modeled with DFT using the range-separated exchange-correlation functional ωPBEh¹⁰¹ (ω=0.2 bohr⁻¹) with an LANL2DZ effective core potential¹⁰² on Zn in DNMT1 and 6–31G*⁹² for the remaining atoms.

For DNMT1, rigid binding energies were computed from single point energies with and without Zn in MD snapshots at around 40, 60, and 100 ns from a 250 ns MD simulation (see ESI). CutC simulations included 2000 step QM/MM minimizations followed by steered molecular dynamics (SMD). SMD in CutC used a 1000 kcal/mol^.Ų harmonic pulling force and 0.5 fs timestep over the reaction coordinate for around 2000 steps. The linear combination of distances (LCOD) reaction coordinates used were: 1) for hydrogen atom transfer the difference between the choline H distance to a C on choline and S(C489); and 2) for cholinyl radical deprotonation the difference between the hydroxyl H atom on cholinyl radical distance to the hydroxyl O atom or to E491 O⁻ (see ESI for starting configurations).

Analysis.

Atom-wise and by-residue sums of Voronoi deformation density (VDD) or Mulliken charges and spins were evaluated on QM/MM SMD snapshots in CutC (every 10 snapshots) or in select MD snapshots for DNMT1, respectively. By-residue sums as well as real-space VDD charges¹⁰³ were employed to reduce basis set sensitivity as in previous work^{35, 62, 64} for CutC. In CutC, hydrogen bonds were identified and quantified using the heuristic half of the potential energy density¹⁰⁴ at the bond critical point (BCPs)¹⁰⁵, as implemented in Multiwfn.¹⁰⁶ Close contacts (< 85% of sum of van der Waals radii) were identified and analyzed as described in the main text. For evaluation of pairwise interaction strength with QM or MM, capping H atoms were added on the backbone vector with a scaled bond length (1.09 Å for C-H, 1.01 Å for N-H). These pairs were geometry optimized in TeraChem^{42, 98} at the B3LYP^107–109/6–31G*⁹² level of theory with heavy atoms and capping H atoms frozen and the protein environment was mimicked with the conductor-like implicit solvent model (COSMO)^{47, 110} with ε=4. Optimizations used the L-BFGS algorithm in Cartesian coordinates, as implemented in DL-FIND¹¹¹, to default thresholds of 4.5 × 10⁻⁴ hartree/bohr for the maximum gradient and 1 × 10⁻⁶ hartree for the change in energy between steps. QM single points for energy decomposition analysis (EDA) were calculated with symmetry adapted perturbation theory (SAPT) at the DF-SAPT0^112–114/jun-cc-pVDZ level of theory, as implemented in Psi4¹¹⁵. MM EDA was carried out with the generalized Born (GB) and surface area (SA) continuum solvation model approach (MM/GBSA) using the MMPBSA.py¹¹⁶ utility with the GB¹¹⁷ “OBC” model II, as previously motivated.¹¹⁸ The same force fields were employed as described previously, and only gas phase terms were retained for comparison to QM results.

3. Results and Discussion

3a. COMT: Charge Transfer in Enzyme Active Sites.

To explore QM region dependence in protein simulation, we begin by summarizing several 0 K QM/MM and finite-temperature dynamics studies we have previously carried out^{34, 62, 68, 119} on the enzyme catechol O-methyltransferase (COMT). COMT is a SAM- and Mg²⁺-dependent MTase⁷² that reacts with catecholamine substrates bound in a bidentate fashion to Mg²⁺ at the active site¹²⁰ (Figure 1). The rate-determining¹²¹ step is direct S_N2 methyl transfer¹²² from a positively charged SAM¹²³ to a negatively charged, deprotonated catecholate^124–125 (CAT) to produce neutral SAH and methylated catechol products (Scheme 1). The free energy barrier for this reaction is estimated from experimental kinetic studies to be 18.1¹²⁶-19.2¹²⁷ kcal/mol. The methyl group transfer process can be well defined by a single linear combination of distances (LCOD) coordinate that is the difference in bond length between the transferring methyl group to the SAM S atom versus the accepting catecholate O⁻ to the methyl group (Figure 1).

Figure 1.

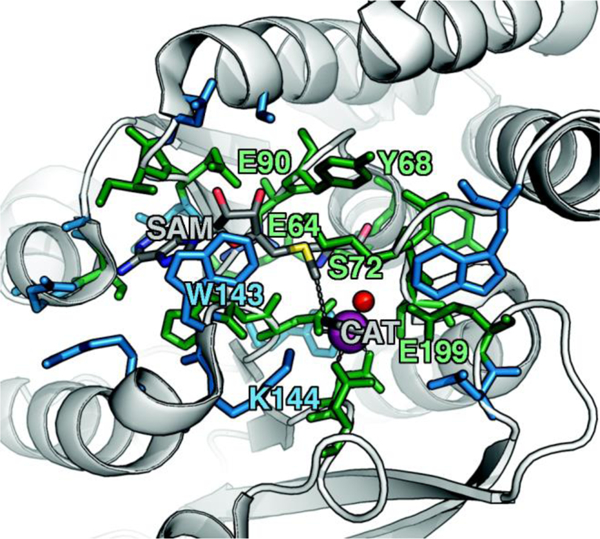
COMT structure with SAM and catecholate (CAT) substrates shown in gray along with Mg²⁺ as a magenta sphere and a water coordinating the Mg²⁺ as a red sphere. The 28 protein residues (518 atoms with H atoms) included in a large QM region, as described in the main text, are shown as sticks. A subset that was identified by systematic analysis of QM regions is shown in green, whereas the remainder is shown in blue. Specific residues of interest are labeled by their single letter residue code and number.

Scheme 1.

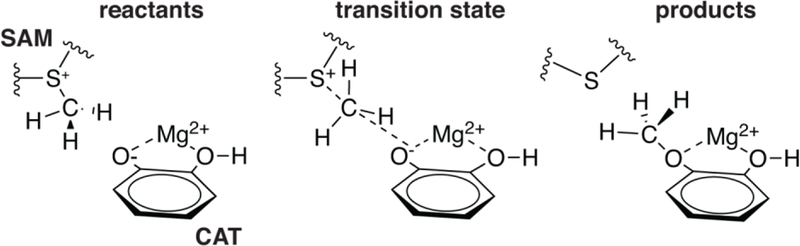
Reaction for COMT-catalyzed methylation of catecholate (CAT) substrate by SAM.

COMT represents a challenging test case for simulation methods, beyond challenges in predicting^{35, 68–70, 128–131} the experimental free energy barrier. Although numerous crystal structures of COMT consistently indicate an unusually short 2.6–2.8 Å non-bonded distance between the donating methyl group on SAM and the catecholate acceptor, classical MD simulations seldom, if ever, sample these distances^{68, 132–133}. Instead, it was observed that large QM regions are essential to sampling these distances^{35, 134}. Furthermore, from small QM region and gas phase cluster studies, it was hypothesized that charge neutralization might occur in the transition state¹³⁵. However, we have since determined^34–35 that a critical role of the enzyme active site is to mediate charge transfer between the substrate and surroundings to increase charge separation at the transition state, an effect that can only be observed with larger QM regions.

Although significant QM region dependence and a mandate for larger QM regions in QM/MM simulation has been noted for numerous properties^{35, 51–55, 58–60}, COMT itself may be a good example of more extreme challenges in QM/MM simulation for enzyme catalysis. The substrates, SAM and CAT, themselves are large at already 64 atoms, and the size of SAM (ca. 15 Å end-to-end) as well as number of polar and charged functional groups means it can form numerous non-covalent interactions with the enzyme active site (Figure 1). In addition to E90, E64, and S72 around SAM, catecholate also has the potential to form strong interactions with a neighboring E199 or K144 (Figure 1).

Thus we revisit and make a comprehensive comparison of several strategies we have developed to understand how changing the QM region changes predictions of catalytic action both in 0 K reaction coordinates^{35, 62} and in room temperature free energy simulations^{34, 68}. Due in part to the ovoid shape of the substrates, radial convergence is very slow in COMT as judged through 0 K E_a and ΔE_rxn values³⁵. Both quantities converge only at around 500 atoms in the QM region, with small QM regions significantly overestimating asymptotically large QM region limits, and even qualitative discrepancies are observed such as endothermic reactions for the smallest QM regions³⁵ (Figure 2). In such a radial convergence study, residues are included at increasingly large distance cutoffs from a central point in the active site, thus providing limited guidance on which residues are essential to include within a given cutoff. For that reason, we developed methodologies designed to enable systematic QM region construction.

Figure 2.

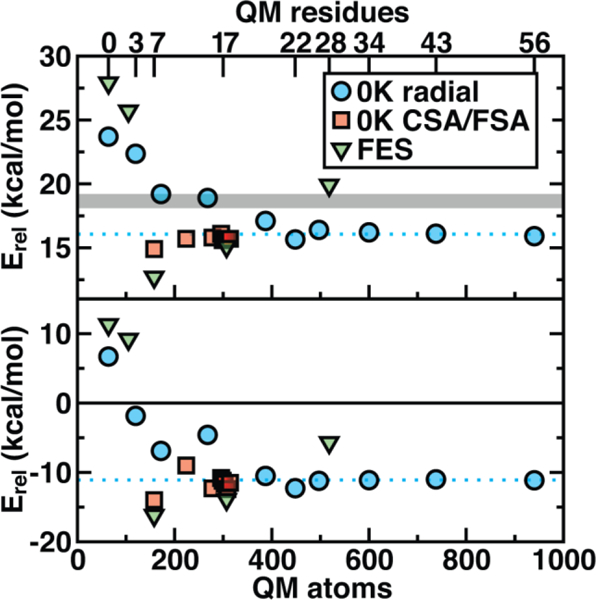
Barrier heights (top) and reaction energies (bottom) in kcal/mol for methyl transfer in COMT versus the number of atoms in the QM region obtained three ways: 0 K QM/MM properties from radially increasing distance cutoffs (blue circles, from Ref. 35), systematically constructed regions (red squares, from Ref. 62) and 300 K QM/MM free energy dynamics (green triangles, from Ref. 34). (top) ΔG^‡ at 300 K or the 0 K E_a with the experimental ΔG^‡ range^126–127 indicated as a gray shaded region that should only be compared to the green triangles. (bottom) ΔG_rxn at 300 K or the 0 K ΔE_rxn. In both plots, the asymptotic limit from the average of the three largest 0 K radial QM regions is shown as a blue dotted line and should only be compared to the blue circles and red squares. Approximate protein residue counts for each QM region size are labeled on the x-axis at top.

In charge shift analysis (CSA)^{35, 62}, we carry out QM/MM single points with large (ca. 1000 atom) QM regions on the protein once with the substrates/cofactors present and then rigidly removed. We compute the change in by-residue-summed partial charges on surrounding residues and determine them to be essential for a QM treatment if the change is above a threshold (typically, |0.04–0.05 e|). Beyond obvious residues (e.g., Mg²⁺-coordinating D141, D169, and N170 or hydrogen bonding E64), this approach revealed^{35, 62} surprising interactions with nonpolar residues, such as a V42 proximal to the substrates. Conversely, proximal charged residues need not necessarily be detected by this method if charge transfer to the substrates is limited.

The limitation of CSA is that it requires a 1000-atom QM calculation, which we circumvent in the complementary Fukui shift analysis (FSA) approach^{62, 64}. In that method, we compute the by-residue condensed Fukui function of the core active site substrates (e.g., in COMT this corresponds to SAM, catecholate, and Mg²⁺) in the presence and absence of each additional residue one residue at a time, making FSA parallelizable. The Fukui function¹³⁶ represents a measure of the substrate’s electrophilicity or nucleophilicity, and the condensed¹³⁷, by-substrate-summed form simply represents what fraction of an added or removed electron is added or removed from the substrates.

Overall, CSA and FSA applied to COMT each reveal around 16 essential residues around the substrates or < 300 atoms in comparison to 500 atoms from the radially converged region. The two methods predict 14 residues in common, despite computing fundamentally distinct quantities, with the non-overlapping residues being E64 and A73 for CSA and G66 and Y71 for FSA. The former CSA residues can be rationalized as only interacting with the substrate by mediation through many-body effects absent from FSA, whereas FSA may detect electronic interactions not mediated through charge transfer. Overall, QM/MM E_a and ΔE_rxn values obtained with CSA and FSA QM regions (ca. 300 atoms) were within < 1 kcal/mol of the asymptotic limits (ca. 500–1000 atoms) and in significantly improved agreement over radial QM regions of comparable size⁶² (Figure 2).

We further developed the charge deletion analysis (CDA) method to determine if any CSA- or FSA-selected residues could be judged as false positives. In CDA, we constructed a QM region consisting of the union of the CSA and FSA residues, and then we moved each residue back to the MM region one by one to determine if this caused a change to the by-residue-summed partial charges on the active site substrates or on neighboring residues. This approach also gave a ranking to residues selected by CSA or FSA and allowed us to identify even smaller QM regions that should contain the most essential residues⁶². These 150–200 atom QM regions constructed from CDA-ranked CSA/FSA residues were within approximately 1 kcal/mol of the asymptotic limit of E_a and showed slightly poorer agreement for ΔE_rxn. Overall, agreement was dramatically improved over radial QM regions of equivalent size, and agreement was found to be best when the smaller QM region yielded consistent electronic structure properties (e.g., charge separation in the transition state) with the larger QM regions.

In a recent study³⁴, we sought to address whether these observations applied to first-principles QM/MM free energy simulations. Thus, we selected 5 QM regions that merged the principles of the radial study with the systematic methods we introduced: 1) a minimal QM region, 2) including Mg²⁺-coordination sphere, 3) including the top-ranked residues from CDA, 4) the consensus residue set from CSA/FSA, and 5) a 0 K-asymptotically converged, 518 atom QM region. Similar trends of overestimating barrier heights and predicting endergonic reactions are observed for the smallest QM regions (Figure 2). However, more variability is observed³⁴ in the larger (ca. 150–500 atom) QM regions for free energy simulation than occurred at 0 K⁶² (Figure 2). Although the CSA/FSA region is by far in the best agreement with region 5, the discrepancy between the two regions is much larger than that for the equivalent at 0 K (Figure 2). This discrepancy arose because i) differing QM regions led to sampling different trajectories and dynamics and ii) during dynamics residue proximity to the active site changed and sampled orientations that were not considered during CSA/FSA analysis. Understanding how this electronic structure evolves is essential to developing methods that go beyond CSA^{35, 62} or FSA^{62, 64} by incorporating dynamics⁶⁵. It is thus also useful to understand what electronic properties give rise to such slow convergence of energetics in the COMT active site.

From our recent study of QM/MM free energy simulation convergence³⁴, we now examine the residue-residue coupling of electronic properties from the largest QM region in that work (518 non-link atoms, 28 protein residues plus substrates, see Figure 1). Specifically, we compute the by-residue Mulliken partial charge sums at every timestep of the 210 ps dynamics. If partial charge sums on each residue show little variation, an MM description with a fixed point-charge force field should adequately describe such residues. Thus, we investigate potential couplings by computing the covariance matrix of the by-residue partial charge sums (Figure 3). To compare the three types of residues (i.e., with zero, one, or two coordinating QM residues on either side along the protein chain) in this QM region on equal footing, the by-residue sum always includes both sidechain and backbone atoms. Isolating one example residue, Glu90, which is coordinated by the two Ile89 and Ile91 QM residues, reveals a comparable standard deviation of the charge for the sidechain-only by-residue sum (0.023 e over 0.25 ps) in comparison to the full by-residue sums (0.028 e over 0.25 ps) reported here. Further comparison of backbone and sidechain-derived effects will be the focus of future work.

Figure 3.

Covariance matrix of Mulliken partial charges over 200 ps of QM/MM dynamics across the COMT methyl transfer reaction coordinate colored on a symmetric logarithmic scale according to inset colorbar (positive in blue, zero white, and red negative). The diagonal represents the variance of charges for each residue. Residues are annotated by their single letter code and residue number at top because the matrix is symmetric. Thick lines correspond to the QM region in which a residue or substrate first appears, and residues are ordered by sequence within each QM region grouping, as described in the main text.

Since the matrix is computed over the full reaction coordinate, SAM and catecholate have the largest individual variances and pairwise covariance as methyl transfer is associated with redistribution of their charges (Figure 3). The Mg²⁺ cation, which is essential for COMT catalysis⁷², has more moderate variance and is most strongly coupled to the catecholate charge, which is reasonable since catecholate remains doubly coordinated to Mg²⁺ throughout the reaction (see Figures 1 and 3).

Somewhat surprisingly, D141, D169, N170, and water which all also coordinate the Mg²⁺ have overall low covariance with Mg²⁺, each other, and other protein residues (Figure 3). The only exception to this observation is the neighboring residues D169 and N170, which exhibit significant covariation that is still less than other adjacent residue pairs (e.g., W143/K144), including those with neutral residues (e.g., A67/Y68 or Y71/S72, see Figure 3). The observation of enhanced covariance between neighboring residues suggests some component of backbone participation in the overall factors that determine charge coupling. This confirms our earlier suggestions³⁴ of reduced individual charge fluctuation for the Mg²⁺-coordinating residues in comparison to even non-polar residues more distant from the active site. These observations in COMT point to potentially reduced fluctuations and coupling between residues immobilized by binding to metals or co-factors, a common feature of metalloenzymes.

Although couplings between core active site residues and the Mg²⁺ coordination sphere are quite low, there are significant charge couplings between SAM/catecholate and other protein residues. Most of these residues reside in regions 3 and 4, including V42, E64, S72, and E199, reinforcing not just expected hydrogen bonding interaction partners but the surprising (i.e., V42) interactions noted through static CSA/FSA results⁶² (Figure 3). These observations highlight that distance-based determination of QM region, which is frequently used in convergence studies^{35, 53}, is an incomplete guide with regard to whether residues are coupled to each other or the active site. The region 3 and 4 residues also have among the strongest covariance within the individual region subset (Figure 3). For intra-region coupling in the 10 residues designated as region 4, E64-Y71/S72 and E64/S119 covariances are observed, consistent with these residues forming hydrogen bonds during the reaction. Interestingly, covariances between substrate-adjacent, nonpolar M40 and charged E64 are nearly as high as some of these polar/charged hydrogen-bonding interactions (Figure 3). In contrast, region 5 covariances are small both internally and with the other regions (Figure 3). The most notable exceptions to this analysis for region 5 are i) L198, which is backbone adjacent to the high-variance, charged E199 and ii) similarly the E90-adjacent I89 (Figure 3). When we observed differences in QM/MM free energy barriers between simulations with only region 4 vs. region 5 residues in the QM region, we attributed³⁴ this difference to specific residues such as K144 that were missing from region 4. Interestingly, analysis of the covariance on the overall reaction coordinate, however, does not reveal a critical coupling between K144 or other region 5 residues and the core substrates (Figure 3).

In addition to overall covariance across the reaction coordinate, we computed individual covariance matrices for reactant-(R), transition-state-(TS), and product-(P) like windows from the umbrella sampling simulations that individually correspond to 15 ps of dynamics. The R and P windows are the extrema from our umbrella-sampling path, with the methyl group fully on SAM in the former and a fully methylated catechol in the latter. To select the TS window, we determined the 0.1 Å LCOD region around the maximum of the QM/MM free energy surface to be $\Delta =d\left(S-C\right)-d\left(C-O\right)=0.28-0.38\AA$ We then determined that the window with a target Δ = 0.30 Å sampled this range of Δ values 95% of the time and selected it as our TS region. Comparison of R, TS, and P covariance matrices reveal notable differences in the three points along the reaction coordinate, reinforcing the significant reorganization of electronic structure in the enzyme active site along the reaction coordinate (Figure 4).

Figure 4.

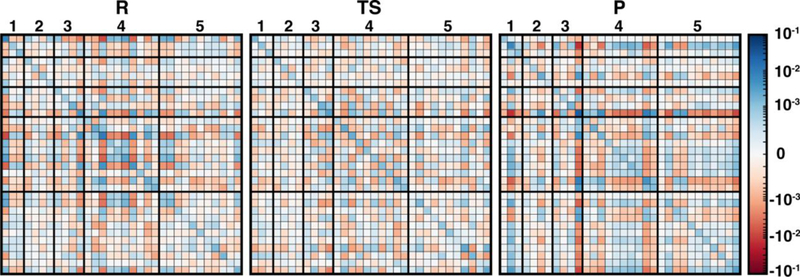
Covariance matrices of Mulliken partial charges for 15 ps each of R, TS, and P-sampled structures colored on a symmetric logarithmic scale according to inset colorbar (positive in blue, zero white, and red negative). The diagonal represents the variance of charges for each residue. Thick lines and associated numbers correspond to the QM region in which a residue or substrate first appears, as described in the main text.

Although SAM has one of the largest variances and couplings with other residues (e.g., E64 and S72) in the R window, as SAH in the P window its couplings and variance are among the lowest of all residues (Figure 4). Conversely, CAT variance is highest in the product state, with strong coupling to S119 as well as E199 likely due to the formation of a low barrier, charge-assisted hydrogen bond in the product³⁴ (Figure 4). In the TS window, the core substrates have markedly decreased covariance with each other or with any other residues in comparison to R or P (Figure 4). As a result, covariance of region 5 residue pairs such as W143/K144 or K144/L198 in the TS are of similar magnitudes to the strongest observed in other QM regions. Comparing R to P windows, it is evident that, although both covariance matrices have larger covariance magnitudes than the TS window, the contributions from more remote residues decreases across the reaction coordinate, with strong coupling of E64 and S72 in the R window absent in the P window (Figure 4). Instead in the product state, E199 interactions dominate with reduced coupling of residues to E64 and S119 (Figure 4).

Overall, covariance of charges sampled in different portions of the reaction coordinate, computed here for the first time on range-separated hybrid DFT QM/MM free energy simulation dynamics, provides distinct insight into how electronic structure evolves across a reaction coordinate. Sensitivity of the COMT reaction coordinate to QM region is likely related to the fact that the electronic structure evolves so significantly both during dynamics and across the reaction coordinate.

3b. CutC: Electronic and geometric structure in radical reactions.

CutC¹³⁸ is an abundant glycyl radical enzyme (GRE)^139–140 that catalyzes degradation of choline to trimethylamine (TMA) and acetaldehyde in the human gut microbiome (Scheme 2). After formation of a stable α-carbon glycyl radical at G821 by an activating enzyme, CutD⁷⁴, the formation of a short-lived and reactive cysteine radical, C489, has been proposed^73–74 that can then initiate choline decomposition via C-H abstraction. The resulting cholinyl α-hydroxyalkyl radical likely undergoes deprotonation by an adjacent general base E491, weakening the C-N bond and leading to cleavage, in contrast to 1,2-migration pathway suggested for other GREs¹⁴¹.

Scheme 2.

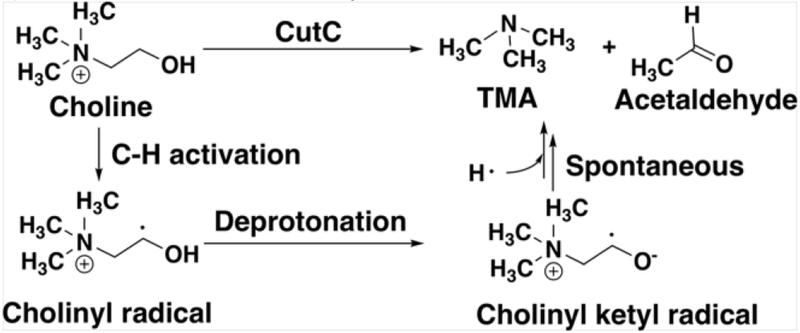
Putative reaction pathway for CutC-catalyzed choline degradation to trimethylamine (TMA) and acetaldehyde.

Although the crystal structure of CutC with bound choline substrate⁷³ can be used to infer the mechanism, QM/MM simulation can provide valuable insight to the dynamic and electronic rearrangements that occur during catalysis in the CutC active site. We focus on the two most essential and poorly understood steps in the CutC reaction mechanism: 1) short-lived cysteinyl radical formation and 2) cholinyl radical (Cho•) deprotonation (Scheme 2). Alternative mechanisms besides direct elimination for Cho•were ruled out based on stability of the relevant intermediates in both the gas phase and an implicit solvent environment that approximates the enzyme active site (ESI, Table S8 and Figure S1). The MD equilibration of CutC sampled choline dihedral configurations in the active site not expected to be reactive, although the reactive orientation was the predominant species (ESI, Figures S2-S3).

Candidate QM region residues were determined using the systematic³⁵ CSA method^{34, 62, 64}. With CSA, electronic reorganization was assessed in a large QM region that contained all residues within 6.5 Å of the choline substrate (i.e., 925 atoms) after C489A mutation and choline removal, as outlined in Sec. 2 (ESI, Table S4). For this CSA step, no geometry optimization is carried out of the greater protein except of the replaced methyl hydrogen atoms in the C489A mutation. Mutagenesis studies had identified¹³⁸ Y208, D216, F395, E491, T502, and Y506 as relevant for catalysis. Due to the less polar substrate and active site, CutC charge shifts are lower than observed in COMT and are largest for N393, E491, and D216 (Figure 5 and ESI, Figure S4 and Table S7). After setting a reduced threshold of |0.02| e for the charge shift to account for reduced polarity, 10 residues (ca. 200 atoms), charged (E491, D216), polar (Y208, Q333, Q393), and nonpolar (W501, M336, G488, C489, V490), are selected for the QM region, including D216 and E491 as well as Y208, but not the less-choline-proximal T502 and Y506 residues suggested by experimental mutagenesis¹³⁸ (ESI, Figure S4). In addition to CSA selected residues, the loop (i.e., V819-S823) containing G821 responsible for forming the C489 radical was also included (ESI, Table S7). Residues not detected by CSA are treated at the MM level of theory during SMD, which is expected to be sufficient due to the absence of charge transfer between the residues and the substrate, and subsequent electronic structure analysis was carried out on > 1000 atom QM region snapshots (ESI, Table S7).

Figure 5.

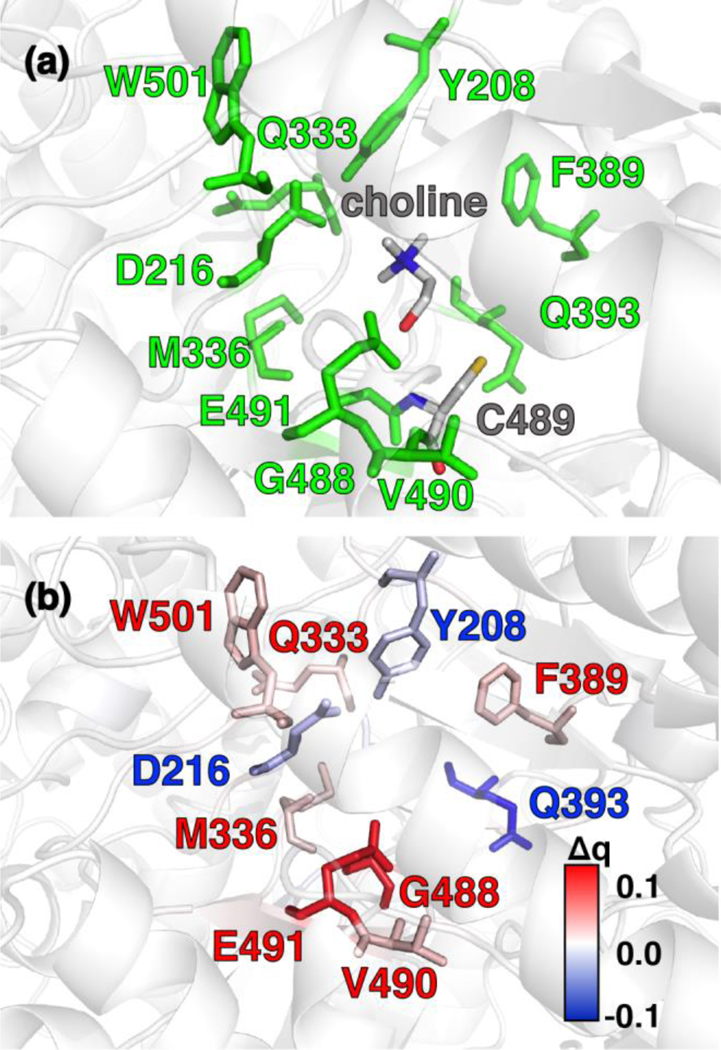
(a) CutC active site structure with choline substrate and cysteinyl radical (C489) shown in gray. Protein residues that were identified by charge shift analysis of QM regions are shown in green. (b) Difference of residue VDD charge upon substrate removal of the choline and residue mutation of C489 to alanine. Residues color-coded in blue and red correspond to loss and gain of partial charge upon substrate removal and residue mutation, respectively (as shown in inset color bar). All residues with Δq ≥ |0.015| e are shown as sticks. Residues of interest are labeled by their single letter residue code and number.

To study the essential reaction steps for CutC, we map reaction coordinates with LCODs in SMD for C-H abstraction (i.e., the difference of S(C489)^…H and C(Cho)-H distances) and O-H deprotonation (i.e., the difference of O-(E491)^…H and O(Cho)-H and distances), as described in the Computational Details. These LCODs correspond to mapping the transfer of H atom and H⁺, respectively, but any spontaneous events that occur during these processes can also be observed during our SMD run. Because our SMD pulling speeds are too high to provide quantitative estimates of barrier heights¹⁴², we focus instead on qualitative geometric rearrangements and on electronic structure (i.e., spin and charge transfer) changes that occur across the reaction coordinate.

For the C-H abstraction step, the H atom is transferred to the thiyl radical of C489 (Figure 6). The Cho and C489 donor/acceptor atom separation is reduced to around 2.9 Å at the moment of transfer in comparison to a 3.9 Å separation in reactants and products (Figure 6). At this point of minimum separation, the C-H distance is slightly shorter than the S-H distance (1.37 Å vs. 1.56 Å), consistent with the fact that equilibrium C-H bond (1.09 Å) is shorter than the equilibrium S-H bond (1.33 Å) (Figure 6). Across this reaction coordinate, we also observe spontaneous proton transfer from the hydroxyl group of choline to the carboxylate group of E491 (Figure 6). In this case, the proton is shared between Cho and E491, with oscillation consistent with a low barrier, charge-assisted hydrogen bond¹⁴³ observed in the reaction coordinate, where the longer 1.6 Å O(Cho)-H distances correspond to the proton residing predominantly on E491 (Figure 6). This observation of spontaneous proton transfer is consistent with the expected increased acidity of the hydroxyl proton on a radical, as it is known that the pK_a values of α-hydroxy radicals can be reduced¹⁴⁴ due to the formation of a stable ketyl radical anion.

Figure 6.

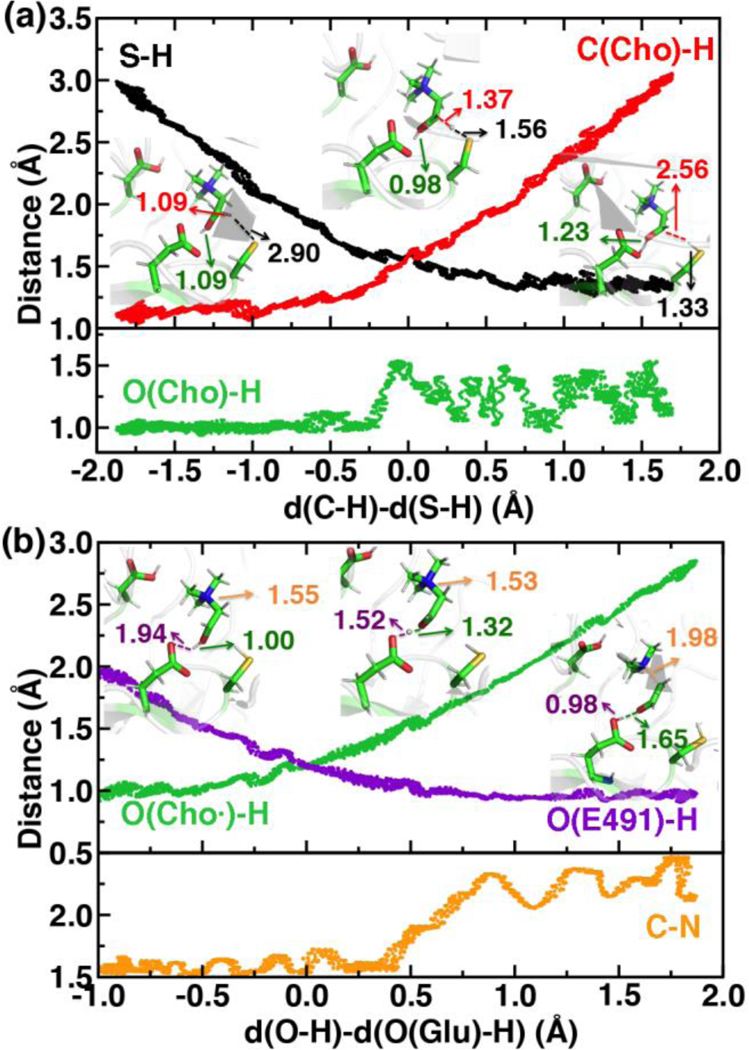
Distances along independent SMD trajectories defined by the LCODs described in the main text. (a) Choline C-H abstraction by cysteinyl radical S (C489) is shown, where the green line in the second pane indicates the choline hydroxyl O-H distance and black and red lines represent the S-H and the C-H distances, respectively. (b) Cholinyl radical deprotonation by E491 is shown, where the yellow line in the second pane represents the C-N distance, and purple and green lines represent O(E491)-H and O(Cho^.)-H distances, respectively. Select snapshots are shown in inset with the respective distances annotated.

For the deprotonation of Cho• hydroxyl, we studied proton transfer from the hydroxyl to E491, increasing the separation of E491 and Cho• during deprotonation to ensure that the proton is fully transferred and no longer shared (Figure 6). Starting from an initial structure where E491 O- is nearly 2.0 Å from the Cho• hydroxyl, driving forward separation and full transfer of the proton to E491 causes spontaneous cleavage of the deprotonated Cho• C-N bond (Figure 6). Although oscillations in C-N bond length occur over the full reaction coordinate, C-N bond cleavage initiates at LCOD values beyond 0.5 Å, which corresponds to full localization of the proton on E491 and Cho• O^−…H distances of slightly greater than the longest distances (i.e., > 1.5 Å) observed in the previous reaction coordinate (Figure 6). As soon as the C-N bond cleaves, it reaches a value greater than 2.0 Å, leading to unambiguous formation of trimethylamine (TMA) and acetaldehyde. Although direct elimination has been hypothesized⁷³, this is the first computational observation of spontaneous C-N cleavage in CutC. Slower pulling speeds or alternative sampling schemes are needed in further work to quantify the energy barrier in this step. During the trajectory, the acetaldehyde radical also rearranges, with formation of a planar geometry at the carbonyl oxygen and a shortening of the C-O distance to a double bond (Figure 6 and ESI, Figure S5). This rearrangement can also be rationalized in terms of the CutC active site, which orients choline such that the radical p orbital is antiperiplanar to the C-N bond. This orientation enables hyperconjugation between the p orbital and C–N σ* orbital to weaken the C-N bond and enable direct TMA elimination. When we separately considered the pathway for protonation of the TMA group in Cho• by a protonated D216, we observed inversion of the TMA improper, C-N bond cleavage and acetaldehyde radical formation with a strong hydrogen bond to E491 as well (ESI, Figure S6). However, we ruled out this step because the D216 proton starts quite far (~4 Å) from the N acceptor on the Cho•, requiring significant movement of the substrate for this step to occur (ESI, Figure S6).

Mulliken spins of the C489 S and choline C confirm that our SMD approach captures the H atom abstraction (Figure 7). As the hydrogen bond of the Cho• radical forms to E491, spin starts to accumulate on the O atom of Cho• (Figure 7). This indicates ketyl radical anion character with spin delocalization increasing the acidity of the hydroxyl group. Although the spin is split between the carbon and oxygen atom, the total spin on those two species is complementary to the S atom spin, indicating that only those two atoms accept the radical from C489 (Figure 7). During O-H deprotonation, spin remains on Cho•until the TMA elimination begins (Figures 6 and 7). The cleavage of the C-N bond is accompanied by the rearrangement of the radical: some small amount of spin accumulates on the N atom along with a transition of a significant amount of the spin to the other C atom on the newly formed acetaldehyde radical fragment (Figure 7). In comparison, the forced TMA protonation step that also produces TMA elimination leads to less net spin on the nitrogen atom of the TMA fragment (ESI, Figure S7).

Figure 7.

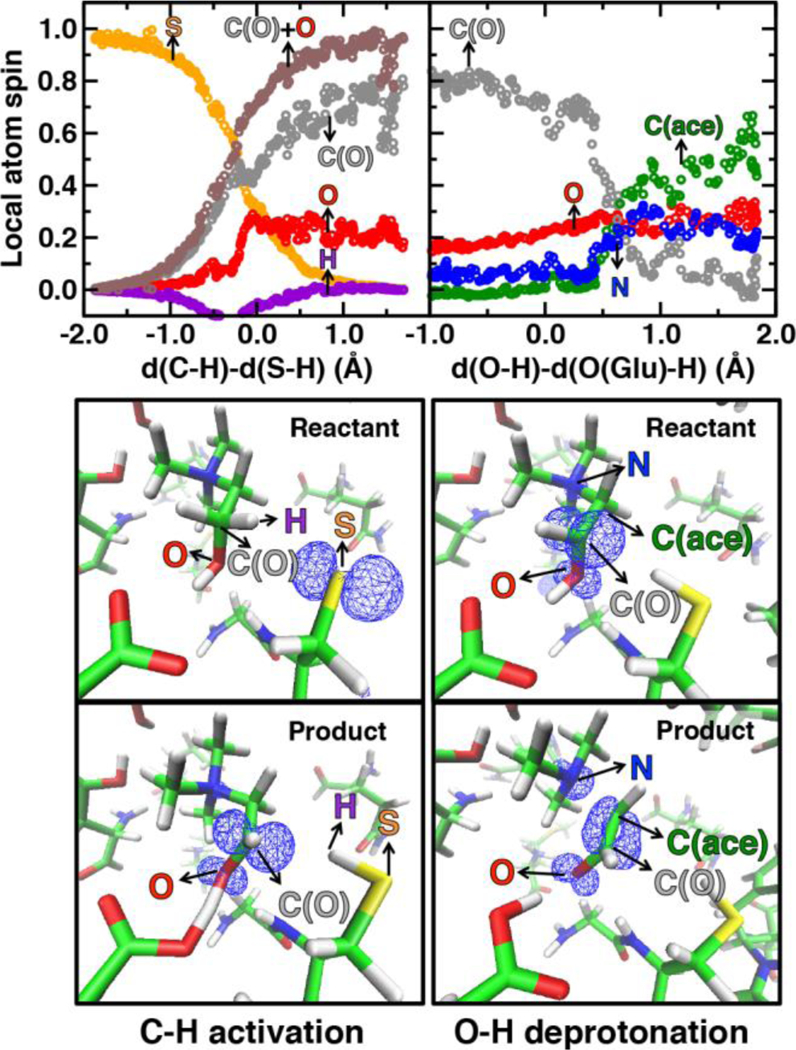
(top) Variation of local atom spin along the reaction coordinate of C-H abstraction (left pane) and of O-H deprotonation (right pane). The atom spin of S, O, N, and H are colored orange, red, blue, and purple, respectively. C(O) and C(ace) refers to the alpha- and beta- hydroxyl carbon atom, and are colored by grey and green, respectively. (bottom) Spin density distribution of typical reactant and product snapshots in H abstraction, and O-H deprotonation, respectively, where the spin density isosurface value is set to 0.01.

During Cho• deprotonation, spins appear delocalized over several species. Analysis of charges on these fragments can help rationalize some of these observations (Figure 8). The total charge over all of fragments originating from Cho• decreases over the course of C-N bond cleavage from around +0.8 e to +0.6 e, reduced from the nominal +1 charge that would be expected (Figure 8). We decompose this charge into i) the proton that is transferred to E491, ii) the acetaldehyde radical fragment, and iii) eliminated TMA (Figure 8). From this decomposition, we observe that the charge on the transferring proton (+0.5 e) is relatively constant, suggesting further that the two remaining fragments are nearly neutral after deprotonation (Figure 8). This deviation is particularly apparent for TMA, which has a reduced partial charge from +0.6 e to +0.2 e at the end of the reaction step, suggesting that the appearance of the radical spin on the N atom of TMA arises in part because TMA is being eliminated as a neutral species, rather than a cation (Figure 8). The weak negative net charge on the acetaldehyde radical is not obviously as significant, as it was instead positive in the case of forced TMA protonation following fragmentation, likely due to differences in the degree of hydrogen bonding with E491 (ESI, Figure S8).

Figure 8.

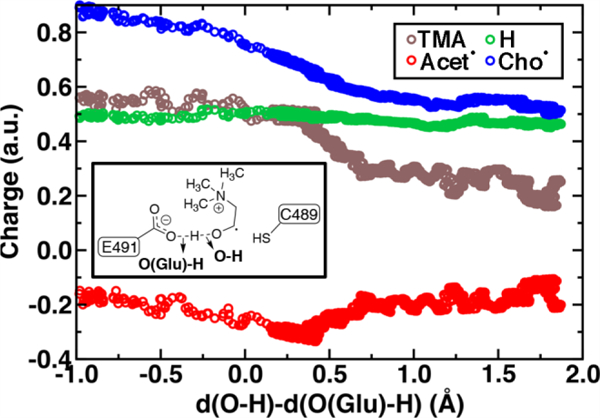
By-fragment-summed partial charges along the cholinyl radical deprotonation reaction coordinate: total cholinyl radical (Cho^., blue circles) and its substituent transferring H+ (green circles), TMA (brown circles), and acetaldehyde radical (Acet^., red circles). A skeleton structure of the distances in the LCOD reaction coordinate is shown in inset.

Finally, we return to the nature of the non-covalent interactions in the active site of CutC that could be responsible for imparting its reactivity. Thus far, we have identified the E491-Cho interaction to be essential for TMA elimination, whereas we found protonation by D216 to be less plausible (ESI, Figures S6-S8). Earlier experimental work⁷³ had also suggested C-H^…O interactions between TMA and adjacent D216, Y506, and Y208 could play an important role in positioning choline during the reaction. To quantify the relative role of C-H^…O and O-H^…O hydrogen bonds (HBs), we evaluate close contacts, defined as cases where two heavy atoms are within 85% or less of the sum of the distance of their van der Waals’ radii, in the CutC crystal structure and our SMD trajectories (see Computational Details). In the entire CutC crystal structure, 15 close contact residue pairs (12 O^…O and 3 N^…O) are observed that represent potential HB interactions, with most (10 of 15) being categorized as sidechain-sidechain (ESI, Table S9). The interaction energies of the pairs of residues are all favorable, whether calculated with QM or MM methods with minimum total interaction strengths of around 4 kcal/mol (ESI, Text S1). HB energies can also be directly estimated from the quantum theory of atoms in molecules (QTAIM) approach^104–105 and are found to be at least 11 kcal/mol, with the HB energy well correlated to heavy atom distances (Figure 9). None of the heavy atom distances in putative C-H^…O HBs were within close contact distance cutoffs (3.2–3.7 Å, vs. < 2.7 Å for a C^…O close contact). As a result, at most weakly favorable interactions are observed between these choline-residue pairs of 2.9 kcal/mol evaluated with SAPT0, and some interactions are weakly unfavorable (ESI, Text S1). QTAIM HB energies for these pairs are also significantly smaller than for their O^…O counterparts (0.7 to 4.0 kcal/mol), commensurate with the longer heavy atom separations (Figure 9).

Figure 9.

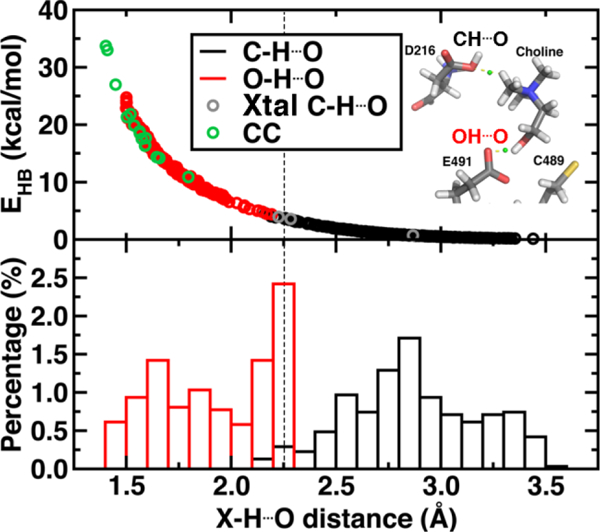
(top) Hydrogen bond energy (E_HB, in kcal/mol) versus X-H^…O distance for i) snapshot MD distances with X=O (red circles), X=C (black circles), ii) all observed close contacts in crystal structures (CC, green circles), and the X=C non-covalent interactions observed in CutC (Xtal C-H^…O, gray circles). A snapshot showing the C-H^…O and O-H^…O hydrogen bond is provided in inset with the BCP shown as a green sphere. (bottom) Normalized distribution of CH^…O and OH^…O distances from MD snapshots as described for the top pane. A qualitative cutoff between CH^…O and OH^…O distances is indicated by a vertical dashed line at 2.25 Å.

Examining all C-H^…O and O-H^…O interactions sampled during our reaction coordinates confirms the observations made on the crystal structure (Figure 9). Most C-H^…O interactions range from 2.25 to 3.5 Å, whereas nearly all O-H^…O hydrogen bonds have an H^…O separation that ranges from 1.7 to 2.25 Å (Figure 9). Due to the high order dependence on separation of hydrogen bond strength energies, C-H^…O HBs are dramatically weaker than O-H^…O HBs (i.e., 0–5 kcal/mol vs. 5–25 kcal/mol). Notably, the charge assisted O-H^…O HB between the Cho^. hydroxyl and E491 is expected to have a significant HB energy (i.e., > 15 kcal/mol) far in excess of the total contribution of the three C-H^…O HBs (i.e., ~6–7 kcal/mol). Thus, while C-H…O interactions are expected to be useful for positioning the choline substrate, the E491 hydrogen bonding interaction is expected to play the dominant role.

3c. DNMT1: considerations for structural metal cofactors.

Metalloproteins present unique challenges for simulation, owing to the need to accurately describe the metalorganic bond at the cofactor site as well as noncovalent interactions in the broader active site. Metals typically play either a catalytic role, e.g., as in the heme in cytochrome P450¹⁴⁵ or a structural role.^146–148 Here, we study DNMTs, which are members of the broad class of MTases introduced in Sec. 3a and examples where bound metals play a structural role. In humans, DNMTs are responsibly for methylating the 5’ position of cytosine bases in CpG-rich islands using SAM as the methyl donor¹⁴⁹, an essential epigenetic process that is crucial for cell fate determination, gene silencing and genome stability¹⁵⁰. We focus on DNMT1, which has been structurally characterized⁷⁶ with its four native Zn metal binding sites (Figure 10). Three of the sites (Zn1, Zn2, and Zn4) are adjacent to the DNA binding domain, whereas the remaining site, Zn3, is more distant (Figure 10). In all cases, Zn is tetrahedrally coordinated, but in both Zn1 and Zn3 the coordination is 3Cys-1His in contrast to the 4Cys coordination for the other two sites (Figure 10). Disruption of DNA methylation upon exposure to toxic metals (e.g., Cd, As, and Ni) has been implicated in cancer¹⁵¹, and there is some evidence that these toxic metals could be replacing native Zn metal¹⁵². QM/MM modeling of the electronic structure around Zn binding sites could provide crucial insight into how substitution by Cd¹⁵³ or As¹⁵¹ might occur and disrupt DNMT activity in a Zn-site-dependent manner.

Figure 10.

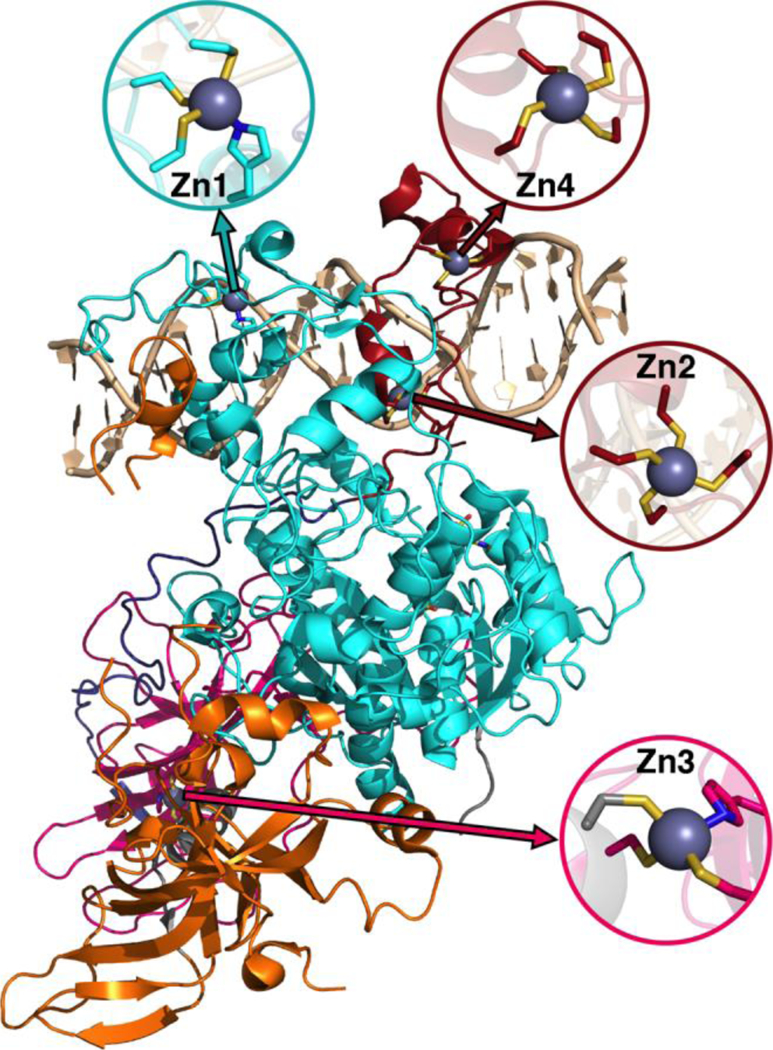
Structure of DNMT1 with DNA bound and separately colored protein chains. Each of the Zn sites in the crystal structure is shown in an inset with the relevant site on the protein indicated by arrows. Zn site numbering corresponds to the numbering in the experimental crystal structure. Zn is shown as a gray sphere, Cys S is shown in yellow, His N is shown in blue, and carbon atoms are colored according to the chain to which they belong.

Here, we focus on the Zn2 site, which is close to both the DNA-protein interface and the methyltransferase catalytic site (Figure 10). We carried out 250 ns of MD to observe the sampled Zn-S(Cys) distances at the 4Cys Zn2 binding site (ESI, Figure S9). All Zn-S bond lengths between Zn and Cys13, Cys16, Cys19, or Cys51 average around 2.4 Å but sample distances as short as 2.0 and as long as 2.8 Å (ESI, Figure S9). Most close contacts observed in the crystal structure are not observed after equilibration (ESI, Table S9 and Text S1). QM-only geometry optimizations of 300-atom QM cluster models confirm the good performance of ZAFF⁸⁵ for the covalent Zn-S bond lengths: average MD-sampled bond lengths are in agreement with QM-optimized bond lengths (ESI, Figure S9 and Table S10). The 0.8-Å range of sampled Zn-S distances suggests that multiple snapshots should indeed be investigated in the context of computing energetics of Zn²⁺ displacement from binding sites. The good correspondence of QM and MM bond lengths suggests this sampling can be achieved at the more efficient MM level of theory, unlike COMT where we showed first principles sampling was essential (see Sec. 3a).

Although we have already discussed QM region convergence in the context of COMT, convergence of properties around the structural Zn²⁺ ion merits some attention. Here, we define QM regions by including a residue if any of that residue’s atoms are within a radial distance cutoff of the Zn²⁺ ion. Radial convergence studies are carried out both because the Zn2 site is near the surface of DNMT1, making the extraction of a large QM sphere for CSA^{35, 62} challenging. Starting from a minimal 3 Å radius QM region 1 that incorporates only Zn2 and the four coordinating Cys residues (net charge: −2, 49 atoms with link H atoms), we constructed six additional QM regions: 5 Å, 6 Å, 7 Å, 8 Å, 9 Å, and 10 Å (Figure 11 and ESI, Table S10 and Figure S10). The largest QM region 7 contains 417 atoms including link H atoms has zero net charge (ESI, Table S10 and Figure S10). Only the three smallest QM regions have a modest net charge of −2 or −1, whereas the remaining four regions are neutral, and most QM regions have 8 or fewer covalent cuts (ESI, Table S10).

Figure 11.

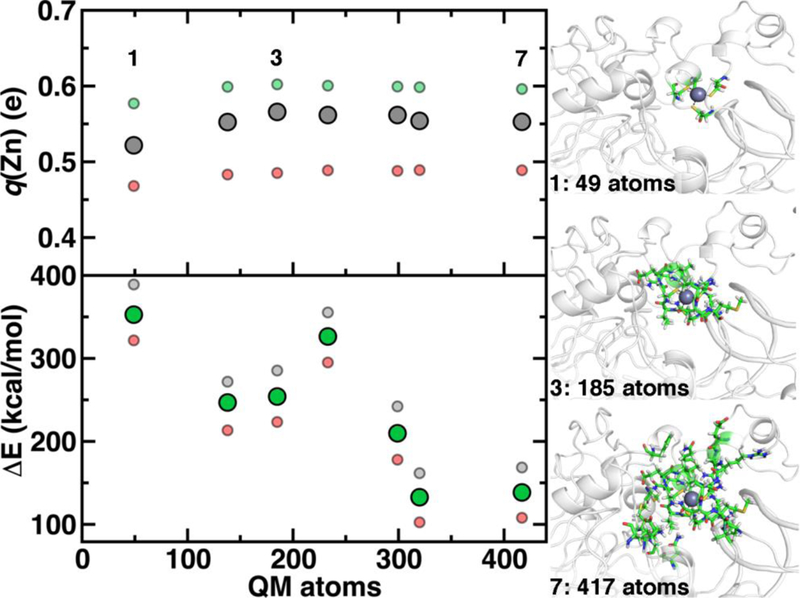
Dependence of properties with QM region size: Zn Mulliken partial charge (q(Zn), in e) shown at top left and rigid binding energy (ΔE, in kcal/mol) shown at bottom left. For each property, three snapshots are computed (40 ns in gray, 60 ns in red, and 100 ns in green), and the middle range symbol is shown in large solid symbols, whereas the upper and lower quantities are shown as translucent, smaller symbols. QM regions 1, 3, and 7 are shown at right in ball and stick representation.

We evaluate key electronic structure and energetic properties with these seven QM regions to determine QM/MM QM region dependence for DNMT1. As a measure of the electronic structure, we evaluate the Mulliken partial charge of Zn²⁺ in the holoenzyme and focus on its variation with QM region size rather than absolute charges that will be more sensitive to the partial charge scheme. Next, we evaluate a rigid binding energy of Zn²⁺, which provides an upper bound estimate of the binding strength of Zn²⁺ to the active site residues and thus how easily it can be displaced by other metals. We evaluate the Zn²⁺ rigid binding energy, ΔE, as:

$$\Delta E=E(Zn/DNMT1)-E(DNMT1)-E(Z{n}^{2+})$$ (2)

where each energy corresponds to the QM/MM single point energies of DNMT1 with Zn bound, DNMT1 without Zn²⁺, and the energy of isolated Zn²⁺, respectively. No geometry optimization of the DNMT1 is carried out after the rigid Zn²⁺ removal.

We compute both Mulliken partial charges and ΔE values for all 7 QM regions on three uncorrelated snapshots from MD obtained at around 40, 60, and 100 ns to determine the effect of configuration on QM region convergence. Significant variation is indeed observed among the three snapshots for any given QM region, with the snapshots with generally more positively charged Zn²⁺ also having higher ΔE values (Figure 11). Qualitatively, Mulliken charges appear QM region insensitive, with only QM region 1 having slightly more neutral Zn²⁺ than all other QM regions (Figure 11). In comparison, QM region 2 adds several residues, including a positively charged Arg12 near the Zn²⁺ site, but primarily residues adjacent to each of the Cys in the sequence, potentially stabilizing the coordinating Cys to be more electron-withdrawing (ESI, Table S10). Overall, the variation within a QM region over the three snapshots is at least 0.12 e, whereas the variation for a given snapshot by QM region is at most around 0.03 e (Figure 11). Thus, making this comparison allows us to determine that Zn²⁺ Mulliken charges are more configurationally sensitive than QM-region sensitive.

Repeating this analysis on ΔE, we observe a very different trend: variations of around 50–70 kcal/mol across the three snapshots for a fixed QM region are smaller than variations in average ΔE for differing QM regions (i.e., 355 kcal/mol for 1 vs. 138 kcal/mol for 7) (Figure 11). Excluding QM region 4, ΔE generally decreases as the QM region increases, with only QM region 6 (320 atoms) within good agreement of region 7 (132 kcal/mol for 6 vs. 138 kcal/mol for 7) (Figure 11). Reviewing residues present in QM region 4 but absent in 3 suggests that ΔE increases for 4 because Arg50, proximal to the Zn²⁺ binding site, is introduced in 4 and interacts strongly with Cys51 altering its binding strength to Zn²⁺ (ESI, Table S10).

To rationalize why ΔE is so sensitive to the QM region, we examined how by-residue-summed partial charges change in QM region 7 when Zn²⁺ is removed (Figure 12). Although most of the charge is gained on the 4 coordinating Cys residues, this gain is highly asymmetric: Cys13 and Cys51 gain 0.24 and 0.18 e, whereas Cys16 and Cys19 gain only 0.11 and 0.05 e, respectively, likely due to indirect influence of other neighboring QM residues (Figure 12 and ESI, Table S11). In addition to the covalently bound residues, Arg12, which is included in 2 and larger QM regions, gains 0.20 e, more than most Cys residues (ESI, Table S6). Other residues have significant shifts in charge, even when further away, such as Gln20 in 3 that is neutral but gains 0.06 e when Zn²⁺ is removed (Figure 12 and ESI, Table S11). Overall, no significant difference is observed for charge shift magnitudes between non-polar active site residues (e.g., G14, V15, V18, M54), polar but neutral residues (Q20), or charged residues (e.g., E17, R12, R50), in accordance with previous observations^{35, 62} of charge shifts in COMT (Figure 12). Significant differences in the electrostatic environment for large QM region simulations thus stabilize Zn²⁺ removal over minimal QM regions via more physical delocalization of charge.

Figure 12.

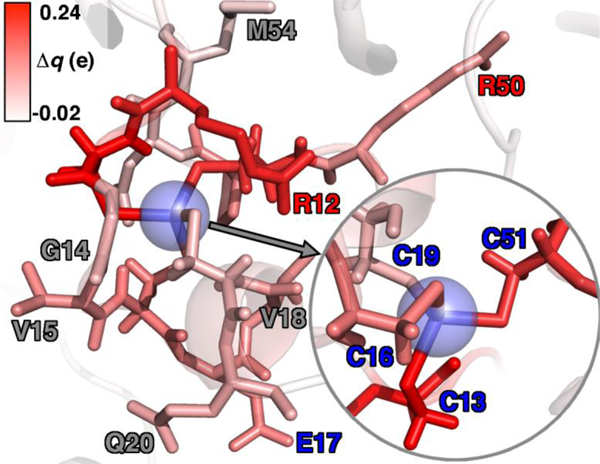
Difference of by-residue-summed Mulliken charges upon removal of Zn²⁺ in QM region 7 QM/MM simulations colored according to color bar in top left inset. All residues with Δq > |0.03| are shown as sticks, with key residues labeled by the single letter residue code and number colored for according to the formal charge (positive in red, neutral in gray, and negative in blue). Zn is not present in the simulation but its position is shown as a translucent blue sphere, and the coordinating Cys residues are shown in the inset at right.

4. Conclusions

In this work, we have studied the electronic structure and reactivity of three diverse enzymes with QM/MM simulation: i) the Mg²⁺-dependent catechol O-methyltransferase (COMT), ii) the glycyl radical enzyme choline trimethylamine lyase (CutC), and iii) Zn²⁺-dependent DNA methyltransferase (DNMT1).

In COMT, a system with a catalytic metal ion and a bulky SAM cofactor, we noted large differences in predictions depending on the means by which QM regions were constructed, ranging from minimal regions, to radially enlarged regions, and finally systematic construction methods, due to the numerous non-covalent substrate-protein interactions in the active site. To explain why techniques to reduce the sizes of QM regions for 0 K reaction coordinates were less successful when applied to QM/MM free energy simulations, we analyzed covariance matrices of the by-residue-summed partial charges. We observed long-range coupling between active site residue charges and distant residues and found that the pattern of couplings varied dynamically along the reaction coordinate.

We next studied CutC as a case where radical chemistry presents challenges to model both charge transfer and the evolution of spin densities. From systematic QM/MM analysis, fewer non-covalent interactions were observed to play essential roles in the CutC active site. By mapping out reaction coordinates with QM/MM steered MD, we observed that initiating one bond cleavage event triggered other reaction events. Using this approach, we provided evidence for spontaneous decomposition of the substrate into products following deprotonation of the cholinyl substrate radical. Through electronic structure analysis of the non-covalent interactions in the active site, we concluded that the E491 to choline O-H^…O charge-assisted hydrogen bond likely dominates over weaker but still favorable C-H^…O interactions.

To illustrate the tradeoffs faced when modeling a transition metal that plays a structural role, we studied the Zn²⁺ binding site of DNMT1. Here, we noted the important role of sampling and averaging over configurations through a robust MM force field. We also observed rapid convergence in small QM regions of some properties (i.e., Mulliken charge of Zn) dictated by nearest neighbor interactions, whereas others that involve significant perturbations to the electrostatic environment (i.e., rigid Zn binding energy) had slower convergence in line with observations on COMT.

These three diverse cases enable us to provide some general recommendations regarding QM/MM simulation of enzymes. Dynamical sampling of distinct geometric configurations provides essential insight into enzyme catalysis. Nevertheless, the effect of QM region size can dominate over the benefits of extensive sampling in cases where the electrostatic environment provided by the MM treatment is too different from the charge transfer allowed in the QM environment (e.g., with strong, charge-assisted hydrogen bonds or other non-covalent interactions). Systematic QM region construction methods provide useful insight by detecting difficult-to-describe interactions with MM. When properties are dominated by through-bond interactions, small QM regions may be sufficient, especially for select metallocofactor properties. Thus, when studying new proteins, researchers will always benefit from QM region sensitivity analysis of properties being studied, and systematic tools should make this analysis straightforward. Beyond these considerations, outstanding challenges remain for computational enzyme modeling, including: accelerating sampling, improving QM methods along with MM embedding, and improved sampling considerations in systematic QM/MM partitioning, which are underway in our group.