Behavioural and neural evidence for self-reinforcing expectancy effects on pain

Abstract

Beliefs and expectations often persist despite disconfirming evidence. We examine two potential mechanisms underlying such ‘self-reinforcing’ expectancy effects in the pain domain: Modulation of perception and biased learning. In two experiments, cues previously associated with symbolic representations of high or low temperatures preceded painful heat. We examined trial-to-trial dynamics in participants’ expected pain, reported pain, and brain activity. Subjective and neural pain responses assimilated towards cue-based expectations, and pain responses in turn predicted subsequent expectations, creating a positive dynamic feedback loop. Furthermore, we found evidence for a confirmation bias in learning: Higher- and lower-than-expected pain triggered greater expectation updating for high- and low-pain cues, respectively. Individual differences in this bias were reflected in the updating of pain-anticipatory brain activity. Computational modeling provided converging evidence that expectations influence both perception and learning. Together, these effects promote self-reinforcing expectations, helping to explain why beliefs can be resistant to change.

Introduction

Our past experiences drive our expectations about the future. This principle is a fundamental tenet underlying learning theory^1,2. At the same time, our expectations can strongly influence how we experience events. This principle underlies decades of work on placebo effects^3–9, top-down influences on perception^10–13, and predictive coding^14–19. The bidirectional interaction between expectations and experience can result in self-reinforcing phenomena—so-called “self-fulfilling prophecies”—in many areas of human endeavor, including placebo and nocebo effects in medicine, stereotype effects on performance and behaviour, and economic growth and recession²⁰.

One domain in which self-reinforcing expectancy effects may be particularly powerful, and have important clinical implications, is pain perception. Previous studies have found that expectations about pain intensity—induced by previous experiences and/or instructions—result in the adjustment of pain responses toward the expected pain level^5,16,21–23. Moreover, several studies have shown that expectancy effects on pain persist, or even grow over time, in the absence of confirming evidence^24–31. Such self-reinforcing expectancy effects are inconsistent with conventional reinforcement-learning principles^1,32. In standard models of reinforcement learning, discrepancies between expected and actual outcomes—or ‘prediction errors’—trigger expectation updating, such that expectations that are not confirmed by experience will extinguish.

The behavioural and brain mechanisms underlying resistance to extinction are largely unknown, and previous studies have not empirically demonstrated reciprocal, positive associations between expectations and experience. Thus, the idea of ‘self-fulfilling prophecies’ in brain-behaviour systems remains a theoretical conjecture. Here, we address this question in a laboratory setting, examining trial-to-trial dynamics in behaviour and fMRI activity related to expectations and pain. In two studies, we independently manipulated predictive cues and painful stimulus intensity, which allowed us to decouple the bidirectional influences of expectation and pain on one another.

Using this platform, we examine two non-mutually exclusive ways in which expectations about pain can be self-reinforcing. First, expectations may modify the perceptual processing of nociceptive input, such that people actually feel what they expect. Findings that placebo and nocebo manipulations—involving suggestions of decreased and increased symptoms, respectively—influence pain-related activation in the spinal cord provide evidence that expectations can modify pain processing at a very early stage^33,34. Similar modulation of perceptual processing may account for expectancy effects on appetitive experiences³⁵. If the assimilation of sensory input toward expectations occurs at a processing stage prior to prediction-error computation, prediction errors will be diminished and hence expectation updating will be impeded.

A second possible mechanism underlying self-reinforcing expectancy effects is that expectations may bias experience-based learning. Specifically, people may update their expectations more when new evidence confirms, compared to when it disconfirms, their initial beliefs. Consistent with this idea, prior information about reinforcement probabilities can bias choices and suppress learning-related brain activation in probabilistic reward-learning tasks^36–40. Expectations may induce biases in both (a) evaluation, i.e., the reinforcement value assigned to outcomes^38,41, and (b) learning, i.e., the degree to which new outcomes trigger expectation updating³⁷.

In the present study, we provide evidence that cue-based expectations influence both pain perception and learning. Higher pain expectations predicted larger subjective and neural pain responses, and larger pain responses in turn predicted higher subsequent expectations, generating a positive feedback loop between expectations and pain. Additionally, expectation updating for high-pain cues was strongest following higher-than-expected pain, while updating for low-pain cues was strongest following lower-than-expected pain, consistent with a confirmation bias in learning. Together, these effects promote persistent effects of initial expectations on pain in the face of predominantly disconfirming evidence.

Results

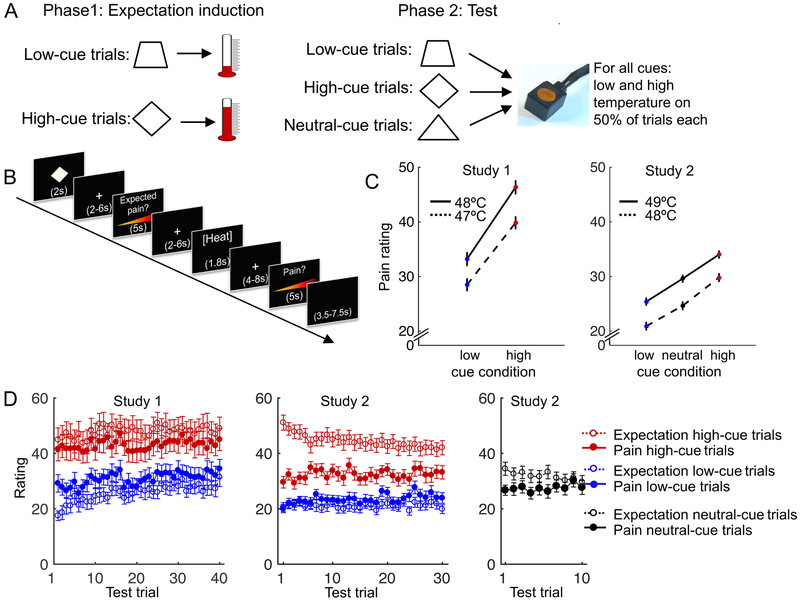
In two studies (N = 28 and N = 34), participants performed a learning procedure followed by a test phase²⁷. During learning, participants viewed abstract visual cues paired with symbolic representations of heat, i.e., pictures of thermometers (Figure 1A). Some cues (low-pain cues) were consistently followed by low-temperature pictures (25–51% of the thermometer scale), and other cues (high-pain cues) were consistently followed by high-temperature pictures (73–93% of the thermometer scale). The purpose of this procedure was to create learned, conceptual associations between cues and heat intensity. In the subsequent test phase, both types of cues were repeatedly followed by noxious contact heat stimuli applied to participants’ inner forearm (47–48°C; Study 1) or lower leg (48–49°C; Study 2). Importantly, unbeknownst to the participants, heat intensities during the test phase were matched for all cues (Figure 1A), allowing a test of the causal effects of the cues on pain. Participants rated how much pain they expected following each cue, and how much pain they experienced following each heat stimulus (Figure 1B). We focused our analyses on the test phase, including pain ratings in both studies and fMRI activity in Study 2. We previously reported the cue effects on pain ratings and skin-conductance responses in Study 1²⁷. Other results, including those on learning dynamics and computational modeling, were not included in previous reports.

Figure 1.

Experimental design and behavioural results. A. Cue-outcome pairings in the conditioning and test phase. Ten neutral-cue trials were included in Study 2 only. B. One test-phase trial in Study 2. Study 1 had slightly shorter interstimulus intervals. C. Pain rating as a function of stimulus temperature and cue type. Heat was applied to the inner forearm in Study 1 and to the, less sensitive, lower leg in Study 2, which explains the overall lower pain ratings in Study 2. Error bars indicate within-subject standard errors. Plots for Study 1 and Study 2 are based on data from 28 and 34 participants, respectively. D. Average expected (open circles) and experienced (filled circles) pain ratings as a function of cue type and trial. The difference between red and blue filled circles is the effect of cue type on pain ratings, which was robust in both studies, and did not disappear over time. The difference between red and blue open circles is the effect of cue type on pain expectations, which remained stronger than the effect on pain ratings throughout the test phase. Error bars indicate between-subject standard errors. Plots for Study 1 and Study 2 are based on data from 28 and 33 participants, respectively (one participant in Study 2 misunderstood the expected-pain rating procedure, and was excluded from all analyses and figures involving pain expectations).

We analyzed the behavioural and Neurologic Pain Signature (NPS) results using multi-level regression analyses on the single-trial data (also see Methods). Unless otherwise stated, the reported t-tests are tests of the distribution of the first-level regression coefficients against 0, and the reported confidence intervals (CI) are the 95% confidence intervals of the regression coefficients. We used bootstrapping for significance testing, which does not require the assumption of normality for valid inference.

Cue effects on pain ratings

As expected, participants’ pain ratings increased with increasing temperature (t(27) = 9.4, bootstrap p < .001, Cohen’s d = 1.9, CI = 2.2 to 3.2 and t(33) = 9.4, bootstrap p < .001, d = 1.9, CI = 3.5 to 5.1 in Study 1 and Study 2, respectively). Importantly, pain ratings were higher following high- than low-pain cues (Figure 1C; t(27) = 7.6, bootstrap p < .001, d = 1.5, CI = 4.6 to 7.5 and t(33) = 8.9, bootstrap p < .001, d = 1.6, CI = 3.4 to 5.2 in Study 1 and Study 2, respectively). In Study 1, the effect of cue type on pain rating was stronger for more intense heat, reflected in an interaction between cue type and temperature (t(27) = 3.2, bootstrap p < .001, d = .91, CI = .17 to .41). In Study 2, the effect of cue type did not differ between the two temperatures (t(33) = .54, bootstrap p = .50, CI = −.48 to .26). In Study 2, we also included test trials with a novel, ‘neutral’ cue that had not been presented during the learning phase. Pain ratings on neutral-cue trials fell between those for low- and high-pain cues, and pain ratings for all three cue types differed significantly from each other, for both temperature levels (all bootstrap ps < .001; Figure 1C).

The effect of cue type on pain rating was stable across test trials even though the cues no longer predicted heat intensity, providing initial evidence for potential ‘self-reinforcing’ effects (Figure 1D). There was a trend towards a negative interaction between cue type and time (trial number) during the test phase (t(27) = 1.8, bootstrap p = .07, d = .38, CI = −.04 to −.0004 and t(33) = 2.1, bootstrap p= .05, d = .34, CI = −.04 to −.0004 in Study 1 and Study 2, respectively), reflecting a slight decrease in the cues’ effects on pain over time. However, the effect of cue type was still large and highly significant at the end of the test phase (pain rating on the last high- vs. the last low-cue trial: t(27) = 4.6, p < .001, d = .87 and t(33) = 5.9, p < .001, d = 1.0 in Study 1 and Study 2, respectively).

Cue effects on pain expectations

Analyses of expected-pain ratings showed that, in both studies, participants expected higher pain following high- than low-pain cues (Figure 1D; t(27) = 10.0, bootstrap p < .001, d = 1.9, CI = 8.9 to 13.1 and t(32) = 13.5, bootstrap p < .001,d = 2.5, CI = 10.0 to 13.2 in Study 1 and Study 2, respectively). Furthermore, pain expectations for high-pain cues were consistently worse than experience (t-tests on average expected minus average experienced pain, t(27) = 7.5, p < .001, d = 1.4, CI = 3.5 to 6.2 and t(32) = 7.1, p < .001, d = 1.2, CI = 8.6 to 15.5 in Study 1 and Study 2, respectively), whereas pain expectations for low-pain cues were consistently better than experience (t-tests on average expected minus average experienced pain, t(27) = 4.5, p < .001, d = .85, CI = −7.5 to −2.8 and t(32) = 3.1,p = .005, d = .54, CI = −3.8 to −.77 in Study 1 and Study 2, respectively), indicating a lack of extinction. Pain expectations for the neutral cues fell between those for low- and high-pain cues. In contrast to the low- and high-cue trials, pain and expected-pain ratings on neutral-cue trials converged over time (Figure 1D).

Cue effects on pain-related brain activity

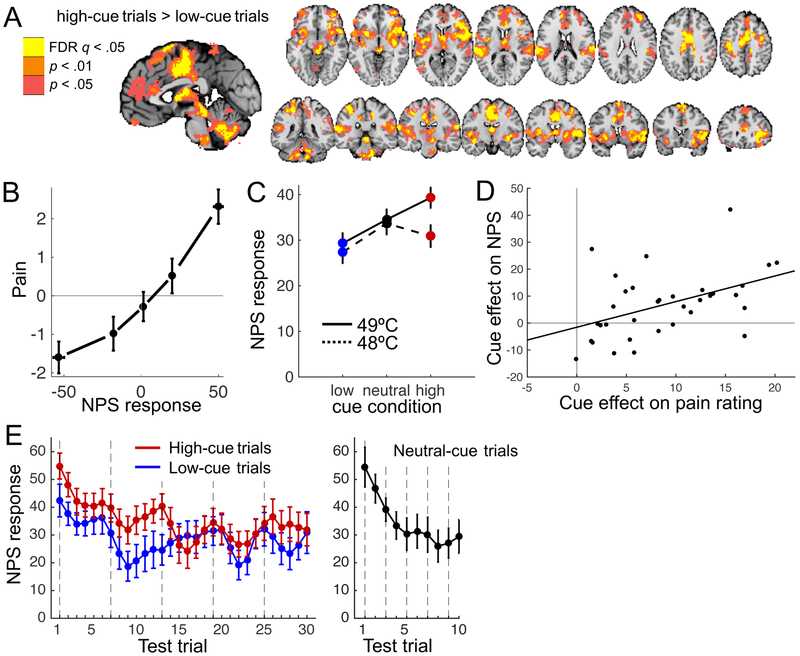
We previously reported that, like pain ratings, heat-evoked skin conductance responses were also larger following high- than low-pain cues²⁷. In Study 2, we examined the effects of the cues on pain-related brain activity. Heat-evoked activity in several areas—including the anterior midcingulate cortex (aMCC), insula, thalamus, and parts of the midbrain—was stronger on high- than low-cue trials (Figure 2A). These brain areas have been related to various aspects of pain processing^42–45. For example, electrical stimulation of the insula can produce pain in humans⁴⁶, and lesions and pharmacological inactivation of the ACC disrupt pain-avoidance behaviours in animals^47,48. However, all these brain areas have also been associated with cognitive and emotional functions that are unrelated to pain; hence they are not specific to pain.

Figure 2.

Cue effects on heat-evoked brain activity. A. Heat-evoked brain activity on high- vs. low-cue trials. Colored regions indicate stronger activity when heat was preceded by a high- than a low-pain cue. All colored regions were significant at q<0.05, FDR-corrected. For the purpose of display, we pruned the results using two additional, less conservative levels of voxel-wise threshold. B. Pain rating as a function of NPS response. We sorted each participant’s pain ratings into five bins according to their single-trial NPS response (both mean-centered), and plotted the group-average data for each bin. Error bars indicate within-subject standard errors. C. NPS response as a function of stimulus temperature and cue type. D. Across-subject correlation between the effects of cue type on pain rating and on the NPS response (r(32) = .46, p = .007, R² = .21, CI = .15 to .95). E. Average NPS response as a function of cue type and trial. Before plotting, the effect of temperature was regressed out and single-trial NPS responses were smoothed using locally weighted scatterplot smoothing. Vertical lines indicate the first trial of each scan run (heat was applied to a new skin site in each run). Note that the ten neutral-cue trials were evenly distributed amidst the low- and high-cue trials (one neutral-cue trial was presented during each series of 3 low- and 3 high-cue trials). Error bars indicate between-subject standard errors. All plots are based on data from 34 participants.

To address this issue, we recently developed a multivariate pattern of fMRI activity found to be sensitive and specific to physical pain in multiple previous studies^49–52: The Neurologic Pain Signature (NPS)⁵³. We computed the strength of expression of the NPS by calculating the dot product of the NPS pattern weights and the activation map for each heat application period (obtained from the subject-level fMRI analysis; see Methods). This resulted in one scalar value—the NPS response—per trial for each participant.

As expected, higher NPS responses predicted higher pain ratings within participants, controlling for temperature and cue type (t(33) = 3.1, bootstrap p< .001, d = .53, CI = .01 to .03; Figure 2B), and NPS responses were stronger for 49°C than for 48°C heat (t(33) = 3.9, bootstrap p < .001, d = .77, CI = 2.8 to 7.1; Figure 2C). Importantly, NPS responses were larger on trials with high- than low-pain cues (main effect of cue type, t(33) = 3.2, bootstrap p < .001, d = .63, CI = 1.3 to 4.4; Figure 2C), indicating that the cues modulated the nociceptive and/or pain-generation processes that drive the NPS response. Furthermore, individual differences in the cue effect on pain rating predicted the magnitude of participants’ cue effect on the NPS response (r(32) = .47, p = .007; Figure 2D). The effect of cue type was larger for more intense heat, as reflected in a Cue type × Temperature interaction (t(33) = 2.0, bootstrap p = .04, d = .37, CI = .25 to 5.1). Follow-up t-tests showed that NPS responses were significantly larger on high- than low-cue trials for 49°C heat (t(33) = 3.1, p = .004, d = .53), but not necessarily for 48° heat (t(33) = 1.9, p = .07, d = .33). Comparisons with neutral-cue trials showed that for 49°C heat, there was a trend toward lower NPS responses following low vs. neutral cues (t(33) = 1.9, p = .06, d = .33), but no significant difference between neutral and high cues (t(33) = 1.4, p = .17). For 48°C heat, the NPS response on neutral-cue trials did not differ significantly from the NPS response on either low- (t(33) = 1.7, p = .11) or high-cue trials (t(33) = 0.7, p = .49).

Although the cue effect on the NPS response was numerically strongest in the first half of the test phase (Figure 2E), there were no significant interactions between cue type and the linear (t(33) = 1.5, bootstrap p = .12, d = .21, CI = −.13 to .03) or quadratic (t(33) = 0.8, bootstrap p = .37, d = .15, CI = −.002 to .005) effects of time. Thus, we cannot say definitively whether the cue effect on the NPS extinguished over time, but it appears to persist throughout the test phase. Together, these findings show that the cues robustly and persistently modulated both behavioural and brain markers of pain.

Reciprocal positive associations between expectations and pain

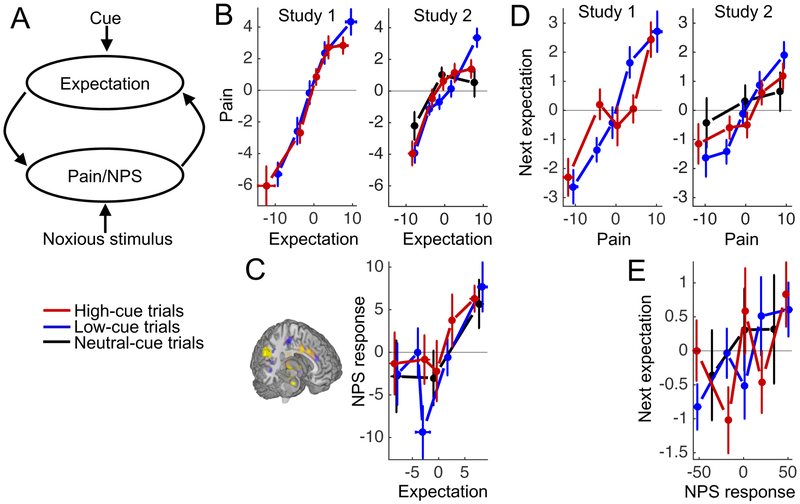
The resistance to extinction of the cue effects on pain may be supported by reciprocal positive influences of expectations and pain perception on one another: Expectations modify pain perception, and this modified perception drives subsequent expectations, resulting in the maintenance of expectations even when these do not reflect sensory input (Figure 3A). To examine evidence for both halves of this putative reciprocal circuit, we first analyzed the effects of expectations on subsequent pain ratings and NPS responses (left arrow in Figure 3A), and then analyzed the effects of pain ratings and NPS responses on subsequent cue-based expectations (right arrow in Figure 3A). We controlled for cue type and temperature in all four analyses.

Figure 3.

Bidirectional effects of expectations and pain on one another. A. Dynamic feedback circuit through which expectations can become self-reinforcing. B. Pain rating as a function of expected pain and cue type. We sorted each participant’s pain ratings for the low- and high-cue trials into five bins, according to their trial-specific expected-pain ratings (both mean-centered), and plotted the group-average data for each bin. As there were fewer neutral-cue trials, we used three bins for the neutral-cue condition. Note that we binned the data for plotting purposes, but used single-trial measures in our statistical analyses. C. NPS response as a function of expected pain and cue type. D. Cue-based pain expectation as a function of cue type and the previous pain rating for that cue. E. Cue-based pain expectation as a function of cue type and the previous NPS response for that cue. All error bars indicate between-subject standard errors. All plots for Study 1 and 2 are based on data from 28 and 33 participants, respectively.

Consistent with the first half of the reciprocal circuit—expectation effects on subsequent pain—higher pain expectations predicted higher pain ratings in both studies (t(27) = 8.8, bootstrap p < .001, d = 1.5, CI = .37 to .61 and t(32) = 7.4, bootstrap p < .001, d = 1.4, CI = .25 to .41, in Study 1 and 2, respectively; Figure 3B). Higher pain expectations also predicted higher NPS responses in Study 2 (t(32) = 4.2, bootstrap p < .001, d = .71, CI = .26 to .74; Figure 3C). Furthermore, a multilevel-mediation analysis showed that trial-to-trial variation in NPS response formally mediated the effect of expectations on pain ratings (controlled for cue type and temperature; p < .001, d = .70). When controlled for NPS response, the effect of expectations on pain ratings remained highly significant (path c’, p < .001, d = 1.1), implying a partial mediation.

Consistent with the second half of the reciprocal circuit—pain effects on subsequent expectations—higher pain ratings on a trial predicted higher pain expectations the next time the same cue was presented (t(27) = 8.0, bootstrap p < .001, d = 1.4, CI = .17 to .29 and t(32) = 4.5, bootstrap p < .001, d = .90, CI= .10 to .22, in Study 1 and 2, respectively; Figure 3D). In Study 2, there was a non-significant trend in the same direction for the NPS response: Higher NPS responses on a trial predicted higher pain expectations the next time the same cue was presented (t(32) = 1.2, bootstrap p = .10, d = .27, CI = −.001 to .01; Figure 3E). Together, these results suggest that expectations modified pain perception, and that participants updated their expectations based on new pain experiences.

Confirmation bias in expectation updating

Bidirectional interactions between expectations and experience can contribute to persistent expectations in spite of inconsistent evidence. Importantly, however, the component of the pain response that is affected by prior expectations may differ from the component that drives expectation updating. Specifically, if expectancy-based pain modulation occurs at a processing stage subsequent to prediction-error signaling, expectancy effects on pain may not carry over to affect subsequent expectations (also see Discussion). Moreover, even if there is a closed feedback loop between pain and expectations, this is sufficient for the creation of self-reinforcing expectancy effects only when experience fully conforms to the expectation. If experience adjusts only partially towards expectations, as was the case in our studies (Figure 1D), we would expect a weakening of expectations and eventual extinction over time. Thus, to explain our findings of persistent cue effects on expected- and experienced-pain ratings, an additional mechanism is needed. One possible additional mechanism is a confirmation bias in learning³⁷: stronger expectation updating when new experiences are consistent, than when they are inconsistent, with the initial expectation of high or low pain.

In our paradigm, a confirmation bias would be reflected in strongest expectation updating when high- and low-pain cues are followed by, respectively, higher- and lower-than-expected pain. For conciseness, we refer to these as aversive and appetitive pain prediction errors, respectively, although this is not meant to suggest that lower-than-expected pain is processed by the same system as reward or pleasure. In reinforcement-learning models, the degree of expectation updating following prediction errors is controlled by the learning rate. Thus, a confirmation bias can be statistically formalized as an interaction between cue type (high- vs. low-pain cue) and prediction error sign (aversive vs. appetitive) on learning rate. Prediction errors and learning rate are typically inferred from behavioural or autonomic data, but the trial-specific expectation and pain ratings in our paradigm provide direct estimates of these variables on each trial, requiring fewer assumptions about latent variables and providing an empirical estimate of learning in each condition. Specifically, we defined an estimated prediction error $\left(\widehat{\delta }\right)$ on each trial t as the difference between the ratings of pain (P) and expected pain $(E):{\widehat{\delta }}_t=P_t-E_t$ Additionally, we defined an estimate of trial-specific learning rate $\left(\widehat{\mathrm{\alpha }}\right)$ as the change in expected-pain rating across two successive presentations of the same cue c (trials t and t^′), divided by the most recent prediction error for that cue: ${\widehat{\mathrm{\alpha }}}_{c,t}=\left(E_{c,t^{\prime }}-E_{c,t}\right)/{\widehat{\delta }}_t$. We report additional model-based analyses in the ‘Computational models’ section.

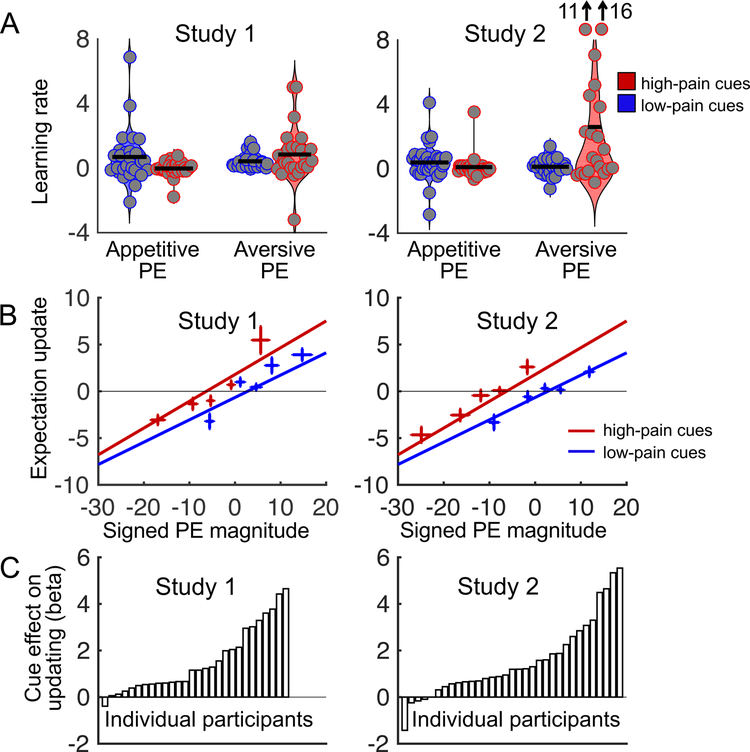
In Study 1, estimated learning rate did not differ between high- and low-pain cues (t(25) = 0.2, bootstrap p = .81, d = .05, CI = −.12 to .16), but was marginally higher for aversive than appetitive prediction errors (t(25) = 1.2, bootstrap p = .07, d = .31, CI = −.03 to .33). Importantly, learning rates were highest for appetitive prediction errors following low-pain cues and for aversive prediction errors following high-pain cues, resulting in an interaction between cue type and prediction error sign (t(25) = 2.5, bootstrap p < .001, d = .68, CI = .08 to .28; Figure 4A), consistent with a confirmation bias. Study 2 confirmed these findings. In Study 2, participants showed higher estimated learning rates for high- than low-pain cues (t(20) = 2.5, bootstrap p < .001, d = .49, CI = .17 to .95) and for aversive than appetitive prediction errors (t(20) = 2.1, bootstrap p = .005, d = .40, CI = .08 to .94). As in Study 1, learning rates were highest for appetitive prediction errors following low-pain cues and aversive prediction errors following high-pain cues, resulting in an interaction between cue type and prediction error sign (t(20) = 2.4, bootstrap p < .001, d = .46, CI = .16 to 1.1; Figure 4A). Thus, learning rates were consistent with a confirmation bias in both studies. We also performed the same analysis on raw expectancy updates (not divided by prediction error), which yielded similar results (Supplementary Results and Supplementary Figure 1), demonstrating that the results are not driven disproportionately by high learning rates on trials with very small prediction errors.

Figure 4.

Confirmation bias in expectation updating. A. Estimated learning rate as a function of prediction error sign and cue type in each study. PE = prediction error. The grey dots indicate individual participants, and the horizontal black lines are the mean values in each condition. The two individual data points at the top of the last condition (learning rates for aversive prediction errors on high-cue trials) in Study 2 fall outside the range of the figure; estimated learning rates for these points are 11 and 16. For Study 1, the first three conditions include data from 28 participants, and the last condition includes data from 26 participants. For Study 2, the first three plots include data from 33 participants, and the last plot includes data from 21 participants. Fewer participants contributed to the last condition because some participants never experienced aversive prediction errors on high-cue trials. B. Expectation updating as a function of signed prediction error magnitude and cue type in each study. Negative and positive prediction errors indicate lower- and higher-than-expected pain, respectively. Negative and positive expectation updates indicate decreases and increases in pain expectations, respectively. We sorted each participant’s low- and high-cue trials into five bins according to signed prediction error magnitude, and plotted the group-mean signed expectation updates for each bin. Lines show linear fits to unbinned single-trial data. Note that there was a significant main effect of cue type but no significant interaction between prediction error and cue type. Plots for Study 1 and 2 are based on data from 28 and 33 participants, respectively. Error bars indicate between-subject standard errors. C. Effect of cue type on expectation updating in each participant (first-level regression coefficients).

The previous analysis considered the sign, but not the magnitude, of prediction errors. Also, a limitation of the previous analysis is that there were relatively few high-cue trials with aversive prediction errors (on average 9.1 and 4.2 trials per participant in Studies 1 and 2, respectively) and low-cue trials with appetitive prediction errors (on average 8.7 trials per participant in both studies). Two participants in Study 1 and 12 participants in Study 2 never experienced aversive prediction errors on high-cue trials, and hence were excluded from the previous analysis (leaving 26 and 21 participants in Studies 1 and 2, respectively).

To address these issues, we conducted an additional analysis in which we tested for effects of cue type and signed prediction error magnitude on (signed) expectation updating. All participants were included in this analysis. As expected, expectation updating increased with increasing prediction error magnitude (t(27) = 12.7, bootstrap p < .001, d = 2.3, CI = .30 to .42 and t(32) = 7.1, bootstrap p< .001, d = 1.6, CI = .22 to .34 in Studies 1 and 2, respectively; Figure 4B). In addition, there was a main effect of cue type (t(27) = 4.8, bootstrap p < .001, d = 1.6, CI = .76 to 1.2 and t(32) = 5.0, bootstrap p < .001, d = 1.1, CI = .86 to 1.6 in Study 1 and 2, respectively), indicating that high-pain cues, relative to low-pain cues, caused an upward shift in expectation updating. There was no Prediction error × Cue type interaction (bootstrap p > .17 in both studies), suggesting that this cue effect on expectation updating was independent of prediction error magnitude. Together, these effects reflect that upward updating of pain expectations following aversive prediction errors was stronger for high- than low-pain cues, while downward updating of pain expectations following appetitive prediction errors was stronger for low- than high-pain cues (Figure 4B). Thus, the cues influenced expectation updating in accordance with a confirmation bias. Finally, the effect of the cues on expectation updating varied substantially across participants (Figure 4C).

Computational models

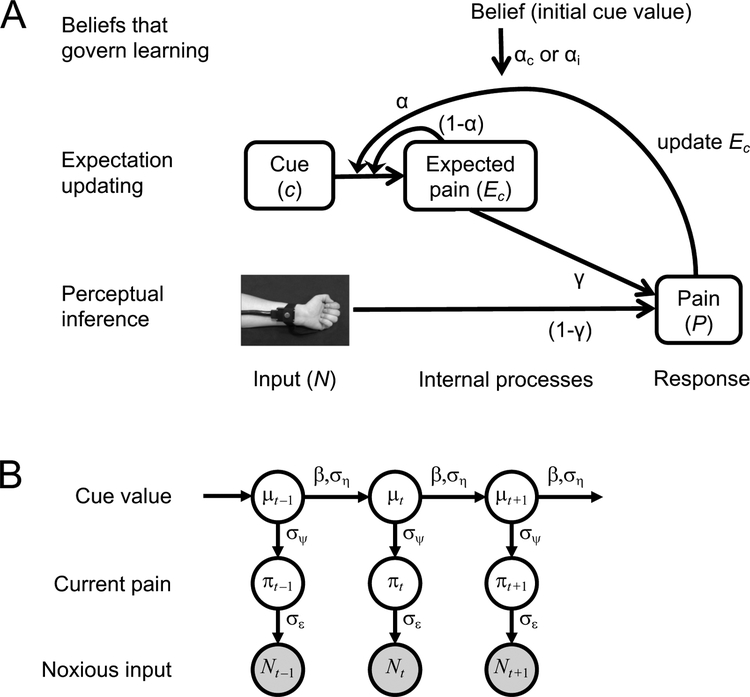
To formalize and quantify the latent processes that we hypothesized to underlie the observed cue effects, we developed two computational models: a reinforcement learning model and a Bayesian model. The two models embody the same ideas from different perspectives and are formally closely related; hence, they can be seen as complementary rather than competing. The reinforcement learning model explains pain perception as a mechanistic process involving prediction and error correction, whereas the Bayesian model explains it at a rational level in terms of probabilistic inference. Full descriptions of the models, and their equations, can be found in the Methods; here we provide a brief overview of their main points. The models observe the sequence of cues and noxious stimuli presented to participants; each cue is initially associated with a low or high pain value. Both models contain (i) a perceptual inference mechanism, which models the pain experienced on a given trial as a weighted average of the sensory (noxious) input and cue-based pain expectation, and (ii) a learning mechanism, which governs how each new pain experience is used to update the predictive value (expectation) of the cue that preceded it (Figure 5). Model 1, the reinforcement learning model, assumes that participants represent expectations and pain outcomes as point values that are updated based on prediction error, as in standard reinforcement learning models. It has three free parameters (which are estimated for each participant) that control the relative weighting of expectations and sensory input during perceptual inference, and the learning rates for cue-pain associations following cue-consistent and cue-inconsistent prediction errors (see below). Model 2, the Bayesian model, assumes that participants track not only the expected values of cue-pain associations but also their uncertainties (variances), and it determines the influence of expectations on pain and the learning update following a given trial based on these uncertainty estimates. Both expected values and variances are updated over time.

Figure 5.

Computational models capturing effects of cue-based expectations on pain and confirmation bias on expectation updating. A. Reinforcement learning model (Model 1). Perceptual inference within a trial combines expectations with noxious input to determine perceived pain. The γ parameter controls the relative impact of these two sources. Learning between trials involves updating the expectation for the current cue toward the current perceived pain. Experience-resistant expectations are modeled by assuming different learning rates, the α_c and a parameters, when the direction of prediction error is, respectively, consistent and inconsistent with the cue’s initial low or high pain association. B. Bayesian model (Model 2). Pain perception and expectation are products of Bayesian inference with respect to a generative model of the task environment that extends the classic Kalman filter. Note that arrows in this diagram indicate statistical dependencies in the subject’s generative model, not dynamics of the subject’s state of knowledge as in Figure 5a. Under the generative model, the mean threat level signaled by each cue (μ_c, index c suppressed in figure) drifts randomly from trial to trial, with step size determined by the σ_η parameter. The current threat level (or objectively correct pain level, π_t) on any trial t deviates randomly from μ_t, with standard deviation equal to the σ_ψ parameter. The noxious input (N_t) is a noisy indicator of π_t, with standard deviation equal to the σ_ε parameter. Inference within a trial (not shown) combines the current belief about with the observed value of N_t to estimate the current value of π_t; this estimate is the subject’s experienced level of pain (P_t). Inference across trials combines the beliefs about μ_t and π_t to estimate μ_t+1; this is the subject’s reported expectation the next time this cue is presented (E_t+1). Experience-resistant expectations are modeled by letting cue-pain associations drift in the directions of their initial values between trials, to a degree governed by the β parameter. Model 2 is formally nearly equivalent to Model 1, except that it assumes γ and α adapt from trial to trial to reflect the subject’s current level of uncertainty (Eqs. 3.1, 3.3, 3.6).

Model 1: Reinforcement learning model

Model 1 is a mechanistic model expressed in the framework of reinforcement learning. The perceptual inference component of this model computes the pain evoked by a noxious stimulus as a weighted average of the current sensory input (stimulus intensity) and the current cue-based expectation. The weighting of sensory input versus expectation is controlled by a parameter γ ∈ [0,1], which is constant across trials. Higher γ yields a stronger impact of expectations on pain. The learning component of this model assumes that each new pain experience triggers the updating of the relevant cue’s pain expectation in proportion to the prediction error (pain minus expected pain), according to a standard reinforcement-learning algorithm (delta rule)³². A learning-rate parameter, α, controls the degree of expectation updating: High values of α result in strong updating toward the latest pain experience, whereas low values of α result in strong updating toward the latest pain experience, whereas low values of a result in more slowly varying expectations. To model confirmation bias, we assume that on each trial one of two different learning rates is used—α_c or α_i—depending on whether the sign of the prediction error is consistent or inconsistent, respectively, with the cue’s initial low or high pain association (as acquired in the learning phase). If α_c is higher than α_i this implies a confirmation bias. Thus, this model has three free parameters: γ, α_c and α_i. Parameter γ controls the impact of the current expectation on pain, and α_c and α_i govern learning and its dependence on initial beliefs.

Model 2: Bayesian model

Model 2 considers pain perception and learning in terms of Bayesian inference, representing expectations and perceived pain as probabilistic beliefs obeying Gaussian probability distributions^16,54–56. Under this model, perceived pain is treated as the subject’s inferred belief regarding how threatening (in terms of potential tissue damage) a situation truly is. The perceptual inference component of the model computes this belief on each trial in a Bayesian fashion, by combining prior expectations based on environmental cues with current nociceptive input. The mean of the resulting posterior belief is a weighted average of these two sources, as in Model 1, but their relative impact depends on their precisions (inverse variances), such that more precise expectations are weighted more heavily. The learning component of the model is based on a Kalman filter, which tracks estimates of the mean level of potential harm signaled by each cue (i.e., the objectively correct cue-pain association) as well as the precision of those estimates^57,58. The effective learning rate on each trial depends on the precision of the expectation at the onset of that trial, with less precise expectations leading to greater updating based on current perceived pain. In addition, the Kalman filter assumes that the objective cue-pain associations vary over time according to a Gaussian random walk process, adding some uncertainty to the cue-based pain expectations after each trial. To model a persistent influence of initial expectations, we incorporated an assumption that the dynamics of the random walk can be biased toward the values of the initial cue-pain associations (see “Comparison of Models 1 and 2” in the Methods for an explanation of how this relates to biased learning). The amount of bias is controlled by free parameter β ∈ [−1,1]: If β equals 0 the random walk process has no directional bias, values of β above 0 yield a drift toward the initial cue- based pain expectations (bias toward initial beliefs), and values of β below 0 yield a drift in the opposite direction of the initial expectations (bias away from initial beliefs). Besides β, this model has three parameters characterizing the subject’s belief about the generating process: the variance of the random walk process $\left({\mathrm{\sigma }}_{\mathrm{\eta }}^2\right)$, the variance in level of harm on a given trial around the average predicted by the current cue $\left({\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)$, and the variance of noise in the noxious input $\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\right)$. Only the ratios among these three parameters matter; hence we fixed ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$ to 1 and estimated ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ and ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ as free parameters (see Methods). Thus, like Model 1, Model 2 also has three free parameters.

Parameter estimates

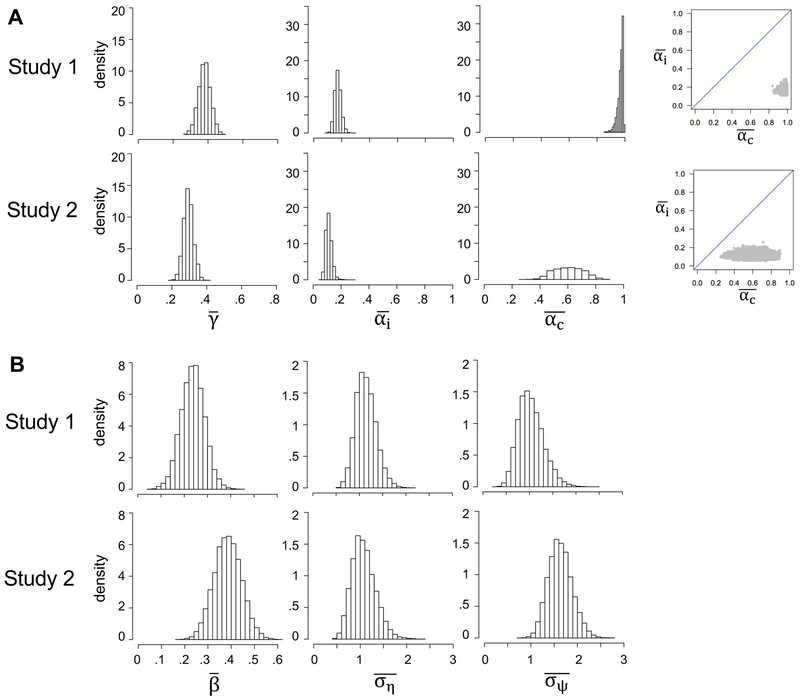
To obtain quantitative estimates of the model parameters, we fit each model (and several reduced versions; see below) to participants’ trial-to-trial sequences of pain and expected-pain ratings, using hierarchical Bayesian parameter estimation (see Methods). The hierarchical procedure assumes every participant has a different set of model parameters, drawn from some population distribution. As we are primarily interested in average participant behaviour, the primary variables of interest are the means of the population distributions, which we denote with overbars (e.g., $\overline{\mathrm{\gamma }}$ denotes the population mean for γ in Model 1). Posterior distributions of the population means for all model parameters are shown in Figure 6. The estimated population distributions of each parameter are shown in Supplementary Figure 2.

Figure 6.

Posterior distributions for the group-level means of the models’ parameters. A. Model 1: γ controls the impact of expectations vs. nociceptive input on pain (higher values cause a stronger weighting of expectations); α_c and α_i are learning rates for cue-consistent and cue-inconsistent prediction errors. The rightmost panels are joint density plots of ${\overline{\mathrm{\alpha }}}_c$ and ${\overline{\mathrm{\alpha }}}_i$ (dots are samples from the MCMC), showing that ${\overline{\mathrm{\alpha }}}_c$ is reliably greater than ${\overline{\mathrm{\alpha }}}_{\mathrm{i}}$. B. Model 2: β controls the drift of expectations toward (if β > 0) or away from (if β < 0) their initial values after each update; ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ is the assumed variance in pain on any given trial; ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ is the assumed variance of the random walk process (random variation in pain across trials). ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ and ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ are estimated relative to the variance of contributions to noxious input unrelated to pain (${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$, which was fixed at 1 to eliminate redundancy in model parameters).

The posterior distribution of ÿ in Model 1 (Study 1: median = .38, 95% credible interval [CI] = .32 to .45; Study 2: median = .29, 95% CI = .24 to .35) suggests that perceived pain is jointly determined by expectations and noxious input, and that, for the average participant, noxious input is weighted roughly twice as strong as expectations. Furthermore, ${\overline{\mathrm{\alpha }}}_c$ was considerably higher than ${\overline{\mathrm{\alpha }}}_i$, consistent with a confirmation bias on learning rate: for Study 1, posterior medians were .98 for ${\overline{\mathrm{\alpha }}}_c$ (95% CI = [.93,1.0]) and .16 for ${\overline{\mathrm{\alpha }}}_i$ (95% CI = [.13,.21]); for Study 2, posterior medians were .63 for ${\overline{\mathrm{\alpha }}}_c$ (95% CI = [.42,.80]) and .11 for ${\overline{\mathrm{\alpha }}}_i$ (95% CI = [.07,.16]). At the individual level, the median of the posterior distribution was higher for α_c than for α_i in 100% and 91% of the participants in Studies 1 and 2, respectively (sign tests, ps < .001).

In Model 2, the relative impact of expectations and noxious input on perceived pain (governed by γ in Model 1) is determined on a trial-to-trial basis by the current level of uncertainty about the objective cue-pain association, and by ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$ and ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ (see the Comparison of Models 1 and 2 subsection in the Methods). The average weighting of expectations vs. noxious input in Model 2 (the grand-average estimate of γ_t, as defined in Equation 3.1, using the medians of the group-level parameter estimates) was .40 and .32 in Studies 1 and 2, respectively, resembling the median posterior estimates of $\overline{\mathrm{\gamma }}$ in Model 1. Parameter β in Model 2 indexes the degree to which expectations drift toward (if β > 0) or away from (if β < 0) their initial values after updating, which is a Bayesian way to capture biased learning. In both studies, 100% of the numerical estimate for the posterior distribution of $\overline{\mathrm{\beta }}$ lay above 0 (Study 1: median = .24, 95% CI = .17 to .32; Study 2: median = .36, 95% CI = .27 to .46), consistent with a persistent contribution of initial beliefs.

Model comparison

To further examine evidence for expectation-based pain modulation and a confirmation bias in learning, we fitted three reduced versions of each model that omitted (a) expectancy-based pain modulation (γ = 0 in Model 1a, and ${\mathrm{\sigma }}_{\epsilon }^2$ = 0 in Model 2a), (b) biased learning (α_c = α_i in Model 1b, and β = 0 in Model 2b), or (c) either of those processes (Model 1c and Model 2c). Note that when ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$ is 0 (Models 2a and 2c), there is no unexplained error in the noxious input (Equation 2.1) and therefore no possibility for expectations to affect the inferred pain (Equation 2.7). When ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$ is 0, only the ratio between ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ and ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ matters. Therefore we fixed ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ to 1 and estimated ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ as a free parameter for Models 2a and 2c. We compared the different models using Bayes factors, which quantify how much more likely the data are to occur under one model compared to another model (Table 1). For both studies, Bayes factors clearly favored the full versions of Models 1 and 2 over all their reduced versions, indicating that the data are best explained by models including both expectation-based pain modulation and a confirmation bias in learning. In addition, models with only confirmation bias and only expectancy-based pain modulation were both favored over reduced models with neither component. Also note that Model 1 (the reinforcement learning model) was favored over Model 2 (the Bayesian model), suggesting that participants did not adapt their learning rates or pain inferences over time as a function of the precision of their expectations. Of course this result bears only on the utility of these particular models, and does not imply that reinforcement learning models fit better than Bayesian models in general.

Table 1.

Log_e Bayes factors for all model comparisons. We log-transformed the Bayes factors such that a value of 0 indicates that the data are equally likely to occur under both models. Positive values indicate evidence in favor of the model in the row over the model in the column.

Study 1
	M1	M1a	M1b	M1c	M2	M2a	M2b	M2c
M1	0	391	129	529	57	459	197	592
M1a		0	−262	138	−334	68	−194	201
M1b			0	400	−72	330	69	463
M1c				0	−472	−70	−331	63
M2					0	402	141	535
M2a						0	−261	133
M2b							0	395
M2c								0
Study 2
	M1	M1a	M1b	M1c	M2	M2a	M2b	M2c
M1	0	263	86	334	36	291	153	399
M1a		0	−177	71	−227	28	−109	137
M1b			0	248	−50	205	68	313
M1c				0	−298	−43	−180	65
M2					0	255	118	363
M2a						0	−137	108
M2b							0	246
M2c								0

M1 and M2 are Model 1 and 2, respectively, and a, b and c refer to the reduced models that do not include (a) expectancy-based pain modulation, (b) a confirmation bias, and (c) either of those components.

Model simulations

To assess whether our models capture the key features of the behavioural results, we simulated expectation and pain ratings according to our full and reduced models, using the best-fitting parameter values (Supplementary Figure 3). Only models including both expectancy-based pain modulation (γ > 0 and ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2>0$ in Models 1 and 2, respectively) and biased learning (α_c > α_i and β > 0 in Models 1 and 2, respectively) capture the key features of the data: A persistent cue effect on both expectation and pain ratings, with a stronger cue effect on expectations than on pain. Although expectations become less extreme over time, indicating that learning is taking place, expectations and pain never fully converge. In contrast, models without expectancy-based pain modulation predict that the cues do not affect pain, and models without biased learning predict that expectations and pain converge to the actual noxious-input intensity. Thus, none of these reduced models fits the pattern of data we observed in these studies, qualitatively or quantitatively, indicating that both expectancy-based pain modulation and biased learning towards initial expectations occur.

Persistent effects of initial beliefs on pain as an alternative to biased learning?

The parameter estimates and model comparisons support the existence of a confirmation bias in learning. However, a potential alternative explanation for these results is a persistent influence of participants’ initial expectations on pain perception: The assimilation of pain towards the initial expectation on all trials would reduce cue-inconsistent prediction errors, which could result in an apparent confirmation bias without affecting learning rate per se.

To test this alternative explanation, we extended the perceptual-inference component of Model 1 by adding an effect of the initial expectation acquired during the learning phase, such that pain was computed as a weighted average of the initial expectation, the current (updated) expectation and the noxious input. The weights of these three terms were controlled by parameters λ, γ, and (1 – λ – γ), respectively, where γ, λ ≥ 0 and (γ + λ) ϵ [0,1]. We refer to this extended model as Model 1⁺. We also defined Model 1b⁺ as the corresponding extension of Model 1b. Thus Models 1⁺ and 1b⁺ both include a persistent effect of initial beliefs on pain, and they differ in that Model 1⁺ includes biased learning (α_c > α_i) whereas Model 1b⁺ does not (α_c = α_i). Comparing these models provides a test of whether there was still evidence for a confirmation bias in learning when allowing for a persistent effect of initial beliefs on pain. Bayes factors strongly favored Model 1⁺ over Model 1b⁺ in both studies (log_e Bayes factor = 78 and 102 for Studies 1 and 2, respectively). In addition, Model 1⁺ was favored over our original Model 1 in Study 2 (log_e Bayes factor = 8) but not in Study 1 (log_e Bayes factor = −12). Supplementary Table 1 reports Bayes factors for comparisons of all versions of Model 1. Thus, these results provide mixed support for a persistent effect of initial beliefs on pain perception. More importantly, they strengthen our conclusions regarding confirmation bias in learning rate, showing that this mechanism is strongly supported regardless of any direct, persistent effects of initial beliefs on pain.

Confirmation bias in the updating of pain-anticipatory brain activity

When pain expectations are updated during learning, this likely causes changes in pain-anticipatory brain responses. Specifically, cues followed by more pain than expected (aversive prediction errors) should increase pain-anticipatory activity on subsequent presentations. Conversely, cues followed by less pain than expected (appetitive prediction errors) should reduce pain-anticipatory activity on subsequent presentations. If confirmation biases are present, this updating of anticipatory activity should be particularly strong when the sign of prediction errors is consistent with the cue’s original low or high pain association. Therefore, we hypothesized that the confirmation bias in expectation updating would be paralleled by a confirmation bias in the updating of cue-specific pain-anticipatory brain activity (during the interval between expectation rating and heat onset).

Within-person parametric modulation analyses revealed that anticipatory brain activity increased in proportion to pain expectations in several regions, including the supplementary motor area (SMA), sensorimotor cortex, anterior midcingulate cortex (aMCC), anterior insula and frontal operculum (aINS), temporal pole, and inferior cerebellar vermis (Supplementary Figure 4; p < .001, uncorrected). While anticipatory activity in some regions (aMCC, aINS, temporal pole) is predicted from prior studies^6,59–62, the activation did not reach significance in whole-brain False Discovery Rate (FDR) correction. Preliminary evidence for activation of these regions may reflect increased anticipatory anxiety and alertness with increasing pain expectations.

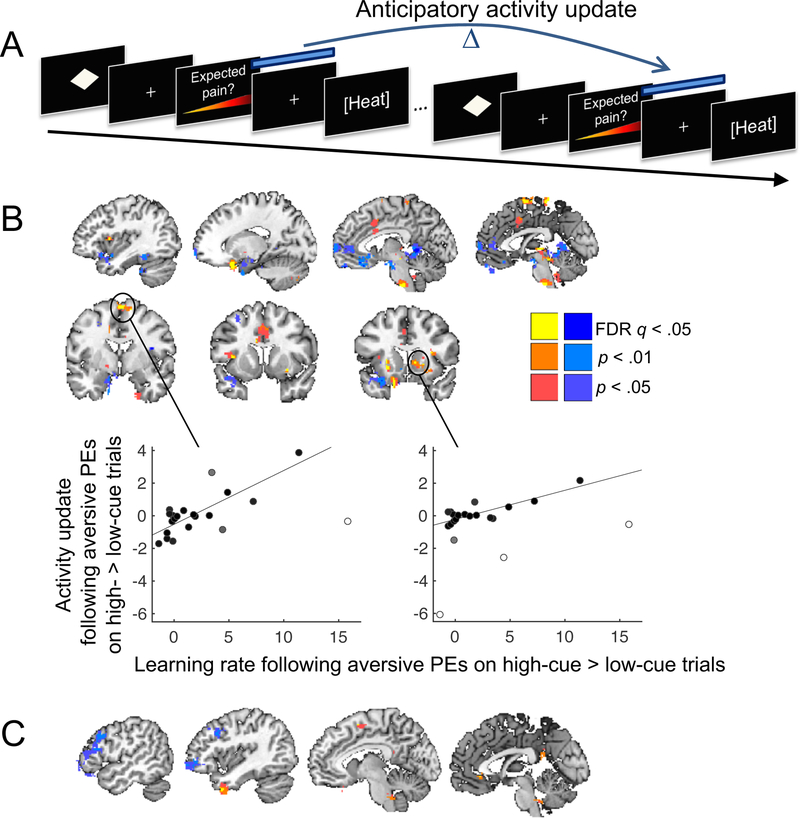
To test for a confirmation bias in the updating of cue-specific pain-anticipatory brain activity, we estimated an fMRI activation map for each pain-anticipation period using single-trial modeling^49,63,64. We then computed the change in anticipatory activity across successive presentations of the same cue, resulting in anticipatory activity ‘update’ images (Figure 7A). To examine evidence for a confirmation bias in the updating of anticipatory activity, we computed contrast images for (i) activity updates following aversive prediction errors that were stronger following high-pain cues than following low-pain cues; and (ii) activity updates following appetitive prediction errors that were stronger following low-pain cues than following high-pain cues. To test whether cue effects on activity updates were related to individual differences in susceptibility to confirmation bias, we added a regressor coding for each participant’s confirmation bias on learning rate (computed directly from the rating data; centered) for the corresponding contrast. Participants who never experienced aversive prediction errors on high-cue trials were excluded from this analysis (leaving 21 participants).

Figure 7.

Confirmation bias in the updating of pain-anticipatory brain activity. A. We computed the change in anticipatory activity across successive trials in which the same cue was presented, separately for trials with higher- and lower-than-expected pain (aversive and appetitive prediction errors, respectively), and tested for effects of cue type. B. Individual differences in confirmation bias on estimated learning rate predict participants’ confirmation bias on anticipatory activity updating following aversive prediction errors. Yellow/red colors indicate positive across-subject correlations between increases in anticipatory activity following aversive prediction errors on high- vs. low-cue trials and estimated learning rate following aversive prediction errors on high- vs. low-cue trials. Blue colors indicate negative correlations. Cluster statistics can be found in Supplementary Table 2. Scatterplots illustrate the correlations in sensorimotor cortex and right striatum. The shading of the points is proportional to each observation’s weight in robust regression; white dots indicate outliers down-weighted by the algorithm. C. Individual differences in confirmation bias on estimated learning rate predict participants’ confirmation bias on anticipatory activity updating following appetitive prediction errors. Yellow/red colors indicate positive across-subject correlations between increases in anticipatory activity following appetitive prediction errors on low- vs. high-cue trials and estimated learning rate following appetitive prediction errors on low- vs. high-cue trials. Blue colors indicate negative correlations. All colored regions were significant at q < 0.05, FDR-corrected. For display purposes, we show the extent of results surrounding FDR-corrected peaks at p < .01 and p < .05 uncorrected. Cluster statistics can be found in Supplementary Table 3. Figures 7B and C are based on data from 21 participants.

At the group-mean level, the cues did not significantly affect anticipatory activity updates following aversive prediction errors after whole-brain FDR correction. However, individual differences in the confirmation bias on learning rate predicted activity for this contrast in several brain regions (q < 0.05, FDR-corrected). In participants with larger confirmation biases, aversive prediction errors following high- relative to low-pain cues resulted in greater increases in anticipatory activity in the aMCC, sensorimotor cortex, mid-insula, striatum (caudate and putamen, but not the nucleus accumbens), a midbrain region encompassing the periaqueductal gray (PAG), a region in the pons, and the inferior cerebellar vermis (Figure 7B; Supplementary Table 2). Note that several, but not all, of those regions overlapped with regions tracking pain expectations (Supplementary Figure 4). Negative correlations (shown in blue in Figure 7B) were found in the ventromedial prefrontal cortex (vmPFC), as well as the dorsal anterior insula and the superior cerebellum. Thus, in individuals with a stronger confirmation bias, aversive prediction errors following high-pain cues (relative to low-pain cues) resulted in increased subsequent anticipatory responses in regions broadly associated with threat and anxiety (aMCC, insula, PAG), and decreased subsequent anticipatory responses in regions commonly associated with appetitive value (vmPFC; see Discussion).

In a complementary analysis, we tested for an effect of cue type on the updating of anticipatory activity following appetitive prediction errors. If learning from aversive and appetitive prediction errors is subserved by one underlying threat/safety system, this analysis should reveal opposite activity patterns to those reported in the previous section. Alternatively, if there are different systems for threat and safety learning, this analysis may reveal different regions. At the group-mean level, the cues did not significantly affect anticipatory activity updates following appetitive prediction errors (FDR corrected). However, individual differences in the confirmation bias on learning rate predicted activity for this contrast in several brain regions. In participants with a greater confirmation bias, appetitive prediction errors following low-pain cues (relative to high-pain cues) resulted in a greater increase in anticipatory activity in the vmPFC and posterior cingulate cortex—both often considered ‘default mode’ regions—as well as the orbitofrontal cortex, temporal pole and pre-SMA (Figure 7C; Supplementary Table 3). Negative correlations (blue in Figure 7C) were found in the lateral PFC. Thus, the vmPFC showed parallel learning effects in analyses of both aversive and appetitive prediction errors. In individuals with a stronger confirmation bias, anticipatory vmPFC responses decreased more following aversive prediction errors on high-cue than low-cue trials, and increased more following appetitive prediction errors on low-cue than high-cue trials. In other respects, however, effects of cue type on anticipatory-activity updating were largely distinct for aversive and appetitive prediction errors.

Discussion

Positive feedback loops between expectations and experiences can create self-fulfilling prophecies—persistent beliefs, behaviours, and decisions that are driven by initial expectations and are resistant to corrective experience. Although such reciprocal systems may operate in many aspects of human behaviour^20,65, empirical studies investigating them are rare, and their underlying mechanisms largely unknown.

Our findings provide evidence that cue-based expectations about pain can become self-reinforcing through their combined effects on perception and learning. First, we identified reciprocal effects of expectations and pain responses on one another: Expectations influenced reported pain and pain-specific brain activity, and these pain responses in turn influenced subsequent expectations. Second, expectation updating was strongest when the direction of prediction errors was consistent with the initial high or low pain value of the preceding cue. Third, computational modeling results provided additional evidence that self-reinforcing expectancy effects on pain result from a combination of expectancy-based pain modulation and a confirmation bias in learning. Fourth, individual differences in confirmation bias in learning predicted confirmation bias in the updating of pain-anticipatory brain activity in regions associated with threat and affective value.

Our results contribute to a basis for understanding self-fulfilling predictions in various domains. In principle, either expectancy effects on perception or a confirmation bias in learning alone, if sufficiently strong, would be sufficient to maintain expectations for a period of time. If perception fully assimilates toward expectations, we always experience what we expect, and learning may be short-circuited. Similarly, if we do not at all learn from expectancy-disconfirming evidence, our initial expectations will be maintained indefinitely. However, extreme biases in perception and learning are unlikely to be functionally advantageous. Complete adjustment of perception to expectations is a form of hallucination, and would prevent the detection of unexpected harmful or rewarding events. Similarly, a complete suppression of learning from expectancy- disconfirming events would prevent adaptive future responding to those events. Our results show that, when combined, even moderate degrees of perception modulation and biased learning can produce persistent expectations, with substantial impacts on perceived pain.

These results complement those of previous computational-modeling studies in other domains that explained effects of prior information on people’s choice behaviour by a modulation of outcome evaluation or a confirmation bias in learning^36–38,41. Although these two mechanisms are computationally distinct—affecting the input to the learning process and the learning rule itself, respectively—they make similar predictions about trial-to-trial dynamics of expected value, and hence are difficult to dissociate based on choice data alone. By directly measuring trial-to-trial dynamics of both expected and perceived outcomes, our paradigm enables the dissociation of these two effects.

Our results also contribute to the discussion about predictive coding and the strength, importance, and locus of ‘top-down’ influences on perception. Previous studies have shown that higher-level cognitive processes, such as expectations and attention, can affect perceptual judgments of stimuli in visual^10–12, pain²³, auditory⁶⁶, and taste¹³ domains. It has recently been questioned whether these findings—specifically those in the visual domain—really reflect the modulation of perception, or merely the interpretation of perceived events⁶⁷. The present study contributes to this debate by showing that expectations modulate pain signaling in the central nervous system in functionally important, and clinically relevant, ways. The NPS is a cerebral pain signature that is strongly affected by noxious-stimulus intensity^49,53 and by drugs that are thought to act in part at a spinal level^53,68. In contrast, changes in reported pain due to reappraisal⁴⁹, pain controllability^69,70, and reward manipulations⁷¹ are not reflected in the NPS response, suggesting that the NPS is largely insensitive to higher-order cognitive processes. Thus, our finding that cue-based expectations modulate the NPS response implies that they affect the cerebral processes that give rise to pain.

With regard to ‘predictive coding’, recent work has proposed that pain perception results from the Bayesian integration of afferent nociceptive input with ‘top-down’ expectations and/or other informational cues^16,54–56, as is also assumed by our Bayesian model. According to these accounts, the precision of each information source determines its influence on perceived pain and the degree of expectation updating; in particular, very precise expectations strongly shape pain and reduce experience-driven expectation updating. Our data are compatible with this view, but they suggest that prior expectancies have an additional effect not captured in standard Bayesian or non-Bayesian learning models. Specifically, our data suggest that initial beliefs about cue-pain associations modify learning rates, creating long-lasting confirmation biases that impede extinction.

Such effects have a history of study in social psychology, under the label of ‘attribution’, which relates to a person’s theory about the causal structure underlying experienced associations^72,73. In short, attributions govern what a person ‘takes away’ or learns from experience. When experiences confirm expectations, individuals attribute experienced effects to the cues that predicted them. When they do not, however, experiences are more likely to be judged to be anomalies or ‘flukes’, or the result of lapses in attention, and discounted. More generally, confirmation biases may reflect a broader principle of regularizing predictions by down-weighting outliers, which is the basis of robust statistics74. This principle can in some cases improve perceptual inference by making our estimates resistant to outliers^75,76; hence it can be seen as a functionally adaptive strength. However, when initial beliefs are no longer valid, e.g., due to a change in the environment, this principle also impedes belief updating, a vulnerability that goes along with its advantages.

Though our data suggest that cues modulate the brain mechanisms underlying pain perception, they do not exclude the possibility that expectations also influence later, post-perceptual processes. That the NPS response partially mediated the effect of expectations on pain ratings suggests that part of this effect is due to modulation of relatively early pain signaling, while another part reflects effects at a later stage (e.g., evaluation or response). Studies using signal-detection theory have shown that placebo treatments can increase observers’ pain criterion values^77,78, implying an effect at the decision or response level. Likewise, a recent study applying evidence-accumulation models of perceptual decision making to a pain-discrimination task suggested that pain-predictive cues introduce response bias to the decision process79. When combining these findings with findings that expectations modify pain-related activity in the spinal cord^33,34, it seems that expectations can affect multiple stages of pain processing and evaluation. The relative strength of early and late expectancy effects likely varies across people and situations, and may depend on the magnitude of expectancy violations. Further specification of the pain-processing stages that are modified by expectations is an important objective for future research.

How prior beliefs affect perception and learning may strongly depend on how those beliefs were acquired as well. In our studies, cue-pain associations were established using a learning procedure in which cues were repeatedly paired with pictures of thermometers displaying low or high heat levels. This procedure differs from conventional classical conditioning as it did not involve primary affective outcomes, and because expectations and pain were reported on each trial. The reinforcement with pictures of thermometers instead of painful heat, which we call ‘symbolic conditioning’, is closely aligned with sensory preconditioning paradigms in animals^80,81and humans⁸², and this type of learning may involve interactions between the hippocampus (traditionally associated with explicit memory) and other value-based learning systems83. In a recent study we found only weak effects of a standard classical conditioning procedure on the NPS70, suggesting that symbolic, conceptual learning procedures may have unique effects. The act of explicitly rating expectations may have important effects as well84. In support of this view, recent work suggests that when threat is engaged by explicit, instruction-driven mechanisms, it produces physiological threat responses via pathways that bypass the amygdala85. It is possible that the expectancy ratings in our paradigm promoted the persistent explicit recall of the initial pain expectations, preventing participants from forgetting these initial expectations. Our Bayesian model captures such ‘resistant priors’ by the drift of expectations toward their initial values after updating, and our extended reinforcement learning model by a persistent effect of initial beliefs on pain. Whether and how the resistance to extinction depends on the specific task structure, such as the presence of explicit expectancy ratings, remains to be tested in future studies.

In addition to perception modulation, confirmation biases in learning appear to be critical for explaining the persistent influences of cues we observed. The reinforcement learning model that included confirmation bias in learning updates outperformed all other models, providing evidence for a contribution of biased learning over and above direct resistant-prior effects. However, we found substantial individual differences in the degree to which participants showed a confirmation bias in learning. Furthermore, individual differences in confirmation bias in learning rate predicted the degree to which participants showed a confirmation bias in the updating of pain-anticipatory activity in several brain regions. When worse-than-expected pain was preceded by a high- relative to a low-pain cue, participants with stronger confirmation biases on learning rate also showed a greater increase in subsequent pain-anticipatory activity in the aMCC, sensorimotor cortex, mid-insula, posterior striatum, PAG and pons. These regions have previously been associated with anticipatory anxiety⁸⁶, pain prediction errors and aversive action policy⁸⁷, and cues predictive of high pain^25,88. The vmPFC showed the opposite correlation: participants with stronger confirmation biases showed greater reductions in anticipatory vmPFC activity following worse-than-expected pain preceded by high- relative to low-pain cues, and greater increases in anticipatory vmPFC activity following less-than-expected pain preceded by low- relative to high-pain cues. Activity in the vmPFC tracked appetitive value in many studies^89–91, and has been shown to negatively track pain expectations⁸⁷. Thus, our results suggest that for high confirmation-bias learners, combining high pain expectancy with worse-than-expected outcomes activates systems associated with anticipatory anxiety, threat, and negative affective value. However, as these results were based on differences between single-trial fMRI activation maps—with low signal-to-noise ratio—and on a relatively small number of participants, they must be considered preliminary, awaiting replication.

The effects of expectations on pain and learning circuits demonstrated in our studies could be applied to the study of chronic pain. Self-reinforcing expectancy effects may facilitate the transition from acute to chronic pain, which is all too common after surgery or injury^92,93. Indeed, the inability to extinguish pain memories has been proposed as a defining aspect of chronic pain^94,95. Relatedly, previous treatment experiences predict people’s analgesic response to subsequent placebo treatments^96–98 and to active medical treatments⁹⁹, suggesting that positive and negative beliefs are important determinants of pain responses. Furthermore, a few studies have demonstrated impaired cue-pain contingency learning in chronic-pain patients, with a particular impairment in safety learning^100,101. If chronic-pain patients expect pain in more situations than healthy people, these deficits may reflect reduced learning from belief-disconfirming (no pain), relative to belief-confirming (pain) outcomes; hence it is possible that many pain patients have a high confirmation-bias phenotype. The interactions between perceptual and learning processes in the development of chronic pain remain to be clarified102. One promising approach would be to quantify effects like those identified in our studies in people at risk for developing chronic pain.

Effects of expectations on perception and learning may also contribute to psychological disorders that are characterized by persistent negative expectations and beliefs, such as anxiety and depression. Recent studies showed that more anxious people are less able to flexibly adapt their learning rate in a dynamic aversive learning task103, and that—unlike healthy people—socially anxious people do not show a positivity bias when updating self-related information based on social feedback104. Whether these findings reflect a confirmation-bias mechanism similar to that observed in our studies—e.g., the down-weighting of evidence that disconfirms previously learned associations or beliefs—is currently unknown. Another open question concerns the potential contribution of fluctuations in mood to our findings. In the reward domain, expectations and prediction errors have been shown to affect people’s self-reported mood on a trial-to-trial basis105. Furthermore, mood can bias how people perceive and learn from rewards, especially in people with high mood instability106. Future research is needed to further investigate the interactions between expectations, mood and affective learning.

A limitation of our studies is that prediction errors were inconsistent with the initial cue-pain associations on most of the trials. According to our models, a larger proportion of ‘cue-consistent’ prediction errors should produce even stronger persistence of cue-based expectations and pain modulation over time. Future studies could increase the proportion of consistent prediction errors, by using more extreme noxious-stimulus intensities, to test this hypothesis. In addition, it is unknown to which degree our expectation-updating results reflect explicit versus implicit learning processes. We previously demonstrated that self-reported expectations and autonomic anticipatory responses have opposite effects on autonomic pain responses27. Thus, it is possible that there are additional learning processes that also influence pain and operate in parallel to the mechanisms revealed here. Finally, although our results provide strong evidence that the cue effects are highly resistant to extinction, we cannot be sure whether our cue effects will never extinguish, or whether they would eventually extinguish but at a much slower rate than would be expected in the absence of confirmation bias. Studies using a larger number of test trials are needed to differentiate between these possibilities.

To conclude, our findings demonstrate that initial beliefs can become self-fulfilling prophecies through their combined effects on perceptual and learning processes. Future studies may examine the generalizability of our findings to self-reinforcing phenomena in other domains, and the clinical relevance of individual differences in the effects revealed in our studies. These insights can help understand—and may eventually help to counteract—self-fulfilling phenomena in various domains of human behaviour.

Methods

Participants

Thirty participants took part in Study 1 (Behavioural study, previously published by 27), and thirty-four participants took part in Study 2 (fMRI study). We chose the sample sizes based on large effect sizes in previous cue-based pain modulation studies conducted in our lab25. Sample sizes of ~30 provide approximately 80% power to detect an effect size of Cohen’s d = 0.54 or larger, which is near the lower bound of what we would expect for the predictive-cue effects on pain responses. All participants were healthy and reported no history of psychiatric, neurological, or pain disorders, and no current pain. All participants gave informed consent and the experiment was approved by the institutional review board of the University of Colorado Boulder. Participants in Study 1 received $12 per hour, and participants in Study 2 received $24 per hour for their participation.

In Study 1, one participant decided to stop before the end of the experiment because she found the heat too painful, and one participant had to be excluded because of thermode failure. Thus, the final dataset for Study 1 was based on twenty-eight participants (mean age = 25, range = 18–55 years; 25% female). In Study 2 (mean age = 25, range = 18–54 years; 50% female), one participant misunderstood the expected-pain rating procedure, and was excluded from all analyses involving pain expectations.

Experimental task

In both studies, we used a previously established paradigm consisting of a learning phase followed by a test phase (Figure 1A). Before starting the task, we instructed participants that they would learn associations between specific shapes and specific heat levels. We also instructed them that the heat levels would be displayed on a thermometer during the first part of the experiment and applied to their skin during the second part of the experiment. In Study 2, the learning and test phases were both performed within the MRI scanner.

Learning phase

Each trial started with the 2-s presentation of a visual cue (a geometric shape). Following the cue, participants indicated which heat level they expected on a 100-unit vertical VAS with lower and upper anchors of “baseline skin temperature” and “extremely hot”, respectively, which was displayed alongside a picture of a blank thermometer. A few seconds later, the thermometer picture reappeared for 3 s, this time indicating a specific symbolic heat level. Some cues (low-pain cues) were always followed by low heat levels (32–53% of the thermometer scale) and other cues (high-pain cues) were always followed by high heat levels (73–93% of the thermometer scale). The learning phase of Study 1 included three low-and three high-pain cues, and participants completed 20 trials for each cue, in pseudorandom order stratified across time, with the constraint that each block of six trials contained one trial in each cell of the six cue conditions. The learning phase of Study 2 included two low and two high-pain cues, and participants completed 30 trials for each cue, in pseudorandom order stratified across time, with the constraint that each block of four trials contained one trial in each cell of the four cue conditions.

Test phase

Each test trial started with the 2-s presentation of one of the cues from the preceding learning phase, or a novel cue (see below). After this, participants indicated how much pain they expected on that trial, on a horizontal 100-unit VAS with anchors of “no pain” and “worst-imaginable pain”. A few seconds later, a noxious heat stimulus was applied to participants’ left inner forearm (Study 1) or lower leg (Study 2), using a 27-mm diameter CHEPS thermode (ramp rate = 40°C/s; 1 s at peak temperature; peak temperature = 47°C or 48°C in Study 1, and 48°C or 49°C in Study 2). Between stimuli, the thermode maintained a baseline temperature of 32°C. Unbeknownst to the participants, all cues were followed by each of two temperatures on 50% of the trials each, i.e. heat intensity was unrelated to the preceding cue (Figure 1A). Several seconds after heat offset, the VAS re-appeared on the screen and participants rated how much pain they had experienced on that trial. Then, after a variable inter-trial interval, during which an empty screen was displayed, the next trial started. Trial procedures were identical in the two studies, expect for the inter-stimulus intervals, which were somewhat longer in Study 2 (Figure 1B).

We introduced two novel cues in the test phase of Study 1: the words LOW and HIGH, which were instructed to precede low- and high-intensity heat, respectively. In the test phase of Study 2, we introduced three additional cues: The letters L and H, which were instructed to precede low and high heat levels, respectively, and a novel geometric shape (‘neutral’ cue). As previously reported²⁷, the LOW/L vs. HIGH/H cues affected pain responses in a similar way as the geometric shapes that had been paired with low vs. high heat representations during the learning phase. Therefore, we refer to all these cues as low- vs. high-pain cues, and report results based on data pooled across these cue types.

Participants completed 10 test trials for each cue, i.e. a total of 80 and 70 trials in Study 1 and 2, respectively, in pseudorandom order stratified across time: In Study 1 each block of eight trials contained one trial in each cell of the eight cue conditions, and in Study 2 each block of seven trials contained one trial in each cell of the seven cue conditions. In Study 1, the test phase was divided in 5 runs of 16 trials, between which we moved the thermode to a new site on the forearm. In Study 2, the test phase was divided in 5 runs of 14 trials, between which we moved the thermode to a new site on the lower leg. Before starting each new run, we once applied the highest of the two temperatures to the to-be-stimulated skin site, to reduce the impact of site-specific habituation effects¹⁰⁷.

Regression analyses

We conducted multi-level regression analyses on the single-trial behavioural data and, in Study 2, NPS responses (see fMRI analysis) during the test phase, using the Multilevel Mediation toolbox (http://wagerlab.colorado.edu/tools)^25,108,109. We tested the significance of all effects using a bootstrap procedure (10,000 bootstrap samples). All tests were 2-tailed.

We tested the effect of cue type (high- vs. low-pain cue) on pain ratings and NPS responses, in two separate regression models. We also modeled the effects of heat intensity (temperature) and the temperature × cue type interaction. To test whether the effect of cue type extinguished over time, we also modeled the linear and quadratic effects of time (i.e., trial number) and their interactions with cue type. In addition, we modeled the linear and quadratic effects of site-specific repetition to account for pain-adaptation effects due to repeated stimulation¹⁰⁷.

To examine evidence for reciprocal effects of expectations and pain responses on one another, we conducted two additional sets of regression analyses. First, we tested the effect of expected-pain rating on subsequent pain ratings and NPS responses, in two separate regression models. Second, we tested the effects of pain and NPS responses on subsequent expectations, also in two separate regression models. In all four analyses, we also modeled the effects of cue type (low, high, and neutral cues were coded as −1, 1 and 0, respectively) and heat intensity.

Data collection and analysis were not performed blind to the conditions of the experiments. However, we do not believe this increased the risk of bias here because all participants performed experimental conditions in computer-generated sequences, and comparisons in analyses were specified in advance.

Confirmation bias analyses

To examine evidence for a confirmation bias in expectation updating, we conducted a regression analysis on estimated trial-specific learning rate (and a parallel analysis on raw expectation updates) with regressors coding for cue type, prediction-error sign (higher- vs. lower-than-expected pain), their interaction, and temperature. A confirmation bias should manifest as an interaction between cue type and prediction-error sign on estimated learning rate and absolute expectation-update size. Two participants in Study 1 and 12 participants in Study 2 never reported higher-than-expected pain following high-pain cues; these participants were excluded from these analyses. In an additional analysis, we used a continuous regressor for prediction error magnitude instead of prediction-error sign, allowing inclusion of all participants.

We conducted similar confirmation bias analyses on the updating of pain-anticipatory brain activity. The dependent variable in these analyses was the change in pain-anticipatory fMRI activity across successive trials on which the same cue was presented (see fMRI analysis). As aversive and appetitive pain prediction errors (higher- and lower-than-expected pain, respectively) may affect subsequent anticipatory activity in different brain circuits, we separately tested for cue effects on anticipatory activity updating following these two types of prediction errors.

Computational models

Model 1

Model 1 is a process-level model built in the framework of reinforcement learning. This model contains mechanisms for perceptual inference (Equation 1.1) and learning (Equations 1.2 and 1.4), as well as a confirmation-bias mechanism through which initial beliefs bias learning (Equation 1.5). We describe each of these three components of the model in turn.

Perceptual inference.

The model infers the level of perceived pain on trial t, P_t, based on the current noxious input, N_t, combined with the current cue-based pain expectation, E_c,t, for the current cue c. Specifically, P_t is a weighted linear combination of N_t and E_c,t:

$$P_t=(1-\gamma )N_t+\gamma E_{c,t}.$$ [1.1]

Parameter γ (0 ≤ γ ≤ 1) controls the relative weighting of N_t and E_c,t, such that the impact of expectations on pain increases with increasing γ.

Learning.

The model’s learning mechanism governs the updating of cue-based expectations in response to new pain outcomes. On each trial, the discrepancy between P_t and E_c,t elicits a prediction error, δ_t:

$${\delta }_t=P_t-E_{c,t}.$$ [1.2]

This prediction error triggers the updating of the pain expectation for cue c, according to a standard reinforcement-learning algorithm (‘delta rule’ learning)³²:

$$E_{c,t+1}=E_{c,t}+\mathrm{\alpha }{\delta }_t.$$ [1.3]

Note that, given Equation 1.2, the expectation-updating process can also be written as

$$E_{c,t+1}=\mathrm{\alpha }{P}_t+(1-\mathrm{\alpha })E_{c,t},$$ [1.4]

which shows that the new expectation is a weighted average of the most recent pain experience and the old expectation. The amount of updating is determined by the learning-rate parameter α (0 ≤ α ≤ 1): Higher values of a result in stronger updating.

Confirmation bias.

Model 1 implements a confirmation bias in learning by specifying a on each trial depending on whether the sign of δ_t is consistent or inconsistent with the initial low or high pain association of the current cue:

$${\mathrm{\alpha }}_t=\{\begin{array}{l}{\mathrm{\alpha }}_c\text{ if }\left({\delta }_t>0\text{ and }c=c_{\text{high }}\right)\text{ or }\left({\delta }_t<0\text{ and }c=c_{\text{low }}\right)\hfill \\ {\mathrm{\alpha }}_{\text{i}}\text{ if }\left({\delta }_t>0\text{ and }c=c_{\text{low }}\right)\text{ or }\left({\delta }_t<0\text{ and }c=c_{\text{high }}\right).\hfill \end{array}$$ [1.5]

Here c_high and c_low refer to cues that were initially associated with high and low relative pain values, respectively. If α_c is higher than α_i, the model produces a confirmation bias. Note that the neutral cues (present only in Study 2) had not been included in the learning phase, and hence were not expected to have a low or high pain association at the start of the test phase. Therefore, we excluded the neutral-cue trials from all model fitting procedures.

Thus, Model 1 has three free parameters: γ, α_c and α_i. To optimize fits, we initialized the cue-based expectations (E_c,₁) to the first expected-pain rating for cue c in the test phase, separately for each participant. In addition, we modeled the noxious input on each trial (N_t) as the participant’s average pain rating for the temperature presented on that trial, such that N_t and P_t are represented on the same scale.

Persistent effects of initial beliefs.

In the extended model (Model 1⁺) that allowed pain perception to be affected by the initial beliefs acquired during the learning phase, Equation 1.1 was replaced by

$$P_t=(1-\lambda -\gamma )N_t+\gamma E_{c,t}+\lambda M_c.$$ [1.6]

where M_c is the initial value associated with cue c, acquired during the learning phase. We set M_c to the first expected-pain rating for cue c in the test phase (before the first heat stimulus for that cue had been received), separately for each participant. The additional parameter λ controls the relative weighting of this initial belief, with 0 ≤ λ ≤ 1 – γ.

Model 2

Model 2 represents pain perception and learning as Bayesian inferences. Below, we first describe the generative assumptions of this model (Equations 2.1–2.4), followed by its perceptual inference (Equations 2.5–2.8) and learning (Equations 2.9–2.12) components, and a mechanism to capture experience-resistant expectations (Equations 2.13–2.16).

Generative model.

As a Bayesian model, Model 2 attributes to the subject a structured belief, i.e., a generative model, regarding the dynamics and statistics of the task environment. The subject is assumed to engage in optimal Bayesian inference with respect to this generative model, based on the noxious input (i.e., heat stimuli). The subject’s posterior beliefs then determine his or her responses (i.e., reported expectations and pain ratings).

The generative model is assumed to contain two sets of latent variables. The first, π_t, represents the true level of potential harm on each trial, in other words the objectively correct level of pain that the subject should feel. The second, μ_c,t, represents the mean level of potential harm signaled by each cue c at any time, which is the average value for π_t if c is the cue presented on trial t. The subject’s belief about μ_c,_t at the start of trial t (after the cue is presented and before the heat stimulus) determines his or her expected pain intensity, E_t. The subject’s posterior belief about π_t after the heat stimulus has been presented determines the pain report, P_t.

The subject is assumed to treat the observed noxious input, N_t, as an imperfect indicator of π_t, with variance

$$N_t~\mathcal{N}\left({\pi }_t,{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\right).$$ [2.1]

Here $\mathcal{N}\left({\pi }_t,{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\right)$ indicates a Gaussian distribution with mean π_t and variance ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$. This relationship defines a likelihood for the observed value of N_t, which can be combined with the prior based on to μ_c derive a posterior for π_t using Bayes’ rule (perceptual inference, elaborated below).

Model 2 assumes that participants track beliefs about μ_c for each cue (learning) using a Kalman filter, a well-studied model of Bayesian learning that has been used to model learning of reward magnitudes in previous studies^110,111. The Kalman filter assumes a generative model in which π_t is sampled from a Gaussian distribution centered on μ_c,_t with a fixed standard deviation, ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$:

$${\pi }_t~\mathcal{N}\left({\mu }_{c,t},{\mathrm{\sigma }}_{\psi }^2\right).$$ [2.2]

The Kalman filter also assumes that μ_c,_t varies over time (hence the additional index t), according to a Gaussian random walk with mean step size 0 and standard deviation ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$:

$${\mu }_{c,t+1}~\mathcal{N}\left({\mu }_{c,t},{\mathrm{\sigma }}_{\mathrm{\eta }}^2\right).$$ [2.3]

Extending the standard Kalman filter, we assume the subject maintains a conjugate iterative prior on μ_c,_t conditioned on all previous observations:

$${\mu }_{c,t}|N_{t-1}~\mathcal{N}\left(m_{c,t},s_{c,t}^2\right),$$ [2.4]

where N_t-1 = (N₁ …,N_t-1) is the sequence of all prior inputs, and m_c,t and s_c,t are values that the subject tracks as part of learning. That is, m_c,t and s_c,t characterize the subject’s state of knowledge regarding μ_c,_t at the beginning of trial t. Both levels of inference in the model are based on the iterative prior in Equation 2.4.

Perceptual inference.

The iterative prior on μ_c,_t also yields a prior on π_t, before the heat stimulus on each trial, obtained by adding the trial-level variance ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$:

$${\pi }_t|N_{t-1}~\mathcal{N}\left(m_{c,t},s_{c,t}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right).$$ [2.5]

The mean of this prior, m_c,t, is the participant’s reported expectation, E_t, at the beginning of a trial (i.e., after the cue has been observed):

$$E_t\text{=}{m}_{c,t}.$$ [2.6]

Once N_t is observed, it can be combined with the prior in [2.6] to derive a posterior for π_t. Using Bayes’ rule, this posterior can be shown to be:

$${\pi }_t|N_t~\mathcal{N}\left(\frac{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2{m}_{c,t}+\left({\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2\right)N_t}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2},\frac{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\left({\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2\right)}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}\right).$$ [2.7]

The mean of this posterior is the subject’s pain report, P_t, which can also be written as

$$P_t=\frac{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{m}_{c,t}+\frac{{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{N}_t.$$ [2.8]

Thus, as in Model 1, reported pain is a weighted average of the expectation and noxious input. The weights in this case are determined by the uncertainties in the two sources of information (the prior expectation and the observed input), each weighted in proportion to its precision (inverse variance).

Learning.

Once the posterior belief for π_t is calculated, it is used to calculate the posterior distribution for μ_c,_t. As with Equation 2.8, the mean of this posterior can be shown to be a precision-weighted average of the prior belief (Eq. 2.5) and the new observation (N_t):

$${\mu }_{c,t}|N_t~\mathcal{N}\left(\frac{\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)m_{c,t}+s_{c,t}^2{N}_t}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2},\frac{\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}\right).$$ [2.9]

The prior on the next trial is then obtained by adding the variance of the random walk:

$${\mu }_{c,t+1}|N_t~\mathcal{N}\left(\frac{\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)m_{c,t}+s_{c,t}^2{N}_t}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2},\frac{\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}+{\mathrm{\sigma }}_{\mathrm{\eta }}^2\right).$$ [2.10]

By definition, the mean and variance of this iterative prior equal m_c,t+1 and $s_{c,t+1}^2$, respectively. This recursive relation yields update equations for m,

$$m_{c,t+1}=\frac{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{m}_{c,t}+\frac{s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{N}_t,$$ [2.11]

and for s,

$$S_{C,t+1}^2=\frac{\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}+{\mathrm{\sigma }}_{\mathrm{\eta }}^2.$$ [2.12]

Equation [2.11] shows that the new expectation is a weighted average of the most recent noxious input and the old expectation, similar to Model 1.

Biased learning.

To model a persistent influence of initial expectations, we put a bias into the random walk, as a spatial (i.e., directional) inhomogeneity. Specifically, we included a directed component in the dynamics of the generative model, replacing Equation 2.3 with

$${\mu }_{c,t+1}~\mathcal{N}\left((1-\mathrm{\beta }){\mu }_{c,t}+\mathrm{\beta }{M}_c,{\mathrm{\sigma }}_{\mathrm{\eta }}^2\right),$$ [2.13]

where M_c is the initial value associated with cue c during the learning phase. Thus, the participant’s generative model assumes μ_c tends to decay toward or away from M_c, and the direction and strength of this effect are determined by parameter β ∈ [−1,1]. Values of β > 0 yield a decay of toward M_c (persistent beliefs), and values of β < 0 yield a growth of away from M_c (the opposite of persistent beliefs).

This change to the random walk between trials has no impact on inference within a trial. Thus Equations 2.5–2.9 are unchanged. The only change is to the learning step between trials, with the iterative prior in Equation 2.10 replaced by

$${\mu }_{c,t+1}|N_t~\mathcal{N}\left(\frac{(1-\mathrm{\beta })\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)m_{\text{c},\text{t}}+(1-\mathrm{\beta })s_{c,t}^2{N}_t}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}+\mathrm{\beta }{M}_c,\frac{{(1-\mathrm{\beta })}^2\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}+{\mathrm{\sigma }}_{\mathrm{\eta }}^2\right).$$ [2.14]

The corresponding update rules (replacing Equations 2.11–2.12) are then

$$m_{c,t+1}=\frac{(1-\mathrm{\beta })\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{m}_{c,t}+\frac{(1-\mathrm{\beta })s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}{N}_t+\mathrm{\beta }{M}_c$$ [2.15]

and

$$S_{C,t+1}^2=\frac{{(1-\mathrm{\beta })}^2\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)s_{C,t}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{C,t}^2}+{\mathrm{\sigma }}_{\mathrm{\eta }}^2.$$ [2.16]

Equation 2.15 shows how the update of the expectation for the next trial (m_c,_t+1) is biased toward the initial association value for the current cue (M_c), provided β > 0.

In summary, Model 2 has four free parameters: the directional bias of the random walk in cue values (β), the variance of the random walk in cue values $\left({\mathrm{\sigma }}_{\mathrm{\eta }}^2\right)$, the variance in potential harm on any given trial $\left({\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)$, and the noise variance of noxious input $\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\right)$. For the last three parameters, only their ratios matter; hence we fixed ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$ at a value of 1 and estimated the other two. For the reduced models with ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$ fixed to zero, we fixed ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ at a value of 1 and estimated ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$.

As in Model 1, we initialized the mean cue-based expectations (prior to trial 1; m_c,l for each value of c) to the participant’s expected-pain rating following the first appearance of each cue in the test phase, and we modeled the noxious input on each trial (N_t) as the participant’s average pain rating across all trials on which that temperature was presented (to put temperature and pain on the same scale).

Finally, we assumed that the initial variance of the subject’s prior for μ_c,l (i.e., the subject’s uncertainty, $s_{c,1}^2$) was equal to ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ for all cues.

Comparison of Models 1 and 2

Despite their substantial differences in framing, the reinforcement learning and Bayesian models presented here can be seen as embodying a shared set of theoretical principles. The main difference is that the former is cast at an algorithmic or mechanistic level, whereas the latter is cast at a computational level, in terms of optimal statistical inference. Specifically, adjusting expectations toward new observations as in delta-rule learning (Equations 1.3–1.4) can be seen as an algorithmic solution to tracking a moving target as in the Kalman filter (Equation 2.9)^{1,57,112–114}. Likewise, perception as a weighted combination of sensory input and expectations (Equation 1.1) enacts a Bayesian integration of new data and prior beliefs (Equations 2.7 and 2.8), or more generally of different sources of information in proportion to their precisions (inverse variances)^115–118.

To see these connections formally, define a trial-specific weighting parameter in Model 2,

$${\mathrm{\gamma }}_t=\frac{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2+{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}.$$ [3.1]

Then from Equations 2.6 and 2.8, the perceptual inference step in Model 2 yields a mean pain report of

$$P_t=\left(1-{\mathrm{\gamma }}_t\right)N_t+{\mathrm{\gamma }}_t{E}_{c,t},$$ [3.2]

in agreement with the perceptual inference step in Model 1 (Equation 1.1). Thus perceptual inference works the same in both models, except that Model 2 determines the weighting parameter (γ) rationally and dynamically, based on current levels of uncertainty in the current input $N_t\left({\mathrm{\sigma }}_{\mathrm{\epsilon }}^2\right)$ and in the prior for π_t $\left({\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2\right)$ as indicators of the level of potential harm (i.e., of the true value of π_t).

The learning steps of the models can be similarly linked. First consider Model 2 without biased without biased learning (β = 0), and define a trial-specific learning rate,

$${\mathrm{\alpha }}_t=\frac{s_{c,t}^2}{{\mathrm{\sigma }}_{\mathrm{\Psi }}^2+s_{c,t}^2}.$$ [3.3]

From Equations 2.11 and 2.8, the learning step in Model 2 yields a mean expectation on the next trial of

$$E_{c,t+1}={\mathrm{\alpha }}_t{P}_t+\left(1-{\mathrm{\alpha }}_t\right)E_{c,t},$$ [3.4]

in agreement with the learning update in Model 1 (Equation 1.4). Thus learning works the same in both models, except that Model 2 determines the learning rate (α) rationally and dynamically, based on current levels of uncertainty in ${\pi }_t\left({\mathrm{\sigma }}_{\mathrm{\Psi }}^2\right)$ and in the prior for ${\mu }_{c,t}\left(s_{c,t}^2\right)$ as indicators of the objective cue-pain association (i.e., of the true value of μ_c,_t).

With bias in the random walk (governed by β), the learning update in Model 2 (Equation 2.15) becomes

$$E_{c,t+1}={\mathrm{\alpha }}_t(1-\mathrm{\beta })P_t+\left(1-{\mathrm{\alpha }}_t\right)(1-\mathrm{\beta })E_{c,t}+\mathrm{\beta }{M}_c.$$ [3.5]

Thus the initial belief directly contributes to the learning update, similar to its role in perceptual inference in Model 1⁺. A second interpretation of Model 2’s learning update (also equivalent to Equation 2.15) that is closer to the primary Model 1 can be obtained by defining an error-dependent learning rate,

$${\tilde{\mathrm{\alpha }}}_t=(1-\mathrm{\beta }){\mathrm{\alpha }}_t+\mathrm{\beta }\frac{M_c-E_{c,t}}{P_t-E_{c,t}}.$$ [3.6]

Using this definition, Equation 2.15 can be rewritten as

$$E_{c,t+1}={\tilde{\mathrm{\alpha }}}_t{P}_t+\left(1-{\tilde{\mathrm{\alpha }}}_t\right)E_{c,t},$$ [3.7]

paralleling Equation 1.4. Moreover, similar to α_c and α_i in Model 1 (see Equation 1.5), a positive value of β implies that ${\tilde{\mathrm{\alpha }}}_t$ is larger when the prediction error moves the expectation toward the initial association (i.e., P_t - E_c,_t and M_c - E_c,_t have the same sign) and smaller otherwise. The main difference is that Model 1 implements biased learning by assuming two fixed learning rates for cue-consistent and cue-inconsistent prediction errors, whereas (under the interpretation of Eqs. 3.6–3.7) Model 2 implements biased learning by allowing learning rate to vary continuously as a function of the relationships among E_c, M_c and P_t.

Model fitting

To estimate the model parameters and assess relative predictive quality of each of the models, we implemented the models in Stan¹¹⁹. Stan enables Bayesian inference through Markov chain Monte Carlo (MCMC) sampling from the posterior distribution over model parameters. Note that the choice to estimate the models using Bayesian methods is unrelated to the assumption in Model 2 that subjects learn using Bayesian inference. Both Model 1 and Model 2 were fitted hierarchically, such that the model parameters of each participant are sampled from a group-level distribution. In this way, the information in the individual data is aggregated, while still respecting individual differences¹²⁰. In the Bayesian framework, this means that each individual-level parameter is assigned a group-level prior distribution, whose distribution parameters (i.e., hyperparameters) are assigned prior distributions (i.e., hyperpriors).

Group-level distributions for α_c, α_i and γ in Model 1 and parameter β in Model 2 were assumed to be beta distributions. The hyperparameters defining each of these beta distributions were assigned uniform hyperpriors on the interval [0,10]. Parameters ${\mathrm{\sigma }}_{\mathrm{\eta }}^2$ and ${\mathrm{\sigma }}_{\mathrm{\Psi }}^2$ in Model 2 were assumed to have half-Cauchy distributions. In both models, subjects’ expectation and pain ratings were assumed to be normally distributed around the model’s point predictions. The variances of both of these normal distributions (i.e., error variances) were each assumed to have a half-Cauchy group-level distribution. We used uniform distributions on the interval [0,10] as hyperpriors for the scale parameters governing the half-Cauchy distributions. These priors and hyperpriors were chosen for their uninformative nature¹²¹.

For both models, the number of burn-in iterations was set at 5,000, the number of posterior samples taken was set at 10,000, and 4 MCMC chains were run with overdispersed starting values. All chains showed proper convergence, as assessed by visual inspection, and all Rhat values were less than 1.1.

For model comparison, we used the bridge sampling algorithm^122–124 in R to obtain Bayes factors¹²⁵. The Bayes factor provides a relative metric between two models’ predictive performances. A Bayes factor of 1 corresponds to both models performing equally well. A Bayes factor of 5, for example, can be interpreted as the data being 5 times as likely under the first model compared to the second. Furthermore, the Bayes factor automatically incorporates parsimony, so that less complex models are preferred over more complex models when they would fit equally well under maximum likelihood.

FMRI acquisition and preprocessing

Imaging acquisition

In Study 2, we acquired whole-brain fMRI data on a Siemens 3T Trio scanner at the Center for Innovation and Creativity in Boulder. Structural images were acquired using high-resolution T1 spoiled gradient recall images (SPGR) for anatomical localization and warping to a standard space. Functional images were acquired with an echo-planar imaging sequence (TR = 1300 ms, TE = 25 ms, field of view = 220 mm, 3.4×3.4×3.0 mm voxels, 26 slices, parallel imaging, SENSE factor 2). Each test-phase run lasted 430 s (331 TRs). Visual stimuli were presented via a mirror attached to the head coil, and ratings were made using a track ball.

Preprocessing

Prior to preprocessing, global outlier time points (i.e. “spikes” in the BOLD signal) were identified by computing both the mean and the standard deviation (across voxels) of values for each image for all slices. Mahalanobis distances for the matrix of slice-wise mean and standard deviation values (concatenated) × functional volumes (time) were computed, and any values with a significant χ2 value (corrected for multiple comparisons based on the more stringent of either false discovery rate or Bonferroni methods) were considered outliers. On average 4.6% of images were outliers (SD = 1.9). The output of this procedure was later used as a covariate of noninterest in the first-level models.

Functional images were slice-acquisition-timing and motion corrected using SPM8 (Wellcome Trust Centre for Neuroimaging, London, UK). Structural T1-weighted images were coregistered to the first functional image for each subject using an iterative procedure of automated registration using mutual information coregistration in SPM8 and manual adjustment of the automated algorithm’s starting point until the automated procedure provided satisfactory alignment. Structural images were normalized to MNI space using SPM8, interpolated to 2×2×2 mm voxels, and smoothed using a 6mm full-width at half maximum Gaussian kernel. We discarded the first 6 volumes of each run, and then concatenated the 5 test-phase runs for each participant. A high-pass filter of 180 seconds was used.

fMRI analysis

We conducted first-level (individual participants) general linear model (GLM) analyses in SPM8, employing the single trial, or “single-epoch”, design and analysis approach^49,63,64. To estimate single-trial pain responses, we constructed a GLM design matrix with separate regressors for the 1.8-s heat-application period in each trial. We also modeled periods of cue presentation (2 s), expected-pain rating (VAS onset to response), pain anticipation (expected-pain rating response to heat onset), and pain rating (VAS onset to response). All task variables were modeled as boxcar regressors, convolved with the canonical hemodynamic response function. Other regressors of non-interest (nuisance variables) were i) “dummy” regressors coding for each run (intercept for each but the last run); ii) linear drift across time within each run; iii) the 6 estimated head movement parameters (x, y, z, roll, pitch, and yaw), their mean-zeroed squares, their derivatives, and squared derivatives for each run (total 24 columns per run); iv) indicator vectors for outlier time points identified based on their multivariate distance from the other images in the sample (see above); v) indicator vectors for the first two images in each run.

In a second GLM we used separate regressors for each single-trial pain-anticipation period. The only difference between this GLM and the one reported above is that the pain-anticipation periods, instead of the heat-application periods, were modeled on a single-trial basis.

One important consideration in single-trial analysis is that trial estimates can be strongly affected by acquisition artifacts that occur during that trial (e.g. sudden motion, scanner pulse artifacts). For this reason, we calculated trial-by-trial variance inflation factors (VIFs; a measure of design-induced uncertainty, in this case due to collinearity with nuisance regressors), and trials with VIFs that exceeded 2.5 were excluded from the analyses. The average number of excluded trials was 2.3 per participant (SD = 2.2).

NPS analyses

We calculated the strength of expression of the NPS pattern for each single-trial heat activation map, by taking the dot product of the vectorized activation image $\left({\overrightarrow{\beta }}_{map}\right)$ with the NPS pattern weights $\left({\overrightarrow{w}}_{map}\right)$, i.e., ${\overrightarrow{\beta }}_{map}^T{\overrightarrow{w}}_{map}$, yielding a continuous scalar value. We used the single-trial NPS responses in our regression analyses.

Anticipatory activity updating analysis

To examine evidence for a confirmation bias in the updating of pain-anticipatory brain activity, we computed the change in pain-anticipatory activity across successive presentations of a given cue. Specifically, we created ‘delta’ (or ‘update’) images by subtracting the single-trial activation map on trial t from the single-trial activation map for the next trial on which the same cue c was presented, i.e., activation map_c,t+1 - activation map_c,t. We then separately computed each participant’s mean update image following aversive prediction errors on low-cue trials, aversive prediction errors on high-cue trials, appetitive prediction errors on low-cue trials, and appetitive prediction errors on high-cue trials. Finally, we computed the following two contrasts: (i) the update of anticipatory activation following aversive prediction errors on high-cue > low-cue trials; and (ii) the update of anticipatory activation following appetitive prediction errors on low-cue > high-cue trials.

We conducted a second-level (group) analysis on each of these two contrasts using robust regression, which minimizes the influence of outliers¹²⁶, and included a regressor coding for individual differences in estimated learning rate (a) between high-cue and low-cue trials (either for aversive or appetitive prediction errors, for the corresponding contrast). We applied a gray-matter mask, and used false discovery rate (FDR) to correct for multiple comparisons in whole-brain voxel-wise analyses.

Activation clusters, reported in the Supplementary Tables, were defined as FDR-corrected voxels (q < 0.05) contiguous with voxels at uncorrected p < 0.001 and p < 0.01. In the figures in the main manuscript, we show FDR-corrected voxels (q < 0.05) contiguous with voxels at uncorrected p < 0.01 and p < 0.05, for display purposes.

Data Availability

The single-trial behavioural and NPS data, needed to reproduce all behavioural and NPS analyses in the paper, are available through the Open Science Framework repository, https://osf.io/bqkz3/. The fMRI data, needed to reproduce the analyses on anticipatory brain activity, is available from the corresponding author upon request.

Code Availability

Our modeling code (all versions of our computational models) is available through the Open Science Framework repository, https://osf.io/bqkz3/. The code we used to conduct all other analyses (multilevel regression, mediation and fMRI analyses) is available via https://github.com/canlab.