Network topologies that can achieve dual function of adaptation and noise attenuation

Abstract

Many signaling systems execute adaptation under circumstances that require noise attenuation. Here, we identify an intrinsic trade-off existing between sensitivity and noise attenuation in the three-node networks. We demonstrate that, although fine-tuning timescales in three-node adaptive networks can partially mediate this trade-off in this context, it prolongs adaptation time and imposes unrealistic parameter constraints. By contrast, four-node networks can effectively decouple adaptation and noise attenuation to achieve dual function without a trade-off, provided that these functions are executed sequentially. We illustrate ideas in seven biological examples, including Dictyostelium discoideum chemotaxis and p53 signaling network, and find that adaptive networks are often associated with a noise attenuation module. Our approach may be applicable to finding network design principles for other dual and multiple functions.

In brief

Minimizing the trade-off between sensitivity and noise attenuation dictates the design principle for the dual function of adaptation and noise attenuation.

Introduction

A fundamental challenge in biology is to understand how the signaling systems in living organisms are able to accurately respond to the external signals and robustly carry out their functions. General design principles have been found to link recurrent network motifs to specific biological functions, such as reliable cell decisions (Brandman et al., 2005), robust biological oscillations (Novak and Tyson, 2008; Tsai et al., 2008; Zhang et al., 2017), faithful noise resistance (Hornung and Barkai, 2008), optimal fold-change detection (Adler et al., 2017), cell polarization (Chau et al., 2012) and adaptation (Ma et al., 2009).

The function of adaptation, referring to the system’s ability to react to a change of signal and return to the pre-stimulated level, is vital for living systems to sense a wide range of change (Alon et al., 1999; Gardner et al., 2000). Such response terminates the signal response after an appropriate time (Ferrell, 2016; Weill et al., 2012) and resists the changed environment to maintain their own stability (Muzzey et al., 2009). For example, bacteria maintain their sensitivity to chemical gradients over a wide range of attractant or repellent concentrations (Barkai and Leibler, 1997). Adaptive Msn2 localization pulse under oxidative stress induced by H₂O₂ plays an important role for yeast to survive environmental challenges (Hao and O’Shea, 2011; Levine et al., 2013). Besides, adaptation of E(spl) mediated by miR-7 through an incoherent feed-forward loop helps to drive the final state to the previous value after the upstream signal changes dramatically, which stabilizes the developmental process of drosophila (Li et al., 2009). Adaptive behavior can be measured collectively by two quantities: sensitivity and precision. Sensitivity describes how large the magnitude of the relative output response is whereas precision depicts how close the pre- and poststimulus steady states are (Figure 1A). An exhausted search on all possible three-node enzyme networks shows that the adaptation can be achieved by networks containing at least one of two core motifs: a negative feedback loop with a buffering node (NFBLB) and an incoherent feedforward loop with a proportioner node (IFFLP) (Ma et al., 2009). Similarly, negative feedback loops and incoherent feedforward loops are also core motifs in three-node adaptive gene regulation networks (Shi et al., 2017).

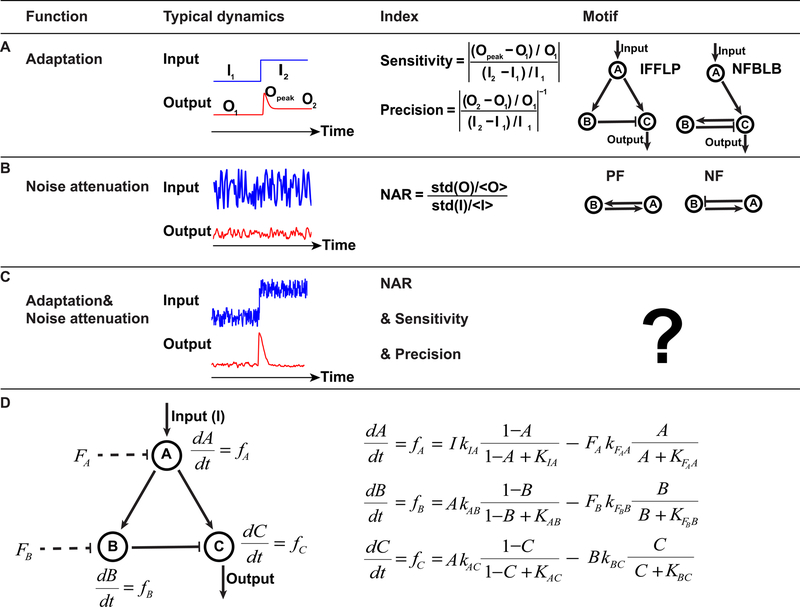
Figure 1. Searching for circuits capable of adaptation and noise attenuation.

(A) Typical dynamics, functional characterization and motifs of adaptation.

(B) Typical dynamics, functional characterization and motifs of noise attenuation.

(C) Expected dynamics and characterization of dual function.

(D) Illustration of mathematical model for a three-node network IFFLP.

Signaling systems also need to resist noise to enable reliable responses. It has been found that feedback loops play important roles in noise attenuation (Figure 1B). For instance, negative feedback (NF) typically reduces cell-cell variations (Alon, 2007; Becskei and Serrano, 2000; Fritsche-Guenther et al., 2011; Hansen et al., 2018; Ji et al., 2013). On the other hand, positive feedback (PF) can attenuate noise better than NF while the sensitivity is maintained (Hornung and Barkai, 2008). By counting on timescales of feedback loops, linking fast and slow positive feedback loops is able to maintain a high state and resist large noise (Brandman et al., 2005). Moreover, the signed activation time, which describes the difference between deactivation and activation time, is a key feature that measures the ability of noise reduction in a regulatory system (Wang et al., 2010).

Since adaptive systems are often operated in noisy circumstances (Colin et al., 2017; Sartori and Tu, 2011), how to achieve noise attenuation and adaptation simultaneously is clearly a challenging task. In equilibrium systems in which the detailed balance condition is satisfied, reducing noise and maintaining high sensitivity cannot be achieved simultaneously based on the fluctuation dissipation theorem (Van Kampen, 2007). However, most sensory and regulatory systems are non-equilibrium; external metabolic energy is consumed to drive the dynamics of the system. It has been demonstrated that it is possible for a system to have both high sensitivity and low fluctuation (Sartori and Tu, 2015). In terms of network topologies, the investigation of intrinsic noise and adaptive response shows that negative feedback loop has a higher response magnitude than incoherent feedforward loop for a given intrinsic noise level (Shankar et al., 2015). Moreover, timescale plays a critical role of noise attenuation in adaptive systems. Adaptive systems may behave as a bandpass filter so that high-frequency extrinsic noise can be averaged out through response time while low-frequency extrinsic noise can be filtered by adaptation time (Sartori and Tu, 2011).

Instead of exploring adaptation properties and noise resistance in some classic adaptive networks (e.g. IFFLP and NFBLB) (Shankar et al., 2015) or experimentally observed networks (Sartori and Tu, 2011), we ask the design principle of low noise and perfect adaptation from the bottom-up. What kind of network topologies can maintain adaptation and reduce noise simultaneously? If such networks exist, what are the underlying design principles?

Here, we systematically investigate the design principles that link network topologies to dual function in both three- and four-node networks (Figure 1C). We first use three-node networks as a minimal framework and enumerate all possible network topologies to reveal the trade-off between sensitivity and noise attenuation capability. In order to mediate such trade-off, we also tune the timescale of nodes in three-node adaptive networks. This strategy can result in better dual function but introduces some “costs”. Then we turn our attention to four-node networks, whose flexibility may provide ways to achieve dual function and overcome the limitations of three-node networks. We sequentially combine noise attenuation modules with adaptive modules in four-node networks to investigate how different strategies influence the compatibility for dual function. Our analysis suggests that despite the simplicity of the modules for single function, achieving multiple functions simultaneously requires that different functional modules work coherently in both time scales and topologies. We further explore a larger four-node network space with an evolution algorithm and the design principle of sequential combination emerges again. Examination on seven biological systems shows that adaptive networks are often sequentially coupled with a noise attenuation module.

Results

Sensitivity, precision, and noise amplification rate

We aim to explore the design principle for network executing both adaptation and noise attenuation. The adaptation behavior and noise propagation process are captured by three quantities. The adaptation behavior can be described by two quantities: sensitivity and precision (Ma et al., 2009). Sensitivity and precision are defined as follows:

$$Sensitivity=\left|\frac{\left(O_{peak}-O_1\right)/O_1}{\left(I_2-I_1\right)/I_1}\right|,$$

and

$$Precision={\left|\frac{\left(O_2-O_1\right)/O_1}{\left(I_2-I_1\right)/I_1}\right|}^{-1},$$

where O₁ and O₂ are output values in steady state under the input signal I₁ and I₂ respectively, and O_peak is the transient peak value when the input signal changes from I₁ to I₂ (Figure 1A). Sensitivity describes the size of the output jump while the precision represents how close the pre- and poststimulus output levels are after a persistent change of input signal. The system noise level in the output is described using the standard Noise Amplification Rate (Hornung and Barkai, 2008; Wang et al., 2010):

$$NAR=\frac{std(O)/mean(O)}{std(I)/mean(I)},$$

where I denotes the input signal fluctuating around I₁ or I₂ and O is the corresponding output level in steady state (Figure 1B). Thus, according to definition of three quantities, networks capable of dual function should have large sensitivity, high precision and low NAR (Figure 1C).

We use enzymatic regulatory networks and Michaelis-Menten rate equations to model both three-node and four-node networks (see STAR Methods). An enzymatic regulatory network with IFFLP topology is illustrated in Figure 1D as an example. Enzyme A is activated by input (I) and active enzyme A activates both enzyme B and C. In contrast to enzyme A, active enzyme B can deactivate enzyme C, thus forming an incoherent feedforward loop. Since both node A and node B have only positive incoming links, basal deactivating enzymes are added to regulate the two nodes. With the assumption that the total concentration of each enzyme is a constant, the network is modeled as ordinary differential equation with three variables (Figure 1D). Each variable represents the concentration of active enzyme and f_i (i = A, B, C) is the reaction rate of active enzyme. Each term in f_i takes the form of Michaelis-Menten equation with Michaelis-Menten constant K and catalytic rate constant k. Any three- or four-node network follows the same way to construct the model. Given all the values of k_IA, K_IA, $k_{F_A}{}_A$, ⋯, sensitivity and precision are calculated through the dynamics of enzyme C when input changes from I₁ to I₂, and NAR is derived by linear noise approximation when input fluctuates around I_ss (I_ss = I₁ or I₂) with autocorrelation time τ₀ (see STAR Methods).

There exists an intrinsic trade-off between robust adaptation and noise attenuation in three-node networks

We first try to answer whether three-node networks can robustly execute adaptation and buffer noise simultaneously. For each network topology, we measure its robustness by using the Q value, which is defined by the number of parameter sets that can yield the target functions (Ma et al., 2009). To be more precise, we sample 10,000 parameter sets for each topology and quantify three Q values: Q_A for adaptation, Q_N for noise attenuation, and Q_A&N, for dual function. Here, adaptation is defined by sensitivity>1 and precision>10, and noise attenuation is defined by NAR<0.2. Dual function of adaptation and noise attenuation is achieved if sensitivity>1, precision>10 and NAR<0.2 are satisfied simultaneously. In our simulation, the initial input (I₁ = 0.4) increases by 12.5% (I₂ = 0.45). If the output first changes more than 12.5% and finally goes to its steady state that is less than 1.25% different from the initial state, sensitivity is larger than 1 and precision is larger than 10. If NAR<0.2, the normalized standard deviation (i.e., coefficient of variation) of output is smaller than one-fifth of that of input. There are total 16,038 possible three-node network topologies, and only 395 networks have been found as the robust adaptation networks (Q value is larger than 10) (Ma et al., 2009). However, since finite sampling of parameters may lead to some randomness in Q values and the threshold Q=10 for defining adaptive network can be somewhat arbitrary, to avoid missing some other possible adaptation networks, we enumerate all three-node networks rather than taking directly the 395 adaptation networks found previously to investigate the dual function.

Enumeration of all possible 16,038 three-node network topologies shows that none of them leads to robust dual function. Figure 2A shows the Q_A – Q_N − Q_A&N space of 16,038 three-node network topologies. Among all these network topologies, 4.65% can achieve non-zero Q_A and 96.97% non-zero Q_N. However, there is no parameter set that can meet the criterion of dual function for all 16,038 networks (Q_A&N = 0). Although there are nonzero Q_A&N for several network topologies when the sample size of parameter sets increases to 10⁶, the maximal Q_A&N is less than 10. These results indicate that some network topologies may have good performance of individual function but are still difficult to achieve dual function. For example, circuits (a circuit is defined as a network topology with certain specific parameters) buffering noise always show little response to external stimuli while adaptive circuits with high sensitivity usually accompany with large noise (Figures 2B and 2C).

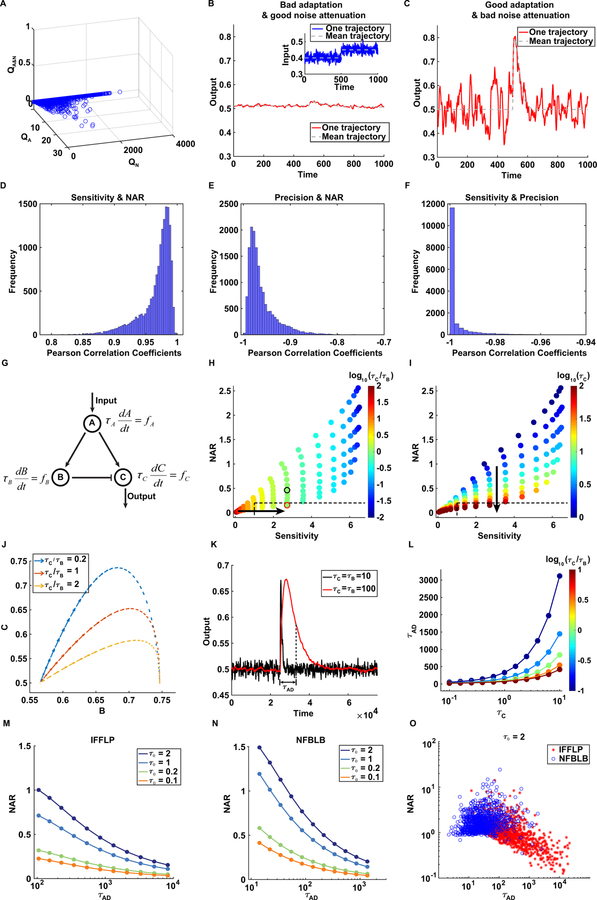
Figure 2. The trade-off between robust adaptation and noise attenuation in three-node networks.

(A) Q values (including Q_N, Q_A and Q_A&N) of 16038 three-node network topologies. Q_A&N are zero for all three-node network topologies.

(B-C) Two kinds of typical output of IFFLP with two different parameter sets. Inset in (B): The blue solid line represents one trajectory of the input signal and the gray dashed line is the average of all random trajectories. In both (B) and (C), the red solid line is one output trajectory under noisy input, and the gray dashed line the mean behavior of output. Both the output in (B) and (C) have high precision, but the dynamics in (B) shows good noise attenuation with low sensitivity while the one in (C) has a high sensitivity with large fluctuations.

(D-F) The histograms of Pearson’s correlation coefficients of sensitivity-NAR, precision-NAR and sensitivity-precision in 16,038 three-node network topologies. Sensitivity, precision and NAR are log-transformed before calculating Pearson’s correlation coefficients. (G) Network topology of IFFLP with timescales τ_A, τ_B and τ_C.

(H-I) The scatter diagrams of sensitivity and NAR for IFFLP. All parameters except τ_B and τ_C are fixed. Here, log (τ_B) is sampled from 0 to 2 with an increment 0.2 and so is log (τ_C), leading to 121 pairs of sensitivity and NAR. The only difference between (H) and (I) is the content of color bar. The color bar in (H) and (I) indicate the values of τ_C/τ_B and τ_C, respectively. The lower-right rectangle bounded by the black dashed line represents the functional region for dual function, i.e., sensitivity>1 & NAR<0.2 & precision>10. The black and the red circle in (H) are corresponding to τ_C = τ_B = 10 and τ_C = τ_B = 100, respectively.

(J) The phase plane of nodes B and C for IFFLP. When the input signal changes from I₁ and I₂, the trajectory of B and C are drawn for different ratios of τ_C to τ_B. The start point of the trajectory is the stable point under I₁ while the end point is the stable point under I₂.

(K) Comparison of the dynamics under two sets of τ_C under τ_B· τ_C = τ_B = 10 and τ_C = τ_B = 100 are corresponding to the black circle point and red circle point in (H), respectively. Adaptation time τ_AD is illustrated for the dynamics under τ_C = τ_B = 100.

(L) τ_AD as a function of τ_B and τ_C for IFFLP.

(M-N) NAR as a function of adaptation time for different timescales of input noise in IFFLP (M) and NFBLB (N). Kinetic parameters except τ_B and τ_C are the same as those used in Figures 2H-2L (for IFFLP) or Figures S1E and S1F (for NFBLB). For a fixed autocorrelation time of input noise τ₀, as τ_B and τ_C are tuned proportionally (with τ_C/τ_B = 1), NAR and adaptation time τ_AD very accprdingly.

(O) Scatter diagram of NAR and adaptation time for IFFLP and NFBLB when τ₀ = 2. In the diagram, 1,000 points satisfying adaptation i.e., sensitivity>1 & precision>10 are illustrated for both IFFLP and NFBLB. See Figures S1G–S1I for the same diagram with τ₀ = 1, 0.2 and 0.1.

To dissect the difficulty of achieving dual function, we investigate the interdependencies among three quantities (sensitivity, precision and NAR). Pearson’s correlation coefficients are calculated to measure correlations among three quantities for all 16038 network topologies (Figures 2D–2F). It can be seen that sensitivity is highly positively correlated with NAR, with Pearson’s correlation coefficients ranging from 0.8 to 1 (Figure 2D). This means that larger sensitivity generally results in higher NAR, which implies a trade-off between adaptation and noise attenuation, hindering the achievement of dual function. In contrast to sensitivity, precision is negatively correlated with NAR, which benefits dual function (Figure 2E). It should be noted that adaptation alone requires to overcome the negative correlation between sensitivity and precision (Figure 2F), which results in an IFFLP or NFBLB architecture in three-node adaptive networks (Ma et al., 2009). Additionally, a similar analysis in three-node transcriptional regulatory networks (see STAR Methods) further confirms the trade-off between adaptation and noise attenuation (Figures S1A–S1D).

Fine-tuning timescales in three-node networks can partially mediate the trade-off between sensitivity and NAR with a cost

In order to minimize the trade-off between sensitivity and NAR, we analyze the effect of timescales on these two quantities. We use IFFLP as an example to illustrate how timescale modification is performed (Figure 2G). First, for the three-node network modeled by $\frac{dA}{dt}=f_A\left(I,A,B,C\right)$, $\frac{dB}{dt}=f_B\left(A,B,C\right)$, and $\frac{dC}{dt}=f_C\left(A,B,C\right)$, we choose one set of parameters capable of good precision (i.e., precision>10) (see Table S1 for parameters). Then with all of the parameters in f_A, f_B and f_C fixed, we introduce three parameters, τ_A, τ_B and τ_C to simulate a new system ${\tau }_A\frac{dA}{dt}=f_A$, ${\tau }_B\frac{dB}{dt}=f_B$ and ${\tau }_C\frac{dC}{dt}=f_C$, where tuning τ_A, τ_B or τ_C can change the timescale of the corresponding node. Since changing τ_A, τ_B or τ_C has no influence on precision, we can investigate how timescales affect sensitivity and NAR. For IFFLP, when τ_A is fixed as a constant (τ_A = 1), smaller ratio of τ_C to τ_B > results in higher sensitivity (Figure 2H). With fixed ratio of τ_C to τ_B, larger τ_C leads to smaller NAR but has little effect in sensitivity (Figure 2I). Similar results can be obtained for NFBLB (Figures S1E and S1F; see Table S2 for parameters). The reason for smaller ratio of τ_C to τ_B leading to higher sensitivity can be given in this way: small ratio of τ_C to τ_B causes a steep slope of the node C trajectory at the initial response when the input intensity changes from I₁ to I₂, and therefore the maximum of node C in the phase plane becomes large (Figure 2J). This can be further validated by mathematical analysis (see STAR Methods). With fixed ratio of τ_C to τ_B, analytical derivation of NAR using linear noise approximation shows that NAR is a decreasing function of τ_C when τ_C is large enough compared to the autocorrelation time of input noise (see STAR Methods). In fact, with more general form of rate equations (i.e., whether it is enzymatic regulation or transcriptional regulation), IFFLP and NFBLB still obey the same monotonicity of sensitivity and NAR as functions of τ_B and τ_C (see STAR Methods).

Taken together, one feasible strategy for reducing the trade-off in IFFLP or NFBLB is to increase τ_C for small NAR while decreasing the ratio of τ_C to τ_B to ensure high sensitivity. For instance, when we fix a small ratio τ_C/τ_B and increase τ_C to ten times, noise can be greatly reduced while sensitivity is almost unchanged (Figure 2K). However, the cost to improve dual function by adjusting timescales is a large increase of the adaptation time τ_AD that is defined as the time required for the output to return to halfway between the peak value and the steady-state value after change of the input (Barkai and Leibler, 1997) (Figures 2K and 2L). That is to say, to obtain a small NAR while maintaining adaptation, the system is required to take a long adaptation time, which depends on the timescale of input noise and network topology. If the time scale of the input noise is faster (corresponding to smaller autocorrelation time), the adaptation time required to reach a certain level of NAR will be shorter for both IFFLP (Figure 2M) and NFBLB (Figure 2N). Sampling within the same parameter space, NFBLB tends to have shorter adaptation time while IFFLP can reach smaller NAR (Figures 2O and S1G–S1I). Overall, there is a trade-off between NAR and adaptation time.

In fact, for all adaptive three-node networks (not limited to simple IFFLP or NFBLB), the trade-off between sensitivity and NAR can be partially lifted by fine-tuning the timescales of node B and node C to obtain both high sensitivity and low NAR (see STAR Methods). However, besides the side effect of increasing the adaptation time, changing the timescales is equivalent to expanding the search space of kinetic parameters, which may be out of biologically realistic range.

Combinations of function-specific modules in four-node networks can achieve dual function

Since dual function in three-node networks is difficult to obtain, we next study four-node networks as more nodes often provide more flexibility in controlling functions. If we just consider networks that contain at least one direct or indirect causal link from the input node to the output node and exclude redundant networks that are topologically equivalent, the number of possible four-node networks is 19,805,472, which is about 1,200 times more than that of possible three-node networks (16,038). Besides, compared to three-node networks, the number of parameters in a four-node network is typically larger, leading to an exponentially increase in the volume of the parameter space to be sampled. Thus, enumeration with effective parameter sampling of all four-node networks is computationally too expensive. Alternatively, we construct four-node networks by assembling two function-specific modules: adaptation module and noise attenuation module. A straightforward strategy is the sequential connection of these two modules, including N-A types and A-N types (Figure 3A), where N represents noise attenuation and A represents adaptation. N-A types indicate that the input signal passes through an upstream noise attenuation module and then the downstream adaptation module, while A-N types require that the adaptation module is placed upstream of the noise attenuation module. We choose IFFLP and NFBLB as adaptation modules (red nodes in Figure 3B) while PF and NF as noise attenuation modules (blue nodes in Figure 3B). Thus, by combining minimal adaptation modules and noise attenuation modules, we obtain eight four-node networks including four N-A types (the first row of Figure 3B) and four A-N types (the second row of Figure 3B). These networks do not have redundant links and thus may constitute minimal four-node networks capable of dual function. Since we allow the input node and the output node to be the same for these modules, IFFLP and NFBLB can be reduced to two-node adaptive networks in Figure 3B.

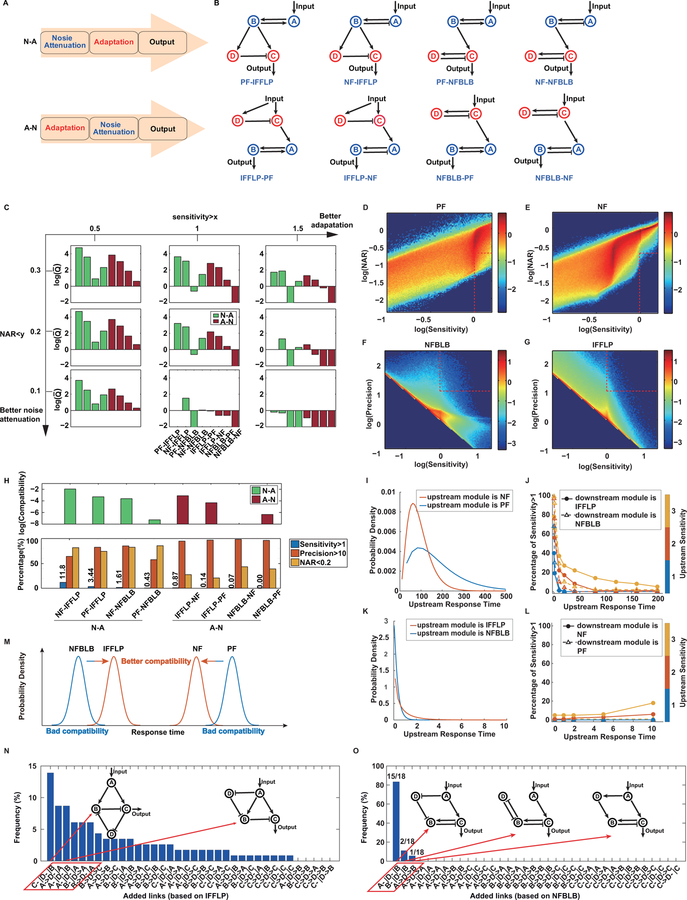
Figure 3. Dual function can be achieved by module combination in four-node networks.

(A) Two strategies for sequential combination of adaptation module and noise attenuation module.

(B) Eight networks obtained by two different ways of module combination shown in (A). Red nodes represent the adaptation module (IFFLP or NFBLB) and blue nodes the noise attenuation module (PF or NF).

(C) $\overline{\text{Q}}$ of dual function for the eight four-node networks in (B). $\overline{\text{Q}}$ is defined as the averaged Q value calculated by eight repeated simulations and modified by adding 10⁻⁸ to ensure $\text{log}\left(\overline{\text{Q}}\right)$ is well-defined. For each bar graph, the criterion for dual function is determined by the x coordinate and y coordinate: sensitivity>x & NAR<y & precision>10. Green bars represent N-A networks and red bars A-N networks.

(D-E) The joint histogram of sensitivity and NAR for noise attenuation modules: PF (D) and NF (E). The color bar indicates the density of parameter sets in a given region. The lower-right rectangle bounded by the red dashed line represents the functional region of noise attenuation, i.e., sensitivity>1 & NAR<0.2.

(F-G) The joint histogram of sensitivity and precision for adaptation modules: NFBLB (F) and IFFLP (G). The color bar indicates the density of parameter sets in a given region. The upper-right rectangle bounded by the red dashed line represents the functional region of adaptation, i.e., sensitivity>1 & precision>10.

(H) Compatibilities (upper panel) and percentages of assembled circuits satisfying sensitivity>1, precision>10 or NAR<0.2 (lower panel) for the eight four-node networks. The four N-A networks are ranked by percentages of assembled circuits satisfying sensitivity>1 and so are the four A-N networks.

(I) Distribution of the upstream response time in N-A networks. For each noise attenuation module (PF or NF), only circuits satisfying sensitivity>1 & NAR<0.2 are chosen to calculate the response time and the probability density is fitted using the Gamma distribution. The shape parameter and the scale parameter of the Gamma distribution are estimated to be: (2.14, 79.38) for PF and (3.06, 30.09) for NF.

(J) The percentage of assembled N-A circuits satisfying sensitivity>1 as a function of the upstream response time and the upstream sensitivity. For a given upstream output with specific response time and sensitivity, 200 adaptation circuits (100 for IFFLP module and 100 for NFBLB module) satisfying sensitivity>1 & precision>10 are chosen as downstream circuits to calculate the sensitivity of assembled circuits.

(K) Distribution of the upstream response time in A-N networks. For each adaptation module (IFFLP or NFBLB), only circuits satisfying sensitivity>1 & precision>10 are chosen to calculate the response time and the probability density is fitted using the Gamma distribution. The shape parameter and the scale parameter of the Gamma distribution are estimated to be: (0.57, 1.22) for IFFLP and (1.09, 0.27) for NFBLB.

(L) The percentage of assembled A-N circuits satisfying sensitivity>1 as a function of the upstream response time and the upstream sensitivity. For a given upstream output with specific response time and sensitivity, 200 noise attenuation circuits (100 for PF module and 100 for NF module) satisfying sensitivity>1 & NAR<0.2 are chosen as downstream modules to calculate the sensitivity of assembled circuits.

(M) Schematic illustration of the relationship between compatibility and response time of modules in both N-A and A-N networks. The distributions of response time for the four modules are sketched using Gaussian distributions with the same variance and different mean values.

(N) Frequency of 36 IFFLP-based topologies among 115 four-node circuits obtained by the evolution algorithm. The 36 IFFLP-based four-node topologies are ranked by their percentages of occurrence. Topologies in the red parallelogram are those whose percentages of occurrence are larger than 5%. Inset: #1 and #3 ranking topologies.

(O) Frequency of 36 NFBLB-based topologies among 18 four-node circuits obtained by the evolution algorithm. The 36 NFBLB-based four-node topologies are ranked by their percentages of occurrence. Inset: the three appeared topologies (whose labels are marked in the red parallelogram).

We explore the capability of these A-N and N-A networks to achieve dual function. As an illustration, the Q value of PF-IFFLP type is computed as follows. First, we randomly assign 2 × 10⁶ parameter sets for PF and IFFLP, respectively. For IFFLP, circuits capable of adaptation are recorded and we use a to denote the number of these adaptive circuits. For PF, circuits capable of noise attenuation are selected out and its number is denoted by n. Here, the criterion for an adaptation circuit is sensitivity>1 & precision>10 while the criterion for a noise attenuation circuit is modified as sensitivity>1 & NAR<0.2. The reason why sensitivity>1 is added to the criterion for noise attenuation is that we expect to maintain the system’s sensitivity when the signal is passing through the noise attenuation module. Because of the extremely low percentage of functional NF circuits (~0.0036%, Figure S2A), we increase the number of sampling parameter sets to 2 × 10⁶. Then, we assemble function-specific circuits to construct a × n and characterize corresponding dynamic behaviors to calculate the Q value.

We first compute the Q values for the eight networks listed in Figure 3B under different thresholds of sensitivity and NAR (Figure 3C). For each bar graph, the criterion for dual function is determined by the x coordinate and y coordinate: sensitivity>x & NAR<y & precision>10. We define $\overline{\text{Q}}$ as the averaged Q value calculated by eight repeated simulations and it is modified by adding 10⁻⁸ to ensure $\text{log}\left(\overline{\text{Q}}\right)$ is well-defined. Green bars denote four N-A networks: PF-IFFLP, NF-IFFLP, PF-NFBLB, NF-NFBLB while red bars denote four AN networks: IFFLP-PF, IFFLP-NF, NFBLB-PF, NFBLB-NF. The results show that combinations of function-specific modules in four-node networks can lead to dual function (Figure 3C). With sensitivity>1 & NAR<0.2 & precision>10 as the criterion, seven of the eight four-node network topologies (excluding NFBLB-NF) can achieve non-zero Q values. Although stricter criteria result in smaller Q values, the Q value rankings of the eight networks are almost consistent under different combinations of thresholds of sensitivity and NAR. Moreover, most N-A networks perform better than A-N networks with the same adaptation and noise attenuation modules except for the combination of PF and NFBLB, and networks with IFFLP have higher Q values than those with NFBLB.

Next, we investigate which factors affect Q values of assembled four-node networks. Clearly, the robustness of each component module, i.e., the number of adaptive circuits a or the number of noise attenuation circuits n can affect Q values since the network topology with larger a or n has the greater potential to generate more parameter sets capable of dual function. With sufficient simulations, we find that adaption modules NFBLB and IFFLP do not share a same value of a, neither do noise attenuation modules PF and NF. Furthermore, n of PF is about fifty times larger than that of NF, while a of NFBLB is roughly double that of IFFLP (Figure S2A). A closer look at the robustness of four modules (PF, NF, IFFLP and NFBLB) is shown in Figures 3D–3G. Joint distributions of sensitivity and NAR for noise attenuation modules show that PF has a broader and denser functional region than NF, implying a larger n (Figures 3D and 3E). For adaptation modules, the functional region of NFBLB is larger than IFFLP, indicating a larger a for NFBLB (Figures 3F and 3G).

However, more robust component modules cannot guarantee to constitute better dual function. For instance, PF-IFFLP performs better dual function than PF-NFBLB despite that NFBLB module can achieve more robust adaptation than IFFLP module. Thus, we define the compatibility as the probability of successful combination of adaptation modules and noise attenuation modules, i.e.,

$$Compatibility=\frac{Q}{a\times n}.$$

We use this quantity to measure the level of compatibility of the two modules when combined sequentially to perform the dual function (upper panel in Figure 3H). Given the same adaptation and noise attenuation modules, N-A networks have better compatibilities thus better performance than A-N networks, except PF-NFBLB. For N-A networks, topologies with NF in the upstream have better compatibilities than those with PF when the downstream module is fixed, and IFFLP in the downstream leads to better compatibility than NFBLB. The A-N networks obey similar rules, where IFFLP-NF is more compatible than others.

The response time of upstream module is a key factor for dual function

To identify the key factor that determines the compatibility between modules, we investigate how sensitivity, precision and NAR are affected in the eight assembled four-node networks. The lower panel in Figure 3H shows the percentages of parameter sets in the eight networks that meet the requirement of sensitivity, precision and NAR for dual function. It can be seen that less than 10 percent of parameter sets can satisfy sensitivity>1 for all eight networks except NF-IFFLP. Instead, percentages of parameter sets for good precision and NAR are relatively high. Thus, loss of sensitivity after module combination can be the bottleneck to achieve dual function. Furthermore, the order of N-A networks sorted by percentages of sensitivity>1 is consistent with that sorted by compatibility, indicating the impact of sensitivity on the compatibility.

Since the downstream module receives the output of the upstream module, the output dynamics of the upstream module plays a role in the downstream output sensitivity. Two quantities can be used to collectively characterize the upstream output dynamics: sensitivity and response time (the time required to reach halfway to the peak value). However, we pay particular attention to the upstream response time, because the upstream circuits (noise attenuation circuits or adaptation circuits) with different topologies have been limited to those with the same requirement of sensitivity (i.e., sensitivity>1) but with no restriction in response time. Thus, in what follows, we investigate how the upstream response time affects the downstream output sensitivity and its dependence on network topology.

First, we focus on N-A networks. As the noise attenuation module, PF tends to have longer response time than NF (Figure 3I). Such difference of response time between PF and NF may cause divergence in the output sensitivity of PF-A and NF-A (where A represents adaptation module IFFLP or NFBLB). To test this hypothesis, we construct a series of dynamics to imitate the outputs of the upstream noise attenuation module where response time and sensitivity of the upstream outputs can be assigned manually. The general form of the dynamics is defined as following:

$$O^{up}(t)=\{\begin{array}{c}\hfill O_1^{up},t<T_0\\ \hfill O_1^{up}+\left(O_2^{up}-O_1^{up}\right)\frac{t-T_0}{T_{on}^{up}+t-T_0},t\ge T_0\end{array}.$$

In this dynamics, O^up(t) increases from its prestimulus steady-state value $O_1^{up}$ after the input changes from I₁ to I₂ at time T₀, and finally stabilizes at $O_2^{up}$. The sensitivity and the response time of O^up(t) are given by $\frac{\left|\left(O_2^{up}-O_1^{up}\right)/O_1^{up}\right|}{\left|\left(I_2-I_1\right)/I_1\right|}$ and $T_{on}^{up}$, respectively. Then we calculate the sensitivity of assembled N-A circuits, in which the output of the upstream noise attenuation module is replaced by O^up(t). By varying $O_2^{up}$ (with fixed $O_1^{up}$) and $T_{on}^{up}$, we can change the upstream sensitivity and the upstream response time respectively, and study how these two quantities affect the sensitivity of assembled circuits. Figure 3J shows that the percentage of the assembled circuits satisfying sensitivity>1 decreases with increasing upstream response time for a given upstream sensitivity whether the downstream module is IFFLP or NFBLB. However, to maintain a high output sensitivity, IFFLP can tolerate longer upstream response time than NFBLB given the same level of the upstream sensitivity. These results indicate that, in order to generate a high output sensitivity for N-A networks, the upstream noise attenuation module should be fast enough and the downstream adaptation module need to allow long upstream response time. Thus, NF is a more compatible upstream module than PF because of its shorter response time and IFFLP is a more compatible downstream module than NFBLB since IFFLP relaxes the requirement of fast upstream dynamics.

Next, we conduct a similar study in A-N networks. Distributions of response time indicate that IFFLP tends to have longer response time than NFBLB as the adaptation module (Figure 3K). Then we construct a series of dynamics to imitate the outputs of the upstream adaptation module, which are defined by following equations:

$$O^{up}\left(t\right)=\{\begin{array}{r}\hfill O_1^{up},\\ \hfill O_1^{up}+\frac{O_{peak}^{up}-O_1^{up}}{1-e^{-1}}\left(1-e^{-\left(t-T_0\right)\frac{\text{ln}\left(\frac{2e}{(e+1)}\right)}{T_{on}^{up}}}\right),\\ \hfill O_2^{up}+\left(O_{peak}^{up}-O_2^{up}\right)e^{-\frac{ln2}{T_{off}^{up}}\left(t\frac{T_{on}^{up}}{\text{ln}\left(\frac{2e}{e+1}\right)}-T_0\right)},\end{array}\begin{array}{l}t<T_0\hfill \\ T_0\le t<T_0+\frac{T_{on}^{up}}{\text{ln}\left(\frac{2e}{e+1}\right)}\hfill \\ t\ge T_0+\frac{T_{on}^{up}}{\text{ln}\left(\frac{2e}{e+1}\right)}\hfill \end{array}.$$

In this dynamics, O^up(t) initially increases from $O_1^{up}$ to the peak value $O_{peak}^{up}$ and then eventually decreases to $O_2^{up}$ with half-time $T_{off}^{up}$. The sensitivity and the response time of O^up(t) are given by $\frac{\left|\left(o_{peak}^{up}-o_1^{up}\right)/o_1^{up}\right|}{\left|\left(I_2-I_1\right)/I_1\right|}$ and $T_{on}^{up}$, respectively. Using the constructed adaptation dynamics, we can explore how response time and sensitivity of upstream adaptation module outputs affect sensitivity of assembled circuits with PF or NF as the downstream module. Figure 3L illustrates that the percentage of assembled circuits satisfying sensitivity>1 increases with increasing upstream response time, which is opposite to the N-A networks. Given the same upstream sensitivity and upstream response time, A-NF can maintain sensitivity better than A-PF. These results indicate that, to maintain downstream output sensitivity, the upstream adaptation module should be slow enough and downstream noise attenuation module should allow relative short upstream response time. The possible reasons can be: a fast response in the upstream adaptation module will be severely filtered by the downstream noise attenuation module (as a low-pass filter), which is harmful for high sensitivity; a fast downstream noise attenuation module has high cutoff frequency and thus retains most of the high-frequency signal, which is beneficial for high sensitivity. As a result, IFFLP, the one with longer response time, has better compatibility than NFBLB as an upstream module, and NF is more compatible as a downstream module because of its higher cutoff frequency than PF. It should be noted that NFBLB-NF can better maintain sensitivity than NFBLB-PF (lower panel in Figure 3H) but has worse compatibility (upper panel in Figure 3H), which results from lower percentage of adaptation circuits in NFBLB-NF (Figure S2B).

The relationship between compatibility and response time of modules in both N-A and A-N networks is summarized in Figure 3M. We notice that response time of these modules is limited by their individual function topologies. For adaptation modules, sensitivity is negatively correlated with response time (Figures S2C and S2D), so high sensitivity often leads to short response time. Within the limit of short response time, IFFLP shows longer response time than NFBLB, thus leading to better compatibility. For noise attenuation modules, NAR is also negatively correlated with response time (Figures S2E and S2F) and thus longer response time usually results in lower NAR, i.e., less noise. To match the response time of adaptation modules, NF is more compatible than PF because of its shorter response time. As a result, a combination of NF and IFFLP optimizes the compatibility and thus maximizes the success rate of the dual function.

Evolution algorithm demonstrates the high performance of dual function for N-A networks

The four-node networks considered in the previous sections are limited to a special class in which two functional modules (adaptation and noise attenuation) are sequentially connected. It would be ideal to expand the search to more classes of four-node networks in order to see if new types of dual function topology would emerge, although, as discussed before, it is not feasible to enumerate all four-node networks. Since adaptation necessarily requires three nodes (i.e., input node, output node and the control node), we focus on the four-node networks containing a minimal three-node adaptive network but allowing the fourth node D with more flexibility. Specifically, we limit ourselves to explore the set of four-node networks with the fourth node D connecting to a three-node IFFLP or NFBLB network via two additional links. The two additional links are one incoming link to and one outgoing link from node D, i.e., node i ⟹ node D ⟹ node j, i, j ∈ {A, B, C} and the combination of signs of these two links can be (+,+), (−,−), (+,−) or (−,+). Thus, there are total 3×3×4=36 different realizations of the two additional links when added to a three-node minimal adaptive network. By this method we construct two subsets of networks in the whole four-node network space, i.e., the IFFLP-based subset and the NFBLB-based subset, each of which has 36 different four-node networks. Note that these sets include N-A networks (added links are A ⟹ D ⟹ A) and A-N networks (added links are C ⟹ D ⟹ C).

To find the network topologies in these subsets that best perform the dual function, we employ an evolution algorithm (François and Hakim, 2004). For each subset, the algorithm begins with an initial collection of circuits whose topologies are randomly chosen from the subset and parameters randomly assigned. Through many rounds of growth and selection, the circuit collection evolves towards higher performance of the dual function (see STAR Methods).

For the IFFLP-based subset, we obtain 115 circuits capable of dual function from 400 implementations of the evolution algorithm. Six network topologies emerge with relatively high occurrences among the 115 functional circuits (Figure 3N). Two of the six networks (ranked #2 and #4) are N-A networks, in which added links A→D—|A and A—|D—|A form one negative and one positive feedback loop, respectively. This is consistent with fact that NA networks have advantage over A-N networks found previously. Interestingly, some new dual function four-node networks emerge. The network with the highest frequency of occurrence has added links C—|D—|B, forming a coherent feedforward loop from node A to node B (i.e., A→C—|D—|B and A→B; see the inset of Figure 3N). The #3 ranking network with added links A—|D—|B also has a coherent feedforward loop from node A to node B (i.e., A—|D—|B and A→B; see the inset of Figure 3N). For these two networks, the additional coherent feedforward loop is analogous to coherent type 4 (Mangan and Alon, 2003), which delays the activation of node B and thus may enhance the transient response of node C. Comparisons between these two networks and IFFLP show that the additional links C—|D—|B or A—|D—|B benefit high sensitivity (Figure S3A) with little effect on noise buffering capability (Figure S3B). Moreover, IFFLP added with C—|D—|B or A—|D—|B can achieve higher sensitivity than IFFLP given the same level of NAR (Figure S3C), which essentially results from slow response of node B caused by the additional coherent feedforward loop (Figure S3D). For the other two networks with added links B—|D→A and B→D—|A, the additional negative feedback loop through node A coupled with IFFLP results in smaller adaptation error (Ma et al., 2009).

For the NFBLB-based subset, only 18 circuits capable of dual function are obtained from 400 implementations. This is consistent with the previous conclusion that N-A and A-N networks containing NFBLB show worse performance of dual function than those containing IFFLP. The 18 circuits correspond to only three topologies (Figure 3O). Similar to the IFFLP-based subset, two of the three topologies (ranked #1 and #3) have an additional coherent feedforward loop from node A to node B (A—|D—|B or A→D→B), which may achieve high sensitivity by delaying the response of node B. The third topology (ranked #2) has links B— |D—|B, a positive feedback loop which also slows down the activation of node B and thus enhances sensitivity. As expected, simulation results show that all of the three topologies improve sensitivity without compromising noise buffering capability compared with NFBLB (Figures S3E–S3G). Further investigations on node B validate that the additional loop (coherent feedforward loop or positive feedback loop) indeed slows down the response of node B to improve dual function in these three topologies (Figure S3H).

We also investigate the robustness of dual function for the IFFLP- and NFBLB-based subset, and find that top-ranked topologies obtained by the evolution algorithm also have higher robustness (Figures S3I–S3L). To avoid zero Q values for almost all topologies, we calculate Q values using a relaxed criterion for dual function, i.e., sensitivity>0.8 & precision>10 & NAR<0.3. For the IFFLP-based subset, the #1 and #3 ranking topologies obtained by the evolution algorithm (Figure 3N) have the top 2 Q values and the N-A network with added links A—|D—|A has the 7^th highest Q value (Figure S3I). Moreover, different thresholds of sensitivity and NAR have little effect on the Q value rankings of 36 IFFLP-based topologies (Figure S3J). For the NFBLB-based subset, the three topologies with highest Q values are exactly those obtained by the evolution algorithm (Figures S3K and S3L).

The design principles for dual function revealed by exploring a larger four-node network space are consistent with those found in previous sections. The first thing is that N-A networks still show relatively high performance of dual function even within a larger network space. Second, besides the sequential connection of two modules, all the new topologies emerged achieve more robust dual function by a better performance in adaptation function, in particular by enhancing the sensitivity. This is consistent with our finding that maintaining sensitivity while reducing noise is the key for the dual function. This can be accomplished either directly by the sequential connection of two modules (e.g. N-A networks) or indirectly by ways of enhancing sensitivity.

Biological examples

In previous sections, we have used three- and four-node networks as coarse-grained approximation to biological networks. Although the vast majority of biological networks are more complex and tend to have more than three or four nodes, many of them are likely to be abstracted into simpler networks with proper coarse-graining. Also, despite the apparent complexity, the underlying core network topology responsible for robustly executing the biological function might be simpler. Thus, the principles obtained from the simple three- or four-node networks may also help to understand more complex biological systems.

By examining several adaptation networks in literatures (Batchelor et al., 2011; Beltrami and Jesty, 1995; Bode and Dong, 2004; Bonner and Savage, 1947; Cesarman - Maus and Hajjar, 2005; Ferrell, 2016; Jackson and Nemerson, 1980; Li et al., 2009; O’Donnell et al., 2005; Ohashi et al., 2014; Shah et al., 2016; Sinha and Häder, 2002; Tago et al., 2015; Zhang and Lozano, 2017; Zhang et al., 2014), we found that the positive or negative feedback loop is often coupled with the adaptation module (Figure 4A). For example, in Dictyostelium discoideum, under the change of ligand cAMP, Gβγ subunit on the membrane is activated and then modulates RasGEF (guanine nucleotide exchange factor) along with RasGAP (GTPase-activating protein). RasGEF activates Ras, whereas RasGAP inactivates Ras. So Gβγ, RasGEF, RasGAP and Ras constitute an adaptation module. Meanwhile, PIP3, a vital intermediate molecular in the downstream of Ras, is involved in a positive feedback loop composed of PI3K, PIP3, RacGEF, Rac and F-actin. Since positive feedback is a noise attenuation module, co-occurrence of these two kinds of signaling pathways can be roughly regarded as an A-N network. Here, we use Dictyostelium discoideum chemotaxis network and p53 activation as biological examples to study whether these modularized signaling pathways can perform robust dual function.

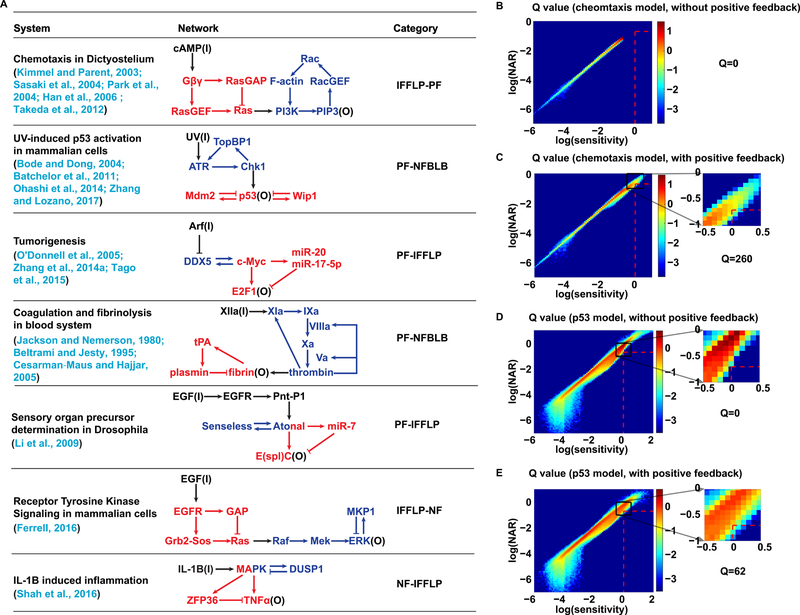
Figure 4. Examples of biological systems capable of dual function.

(A) A list of biological systems that include both adaptation module and noise attenuation module. Biological process (along with the references), network topology and category of module combination are illustrated for each system.

(B-C) The joint histogram of NAR-Sensitivity without and with the positive feedback loop between PI3K and PIP3 in the chemotaxis model. The color bar indicates the density of parameter sets in a given region. The area bounded by red dashed line is the region of dual function, i.e., sensitivity>1 & NAR<0.2 & precision>10. The corresponding Q value is indicated on the right.

(D-E) The joint histogram of NAR-Sensitivity without and with the positive feedback loop between ATR and TopBP1 in the p53 model. The color bar indicates the density of parameter sets in a given region. The area bounded by red dashed line is the region of dual function, i.e., sensitivity>1 & NAR<0.2 & precision>10. The corresponding Q value is indicated on the right.

Dictyostelium discoideum chemotaxis

Chemotaxis describes the directional movement of biological system when exposed to a chemical gradient. This behavior is crucial for organisms to seek for food, chase a signaling cue or avoid harmful environment, and is observed in many organisms such as bacteria (Barkai and Leibler, 1997; Berg and Brown, 1972), amoebae (Bonner and Savage, 1947), neutrophils (Li et al., 2002) and tumor cells (Roussos et al., 2011). In chemotaxis systems like bacteria and amoebae, perfect adaptation to changes in chemoattractant is essential to gradient sensing. At the same time, these systems face with diverse kinds of noise such as receptor-ligand binding noise (Berg and Purcell, 1977; Sartori and Tu, 2011), chemoattractant fluctuations and intrinsic noise (Sartori and Tu, 2011). In Escherichia coli and Dictyostelium discoideum chemotaxis system, adaptation is driven by hydrolysis of SAM, ATP or GTP (high-energy biomolecules under physiological conditions), which makes the system far from equilibrium and the detailed balance condition broken. Therefore, it is feasible for bacteria and amoebae to buffer noise while responding and adapting to signal change (Sartori and Tu, 2015).

The signaling pathways of Dictyostelium discoideum chemotaxis have been well studied (Han et al., 2006; Kimmel and Parent, 2003; Park et al., 2004; Sasaki et al., 2004; Takeda et al., 2012). The whole regulatory network can be regarded as a IFFLP-PF type network (Figures 4A and S4A). Signaling from the ligand (cAMP) to Ras constitutes the adaptation module. The ligand binds to the G-protein coupled receptor (GPCR), activating the GPCR. Upon activation of GPCR, the heterotrimeric G-protein dissociates into a Gα subunit and a free Gβγ subunit. The free Gβγ subunit activates both RasGEF and RasGAP. RasGEF catalyzes GDP-bound Ras (inactive form of Ras) to GTP-bound Ras (active form of Ras), while RasGAP converts active Ras to its inactive form by catalyzing GTP hydrolysis. Hence, the regulations of Ras form an incoherent feedforward loop, which is the core of the adaptation module (Takeda et al., 2012). Downstream of the adaptation module is the noise attenuation module, characterized by the positive feedback loop between PI3K and PIP3. Accumulation of upstream output Ras activates PI3K on the plasma membrane. Active membrane PI3K phosphorylates the membrane lipid PIP2 into PIP3, a second messenger. Accumulation of PIP3 activates Rac by stimulating the activity of RacGEF, and activation of Rac leads to polymerization of F-actin. F-actin polymerization promotes the localization of PI3K on the plasma membrane from cytoplasm. Thus, PIP3 can facilitate the membrane localization of PI3K through F-actin polymerization and forms a positive feedback loop with PI3K.

By merging the multi-steps in the linear pathway of regulation from PIP3 to PI3K into one step, this system can be simplified to seven species (Figure S4B) and modeled by following equations:

$$\frac{d{G}_{\beta \gamma }}{dt}=k_1\cdot cAMP\cdot \left(G_{\beta \gamma 0}-G_{\beta \gamma }\right)-k{d}_1\cdot G_{\beta \gamma }$$

$$\frac{dRasGEF}{dt}=k_2\cdot G_{\beta \gamma }-k{d}_2\cdot RasGEF$$

$$\frac{dRasGAP}{dt}=k_3\cdot G_{\beta \gamma }-k{d}_3\cdot RasGAP$$

$$\frac{dRas}{dt}=k_4\cdot RasGEF\cdot \left(Ra{s}_0-Ras\right)-k{d}_4\cdot RasGAP\cdot Ras$$

$$\frac{dPI3K}{dt}=k_5\cdot Ras\cdot PI3K_m-k{d}_5\cdot PI3K$$

$$\frac{dPI3K_m}{dt}=k_7\cdot \left(PI3K_0-PI3K_m-PI3K\right)\cdot \left(PIP3+k_{70}\right)-k{d}_7\cdot PI3K_m-k_5\cdot Ras\cdot PI3K_m+k{d}_5\cdot PI3K$$

$$\frac{dPIP3}{dt}=k_6\cdot PI3K\cdot \frac{P_0-PIP3}{P_0-PIP3+K_6}-k{d}_6\cdot PIP3.$$

To investigate the importance of noise attenuation module, we destroy positive feedback by artificially deleting the regulation from PIP3 to PI3K as comparison. This is achieved by replacing PIP3 with a (arbitrary) constant 0.44 in the equation of PI3K_m (other choices of the constant gave the same results). Parameters of upstream adaptation module are selected to achieve an adaptive response of Ras (Table S3). Parameters of downstream module with or without positive feedback are randomly chosen with a sample size of 10⁶ (Table S3). The adaptation precision of PIP3 is well maintained because of the good precision of Ras. The distributions of sensitivity and NAR without and with positive feedback are shown in Figures 4B and 4C, respectively. The area bounded by red dashed line is the region of dual function, within which the network with positive feedback (Figure 4C) has a higher Q value than that without (Figure 4B). Moreover, the superiority of the network with positive feedback in the Q value remains consistent for different combinations of thresholds of sensitivity and NAR (Figure S4C). It demonstrates the critical role of positive feedback as a downstream noise attenuation module in the IFFLP-PF network of Dictyostelium discoideum chemotaxis to achieve dual function.

p53 activation

In mammalian cells, tumor suppressor p53 is a common mediator of many stress-related signaling pathways and plays a role in cell cycle arrest, senescence and apoptosis (Zhang and Lozano, 2017). However, different kinds of stresses can induce distinct temporal dynamics of p53, which may encode different information (Batchelor et al., 2011; Levine et al., 2013). For example, double-strand breaks (DSBs) caused by γ-radiation can lead to stereotyped pulses of p53, while single-stranded DNA (ssDNA) damage caused by UV light can induce a dose-dependent adaptive dynamics of p53 (Batchelor et al., 2011).

The signaling pathway involved in response to UV can be regard as a PF-NFBLB type network (Figure 4A). Exposure to UV light can cross-link adjacent cytosine or thymine bases and create pyrimidine dimers, leading to ssDNA damage (Sinha and Häder, 2002). ssDNA damage lesions lead to recruitment of ATR and phosphorylation of ATR itself. Then the kinase activity of ATR is stimulated by TopBP1 with the help of other regulators such as Rad17 and 9-1-1 complexes (Zhang and Lozano, 2017). Once stimulated, ATR phosphorylates Chk1 and activation of ATR-Chk1 checkpoint pathway further increases the accumulation of TopBP1 to the DNA damage lesions, thus creating a positive feedback loop between ATR and TopBP1 (Ohashi et al., 2014). Phosphorylation of p53 by Chk1 can activate p53 for DNA-binding, which enhances the expression of the target genes such as those related to DNA-repair processes, cell-cycle arrest, and apoptosis (Bode and Dong, 2004). The function of p53 can be controlled by two negative regulators, Mdm2 and Wip1, both of which are also target genes of p53. Mdm2 is a ubiquitin E3 ligase and can induce p53 degradation through the ubiquitin-proteasome pathway, while Wip1 is a phosphatase that can dephosphorylate p53 and thus reduce the activity of p53 (Batchelor et al., 2011). So, in this network, ATR-Chk1-TopBP1-ATR forms the positive feedback loop, while Mdm2 and Wip1 act as the negative regulators of p53 and thus form two negative feedback loops with p53.

Dynamics of the signaling network can be modeled by following equations:

$$\frac{dATR}{dt}=k_1\cdot UV\cdot \left(TopBP1+l_1\right)\cdot \left(AT{R}_0-ATR\right)-k{d}_1\cdot ATR$$

$$\frac{dTopBP1}{dt}=k_2\cdot Chk1\cdot \left(TopBP{1}_0-TopBP1\right)-k{d}_2\cdot TopBP1$$

$$\frac{dChk1}{dt}=k_3\cdot ATR\cdot \frac{Chk{1}_0-Chk1}{K_3+Chk{1}_0-Chk1}-k{d}_3\cdot \frac{Chk1}{K{d}_3+Chk1}$$

$$\frac{dp{53}_{inactive}}{dt}=k{g}_4-k{d}_4\cdot p{53}_{inactive}+k_4\cdot Wip1\cdot \frac{p{53}_{active}}{K_4+p{53}_{active}}-k_5\cdot Chk1\cdot \frac{p{53}_{inactive}}{K_5+p{53}_{inactive}}$$

$$\frac{dp{53}_{active}}{dt}=k_5\cdot Chk1\cdot \frac{p{53}_{inactive}}{K_5+p{53}_{inactive}}-k_4\cdot Wip1\cdot \frac{p{53}_{active}}{K_4+p{53}_{active}}-k{d}_5\cdot Mdm2\cdot \frac{p{53}_{active}}{K{d}_5+p{53}_{active}}$$

$$\frac{dMdm2}{dt}=k_6\cdot \frac{p{53}_{active}}{K_6+p{53}_{active}}-k{d}_6\cdot \frac{Mdm2}{K{d}_6+Mdm2}$$

$$\frac{dWip1}{dt}=k_7\cdot \frac{p{53}_{active}}{K_7+p{53}_{active}}-k{d}_7\cdot \frac{Wip1}{K{d}_7+Wip1}.$$

Using this p53 model, we perform the same simulations as the chemotaxis model. Positive feedback can be eliminated the by replacing TopBP1 with a (arbitrary) constant 0.5 in the equation of ATR (other choices of the constant gave the same results) and other parameters are shown in Table S4. We find that the positive feedback loop as the upstream noise attenuation module can increase the parameter region for dual function (Figures 4E, 4F and S4D), indicating that such PF-NFBLB network for p53 dynamic is able to perform robust dual function.

Discussion

A longstanding question in biology is how complex biological networks in the cell perform sophisticated regulatory functions with a remarkable degree of accuracy, reliability, and robustness. Do “universal” design principles underlie cellular systems? Rather than searching for naturally occurring circuits on a case-by-case basis, one strategy is to understand the design logic from the bottom-up to achieve single or multiple functions (Lim et al., 2013; Zhang and Tang, 2019).

Here we have investigated both three- and four-node networks to search for the design principle for the dual function of adaptation and noise attenuation. An intrinsic trade-off was found to exist in three-node networks between system sensitivity, which is required in adaptation, and noise attenuation. Although fine-tuning timescales in three-node adaptive networks can partially mediate such trade-off, it introduces prolonged adaptation time and additional parameter constraints. Our results show that the required adaptation time to reduce noise can be unrealistically long. For example, to achieve a noise reduction of NAR=0.1, the adaptation time has to be about 10,000 times longer than the autocorrelation time of the input noise (Figures S1G–S1I). A too slow adaptation time can be harmful for detecting rapid changes of signal (Andrews et al., 2006; Berg, 1988), leading to a further tradeoff between noise buffering capability and signal tracking ability.

In four-node networks, the dual function can be achieved robustly. The key challenge of maintaining system sensitivity while reducing noise can be met, via sequential combination of two sub-function modules. By evaluating effects of response times in noise attenuation and adaptation modules on the functional performance, we found that the combination of slow adaptation module and fast noise attenuation module can achieve better dual function. Our work highlights the importance of time scales in the relationship between topology and function. In some cases, timescale can be a key factor linking topology to function. For adaptation alone, the determining factor is topology (Ma et al., 2009). On the other hand, noise attenuation is closely related to timescale. Many works have shown how output noise depends on kinetic parameters such as degradation rate (Hornung and Barkai, 2008; Paulsson, 2004). Since different topologies can have distinct timescales, topology can therefore play a crucial role in noise resistance. For example, compared with NF, PF slows down the dynamics and therefore enhances noise buffering for a given steady susceptibility (Hornung and Barkai, 2008) or transient sensitivity (Figures 3D and 3E). Interlinked fast and slow positive feedback loops have a short activation time and a long deactivation time, resulting in the small fluctuation of the on state (Brandman et al., 2005). Our work of exploring the criterion to combine adaptation module and noise attenuation module follows the similar scenario: the topology determines the response time and therefore determines compatibility (Figure 3M). In N-A networks, NF has shorter response time, which is beneficial for high sensitivity after combination, so NF is more compatible than PF as an upstream module. In A-N networks, IFFLP, the one with longer response time, maintains a higher percentage of sensitive output and thus has better compatibility than NFBLB as an upstream module. Thus, together with previous works, our finding highlights the significance of timescale and its dependence on the network topology in reverse engineering.

In biological systems, ample examples of singling pathways adopt the topologies capable of the dual function of adaptation and noise attenuation. In two cases, Dictyostelium discoideum chemotaxis and p53 signaling network, we showed that these networks can effectively resist the noise while performing adaptation. Although many regulatory networks could be highlighted as in Figure 4 using sequentially connected modules, our explorations on many existing systems have suggested that in many adaptive systems a positive feedback loop or negative feedback loop is coupled with an adaptation module, creating an expanded dual-function module. In addition, the detail dynamics induced by such added positive/negative feedback is clearly related to noise attenuation in our analysis – an area not explored in previous studies that have focused only on adaptation. Interestingly, we found that in biological systems N-A networks appear more frequently than A-N networks. This is consistent with our finding that N-A architecture has higher compatibility for dual function. However, some adaptive systems such as chemotaxis network in Dictyostelium discoideum (Han et al., 2006; Kimmel and Parent, 2003; Park et al., 2004; Sasaki et al., 2004; Takeda et al., 2012) and EGFR signaling pathway in mammalian cells (Ferrell, 2016) adopt the A-N architecture. One possible reason is that placing adaptation module in the upstream may be advantageous if the same upstream signal activates several downstream pathways of different characters (Levchenko and Iglesias, 2002). Since noise attenuation module is generally non-adaptive, placing noise attenuation module in the upstream may also cause persistent activation of downstream signaling pathways. Thus, it is conceivable that A-N networks could be more suitable in certain circumstances.

In this work, the noise is assumed only from the input signal. Besides extrinsic noise due to the input fluctuation, the adaptation module also faces with intrinsic noise in the adaptation reaction (Colin et al., 2017; Sartori and Tu, 2011). Such noise exhibits different characteristics (e.g. frequency and amplitude), and may require different mechanisms to attenuate (Colin et al., 2017; Sartori and Tu, 2011; Shankar et al., 2015). Therefore, different design principles may emerge when considering mixed sources of noise.

Although this work was limited to enzymatic regulatory networks, our approach can be naturally extended to other types of regulations or forms of networks. For instance, the topologies for three-node adaptive networks with transcriptional regulation can still be grouped into the same two categories: NFBLB and IFFLP (Shi et al., 2017). Furthermore, other types of modules can also be used for network assembly. For adaptation, besides negative feedback and incoherent feedforward, mechanisms such as state-dependent inactivation and antithetical integral feedback could generate perfect adaptation (Briat et al., 2016; Ferrell, 2016; Friedlander and Brenner, 2009). For noise attenuation, linear cascades, time delay, and zero-order kinetics can also buffer noise (Hornung and Barkai, 2008). It would be interesting to systematically investigate the design principles for dual function made of other or mixed regulation types and functional modules, especially considering that the time scales of different regulations and modules can be very different.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Lei Zhang (zhangl@math.pku.edu.cn).

METHOD DETAILS

Mathematical model

Enzymatic regulatory networks

We use enzymatic regulatory networks and Michaelis-Menten rate equations to model both three-node and four-node networks (Ma et al., 2009). An enzymatic regulatory network with IFFLP topology is illustrated in Figure 1D as an example. Each node (representing an enzyme) is assumed to have active form and inactive form, with the total concentration as a constant (set to be 1). A positive regulation from node i to node j (denoted by i→j) implies that the inactive form of the enzyme j can be converted to its active form by active enzyme i. Similarly, a negative regulation from node i to node j (denoted by i—|j) implies that the active form of enzyme j can be converted to its inactive form by active enzyme i. If the node i has only positive (or negative) incoming regulations, a basal enzyme (F_i) with constant concentration (set to be 0.5) is assumed to deactivate (or activate) the node. Thus, a three-node enzymatic regulatory network can be modeled by following equations:

$$\frac{dA}{dt}=f_A=I{k}_{IA}(1-A)\frac{1-A}{1-A+K_{IA}}+\sum _i{X}_i{k}_{X_{i}A}\frac{1-A}{1-A+K_{X_{i}A}}-\sum _i{Y}_i{k}_{Y_{i}A}\frac{A}{A+K_{Y_{i}A}},$$

$$\frac{dB}{dt}=f_B=\sum _i{X}_i{k}_{X_{i}B}\frac{1-B}{1-B+K_{X_{i}B}}-\sum _i{Y}_i{k}_{Y_{i}B}\frac{B}{B+K_{Y_{i}B}},$$

$$\frac{dC}{dt}=f_C=\sum _i{X}_i{k}_{X_{i}C}\frac{1-C}{1-C+K_{X_{i}C}}-\sum _i{Y}_i{k}_{Y_{i}C}\frac{C}{C+K_{Y_{i}C}},$$

where I is the input intensity, and A, B and C are concentrations of the three enzymes in active form, respectively. Since the total concentration of each enzyme is set to be 1, 1 − A, 1 − B and 1 − C represents concentrations of the three enzymes in inactive form, respectively. X_i in each equation represents the activating enzymes of the node while Y_i the deactivating enzymes. Each term in above equations takes the form of Michaelis-Menten equation where capitalized K denotes Michaelis-Menten constant and lowercase k denotes the catalytic rate constant. For a four-node network there is an additional equation for node D:

$$\frac{dD}{dt}=f_D=\sum _i{X}_i{k}_{X_{i}D}\frac{1-D}{1-D+K_{X_{i}D}}-\sum _i{Y}_i{k}_{Y_{i}D}\frac{D}{C+K_{Y_{i}D}}.$$

Unless otherwise specified, all our simulations are based on enzymatic regulatory networks.

Transcriptional regulatory networks

The transcriptional regulatory network depicts interactions among genes’ products where each gene product can regulate the transcriptional activity of other genes as the transcription factor (TF). In a transcriptional network topology, nodes and links represent gene products and transcriptional regulations respectively. In our model, transcriptional regulations are assumed to only affect the gene activation and have no effect on the degradation of gene products. If multiple TFs regulate the same gene, AND logic (i.e., the gene expression is active if all activators are at high concentrations and all repressors at low concentrations) is applied. By modeling the regulated production rate with Hill function and the degradation rate with linear function, the three-node transcriptional regulatory network with AND logic can be modeled by following equations:

$$\frac{dA}{dt}=f_A=v_A\frac{I^{n_{IA}}}{I^{n_{IA}}+K_{IA}^{n_{IA}}}\prod _i\frac{X_i^{n_{X_{i}A}}}{X_i^{n_{X_{i}A}}+K_{X_{i}A}^{n_{X_{i}A}}}\prod _j\frac{K_{Y_{i}A}^{n_{Y_{i}A}}}{Y_i^{n_{Y_i}A}+K_{Y_{i}A}^{n_{Y_i}A}}-\frac{A}{{\tau }_A},$$

$$\frac{dB}{dt}=f_B=v_B\prod _i\frac{X_i^{n_{X_{i}B}}}{X_i^{n_{X_{i}B}}+K_{X_{i}B}^{n_{X_{i}B}}}\prod _j\frac{K_{Y_{i}B}^{n_{Y_{i}B}}}{Y_i^{n{Y}_{i}B}+K_{Y_{i}B}^{n_{Y_{i}B}}}-\frac{B}{{\tau }_B},$$

$$\frac{dC}{dt}=f_C=v_C\prod _i\frac{X_i^{n_{X_{i}C}}}{X_i^{n_{X_i}C}+K_{X_{i}C}^{n_{X_{i}C}}}\prod _j\frac{K_{Y_{i}C}^{n_{Y_{i}C}}}{Y_i^{n_{Y_{i}C}}+K_{Y_{i}C}^{n_{Y_{i}C}}}-\frac{C}{{\tau }_C},$$

where I is the input intensity, and A, B and C are concentrations of the three gene products respectively. Each gene product has a degradation rate constant ${\tau }_i^{-1}$ and a maximal production rate ν_i (i = A, B, C). X_i in each equation represents the activator of the node while Y_i the repressor. The Hill function representing positive regulation (e.g. $\frac{X_i^{n_{X_{i}A}}}{X_i^{n_{X_{i}A}}+K_{X_{i}A}^{n_{X_{i}A}}}$) has two parameters K and n, which denote the activation coefficient and Hill coefficient, respectively. Likewise, the Hill function representing negative regulation (e.g. $\frac{K_{Y_{i}A}^{n_{Y_{i}A}}}{Y_i^{n_{Y_{i}A}}+K_{Y_{i}A}^{n_{Y_{i}A}}}$) also has parameters K and n, except that K is termed as the repression coefficient. When calculating Q values for 16,038 three-node transcriptional regulatory networks, above equations are normalized by setting $v_i={\tau }_i^{-1}$ for parameter reduction.

Calculation of sensitivity, precision and NAR

In our simulations, we set I₁ = 0.4 and I₂ = 0.45. When calculating Q values for enzymatic regulatory networks, the Latin hypercube method is used to sample the catalytic rate constants k’s and Michaelis-Menten constants K’s, which are from log-uniform distributions with the parameter ranges [0.1,10] and [0.001,1000], respectively. For transcriptional regulatory networks, the degradation rate constants ${\tau }_i^{-1}$‘s and the activation (or repression) coefficients K’s are sampled from log-uniform distributions with ranges [0.1,10] and [0.001,1000], respectively; the Hill coefficient n is sampled based on uniform distribution from 1 to 4.

By performing ODE simulation, the deterministic dynamics for a given circuit is obtained and thus the sensitivity and the precision are calculated directly according to their definitions. We use linear noise approximation (LNA) (Elf and Ehrenberg, 2003; Paulsson, 2004) to calculate NAR. By assuming the noise is only from the input signal I and autocorrelation function of fluctuations exponentially decays with timescale τ₀ = 1/ω (ω is set to 0.5 unless otherwise specified), Ornstein-Uhlenbeck process is applied to approximate the dynamics of I:

$$\frac{dI}{dt}=-\frac{I-I_{ss}}{{\tau }_0}+\sqrt{\frac{2{\eta }_0^2}{{\tau }_0}}{\xi }_t$$

where ξ_t = is the white noise satisfying 〈ξ_t〉 = 0 and 〈ξ_tξ_s〉 = δ (t − s), and ${\eta }_0^2$ is the variance of I as t → ∞. We set I_ss = I₁ and I₂ to calculate the NAR when system is at the steady state under I₁ and I₂ respectively. For saving calculation costs, we linearize the model to obtain an approximate NAR instead of a long-time simulation. According to LNA, we can solve the following equation to get NAR:

$$M\eta +\eta M^T+D=0.$$

In three-node networks, the matrix M, η, D are

$$M=\left[\begin{array}{cccc}-\frac{1}{{\tau }_0}& 0& 0& 0\\ \frac{\partial f_A}{\partial I}& \frac{\partial f_A}{\partial A}& \frac{\partial f_A}{\partial B}& \frac{\partial f_A}{\partial c}\\ \frac{\partial f_B}{\partial I}& \frac{\partial f_B}{\partial A}& \frac{\partial f_B}{\partial B}& \frac{\partial f_B}{\partial C}\\ \frac{\partial f_C}{\partial I}& \frac{\partial f_C}{\partial A}& \frac{\partial f_B}{\partial B}& \frac{\partial f_C}{\partial C}\end{array}\right],\eta =\left[\begin{array}{cccc}{\eta }_0^2& cov(I,A)& cov(I,B)& cov(I,C)\\ cov(I,A)& {\eta }_A^2& cov(A,B)& cov(A,C)\\ cov(I,B)& cov(A,B)& {\eta }_B^2& cov(B,C)\\ cov(I,C)& cov(A,C)& cov(B,C)& {\eta }_C^2\end{array}\right],D=\left[\begin{array}{cccc}\frac{2{\eta }_0^2}{{\tau }_0}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right].$$

Then NAR is just $\sqrt{\frac{{\eta }_C^2/{\langle C\rangle }^2}{{\eta }_0^2/I_{SS}^2}}$ (〈·〉) denotes the steady-state value of the node). In practice, we transformed M_ij to $M_{ij}\frac{x_j}{x_i}$, η_ij to $\frac{{\eta }_{ij}}{x_i{x}_j}$, D_ij to $\frac{D_{ij}}{x_i{x}_j}$, where x₁ = I_ss, x₂ = 〈A〉, x₃ = 〈B〉, x₄ = 〈C〉 so that we can get the square of NAR directly by dividing the last element in new η by the first element. These matrices are evaluated in steady state. As there are two different levels of input signal (i.e., I₁ and I₂), we have two steady states and thus two values of NAR. When calculating Q values, the larger value of NAR is used. The method above can easily expand to four-node network. In fact, the NAR obtained by LNA can well approximate that obtained by a long-time simulation of stochastic differential equation (Figure S2G).

Analytical derivation of NAR and sensitivity

IFFLP with general form of regulations

To simplify the derivation, we assume that the dynamics of node A is the same as the input I. Then equations of IFFLP can be written as

$$\{\begin{array}{l}{\tau }_B\frac{dB}{dt}=f_B(A,B)\hfill \\ {\tau }_C\frac{dC}{dt}=f_C(A,B,C)\hfill \end{array}.$$

First we use LNA to derive NAR for the above system. We assume the fluctuation of A is an Ornstein-Uhlenbeck process with time scale τ₀ = 1/ω and variance ${\eta }_0^2$. Then we can calculate

$$M=\left(M_{ij}\right)=\left(\begin{array}{ccc}-\omega & 0& 0\\ k_1/{\tau }_B& -k_2/{\tau }_B& 0\\ k_4/{\tau }_C& -k_5/{\tau }_C& -k_6/{\tau }_C\end{array}\right)$$

and

$$D=\left(\begin{array}{ccc}2{\eta }_0^2\omega & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),$$

where $k_1=\frac{\langle A\rangle }{\langle B\rangle }\frac{\partial f_B}{\partial A}$, $k_2=-\frac{\partial f_B}{\partial B}$, $k_4=\frac{\langle A\rangle }{\langle C\rangle }\frac{\partial f_C}{\partial A}$, $k_5=-\frac{\langle B\rangle }{\langle C\rangle }\frac{\partial f_C}{\partial B}$, $k_6=-\frac{\partial f_C}{\partial C}$. All k_i (i = 1,2,4,5,6) are positive according to the sign of regulations in IFFLP. ⟨A⟩, ⟨B⟩, ⟨C⟩ denote steady states of A, B, C respectively. By solving the equation with respect to η

$$M\eta +\eta M^T+D=0,$$

we get the expression of NAR:

$$\text{NAR}=\sqrt{\frac{{\eta }_C^2}{{\eta }_A^2}}=\sqrt{\frac{{\left(k_1{k}_5-k_2{k}_4\right)}^2\left(k_2{\tau }_C+k_6{\tau }_B+{\tau }_B{\tau }_C\omega \right)+k_2{k}_6{k}_4^2{\tau }_B^2\omega }{k_2{k}_6\left(k_2{\tau }_C+k_6{\tau }_B\right)\left(k_2+\omega {\tau }_B\right)\left(k_6+\omega {\tau }_C\right)}}=\sqrt{\frac{{\left(k_1{k}_5-k_2{k}_4\right)}^2\left(k_2\left(\frac{{\tau }_B}{{\tau }_C}\right)\frac{1}{{\tau }_B}+k_6{\left(\frac{{\tau }_E}{{\tau }_C}\right)}^2\frac{1}{{\tau }_B}+\left(\frac{{\tau }_B}{{\tau }_C}\right)\omega \right)+k_2{k}_6{k}_4^2{\left(\frac{{\tau }_B}{{\tau }_C}\right)}^2\omega }{k_2{k}_6\left(k_2+k_6\left(\frac{{\tau }_B}{{\tau }_C}\right)\right)\left(k_2/{\tau }_B+\omega \right)\left(k_6\frac{{\tau }_B}{{\tau }_C}\right)+\omega {\tau }_B)}}.$$

From the expression of NAR, we can easily find that NAR is a decreasing function of τ_C (or τ_B) if ${\tau }_B{\tau }_C\ge \frac{k_2{k}_6}{{\omega }^2}$ when the ratio of τ_C to τ_C is fixed as a constant.

Then we approximate sensitivity by linearizing the system around steady state ⟨A⟩, ⟨B⟩, ⟨C⟩:

$$\left[\begin{array}{c}\frac{d\mathrm{\Delta }B}{dt}\\ \frac{d\mathrm{\Delta }C}{dt}\end{array}\right]=\left[\begin{array}{cc}\frac{-k_2}{{\tau }_B}& 0\\ -\frac{k_5\langle C\rangle }{{\tau }_C\langle B\rangle }& \frac{-k_6}{{\tau }_C}\end{array}\right]\left[\begin{array}{l}\mathrm{\Delta }B\hfill \\ \mathrm{\Delta }C\hfill \end{array}\right]+\mathrm{\Delta }A\left[\begin{array}{l}\frac{k_1(B\rangle }{{\tau }_B\langle A\rangle }\hfill \\ \frac{k_4\langle C\rangle }{{\tau }_C\langle A\rangle }\hfill \end{array}\right]$$

where ⟨A⟩, ⟨B⟩, ⟨C⟩ denote the steady states of A, B, C. The condition of perfect adaptation is assumed, that is, k₁k₅ – k₂k₄ = 0. By solving above equations, we get the expression of ΔC(t):

$$\mathrm{\Delta }C(t)=\frac{k_4\langle C\rangle }{{\tau }_C\langle A\rangle }\mathrm{\Delta }A\frac{e^{{\lambda }_{2}t}-e^{{\lambda }_{1}t}}{{\lambda }_2-{\lambda }_1}$$

where ${\lambda }_1=-\frac{k_2}{{\tau }_B}$, ${\lambda }_2=-\frac{k_6}{{\tau }_C}$. Let ΔC′(t) = 0, and we obtain the peak time of ΔC:

$$t_{peak}=\frac{\text{ln}\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}{{\lambda }_1-{\lambda }_2}=\frac{{\tau }_C\text{ln}\left(\frac{k_6{\tau }_B}{k_2{\tau }_C}\right)}{\left(k_6-k_2\frac{{\tau }_C}{{\tau }_B}\right)}.$$

Then the highest (or lowest) value of ΔC is:

$$\mathrm{\Delta }C\left(t_{peak}\right)=\mathrm{\Delta }A\frac{k_4\langle C\rangle }{{\tau }_C\langle A\rangle }\frac{1}{-{\lambda }_1}{\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^{\frac{{\lambda }_2}{{\lambda }_1-{\lambda }_2}}=\frac{k_4\langle C\rangle }{k_2\langle A\rangle }\frac{{\tau }_B}{{\tau }_C}{\left(\frac{k_6{\tau }_B}{k_2{\tau }_C}\right)}^{\frac{1}{\frac{k_2{\tau }_C}{k_6{\tau }_B}-1}}\mathrm{\Delta }A.$$

The sensitivity is derived naturally:

$$\text{Sensitivity}=\left|\frac{\mathrm{\Delta }C\left(t_{peak}\right)/\langle C\rangle }{\mathrm{\Delta }A/\langle A\rangle }\right|=\frac{k_4}{k_6}\frac{k_6{\tau }_B}{k_2{\tau }_C}{\left(\frac{k_6{\tau }_B}{k_2{\tau }_C}\right)}^{\frac{1}{\frac{k_2{\tau }_C}{k_6{\tau }_B}-1}}=\frac{k_4}{k_6}{\left(\frac{k_2{\tau }_C}{k_6{\tau }_B}\right)}^{\frac{\frac{k_2{\tau }_C}{k_2{\tau }_B}}{1-\frac{k_2{\tau }_C}{k_6{\tau }_B}}}$$

From the expression of sensitivity, it can be seen that sensitivity is a constant when $\frac{{\tau }_C}{{\tau }_B}$ is fixed. Furthermore, smaller ratio of τ_C to τ_B causes larger sensitivity because of decreasing function $\frac{x}{X^{1-x}}$.

Next, we show the special case in enzymatic regulatory IFFLP. If conditions of perfect adaptation are assumed, that is, (1 −B) ≫ K_AB and $B\ll K_{F_{B}B}$, equations of enzymatic regulatory IFFLP can be written as

$$\{\begin{array}{l}{\tau }_B\frac{dB}{dt}=A{k}_{AB}-F_B\frac{k_{F_{B}B}}{K_{F_{B}B}}B\hfill \\ {\tau }_C\frac{dC}{dt}=A{k}_{AC}\frac{1-C}{1-C+K_{AC}}-B{k}_{BC}\frac{C}{C+K_{BC}}\hfill \end{array}.$$

Then we have $k_1=k_2=k_{F_{B}B}{F}_B/k_{F_{B}B}$, $k_4=k_5=\frac{k_{AC}\langle A\rangle (1-\langle C\rangle )}{\left(1-\langle C\rangle +K_{AC}\right)\langle C\rangle }=\frac{k_{BC}\langle B\rangle }{\langle C\rangle +K_{BC}}$, $k_6=\left[\frac{K_{AC}\langle C\rangle }{\left(1-\langle C\rangle +K_{AC}\right)(1-\langle C\rangle )}+\frac{K_{BC}}{\langle C\rangle +K_{BC}}\right]k_4$. The expressions of NAR and sensitivity can thus be obtained directly:

$$\text{NAR}=\sqrt{\frac{k_4^2{\tau }_B^2\omega }{\left(k_1{\tau }_C+k_6{\tau }_B\right)\left(k_1+\omega {\tau }_B\right)\left(k_6+\omega {\tau }_C\right)}}=\frac{k_4^2{\left(\frac{{\tau }_B}{{\tau }_C}\right)}^2\omega }{\left[k_1+k_6\left(\frac{{\tau }_B}{{\tau }_C}\right)\right]\left[k_6\left(\frac{{\tau }_B}{{\tau }_C}\right)+\omega {\tau }_B\right]\left(k_1/{\tau }_B+\omega \right)},$$

and

$$\text{Sensitivity }=\left|\frac{\mathrm{\Delta }C\left(t_{\text{peak}}\right)/\langle C\rangle }{\mathrm{\Delta }A/\langle A\rangle }\right|=\frac{k_4}{k_6}{\left(\frac{k_1{\tau }_C}{k_6{\tau }_B}\right)}^{\frac{\frac{k_1{\tau }_C}{k_6{\tau }_B}}{1-\frac{k_1{\tau }_C}{k_6{\tau }_B}}}.$$

When $\frac{{\tau }_C}{{\tau }_B}$ is fixed, we can see that sensitivity is a constant and NAR is a decreasing function of τ_B (or τ_C) if ${\tau }_B{\tau }_C\ge \frac{k_1{k}_6}{{\omega }^2}$.

NFBLB with general form of regulations

To simplify the derivation, we assume that the dynamics of node A is the same as the input I. Then equations of NFBLB are

$$\{\begin{array}{l}{\tau }_B\frac{dB}{dt}=f_B(B,C)\hfill \\ {\tau }_C\frac{dC}{dt}=f_C(A,B,C)\hfill \end{array}$$

First we use LNA to derive NAR for the above system. We assume the fluctuation of A is an Ornstein-Uhlenbeck process with time scale τ₀ = 1/ω and variance ${\eta }_0^2$. Then we can calculate

$$M=\left(M_{ij}\right)=\left(\begin{array}{ccc}-\omega & 0& 0\\ 0& -k_1/{\tau }_B& k_2/{\tau }_B\\ k_3/{\tau }_C& -k_4/{\tau }_C& -k_5/{\tau }_C\end{array}\right)$$

and

$$D=\left(\begin{array}{ccc}2{\eta }_0^2\omega & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),$$

where $k_1=-\frac{\partial f_B}{\partial B}$, $k_2=\frac{\langle C\rangle }{\langle B\rangle }\frac{\partial f_B}{\partial C}$, $k_3=\frac{\langle A\rangle }{\langle C\rangle }\frac{\partial f_C}{\partial A}$, $k_4=-\frac{\langle B\rangle }{\langle C\rangle }\frac{\partial f_C}{\partial B}$, $k_5=-\frac{\partial f_C}{\partial C}$. All k_i (i = 1,2,3,4,5) are positive according to the sign of regulations in NFBLB. ⟨A⟩, ⟨B⟩, ⟨C⟩ denote steady states of A, B, C respectively. By solving the equation with respect to η.

$$M\eta +\eta M^T+D=0,$$

we get the expression of NAR:

$$\text{NAR}=\sqrt{\frac{{\eta }_C^2}{{\eta }_A^2}}=\sqrt{\frac{k_3^2\left[k_1^2\left(k_1{\tau }_C+k_5{\tau }_B+{\tau }_B{\tau }_C\omega \right)+\left(k_1{k}_5+k_2{k}_4\right){\tau }_B^2\omega \right]}{\left(k_2{k}_4+k_1{k}_5\right)\left(k_5{\tau }_B+k_1{\tau }_C\right)\left({\tau }_B{\tau }_C{\omega }^2+k_5{\tau }_B\omega +k_1{\tau }_C\omega +k_2{k}_4+k_1{k}_5\right)}}=\sqrt{\frac{k_3^2\left[k_1^2\left(k_1\frac{1}{{\tau }_C}{\left(\frac{{\tau }_C}{{\tau }_B}\right)}^2+k_5\frac{1}{{\tau }_C}\left(\frac{{\tau }_C}{{\tau }_B}\right)+\left(\frac{{\tau }_C}{{\tau }_B}\right)\omega \right)+\left(k_1{k}_5+k_2{k}_4\right)\omega \right]}{\left(k_2{k}_4+k_1{k}_5\right)\left[k_5+k_1\left(\frac{{\tau }_C}{{\tau }_B}\right)\right]\left[{\tau }_C{\omega }^2+k_5\omega +k_1\left(\frac{{\tau }_C}{{\tau }_B}\right)\omega +\frac{1}{{\tau }_C}\left(\frac{{\tau }_C}{{\tau }_B}\right)\left(k_2{k}_4+k_1{k}_5\right)\right]}}.$$

From the expression of NAR, we can easily find that NAR is a decreasing function of τ_C (or τ_B) if ${\tau }_B{\tau }_C>\frac{k_1{k}_5+k_2{k}_4}{w^2}$ when the ratio of τ_B to τ_C is fixed as a constant.

Then we approximate sensitivity by linearizing the system around steady state (⟨A⟩, ⟨B⟩, ⟨C⟩):

$$\left[\begin{array}{c}\frac{d\mathrm{\Delta }B}{dt}\\ \frac{d\mathrm{\Delta }C}{dt}\end{array}\right]=\left[\begin{array}{cc}-\frac{k_1}{{\tau }_B}& \frac{k_2\langle B\rangle }{{\tau }_B\langle R\rangle }\\ -\frac{k_4\langle C\rangle }{{\tau }_C\langle B\rangle }& -\frac{k_5}{{\tau }_C}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }B\\ \mathrm{\Delta }C\end{array}\right]+\mathrm{\Delta }A\left[\frac{k_3\langle C\rangle }{{\tau }_C\langle A\rangle }\right]$$

where (⟨A⟩, ⟨B⟩, ⟨C⟩ denote the steady states of A, B, C. The condition of perfect adaptation is assumed, that is, k₁ = 0. By solving above equations, we get the expression of ΔC(t):

$$\mathrm{\Delta }C(t)=\frac{k_3\langle C\rangle }{{\tau }_C\langle A\rangle }\mathrm{\Delta }A\frac{e^{{\lambda }_{2}t}-e^{{\lambda }_{1}t}}{{\lambda }_2-{\lambda }_1}$$

where ${\lambda }_1=\frac{-\frac{k_5}{{\tau }_C}+\sqrt{{\left(\frac{k_5}{{\tau }_C}\right)}^2-4\frac{k_4{k}_2}{{\tau }_B{\tau }_C}}}{2}$, ${\lambda }_2=\frac{-\frac{k_5}{{\tau }_C}\sqrt{{\left(\frac{k_5}{{\tau }_C}\right)}^2-4\frac{k_4{k}_2}{{\tau }_B{\tau }_C}}}{2}$. Let ΔC′(t) = 0, and we obtain the peak time of ΔC:

$$t_{peak}=\frac{\text{ln}\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}{{\lambda }_1-{\lambda }_2}=\frac{\text{ln}\left(\frac{-\frac{k_5}{{\tau }_C}\sqrt{{\left(\frac{k_5}{{\tau }_C}\right)}^2-4\frac{k_4{k}_2}{{\tau }_B{\tau }_C}}}{--\frac{k_5}{{\tau }_C}+\sqrt{{\left(\frac{k_5}{{\tau }_C}\right)}^2-4\frac{k_4{k}_2}{{\tau }_B{\tau }_C}}}\right)}{\sqrt{{\left(\frac{k_5}{{\tau }_C}\right)}^2-4\frac{k_4{k}_2}{{\tau }_B{\tau }_C}}}.$$

Then the highest (or lowest) value of ΔC is:

$$\mathrm{\Delta }C\left(t_{peak}\right)=\mathrm{\Delta }A\frac{k_3\langle C\rangle }{{\tau }_C\langle A\rangle }\frac{1}{-{\lambda }_1}{\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^{\frac{{\lambda }_2}{{\lambda }_1-{\lambda }_2}}.$$

The sensitivity is derived naturally:

$$\text{Sensitivity }=\left|\frac{\mathrm{\Delta }C\left(t_{peak}\right)/\langle C\rangle }{\mathrm{\Delta }A/\langle A\rangle }\right|=\frac{k_3}{{\tau }_C}\frac{1}{-{\lambda }_1}{\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^{\frac{{\lambda }_2}{{\lambda }_1-{\lambda }_2}}.$$

The expression of sensitivity and t_peak also holds for complex eigenvalues. However, the monotonicity with $\frac{{\tau }_C}{{\tau }_B}$ τ_C is easy to analysis when eigenvalues are both negative real number. So only the situation with negative real eigenvalues is considered.

Let $x=\sqrt{{\left(k_5\right)}^2-4\frac{k_2{k}_4{\tau }_C}{{\tau }_B}}$, ${\lambda }_1=\frac{-k_5+x}{2{\tau }_C}$, ${\lambda }_2=\frac{-k_5-x}{2{\tau }_C}$, then

$$\text{Sensitivity }=\frac{\frac{\mathrm{\Delta }C\left(t_{peak}\right)}{\langle C\rangle }}{\frac{\mathrm{\Delta }A}{\langle A\rangle }}=\frac{k_3}{{\tau }_C}\frac{1}{-{\lambda }_1}{\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^{\frac{{\lambda }_2}{{\lambda }_1-{\lambda }_2}}\propto \frac{1}{k_5-x}{\left(\frac{k_5+x}{k_5-x}\right)}^{\frac{k_5+x}{-2x}}\propto \frac{1}{1-x/k_5}{\left(\frac{1+x/k_5}{1-x/k_5}\right)}^{\frac{1+x/k_5}{-2x/k_5}}.$$

Use x to denote x/k₅, and let $f\left(x\right)=\frac{1}{1-x}{\left(\frac{1+x}{1-x}\right)}^{\frac{1+x}{-2x}}$, x ∈ (0,1). According to the monotonicity of f(x), sensitivity is an increasing function with x, and thus a decreasing function with $\frac{{\tau }_C}{{\tau }_B}$.

Fine-tuning timescales in three-node networks

For a three-node network capable of perfect adaptation, we aim to maintain sensitivity and lower NAR by tuning τ_B and τ_C. Here, S denotes sensitivity and N denotes NAR. Maintaining sensitivity means

$$\frac{\partial \text{S}}{\partial {\tau }_B}\mathrm{\Delta }{\tau }_B+\frac{\partial \text{S}}{\partial {\tau }_C}\mathrm{\Delta }{\tau }_C=0$$

by neglecting the high-order terms. Similarly, lowering NAR means

$$\frac{\partial N}{\partial {\tau }_B}\mathrm{\Delta }{\tau }_B+\frac{\partial N}{\partial {\tau }_C}\mathrm{\Delta }{\tau }_C<0$$

by neglecting the high-order terms. Taking the first equality and the second inequality together, we have

$$\left(\frac{\partial N}{\partial {\tau }_C}-\frac{\partial N}{\partial {\tau }_B}\frac{\frac{\partial \text{S}}{\partial {\tau }_C}}{\frac{\partial \text{S}}{\partial {\tau }_B}}\right)\mathrm{\Delta }{\tau }_C<0.$$

For instance, if $\left(\frac{\partial N}{\partial {\tau }_C}-\frac{\partial N}{\partial {\tau }_B}\frac{\frac{\partial \text{S}}{\partial {\tau }_C}}{\frac{\partial \text{S}}{\partial {\tau }_B}}\right)>0$, we can reduce τ_C, i.e., Δτ_C < 0, and set $\mathrm{\Delta }{\tau }_B=-\frac{\frac{\partial \text{S}}{\partial {\tau }_C}}{\frac{\partial \text{S}}{\partial {\tau }_B}}\mathrm{\Delta }{\tau }_C$ in order to lower NAR while maintaining sensitivity. It is similar to the case of $\left(\frac{\partial N}{\partial {\tau }_C}-\frac{\partial N}{\partial {\tau }_B}\frac{\frac{\partial \text{S}}{\partial {\tau }_C}}{\frac{\partial \text{S}}{\partial {\tau }_B}}\right)<0$.

Module combination in four-node networks

We take PF-IFFLP as an example to show how to construct equations and parameters of the assembled four-node network. Before module combination, we assume that equations of PF are

$$\begin{gathered} \frac{dA}{dt}=I{k}_{IA}^{up}(1-A)\frac{1-A}{1-A+K_{IA}^{up}}+B{k}_{BA}^{up}\frac{1-A}{1-A+K_{BA}^{up}}-F_A{k}_{FAA}^{up}\frac{A}{A+K_{F_{A}A}^{up}}, \\ \frac{dB}{dt}=A{k}_{AB}^{up}\frac{1-B}{1-B+K_{AB}^{up}}-F_B{k}_{FB}^{up}\frac{B}{B+K_{FB}^{up}}, \end{gathered}$$

and those of IFFLP

$$\begin{gathered} \frac{dC}{dt}=I{k}_{IC}^{dw}\frac{1-C}{1-C+K_{IC}^{dw}}-D{k}_{DC}^{dw}\frac{C}{C+K_{DC}^{dw}}, \\ \frac{dD}{dt}=I{k}_{ID}^{dw}\frac{1-D}{1-D+K_{ID}^{dw}}-F_D{k}_{FD}^{dw}\frac{D}{D+K_{FD}^{dw}}. \end{gathered}$$

However, in PF-IFFLP, node C and node D receive the regulation from node B rather than the input I. So, to obtain equations of PF-IFFLP, we need replace variable I with variable B in equations of node C and node D while keeping other equations unchanged, i.e.,

$$\begin{gathered} \frac{dA}{dt}=I{k}_{IA}^{up}(1-A)\frac{1-A}{1-A+K_{IA}^{up}}+B{k}_{BA}^{up}\frac{1-A}{1-A+K_{BA}^{up}}-F_A{k}_{F_{A}A}^{up}\frac{A}{A+K_{FA}^{up}}, \\ \frac{dB}{dt}=A{k}_{AB}^{up}\frac{1-B}{1-B+K_{AB}^{up}}-F_B{k}_{F_{B}B}^{up}\frac{B}{B+K_{F_{B}B}^{up}}, \\ \frac{dC}{dt}=B{k}_{IC}^{dw}\frac{1-C}{1-C+K_{IC}^{dw}}-D{k}_{DC}^{dw}\frac{C}{C+K_{DC}^{dw}}, \\ \frac{dD}{dt}=B{k}_{ID}^{dw}\frac{1-D}{1-D+K_{ID}^{dw}}-F_D{k}_{F_{D}D}^{dw}\frac{D}{D+K_{F_{D}D}^{dw}}. \end{gathered}$$

Equations and parameters for other assembled four-node networks can be obtained in a similar way.

Evolution algorithm

The evolution algorithm (François and Hakim, 2004) begins with an initial circuit collection including different networks with random parameters. Then the circuit collection evolves towards dual function with many rounds of growth and selection. In the growth phase, the circuit collection is doubled by adding a mutated copy of each circuit in the collection. The mutation of each circuit is carried out as following: (1) randomly select one parameter based on the equal probability principle; (2) modify the chosen parameter by multiplying a random number uniformly distributed between 0 and 2. In the selection phase, high-performance circuits are selected to form a new circuit collection with the original size. The performance of dual function is measured using a score function, which reaches maximum score when the circuit performs dual function (i.e., sensitivity>1, precision>10, NAR<0.2). Here, the size of the initial circuit collection is set to be 1000, so each network in the subset will have about 27~28 (1000÷36≈ 27.8) different parameter sets in average. The score function we use is defined as the product of three factors, each of which ranges from 0 to 1. The first factor is defined by the minimum between the value of sensitivity and 1. The second factor is the minimum between precision/10 and 1. The third factor is the minimum between 0.2/NAR and 1. These three factors reflect how close the circuit’s sensitivity, precision and NAR approach to corresponding thresholds. The evolution process is terminated if the circuit with score=1 (i.e., capable of dual function) occurs or the maximum number of iterations (set to be 300) is reached.

DATA AND CODE AVAILABILITY STATMENT

This paper presents no new data or code to make available.

Highlights.

• An intrinsic trade-off exists in three-node networks

• Tuning timescales can partially mediate this trade-off with a cost

• Sequential assembly in four-node networks can effectively decouple two functions

• Biological adaptive networks are often associated with a noise attenuation module