Abstract
Characterising quantum processes is a key task in the development of quantum technologies, especially at the noisy intermediate scale of today’s devices. One method for characterising processes is randomised benchmarking, which is robust against state preparation and measurement (SPAM) errors, and can be used to benchmark Clifford gates. A complementing approach asks for full tomographic knowledge. Compressed sensing techniques achieve full tomography of quantum channels essentially at optimal resource efficiency. So far, guarantees for compressed sensing protocols rely on unstructured random measurements and can not be applied to the data acquired from randomised benchmarking experiments. It has been an open question whether or not the favourable features of both worlds can be combined. In this work, we give a positive answer to this question. For the important case of characterising multi-qubit unitary gates, we provide a rigorously guaranteed and practical reconstruction method that works with an essentially optimal number of average gate fidelities measured respect to random Clifford unitaries. Moreover, for general unital quantum channels we provide an explicit expansion into a unitary 2-design, allowing for a practical and guaranteed reconstruction also in that case. As a side result, we obtain a new statistical interpretation of the unitarity – a figure of merit that characterises the coherence of a process. In our proofs we exploit recent representation theoretic insights on the Clifford group, develop a version of Collins’ calculus with Weingarten functions for integration over the Clifford group, and combine this with proof techniques from compressed sensing.
I. INTRODUCTION
As increasingly large and complex quantum devices are being built and the development of fault tolerant quantum computation is moving forward, it is critical to develop tools to refine our control of these devices. For this purpose, several improved methods for characterizing quantum processes have been developed in recent years.
These improvements can be grouped into two broad categories. The first category includes techniques such as randomised benchmarking (RB) [1–7] and gate set tomography (GST) [8], which are more robust to state preparation and measurement (SPAM) errors. These techniques work by performing long sequences of random quantum operations, measuring their outcomes, and checking whether the resulting statistics are consistent with some physically-plausible model of the system. In this way, one can characterise a quantum gate in terms of other quantum gates, in a way that is insensitive to SPAM errors.
The second category [9–13] provides more detailed tomographic information. It includes techniques such as compressed sensing [14–20], matrix product state tomography [21, 22], and learning of local Hamiltonians and tensor network states [23, 24]. These methods exploit the sparse, low-rank or low entanglement structure that is present in many of the physical states and processes that occur in nature. These techniques are less resource-intensive than conventional tomography, and therefore can be applied to larger numbers of qubits. Convex optimization techniques, such as semidefinite programming, are then used to reconstruct the underlying quantum state or process.
A recent line of work [25, 26] has attempted to unify these two approaches to a quantum process tomography scheme, that is both robust to SPAM errors, and can handle large numbers of qubits (provided the quantum process has some suitable structure). To achieve this goal, it turns out that the proper design of the measurements is crucial. SPAM-robust methods such as randomised benchmarking are known to require some kind of computationally-tractable group structure, such as that found in the Clifford group. Clifford gates are motivated by their abundant appearance in many practical applications, such as fault-tolerant quantum computing [3, 27].
In contrast, compressed sensing methods typically require measurements with less structure in this context, in that their 4th-order moments are close to those of the uniform Haar measure. Thus, the key technical question is whether the seemingly conflicting requirements of sufficient randomness and desired structure in the measurements can be combined.
In this work, we show that the answer is indeed yes. In layman’s terms, we demonstrate that Clifford-group based measurements are also sufficiently unstructured that they can be used for compressed sensing. Thus, we develop methods for quantum process tomography that are resource efficient, robust with respect to SPAM and other errors, and use measurements that are already routinely acquired in many experiments.
In more detail, we provide procedures for the reconstruction from so-called average gate fidelities (AGFs), which are the quantities that are measured in randomised benchmarking. It was established that the unital part of general quantum channels can be reconstructed from AGFs relative to a maximal linearly independent subset of Clifford group operations [25]. We generalise this result by noting that the Clifford group can be replaced by an arbitrary unitary 2-design and also explicitly provide an analytic form of the reconstruction.
Our main result is a practical reconstruction procedure for quantum channels that are close to being unitary. Let d be the Hilbert space dimension, so that a unitary quantum channel can be described by roughly d2 scalar parameters. The protocol is rigorously guaranteed to succeed using essentially order of d2 AGFs with respect to randomly drawn Clifford gates, and we also prove it to be stable against errors in the AGF estimates. In this way we generalise a previous recovery guarantee [26] from AGFs with 4-designs to ones with the more relevant Clifford gates.
Conversely, we prove that the sample complexity of our reconstruction procedure is optimal in a simplified measurement setting. Here, we assume that independent copies of the channel’s Choi state are measured and use direct fidelity estimation [23, 28] and information theoretic arguments [9] to show that the dimensional scaling of our reconstruction error is optimal up to log-factors. As a side result, we also find a new interpretation of the unitarity [4] – a figure of merit that captures the coherence of noise. We show that this quantity can be estimated directly from AGFs, rather than simulating purity measurements [4].
In summary, we provide a protocol for quantum process tomography that fulfils all of the following desiderata:
It should be based on physically reasonable and feasible measurements,
make use of them in a sample optimal fashion,
exploit structure of the expected/targeted channel (here low Kraus rank reflecting quantum gates), and
be stable against SPAM and other possible errors.
In this sense, we expect our scheme to be of high importance and practically useful in actual experimental settings in future quantum technologies [29]. It adds to the information obtained from mere randomised benchmarking in that it provides actionable advice, especially regarding coherent errors. Such advice is particularly relevant for fault tolerant quantum computation: Refs. [30, 31] indicate that it is coherent errors that lead to an enormous mismatch between average errors, which are estimated by randomised benchmarking, and worst-case errors, reflected by fault tolerance thresholds.
Our main technical contributions are results for the second and fourth moments of AGF measurements with random Clifford gates. For the second moment we provide an explicit formula improving over the previous lower bound [26]. In the case of trace-preserving and unital maps, our analysis gives rise to a tight frame condition. In order to prove a bound on the fourth moment, we derive – as a more universal new technical tool – a general integration formula for the fourth-order diagonal tensor representation of the Clifford group. The proof builds on recent results on the representation theory of the multi-qubit Clifford group [32–34]. Our result is the Clifford analogue to Collins’ integration formula for the unitary group [35, 36] for fourth orders, which we expect to also be useful in other applications. In the following, we present the precise formulation of our results. The proofs and technical contributions are given in Section IV.
II. MAIN RESULTS
A linear map from the set of Hermitian operators on a d-dimensional Hilbert space to itself is referred to as map. A quantum channel is a completely positive map that in addition preserves the trace of a Hermitian operator and, thus, maps quantum states to quantum states. A map is unital if the identity operator (equivalently, the maximally mixed state) is a fixed point of the map. We define the average gate fidelity (AGF) between a map and a quantum gate (i.e. a unitary quantum channel) associated with a unitary matrix U ∈ U(d) as
| (1) |
where the integral is taken according to the uniform (Haar) measure on state vectors.
The Clifford group constitutes a particularly important family of unitary gates that feature prominently in state-of-the-art quantum architectures. Moreover, it was shown that for many-qubit systems (i.e. d = 2n), any unital and trace-preserving map is fully characterised by its AGFs (1) with respect to the Clifford group [25]. A detailed analysis of the geometry of unital channels was previously given in Ref. [37]. There, it was shown that a quantum channel is unital if and only if it can be written as an affine combination of unitary gates. (Affine here means that the expansion coefficients sum to 1. Unlike convex combinations, they are however not restrict to being non-negative.) Motivated by the result for Clifford gates, one can ask more generally: What are the sets of unitary gates that span the set of unital and trace-preserving maps?
A general answer to this question can be given using the notion of unitary t-designs. Unitary t-designs [38, 39] (and their state-cousins, spherical t-designs [40, 41], respectively) are discrete subsets of the unitary group U(d) (resp. complex unit sphere) that are evenly distributed in the sense that their average reproduces the Haar (resp. uniform) measure over the full unitary group (resp. complex unit sphere) up to the t-th moment. The multi-qubit Clifford group, for example, forms a unitary 3-design [42–44]. For spherical designs, a close connection between informational completeness for quantum state estimation and the notion of a 2-design has been established in Ref. [41], see also Refs. [45–47]. A similar result holds for quantum process estimation, and is the starting point of our work. Indeed, the following is essentially due to Ref. [48]. We give a concise proof in form of the slightly more general Theorem 39 in Section IV F.
Proposition 1
(Informational completeness and unitary designs). Let be the gate set of a unitary 2-design, represented as channels. Every unital and trace-preserving map can be written as an affine combination of the . The coefficients are given by , where C = d(d+1)(d2−1).
Hence, every unital and trace-preserving map is uniquely determined by the AGFs with respect to an arbitrary unitary 2-design.
Clifford gates are a particularly prominent gate set with this 2-design feature. However, its cardinality scales superpolynomially in the dimension d. For explicit characterisations, this is far from optimal. However, in certain dimensions there exist subgroups of the Clifford group with cardinality proportional to d4 that also form a 2-design [39, 49]. More generally, order of d4 log(d) Clifford gates drawn i.i.d. uniformly at random are an approximate 2-design [50]. From Proposition 1, we expect that such randomly generated approximate 2-designs yield approximate reconstruction schemes for unital channels.
Our main result focuses on the particular task of reconstructing multi-qubit unital channels that are close to being unitary, i.e. well-approximated by a channel of Kraus rank equal to one. Techniques from low-rank matrix reconstruction [9, 10, 14, 15, 20, 51] allow for exploiting this additional piece of information in order to reduce the number of AGFs required to uniquely reconstruct an unknown unitary gate.
Suppose we are given a list of m AGFs
| (2) |
– possibly corrupted by additive noise ϵi – between the unknown unitary gate and Clifford gates that are chosen uniformly at random. In order to reconstruct from these observations, we propose to perform a least-squares fit over the set of unital quantum channels, i.e.
| (3) |
We emphasise that this is an efficiently solvable convex optimisation problem. The feasible set is convex since it is the intersection of an affine subspace (unital and trace-preserving maps) and a convex cone (completely positive maps).
Valid for multi-qubit gates (d = 2n), our second main result states that this reconstruction procedure is guaranteed to succeed with (exponentially) high probability, provided that the number m of AGFs is proportional (up to a log(d)-factor) to the number of degrees of freedom in a general unitary gate. The error of the reconstructed channel is measured with the Frobenius norm in Choi representation ‖ · ‖, see Section IV for details. Here, we give a concise statement for the case of unitary gates. A more general version – Theorem 19 in Section IV – shows that the result can be extended to cover approximately unitary channels.
Theorem 2
(Recovery guarantee for unitary gates).
Fix the dimension d = 2n. Then,
| (4) |
noisy AGFs with randomly chosen Clifford gates suffice with high probability (of at least 1−e−γm) to reconstruct any unitary quantum channel via (3). This reconstruction is stable in the sense that the minimiser of (3) is guaranteed to obey
| (5) |
The constants , c, γ > 0 are independent of d.
We note the following:
Eq. (5) shows the protocol’s inherent stability to additive noise. This stability, combined with the robustness of randomised benchmarking against SPAM errors, results in an estimation procedure that is potentially more resource-intensive, but considerably less susceptible to experimental imperfections and systematic errors than many other reconstruction protocols [9, 12, 28].
The proof can be verbatim adapted to an optimisation of the ℓ1-norm instead of the ℓ2-norm in Eq. (3), resulting in a slightly stronger error bound.
The theorem achieves a quadratic improvement (up to a log-factor) over the minimal number of AGFs required for a naive reconstruction via linear inversion for the case of noiseless measurements. But what is the number of measurements required to obtain the AGFs and to suppress the effect of the measurement noise in the reconstruction error (5)? For randomised benchmarking setups a fair accounting of all involved errors is beyond the scope of the current work. But in order to show that the scaling of the noise term in our reconstruction error (5) is essentially optimal, we consider the conceptually simpler measurement setting where the channel’s Choi state is measured directly. In Section IV E we prove upper and lower bounds to the minimum number of channel uses sufficient for a reconstruction via Algorithm (3) with reconstruction error (5) bounded by . This number of channel uses scales as up to log-factors. The upper bound relies on direct fidelity estimation [28]. In order to establish a lower bound we extend information theoretic arguments from Ref. [9] to rank-1 measurements.
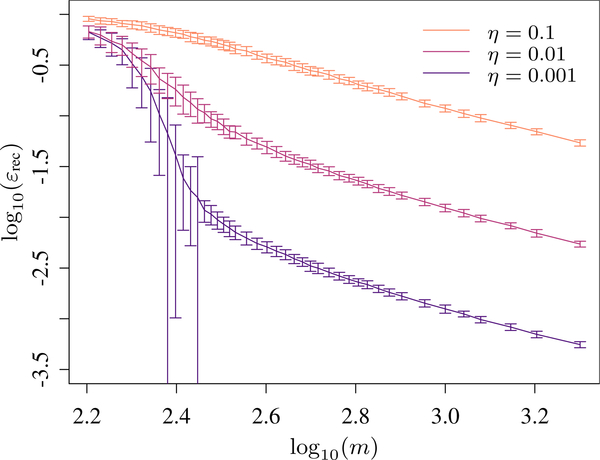
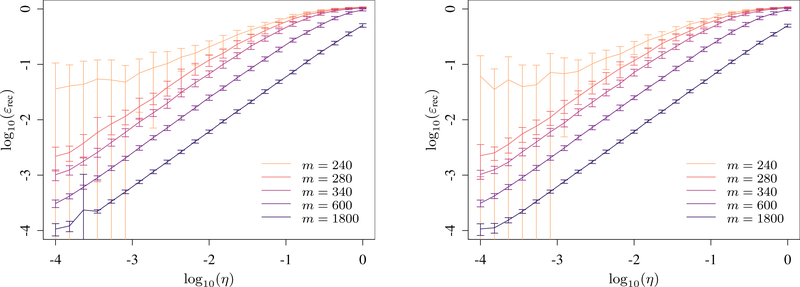
Finally, we note that the reconstruction (3) can be practically calculated using standard convex optimization packages. A numerical demonstration is shown in Figure 1 and discussed in more detail in Section IV H. There we also show that measuring AGFs with respect to Clifford unitaries seems to be comparable to Haar-random measurements, even in the presence of noise. This confirms an observation that was already mentioned in Ref. [26].
Figure 1.
Reconstruction of a Haar random 3-qubit channel using the optimization (3): The plots show the dependence of the observed average reconstruction error on the number of AGFs m for different noise strengths . The error bars denote the observed standard deviation. The averages are taken over 100 samples of random i.i.d. measurements and channels (nonuniform). The Matlab code and data used to create these plots can be found on GitHub [52].
The proof of Theorem 2 is presented in Section IV D. The AGFs can be interpreted as expectation values of certain observables, which are unit rank projectors onto directions that correspond to elements of the Clifford group. In contrast, most previous work on tomography via compressed sensing feature observables that have full rank, e.g. tensor products of Pauli operators. Since we now want to utilize observables that have unit rank, a different approach is needed. One approach, developed by a subset of the authors in [26] is to use strong results from low rank matrix reconstruction and phase retrieval [20, 47, 53–55]. These methods [20, 55] require measurements that look sufficiently random and unstructured, in that their 4th-order moments are close to those of the uniform Haar measure. The multi-qubit Clifford group, however, does constitute a 3-design, but not a 4-design. In Ref. [26] this discrepancy is partially remedied by imposing additional constraints (a “non-spikiness condition”, see also Ref. [56]) on the unitary channels to be reconstructed. In turn, their result also required these constraints to be included in the algorithmic reconstruction which renders the algorithm impractical [57]. Moreover, important classes of channels, e.g. Pauli channels, do in general not satisfy this condition. Here, we overcome these issues by appealing to recent works that fully characterise the fourth moments of the Clifford group [32, 33]. In order to apply these results, we develop an integration formula for fourth moments over the Clifford group. This formula is analogous to the integration over the unitary group know as Collins’ calculus with Weingarten functions [35]; see Section IV A. Equipped with this new representation theoretic technique we show in Section IV C that the deviation of the Clifford group from a unitary 4-design is – in a precise sense – mild enough for the task at hand.
Our final result addresses the unitarity of a quantum channel. Introduced by Wallman et al. [4], the unitarity is a measure for the coherence of a (noise) channel . It is defined to be the average purity of the output states of a slightly altered channel [58]
| (6) |
that flags the absence of trace-preservation and unitality. The unitarity can be estimated efficiently by using techniques similar to randomised benchmarking [59]. It is also an important figure of merit when one aims to compare the AGF of a noisy gate implementation to its diamond distance [30, 31] – a task that is important for certifying fault tolerance capabilities of quantum devices.
Although useful, the existing definition of the unitarity (6) is arguably not very intuitive. Here, we try to (partially) amend this situation by providing a simple statistical interpretation:
Theorem 3
(Operational interpretation of unitarity). Let be the gate set of a unitary 2-design. Then, for all hermicity preserving maps
| (7) |
where the variance is computed with respect to drawn randomly from the unitary 2-design.
The proof of the theorem is given in Section IV F. Note that the variance is taken with respect to unitaries drawn from the unitary 2-design and not the variance of the average fidelity with respect to the input state as calculated, e.g. in Ref. [60].
III. CONCLUSION AND OUTLOOK
In this work we address the crucial task of characterising quantum channels. We do so by relying on AGFs of the quantum channel of interest with simple-to-implement Cliffords. More specifically, we start by noting that (i) the unital part of any quantum channel can be written in terms of a unitary 2-design with expansion coefficients given by AGFs. As a consequence, for certain Hilbert space dimensions d, the unital part can be reconstructed from d4 AGFs with Clifford group operations by a straight-forward and stable expansion formula. (ii) As the main result, we prove for the case of unitary gates that the reconstruction can be practically done using only essentially order of d2 random AGFs with Clifford gates. In a simplified measurement setting, we show that this setting is provably resource optimal in terms of the number of channel invocations. For the proof, we derive a formula for the integration of fourth moments over the Clifford group, which is similar to Collins’ calculus with Weingarten functions. This integration formula might also be useful for other purposes. (iii) We prove that the unitarity of a quantum channel, which is a measure for the coherence of noise [4], has a simple statistical interpretation: It corresponds to the variance of the AGF with unitaries sampled from a unitary 2-design.
The focus of this work is on the reconstruction of quantum gates. Here, the assumption of unitarity considerably simplifies the representation-theoretic effort for establishing the fourth moment bounds required for applying strong existing proof techniques from low rank matrix recovery. These extend naturally to higher Kraus ranks and we leave this generalisation to future work. Existing results [61, 62] indicate that the deviation of the Clifford group from a unitary 4-design may become more pronounced when the rank of the states/channels in question increases. This may lead to a nonoptimal rank-scaling of the required number of observations m. In fact, a straightforward extension of Theorem 2 to the Kraus rank-r case already yields a recovery guarantee with a scaling of m ~ r5d2 log(d).
Practically, it is important to explore how this protocol behaves when applied to data obtained from interleaved randomised benchmarking experiments. In Ref. [25], the authors show how to use interleaved randomised benchmarking experiments to measure the AGF between a known Clifford and the combined process of an unknown gate concatenated with the average Clifford error process. In order to obtain tomographic information about the isolated unknown gate, the authors had to do a linear inversion of the average Clifford error. However, in most cases, we expect the average Clifford error to be close to a depolarizing channel which has very high rank. Thus, building on our intuition obtained for quantum states [63] and using our techniques, we could obtain a low-rank approximation to the combined unknown gate and average Clifford error, which under the assumption of a high rank Clifford error, would naturally pick out the coherent part of the unknown gate.
IV. DETAILS AND PROOFS
In this section we provide proofs and further details of the results of the work. Section IV A–IV C develop the prerequisites to prove the recovery guarantee, Theorem 2, in Section IV D. The optimality of this result is addressed in Section IV E. The expansion of unital maps in terms of a unitary 2-design, Proposition 1, is derived in Section IV F. In Section IV G, we show that the unitarity of a hermiticity preserving map can be expressed as the variance of its average gate fidelity with respect to a unitary 2-design. We also discuss possible implications. Finally, Section IV H provides further details of the numerical demonstration of the protocol.
We start by specifying the notation that is used subsequently. For a vector space V we denote the space of its endomorphisms by L(V). In particular, let Hd denote the space of hermitian operators on a d-dimensional complex Hilbert space. We label the vector space of endomorphisms on Hd by L(Hd) and denote its elements with calligraphic letters. For every map , we define its adjoint with respect to the Hilbert-Schmidt inner product (·,·) on Hd. We denote the subset of completely positive maps by CP(Hd) ⊂ L(Hd). Quantum channels are elements of CP(Hd) that are trace preserving (TP), i.e. for all X ∈ Hd. This condition is equivalent to the identity matrix Id ∈ Hd being a fixed point of the adjoint channel, . Similarly, a map (or channel) that itself has the identity as a fixed-point, , is called unital. The affine subspace of TP and unital maps is denoted by Lu,tp(Hd) ⊂ L(Hd). We further denote the linear hull of by .
Most of our results feature a norm on L(Hd), which is naturally induced on by the average gate fidelity (AGF) (1) in the following way. We define the inner product on L(Hd) as
| (8) |
and denote the induced norm on L(Hd) by . The pre-factors are chosen such that unitary channels have unit norm.
Note that this inner product is proportional to the previously defined Hilbert-Schmidt inner product applied to the Choi and Liouville representations:
| (9) |
see Refs. [64, 65] and also [30, Proposition 1]. We choose the convention that Choi matrices of quantum channels have unit trace, i.e. . Furthermore, for X ∈ Hd we will encounter the Schatten norms and , where μmax(Y) denotes the maximum eigenvalue of a Hermitian matrix Y. For a vector y ∈ ℝm and q ∈ ℕ the ℓq-norm is defined by .
For a map we define the random variable
| (10) |
where is a unitary channel with U either chosen uniformly at random from the full unitary group U(d), or the Clifford group Cl(d), depending on the context. The main technical ingredients for the the proofs of our main results are an expression for the second and fourth moment of . To this end, an integration formula for the first four moments over the Clifford group is developed in Section IV A. We then derive an explicit expression for the second moment of in Section IV B and an upper bound on the fourth moment of in Section IV C. These bounds are essential prerequisites for applying strong techniques from low-rank matrix reconstruction to prove our recovery guarantee, Theorem 2, for unitary gates in Section IV D.
A. An integration formula for the Clifford group
One of the main technical ingredients of the proof is an explicit formula for integrals of the diagonal action of the Clifford group Cl(d). More precisely, for a unitary representation R : G → L(V) of a subgroup G ⊂ U(d) carried by a vector space V, we define ER : L(V) → L(V) (“twirling”) as
| (11) |
where μ is the invariant measure induced by the Haar measure on U(d).
For we denote the diagonal action of a subgroup G of by , i.e.
| (12) |
Note that if G is a subgroup of the unitary group U(d) then is a unitary representation. The main result of this chapter is an explicit expression for for arbitrary A ∈ L(V).
For , where the integration is carried out over the entire unitary group, an explicit formula was derived in Refs. [35, 36]. It is instructive to review the result of Ref. [36] and its proof first. Our derivation of the analogous expression for the Clifford group follows the same strategy and makes use of many of the intermediate results.
1. Integration over the unitary group U(d)
To state the result we have to introduce notions from the representation theory of which can be found, e.g., in Refs. [35, 36, 66, 67]. Schur-Weyl duality relates the irreducible representations of the diagonal action of GL(V) to the irreducible representations of the natural action of the symmetric group Sn on V. Recall that the representation decomposes into irreducible representations labelled by partitions λ = (λ1,λ2, …, λl(λ)) of n into l(λ) ≤ d integers, i.e. . For short, we denote a partition of n by λ ⊢ n and dimensions of the Weyl-modules Wλ by Dλ.
Let be an orthonormal basis of . We define the representation by linearly extending
| (13) |
The irreducible representations of , are also labelled by partitions λ ⊢ n. The dimensions of the Specht-modules Sλ are denoted by dλ. Since the actions of and commute, they induce a representation of U(d)×Sn on that decomposes into irreducible representations as follows:
Theorem 4
(Schur-Weyl decomposition). The action of U(d)×Sn on is multiplicity free and decomposes into irreducible components as
| (14) |
on which U(d) × Sn acts as .
We denote the orthogonal projections on Wλ ⊗ Sλ by Pλ and the character on the irreducible representation of Sn by . The orthogonal projectors can be written as
| (15) |
see, e.g. Ref. [68, Eq. (12.10)]. In terms of these projectors can be calculated using the following theorem.
Theorem 5
(Integration over the unitary group U(d)). Let A ∈ L(V). Then, for and G = U(d),
| (16) |
This formula differs slightly from the original statement presented in Ref. [36]. The more common formulation presented there follows from evaluating the expression of Theorem 5 using a standard tensor basis of L(V ) [69]. However, here we have opted for a presentation of Theorem 5 that is easier to generalise beyond the full unitary group.
In the remainder of this section, we present a proof of Theorem 5 following the strategy of Ref. [36]. The commutant of a subset is the subset of L(V ) defined by
| (17) |
It is straight-forward to verify the following well-known properties of ER:
Lemma 6
(Properties of ER). Let R be a unitary representation of a subgroup G ⊆ U(d). Then, for all A ∈ L(V ) and B ∈ Comm(R(G)), the map ER (defined in Eq. (11)) fulfils
| (18) |
| (19) |
| (20) |
The last statement of Lemma 6 implies that is in the commutant of for all A ∈ L(V ). Using the decomposition of Theorem 4 and Schur’s Lemma we therefore conclude that acts as the identity on the Weyl-modules,
| (21) |
with Eλ ∈ L(Sλ). In general, the direct sum of endomorphisms acting on the irreducible representations of a group is isomorphic to the group ring which consists of formal (complex) linear combinations of the group elements [67, Propositon 3.29]. We denote the group ring of Sn by .
To derive an explicit expression of the coefficient of the expansion of in , we introduce the map Φ : L(V ) → L(V)
| (22) |
We will make use of the following properties of the map Φ.
Lemma 7
(Properties of Φ). For all A ∈ L(V ) and
| (23) |
| (24) |
| (25) |
Proof. 1. Since is in for all σ ∈ Sn, we can apply Lemma 6 to get
| (26) |
which establishes the first statement.
2. Since the commutant is isomorphic to the group ring, it suffices to proof the statement for all with τ ∈ Sn. In this case, using the cyclicity of the trace for the first equality, we find
| (27) |
Here we have used that for all τ, σ ∈ Sn.
3. Using Theorem 4 (Schur-Weyl duality), we can rewrite Φ(Id) as
| (28) |
The explicit expression (15) for the projectors identifies Φ(Id) as
| (29) |
Since the {Pλ} are a complete set of orthogonal projectors, the inverse of Φ(Id) is given by
| (30) |
□
We are now in position to give a concise proof of Theorem 5:
Proof of Theorem 5. From Eqns. (23) and (24) we conclude and, thus, . Inserting the expression (25) for Φ(Id)−1 and the definition (22) of Φ yields the expression of the theorem. □
2. Integration over the Clifford group
We now turn our attention to the Clifford group and aim at an analogous result to Theorem 5 for with A ∈ L(V ). As the former result for the unitary group, the result for the Clifford group heavily relies on a characterisation of the commutant of . The required results for the Clifford group were derived in Ref. [32] and apply to multi-qubit dimensions d = 2n. This paper introduces the orthogonal projection
| (31) |
where are the multi-qubit Pauli matrices. In fact, the d2-dimensional range of Q forms a particular stabiliser code. We denote by Q⊥ = Id−Q the orthogonal projection onto the complement of this stabiliser code. The orthogonal projection Q commutes with every . Thus, Q acts trivially on the Specht modules Sλ in the SchurWeyl decomposition (14). Following the notation conventions from Ref. [32], we denote the subspace of the Weyl module Wλ that intersects with the range of Q by and its dimension as . Analogously, the orthogonal complement of shall be with dimension . We are now ready to state the main result of this section.
Theorem 8
(Integration over the Clifford group Cl(d)). Let A ∈ L(V ). Then,
| (32) |
To set-up the proof we summarise the necessary results of Ref. [32] in the following theorem:
Theorem 9
(Representation theory of the Clifford group [32]). Whenever are non-trivial, the action of Cl(d)×S4 on is multiplicity free and decomposes into irreducible components
| (33) |
on which Cl(d) × S4 acts as .
The dimensions of are of polynomials in d of degree 4 and the dimensions of are either vanishing or polynomials in d of degree 2.
From Theorem 9 we learn that an element of the commutant of the diagonal action of the Clifford group can be written in the form
| (34) |
where are linear operators acting on the Specht modules Sλ.
To expand elements of , we define the map , with Φ from (22). The map has properties comparable to the map Φ, but is adapted to the diagonal representation of the Clifford group.
Lemma 10
For all A ∈ L(V ) and
| (35) |
| (36) |
| (37) |
Proof.
Since and are in for all σ ∈ S4, we can again apply Lemma 6 to get and likewise for Q⊥ instead of Q. Inserting this in the definition of yields the first statement.
- From the expansion of elements in (34), we conclude that B can be expressed as B = QB1 + Q⊥B2, where B1 and B2 are in the group ring . Hence, it suffices to show the statement, , for and . In the first case, we find
where property (19) from Lemma 6 has been used in the second step. The proof of Q⊥ is analogous.(38)
With these statements for the Clifford group at hand, we can proceed to prove Theorem 8.
Proof of Theorem 8. Eq. (35) in Lemma 10 and 36 in Lemma 10 can be combined to conclude and, thus, . The expression for was derived in Lemma 10, Eq. (37). Together with the definition of the expression of the theorem follows after some simplification. □
B. The second moment
The main result of this section is the following expression for the second moment of defined in Eq. (10). We shall use this statement multiple times in the proofs of our main results.
Lemma 11
(The 2-nd moment for U(d)). Let be a map. Then
| (41) |
for defined in Eq. (10).
For trace-annihilating and Id-annihilating maps, one arrives at a much simpler expression:
Corollary 12
(Expression for trace-annihilating and Id-annihilating maps). Let be a map that is trace-annihilating and Id-annihilating. Then the second moment of is
| (42) |
Proof. This follows directly from Lemma 11 and the observation that being trace-annihilating translates to and and being Idannihilating further requires . □
Before proving Lemma 11, we derive a general expression for the k-th moment of . To this end, recall that by Choi’s theorem an endomorphism of Hd (i.e. a hermiticity preserving map) can be decomposed as
| (43) |
where λi ∈ ℝ and T1, …, Tr are linear operators with unit Frobenius norm. In this decomposition, the random variable from Eq. (10), with takes the form
| (44) |
and its k-th moment can be expressed as follows:
Lemma 13
(k-th moment of ). For k ∈ ℕ and Ti defined by Eq. (43) we have
| (45) |
Proof. We can rewrite the k-th unitary moment of as
| (46) |
where in the last line we evaluated the trace in an orthonormal basis {|m〉 | m ∈ {1, …, dk}} for . Using the expression for of Theorem 5 we get
| (47) |
□
Proof of Lemma 11. We evaluate the expression of Lemma 13 for the case k = 2. To this end recall that the irreducible representations of S2 are the symmetric  and antisymmetric representation
and antisymmetric representation 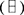 . The central projections are given by
. The central projections are given by  and
and  [67], where is the bipartite flip operator . The dimensions are
[67], where is the bipartite flip operator . The dimensions are 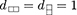 ,
, 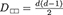 and
and 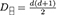 . For we introduce the following short-hand notation
. For we introduce the following short-hand notation
| (48) |
Rearranging the terms in the first statement of the Lemma 13 then yields
| (49) |
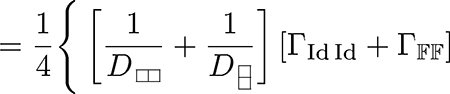 |
(50) |
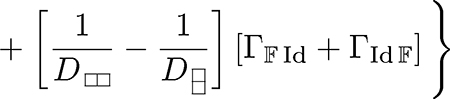 |
(51) |
| (52) |
The four Γ-terms can be evaluated explicitly. For the first term, we obtain
| (53) |
The second terms reads
| (54) |
and the third term can be written as
| (55) |
Moreover, a computation that closely resembles this reformulation yields and the claim follows. □
C. A fourth moment bound
The main result of this section is an upper bound for the fourth moment of when is a Haar random Clifford operation. To gain some intuition, let us first derive an upper bound on the fourth moment taken with respect to the full unitary group. Note that a similar bound has already been derived in Ref. [26].
Lemma 14
(4-th moment bound for U(d)). Let be a map. Then for defined in Eq. (10)
| (56) |
with some constant independent of the dimension d.
Proof. Applying Cauchy-Schwarz to an individual summand on the right hand side of Lemma 13 yields for all k
| (57) |
which is independent of the permutation τ ∈ Sk. We may therefore conclude
| (58) |
From Theorem 9 we observe that for k = 4
| (59) |
for some constant independent of d. Thus, Eq. (58) implies the desired bound. □
In an analogous way we can derive a sufficient bound on the fourth moment of when the average is performed over the Clifford group. The result will be stated in Lemma 18. To get the correct dimensional pre-factors in the bound, we have to rely on particular properties of the projection Q of Eq. (31) appearing in the representation theory of the fourth order diagonal action of Clifford group in Theorem 8. The following technical result takes care of this issue.
Lemma 15
(Properties of the projection Q). For and Q defined in Eq. (31)
| (60) |
This bound is tight. In fact, one can show that it is saturated if all Ti’s are chosen to be the same stabiliser state. The proof of Lemma 15 requires two other properties of multi-qubit Pauli matrices W1, …, Wd2. The first property is summarised by the following lemma.
Lemma 16
(Magnitude of multi-qubit Pauli matrices). For A, B ∈ L(ℂd),
| (61) |
for all j, k ∈ {1, …, d2}.
Proof. This statement follows directly from Cauchy-Schwarz and the unitary invariance of the Frobenius norm:
| (62) |
□
The second property is that the two multi-qubit flip operator can be expanded in terms of tensor products of Pauli matrices.
Lemma 17
(Multi-qubit flip operator in terms of Pauli matrices).
| (63) |
Proof. The re-normalised Pauli matrices form an orthonormal basis of Hd:
| (64) |
We can extend this to a basis of by considering all possible tensor products of Pauli matrices. Expanding the flip operator in this basis yields
| (65) |
as claimed. □
We are now equipped to prove Lemma 15.
Proof of Lemma 15. We start by inserting the definition of Q, (31). Fixing w.l.o.g. an order of the indices, we obtain
| (66) |
| (67) |
| (68) |
where we defined . These numbers obey
| (69) |
In addition, Lemma 16 implies
| (70) |
Equation (68) can be viewed as a complex-valued inner product between two d2-dimensional vectors indexed by k and l. This expression can be upper bounded by the Cauchy-Schwarz inequality:
| (71) |
| (72) |
| (73) |
The first square-root can be bounded in the following way
| (74) |
Here, we have applied the magnitude bound (70) for in the second line and applied Lemma 17.
The second square root can be bounded in a complete analogous fashion, i.e.
| (75) |
Inserting both bounds into Eq. (73) yields the desired claim. □
Having established Lemma 15, we will now state the bound on the fourth moment of when the average is performed over the Clifford group.
Lemma 18
(4-th moment bound for Cl(d)). Let be a map. For defined in Eq. (10), it holds
| (76) |
where ‖ · ‖1 denotes the trace (or nuclear) norm and the constant C > 0 is independent of d.
Proof. As for the unitary group, we can rewrite the k-th moment of for the Clifford group as
| (77) |
using a basis {|m〉 | m ∈ {1, …, dk}} for (ℂd)⊗k. The expression for with k = 4 was derived in Theorem 8. It implies that
| (78) |
We may bound the first trace term by
| (79) |
where we have used Cauchy-Schwarz and applied Lemma 15 in the last line. For the second trace term a looser bound suffices:
| (80) |
for all τ ∈ S4. This follows directly from Cauchy-Schwarz. Altogether we conclude that
| (81) |
with some constant C > 0 independent of d. The last step follows from the dimensions given in Theorem 9. □
D. Proof of Theorem 2 (recovery guarantee)
We consider the following measurements: For a map the measurement outcomes f ∈ ℝm are given by
| (82) |
where are random Clifford channels and ϵ ∈ ℝm accounts for additional additive noise.
To make use of the proof techniques developed for low rank matrix reconstruction [20, 55], we will in the following work in the Choi representation of channels. This has the advantage, that the Kraus rank directly translates to the familiar matrix rank. We define the Choi matrix of a map as
| (83) |
where is the maximally entangled state vector. The Choi matrix of a map is positive semi-definite if and only if the map is completely positive. We denote the cone of positive semi-definite matrices by . A channel is trace-preserving and unital if and only if both partial traces of the Choi matrix yield the maximally mixed state, i.e. . We will denote the set of Choi matrices that correspond to channels in Lu,tp by J(Lu,tp). Furthermore, we define J(Vu,tp,0) as the set of Choi matrices corresponding to trace- and identityannihilating channels, i.e., both partial traces of operators in J(Vu,tp,0) vanish. Moreover, recall that the inner product on Lu,tp we introduced in (8) coincides with the Hilbert-Schmidt inner product of the corresponding Choi matrices (9). Adhering to this correspondence, we slightly abuse notation and use and interchangeably.
To formalise the robustness of our reconstruction we need to introduce the following notation. For a Hermitian matrix Z ∈ Hd let λ be the largest eigenvalue with an eigenvector v. We write Z|1 = λ |v〉〈v| for the best unit rank approximation to Z and Z|c := Z − Z|1 denotes the corresponding “tail”.
In terms of the Choi matrix of the measurement outcomes f ∈ ℝm read
| (84) |
The underlying linear measurement map is given by
| (85) |
Since unital and trace preserving maps have trace normalised Choi matrices the second trace-term of the measurement map is just a constant shift. We also define the set of measurement matrices that encode the measurement map as , where each is a gate that is chosen uniformly at random (according to the Haar measure) from the multi-qubit Clifford group.
In the Choi representation, we want to consider the optimisation problem
| (86) |
where we allow the minimisation of an arbitrary ℓq-norm. The optimisation problem (3) is equivalent to (86) for q = 2.
We are interested in using the optimisation procedure (86) for the recovery of unitary quantum channels. In this section, we will derive the following recovery guarantee:
Theorem 19
(Recovery guarantee). Let be the measurement map (85) with
| (87) |
Then, for all given noisy observations , the minimiser Z♯ of the optimization problem (86) fulfils for p ∈ {1,2}
| (88) |
with probability at least over the random measurements. The constants , , c, cf > 0 only depend on each other.
The recovery guarantee of Theorem 2 is the special case of Theorem 19 for q = 2 and p = 2 restricted to measurements of a unitary quantum channel. In contrast, the more general formulation of Theorem 19 allows for a violation of the unit rank assumption. The first term (88) is meant to absorb violations of this assumption into the error bound. We note in passing that the choice of p = 1 actually yields a tighter bound compared to p = 2.
More generally, one can ask for a recovery guarantee if the measured map X can not be guaranteed to be unital or trace preserving. From Eq. 171 one observes that as long as the map X is trace normalised the measured AGFs are identical to the average fidelities of the projection Xu,tp of X onto the affine space of unital and trace-preserving maps. But since Xu,tp is not necessarily positive, it is not straight-forward to apply Theorem 19 to Xu,tp. We expect the reconstruction algorithm to recover the trace-preserving and unital part of an arbitrary map. The reconstruction error (88) is expected to additionally feature a term proportional to the distance of X to the intersection of Lu,tp with the cone of positive semi-definite matrices.
Another way to proceed is to use a trace-norm minimisation subject to unitality, trace-preservation and the data constraints . The derivation of Theorem 19 readily yields a recovery guarantee for the trace-norm minimisation that is essentially identical to Theorem 19. See Ref. [20] for details on the argument. The main difference is that such a recovery guarantee does not need to assume complete positivity of the map that is to be reconstructed. Correspondingly, the result of the trace-norm minimisation is not guaranteed to be positive semi-definite. This implies that the robustness of this algorithm against violations of the unitality and tracepreservation is different compared to (86). For example, the AGFs of a not necessarily unital or trace-preserving map to unitary gates coincide with the AGFs of its unital and tracepreserving part as long as X is still normalised in tracenorm. This is a consequence of Eq. 171. Thus, a trace-norm minimisation will reconstruct Xu,tp up to an error given by and noise. We leave a more extensive study of the robustness of the discussed reconstruction algorithms against violations of this particular model assumption to future work.
The proof of the recovery guarantee relies on establishing the so-called null space property (NSP) for the measurement map . We refer to Ref. [70] for a history of the term. The NSP ensures injectivity, i.e. informational completeness, of the measurement map restricted to the matrices that should be recovered. Informally, for our purposes, a measurement map obeys the NSP if no unit rank matrix in J(Vu,tp,0) is in the kernel (nullspace) of .
Definition 20
(Robust NSP, Definition 3.1 in Ref. [20]). satisfies the null space property (NSP) with respect to ℓq with constant τ > 0 if for all X ∈ J(Vu,tp,0)
| (89) |
The factor 1/2 in front of the first term of (89) is only one possible choice. In fact, one can instead introduce a constant with value in (0,1). The constants appearing in Theorem 19 then depend on the specific value of the pre-factor. In particular, the different choices of the pre-factor in the definition of the NSP result in different trade-offs between the constant c that appears in the sampling complexity and the constant that decorates the model-mismatch term in the reconstruction error. For the simplicity, we leave these dependencies implicit.
The main consequence of the NSP that we require is captured by the following reformulation of Theorem 12 of [20].
Theorem 21
Fix p ∈ {1, 2} and let satisfy the NSP with constant τ > 0. Then, for all Y, Z ∈ J(Lu,tp)
| (90) |
In fact, the measurement of (84) obeys the NSP. More precisely:
Lemma 22
Let be the measurement map defined in (85) with m ≥ cd2 log(d). Then A obeys the NSP property with constant τ = C−1d(d + 1)m−1/q with probability of at least . The constants C, c, cf > 0 only depend on each other.
The proof of Lemma 22 is developed in the subsequent section.
Proof of Theorem 19. With the requirements of Lemma 22 we can apply Theorem 21 and set , the reconstructed result of the algorithm, as well as Y = X. The theorem’s statement then reads
| (91) |
because ‖X‖1 = ‖Z‖1 = 1 is true for arbitrary Choi matrices of (trace-preserving) quantum channels. The second term is dominated by
| (92) |
where the last step follows from being the minimiser of (86). Thus, we can replace it by any point in the feasible set including X on the right hand side of the first line. Inserting (92) and the NSP constants of Lemma 22 into (91) the assertion of the theorem follows. □
In the remainder of this section, we will establish the NSP for our measurement matrix as summarised in Lemma 22.
Establishing the null space property
To prove Lemma 22 at the end of this section we start with deriving a criterion for the NSP property following the approach taken in Refs. [12, 20].
Lemma 23
A map obeys the null space property with respect to ℓq-norm with constant τ > 0 if
| (93) |
with
Proof. For matrices X with the property the NSP condition (89) is satisfied independently of the map . Hence, to establish the NSP for a specific map it suffice to show that the condition (89) holds for all . The additional assumption of ‖Z‖2 = 1 is no restriction since both sides of (89) are absolutely homogeneous functions of the same degree. By definition, for all X ∈ Ω we have ‖X|1‖2 ≤ ‖X‖2 ≤ 1. Therefore, for X ∈ Ω
| (94) |
implies the NSP condition (89). Using the norm inequality yields the criterion of the lemma. □
Recall that every rank-r matrix X obeys . This motivates thinking of the matrices of Ω as having effective unit rank since the norm ratio bounded in . More precisely, the following statement holds:
Lemma 24
(Ratio of 1 and 2-norms). Every matrix X ∈ Ω has effective unit rank in the following sense:
| (95) |
Proof. From ‖X|1‖2 ≤ 1 and the definition of Ω it follows that . Hence . Therefore, we have that ‖X‖1 ≤ ‖X|1‖1 + ‖X|c‖1 ≤ 3 from which the assertion follows, because every X ∈ Ω has unit Frobenius norm. □
In summary, we want to prove a lower bound on the ℓq-norm of the measurement outcomes for trace- and identity annihilating channels with effective unit Kraus rank. The proof uses Mendelson’s small ball method. See Ref. [12, Lemma 9] for details of the method as it is stated here, which is a slight generalisation of Tropp’s formulation [71] of the original method developed in Refs. [72, 73]. Mendelson’s proof strategy requires multiple ingredients. These necessary ingredients will become obvious from the following theorem, which can be found in Ref. [71] and lies at the heart of the small ball method.
Theorem 25
(Mendelson’s small ball method). Suppose that contains m measurements of the form fk = Tr[AkX] where each Ak is an independent copy of a random matrix A. Fix E ⊆ J(Vu,tp,0) and ξ > 0 and define
| (96) |
| (97) |
where the k’s are i.i.d. Rademacher random variables, i.e. are uniformly distributed in {−1, 1}. Then, with probability of at least , where t ≥ 0,
A lower bound of thus requires two main ingredients: 1.) a lower bound on the so-called mean empirical width Wm(E;A) and 2.) an upper bound on the socalled marginal tail function Q2ξ(E;A). We will derive those bounds for E = Ω and our measurement map at hand.
Bound on the mean empirical width
With a different normalisation the following statement is derived in Ref. [74].
Lemma 26
Fix d = 2n and suppose that the measurement matrices are given by with a gate chosen uniformly from the Clifford group for all i. Also, assume that m ≥ d2 log(d). Then
| (98) |
The proof is analogous to the one in Refs. [12, 26, 55]. In order to adjust the normalisation we provide a short summary.
Proof. For Z ∈ Ω it holds that
| (99) |
The constant shift by the identity matrix does not appear hear since every Z ∈ Ω is trace-less. Thus, we can set . Applying Hölder’s inequality for Schatten norms to the definition of the mean empirical width yields
| (100) |
where we have used the effective unit rank of Z, Lemma 24. Also, the ϵi’s in the definition of H form a Rademacher sequence. The non-commutative Khintchine inequality, see e.g [75, Eq. (5.18)], can be used to bound this sequence
| (101) |
and J(Ci)2 = J(Ci) further simplifies the remaining expression. Moreover, and a Matrix Chernoff inequality for expectations (with parameter θ = 1), see e.g. [76, Theorem 5.1.1] implies
| (102) |
where the second inequality follows from the assumption m ≥ d2 log(d). Inserting this bound into Eq. (101) yields
| (103) |
and the claim follows from combining this estimate with the bound (100) and log(2d2) ≤ 4log(d). □
Bound on the marginal tail function
Here, we establish an anti-concentration bound to the marginal tail function. The precise result is summarised in the following statement.
Lemma 27
Suppose the random variable A ∈ Hd is given by , where is a Clifford channel drawn uniformly from the Clifford-group Cl(d). For it holds that
| (104) |
where is the constant from Lemma 28.
This statement follows from applying the Paley-Zygmund inequality to the non-negative random variable defined in Eq. (10). For this purpose, we will make use of the bounds on the second and fourth moment of derived in Section IV B and Section IV C, respectively. In particular, we establish the following relation between the second and fourth moment of . This is one of the technical core result of this work.
Lemma 28
Let be a map with of effective unit rank, i.e. with some constant c > 0, then
| (105) |
for some constant independent of the dimension d.
Proof. Since the Clifford group is a unitary 3-design [42, 43], Corollary 12 implies
| (106) |
Furthermore, the effective unit rank assumption, , together with Lemma 18 yields for the fourth moment
| (107) |
for some constant independent of d. Combining these two equations, the statement of the proposition follows. □
Note that with the help of Lemma 14 one arrives at the same conclusion for the moments of when the average is taken over the unitary group. This reproduces the previous technical core result of Ref. [26].
Proof of Lemma 27. In the following we always understand by the map in L(Hd) with Choi matrix . In terms of the random variable , Eq. (10), the marginal tail function can be expressed as
| (108) |
Here we again used that every Z ∈ Ω is trace-less. Consequently, the shift by the identity matrix in the measurements Ai vanishes. Using Lemma 28, the theorem follows by a straight-forward application of the Paley-Zygmund inequality,
| (109) |
where and is required to fulfil . According to Corollary 12 and the normalisation of T ∈ Ω we have . □
Completing the proof of Lemma 22 We are finally in position to deliver the proof for the NSP of . With the bounds on the mean empirical width, Lemma 26, and the marginal tail function, Lemma 27, Mendelson’s small ball method, Theorem 25, yields the following lemma:
Lemma 29
Suppose that contains
| (110) |
measurements of the form fk = Tr[AkX] where each is given by an independent and uniformly random Clifford unitary channel Ci. Fix Ω ⊂ J(Vu,tp,0) as defined in Lemma 23. Then
| (111) |
with probability at least over the random measurements. The constants C, c, cf > 0 only depend on each other.
Proof. Combining the Lemmas 25, 26, and 27 yields with probability at least that
| (112) |
where we have chosen . The statement follows from the scaling (110) of m. □
From Lemma 29 and Lemma 23 the assertion of Lemma 22 directly follows.
E. Sample optimality in the number of channel uses
The compressed sensing recovery guarantees, Theorem 2 and Theorem 19, focus on the minimal number of AGFs m that are required for the reconstruction of a unital and tracepreserving quantum channel using the reconstruction procedure (3) and (86), respectively. This can be regarded as the number of measurement settings. But already the measurement of single fidelities up to some desired additive error will require a certain number of repetitions of some experiment. Therefore, to quantify the total measurement effort a more relevant figure of merit is the minimum number of channel uses M required for taking all the data used in a reconstruction.
We will show that the equivalent algorithms (3) and (86) reach an optimal parametric scaling of the required number of channel uses in a simplified measurement setting. To this end, we first combine the direct fidelity estimation protocol of Ref. [28] with our recovery strategy to provide an upper bound on the number of channel uses required for the reconstruction of a unitary gate up to a constant error. Second, following the proof strategy of Ref. [9, Section III], we derive a lower bound on the number of channel uses required by any POVM measurement scheme of AGFs with Clifford gates and any subsequent reconstruction protocol that only relies on these AGFs.
1. Measurement setting
In order to obtain an optimality result we consider a measurement setting that is arguably simpler than the one in randomised benchmarking and more basic from a theoretical perspective. We consider a unitary channel given by a unitary U ∈ U(d) and measurements given by Clifford channels with Ci ∈ Cl(d). Using the identities (8) and (9) the AGFs are determined by
| (113) |
In this section, we consider as a pure state vector in ℂd ⊗ ℂd, i.e., as the state vector corresponding to the Choi state of the channel . This state can be prepared by applying the operation U to one half of a maximally entangled state.
2. An upper bound from direct fidelity estimation
We will now derive an upper bound on the number of channel uses required in the reconstruction scheme (86). We note that our measurement values (113) are also fidelities of the quantum state vectors and and use direct fidelity estimation [28] (see also [23]) to estimate these fidelities. Importantly, each is a stabiliser state and we view it as the “target state” in the direct fidelity estimation protocol [28]. Then is a well-conditioned state with parameter α = 1. One of the main statements of Ref. [28] is that the fidelity fi can hence be estimated from μ ≥ μ0 many Pauli measurements, where . Here, δ0 > 0 is the maximum failure probability, and εF > 0 is the accuracy up to which the fidelity fi is estimated. This implies that the estimation error is bounded as
| (114) |
For our channel reconstruction, we measure many fidelities, each up to error εF, see Theorem 2. For a maximum failure probabilities of the single fidelity estimations δ0 and a desired failure probability δ of all the m estimations it is sufficient to require δ ≤ mδ0, since (1−δ0)m ≥ 1 − mδ0. Moreover, in order for the reconstruction error (5) to be bounded as
| (115) |
where , we require
| (116) |
Thus, a constant bound εrec of the reconstruction error can be achieved with a number of channel uses M in
| (117) |
3. Information theoretic lower bound on the number of channel uses
In this section we derive a lower bound on the number of channel uses that holds in a general POVM framework. Up to log-factors, it has the same dimensional scaling as the upper bound (117) from direct fidelity estimation.
We extend the arguments of Ref. [9, Section III] to prove a lower bound on the number of channel uses required for QPT of unitary channels from measurement values of the form (113). We consider each of these values to be an expectation value in a binary POVM measurement setting given by the unit rank projector are applied to the Choi state . Then we are in the situation of [9, Section 3], which proves a lower bound for the minimax risk – a prominent figure of merit for statistical estimators.
Let us summarise this setting. We denote by the set of density matrices and by the set of all two-outcome positive-operator-valued measurements (POVMs), each of them given by a projector π ∈ Hd. Next, we assume that we measure M copies of an unknown state in a sequential fashion. By Yi we denote the binary random variable that is given by choosing the i-th measurement and measuring ρ. These are mapped to an estimate . Any such estimation protocol is specified by the estimator function and a set of functions {Πi}i∈[M] that correspond to the measurement choices, where , i.e., the i-th measurement choice Πi only depends on previous measurement outcomes. Let ε > 0 be the maximum trace distance error we like to tolerate between the estimation and ρ. Then the minimax risk is defined as
| (118) |
where we denote by Y the vector consisting of all random variables Yi. An estimation protocol minimising the minimax risk has the smallest possible worst-case probability over the set of quantum states.
The following theorem provides a lower bound on the minimax risk for the estimation of the Choi matrix of a unitary gate from unit rank measurements.
Theorem 30
(Lower bound, unit rank measurements). Fix a set of rank-1 measurements. For ε > 0 the minimax risk (118) of measurements of M copies is bounded as
| (119) |
where c1 and c2 are absolute constants.
Before providing a proof for this theorem let us work out its consequences. If the measurements project onto Clifford unitaries, we get the following lower bound on the minimax risk.
Corollary 31
(Lower bound, Clifford group). Let ε > 0 and consider measurements of the form (113) given by Clifford group unitaries on M copies. Then the minimax risk (118) is bounded as
| (120) |
where c3 and c2 are absolute constants.
Proof. The cardinality of the n-qubit Clifford group (d = 2n) is bounded as
| (121) |
[77]. This implies that in case of our Clifford group measurements we have . □
In every meaningful measurement and reconstruction scheme the minimax risk needs to be small. The corollary implies that, in the case of Cliffords, the number of copies M need to scale with the dimension as
| (122) |
where we have assumed ε > 0 to be small. This establishes a lower bound on the number of channel uses that every POVM measurement and reconstruction scheme requires for a guaranteed successful recovery of unitary channels from AGFs with respect to Clifford unitaries.
From the argument as it is presented here it is not possible to extract the optimal parametric dependence of the number of channel uses M on the desired reconstruction error ε. For quantum state tomography such bounds were derived in Ref. [78] by extending the argument of Ref. [9] and constructing different ε-packing nets. By adapting the ε-packing net constructions of Ref. [78] to unitary gates one might be able to derive a optimal parametric dependence of M on ε. But it is not obvious how one can incorporate the restriction of the measurements to unit rank in the argument of Ref. [78]. We leave this task to future work.
In the remainder of this section we prove Theorem 30. The proof proceeds in two steps. At first we derive a more general bound on the minimax risk, Lemma 32, that follows mainly from combining Fano’s inequality with the data processing inequality, see e.g. [79]. This is a slight generalization of Lemma 1 of Ref. [9] adjusted to the situation where the outcome probabilities of the POVM measurements do not necessarily concentrate around the value 1/2. Lemma 32 assumes the existence of an ε-packing net for the set of unitary gates whose measurement outcomes are in a small interval to establish a lower bound on the minimax risk. Hence, in order to complete the proof, we have to establish the existence of a suitable packing net, Lemma 36, in a second step. Combining the general bound of Lemma 32 and the existence of the packing net of Lemma 36, the proof of Theorem 30 follows.
We begin with the general information theoretic bound on the minimax risk.
Lemma 32
(Lower bound to the minimax risk). Let ε > 0 and 0 < α < β ≤ 1/2. Assume that there are states ρ1, …, ρs ∈ PosD and orthogonal projectors π1, …, πn ∈ PosD such that
| (123) |
| (124) |
for all i ≠ j ∈ [s] and k ∈ [n]. Then the minimax risk (118) of M single measurements is bounded as
| (125) |
where h denotes the binary entropy.
Proof. We start by following the proof of [9, Lemma 1]: Let X be the random variable uniformly distributed over [s] and let Y1, …, YM be the random variables describing the M single POVM measurements performed on ρX. Consider any estimator of the state ρX from the measurements Y and define
| (126) |
Then, for all i ∈ [s],
| (127) |
Following Ref. [9], we combine Fano’s inequality and the data processing inequality for the mutual information I(X;Z) = H(X) − H(X|Z), where H denotes the entropy and conditional entropy, to obtain
| (128) |
| (129) |
Now we start deviating from Ref. [9]. We use that I(X;Y ) = I(Y;X), the chain rule, and the definition of the conditional entropy to obtain
| (130) |
| (131) |
| (132) |
| (133) |
Now we use that
| (134) |
and
| (135) |
where h is the binary entropy, to arrive at
| (136) |
| (137) |
□
To apply Lemma 32 we need to proof the existence of an ε-packing net consisting of unitary quantum gates with the properties (123) and (124). The construction of such a suitable ε-packing net will use the fact that the modulus of the trace of a Haar random unitary matrix is a sub-Gaussian random variable. This can be viewed as a non-asymptotic version of a classic result by Diaconis and Shahshahani [80]: the trace of a Haar random unitary matrix in U(d) is a complex Gaussian random variable in the limit of infinitely large dimensions d.
The trace of Haar random unitaries is sub-Gaussian
The statement follows from the fact that the moments of the modulus of the trace of a Haar random unitary are dominated by the moments of a Gaussian variable.
Proposition 33
For all d,k ∈ ℤ+
| (138) |
with equality if k ≤ d.
Proof. Denote by S := |Tr(U)|2 the random variable with U ∈ U(d) drawn from the Haar measure. Let be an orthonormal basis of (ℂd)⊗k. The k-th moment of S is given by
| (139) |
Applying Theorem 5, we get
| (140) |
| (141) |
| (142) |
| (143) |
Since Tr(Pλ) = dλDλ, we conclude
| (144) |
The last equality can be seen from the orthogonality relation of the characters of the symmetric group, see e.g. Ref. [67, Chapter 2] for more details. Note that the second inequality is saturated in the case where k ≤ d since in this case the restriction l(λ) ≤ d is automatically fulfilled. □
As a simple implication of the previous lemma is that the random variable S = |Tr(U)|2 has subexponential tail decay.
Lemma 34
Let S be a real-valued random variable that obeys for all k ∈ ℕ. Then, the right tail of X decays at least subexponentially. For any t ≥ 0,
with .
This is a consequence of a standard result in probability theory that can be found in many textbooks, e.g. [81] and [82, Section 7.2]. We present a short proof here in order to be self-contained.
Proof. We use Markov’s inequality, Proposition 33, and Stirling’s bound to obtain for any k ∈ ℕ
| (145) |
In order to prove the tail bound, we choose t ≥ 0 arbitrary and let k be the largest integer that is smaller or equal to t (k = ⌊t⌋). Then
Here, we have used and t ≤ k + 1. □
Random variables with subgaussian tail decay – subgaussian random variables – are closely related to random variables with subexponential tail decay: X is subgaussian if and only if X2 is subexponential.
Thus, Proposition 33 highlights that the trace of a Haarrandom unitary is a subgaussian random variable. This is the aforementioned generalization of the classical result by Diaconis and Shashahani.
A packing net with concentrated measurements
The proof of existence of an ε-packing net to apply Lemma 32 uses a probabilistic argument as in Ref. [9]. Here, the strategy is the following: We assume we are already given an ε-packing net of a size s−1 that satisfies the desired concentration condition (124). We then show that a Haar random unitary gate also fulfils the concentration condition and is ε-separated from the rest of the net with strictly positive probability. Consequently, if one can be lucky to randomly arrive at a suitable ε-packing net of size s in this way then it must also exist.
We start by deriving an anti-concentration result for the Choi matrix of a unitary channel given by a Haar random unitary U in U(d).
Lemma 35
Let be a unitary gate. For all ε > 0
| (146) |
with κ > 0 being the constant from Lemma 34.
Proof. Due to the unitary invariance of the trace-norm and the Haar measure, it suffice to show the statement for . For a unitary channel with Choi-matrix and Kraus-operator U ∈ U(d) we have
| (147) |
For the first equation we calculate the set eigenvalues of , which is . Introducing the random variable SU := |Tr(U)|2, we can rewrite the probability as
| (148) |
| (149) |
From Lemma 34 we know that
| (150) |
from which the assertion follows. □
The anti-concentration result of Lemma 35 implies the existence of a large ε-packing net of unitary quantum channels. The desired concentration of the measurement outcomes can be established using Lemma 34. In summary we arrive at the following assertion:
Lemma 36
(Packing net with concentrated measurements). Let , and C1, …, CK ∈ U(d). Then, for any number , there exist U1, …, Us ∈ U(d) such that for all i, j ∈ [s] with i ≠ j and for all k ∈ [K]
| (151) |
| (152) |
Proof. As outlined above the existence of the described ε-packing net follows inductively from the fact that if one adds a Haar random unitary gate to an ε-packing of size s−1 that already fulfils all requirements of the lemma the resulting set has still a strictly positive probability to be an ε-packing net with the desired concentration property (152).
We start with bounding the probability that the resulting set fails to be an ε-packing net. Let us denote the probability that a Haar random is not ε-separated from by . In other words, is the probability that there exists with
| (153) |
Taking the union bound for all , Lemma 35 implies that
| (154) |
with . Thus, for we ensure that .
We now also have to upper bound the probability of not having a concentration property
| (155) |
with respect to K different unitaries C1, …, CK.
Using the unitary invariance of the Haar measure and taking the union bound, the tail-bound for the squared modulus of the trace of a Haar random unitary, Lemma 34, yields
| (156) |
for β ≥ 2. In order for to be at most 1/2, we need that
| (157) |
In summary, we have established that as long and the achievable concentration is β ≥ (log(2K) + 2)/(κd2). Hence, in this parameter regime there always exist at least one additional unitary gate extending the ε-packing net. Inductively this proves the existence assertion of the lemma. □
Having established a suitable ε-packing net, we can now apply Lemma 32 to derive the lower bound on the minimax-risk for the recovery of unitary gates from unit rank measurements of Theorem 30, the main result of this section.
Proof of Theorem 30. We will apply Lemma 32 with α = 0 and
| (158) |
and we use that h(β) ≤ 2β log(1/β) for β ≤ 1/2. Combining the Lemmas 32 and 36 we obtain
| (159) |
| (160) |
where, in Lemma 36 we have chosen s to be the strict upper bound minus one. Finally, we simplify the bound by choosing large enough constants c1 and c2. □
F. Expansion of quantum channels in average gate fidelities
In this section, we give a instructive proof of the result of [48] that the linear span of the unital channels coincides with the linear span of the unitary ones, even if one restricts to the unitaries from a unitary 2-design. We also link this finding to AGFs. On the way, we establish the simple formula of Proposition 1 that allows for the reconstruction of unital and trace-preserving maps from measured AGFs with respect to a arbitrary unitary 2-design, e.g. Clifford gates.
In Lemma 11 we derived an explicit expression for the second moment of the random variable . For , the linear hull of unital and trace-preserving maps, and uniformly drawn from a unitary 2-design the expression in fact indicates that a unitary 2-design constitutes a Parseval frame for . More abstractly, this observation stems from the general fact that irreducible unitary representations form Parseval frames on the space of endomorphisms of their representation space. For this reason it is instructive, to derive the connection explicitly in the ‘natural’ representation-theoretic language. We begin with formalising the connection between irreducible representations and Parseval frames.
Lemma 37
(Irreps form a Parseval frame). Let R : G → L(V ) be an irreducible unitary representation of a group G. Then the set forms a Parseval frame for the space L(V ) equipped with the Hibert-Schmidt inner product A, B ↦ Tr[A†B], in the sense that
| (161) |
for all A ∈ L(V ).
Proof. Since L(V ) is generated as an algebra by {R(g)}g∈G (see e.g. [67, Proposition 3.29]), it suffices to show the statement for A = R(g) with g ∈ G. Due to the invariance of the Haar measure, the map TG is covariant in the sense that TG(R(g)B) = R(g)TG(B) for all B ∈ L(V ). In particular, for B = Id, we thus get TG(R(g)Id) = R(g)TG(Id). With the character of the representation, we have
| (162) |
from the well-known expression for projection onto a representation space in terms of the character, see e.g. Ref. [67, Chapter 2.4]. Thus, we have established that SR(R(g)) = R(g) for all g ∈ G. □
Applying this lemma to unitary channels, we can derive the following expression for the orthogonal projection onto the linear hull of unital and trace-preserving maps.
Theorem 38
Let be a unitary 2-design. The orthogonal projection onto the linear hull of unital and trace-preserving maps is give by
| (163) |
with coefficients
| (164) |
where C := d(d + 1)(d2 − 1).
Proof. Throughout the proof, we denote the unitary channel representing the unitary U ∈ U(d) on space of Hermitian operators Hd by . The vector space Hd is a direct sum of the space of trace-less hermitian matrices, and of . The group of unitary channels acts trivially on , and irreducibly on . In particular, is “block-diagonal” with respect to this decomposition, where is the irreducible (d2 − 1)-dimensional block. More generally, the projection of a map onto the linear hull of unital and trace-preserving maps is of the form . The map is trace-preserving and unital if and only if . For the map we have
| (165) |
Using this formula, Lemma 37 for the choice , and the fact that a group integral over a non-trivial irrep vanishes [83], we find
| (166) |
Hence, for we obtain the completeness relation
| (167) |
For in the ortho-complement of the left hand side of Eq. (167) vanishes. The expression, thus, defines the orthogonal projection onto . The projection can be reexpressed in terms of the AGF. With the help of Eqs. (8, 9),
| (168) |
Hence,
| (169) |
with expansion coefficients
Since the integrand in Eq. (169) is linear in , the completeness relation continues to hold if the Haar integral is replaced by the average
| (170) |
over any unitary 2-design . □
In the proof, we have used that linear hull of the unital and trace-preserving maps is given by the space of block diagonal matrices . If is not unital and tracepreserving, the image will thus be equal to , with the off-diagonal blocks set to zero. In particular, the two-norm deviation of a map from its projection onto is given by
| (171) |
Based on the arguments used to establish Theorem 38, we can derive the following variant, which includes a converse statement.
Theorem 39
(Informational completeness and unitary designs). Let be a set of unitary channels. Then the following are equivalent:
Every unital and trace-preserving map can be written as an affine combination of the , with coefficients given by , where C = d(d + 1)(d2 − 1).
The set forms a unitary 2-design.
Proof. To show that (ii) implies (i) we apply Theorem 38. From Eq. (167) we can read of that
| (172) |
Thus, the linear expansion of in terms of the unitary 2-design is affine.
It remains to establish the converse statement. Let be a set of unitary channels fulfilling
| (173) |
for all .
A handy criterion for verifying that is a unitary 2-design can be formulated in terms of its frame potential
| (174) |
where again Uk is the unitary matrix defining the unitary channel . A set of unitary gates is a unitary 2-design if and only if P = 2 [39, Theorem 2]. In fact, Eq. (173) allows to calculate the frame potential as follows.
Inserting (the depolarising channel), we find that
| (175) |
Note that this implies that the set constitutes a unitary 1-design. Therefore, Eq. (173) takes the form
| (176) |
for all . Let the left hand side of Eq. (176) define a linear operator . Then Eq. (176) implies
| (177) |
| (178) |
| (179) |
and hence
| (180) |
This completes the proof. □
Note that for quantum channels, the affine expansion is almost convex in the sense that .
G. A new interpretation for the unitarity
In this section, we provide a proof for Theorem 3 and elaborate on its implications. The proof is most naturally phrased by decomposing the linear hull of unital and trace preserving maps into endomorphism acting on the spaces that carry irreducible representations of the unitary channels. In the proof of Theorem 38 we have explicitly seen that the projection of any map onto has the block-diagonal structure:
where . For channels that are already unital and trace preserving, this projection acts as the identity and x1 = 1. Particular examples of this class are unitary channels and the depolarizing channel acting as on X ∈ Hd. Unitary channels are also special in the sense that they are normalised with respect to the inner products defined in Eqs. (8), (9) and (168):
In fact, unitary channels are the only maps with this property (provided that we also adhere to our convention of normalizing maps with respect to the trace-norm of the Choi matrix). Combining this feature with the “block diagonal” structure of unitary channels yields
This computation implies that a map is unitary if and only if
equals one. Otherwise the unitarity is strictly smaller. For instance, for the depolarizing channel. This definition of the unitarity is equivalent to the one presented in Eq. (6), see [4, Proposition 1]. The argument outlined above succinctly summarises the main motivation for this figure of merit: it captures the coherence of a noise channel .
Equipped with this characterisation of the unitarity, we can now give the proof for the interpretation of the unitarity as the variance of the AGF with respect to a unitary 2-design.
Proof of Theorem 3. The unitarity may be expressed as
| (181) |
Eq. (175) allows us to rewrite x1 as an average over a unitary 1-design :
Let us now assume that the set is also a 2-design. Then, Eq. (166) implies
Inserting both expressions into Eq. (181) yields
where we have used linearity of the expectation value and the fact that the random variable is real-valued. Finally, we employ the relation between and presented in Eq. (168) to conclude
because variances are invariant under constant shifts and depend quadratically on scaling factors. This establishes Theorem 3. □
We conclude this section with a more speculative note regarding the possible applications for Theorem 3. A direct estimation procedure for the unitarity has been proposed in Ref. [4]. Inspired by randomised benchmarking, this procedure is robust towards SPAM errors, but has other drawbacks: Estimating the purity of outcome states directly is challenging, because the operator square function is not linear. Although Wallman et al. have found ways around this issue, their approaches are not yet completely satisfactory.
We propose an alternative approach based on Theorem 3. It might be conceivable that techniques like importance sampling could be employed to efficiently estimate this variance – and thus the unitarity – from “few” samples. The fourth moment bounds computed here could potentially serve as bounds on the “variance of this variance” and help control the convergence.
H. Numerical demonstrations
We emphasise that the main contributions of this work are of theoretical nature (we prove several Theorems). Nonetheless, we would also like to demonstrate the practical feasibility of our reconstruction procedure (3) and discuss some of its subtleties. The Matlab code for our numerical experiments can be found on GitHub [52].
Let denote a unitary quantum channel. Given measurements fi from Eq. (84) with Clifford unitaries Ci we approximately recover using the semi-definite program (SDP) (86) with q = 2. In the numerical experiments we draw a three-qubit unitary channel uniformly at random, the m Clifford unitaries for the measurements uniformly at random, and the noise ϵ ∈ ℝm uniformly from a sphere with radius η, i.e., .
Then we solve the SDP using Matlab, CVX and SDPT3. The resulting average reconstruction error is plotted against the number of measurement settings m and the noise strength η in Figure 1 and Figure 2 (left), respectively. As a comparison we run simulations for Haar random unitary measurements, see Figure 2 (right). We find that the measurements based on random Clifford unitaries perform equally well as measurements based on Haar random unitaries. This is in agreement with a similar observation made for the noiseless case by two of the authors in Ref. [26].
Figure 2.
Comparison of the reconstruction (3) from AGFs (2) with random Clifford unitaries (left) and Haar random unitaries (right). The plots show the dependence of the observed average reconstruction error , on the noise strength for 3 qubits and different numbers of AGFs m. The error bars denote the observed standard deviation. The averages are taken over 100 samples of random i.i.d. measurements and channels (non-uniform). The Matlab code and data used to create these plots can be found on GitHub [52].
We observed that sometimes the SDP solver cannot find a solution. We also tested the use of Mosek instead of SDPT3. We find that the Mosek solver is faster but has more problems finding the correct solution. For the cases where the SDP solver does not exit with status “solved” we relax the machine precision on the equality constraints in the SDP (86) and change the measurement noise by a machine precision amount. More explicitly, for an integer j ≥ 0 we try to solve
| (182) |
where eps denotes the machine precision and Tr1 and Tr2 the partial traces on L(ℂd ⊗ ℂd). We successively try to solve these SDPs for j = 0,1,2, …, 6. Moreover, we change the measurement noise ϵ′ + ζ in each of these trials, where each ζi = eps · gi with is an independent normally distributed random number. For the Clifford type measurement (Figures 1 and 2 left) a total of 24400 channels were reconstructed and j was increased 1865 many times in total. For the Haar random measurement unitaries (Figure 2 left) a total of 12900 channels were reconstructed and j was increased 950 times. So, we observed that with a probability of ~ 7.5% the SDP solver cannot solve the given SDP with machine precision constraints.
Some of the error bars in the plots in Figures 1 and 2 might seem quite large, which we would like to comment on. Note that in compressed sensing it is typical to have a phase-transition from having no recovery for too small numbers of measurements m to having a recovery with very high probability once m exceeds a certain threshold. This phase transition region becomes smeared out if the noise strength is increased. For those m in the phase transition region the reconstruction errors are expected to fluctuate a lot, which we observe in the plots.
The slope of the linear part of plots εrec(m) in Figure 1 is roughly δεrec(m)/δm ≈ −1.3. This means that the reconstruction error scales like εrec(m) ~ m−1.3, which is better than Theorem 2 suggests. The reason for this discrepancy is that the theorem also bounds systematic errors and even adversarial noise whereas in the numerics we have drawn i uniformly from a sphere, i.e., i are i.i.d. up to a rescaling.
ACKNOWLEDGEMENTS
We thank Steven T. Flammia, Christian Krumnow, Robin Harper, and Michaeł Horodecki for inspiring discussions and helpful comments. RK is particularly grateful for a “peaceful disagreement” (we borrow this term from Ref. [84]) with Mateus Araújo that ultimately led to our current understanding of the relation between Clifford gates and tight frames. We used code from references [85–87] to run our simulations. The work of IR, RK, and JE was funded by AQuS, DFG (SPP1798 CoSIP, EI 519/9-1, EI 519/7-1, EI 519/14-1), the ERC (TAQ) and the Templeton Foundation. Parts of YKL’s work were carried out in the context of the AFOSR MURI project “Optimal Measurements for Scalable Quantum Technologies.” Contributions to this work by NIST, an agency of the US government, are not subject to US copyright. Any mention of commercial products does not indicate endorsement by NIST. DG’s work has been supported by the Excellence Initiative of the German Federal and State Governments (ZUK 81), the ARO under contract W911NF-14-1-0098 (Quantum Characterization, Verification, and Validation), Universities Australia and DAAD’s Joint Research Co-operation Scheme (using funds provided by the German Federal Ministry of Education and Research), and the DFG (SPP1798 CoSIP, project B01 of CRC 183). The work of MK was funded by the National Science Centre, Poland within the project Polonez (2015/19/P/ST2/03001) which has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 665778.
References
- [1].Knill E, Leibfried D, Reichle R, Britton J, Blakestad RB, Jost JD, Langer C, Ozeri R, Seidelin S, and Wineland DJ, Randomized benchmarking of quantum gates, Phys. Rev. A 77, 012307 (2008), 0707.0963. [Google Scholar]
- [2].Magesan E, Gambetta JM, and Emerson J, Characterizing quantum gates via randomized benchmarking, Phys. Rev. A 85, 042311 (2012), arXiv:1109.6887 [quant-ph]. [Google Scholar]
- [3].Magesan E, Gambetta JM, and Emerson J, Scalable and robust randomized benchmarking of quantum processes, Phys. Rev. Lett. 106, 180504 (2011), arXiv:1009.3639 [quant-ph]. [DOI] [PubMed] [Google Scholar]
- [4].Wallman J, Granade C, Harper R, and Flammia ST, Estimating the coherence of noise, New J. Phys. 17, 113020 (2015), arXiv:1503.07865 [quant-ph]. [Google Scholar]
- [5].Wallman JJ, Randomized benchmarking with gate-dependent noise, arXiv:1703.09835 [quant-ph]. [Google Scholar]
- [6].Helsen J, Wallman J, Flammia ST, and Wehner S, Multi-qubit randomized benchmarking using few samples, (2017), arXiv:1701.04299. [Google Scholar]
- [7].Wallman JJ and Flammia ST, Randomized benchmarking with confidence, New J. Phys. 16, 103032 (2014), arXiv:1404.6025 [quant-ph]. [Google Scholar]
- [8].Blume-Kohout R, King Gamble J, Nielsen E, Mizrahi J, Sterk JD, and Maunz P, Robust, self-consistent, closed-form tomography of quantum logic gates on a trapped ion qubit, arXiv:1310.4492 [quant-ph]. [Google Scholar]
- [9].Flammia ST, Gross D, Liu Y-K, and Eisert J, Quantum tomography via compressed sensing: error bounds, sample complexity and efficient estimators, New J. Phys. 14, 095022 (2012), arXiv:1205.2300 [quant-ph]. [Google Scholar]
- [10].Baldwin CH, Kalev A, and Deutsch IH, Quantum process tomography of unitary and near-unitary maps, Phys. Rev. A 90, 012110 (2014), arXiv:1404.2877. [Google Scholar]
- [11].Kliesch M, Kueng R, Eisert J, and Gross D, Improving compressed sensing with the diamond norm, IEEE Trans. Inf. Th. 62, 7445 (2016), arXiv:1511.01513. [Google Scholar]
- [12].Kliesch M, Kueng R, Eisert J, and Gross D, Guaranteed recovery of quantum processes from few measurements, arXiv:1701.03135 [quant-ph]. [Google Scholar]
- [13].Holzäpfel M, Baumgratz T, Cramer M, and Plenio MB, Scalable reconstruction of unitary processes and Hamiltonians, Phys. Rev. A 91, 042129 (2015), arXiv:1411.6379 [quant-ph]. [Google Scholar]
- [14].Gross D, Liu Y-K, Flammia ST, Becker S, and Eisert J, Quantum state tomography via compressed sensing, Phys. Rev. Lett. 105, 150401 (2010), arXiv:0909.3304 [quant-ph]. [DOI] [PubMed] [Google Scholar]
- [15].Gross D, Recovering low-rank matrices from few coefficients in any basis, IEEE Trans. Inf. Th. 57, 1548 (2011), arXiv:0910.1879 [cs.IT]. [Google Scholar]
- [16].Liu Y-K, Universal low-rank matrix recovery from Pauli measurements, Adv. Neural Inf. Process. Syst, 1638 (2011), 1103.2816. [Google Scholar]
- [17].Shabani A, Kosut RL, Mohseni M, Rabitz H, Broome MA, Almeida MP, Fedrizzi A, and White AG, Efficient measurement of quantum dynamics via compressive sensing, Physical Review Letters 106, 100401 (2011), arXiv:0910.5498 [quant-ph]. [DOI] [PubMed] [Google Scholar]
- [18].Kalev A, Kosut RL, and Deutsch IH, Quantum tomography protocols with positivity are compressed sensing protocols, npj Quantum Information 1, 15018 (2015), arXiv:1502.00536. [Google Scholar]
- [19].Kueng R, Low rank matrix recovery from few orthonormal basis measurements, in Sampling Theory and Applications (SampTA), 2015 International Conference on (2015) pp. 402–406. [Google Scholar]
- [20].Kabanava M, Kueng R, Rauhut H, and Terstiege U, Stable low-rank matrix recovery via null space properties, arXiv:1507.07184 [cs.IT]. [Google Scholar]
- [21].Cramer M, Plenio MB, Flammia ST, Somma R, Gross D, Bartlett SD, Landon-Cardinal O, Poulin D, and Liu Y-K, Efficient quantum state tomography, Nat. Commun. 1, 149 (2010). [DOI] [PubMed] [Google Scholar]
- [22].Lanyon B, Maier C, Holzapfel M, Baumgratz T, Hempel C, Jurcevic P, Dhand I, Buyskikh A, Daley A, Cramer M, Plenio M, Blatt R, and Roos C, Efficient tomography of a quantum many-body system, Nat. Phys. 13, 1158 (2017), 1612.08000. [Google Scholar]
- [23].da Silva MP, Landon-Cardinal O, and Poulin D, Practical characterization of quantum devices without tomography, Phys. Rev. Lett. 107, 210404 (2011). [DOI] [PubMed] [Google Scholar]
- [24].Landon-Cardinal O and Poulin D, Practical learning method for multi-scale entangled states, New J. Phys. 14, 085004 (2012). [Google Scholar]
- [25].Kimmel S, da Silva MP, Ryan CA, Johnson BR, and Ohki T, Robust extraction of tomographic information via randomized benchmarking, Phys. Rev. X 4, 011050 (2014). [Google Scholar]
- [26].Kimmel S and Liu YK, Phase retrieval using unitary 2-designs, in 2017 International Conference on Sampling Theory and Applications (SampTA) (2017) pp. 345–349, 1510.08887. [Google Scholar]
- [27].Nielsen MA and Chuang IL, Quantum computation and quantum information (Cambridge University Press, 2010). [Google Scholar]
- [28].Flammia ST and Liu Y-K, Direct fidelity estimation from few Pauli measurements, Phys. Rev. Lett. 106, 230501 (2011). [DOI] [PubMed] [Google Scholar]
- [29].Acin A, Bloch I, Buhrman H, Calarco T, Eichler C, Eisert J, Esteve D, Gisin N, Glaser SJ, Jelezko F, Kuhr S, Lewenstein M, Riedel MF, Schmidt PO, Thew R, Wallraff A, Walmsley I, and Wilhelm FK, The European quantum technologies roadmap, (2017), arXiv:1712.03773 [quant-ph]. [Google Scholar]
- [30].Kueng R, Long DM, Doherty AC, and Flammia ST, Comparing experiments to the fault-tolerance threshold, arXiv:1510.05653 [quant-ph]. [DOI] [PubMed] [Google Scholar]
- [31].Wallman JJ, Bounding experimental quantum error rates relative to fault-tolerant thresholds, arXiv:1511.00727 [quant-ph]. [Google Scholar]
- [32].Zhu H, Kueng R, Grassl M, and Gross D, The Clifford group fails gracefully to be a unitary 4-design, arXiv:1609.08172 [quant-ph]. [Google Scholar]
- [33].Helsen J, Wallman JJ, and Wehner S, Representations of the multi-qubit Clifford group, arXiv:1609.08188 [quant-ph]. [Google Scholar]
- [34].Gross D, Nezami S, and Walter M, Schur-Weyl Duality for the Clifford Group with Applications, arXiv preprint arXiv:1712.08628 (2017). [Google Scholar]
- [35].Collins B, Moments and cumulants of polynomial random variables on unitary groups, the Itzykson-Zuber integral, and free probability, Int. Math. Res. Not. 2003, 953 (2003), math-ph/0205010. [Google Scholar]
- [36].Collins B and Sniady P, Representations of Lie groups and random matrices, Trans. Amer. Math. Soc. 361, 3269 (2009). [Google Scholar]
- [37].Mendl CB and Wolf MM, Unital quantum channels - convex structure and revivals of Birkhoff’s theorem, Comm. Math. Phys. 289, 1057 (2009), arXiv:0806.2820 [quant-ph]. [Google Scholar]
- [38].Dankert C, Cleve R, Emerson J, and Livine E, Exact and approximate unitary 2-designs and their application to fidelity estimation, Phys. Rev. A 80, 012304 (2009). [Google Scholar]
- [39].Gross D, Audenaert K, and Eisert J, Evenly distributed unitaries: on the structure of unitary designs, J. Math. Phys. 48, 052104, quant-ph/0611002. [Google Scholar]
- [40].Delsarte P, Goethals J, and Seidel J, Spherical codes and designs, Geom. Dedicata 6, 363 (1977). [Google Scholar]
- [41].Renes JM, Blume-Kohout R, Scott AJ, and Caves CM, Symmetric informationally complete quantum measurements, J. Math. Phys. 45, 2171 (2004), quant-ph/0310075. [Google Scholar]
- [42].Zhu H, Multiqubit Clifford groups are unitary 3-designs, arXiv:1510.02619 [quant-ph]. [Google Scholar]
- [43].Webb Z, The Clifford group forms a unitary 3-design, arXiv:1510.02769 [quant-ph]. [Google Scholar]
- [44].Kueng R and Gross D, Qubit stabilizer states are complex projective 3-designs, arXiv:1510.02767 [quant-ph]. [Google Scholar]
- [45].Scott AJ, Tight informationally complete quantum measurements, J. Phys. A Math. Gen. 39, 13507 (2006), quantph/0604049. [Google Scholar]
- [46].Appleby DM, Symmetric informationally complete-positive operator valued measures and the extended Clifford group, J. Math. Phys. 46, 052107 (2005), quant-ph/0412001. [Google Scholar]
- [47].Gross D, Krahmer F, and Kueng R, A partial derandomization of PhaseLift using spherical designs, J. Fourier Anal. Appl. 21, 229 (2015), arXiv:1310.2267 [cs.IT]. [Google Scholar]
- [48].Scott AJ, Optimizing quantum process tomography with unitary 2-designs, J. Phys. A 41, 055308 (2008). [Google Scholar]
- [49].Chau HF, Unconditionally secure key distribution in higher dimensions by depolarization, IEEE Trans. Inf. Theory 51, 1451 (2004). [Google Scholar]
- [50].Ambainis A, Bouda J, and Winter A, Nonmalleable encryption of quantum information, J. Math. Phys. 50, 042106 (2009), arXiv:0808.0353. [Google Scholar]
- [51].Fazel M, Hindi H, and Boyd S, A rank minimization heuristic with application to minimum order system approximation, in Proceedings American Control Conference, Vol. 6 (2001) pp. 4734–4739. [Google Scholar]
- [52].Roth I, Kueng R, Kimmel S, Liu Y-K, Gross D, Eisert J, and Kliesch M, Quantum process tomography with average gate fidelities, GitHub repository https://github.com/MartKl/Quantum_process_tomography_with_average_gate_fidelities (2017). [Google Scholar]
- [53].Candès EJ, Strohmer T, and Voroninski V, Phaselift: exact and stable signal recovery from magnitude measurements via convex programming. Commun. Pure Appl. Math. 66, 1241 (2013), arXiv:1109.4499 [cs.IT]. [Google Scholar]
- [54].Candès E and Li X, Solving quadratic equations via PhaseLift when there are about as many equations as unknowns, Found. Comput. Math. 14, 1017 (2014), arXiv:1208.6247 [cs.IT]. [Google Scholar]
- [55].Kueng R, Rauhut H, and Terstiege U, Low rank matrix recovery from rank one measurements, Appl. Comp. Harm. Anal. (2015), arXiv:1410.6913 [cs.IT]. [Google Scholar]
- [56].Krahmer F and Liu YK, Phase Retrieval Without Small-Ball Probability Assumptions, IEEE Trans. Inf. Th. 64, 485 (2018), 1604.07281. [Google Scholar]
- [57].The cardinality of the Clifford group grows superpolynomially in the Hilbert space dimension d. Therefore, the non-spikiness with respect to the Clifford group quickly corresponds to a demanding number of constraints. In fact, about 108 and 1013 constraints are already required for 3-qubits and 4-qubits, respectively.
- [58]. is defined so that and for all traceless X.
- [59].Feng G, Wallman JJ, Buonacorsi B, Cho FH, Park DK, Xin T, Lu D, Baugh J, and Laflamme R, Estimating the coherence of noise in quantum control of a solid-state qubit, Phys. Rev. Lett. 117, 260501 (2016), arXiv:1603.03761 [quant-ph]. [DOI] [PubMed] [Google Scholar]
- [60].Magesan E, Blume-Kohout R, and Emerson J, Gate fidelity fluctuations and quantum process invariants, Phys. Rev. A 84, 012309 (2011). [Google Scholar]
- [61].Kueng R, Zhu H, and Gross D, Low rank matrix recovery from Clifford orbits, arXiv:1610.08070 [cs.IT]. [Google Scholar]
- [62].Kueng R, Zhu H, and Gross D, Distinguishing quantum states using Clifford orbits, arXiv:1609.08595 [quant-ph]. [Google Scholar]
- [63].Riofrio CA, Gross D, Flammia ST, Monz T, Nigg D, Blatt R, and Eisert J, Experimental quantum compressed sensing for a seven-qubit system, Nat. Commun 8, 15305 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Horodecki M, Horodecki P, and Horodecki R, General teleportation channel, singlet fraction, and quasidistillation, Phys. Rev. A 60, 1888 (1999). [Google Scholar]
- [65].Nielsen MA, A simple formula for the average gate fidelity of a quantum dynamical operation, Phys. Lett. A 303, 249 (2002), quant-ph/0205035. [Google Scholar]
- [66].Goodman R and Wallach NR, Symmetry, representations, and invariants (Springer, Berlin, 2009). [Google Scholar]
- [67].Fulton W and Harris J, Representation theory, Vol. 129 (Springer Science & Business Media, 1991). [Google Scholar]
- [68].Wigner EP, Group theory and its application to the quantum mechanics of atomic spectra (Academic Press, London, 1959). [Google Scholar]
- [69].This way of stating the result of Ref. [36] was brought to our attention by study notes of K. Audenaert.
- [70].Foucart S and Rauhut H, A mathematical introduction to compressive sensing (Springer, Heidelberg, 2013). [Google Scholar]
- [71].Tropp JA, Convex recovery of a structured signal from independent random linear measurements, in Sampling Theory, a Renaissance, edited by Pfander EG (Springer, 2015) pp. 67–101, arXiv:1405.1102. [Google Scholar]
- [72].Mendelson S, Learning without concentration, J. ACM 62, 21:1 (2015), arXiv:1401.0304 [cs.LG]. [Google Scholar]
- [73].Koltchinskii V and Mendelson S, Bounding the smallest singular value of a random matrix without concentration, International Mathematics Research Notices 2015, rnv096 (2015), arXiv:1312.3580 [math.PR]. [Google Scholar]
- [74].Kimmel S and Liu YK, Phase retrieval using unitary 2-designs, in 2017 International Conference on Sampling Theory and Applications (SampTA) (2017) pp. 345–349, 1510.08887. [Google Scholar]
- [75].Vershynin R, Introduction to the non-asymptotic analysis of random matrices, arXiv:1011.3027 [math.PR]. [Google Scholar]
- [76].Tropp JA, User friendly tools for random matrices. An introduction. Preprint (2012). [Google Scholar]
- [77].Calderbank AR, Rains EM, Shor PW, and Sloane NJA, Quantum error correction via codes over GF(4), IEEE Transactions on Information Theory 44, 1369 (1998), arXiv:quant-ph/9608006. [Google Scholar]
- [78].Haah J, Harrow AW, Ji Z, Wu X, and Yu N, Sample-optimal tomography of quantum states, arXiv:1508.01797 [quant-ph]. [Google Scholar]
- [79].Cover TM and Thomas JA, Elements of information theory (John Wiley & Sons, 2012). [Google Scholar]
- [80].Diaconis P and Shahshahani M, On the Eigenvalues of Random Matrices, Journal of Applied Probability 31, 49 (1994). [Google Scholar]
- [81].Vershynin R, Introduction to the non-asymptotic analysis of random matrices, in Compressed Sensing: Theory and Applications (Cambridge University Press, 2012) pp. 210–268, arXiv:1011.3027 [math.PR]. [Google Scholar]
- [82].Foucart S and Rauhut H, A mathematical introduction to compressive sensing (Springer, 2013). [Google Scholar]
- [83]. More explicitly, for X ∈ Hd we can calculate. using Theorem 5.
- [84].Araújo M, More Quantum, (2016). [Google Scholar]
- [85].Johnston N, QETLAB: A MATLAB toolbox for quantum entanglement, version 0.9, http://qetlab.com (2016).
- [86].Magesan E, Random Clifford sampler for Matlab, (2011). [Google Scholar]
- [87].da Silva MP, QIP Matlab Library, https://github.com/marcusps/QIP.m (2012).