Continuous Phase Estimation for Phase-Locked Neural Stimulation Using an Autoregressive Model for Signal Prediction

Abstract

Neural oscillations enable communication between brain regions. Closed-loop brain stimulation attempts to modify this activity by stimulation locked to the phase of concurrent neural oscillations. If successful, this may be a major step forward for clinical brain stimulation therapies. The challenge for effective phase-locked systems is accurately calculating the phase of a source oscillation in real time. The basic operations of filtering the source signal to a frequency band of interest and extracting its phase cannot be performed in real time without distortion. We present a method for continuously estimating phase that reduces this distortion by using an autoregressive model to predict the future of a filtered signal before passing it though the Hilbert transform. This method outperforms published approaches on real data and is available as a reusable open-source module. We also examine the challenge of compensating for the filter phase response and outline promising directions of future study.

I. Introduction

Oscillatory synchrony of the local field potential (LFP) between brain regions appears to be correlated with the strength of communication between these regions [1]–[3]. Manipulating synchrony might alter network structure and/or its behavioral correlates, with both experimental and clinical applications [2], [3]. To test this, we must first develop methods to reliably modify oscillatory synchrony.

One possible method for modifying synchrony is closed-loop, phase-locked stimulation. In this paradigm, stimulation pulses are delivered to a target region at a particular phase of a band-limited recording from a source region. In [3], for example, Siegle and Wilson delivered optical pulses to a rat hippocampus on either the rising or falling phase of local 4–12 Hz (theta) oscillations. Even with an extremely basic method of phase identification—mapping maxima and minima of the filtered signal to 0° and 180°, respectively—the paradigm produced a small but significant behavioral effect. Thus, we hypothesize that a more flexible and reliable algorithm for real-time phase estimation could yield even stronger effects.

In [4], Chen et al. describe a more sophisticated method that can estimate the phase of any sample of a real-time recording, rather than just identifying peaks and troughs. They used a pipeline of passband optimization, zero-phase filtering, autoregressive (AR) model-based prediction, and the Hilbert transform to compute each phase estimate. As the processing must occur in real time, it would be impractical to repeat this computation for every sample, so they used an analysis frequency much lower than the sampling rate. For their tests, they analyzed 10 samples per second, with a band of interest of 4–9 Hz. This allowed at least one phase estimation per oscillatory cycle. To target a specific phase for stimulation given these sparse estimates, they also estimated the instantaneous frequency (IF) from the Hilbert transform output and used this to predict a future time at which the oscillation would reach the target phase.

The algorithm in [4] has higher phase resolution than [3], but sacrifices temporal resolution in that it only analyzes one sample per estimation period. Using the parameters in [4], the identified phase may precede the target phase of a given cycle by as much as 100 ms (0.9 cycles). Since the frequency characteristics of LFPs can be highly dynamic, the correct temporal delay to reach the target phase becomes less certain as the angular distance to be traversed increases. This adds uncertainty to the ultimate stimulation phase even if the estimated phase is precise. Our algorithm, based on [4] and presented below, efficiently outputs a phase for each input sample (“continuously”), allowing the stimulation delay to be reduced and thus the accuracy to be increased.

Even when not adding a phase-dependent delay after phase estimation, another source of stimulation phase variance in real systems is transmission delay, defined as the total elapsed time between the recorded sample that triggers a stimulation and the pulse itself. For instance, the standard deviation of this delay in [3] was about 7 ms, or greater than 30° at their highest frequency of 12 Hz. To minimize transmission delay variance, we compared phase event timestamps to the sample clock within our stimulation procedure, allowing compensation for transmission delay.

II. Methods

A. Algorithm Testing and Data Collection

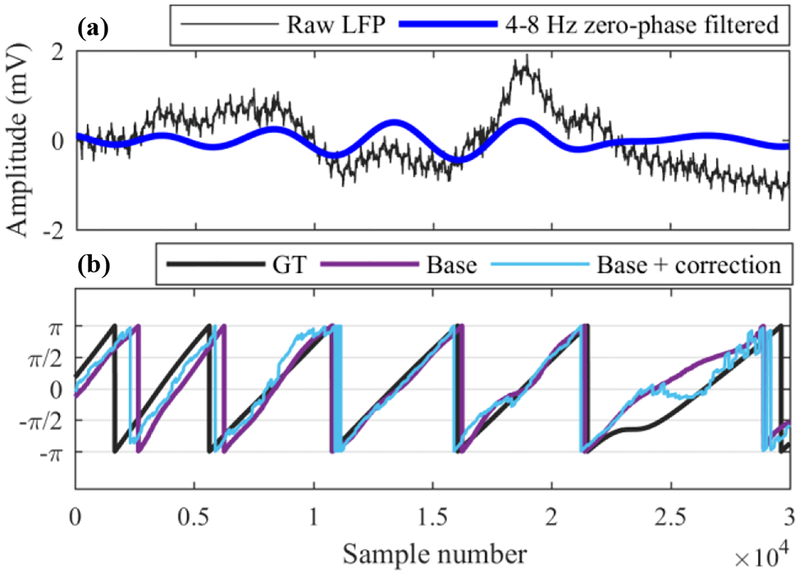
LFP datasets were collected via the Open Ephys electrophysiology system [5] at a sampling rate of 30 kHz (Fig. 1(a)). During 30-minute sessions, we recorded LFPs from the infralimbic cortex (IL) and basolateral amygdala (BLA) of male Long-Evans rats (Charles River Laboratory, MA). We stimulated BLA with charge balanced biphasic pulses (pulse width: 90 μs, and pulse amplitude: 100 μA) approximately once every second, locked to the 4–8 Hz phase of IL LFP using the base phase estimator described below. All procedures involving animal models were approved by the Institutional Animal Care and Use Committee.

Figure 1.

Example second of raw and theta-band zero-phase filtered LFP data recorded from IL (a) and corresponding ground truth (GT) phase and phase estimates with and without frequency-based correction (b).

B. Offline Ground Truth Phase

We obtained a ground truth phase using the filter-Hilbert method [6]. First, we zero-phase filtered each full raw dataset (MATLAB’s “filtfilt”) using a 2nd-order Butterworth bandpass filter with 3 dB cutoff frequencies at 4 and 8 Hz (Fig. 1(a)). We obtained the phase ϕ(t) at each timepoint t from the complex analytic signal z(t), defined in terms of the filtered signal x(t), its Hilbert transform H{x(t)}, and the imaginary unit j:

$$z\left(t\right)=x\left(t\right)+jH\left\{x\left(t\right)\right\}$$ (1)

$$\varphi \left(t\right)=\text{arg }z\left(t\right)$$ (2)

Note that the instantaneous frequency ω(t), used below, can be defined as the slope of the unwrapped phase:

$$\omega \left(t\right)={\varphi }_{\text{uw}}\left(t+1\right)-{\varphi }_{\text{uw}}\left(t\right)$$ (3)

The unwrapped phase ϕ_uw(t) is the phase ϕ(t) with each sample-to-sample difference of greater than π radians in magnitude replaced with its smallest equivalent modulo 2π.

C. Continuous Real-Time Phase Estimator

Our base real-time phase algorithm effectively adapts the offline algorithm to operate causally, with additional steps to reduce distortion. First, instead of zero-phase filtering, we simply applied the same Butterworth bandpass filter in the forward direction only (e.g. using the “filter” function when simulating in MATLAB). We found that this was less error-prone than the method of short-time zero-phase filtering used in [4], but see below for further discussion.

Second, we adapted the Hilbert transform step to operate without distortion on short buffers of current data containing about 160 samples per iteration. Since the Hilbert transform, and thus the phase via analytic signal, relies on Fourier decomposition, its input must be long enough to capture the oscillatory characteristics of the signal. Furthermore, since the discrete Fourier transform assumes a periodic signal, the jump discontinuity between the start and end of successive data segments creates an edge distortion at both ends of the transform’s output. To output an accurate phase for the most recent samples on each analysis iteration, we must therefore pad current data with both past and predicted future filtered data. Chen et al. used an AR model for prediction, and we adopted the same strategy.

We used a Hilbert input buffer of 8192 samples in total, which spans about 1.1 cycles of a 4 Hz oscillation at our sampling rate of 30 kHz. Of these, if there were n current samples, the 7168–n first samples were from past data and the 1024 last samples were predicted future data. To predict future samples, we applied an AR(20) model:

$$x\left[t\right]=\sum _{k=1}^{20}{\alpha }_{k}x\left[t-k\right],$$ (4)

where α₁, …,α₂₀ are the model parameters. We chose 20 as the model order based on the optimal order found in [4]; however, we later found that using an order as low as 3 yielded similar results. We did not fit the model on every iteration; rather, an asynchronous thread refitted it every 50 ms on the past and current portions of the latest Hilbert input buffer. We used the Burg lattice method for AR model fitting.

After filling the Hilbert input buffer, the phase was estimated as in the offline algorithm (1–2). The phases of the current timepoints were extracted from the longer buffer, converted to degrees, and passed through a final “glitch correction” step before stimulation scheduling. Glitch correction removed short negative phase excursions at buffer edges and most jumps of larger than 180° (other than normal phase wraps at wave troughs). An example of the final estimated phase is shown in Fig. 1(b).

D. Phase Detection and Stimulation Scheduling

To minimize the stimulation phase variation, we paired the continuous phase estimator with a stimulation program that equalized round-trip delay. This program received software events from the Open Ephys GUI whenever the estimated phase crossed a certain threshold. It then measured the delay in real time by comparing the event timestamps with a counter tied to the acquisition sample clock. Each closed-loop run consisted of an initial delay measurement period lasting about 5 minutes, followed by the 30-minute stimulation session.

During the measurement period, the stimulation program received events and maintained a running maximum of the acquisition-to-reception delay. This delay was variable due to both USB and software buffering in the data acquisition system, but large spikes in delay were rare. Once it appeared that the running maximum was exceeding most events’ delay, we locked this maximum to prevent it from changing during the stimulation session. We also sometimes added up to 30 samples (1 ms) of extra delay to protect against unexpected future increases. Finally, we converted this total “target” delay to degrees at 6 Hz and set the phase event threshold to the target phase minus this offset. A typical offset was 65°.

During the stimulation session, we stimulated at most once per second. Each time the stimulation program received an event, it waited until the current delay was greater than or equal to the target delay before firing the pulse. Each time a pulse fired, we sent a digital event back to the acquisition software. We then used the timestamp difference between the threshold crossing and stimulation events to analyze delay.

E. Phase Estimator with Frequency-Based Correction

Although we had limited success with using zero-phase filtering in the real-time phase estimator, we explored other methods to compensate for the phase distortion caused by filtering causally. Our preferred approach was a correction based on the known filter phase response. We estimated the IF in real time by applying (3), identified the corresponding filter phase response, then subtracted this correction from the phase estimate right before the glitch correction step.

We have prototyped this method in MATLAB and tested it on recorded data. Then, to improve its performance, we made three modifications. First, to balance smoothness of the final phase with accuracy, we averaged the IF within each buffer. Second, we modified the Hilbert input buffer by lengthening it by a factor of 2 and changing the amount of predicted data such that the current points fell at the center of the transform. This was important because the Hilbert transform edge distortions affect the IF dramatically, causing wide oscillations whose amplitude increase with distance from the buffer center and decrease overall with the length of the buffer. Finally, we found that dividing the correction factor by 2 before applying it improved results (possibly by mitigating the effect of extreme values). An example of the final corrected phase estimate is shown in Fig. 1(b), and its performance summarized in Table I.

TABLE I.

Statistics of estimated phase error relative to ground truth

Method	Mean ± 95% CI	Circ. Variance
Siegle and Wilson [3]a	−14.18 ± 0.43°	0.5421
Chen et al. [4]b	−5.43 ± 0.47°	0.5390
[4], no passband optimizationb	0.34 ± 0.52°	0.5817
Our method (base)	−2.56 ± 0.01°	0.4978
Our method + phase correction	−1.75 ± 0.01°	0.4584

^a.Only detects peaks (0°) and troughs (180°)

^b.Phases calculated at t₀ (one per buffer), before stimulation time estimation

III. Results

To assess phase-locking performance, we measured the circular mean and variance of real-time phase errors from the ground truth or target. Since an angular offset can usually be applied to the target to minimize mean phase error, the variance is usually a more meaningful measure of quality. However, for methods that only identify certain phases, such as the one in [3] that only detects peaks and troughs, stimulation phase accuracy depends heavily on the target phase. While adding a stimulation delay could still reduce the mean error, it would come at the cost of increased variance.

The phase-locking error derives from two broad sources: the phase estimate and the process of stimulation scheduling and delivery. We hypothesized that continuous estimation would reduce the variance of scheduling-derived error. Below, we compare our method to implementations of [3] and [4] in both types of error. Of our ten experimental sessions, the five with the lowest variance in both types of phase error are included for analysis, for a total of seven sessions.

A. Phase Estimate Accuracy

The phase estimate error compares the 4–8 Hz phases estimated by each algorithm to the ground truth, without regard for stimulation scheduling or transmission delay. For all methods, we excluded from results samples that may have coincided with stimulation artifacts. Based on visual inspection, this resulted in discarding the 1 ms preceding each digital stimulation marker. Also, since [3] and [4] are not continuous estimators, they each only output a phase corresponding to a small subset of the remaining samples: those identified as peaks and troughs for [3] and ten evenly-spaced samples per second for [4].

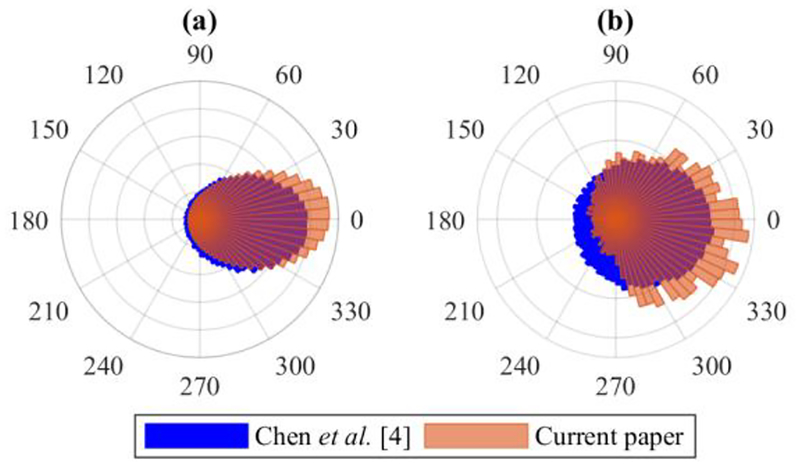
Table I shows the mean and circular variance (ranging from 0 to 1) of the error of each method; Fig. 2(a) compares our result with [4]. Our base method estimates phases more accurately on average and with less variance than both published methods. Adding phase correction further decreases the absolute mean error by 32% and the variance by 7.9%.

Figure 2.

Error of our estimated phases using frequency-based correction (a) and stimulus phases (b) compared to the algorithm in [4].

B. Stimulation Phase Accuracy

The stimulation phase error for each method is defined as the angular distance from the target phase of the ground truth phases at which stimulations either occurred (for our base method) or were scheduled to occur (for other, simulated methods). For [3], we defined the target phase to be the same as the phase being detected, although this is a somewhat arbitrary choice as Siegle and Wilson only aimed to stimulate sometime in the half-cycle following each detected peak or trough. The target phase for [4] was always 0°, and for our method was 180° for six of the sessions and 0° for the other.

Stimulation times for [4] are based on their formula [4, eq. (11)] that uses current phase and IF to predict future phase. Although Chen et al. did not test their algorithm in a real-time system, we assume that any implementation would allow for precise timing according to this formula. In contrast, the method in [3] does not schedule stimulation times precisely, but the authors include a histogram of stimulation delays [3, Fig. 3C]. We modeled this delay process with a gamma distribution (shape = 8, scale = 2.5) and added randomly drawn values from this to each sample time to obtain simulated stimulation times.

Table II shows the stimulation phase error statistics; Fig. 2(b) compares our base stimulation error with [4]. Our method times stimulations closer to the target phase on average and with less variance than both published methods. Although Siegle and Wilson’s method also achieves a relatively low variance, its performance is highly dependent on the target phase, as discussed previously. Note that our phase error variance only increased by 24% between the estimate and stimulation, compared to a 48% increase for [4], even though their stimulation scheduling formula takes instantaneous frequency into account while ours does not.

TABLE II.

Statistics of stimulation phase error relative to target

Method	Mean ± 95% CI	Circ. Variance
Siegle and Wilson [3]a	56.75 ± 0.56°	0.6344
Chen et al. [4]b	−10.85 ± 1.13°	0.7973
[4], no passband optimizationb	−18.78 ± 1.22°	0.8111
Our method (base)	−0.42 ± 1.92°	0.6196

^a.Stimulation errors assume a target equal to the detected phase (0° for peaks and 180° for troughs)

^b.Errors are for a target stimulation phase of 0°

IV. Discussion

Closed-loop stimulation is a promising method of altering neural communication, but locking stimulation precisely to the phase of an LFP oscillation has been a challenge. Siegle and Wilson have shown that even rough phase locking can be enough to induce observable changes in behavior. However, precise and accurate locking is likely to be dramatically more effective and will allow us to study the specific effects of fine-grained manipulations on directional connectivity and coherence. The continuous phase estimation method presented here allows stimulation to be targeted to any phase and improves on published algorithms in both phase estimate and stimulation phase error. Furthermore, it is implemented in open-source software freely available for use with the Open Ephys system at our GitHub page, https://github.com/tne-lab.

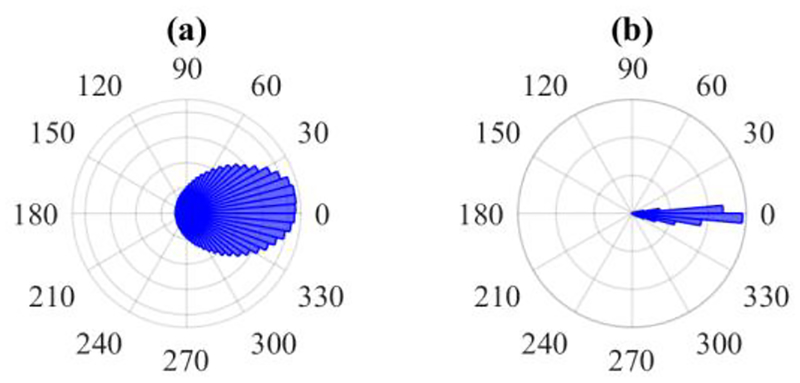
Nevertheless, there is still much room for improvement in phase locking precision. Most of the error variance in our base phase estimate comes from the bandpass filter’s variable phase response as a function of frequency (Fig. 3). Although the exact frequency spectrum at a specific point in a non-stationary signal cannot be determined, and especially not in a real-time system, one may still attempt to approximately compensate for the filter’s phase response. Our basic attempt to do so was the instantaneous-frequency-based correction, which does improve the base estimate, but only modestly. Within the framework of applying a frequency-based correction onto the base phase, future work should focus on further exploring the problem of local frequency estimation to find the measure that yields the best results after correction. For instance, the two methods presented in [7] may yield more accurate causal estimates of instantaneous frequency.

Figure 3.

Effect of causal filtering on phase estimate error versus all other changes necessitated by real-time operation. (a) Difference between post-processed phase with causal and zero-phase filtering. (b) Difference between real-time phase and post-processed phase with causal filtering.

Other strategies might also be more effective at reducing phase distortion from filtering. The following two are probably worthy of further investigation:

A. Zero-Phase Filtering

In contrast to [4], our phase estimator does not use zero-phase filtering before the Hilbert transform. We tested a zero-phase filtering step, but the ability to predict future data starting from the most recent timepoint (without the problem of edge distortion) when filtering forward outweighed the reduced phase distortion zero-phase filtering produces outside of buffer edges. Also, when training AR models on our zero-phase-filtered buffers, we found that the predictions often grew without bound. Nevertheless, future work should firmly establish whether incorporating zero-phase filtering in some way may improve the results of the base estimator.

B. Passband Optimization

The phase responses of infinite impulse response (IIR) bandpass filters (such as Butterworth filters) are closest to 0 near the center of the passband. Thus, the mean absolute phase distortion caused by filtering might be reduced if the passband were periodically recentered onto the signal of interest’s dominant frequency. This center frequency could be estimated by various methods, including causal IF (3) and Fourier-based algorithms.

Chen et al. narrow the passband down from 4–9 Hz on each iteration to include only the frequencies of peak power, using an AR model-based estimate of power spectral density [4]. This step reduces the phase estimate variance by 7.3% and the stimulation phase variance by 1.7%, and moves the mean stimulation phase 42% closer to the target (Tables I–II). Since the phase responses of IIR bandpass filters increase in steepness inversely with the width of the passband, a better strategy might be to simply shift the passband without narrowing it, unless contamination by oscillations at nearby frequencies is a concern. As with frequency-based direct phase correction, future work should also focus on finding the best local frequency metric for updating the passband.