The Aristotle Classifier: Using the whole glycomic profile to indicate a disease state.

Abstract

“The totality is not, as it were, a mere heap, but the whole is something besides the parts.” --Aristotle.

We built a classifier that uses the totality of the glycomic profile, not restricted to a few glycoforms, to differentiate samples from two different sources. This approach, which relies on using thousands of features, is a radical departure from current strategies, where most of the glycomic profile is ignored in favor of selecting a few features, or even a single feature, meant to capture the differences in sample types. The classifier can be used to differentiate the source of the material; applicable sources may be different species of animals, different protein production methods, or, most importantly, different biological states (disease vs. healthy). The classifier can be used on glycomic data in any form, including derivatized monosaccharides, intact glycans, or glycopeptides. It takes advantage of the fact that changing the source material can cause a change in the glycomic profile in many subtle ways; some glycoforms can be upregulated; some downregulated; some may appear unchanged, yet their proportion – with respect to other forms present – can be altered to a detectable degree. By classifying samples using the entirety of their glycan abundances, along with the glycans’ relative proportions to each other, The Aristotle Classifier is more effective at capturing the underlying trends than standard classification procedures used in glycomics, including PCA (Principal Components Analysis). It also outperforms workflows where a single, representative glycomic-based biomarker is used to classify samples. We describe The Aristotle Classifier and provide several examples of its utility for biomarker studies and other classification problems using glycomic data from several sources.

Graphical abstract

Introduction

Glycomic and glycoproteomic analyses offer unique approaches to diagnose and monitor diseases because glycosylation profiles change when cellular conditions change. Numerous examples in the literature show that specific glycans^1–6 or glycopeptides^7–10 can be used to discriminate healthy patients from those with various diseases. Disease classification, based on glycomic profiles, shows promise for an extensive and diverse set of ailments, including arthritis,⁹ cirrhosis,¹⁰ heart disease,³ Alzheimer’s Disease,¹¹ Parkinson’s Disease,⁴ chronic inflammatory disease,⁵ galactosaemia,⁶ and several cancers.^{1, 2, 7, 8}

One unique feature of glycomic data, distinct from genomic and proteomic data, is the consistent heterogeneity present on any glycosylated protein. While glycan heterogeneity is often viewed as a disadvantage, because the glycosylation signal of a protein of interest is distributed across many different glycoforms, presenting each form in substoichiometric quantities,¹² glycan heterogeneity offers a unique opportunity in the field of biomarker discovery because it affords researchers multiple features that can be used to classify a sample as “diseased” or “healthy.” Currently, glycomics researchers do not leverage information across the full glycosylation profile of a sample; rather, the standard approach in the field is to select a single feature^{6, 8} or a few features^{2, 4} that best discriminate the samples in a healthy or disease group. However, this approach necessarily eliminates information that could be beneficial in classifying samples.

We hypothesized that the current best practice in glycomics-based biomarker studies misses out on an opportunity to improve classification of samples (as disease/healthy for example). While only one or a few features are used currently for classification, all of the glycan signatures could be considered as interrelated features, which, en masse, could do a better job of defining disease than any individual component. Figure 1 exemplifies the concept using an artistic analogy. Figure 1A shows six separate image fragments which, in isolation, are not highly useful at classifying the object that they depict. These six fragments are analogous to six different glycoforms being considered as potential disease biomarkers. When these six images are viewed in context to each other (Figure 1B), they, are more useful at revealing the underlying object they represent; by analogy, in glycomics analyses, one can consider the glycans in context to each other by comparing samples’ glycan ratios instead of the glycans’ absolute abundances. The idea of considering a few selected glycan peak ratios as potential biomarkers is certainly not new, but the idea of using thousands of glycan ratios as a single scorable unit has never been considered in this field (to our knowledge.) This concept, by analogy, is represented in Figure 1C. Viewing the entire portrait (1C) is the most useful in classifying the image as a woman, compared to the fragmented data in Figures 1A or 1B. We sought to develop a new strategy for using glycomics data, using a “whole is greater than the parts” model, where all the glycans, and their relationships to each other are used to classify glycomic samples.

Figure 1:

Images from “On the Beach” by Victor Laredo. This art is taken from the New York Public Library Public Domain Collection at https://digitalcollections.nypl.org/items/5a11fd80–2892-0132–98d5–58d385a7bbd0 1A) Represents six image fragments which, individually, are difficult to use to identify the painting’s subject. 1B) The objects, arranged in the correct position and proportion to each other, are more telling of the underlying portrait. 1C) The entire portrait provides the most clarity for object identification.

The key barrier to overcome in classifying samples in this way is data analysis. There is no obvious parallel analysis strategy that could be borrowed from the field of proteomics, since the goal of a proteomics experiment is typically to find one feature, a protein, or a very small sub-set of features that can classify the sample. To find and use every relevant feature, one must consider sophisticated analysis tools that handle multiple data inputs. Principal Components Analysis (PCA) is a standard statistical approach used extensively in glycomics-based biomarker discovery efforts.^2,4,7,9 It can be used to show how well data sets are separable from each other; classification using all the glycan abundances (but not all their ratios) can be done using this method. PCA is an unsupervised learning method, and it does not explicitly attempt to separate the samples by class; rather it is a dimensionality reduction technique.¹³ Therefore, it typically does a sub-optimal job of identifying useful trends in the data that can be used to classify samples. Supervised machine learning approaches, which are not yet used in glycomics analyses but certainly are used in other fields, do a better job of classifying data compared to unsupervised methods.^14,15 Their biggest disadvantage is the large number of patients’ samples that are needed to correctly classify the data.^14–16 The requirement of large patient data sets is particularly detrimental in many early biomarker discovery campaigns, especially when the disease to be studied is rare or samples are difficult to acquire. Without large sample sets, supervised machine learning algorithms are prone to overfitting, particularly in the domain of biomarker discovery, where the number of potential features to consider can be large.¹⁷ In fact, the primary cause of the lack of reproducibility in identifying biomarkers from ‘omics data by machine learning methods is overfitting.¹⁸ To address the aforementioned limitations, we devised a new machine learning classification algorithm for glycomics data that does better at classifying data than unsupervised methods (like PCA) while avoiding the known issues of supervised machine learning methods, which are prone to overfitting the training data and require larger data sets to correctly classify samples. The Aristotle Classifier is described in detail in the methods section; the code is open-source, and we demonstrate herein the classifier’s value over the current best practices in the field of glycomic-based biomarker discovery.

Methods

Software Overview:

The Aristotle Classifier was built in R Studio, using R version 3.5.0. The version of the classifier used for all analyses in this manuscript is included as two text files in Supplemental Data. These text files also contain basic operating instructions, including which values must be input for the software to run and reasonable ranges for those values. The Aristotle Classifier is comprised of two parts; Part I builds the feature set that will be queried by Part II. A descriptive overview of each component follows.

Part I: Feature Building.

A matrix of data, including all the desired glycan peak intensities for all the samples to be classified, must be imported into R. The features need to be present in rows, and each sample needs to be represented in a single column in the matrix. The quantitative inputs could be raw peak intensities, abundances normalized to an internal standard, or relative abundances (percentages) of each glycan type. The last feature (the last row) of the matrix must contain a “1” for every sample. Including this feature is the simplest way to ensure that individual peaks, ratios of two peaks, and ratios of three peaks are all considered after the matrix math below is conducted. The code in Part I uses linear algebra to transform the input matrix into a nonredundant matrix that contains more features for each sample. The features include: all of the individual glycan abundances (however they were provided), along with all possible ratios of any two glycan abundances, along with all possible ratios that comprise three glycans. The algorithm that accomplishes Part I contains a redundancy reduction step that assures that each feature is only represented once in the larger matrix.

Part II: Feature Identification and Scoring.

The user must identify a set of at least six known samples for each of the two groups being classified (ex: disease vs healthy). These identified samples are input into line 39 of the scoring algorithm. The identified samples are used for feature selection. If all the samples’ classification groups are known, and the goal of running the code is to determine how well the glycan profile differentiates the samples into their two groups, all of the available samples should be used for feature identification and scoring. (These are input on line 39.) If the goal of running the code is to do a validation experiment, or if the goal is to score samples of an unknown sample type, a subset of the samples can be input on line 39. The samples used on line 39 would then comprise the training set for the algorithm. While at least six known samples from each of the two groups are needed for training, hundreds of samples can be tested at a time.

Once the algorithm commences, four training samples from Group 1 and four training samples from Group 2 are randomly selected from the list of known samples that the user had included on line 39. Each feature (which is an individual glycan signal or a peak ratio) is individually assessed to determine if it discriminates the sample type (Group 1 vs Group 2). To be considered a discriminating feature, all four values for the feature from the samples from Group 1 need to be higher (or lower) than all four values from the selected training samples from Group 2. Each feature (peak or ratio) generated from Part I is assessed in this way to determine the set of discriminating features. The discriminating features are selected for the scoring step, and the non-discriminating features are ignored. For each selected feature, a boundary is calculated that falls between the two groups.

A scoring step follows feature selection. Every sample that was not picked for the feature selection step is subjected to scoring, using an unsupervised scoring routine. For each selected feature in each sample, the sample gets a positive score if the feature size falls on the same side of the boundary as the features in the four training samples from Group 1. The feature gets a negative score if the value for the feature is on the same side of the boundary as the four training samples from Group 2. This process proceeds for each selected feature and each sample to be scored. Each sample that is being scored is treated the same way, regardless of whether it belonged to Group 1, Group 2, or had an unknown classification. After this scoring step is completed, all the scores for all the features are added for each sample, and each sample gets a single score that represents its similarity to the Group 1 or Group 2 training samples. A score >0 indicates that the sample is more similar to the Group 1 samples. A score <0 indicates the sample is more similar to Group 2.

The entire process, starting with randomly selecting four training samples from each group for feature selection, is repeated hundreds of times, with 1000 rounds being an effective number to use in routine testing of large data sets. Repeating the test multiple times assures that many possible groupings of the samples are considered. The results of all the rounds of feature selection and scoring are weighted equally and combined, providing a single score for each sample upon completion. Unless a very large number of very diverse samples are present, repeating the feature selection/scoring step more than 1000 times does not change the final outcome of the group assignments. Currently, the user can set the repeat number to be any value between 1 and 5000. To find the optimal repeat value, users can start with a low number, such as 50 or 100, and determine whether or not all of the examples are classified in the same way upon replicate analyses. Once the user conducts the experiment with a sufficient number of repeats, the results will not change upon replicating the experiment. Conversely, users could select a large number of repeats by default, ex 3,000. In this case, the experiment would be highly reproducible, but the calculation time might be large if a very large dataset is being analyzed.

Data used for testing.

The data used to test The Aristotle Classifier come from three sources. The first set of data is a group of 128 random “samples,” each with 20 random glycan features, which was generated in R by building a 128×20 matrix of random numbers. This matrix is available in Supplemental Data. A second source of data includes the normalized monosaccharide abundances for liver fibrosis and ovarian cancer. These data are found in the Supplemental Materials associated with reference 1. Finally, a set of mass spectrometry data of IgG glycopeptides was freshly acquired for these studies. The preparation and analyses of these samples is described next. The peak abundances for the glycopeptides are also available in Supplemental Data.

Sample preparation for IgG2 glycopeptides.

Two aliquots of Human IgG samples (100 μg each), were dissolved in 10X glycobuffer, pH 5.5. One of the sample aliquots was treated with 2.0 μL of α2–3,6,8,9 Neuraminidase A and the other, with an identical volume of deionized water. Both samples were incubated for 1 week at 37 °C. After the incubation period, the pH of the samples was adjusted, to pH 8.0, with 300 mM NH₄OH followed by the addition of 50 mM ammonium bicarbonate buffer (pH 8.0), giving a final IgG sample concentration of 4 mg/mL. Each sample was (separately) denatured by adding GdnHCl to a final concentration of 6 M followed by reducing disulfides via the addition of DTT to give a final concentration of 10 mM. The reaction was allowed to continue for 1 h at room temperature. Subsequently, IAM was added to a final concentration of 25 mM, and the samples were incubated for 1 h in the dark. Excess IAM in the reaction mixture was neutralized by adding DTT (30 mM final concentration) and by proceeding the reaction for 30 mins at room temperature. Subsequently, the resulting samples were subjected to centrifugal filtration (10 kDa molecular weight cutoff filters) and buffer exchanged with 50 mM NH₄HCO₃ twice. The samples were diluted with ammonium bicarbonate buffer (pH 8.0) to a final concentration of 1 μg/μL. Finally, trypsin digestion was performed on both samples by adding trypsin at a protein-to-enzyme ratio of 30:1 (w/w) and incubating 20 hours at 37 °C, and 1 μL of formic acid for every 100 μL of sample solution was added to stop the digestion. The digested protein samples were aliquoted and stored at −20 °C until the analysis was performed.

After preparing tryptic digests of native and desialylated IgG samples separately, IgG native samples, at 0.05 μg/μL concentration, were prepared by, first diluting the 0.9 μg/μL original IgG tryptic digest solution to 0.45 μg/μL (stock 1) with deionized water, followed by a second dilution of appropriate volume of stock 1 with water. These samples are henceforth referred to as Group 1. Then, 0.05 μg/μL IgG Desialo 20% mixed sample was prepared by mixing appropriate volumes of the tryptic digests of IgG native stock 1 (0.45 μg/μL) and IgG desialo 0.1 μg/μL sample solution (generated by diluting original IgG desialylated sample (0.9 μg/μL) with water), while keeping the final concentration of both native and IgG desialo 20% mixed samples at 0.05 μg/μL. These samples are henceforth referred to as Group 2.

LC-MS of 42 glycopeptide samples.

Analysis of glycoprotein digests was performed by separating glycopeptides on a reverse phase C18 capillary column (3.5 μm, 300 μm i.d. ×10 cm, Agilent Technologies, Santa Clara, CA) using a Waters Acquity high performance liquid chromatography system (Milford, MA) followed by mass spectrometric data acquisition in an Orbitrap Fusion Tribrid mass spectrometer (Thermo Scientific, San Jose, CA). For each run, 3 μL of a sample was injected with a mobile phase flow rate of 10 μL/min. A gradient elution was performed for the separation with two mobile phases: mobile phase A consists of 99.9% water plus 0.1% formic acid, while the mobile phase B consists of acetonitrile with 0.1% formic acid. The LC separation gradient used for the run was as follows: 5% mobile phase B for 3 mins, 5% to 20% linear increase of B in 22 mins, and ramp to 90% B in 20 mins, decrease the B to 5% in 5 mins, followed by re-equilibrating the column at 5% B for another 10 mins. To minimize sample carryover, blank runs were performed either in between each run or after a pair of runs, as described below.

A total of 42 samples were acquired, 21 from each group. The LC-MS analyses always alternated between samples from Group 1 and Group 2. For the first 12 samples acquired, Group 1 and Group 2 samples were alternately acquired by including a blank in between each run. The remaining 30 samples were analyzed 3 weeks after the first set of data was acquired. For the second data set, 15 replicates of IgG native (Group 1) and IgG desialo 20% Mixed (Group 2) sample pairs (0.05 μg per μL injection) were acquired under identical LC conditions, including a blank after each pair of the samples.

MS conditions:

ESI-MS in the positive ion mode was used with a heated electrospray source held at 2.3 kV. The ion transfer tube and the vaporizer temperature were set at 300 °C and 20 °C, respectively. The full MS scans for the m/z range of (400 – 2000) were performed in the Orbitrap at a resolution of 60,000 (m/z 200) and the AGC target and the maximum injection time for the full MS scan was 4× 10⁵ and 50 ms, respectively. CID data were acquired in a data dependent manner to confirm the compositions of the glycopeptides. CID spectra were collected in the ion trap with “Rapid” scan rate, with a repeat count of one within an exclusion duration of 30 s. For CID, an AGC target of 2×10³ was used, and the maximum injection time was 300 ms. The isolation mass window for the parent ion selection for the CID MS/MS was 2 Da, and the selected ions were fragmented by applying 35% of collision energy for 10 ms. After the glycopeptide ions were confidently identified using established procedures,^{19, 20} thirteen glycopeptides from IgG2 were selected for quantitative analysis for this study. The raw abundance of each glycoform at the 50% abundance of extracted ion chromatograms were recorded, and these raw abundances were transformed into percents by summing the 13 contributing IgG2 glycan abundances in each file and dividing the individual abundances by the total, as previously described.²¹ A table of all the glycoforms’ relative abundances for each of the 42 samples is found in Supplemental Data.

Data Analysis.

All data reported from The Aristotle Classifier were generated using the version of the code supplied in Supplemental Data. All data were processed in R, version 3.5.0. The number of replicate feature selection steps (k, line 39) was set to 1000. All experiments were repeated at least once to assure that the group assignments did not vary from run to run. PCA and k-means clustering was performed in Excel using XLSTAT.

Results and Discussion:

The Aristotle Classifier Is Better than PCA for Discriminating Sets of Glycomic Data.

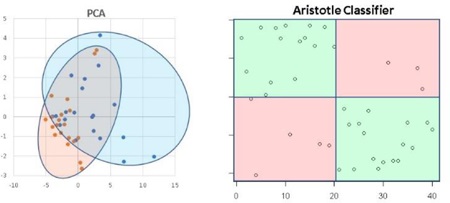
Principal Components Analysis is the gold standard for exploring variability in glycomic datasets, and it is similar to The Aristotle Classifier in that it can use all of the available glycan abundances to classify samples. We compared The Aristotle Classifier’s utility in classifying data versus PCA. Figure 2 shows two examples of data classification by PCA versus The Aristotle Classifier. Two different data types, from two different labs, were used for the comparison. In one case, ESI-MS data of two groups of IgG2 glycopeptide samples were compared. One group contained the native IgG2 glycopeptide profile. The second group was purposely adulterated with a small fraction of IgG2 that had been partially desialylated. For these samples, The Aristotle Classifier correctly assigned 98% of the data (4¼2 samples) to their correct groups; by contrast, the PCA plot had substantially overlapping regions for the two different sample groups, where 12 of the 42 samples could not be uniquely classified into one group or the other. In a second comparative example, glycomics data from liver fibrosis patients (Stage 3 and 4) versus healthy controls were compared; the glycan abundances for these samples are available in reference 1. The Aristotle Classifier was able to correctly assign 81% of the data (17/21 samples), while PCA, again, is substantially less useful in separating the two groups into their respective classes. Based solely on the PCA results of these two sample sets, it would appear that the underlying glycomics data would not be very useful in discriminating the groups; yet, when the data are subjected to The Aristotle Classifier, the discriminating potential of the glycan signals becomes evident. An additional example comparing PCA results for glycomics data and results from The Aristotle Classifier is provided in Supplemental Data (Figure S1). In every case tested thus far, The Aristotle Classifier is more useful for separating the samples into their respective classes than PCA.

Figure 2:

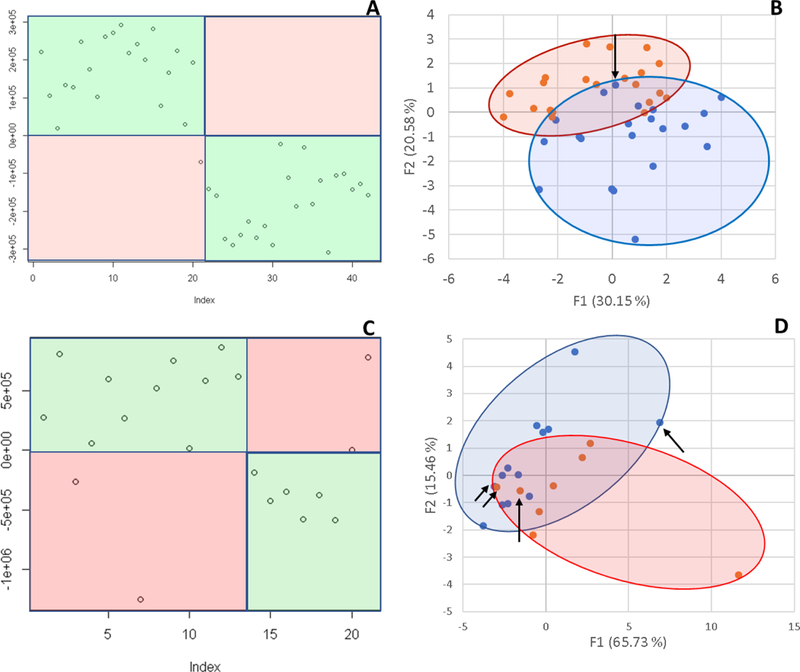
Comparison of The Aristotle Classifier vs PCA for two different data sets. 2A) Results from the Aristotle Classifier for distinguishing a total of 42 IgG2 glycopeptide samples; 21 samples are in each group. Correctly classified samples show up in green fields. Forty-one of 42 samples are correctly classified. 2B) Principal Components Analysis of the same 42 glycopeptide samples from 2A. 2C) Results for classifying glycomic data from healthy controls (13) or liver fibrosis patients (8) using The Aristotle Classifier. In this case 17/21 are correctly classified. 2D) PCA of the same 21 samples in Figure 2C. Arrows in 2B and 2D indicate the samples that were misclassified by the Aristotle Classifier.

Why didn’t The Classifier get the right answer every time? In Figure 2A, only one sample was mis-assigned. In Figure 2C, four samples were not classified correctly. Understanding whether these classification errors could have been prevented using another tool is one useful way to help understand how good an algorithm is. We first asked: Could PCA have done better on these mis-classified samples? The arrows on the PCA plots in Figure 2B and2D show where the mis-assigned samples reside on the PCA plots. None of the mis-assigned samples could have been correctly assigned by a PCA approach. We additionally asked: Could a different clustering approach have done better than the Aristotle Classifier? To find out, we subjected both datasets used in Figure 2 to k-means clustering. For the IgG data, 10 of the 42 samples were mis-classified; for the liver fibrosis data, 9 of the 21 files were misclassified. These tests demonstrate that the classification errors encountered by The Aristotle Classifier could not have been reduced by another approach. Furthermore, we noticed that both PCA and k-means clustering were more error prone on the liver fibrosis data set, compared to the IgG data; this finding indicates that the glycan features in the liver fibrosis data set are innately less useful for discriminating the samples, so it is not surprising that the Aristotle Classifier, which mis-classified four of the liver samples, had a lower accuracy on this set than on the IgG data set.

The Aristotle Classifier has no training bias; small training sets and large validation sets obtain equivalent results.

The single-biggest challenge in biomarker discovery is that potential biomarkers can appear to be effective in small sample sets, but they frequently fail to perform as well in larger validation studies.¹⁸ We demonstrate this “validation failure” problem below. Small training sets will always perform better than larger validation sets unless one can completely remove training bias, or model overfitting. The Aristotle Classifier’s scoring algorithm does not attempt to maximize the accuracy of the model, resulting in equal performance for training and validation samples, as demonstrated in Figure 3.

Figure 3:

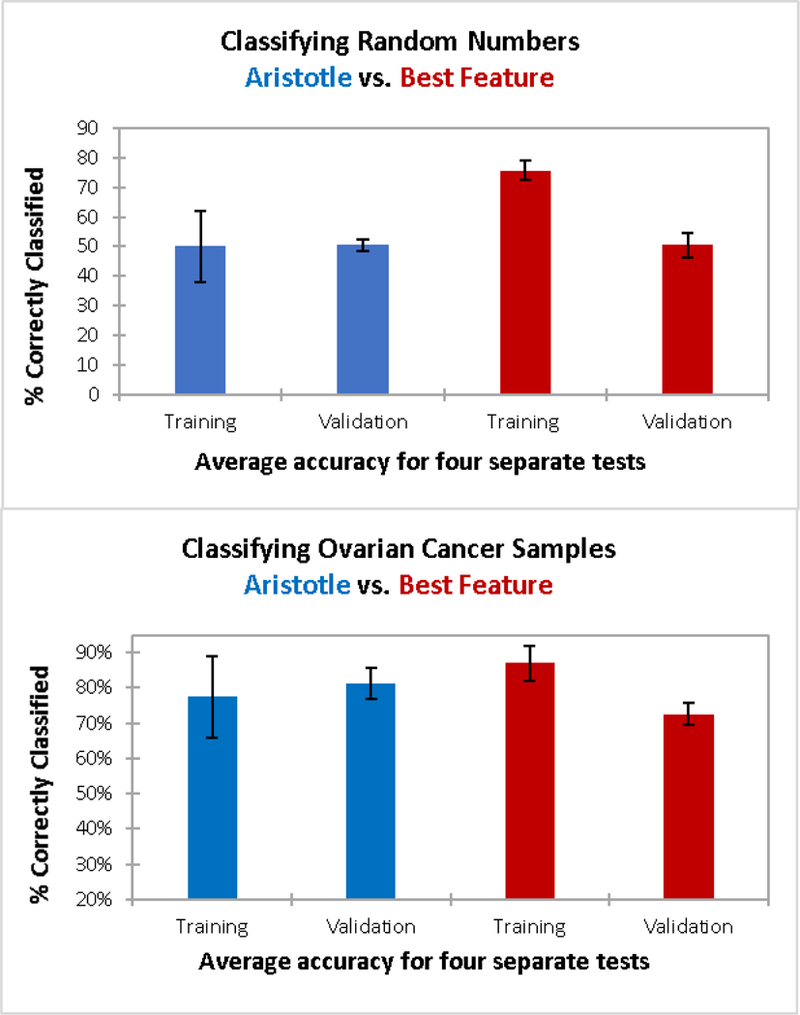
Training and validation results for classifying two different datasets: 3A) Classification of sets of random numbers. Each “sample” has 20 random numbers as features; 30 samples were used for training; 98 samples were used for validation in a four-fold cross validation. The Aristotle Classifier (blue) and the selection of the most discriminating feature in the training set (red) were both used to classify the data. 3B) Classification of glycomic data from a total of 146 samples (59 ovarian cancer patients; 87 healthy controls.) Here, 30 samples were used for training and 116 were used for validation. The same two methods as in 3A are used to classify the data. In both 3A and 3B, The Aristotle Classified exhibits no training bias. Additionally, it outperforms the traditional method in classifying ovarian cancer samples; it had higher accuracy in the validation experiment in 3B.

Two different types of data sets were selected to demonstrate The Aristotle Classifier’s lack of training bias. One dataset is a large matrix of random numbers (available in Supplemental Data); the other is a set of glycomics data from Stage III ovarian cancer patients vs. healthy controls (See Reference 1). The matrix of random numbers has 20 rows, mimicking 20 “features” for each of the 128 columns, where each column represents a “sample.” The matrix, therefore, has a total of 2560 random numbers (20*128), generated in R. The first 64 columns were randomly assigned as samples from Group 1, and the latter 64, as Group 2. For both the cancer dataset and the matrix of random numbers, the columns in the matrix (corresponding to patient samples in the cancer case or “random samples” in the matrix of random numbers) were divided into sets of training data and validation data. Each training set contained 15 randomly selected examples from Group 1 and 15 examples from Group 2. Data not selected for training were used for validation. For both the random matrix and the ovarian cancer data, four sets of training and validation data were generated and scored. The Aristotle Classifier was used to score each set of training data, and the trained model was then used to score the validation samples. For comparison purposes, the best discriminating feature in each group of 30 training samples was also used to score the corresponding validation samples.

Figure 3A shows results from classifying the matrix of random numbers by the two different approaches described above. The left side of the figure (blue bars) are results from The Aristotle Classifier; the red bars show data for the comparison approach, selecting the best feature of the training set to score the validation set. Since the data are random numbers assigned into random groups, no underlying trend predicting the group assignments should be identifiable. Thus, any algorithm without training bias would only be able to classify the samples correctly about 50% of the time, no better than random chance. The Aristotle Classifier assigned between 33 and 60% of the training samples “correctly” for the four different training sets, and the average accuracy for the training sets was 50%. These results were replicated in the validation sets; 48–52% of the validation samples were correctly assigned. (Note: The range of results in the validation sets was smaller than that of the training sets because the sample size of the validation sets was much greater.) The beauty of these results is best appreciated when they are contrasted with results from using a single best “feature” to score the data, shown in red in Fig 3A. In this comparison approach, each training set of 30 samples has at least one feature that discriminates the data very well. On average, 76% of the training samples could be “correctly classified.” Yet, in every case tested, a very large drop off occurs between training and validation, using a single best feature and 30 training samples. The average drop -from training to validation – was from 76% to 50%. These results emphasize the danger in using small data sets for biomarker discovery if a single best glycan signature is sought. When only 30 training samples are used, an effective biomarker can almost always be “found” using the traditional approach of comparing about 20 different glycan features and picking a single best one, but that selected feature will very likely not perform well in validation studies.

The data in Figure 3B show how data from ovarian cancer patients vs. healthy controls are classified, using either The Aristotle Classifier or using a single best glycan feature. These data show a second example of The Aristotle Classifier discriminating samples without training bias, while the comparator method does less well at discriminating data and introduces training bias. In this case, glycomics data from 15 healthy controls and 15 ovarian cancer patients are used for the training set and the remaining 116 samples are used for validation. Again, the experiment was repeated four times with randomly selected samples. The Aristotle Classifier correctly assigned an average of 77% of the training samples, and 81% of the validation samples. By contrast, the standard classification approach, where one selects a single best feature from the training set, results in a far less desirable outcome. First, a considerable drop-off between the training and validation was observed in every test, averaging about a 14% drop in accuracy between training and validation. Second, the validation results were lower than the validation results for The Aristotle Classifier in every test.

The Aristotle Classifier Can Distinguish Unusually Subtle Changes in Glycomic Profiles.

We built The Aristotle Classifier with the goal of distinguishing changes in clinical glycomics samples. These samples are challenging to classify in part because the glycomic change from healthy state to disease state can be quite subtle. To test the utility of the classifier on these types of challenging cases, we generated two groups of glycopepitde data with very minor changes in the glycomic profile between the two groups. The first group contains 21 samples, each containing native IgG2 glycopeptides. The second group of 21 samples contains 80% native IgG2 glycopeptides, adulterated with 20% IgG2 that had been partially desialylated. Each of the 42 sample was individually analyzed, and the quantities of 13 identified glycoforms for each sample are shown in Figure 4, with the Group 1 data depicted on the left side for each glycoform feature and the Group 2 data depicted on the right. The data in Figure 4 demonstrate that the samples cannot be discriminated by any single glycoform in the group. Clearly, being able to correctly classify these samples as “Group 1” or “Group 2” represents a challenging informatics problem. The Aristotle Classifier was able to classify these samples with 98% accuracy, with just one sample mis-classified. The classification results are shown in Figure 2A. Since the data in Figure 3 show that the Aristotle Classifier does not suffer from training bias, and the data in Figure 2 demonstrate that the classifier does better than PCA at classification problems, the ability to correctly classify the challenging samples shown in Figure 4 represents a significant step forward in glycomic analyses.

Figure 4:

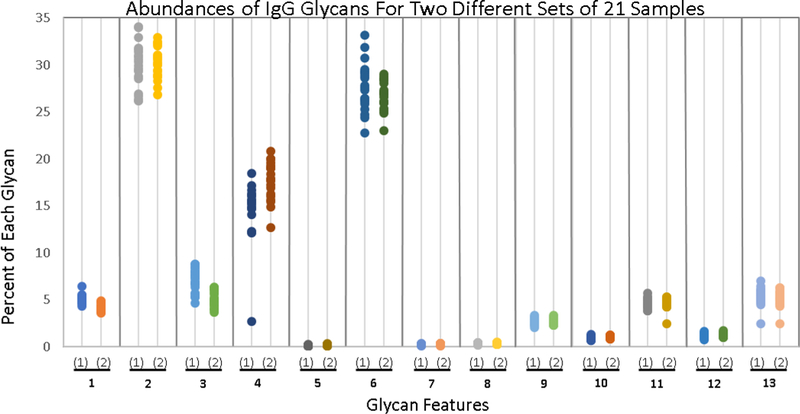
Comparison of the abundance of 13 different glycoforms in two groups of IgG2 samples (42 samples total; 21 in each group.) Group One comprises 21 native IgG2 samples; Group Two’s IgG2 glycoforms were modified slightly, as described in the text. The percent of each of the 13 different glycoforms is plotted; samples are grouped according to whether or not they contain the native IgG2 glycan profile. Not one of the thirteen glycans can be used to classify the samples as belonging to either Group 1 or Group 2; yet these samples are readily discriminated by The Aristotle Classifier, as shown in Fig 2A.

Could the algorithm do even better than what is shown here? Because this algorithm, by design, does not attempt to maximize the accuracy of the training data --it doesn’t minimize a cost function--it is not tunable in the way that most supervised machine learning algorithm would be tuned. While in some cases, lack of tunability is a disadvantage, this approach is the feature that removes training bias. Improved performance can be elicited by paying attention to the data being supplied to the algorithm. For example, the IgG glycoform abundances were input as normalized values – for each sample, the sum of all glycan abundances was 100%. This approach generally gives better results than using the raw abundances. As with any classification algorithm, performance also improves with lower variability in the measured features, so working to achieve reproducible MS conditions is a valuable time investment for enhanced classification accuracy. For glycan-based biomarker studies, an optimal outcome will require careful attention to collecting the best possible data, processing the data as normalized peak areas instead of using raw abundances, application of the Aristotle Classifier as described here, and, perhaps most importantly, analyzing a protein’s glycans that have a distinct change as a result of the disease state.

Conclusion

The Aristotle Classifier was built to support clinical glycomics studies. It addresses the need for a tool that can classify samples into groups based on the glycomic profile of those samples; it excels at challenging cases where the glycomic differences in the samples are subtle and concealed by other variability in the data. The Classifier uses a scoring routine that does not minimize a cost function; therefore, it does not introduce training bias. It classifies glycomic data better than the leading unsupervised method used in glycomics, PCA, as shown in numerous examples with diverse datasets. The source code for The Aristotle Classifier is provided in the Supplemental Data. Any researcher can take advantage of this new machine learning tool for classifying glycomics data. While the tool has been built specifically for glycomics analyses, we envision that The Aristotle Classifier may be useful for classification problems in other fields. Studies beyond the field of glycomics are under investigation.

Supplementary Material

1

Figure S1: Results from The Aristotle Classifier and PCA for a set of 40 glycomics samples: 20 are from ovarian cancer patients; 20 are from healthy controls.

2

Text File 1: Source code for Part I of the Aristotle Classifier

3

Text File 2: Source code for Part II of the Aristotle Classifier

4

Workbook: Page 1: List of random numbers used to generate data for Figure 3. Page 2: IgG glycopeptide abundances for 42 samples analyzed herein.