Estimating the receiver operating characteristic curve in matched case control studies

Abstract

The matched case-control design is frequently used in the study of complex disorders and can result in significant gains in efficiency, especially in the context of measuring biomarkers; however, risk prediction in this setting is not straightforward. We propose an inverse-probability weighting approach to estimate the predictive ability associated with a set of covariates. In particular, we propose an algorithm for estimating the summary index, area under the curve corresponding to the Receiver Operating Characteristic curve associated with a set of pre-defined covariates for predicting a binary outcome. By combining data from the parent cohort with that generated in a matched case control study, we describe methods for estimation of the population parameters of interest and the corresponding area under the curve. We evaluate the bias associated with the proposed methods in simulations by considering a range of parameter settings. We illustrate the methods in two data applications: (1) a prospective cohort study of cardiovascular disease in women, the Women’s Health Study, and (2) a matched case-control study nested within the Nurses’ Health Study aimed at risk prediction of invasive breast cancer.

1 |. INTRODUCTION

The matched case-control study design is widely utilized in biomedical investigations. Matching of cases to controls on one or more confounders can result in significant gains in efficiency.^1–3 Case control studies are often nested within a large prospective cohort, and are useful when the outcome of interest is rare. In many settings, the measurement of the biomarker(s) on all individuals in a prospective cohort is prohibitively expensive. This study design enables researchers to balance the number of cases and controls within matching strata defined by previously known confounding factors and to collect biomarker measurements only on the selected subset of subjects. While matched studies are primarily geared toward estimation of the association between exposure (or biomarker) and outcome, prediction in this setting is not straightforward. In this paper, we describe an inverse-probability weighting approach to estimate the area under the curve (AUC) associated with the Receiver Operating Characteristic (ROC) curve in a matched case control study. We consider settings in which the aim is to estimate the predictive ability of a pre-defined set of covariates that could include both novel biomarkers in conjunction with traditional risk factors with respect to a binary outcome.

In a typical matched case control study, all or a subset of cases is randomly selected from a prospective cohort. Each selected case is matched to one or more randomly selected controls on confounding factors such as age, gender etc. -and this selection results in a sample of controls that is no longer representative of the population. This also implies that statistical analysis of a matched case control study has to take the matching into account. An unmatched analysis of matched data can result in biased estimates of the biomarker-outcome association.^3,4 Conditional logistic regression models are commonly employed to estimate the magnitude and significance of the association of one or more biomarkers with an outcome.^5,6 The statement of the conditional logistic regression model includes matching stratum-specific intercepts. However, in this model, the association of a biomarker with outcome is estimated by maximization of the conditional likelihood, which eliminates the stratum-specific intercepts as nuisance parameters. Since these models do not provide estimates of the stratum specific intercepts, they are not appropriate for direct estimation of prediction and related statistics.

The accuracy of classification of cases and controls according to an algorithm can be visualized through a ROC curve. However, direct estimation of the ROC curve using data from matched case control studies can result in estimates that are attenuated toward the null.⁷ Several papers in the literature have described the use and estimation of the covariate adjusted ROC curve (AROC), which is a measure of the covariate adjusted classification accuracy and is useful for evaluating the predictive ability of a new biomarker.^8–11 Other related works in the literature include methods for estimating the ROC curve and associated summary indices using data from nested case control studies.^12–14 Our proposed methods build upon the work by Qian et al, who proposed a multiple step likelihood-based approach for parameter estimation and prediction in matched case-control studies.¹⁵ In this paper, the authors describe methods for estimating the effects of matching factors and biomarkers in a matched case control study by augmenting the data collected in the matched study with information from the parent cohort. We extend the methods from the aforementioned work¹⁵ for estimation of the ROC curve associated with a pre-defined set of covariates by incorporating an inverse-probability weighting procedure that accounts for the non-random sampling of controls in the matched study. While the approach of incorporating inverse-probability weighting has been previously used to adjust for non-random sampling, our paper illustrates the utility of combining the parameter estimation procedure described in the work of Qian et al¹⁵ with sampling weights to estimate unbiased estimates of AUC in matched studies. Moreover, through simulation studies and with two contrasting data applications, we illustrate the impact of the associations of the matching factors with the outcome and biomarkers of interest on AUC estimation in matched studies.

The paper is structured as follows: In Section 2, we introduce notation, describe the approach for parameter estimation and the calculation of matching stratum specific weights for ROC and AUC estimation. In Section 3, we present results from extensive simulation studies and compare the performance of the proposed approach to AUC estimation to naive methods based on conditional logistic regression and logistic regression. In Section 4, we apply our proposed methods to data from two applications: In the first, we use data on the full longitudinal cohort in the Women’s Health Study of 24532 women, of whom 559 women were observed to develop incident cardiovascular disease during follow up.^16–18 Nested within this cohort, we generate age-matched case control datasets from which we obtain AUC estimates using the proposed methods. The distribution of AUC estimates using proposed methods is compared to the corresponding AUC estimate from the full cohort (gold standard). In a second application, we use data generated in a breast cancer study of 437 patient cases and 775 matched controls nested within the Nurses’ Health Study.¹⁹ In Section 5, we discuss limitations of the proposed approach and consider extensions to related settings.

2 |. METHOD

In Section 2.1, we present the notation and define the population model. In Section 2.2, we briefly summarize the approaches to obtain unbiased estimates of the parameters governing the population model.¹⁵ In Sections 2.3–2.4, we propose a weighted estimator of the AUC that adjusts for the distortion of the prevalence of cases to controls within covariate strata as a result of matching. In Section 2.5, we describe a bootstrap sampling procedure for estimating the standard error (SE) of the AUC estimator.

2.1 |. Notation

Let Y denote a binary response variable (1=case, 0=control), X = (X₁, … , X_p)^T denote a 1 × p vector of biomarkers and other variables of interest, and Z = (Z₁, … , Z_q)^T denote a 1 × q vector of variables used in matching. We assume the following logistic regression model at the population level to describe the association of outcome (Y) with biomarkers X and matching variables Z:

$$\text{logit}(Pr(Y=1|X,Z))=\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}X+{\mathit{\gamma }}^{\text{T}}Z,$$ (1)

where β = (β₁, … , β_p)^T and γ = (γ₁, … , γ_q)^T. We assume that the primary parameters of interest are β.

As in a typical 1 : m matched case control study, we assume that N subjects are enrolled such that each case is matched to m controls based on the matching variables, Z. In this setting, we assume that all or a random sample of the cases in the population are included in the study, with selection of controls according to the matching by variables Z. To implement the matching, we assume that the matching variables Z are used to create K matching strata.

2.2 |. Parameter estimation

Here, we describe the procedure for estimation of the parameters α, β, γ governing the population logistic regression model in Equation 1 based on the methods proposed in the work of Qian et al.¹⁵

Let V denote the binary variable indicating if a subject is sampled into the matched case-control study (ie, 1 = yes, 0 = no). We assume that given (Y, Z), the sampling probability does not depend on X. In other words, Pr(V = 1|Y, Z, X) = Pr(V = 1|Y, Z). In a 1 : m matched case control study design, the following holds:

$$Pr(Y=1|V=1,Z)=\frac{Pr(Y=0|V=1,Z)}{m}.$$

Thus, under 1 : m matching, it follows that

$$\frac{Pr(Y=1|Z,X,V=1)}{Pr(Y=0|Z,X,V=1)}=\frac{Pr(Y=1|Z,X)}{Pr(Y=0|Z,X)}\times \frac{Pr(Y=0|Z)}{Pr(Y=1|Z)}\times \frac{1}{m}.$$

Therefore, from (1), the probability that a case is sampled into the matched case-control study is

$$\text{logit}(Pr(Y=1|X,Z,V=1))=\alpha +f(Z)+{\mathit{\beta }}^{\text{T}}X+{\mathit{\gamma }}^{\text{T}}Z,$$ (2)

where $f(Z)=\text{log}\{\frac{Pr(Y=0|Z)}{Pr(Y=1|Z)}\}-\text{log}(\text{m})$. The term f (Z) plays an important role in the estimation of α and γ.¹⁵

According to the methods described in the work of Qian et al,¹⁵ we summarize both the Two-stage procedure and Simultaneous procedures for estimation of the parameters, β, γ in the population logistic regression model 1.

1. Estimating the offset, f (Z): To estimate f (Z), we use data from the parent cohort study and fit a logistic regression model treating Y as the outcome and Z as the predictors of interest. By obtaining the estimate of $\text{log}\{\frac{Pr(Y=0|Z)}{Pr(Y=1|Z)}\}$ from the logistic regression model, the offset $f(Z)=\text{log}\{\frac{Pr(Y=0|Z)}{Pr(Y=1|Z)}\}-\text{log}(\text{m})$ is estimated.

2. Two-stage procedure: According to this algorithm, β and α, γ are estimated in two separate steps.

   1. Estimating β: Using the data from the 1 : m matched case control study, we fit a conditional logistic regression model by including the biomarkers X as predictors and obtain maximum likelihood estimates of β.
   2. Estimating α, γ: Using the data from the matched case control study, we fit a logistic regression model where Y is the outcome and Z the vector of predictors, while simultaneously including the offset $f\widehat{(}Z)+\widehat{\mathit{\beta }}X$ estimated in the previous step.

3. Simultaneous procedure: According to this algorithm, β, α, γ are estimated together in one model. As shown in equation 2, by including the offset f (Z), β, α, γ can be simultaneously estimated in a logistic regression model fit to the matched case control study data.

2.3 |. Sampling weights

As discussed in other works,^8–10 direct estimation of the AUC using data from matched case control studies can result in severely biased estimates. This phenomenon is driven by the fact that the selected set of controls are no longer representative of a random sample from the population; therefore, AUC estimates can be severely biased especially in settings in which the biomarker is strongly correlated with the matching variables. For example, matched datasets are obtained often by matching on fasting status, which can be related to the levels of one or more biomarkers.

Within each matching strata 1, … , K based on Z, we propose an inverse probability weighting approach to obtain a weighted AUC estimator. The proposed weights are implemented with the goal of recovering the stratum specific relative proportion of cases and controls in the original cohort.

Let n_k0, n_k1 denote the number of controls and cases in the k^th matching stratum of the cohort, respectively. In a 1 : m matched case control study, let j_k and mj_k denote the number of cases and controls selected in the k^th stratum. The proposed weights for each case and control within the k^th stratum are:

$$w_{k,\text{case}}=\frac{n_{k1}}{j_k};w_{k,\text{control}}=\frac{n_{k0}}{m{j}_k}.$$

The proposed weights (w_k,case, w_k,control) result in the re-calibrating the weighted proportion of cases to controls in each stratum of the matched dataset to equal that in the original cohort.

2.4 |. Weighted AUC estimator

We propose the following algorithm to estimate the AUC incorporating the effects of the matching variables Z and biomarkers X:

1. Estimate parameters α, β, γ in the population logistic model as described in Section 2.2.

2. For each subject in the matched case control study, the linear score $\widehat{S}=\widehat{\alpha }+\widehat{\mathit{\beta }}X+\widehat{\mathit{\gamma }}Z$ is calculated.

3. The weights (w_k,case, w_k,control) for each subject in the matched case control study is calculated, as described in Section 2.3.

4. Using estimated linear score, the weighted ROC curve and associated AUC is calculated as follows:

   Let S = {S₁, … , S_N} denote the linear score based on the population logistic model (Equation (1)), for each subject 1, … , N in the matched case control study. As described in the work of Pepe,²⁰ we define a binary test for predicting outcome Y using a threshold s as:

   $$\text{Predict Y}=1\text{ if }S\ge s$$

   $$\text{Predict Y}=0\text{ otherwise.}$$
   For each threshold s, let TPF(s) = Pr(S ≥ s | Y = 1) and FPF(s) = Pr(S ≥ s | Y = 0) denote the true positive fraction and false positive fraction, respectively. The corresponding estimates from the matched case control study, adjusting for the weights are:

   $$\widehat{TPF(s)}=\frac{{\sum }_{i:Y_i=1}{w}_i*1[{\widehat{S}}_i\ge s]}{{\sum }_{i:Y_i=1}{w}_i}$$

   $$\widehat{FPF(s)}=\frac{{\sum }_{i:Y_i=0}{w}_i*1[{\widehat{S}}_i\ge s]}{{\sum }_{i:Y_i=0}{w}_i}$$

   The associated area under the curve is calculated from the weighted ROC curve.

2.5 |. Confidence intervals

We propose a bootstrap sampling procedure for obtaining confidence intervals (CIs) for the true AUC.

1. Obtain b bootstrap samples, each generated by sampling the matched sets with replacement. We note that this bootstrap sampling procedure ensures that the matched structure of the original dataset is preserved.

   Based on the b^th bootstrap sample:

   1. Estimate α, β, γ as described in Section 2.2. We note that the offset $\widehat{f(Z)}$ is that based on the parent cohort and is estimated in each bootstrap sample as described in Section 2.3.
   2. Using the weights calculated from the parent cohort, re-estimate the AUC based on the procedure described in Section 2.4.

2. Obtain the desired CI based on the percentiles of the distribution of the AUC estimates from the b bootstrap samples. We recommend the accelerated bias-corrected percentile limits (BCa) that corrects for the skewness and bias of the bootstrap distribution.²¹

3 |. SIMULATION

We present results from simulation studies considering a range of parameter values corresponding to the population logistic regression model. Through simulations, we compare the performance of naive estimators of AUC using logistic and conditional logistic regression models to the proposed weighted AUC estimator presented in Section 2.

3.1 |. Simulation strategy

Based on 500 simulated datasets, averages $\left(\overline{AUC}\right)$ and associated 95% CIs are reported. In each dataset, we estimate the AUC according to the following strategies:

• Logistic regression (LR): We fit a logistic regression based on Equation (1) to the matched case-control dataset (ignoring the matching) and obtain $\widehat{\mathit{\beta }}$, $\widehat{\alpha }$, and $\widehat{\mathit{\gamma }}$. Using the estimated linear predictor $(\widehat{\alpha }+\widehat{\mathit{\beta }}X+\widehat{\mathit{\gamma }}Z)$, we obtain both unweighted and weighted AUC estimates.

• Conditional logistic regression (CLR): We fit a conditional logistic regression model using the matched case control dataset, treating Y as the outcome and X as the predictor in the model and estimate $\widehat{\mathit{\beta }}$. Using the estimated linear predictor $\left(\widehat{\mathit{\beta }}X\right)$ as the prediction score, we obtain both unweighted and weighted AUC estimates. Note that in this process, we implicitly set $\widehat{\alpha }=\widehat{\mathit{\gamma }}=0$ when estimating the linear predictor.

• Proposed estimators: Based on the procedure described in Section 2.2, we estimate α, γ, β using either the two-stage or simultaneous approaches for parameter estimation.¹⁵ Using the estimated linear predictor $(\widehat{\alpha }+\widehat{\mathit{\beta }}X+\widehat{\mathit{\gamma }}Z)$, we obtain both unweighted and weighted AUC estimates.

In each of 500 datasets, we used a bootstrap distribution of weighted AUC estimates as described in Section 2.5 to obtain a 95% CI for the true AUC. The bootstrap distribution was estimated based on b = 2000 bootstrap samples, of the same size as the original dataset. Coverage probabilities were calculated as the proportion of simulated datasets (out of 500) in which the 95% CI included the true AUC.

For each setting, we simulate data (Y, Z, X) for a large number of subjects (N= 10000) of a hypothetical population assuming the population logistic regression model in Equation 1. From the simulated population, we draw a matched case control dataset of size n = 200, by matching on the variable Z.

Binary matching variable, Z:

For all subjects in the population, we simulate a matching variable Z, where Z ~ Bernoulli(0.5) and the biomarker X as follows: X | Z = 0 ~ N(0, 1) and X | Z = 1 ~ N(δ, 1). Here, δ represents the parameter quantifying the shift in mean levels of biomarker X, through Z. By setting values of the parameters α, β, γ, we calculate the linear predictor as α + βX + γZ and corresponding values of the Pr (Y = 1 | X, Z) for each subject. We simulate the outcome Y for each subject as a Bernoulli random variable with probability p = Pr (Y = 1 | X, Z). From the simulated population, a matched case control study of size n = 200 is drawn as follows: A random sample of cases (Y = 1) of size n is selected. For each selected case, a matching control (Y = 0) is selected, such that the case and its matched control have the same value of Z.

Continuous matching variable, Z:

To generate the large population dataset, we simulate a matching variable Z, where Z ~ N(μ = 0, σ² = 1.5). Z is categorized into 10 strata (denoted W) according to deciles of its distribution. For all subjects in the population, we simulate the biomarker X ~ N(ρW, σ² = 1 – ρ²). Here, ρ represents the parameter quantifying the effect of the matching variable Z (or equivalently W) on the biomarker X, through both its mean and variance. The random variable Y is simulated as described above and a matched case control dataset is drawn by matching on W.

In all simulations, we fix β = 0.5. We consider different strengths of the effect of the matching variable Z with respect to Y by varying the value of γ = {0, 0.25, 0.50, 0.75}. In the simulations involving a binary matching variable, we vary δ between the values δ = 0, 0.5, 1. In the setting involving a continuous matching variable, we vary ρ between the values ρ = {0, 0.35, 0.5}. In each simulation scenario, we fix α such that the prevalence of cases in the population is 10%.

3.2 |. Results: Binary matching variable

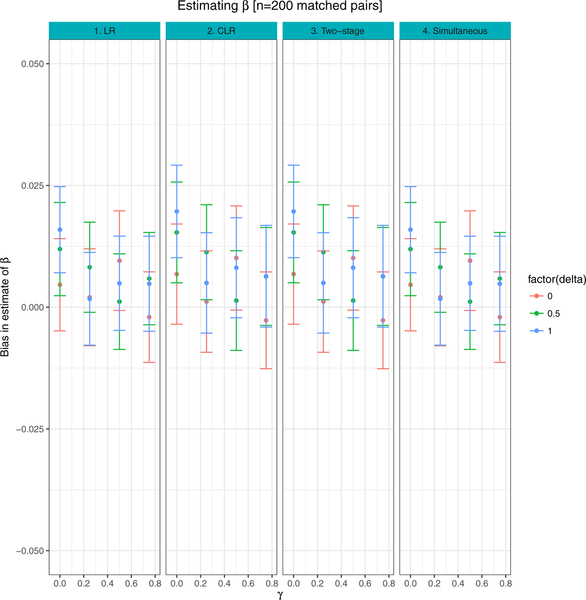
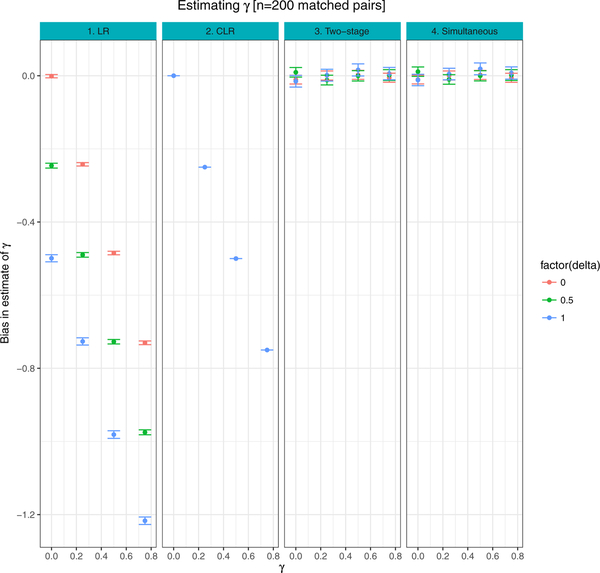
Figure 1 presents the mean bias associated with estimates of AUC, comparing both the naive estimates of AUC to weighted estimates. Figures 2–3 show the average bias associated with estimates of β, γ, based on LR, CLR and the proposed two-stage and simultaneous methods described in Section 2. In Figures 1–3, the 95% CI for bias is calculated as avg ± 1.95 * SE across 500 simulated datasets.

FIGURE 1. Binary matching variable:

Comparison of bias between weighted and naive approaches, when parameter estimates are based on logistic regression (LR), conditional logistic regression (CLR) and the proposed procedures (Two-stage and Simultaneous). Results are averages of 500 simulated datasets, each of n = 200 matched case control pairs

FIGURE 2. Binary matching variable:

Comparison of bias between β estimates from logistic regression (LR), conditional logistic regression (CLR) and the proposed procedures (Two-stage and Simultaneous). Results are averages of 500 simulated datasets, each of n = 200 matched case control pairs

FIGURE 3. Binary matching variable:

Comparison of bias between γ estimates from logistic regression (LR), conditional logistic regression (CLR) and the proposed procedures (Two-stage and Simultaneous). Results are averages of 500 simulated datasets, each of n = 200 matched case control pairs

See Tables 1–3 for average AUC (weighted and unweighted) comparing LR, CLR and proposed methods (Two-stage and Simultaneous). The 95% CIs for true AUC are based on the 2.5^th and 97.5^th percentiles of the distribution of AUC estimates in the 500 simulated datasets. Coverage probabilities are associated with 95% CIs obtained using proposed, bootstrap methods based on weighted AUC estimates.

TABLE 1. Binary matching variable:

Estimates of AUC (weighted and unweighted) comparing logistic regression regression (LR), conditional logistic regression (CLR) and proposed methods (Two-stage and Simultaneous). 95% confidence intervals (CI) for true AUC are based on the 2.5^th and 97.5^th percentiles of AUC estimates from 500 simulated datasets. Coverage probabilities are associated with 95% CIs obtained using proposed, bootstrap methods based on weighted AUC estimates. Results are averages of 500 simulated datasets, each of n = 200 matched case control pairs and where δ = 0

Model	γ	AUC	A$\widehat{U}$C [95% CI]		Coverage Probability
			Unweighted	Weighted
LR	0	0.64	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.99
CLR	0	0.64	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.99
Two-stage	0	0.64	0.64 [0.58 – 0.69]	0.64 [0.59 – 0.69]	0.99
Simultaneous	0	0.64	0.64 [0.58 – 0.69]	0.64 [0.59 – 0.69]	0.99
LR	0.25	0.64	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.99
CLR	0.25	0.64	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.98
Two-stage	0.25	0.64	0.63 [0.57 – 0.69]	0.64 [0.58 – 0.69]	0.99
Simultaneous	0.25	0.64	0.63 [0.57 – 0.69]	0.64 [0.58 – 0.69]	0.99
LR	0.50	0.65	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.70]	0.94
CLR	0.50	0.65	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.93
Two-stage	0.50	0.65	0.62 [0.56 – 0.68]	0.65 [0.60 – 0.71]	0.99
Simultaneous	0.50	0.65	0.62 [0.56 – 0.68]	0.65 [0.60 – 0.71]	0.99
LR	0.75	0.67	0.63 [0.58 – 0.68]	0.63 [0.58 – 0.69]	0.82
CLR	0.75	0.67	0.63 [0.58 – 0.68]	0.63 [0.58 – 0.68]	0.81
Two-stage	0.75	0.67	0.61 [0.55 – 0.67]	0.67 [0.62 – 0.71]	0.99
Simultaneous	0.75	0.67	0.61 [0.55 – 0.67]	0.67 [0.62 – 0.71]	0.99

TABLE 3. Binary matching variable:

Estimates of AUC (weighted and unweighted) comparing logistic regression regression (LR), conditional logistic regression (CLR) and proposed methods (Two-stage and Simultaneous). 95% confidence intervals (CI) for true AUC are based on the 2.5^th and 97.5^th percentiles of AUC estimates from 500 simulated datasets. Coverage probabilities are associated with 95% CIs obtained using proposed, bootstrap methods based on weighted AUC estimates. Results are averages of 500 simulated datasets, each of n = 200 matched case control pairs and where δ = 1

Model	γ	AUC	A$\widehat{U}$C [95% CI]		Coverage Probability
			Unweighted	Weighted
LR	0	0.65	0.64 [0.59 – 0.68]	0.64 [0.59 – 0.68]	0.97
CLR	0	0.65	0.63 [0.58 – 0.67]	0.65 [0.60 – 0.70]	0.99
Two-stage	0	0.65	0.63 [0.57 – 0.68]	0.66 [0.61 – 0.70]	0.99
Simultaneous	0	0.65	0.63 [0.57 – 0.68]	0.66 [0.61 – 0.70]	0.99
LR	0.25	0.67	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.81
CLR	0.25	0.67	0.62 [0.57 – 0.67]	0.66 [0.61 – 0.71]	0.98
Two-stage	0.25	0.67	0.61 [0.55 – 0.67]	0.67 [0.62 – 0.72]	0.99
Simultaneous	0.25	0.67	0.61 [0.55 – 0.67]	0.67 [0.62 – 0.72]	0.99
LR	0.50	0.69	0.64 [0.59 – 0.69]	0.64 [0.58 – 0.69]	0.54
CLR	0.50	0.69	0.63 [0.58 – 0.68]	0.68 [0.63 – 0.73]	0.97
Two-stage	0.50	0.69	0.60 [0.55 – 0.66]	0.69 [0.65 – 0.74]	1.00
Simultaneous	0.50	0.69	0.60 [0.55 – 0.66]	0.69 [0.65 – 0.74]	1.00
LR	0.75	0.71	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.25
CLR	0.75	0.71	0.63 [0.57 – 0.68]	0.69 [0.64 – 0.73]	0.88
Two-stage	0.75	0.71	0.60 [0.55 – 0.66]	0.71 [0.67 – 0.75]	0.97
Simultaneous	0.75	0.71	0.60 [0.55 – 0.66]	0.71 [0.67 – 0.75]	0.98

When γ = δ = 0, the matching variable Z has no effect on the outcome Y either directly through the logistic model in Equation (1) or through the biomarker X. In this setting, the sampled sets of cases and controls in the study are equivalent to random samples from the population of all cases and controls, and thus, weighted and unweighted estimates from all three approaches (LR, CLR and proposed strategy) result in unbiased estimates of the true AUC (Figure 1, Table 1).

When δ = 0, γ > 0, the matching variable Z is independent of the biomarker, X, and Z has a direct effect on the outcome Y through the logistic model in Equation (1). Here, the matched sampling of controls into the study is no longer equivalent to selecting a random sample of controls. Moreover, estimation of the linear predictor requires unbiased estimates of parameters α, β, γ. When estimation of parameters is based on the CLR model, we set $\widehat{\alpha }=\widehat{\gamma }=0$, resulting in biased estimates of the linear predictor. When the effect of the matching variable on outcome is strong (γ = 0.75), the weighted AUC estimate based on LR or CLR is less than optimal reflecting the bias in parameter estimation - the 95% CI for the true AUC based on the bootstrap distribution of weighted AUC estimates is 0.82 and 0.81, respectively (Table 1). When δ = 0, γ > 0, estimates of γ, β based on the proposed procedures are nearly unbiased (Figures 2–3); however, the unweighted AUC estimate is biased towards the null, reflecting the skewed sampling of controls into the study. On the other hand, the weighted AUC estimate based on the proposed methods is unbiased when δ = 0 and for varying values of γ, with coverage probabilities of 0.99 (Figure 1, Table 1).

When δ > 0 and γ > 0, the matching variable Z has both a direct effect on Y through the logistic model (Equation (1)) and an indirect effect on Y through its association with biomarker X. For example, consider the setting when β = 0.5, δ = 1.0, γ = 0.75, resulting in a true AUC of 0.71. The weighted AUC estimate based on both the two-stage and simultaneous procedures was 0.71 (95% CI: 0.67 – 0.75), with coverage probabilities of 0.97 and 0.98, respectively. All other approaches showed modest to large bias towards the null (Figure 1, Tables 2–3). Figures 2–3 show that estimates of β, γ are unbiased under both simultaneous and two-stage parameter estimation strategies, across a range of values of δ, γ.

TABLE 2. Binary matching variable:

Estimates of AUC (weighted and unweighted) comparing logistic regression regression (LR), conditional logistic regression (CLR) and proposed methods (Two-stage and Simultaneous). 95% confidence intervals (CI) for true AUC are based on the 2.5^th and 97.5^th percentiles of AUC estimates from 500 simulated datasets. Coverage probabilities are associated with 95% CIs obtained using proposed, bootstrap methods based on weighted AUC estimates. Results are averages of 500 simulated datasets, each of n = 200 matched case control pairs and where δ = 0.5

Model	γ	AUC	A$\widehat{U}$C [95% CI]		Coverage Probability
			Unweighted	Weighted
LR	0	0.64	0.64 [0.59 – 0.69]	0.64 [0.59 – 0.69]	0.99
CLR	0	0.64	0.63 [0.59 – 0.69]	0.64 [0.59 – 0.70]	0.99
Two-stage	0	0.64	0.63 [0.58 – 0.69]	0.64 [0.59 – 0.70]	0.99
Simultaneous	0	0.64	0.63 [0.58 – 0.69]	0.64 [0.59 – 0.70]	0.99
LR	0.25	0.65	0.64 [0.59 – 0.69]	0.64 [0.58 – 0.69]	0.95
CLR	0.25	0.65	0.63 [0.58 – 0.69]	0.65 [0.60 – 0.70]	0.99
Two-stage	0.25	0.65	0.62 [0.56 − 0.68]	0.65 [0.60 – 0.71]	0.99
Simultaneous	0.25	0.65	0.62 [0.57 – 0.68]	0.65 [0.60 – 0.70]	0.99
LR	0.50	0.67	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.80
CLR	0.50	0.67	0.63 [0.58 – 0.68]	0.65 [0.60 – 0.71]	0.96
Two-stage	0.50	0.67	0.61 [0.55 – 0.67]	0.67 [0.62 – 0.72]	0.99
Simultaneous	0.50	0.67	0.61 [0.56 – 0.67]	0.67 [0.62 – 0.72]	0.99
LR	0.75	0.69	0.64 [0.58 – 0.69]	0.64 [0.58 – 0.69]	0.53
CLR	0.75	0.69	0.63 [0.58 – 0.69]	0.66 [0.61 – 0.72]	0.85
Two-stage	0.75	0.69	0.60 [0.55 – 0.66]	0.69 [0.65 – 0.73]	0.99
Simultaneous	0.75	0.69	0.60 [0.55 – 0.66]	0.69 [0.65 – 0.73]	0.99

In Tables 1–3, we note that the empirical coverage probabilities obtained based on the proposed bootstrap procedure exceeds the nominal level of 95%, indicating that the bootstrap procedure over-estimates the true variances of the estimators.

3.3 |. Results: Continuous matching variable

The results for this setting are presented in the Supplementary material. Supplementary Figures 1–3 present the mean bias associated with estimates of AUC (weighted and unweighted), β and γ, respectively, based on LR, CLR and the proposed two-stage and simultaneous methods. In Supplementary Figures 1–3, the 95% CI for bias is calculated as avg ± 1.95 * SE across 500 simulated datasets. See Supplementary Tables 1–3 for average AUC (weighted and unweighted) comparing LR, CLR and proposed methods (two-stage and simultaneous). The 95% CIs for true AUC are based on the 2.5^th and 97.5^th percentiles of the distribution of AUC estimates in the 500 simulated datasets. Coverage probabilities are associated with 95% CIs obtained using proposed, bootstrap methods based on weighted AUC estimates.

As in the binary matching variable setting, when γ = ρ = 0, the sampled sets of cases and controls in the study are equivalent to random samples from the population of all cases and controls - and thus weighted and unweighted estimates from all approaches (LR, CLR, two-stage, simultaneous) result in unbiased estimates of the true AUC (Supplementary Figure 1, Supplementary Table 1). When both ρ and γ are large, estimates of β and γ from the simultaneous approach show significant bias (Supplementary Figures 2–3) when compared to that from the two-stage method. Moreover, for settings where γ is large, estimates of γ from the two-stage shows a modest residual bias - this result is likely due to the fact that the matching is based on the discretized variable W, but the population logistic regression model is a function of the continuous variable Z. Interestingly, when ρ > 0, so that Z and X are correlated, and when γ is modest, the weighted AUC estimates from CLR have modest bias when compared to that from LR - for example, when ρ = 0.5, γ = 0.25, the coverage probability associated with CLR is 0.98, whereas that associated with LR is 0.10 (Supplementary Table 3). In this setting, the bias resulting from the exclusion of Z in the CLR model is offset by the association between X and Z. For a continuous matching variable that has strong effects on outcome and the biomarker, the proposed two-stage approach incorporating inverse-probability weights achieves minimum bias with respect to AUC and associated empirical coverage probability that approaches 95%.

The R code and associated functions used for generating the simulation results is included in the Supplementary material.

4 |. APPLICATIONS

We illustrate the proposed methods for AUC estimation in two data applications in the Women’s Health Study and Nurses Health Study, respectively. In a study of cardiovascular disease risk prediction within the Women’s Health Study, we illustrate the bias observed in AUC estimation approaches that do not adjust for the matched sampling of cases and controls, in a setting where the biomarker of interest (high density lipoprotein (HDL) cholesterol) has strong associations with the outcome (cardiovascular disease) and the matching variable (age).^16–18 In a second application involving a breast cancer study nested within the Nurses Health Study, we see no significant differences in AUC estimates using proposed methods when compared to an approach that ignores the matched sampling, in a setting where the matching factors are neither strongly associated with outcome (breast cancer) nor correlated with the biomarkers of interest (set of three endogenous hormones).¹⁹

The results for this setting are presented in the Supplementary material.

4.1 |. Women’s health study

The Women’s Health Study (WHS) is a prospective cohort study of cardiovascular disease in women.¹⁶ Participants provided informed consent and the study was approved by the institutional review board of Brigham and Women’s Hospital. As described in,¹⁸ 24558 women had complete data on risk factors and known cardiovascular disease status at eight years after entry. For this analysis, cases were defined as women with an observed diagnosis of cardiovascular disease within 8 years of follow up. Since less than 2% of the women were lost of follow up before 8 years, all women without an observed diagnosis of cardiovascular disease within 8 years were designated as controls. After further excluding 26 women as they belonged to age strata (defined by year) that had either only cases or only controls, this analysis is based on the remaining 24532 women, including 559 cases. In this application, we considered age as the matching variable and HDL cholesterol as the biomarker of interest. We obtained age matched case control datasets of various sample sizes nested with the full prospective cohort and compared the distribution of AUC estimates from the matched case control datasets to the AUC estimated from the full cohort (gold standard).

In the WHS cohort of 24532 women, the median age at entry was 52 years, with a range of 45 to 83 years. The gold standard estimate of AUC based on the full prospective cohort was obtained from a logistic regression model with age (in years) and HDL cholesterol (log transformed) as covariates. In this model, age and HDL cholesterol were both statistically significant predictors of cardiovascular disease, with β_age = 0.09, p < 2⁻¹⁶ and β_lnHDL = −1.68, p < 2⁻¹⁶, respectively. The AUC estimate from this full cohort based model was 0.741. In addition, age was a significant predictor of HDL cholesterol - in a linear model with log transformed HDL cholesterol as outcome and age as the predictor, we observed β_age = 0.001, p = 2.37⁻⁶. Moreover, as expected, age was a significant predictor of cardiovascular disease in a logistic regression model, with β_age = 0.09, p < 2⁻¹⁶.

From the cohort of 24532 women, 250 age matched case control datasets were sampled, of size 100, 200 or 400 pairs. From each matched dataset, AUC estimates were obtained by: (A) using proposed methods to estimate AUC associated with age and HDL cholesterol; (B) using methods described in the work of Qian et al¹⁵ to estimate parameters for age and HDL, with the corresponding linear predictor used to estimate AUC; (C) fitting a conditional logistic regression (CLR) model with HDL cholesterol as the only covariate, with the corresponding linear predictor used for AUC estimation; (D) fitting a logistic regression model with age and HDL cholesterol as covariates, with the corresponding linear predictor for AUC estimation. Approaches (B), (C) and (D) do not account for the matched sampling of cases and controls when estimating the ROC curve.

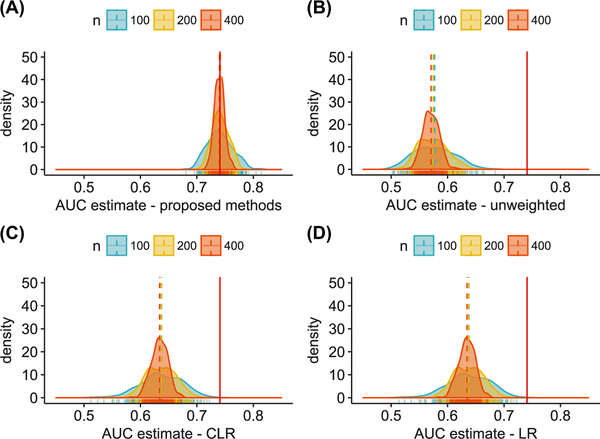
Figure 4, panels (A)-(D) present the distribution of AUC estimates from the 250 matched datasets, from each of the four methods described above. The AUC estimated from the full cohort is shown in each panel by the vertical, solid, red line (AUC = 0.741). In panel (A), we see that the distribution of AUC estimates using proposed methods is centered at 0.74 for all sample sizes considered, with ranges of (0.68 − 0.81), (0.70 − 0.78) and (0.72 − 0.77), for n equal to 100, 200 and 400 matched pairs, respectively. In comparison, estimates obtained by ignoring the matched sampling suffer from significant bias. In panel (B), we present AUC estimates from a linear predictor in which parameters for age and HDL cholesterol are estimated based on methods described in the work of Qian et al¹⁵ but without sampling weights; in this setting, AUC estimates are centered at 0.57 for all sample sizes considered, with ranges of (0.50 − 0.68), (0.51 − 0.66) and (0.53 − 0.62), for n equal to 100, 200 and 400 matched pairs, respectively. In panel (C), we present AUC estimates from a linear predictor including only HDL cholesterol in which the regression coefficient is estimated using conditional logistic regression. In this case, the linear predictor is incorrectly excluding the effect of age and the AUC estimation procedure does not account for the matched sampling - in this setting, AUC estimates are centered at 0.64 for all sample sizes considered, with ranges of (0.51 − 0.74), (0.55 − 0.71) and (0.59 − 0.67), for n equal to 100, 200 and 400 matched pairs, respectively. In panel (D), we present the AUC estimates from a linear predictor including both age and HDL cholesterol obtained from a logistic regression model in each matched dataset. In this analysis, the regression coefficients associated with age and HDL cholesterol and the corresponding AUC estimates are biased as the matched sampling is ignored; in this setting, AUC estimates are centered at 0.64 for all sample sizes considered, with ranges of (0.51 − 0.74), (0.55 − 0.71) and (0.59 − 0.67), for n equal to 100, 200 and 400 matched pairs, respectively.

FIGURE 4. Women’s Health Study:

Distribution of AUC estimates from 250 age matched case control datasets of size n pairs (n = 100, 200, 400) drawn from the WHS cohort that included 24532 participants of whom 559 had observed events (incident cardiovascular disease). The AUC estimated from the full cohort from a model including age and HDL was 0.741 (shown by solid, red line in each panel). The distribution of AUC estimates from the matched datasets for each sample size n is shown in panels (A)-(D). AUC was estimated using proposed methods [panel (A)]; AUC estimates using methods described in the work of Qian et al¹⁵ but without sampling weights [panel (B)]; AUC estimates from a conditional logistic regression model with HDL as covariate [panel (C)]; and AUC estimates from a logistic regression model with age and HDL [panel (D)]. Methods in (B), (C) and (D) do not account for the matched sampling

In summary, all approaches that ignore the matched sampling of cases and controls exhibit severe bias, such that the range of AUC estimates does not include the AUC estimated from the full cohort (Figure 4), Panels (B), (C), (D)). This analysis illustrates the extent to which the skewed distributions of the matching factor and biomarker levels in the controls results in distorting AUC estimates in a naive analysis. In contrast, the proposed algorithm that appropriately adjusts for the matched study design results in AUC estimates that are centered at the value obtained from the full, prospective cohort.

4.2 |. Nurses’ health study

We illustrate our algorithm using data from a matched case control study of 437 cases with breast cancer and 775 controls, nested within the Nurses’ Health Study. The aims of this study were to evaluate whether the inclusion of seven endogenous hormones (plasma estradiol, estrone, estrone sulfate, testosterone, dehydro epiandrosterone sulfate (DHEAS), prolactin, and sex hormone-binding globulin (SHBG)) improved risk prediction for postmenopausal invasive breast cancer.¹⁹ Improvement in prediction was assessed based on change in AUC when adding each hormone individually to reference models that included either the Gail or the Rosner-Colditz risk score. The Gail score includes age at menarche, number of previous breast biopsies, presence of atypical hyperplasia at biopsy, age at first birth, number of first degree relatives with a history of breast cancer, and age. The details on the Gail and Rosner-Colditz risk scores can be found in previous publications.^22–24 While breast cancer risk-prediction models have been developed to identify women at high risk, these models have not previously included endogenous hormone levels, which are risk factors for postmenopausal breast cancer.

The Nurses’ Health Study was initiated in 1976 with a cohort of 121,700 US female registered nurses aged 30–55 years. Women completed a baseline questionnaire and have been observed biennially by questionnaire to update exposure status and disease diagnoses. From 1989 to 1990, 32,826 participants (age 43 to 69 years) provided blood samples.²⁵ From 2000 to 2002, 18,743 women provided a second blood sample (age 53 to 80 years).²⁶ Follow-up of the blood cohort was 97% in 2010. This study was approved by the Committee on the Use of Human Subjects in Research at Brigham and Women’s Hospital (Boston, MA). Patient cases, who were postmenopausal and not using hormone therapy (HT) at time of first blood draw, were diagnosed with invasive breast cancer after the initial blood collection but before June 1, 2010, and were matched to one or two controls on birth year (± 2 years), month (± 1 month) and time of day (± 2 hours) of blood draw and fasting (< 8 or ≥ 8 hours). Endogenous hormones were measured from blood samples collected at the time of the first blood draw during 1989 to 1990. In total, 437 patient cases and 775 controls with data on all seven hormones (plasma estradiol, estrone, estrone sulfate, testosterone, DHEAS, prolactin, SHBG) and the variables included in the Gail risk prediction model for breast cancer were included in the analysis.¹⁹

The measurements of each of seven endogenous hormones in the matched case control study were log₂ transformed prior to inclusion in the analysis. As reported in the work of Tworoger et al,¹⁹ each of the seven individual hormones was significantly associated with invasive breast cancer risk in logistic regression models, while adjusting for matching factors. Using stepwise regression with adjustment for matching factors, three of the seven endogenous hormones remained statistically significant, namely estrone sulfate, testosterone and prolactin. In our analysis, we estimated the AUC associated with this set of three hormones in combination with the Gail score and matching factors.

The analysis involved four steps as follows. First, the estimates of β = {β₁, … , β₄} corresponding to the three hormones (estrone sulfate (X₁), testosterone (X₂), prolactin (X₃) and Gail score, respectively, were obtained from a conditional logistic regression model in the dataset of 437 patient cases and 775 matched controls. Second, the offset f (Z) was estimated based on the parent cohort, after excluding women who were pre-menopausal and using hormone therapy (HT). The offset f (Z) was estimated using 12,506 participants in the Nurses’ Health Study, of whom 774 were breast cancer cases. Third, the parameter estimates α, γ were estimated by fitting a logistic regression model to the data from the matched case control study, while controlling for the term $\widehat{f}(Z)+{\widehat{\beta }}_1{X}_1+{\widehat{\beta }}_2{X}_2+{\widehat{\beta }}_3{X}_3+{\widehat{\beta }}_4$ Gail Score in the model. Fourth, a 95% CI for the AUC associated with the set of three hormones, Gail score and matching factors was estimated, based on the percentiles of the 250 weighted AUC estimates obtained in bootstrap samples.

In conditional logistic regression models including the three hormones and Gail score, the odds ratios for a doubling of hormone levels were 1.33 (95% CI: 1.17 – 1.51), 1.15 (95% CI: 0.96 – 1.37), and 1.22 (95% CI: 1.02 – 1.46), for estrone sulfate, testosterone, and prolactin, respectively. In the parent cohort, the offset f (Z) was estimated in a logistic regression model including all matching factors - of these factors, only time of blood draw was a statistically significant predictor of breast cancer risk. Timing of blood draw between 1pm-12am was associated with an odds ratio of 1.32 (95% CI: 1.06 – 1.65), compared to the reference time interval of 8am - 12pm. Age at blood draw was not statistically significant, possibly due to restricting the study to include only post menopausal women.

The parameters γ associated with the matching factors were estimated in a logistic regression model in the matched case control dataset, by including $\widehat{f}(Z)+{\widehat{\beta }}_1{X}_1+{\widehat{\beta }}_2{X}_2+{\widehat{\beta }}_3{X}_3+{\widehat{\beta }}_4$ Gail Score as an offset. In this model, age remained insignificant, but timing of blood draw remained statistically significant. The weighted AUC estimate associated with the model including all three hormones, Gail score and matching factors was 0.60 (95% CI: 0.57–0.64). In comparison, the weighted AUC estimate associated with the model including the Gail score and matching factors was 0.57 (95% CI: 0.53, 0.60). The results from our proposed weighted methods show close agreement with that reported in the work of Tworoger et al,¹⁹ in which the authors report an AUC of 0.61 (95% CI: 0.58 – 0.64) in a logistic regression model with three hormones, Gail score and matching variables.

In this application, the weighted and unweighted estimates of AUC were in close agreement. Mirroring trends observed in the simulations, we note that when the matching factors are neither strongly associated with outcome nor correlated with the biomarkers, the estimates from proposed methods show close agreement with standard unweighted methods based on logistic regression.

5 |. DISCUSSION

In the context of a matched case control study, we propose an inverse-probability weighting procedure in combination with the parameter estimation approaches described by Qian et al¹⁵ to estimate the AUC associated with a pre-defined set of covariates for predicting a binary outcome. The proposed methods are evaluated in simulations and illustrated using two applications involving a cardiovascular risk prediction study and a breast cancer matched case control study. We compare the performance of the proposed algorithm to naive methods using data from the Women’s Health Study; in this analysis, we illustrate the significant bias observed in AUC estimation approaches that do not adjust for the matched sampling of cases and controls, when the biomarker of interest (high density lipoprotein (HDL) cholesterol) has significant associations with the outcome (cardiovascular disease) and the matching variable (age).^16–18 In a second application involving a breast cancer study nested within the Nurses Health Study, we observed no significant differences in AUC estimates using proposed methods when compared to an approach that ignores the matched sampling, as a result of the matching factors not being associated with the outcome (breast cancer) and showing no significant association with the biomarkers of interest.¹⁹ These contrasting applications highlight specific conditions involving the distributions of the matching factors, biomarkers and outcome that influence AUC estimation in matched case control studies.

The proposed algorithm was evaluated in a series of simulation studies in which the effects of several factors was manipulated including: (1) the strength of association of matching factors with outcome; (2) the correlation between matching factors and biomarkers; and (3) sample size. We compared the bias associated with the proposed methods to estimates obtained without weighting and from prediction scores obtained from logistic regression models that adjust for the matching factors. Our proposed procedure was the only approach that achieved nearly unbiased estimates of the AUC, when there is a strong effect of the matching variables with respect to outcome and/or high correlation between biomarkers and matching variables - these conditions reflect those in which a matched study design is most appropriate. Moreover, in settings of a continuous matching variable, simulation results showed that the proposed weighted AUC estimator based on the Two-stage parameter estimation approach showed smaller bias when compared to the Simultaneous parameter estimation approach.

The proposed methods were developed for hypothesis driven studies in which a pre-defined set of covariates are evaluated with respect to a binary outcome. Matched case control studies are also frequently conducted in investigations employing high throughput metabolomic and proteomic technologies, in which a large number of measurements are made in each subject. It will be useful to extend methods for AUC estimation in high dimensional data settings in which a biomarker discovery and validation procedure precedes model development and prediction.