The avalanche-like behaviour of large-scale haemodynamic activity from wakefulness to deep sleep

Abstract

Increasing evidence suggests that responsiveness is associated with critical or near-critical cortical dynamics, which exhibit scale-free cascades of spatio-temporal activity. These cascades, or ‘avalanches’, have been detected at multiple scales, from in vitro and in vivo microcircuits to voltage imaging and brain-wide functional magnetic resonance imaging (fMRI) recordings. Criticality endows the cortex with certain information-processing capacities postulated as necessary for conscious wakefulness, yet it remains unknown how unresponsiveness impacts on the avalanche-like behaviour of large-scale human haemodynamic activity. We observed a scale-free hierarchy of co-activated connected clusters by applying a point-process transformation to fMRI data recorded during wakefulness and non-rapid eye movement (NREM) sleep. Maximum-likelihood estimates revealed a significant effect of sleep stage on the scaling parameters of the cluster size power-law distributions. Post hoc statistical tests showed that differences were maximal between wakefulness and N2 sleep. These results were robust against spatial coarse graining, fitting alternative statistical models and different point-process thresholds, and disappeared upon phase shuffling the fMRI time series. Evoked neural bistabilities preventing arousals during N2 sleep do not suffice to explain these differences, which point towards changes in the intrinsic dynamics of the brain that could be necessary to consolidate a state of deep unresponsiveness.

1. Introduction

Human consciousness remains a poorly understood phenomenon, difficult to define let alone to reduce to neurobiological explanation [1]. Independent theoretical efforts have converged on certain features characteristic of the conscious state. The first-person approach based on phenomenology leads to the hypothesis that complex brain dynamics are associated with conscious awareness as a consequence of information integration (accounting for the unitary character of consciousness) coexisting with an ample repertoire of possible states or configurations (accounting for the richness of conscious experience) [2–4]. On the other hand, the third-person approach of cognitive neuroscience (aligned with the viewpoint of functionalism) [5] suggests that conscious access plays a key role in the massive broadcasting of sensory information throughout the cortex, thus allowing its accessibility by multiple independent and parallel processes [6,7]. Long-range broadcasting occurs at the threshold for conscious access; in other words, small sensory perturbations can be amplified in a nonlinear fashion [8,9]. Both theories have received support from neuroimaging studies of conscious information access and temporally extended states of reduced responsiveness, as well as from experiments based on measuring the response to externally induced magnetic perturbations, which represents a proxy for the repertoire of potential brain states [10–12].

The hypothesis that conscious wakefulness depends on critical or near-critical non-equilibrium dynamics offers a parsimonious explanation for the properties described in the above paragraph [13]. It is well established in statistical mechanics that the correlation length diverges in a system undergoing a second-order phase transition. Such divergence would endow the brain with capacity for the long-range broadcasting of information [14,15]. The amplification of sensory stimuli during all-or-none conscious access is indicative of the high susceptibility of neural activity to external perturbations [16], suggesting that the dynamics are poised close to criticality. A similar consideration applies to the number of metastable states, peaking at criticality and thus potentially accounting for the large repertoire of brain configurations associated with conscious awareness [17]. In the absence of fine-tuning of control parameters, self-organized criticality provides a plausible framework consistent with these constraints, while also predicting the presence of scale-free cascades of spatio-temporal activity (‘avalanches’) extending up to the complete size of a finite system [18].

Empirical support for critical (or slightly subcritical and externally driven) neuronal dynamics is ample, and much of this support relates to the measurement and characterization of neuronal avalanches. Power-law distributions for avalanche size distributions were first measured using local field potentials (LFPs) in organotypic slice cultures in vitro [19]. Further in vitro experiments measuring LFPs supported and extended these results, followed by in vivo confirmations in awake and anaesthetized rats and cats [20–25], awake monkeys [22,26–28] and humans [29]. Voltage [30] and two-photon imaging [31] provided further evidence in awake mice. Finally, human experiments based on non-invasive neuroimaging methods such as electroencephalography (EEG) [32–34], magnetoencephalography (MEG) [35] and functional magnetic resonance imaging (fMRI) [36] yielded results supporting the criticality hypothesis. In particular, fMRI revealed avalanche-like¹ events encompassing the whole grey matter, a result consistent with scale-free dynamics in a finite size system [35,36]. The functional benefits of critical dynamics in terms of information processing and storage received wide attention and experimental support [37–40]. However, a strong point has also been made for subcritical and slowly driven dynamics as those better representing the empirical data [41,42].

The conjecture that criticality conveys advantage through the capacity for optimal or near-optimal information processing, compounded with the correspondence between signatures of conscious awareness and features of the critical state, naturally leads to the hypothesis that the distribution of neuronal avalanches should reflect the level of consciousness. To date, experiments to evaluate this hypothesis have been conducted on different organisms, using diverse neural activity recording techniques and methods for the induction of unconscious states. The first evidence of criticality in a physiological system emerged from studies reporting scale-free behaviour in the distribution of arousals, which was explained using a model based on self-organized criticality [43,44]. Further experiments yielded mixed results, with empirical support for this hypothesis stemming mostly from intracranial LFP recordings during non-rapid eye movement (NREM) human sleep [29], as well as from EEG [45], voltage [30,46] and two-photon [31] imaging in anaesthetized animals. However, experiments suggesting invariant neural avalanche statistics from wakefulness to deep sleep were also reported [24].

While the effects of human sleep on the scale-free behaviour of signals related to autonomic nervous system regulation have been intensively investigated [47–51], no experiment to date evaluated how the progressive loss of consciousness and vigilance occurring during human NREM sleep impacts on the scale-free properties of whole-brain activity as recorded using fMRI. Contrasting with the specificity of avalanching behaviour across precise cortical areas and layers [31], fMRI provides global and indirect estimates of brain activity with millimetric spatial resolution. This could help circumvent possible sources of heterogeneity by integrating local dynamics by means of the less specific haemodynamic responses required to satisfy metabolic demands. In other words, the macroscale description provided by fMRI could reveal emergent mechanisms that are hidden at microscale descriptions [52]. To address this possibility, we investigated the scale-free behaviour of avalanche-like activity in fMRI recordings measured during wakefulness and all stages of NREM sleep (N1, N2 and N3, also known as light sleep 1 and 2 and deep sleep, respectively) [53].

2. Methods

2.1. NREM sleep fMRI data

An fMRI sleep dataset from a previously published study was used [54]. A total of 71 non-sleep-deprived subjects were selected from a larger dataset on the basis of successful multimodal polysomnographic data recording and quality assessment (written informed consent, approval by the local ethics committee). All subjects were scanned during the evening (starting from approx. 20.00) and instructed to close their eyes and lie still and relaxed. Functional data acquisition comprised 52 min. A group of 58 subjects was formed out of the original dataset by excluding subjects who did not fall asleep. Sleep stages were scored manually by an expert according to the American Academy of Sleep Medicine criteria [53]. The resulting hypnograms were scanned for contiguous epochs of wakefulness, N1, N2 and N3 sleep. Subjects who did not reach all these stages were excluded from the analysis, leading to a balanced dataset of 18 subjects allowing paired comparisons between stages. Data from an MRI water phantom were collected to serve as a null model, and preprocessing of the data followed the same pipeline used for the participants.

All participants reached N3 sleep, but spent a variable amount of time in intermediate stages. Statistics concerning the sampling of each sleep stage are presented in section 5 of the electronic supplementary material, together with analyses showing that our results are not biased by variable sampling of the different stages.

2.2. EEG and fMRI recording

EEG was recorded via a cap (modified BrainCap MR, Easycap, Herrsching, Germany) during fMRI acquisition (1505 volumes of T2*-weighted echo planar images, repetition time (TR)/echo time (TE) = 2080/30 ms, matrix 64 × 64, voxel size 3 × 3 × 2 mm³, distance factor 50%; filed of view (FOV) 192 mm²) at 3 T (Siemens Trio, Erlangen, Germany) with an optimized polysomnographic setting (chin and tibial electromyography (EMG), electrocardiography, electro-oculography recorded bipolarly (sampling rate 5 kHz, low pass filter 1 kHz), 30 EEG channels recorded with FCz as the reference (sampling rate 5 kHz, low pass filter 250 Hz), and pulse oximetry and respiration recorded via sensors from the Trio (sampling rate 50 Hz)) and MR scanner-compatible devices (BrainAmp MR+, BrainAmp ExG; BrainProducts, Gilching, Germany). MRI and pulse artefact correction were performed based on the average artefact subtraction (AAS) method [55] as implemented in Vision Analyzer 2 (Brain Products, Germany) followed by objective (CBC parameters, Vision Analyzer) ICA-based rejection of residual artefact-laden components after average artefact subtraction resulting in EEG with a sampling rate of 250 Hz.

2.3. Image pre-processing

Using Statistical Parametric Mapping (SPM8), echo planar imaging (EPI) data were realigned, normalized (Montreal Neurological Institute space) and spatially smoothed (Gaussian kernel, 8 mm³ full width at half maximum). Cardiac-, respiratory-, and motion-induced noises were regressed out using the RETROICOR method [56]. The data were band-pass filtered in the range 0.01–0.10 Hz using a sixth-order Butterworth filter.

2.4. Point-process transformation

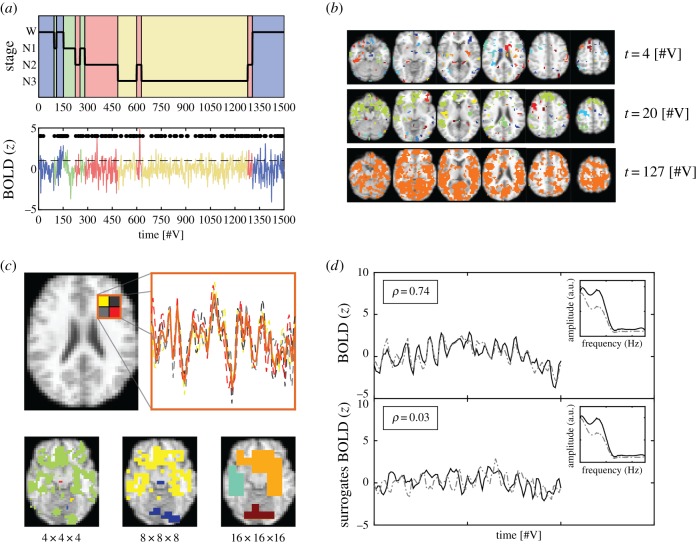
The criteria to determine the activation of each voxel at a specific time were based on transforming the continuous blood oxygen level-dependent (BOLD) time series into a point process [36,57]. Note that thresholding and binarization of time series for avalanche analysis are not exclusive to fMRI, but apply to other data-recording techniques as well, such as LFP, EEG, MEG, voltage and two-photon imaging. The BOLD time series corresponding to each voxel were first normalized by subtracting their mean and dividing by their standard deviation (s.d. of the full time series). A voxel was considered active in volumes when its normalized activity was larger than a threshold value (1 s.d.); otherwise, it was considered inactive. This resulted in the transformation of the fMRI data into a spatio-temporal point process consisting only of binary values [58]. In figure 1a (upper panel), the hypnogram of a randomly selected subject is shown, with sleep stages indicated using different background colours. An example BOLD time series from a randomly selected voxel (using the same colour code as in the hypnogram) is shown in figure 1a (bottom panel). Super-threshold events comprising the point process are shown as black dots (the back dashed line indicates the 1 s.d. threshold).

Figure 1.

Methodological outline. (a) Upper panel: example hypnogram showing the progression of sleep stages from wakefulness (blue) towards N1 (green), N2 (red) and N3 sleep (yellow). Bottom panel: BOLD signal from a randomly chosen voxel, with the corresponding sleep stages indicated using the same colour coding. Black dots represent the super-threshold values that constitute the point process. (b) Examples of the distribution of whole-brain binary activations into small (t = 4), medium (t = 20) and large (t = 127) cluster sizes. (c) Scheme of the data spatial down-sampling procedure (coarse graining). BOLD signals from voxels comprising a super-voxel were first extracted and then averaged to yield the coarse-grained signal (upper panel). Axial slices showing cluster distributions after two successive coarse-graining steps are shown in the lower panel. (d) Two correlated BOLD signals (upper panel) and their corresponding surrogates obtained after phase shuffling (lower panel). The preserved power spectra of the signals are shown in the insets. In all panels, time is represented in units of elapsed fMRI volumes [#V]. (Online version in colour.)

2.5. Connected clusters of co-activated voxels

Connected components composed of co-activated voxels are here referred to as clusters. Clusters correspond to connected groups of simultaneously activated voxels, where connection is understood as a first-neighbour relationship in a cubic lattice, and activation is understood as super-threshold BOLD signal values. Thus, each fMRI volume consisted of isolated clusters spread throughout the cortical and subcortical grey matter. The size of each cluster was obtained by counting the total number of voxels belonging to it. Cluster sizes presented a large variability; as shown in figure 1b, at different times the activity could be distributed into small (t = 4), intermediate (t = 20) and large (t = 127) clusters (all times are given in terms of elapsed fMRI volumes). In particular, in this last example it can be seen that all activated voxels coalesce into a brain-wide cluster. To obtain cluster size distributions per sleep stage, cluster sizes were normalized by their total number, and then data from all participants were averaged within bins of sizes determined by a logarithmic scale. The distributions pool cluster sizes across all times for each sleep stage.

2.6. Power-law distributions

Distributions of cluster sizes were obtained per sleep stage. Plotting these distributions using logarithmic binning suggested behaviour of the form P(s) = s^−α. The scaling exponent α was computed using the method of maximum-likelihood estimators (MLEs) by Clauset et al. [59]. The scaling parameter was estimated from the cumulative density function (CDF) instead of the probability density function (PDF) since this reduces bias related to the tail of the distribution and the binning of the data. The method of MLEs excluded values below a lower bound (determined for each individual distribution) to avoid bias in the estimation [59].

2.7. Statistical testing

The exponent α was computed for each subject and sleep stage, and then compared across sleep stages using a non-parametric version of ANOVA (Kruskal–Wallis test). Post hoc non-parametric Wilcoxon signed-rank and permutation tests were conducted to evaluate differences between pairs of sleep stages.

2.8. Coarse graining

To leverage the high spatial and whole-brain resolution of fMRI, avalanche-like behaviour was studied at different levels of spatial resolution by means of spatial down-sampling of the data (coarse graining). Coarse-grained voxels were obtained by averaging the BOLD signals from their corresponding sub-voxels [60]. An example of this procedure is shown in figure 1c, representing an axial slice (upper panel, left) with a super-voxel divided into four sub-voxels whose signals (upper panel, right) are averaged. Starting from an original voxel resolution of 4 × 4 × 4 mm, only two coarse-graining steps could be performed before excessively downgrading the spatial resolution of the data (bottom panel). The resulting resolutions were then 8 × 8 × 8 mm and 16 × 16 × 16 mm. Observables following a scale-free distribution are expected to remain approximately constant upon coarse graining of the data.

2.9. BOLD time-series phase shuffling

BOLD signals were phase shuffled to construct null models using signals that contain the same spectrum as the original versions, but with scrambled phases (surrogates). This procedure was implemented by applying a fast Fourier transform (FFT) to transform BOLD signals into the frequency domain, and subsequently reversing the FFT after adding a random phase to obtain the surrogate time series. Figure 1d shows two examples of BOLD signals (upper panel) and their corresponding surrogates (bottom panel). After phase scrambling, the Pearson correlation coefficient between the signals was reduced from ρ = 0.74 to ρ = 0.03. The preserved spectra of the signals are shown as insets (smoothed using a Savitzky–Golay filter for better visualization).

2.10. Robustness against threshold change

While the threshold value of 1 s.d. was chosen by default based on previous work [36], the analyses were repeated using binarization thresholds ranging between 0 and 1.5 s.d. (in steps of 0.25).

3. Results

3.1. Power laws

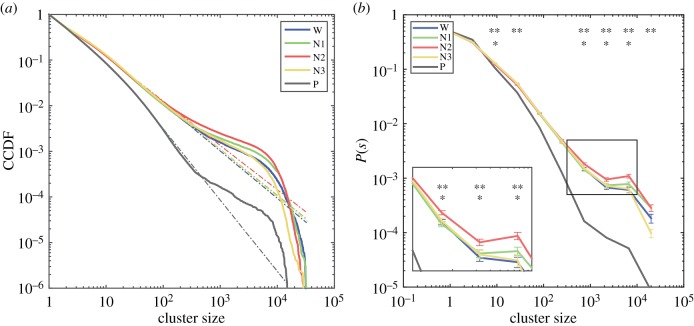
We show in figure 2a the complementary cumulative distribution functions (CCDFs) for cluster sizes per sleep stage (wakefulness (W), N1, N2 and N3 sleep) obtained following the procedure explained in §2.5. In figure 2b we show the normalized cluster size distributions, where P(s) represents the probability of obtaining a cluster of size s by randomly selecting from all clusters within a given sleep stage. Except for the distribution corresponding to the water phantom, power-law scaling was observed for all sleep stages up to sizes ≈10³. In particular, we observed non-zero probability of finding clusters of approximately 10⁴ co-activated voxels which, at this particular resolution, represents most of the grey matter voxels in the brain. Conversely, such extreme events were not observed for the water phantom. Applying a non-parametric Kruskal–Wallis test to each bin, we observed that the effect of sleep stage on P(s) was significant (p < 0.05, Bonferroni corrected for multiple comparisons) at the tail of the distribution (i.e. sleep stage showed a significant effect on the likelihood of measuring extreme events of co-activated clusters), as well as at the rest of the distributions. Post hoc Wilcoxon signed-rank tests (p < 0.05, Bonferroni corrected for multiple comparisons) revealed that differences could be predominantly attributed to larger P(s) for N2 sleep versus wakefulness.

Figure 2.

Distributions of cluster sizes. (a) The complementary cumulative distribution functions (CCDFs) for cluster sizes (colour coded for wakefulness, N1, N2 and N3 sleep). (b) The normalized probability density functions for cluster sizes (colour coded as in (a)). The inset zooms in to the tail of the distributions, where significant effects of stage on P(s) were found (** significant effect of sleep stage on P(s), * significant difference of P(s) between wakefulness and N2 sleep). (Online version in colour.)

The electronic supplementary material (section 1) contains results obtained from fitting other distributions to the data (lognormal, power law with exponential cut-off, and truncated power law), and comparing them versus power laws. This analysis supports the presence of power-law behaviour in the cluster size distributions. The goodness of fit values obtained using models with one additional free parameter (lognormal and power law with exponential cut-off) were comparable to those from unmodified power laws, and the estimated parameters indicated that the fitted distributions presented asymptotic power law behaviour (i.e. the optimal parameters yielded power laws as limiting cases). Sections 2, 3 and 4 of the electronic supplementary material contain the CCDFs of each individual participant with the corresponding best-fitting power laws, truncated power laws and power laws with exponential cut-off, respectively.

3.2. Scaling parameters

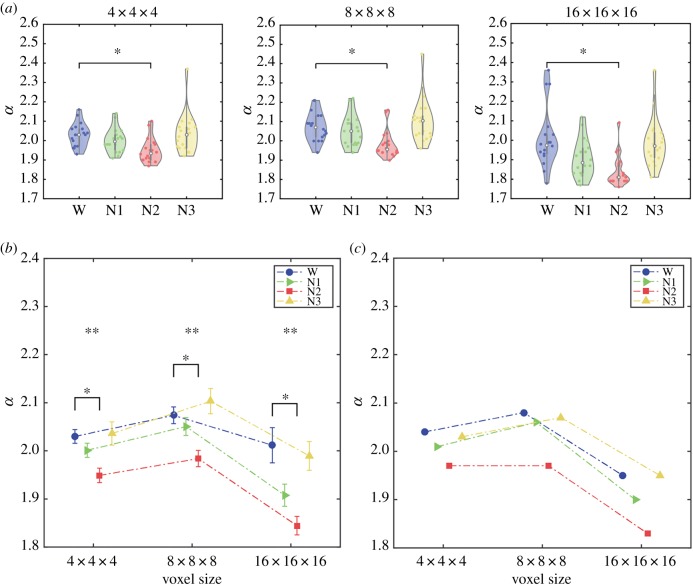
While comparing P(s) in bins where the scaling relationship no longer holds (i.e. the tail of the distribution) may be intuitive [29], a more adequate comparison of the distributions can be performed by applying the method of MLEs to the CDFs of the PDFs plotted in figure 2. Figure 3a (leftmost panel) presents violin plots for the estimated scaling parameters α for all participants and separated per sleep stage (the α value for the water phantom was estimated as ≈2.5). We applied the non-parametric Kruskal–Wallis test to reject the null hypothesis that wakefulness/sleep stage did not have an effect on α (p = 0.0012). We then applied non-parametric Wilcoxon signed-rank tests for the post hoc comparison of α between wakefulness and all sleep stages. After correcting for multiple comparisons, we found that the mean α value was significantly lower in N2 sleep than in wakefulness (p = 0.0018). We also compared the goodness of fit (Kolmogorov–Smirnov statistic) between wakefulness and all sleep stages (Wilcoxon signed-rank test, Bonferroni corrected). We observed significantly better goodness of fit for the wakefulness distribution versus the N2 sleep distribution (p = 0.01), but not for N1 (p = 0.06) or N3 sleep (p = 0.91). The scaling parameters α estimated from lognormal, power law with exponential cut-off and truncated power-law distributions were very close to those obtained using full power laws, and the statistical analyses yielded identical results to those presented in figure 3a (see section 1 of the electronic supplementary material), thus indicating that the tails of the distributions in figure 2 did not drive our results.

Figure 3.

Scaling parameter α for different granularities of the data. (a) Violin plots of α values. A significant effect of sleep stage on α was found for all resolutions (4 × 4 × 4: p = 0.0012; 8 × 8 × 8: p = 0.0002; 16 × 16 × 16: p < 0.0001). Post hoc tests showed that α decreased from wakefulness to N2 sleep for all resolutions (4 × 4 × 4: p = 0.0018; 8 × 8 × 8: p = 0.0018; 16 × 16 × 16: p = 0.0006). (b) Means and standard errors of α for each resolution. ANOVA tests revealed a significant effect of stage across all resolutions (4 × 4 × 4: p = 0.0029; 8 × 8 × 8: p = 0.0007; 16 × 16 × 16: p = 0.0002). (c) Scaling parameter values α for cluster size distributions obtained by pooling values for all subjects. (Online version in colour.)

3.3. Coarse graining

Taking advantage of the high spatial resolution and whole-brain coverage of fMRI, we applied successive coarse-graining steps to assess the stability of our results. In figure 3a we present violin plots for the three granularities and observed a significant effect of stage on α for all of them (Kruskal–Wallis test; 4 × 4 × 4: p = 0.0012; 8 × 8 × 8: p = 0.0002; 16 × 16 × 16: p < 0.0001; all units in mm). Also, for all three granularities post hoc tests showed that α was significantly reduced from wakefulness to N2 sleep (Bonferroni-corrected Wilcoxon signed-rank test; 4 × 4 × 4: p = 0.0018; 8 × 8 × 8: p = 0.0018; 16 × 16 × 16: p = 0.0006; all units in mm). We verified the assumptions of parametric ANOVA by applying Shapiro–Wilk and Levene's tests for normality and homoscedasticity, respectively. An ANOVA test rejected the null hypothesis that the mean α was independent of stage (ANOVA; 4 × 4 × 4: p = 0.0029; 8 × 8 × 8: p = 0.0007; 16 × 16 × 16: p = 0.0002, all units in mm). Finally, we used a permutation test between groups (10.000 permutations) to further show that N2 sleep presented a significantly smaller scaling parameter than wakefulness for all granularities (4 × 4 × 4: p = 0.0015; 8 × 8 × 8: p = 0.0033; 16 × 16 × 16: p = 0.0006, all units in mm).

We also constructed distributions of cluster sizes for all subjects combined (per sleep stage) and used the method of MLEs to estimate the corresponding α value. The estimated values for all subjects pooled into the same distribution are shown in figure 3c, which displays values consistent with those of figure 3b (i.e. α estimated independently per subject and then averaged).

3.4. Phase shuffling

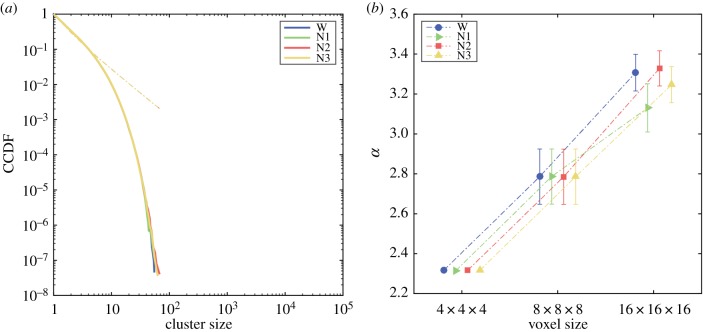
We repeated the analyses presented in the previous sections but after randomly shuffling the phases of the BOLD time series corresponding to each voxel. These surrogate time series are in principle uncorrelated and can be used to construct null models to compare the findings obtained from the preserved time series. Neither the CCDFs for cluster sizes (figure 4a) nor the estimated α values (figure 4b) presented significant differences between stages. It is also clear that phase shuffling eliminated the scale invariance reported in figure 3 from the data. Not only did the cluster size distributions not follow a power law (all P(s) collapsed into the same exponentially decaying distribution), but furthermore coarse graining altered the scaling parameter, which should have remained approximately constant for a scale-free power-law distribution (compare with figure 3b and figure 3c). Section 6 of the electronic supplementary material shows that the CCDFs for cluster sizes using the shuffled data can be fitted with a power law with exponential cut-off (the corresponding exponents appear as the slopes of the dashed lines in figure 4a). The optimal cut-off parameter was, on average, 10⁹ larger than those estimated for the unshuffled data, consistent with the strong exponential decay seen in figure 4a.

Figure 4.

Results obtained for the phase-shuffled BOLD time series. (a) Complementary cumulative distribution functions (CCDFs) for cluster sizes obtained using the surrogate time series. The dashed lines indicate the exponent of the best fit using power laws with exponential cut-off. The cut-off parameters β were, on average, 10⁹ larger than for the unshuffled data. (b) Means and standard errors of α values for each level of granularity. Note that there are no significant differences between stages, and that the α values change significantly as a consequence of coarse graining. (Online version in colour.)

3.5. Correlations between scaling exponents and prevalence of sleep grapho-elements

To assess the possibility that the simultaneous co-activation of voxels due to the onset of sleep spindles and K-complexes during N2 sleep could affect the scaling parameters (figure 2), we correlated the α values obtained from the MLE estimation with the total number of grapho-elements of each class across all participants (non-parametric Spearman rank correlation). Neither correlations with the total number of sleep spindles (ρ = −0.31, p = 0.2) nor K-complexes (ρ = 0.05, p = 0.83) were found to be significant.

3.6. Robustness against the point-process threshold

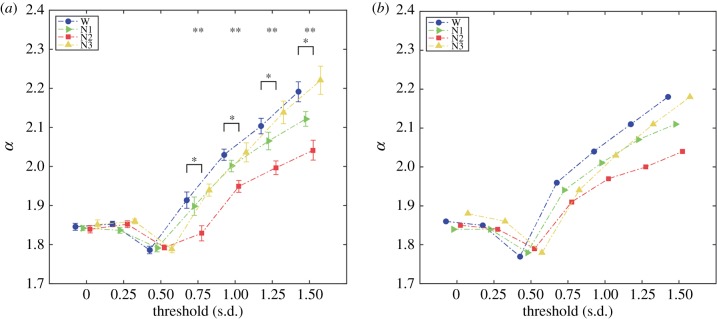
We repeated the analysis for different thresholds in the process of transforming BOLD time series into a spatio-temporal point process. Figure 5a shows the mean value of the estimated α for each threshold. Applying the Kruskal–Wallis test we found significant differences for the upper range of thresholds, beginning with 0.75. For these thresholds, post hoc non-parametric Wilcoxon signed-rank tests showed differences between wakefulness and N2 sleep. Parametric ANOVA and permutation tests agreed with these results. The scaling parameters estimated from distributions pooling all subjects per sleep stage are shown in figure 5b and agree with those presented in figure 5a.

Figure 5.

α values across binarization thresholds. (a) Means and standard errors of the estimated α as a function of the binarization threshold. An effect of stage on α (**p < 0.05, Kruskal–Wallis test) was observed for all thresholds above 0.75 s.d. Post hoc tests revealed significantly higher α values (*p < 0.05, Wilcoxon signed-rank test) in wakefulness versus N2 sleep for all thresholds above 0.75 s.d. (b) α values obtained from distributions pooling all subjects within each sleep stage. (Online version in colour.)

3.7. Two-point spatial correlation function

As an alternative marker of scale-free behaviour, we followed Expert et al. [60] in computing the spatial correlation function 〈C(r)〉. The procedure for computing 〈C(r)〉 and the obtained results are presented in section 7 of the electronic supplementary material.

4. Discussion

We probed for the first time the scale-invariant properties of whole-brain fMRI data from wakefulness to deep sleep. Adopting the theoretical and methodological framework of critical phenomena, we obtained evidence that the likelihood of large-scale events encompassing most grey matter voxels is modulated throughout the human sleep–wake cycle. We begin with a general discussion on the validity of interpreting our results as linked to critical phenomena, followed by their relationship with the neurophysiology of human sleep, and finally by considering the possible connection between the states of reduced responsiveness and departures from criticality.

Our use of ‘avalanche-like events’ to describe extreme events in the tail of the distribution P(s) relates to the difficulty of inferring certain features characteristic of avalanching phenomena from fMRI recordings. fMRI data are severely sub-sampled in the temporal domain relative to other methods that have been used in experiments to evaluate neuronal avalanches (e.g. LFP, EEG, MEG, voltage and two-photon imaging) [19–35,46]. These methods rely on the selection of an appropriate temporal bin size Δt, during which binary events are detected and averaged. The limitation of fMRI is analogous to a relatively large and fixed Δt that is constrained by the low temporal sampling rate. In a similar way that the avalanche size distributions deviate from power-law behaviour when spatially sub-sampled [27,29,61], the detection of ‘avalanche-like’ events in fMRI data results in exponentially decaying distributions for avalanche size as a function of time, as shown in fig. 4c in [36]. The separation of time scales observed in models of self-organized criticality [18] is less manifest in avalanches from electrophysiological recordings [41] and even more so in fMRI data. While Priesemann et al. [41] argued that external forcing of a subcritical state could eliminate the separation of time scales, it is difficult to disentangle this possibility from temporal sub-sampling in the case of fMRI data. Tracking the temporal evolution of avalanches in fMRI data presents another difficulty: the possibility that multiple cascades of activity originate in different cortical areas, leading to the problem of distinguishing them based on the comparatively low temporal resolution of this imaging method. Our proposed solution is to assume that co-activated clusters represent ‘time slices’ of ongoing events originating throughout different parts of the cortex, and then assessing the power-law behaviour of the resulting cluster size distribution [36].

In contrast to the temporal resolution, fMRI provides whole-brain coverage with millimetric spatial resolution and, as such, it is in principle a relatively good neuroimaging method to investigate the spatial properties of mesoscopic and macroscopic cascading events, which can be severely affected by sub-sampling effects in other imaging modalities [27,29,41]. The distributions for the size of co-activated clusters, P(s), follow power laws with robust scaling exponents, consistent with a previous report [36]. Importantly, the emergence of power laws for the distribution of cluster sizes could be traced to the collective behaviour of the BOLD time series, since power-law scaling did not emerge from the phase-shuffled data (figure 4a). While different sleep stages showed variations in the scaling parameter α, the impact of coarse graining was comparatively low relative to that observed in the phase-shuffled data (figure 3c), as expected for scale-invariant cluster distributions (figure 4b). Finally, different alternative statistical models were investigated (including truncated and exponentially truncated power laws), yielding results consistent with standard power-law distributions. It must be noted that the existence of scale-free avalanches in neural tissue remains a debated issue [62–64]. The most studied models of self-organized criticality consist of homogeneous units arranged in a lattice [65]; however, the brain must be ultimately understood as a system consisting of complex interacting units linked by a network of long-distance connections [66].

Critical branching processes are expected to produce cascade distributions with scaling exponent α = 3/2. However, the scaling exponents observed in our data were higher than this value (≈2). The scaling exponents for neuronal avalanches reported in the literature are variable as well, ranging from values close to 3/2 [19] to >2 [19,21–23,25,26]. These discrepancies have been generally attributed to the limitations of experimental set-ups and recording techniques, e.g. slow waves of activity present in reduced preparations [24], spacing between units in electrode arrays [67] and finite size and/or volume conduction effects in EEG data [34]. Besides finite size effects [68], we can expect departures from theoretical predictions since in fMRI data the characteristic times of signal transmission are related to the unusual hydrodynamics of the vascular system, and not directly related to the sequences of neural spikes. We must note, however, that scaling parameters α ≈ 2 were reported in previous work addressing the statistics of observables related to sleep physiology (e.g. the duration of arousals [43,44,69]), and can depend upon environmental variables such as temperature [70]. Furthermore, the Gutenberg–Richter law for the amplitudes of different earthquakes also shows power-law exponents α ≈ 2 [71].

We observed that the scaling parameter values remained approximately constant for different levels of coarse graining (figure 3b), especially when compared with the phase-shuffled data (figure 4b). This is consistent with the scale-free behaviour of critical systems [60]. The differences we observed likely relate to the fact that not all distributions closely followed a power law, as also reported by previous authors assessing neuronal avalanches in vivo in humans [29]. Regardless, we did not observe a radical departure from power-law distributions following unconsciousness, as reported from voltage imaging experiments in mice [30]. However, the goodness of fit was significantly reduced in N2 sleep relative to wakefulness. Our result is similar to that reported for LFP recordings in humans [29]; in particular, that differences comprise changes in the scaling parameter, as well as the higher prevalence of events in the tail of the distributions during sleep relative to wakefulness. Insofar as criticality is associated with rapid response to external perturbations (i.e. high susceptibility), this result could be related to the persistence of covert responsiveness and off-line information processing during sleep [72] (likely due to the influence of deep-brain neuromodulatory centres), which is absent in pharmacologically induced loss of consciousness.

Our results were specific to the contrast between wakefulness and N2 sleep, while N1 sleep presented an intermediate value between wakefulness and N2 sleep. The differences do not seem to be scale dependent (as they were manifest after coarse graining of the data), cannot be dismissed as trivial consequences of the correlation structure of the data (since they were not observed after phase shuffling) and were robust across a range of binarization thresholds. Decreased α values indicate a less pronounced slope and increased probability of large clusters occurring during N2 sleep, consistent with a previous study based on LFP recordings [29]. While both N2 and N3 sleep are regarded as stages of unresponsiveness, ample evidence supports sporadic reports of conscious mentation upon awakening [73–75], which could be related to local aspects of sleep [76–79]. The specificity of the changes to N2 sleep could in principle relate to neurophysiological processes that parallel the descent into deep sleep. As opposed to diffuse neuromodulatory mechanisms that help maintain a near-critical state across all sleep stages, differences in local dynamics could account for changes in the value of the scaling parameter. The opening of calcium-dependent potassium channels (K⁺) during deep sleep could cause hyperpolarization and bistability at the cell level [80]. K-complexes, large deflections in the EEG signal that serve a protective role against arousals, emerge during N2 sleep as a consequence of this process. The especially wide cortical distribution of K-complexes could bias the scaling parameters, independently of the background activity, and thus impact on the shape of the distributions [72]. However, we did not find a significant correlation between the number of K-complexes/sleep spindles and the scaling exponents obtained for N2 sleep. The fact that extreme haemodynamic events are not observed with higher probability during N3 sleep could be linked to specific processes associated with the stabilization of deep sleep, as well as with a shift towards low electrophysiological frequencies that might not be reflected in the haemodynamic signal measured with fMRI [81,82]. It must be noted that, since N3 sleep presents stronger sleep inertia than earlier stages and less bursts in the theta and alpha ranges (e.g. as caused by arousals) [80], smaller cluster sizes could be expected during deep sleep; however, the same line of reasoning leads us to expect a higher number of large clusters (and, correspondingly, a smaller scaling parameter) for wakefulness, which was not observed. Finally, it could be the case that the standard sleep stages are too coarse, so that different contributions to α arise from finer subdivisions of N2 and N3 sleep [83].

In recent years, different theories have proposed numerical metrics to determine the level of conscious awareness present in a given physical system. Examples of these metrics include neural complexity [2], information integration (Φ) [4], causal density [84] and thermodynamic entropy [85]. A common objection to these metrics is the conceivability of abstract or physical systems realizing arbitrarily large values, leading either to their dismissal or to the commitment with a panpsychist worldview. A recent example is the online discussion between Scott Aaronson and Giulio Tononi² concerning the possibility (argued by Aaronson) of reaching arbitrarily large values of Φ either by abstract mathematical operations (iterative multiplication by a Vandermonde matrix with coefficients in a finite field with p elements, with p a sufficiently large prime number) or by a conceivable physical implementation (logic gates connected by an expander graph). These difficulties do not imply that, in principle, it should not be possible to devise a numerical quantity with the following two properties: (i) its value associated with a given physical system increases with the level of conscious awareness of said system and (ii) physical systems that are (by common sense) considered unconscious (e.g. regularly assembled logic gates) yield low values. In contrast to the problem of providing a scientific explanation for the subjectively felt qualities of conscious experience (the ‘hard problem of consciousness’) [86], Aaronson dubbed the discovery of a metric with the aforementioned properties the ‘pretty hard problem of consciousness’ since, as opposed to the former, it seems more scientifically tractable. Drawing connections between metrics related to critical phenomena (e.g. scaling exponents) and states of consciousness could represent an interesting contribution towards tackling the pretty hard problem of consciousness. Clearly, criticality does not per se offer a solution, since critical phenomena are ubiquitous in nature and regarded as unconscious by overwhelming consensus. However, such connection narrows the space of counterexamples to the set of self-organized many-body physical systems, thus excluding constructs such as logic gates coupled by expander graphs. It could be argued that such narrowing represents a step forward, which might not come as a surprise since (as opposed to the aforementioned theories) the criticality hypothesis is both explicit about the numerical metrics to be computed and the physical laws that assign them meaning. Convergent evidence from studies directly addressing functional integration as a function of neural dynamics during sleep add support to a relationship between our results and the predictions of integrated information theory [87,88].

It must be emphasized, however, that human sleep represents by itself a limited model to evaluate these claims, since neural processes related to loss of wakefulness (and not to loss of consciousness per se) could affect our results. While our analysis seems to rule out an effect of sleep grapho-elements that are not directly linked to loss of conscious awareness, the complex neuromodulatory and neurophysiological processes underlying loss of vigilance and unresponsiveness during sleep are difficult to disentangle from those associated with impaired levels of consciousness [80,86]. This is especially clear in the similar α values measured during wakefulness and N3 sleep. Thus, other experimental models (such as general anaesthesia or patients with disorders of consciousness) should be evaluated using this methodology in future studies.

In conclusion, we observed scale-free whole-brain fMRI activity consistent with critical or near-critical dynamics. The distributions of sizes of co-activated clusters were close to power laws, and the scaling exponents of those power laws reflected the transitions between sleep stages. A deep sleep stage (N2) was robustly associated with an increased probability of observing extreme events in the tail of the distribution. The information-processing capabilities that critical dynamics bestow upon the human cortex are highly suggestive of a potential role in the emergence and maintenance of conscious awareness. While several quantitative metrics have been proposed to estimate the level of conscious awareness based on empirical observations, those associated with signatures of criticality present the advantages of being motivated in terms of fundamental physical laws, not requiring the postulation of ad hoc mechanisms for their emergence in living neural tissue, and being harder to dismiss by arguments based on trivial counter-examples that should produce high levels of conscious awareness.

Ethics

All subjects signed written informed consent approved by the local ethics committee.

Data accessibility

The datasets supporting this article (https://doi.org/10.5061/dryad.78v68ss) and the codes required to reproduce them (https://github.com/HBocaccio/Avalanches_Sleep_fMRI_2019) have been uploaded as part of the electronic supplementary material.

Authors' contributions

H.L. designed and supervised the experiments; E.T. coordinated data analyses and co-wrote the manuscript; H.B. conducted data analyses and co-wrote the manuscript; M.F.V. coordinated data analyses and revised the manuscript; C.P. helped to draft an early version of the manuscript; M.N.C., S.M.S. and G.D.P. revised the manuscript and contributed to the discussion. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

Data acquisition was supported by the Bundesministerium für Bildung und Forschung (grant no. 01 EV 0703) and the LOEWE Neuronale Koordination Forschungsschwerpunkt Frankfurt (NeFF). H.B., S.M.S. (doctoral) and C.P. (postdoctoral) are funded by fellowships from CONICET (Argentina).