Abstract
Typical approaches to patient-specific haemodynamic studies of cerebral aneurysms use image-based computational fluid dynamics (CFD) and seek to statistically correlate parameters such as wall shear stress (WSS) and oscillatory shear index (OSI) to risk of growth and rupture. However, such studies have reported contradictory results, emphasizing the need for in-depth multi-modality haemodynamic metric evaluation. In this work, we used in vivo 4D flow MRI data to inform in vitro particle velocimetry and CFD modalities in two patient-specific cerebral aneurysm models (basilar tip and internal carotid artery). Pulsatile volumetric particle velocimetry experiments were conducted, and the particle images were processed using Shake-the-Box, a particle tracking method. Distributions of normalized WSS and relative residence time were shown to be highly yet inconsistently affected by minor flow field and spatial resolution variations across modalities, and specific relationships among these should be explored in future work. Conversely, OSI, a non-dimensional parameter, was shown to be more robust to the varying assumptions, limitations and spatial resolutions of each subject and modality. These results suggest a need for further multi-modality analysis as well as development of non-dimensional haemodynamic parameters and correlation of such metrics to aneurysm risk of growth and rupture.
Keywords: cerebral aneurysm, particle image velocimetry, 4D flow MRI, wall shear stress, oscillatory shear index, relative residence time
1. Introduction
It is estimated that about 3% of the population harbours an unruptured intracranial aneurysm (IA) [1]. If detected, clinicians must assess and balance risk of rupture with risk of treatment of the cerebral aneurysm [2,3]. However, accurately assessing risk of rupture in IAs is difficult as the specific mechanisms that cause an aneurysm to form, grow and rupture remain largely unknown.
Previous studies have demonstrated that haemodynamics plays a critical role in the growth and rupture of an IA [4–8]. However, despite a large volume of studies that have investigated the influence of several haemodynamic variables on risk of rupture, contradictory and ultimately inconclusive results have been reported. Wall shear stress (WSS) has received much attention but has been perhaps the most controversial haemodynamic parameter [8]. Both low [4,9–12] and high [13,14] WSS have been shown to indicate elevated risk of rupture. High WSS gradients, high oscillatory shear index (OSI) and high relative residence time (RRT) have also been reported to increase risk of rupture [4,8,11,15]. Studies have also explored the presence and effect of chaotic flow and high-frequency fluctuations in cerebral aneurysms [3,6,16]. Other haemodynamic variables identified as potentially increasing the risk of rupture include concentrated inflow jets, larger shear concentration, lower viscous dissipation and complex and unstable flow patterns [6,13,14].
Computational fluid dynamics (CFD) has been the predominant methodology used to study haemodynamics in cerebral aneurysms [2,4,9,10,14,16]. However, limited CFD validation and disputed CFD assumptions such as laminar flow remain issues limiting its clinical acceptance [17]. It has also been shown that CFD results can vary significantly based on solver parameters, even when similar geometries and boundary conditions are used [5,18]. Velocity fields obtained from both in vivo and in vitro 4D flow MRI have also been used, but the low spatio-temporal resolution is a major limitation of this modality [5,10,19]. Although high-resolution 4D flow MRI has been shown to capture complex flow patterns [19], studies have demonstrated that the low resolution causes an underestimation of velocity and WSS magnitudes, particularly when compared with CFD or particle image velocimetry (PIV) [2,5,10,20]. Few experimental PIV studies have been conducted in this domain. Among such studies, planar and stereo PIV (2D-2 velocity component) have been the most common [3,11,15,19,21]. Other studies have taken two-dimensional data at several parallel planes in a ‘sliced planar’ (3D-2 velocity component) configuration and subsequently reconstructed the third velocity component [6,22]. Despite the high three-dimensionality known to exist in cerebral aneurysm geometries, to date, only one steady-flow 4D tomographic (TOMO) PIV (3D-3 velocity component) study has been reported [5]. Furthermore, PIV studies are most often used only to compare flow patterns and validate CFD models and simulations [5,11,19]; only a few have reported WSS and even fewer (if any) OSI and RRT [6,15]. Multi-modality-type studies have compared in vivo 4D flow MRI and CFD [9,10,17,23], many treating CFD as the ‘ground-truth’ modality due to its increased resolution and accuracy; however, the higher physiological fidelity method is debatable. Due to this ‘ground-truth’ concern, studies which directly compare 4D flow MRI, CFD and PIV are often restricted to in vitro and in silico validation-based analysis [3,5,19,22], limiting their clinical translational ability due to the lack of in vivo data.
In this work, we use a multi-modality approach, including in vivo measurements, in vitro experiments and in silico modelling, in a unique way, where the in vivo 4D flow MRI was used as boundary conditions for the CFD and particle velocimetry. We conducted one of the first reported pulsatile volumetric particle velocimetry studies using two patient-specific aneurysm models. As opposed to traditional TOMO-PIV studies which use interrogation window correlation, we used Shake-the-Box (STB) [24], a particle tracking methodology, which has, to the authors' knowledge, never been used in this domain and demonstrated significant improvements in the current experimental methodologies for this application. All three modalities maintained different assumptions and limitations, and—due to the low spatio-temporal resolution and high noise inherent to 4D flow MRI—some uncertainty in the prescribed boundary conditions existed which manifested into flow variations across modalities. Here, we investigate the effects of these factors on the resulting haemodynamic metrics including time-averaged WSS (TAWSS), OSI and RRT. The multi-modality approach of this work was intended to take some initial steps towards bridging the gaps between modalities and understanding how to synthesize information by leveraging the strengths of each method and compensating for the weaknesses, thereby enhancing the clinical translational ability of such haemodynamic analysis.
2. Material and methods
2.1. In vivo 4D flow MRI and magnetic resonance angiography imaging
The two aneurysm models used were a basilar tip aneurysm, MRI imaged at San Francisco VA Medical Center, and an internal carotid artery (ICA) aneurysm, MRI imaged at Northwestern Memorial Hospital (NMH). Both aneurysms were imaged on a 3 T MRI scanner (Skyra, Siemens Healthcare, Erlangen, Germany). At San Francisco VA Medical Center, the Siemens WIP sequence, an ECG-gated RF spoiled 4D flow MRI sequence, was used with gadolinium contrast, while at NMH no contrast was used. The 4D flow scan parameters for both imaging studies are given in table 1. The in vivo 4D flow MRI data will be referred to simply as ‘4D flow’ herein.
Table 1.
4D flow MRI parameters and resolutions. (TE, echo time; TR, repetition time.)
| geometry | TE/TR (ms) | flip angle (°) | velocity encoding (venc) (cm s−1) | temporal resolution (ms) | spatial resolution (mm) |
|---|---|---|---|---|---|
| basilar tip | 3.46/6.33 | 12 | 100 | 40.5 | 1.25 × 1.25 × 1.33 |
| ICA | 2.997/6.4 | 15 | 80 | 44.8 | 1.09 × 1.09 × 1.30 |
All 4D flow data were corrected for noise, velocity aliasing and phase offset errors caused by eddy currents and concomitant gradient terms. In addition to 4D flow, contrast-enhanced magnetic resonance angiography (CE-MRA) data with a spatial resolution of 0.7 × 0.7 × 0.7 mm3 for the basilar tip aneurysm and non-contrast time of flight (TOF) angiography with a spatial resolution of 0.4 × 0.4 × 0.6 mm3 for the ICA aneurysm were acquired in the same scanning sessions and used to create the in vitro models.
2.2. Image segmentation and model fabrication
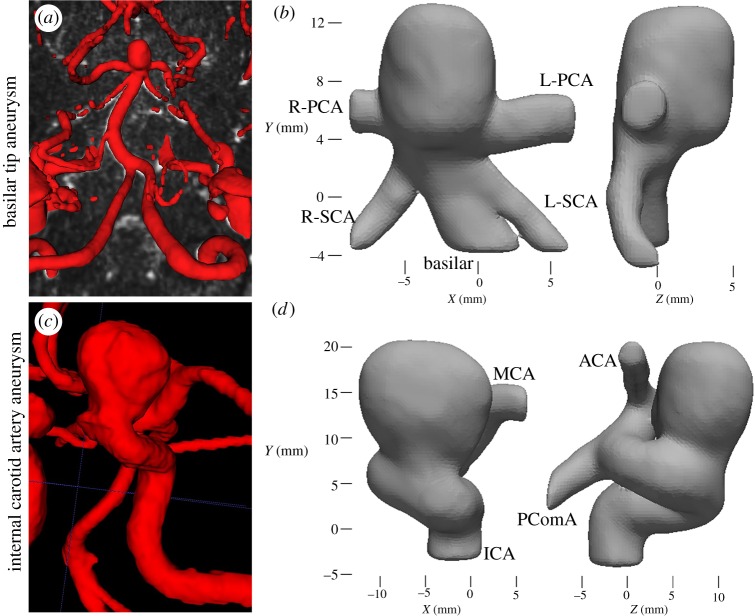
For the basilar tip aneurysm, CE-MRA images were segmented using an in-house VTK-based software. A three-dimensional (3D) iso-surface was computed by selecting a threshold intensity value that defined the intra-luminal volume of the vessel. The threshold was adjusted to match the iso-surface to the MR luminal boundaries. For the ICA aneurysm, TOF images were segmented with an open-source ITK-Snap software, using thresholding and volume growth techniques. A modelling software, Geomagic Design (3D Systems, Rock Hill, SC, USA), was used to separate the inflow and outflow vessels of the aneurysm from the remaining cerebral vasculature (figure 1a,c). The resulting surface (STL), shown in figure 1b,d, was used for CFD simulations and PIV flow phantom fabrication. Note that the STL surfaces in figure 1 are zoomed in and clipped such that they do not reflect the full branch lengths. For the flow phantoms, inlet and outlet vessels were extended in order to connect the model to the flow loop. A positive-space model of the vascular geometry was 3D printed (ProJet printer—3D Systems), embedded into a tear-resistant silicone block and then cut from the block. A low melting point metal (Cerrobend 158 Bismuth alloy) was cast into the block, and the block was then cut away. The metal model was embedded in optically clear polydimethylsiloxane silicone (PDMS—Slygard 184) which was allowed to cure until hardened, then the metal was melted out from the clear PDMS.
Figure 1.
Segmentation from (a) in vivo vasculature showing patient-specific basilar tip aneurysm to the (b) associated in vitro model. Note that the in vitro basilar tip model was mirrored when compared with the in vivo. (c) In vivo vasculature for patient-specific ICA aneurysm and the (d) in vitro segmented model (PCA, posterior cerebral artery; SCA, superior cerebellar artery; MCA, middle cerebral artery; ACA, anterior cerebral artery; PComA, posterior communicating artery). (Online version in colour.)
2.3. In vitro flow loop
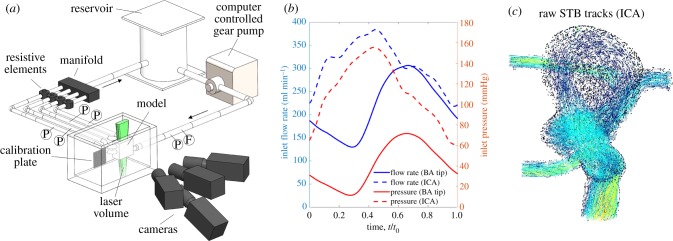
An in vitro flow loop (figure 2a) was designed to simulate in vivo flow conditions. The working fluids, detailed in table 2, were blood analogues consisting of water, glycerol and urea. Water, glycerol and urea blood analogues have been demonstrated to provide good user-control and flexibility over the balance of fluid density, viscosity and index of refraction, as well as yield densities more consistent with blood than water, glycerol and sodium iodide (NaI) solutions [25]. The pulsatile inflow waveforms (figure 2b) were extracted from the in vivo 4D flow MRI data and generated by a computer-controlled gear pump. Average flow rates for the outlet vessels were controlled using resistive elements to match the 4D flow outlet flow rate ratios. Flow details for both geometries are provided in table 3.
Figure 2.
(a) Schematic of the flow loop set-up, including the camera and calibration plate. F indicates locations of ultrasonic flowmeters and P indicates locations of pressure transducers. (b) Inflow flow rate and pressure taken from the upstream flowmeter and pressure transducer for both geometries. The phase of the pulsatile cycle is displayed as it was extracted from 4D flow MRI. (c) Sample STB tracks for the ICA geometry. (Online version in colour.)
Table 2.
Blood analogue working fluids used for both geometries. Nano-pure water, technical grade glycerol (99%; McMaster-Carr) and 99+% urea (Fischer Scientific) were used.
| blood analogue composition (wt%) |
|||||
|---|---|---|---|---|---|
| geometry | water | glycerol | urea | density (kg m−3) | kinematic viscosity (m2 s−1) |
| basilar tip | 44.8 | 32.8 | 22.4 | 1103 | 3.04 × 10−6 |
| ICA | 45.3 | 29.7 | 25.0 | 1132 | 3.50 × 10−6 |
Table 3.
Flow cycle information for both aneurysm geometries.
| Reynolds number |
||||
|---|---|---|---|---|
| geometry | max | min | Womersley number | cycle period, T (s) |
| basilar tip | 500 | 150 | 2.73 | 0.77 |
| ICA | 300 | 130 | 5.33 | 0.54 |
2.4. Volumetric particle velocimetry measurement technique
Particle images were captured using an Nd-YLF laser (Continuum Terra-PIV; λ = 527 nm) and four high-speed cameras (Phantom Miro). In the camera configuration (figure 2a), the centre camera was not angled, while the other three were angled about 30° from the geometry plane. The magnification of all cameras was approximately 30 µm pixel−1. Flow was seeded with 24 µm fluorescent particles, and long-pass filters filtered the laser light from the images. The index of refraction of the working fluid was matched to that of the PDMS model (n = 1.4118), and the model was submerged in the working fluid to reduce optical distortion. Time-resolved images (1216 × 1224 pixels for basilar tip and 1088 × 1320 pixels for ICA) were captured at 2000 Hz, corresponding to a maximum particle displacement between frames of approximately 10 pixels. Three full pulsatile cycles for the basilar tip aneurysm and four cycles for the ICA aneurysm were captured.
Particle images were processed using DaVis 10.0 (LaVision Inc.). Calibration images were captured using a dual-plane calibration target. The perspective calibration error was approximately 0.25 pixels for each camera in both experiments and volume self-calibration corrected these errors to less than 0.03 pixels [26]. STB, a particle tracking-based algorithm, was used to process the velocity fields. Sample STB tracks are shown in figure 2c. STB requires time-resolved data, using the previous time step to iteratively add predicted particle locations in the next time step. The predicted particle locations are refined by iteratively ‘shaking’ them within a tolerance, minimizing the residual between the subsequent particle image and the predicted particle image. STB was done using 12 iterations for both the outer (adding particles) and inner (particle position refinement) loops with an allowed particle triangulation error of 1.5 voxels and particle position shaking of 0.1 voxels. As opposed to planar and stereo PIV [27–29], currently no methods to evaluate uncertainty in volumetric PIV/STB processing have been reported. However, the calibration errors were consistent with those observed in well-controlled TOMO-PIV experiments. To further ensure the accuracy of the STB data, a portion of data was processed using the traditional TOMO-PIV multiplicative algebraic reconstruction technique (MART) processing [30]. Due to the complex, highly curved aneurysm geometries which amplify small and unavoidable refractive index mismatches within the test section, ghost particles (falsely triangulated 3D particles) were expected to be higher using MART. Ghost particles can create significant bias error in resulting velocity fields [24,31]. When compared with MART, STB's use of temporal information reduced the percentage of estimated ghost particles from about 10% to less than 1%. STB also reduced computation time by at least a factor of 10 per dataset. The volumetric STB data will be referred to as ‘STB’ herein.
2.5. Computational fluid dynamics simulation
CFD simulations were performed using Fluent 18.1 (ANSYS) to solve the governing Navier–Stokes equations. An unstructured tetrahedral mesh was generated on the domain using HyperMesh 14.0 (Altair Engineering, Troy, MI, USA). Incompressible, Newtonian flow with density of 1060 kg m−3 and dynamic viscosity of 0.0035 Pa s was modelled. Laminar flow and rigid walls were assumed. Patient-specific waveforms obtained from 4D flow were prescribed at the inlet and outlets of the CFD models. A pressure-based coupled algorithm was used to solve the momentum and pressure-based continuity equations. A second-order Crank–Nicolson scheme was used in time discretization and a third-order MUSCL scheme was used for discretization of the momentum equations. A mesh with a nominal cell size of 150 µm and time step of 1.5 ms was used. These values provided sufficient resolution of the flow based on mesh independence and temporal resolution testing. Three cardiac cycles were simulated, and the results obtained for the last cycle were used for comparisons with the other modalities.
2.6. Post-processing
All modalities were registered to and masked by the STL geometry obtained from MRA segmentation. The unstructured STB and CFD data were gridded to isotropic resolutions of 0.3 and 0.4 mm3 for the basilar tip and ICA aneurysms, respectively, using inverse-squared radial distance weighted averaging. An initial radius of half the grid size was used to search for the nearest unstructured vectors; however, this radius was extended to ensure a minimum of three unstructured vectors for each averaging calculation. For the STB gridding, unstructured velocity fields were temporally grouped at a 5 : 1 and 3 : 1 ratio for the basilar tip and ICA aneurysms, respectively, such that each unstructured field was used in only a single group. This increased the number of unstructured particles per gridded time step but reduced the effective temporal resolution to 2.5 and 1.5 ms for the basilar tip and ICA aneurysms, respectively. The gridded STB data were filtered using proper orthogonal decomposition with the entropy line fit autonomous thresholding method [32,33]. A single pass of universal outlier detection (UOD) [34] and phase averaging of the STB pulsatile cycles were subsequently done. ‘Virtual voxel averaging’ was spatially performed to bring the STB and CFD data to the 4D flow spatial resolution.
WSS was computed using thin-plate spline radial basis functions, which performs smoothing surface fits and reduces errors in the inherently noisy gradient calculation [35]. A normal vector at each surface point was computed by mapping the velocity coordinate to the equivalent STL-surface point and computing the inward facing normal from a surface fit of 25 adjacent STL-surface points. Two passes of UOD were used to eliminate erroneous normal vectors. For the voxel averaged (VA) datasets, wall normals were extracted from their full resolution equivalent. For the 4D flow, the full resolution CFD was used. WSS was computed according to the following equations [36]:
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
where τx, τy and τz are the WSS components in the x, y and z directions, τmag is the WSS magnitude, µ is the dynamic viscosity and (nx, ny, nz) is the unit normal.
The in-house WSS code, including the wall normal and velocity gradient calculations, was validated using analytical 3D Poiseuille flow data. Biases in the near-wall discrete velocity gradients, whose magnitudes vary based on each specific point's distance from the wall, are a known issue [6,35]. Thus, similar to that done in Yagi et al. [6], the WSS calculation was extended to use gradients beyond the biased near-wall region, mitigating the spatial variation of this bias to about 5% but allowing WSS magnitude bias errors of up to 25% (based on the validation testing). Thus, all WSS magnitudes reported here are expected to have a consistent bias and should be considered only relative to other values reported here.
TAWSS was computed according to the following equation:
| 2.5 |
where τw is the WSS vector and T is the duration of the pulsatile cycle. OSI was subsequently computed according to the following equation:
| 2.6 |
OSI is a non-dimensional parameter ranging from 0 to 0.5, where 0 indicates no oscillatory WSS throughout the pulsatile cycle and 0.5 indicates purely oscillatory WSS. RRT was computed using the following equation:
| 2.7 |
RRT is a measure of the flow stagnation or the residence of fluid particles near the wall. High RRT is typically considered as an indicator of flow disturbances [37], thrombus-prone regions [38] and flow separation regions which are believed to facilitate aneurysm growth [8].
3. Results
3.1. Comparing flow structures and velocity distributions across modalities
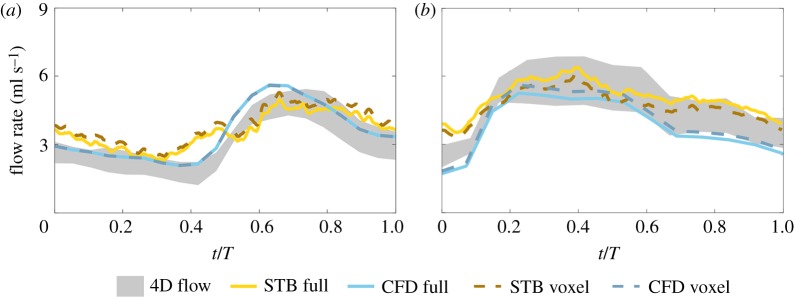
The inlet flow rate was computed from the velocity fields for all modalities in the basilar tip and ICA aneurysms to ensure agreement across modalities and is shown in figure 3a,b, respectively. The shaded 4D flow inflow rates highlight the difference between the computed inflow and outflow rates and demonstrate the uncertainty of prescribed in vitro boundary conditions. All reported 4D flow inflow rates are based on the average of the total inflow and outflow rates. The maximum inlet flow rate in the basilar tip aneurysm was 4.81, 4.97 and 5.61 ml s−1 for the 4D flow and full resolution STB and CFD, respectively. The average inlet flow rate was 3.09 ml s−1 for the 4D flow, 3.58 ml s−1 for STB and 3.51 ml s−1 for CFD. The trend of the inflow waveforms was similar for all modalities, with STB maintaining the largest temporal variability as expected. For the ICA aneurysm, the maximum inflow rate was 5.81, 6.40 and 5.26 ml s−1 for the 4D flow, and full resolution STB and CFD, respectively. The average inlet flow rate was 4.54 ml s−1 for 4D flow, 5.07 ml s−1 for STB and 3.79 ml s−1 for CFD. Again, the general inflow waveform trend showed reasonable agreement across all modalities.
Figure 3.
Inlet flow rates for all modalities in the (a) basilar tip aneurysm and (b) ICA aneurysm. The flow rate of 4D flow is shaded to show the discrepancy of the total inflow and outflow flow rates. (Online version in colour.)
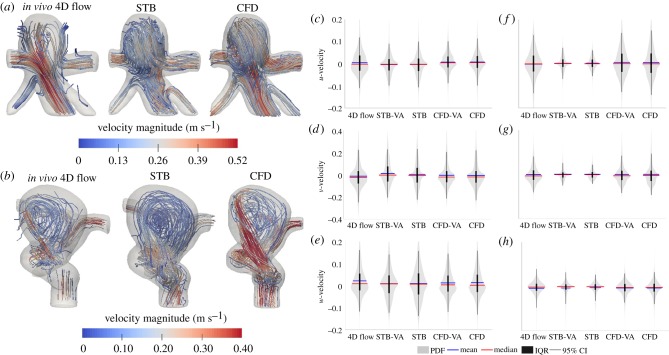
Figure 4 shows the instantaneous 3D velocity stream-tracers for each modality and geometry at peak systole. In the basilar tip aneurysm (figure 4a), initial observation shows qualitative agreement of the flow patterns across all modalities. Flow enters from the basilar artery and about 20% (by flow rate) exits through the superior cerebellar arteries. The remainder of the flow extends into the right distal posterior region of the aneurysmal sac, swirls to the left proximal anterior portion of the sac and exits the posterior cerebral arteries. In the ICA aneurysm (figure 4b), flow enters from the curving ICA and some flow rotates through the aneurysmal sac before re-entering the distal ICA. About half of the flow exits through the middle cerebral artery and the remainder splits between the anterior cerebral artery and posterior communicating artery. The swirling flow in the aneurysmal sac was qualitatively similar for the 4D flow and CFD, while for the STB, the swirling was more centred in the sac and the impinging jet was weaker. The velocity distributions in the aneurysmal sac for all modalities throughout the pulsatile cycle are shown in figure 4c–e for the basilar tip aneurysm and in figure 4f–h for the ICA aneurysm. The distributions highlight some velocity field differences across the modalities. Similar velocity distributions and velocity ranges were observed across all modalities for the basilar tip aneurysm. For the u-velocity component, 95% confidence interval (CI) ranges were ±11.4 cm s−1 for 4D flow, ±10.5 cm s−1 for STB and ±10.6 cm s−1 for CFD. For the v-velocity component, the 95% CI ranges were ±23.7, ±22.9 and ±22.6 cm s−1 for 4D flow, STB and CFD, respectively. The ranges for the w-velocity were ±13.9 cm s−1 for 4D flow, ±14.7 cm s−1 for STB and ±14.5 cm s−1 for CFD. In the ICA aneurysm, all modalities maintained similar distribution shapes; however, STB maintained lower magnitude ranges of the velocity distributions than 4D flow and CFD. For example, for the u-velocity component, STB maintained a 95% CI range of ±6 cm s−1 while 4D flow MRI and CFD maintained 95% CI ranges of ±14 cm s−1. For the v-velocity, 95% CI ranges were ±9 cm s−1 for STB and ±17 cm s−1 for 4D flow and CFD while for the w-velocity, they were ±6 cm s−1 for STB, ±7 cm s−1 for CFD and ±8 cm s−1 for 4D flow.
Figure 4.
Velocity field instantaneous streamlines for the MRI and full resolution STB and CFD at peak systole for the (a) basilar tip aneurysm and (b) ICA aneurysm. (Note: the two aneurysm geometries (a) and (b) are not shown at the same spatial scale.) Distributions of all velocity components throughout the entire pulsatile cycle, spatially limited to the aneurysmal sac only for the (c–e) basilar tip and (f–h) ICA aneurysm. The width of the probability density function (PDF) shows relative distribution density. The mean and median values, IQRs and 95% CIs are indicated. Violin plots were made from code adapted from [39]. (Online version in colour.)
3.2. Evaluating time-averaged wall shear stress, oscillatory shear index and relative residence time across modalities and spatial resolutions
The previous results demonstrate that each modality represented the same underlying process, maintaining similar large-scale flow features but with notable flow-field variations resulting from uncertainties in the segmentation and boundary conditions, as well as differing spatio-temporal resolution, flow properties and regime assumptions, and limitations across modalities. Next, the effects of such variations on subsequent haemodynamic metrics were evaluated.
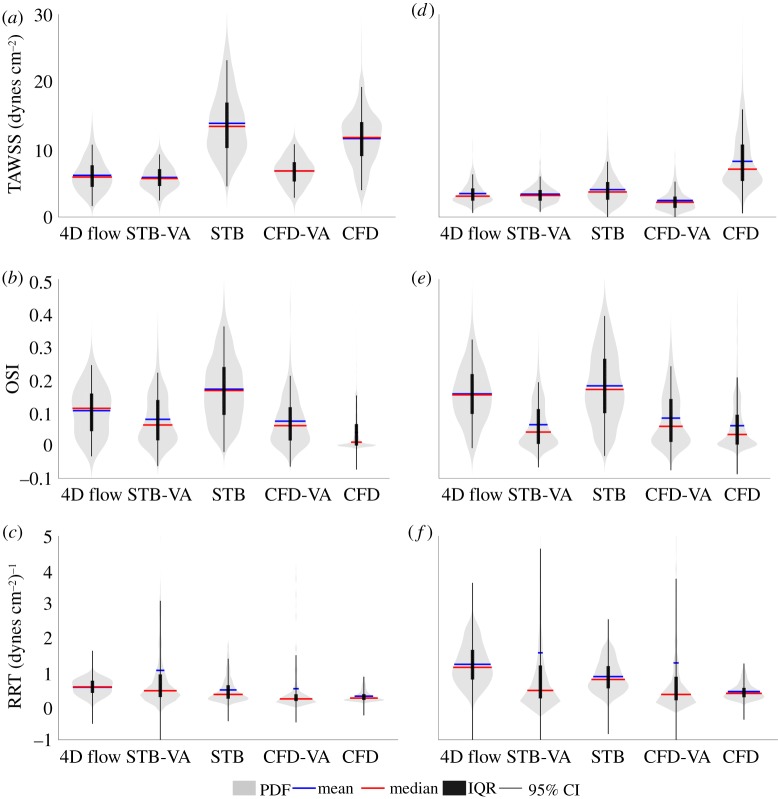
Figure 5 shows the distributions of TAWSS, OSI and RRT in the aneurysmal sac for all modalities for the basilar tip aneurysm (figure 5a–c) and ICA aneurysm (figure 5d–f). The distributions of the TAWSS varied significantly across all five datasets. For the basilar tip aneurysm, the average TAWSS was 6.19 dynes cm−2 for the 4D flow, 13.88 dynes cm−2 for the full resolution STB and 11.61 dynes cm−2 for the full resolution CFD. When voxel averaged, the average TAWSS decreased to 5.88 dynes cm−2 for the STB, a 58% drop, and to 6.81 dynes cm−2 for the CFD, a 41% decrease. For the ICA aneurysm, the TAWSS distributions of the 4D flow, full resolution STB, and VA STB and CFD showed agreement. The average TAWSS for STB had only a small change from 4.06 to 3.40 dynes cm−2 when voxel averaged. The average CFD TAWSS decreased 70% from 8.25 to 2.46 dynes cm−2 when voxel averaged. The full resolution CFD WSS distribution maintained a larger spread of WSS values than all other modalities and maintained the largest WSS magnitudes. Similar OSI distributions for the basilar tip aneurysm were observed for all modalities except the full resolution CFD. The average OSI of the STB changed from 0.17 to 0.08, while CFD went from 0.04 to 0.07 when voxel averaged. For the ICA aneurysm, good agreement of the OSI distribution and averages was observed between 4D flow and STB. The VA STB and CFD and full resolution CFD OSI distributions and averages matched well. Voxel averaging changed the average OSI from 0.18 to 0.06 for STB and from 0.06 to 0.08 for CFD. The average RRT in the basilar tip aneurysm was 0.55, 0.47 and 0.29 (dynes cm−2)−1 for the 4D flow, and full resolution STB and CFD, respectively. When voxel averaged, these values changed to 1.05 (dynes cm−2)−1 for STB and 0.50 (dynes cm−2)−1 for CFD. RRT distributions in the ICA aneurysm showed more variation across modalities. The average RRT in the ICA aneurysm was 1.22, 0.86 and 0.42 (dynes cm−2)−1 for the 4D flow, and full resolution STB and CFD, respectively. Voxel averaging increased the average RRT to 1.56 (dynes cm−2)−1 for STB and to 1.27 (dynes cm−2)−1 for CFD. Overall, OSI showed the best agreement of CIs and interquartile ranges (IQRs) across modalities for both geometries, while TAWSS showed the largest variation of distributions across modalities and RRT maintained the largest variance of 95% CIs, demonstrating the effect of the unbounded RRT calculation.
Figure 5.
Distribution of (a) TAWSS, (b) OSI and (c) RRT in the basilar tip aneurysm, where the width of PDF shows relative distribution density. Distribution of (d) TAWSS, (e) OSI and (f) RRT in the ICA aneurysm. The mean and median values, IQRs and 95% CIs are indicated. Violin plots were made from code adapted from [39]. (Online version in colour.)
Given the flow-field variations across modalities, it is important to investigate and compare the normalized spatial distributions of the haemodynamic metrics. Figure 6 illustrates the WSS distribution at peak systole (figure 6a,d), and the OSI (figure 6b,e) and RRT (figure 6c,f) distributions. Each modality's WSS, OSI and RRT distributions were normalized by its respective mean value. Even when normalized, the WSS spatial distributions showed large variation across modality and resolution. For the basilar tip aneurysm (figure 6a), the full resolution CFD exhibited a large region of low WSS at the proximal anterior portion of the aneurysmal sac. Conversely, the full resolution STB showed no region of low WSS and 4D flow maintained a much smaller region of low WSS at that location. Similarly, for the ICA aneurysm normalized WSS (figure 6d), all modalities maintained uniquely different distributions. For both geometries, the normalized RRT distributions also varied significantly across modalities. Although still maintaining some differences, the normalized OSI spatial distributions showed the best agreement across modalities for both geometries. Furthermore, comparing STB-VA versus STB and CFD-VA versus CFD, the low spatial resolution and voxel averaging significantly altered the normalized WSS and RRT distributions, but the OSI distributions maintained better agreement.
Figure 6.
Normalized WSS distribution at peak systole for all modalities in the (a) basilar tip aneurysm and (d) ICA aneurysm. Normalized OSI distribution for all modalities in the (b) basilar tip aneurysm and (e) ICA aneurysm. Normalized RRT distribution in the (c) basilar tip and (f) ICA aneurysm. Normalization of the WSS, OSI and RRT was done for each modality using its own mean value. (Note: the two aneurysm geometries are not shown at the same spatial scale.) (Online version in colour.)
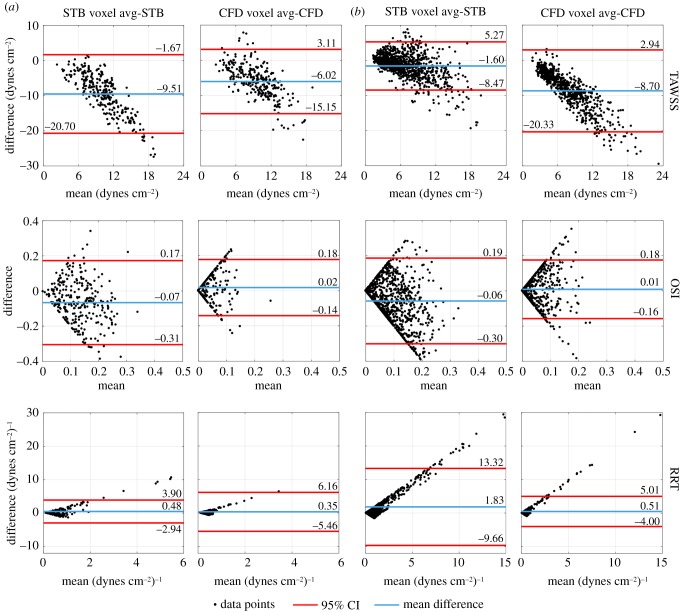
To investigate the effect of spatial resolution on TAWSS, OSI and RRT in more detail, figure 7 illustrates the Bland–Altman analysis comparing the voxel averaged and full resolution STB and CFD across the entire flow domain. Using an intra-modality comparison here isolates the effect of spatial resolution. In both aneurysms, a proportional difference of the TAWSS was observed where the TAWSS magnitude of the VA datasets was less than that of the full resolution, in agreement with the results in figure 5. The average differences were −9.51 and −6.02 dynes cm−2 for the STB and CFD, respectively, in the basilar tip aneurysm (figure 7a). For the ICA aneurysm (figure 7b), the average TAWSS difference was −1.60 dynes cm−2 for STB and −8.70 dynes cm−2 for CFD. The average OSI difference magnitude across all cases was 0.04, with a maximum difference magnitude of 0.07. The spread of OSI points was relatively symmetric, demonstrating no significant proportional differences. The average RRT difference was 0.48 (dynes cm−2)−1 for the STB and 0.35 (dynes cm−2)−1 for the CFD in the basilar tip aneurysm, and 1.83 and 0.51 (dynes cm−2)−1 for the STB and CFD, respectively, in the ICA aneurysm. A proportional difference was observed with the RRT, but in this case, the RRT of the VA datasets was larger in magnitude than that of the full resolution. Thus, figure 7 confirms the varying behaviour and sensitivity of each metric to spatial resolution.
Figure 7.
Bland–Altman analysis of TAWSS, OSI and RRT, comparing VA STB to full resolution STB and VA CFD to full resolution CFD in the (a) basilar tip aneurysm and (b) ICA aneurysm. The mean difference and 95% CIs are indicated. (Online version in colour.)
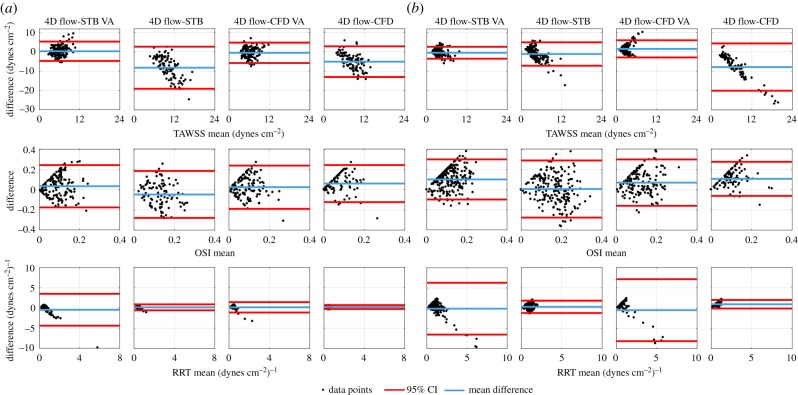
The Bland–Altman analysis was performed to specifically compare the in vitro and in silico TAWSS, OSI and RRT in the aneurysmal sac to that of the in vivo 4D flow data as well as how the spatial resolution of the in vitro and in silico datasets affects the comparison (figure 8). In the basilar tip aneurysm (figure 8a), the mean TAWSS difference was −8.19 and −5.05 dynes cm−2 for STB and CFD, respectively. This changed to 0.36 dynes cm−2 for STB-VA and −0.49 dynes cm−2 for CFD-VA. The 95% CIs for the VA data reduced in range by 54% for STB and 34% for CFD when compared with the full resolution intervals. Similarly, for the ICA aneurysm (figure 8b), the mean TAWSS difference was −1.12 dynes cm−2 for STB and −7.86 dynes cm−2 for CFD. The 95% CI limits reduced by 49 and 64% for STB-VA and CFD-VA, respectively, when compared with the full resolution data. Thus, the VA datasets generally maintained a better match to the 4D flow TAWSS than the full resolution datasets. For OSI, the mean difference was −0.05 and 0.06 for STB and CFD, respectively, in the basilar tip aneurysm. Voxel averaging had a small effect, where the mean difference changed to 0.04 for STB and to 0.03 for CFD, while the 95% CIs reduced by only 9% for STB and 17% for CFD. Mean OSI differences of 0.01 for STB, 0.10 for STB-VA, 0.11 for CFD and 0.07 for CFD-VA were observed in the ICA aneurysm. The interval ranges decreased by 29% when voxel averaged for the STB and increased by 36% when voxel averaged for the CFD. In the basilar tip aneurysm, the mean RRT difference was 0.16 and −0.45 (dynes cm−2)−1 for the full resolution and VA STB, respectively, and 0.24 and 0.17 (dynes cm−2)−1 for the full resolution and VA CFD, respectively. The CI ranges increased fivefold for the STB when voxel averaged and threefold for the CFD when voxel averaged. For the ICA aneurysm, the mean RRT difference was 0.33 (dynes cm−2)−1 for the full resolution STB and −0.13 (dynes cm−2)−1 for the VA STB. The mean RRT difference was 0.97 and −0.50 (dynes cm−2)−1 for the full resolution and VA CFD, respectively. The CIs maintained about a fourfold increase in range for the VA STB dataset when compared with the full resolution while the CFD maintained about a sevenfold increase.
Figure 8.
Bland–Altman analysis of TAWSS, OSI and RRT, comparing in vivo 4D flow MRI to STB-VA, full resolution STB, CFD-VA and full resolution CFD in the (a) basilar tip aneurysm and (b) ICA aneurysm. The mean difference and 95% CIs are indicated. (Online version in colour.)
4. Discussion
In this work, the effects of spatio-temporal resolution and varying flow assumptions and limitations across modalities on resultant haemodynamic metrics were assessed. The unique implementation of three modalities—where the in vivo 4D flow MRI data informed the in vitro STB and in silico CFD—in two time-varying aneurysm flow domains is a significant contribution of this work and provided an enhanced evaluation of the haemodynamic metrics. A major challenge for any multi-modality study that uses in vivo measurements is that no ‘ground-truth’ flow field can be established. The 4D flow MRI maintains the highest possible level of physiological fidelity because it does not require segmentation or assumptions on the flow regime and properties. However, the low spatio-temporal resolution, voxel averaging and typically high noise compromise the accuracy and overall reliability of calculated haemodynamic metrics. In vitro or in silico modalities maintain higher resolution and accuracy, but uncertainty in the segmentation and boundary conditions compromises the fidelity, as do modality-specific assumptions (i.e. Newtonian fluid, laminar flow for CFD), solver parameters [5,18] and experimental limitations regarding inflow conditions and noise. In general, each modality yields a unique set of strengths and weaknesses as well as varying accuracy, physiological fidelity and resolution. The results here demonstrated that WSS, OSI and RRT maintained differing behaviour when subjected to these flow domain variations across modalities. Thus, this analysis can provide a framework for improving the robustness and universality of haemodynamic-based risk of rupture assessments through additional multi-modality studies that develop methods to optimally synthesize information across modalities in order to enhance the accuracy, fidelity and clinical utility of in vivo haemodynamic representations.
Low WSS regions and their impact on the risk of growth and rupture have received much attention [4,8–11,15]. As seen in figure 6, all modalities had uniquely different regions of normalized low WSS and RRT in the aneurysmal sacs of both geometries, even across cases which had strong agreement in the flow patterns and velocity distributions (i.e. 4D flow and CFD for the ICA aneurysm). In this study, one WSS calculation methodology was used and variations in the proximity of the velocity vectors to the wall were mitigated to ensure consistent calculation bias across cases. Furthermore, Cebral et al. [14] showed inflow waveform changes can cause variability in the magnitude but not spatial variation of haemodynamic metrics and van Ooij et al. [10] demonstrated similar findings regarding spatial resolution. However, WSS and RRT calculations are highly sensitive to the near-wall velocity field, and across modalities, different accuracy and resolution in the near-wall region are expected. CFD is highly resolved in the near-wall region and enforces the no-slip boundary condition, ensuring zero flow at the wall. Conversely, resolving the no-slip condition for MRI or STB is unlikely and in MRI, the low velocity flow is known to maintain substantially higher noise. Compounding ancillary factors such as variations in inlet flow conditions, the Newtonian fluid assumption and physical aneurysm orientation can plausibly influence resulting haemodynamic forces, though future work is needed to expand the specific relationships. Moreover, these factors, some of which could be time or spatially varying, hinder the robustness of both WSS and RRT and their ability to inform aneurysm stability. For example, the assessed stability of the basilar tip aneurysm here would likely be different based on the WSS distribution obtained from the full resolution CFD versus that obtained from the full resolution STB. Furthermore, studies which investigate haemodynamic variables in order to determine which variables have a statistically significant difference between stable and unstable aneurysms, regardless of modality, would be influenced by these factors, possibly confounding statistically significant results.
The effect of voxel averaging and spatial resolution on haemodynamic metric magnitudes has also been a growing concern. Roloff et al. [5] demonstrated reductions in velocity magnitude by as much as 10–20% because of voxel averaging. Van Ooij et al. [10] reported that WSS values for 4D flow MRI were lower than that of CFD but increased if the MRI spatial resolution was increased. Figure 8 is in agreement with this notion, demonstrating that datasets with similar spatial resolutions have similar TAWSS magnitudes and lowering the spatial resolution generally lowers the WSS magnitude. In figure 7, reduction (bias error) in TAWSS caused by virtual voxel averaging within the same modality was about 6.46 dynes cm−2, corresponding to a roughly 72% error when normalizing by the mean TAWSS across all datasets. The effect of spatial resolution on OSI and RRT by contrast has received very limited attention. The average RRT error caused by voxel averaging was 0.79 (dynes cm−2)−1, a 125% error when normalizing by the mean RRT across all datasets. However, the average OSI bias error caused by voxel averaging was 0.04, a 50% error when normalized by the mean OSI across all datasets. Furthermore, in figure 8, comparing the in vitro and in silico datasets to the in vivo 4D flow, OSI had the most consistent 95% CI bounds across all modalities as well as across full resolution and VA datasets within the same modality.
Overall, OSI was more robust to varying limitations, assumptions and spatial resolution, and maintained more consistent magnitude and spatial distributions than both TAWSS and RRT. OSI yielded no proportional or significant bias errors for all datasets and comparisons. Because OSI is a non-dimensional parameter, its magnitude is less affected by bias errors than equivalent dimensional parameters, as bias scale errors in the WSS magnitude would cancel out in the OSI calculation (equation (2.6)). As previously discussed, bias errors are unavoidable across all modalities and subjects and are attributed, at least in part, to the assumptions and spatial resolution of the data as well as calculation methodologies. Thus, OSI and other non-dimensional parameters offer the potential for more consistent haemodynamic risk analysis across a cohort of varying geometries and 4D flow resolutions than equivalent dimensional parameters. This is a notion that should be explored and expanded in future studies.
There were several limitations of this study. The inlet vessel of the in vitro models had to be curved slightly for experimental and manufacturing reasons. This could have had some effect on inflow conditions of the STB experiment, possibly preventing a fully developed inflow. However, given the natural tortuosity of the cerebral vasculature, the exact in vivo inflow conditions would be complex and not necessarily fully developed. For example, in figure 1c, the in vivo inflow of the ICA geometry contains a significant curve, similar to what was manufactured for this study. Furthermore, passive resistance valves were used to control the outlet flow rates such that only the average flow rate throughout the pulsatile cycle in each vessel could be controlled. Thus, the amplitude of pulsatility in each vessel could not be controlled and differences in the outlet flow rate pulsatility amplitude of the smaller vessels were observed. Small batches of the working fluid were made for each geometry test such that the working fluids were slightly different. However, because no cross-geometry comparisons were done, this did not impact the results. Uncertainty quantification methods are widely available for PIV but have yet to be reported for STB and are needed so these datasets can be used as robust validation test cases for CFD simulations. While virtual spatial voxel averaging was done here, this process does not exactly replicate that of MRI voxel or ensemble averaging. Thus, additional studies are needed to further explore the possible effects of voxel averaging on velocity and post-processing metrics identified in this study using higher fidelity voxel averaging techniques. Bias errors in discrete WSS calculations are well documented in the literature [6,35]. From the WSS algorithm validation done for this study, a consistent bias error was a known issue. Furthermore, although the working fluid was highly controlled and optimized, the STB and CFD dynamic viscosities differed by 4 and 13% for the basilar tip and ICA aneurysms, respectively, and for the in vivo 4D flow, the viscosity was not explicitly known and had to be assumed. These viscosity variations could plausibly have caused minor differences in the near-wall flow and thus WSS for each modality, but this effect was not expected to be significant nor alter the conclusions of this work. Therefore, all WSS, OSI and RRT values reported in this study can validly be interpreted in a relative sense, but global values of these metrics cannot be extrapolated from this study.
5. Conclusion
In this study, we conducted a multi-modality comparison using in vivo 4D flow MRI, in vitro volumetric flow velocimetry data and in silico CFD in order to investigate the robustness of TAWSS, OSI and RRT to inherent boundary condition uncertainties and modality-specific assumptions. Here, STB processing of particle images significantly reduced reconstruction errors, advancing the state-of-the-art experimental capability and fidelity among cerebral aneurysm studies. The notable differences of WSS and RRT distributions across modalities demonstrated that more in-depth and comprehensive sensitivity analysis of specific assumptions and limitations on such metrics is needed. Furthermore, non-dimensional parameters, such as OSI, were shown to be more robust and consistent to varying modalities and spatial resolutions, a finding which can improve flow metrics associated with aneurysm risk of rupture in future work. However, given the limitations of this study, additional work is needed to further investigate these findings.
Data accessibility
Data used in this study have been published and are available in the Purdue University Research Repository (Title: In vitro Volumetric Particle Velocimetry, Computational Fluid Dynamics (CFD), and in vivo 4D Flow MRI Hemodynamic Data in Two Patient-Specific Cerebral Aneurysms. URL: https://purr.purdue.edu/publications/3136/1). Processing codes used for this study are available at https://github.com/mbrindise/IAHemodynamics.
Authors' contributions
M.C.B. conducted the particle velocimetry experiments, carried out data analysis and drafted the manuscript; S.R. and B.D. completed the flow simulations and manufactured the in vitro models; S.S., M.M. and D.S. obtained and pre-processed all in vivo data; and V.L.R. and P.P.V. designed and oversaw the study and all data analysis. All authors contributed to data analysis, critically reviewed and edited the manuscript and gave final approval for publication.
Competing interests
The authors have no conflicts of interest to report.
Funding
This study is funded by American Heart Association pre-doctoral fellowship (grant no. 17PRE33670268) to M.C.B. and NIH awards nos. R21 NS106696 and R01 HL115267 (V.L.R.).
References
- 1.Vlak MHM, Algra A, Brandenburg R, Rinkel GJE. 2011. Prevalence of unruptured intracranial aneurysms, with emphasis on sex, age, comorbidity, country, and time period: a systematic review and meta-analysis. Lancet Neurol. 10, 626–636. ( 10.1016/S1474-4422(11)70109-0) [DOI] [PubMed] [Google Scholar]
- 2.Rayz VL, Abla A, Boussel L, Leach JR, Acevedo-Bolton G, Saloner D, Lawton MT. 2015. Computational modeling of flow-altering surgeries in basilar aneurysms. Ann. Biomed. Eng. 43, 1210–1222. ( 10.1007/s10439-014-1170-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ford MD, Nikolov HN, Milner JS, Lownie SP, Demont EM, Kalata W, Loth F, Holdsworth DW, Steinman DA. 2008. PIV-measured versus CFD-predicted flow dynamics in anatomically realistic cerebral aneurysm models. J. Biomech. Eng. 130, 021015 ( 10.1115/1.2900724) [DOI] [PubMed] [Google Scholar]
- 4.Xiang J, Natarajan SK, Tremmel M, Ma D, Mocco J, Hopkins LN, Siddiqui AH, Levy EI, Meng H. 2011. Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 42, 144–152. ( 10.1161/STROKEAHA.110.592923) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roloff C, Stucht D, Beuing O, Berg P. 2018. Comparison of intracranial aneurysm flow quantification techniques: standard PIV vs stereoscopic PIV vs tomographic PIV vs phase-contrast MRI vs CFD. J. Neurointerv. Surg. 11, 275–282. ( 10.1136/neurintsurg-2018-013921) [DOI] [PubMed] [Google Scholar]
- 6.Yagi T, Sato A, Shinke M, Takahashi S, Tobe Y, Takao H, Murayama Y, Umezu M. 2013. Experimental insights into flow impingement in cerebral aneurysm by stereoscopic particle image velocimetry: transition from a laminar regime. J. R. Soc. Interface 10, 20121031 ( 10.1098/rsif.2012.1031) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cebral JR, Raschi M. 2013. Suggested connections between risk factors of intracranial aneurysms: a review. Ann. Biomed. Eng. 41, 1366–1383. ( 10.1007/s10439-012-0723-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Meng H, Tutino VM, Xiang J, Siddiqui A. 2014. High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. Am. J. Neuroradiol. 35, 1254–1262. ( 10.3174/ajnr.A3558) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Boussel L, et al. 2008. Aneurysm growth occurs at region of low wall shear stress: patient-specific correlation of hemodynamics and growth in a longitudinal study. Stroke 39, 2997–3002. ( 10.1161/STROKEAHA.108.521617) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.van Ooij P, Potters WV, Guédon A, Schneiders JJ, Marquering HA, Majoie CB, Vanbavel E, Nederveen AJ. 2013. Wall shear stress estimated with phase contrast MRI in an in vitro and in vivo intracranial aneurysm. J. Magn. Reson. Imaging 38, 876–884. ( 10.1002/jmri.24051) [DOI] [PubMed] [Google Scholar]
- 11.Kojima M, Irie K, Ikeda S, Fukada T, Arai F, Hirose Y, Negoro M. 2012. The hemodynamic study for growth factor evaluation of rupture cerebral aneurysm followed up for five years. J. Biomed. Sci. Eng. 5, 884–891. ( 10.4236/jbise.2012.512A112) [DOI] [Google Scholar]
- 12.Xu J, Yu Y, Wu X, Wu Y, Jiang C, Wang S, Huang Q, Liu J. 2013. Morphological and hemodynamic analysis of mirror posterior communicating artery aneurysms. PLoS ONE 8, e55413 ( 10.1371/journal.pone.0055413) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Castro MA, Putman CM, Sheridan MJ, Cebral JR. 2009. Hemodynamic patterns of anterior communicating artery aneurysms: a possible association with rupture. Am. J. Neuroradiol. 30, 297–302. ( 10.3174/ajnr.A1323) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cebral JR, Mut F, Weir J, Putman C. 2011. Quantitative characterization of the hemodynamic environment in ruptured and unruptured brain aneurysms. Am. J. Neuroradiol. 32, 145–151. ( 10.3174/ajnr.A2419) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tanoue T, Tateshima S, Villablanca JP, Vinuela F, Tanishita K. 2011. Wall shear stress distribution inside growing cerebral aneurysm. Am. J. Neuroradiol. 32, 1732–1737. ( 10.3174/ajnr.A2607) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Valen-Sendstad K, Mardal KA, Steinman DA. 2013. High-resolution CFD detects high-frequency velocity fluctuations in bifurcation, but not sidewall, aneurysms. J. Biomech. 46, 402–407. ( 10.1016/j.jbiomech.2012.10.042) [DOI] [PubMed] [Google Scholar]
- 17.Berg P, Stucht D, Janiga G, Beuing O, Speck O, Thévenin D. 2014. Cerebral blood flow in a healthy circle of Willis and two intracranial aneurysms: computational fluid dynamics versus four-dimensional phase-contrast magnetic resonance imaging. J. Biomech. Eng. 136, 041003 ( 10.1115/1.4026108) [DOI] [PubMed] [Google Scholar]
- 18.Berg P, et al. 2015. The computational fluid dynamics rupture challenge 2013—phase II: variability of hemodynamic simulations in two intracranial aneurysms. J. Biomech. Eng. 137, 121008 ( 10.1115/1.4031794) [DOI] [PubMed] [Google Scholar]
- 19.van Ooij P, Guedon A, Poelma C, Schneiders J, Rutten MCM, Marquering HA, Majoie CB, Vanbavel E, Nederveen AJ. 2012. Complex flow patterns in a real-size intracranial aneurysm phantom: phase contrast MRI compared with particle image velocimetry and computational fluid dynamics. NMR Biomed. 25, 14–26. ( 10.1002/nbm.1706) [DOI] [PubMed] [Google Scholar]
- 20.Cibis M, Potters WV, Gijsen FJ, Marquering H, Van Ooij P, Van Bavel E, Wentzel JJ, Nederveen AJ. 2016. The effect of spatial and temporal resolution of cine phase contrast MRI on wall shear stress and oscillatory shear index assessment. PLoS ONE 11, e0163316 ( 10.1371/journal.pone.0163316) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Roloff C, Bordás R, Nickl R, Mátrai Z, Szaszák N, Szilárd S, Thévenin D. 2013. Investigation of the velocity field in a full-scale model of a cerebral aneurysm. Int. J. Heat Fluid Flow 43, 212–219. ( 10.1016/j.ijheatfluidflow.2013.06.006) [DOI] [Google Scholar]
- 22.Raschi M, Mut F, Byrne G, Putman CM, Tateshima S, Vinuela F, Tanoue T, Tanishita K, Cebral JR. 2012. CFD and PIV analysis of hemodynamics in a growing intracranial aneurysm. Int. J. Numer. Methods Biomed. Eng. 28, 72–86. ( 10.1002/cnm.1459) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jain K, Jiang J, Strother C, Mardal KA. 2016. Transitional hemodynamics in intracranial aneurysms—comparative velocity investigations with high resolution lattice Boltzmann simulations, normal resolution ANSYS simulations, and MR imaging. Med. Phys. 43, 6186–6198. ( 10.1118/1.4964793) [DOI] [PubMed] [Google Scholar]
- 24.Schanz D, Gesemann S, Schröder A. 2016. Shake-the-Box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57, 1–27. ( 10.1007/s00348-016-2157-1) [DOI] [Google Scholar]
- 25.Brindise MC, Busse MM, Vlachos PP. 2018. Density- and viscosity-matched Newtonian and non-Newtonian blood-analog solutions with PDMS refractive index. Exp. Fluids 59, 173 ( 10.1007/s00348-018-2629-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wieneke B. 2008. Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45, 549–556. ( 10.1007/s00348-008-0521-5) [DOI] [Google Scholar]
- 27.Bhattacharya S, Charonko JJ, Vlachos PP. 2017. Stereo-particle image velocimetry uncertainty quantification. Meas. Sci. Technol. 28, 015301 ( 10.1088/1361-6501/28/1/015301) [DOI] [Google Scholar]
- 28.Xue Z, Charonko JJ, Vlachos PP. 2014. Particle image velocimetry correlation signal-to-noise ratio metrics and measurement uncertainty quantification. Meas. Sci. Technol. 25, 115301 ( 10.1088/0957-0233/25/11/115301) [DOI] [Google Scholar]
- 29.Charonko JJ, Vlachos PP. 2013. Estimation of uncertainty bounds for individual particle image velocimetry measurements from cross-correlation peak ratio. Meas. Sci. Technol. 24, 065301 ( 10.1088/0957-0233/24/6/065301) [DOI] [Google Scholar]
- 30.Herman GT, Lent A. 1976. Iterative reconstruction algorithms. Comput. Biol. Med. 6, 273–294. ( 10.1016/0010-4825(76)90066-4) [DOI] [PubMed] [Google Scholar]
- 31.Elsinga GE, Westerweel J, Scarano F, Novara M. 2011. On the velocity of ghost particles and the bias errors in tomographic-PIV. Exp. Fluids 50, 825–838. ( 10.1007/s00348-010-0930-0) [DOI] [Google Scholar]
- 32.Brindise MC, Vlachos PP. 2017. Proper orthogonal decomposition truncation method for data denoising and order reduction. Exp. Fluids 58, 28 ( 10.1007/s00348-017-2320-3) [DOI] [Google Scholar]
- 33.Sirovich L. 1987. Turbulence and the dynamics of coherent structures, I–III. Q. Appl. Math. 45, 561–571. ( 10.1090/qam/910462) [DOI] [Google Scholar]
- 34.Westerweel J, Scarano F. 2005. Universal outlier detection for PIV data. Exp. Fluids 39, 1096–1100. ( 10.1007/s00348-005-0016-6) [DOI] [Google Scholar]
- 35.Karri S, Charonko J, Vlachos PP. 2009. Robust wall gradient estimation using radial basis functions and proper orthogonal decomposition (POD) for particle image velocimetry (PIV) measured fields. Meas. Sci. Technol. 20, 045401 ( 10.1088/0957-0233/20/4/045401) [DOI] [Google Scholar]
- 36.Stalder AF, Russe MF, Frydrychowicz A, Bock J, Hennig J, Markl M. 2008. Quantitative 2D and 3D phase contrast MRI: optimized analysis of blood flow and vessel wall parameters. Magn. Reson. Med. 60, 1218–1231. ( 10.1002/mrm.21778) [DOI] [PubMed] [Google Scholar]
- 37.Xu L, Liang F, Gu L, Liu H. 2018. Flow instability detected in ruptured versus unruptured cerebral aneurysms at the internal carotid artery. J. Biomech. 72, 187–199. ( 10.1016/j.jbiomech.2018.03.014) [DOI] [PubMed] [Google Scholar]
- 38.Rayz VL, Boussel L, Ge L, Leach JR, Martin AJ, Lawton MT, Mcculloch C, Saloner D. 2010. Flow residence time and regions of intraluminal thrombus deposition in intracranial aneurysms. Ann. Biomed. Eng. 38, 3058–3069. ( 10.1007/s10439-010-0065-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hoffmann H. 2015. violin.m—simple violin plot using Matlab default kernel density estimation. INRES (University of Bonn), Bonn, Germany. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data used in this study have been published and are available in the Purdue University Research Repository (Title: In vitro Volumetric Particle Velocimetry, Computational Fluid Dynamics (CFD), and in vivo 4D Flow MRI Hemodynamic Data in Two Patient-Specific Cerebral Aneurysms. URL: https://purr.purdue.edu/publications/3136/1). Processing codes used for this study are available at https://github.com/mbrindise/IAHemodynamics.