Recovering gene interactions from single-cell data using data diffusion

Abstract

Single-cell RNA-sequencing technologies suffer from many sources of technical noise, including under-sampling of mRNA molecules, often termed ‘dropout’, which can severely obscure important gene-gene relationships. To address this, we developed MAGIC (Markov Affinity-based Graph Imputation of Cells), a method that shares information across similar cells, via data diffusion, to denoise the cell count matrix and fill in missing transcripts. We validate MAGIC on several biological systems and find it effective at recovering gene-gene relationships and additional structures. MAGIC reveals a phenotypic continuum, with the majority of cells residing in intermediate states that display stem-like signatures and uncovers known and previously uncharacterized regulatory interactions, demonstrating that our approach can successfully uncover regulatory relations without perturbations.

One Sentence Summary: Graph diffusion-based imputation method recovers missing transcripts in scRNA-seq data, yielding insight into the epithelial-to-mesenchymal transition.

In brief - A new algorithm overcomes limitations of data loss in single cell sequencing experiments

Abstract highlights:

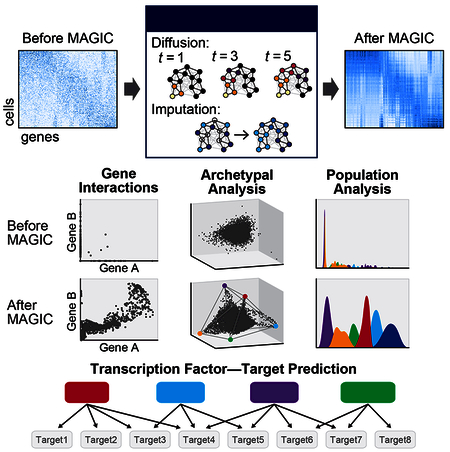
1. MAGIC restores noisy and sparse single-cell data using diffusion geometry.

2. Corrected data is amenable to myriad downstream analyses.

3. MAGIC enables archetypal analysis and inference of gene interactions.

4. Transcription factor targets can be predicted without perturbation after MAGIC. In brief - A new algorithm overcomes limitations of data loss in single cell sequencing experiments

INTRODUCTION

Single cell RNA-sequencing (scRNA-seq) is fast becoming one of the most widely used technologies in biomedical investigation. However, a vexing challenge in single cell genomics is that the observed expression counts capture a small random sample (typically 5–15%) of the transcriptome of each cell (Grun et al., 2014; Stegle et al., 2015). In the case of lowly expressed genes, this can lead to lack of detection of an expressed gene, a phenomenon called “dropout”. This impacts the signal for every gene, leading to loss of gene-gene relationships in the data, obscuring all but the strongest relationships. To overcome this sparsity, most methods aggregate cells, collapsing thousands of cells into a small number of clusters. Alternatively, other methods aggregate genes (e.g. PCA), creating “meta-genes”. While these approaches cope with sparsity to some extent, they lose single-cell or single-gene resolution.

To address these issues, we develop MAGIC (Markov Affinity-based Graph Imputation of Cells), a computational approach for recovering missing gene expression in single cell data. MAGIC leverages the large sample sizes in scRNA-seq (many thousands of cells) to share information across similar cells via data diffusion. MAGIC imputes likely gene expression in each cell, revealing the underlying biological structure. MAGIC uses signal-processing principles similar to those used to clarify blurry and grainy images. We validate MAGIC on several biological systems and find it effective at recovering gene-gene relationships and additional structures.

RESULTS

The MAGIC algorithm

MAGIC relies on structure in the data; possible cell states are constrained by regulatory mechanisms creating interdependencies between genes (Amir el et al., 2013). While data is observed in a high dimensional measurement space, cell phenotypes can be approximately embedded in a substantially lower dimensional manifold. This manifold can be represented using a nearest neighbor graph, where each node represents a cell, and edges connect most similar cells, based upon gene expression. Nearest neighbor graphs have been used to faithfully recover subpopulations (Levine et al., 2015; Shekhar et al., 2016) and developmental trajectories (Bendall et al., 2014; Haghverdi et al., 2015; Haghverdi et al., 2016; Setty et al., 2016). However, MAGIC uses a diffusion operator (Coifman and Lafon, 2006a) to learn the underlying manifold and map cellular phenotypes to this manifold, restoring missing transcripts in the process.

MAGIC takes an observed count matrix and recovers an imputed count matrix representing the likely expression for each individual cell, based on data diffusion between similar cells. For a given cell, MAGIC first identifies the cells that are most similar and aggregates gene expression across these highly similar cells to impute gene expression that corrects for dropout and other sources of noise. However, due to data sparsity, nearest neighbors in the raw data do not necessarily represent the most biologically similar cells. Therefore, we use data diffusion to construct a weighted affinity matrix representing a more faithful neighborhood of similar cells, and then use this matrix to restore the data. With a sufficient number of cells, this process (illustrated in figure 1) increases weights on cells that share similarity across a majority of biological processes.

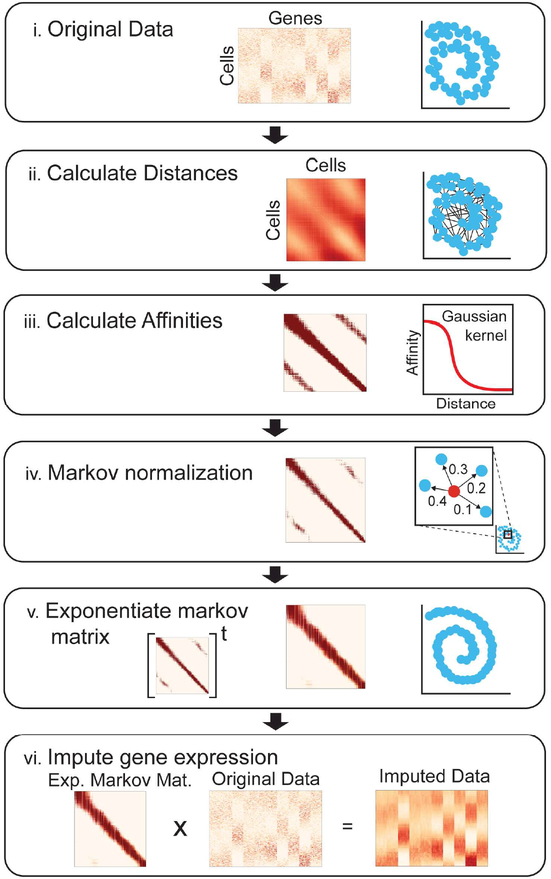
Fig 1: Steps of the MAGIC algorithm:

(i) The input data consists of a matrix of cells by genes (middle) of the data (right). (ii) We compute a cell by cell distance matrix. (iii) The distance matrix is converted to an affinity matrix (middle) using a Gaussian kernel. A graphical depiction of the kernel function is shown (right). (iv) The affinities are normalized, resulting in a Markov matrix (middle). The normalized affinities are shown for a single point as transition probabilities (right). (v) To perform diffusion we exponentiate the Markov matrix to a chosen power t. (vi) We matrix multiply the exponentiated Markov matrix (left) with the original data matrix (middle) to obtain a denoised and imputed data matrix (right). See also Figure S1.

Constructing the affinity matrix proceeds as follows: first PCA is used as a preprocessing step, similar to other graph-based approaches (Haghverdi et al., 2016; Setty et al., 2016; Shekhar et al., 2016). MAGIC uses an adaptive (width) Gaussian kernel to convert distances into affinities, so that similarity between two cells decreases exponentially with their distance. The adaptive kernel serves to equalize the effective number of neighbors for each cell, which helps recover finer structure in the data, whereas the non-adaptive kernel collapses the data into the densest regions (Figure S1A, B). From the affinity matrix we create a Markov transition matrix,M, representing the probability distribution of transitioning from one cell to another in a single step.

Technical noise prevents distinguish between similarity due to biological correspondence versus spurious chance. Mimicking scRNA-seq, if we randomly subsample a fraction of the transcripts, the expression observed across identical cells can appear dissimilar. However, these cells likely share many neighbors, whereas spurious edges connect cells that share few neighbors. Raising M, to the power t results in a matrix where each entry represents the probability that a random walk of length t starting at cell i will reach cell j (Figure 1v), a process akin to diffusion. While the exponentiated Markov affinity matrix increases the number of cell neighbors, unlike the effect of increasing k in knn-imputation, MAGIC does not bluntly smooth and average over increasingly distant cells. Instead, exponentiation refines cell affinities, increasing the weight of similarity along axes that follow data density, thus phenotypically similar cells have strongly weighted affinities, whereas spurious neighbors are down-weighted.

In the imputation step, MAGIC learns from cells in each neighborhood through multiplying the transition matrix by the original data matrix. (Figure 1vi), effectively restoring cells to the underlying manifold. In this data diffusion process, cells share information through local neighbors in a process that is mathematically akin to diffusing heat through the data, where raising the diffusion operator to the t-th power is akin to a t-step random walk through the data. Exponentiation is essentially a low-pass filter on the eigenvalues, which serves to eliminate noise dimensions with small eigenvalues, while simultaneously learning the manifold structure. While we use PCA to gain more robustness for computing the affinity matrix, the imputation is performed using the count matrix before PCA. Thus, while we average data across cells, each individual cell retains a unique neighborhood, resulting in a unique expression vector.

To select an optimal t, we consider the impact of t on the final imputed data. We evaluate the degree of change between the imputed data at time t and time t-1 and stop after this value stabilizes. As t increases, we observe two regimes (Figure S1C,D), a rapidly changing imputation regime and, after convergence, a smoothing regime. In the imputation regime, the first few steps of diffusion learn the manifold structure and remove the noise dimensions. As t increases we rapidly capture relations between cells that are biologically very similar, and only appeared different due to collection artifacts. At larger values of t, the structure of the data has already been recovered and diffusing further would smooth out trends that likely represent real biology. The knee-point (Figure S1C), determines an optimal t. A synthetic dataset demonstrates that best correspondence between the ground truth and imputed data is achieved at the defined optimal t (Figure S1D). See STAR for more details.

MAGIC Enhances Structures in Bone Marrow

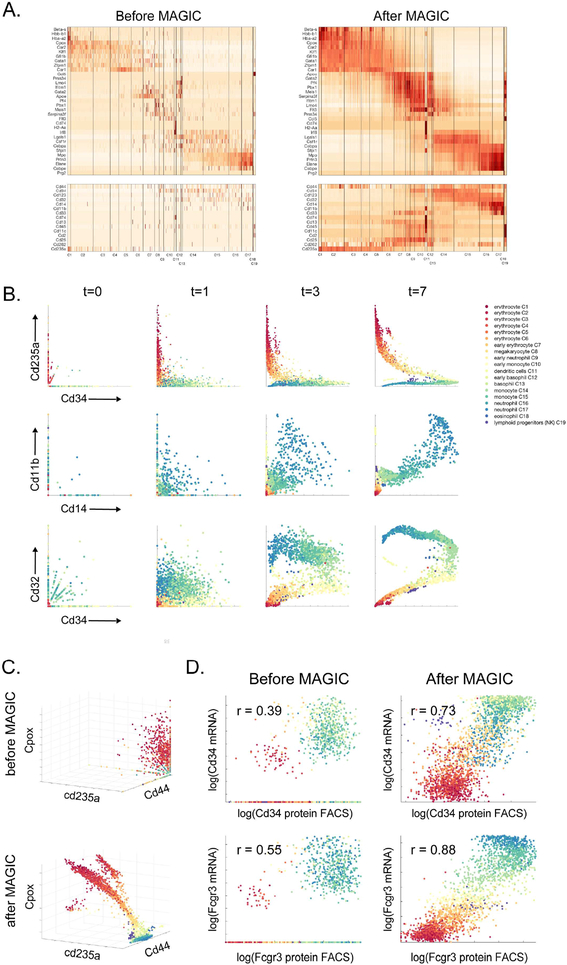
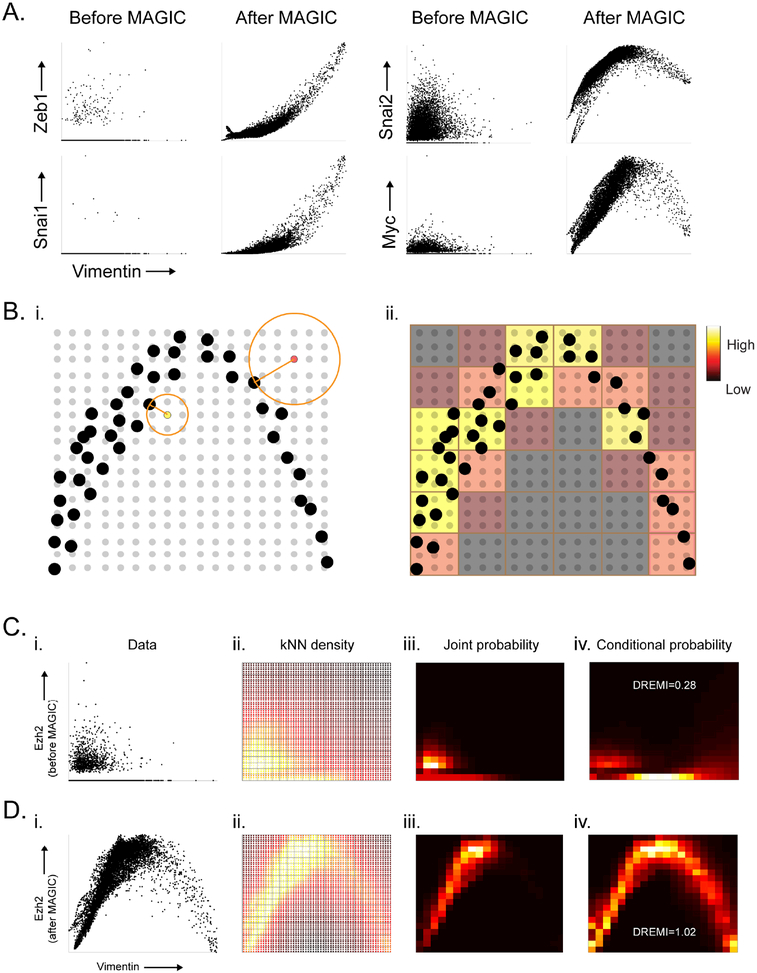
We first evaluated MAGIC on a mouse bone marrow dataset (Paul et al., 2015), collected with MARS-seq2 (Jaitin et al., 2014). The data matrix is sparse and cells are missing many canonical genes in their respective cell types (Figure 2A,B). At the transcript level, canonical surface markers typically used to identify immune subsets are lowly expressed and hence detected at low levels. For example, in the monocyte clusters C14, C15 only 1.6% cells express CD14 and 5.8% cells express CD11b and only 10% of the dendritic cells (cluster C11) express CD32. After MAGIC (npca=100, ka=4, t=7), 94% of monocytes express CD14, 98% express CD11b and 97% of dendritic cells express CD32 at significant levels (Figure S2A).

Fig 2: MAGIC applied to mouse myeloid progenitor data:

Mouse bone marrow dataset (Paul et al., 2015). A) Gene expression matrix for hematopoietic genes (top) and characteristic surface markers of immune subsets (bottom) before and after MAGIC. See also Figure S2A. B) Scatter plots of several gene-gene relationships after different amounts of diffusion. In these scatter plots, each dot represents a single cell, plotted according to its expression values (measured at t=0 and imputed for t=1,3,7), and colored based on the clusters identified in (Paul et al., 2015). C) Shows before and after MAGIC of a 3D relationships (with diffusion time t=7). D) FACS measurements of CD34 and FCGR3 protein levels versus transcript levels, before and after MAGIC. Both FACS measurements and mRNA levels are log-scaled as per FACS conventions.

The sparsity of the data is more evident when viewing the data with biaxial plots (Fig 2B, t=0). It is rare for both genes to be observed simultaneously in any given cell, obscuring relationships between genes. MAGIC restores missing values and relationships, recreating the biaxial plots typically seen in flow cytometry. Figure 2B shows established relationships during hematopoiesis that are undetectable in the raw data. By superimposing the reported clusters onto the biaxial plots we see that cells are grouped by cluster and gene-gene relations gradually change between clusters as the cells mature and differentiate. Also demonstrated are the effects of the diffusion process: a clear and well-formed structure emerges as t (number of time the matrix is exponentiated) grows. Figure 2C demonstrates gene-gene relationships in 3 dimensions. Little structure is visible in the raw data, yet after MAGIC we observe the emergence of a continuous developmental trajectory.

To provide further validation, we utilize the index sorting available with MARS-seq2 (Paul et al.,2015), providing FACS based measurement for CD34 and FCGR3. While the data has poor correlation between protein and original mRNA, after MAGIC, this correlation substantially increases for both proteins: FCGR3 from 0.55 to 0.88 and CD34 from 0.39 to 0.73 (Figure 2D). We note that a comparison between protein and transcriptomic data found a correlation of up to 0.6 between in mRNA and protein in bulk data (Greenbaum et al., 2003).

MAGIC Retains and Enhances Cluster Structure in Neuronal Data

We next evaluated MAGIC on two datasets measuring neuronal cells (Shekhar et al., 2016; Zeisel et al., 2015) known to have a high degree of functional specificity. Therefore, end-state differentiated neural cells are expected to have well-separated cluster structure.

We analyzed a mouse retina dataset collected with drop-seq (Shekhar et al., 2016). Following (Shekhar et al., 2016), we clustered the cells (using the original data) with Phenograph (Levine et al., 2015) (k=30). To verify that MAGIC preserves cluster structure, we ran MAGIC (npca=100, ka=10, t=6), re-clustered the post-MAGIC data and computed the rand index (a measure of similarity between clustering solutions (Rand, 1971)) between the pre-MAGIC and post-MAGIC clusters, resulting in a rand index of 0.93.

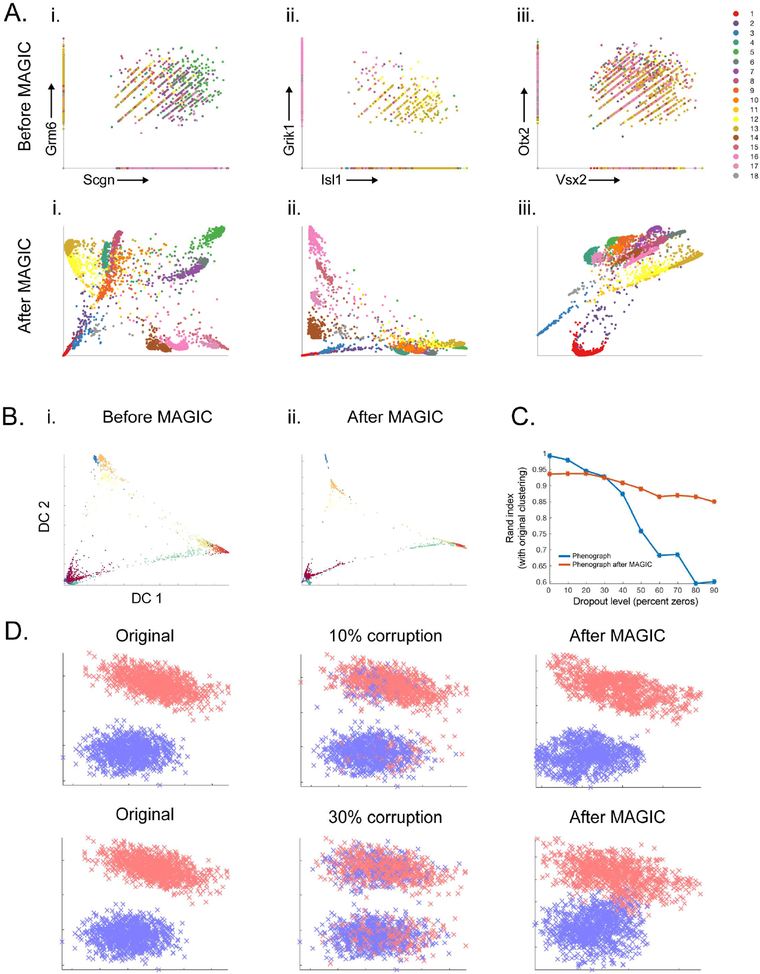
MAGIC extends beyond clustering to highlight heterogeneity and gene-gene relationships within each cluster. We plotted various gene-gene interactions before and after MAGIC, and colored cells by their pre-MAGIC cluster, finding gene-gene relations that vary across clusters (Figure 3A). For example, the ON bipolar cone markers SCGN and GRM6 relate to each other differently in different clusters of cells. In clusters 5–7 SCGN and GRM6 are both highly expressed and show a positive relationship (Figure 3Ai). Clusters 14–17 have high expression of SCGN and low expression of GRM6 and show a negative relationship within the clusters. These trends and distinctions are not detectable prior to MAGIC and would be missed by simple population averaging.

Fig 3: MAGIC preserves cluster structure.

A) Mouse retinal bipolar cells from (Shekhar et al., 2016) showing 2D relationships before and after MAGIC. Cells colored by Phenograph clusters and show differing trends among clusters. B-C): Mouse cortex and hippocampus cells (Zeisel et al., 2015). B) Diffusion components before MAGIC (i) and after MAGIC (ii) colored with clusters, MAGIC does not merge clusters. C) Rand index (Y-axis) of Phenograph clustering after dropout, with MAGIC (red) or without MAGIC (blue), against Phenograph original data. D) Synthetic mixture of two Gaussians embedded in high dimension (original, left), 10% and 30% of the values are corrupted by randomly switching values between the clusters (middle). MAGIC is able to fix the majority of the corruptions (right); 98% recovery for 10% corruption and 81% recovery for 30% corruption.

Next, we assessed MAGIC’s ability to maintain clusters using a deeply sequenced mouse cortex dataset from (Zeisel et al., 2015) collected with smart-seq2 (Islam et al., 2014). MAGIC preserved the discrete nature of the clusters and did not add spurious intermediate states between them; diffusion components remain the same before and after MAGIC (Figure 3B). The relatively deep sampling of this dataset enabled a systematic evaluation, where we dropout transcripts from the original data, cluster, and compare the original clustering, before and after MAGIC. We dropped out up to 90% of the data and compared clustering solutions. While clustering on the dropped out data steadily decreases in quality (dipping to rand index 0.6 at 80% dropout), clustering after MAGIC retains a consistent quality (Rand index 0.89–0.94) throughout all levels of dropout, including 90% (Figure 3C).

Evaluating MAGIC’s accuracy and robustness

To illustrate MAGIC’s ability to correct for contamination (e.g. ambient mRNA or cell barcode swapping), we generated a synthetic test case creating two cell clusters (Gaussian mixture in high dimensions) and then randomly selected a fraction of matrix entries and switched their values between clusters (10% and 30% corruption). We used MAGIC (ka=10, t=4, npca=10) to correct this high-frequency noise. Figure 3D shows that while corruption leads to placing cells in the wrong clusters, MAGIC is able to correct this; 98% recovery for 10% corruption and 81% recovery for 30% corruption.

To quantitatively evaluate the accuracy of MAGIC’s imputation, we created two synthetic datasets where ground truth is known. By directly comparing the original and imputed data, we found that MAGIC was able to correctly recover ground truth data both qualitatively and quantitatively (Figures S2B-C, S3A-B). MAGIC can also capture multivariate relations effectively -- surprisingly the agreement between the original and imputed data is even higher in the case of gene-gene correlations (Figure S3Aii), likely because these correlations are part of the structure that MAGIC harnesses for its imputation. We performed systematic robustness analysis on our EMT dataset and find that MAGIC is robust to sub-sampling of cells (Figure S3C) and to different parameters (Figures S3D-E). See STAR for full details.

Characterizing the Epithelial-to-Mesenchymal Transition

We chose to study EMT, a cell state transition during which cells gradually lose epithelial markers (including E-cadherin, Epcam and epithelial cytokeratins), and gain mesenchymal markers (including Vimentin, Fibronectin and N-cadherin) (Nieto et al., 2016). At a transcriptional level, multiple drivers of EMT have been characterized and include the transcription factors ZEB1, SNAIL (SNAI1) and TWIST1. However, knowledge of the EMT process has been largely derived from studies comparing the extreme states of the EMT, i.e. the beginning epithelial state with the endpoint mesenchymal state. Moreover, most studies have been conducted in bulk where the state of individual cells is not resolved. Hence, while the initiation and the final outcome of EMT are well characterized, little is known about intermediary states.

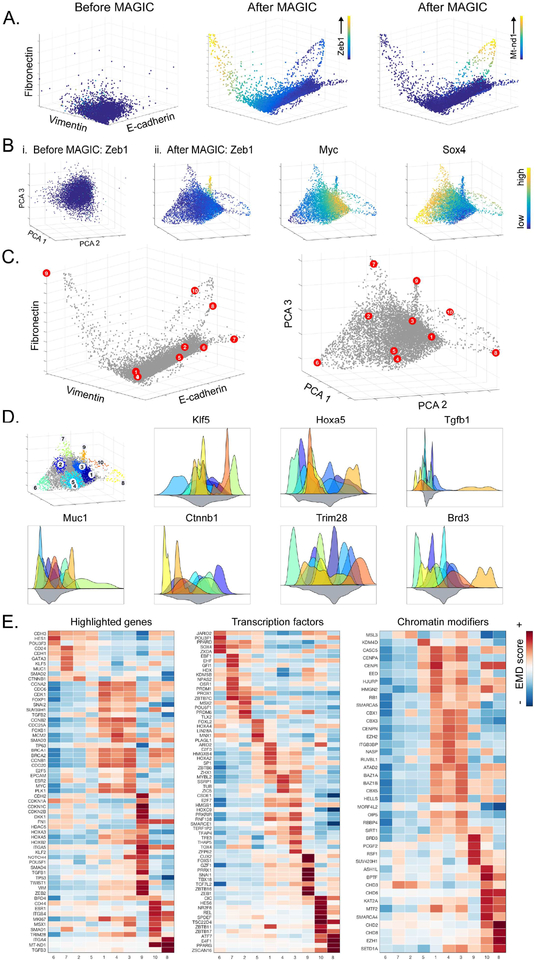
Transformed mammary epithelial cells (HMLE) were induced to undergo the EMT via TGFβ treatment (8 days) and measured using inDrops (Klein et al., 2015). We observe that induction of EMT is asynchronous; each cell progresses along the transition at a different rate. Consequently, on days 8 and 10, we see that cells reside in all phases along the continuum of the EMT. MAGIC unveils a continuum of transitional states that comprise EMT. Before MAGIC, the canonical decrease in CDH1 (E-cadherin) coinciding with an increase in VIM (Vimentin) and FN1 (Fibronectin) is obscured. After MAGIC (npca=20, ka=10, t=6) this relationship is successfully recovered (Figure 4A). ZEB1, a key transcription factor known to induce EMT (Lamouille et al., 2014), progressively increases as VIM and FN1 increase. Another progression revealed by MAGIC involves two branches that deviate from the main structure, which display an increase in mitochondrial RNA, reflecting a progression into apoptosis (Figure 4A). The apoptotic state is supported by the rise of additional apoptotic markers in these cells (data not shown).

Fig 4: MAGIC recovers a state space in EMT data.

EMT data collected 8 and 10 days after TGFβ-stimulation of HMLE breast cancer cells. A) 3D scatterplots between canonical EMT genes CDH1, VIM, and FN1. (Left) Before MAGIC (Middle) after MAGIC with cells colored by the level of ZEB1 and (Right) MT-ND1. See also Figure S3. B) 3D PCA plots before MAGIC (i) and after MAGIC (ii) with cells colored by levels of ZEB1, MYC and SOX4 respectively. C) 3D scatter plots after MAGIC, red dots represent each of the 10 archetypes in the data. Plotted by (Left) CDH1, VIM and FN1, and (right) PCA. D) (Left) most archetypal neighborhoods, cell colored by archetype, grey cells are not associated with any archetype. Histograms represent distributions of genes in archetypal neighborhoods, color-coded by the colors shown in the leftmost plot. E) A subset of differentially expressed genes for each archetype including highlighted genes, transcription factors and chromatin modifiers. Additional differentially expressed genes are shown in table S1. See also Figure S4.

Characterizing Intermediate States during EMT

A surprising revelation is that most of the cells (79%) reside in an intermediate state that is neither epithelial, nor mesenchymal. Moreover, the intermediate cells are highly heterogeneous, occupying a multi-dimensional manifold that does not seem to follow a simple one-dimensional progression. Thus, next characterized this structure and in particular, its boundaries. We used archetypal analysis (Cutler and Breiman, 1994) to characterize the extreme phenotypic states (Shoval et al., 2012), and states that lie in between these extrema. While archetypal analysis has been used to characterize single-cell data (Korem et al., 2015), MAGIC learns a better-formed structure that is amenable to archetypal analysis (Figures 4A,B).

Archetype analysis identified 10 archetypes (AT) in our data. While these archetypes represent extrema in a higher-dimensional space, Figure 4C shows their projection onto two different 3D plots. We use the neighborhood of cells around each archetype to characterize the gene expression profile for that archetype (see STAR) and find unique gene expression patterns for each AT (Figure 4D). We performed differential gene expression analysis (see STAR) to gain a more comprehensive characterization of each AT (Figures 4E, Supplementary Table 1). These archetypes fall into the following categories: ‘epithelial’ – AT6, AT7, ‘intermediary’ – AT1 to AT5, ‘mesenchymal’ – AT9, and ‘apoptotic’ – AT8, AT10. We performed 100 random sub-samplings of the cells and found that we repeatedly identified a very similar set of ATs, where similarity was quantified by correlating AT gene expression (Figure S4A), demonstrating the ATs are robust.

The epithelial ATs (AT6 and AT7) are defined by strong epithelial marker expression including CDH1, CDH3, MUC1 and CD24. The transcriptional profile of AT7 includes higher ESR2 and GATA3, commonly associated with the luminal mammary epithelial cells, and higher CD24 and CDH1, suggesting a more differentiated epithelial phenotype than AT6. Of note, AT6 and AT7 express high levels of SOX4, recently shown to be a master regulator of a TGFβ-induced EMT (Tiwari et al., 2013). The mesenchymal AT9 is characterized by high expression of core EMT TFs SNAI1, ZEB1, SMAD4, TGFB1, TWIST1 (see Figure 4E). Thus, AT9 may represent a gene expression program of cells that have undergone EMT in response to TGFβ.

Our analysis highlights five intermediate ATs (AT1–5), which reside along a continuous spectrum of phenotypes, supporting recent findings suggesting that cells undergoing the EMT move through a series of partial and/or metastable cell states (Nieto et al., 2016; Tam and Weinberg, 2013). AT2 shows a similar gene expression profile as AT7, including upregulation of SOX4 and is closest to the epithelial state. However, AT2 expresses a recently characterized partner in EMT, KLF5 (David et al., 2016). AT3 is closest to the mesenchymal state, with SMAD3 and mesenchymal regulator MSX1 upregulated. AT1 3,4 all express a large number of chromatin modifiers, including EZH2, and several CBX genes, suggesting that these might play a role in the reprogramming. ATs 1,4,5 segregate from the other ATs with concomitant increase in multiple embryonic genes (including TRIM28, FOXB1, HOXA5, HOXB2, HOXA3). Indeed, it has been postulated that epithelial cells undergoing EMT may revert to a more primitive state before acquiring the ability to differentiate into a mesenchymal cell (Ben-Porath et al., 2008). Together these data suggest AT1,4, have entered into a marked reprogramming phase of the EMT, while AT3 is further along this reprogramming phase, further supported by the increasing levels of VIM, along this progression. Gene set enrichments for the ATs appear in table S1.

Applying a similar archetypal analysis to the data prior to MAGIC fails to find distinct archetypes that differ in their expression profiles (Figure S4B-D). Further, genes involved in the EMT process do not vary across the identified archetypes. Thus the structure revealed by MAGIC enabled the characterization of previously unappreciated intermediate states.

MAGIC reveals gene-gene relationships

The core-regulatory circuit defining EMT has been well established, with both ZEB1 and SNAIL1 as potent repressors of the epithelial phenotype. However, the breadth of targets regulated by these EMT-TFs remains largely unknown. Defining the EMT circuitry, and importantly, the timing of different regulatory factors, can shed light upon how this state transition occurs.

The asynchronous nature of the data allows us to explore temporal trends as cells progress from the epithelial to the mesenchymal state. We organize the cells along a pseudo-time progression, using VIM expression as a proxy for EMT state. Thus, we can observe temporal trends of regulatory factors along this transition. However, TFs are typically expressed at low levels and the signal is obscured. For example, the biaxial plots of both ZEB1 and SNAI1 against VIM lack any discernable trend (Figure 5A). However, after imputation, the rise in these key TFs is revealed, recapitulating their known temporal trends.

Fig. 5: Gene-Gene Relationships and kNN-DREMI.

A) 2D scatterplots before and after MAGIC. B) Illustrates the computation of kNN-based density estimation on an 18 × 18 grid, shown as gray points with data points shown in black. Each grid point (yellow, and red grid points are examples) is given density inversely proportional to the volume of a circle with radius r equal to the distance to its nearest data neighbor (black point). After density estimation on the grid-points, the grid is coarse grained into a 6×6 discrete density estimate (red and yellow squares show coarse grained partitions) by accumulation of all densities within each square bin. C) The steps for computing kNN-DREMI are shown for EZH2 (Y-axis) and VIM (X-axis) before MAGIC, with (i) a scatter plot, (ii) kNN-based density estimation on a fine grid (60×60), (iii) coarse-grained joint probability estimate on probability to obtain conditional probability density, resulting in 20 × 20 partition, and (iv) normalization of joint kNN-DREMI = 0.28. D) Same steps as (C) shown after MAGIC resulting in a kNN-DREMI = 1.02. See also Figure S5.

A considerable number of regulators peak at intermediate levels of VIM (e.g. MYC and SNAI2, Figure 5A). The activity of these genes is restricted to intermediate states, whereas their expression is similarly low in both the epithelial and mesenchymal states and would hence be missed by studies that focus only on end states. To systematically explore gene-gene interactions, we need a quantitative metric to score statistical dependency between genes, which takes into account non-linearity observed in the data (e.g. MYC and SNAI2).

To quantify relationships, we adapted DREMI (Krishnaswamy, 2014) to scRNA-seq data, which measures statistical dependency between genes. DREMI captures the functional relationship between two genes across their entire dynamic range. The key change to kNN-DREMI is the replacement of the heat diffusion based kernel-density estimator from (Botev et al., 2010) by a k-nearest neighbor based density estimator (Sricharan et al., 2012) (Figure 5B), which has been shown to be an effective method for sparse and high dimensional datasets (STAR). Moreover, we show that kNN-DREMI is highly robust over a wide range of parameters (Figures S5A).

We illustrate this computation using the relationship between VIM and EZH2 on the same data before MAGIC (Figure 5C) and after MAGIC (figure 5D). We note that Figure 5C is representative of almost any pair of genes in the data, even gene-pairs that are known to be related. The kNN-DREMI score between VIM and EZH2 is 0.28 and 1.02, before and after MAGIC respectively. For perspective, Figure S5B shows a histogram of DREMI scores of 10,000 random gene pairs. Note, there is limited correlation between DREMI before and after MAGIC (Figure S5C), indicating that MAGIC does not simply shift the values. Moreover, DREMI is able to capture gene-gene dependencies beyond correlation (Figure S5D,E).

Characterizing Expression Dynamics Underlying EMT

We next constructed a genome-wide view of expression dynamics during the course of EMT to assess which genes change, when and how. We filtered out apoptotic cells (based MT-ND1 expression) and use the remaining cells to compute kNN-DREMI between VIM and all genes. We found that the majority of the genes demonstrate a temporal trend that follows VIM and selected 13,487 genes having kNN-DREMI > 0.5 with VIM for further study.

We used the DREVI plot (Figure 5Div) to cluster genes based on the shape and timing of their relationship with VIM (see STAR). This resulted in 22 groups of genes with distinct temporal trends. This clustering filters noise by averaging over trends with roughly similar shape and timing. We then fit a spline curve to each cluster, estimate the timing of peak expression, and order the clusters based on this timing.

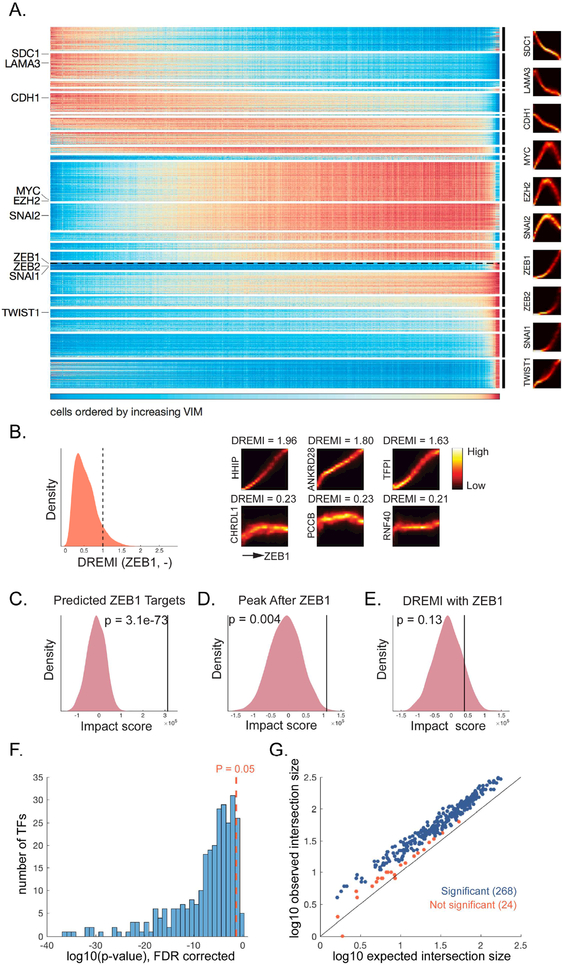
The result is a global map of the pseudo-temporal gene dynamics leading to the mesenchymal state (Figure 6A), with the majority of the genes (2/3 of the genome) participating in this transition with clear temporal trends. We observe clusters of genes that change expression in waves as VIM rises, with three modes of behavior that vary in their timing. The first set of clusters decrease with VIM, for example, SDC1 and LAMA3, which are both involved with cell adhesion and binding. There are genes that increase and then decrease before entering the mesenchymal state, including MYC and EZH2. Finally, as cells transition into the mesenchymal state, a large number of genes monotonically increase, including the canonical EMT-TFs ZEB1, TWIST, SNAIL and SLUG. A full list of genes and their associated clusters appear in Table S2.

Fig. 6: Gene Expression Dynamics Underlying EMT and TF target predictions.

(A) Expression of genes (Y-axis) ordered by DREVI-based clustering and by peak expression along VIM (X-axis). ZEB1 is highlighted with dashed line. Representative DREVI plots with VIM shown to the right. B) (Left) Distribution of kNN-DREMI with ZEB1. The dashed line marks the threshold for genes that we include in the prediction. (Right) DREVI plots and DREMI values for a set of example genes above the threshold (top row) and below threshold (bottom row). C) Impact score of the predicted ZEB1 targets. D) Impact score of all genes that peak after ZEB1. E) Impact score of all genes with kNN-DREMI against ZEB1 >= 1. F) Histogram of 292 FDR corrected p-values (log transformed) obtained using a hypergeometric test on TF-target predictions soverlap with targets obtained from ATAC-seq data, 268 out of 292 TFs have p-value < 0.05. G) Expected number of genes in intersection (log10 scale, X-axis) based on the hypergeometric distribution, versus the observed intersection (log10 scale, Y-axis). For all TFs except one, the observed intersection is higher than expected from random. For 268 TFs (blue points) the difference is significant, and 24 (red points) are not significant. See also Figure S6.

To ensure these pseudo-temporal dynamics are robust and representative of EMT, we repeated this analysis with three other canonical markers of the mesenchymal state, CDH2, ITGB4 and CD44. The resulting gene dynamics are both visually and quantitatively similar for all four markers of EMT progression (Figure S6A-B).

Characterization of ZEB1 Targets

We have shown that MAGIC can recover gene-gene relationships, as well as a fine-grained pseudo-time ordering of gene activation. This offers the possibility of directly learning gene regulatory networks at large scales without perturbation. While DREMI only suggests statistical dependency, incorporating pseudo-time can indicate a causal relationship. In case of activation, we assume that target’s expression should peak after the TF. Thus, we harness the temporally ordered clusters to limit potential targets only to those that peak after the regulator. Additionally, the expression of the regulator should be strongly informative of the expression of its targets, meaning we should only consider genes that have strong kNN-DREMI with the TF. These two criteria combined can predict a set of candidate targets for each TF (see STAR).

With respect to the transcriptional targets of the EMT-TFs, it is clear that a certain level of redundancy exists. However, a recent study suggests that there are actually profound differences in the transcriptional programs they induce (Ye et al., 2015). We focused on ZEB1, a key regulator of EMT whose transcriptional targets remain poorly defined to date. We found 4,509 genes that changed with EMT and peaked along with or after ZEB1 (Figure 6A), and among these 1,085 genes had DREMI >= 1 with ZEB1 (Figure 6B). We predict that ZEB1 activates these genes, either directly or indirectly. See Table S3 for full list of targets.

To validate our predicted targets of ZEB1, we used a variant of the HMLE cell line, where ZEB1 can be over-expressed using a Dox-inducible promoter. We measured the cells after two days of continuous Dox treatment (see STAR), which is sufficient to induce significant numbers of mesenchymal cells (10% of the cells). In the ZEB1 induction, we expect ZEB1 targets to be up-regulated relative to other genes. For a given set of genes (e.g. list of predicted targets), we define an impact score, which compares the relative ranking of gene expression between the ZEB1 and TGFβ inductions (see STAR).

Our predicted ZEB1 targets are indeed up-regulated in the ZEB1 induction with a significance of p=3.1E-73, against a background of all genes involved in EMT (Figure 6C). Including all 4,509 genes that peak after ZEB1 results in a significant but diminished impact score (Figure 6D, p=0.004), indicating that while ZEB1 is a key regulator of EMT, there are additional regulatory factors at play in the TGFβ-induced EMT, even during late stages of the transition. Predicting targets based on DREMI with ZEB1 alone results in an impact score that is not significant (Figure 6E, p=0.13). We note that our prediction focuses only on genes activated by Zeb1, whereas Zeb1 is also a potent repressor, indeed among these high DREMI genes, ~1/3 are negatively correlated with ZEB1.

Our top predicted targets include many genes known to be involved in EMT, including SNAI1, ZEB2, BMP (bone morphogenic) antagonist family proteins and MMP (matrix metaloproteinase) family proteins such as MMP3. In addition, we see proteins involved in cell cycle, remodeling of cell cytoskeleton, extracellular matrix remodeling, and cell migration. This includes: CDKN1C, a negative regulator of proliferation, RHOA, involved in reorganization of the actin cytoskeleton and regulates cell shape, attachment, and motility, CCBE1, involved in extracellular matrix remodeling and migration, and interestingly NTN4, normally involved in neural migration. While these genes are less known in their EMT involvement, their phenotypic annotations match with known phenotypic changes involved in EMT, providing further evidence that ZEB1 is critical in activating a myriad of processes that result in cellular trans-differentiation. Thus we have demonstrated that combining MAGIC, pseudo-time and kNN-DREMI, we are able to predict regulatory targets, without perturbation.

Systematic Validation of an EMT regulatory network

To build a global regulatory network of EMT, we selected all TFs that change considerably along EMT (kNN-DREMI with VIM is >0.5) and predicted targets of each using the analysis applied to ZEB1. This resulted in a large regulatory network consisting of 719 regulators over a total of 11,126 targets (Supplementary Table 3). To systematically validate our target predictions, we used ATAC-seq (Assay for Transposase-Accessible Chromatin using sequencing) (Buenrostro et al., 2013) as an independent and well-accepted approach for target prediction (STAR) (Kundaje et al., 2015). ATAC-seq was carried out on HMLE cells 8 days following TGFb stimulation. Cells were FACS sorted by CD44+ to enrich for the mesenchymal population. We used the ATAC-seq peaks combined with motif analysis to derive a set of targets for each TF using standard approaches (STAR). Note, we do not expect the two approaches to perfectly align: our predictions identify both direct and indirect targets of a TF, whereas ATAC-seq only captures direct targets. ATAC-seq identifies binding of TFs that are activating, poised or inhibiting, whereas our predictions only focus on TF activation. Nevertheless, if our predictions are accurate, we expect a significant overlap between the two sets.

For each of 292 TFs in our predicted regulatory network, for which we also had ATAC-seq based predictions, we used the hypergeometric distribution to assess the significance of overlap between the two target sets and false discovery correction (FDR), to correct for multiple hypothesis testing (STAR). We find the overlap is greater than expected for 291/292 TFs, and after FDR this overlap is significant for 268/292 TFs (Figures 6F,G). Thus our predictions significantly overlapped with targets derived from ATAC-seq for 92% of the TFs tested.

To directly evaluate the gene-gene relationships recovered by MAGIC, we compared DREMI scores between targets and non-targets, for each of 418 TFs, and compared the distribution of DREMI scores using a one-sided Kolmogorov-Smirnoff (KS) test (STAR). In this analysis we comprehensively evaluate all TFs with ATAC-seq based predictions (regardless of their relationship to VIM) and all targets, regardless of pseudo-time ordering. We find that 372/418 TFs have significantly higher DREMI score with their ATAC-seq based targets than with other genes with p < 0.05, whereas many of these are insignificant before MAGIC. Figure S6D shows distributions for ZEB1, SNAI1 and MYC, after MAGIC all have significant KS scores (p=4.7e-25, p=3e-25 and p=e-8 respectively), whereas none of these are significant prior to MAGIC (p=0.16, p=0.99 and p=0.99 respectively).

In summary, we validated a computational approach to build a large-scale regulatory network from scRNA-seq data without genetic perturbations.

Comparison of MAGIC to Other Methods

We compare MAGIC to kNN-imputation and diffusion maps using a few known gene-gene relationships from the bone marrow (Figure 7A) and EMT (Figure 7B) datasets. Contrary to MAGIC, the simpler kNN-imputation approach fails to recover the known gene-gene relationships (Figure 7, peach). Unlike simple smoothing over a kNN-graph, which is limited to local information, by propagating data using the diffusion operator, MAGIC is able to recover data using longer range, global features. In essence, this pulls in noisy outlier data to the manifold and restores the structure.

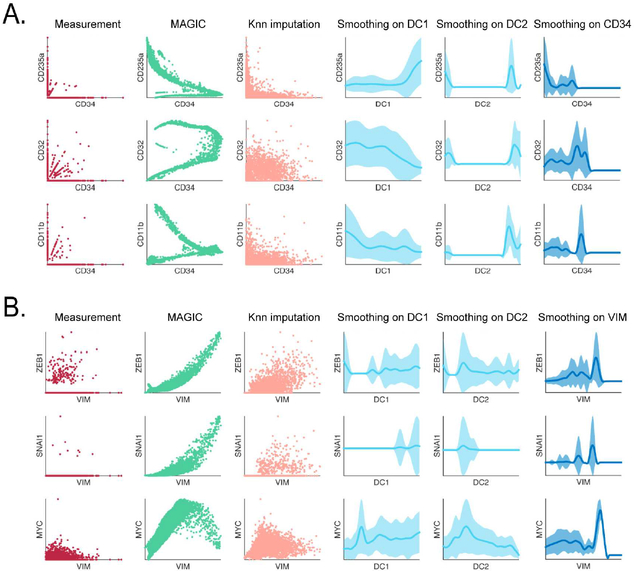
Fig. 7: Comparison of MAGIC to other imputation and smoothing methods.

A) Comparison shown on bone marrow data (as in Figure 2), raw data (first column), MAGIC imputed (second column). The other columns show kNN-based imputation, smoothing on diffusion components 1 to 2, and smoothing on CD34, respectively. B) The same as in A but for the EMT data. See also Figure S7.

A popular aggregation approach utilizes diffusion maps (Coifman and Lafon, 2006a), which like MAGIC, compute a diffusion operator that defines similarity between data points along a manifold. However, diffusion maps find diffusion components (DCs), a nonlinear equivalent to a PCA, which have been recently utilized to find pseudotime trends in developmental systems (Haghverdi et al., 2015; Haghverdi et al., 2016; Setty et al., 2016). Moving average approaches have been successfully used to observe gene trends along DCs, smoothing along a single diffusion component, one gene at a time. This performs well when DCs correspond to tight developmental pseudo-time trajectories, and only for developmentally related genes, whose major component of variation is singular. Moreover, because smoothing occurs one gene at a time, the approach cannot be used to reveal gene-gene relationships. MAGIC, by contrast, uses the diffusion operator to propagate gene expression information between similar cells, taking all diffusion components and genes into account simultaneously in its inference.

The difference is illustrated in Figure 7, sky blue: while smoothing along DC1 (corresponding to erythrocytes) results in a roughly correct trend for CD235a (an erythrocyte marker), the relationship is entirely incorrect for markers belonging to other lineages such as CD11B. Moreover, this approach is unable to recover gene-gene relationships even in cases like CD335a and CD34, whose trends both follow DC1 relatively well. Additionally, the EMT dataset does not follow a simple trajectory and therefore diffusion components fail to capture trends for even the most canonical TFs in this process. For instance, ZEB1 or SNAIL vs VIM shows a fluctuating rather than positive trend.

We also compare MAGIC to methods used to fill in missing data, SVD-based low-rank data approximation (LRA) (Achlioptas and McSherry, 2007) and Nuclear-Norm-based Matrix Completion (NNMC) (Candes and Recht, 2012). Both methods have a low-rank assumption, i.e., like MAGIC, they assume that the intrinsic dimensionality of the data is much lower than the measurement space and utilize a singular value decomposition (SVD) of the data matrix. We compared the performance of the three techniques on synthetic and real data (Figure S7), where we demonstrate MAGIC is uniquely well suited to handle the dropout rampant in scRNA-seq data (STAR). A likely explanation for NNMC’s poor performance is that it “trusts” non-zero values and only attempts to impute possibly missing zero values. Whereas in scRNA-seq, dropout of molecules impacts all genes and even non-zero genes are likely lower than their true count in the data. Hence NNMC is poorly suited to this data type. LRA, a linear method, cannot separate the exact manifold from external noise, likely due to its inability to find non-linear directions in the data.

Discussion

Here, we presented MAGIC, an algorithm to alleviate sparsity and noise due to stochastic mRNA capture and recapitulate gene-gene interactions in single-cell data. The cost of sequencing limits our ability to measure large numbers of cells at depth, ensuring MAGIC’s utility even as scRNA-seq technology improves. Further, MAGIC can be used in newer single-cell technologies such as single-cell ATAC-seq, which suffer from similar sparsity and noise. Unlike other imputation algorithms, which simply fill in “missing values”, MAGIC uses diffusion of values between similar cells along an affinity-based graph structure, to correct the entire data matrix and restore it to its underlying manifold structure. This diffusion is akin to low-pass filtering of the graph spectrum. Previously, low-pass filtering has only been applied to structured data, i.e. data that has a given temporal or spatial ordering such as images or audio signals (Buades et al., 2005). Here, we extend this operation to data without such ordering, by learning a manifold structure de novo via the diffusion operator and filtering on the manifold structure. MAGIC is versatile and is able to denoise and correct a wide range of structures and is particularly well suited for structures underlying cell states and phenotypes.

MAGIC assumes cell phenotypes can be approximately embedded in a substantially lower dimensional structure, which can be of any shape and even comprise of well-separated components. Cells are regulated to reside within the boundaries of a restricted portion of the state space, i.e., a subspace. Moreover, gene-gene relationships ensure that these subspaces exist as lower-dimensional objects relative to the full measurement space. MAGIC’s key assumption is that such a subspace corresponds to low frequency trends in the data (technically the affinity graph representing the data) containing biological signals of interest, while noise, including dropout, are high frequency. Thus, low frequency batch effects or artifacts will not be removed and genes behaving in a noisy (high frequency) fashion may be smoothed out.

The diffusion time parameter determines the extent of smoothing performed by MAGIC. We recommended a diffusion time that retains biological signals but removes ‘intrinsic’ noise, such as bursting, as these cannot be distinguished from the large degree of technical noise in scRNA-seq data. Additionally, the number of cells affects the frequency of signals in the data. For instance, the same signal (such as EMT) can be high frequency if only a few cells are undergoing EMT, but this signal is captured as the cell number increases. Our data contained only 1% meshenchymal cells, but with thousands of cells we recovered the process in detail, including its regulatory process. Thus, while MAGIC is able to find gross structures using only hundreds of cells, increasing cell number enables MAGIC to find increasingly fine structures and more signals in the data.

We evaluated MAGIC on four different scRNA-seq datasets from different biological systems and measurement technologies. MAGIC recovers fine phenotypic structure in the data, including well-separated clusters (Figure 3), bifurcating developmental trajectories (Figure 2), as well as heterogeneous state transitions (Figure 4). Additionally, MAGIC refines cluster structure, trajectories and gene-gene relationships, and enables a myriad of subsequent analysis techniques. In the case of EMT, MAGIC recovered a complex structure that is not well represented by a simple trajectory. We applied archetypal analysis to characterize this complex structure and reveal several previously-unappreciated intermediate states.

We expect MAGIC to be broadly applicable to any single-cell genomics dataset, boosting the signal and the interpretability of the data. As with all post-processing, care must be taken when applying downstream tools. For example, most tools to detect differentially expressed genes (DEGs) assume sparsity and would likely over-estimate DEGs post-MAGIC. Thus, we recommend the earth-mover distance (EMD) used in the archetype analysis (STAR). We recommend running diffusion map analysis directly on the raw data (otherwise this could lead to over smoothing). On the other hand, MAGIC imputed data is well-suited to visualize trends along the diffusion components. Most cells no longer have zeros, but instead have very small values that can be interpreted as the probability a cell is expressing the transcript, thus we recommend treating the very low values as zero, i.e. the cell is not expressing that transcript.

Finally, the most important application is MAGIC’s ability to recover gene-gene relationships which are largely obscured in scRNA-seq data. We validated our approach using: 1) synthetic data, 2) known relationships, 3) by comparing Zeb1 overexpression-based EMT induction with a TGFb-induced EMT, and 4) an extensive systematic validation using ATAC-seq. For network learning, we developed an adaptation of DREMI (Krishnaswamy, 2014), termed kNN-DREMI, to quantify the strength of non-linear and noisy gene-gene relationships. Post-MAGIC, we inferred regulatory relationships and validated predicted targets of a large-scale regulatory network involving hundreds of TFs and over 10,000 target genes. Another approach to learn gene-gene interactions is based on perturbations through the combination of scRNA-seq with CRISPR(Dixit et al., 2016). However, these methods require a preselected set of genes to perturb, often disrupt the system in unintended ways, and require considerable experimental efforts that are not always applicable, e.g., the case of clinical tissue. Our approach requires no perturbations or other experimental manipulations, and can be applied to primary tissue and clinical samples. This offers the possibility of discovering rogue regulatory pathways in cancer, autoimmune disease and developmental disorders, in a patient specific manner, potentially suggesting therapeutic interventions.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dana Pe’er (peerd@mskcc.org).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

We used female HMLE breast cancer cell lines in this study. The cell lines were not authenticated. HMLE and all derived cell lines used in this work were cultured in MEGM (Mammary Epithelial Cell Growth Medium) media (Lonza, USA, CC-3051) at 37 °C. Cells were cultured in round tissue culture dishes 10cm in diameter (Corning, USA) and split to a ratio of 1:7 every 2 to 3 days or once they reached 80% confluence on a plate. All cell dissociations were performed using TrypLE^™ (Ambion, USA) reagent.

METHOD DETAILS

TGF-beta and Zeb1 induction of EMT

EMT was induced in HMLE cells by addition of Recombinant Human TGF-β1 (HEK293 cell derived) (PeproTech, USA 100–21) to a final concentration of 5ng/ml. EMT was also induced by overexpression of Zeb1 transcription factor. HMLE cells transfected with FUW plasmid, a tetracycline operator, and minimal CMV promoter were used and Zeb1 gene overexpression was induced by addition of doxycycline (Sigma, D3447) to a final concentration of 1mg/ml. All cells under induction were passaged once they reached 80% confluence.

ATAC-seq profiling of TGF-beta induced EMT

HMLE cells were induced with TGF-beta (5 ng/mL, replenished every day) and grown for 8 days. TGF-beta induced HMLE cells were removed from the cell culture plate with TrypLE treatment, washed twice in 1X PBS buffer, and stained with DAPI dye and Anti-Human/Mouse CD44 (PE-Cyanine 7) antibody. The stained cells were then analyzed by flow cytometry and the top 3% (n=48,000) CD44 positive cells (mesenchymal population) were FACS sorted into a collection tube. FACS sorted cells were first lysed with 10 mM Tris-HCl [pH 7.4], 10 mM NaCl, 3 mM MgCl2 and 0.1% IGEPAL CA-630 buffer. The resulting nuclei suspension was pelleted and fragmented using Tn5 transposase reaction mix (Illumina), purified (Qiagen) and PCR amplified for sequencing following the protocol published previously (Buenrostro et al., 2013).

Single-cell RNA-seq profiling of EMT

Single-cell RNA-seq was performed using the inDrops platform (Klein et al., 2015; Zilionis et al., 2017), a droplet microfluidics based single-cell isolation and mRNA barcoding technology. Briefly, the cell culture flasks containing HMLE cells were treated with 2 mL TrypLE^™ Express Enzyme (1X) no-phenol-red for 10 min at 37ºC, washed three times with 1X PBS containing 0.05% (w/v) BSA, and strained through 40 μm size mesh. The resulting suspension of single-cells was supplemented with 16% (v/v) Optiprep and 0.05% (w/v) BSA and encapsulated into 3 nL droplets together with custom-made DNA barcoding hydrogel beads and RT/lysis reagents. The cell encapsulation was set at ~30,000 cells per hour using a cell barcoding chip (v2) (Droplet Genomics), and over 75% of cells entering microfluidics chips were co-encapsulated with one DNA barcoding hydrogel bead. After loading cells, hydrogel beads and RT/lysis reagents into microfluidic droplets, the composition of a RT reaction under which cDNA synthesis was carried out was 155 mM KCl, 50 mM NaCl, 11 mM MgCl₂, 135 mM Tris-HCl [pH 8.0], 0.5 mM KH₂PO₄, 0.85 mM Na₂HPO₄, 0.35 % (v/v) Igepal-CA630, 0.02 % (v/v) BSA, 4.4% (v/v) Optiprep, 2.4 mM DTT, 0.5 mM dNTPs, 1.3 U/ml RNAsIN Plus, and 11.4 U/ml SuperScript-III RT enzyme. After cell encapsulation the tube containing the emulsified components was exposed to 365 nm light to photo-release DNA barcoding primers attached to the hydrogel beads. The RT reaction was initiated by transferring the tube to 50ºC for 1-hour and terminated by incubating for 15 min at 75ºC. Post-RT droplets were chemically broken to release barcoded cDNA, which was then purified and amplified. At the final step, libraries were amplified using trimmed PE Read 1 primer (PE1): 5’-AATGATACGGCGACCACCGAGATCTACACTCTTTCCCTACACGA and indexing PE Read 2 primer (PE2): 5’-CAAGCAGAAGACGGCATACGAGAT[index]GTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT, where [index] encoded one of the following sequences: CGTGAT, ACATCG, GCCTAA, TGGTCA, CACTGT or ATTGGC). Multiplexing of PCR libraries allowed for the pooling of different samples onto one lane of Illumina HiSeq2500 flow cell when desired. To prepare the cells for scRNA-seq experiments, they were cultured to 70% confluence and dissociated from the plate with the addition of 3ml of trypsin for 5 mins at 37 °C. After dissociation cells were kept at +4 °C at all times in MEGM-complete media. Two 1x PBS (Ambion, USA) washes were performed on the dissociated cells and cell viability was evaluated using trypan blue staining prior to scRNA-seq. All inDrops experiments were performed with cell viability exceeding 90%.

Overview of the MAGIC Algorithm

MAGIC begins with an n-by-m count matrix D, representing the observed transcript counts of m genes in n cells and returns an imputed count matrix D_imputed The expression of each individual cell, a row in D, defines a point in the high-dimensional measurement space representing the cell’s observed phenotype. The counts in the imputed data matrix D_imputed represent the likely expression vectors (phenotypes) for each individual cell, based on data diffusion between similar cells.

Key to the success of our graph-based method is a faithful neighborhood of similar cells, based on a good similarity metric. Given the sparsity of the data, finding the k-nearest neighbors in the raw data using a simple similarity metric is unlikely sufficient to find cells whose biology is most similar. Therefore, MAGIC builds its affinity matrix in four steps: (i) A data preprocessing step, which is PCA in the case of scRNA-seq. (ii) Converting distances to affinities using an adaptive Gaussian Kernel, so that similarity between two cells decreases exponentially with their distance. (iii) Converting the affinity matrix A into a Markov transition matrix M, representing the probability distribution of transitioning from each cell to every other cell in the data in a single step. (iv) Data diffusion through exponentiation of M, to filter out similarity based on high frequencies that typically represent noise and increase the similarity based on strong trends in the data. Once the affinity matrix is constructed, the imputation step of MAGIC involves sharing information between cells in the resulting neighborhoods through matrix multiplication D_imputed = M^t * D(Figure 1.vi).

Using PCA for data preprocessing

MAGIC can be generally applied to any type of high dimensional single cell data to remove noise and clarify structure in the data. However, before a cell-cell distance matrix is computed, each data-type typically requires specific pre-processing and normalization steps. Pre-processing is particularly important in the case of scRNA-seq to ensure that distances between cells reflect biology rather than experimental artifact. We perform two operations on the data which are typically applied to single-cell RNA-sequencing datasets (Haghverdi et al., 2016; Setty et al., 2016; Shekhar et al., 2016): 1) library size normalization on the cells, and 2) principal component analysis (PCA) on the genes.

ScRNA-seq data entails substantial cell-to-cell variation in library size (number of observed molecules) which is largely due to technical variation occurring due to multiple enzymatic steps, such as lysis efficiency, mRNA capture efficiency and the efficiency of multiple amplification rounds(Grun et al., 2014). For example, the cell barcode associated with each cell can have a substantial effect on the PCR efficiency and subsequently the number of transcripts in that cell. Therefore, we normalize transcript abundances (library size), so that each cell will have an equal transcript count.

Given a m ∗ n data matrix D, the normalized data matrix is defined as follows:

$$Libsize=rowsum\left(D\right);$$

$$D_{norm}(i,j)=\frac{D(i,j)}{{\displaystyle {\sum }_{k=1}^{n}D(i,k)}}*median(Libsize)$$

This effectively eliminates cell size as a signal in the measurement for the purposes of constructing the affinity matrix and thus the resulting weighted neighborhood is not biased by cell size.

Second, we apply principal component analysis (PCA) to further increase the robustness and reliability of the constructed affinity matrix. While dropout renders single cell RNA-seq data extremely noisy, the modularity of gene expression provides redundancy in the gene dimensions, which can be exploited. Therefore, we perform PCA dimensionality reduction to retain ~70% of the variation in the data, which typically results in 20 to 100 robust dimensions for each cell.

$$D_{pca}=pca\left(D,0.70\right)$$

The cell-cell affinity matrix is computed off of these PCA dimensions, but imputation is performed on the full data matrix. While MAGIC still gives reasonable results without preprocessing with PCA, it gives the diffusion a better starting point, resulting in quicker and more robust computation. We also note that MAGIC is relatively robust to the number of principle components selected, within a reasonable range (Figure S3D).

Constructing MAGIC’s Markov Affinity Matrix

One of the most critical steps in MAGIC is computing the affinity matrix M. M defines the graph structure and cell neighborhoods; MAGIC can only succeed if the affinity matrix faithfully represents the geometry of the data. We compute a similarity matrix by applying a kernel function to the distance matrix using the following steps:

• 1)Computation of a cell-cell distance matrix Dist (Figure 1.ii).
• 2)Computation of the affinity matrix A based on Dist, via an adaptive Gaussian kernel (Figure 1.iii).
• 3)Symmetrization of A using an additive approach
• 4)Row-stochastic Markov-normalization of A (so each row sums to 1) into Markov matrix M. (Figure 1.iv)

We compute a similarity matrix by applying a kernel function to the distance matrix. After data processing (in a technology-dependent manner), MAGIC computes a cell-cell distance matrix Dist based on a cell-cell Euclidian distance. Distances are then converted into an affinity matrix A using a Gaussian kernel function that emphasizes close similarities between cells, as follows

$$A(i,j)=e^{-{(\frac{Dist(i,j)}{\sigma })}^2}$$

Using the Gaussian kernel, similarity between two cells decreases double exponentially with their distance. With a negative double exponential function, distances beyond the standard deviation σ rapidly drop off to zero and hence the choice of σ, the kernel width, is a key parameter. If σ is too small, the graph becomes disconnected leading to noise and instability. If σ is too large, distinct and distant phenotypes will be collapsed and averaged together, losing resolution and structure in the data. However, cell phenotypic space is not uniform: a stem cell can be orders of magnitude less frequent than a mature cell type and transitional cell states are also rare. Therefore, s that would be appropriate for a mature cell type would be far too coarse to capture fine details of the differentiation in progenitor cell types.

Without proper care, denser phenotypes can dominate the imputation. Cells in dense areas have more neighbors and therefore exert more influence than cells with fewer neighbors. Moreover, dense phenotypes are further reinforced during diffusion, where dense phenotypes iteratively attract more and more cells towards them and dominate the data (Figure S1A,B). MAGIC uses an adaptive Gaussian kernel to equalize the effective number of neighbors for each cell, thereby diminishing the effect of differences in density. Instead of fixing a single value for the kernel width σ, we adapt this value for each cell, based on its local density. Specifically, to equalize the number of neighbors we set the value σ(i) for each cell i to the distance to its kath nearest neighbor:

$$\sigma \left(i\right)=distance\left(i,neighbor(i,ka)\right)$$

Thus the kernel is wider in sparse areas and smaller in dense areas. To maximize our sensitivity to recover fine structure, we choose ka to be as small as possible, such that the graph remains connected. We note that MAGIC is relatively robust to selection of ka, within a reasonable range (Figure S3D).

Comparing non-adaptive to the adaptive kernel on the EMT data in Figure S1A, we see that the non-adaptive kernel coarsely captures only the single strongest trend in the data, whereas the adaptive kernel does not collapse the data, but rather imputes finer structures. Figure S1B shows this on synthetic data with 3 rotated sinusoidal arms. The adaptive kernel can impute the fine details of the geometry while the fixed bandwidth kernel averages the sinusoidal features into a line.

To improve computational efficiency and robustness, we ensure sparsity in the resulting affinity matrix A and allow each cell to have at most k neighbors. Since the standard deviation of the kernel bandwidth is set locally to the distance to the ka-th neighbor we set k = 3ka to ensure that the kNN graph covers the majority of the Gaussian kernel function. All additional affinities (which are already close to zero) are set to zero.

Another important factor in MAGIC’s success is the quality of the diffusion process that occurs when the affinity matrix is powered. A good process would smooth the data in a manner that follows the shape of the underlying manifold. It has been shown (Coifman and Lafon, 2006b) that to mimic a discretized diffusion that achieves these properties, the affinity matrix must be symmetric and positive semidefinite, with eigenvalues in the range of zero to one. Negative eigenvalues would simply flip back and forth at each powering, leading to instability. With values greater than one, things would be sensitive to outliers and powering would wildly amplify.

The adaptive kernel results in an asymmetric affinity matrix where A(i,j) ≠ A(j,i), which we need to symmetrize to achieve these desired properties for A. We take the additive approach to symmetrization, which averages the affinities, helps pull in outliers and denoises the data. We construct the symmetric affinity matrix as:

$$A=A+A\text{'}$$

The final step is the row-stochastic normalization that renders the affinity matrix into a Markov transition matrix M. Each row represents a probability distribution, where M(i,j) is the probability of cell transitioning to cell j. Each row must sum to 1, which we achieve simply by dividing each entry in A by the sum of row affinities.

$$M(i,j)=\frac{A(i,j)}{{\displaystyle {\sum }_{k}A(i,k)}}$$

We note that we want a cell’s own observed values to have the highest impact on the imputation of its own values, thus our transition matrix allows for self-loops and these are the most probable steps in the random walk. The distance between a cell and itself is zero, therefore its weight in the affinity matrix before normalization is 1 (regardless of σ) ensuring the measured values in each cell retains a high weight in its imputation.

An adaptive kernel was previously used to handle the lack of uniformity in biological data in (Haghverdi et al., 2016). However, the key differences between approaches involve time-scale of diffusion. The kernel in (Haghverdi et al., 2016) sums up walks of all length scales after removal of the first eigenvector. By contrast, we prescribe a particular time scale of diffusion, based on convergence so as not to over-smooth in the context of imputation.

Markov affinity based graph diffusion

Due to sources of technical noise, such as drop out and others, one cannot distinguish between similarity due to biological correspondence vs spurious chance. This is demonstrated using a synthetically generated Swiss roll (with Gaussian noise) presented in figure 1. While most nearest-neighbor edges follow the spiral, there are many short cut edges that cut across the spiral (Figure 1.ii), which result in the off-diagonal affinities in Figure 1.iii. Consider the following thought experiment, starting with an identical cell, mimicking scRNA-seq, if we randomly subsample on a small fraction of the transcripts each time, the expression observed across these cells can appear dissimilar. However, each pair of cells are likely to at least share many neighbors that overlap with each of them. Whereas spurious edges would have similarity in the raw data, but these would not be supported by shared neighbors. Thus, exponentiation refines cell affinities, increasing the weight of similarity along axes that follow the data manifold. Following the exponentiation of M, phenotypically similar cells should have strongly weighted affinities, whereas spurious neighbors are down-weighted.

Raising M to the power t results in a matrix where each entry M^t(i,j) represents the probability that a random walk of length t starting at cell i will reach cell j, thus we call t the “diffusion time”. While the powered Markov affinity matrix increases the number of cell neighbors, unlike the effect of increasing k in knn-imputation, MAGIC does not bluntly smooth and average over increasingly distant cells. In MAGIC, even as t increases, reweighting also occurs: dense areas of the data result in more possible paths and thus weights are concentrated in these areas. Importantly, the closest neighbors remain with the highest probability: (i) The probability of a path is the product of its steps and hence longer paths are less likely; (ii) There will be many paths that linger in the region, points that are very close to each other will have many paths that are circular or back and forth that reach each other, including self-loops.

Powering M has the effect of low-pass filtering the eigenvalues of the Markov transition matrix. Markov matrices have nicely structured eigenvalues, in the range of [1, 0] with 1 being the highest eigenvalue, and 0 the lowest possible eigenvalue. Much like PCA, the magnitude of the eigenvalue is an indication of its importance in explaining (non-linear) variability of the associated eigen-dimension. Thus when a Markov matrix is powered, it decreases the magnitude of all the eigenvalues besides 1, and diminishes the importance of noise dimensions with near-zero explanatory power. In this process, the signal is filtered out from the noise. Thus, as t increases, similarity based on high frequency trends (which often correspond to technological noise) decreases and the affinity matrix represents similarity along lower frequency trends that follow data density. As a result, after the powering of M, phenotypically similar cells should have a strong weighted entry, whereas spurious neighbors are down-weighted. In our toy example, there are no off-diagonal entries in Figure 1.v.

Diffusion time for Markov Affinity Matrix

A key parameter in MAGIC is the amount of diffusion, or the power the Markov Affinity Matrix is raised to before the imputation step D_imputed = M^t * D. We need a method to determine the optimal value of t for a given dataset, that removes noise and effectively impute missing values, without over-smoothing the data. We assume that the data lies on a lower dimensional manifold, which is obscured by dropout and additional sources of noise in the data. The true manifold structure of the data is captured by the top eigenvectors of M, whereas the rest of the eigenvectors likely represent noise. The eigenvalues, which are in the range [1,0], are gradually reduced by exponentiation.

We divide the possible diffusion times into two regimes, an imputation regime and a smoothing regime. The first few steps of diffusion, which we call the imputation regime, diminishes the noise dimensions, bringing these small eigenvalues to zero and removing most of the noise in the data including dropout. As t increases, cells learn missing values from their neighbors and we rapidly capture proper relations between cells that are biologically very similar, and were only separated by collection artifacts. Thus, in the imputation regime, the imputed matrix rapidly changes from iteration to iteration.

In the smoothing regime, t is sufficiently large to have recovered the manifold with most of the noise removed. Once diffusion creates a common support for cells, diffusing further would smooth out lower frequency trends in the data that likely represent real biology. Therefore, optimal tuning of t relies on quantifying the point where the noise removal turns into signal removal. Since typically noise is of different frequency than the signal itself (i.e., high- versus low-frequency respectively), we initially expect to see a rapid change in the data as high-frequency information is being removed. Then, slower change, or convergence ensues. We therefore expect a regime change in terms of the convergence, or rate of data change, as a function of t. To quantify rate of change, we use the coefficient of determination (Rsq), between the imputed data at time t and time t-1, and choose a point after this value stabilizes. So that our metric is not dominated by few highly expressed genes, we normalize by dividing each gene by its sum. We then compute, for each t:

$$\text{R-sq}\left(\text{data\_t, data\_}\left(\text{t-1}\right)\right)\text{ = 1 - SSE}\left(\text{data\_t, data\_}\left(\text{t-1}\right)\right)\text{ / SST}\left(\text{data\_t, data\_}\left(\text{t-1}\right)\right)$$

Where SSE is the sum of squared error and SST is the sum of squared total. Since R-squared is a normalized measure, between 0 and 1, we reason that the decay has approximately converged after it has gone below 0.05, i.e., less than 5% change from the previous t. To make this robust we select the second t after the decay has gone below 0.05 as the optimal t. We note that t is robust to a range of values of around the optimal t (Figure S3D), further supporting its selection.

In Figure S1C we plot 1 - R-sq(data_t,data_(t-1)) versus t to inspect how the rate of change decreases and converges. We show that there are two regimes: an imputation regime, and following convergence, a smoothing regime.

We created a ground truth dataset to test our approach for selecting t. We generated 2000 points on a random tree structure that was generated using a random walk process where points accumulate adjacent to existing points, with 4 branches and rotated it in 1000 dimensions (Figure S1Di). We then simulated dropout on this tree by subtracting random values sampled from an exponential distribution to achieve 0%, 2%, 39% and 79% zeros respectively. For each of these noise levels, we ran MAGIC on the dropped out data for increasing t values (t=1–8) and computed the convergence, as described in the previous section (Figure S1Dii). As expected, we find that increasing levels of noise causes convergence to occur at higher values of t. The optimal t is selected at t=0, t=3, t=4 and t=6 for the increasing noise levels respectively. To determine if these values correspond to actual optimal levels of t, we quantify the Rsq of the imputed data with the original data before dropout. We reason that the R-squared should be relatively low at low t, then increase and peak at the optimal t, after which it decreases for larger t. The closest match between the ground truth and imputed data is indeed corresponds very well with the optimal t for all tested noise levels (Figure S1Diii) and also looks good visually (Figure S1Div). Moreover, we see that the Rsq remains fairly stable as we increase t beyond the optimal value and the quality of imputation remains good even as we increase t (Figure S1Diii,iv).

Imputation after graph diffusion

Once M^t is computed, we have a vector of weighted neighbors associated with each cell in our data. We can now use this robust neighborhood operator to impute and correct data using the library-size normalized count matrix (before PCA). Thus, while we use PCA to gain more robustness for the computation of M, the imputation D_imputed = M^t * D.is performed at the resolution of individual genes.

The imputation step of MAGIC involves information transfer from cells in the cell neighborhoods and right-multiplying M^t by the original data matrix. D_imputed = M^t * D. (Figure 1.vi). When a matrix is applied to the right of the Markov Affinity matrix it is considered a backward diffusion operator and has the effect of replacing each entry.D(i,j) that is gene j in cell i, with the weighted average of the values of the same gene in other cells (weighted by M^t).

$$D_{imputed}(i,j)={\displaystyle {\sum }_{k=1}^n{M}^t}(i,k)*D(k,j)$$

This process effectively restores the missing data to the underlying manifold, which captures the majority of the data.

In the final step of MAGIC, we re-scale the count matrix. The MAGIC process resembles heat diffusion in the graph, which has the effect of spreading out molecules, but keeping the total sum constant. This means that the average value of each non-zero matrix entry decreases after imputation. To match the observed expression levels (per cell), we rescale the values so that the max value for each gene equals the 99^th percentile of the original data. Thus cells with high expression of a gene are brought up to similar levels as the original data and all other values are proportionally scaled up with them.

$$D_{rescaled}(i,j)=D_{imputed}(i,j)*\frac{percentile({\overrightarrow{D}}_j,.99)}{\text{max}({\overrightarrow{D}}_{imputed,j})}$$

MAGIC pulls outliers into the data manifold

MAGIC is able to pull outlier data into the manifold due to the properties of diffusion with an adaptive kernel. As the Markov affinity matrix M is an asymmetric matrix, the walking probabilities from a particular cell, i.e., M(i, x) are not the same as the walking probabilities to the cell M(x,i). The gene values for a particular cell i, are the weighted averages of other cells based on the i-th row M(i,:). This row reflects the probability that if you start at cell i, you end up at a cell x in t steps. As the matrix is exponentiated, if cell x is an outlier cell, then there will not be many paths from i to x, and thus this entry in the Markov matrix M(i,x) gets down-weighted. Therefore cell i’s values D(i,j) will not veer towards the values of the outlier cell x. On the other hand cell x’s corrected values come from the x-th row M(x,:), and since cell x is an outlier its nearest neighbors will be on the manifold (and may include cell i). Thus the probability of x walking to the manifold is very high and thus cell x’s values will become closer to its manifold neighbors and cell x gets brought into the manifold as t increases. Due to use of the adaptive bandwidth for the Gaussian kernel, cell x is guaranteed to have k nearest-neighbors (based on our setting the kernel sigma to the distance to the kth neighbor) and those neighbors are likely to be on the manifold to aid the pulling in of outliers. See Figures 2, 4, S1 for examples of denoised manifolds after MAGIC.

Evaluation of the Synthetic Worm Dataset

To quantitatively evaluate the accuracy of MAGIC’s imputation, we created a validation dataset that was based on bulk transcriptomic data from 206 developmentally synchronized C. elegans young adults, measured at regular time intervals during a 12-hour developmental time-course using microarrays (Francesconi and Lehner, 2014). Do to the noise prevalent in early microarray experiments, similar to the analysis performed in the original publication of the data, we select only genes that load to the first two PCA components of the data. This results in a data matrix with 206 worms and 9861 genes.

We down-sampled this data to emulate the sparsity found in scRNA-seq data (Figure S2B-C). The log-scaled expression levels were exponentiated, and then each entry was downsampled using an exponential distribution such that the result had 80% and 90% of the values set to 0. Then the data was log-scaled and normalized based on z-score. We applied MAGIC (with parameters npca=20, ka=3, t=5) to this synthetically “dropped out” data and then compared between the original and imputed data. We note that this dataset is particularly challenging as it only contains 206 samples, whereas MAGIC is primarily intended for datasets consisting of thousands of samples, as is the case for most single cell datasets.

Based on the expression matrix, the imputed data largely matches the original data (Figure S2B). To zoom into finer structure and illustrate MAGIC’s ability to recover key trends in the data, we select 3 genes (C27A7.6, ERD2 and C53D5.2) based on their non-monotonic developmental time trends and compare the original and imputed shapes for each of these trends. For each gene, we find close concordance in the developmental trend between the original and imputed data (Figure S2B).

We quantitatively evaluate MAGIC’s accuracy by directly comparing the original and imputed values. At dropout of 90%, the R² increases from 7% to 43% and for 80% dropout, the R² increases from 13% to 53%. The agreement between the original and imputed data is even higher in the case of gene-gene correlations than that of the univariate case. For example, the agreement in gene-gene correlations between the original data and data with 90% of the values dropped out is 0.12. MAGIC recovers most of the gene-gene correlations so that after imputation we have a R² of 0.65. For 80% of the values at zero, MAGIC improves from 0.35 to 0.78.

Validation Using a Synthetic EMT Dataset

We used the MAGIC-imputed count matrix of the EMT data as the “ground truth” of a synthetically created dataset and then re-created synthetic dropout. Starting with data from 7523 HMLE cells 8–10 days after TGFB treatment, we first imputed the data with MAGIC (npca=20, ka=10, t=6) and then we induce dropout by down-sampling using an exponential distribution such that 0%, 60%, 80% and 90% of the values are set to 0. We then re-imputed the data using MAGIC. We show that MAGIC can also capture multivariate relations effectively -- the agreement between the original and imputed data is even higher in the case of gene-gene correlations than that of the univariate case (Figure S3Aii).

With 90% zeros, the R² between the original data and the down-sampled data is brought down to 0.04 and MAGIC corrects the data so that the R² rises back to 0.7 (Figure S3Ai). We see that with 80% zeros, we have R² of 0.09 after dropout, which is corrected to 0.81 after imputation. An important feature of MAGIC is that it is particularly good at capturing the “shape” of the data (Figure S3B). We note that the imputed data is less noisy and more accurately adheres to a low dimensional manifold. However, MAGIC may additionally remove some stochastic biological variation, as it removes unstructured, high frequency variation.

Robustness of MAGIC to Subsampling

An important feature of any algorithm is its robustness to input parameters and subsampling of the data (in this case, cells). First, we consider the sensitivity of MAGIC to subsampling of cells. We start with the 7523 cells collected in the EMT HMLE data and consider the imputation result on the full data as the ground truth. For this analysis, we only consider the 9,571 genes that are expressed in more than 250 cells, to ensure these genes will likely remain present in each subsample. More generally, we expect the quality of the imputation to depend on gene expression, both the absolute expression level of a gene when it is observed, as well as how frequently (in how many cells) it is observed. To take this into account, we divide remaining genes into two groups, based on the mean log expression in the raw data, highly expressed genes (3,190 genes) and lowly expressed genes (6,381 genes). We subsampled cells to different degrees, uniformly at random (100 iterations each). For each subsampled dataset, we remove any genes that have no expression and impute the remaining genes using MAGIC (for the same set of parameters). For each imputed matrix, we compute the correlation-squared R², per entry against the ground truth (full dataset). Figure S3C shows the mean correlation-squared across 100 iterations with 1-standard deviation represented by the error bars. MAGIC is highly robust to subsampling of cells across both groups of genes. Even for a subsample with only 1000 cells, we obtain R² > 0.94 among highly expressed genes and R² > 0.61 among lowly expressed genes (with standard deviation < 0.01 for both).

Since our main interest lies in the quality of imputed cells, for each imputed cell (represented as a vector of gene counts) we compute the correlation-squared R², against the ground truth for the same cell and average the result over all cells. This “cell-centric” view of the data (Figure S3C, middle column) produces the same results and quality as the correlation observed across the full matrix. As demonstrated in previous analysis, MAGIC learns a lower dimensional manifold where cells reside and inferred cells adhere to this learned structure.

However, a “gene centric” view of each imputed gene (represented as a vector of cells), gives slightly different results (Figure S3C, right). While we have good agreement when large numbers of cells are subsampled, e.g. when sampling 5000 cells averaged over all genes, R² > 0.89 (std. < 0.01) on the set of highly expressed genes and R²> 0.78 (std. < 0.01) for the lowly expressed genes. This correspondence declines linearly with the number of cells subsampled, so that with only 1000 cells, we find R² > 0.49 (std. < 0.01) on the set of highly expressed genes and > 0.29 (std. < 0.01) for the lowly expressed genes. Most genes are only observed in a fraction of cells, thus as the number of cells decline, so does the number of observations we have for any given gene. We find that we are successful at inferring genes that have high loadings on the top PCA (or diffusion) components. That is, some genes behave in a more structured manner, and MAGIC is good at inferring these genes. But, not all genes exhibit such structured expression. Importantly, we have the ability to predict in advance (based on their PCA loadings), which genes we are likely able to impute well.

Robustness of MAGIC to Parameters

MAGIC requires three key input parameters, ka (to set the adaptive kernel to the distance of the kth nearest neighbor), t (the number of times M is powered) and npca (the number of PCA components used to construct the affinity matrix). While we proposed criteria to guide the choice of these parameters, we also analyze MAGIC’s robustness to their exact values.

MAGIC uses an adaptive kernel for cell-cell affinity computation, where σ, the width of the Gaussian kernel at each point is set to the distance to its k^th nearest neighbor (denoted ka (“adaptive k”)). We generally pick ka such that it is the smallest value that still results in a connected graph. We test MAGIC’s robustness to ka, applying a range of ka values to the EMT data, with t set to 6 and npca to 20. To avoid the possibility of correlation being dominated by a small number highly expressed genes, we use z-score values for each gene in the imputed matrix. Then, we compute the R² of the post-imputation data for each pair of ka settings (Figure S3D). MAGIC is highly robust for a suitable range of ka values (between 10–30), the average R² value for ka = 10–30 is 0.95 (std 0.05). However, a very large value of ka (60–120) over-smooths the graph resulting in a weaker correlation score with other settings of ka (mean 0.56, std 0.27).

Next, we consider robustness of MAGIC to the diffusion time (t), by applying MAGIC to a range of values, keeping other variables fixed (npca=20, ka=10, Figure S3D,E). Again, we find that MAGIC is robust to a suitable range of t (6 – 24). In particular, the average R² value for t=6–24 is 0.90 with a standard deviation of 0.10. However, a very large value of t (64–128) over-smooths the graph resulting in a weaker correlation. Moreover, we show that our criteria for selecting the optimal diffusion time t, is robust. The Optimal t was computed on 20 subsamples of 50% of the EMT data, resulting in tight reproducibility (Figure S3Eii).

Lastly, we consider robustness of MAGIC to the number of PCA (npca) components used to build the affinity matrix. We compute MAGIC based on a range of values of npca, holding other parameters fixed (k_a=10, t=6). As shown in Figure S3D, we find that MAGIC is highly robust to the choice of npca. In particular, for npca>= 16, the average R² is 0.94 with a std of 0.05. However, as expected, since few number of PCA components do not capture enough variance in the data, we observe low correlation between small and high npca. Overall we conclude that MAGIC is robust to a wide range of parameters, around the level that our heuristics for ka, t and npca provide. Thus changes in these parameters should have minimal effect on imputed results.

Recovering cluster structure with MAGIC

While MAGIC recovers structure by diffusing values between neighboring cells, values should not exchange between different clusters. Cluster structure should therefore be maintained even after running MAGIC. To show this we computed a diffusion map on the original data and on the data after MAGIC. Figure 3B shows the first two diffusion components of the original data (i) and data after MAGIC (ii) colored by Phenograph clustering on the original data (k=50). While the diffusion map after MAGIC appears to have less noise, the two diffusion maps show the same cluster structure.

Next, to investigate the ability of MAGIC to preserve and recover cluster structure in the face of dropout, we performed manual dropout on a dataset of 3005 mouse neurons (Zeisel et al., 2015). This dataset has relatively high numbers of molecules (~19% non zero values) and is therefor particularly suited for downsampling. We downsampled up to 90% zeros by subtracting random values sampled from an exponential distribution. We first performed clustering on the original data (after library size correction and log transformation with pseudocount 0.1) using Phenograph (k=50). We then downsampled to different levels of dropout and for each level either ran MAGIC (t=6, npca=20, k=30, ka=10) and clustered using Phenograph, or directly ran Phenograph on the down-sampled data. The clustering solutions before and after MAGIC were compared using the Rand index, which measures the correspondence between the two clustering solutions. The Rand index gives a value of between 0 and 1, with a value of 1 signifying a perfect correspondence. Figure 3C shows the Rand index, for Phenograph performed without and with MAGIC, as a function of the dropout level. Phenograph with MAGIC performs significantly better after dropout (after at least 40% zeros). At 0–10% dropout the original data performs slightly better (inclustering correspondence to the original data), we note however, that even the original data has substantial drop-out and thus MAGIC is likely finding additional structure in the data.

MAGIC corrects ambient RNA and mixed barcodes

MAGIC removes high-frequency signal, which typically relates to sources of noise. In addition to correcting for drop-out, MAGIC can correct for additional sources of error in scRNA-seq, including ambient RNA in the media, barcode swapping between cells and other spurious sources of molecules. To illustrate this ability, we generate a test case with artificially contaminated cells, by assigning molecules to the wrong cell.

First, we generated a Gaussian mixture in high dimensions (2000 cells in 1000 dimensions) consisting of two clusters (1000 cells each) (Figure 3D, original). We then randomly select pairs of cells (one from each cluster) and a random gene, and swap their values, for some fraction of the data (Figure 3D, 10% and 30% corruption). Finally, we imputed the data with MAGIC (ka=10, t=4, npca=10) (Figure 3D, After MAGIC). Figure 3D shows that while corruption creates significant noise, i.e. cells in the wrong clusters, MAGIC is able to correct this; 98% recovery for 10% corruption and 81% recovery for 30% corruption.

Creation of Synthetic Datasets

We created several synthetic datasets to demonstrate the effects of dropout, noise and recovery after application of MAGIC. We have already described datasets created for measuring the ability of MAGIC to recover ground truth, i.e., the artificially dropped-out worm and EMT datasets. Here we describe datasets used to quantify MAGIC’s ability to correct contamination, denoise data along non-linear manifolds and to validate our criteria for the optimal diffusion time t.

Creation of corruption dataset

To illustrate the ability of MAGIC to correct for contamination in the transcriptome (potentially due to ambient mRNA or other errors), we generate a test case with artificially contaminated cells. First, we generated a Gaussian mixture in high dimensions (2000 cells in 1000 dimensions) consisting of two clusters (1000 cells each) (Figure 3D, original). We then randomly selected a fraction of the matrix entries and switched their values between the two clusters (Figure 3D, 10% and 30% corruption) in order to evaluate MAGIC’s ability to recover the true entries.

Creation of tree structure dataset

To test whether our method for choosing the optimal t does indeed find an optimal t we created a ground truth dataset. We generated 2000 points on a random tree structure that was generated using a random walk process (diffusion-limited aggregation) where points accumulate adjacent to existing points, with 4 branches and rotated it in 1000 dimensions (Figure S1Di). We then simulated dropout on this tree by subtracting random values sampled from an exponential distribution to achieve 0%, 2%, 39% and 79% zeros respectively (Figure S1Dii,iv).

Creation of Swiss roll datasets

To illustrate the MAGIC algorithm, we generated a Swiss roll dataset. A Swiss roll is a prototypical example of a higher dimensional dataset with a continuous lower dimensional manifold. We first generated a 2-dimensional Swiss roll sampled at 1000 points. The data is embedded in 10 dimensions by random rotation via a randomly generated QR transformation. Then these 10 dimensions are extended to 100 dimensions by replicating each dimension 10 times with additional Gaussian noise. We added Gaussian noise with mean 0 and standard deviation 2.5. The first two PCA components of this data, illustrating the Swiss roll shape is shown in Figure 1Aii.

For Figure S7C, the Swiss roll consisted of 2000 points. A Gaussian noise of mean 0 and standard deviation 0.35 was added to create a noisy Swiss roll. This was then embedded into 5000 dimensions via QR transformation. The first two PCA components of this data is shown in Figure S7C. In Figure S7D, we added dropout by subtracting values per data-point from an exponential distribution with in the inner part of the Swiss Roll and decreasing to towards the outer part of the spiral.

MAGIC compared to Diffusion Maps

Diffusion Maps were developed as a nonlinear dimensionality reduction technique (a type of Kernel PCA) to find major (non-linear) directions of variation in high dimensional datasets by Coifman and Lafon in 2005 (Coifman and Lafon, 2006a). The main idea behind diffusion maps is that solutions of the heat equation over a manifold provide global representation of its intrinsic dimensions. When applied in a data analysis setting, this corresponds to finding the eigen-decomposition of a diffusion operator, i.e., a Markov-normalized affinity matrix that defines similarity between data points along a manifold. This operator is exponentiated to achieve diffusion, i.e., longer range connectivity between data points via global random walks over the data. Finally, this operator is eigendecomposed to find diffusion components (a nonlinear analogue to PC components)(Coifman and Lafon, 2006a). Diffusion maps are primarily used provide an embedding of the data in a new coordinate system in which Euclidean distances are equivalent to diffusion distances.

Recent applications in biology have used the fact that diffusion components encode major nonlinear trends in the data to find “pseudotime trends” that often correspond to progression of development (Haghverdi et al., 2015; Haghverdi et al., 2016; Setty et al., 2016). Therefore, these components have value even when observed individually, rather than as coordinates of an embedded space.

Diffusion maps are not designed to recover the original data features and do not perform manifold denoising or imputation (i.e., correct the features to the original high-dimensional representation of a clean manifold), but rather they find a separate representation, typically low dimensional, of trends in the data. Smoothing has been used to recover gene trends along individual diffusion components, but this is not equivalent to recovering the data taking all components into account (See Figure 7, sky blue).

MAGIC, by contrast, attempts to restore and correct the data (gene measurements) itself. To achieve this, MAGIC considers the propagation of information via a data diffusion process directly applied to the data. It recovers each gene in each cell as a weighted average of its neighbors based on a walking probability, i.e., each cell X gets values from other cells Y proportional to the probability of a random walk proceeding from X to Y. In essence this restores outlier data to the manifold and clarifies manifold structure of the data. The mathematical foundation for our method is rooted in the emerging field of graph signal processing (Shuman et al., 2013), which considers the spectrum of a graph as a Graph Fourier Transform, and applies filters to this spectrum. By applying the diffusion operator directly to the data, we essentially achieve a low pass filter on the data. Fourier transforms are traditionally applied in image processing or audio processing where there is time-or-space order, also called structure to the data. Our contribution generalizes this approach to unstructured data.

MAGIC versus Pseudotime-based Imputation

We compare MAGIC to pseudotime analysis based on diffusion components (Figure 7). Pseudo-time refers to methods that derive one dimensional orderings of cells in data, which may reflect the order of differentiation or other types of cellular progression (Bendall et al., 2014; Haghverdi et al., 2016; Setty et al., 2016). Such methods have had recent success in inferring certain types of trends in data. We further motivate the necessity of MAGIC by showing their inability to correctly infer gene-interactions or even developmental trends in sparse single-cell RNA-sequencing data that has more complex structure.

For this purpose, we used the first two diffusion components, as in (Haghverdi et al., 2016), which captures the main non-linear progressions in the data(Coifman and Lafon, 2006a), as well as known markers of the transition, CD34 for bone marrow and VIM for EMT. Just as in MAGIC, the diffusion operator is computed using distances computed off of 20 principle component dimensions. On each pseudo-time trajectory, we perform a sliding window convolution using a Gaussian kernel with bandwidth set by Silverman’s rule of thumb (Silverman, 1986) (to the standard deviation of the data) to impute averaged values of particular genes in the data (Figure 7, sky blue).

Compared to MAGIC (2^nd column, green), the trends inferred by pseudotime-based imputation are noisy, fluctuating, and do not corroborate the known biology. For instance, ZEB and SNAIL are both associated with the mesenchymal state and should go up with EMT progression, and yet their trends still show fluctuation and downward inflections. Thus, we conclude that MAGIC, with its implicit consideration of all diffusion components simultaneously (as contained in the diffusion operator itself), and unique treatment of each cell, is unique in its ability to restore of gene-gene relationships and behavioral trends in single-cell RNA-sequencing data.

Comparison of MAGIC to Other Methods

We compare MAGIC to current state-of-the-art methods to fill in missing data and reduce noise, SVD-based low-rank data approximation (LRA) (Achlioptas and McSherry, 2007) and Nuclear-Norm-based Matrix Completion (NNMC)(Candes and Recht, 2012). Both methods have a low-rank assumption, i.e., like MAGIC, they assume that the intrinsic dimensionality of the data is much lower than the measurement space and utilize a singular value decomposition (SVD) of the data matrix. The singular-value decomposition of the data matrix, is a factorization of the form D = UEV^* where U contains the left singular vectors of D,V contains the right singular vectors of D, and E contains the singular values along the diagonal. Note, PCA also uses SVD for its dimensionality reduction.

The two methods we compare against MAGIC work as follows:

• 1)SVD-based low-rank data approximation (LRA)(Achlioptas and McSherry, 2007): This method for derives a low-rank approximation of a higher rank data matrix. After performing SVD, a lower rank version of D,D_low is created by taking only the first k columns of U and E and only the first k rows of V^*. This is because the first singular vectors, like PCA vectors, explain a larger variation in the data, while the subsequent vectors may correspond to noise. Therefore, the elimination of the lower singular vectors effectively de-noises the data, albeit, only using linear directions of variation.
• 2)Nuclear-Norm-based Matrix Completion (NNMC)(Candes and Recht, 2012): This technique is designed to recover missing values in data matrices, which could potentially address the dropout issue. MNMC restores “missing values” so that the rank of the data matrix is not increased, as computed through a linear programming optimization. However, since minimizing the rank of a matrix is a non-convex optimization, they optimize a convex proxy for rank, which is the nuclear norm (sum of all singular values) of a matrix.

First, we compared the performance of the three techniques on a two-dimensional Swiss roll (See Figure S7). We added Gaussian noise along the Swiss roll (Figure S7C), and then embedded the Swiss roll into 5000 dimensions via a random QR rotation matrix. Results show that only MAGIC is able to denoise even relatively simple Gaussian noise. While LRA can take off noise from outside the plane of the Swiss roll (by decreasing rank and essentially discarding noise dimensions), NNMC seems incapable of even that. NNMC is only concerned with retaining rank, and so it can fill in data arbitrarily so as not to increase rank.

The real advantage of MAGIC becomes clear when we add dropout, typical of scRNA-seq data (Figure S7D). Dropout was added to create 80% zeros, creating regions of different densities in the data. We find that only MAGIC is able to correct for dropout and restore the Swiss Roll. The “recovered” LRA looks identical to the noisy, dropped out LRA, and the “recovered” NNMC looks cloud-like. We conclude that MAGIC is uniquely well suited to handle the dropout rampant in scRNA-seq data.

We also compared all 3 techniques on 8 known biological relationships in our data (Figure 7A,B). In each case, NNMC performs poorly, generally only imputing a single linear shape. Occasionally the direction of correlation is also incorrect in NNMC. For, instance, the Cdh1 vs Cdh2 (E-cadherin vs N-cadherin) edge shown in Figure S7A, is known to have a negative relationship. However, NMMC imputes a positive correlation between these genes. Additionally, NMMC finds no relationship between the well-known negative correlation between canonical EMT markers E-cadherin and Vimentin. A possible explanation for this poor recovery is that NMMC “trusts” non-zero values and only attempts to impute possibly missing zero values. Whereas in scRNA-seq dropout of molecules impacts all genes and even non-zero genes are likely lower than their true count in the data. Hence NMMC is poorly suited to this data type.

LRA performs slightly better, as the most significant components of the SVD do usually contain the hyperplanes of the data manifold. However, it cannot separate the exact manifold from external noise, likely due to its inability to find non-linear directions in the data. Therefore, it cannot impute the fine-grained structure that MAGIC imputes as shown throughout Figure S7. For instance, in Figure S7Ai we see that MAGIC is the only method that is able to impute the details of the sparser branches, which contain the mesenchymal and apoptotic cells, while the other methods only impute a cloud shape. In the Bone marrow data shown in Figure S7B, we see that MAGIC is the only method that is able to clarify the developmental trajectory seen in Figure S7Bi into an arc with myeloid cells developing to one arm and erythroid cells developing in the other.

QUANTIFICATION AND STATISTICAL ANALYSIS

Archetype analysis using PCHA

Recently, archetypal analysis (Cutler and Breiman, 1994) has been proposed as a method for characterizing high dimensional biological data (Korem et al., 2015; Shoval et al., 2012). Under this model, the cellular phenotypic space is fit to a low dimensional convex polytope. While the actual phenotypic space is non-convex, we search for a low-dimensional convex polytope that closely approximates the data. The corners of this polytope represent extreme phenotypic states at the data extrema, with other points being convex combinations of these extrema.

While archetypal analysis has previously been applied to single cell data that was not imputed (Korem et al., 2015), we find that MAGIC is an essential step into finding meaningful archetypes (Figure S4B-D). Before MAGIC the data is dominated by noise and as a result there are no apparent extreme states. After MAGIC (Figure 4) we can observe the shape of the phenotypic landscape and clearly see “corners” or extreme states in the data (compare to Figure S4B). To find the archetypes of our EMT data we use the Principal Convex Hull Analysis (PCHA) method (Mørup and Hansen, 2012) on the PCA projection of the imputed data, which scales efficiently with the number of cells and has previously been used successfully in single cell data analysis (Korem et al., 2015).

To make the archetypal analysis more robust, the dimensionality of the data is reduced via PCA (Korem et al., 2015; Shoval et al., 2012). Since volume increases exponentially with the dimension, the number of data points needed to robustly approximate the polytope also grows exponentially with the dimension. We observe that 90% of the variance of the imputed data is explained by 10 PC components, allowing us to robustly estimate the polytope in a dramatically reduced dimension that still captures the dominant dimensions of variation. Moreover, since PCA is a linear transformation, the convex hull of the data in PCA-dimensions is a subset of the convex hull of the original data and therefore the archetypes obtained are indeed extreme points of the original data.

We use the first 10 PC components for the PCHA method, and search for 10 archetypes, whose convex-hull closely approximate the data. To ensure a compact and concise shape that best approximates the data, the archetypes must exist in the convex hull of the data and in turn the convex hull of the archetypes must closely approximate the data. Each archetype is a specific convex combination of the data points. In particular, let $X=\{x_1,x_2,\mathrm{...},x_N\},x_i\in {ℝ}^m$ be the data points, we define an archetype $Z_j={\displaystyle {\sum }_{i=1}^N{c}_{ij}{x}_i}$, where $0\le c_{ij}\le 1,{\displaystyle {\sum }_i{c}_{ij}=1}$ In matrix form, for p archetypes Z = XC, where $X\in {ℝ}^{m\times N}$ is the data matrix, $C\in {ℝ}^{N\times p}$ is the coefficient matrix and $Z\in {ℝ}^{m\times p}$ is the matrix of archetypes. The constraints ${\displaystyle {\sum }_i{c}_{ij}=1}$ and $0\le c_{ij}\le 1$ imply that each archetype is within the convex hull of the data points.

The goal in archetypal analysis is to identify an optimal set of archetypes so that the convex combination of the archetypes can re-approximate the data points. Mathematically, $\widehat{X}={\displaystyle {\sum }_{j=1}^p{s}_{ji}{z}_j}$, where $0\le s_{ji}\le 1,{\displaystyle {\sum }_j{s}_{ji}=1}$ so that $\widehat{X}$ best approximates the original data points. In matrix notation, $\widehat{X}=ZS=XCS$ where $S\in {ℝ}^{p\times N}$ is the matrix of coordinates S_ji. This second constraint implies that the data can be well approximated by a convex combination of the archetypes, which in turn implies that the archetypes must lie on or near the convex hull of the data; hence making them the extreme states of the data. The PCHA method minimizes the difference between the original data X and the estimated data $\widehat{X}$ with the objective function defined as $\left|\right|X-\widehat{X}|{|}_2^2=||X-XCS|{|}_2^2$, where the minimum is obtained via a projective gradient descent scheme (Mørup and Hansen, 2012).

To summarize, the computation of the archetypes: Let $X\in {ℝ}^{N\times m}$ be the imputed data matrix, where n is the number of cells and m is the number of genes.

1. [U,Y] = pca(X) where $U\in {ℝ}^{m\times 10}$ is the principal component coefficient matrix and Y ∈ ℝ^{N × 10} is the matrix of the principal component scores (projection of X onto U) We note that the number of principle components, 10 in the EMT dataset, is data dependent.

2. K = pcha(Y,10), where $K\in {ℝ}^{10\times 10}$ are the archetypes on the PCA projection.

3. $K_{full}=K\times U\text{'}$, where $K_{full}\in {ℝ}^{10\times m}$ is the estimated set of archetypes on the original phenotypic space.

Differential expression of the archetypes

An archetype is a weighted sum of cells, which allows us to construct archetypal-neighborhoods, consisting of cells most similar to the archetype. The neighborhoods are constructed by assigning cells to their nearest archetype based on the diffusion distance, as long as this distance is within a bounded proximity from the archetype. Diffusion distance is defined as the Euclidean distance on the diffusion map representation of the data, i.e., using diffusion components as a coordinate system (Nadler et al., 2005), denoted by DM(t) which is constructed as follows:

1. [P,Q,R] = eig(M), where $M\in {ℝ}^{N\times N}$ is the same Markov matrix as for MAGIC (constructed as described above) and P,Q,R are the matrices of the right eigenvectors, eigenvalues and left eigenvectors of respectively

2. DM(t) = P × Q^t, We used the same value for t as we used for imputation (t = 6)

3. Then, the diffusion distance between any two points x_i and x_j for diffusion time t is computed as $D_{diff}(t,x_i,x_j)=\left|\right|DM(t,x_j)|{|}_2$.

To assign similar cells to each archetype we define a neighborhood of radius r_i for each archetype z_i as ${\mathcal{N}}_{z_i}=\{x_j:D_{diff}(t,z_i,x_j)\le r_i,\text{for all\hspace{0.17em}}j\}$, where $r_i=\frac{1}{2}{\text{min}}_{j\ne i}\left(D_{diff}(t,z_i,z_j)\right)$. This choice of the radius guarantees that the neighborhoods span a similar range on the manifold for each archetype.

These archetypal neighborhoods now enable us to characterize the gene expression profiles as distributions around each archetype and compare these distributions between the archetypes. For quantifying differences between distributions, we use earth mover’s distance (EMD) (Levina and Bickel, 2001), a nonparametric measure of the distance between two distributions that quantifies the flow required to morph one distribution to another. It is defined as the L1 norm of the cumulative density functions, $D_{EMD}=\left|\right|CD{F}_1-CD{F}_2|{|}_1$ and has successfully been used to quantify gene expression differences in single cell data (Levine et al., 2015).

We find the genes whose expression maximally distinguishes each archetype against background gene expression. For each archetype, the background is constructed using all cells that are not a member of the archetypal neighborhood, excluding apoptotic cells. However, due to density differences in the data, simply combining the remaining cells over-represents some archetypes and underrepresents others. Therefore, we create a background distribution by randomly subsampling an equal number of cells from each archetypal neighborhood. For each archetype, we compute the EMD to background for each gene. To ensure robustness, we perform this subsampling and EMD computation 100 times and use the average score for each gene. Finally, we select the genes that have the largest average EMD distance to background as distinguishing features for each archetype. Note that MAGIC is absolutely essential in getting distinct differentially expressed genes between the different archetypes, compare Figures 4D,E (differential expressed genes after MAGIC) with Figure S4C,D (same analysis before MAGIC).

Robustness analysis of archetypes

To determine whether the 10 archetypes that we found are robust, we randomly downsampled the EMT data to 90% of the 7523 cells 100 times and reran the archetype analysis (with the same parameters) each time. Each of 100 subsamples resulted in 10 archetypes. To quantify the robustness between subsamples, for each archetype we computed the Pearson correlation with all 99 replicates of that archetype. Figure S4A shows a 3D PCA plot of the EMT data, with the archetypes from each replicate plotted. Each color represents one archetype, and the multiple points per color show the 100 replicates per archetype. Each archetype is annotated with the average Pearson correlation between pairs of replicates. The Pearson correlation was > 0.95 for 9/10 archetypes and closer to 1 in most cases.

Computation of kNN-DREMI

To quantify relationships, we adapt DREMI (conditional-Density Resampled Estimate of Mutual Information) (Krishnaswamy, 2014) to scRNA-seq data. The main idea underlying DREMI is the use of conditional density instead of joint density, thus capturing the functional relationship between two genes across their entire dynamic range. The key change in kNN-DREMI is the replacement of the heat diffusion based kernel-density estimator from (Botev et al., 2010) by a k-nearest neighbor based density estimator(Sricharan et al., 2012), which has been shown to be an effective method for sparse and high dimensional datasets. This involves a local computation involving only the k-nearest neighbors for each cell, which scales linearly with the number of cells. Moreover, while density estimation becomes prohibitively slow at higher dimensions and requires exponentially more data for stable estimates (Scott, 2015), a neighbor-graph has no dimensions and is only dependent on a good affinity matrix. The steps of kNN-DREMI include.

1. Kernel density estimation to compute p(x,y) for two variables x and y.

2. Coarse-graining of KDE into larger discrete bins for entropy computation.

3. Normalization of the coarse-grained KDE to compute $p(y|x)=\frac{p(x,y)}{p(x)}$

4. Entropy and mutual information computation based on the discrete bins.

1). Computation of joint density using kNN:

In the first step, the joint density is computed using k-nearest neighbors on a fine grid of points (Figure 5B). To be able to capture fine, non-parametric structures in the data, we partition the 2-dimensional space into a fine grid of points uniformly spaced points (gray dots). For each grid point, we compute its density based on the distance to its kth nearest neighbor, where neighbors are the actual data points (black dots). Figure 5B shows two data points colored by density based on their distance to the nearest neighboring data-point (k=1). More generally, the density at each grid point is calculated by:

$$\frac{k}{N*V(r,d)}$$

Where N is the total number of data-points and r is set to the distance to the kth neighbor. Then the volume of a d-dimensional ball of radius r is given by:

$$V(r,d)=\frac{{\pi }^{d/2}}{\Gamma (\frac{d}{2}+1)}*r^d$$

kNN-based density estimation has been shown to be particularly robust approach to handle sparse data (Sricharan et al., 2012). Since we are computing pairwise relationships, d=2 in this context. We set k=10 for robustness against outliers and construct a grid of 60×60 points to capture fine structure in the data.

2). Coarse graining the density estimate:

While the KDE is computed on a fine-grid, to achieve robustness, the discrete mutual information is computed on a coarser grid (Figure 5Bii). While density estimate is intended to smooth and fill in gaps in the data requiring a finer scale of resolution, having a coarser-scale resolution for mutual information renders the mutual information more robust. A coarse grid can identify clear relationships and is less dependent on noise and irregularities in the partitions. Therefore, we accumulate the density estimates for each grid point into a coarser 20×20 grid on which to compute entropy.

3). Computation of conditional density using a kNN-method:

To capture the functional relationship between two genes over their full dynamics range, we use the conditional density rather than joint density. For instance, in Figure 5Di we see that the left half of the relationship is much more densely sampled than the right half and that the joint density (shown in Figure 5Diii) only picks up signal in the left half. By contrast, the conditional density estimate (shown in Figure 5Div) picks up the relationship in both halves revealing that EZH2 peaks at intermediate levels of Vimentin and subsequently declines.

To compute the conditional density estimate, we simply column-normalize the joint density estimate, i.e., divide the joint density estimate by the marginal. More formally, for joint density estimate on a n * n matrix G, to condition on the columns, divide each entry by the column-total:

$$G(i,j)=\frac{G(i,j)}{{\displaystyle {\sum }_{k}G(i,k)}}$$

We call the resulting matrix (e.g. Figure 5Div) DREVI (Density reweighted visualization), essentially producing a 20×20 image that captures the shape of the gene-gene relationship, which we can visualize, vectorize and apply curve fitting to this representation of the relationship.

4). Computation of Mutual Information from conditional density.

The final step of kNNDREMI is the computation of entropy and mutual information using the coarse-grained conditional density estimate from step 3. In the discrete case where X and Y can take on values between 1 and m, mutual information between two variables X and Y is generally computed as the difference between the entropy of Y, and its conditional entropy after conditioning on X:

$$I\left({\rm X}:Y\right)=H\left(Y\right)–H\left(Y|X\right)$$

Here H is the Shannon Entropy is:

$$H(Y)={\displaystyle \sum _{y=1}^m-}p(y)\text{log}(p(y|x))$$

Conditional Shannon Entropy is given by:

$$H(Y|X)={\displaystyle \sum _{x}p(x)}{\displaystyle \sum _y-p(y|x)\text{log}(p(y|x))}$$

After computation of the coarse-grained conditional density estimates, we simply compute the mutual information using the equation above. Effectively, this simply added another level of conditioning to the original formulation of mutual information:

$$DREMI(X:Y)=H(Y|X)-H(Y\left|X\right|X)$$

We illustrate this computation using the relationship between VIM and EZH2, revealing a clear non-linear relationship between the two variables (Figure 5D). kNN-based kernel density estimation is computed on a fine grid (panel ii), which is aggregated into a coarser grid (panel iii) and converted to a conditional density estimate by column normalization. The resulting DREVI image (panel iv) provides us with a non-parametric, vectorized representation of the gene-gene relationship, enabling quantification and comparison between different gene pairs. Finally the kNN-DREMI score is the mutual information computed on the conditional density estimate.

MAGIC substantially increases our ability to detect gene-gene relationships, whereas the pre-MAGIC DREMI range is between 0–0.4, after MAGIC, this range increases to 0–1.7 (Figure S5B), with the mode shifting from 0 to 0.2. We note that there is almost no correlation between the DREMI scores before and after MAGIC (Figure S5C) and moreover, we find gene pairs with very high-DREMI after MAGIC, across the entire range of DREMI scores before MAGIC. We see that if the correlation coefficient is high then DREMI will also be high. However, there are additional relationships (highlighted in the box in Figure S5D) that only DREMI identifies (Figure S5E,F).

Robustness analysis of kNN-DREMI

kNN-DREMI requires three parameters to compute the DREMI score between two gene expression vectors; the number of neighbors for kNN density estimation (k), the size of the fine-grained grid on which kNN density is computed (nGrid---square root of grid size), and the number of bins in the coarse grid (nBin). We choose k such that it is small enough to focus on local density and large enough to ensure robustness, setting k=10. nBin should be chosen such that enough resolution exists to capture mutual information across a range of relationships, but small enough such that each bin has a fairly large amount of data points. We set nBin to 20, thus giving 400 bins. Finally, nGrid should be significantly larger than nBin such that multiple grid points exist within each coarse bin. As a rule of thumb we set this value to 3 times nBin, thus 60. While our parameter choices are based on reason, we wish to ensure that the DREMI score is relatively robust to these choices. We evaluated robustness to changes in the three parameters (see Figure S5A). We computed kNN-DREMI for 3000 random gene pairs of the EMT data for the following parameter values: k = [1 2 5 10 20], nBin = [5 10 20 30 40], and nGrid = [20 30 60 90 120], around the default parameter setting k=10, nBin=20 and nGrid=60. To quantify robustness we computed R² between each pair of parameter settings, for each of the three parameters. Figures S5A show that the kNN-DREMI score is highly robust to changes of the parameters within a reasonable range.

Clustering and Ordering Using DREVI

To characterize the dynamics of gene expression during EMT we first require a pseudo-time representing EMT progression. We decided to use the expression level of the canonical EMT marker Vimentin as a pseudo-time representing EMT progression (we get similar results using alternative genes as markers, see Figure S6A). We performed the following steps:

1. Filter the genes to include only those that have clear temporal trends along EMT progression based on DREMI with Vimentin.

2. Shape based clustering of the genes, by representing each gene with its vectorized DREVI with Vimentin and clustering these images.

3. Estimate the timing of peak gene expression for each cluster based on a spline curve, fit to the cluster’s geometric mean.

4. Order the clusters based on their peak timing.

First, we filtered the data. We removed apoptotic cells, based on expression of the mitochondrial gene MT-ND1 (normalized expression > 5). Next, we removed genes that are expressed in less than 5 cells, as these have a very low signal-to-noise ratio. We computed DREMI between Vimentin and all genes and removed genes that had less than 0.5 DREMI with Vimentin (the bottom ⅓), as these are likely uninvolved with EMT. We consider the remaining genes (whose DREMI with vimentin is greater than 0.5) the set of EMT related genes, and limit the rest of the analysis to these genes.

The remaining genes have a temporal trend with Vimentin, resulting in a DREVI image with structure. We vectorized their DREVI images resulting in a 400×1 vector for each gene, which captures the shape of the temporal trend (see Figure 5Div). Rather than clustering the genes based on their gene expression, we clustered them based on this vectorized DREVI image, representing their dynamics along EMT. We used correlation as a similarity metric, as relative intensities better capture the temporal trends of each gene.

Correlation distance between vectorized DREVI images x_s and x_t is defined as follows:

$$d_{st}=1-\frac{(x_s-{\overline{x}}_s)(x_t-{\overline{x}}_t{)}^{\prime }}{\sqrt{(x_s-{\overline{x}}_s)(x_s-{\overline{x}}_s{)}^{\prime }}\sqrt{(x_t-{\overline{x}}_t)(x_t-{\overline{x}}_t{)}^{\prime }}}$$

where

$${\overline{x}}_s=\frac{1}{n}{\displaystyle \sum _j{x}_{sj}}$$

and

$${\overline{x}}_t=\frac{1}{n}{\displaystyle \sum _j{x}_{tj}}$$

We constructed an agglomerative hierarchical cluster tree from correlation distances using complete linkage. Complete linkage uses the largest distance between objects in the two clusters, r and s, to define distance between clusters:

$$d(r,s)=\text{\hspace{0.17em}max}\left(dist(x_{ri},x_{sj})\right),i\in (1,\mathrm{...},n_r),j\in (1,\mathrm{...},n_s)$$

Clusters were merged until reaching a stopping criteria of d(r,s) < 1.2. This clusters the genes based on their relationship with Vimentin and results in 22 clusters with distinct temporal trends that differ based on shape and timing of the curve (Supplementary Table 2).

We estimated the timing of peak gene expression for each cluster based on a spline curve fit to the cluster’s geometric mean. The average DREVI plot per cluster was computed by taking the geometric mean of the vectorized DREVI plots. Because these clusters share roughly a similar shape, averaging over a number of genes clarifies the shape of the curve and reduces spurious noise that could mislead peak finding at the level of individual genes. We then fit a spline curve to this averaged DREVI image. The smoothing spline s is constructed for the smoothing parameter p and the weights w_i. The smoothing spline minimizes

$$p{{\displaystyle \sum _i{w}_i\left(y_i-s(x_i)\right)}}^2+(1-p){{\displaystyle \int \left(\frac{d^{2}s}{d{x}^2}\right)}}^{2}dx$$

where x and y are the coordinates of the 20×20 DREVI image, and weights w are the normalized density values in the averaged DREVI image. The default smoothing parameter p = 0.9 (approximately 1/(1+h³/6) is used, where h is the average spacing of the data points).

Clusters were then ordered based on the timing of their peak expression, genes in cluster 1 peak early along the Vimentin trajectory, while cluster 22 peaks late. The resulting clusters and their ordering appears in Figure 6A and Supplementary Table 2.

Event ordering robustness to EMT-proxy

The DREVI based clustering and event-ordering approach has considerable dependency on the pseudo-time, in our case, the expression of Vimentin as a marker of EMT progression leading to the mesenchymal phenotype. To ensure that the resulting clustering and ordering of genes is robust to the specific EMT marker selected, we repeated our analysis using three other known EMT markers (CDH2, ITGβ4 and CD44). We used each the expression of each of these genes as a proxy for EMT progression and followed the steps described above, replacing Vimentin with CDH2, ITGβ4 and CD44 respectively, resulting in 4 different clustering solutions and the gene ordering associated with each. The resulting heat-maps for each of these solutions look qualitatively similar (Figure S6A).

To evaluate similarity between clustering solutions we use Rand Index, which gives a score between 0 and 1 (0 indicating no similarity, 1 indicating perfect similarity). We obtain rand index > 0.86 (average rand index = 0.89) indicating a high degree of similarity between the clustering results (Figure S6B) between all pairs of genes used as EMT proxies. To evaluate similarity between the gene orderings, we compute Spearman correlation between all pairs of orderings. We obtain correlation > 0.70 (average correlation = 0.77) indicating that the ordering is consistent (Figure S6B). Combined, these results show that our characterization of gene expression dynamics along EMT gives consistent results for four different canonical EMT markers.

Transcription Factor Target Prediction

We can combine DREMI with the pseudo-temporal ordering of genes to predict candidate targets of regulatory genes. We make two assumptions:

1. A TF should be predictive of its targets’ expression, evaluated as a high DREMI score between TF and its target.

2. Positively regulated targets reach maximal activation at the same time or following the peak activation of the TF during EMT progression.

Statistical dependency has frequently been used to infer regulatory networks (Friedman et al., 2000) including between individual cells (Sachs et al., 2005). Thus, X such that DREMI(TF, X) > threshold is a potential regulatory target of the TF. However, statistical dependency alone is insufficient to indicate a regulatory or causal relationship. Statistical dependency does not indicate the direction of influence and in many cases can be caused due to co-regulation by a common factor.

Temporal data is often used to suggest causality. While we only measure a single time point, due to the asynchronous nature of progression through EMT, we can instead use pseudo-time to provide further support for gene regulation. Specifically, we use the DREVI-based gene ordering (Figure 6A) and consider genes that peak at the same time or following the peak of the TF during EMT progression.

Thus for a given TF, our predicted targets are genes that match both the DREMI and the ordering based criteria. In the case of ZEB1, which we subsequently validate, we consider targets where DREMI(ZEB1, X) > 1 (95 percentile), a total of 1667 genes. There are 4509 genes that peak with or after ZEB1. Intersecting these two criteria results in 1085 genes, that we consider our predicted targets of Zeb1 activation (Supplementary Table 3).

Validation of Zeb1 Targets

To validate our prediction of 1085 targets of ZEB1, we collected an additional scRNA-seq dataset of 3500 cells from an engineered cell line that has Zeb1 under a DOX-inducible promoter and induced EMT by directly up-regulating ZEB1. This cell line is identical to the wild-type HMLE cell line except that Zeb1, a key regulator of EMT, is under a Dox inducible promoter. We measured the cells after two days of continuous Dox treatment, which is sufficient to induce significant numbers of mesenchymal cells (10% of the total cell population). This data thus enables the comparison of EMT that is induced via TGFβ stimulation to EMT that is induced directly and exclusively via Zeb1 over-expression.

TGFB-induction activates multiple pathways, including Zeb1, to drive the cells towards the mesenchymal phenotype. By contrast, zeb1-induction is likely to “skip” several steps involved in the transition and directly induce a concise transcriptional program typically activated at later stages of the transition. Thus, in the Zeb1-induction, targets that fall under Zeb1’s regulatory cascade (direct and indirect targets) will have higher gene expression, relative to genes that are not targeted by Zeb1. Therefore, we validate our predicted Zeb1 targets by comparing their relative expression under TGFβ versus zeb1 induction of EMT and expect that genes regulated by Zeb1 to be ranked significantly higher in the Zeb1 induction.

For a given set of genes G, we define an impact score to quantify the impact of perturbation (the Zeb1 induction in this case) on the ranking of that gene set. We rank the genes from highest to lowest (based on mean expression) for each of TGFβ versus zeb1 inductions, and sum the ranks of the gene set under each condition. The impact score is the average difference between the summed ranks of the two conditions, in N subsamples of G of fixed size S. This subsampling procedure controls for the size of G, as p-values will be biased towards 0 given larger sized gene sets G.

Let r_t(g) and r_z(g) denote the rank of gene g (based on its mean expression as described above) in TGFβ-induction and zeb1-induction respectively. Then:

$$impactscore(G)=\frac{1}{N}{\displaystyle \sum _{j=1}^N\left({\displaystyle \sum _{i=1}^s{r}_z(g_i^j)-{\displaystyle \sum _{i=1}^s{r}_t(g_i^j)}}\right),}$$

Here, we set S=200 and N = 1000.

A large impact score corresponds to an increase in relative expression of the predicted targets under Zeb1 induction but not in TGFβ induction. To compute the significance of this impact score, we produce subsamples of size S of the background gene set (all genes involved in EMT, DREMI with VIM > 0.5) and compute the impact score of those (as above) and repeat this M times, with M set to 1000. The p-value is the fraction of subsamples that have equal or greater impact score than the predicted gene set G.

ATAC-seq Processing Pipeline

To systematically validate our target predictions, we used ATAC-seq (Assay for Transposase-Accessible Chromatin using sequencing) (Buenrostro et al., 2013) as an independent and well-accepted approach for target prediction (Buenrostro et al., 2013; Kundaje et al., 2015).

The following filtering and analysis steps were carried out in order to go from raw sequencing data from the ATAC-seq protocol to calling peaks:

1. Adapters and low quality bases were trimmed from reads using Trimmomatic v0.36 in paired end mode. Minimum retained read length is 30bp, and first/last 5bp are trimmed off the ends if low-quality. Also use a sliding window to trim reads if below quality phred score 10. Nextera transposase adapters from Trimmomatic were used to detect adapter contamination.

2. Reads were aligned with bowtie2 using default parameters for paired-end reads to hg19.

3. Alignments were filtered with MAPQ below 10 using samtools after which the bam file was sorted by chromosome and position.

4. Duplicates were removed with MarkDuplicates from picard with default parameters, except REMOVE_DUPLICATES option is set to true so that duplicates are removed instead of flagged.

5. All reads that map to the mitochondrial genome were removed.

6. Peaks were called using MACS2 in paired-end mode with an FDR of 0.1

ATAC-seq Validation of TF-target Predictions

Once we identified robust peaks from the ATAC-seq data, we used the following procedure to obtain TF targets from the ATAC-seq peaks. To quantify which TFs bind at the peaks we computed TF motif binding scores for a large set of known TFs based on the motif database cisPB(Weirauch et al., 2014), obtained from the meme suite’s motif databases. We used FIMO(Grant et al., 2011), with default parameters, to identify binding motifs and peak locations with significant predicted binding were associated with their closest gene. This resulted in a list of targets for each of 418 TFs with significant biding scores.

There was a set of 292 TFs for which we both had computationally predicted targets (TFs with knn-DREMI>0.5) and ATAC-seq predicted targets (as described above), for we could compare the two sets of predicted genes. A significant overlap between these two independent sets of predictions, derived from different biological replicates, different technologies (scRNA-seq verses ATAC-seq) and two computational approaches for prediction (DREMI verses motif analysis) would indicate that these independently derived predictions are likely correct. For each TF, we use the hypergeometic distribution to compute the significance of the intersection between its two target sets:

$$P(X=k)=\frac{\left(\begin{array}{c}N\\ k\end{array}\right)\left(\begin{array}{c}N-K\\ n-k\end{array}\right)}{\left(\begin{array}{c}N\\ n\end{array}\right)}$$

Here, N = total number of genes, K = size of the ATAC-seq target set, n is the size of our predicted target set, and k is the observed intersection size. We use the one-sided hypergeometric test to test whether our observed intersection is significantly larger than is expected from random. Almost all TFs, 291/292, have a higher overlap than expected by chance, after false discovery correction we find that 268 out of 292 TFs (92%) have a significant intersection size (Figure 6F,G).

Additionally, for each of 418 TFs that we obtained ATAC-seq targets for, we compare the distribution of the DREMI scores between TF to all targets with the DREMI-scores of all non-targets. We then computed a one-sided KS-test on these distributions to determine if the DREMI values of the ATAC-seq targets are significantly higher than the DREMI values of the non-targets. We find that 372 out of 418 TFs (89%) have p < 0.05, and thus have a significantly higher DREMI score with their ATAC-seq targets than with other genes. This is not the case for data prior to DREMI (Figure S6D)

DATA AND SOFTWARE AVAILABILITY

Python, Matlab and R implementations of MAGIC are available on GitHub: https://github.com/DpeerLab/magic or https://github.com/KrishnaswamyLab/magic

SEQC single-cell analysis pipeline is available on GitHub: https://github.com/dpeerlab/seqc

Single-cell RNA-seq and ATAC-seq data are accessible through GEO Series accession number GSE114397 (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE114397)

Supplementary Material

1. Fig. S1: Adaptive kernel and optimal t, related to Figure 1.

A) Comparison between Adaptive and Non-adaptive Kernels. 3D-scatterplot of CDH1, VIM and FN1, colored by ZEB1 expression after MAGIC performed with different amounts of diffusion (t=0,1,3,6), using a non-adaptive kernel. The fixed kernel alters and deforms the shape of the data as cells in denser regions have more neighbors, while cells in sparse areas have fewer cells to exchange information. The same data with the adaptive kernel used in MAGIC revealing finer structures in the data. B) Synthetic data generated on a manifold that has three sinusoidal arms, without added noise, with Gaussian noise, denoised using MAGIC with the nonadaptive kernel, and denoised using MAGIC with the adaptive kernel. Only the adaptive kernel recovers the true underlying manifold. C) Convergence behavior for optimal t analysis for: EMT data, the hematopoiesis data (Paul et al., 2015), and the mouse retinal cell data (Shekhar et al., 2016), with optimal t values of 6, 7 and 6 respectively (shown by arrows). D) (i) PCA on a randomly generated tree with 4 branches rotated into higher dimensions. (ii) Convergence behavior for optimal t analysis for different amounts of dropout noise added to the random tree. Dropout was done to achieve 0%, 2%, 39% and 79% zeros. More noise results in convergence at a higher t. (iii) For the same tree and noise levels, the R-squared of the imputed data versus the ground truth data (with no dropout noise) is shown. Maximum R-squared corresponds to the optimal t. (iv) PCA on the same tree with different amounts of dropout noise (rows) at different levels of imputation (columns). Green boxes show the optimal t value for each level of dropout.

9. Table S2. Clusters of EMT transitional time trends, related Figure 6.

List of each gene, which cluster they belong to, and their DREMI (density resampled estimate of mutual information) with VIM.

10. Table S3. Predicted targets for ZEB1 and other transcription factors, related Figure 6.

Predictions of ZEB1 targets were validated by a DOX overexpression experiment. Other targets were validated with ATAC seq.

2. Fig. S2: MAGIC recovers trends in the data, related to Figure 2.

A) MAGIC reveals multi-modal gene distributions in bone marrow data shown in Figure 2. Histograms per cell cluster for CD11b and CD32 computed using kernel density estimation on the data before (top) and after (bottom) MAGIC. Due to drop-out before MAGIC, most density is concentrated unimodally at zero. After MAGIC we observe unique multi-modal distributions per gene, with different cell clusters represented by different peaks, matching known expression in these immune subsets. B) The gene expression matrix with 206 worms sorted by developmental time along the Y-axis, and genes (along columns) clustered hierarchically. Left: the original matrix, Middle: the matrix after dropout resulting in 80% of the values set to 0, and Right: restored values after MAGIC. C) Scatter plots of gene expression (Y-axis) as a function of developmental time (X-axis) for C27A7.6 and C53D5.2. Left: the original gene expression versus time, Middle: gene expression after dropout, Right: after MAGIC (with diffusion time t=5).

3. Fig. S3: Validation and robustness of MAGIC, related to Figure 4.

Ai) Line plots showing the recovery of values (R2 of imputed values with original values) after MAGIC at various diffusion times t. The different curves show recovery for different levels of dropout (purple=0%, yellow=60%, red=80%, blue=90%). (ii) Shows line plots quantifying the recovery of gene-gene correlations after MAGIC with various diffusion times. The original correlation matrix is compared to the imputed correlation matrix and the match is quantified by R2. Bi) 2D scatter plot of canonical EMT genes E-cadherin and Vimentin, colored by ZEB1, before artificial dropout. Bii) The plot of (Bi) after 80% dropout. Biii) sample scatterplot as Bi after MAGIC, Biv) 3-D scatterplot of E-cadherin, Vimentin and Fibronectin after MAGIC. C) R2 of original to re-imputed values on 9,571 genes divided into two groups based on expression levels (blue = 6381 high expressing genes, red = 3190 low expressing). The R2 was computed (original vs imputed) per value, per cell and per gene for different levels of cell subsampling. The line plots show average and standard deviation between full and subsampled data. D) The robustness to various parameters of MAGIC including ka, t and number of PCA components. E) (i) 3D scatter plots of CDH1, VIM, and FN1 colored by Zeb1 are shown. The green box signifies the optimal t. (ii) Robustness of optimal t computation. Optimal t analysis was performed on 20 subsamples of 50% of the EMT data. Shown is the mean and standard deviation (error bars).

4. Fig. S4: MAGIC enables archetype analysis, related to Figure 4.

A) Robustness of the EMT archetype analysis shown on the 3D PCA plot. The EMT data was subsampled to 90% of the cells 100 times and archetypes (colors in plot) were inferred for each subsample. For each archetype the average Pearson correlation is shown between the 100 replicates of each archetype. B) Archetype analysis on the same data as Figure 4, before MAGIC. 3D scatter plots annotated by red dots representing each of the 10 archetypes in the data. (Left) Canonical EMT genes CDH1, VIM and FN1, and (right) 3D PCA plot. Note, two archetypes pinpoint outlier cells and are removed from further analysis. C) Leftmost plot shows 3D PCA plot of archetypal neighborhoods, with each cell colored by its associated archetype, grey cells are not associated with any archetype. The remaining panels show histograms representing the distributions of various genes in archetypal neighborhoods, color-coded by the colors shown in the leftmost plot. Most of the data is zero and does not capture the heterogeneity captured in the same analysis after MAGIC (Figure 4D). D) A subset of differentially expressed genes for each archetype including the set of highlighted genes from Figure 4E. Here we see little difference across the archetypes found on this data.

5. Fig. S5: Evaluation of kNN-DREMI, related to Figure 5.

A) Heatmap depicting R2 between DREMI values computed using different parameter choices, over 3000 pairs of randomly chosen genes, showing robustness of kNN-DREMI to a range of values for k, the nearest neighbor cardinality for the density estimate, nBin, number of bins used for coarse graining density estimate and computation of mutual information, and nGrid, the grid size on which kNN-based density is estimated. B) Histogram of kNN-DREMI values over gene pairs in EMT data. C) kNN DREMI before (X-axis) and after (Y-axis) MAGIC colored by density. Each point represents one of 28910 relationships between VIM and all other genes present in our EMT dataset. Scatterplot indicates a higher range of kNN-DREMI (0–1.6 versus 0–0.4) after imputation and values do not correlate well with their pre-MAGIC values. D) Absolute Pearson correlation computed on the same post-MAGIC gene-gene relationships versus kNN-DREMI. The black box indicates a region of low Pearson correlation but high kNN-DREMI (r<0.05, DREMI>0.9). E) 6 gene-gene relationships (3-well known, and 3 picked from the black box in D) from EMT data after imputation, with Pearson correlation and kNN-DREMI scores shown, indicating that kNN DREMI is much more effective at recognizing non-linear relationships. F) Similar analysis as is shown in (E) for the bone marrow data.

6. Fig. S6: Robustness of pseudo-temporal ordering of genes to reference EMT marker, related to Figure 6.

To obtain an ordering of genes that activate during the EMT progression we use VIM as a marker of EMT progression. To show that this ordering is robust, we re-compute the clustering and gene ordering using three additional canonical EMT markers: CDH2 (NCADHERIN), ITGB4 (CD104) and CD44. A) Shows gene expression (X-axis) versus EMT marker expression (Y-axis) similar to Figure 5A. B) Shows the correlation between the different gene orderings using Rand Index and rank correlation. C) Histograms of DREMI scores of Zeb1 versus all genes for the EMT data before MAGIC (red) and after MAGIC (blue). D) PDFs computed using kernel density estimation of DREMI values of three TFs (ZEB1, SNAI1 and MYC) versus all other genes for the EMT data. The DREMI values were split into ATAC-seq derived targets (blue) and non-targets (red) and the distributions were computed for the data before MAGIC (top row) and after MAGIC (bottom row). For each plot we computed the Two sided KS test that the DREMI values of the targets are bigger than the DREMI values of the non-targets. For the values before MAGIC none of the TFs are significant, while after MAGIC all TFs are significant.

7. Fig. S7: Comparison of MAGIC to other imputation methods, related to Figure 7.

A) Comparison of recovery with NNMC (Candes and Recht, 2012), Low-Rank Approximation (LRA) (Achlioptas and McSherry, 2007) and MAGIC on various edges of the EMT Dataset. Ai) 3D Scatter plot of VIM, CDH1 and FN1, with cells colored by ZEB1. Only MAGIC is able to impute the finer branches leading to the stable mesenchymal state (high ZEB1) and apoptosis. Aii) Scatterplot of CDH1 versus VIM showing a clear negative relationship after MAGIC, while other methods are able to only catch slight negative correlation. Aiii) Ezh2 versus VIM: only MAGIC is able to impute a negative quadratic relationship. Aiv) Linear relationship of ZEB1 versus SNAI1 imputed by all methods. Av) Non-linear negative relationship between N-cadherin and E-cadherin, B) Comparison of imputation methods on gene-gene associations from the bone marrow dataset (Figure 1). Bi) 3D scatterplot of CD34 (a progenitor marker), GATA1 (an erythropoiesis marker) and GATA2 (a developmental marker) colored by cluster ID, shows MAGIC connecting clusters into an arc where only the erythroid branch shows increase in GATA1. Bii) CD34 versus CD235a (an erythroid marker), where MAGIC successfully imputes a negative relationship in only the erythroid branch of the data. NNMC imputes a positive relationship and LRA shows a fuzzy relationship. Biv) CEBPA (a myeloid marker). versus MEIS1 (an erythroid marker) shows a negative relationship on erythrocytes as imputed by MAGIC and mild positive relationship on myeloid cells. Bv) Positive relationship between CEBPA and ELANE (neutrophil markers). imputed by LRA and MAGIC, although MAGIC shows the more pronounced positive relationship expected for these markers. C) Comparison of imputation methods on synthetic Data. We use a 2D Swiss roll, embedded in 5000 dimensions (by QR rotation) with Gaussian and dropout noise. First two PCA components of the noiseless high-dimensional Swiss roll and Swiss roll after Gaussian noise are shown, as well as the same PCA components of the Swiss roll after imputation by NNMC, LRA and MAGIC. Only MAGIC is able to reverse Gaussian noise along the Swiss Roll. D) Shows similar data as C, but recovery after the addition of Gaussian noise along with random dropout. The dropout was also increased along the curve of the Swiss Roll. Only MAGIC is able to recover the coiling shape of the Swiss roll after dropout.

8. Table S1. Differentially expressed genes for each archetype, related Figure 4.

Signed EMD scores, and expression levels are shown for top differentially expressed genes in 5 gene sets for each of the 10 archetypes on EMT data. The 5 gene sets are 1) transcription factors from Animal TF DB, 2) chromatin modifiers from Animal TF DB, 3) embryonic stem cell genes from (Wong et al., 2008) 4) Cell differentiation markers from Broad GSEA, 5) Cell cycle genes (Whitfield et al., 2002).

Pseudo-code of the MAGIC procedure:

MAGIC(D,t)

 D = preprocess(D)

 Dist = compute_distance_matrix(D)

 A = compute_affinity_matrix(Dist)

 M = compute_markov_affinity_matrix(A)

 D_imputed = M^t * D

 D_rescaled = Rescale (D_imputed)

 D_imputed = D_rescaled

            END